1 Introduction

The Efimov effect is a remarkable phenomenon, which is an excellent illustration of the variety of possibilities arising when we transit from the two-body to the three-body problem. In 1970 Efimov [1, 2] proposed that three-body systems with short range interaction can have an infinite number of bound states when none of the two-particle subsystems has bound states but at least two of them have infinite scattering lengths. In such a case the scattering length a is much lager than the range of the interaction \(r_0\). The simplest situation described by Efimov [2] corresponds to three identical neutral bosons interacting via short-range resonant interactions treated in the zero-range theory framework. In this theory it is assumed that the short-range region details of the interaction can be neglected and the wave function in the asymptotically free region can be parametrized by the scattering length. In order to reproduce correctly the two-body wave function in the region outside of the range of interaction \(r_0\) one can use the Bethe–Peierls boundary conditions [3] for the three-body wave function \(\varPsi \) when the two particles separated by r come in contact

$$\begin{aligned} - \frac{1}{r\varPsi } \frac{\partial r \varPsi }{\partial r} \xrightarrow [{r \rightarrow 0}]{} \frac{1}{a} . \end{aligned}$$
(1)

The simplification which is used in the zero-range theory is to keep the same form of the wave function down to \(r=0\), although this is unphysical at distances \(r < r_0\). To describe the three-body system Efimov used the free Schrödinger equation written in hyperspherical coordinates [4] with Bethe–Peierls boundary conditions (1) which lead to the equation for a radial function

$$\begin{aligned} \left( - \frac{d^2}{d R^2} - \frac{1}{R} \frac{d}{d R} + \frac{s_n^2}{R^2} \right) F_n (R) = E F_n (R) , \end{aligned}$$
(2)

where R is the hyperradius and \(s_n\) is a solution of the following transcendental equation [2, 5]

$$\begin{aligned} - s_n \cos \left( s_n \frac{\pi }{2} \right) + \frac{8}{\sqrt{3}} \sin \left( s_n \frac{\pi }{6}\right) = 0. \end{aligned}$$
(3)

All the solutions of equation (3) are real, except one \(s_0 = 1.0062378 i\) which is purely imaginary, which results in an attractive effective potential in equation (2) for \(n=0\). This attraction is the origin of the Efimov effect. In order to prevent the Thomas collapse [6] an additional three-body boundary condition can be used to fix some of the three-body observables (the ground state energy or the particle-dimer scattering length). This boundary condition breaks the scale invariance under arbitrary scale transformations but still keeps the scale invariance under some discrete set of scale transformation with scaling factors being powers of \(\lambda =\exp {(\pi /|s_0|)}\). Thus, in the limit \(a \rightarrow \infty \) there is an infinite number of bound states, forming a geometric series of energies accumulated at the threshold. The following relationship holds for three identical bosons

$$\begin{aligned} \lim \limits _{n\rightarrow \infty }\dfrac{E_{n+1}}{E_n}=\exp (-{2\pi }/{|s_0|})\equiv \lambda ^{-2} \approx \frac{1}{515.035}\approx \frac{1}{22.7^2}. \end{aligned}$$
(4)

One of the best theoretically predicted three-body system with an excited state of the Efimov type is a naturally existing molecule of the helium trimer \(^4\)He\(_3\) (see, [7, 8] and refs. therein). The interaction between two helium atoms is quite weak and supports only one bound state with the energy about 1 mK and a rather large scattering length about 100 Å. Only recently the long predicted weakly-bound excited state of the helium trimer was observed for the first time using a combination of Coulomb explosion imaging and cluster mass selection by matter wave diffraction [9].

The first experimental evidence of the Efimov resonance was observed in an ulracold gas of \(^{133}\)Cs atoms in 2006 [10]. Experimentally, they observed a giant three-body recombination loss when the strength of two-body interaction was varied. More recently, the second Efimov resonance has been observed and the scaling factor for the Efimov period has been found to be 21.0 [11, 12], close to the universal ratio \(\lambda = 22.7\) in a homonuclear system [1]. It was shown in [13,14,15] that the universal Efimov scaling is also valid for systems of non-identical particles. In particular, for a system composed of two heavy and one light atom the scaling factor \(\lambda \) (it depends only on the masses of the particles) gets smaller as the mass imbalance increases. Experimentally, heteronuclear Efimov states have been searched for in \(^{41}\)K\(^{87}\)Rb\(_2\) [16], \(^{40}\)K\(^{87}\)Rb\(_2\) [17], \(^{39}\)K\(^{87}\)Rb\(_2\) [18], \(^{7}\)Li\(^{87}\)Rb\(_2\) [19], \(^{6}\)Li\(^{133}\)Cs\(_2\) [20, 21] systems. Recent reviews on Efimov effect could be found in [22, 23].

There is a growing interest in the investigation of He\(_2\)—alkali-atom van-der-Waals systems, that are expected to be of Efimov nature. In addition to the Helium dimer, the He–alkali-atom interactions are even shallower and also support weakly bound states. In triatomic \(^4\)He\(_2\)–alkali-atom systems presence of Efimov levels can be expected. Three-body recombination and atom–molecular collision in Helium–Helium–alkali-metal systems at ultracold temperatures have been studied using adiabatic hyperspherical representation in Ref. [24,25,26]. Here we use the Faddeev equations in total angular momentum representation to calculate the \(^4\)He\(_2{}^{6;7}\)Li binding energies and a scattering length, which has not been studied before.

2 Method

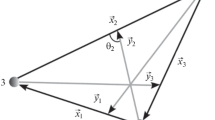
The configuration space of three particles after elimination of the center of mass can be described in terms of three sets of Jacobi coordinates

$$\begin{aligned} \begin{array}{rcl} \mathbf{x}_i&{}=&{}\displaystyle \left( \frac{2m_j m_k }{m_j+m_k}\right) ^{1/2} (\mathbf{r}_j-\mathbf{r}_k)\\ \mathbf{y}_i&{}=&{}\displaystyle \left( \frac{2m_i (m_j +m_k )}{m_i +m_j +m_k }\right) ^{1/2} \left( \mathbf{r}_i-\displaystyle \frac{m_j \mathbf{r}_j+m_k \mathbf{r}_k}{m_j+m_k }\right) \end{array} \end{aligned}$$
(5)

The set of coordinates i describes a partitioning of the three particles into a pair (jk) and a separate particle i. The Jacoby vectors with different indexes are related by an orthogonal transform

$$\begin{aligned} \mathbf{x}_j = \mathsf{c}_{ji}{} \mathbf{x}_i+ \mathsf{s}_{ji} \mathbf{y}_i \quad \mathbf{y}_j = -\mathsf{s}_{ji} \mathbf{x}_i + \mathsf{c}_{ji}{} \mathbf{y}_i \,. \end{aligned}$$
(6)

The coefficients \(c_{ji}\) and \( s_{ji}\) are expressed through the masses of the particles

$$\begin{aligned} \mathsf{c}_{ji}= & {} -\left( \frac{\mathrm{m}_i \mathrm{m}_j}{(\mathrm{m}_i + \mathrm{m}_k) (\mathrm{m}_j + \mathrm{m}_k)} \right) ^{1/2}, \quad \mathsf{s}_{ji}=(-1)^{j-i} \mathrm{sign}(j-i) \left( 1-\mathsf{c}_{ji}^2 \right) ^{1/2} \end{aligned}$$

and satisfy \(c^2_{ji}+s^2_{ji}=1\).

The three-body system is described by the Hamiltonian

$$\begin{aligned} H=H_0+\sum _i V_i (\mathbf{x}_i )\,, \end{aligned}$$
(7)

where \(H_0\) stands for the kinetic energy of the three particles and \(V_i (\mathbf{x}_i )\) is the interaction potential acting in the pair i. Faddeev decomposition represents the wave function \(\varPsi \) in terms of the Faddeev components \(\varPhi _i\)

$$\begin{aligned} \varPsi =\sum _i \varPhi _i(\mathbf{x}_i, \mathbf{y}_i) \, , \end{aligned}$$
(8)

which satisfy the following set of equations [27]

$$\begin{aligned} (-\varDelta _{\mathbf{x}_i} -\varDelta _{\mathbf{y}_i}+ V_i(\mathbf{x}_i) - E) \varPhi _i(\mathbf{x}_i, \mathbf{y}_i) = V_i(\mathbf{x}_i) \sum _{k\ne i} \varPhi _k(\mathbf{x}_k, \mathbf{y}_k) \ , \end{aligned}$$
(9)

where E is the total energy of the system. In case of zero total angular momentum the angular degrees of freedom corresponding to collective rotation of the three-body system can be separated [28] and the kinetic energy operator reduces to

$$\begin{aligned} H_{0}=-\frac{\partial ^{2}}{\partial x_i^{2}}-\frac{\partial ^{2}}{\partial y_i^{2}}-\left( \frac{1}{x_i^{2}} +\frac{1}{y_i^{2}}\right) \frac{\partial }{\partial z_i}(1-z_i^{2}) \frac{\partial }{\partial z_i}\,, \end{aligned}$$
(10)

where \(x_i\), \(y_i\) and \(z_i\) are intrinsic coordinates

$$\begin{aligned} x_i=|\mathbf{x}_i|,\quad y_i=|\mathbf{y}_i|,\quad z_i=\frac{(\mathbf{x}_i,\mathbf{y}_i)}{x_iy_i},\quad x_i,y_i\in [0,\infty ),\ \ z_i\in [-1,1] . \end{aligned}$$
(11)

Due to (5) and (6) these coordinates are related by

$$\begin{aligned} x_{j}= & {} \sqrt{\mathsf{c}_{ji}^2 x^2_i+ 2\mathsf{c}_{ji}\mathsf{s}_{ji} x_iy_i z_i +\mathsf{s}_{ji}^2 y_i^2}, \quad y_{j}=\sqrt{\mathsf{s}_{ji}^2 x_i^2 -2\mathsf{c}_{ji}\mathsf{s}_{ji} x_iy_iz_i +\mathsf{c}_{ji}^2 y_i^2},\\ x_j y_j z_j= & {} (\mathsf{c}_{ji}^2 - \mathsf{s}_{ji}^2)x_iy_i z_i - \mathsf{c}_{ji}\mathsf{s}_{ji} (x_i^2 - y_i^2)\,. \end{aligned}$$

As a result we have a set of three-dimensional differential Faddeev equations

$$\begin{aligned} \displaystyle (H_0+V_i(x_i)-E)\phi _i(x_i,y_i,z_i) = -V_i(x_i) \sum _{k\ne i} \phi _k(x_k,y_k,z_k) \,. \end{aligned}$$
(12)

When two particles of a system are identical, the Faddeev equations can be simplified. For example, for the He\(_2\)Li atomic systems particles 1 and 2 corresponding to \(^4\)He atoms are identical and the Faddeev components \(\phi _1(x_1,y_1,z_1)\) and \(\phi _2(x_2,y_2,z_2)\) transform into each other under an appropriate rotation of the coordinate space. Therefore, it is sufficient to consider only two independent Faddeev components. In the case of three identical bosons all the Faddeev components take identical functional form, which makes it possible to reduce the system of three equations (12) to one equation.

Using the fact that the both dimers – \(^4\)He\(_2\) and \(^4\)HeLi – have a unique bound state, the asymptotic boundary condition for a bound state as \(\rho =\sqrt{x^2+y^2}\rightarrow \infty \) and/or \(y\rightarrow \infty \) reads as follows (see [27, 29])

$$\begin{aligned} \begin{array}{rcl} \phi (x,y,z) = \psi _d(x)\exp (\mathrm{i} \sqrt{E-\epsilon _d}\,y) \mathrm{a}_0 (z) + \displaystyle \frac{\exp (\mathrm{i}\sqrt{E}\rho )}{\sqrt{\rho }} A(y/x,z), \end{array} \end{aligned}$$
(13)

where \(\epsilon _d\) stands for the corresponding dimer energy while \(\psi _d(x)\) denotes the dimer wave function. The coefficients \(\mathrm{a}_0\) and A(y / x, z) describe contributions into \(\phi (x,y,z)\) from (2+1) and (1+1+1) channels respectively. The last term can be neglected for the states below the three-body threshold. For bound state calculations Dirichlet or Neumann boundary conditions can also be employed.

3 Results and Discussion

The Li–He interaction is described by the KTTY potential [30], theoretically derived by Kleinekathöfer, Tang, Toennies and Yiu with more accurate coefficients taken from [31, 32]. Calculated values of the binding energy for \(^4\)He\(^6\)Li is 1.512 mK and for \(^4\)He\(^7\)Li is 5.622 mK. Such small values of binding energy give indication on possible existence of Efimov states in the corresponding He\(_2\)Li triatomic systems.

In our calculations we use two different model potentials for He–He interaction—TTY [33] and Przybytek [34]. The purely theoretical TTY potential derived by Tang, Toennies and Yiu [33] is based on the perturbation theory and is described by a relatively simple analytical expression. The recent Przybytek [34] potential includes relativistic and quantum electrodynamics contributions as well as some accuracy improvements. Each of these potentials supports a single weakly bound state of the dimer. Calculated values of the binding energy \(\epsilon _d\) for the corresponding dimers, the inverse wavenumber \(\kappa ^{-1}= (\hbar ^2/2\mu \epsilon _d)^{1/2}\) (\(\mu \) is a reduced mass) and the atom-atom scattering length \(a^{2}\) are presented in Table 1. Atomic masses for different isotopes are taken from [35].

Table 1 Absolute values of dimer energies \(|\epsilon _d|\) (in mK), the inverse wavenumber \(\kappa ^{-1}\) ( in Å) and the scattering length \(a^{2}\) (in Å) for He–He and \(^4\)He–alkali-atoms calculated for the potentials used
Full size table

From Table 1 we can see that the inverse wave number is a good approximation for the scattering length, which indicates that the zero-range potential model (1) is applicable. The calculated binding energy of the helium dimer with Przybytek potential [34] is very close to its recent experimental value of \(-\,151.9 \pm 13.3\) neV \(\approx -\,1.76 \pm 0.15\) mK [36] while the energy obtained with TTY potential [33] is closer to the previous experimental estimation of \(-\,1.1^{+0.3}_{-0.2}\) mK \(\approx -\,95^{+\,25}_{-15}\) neV [37]. The choice of the He–He potential is especially important for \(^4\)He\(^6\)Li, as switching between the two model potentials swaps the order of the two-body thresholds in the system. In the case of TTY potential the lowest two-body threshold corresponds to the \(^6\)LiHe system, while for the Przybytek potential it is the \(^4\)He\(_2\) dimer which is bound stronger.

All He–alkali-atom dimers are weakly bound, but the binding energies of HeLi and HeCs systems are of the same order as the binding energy of the Helium dimer. It suggests that in the corresponding He\(_2\)–alkali-atom triatomic systems Efimov states might exist. Indeed, in calculations [24,25,26, 29] an excited state located very close to the HeLi threshold has been found.

To calculate the binding energy of \(^4\)He\(_2{}^{6}\)Li and \(^4\)He\(_2{}^{7}\)Li trimers, we employed the equations (12), and the bound-state asymptotic boundary condition (13). The details of the numerical procedure are described in [38,39,40]. The three-body interaction is expected to be small as in the case of helium trimer [41] and we do not take it into account. Convergence tables for bound states of the \(^4\)He\(_2{}^7\)Li trimer calculated with the Przybytek potential [34] are shown in Table 2. The bound state energies (with respect to the three-body break-up threshold) are presented for different numbers of grid points. The number of grid points in coordinates x and y are set equal, and the number of grid points in angular coordinate z is varied independently. As it is seen from Table 2, the excited state is much less sensitive to the angular grid. Similar behavior had been observed for the helium trimer [38, 39].

Table 2 Convergence for the \(^4\)He\(_2{}^7\)Li bound states energies with respect to the number of grid points for the Przybytek potential [34]
Full size table
Table 3 Bound-state energies for the He\(_2\)Li systems and helium atom–HeLi dimer scattering length \(a^3\)
Full size table

Our results for \(^4\)He\(_2{}^{7}\)Li and \(^4\)He\(_2{}^{6}\)Li trimers binding energies as well as the results obtained by other authors are summarized in Table 3. The results show that the both potential models support two bound states in the both trimers. The energy of the excited state is very close to the energy of the lowest two-body threshold. Different He–He potentials give 0.3 mK difference in the helium dimer binding energy, which leads to the \(\sim 1.2\) mK difference in the binding energy of the ground state of He\(_2\)Li trimers, although the energy of excited state of He\(_2{}^7\)Li is practically unchanged (difference is \(\sim 0.01\) mK). As is mentioned above, for the He\(_2{}^6\)Li system the lowest threshold is different for different potentials: for TTY it corresponds to the energy of HeLi bound state, while for Przybytek it is the bound state energy of the He\(_2\) dimer. So, for different potentials the absolute value of the excited state energy changes slightly, but the relative energy with respect to the two-body threshold remains practically the same.

Results of other authors in Table 3 are based on solving the Shrödinger equation. The adiabatic hyperspherical approach has been employed in [24,25,26, 43, 44] and variational calculations has been performed in [45,46,47]. The fourth column of Table 3 contains the results obtained by Suno in [25] using the adiabatic hyperspherical method. For the He–Li interaction he has used KTTY potential [30] as in our calculations, but for the He–He interaction the LM2M2 potential [48] has been used. However, LM2M2 and TTY potentials support \(^4\)He\(_2\) with the energies \(\varepsilon _d = -\,1.31\) mK and \(\varepsilon _d = -1.32\) mK, correspondingly [39]. So good agreement between our results and results from [25] are not surprising (see columns 1 and 3 in Table 3).

The fifth column of Table 3 contains the results obtained by Wu et al. [26] using the mapping method within the adiabatic hyperspherical framework [42]. The next two columns are the results of calculations by H. Suno, E. Hiyama and M. Kamimura [43] using the Gaussian expansion method and the adiabatic hyperspherical representation respectively, although with different He–He potentals. They employed the He–He potential suggested by Jeziorska et al. [49], which gives the helium dimer biding energy \(-\,1.74\) mK which is lower than for Przybytek potential. The two methods give different results, but authors in [43] mentioned that the adiabatic hyperspherical representation was less accurate. The next column is the results of calculations by Suno and Esry [24, 44] by the adiabatic hyperspherical method. They also employed the He–He potential from [49], but for Li–He interaction Cvetko potential from [50] has been used. The potential proposed by Cvetko et al. [50] gives the HeLi smaller binding energy than the KTTY potential, namely \(-\,2.8\) mK for \(^4\)He\(^7\)Li and \(-\,0.31\) mK in case of \(^4\)He\(^6\)Li dimer. The ninth column contains the results obtained by Baccarelli et al. [45] with the same potential as in [44], but using a different computation method—variational calculations in terms of distributed Gaussian functions. The last two columns contain the results of Monte Carlo calculations by Di Paola et al. [46] and Stipanović et al. [47] using TTY [33] and HFDB [51] as He–He interactions.

We should also mention the first results obtained by Yuan and Lin [52] using the adiabatic hyperspherical method which gives an upper bound to the ground state \(-\,45.7\) mK for \(^4\)He\(_2{}^7\)Li and \(-\,31.4\) mK for \(^4\)He\(_2{}^6\)Li and the prediction of the bound state energies made by Delfino et al. [53] using the scaling ideas and zero-range model calculations. The preliminary Faddeev calculation using bipolar partial-wave expansion for searching Efimov states in \(^4\)He\(_2{}^7\)Li system have been performed in [29]. In these papers, however, the contribution of higher partial waves was underestimated because of the computational restrictions.

As it has been demonstrated in [29], the excited state of He\(_2{}^7\)Li has a Efimov-type behavior similar to helium trimer system [54]. To check for the Efimov-like state the original Li–He potential has been multiplied by a factor \(\lambda \). An increase of the coupling constant \(\lambda \) makes the potential more attractive and Efimov levels become weaker and disappear with further increase of \(\lambda \). Indeed this situation is observed for the excited state energy of He\(_2{}^7\)Li in contrast to the ground state energy whose absolute value increases continuously with increasing attraction.

The results for the He-atom–HeLi-dimer scattering length are presented in the last line of the Table 3 for each Li isotopes. The helium atom–helium–alkali-atom collisions at ultralow energies are studied in Ref. [55] by Suno and Esry using the adiabatic hyperspherical representation. In particular, they calculated the total cross section also for \(^4\)HeLi + \(^4\)He \(\rightarrow \) \(^4\)HeLi + \(^4\)He elastic scattering. Our estimation of the cross section \(\sigma =4\pi a^2\) at the threshold is \( 5.8\times 10^{-10}\) cm\(^2\) using TTY potential [33] and \(3.8\times 10^{-10}\) cm\(^2\) using Przbytek potential [34]. These values agree with the value \(\approx 3 \times 10^{-10}\) cm\(^2\) obtained in Ref. [55] using SAPT potential [49] at the energy \(10^{-3}\) mK above the threshold.

4 Conclusion

We have used direct solution of the Faddeev equations for the bound-state and scattering problems with zero total angular momentum. The numerical algorithm is based on spline expansion of the Faddeev components combined with the tensor trick preconditioning and the Arnoldi algorithm for eigenanalysis. Calculations of the He\(_2{}^6\)Li and He\(_2{}^7\)Li ground and excited states show that the method is very efficient and allows one to obtain stable convergent results. Apparently, it performs better than the previously exploited method of the bipolar partial-wave expansion. Our results for \(^4\)He\(_2{}^{7}\)Li and \(^4\)He\(_2{}^{6}\)Li trimers binding energies show that different potential models support two bound states in both trimers. The energy of the excited state is very close to the energy of the lowest two-body threshold. In case of the He\(_2{}^6\)Li system the lowest threshold is different for different potentials but the relative energy with respect to the lowest two-body threshold is practically the same.