Local Null Controllability of a Free-Boundary Problem for the Semilinear 1D Heat Equation

Abstract

This paper deals with the local null control of a free-boundary problem for the 1D semilinear heat equation with distributed controls (locally supported in space) or boundary controls (acting at $x=0$). In the main result we prove that, if the final time T is fixed and the initial state is sufficiently small, there exists controls that drive the state exactly to rest at time $t=T$.

1 Introduction

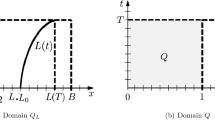
Let $T>0$ be given and let us assume that $f:\mathbb {R}\rightarrow \mathbb {R}$ is a globally Lipschitz continuous function. For any function $L\in C^1([0,T])$ with

$$\begin{aligned} 0<L_* \le L(t) \le B,\quad t\in (0,T), \end{aligned}$$

(1.1)

we will set $Q_L {\,:=\,} \{(x,t) : x\in (0,L(t)), \,\,\, t\in (0,T)\}$. We will consider free-boundary problems for semilinear parabolic systems of the form

$$\begin{aligned} \left\{ \begin{array}{lllll} y_t-y_{xx}+f(y)=v1_{\omega }, &{}\quad (x,t)\in Q_L,\\ y(0,t)=0, \,\,\, y(L(t),t)=0, &{}\quad t\in (0,T),\\ y(x,0)= y^0(x), &{}\quad x\in (0,L_0),\\ L(0)=L_0,\end{array}\right. \end{aligned}$$

(1.2)

with the additional boundary condition

$$\begin{aligned} L'(t)=-y_x(L(t),t),\quad t\in (0,T). \end{aligned}$$

(1.3)

Here, $y=y(x,t)$ is the state and $v=v(x,t)$ is a control; it acts on the system at any time through the nonempty open set $\omega =(a,b)$ with $0<a<b<L_*$; $1_\omega$ denotes the characteristic function of the set $\omega$; we assume that $y^0\in H^1_0(0,L_0)$ and $L(0)=L_0$.

The main goal of this paper is to analyze the null controllability of (1.2). It will be said that (1.2) is null-controllable at time T if, for each $y^0\in H^1_0(0,T)$, there exists $v\in L^2(\omega \times (0,T))$, a function $L\in C^1([0,T])$ satisfying (1.1) and an associated solution $y=y(x,t)$ satisfying (1.2), (1.3) and

$$\begin{aligned} y(x,T)=0, \quad x\in (0,L(T)). \end{aligned}$$

(1.4)

On the other hand, it will be said that (1.2) is approximately controllable in $L^2(0,L(T))$ at time T if, for any $y^0\in H^1_0(0,L_0)$ and any $\varepsilon >0$, there exists a control $v\in L^2(\omega \times (0,T))$, a function $L\in C^1([0,T])$ satisfying (1.1) and an associated state $y=y(x,t)$ satisfying (1.2), (1.3) and

$$\begin{aligned} \Vert y(\cdot ,T)\Vert _{L^2(0,L(T))}\le \varepsilon . \end{aligned}$$

(1.5)

The controllability of linear and semilinear parabolic systems has been analyzed in several papers. Among them, let us mention Fursikov and Imanuvilov (1996), Barbu (2000), Fernández-Cara and Zuazua (2000) and Doubova et al. (2002).

On the other hand, free-boundary problems similar to (1.2), (1.3) have been motivated by different applications, such as:

• Tumor growth and other phenomena from mathematical biology; see Friedman (2006) and Friedman (2012).

• Fluid-solid interaction; see Doubova and Fernández-Cara (2005), Vázquez and Zuazua (2003) and Liu et al. (2013).

• Gas flow through porous media; see Aronson (1983), Fasano (2005) and Vázquez (2007).

• Solidification and related Stefan problems; see Friedman (1982).

• The analysis and computation of free surface flows; see Hermans (2011), Stoker (1957) and Wrobel and Brebbia (1991).

Let us denote by $y^*$ the extension of y by 0. The main result in this paper is the following:

Theorem 1.1

Assume that f is globally Lipschitz continuous, $f(0)=0$, $T>0$ and $B>0$. Also, assume that $0<a<b<L_*<L_0<B$. Then (1.2) is locally null-controllable. More precisely, there exists $\kappa >0$ such that, if $\Vert y^0\Vert _{H^1_0(0,L_0)}\le \kappa$ there exists triplets (L, v, y) with

$$\begin{aligned} \left\{ \begin{array}{ll} L\in C^1([0,T]), &{}\quad L_* \le L(t) \le B,\\ v \in L^2(\omega \times (0,T)), &{}\quad y^* \in C^0\left( [0,T];H^1_0(0,B)\right) ,\end{array}\right. \end{aligned}$$

(1.6)

satisfying (1.2), (1.3) and (1.4).

The proof relies on the following argument:

• 1. First, for each $\varepsilon > 0$, we prove the existence of triplets $(y_\varepsilon ,L_\varepsilon ,v_\varepsilon )$ that are uniformly bounded in an appropriate space and satisfy (1.2), (1.3) and (1.5). To this purpose, we introduce a fixed point reformulation relying suitable linearized problems and we check that, if $y_0$ is sufficiently small, Schauder’s Theorem can be applied.

  In particular, in order to get compactness, we rewrite (1.3) as an equation where the L in the right hand side is given and the L in the left hand side is obtained after integration in time. We use parabolic regularity theory to deduce that $y_x$ is Hölder-continuous near the lateral boundary and, consequently, a $C^1$ function L in the right leads to a $C^{1+\alpha }$ function L in the left.

  Note that it is not easy to prove this for $\varepsilon = 0$. Indeed, it becomes difficult to prove the continuity of the corresponding fixed point mapping; see the details below, in Sect. 3.

• 2. Then, we take limits as $\varepsilon \rightarrow 0$ and we see that, at least for a subsequence, we get convergence to a solution to (1.2)–(1.4).

Remark 1.1

Theorem 1.1 is still true when we consider, instead of (1.2), a boundary controlled system with the control acting just at $x=0$. This can be deduced in a simple way as follows:

• 1. Take $\delta >0$ and solve the following control problem

  $$\begin{aligned}&\left\{ \begin{array}{lllll} {\widetilde{y}}_t-{\widetilde{y}}_{xx}+f({\widetilde{y}})=v1_{(-\delta /2,0)}, &{}\quad (x,t)\in {\widetilde{Q}}_L,\\ {\widetilde{y}}(-\delta ,t)=0, \,\,\, {\widetilde{y}}(L(t),t)=0, &{}\quad t\in (0,T),\\ {\widetilde{y}}(x,0)= {\widetilde{y}}^0(x), &{}\quad x\in (-\delta ,L_0),\\ L(0)=L_0,\end{array}\right. \\&L'(t)=-{\widetilde{y}}_x(L(t),t),\quad t\in (0,T),\\&{\widetilde{y}}(x,T)=0,\qquad x\in (-\delta ,L(T)). \end{aligned}$$

  Here, ${\widetilde{y}}^0$ is the extension of $y^0$ by 0, v is a distributed control with support in the cylinder $(-\delta /2,0)\times (0,T)$ and ${\widetilde{Q}}_L {:=} \{(x,t) : x\in (-\delta ,L(t)), \,\,\, t\in (0,T)\}$.

• 2. Denote by y the restriction to $Q_L$ of the function ${\widetilde{y}}$ and set $h(t)={\widetilde{y}}(0,t)$. Then the triplet (L, h, y) is the solution of the boundary null controllability problem.

Remark 1.2

Appropriately adapted, the techniques in Liu et al. (2013) can be used to prove a result similar to Theorem 1.1. Both approaches [the one in this paper and the one in Liu et al. (2013)] need comparable effort. Here, we first fix the boundary and solve a controllability problem for a non cylindrical domain; then, we carry out a fixed point strategy based on compactness, which is rather natural in view of the parabolic structure of the state equation. On the other hand, the approach in Liu et al. (2013) relies on a reformulation of the problem in a product space that must be chosen conveniently (adequate weights must be introduced) and a remarkable result of the authors of independent interest to handle right hand sides. The argument must be completed with the proof of the contractivity of a fixed point mapping (for small initial data).

Remark 1.3

An even more interesting case is found when the control acts on the free boundary:

$$\begin{aligned} \left\{ \begin{array}{lllll} y_t-y_{xx}+f(y)=0, &{}\quad (x,t)\in Q_L,\\ y(0,t)=0, \,\,\, y(L(t),t)=h(t), &{}\quad t\in (0,T),\\ y(x,0)= y^0(x), &{}\quad x\in (0,L_0),\\ L(0)=L_0,\end{array}\right. \end{aligned}$$

together with (1.3) and (1.4). This control problem needs a deeper analysis.

The rest of this paper is organized as follows. In Sect. 2, we prove a global Carleman inequality, whence we deduce an observability inequality needed to prove the null controllability of a linear variant of (1.2), (1.3). We also establish a regularity property for the function $t \mapsto y_x(L(t),t)$. In Sect. 3, we give the proof of Theorem 1.1. Section 4 deals with some additional comments.

2 A Controllability Result for the Linear Heat Equation in a Non-Cylindrical Domain

2.1 The Problem and the Result

Our final goal is to prove Theorem 1.1. We will use a fixed point argument and, for this purpose, we must first study the null controllability problem for the linear system:

$$\begin{aligned} \left\{ \begin{array}{lllll} y_t-y_{xx}+ a(x,t)y=v1_\omega , &{}\quad (x,t)\in Q_L,\\ y(0,t)=0, \,\,\, y(L(t),t)=0, &{}\quad t\in (0,T),\\ y(x,0)= y^0(x), &{}\quad x\in (0,L_0),\end{array}\right. \end{aligned}$$

(2.1)

where $a\in L^{\infty }((0,B)\times (0,T))$ and the function $L \in C^1([0,T])$ is given and satisfies, $0<a<b<L_*< L(t)<B$.

After an appropriate change of variable, (2.1) can be rewritten in the form

$$\begin{aligned} \left\{ \begin{array}{lllll} w_s - w_{\xi \xi }+ B(\xi ,s)w_\xi +C(\xi ,s)w=h, &{}\quad (\xi ,s)\in (0,L_0)\times (0,S),\\ w(0,s)=0, \,\,\, w(L_0,s)=0, &{}\quad s\in (0,S),\\ w(\xi ,0)= y^0(\xi ), &{}\quad \xi \in (0,L_0),\\ \end{array}\right. \end{aligned}$$

with $B, C\in L^{\infty }((0,L_0)\times (0,S))$ and $h\in L^2((0,L_0)\times (0,S))$.

We can easily verify that there exists a unique solution y to (2.1), with $y^*\in L^2(0,T;H^2(0,B))$ and $y^*_t\in L^2(0,T;L^2(0,B)$. Consequently,

$$\begin{aligned} y^* \in C^0\left( [0,T];H^1_0(0,B)\right) . \end{aligned}$$

Theorem 2.1

For any $y^0 \in H^1_0(0,L_0)$ and $\varepsilon >0$, there exist pairs $(v_\varepsilon ,y_\varepsilon )$ with

$$\begin{aligned} v_\varepsilon \in L^2(\omega \times (0,T)),\quad y^*_\varepsilon \in C^0\left( [0,T];H^1_0(0,B)\right) \end{aligned}$$

satisfying (2.1) and

$$\begin{aligned} \Vert y_\varepsilon (\cdot ,T)\Vert _{L^2(0,L(T))}\le \varepsilon . \end{aligned}$$

(2.2)

Furthermore, the control $\upsilon _\varepsilon$ can be found such that

$$\begin{aligned} \Vert v_\varepsilon \Vert _{L^2(\omega \times (0,T))}\le C_1 \Vert y^0\Vert _{L^2(0,L_0)}, \end{aligned}$$

(2.3)

where $C_1>0$ only depends on $L_*, B, \omega , \Vert L'\Vert _{\infty }, \Vert a\Vert _{L^{\infty }(Q_0)}$ and T.

The proof follows rather standard arguments. The main tool is a global Carleman estimate for the solution to the adjoint system of (2.1), that is given by

$$\begin{aligned} \left\{ \begin{array}{lllll} -\varphi _t-\varphi _{xx}+ a(x,t)\varphi =u, &{}\quad (x,t)\in Q_L,\\ \varphi (0,t)=0, \,\,\, \varphi (L(t),t)=0, &{}\quad t\in (x,T),\\ \varphi (x,T)= \varphi ^0(x), &{}\quad x\in (0,L(T)),\end{array}\right. \end{aligned}$$

(2.4)

where $u \in L^2(Q_L)$ and $\varphi ^0 \in L^2(0,L(T))$.

An immediate consequence of Theorem 2.1 is the following:

Corollary 2.1

For any $y^0\in H^1_0(0,L_0)$, there exists pairs (v, y), with

$$\begin{aligned} v\in L^2(\omega \times (0,T)),\,\,\,y^*\in C^0\left( [0,T];H^1_0(0,B)\right) , \end{aligned}$$

satisfying (2.1) and (1.4). Furthermore, v can be found such that

$$\begin{aligned} \Vert v\Vert _{L^2(\omega \times (0,T))}\le C_2\Vert y^0\Vert _{H^1_0(0,L_0)}, \end{aligned}$$

where $C_2$ only depends on $L_*, B, \omega , \Vert L'\Vert _{\infty }, \Vert a\Vert _{L^{\infty }(Q_0)}$ and T.

This will be recalled in the next section.

2.2 A Global Carleman Inequality for the Linear Heat Equation and its Consequences

Let us first introduce some weight functions. Let us denote the lateral boundary of $Q_L$ by

$$\begin{aligned} \Sigma _L {\,:=\,} \{(x,t) : x=0 \quad \hbox {or}\quad x=L(t),\,\,0<t<T\}. \end{aligned}$$

Lemma 2.1

Let $\omega _0$ be a non-empty open set with ${\overline{\omega _0}}\subset (a,b)$. There exists a function $\eta _0\in C^1({\overline{Q_L}})$ with $\eta _{0,xx}\in C^0({\overline{Q_L}})$ such that

$$\begin{aligned} \left\{ \begin{array}{lllll} \eta _0(x,t)=0,&{}\quad (x,t)\in \Sigma _L,\\ |\eta _{0,x}|>0,&{}\quad (x,t)\in {\overline{Q_L}}{\setminus }(\omega _0\times (0,T)),\\ \displaystyle \eta _0(x,t)=1-\frac{x-b}{l(t)-b},&{}\quad (x,t)\in (b,L(t))\times (0,T). \end{array}\right. \end{aligned}$$

The proof of this Lemma can be found in Fernández-Cara et al. (2016), Lemma 2.1

We introduce now the weight functions

$$\begin{aligned} \alpha (x,t):= & {} \frac{e^{2\lambda \Vert \eta \Vert _{\infty }} -e^{\lambda \eta (x,t)}}{\beta (t)},\\ \xi (x,t):= & {} \frac{e^{\lambda \eta (x,t)}}{\beta (t)}, \end{aligned}$$

where $\beta (t)=t(T-t)$, $\eta (x,t)=\eta _0(x,t)+1$ and $\lambda >0$. The following result contains a Carleman estimate for the solutions to the adjoint systems (2.4); it is inspired by the ideas in Fursikov and Imanuvilov (1996) and the proof is identical to the proof of Theorem 2.2 in Fernández-Cara et al. (2016).

Theorem 2.2

Let $\eta , \alpha , \beta$ and $\xi$ be the functions defined above. There exist positive constants $\lambda _0, s_0$ and $C_0$, only depending on $L_*, B, \omega , \Vert L'\Vert _{\infty }, \Vert z\Vert _{L^\infty (Q_0)}$ and T, such that, for any $s\ge s_0$ and any $\lambda \ge \lambda _0$, we have

$$\begin{aligned}&\displaystyle \iint _{Q_L}e^{-2s\alpha }\left( \frac{1}{s\xi }(\left| \varphi _t\right| ^2 +\left| \varphi _{xx}\right| ^2)+\lambda ^2s\xi \left| \varphi _x\right| ^2 +\lambda ^4s^3\xi ^3\left| \varphi \right| ^2\right) \,dx\,dt\nonumber \\&\qquad + \displaystyle \int _0^T e^{-2s\alpha (L(t),t)}\lambda s\xi (L(t),t) \left| \varphi _x(L(t),t)\right| ^2\,dt\nonumber \\&\qquad + \displaystyle \int _0^T e^{-2s\alpha (0,t)}\lambda s\xi (0,t) \left| \varphi _x(0,t)\right| ^2\,dt\nonumber \\&\quad \le C_0\left( \displaystyle \iint _{Q_L}e^{-2s\alpha }|u|^2\,dx\,dt + \displaystyle \iint _{\omega \times (0,T)}e^{-2s\alpha }\lambda ^4s^3\xi ^3 \left| \varphi \right| ^2\,dx\,dt\right) \end{aligned}$$

(2.5)

In a second step, we will prove an observability inequality for the solutions to the adjoint systems. This is a consequence of the previous Carleman inequality.

Proposition 2.1

There exists a constant $C>0$, only depending on $L_*$, B, $\omega$, $\Vert L'\Vert _{\infty }$, $\Vert z\Vert _{L^\infty (Q_0)}$ and T, such that for any $\varphi ^0\in L^2(0,L(T))$, the associated solution to (2.4) with $u=0$ satisfies

$$\begin{aligned} \int _0^{L_0}|\varphi (x,0)|^2\,dx\le C\iint _{\omega \times (0,T)}|\varphi |^2\,dx\,dt \end{aligned}$$

(2.6)

Proof

Let us take $\lambda =\lambda _0$ and $s=s_0$ in (2.5). Then

$$\begin{aligned} \iint _{Q_L}e^{-2s\alpha }\xi ^3|\varphi |^2\,dx\,dt \le C \iint _{\omega \times (0,T)}e^{-2s\alpha }\xi ^3|\varphi |^2\,dx\,dt \end{aligned}$$

and, consequently,

$$\begin{aligned} \displaystyle \int _{T/4}^{3T/4}\int _0^{L(t)}|\varphi |^2\,dx\,dt\le & {} \displaystyle C\int _{T/4}^{3T/4}\int _0^{L(t)}e^{-2s\alpha }\xi ^3|\varphi |^2\,dx\,dt\nonumber \\\le & {} \displaystyle C\iint _{\omega \times (0,T)}|\varphi |^2\, dx\, dt. \end{aligned}$$

(2.7)

On the other hand, if we introduce the auxiliary function $\psi =e^{t\Vert a\Vert _{\infty }}\varphi$, we find that

$$\begin{aligned} -\frac{1}{2}\frac{d}{dt}\left( \int _0^{L(t)}|\psi |^2\,dx\right) +\int _0^{L(t)} |\psi _x|^2\,dx + \int _0^{L(t)}\left( \Vert a\Vert _\infty +a\right) |\psi |^2\,dx=0, \end{aligned}$$

for all $t\in (0,T)$, whence

$$\begin{aligned} \frac{d}{dt}\left( \int _0^{L(t)}|\psi |^2\,dx\right) \ge 0. \end{aligned}$$

This implies

$$\begin{aligned} \int _0^{L(0)}|\varphi (x,0)|^2\,dx\le e^{T\Vert a\Vert _\infty }\int _0^{L(t)}|\varphi (x,t)|^2\,dx\,\,\,\,\,\,\forall t\in (0,T) \end{aligned}$$

and

$$\begin{aligned} \frac{T}{2}\int _0^{L(0)}|\varphi (x,0)|^2\,dx\le e^{T\Vert a\Vert _\infty }\int _{T/4}^{3T/4}\int _0^{L(t)}|\varphi (x,t)|^2 \,dx\,dt. \end{aligned}$$

(2.8)

From (2.7) and (2.8), we conclude the proof. $\square$

The observability inequality (2.6) leads to the approximate controllability result in Theorem 2.1. The argument is well known; see Fabre et al. (1995) for more details. Thus, let $y^0\in L^2(0,L_0)$ and $\varepsilon > 0$ be given and let us introduce the functional $J_\varepsilon (\cdot ,a,L)$, with

$$\begin{aligned} J_\varepsilon (\varphi ^0;a,L)=\frac{1}{2}\iint _{\omega \times (0,T)}|\varphi |^2\,dx\,dt +\varepsilon \Vert \varphi ^0\Vert _{L^2(0,L(T))} +\left( \varphi (\cdot ,0),y^0\right) _{L^2(0,L_0)} \end{aligned}$$

for all $\varphi ^0\in L^2(0,L(T))$.

Here, $\varphi$ is the solution to (2.4). Using (2.6), it is relatively easy to check that $J_\varepsilon (\cdot ;a,L)$ is strictly convex, continuous, and coercive in $L^2(0,L(T))$, so it possesses a unique minimum $\varphi ^0_\varepsilon \in L^2(0,L(T))$, whose associated solution is denoted by $\varphi _\varepsilon$. Let us now introduce the control $v_\varepsilon =\varphi _\varepsilon 1_\omega$ and let us denote by $y_\varepsilon$ the solution to (2.1) associated to $v_\varepsilon$. Then, either $\varphi ^0_\varepsilon =0$ or we can differentiate the functional at $\varphi _\varepsilon ^0$ and obtain a necessary condition to reach a minimum at $\varphi _\varepsilon ^0$:

$$\begin{aligned} \left\{ \begin{array}{lll} \displaystyle \iint _{\omega \times (0,T)}\varphi _\varepsilon \varphi \,dx\,dt &{}+&{} \varepsilon \left( \displaystyle \frac{\varphi ^0_\varepsilon }{\Vert \varphi ^0_\varepsilon \Vert _{L^2(0,L(T))}},\varphi ^0\right) _{L^2(0,L(T))}\\ &{} +&{} \left( \varphi (\cdot ,0),y^0\right) _{L^2(0,L_0)}=0\\ \forall \varphi ^0\in L^2(0,L(T)), \end{array} \right. \end{aligned}$$

(2.9)

From this and (2.6) for $\varphi ^0=\varphi ^0_\varepsilon$, we get the estimate (2.3). On the other hand, since the systems (2.1) and (2.4) are in duality, we also have

$$\begin{aligned} \iint _{\omega \times (0,T)}\varphi _\varepsilon \varphi \,dx\,dt =\left( \varphi ^0,y_{\varepsilon }(T)\right) _{L^2(0,L(T))} - \left( \varphi (0),y^0\right) _{L^2(0,L_0)} \end{aligned}$$

which, combined with (2.9), yields (2.2).

2.3 The Uniform Hölder-Continuity of $y_x$

We introduce here a class of functions of standard use in the regularity theory of parabolic equations (see Ladyzhenskaja et al. 1968).

Let us fix an integer $m\ge 0$ and $\alpha \in (0,1)$. Let us set $Q_0=(0,B)\times (0,T)$, let $G\subset Q_0$ be a non-empty open set and let us assume the $D^r_tD^s_xu$ is continuous in ${\overline{G}}$ for $2r+s<m+\alpha$. Then, we set

$$\begin{aligned} \langle u\rangle ^{(\alpha )}_{x,G}:= & {} \mathop {\sup }\limits _{(x,t),(x',t)\in {\overline{G}}}\frac{|u(x,t)-u(x',t)|}{|x-x'|^\alpha },\\ \langle u\rangle ^{(m+\alpha )}_{x,G}:= & {} \sum _{2r+s=m}\left\langle D^r_tD^s_xu\right\rangle ^{(\alpha )}_{x,G},\\ \langle u\rangle ^{(\alpha /2)}_{t,G}:= & {} \displaystyle \sup _{(x,t),(x,t')\in {\overline{G}}}\frac{|u(x,t)-u(x,t')|}{|t-t'|^{\alpha /2}},\\ \langle u\rangle ^{\left( \frac{m+\alpha }{2}\right) }_{t,G}:= & {} \sum _{2r+s=m}\left\langle D^r_tD^s_xu\right\rangle ^{\left( \frac{\alpha }{2}\right) }_{t,G}, |u|^{(m+\alpha )}_{G}\\:= & {} \sum _{2r+s\le m}\left\| D^r_tD^s_xu\right\| _{L^{\infty }(G)}+\langle u\rangle ^{(m+\alpha )}_{x,G}+\langle u\rangle ^{\left( \frac{m+\alpha }{2}\right) }_{t,G}. \end{aligned}$$

The space of the functions $u=u(x,t)$, such that $|u|^{(m+\alpha )}_{G}< +\infty$ will be denoted by$K^{m,\alpha }({\overline{G}})$. This is a separable Banach space for $|\cdot |^{m,\alpha }_{G}$. Furthermore, it is easy to check that $K^{m,0}({\overline{G}})=C^m({\overline{G}})$ and, if $m+\alpha <m'+\alpha '$, the embedding $K^{m',\alpha '}({\overline{G}})\hookrightarrow K^{m,\alpha }({\overline{G}})$ is compact.

Let us denote by $N_0$ the norm of $y^0$ in $L^2(0,L_0)$ and let $(\upsilon ,y)$ be a control-state pair furnished by Theorem 2.1. Let $b'$ be given with $b<b'<L_0$ and let us set $R_L {\,:=\,} Q_L\cap \{(x,t): x>b'\}$. From Theorems 10.1 and 11.1 in Ladyzhenskaja et al. (1968) (pp. 204 and 211), we can affirm that $y\in K^{1,\alpha }$ for all $\alpha \in [0,1/2)$, the function $V_L$ with $V_L(t){:=}y_x(L(t),t)$ satisfies $V_L\in C^{0,\alpha }([0,T])$ and, furthermore,

$$\begin{aligned} \Vert V_L\Vert _{C^{0,\alpha }([0,T])}\le C\Vert y\Vert _{L^\infty (Q_L)}, \end{aligned}$$

(2.10)

where the constant $C>0$ only depends on $C_1$ and $N_0$ and $\alpha$ only depends on $L_*$ and B.

Let us write $y={\widehat{y}}+{\widetilde{y}}$, where ${\widehat{y}}$ is the solution to (2.1) with $y^0\equiv 0$ and ${\widetilde{y}}$ is the solution to (2.1) with $v\equiv 0$. Using Gronwall’s Lemma, one can easily prove that

$$\begin{aligned} \Vert {\widehat{y}}\Vert _{L^\infty (Q_L)}\le C\left( \Vert a\Vert _{L^\infty (Q_0)},\Vert L'\Vert _\infty ,B,T\right) \Vert \upsilon \Vert _{L^2(\omega \times (0,T))}. \end{aligned}$$

On the other hand, from the Maximum Principle, we have

$$\begin{aligned} \Vert {\widetilde{y}}\Vert _{L^{\infty }(Q_L)}\le C\left( \Vert a\Vert _{L^\infty (Q_0)},\Vert L'\Vert _\infty ,T\right) \Vert y^0\Vert _{L^{\infty }(0,L_0)}. \end{aligned}$$

Consequently, we see that

$$\begin{aligned} \Vert V_L\Vert _{C^{0,\alpha }([0,T])}\le C_3\Vert y^0\Vert _{L^{\infty }(0,B)}, \end{aligned}$$

(2.11)

where the constant $C_3>0$ only depends on $\Vert a\Vert _{L^\infty (Q_0)},\Vert L'\Vert _\infty , B, T, L_*, \omega$ and $N_0$.

The estimate (2.11) will be crucial in the proof of Theorem 1.1 in the next section.

3 Proof of Theorem 1.1

In a first step, let us assume that $f\in C^1(\mathbb {R})$ and $|f'|$ is uniformly bounded.

We define the function $g:\mathbb {R}\rightarrow \mathbb {R}$ as follows:

$$\begin{aligned} g(s)=\frac{f(s)}{s} \quad \hbox {for},\quad s\ne 0 \quad \hbox {and}\quad g(0)=f'(0). \end{aligned}$$

For any $(z,\ell )\in L^\infty (Q_0)\times C^1([0,T])$ with $L_*\le \ell \le B$ and any $y^0\in H^1_0(0,L_0)$, we consider the following controllability problem

$$\begin{aligned}&\left\{ \begin{array}{lllll} y_t-y_{xx}+g(z)y=v1_\omega , &{}\quad (x,t)\in Q_\ell ,\\ y(0,t)=0, \,\,\, y(\ell (t),t)=0, &{}\quad t\in (x,T),\\ y(x,0)= y^0(x), &{}\quad x\in (0,L_0), \end{array}\right. \end{aligned}$$

(3.1)

$$\begin{aligned}&\qquad \quad \Vert y(\cdot ,T)\Vert _{L^2(0,\ell (T))}\le \varepsilon . \end{aligned}$$

(3.2)

Let us introduce the set

$$\begin{aligned} \mathcal {N} {\,:=\,} \{z\in L^\infty (Q_0) : \Vert z\Vert _{L^\infty (Q_0)}\le R\}, \end{aligned}$$

where $R > 0$ will be defined later. Let $R_1>0$ be given and let us set

$$\begin{aligned} \mathcal {M}=\{\ell \in C^1([0,T]) : L_*\le \ell \le B, \,\, \ell (0)=L_0, \,\, \Vert \ell '\Vert _{\infty }\le R_1 \}. \end{aligned}$$

We will consider the mapping $\Lambda _\varepsilon : \mathcal {N}\times \mathcal {M}\mapsto L^\infty (Q_0)\times C^1([0,T])$, defined as follows:

• $\Lambda _\varepsilon (z,\ell ) = \left( y^*_\varepsilon ,L_\varepsilon \right)$, where $y_\varepsilon$ satisfies (3.1) and (3.2) for $v=\varphi _\varepsilon |_{\omega \times (0,T)}$, $\varphi _\varepsilon$ is the unique minimum of $J_\varepsilon (\cdot ;g(z),\ell )$ and

  $$\begin{aligned} L_\varepsilon (t)=L_0-\int ^t_0 y_{\varepsilon ,x}(\ell (s),s)\,ds \end{aligned}$$

In order to prove Theorem 1.1, we will apply a fixed point technique. First, note that in view of the results in Sect. 2, $\Lambda _\varepsilon$ is well defined. Moreover, one has

$$\begin{aligned} \left\| y^*_\varepsilon \right\| _{L^{\infty }(Q_0)}\le C_4\Vert y^0\Vert _{L^{\infty }(0,L_0)}, \end{aligned}$$

where $C_4$ only depends on $L_*, B, \omega , R_1$ and T,

$$\begin{aligned} \Vert L'_\varepsilon \Vert _{\infty }\le C_3\Vert y^0\Vert _{H^1_0(0,L_0)} \end{aligned}$$

and, consequently,

$$\begin{aligned} |L_\varepsilon (t)-L_0|\le C_3T\Vert y^0\Vert _{H^1_0(0,L_0)} \quad \forall t\in [0,T]. \end{aligned}$$

Therefore, if we take

$$\begin{aligned} R=C_4\Vert y^0\Vert _{L^{\infty }(0,L_0)} \end{aligned}$$

and, we assume that

$$\begin{aligned} \Vert y^0\Vert _{H^1_0(0,L_0)}\le \min \left( \frac{R_1}{C_3},\frac{B-L_*}{C_3T}, \frac{L_0-L_*}{C_3T}\right) , \end{aligned}$$

we find that $\Lambda$ maps $\mathcal {N}\times \mathcal {M}$ into itself.

Let us now prove that, for some $\alpha \in (0,1)$, $\Lambda _\varepsilon$ maps the bounded sets of $L^{\infty }(Q_0)\times C^1([0,T])$ into bounded sets in $K^{0,\alpha }({\overline{Q}}_0)\times C^{1,\alpha }([0,T])$. We will use the results from Ladyzhenskaja et al. (1968) (see Theorems 7.1 and 10.1, Ch. III). Thus, there exists $\alpha \in (0,1/2)$ (only depending on $L_*, B$ and T) such that $y_\varepsilon \in K^{0,\alpha }({\overline{Q}}_0)$ and there exists a constant $C>0$, only depending on $L_*,B,T,\alpha$ and $\Vert y^0\Vert _{H^1_0(0,L_0)}$ such that

$$\begin{aligned} \left| y_\varepsilon \right| ^{0, \alpha }_{Q_0}\le C; \end{aligned}$$

more details can be found in Fernández-Cara et al. (2016).

On the other hand, from (2.10) we already know that

$$\begin{aligned} \Vert L_\varepsilon \Vert _{C^{1,\alpha }}\le C, \end{aligned}$$

where $C>0$ only depends on the previous data and $N_0$. As a consequence, $\Lambda _\varepsilon$ maps $\mathcal {N}\times \mathcal {M}$ into a compact set of $L^\infty (Q_0) \times C^1([0,T])$.

Now, we will show that $(z,\ell )\mapsto \Lambda (z,\ell )$ is a continuous mapping. Thus, let the $(z_n,\ell _n)$ be such that

$$\begin{aligned} (z_n,\ell _n)\rightarrow (z,\ell ) \,\,\hbox {in}\,\,\, L^{\infty }(Q_0)\times C^1([0,T]) \end{aligned}$$

and let us set $(y^*_{\varepsilon ,n},L_{\varepsilon ,n})= \Lambda _\varepsilon (z_n,\ell _n)$.

Obviously, $\Lambda _\varepsilon (z_n,\ell _n)$ converge strongly to some $(y^*_\varepsilon ,L_\varepsilon )$. We must prove that $(y^*_\varepsilon ,L_\varepsilon )=\Lambda _\varepsilon (z,\ell )$. To this purpose, the following result will be used:

Proposition 3.1

Let us consider the mapping $M: \mathcal {N}\times \mathcal {M}\mapsto L^2(0,1)$, where $M(z,\ell )=\psi ^0_\varepsilon$, $\psi ^0_\varepsilon (\zeta )\equiv \varphi ^0_\varepsilon (\zeta \ell (T))$ and $\varphi ^0_\varepsilon$ is the minimizer of $J_\varepsilon (\cdot ;g(z),\ell )$. If $z_n\rightarrow z\in L^\infty (Q_0)$ and $\ell _n\rightarrow \ell$ strongly in $C^1([0,T])$, then $\psi ^0_{\varepsilon ,n}$ converges strongly in $L^2(0,1)$ to $\psi ^0_\varepsilon$.

The proof can be obtained as in Fernández-Cara et al. (2016).

A direct consequence of Proposition 3.1 is that the controls $\upsilon _{\varepsilon ,n}$ associated to the $(z_n,\ell _n)$ converge strongly in $L^2(\omega \times (0,T))$ to the control $v_\varepsilon$ associated to $(y,\ell )$:

$$\begin{aligned} v_{\varepsilon ,n}\rightarrow v_\varepsilon \,\,\,\hbox {strongly in}\,\,\, L^2(\omega \times (0,T)). \end{aligned}$$

Thus, it is straightforward to check that the $(y^*_{\varepsilon ,n},L_{\varepsilon ,n})$ converge to $\Lambda _\varepsilon (z,\ell )$ and, therefore, $\Lambda _\varepsilon$ is continuous.

In view of the previous properties of $\Lambda _\varepsilon$, there exists $\delta >0$ (independent of $\varepsilon$) such that, if $\Vert y^0\Vert _{H^1_0(0,L_))}\le \delta$, Schauder’s Theorem can be applied to the fixed point equation $(y,L)=\Lambda _\varepsilon (y,L)$.

Let $(y_\varepsilon ,L_\varepsilon )$ be a fixed point of $\Lambda _\varepsilon$ for each $\varepsilon >0$. Then, it is clear that $(y_\varepsilon ,L_\varepsilon )$ satisfies, together with $v_\varepsilon$, (1.2), (1.3), (2.2) and (2.3). Moreover, $L_\varepsilon$ and $v_\varepsilon$ are uniformly bounded in $C^{1+\alpha }([0,T])$ and $L^2(\omega \times (0,T))$, respectively. Consequently, our assertion is proved.

Now, at least for a subsequence, one has

$$\begin{aligned} L_\varepsilon \rightarrow L\,\,\,\hbox {strongly in}\,\,\, C^1([0,T])\,\,\hbox {and}\,\,v_\varepsilon \rightarrow v\,\,\hbox {weakly in}\,\,\, L^2(\omega \times (0,T)) \end{aligned}$$

as $\varepsilon \rightarrow 0$. Obviously, (y, L, v) satisfies (1.1) and (1.3). Also, it is clear that y satisfies (1.4).

This proves the result when f is of class $C^1$.

The general case can be easily obtained through a simple approximation process. Hence, The proof of Theorem 1.1 is completed.

4 Additional Comments and Questions

The global null controllability of (1.2), (1.3) is an open question. As noticed in Fernández-Cara et al. (2016), it is open even in the case $f \equiv 0$. It s not clear at all how the existence of a fixed point of $\Lambda _\varepsilon$ can be obtained for large $y^0$.

On the other hand, for higher spatial dimensions, the local null controllability is also open. In view of the previous results and arguments, a natural strategy would be to introduce a mapping of the form

$$\begin{aligned} (z,\ell )\in \mathcal {L}\mapsto \Lambda (z,\ell )=(y^*,L)\in \mathcal {L}, \end{aligned}$$

where v is a minimal $L^2$-norm control that produces a state satisfying

$$\begin{aligned} \Vert y(\cdot \,,T)\Vert _{L^2(\Omega (T))} \le \varepsilon ,\quad x \in \Omega (T). \end{aligned}$$

and $\{ \Omega (t) \}_{t \in [0,T]}$ is a family of sets whose boundaries are parametrized by $\ell$ and try to prove the existence of a fixed point. But, again, this does not seem easy.

Note that, for the proof of Theorem 1.1, we can imagine another strategy: rewrite (1.2), (1.4) as an equation of the form $F(w,L,v) = 0$ in an appropriate Banach space for some $C^1$ mapping F and try to invert this equation near $(0,L_0,0)$. An advantage of this argument is that, in principle, it can be adapted to similar null controllability problems in higher dimension. This will be explored in a forthcoming work.

On the other hand, it is not difficult to prove a result similar to Theorem 1.1 under spherical symmetry hypotheses. Indeed, it suffices to adapt the assumptions on the data $\omega$ and $y^0$ and define the weights appropriately.