1 Introduction

Cable-driven parallel robots (CDPRs) are parallel robots that use flexible cables to guide their end-effectors (EEs) through space. Due to the large workspace and relatively simple design, CDPRs have been widely used in academia and industry (Qian et al. 2018), in applications such as modular CDPRs (Seriani et al. 2016), multiple mobile cranes (Zi et al. 2015), cable-driven cameras (Tanaka et al. 1988) and radio telescope application (Meunier et al. 2009), notably, in a five-hundred-meter aperture spherical radio telescope (FAST) (Duan 1999; Nan 2006). CDPRs that operate in harsh environments can be affected by disturbances such as wind, earthquakes and so on. According to the studies by Nan et al. (2006) and Vogiatzis et al. (2004), wind loading is one of the critical parameters influencing the performance of large telescopes. It can affect both the flexible cable and feed cabin, leading to a deterioration in the performance of the control system, eventually making it unstable. Therefore, it is important to investigate how best to reduce the effects of disturbance in CDPRs, to widen their industrial applications and stabilize such systems.

There are many aspects to consider when developing CDPRs, such as stability analysis of robots (Carricato and Merlet 2012), calculations relating to the workspace (Duan and Duan 2014; Heo et al. 2018) and trajectory planning, and the development of accurate position control algorithms (Schmidt and Pott 2017; Kang et al. 2019). However, for applicability to real robots, cable tension must be modelled accurately. There have been many studies on force control and analyses of friction in pulleys (Kraus et al. 2014; Choi et al. 2017). Kraus et al. 2014 proposed a force control method in which an impulse response was used to establish a second-order system with dead time, and obtained the correlation between dead time and cycle time. Using their system, they developed and implemented a cable force controller. However, they did not consider the effects of external disturbances such as wind, and did not apply disturbance observer based (DOB) control to reduce the effect of disturbance. It is not easy to apply DOB to CDPR systems, because they have eight cables with different features and long delay times are induced by the friction and elongation of pulleys connected in series.

However, DOB control has been successfully applied in many real industrial applications (Ohishi 1987; Umeno and Hori 1991; Natori 2012; Chen et al. 2016; Natori et al. 2008; Sariyildiz and Ohnishi 2015; Li et al. 2017; Yang et al. 2010; Zhu et al. 2005). The DOB control method was first introduced by Ohnishi in (1987), and was further developed by Umeno and Hori (1991). The basic principle of DOB control is that the lumped disturbance can be estimated and input into a feed forward model (Chen et al. 2016).

In this paper, we propose the application of a DOB algorithm to 8-cables CDPRs, with the aim of attenuating the deleterious effects of disturbances in harsh environments. We then evaluate the performance of our algorithm. First, we constructed an experimental setup for system identification, and then used it to test the CDPR system with a step response. Next, for each of the eight cables, we designed and analyzed a DOB controller for a model system with time delay. We then constructed another experimental setup with a mounted eccentric motor to create disturbance, and implemented a DOB algorithm in the CDPR via a programmable logic controller (PLC). We operated the CDPR at specific disturbance frequencies and compared the experimental results with and without the DOB algorithm.

2 CDPR system and system identification

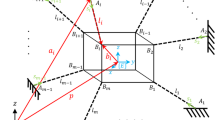
2.1 Fully constrained CDPR system

The designed CDPR system is shown in Fig. 1. It is a six-degree of freedom (DOF) robot with eight cables connecting eight motors, winches, and EEs via pulleys. The robot uses industrial servo drives as hardware and TwinCAT3 software for real-time control. The system parameters are listed in Table 1.

Fig. 1
figure 1

Experimental setup for testing the cable-driven parallel robot (CDPR) control

Full size image
Table 1 Components and parameters of our cable-driven parallel robot (CDPR)
Full size table

2.2 System identification

For system identification, a mathematical model of a dynamical system is constructed based on observations of its inputs and outputs. The input signal used in an identification experiment can have a significant influence on the resulting parameter estimates. Based on the response of a process to a step input, a number of practical parameters can be obtained, such as the dead time and time constant.

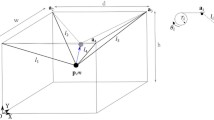
In the first step, we set up the test system to evaluate the model parameters. The system included a motor, servo controller, winch, load cell, pulley and cable connected to a fixed point in the frame. A schematic of the system identification setup is shown in Fig. 2. The step response to the input signal depended on the cable length, \( \delta_{d} \), and was generated by the PLC and controlled via a field bus to the servo driver. The output signal was the force sensor value, \( f \), which was digitized and sent back to the PLC via the field bus.

Fig. 2
figure 2

Schematic of the system identification setup

Full size image

Since the signal passes several layers of communication in discrete time, dead time arises in the control loop. Hence, we repeated the identification process with different cycle times \( T_{c} \) for the controller and field bus in the range 1 to 16 ms and analyzed the dead time \( T_{d} \) between the cable length and load cell value response, as shown in Fig. 3a. There was a linear correlation between cycle time and dead time, as shown in Fig. 3b. The system was a typical spring-mass-damper system with time-discrete control. Therefore, we assumed a second-order system with dead time for the transfer function (Kraus et al. 2014):

$$ G_{p} (s) = \frac{{K_{p} }}{{1 + 2\varsigma T_{w} s + (T_{w} s)^{2} }}e^{{ - T_{d} s}} $$
(1)

where \( K_{p} \), \( \varsigma \), \( T_{w} \) and \( T_{d} \) are the proportional gain, damping ratio, natural period, and dead time, respectively.

Fig. 3
figure 3

Dead time calculation and corrrelation using the measured data. a Dead time calculation between the step input and step output response for a cycle time of 2 ms. b Correlation between dead time and cycle time

Full size image

By sampling the input/output data every 2 ms using the Matlab System Identification Toolbox, as indicated in Fig. 4, we obtained the parameters of the transfer function. The parameters are listed in Table 2. The fit for each cable was greater than 93%.

Fig. 4
figure 4

Comparison between the actual force response (blue line) and estimated force response (red line) for a cycle time of 2 ms (color figure online)

Full size image
Table 2 Parameters of the transfer function
Full size table

3 DOB algorithm

3.1 Basic DOB controller structure

Consider the basic DOB controller structure shown in Fig. 5a. \( U_{c} (s) \), \( U(s) \), \( Y(s) \), \( D(s) \) and \( \mathop D\limits^{ \wedge } (s) \) are, respectively, the command, plant input, output, external disturbance and estimated lumped disturbance. \( G_{p} (s) \), \( G_{n} (s) \) and \( Q(s) \) are the transfer functions of the actual plant, nominal plant and disturbance observer filter to be designed, respectively. From Fig. 4a, the system output is represented:

Fig. 5
figure 5

Block diagram of the basic and proposed disturbance observer based (DOB) controller

Full size image
$$ Y(s) = G_{1} (s)U_{c} (s) + G_{2} (s)D(s) $$
(2)

where

$$ G_{1} (s) = \frac{{G_{p} (s)G_{n} (s)}}{{G_{n} (s) + Q(s)[G_{p} (s) - G_{n} (s)]}} $$
(3)
$$ G_{2} (s) = \frac{{G_{p} (s)G_{n} (s)[1 - Q(s)]}}{{G_{n} (s) + Q(s)[G_{p} (s) - G_{n} (s)]}} $$
(4)

As we can see from (2) to (4), optimal DOB control performance can be achieved with high accuracy of the nominal plant and according to the design of the filter. If the nominal plant matches the real plant and \( Q(s) \) is a low-pass filter with a steady-state gain, the disturbance can be eliminated.

3.2 DOB controller structure with dead time

It is necessary to consider dead time in real systems. Figure 5b shows a block diagram of the basic DOB controller structure shown in Fig. 5a (Li et al. 2017; Zhu et al. 2005). The transfer function of the actual plant is represented as the sum of the real minimum-phase, \( g(s) \), and the real dead time, \( e^{{ - T_{n} s}} \). The transfer function of the nominal plant can also be obtained by multiplying the nominal minimum-phase \( g_{n} (s) \) by the nominal dead time \( e^{{ - T_{d} s}} \). From Fig. 5b, the system output can be obtained as:

$$ Y(s) = G_{1} (s)U_{c} (s) + G_{2} (s)D(s) $$
(5)

where

$$ G_{1} (s) = \frac{{g(s)e^{{ - T_{n} s}} }}{{1 + Q(s)g_{n}^{ - 1} (s)[g(s)e^{{ - T_{n} s}} - g_{n} (s)e^{{ - T_{d} s}} ]}} $$
(6)
$$ G_{2} (s) = \frac{{1 - Q(s)e^{{ - T_{d} s}} }}{{1 + Q(s)g_{n}^{ - 1} (s)[g(s)e^{{ - T_{n} s}} - g_{n} (s)e^{{ - T_{d} s}} ]}} $$
(7)

And the lumped disturbances estimation can be obtained as:

$$ \mathop D\limits^{ \wedge } (s) = e^{{ - T_{d} s}} Q(s)D(s) $$
(8)

Define \( E_{d} (s) \) to be the error between the actual value \( D(s) \) and the estimated value \( \mathop D\limits^{ \wedge } (s) \) of the lumped disturbance:

$$ E_{d} (s) = [1 - Q(s)e^{{ - T_{d} s}} ]D(s) $$
(9)

According to the final-value theorem (8):

$$ \begin{aligned} e_{d} (\infty ) & = \mathop {\lim }\limits_{t \to \infty } e_{d} (t) \\ & = \mathop {\lim }\limits_{s \to 0} sE_{d(s)} \\ & = \mathop {\lim }\limits_{s \to 0} [1 - Q(s)e^{{ - T_{d} s}} ]\mathop {\lim }\limits_{s \to 0} sD(s) \\ & = \mathop {\lim }\limits_{s \to 0} [1 - Q(s)e^{{ - T_{d} s}} ]\mathop {\lim }\limits_{t \to \infty } D(t) \\ & = \mathop {\lim }\limits_{s \to 0} [1 - Q(s)e^{{ - T_{d} s}} ]d(\infty ) \\ \end{aligned} $$
(10)

Set \( Q(s) \) to be a low-pass filter with a steady state gain of 1: \( Q(s) = \frac{1}{{(\tau s + 1)^{m} }} \)

where \( \tau \) is the filter time constant and m is the relative degree, which should not be less than the difference between the order of the denominator and the order of the numerator to conserve the proper value of \( Q(s)g_{n}^{ - 1} (s) \). From (9), we can then obtain the following (10):

$$ \mathop {\lim }\limits_{\omega \to 0} G_{2} (j\omega ) = 0 $$
(11)
$$ e_{d} (\infty ) = 0 $$
(12)

According to (11) and (12), the disturbance can be rejected. Hence, the low pass filter \( Q(s) \) is important as it not only restricts the effective bandwidth of the DOB controller, but also ensures the robustness of the system.

Because the dead time transfer function cannot be handled by a control design algorithm, the first order Pade approximation described below was used:

$$ e^{{ - T_{d} s}} \approx G_{T} (s) = \frac{{1 + \frac{{ - T_{d} s}}{2}}}{{1 - \frac{{ - T_{d} s}}{2}}} $$
(13)

To implement the DOB controller in the CDPR, we converted it from continuous time to discrete time based on a specific sampling time.

4 Experiment

4.1 Experimental setup

According to Vogiatzis et al. (2004), wind loading predominantly affects the frequency range of 0.5 ~ 4 Hz in the case of giant telescopes. Therefore, instead of using wind as a source of disturbance for the CDPR in this study, we used an eccentric motor system to create a 2 Hz rotating frequency, thus simulating low-frequency disturbance. This system was composed of a low-speed direct current motor with an unbalanced mass connected to the shaft. The motor was fastened to the end-effectors via a subsystem so that its vibrations could be transferred. Different vibration frequencies and intensities were created by varying the speed at which the offset mass was rotated (Fig. 6). The speed of the motor was controlled based on the input voltage. The parameters describing the vibration motor system are summarized in Table 3.

Fig. 6
figure 6

Experimental setup of the vibration motor

Full size image
Table 3 Components and parameters of the vibration motor system
Full size table

The controller was implemented as a real-time PLC, as shown in Fig. 7. The position of the CDPR was controlled by an open-loop control system, and the cable tension by a closed-loop control system. The open-loop control system used inverse kinematics with a pulley (Heo et al. 2018) to obtain the desired cable length \( l_{d} \) and move the end-effectors to the desired position. In closed-loop control, a simple P-controller is applied to control the error between the cable tension feedback \( f_{c} \) from the force sensor and the cable tension \( f_{d} \) at the desired position which can be generated by dynamic modeling (Heo et al. 2018).

Fig. 7
figure 7

Block diagram of a CDPR controller using the disturbance observer based (DOB) algorithm

Full size image

Then, the output tension \( f_{O} \) from the P-controller was transformed into the cable length input \( \Delta l \). If we assume that the cable is modelled using a linear stiffness model, the cable length can be obtained as follows:

$$ \Delta l = \frac{{f_{0} L}}{AE} $$

where L is the cable length from the motor winch to the end-effectors, A is the cross-sectional area, and E is the Young’s modulus of the cable.

Finally, the change in cable length, \( \Delta l \), was input to the feedback disturbance estimation, \( \mathop d\limits^{ \wedge } \), from the DOB controller structure, as mentioned above, and the desired cable length, \( l_{d} \), was used to set the cable lengths in the TwinCAT controller, as shown in Fig. 7. The force sensors in each cable were calibrated to supply the actual force \( f_{c} \) to the controller.

4.2 Experiment result

We carried out experimental studies to evaluate the practical performance of the proposed method. The input voltage of the vibration motor was 12 V. The gain of the P-controller (\( K_{p} = diag[0.22] \)), which controlled the cable tension, was tuned manually. For the DOB controller, based on the considerations outlined above, the following filter was selected: \( Q(s) = \frac{1}{{(0.178s + 1)^{2} }} \). We used fast Fourier transform (FFT) to analyze and evaluate the cable tension based on the obtained data. In Fig. 8, we compare the cable tension with P + DOB control (red) and P individual control (blue). It is clear that the performance of all cables improved significantly when the DOB controller was used. According to Fig. 8, the vibrations of cables 2, 4, 5 and 7 were larger than those of the other cables. This is because the mounting location was slightly asymmetric, which affected the tension of the diagonal cables. As shown in Fig. 8, the suspended tension varied from 0.2 to 2.5 N in the case of the DOB controller. In Table 4, we summarize the improvement in cable tension both with and without DOB control. When DOB control was applied, the reduction in cable tension improved significantly, by 40–60%, at the target frequency of 2 Hz, and the amplitude range decreased by 35–50% compared to the case in which DOB control was not applied. DOB control cannot attain perfect static accuracy due to uncertainties in the model and sensor noise.

Fig. 8
figure 8figure 8figure 8

Comparison between cable tension with DOB control (red line) and without DOB control (blue line) based on fast Fourier transform (FFT) analyses. a Cable 1, b cable 2, c cable 3, d cable 4, e cable 5, f cable 6, g cable 7, h cable 8 (color figure online)

Full size image
Table 4 Comparison between the cable-driven parallel robot (CDPR) performance with and without disturbance observer based (DOB) control
Full size table

In Fig. 9, we compare the changed encoder value of 8 motors between the cases with and without DOB control. In the case with DOB control, the changed encoder value of 8 motors was smaller than in the case without DOB control. Figure 9 also shows that, after a long period of time, the changed encoder value was larger in the case with the standard control method and external disturbance, that mean the end-effectors position will be more and more inaccurate.

Fig. 9
figure 9

Comparison of the changed encoder value of 8 motors winch with DOB control (red line) and without DOB control (blue line) (color figure online)

Full size image

5 Conclusion

In this paper, we applied the system identification method to establish a second-order system including dead time, and constructed a test setup to apply the DOB control system to CDPRs. Using the constructed experimental setup, system parameters were measured for all eight cables, and a DOB algorithm was developed based on the values obtained. The aim of this algorithm was to control a second-order system with dead time. Using the CDPR system with the DOB algorithm and a P-controller, an experiment was carried out with disturbances at frequencies of 2 Hz. When DOB control was applied, the reduction in amplitude of the cable tension improved significantly, by 40% to 60%, and the peak to peak improved by 35% to 50% compared to the case without DOB control. Thus, we validated our proposed strategy, namely the application of DOB controllers to CDPR systems.