1 Introduction

Radio frequency (RF) passive components realised in MEMS, MicroElectroMechanical-Systems, technology, widely known as RF-MEMS, are becoming more and more attractive to market segments linked to modern telecommunication systems, with 5G first in line (Iannacci 2015, 2018a; Ma et al. 2019). In fact, RF-MEMS enable the achievement of remarkable characteristics, in terms of high isolation, low loss, wide reconfigurability or tunability, broadband operability and frequency agility (Liu 2010; Lucyszyn 2010; Iannacci 2018b). Moreover, their typical design flexibility makes possible realising complex networks, like multi-state phase shifters, step attenuators and high order switching matrices, in just few square millimetres of silicon (Enz and Kaiser 2013; Iannacci 2013b).

From a different point of view, simulation and modelling of RF-MEMS are not easy tasks, as their behaviour places across different physical domains, i.e. mechanical, electrical and electromagnetic. The availability of a simulation tool for MEMS devices allowing to obtain good accuracy and fast computation times is especially desirable when increasingly complex structures are to be modelled. To this regard, a multi-domain simulation environment was obtained by means of a MEMS model library implemented in an HDL-based (hardware description language) available in most part of commercial software development tools for integrated circuits (ICs). The elementary MEMS components available in the software library are based on the concept of nodal modelling (Del Tin et al. 2007; Bazigos et al. 2014; Iannacci 2013a).

This paper focuses on some improvements of the mentioned models. In particular, Sect. 2.1 discusses the electrostatic model for a rigid suspended transducer plate with 6 geometrical Degrees of Freedom (DoFs) accounting for the presence of holes on its surface. Section 2.2 reports the squeeze-film damping model for the rigid plate (6 DoFs), with holes on the plate surface, as well. Section 2.3 focuses on the flexible beam model (6 DoFs), that has been improved by adding the viscous damping effect. Subsequently, Sect. 3 introduces the working principle of the toggle-switch design. Section 4 reports the results of some reference simulations of the RF-MEMS toggle-switch performed with the discussed compact models, and compares such results with Finite Element Method (FEM) simulations for validation purposes. Finally, Sect. 5 collects some conclusive considerations.

2 Compact models library of MEMS components

The models implemented in the HDL-based software library are obtained by exploiting the concept of compact nodal modelling. Such methodology has been successfully followed by other Authors to build-up MEMS ad-hoc simulation tools (Jing et al. 2002; Fedder GK 2000). The mentioned models characterise the device behaviour by taking into account a reduced number of meaningful points (nodes), that usually coincide with the connectivity points of each elementary MEMS component (e.g. rigid plate corners or flexible beam ends) forming a complete device. As a meaningful example, the schematic of the flexible straight beam with 6 geometrical DoFs at each end, coming from the structural mechanical theory based on matrices (Przemieniecki 1968), is reported in Fig. 1.

Fig. 1
figure 1

The straight flexible beam with 6 geometrical DoFs at each node

Full size image

The complete description of the mechanical behaviour is provided by the forces/torques and displacements/rotations applied to the two beam-ends, each one with 6 DoFs (3 linear displacements and 3 rotations). The description of the elastic behaviour leads to the Stiffness Matrix (K) while the inertia comes in as the Mass Matrix (M). All the matrices are 12 × 12, and the constitutive formula is expressed as:

$$ F = Kx + M\ddot{x} $$
(1)

where F is a 12 × 1 vector representing forces (torques), while x and \(\ddot{x}\) are the displacement and the acceleration 12 × 1 vectors respectively.

In the 6 DoFs rigid plate mechanical model the connectivity points are the four vertexes. The forces applied to those points are then referred to the Centre of Mass (CM) and the corresponding torques are computed by using rigid geometry assumptions. In doing so, the instantaneous orientation angles are utilised. The torques applied to the vertexes are directly transferred to the CM. More details are going to be discussed in the following pages.

2.1 Rigid plate electrostatic model with 6 degrees of freedom (DoFs)

The electrostatic transduction model is based on two well-known formulas for the capacitance and the attractive electrostatic force calculation for two parallel plates (Senturia 2001). However, when the plate tilts with non-zero orientation angles, each point on its surface has a different distance from the underlying electrode. This punctual vertical distance can be determined as a function of the instantaneous orientation angles and of the instantaneous gap between the CM and the substrate zmid, through the computation of the projection along the z-axis of each point using the rotation matrix. A coefficient σ also takes into account the curvature of the field (see Fig. 2).

Fig. 2
figure 2

The length of the electrical field arcs is computed by means of geometrical calculations and depends on the plate rotation angles

Full size image

This has been determined by means of geometrical considerations, taking into account that the field lines are normal to the conductor surfaces and by approximating them with circumference arcs. Finally, the electrostatic force and the capacitance formulas are expressed by two double integrals on the plate area that are analytically computed and displayed as follows:

$$ C = \frac{\varepsilon }{\sigma }\int\limits_{{\frac{ - W}{2}}}^{\frac{W}{2}} {\int\limits_{{\frac{ - L}{2}}}^{\frac{L}{2}} {\frac{dxdy}{{d(z_{mid} ,\vartheta_{x} ,\vartheta_{y} ,\vartheta_{z} )}}} } $$
(2)
$$ F_{z} = \frac{1}{2}\frac{{\varepsilon V^{2} }}{{\sigma^{2} }}\int\limits_{{\frac{ - W}{2}}}^{\frac{W}{2}} {\int\limits_{{\frac{ - L}{2}}}^{\frac{L}{2}} {\frac{dxdy}{{d(z_{mid} ,\vartheta_{x} ,\vartheta_{y} ,\vartheta_{z} )^{2} }}} } $$
(3)

where W and L are the two plate dimensions along the x and y directions, respectively, ε is the dielectric constant of air, V is the applied potential and d(zmid,θx,θy,θz)2 is the punctual vertical distance. The presence of a matrix of holes on the plate surface is accounted for by computing a negative contribution of capacitance and electrostatic force for each hole, subsequently added to the previous formulas. Such negative contributions are calculated with integral formulas similar to (2) and (3), however defined on the restricted domain of each holes (see Fig. 3).

Fig. 3
figure 3

The plate surface is divided into domains, each containing one hole. The negative electrical effects are computed by integrating suitable formulas on such domains

Full size image

This integration is repeated for each hole, and the contributions of negative capacitance and electrostatic force are the results of a summation of integrals, as shown in the following formulas:

$$ C_{ - } = \frac{\varepsilon }{\sigma }\sum\limits_{i = 0}^{n - 1} {\sum\limits_{j = 0}^{m - 1} {\int\limits_{{S_{ij} }} {\frac{dxdy}{{d(z_{mid} ,\vartheta_{x} ,\vartheta_{y} ,\vartheta_{z} )}}} } } $$
(4)
$$ F_{ - } = \frac{1}{2}\frac{{\varepsilon V^{2} }}{{\sigma^{2} }}\sum\limits_{i = 0}^{n - 1} {\sum\limits_{j = 0}^{m - 1} {\int\limits_{{S_{ij} }} {\frac{dxdy}{{d(z_{mid} ,\vartheta_{x} ,\vartheta_{y} ,\vartheta_{z} )^{2} }}} } } $$
(5)

where Sij is the integration domain corresponding to the hole area, while n and m are the numbers of holes along the x and y plate dimensions, respectively. With a similar integral formulation, the contributions to the capacitance and to the electrostatic force due to the fringing field are also calculated. The effect due to the field lines distortion near the plate boundaries and those starting from the plate sidewalls (see Fig. 4), also concerning each hole (see Fig. 5), are calculated by means of an empirical model (Iannacci et al. 2007; Iannacci 2013a; Brusa et al. 2008; Halder et al. 2009, 2010; Tang et al. 2005; Veijola 2005). Once the total electrostatic force and torques are computed, they are applied to plate CM.

Fig. 4
figure 4

The lateral fringing acts on the sidewalls when the plate orientation angles are not zero

Full size image
Fig. 5
figure 5

Distortion of the electrical field lines in the vicinity of each hole. The boundary fringing is empirically assumed to act in an area of width ζ

Full size image

2.2 Rigid plate squeeze-film damping model with 6 degrees of freedom (DoFs)

The squeeze-film damping effect of the rigid plate is based on the model proposed by Bao et al. (2003). It exploits a modified Reynolds equation to allow its computation with reference to squeeze-film damping of plates with holes on their surface. This model considers circular-shaped holes and parallel position between the plate and the underneath surface. For the purposes of this work, such a model was modified to tailor it to the 6 DoFs plate description.

Firstly, the circular hole area corresponding to that of the rectangular opening has been obtained by means of simple geometrical considerations. It is assumed that the model is still valid for rectangular instead of circular ones. Then, in order to face the problem of the damping description extension to 6 geometrical DoFs, the model was applied following an approach similar to the one exploited for the negative electrostatic force computation. In other words, the viscous damping contribution was calculated with a discrete approach. For each hole domain, the velocity of the central opening point along the three axes is obtained starting from the linear plate CM velocities and from the instantaneous angular velocities of the plate CM. It is assumed that the velocity of each point of the sub-domains can be approximated with the one of the respective central point. In addition, the air viscosity variation as the distance between the plate and the substrate approaches the gas molecules mean free path, is taken into account by applying the model reported in (Veijola et al. 1997).

2.3 Flexible beam squeeze-film damping model with 6 degrees of freedom (DoFs)

The squeeze-film damping model for the 6 DoFs flexible straight beam is based on a simplified Reynolds equation, in which the pressure profile is considered to be independent on the longitudinal coordinate (Bao et al. 2003). This is a valid assumption when the beam length is greater than its width (L >  > w). In order to take into account that the beam is a flexible body, and therefore that each point can have a different velocity depending on the forces (torques) applied to its ends, the surface is discretised into sub-elements. In details, a local vertical distance is computed for each element by means of the Hermitian Shape Functions (HSFs) (Przemieniecki 1968). The HSFs are non-dimensional functions describing the distribution of displacement, point by point, along the beam length, as a function of the deformations applied to its ends. Such functions assume a certain geometrical shape for the deformed beam and are defined for each geometrical DoF. The HSFs values ranges between 0 and 1, with the maximum at the node where the stimulus is applied, and zero at the opposite end. The HSFs are normally used in the K and M matrices formulation. For instance, the distribution of the displacement along the z-direction in a generic point x along a beam of length L is:

$$ z(x) = \left[ {1 - \left( {3\left( \frac{x}{L} \right)^{2} + 2\left( \frac{x}{L} \right)^{3} } \right)} \right]Z_{a} + \left[ {\left( {3\left( \frac{x}{L} \right)^{2} - 2\left( \frac{x}{L} \right)^{3} } \right)} \right]Z_{b} $$
(6)

where Za and Zb are the displacements at the beam ends a and b, respectively (see Fig. 6).

Fig. 6
figure 6

Distribution of the superposed node displacements along the beam length

Full size image

By applying the superposition principle, it is possible to consider as well the contributions to the total vertical displacement profile due to the angular rotation around the y-axis at the two ends. Once all the contributions to the punctual z displacements have been determined, they are superposed to the initial gap between the non-deformed beam and the substrate to define the punctual instantaneous gap. Each sub-element is assumed to be rigid and rectangular (see Fig. 7). Therefore, by means of the previous calculations it is possible to define the height of its central point and of its corners.

Fig. 7
figure 7

Discretisation of the beam surface in rigid rectangular elements

Full size image

The geometrical calculations lead to the definition of the instantaneous y-rotation angle for each sub-element and consequently to the assessment of its position. Subsequently, the vertical velocity distribution along the beam length is computed with the same approach. By assuming a constant vertical velocity for each sub-element, the squeeze-film damping force is calculated as a summation along the x-direction across all the elements. Also, in this case the Veijola et al. (1997) model was applied to take into account the air viscosity variation depending on the vertical distance, as previously shown. The issue of how to apply the computed damping forces back to the two beam nodes must be considered. Since the beam is a flexible body, the force in a certain point cannot be directly transferred to another one as it happens in the rigid plate. To circumvent this problem, the approach proposed by Jing et al. (2002) was adopted. It exploits again the HSFs as weight functions to determine the effective contribution of the forces distributed along the beam length, at the two ends. For instance, the viscous damping force applied to the a node is:

$$ F_{za} = \frac{L}{n}W^{3} \sum\limits_{i = 0}^{n - 1} {\mu \left( {z\left( \frac{i}{n} \right)} \right)\frac{{v\left( \frac{i}{n} \right)}}{{z\left( \frac{i}{n} \right)^{3} }}g\left( {\vartheta_{y} \left( \frac{i}{n} \right)} \right)\left( {1 - 3\left( \frac{i}{n} \right)^{2} + 2\left( \frac{i}{n} \right)^{3} } \right)} $$
(7)

where L and W are the beam length and width along the x and y-axis, respectively, n is the number of elements in which the beam is divided along the x-axis, v(i/n) and z(i/n) are the vertical velocity and the gap of the i-th element respectively. Moreover, g(θ(i/n)) is the relationship between the local element reference system and the fixed one, and finally μ(z(i/n)) is the permittivity of air.

3 MEMS toggle-switch design concept

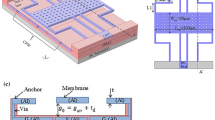
In this section, a brief description of the reference design concept chosen as target of the analysis is provided. The MEMS toggle-switch is a symmetric structure made of two toggle electrostatic transducers, each anchored through two straight short beams, connected through other two flexible beams to a middle rigid plate suspended above the RF-signal path (Gaddi et al. 2003, 2004; Farinelli et al. 2008; Sordo et al. 2013; Rangra et al. 2005). A comprehensive schematic view, including a top view and cross-sections, is provided in Fig. 8. By applying a bias voltage to either the inside or outside electrodes (see Fig. 8c, d), the structure assumes a non-parallel position with respect to the substrate by rotating around the axes of the anchor beams. The resulting deformation makes the RF signal electrode to be lowered or raised from its rest position, changing therefore the shunt capacitance value for the RF signal path and implementing a capacitive switch.

Fig. 8
figure 8

Set of schematic views of the MEMS toggle-switch design concept. a Top view, highlighting the lateral actuator plates and the central electrode, as well as the anchoring points. b Cross-section of the toggle-switch in its rest position. c Cross-section of the down position, when the controlling voltage is imposed to the inner electrodes. d Cross-section of the up position, when the controlling voltage is imposed to the outer electrodes

Full size image

4 Simulation and validation of the MEMS toggle-switch model

In this section, the MEMS toggle-switch is analysed with the compact models previously discussed in this work, and the results are compared for validation purposes with the outcome of Finite Element Method (FEM) simulations, conducted with a commercial software tool, referring to a full-3D model. The schematic reported in Fig. 9 shows the full-3D model of the toggle-switch to be simulated in the FEM environment. In order to simplify the problem, given the symmetry of the structure, just half of the toggle-switch is considered, imposing suitable mechanical constraints on the plane of symmetry.

Fig. 9
figure 9

Finite element method (FEM) model of half portion of the MEMS toggle-switch, highlighting the symmetry plane

Full size image

The schematic of the same structure in Fig. 9 is assemble with the compact models previously discussed, and it is shown in Fig. 10, where the suspended electrode, mechanical anchors and symmetry plane are labelled.

Fig. 10
figure 10

Schematic of the half toggle-switch, corresponding to the one reported in Fig. 9, built with the compact models discussed in this work

Full size image

Once both the FEM full-3D model and the schematic built with compact models are set, the static electromechanical simulation to identify the pull-in behaviour and activation voltage is performed. Figure 11 shows the deformed shape of the FEM full-3D model, when the controlling voltage is applied to the inner (Fig. 11a) and outer (Fig. 11b) electrodes, as previously shown in Fig. 8. The colour scale indicates the extent of the structure displacement along the vertical axis.

Fig. 11
figure 11

Deformed shape of the FEM full-3D model when the inner (a) and the outer (b) electrodes are activated (see Fig. 8). The colour scale indicates the vertical displacement extent

Full size image

The same type of simulation is performed on the schematic based on compact models (see Fig. 10) and the results are compared in the plots shown in Fig. 12, with reference to the case in which inner (Fig. 12a) and outer (Fig. 12b) electrodes are driven with a ramped DC voltage, respectively. As visible in the plots, simulations based on compact models predict rather accurately the pull-in voltage detected by the full-3D FEM model, both concerning the activation of the inner and outer electrodes of the MEMS toggle-switch actuators.

Fig. 12
figure 12

Comparison of the pull-in electromechanical simulation performed on the FEM full-3D model (Fig. 9) and on the schematic based on compact models (Fig. 10), when the inner (a) and outer (b) electrodes are driven, respectively

Full size image

Further validation is reported in the following. The plot in Fig. 13 shows the vertical displacement characteristic in response to an increasing applied voltage, for both the central movable parallel plate of the MEMS toggle-switch and for the inner edge of one of the two lateral transducer electrodes (see Fig. 8c).

Fig. 13
figure 13

Comparison of the pull-in electromechanical simulation performed on the FEM full-3D model (dashed lines) and on the schematic based on compact models (dots), with reference to the vertical displacement both of the central toggle-switch capacitor plate and of the lateral electromechanical actuator

Full size image

The dashed lines reported in the plot refer to the FEM simulations, while the dots report the response of the schematic, based on compact models, already reported and discussed in Fig. 10. Also this further comparison between the full-3D FEM model and the description based on the compact models discussed in the previous pages, exhibits good match between the two different analysis approaches.

Now, in order to exploit the full capabilities of the compact models here discussed, a transient simulation is reported and discussed, thus involving both inertial effect and viscous damping due to viscosity of air. A 0–20 V square pulse is imposed to the inner and outer actuation electrodes (see Fig. 8) with a certain delay, in order not to overlap them. The capacitance of the central plate, also calculated by the implemented compact models (discussed before), is observed as output variable. The response is depicted in Fig. 14.

Fig. 14
figure 14

Transient behaviour of MEMS toggle-switch central plate capacitance, simulated with the compact models (schematic in Fig. 10), when the inner and outer electrodes are driven with delayed square pulse voltages (0–20 V)

Full size image

Depending on which electrode (inner/outer) is driven with the square pulse, the central plate capacitance exhibits variations with respect to its value in the resting position, i.e. 87 fF. In particular, when the inner electrode is driven, the central plate reaches the pull-in and, in turn, the largest capacitance value of 125 fF. On the other hand, when the outer electrode is driven, the central plate raises above the resting position, thus decreasing the capacitance to 68 fF. It should be observed that the mechanical ringing, after each voltage transition, is correctly damped due to the presence of air, by means of the implemented viscous damping formulation previously discussed. Of course, in correspondence to the 0–20 V transition of the bias applied to the inner electrode, no ringing is visible in the capacitance response. This is because the central plate pulls-in, thus touching the underneath electrode.

As final analysis, the transient behaviour of the central plate is now observed against its vertical displacement, when dimensions of the plate itself are varied. Figure 15 shows the actuation transient behaviour for two central plate sizes, i.e. 140 × 140 μm2 and 300 × 300 μm2. It must be noted that the size of the central plate does not affect the electromechanical characteristics of the MEMS toggle-switch, as the actuation electrodes are placed underneath the lateral transducers (see Fig. 8). Having said that, the difference of the two curves has to be inferred exclusively to inertia and viscous damping of the central plate. In particular, the 300 × 300 μm2 plate, with its increased surface, leads to more relevant damping force, slowing down the actuation dynamics of the plate.

Fig. 15
figure 15

Transient actuation response versus time obtained by the MEMS toggle-switch schematic in Fig. 10 for two different geometries for the central plate

Full size image

Eventually, Fig. 16 reports the transient release for the 140 × 140 μm2 and 300 × 300 μm2 central plate. Also in this circumstance, the different viscous damping force due to the modified dimensions, leads to significantly different dynamic responses of the central plate, when the controlling voltage is suddenly zeroed.

Fig. 16
figure 16

Transient release response versus time obtained by the MEMS toggle-switch schematic in Fig. 10 for two different geometries for the central plate

Full size image

5 Conclusions

In this work, a compact modelling approach for the multi-physical mixed-domain simulation of RF-MEMS geometry was discussed and exploited to predict the behaviour of a MEMS toggle-switch geometry. The modelling methodology relies on compact analytical models implemented in a Hardware Description Language (HDL) programming code, thus enabling the exploitation of the software library in all the most diffused frameworks for the development of Integrated Circuits (ICs).

After reporting some details concerning the developed models, the MEMS toggle-switch design concept was introduced. The electromechanical behaviour of the toggle-switch, as predicted by the discussed compact models, was compared to a full-3D model analysed with the Finite Element Method (FEM) approach, for validation purposes. Then, compact models were exploited to observe the dynamic response of the device.

The discussed modelling and simulation methodology represents a suitable tool for the development of innovative MEMS and RF-MEMS designs, as it enable fast and accurate simulation of complex geometries.