1 Introduction

Underwater robots have been widely and successfully used for monitoring, recovery, detection of environment pollution, exploitation of unstructured underwater environments activities, submarine sampling and other tasks (Kaznov and Seeman 2010; Guo et al. 2017; Kelasidi et al. 2016; Shi et al. 2017), and the underwater robots have become essential tools for ecological observations and military reconnaissance applications in littoral regions. Generally, different applications requiring different configurations and size of robots, compared with some streamlined body form with finned and snakelike underwater robots, the spherical robot generate less noise and water disturbance, provide better stealth ability and bio-affinity, and sphere body provide maximum internal space to install more batteries and sensors (Chen et al. 2013; Li et al. 2015). Additionally, due to the central symmetry, spherical body always performance high stability, flexibility, easy for modeling and controlling, and spherical body can realize rotational motions with a 0° turn radius, and most spherical robots are driven by pendulums, rollers or propellers et al. (Jia et al. 2016). From 2012 up to now, our previous team have proposed a spherical amphibious robot, with a deformable mechanical structure, the robot walked on land with legs and swimming underwater with vectored water jet propellers, which provided better overstepping ability and adaptability in littoral regions. And to improve stability while retaining precision, an improved amphibious spherical robot with compact structure was built using 3-D printing technology, in addition, different on-land walking gaits and underwater swimming with PID control method has been designed and implemented for our amphibious spherical robot (He et al. 2014, 2016; Guo et al. 2016, 2018; Pan et al. 2014, 2015).

In recent years, with the increased interest in multi-robot cooperation system of biological monitoring and target rounding up activities, multi robot system are developed rapidly due to their ability to access complex and multi tasks. Biology has inspired researchers in many ways, and inspired by the swarm intelligence, the Nagoya University designed a cellular robotic system (Jiang et al. 2014), in which system all the robots were assumed as cell elements, and the cell elements can be freely combined according to the application requirements. Mccolgan et al. (2015) has presented a coordination algorithm based on the behavior mechanisms observed in fish schooling to coordinate a group of AUVs, four nearest AUVs are required to ensure a stable structure of formation group. Tsiogkas et al. (2015) have proposed and studied three distributed methods for an underwater archaeological inspection scenario under communication constraints, including the greedy allocation method, k-Means method and the linear programming formulation method, and they also illustrated that the k-Means method performs better when communication error rates are lower. Yan et al. (2008) have proposed a path following algorithm for AUV, which combined the backstepping and Lyapunov method and make each AUV’s path parameter synchronization to accomplish the formation task. Wang et al. (2017) introduced the human intelligent into the intelligent UUV formation system, and some simulation results have indicated that the cooperative system of UUVs is able to realize obstacle avoidance. Yu et al. (2016) have designed a leader–follower system with two-layer random switching topologies for the formation control of UUVs, and the follower could track the path of leader in the formation system. Wang et al. (2017) have studied the coordination of multiple robotic fish with applications to underwater robot competition, and a behavior-based hierarchical architecture in connection with cooperative behavior acquisition based on fuzzy RL has been proposed to achieve efficient coordination among multiple robotic fish.

However, it is still problematic to implement actual target rounding up task of multi underwater robots, and most researches about formation control system with large scaled robots basically focused on theoretical analysis, and more importantly, some researches about formation control system of target rounding up with small-scaled amphibious robot has not been carried out at home and abroad. Consequently, with the requirement of target monitoring and rounding up in the wide underwater environment of our small-scaled amphibious spherical robot, an underwater formation control system of multi spherical robot was designed and studied in this paper.

The remainder of this paper is organized as follows: In Sect. 2, we describe our previous design of amphibious spherical robot, the control circuit and communication system, and an adaptive control method of our robot was also designed and analyzed in Sect. 2. Section 3 presents the formation control system of target rounding up with multi robots, the path planning and modeling improvement of dynamic target. In Sect. 4, we describe underwater experiments verifying the formation control system with static and dynamic target. And Sect. 5 will be conclusions and our future work.

2 Adaptive control method of underwater spherical robot

2.1 The related work about amphibious spherical robot

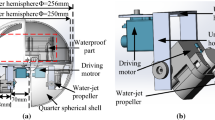
A latest version of the amphibious spherical robot with a larger diameter of 350 mm was designed and fabricated, as presents in Fig. 1, which consisted of two enclosed waterproof shell and two openable quarter-sphere shells, the diameter of the first and second waterproof shell is 280 mm, 320 mm respectively. The diameter of the two openable quarter-sphere shells is 350 mm, and the mass of the robot is approximately 9.408 kg. Electronic devices and batteries were installed inside the hemispherical hull, which was waterproof and provided protection from collisions. Four legs, each of which was equipped with two servo motors and a water-jet propeller, were installed symmetrically in the lower hemisphere of the robot. Driven by the two servo motors, the upper joint and lower joint of a leg were able to rotate around a vertical axis and a horizontal axis, respectively. The water-jet propeller was fixed in the lower joint and could generate a vectored thrust in a specific direction in water. The openable shells could close to form a ball shape, and the robot was propelled by vectored thrusts from four water-jet propellers, and the openable shells could open and the robot walked using its four legs, and the amphibious spherical robot was designed to be able to work in complex environments like coral reefs and pipelines (Fig. 1).

Fig. 1
figure 1

The structure of amphibious spherical robot

Full size image

As illustrated in Fig. 2a, the robot was powered by a set of Li–Po batteries, with a total capacity of 24,000 mAh. Sensors including a global positioning system module, a depth gauge, a micro-electromechanical system, an inertial measurement unit, an industrial camera, and a ToF camera, were installed to sense the status of the robot and the surroundings. Due to the load space of the robot was narrow and enclosed, and in order to reduce the power consumption and heat generation, a Xilinx Zynq-7000 SoC and a Raspberry Pi 3 was used to fabricate the information processing system of robot, and a SoC-based heterogeneous computing architecture was designed to speed up image processing. An acoustic modem and a universal serial bus radio module were used for communication, and the module of the communication system in this paper is the Tritech International Ltd Micron Data Modem, it could provide a means of transferring data acoustically through water. Operation is point to point, between a pair of Micron Data Modems, at operational distances of up to 500 m horizontally and 150 m vertically at a data rate of 40 bits per second. Devices are addressed through a serial electrical interface, which may be controlled directly from a control board with a simple teletype (half-duplex) terminal program. The specification of the Micron Data Modem is illustrated in Fig. 3. The external diameter of the sensor is from 50 mm to 56 mm, and the height is 79 mm. The weight of the Micron Data Modem in air and in water are 235 g and 80 g, respectively, and its depth rating is 750 m, its temperature range is (− 10 °C, 35 °C) (He et al. 2018). The control system of our amphibious spherical robot was designed as Fig. 2b, and the system mainly including five sub-systems: information processing, sensor detection, motor actuating, composite communication, power supply and so on.

Fig. 2
figure 2

The control and communication system of amphibious spherical robot

Full size image
Fig. 3
figure 3

Specification of the Micron Data Modem (He et al. 2018)

Full size image

2.2 Adaptive control method of underwater spherical robot

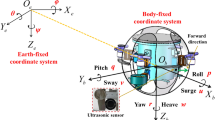
Figure 4 illustrates the kinematic model of the underwater spherical robot. Figure 4a illustrates the coordinates of the spherical robot, including the earth fixed coordinate E-ξζη and the body fixed coordinate O-xyz, and the geometric center O of robot is the origin of body fixed coordinate. The results of the thrust measurements of a water-jet propeller is shown in Fig. 4b. Thrust increases as the input voltage increases. At the maximum voltage of 16.8 V, the maximum thrust is 85 mN, and by controlling the angles of the water-jet propellers and the vertical motor, thrust can be realized in all directions. As illustrates in Fig. 4c, d, the angle of the water-jet propellers can be varied to control the motion of the robot. As depicts in Fig. 4a, the earth fixed coordinate E-ξζη and the body fixed coordinate O-xyz was established, and in the earth fixed coordinate, the position and attitude of robot can be written as (Dong et al. 2012; Krug and Dimitrov 2015):

$$ \eta = \left\{ {x,y,z,\varphi ,\theta ,\psi } \right\} $$
(1)

where (x, y, z) and (φ, θ, ψ) represents the Cartesian position and Euler angle of robot. In the body fixed coordinate of robot, the motion state of robot can be expressed as:

$$ v = \left\{ {u,v,w,p,q,r} \right\} $$
(2)

where u, v and w represent the linear velocity of surge, heave and sway motion, p, q and r represent the angular velocity of rolling, pitching and yawing motion.

Fig. 4
figure 4

Underwater spherical robot and its kinematic model

Full size image

The kinematic model of underwater spherical robot can be written as:

$$ (M_{RB} + M_{A} )\dot{v} + (C_{RB} (v) + C_{A} (v))v + (D_{l} + D_{q} (v))v + g(\eta ) = \tau $$
(3)

where MRB denotes the inertial matrix, MA is the added inertial matrix, CRB(v) is the rigid Coriolis force matrix, CA(v) is the additional mass Coriolis force matrix, Dlv is the linear damping matrix of hydrodynamics, Dq(v)v is the nonlinear damping matrix of hydrodynamics, g(η) is the restoring force and moment matrix, τ is the driving force and moment matrix of robot.

Considering the characteristics of underwater spherical robot and to simplify its dynamic model, we make assumptions as follow: The velocity of robot is less than 0.5 m/s, so its hydrodynamic damping conforms to the condition of low speed motion; the four degrees of freedom motion of the robot has been decoupled; the structure of the robot is symmetrical, the surge and sway motion has the same dynamic characteristics; the robot remain its horizontal attitude in the surge and sway motion, and only a small passive pitching and rolling motion (Yue et al. 2013; Rodrigo et al. 2016; Xu et al. 2014).

The elements of MRB and MA is determined by the mass distribution and geometric configuration of the spherical robot, due to the symmetrical structure and suspended weight of our spherical robot, and the angular velocity of pitching and swaying motion could be ignored, so we could get:

$$ M_{RB} = \left[ {\begin{array}{*{20}c} m & 0 & 0 & 0 & {mz_{G} } & 0 \\ 0 & m & 0 & { - mz_{G} } & 0 & {mx_{G} } \\ 0 & 0 & m & 0 & { - mx_{G} } & 0 \\ 0 & { - mz_{G} } & 0 & {I_{x} } & 0 & { - I_{zx} } \\ {mz_{G} } & 0 & { - mx_{G} } & 0 & {I_{y} } & 0 \\ 0 & {mx_{G} } & 0 & { - I_{zx} } & 0 & {I_{z} } \\ \end{array} } \right] $$
(4)
$$ M_{A} = \left[ {\begin{array}{*{20}c} { - X_{{\dot{u}}} } & 0 & 0 & 0 & 0 & 0 \\ 0 & { - Y_{{\dot{v}}} } & 0 & 0 & 0 & { - Y_{{\dot{r}}} } \\ 0 & 0 & { - Z_{{\dot{w}}} } & 0 & { - Z_{{\dot{q}}} } & 0 \\ 0 & 0 & 0 & { - K_{{\dot{p}}} } & 0 & 0 \\ 0 & 0 & { - M_{{\dot{w}}} } & 0 & { - M_{{\dot{q}}} } & 0 \\ 0 & { - N_{{\dot{v}}} } & 0 & 0 & 0 & { - N_{{\dot{r}}} } \\ \end{array} } \right] $$
(5)

where m  = 9.408 kg is the mass of robot, rG = [xG, yG,zG]T = [0, 0, − 0.0045] T is the center of gravity of robot, rB = [xB, yB, zB]T = [0, 0, 0.0619] T is the center coordinate of buoyancy of robot. Based on the 3D modeling of robot in SolidWorks, the inertia tensor of robot Ix = Iy = 0.0664, Iz = 0.0826, Izx = 0 can be calculated by using integral operation tool in MATLAB. Simultaneously, our spherical robot was assumed as a sphere body, so the numerical solution of tensor term of additional mass could be obtained \( X_{{\dot{u}}} = Y_{{\dot{v}}} = Z_{{\dot{w}}} = 10.3 \), \( Y_{{\dot{r}}} = Z_{{\dot{q}}} = M_{{\dot{w}}} = N_{{\dot{v}}} = 0 \), \( K_{{\dot{p}}} = M_{{\dot{q}}} = 0.088 \), \( N_{{\dot{r}}} = 0.065 \).

The Coriolis force is caused by the earth rotation, and the elements of matrix CRB(v) and CA(v) are determined by MRB and MA separately, so the characteristics of the simplified robot can be expressed as:

$$ C_{RB} = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & {mz_{G} r} & {mw} & { - mv} \\ 0 & 0 & 0 & { - mw} & {mz_{G} r} & {mu} \\ 0 & 0 & 0 & {m(v - z_{G} p)} & { - m(z_{G} q + u)} & 0 \\ { - mz_{G} r} & {mw} & {m(z_{G} p - v)} & 0 & {I_{z} r} & { - I_{y} q} \\ { - mw} & { - mz_{G} r} & {m(z_{G} q + u)} & { - I_{z} r} & 0 & {I_{x} p} \\ {mv} & { - mu} & 0 & {I_{y} q} & { - I_{x} p} & 0 \\ \end{array} } \right] $$
(6)
$$ C_{A} = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 & { - Z_{{\dot{w}}} w} & {Y_{{\dot{v}}} v} \\ 0 & 0 & 0 & {Z_{{\dot{w}}} w} & 0 & { - X_{{\dot{u}}} u} \\ 0 & 0 & 0 & { - Y_{{\dot{v}}} v} & {X_{{\dot{u}}} u} & 0 \\ 0 & { - Z_{{\dot{w}}} w} & {Y_{{\dot{v}}} v} & 0 & { - N_{{\dot{r}}} r} & {M_{{\dot{q}}} q} \\ {Z_{{\dot{w}}} w} & 0 & { - X_{{\dot{u}}} u} & {N_{{\dot{r}}} r} & 0 & { - K_{{\dot{p}}} p} \\ { - Y_{{\dot{v}}} v} & {X_{{\dot{u}}} u} & 0 & { - (M_{{\dot{w}}} w + M_{{\dot{q}}} q)} & {K_{{\dot{p}}} p} & 0 \\ \end{array} } \right] $$
(7)

Due to the low velocity of robot, the flow of robot is Stokes flow, the viscosity coefficient of flow is Cl = 1.01 × 10−4, and its hydrodynamics linear damping matrix can be written as:

$$ D_{l} v = C_{l} \times diag\left\{ {u,v,w,p,q,r} \right\} = 1.01 \times 10^{ - 4} \times diag\left\{ {u,v,w,p,q,r} \right\} $$
(8)

The nonlinear damping matrix of spherical robot can be expressed as:

$$ D_{q} (v)v = \frac{1}{2}C_{d} \rho V_{r}^{2} A = \left[ {\begin{array}{*{20}c} {0.471} & 0 & 0 & 0 & 0 & 0 \\ 0 & {0.471} & 0 & 0 & 0 & 0 \\ 0 & 0 & {0.499} & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} u \\ v \\ w \\ p \\ q \\ r \\ \end{array} } \right] $$
(9)

where Cd is the drag coefficient, and which is different in the vertical and horizontal motions, ρ is the density of the fluid, Vr is the relative velocity of robot and fluid, A is the cross-sectional area of the water surface in the robot’s motion direction.

The restoring force and moment matrix are determined by the gravity and the center of gravity of robot, the buoyancy and the center of buoyancy of robot.

$$ g(\varTheta ) = \left[ {\begin{array}{*{20}c} {0^{3 \times 1} } \\ {(z_{G} W - z_{B} B)\cos \theta \sin f} \\ {(z_{G} W - z_{B} B)\sin \theta + (x_{G} W - x_{B} B)\cos \theta \cos f} \\ { - (x_{G} W - x_{B} B)\cos \theta \sin f} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {0^{3 \times 1} } \\ { - 0.9856\cos \theta \sin f} \\ { - 0.9856\sin \theta } \\ 0 \\ \end{array} } \right] $$
(10)

The driving force and the moment matrix are determined by the distribution of the waterjet propeller and its output thrust.

$$ \tau = LU $$
(11)

where L is the distribution matrix of thrust, U = [FLF, FRF, FRH, FLH] is the vector of output thrust of waterjet propeller. As illustrated in Fig. 3b, the thrust increases as the input voltage increases. Based on the quantitative measurement of force/torque sensors, its linear fitting curve can be obtained:

$$ F = 0.236U^{2} + 1.662U - 1.669 $$
(12)

As illustrated in Fig. 4c, d, when the robot implements horizontal and vertical motion, the distribution matrix LHand LV of thrust can be obtained by analyzing the attitude and installation parameters of all composite actuating systems. The legs are labeled as follows: left front (LF), right front (RF), left hind (LH), and right hind (RH).

$$ L_{H} = \left[ {\begin{array}{*{20}c} {a_{11} } & {a_{12} } & {a_{13} } & {a_{14} } \\ {a_{21} } & { - a_{22} } & {a_{23} } & { - a_{24} } \\ 0 & 0 & 0 & 0 \\ {(z_{G} + z_{H} )a_{21} } & { - (z_{G} + z_{H} )a_{22} } & {(z_{G} + z_{H} )a_{23} } & { - (z_{G} + z_{H} )a_{24} } \\ { - (z_{G} + z_{H} )a_{11} } & { - (z_{G} + z_{H} )a_{12} } & {(z_{G} + z_{H} )a_{13} } & { - (z_{G} + z_{H} )a_{14} } \\ {x_{H} a_{21} - y_{H} a_{11} } & {x_{H} a_{22} - y_{H} a_{12} } & {y_{H} a_{13} - x_{H} a_{23} } & {y_{H} a_{14} - x_{H} a_{24} } \\ \end{array} } \right] $$
(13)

where \( a_{11} = \cos \alpha_{\text{LF}} \), \( a_{12} = \cos \alpha_{\text{RF}} \), \( a_{13} = \cos \alpha_{\text{RH}} \), \( a_{14} = \cos \alpha_{\text{LH}} \), \( a_{21} = \sin \alpha_{\text{LF}} \), \( a_{22} = \sin \alpha_{\text{RF}} \), \( a_{23} = \sin \alpha_{\text{RH}} \), \( a_{24} = \sin \alpha_{\text{LH}} \), \( \alpha_{\text{LF}} \),\( \alpha_{\text{LH}} \),\( \alpha_{\text{RF}} \), \( \alpha_{\text{RH}} \) are the angle of horizontal motor, \( (x_{\text{H}} ,y_{\text{H}} ,z_{\text{H}} ) \) is the coordinate of thruster in horizontal motion state.

$$ L_{V} = \left[ {\begin{array}{*{20}c} {b_{21} a_{11} } & { - b_{22} a_{12} } & { - b_{23} a_{13} } & {b_{24} a_{14} } \\ {b_{21} a_{21} } & {b_{22} a_{22} } & { - b_{23} a_{23} } & { - b_{24} a_{24} } \\ { - b_{11} } & { - b_{12} } & { - b_{13} } & { - b_{14} } \\ { - y_{v} b_{11} } & { - y_{v} b_{12} } & {y_{v} b_{13} } & {y_{v} b_{14} } \\ {x_{v} b_{11} } & { - x_{v} b_{12} } & { - x_{v} b_{13} } & {x_{v} b_{14} } \\ {x_{v} b_{21} a_{21} - y_{v} b_{21} a_{11} } & {y_{v} b_{22} a_{12} - x_{v} b_{22} a_{22} } & {x_{v} b_{23} a_{23} - y_{v} b_{23} a_{13} } & {y_{v} b_{24} a_{14} - x_{v} b_{24} a_{24} } \\ \end{array} } \right] $$
(14)

where \( b_{11} = \cos \beta_{\text{LF}} \), \( b_{12} = \cos \beta_{\text{RF}} \), \( b_{13} = \cos \beta_{\text{RH}} \), \( b_{14} = \cos \beta_{\text{LH}} \), \( b_{21} = \sin \beta_{\text{LF}} \), \( b_{22} = \sin \beta_{\text{RF}} \), \( b_{23} = \sin \beta_{\text{RH}} \), \( b_{24} = \sin \beta_{\text{LH}} \), \( \beta_{\text{LF}} \), \( \beta_{\text{LH}} \), \( \beta_{\text{RF}} \), \( \beta_{\text{RH}} \) are the angle of vertical motor, \( (x_{\text{V}} ,y_{\text{V}} ,z_{\text{V}} ) \) is the coordinate of propeller in vertical motion state.

Then the kinematic model of robot with surge, sway, heave and yaw motion can be expressed as:

$$ \left\{ {\begin{array}{*{20}c} {19.708\dot{u} + 1.01 \times 10^{ - 4} u + 0.471u^{2} = F_{u} } \\ {19.708\dot{v} + 1.01 \times 10^{ - 4} v + 0.471v^{2} = F_{v} } \\ {19.708\dot{w} + 1.01 \times 10^{ - 4} w + 0.499w^{2} = F_{w} } \\ {0.1476\dot{r} + 1.01 \times 10^{ - 4} r = F_{r} } \\ \end{array} } \right. $$
(15)

where Fu, Fv, Fw and Fr are the driving force and moment of waterjet propellers with surge, sway, heave and yaw motion, and can be obtained by the Eqs. (11)–(14).

3 Target rounding up strategy of multi robots

3.1 Path planning of multi robot formation

In this section, according to the desired trajectory, multi robots were assumed to moving towards the target point under the control of their own controllers. As illustrates in Fig. 5, the linear quadratic regulator method was adopted to plan the trajectories of three underwater spherical robots, and these three robots rounding up the target in the form of arc (Sutantyo et al. 2013; Fang et al. 2014; Liang et al. 2016).

Fig. 5
figure 5

The diagram of target rounding up with three robots

Full size image

In the formation control system of multi robot with target rounding up, according to the actual task and application requirements of environment, two or more robots can be selected for formation control system. And in the formation control system, the distance from robot to the target is made up of some straight lines, each line is the ideal trajectory of robot, and each robot moves along the ideal trajectory under its own controller. When the robot arrived at the end of the last line, then the formation system of multi robot can be considered as complete the target rounding up.

The coordinate of robot is defined as (xi, yi), i  = 1, 2, 3…n, and the coordinate of target is defined as (xT, yT), as illustrated in Fig. 6.

Fig. 6
figure 6

Kinematic coordinate model of robot

Full size image

Taking the center point of target as the center, the distance from the center of robot to the target center is the radius, and then we can get

$$ \left( {x - x_{T} } \right)^{2} + \left( {y - y_{T} } \right)^{2} = \sqrt {\left( {x_{1} - x_{T} } \right)^{2} + \left( {y_{1} - y_{T} } \right)^{2} } $$
(16)

The coordinates of the center point of two front legs of robot is (xf, yf), and the coordinates of the center point of the two hinder legs is (xh, yh), the center of gravity of the robot is (xG, yG), the relationship between the center of gravity and the coordinate of legs is:

$$ x_{G} = \begin{array}{*{20}c} {\left( {x_{f} + x_{h} } \right)/2} & {y_{G} = \left( {y_{f} +_{h} } \right)/2} \\ \end{array} $$
(17)

Due to the constraints of robot:

$$ y_{f} \times \cos \theta - x_{f} \times \sin \theta = 0 $$
(18)

For the front and hinder legs of robot

$$ \dot{x}_{f} = V \times \cos \left( {\theta + \phi } \right)\begin{array}{*{20}c} ; & {\dot{y}_{f} = V \times \sin \left( {\theta + \phi } \right)} \\ \end{array} $$
(19)
$$ x_{h} = x_{f} - l \times \cos \theta \begin{array}{*{20}c} ; & {y_{h} = y_{f} - l \times \sin \theta } \\ \end{array} $$
(20)

Here we assume θ with fewer changes and linearized the characteristics of spherical robot

$$ \dot{x}_{h} = \dot{x}_{f} + l \times \sin \theta \times \theta \begin{array}{*{20}c} ; & {\dot{y}_{h} = \dot{y}_{f} - l \times \cos \theta } \\ \end{array} \times \theta $$
(21)

Combined the Eq. (27) with Eqs. (24) and (25), and we could get:

$$ \dot{\theta } = V \times \frac{\sin \phi }{l} $$
(22)

Then the coordinate of the center of gravity of robot can be expressed as

$$ \begin{array}{*{20}c} {x_{G} = x_{f} - \frac{l}{2} \times \cos \theta ;} & {y_{G} = y_{f} - \frac{l}{2} \times \sin \theta } \\ \end{array} $$
(23)

Correspondingly

$$ \dot{x}_{h} = \dot{x}_{f} + \frac{l}{2} \times \sin \theta \times \dot{\theta }\begin{array}{*{20}c} ; & {\dot{y}_{h} = \dot{y}_{f} - \frac{l}{2} \times \cos \theta } \\ \end{array} \times \dot{\theta } $$
(24)

The velocity of robot in the direction of x and y are given by the following:

$$ \left\{ \begin{aligned} \dot{x}_{G} = \frac{l}{2} \times V \times \cos (\theta + \phi ) + \frac{l}{2} \times V \times \cos \theta \cos \phi \hfill \\ \dot{y}_{G} = \frac{l}{2} \times V \times \sin (\theta + \phi ) + \frac{l}{2} \times V \times \sin \theta \cos \phi \hfill \\ \end{aligned} \right. $$
(25)

where V is the velocity of robot, and the kinematic modeling of the robot can be expressed as:

$$ \left[ {\begin{array}{*{20}c} {\dot{x}_{G} } \\ {\dot{y}_{G} } \\ {\dot{\theta }_{G} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\dot{x}_{G} = \frac{l}{2} \times V \times \cos (\theta + \phi ) + \frac{l}{2} \times V \times \cos \theta \cos \phi } \\ {\dot{y}_{G} = \frac{l}{2} \times V \times \sin (\theta + \phi ) + \frac{l}{2} \times V \times \sin \theta \cos \phi } \\ {V \times \frac{\sin \phi }{l}} \\ \end{array} } \right] $$
(26)

where ϕ is the angle of the robot’s current direction and initial direction, l is the distance between the center point of the front and hinder legs.

3.2 Modeling improvement of dynamic target

Assuming that the multi robot formation system rounding up a moving target, and the target is moving in a straight line with constant velocity, the motion state of robot can be formulated as:

$$ \left( {\begin{array}{*{20}c} d \\ s \\ {\Delta \theta } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {\left( {x_{h} - x} \right)\sin \theta_{h} - \left( {y_{h} - y} \right)\cos \theta_{h} } \\ {\left( {x_{h} - x} \right)\cos \theta_{h} + \left( {y_{h} - y} \right)\sin \theta_{h} } \\ {\theta_{G} - \theta_{h} } \\ \end{array} } \right) $$
(27)

The distance between the actual trajectory and the desired shortest (straight line) trajectory of robot is d, the optimal tangential distance of the desired trajectory of robot is s, the angle difference between the current heading angle and ideal heading angle (in the direction of the desired trajectory) is Δθ. Then the modeling of dynamic target is illustrated in Fig. 7. (Oh et al. 2017; Pellegrinelli et al. 2017).

Fig. 7
figure 7

Modeling of dynamic target

Full size image

Then the state equation of robot could be given as follows:

$$ \left( {\begin{array}{*{20}c} {\dot{d}} \\ {\dot{s}} \\ {\Delta \dot{\theta }} \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {\sin \theta_{h} \left( {x_{h} - \dot{x}} \right) - \cos \theta_{h} \left( {y_{h} - \dot{y}} \right)} \\ {\cos \theta_{h} \left( {x_{h} - \dot{x}} \right) + \sin \theta_{h} \left( {y_{h} - \dot{y}} \right)} \\ {\dot{\theta }_{G} - \theta_{h} } \\ \end{array} } \right) $$
(28)

Insert the Eq. (28) into Eq. (27), and we could get:

$$ \left( {\begin{array}{*{20}c} {\dot{d}} \\ {\dot{s}} \\ {\Delta \dot{\theta }} \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {v\sin \left( {\Delta \theta } \right)\cos \left( \varphi \right) + 0.5v\cos \left( {\Delta \theta } \right)\sin \left( \varphi \right)} \\ {0.5v\sin \left( {\Delta \theta } \right)\sin \left( \varphi \right) - v\cos \left( {\Delta \theta } \right)\cos \left( \varphi \right)} \\ {v\frac{\sin \left( \varphi \right)}{l}} \\ \end{array} } \right) $$
(29)

Here we select ΔV  = V − Vh and ϕ are the control variables, then the state equation of robot is given by:

$$ \left( {\begin{array}{*{20}c} {\dot{d}} \\ {\Delta \dot{\theta }} \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {\left( {V_{h} + \Delta V} \right)\sin \left( {\Delta \theta } \right)\cos \left( \varphi \right) + 0.5\left( {V_{h} + \Delta V} \right)\cos \left( {\Delta \theta } \right)\sin \left( \varphi \right)} \\ {\left( {V_{h} + \Delta V} \right)\frac{\sin \left( \varphi \right)}{l}} \\ \end{array} } \right) $$
(30)

4 Experiment testing of target rounding up

To evaluate the feasibility and performance of the formation control system proposed in this paper, we carried out underwater experiments of static and dynamic targets rounding up with two/three spherical robot in a pool with 3 m × 2 m × 1.5 m, and a real-time vision localization system was used to evaluate the trajectory and attitude angle of the robot. As presents in Fig. 8, the experimental platform consists of consists of robot module, image capturing and processing module, and communication module. The overhead camera with resolution of 720 P was installed above the pool to obtain the trajectory of robot during the experiment. All experiments were carried out by the same control algorithm in the same pool, and each one was repeated more than 20 times.

Fig. 8
figure 8

Experimental platform used to conduct our proposed formation control system

Full size image

Firstly, we carried out the formation control experiment of static target rounding up with two spherical robots, a static yellow submarine was assumed as a target in the experiment, one side of the submarine was assuming blocked by other obstacles. Two spherical robots which located at different monitoring positions, moving forward with the nearest distance trajectory toward the target, and finally, the target is rounded up by two robots, Fig. 9 presents the movement changes of two robots from the closest distance to the target from different starting points. The trajectory tracking and attitude angle results of two robots are depicted in Figs. 10 and 11.

Fig. 9
figure 9

The process of static target rounding up

Full size image
Fig. 10
figure 10

The process of static target rounding up

Full size image
Fig. 11
figure 11

Displacement trajectory of the triangular formation

Full size image

As we can see from Figs. 10 and 11, although the two robots occur some deviation in the movement, there was only a slight deviation, the two spherical robots could implement a static target rounding up, and the controller module of the robot was set to ignore minor deviations. The pitching, yawing and rolling angles of two robots were relatively small, so the robot should not jump and there should be no sudden changes in its motion, and the two robots first close the target at the ideal nearest distance and then rounded up the target, and the whole movement process is consistent and stable.

Then, some experiments were carried out with three robots for dynamic target tracking and rounding up. As presents in Fig. 12, one of spherical robot is assumed as a dynamic target, and the other two robots are tracking and rounding up the target robot, in order to reduce the interference between the robots, the two robots on both sides of the target keep the same velocity and distance with the target, and then the two robots speed up and rounding up the target from two sides of the target. The trajectory tracking and attitude angle results of two robots are depicted in Figs. 13 and 14.

Fig. 12
figure 12

The video of dynamic target rounding up

Full size image
Fig. 13
figure 13

Displacement trajectory of dynamic target rounding up

Full size image
Fig. 14
figure 14

Attitude angle of dynamic target rounding up with two robots

Full size image

As we can see from Figs. 13 and 14, the two robots are moving towards the target with the same velocity at first, and gradually accelerated from two side of the target and rounding up the target. Although the trajectory performance of two robots have minor deviations, due to the mutual interference of multi robot and the error of sensors, as the motion continues, the attitude angle of two robot gradually decreased and stabilized. Above all, according to the experimental results of formation control system of target rounding up with multi robots, although there exist some deviations of multi robot’s motion, the overall motion process of multi robot is flexible and stable, which indicates that the small-scaled spherical underwater multi robot can implement static and dynamic targets rounding up with the formation control system designed in this paper, and has practical application feasibility of target monitoring and rounding up with multi underwater robot cooperation et al.

5 Conclusions and future work

In this paper, to meet the practical application requirements of the small-scaled underwater spherical robots in biological monitoring and intelligent surveillance tasks, a cooperative formation control system with static and dynamic target rounding up was proposed and implemented. To address the kinematic model of underwater spherical robot in complex underwater scenarios, a simplified kinematic model of underwater spherical robot with horizontal and vertical motion was established. Then, an adaptive control algorithm was designed to control the underwater spherical robot, which has good robustness and adaptability in practical underwater environment. Using the path planning strategy and modeling optimization of static and dynamic target, a controller based on linear quadratic regulator method was designed to realize static/dynamic target rounding up with multi robots. Evaluation experiments confirmed the feasibility of the proposed system, and the proposed system was capable of rounding up the static and dynamic target with two or three small-scaled underwater spherical robots.

Our future work will focus on high-level applications in actual marine environment with different degrees of freedom motions in ever-changing environments, including automatic target monitoring and rounding up. Additionally, advanced visual algorithms and tools will be used to improve the vision system of robot.