1 Introduction

Resonant accelerometer, their operational principle is detecting resonant frequency shift in the resonator. Detection of frequency shift is more advantageous compared to detecting changes in amplitude, as it less sensitive to effects such as feedthrough coupling from undesired sources and parasitic passive elements (Zou and Seshia 2015; Pedersen and Seshia 2004; Seshia et al. 2002). Thus, as one core device of an inertial navigation system, its precision and quality of property greatly determine the precision and property of the inertial navigation system. The system is widely applied to missile, satellites, rockets, and other aircraft and plays a significant part in guaranteeing the vehicle attitude being stable and the target being accurate (Comi et al. 2010; Suminto 1996). Recently, there are several reports on accelerometer of the novel structures (Wang et al. 2017; Zhao et al. 2016; Ding et al. 2016a, b; Zhang et al. 2015; Yang et al. 2014; Park et al. 2014), measurement methods (Li et al. 2017; Comi et al. 2016; Yan et al. 2016; Park et al. 2016; Zotov et al. 2015; Heng and Li 2013; Shi et al. 2013) and fabricating process (Verma et al. 2016; Han et al. 2013). By the investigation and analysis about the existing literature dates and relevant technologies, it can be found that there are very few studies about external frame and internal structure to design the resonant accelerometer structure.

This paper focuses on the design and simulation of a resonant accelerometer. The structure of the resonant accelerometer is designed according to the external frame and internal structure. The acceleration on proof mass determines the resonance frequency shifts of a pair of resonator, which are proportional to the external acceleration. The pairs of decoupling resonators allow the simultaneous differential measurement of acceleration along two orthogonal axes, while the high sensitivity and low crossaxis sensitivity is guaranteed.

2 Operational principle

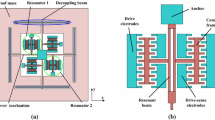
The working principle of the resonant accelerometer is shown in Fig. 1, which mainly consists of a single proof mass, a pair of resonators, levers and elastic beams. When acceleration a is produced in the x direction, in the light of Newton’s second law, this direction will produce an inertia force that can be represented as:

Fig. 1
figure 1

The working principle of the resonant accelerometer

Full size image
$$ F = ma. $$
(1)

In this case, m is mass of the proof mass, F is the inertial force. The acceleration is converted to the inertial forces along the x axis, and the inertia force is applied to the axis of the resonator, changing the original resonant frequency of the resonant beam. According to the theoretical derivation, the corresponding acceleration is obtained by measuring the variation of vibration resonant frequency of the new resonant state.

When the resonant beam vibrate, the natural resonant frequency is:

$$ \omega_{\text{n}} = \sqrt {{{k_{{\text{eff}}} } \mathord{\left/ {\vphantom {{k_{{\text{eff}}} } {M_{{\text{eff}}} }}} \right. \kern-0pt} {M_{{\text{eff}}} }}} , $$
(2)

where \( k_{{\text{eff}}} \) is the equivalent stiffness of the resonator and \( M_{{\text{eff}}} \) is the equivalent mass of the resonant beam.

Assume that the natural resonant frequency of the resonant beam can be expressed as:

$$ \omega^{\prime}_{n} = \omega_{n} \sqrt {1 + \beta a} . $$
(3)

In this case, \( \beta \) is a constant relative to the accelerometer structure. To show the Eq. (3) in the form of Taylor series:

$$ \omega^{\prime}_{n} = \omega_{\text{n}} \left( {1 + \frac{\text{1}}{\text{2}}\beta a - \frac{\text{1}}{\text{8}}\beta^{2} a^{2} + \frac{\text{1}}{{\text{16}}}\beta^{3} a^{3} - \ldots } \right). $$
(4)

Therefore, in the case of higher order terms, the frequency variation of the resonator under the measured acceleration a is:

$$ \Delta \omega = \omega^{\prime}_{\text{n}} - \omega_{\text{n}} = \frac{1}{2}\beta a\omega_{\text{n}} . $$
(5)

It can be seen from the Eq. (5), in a certain acceleration input range, the measured acceleration is linearly proportional to the change in natural resonant frequency. Therefore, the measurement of the measured acceleration can be achieved by measuring the variation in the natural resonant frequency. However, the high order terms of the acceleration a in the Eq. (4) influences the linearity of the accelerometer scale factor. That is, the linear degree of the accelerometer is determined by the nonlinearity of the change in frequency in terms of \( 1/8\beta^{2} a^{2} \) and its subsequent terms. The influence of higher order terms on \( \Delta \omega \) are negligible by properly designing the value of \( \beta \).

3 Structure design and simulations

In order to realize the measurement of high performance accelerometer by simple and optimized structure design, this paper divides the resonant accelerometer structure into two parts, namely the external frame and the internal structure, as shown in Fig. 2, in which the internal structure includes the mass, resonators and elastic beams.

Fig. 2
figure 2

The resonant accelerometer structure

Full size image

The external frame mainly plays the role of supporting the internal structure, how to avoid the energy of the resonator transferred to the external frame, avoid the external frame’s vibration in the system operating frequency range, are problems that needs to be solved in the external frame design. The internal structure is the main body of the accelerometer, the sensitivity of the entire accelerometer is replaced by the sensitivity of the resonator in design. So in the actual design, establishing the whole structure of mechanical model and mathematical model, getting the relationship between force and frequency characteristics, and obtaining sensitivity formula by analysis of the structure.

3.1 External frame

The core idea of external frame design is that external structural rigidity is much greater than the internal structure, which can be decoupled from the internal structures. Figure 3 shows the structure of external frame, Fig. 4 shows the width of external frame beam. Take the microelements b 1, b 2, on the side of the external frame. When b 1 increases, the equivalent of the microelement of the stiffness k 1 increases, reflected in the characteristics “board” of the external frame. When b 2 increases, the equivalent of the microelement of the stiffness k 2 is reduced, reflected in the characteristics “beam” of the external frame. And b 1, b 2 belong to the width of the beam, so, with b 1, b 2 increases, k 1 , k 2 must have an intersection, and this point is the theoretical optimum width of the beam. The optimal design of external frame parameters was carried out with six sets of structural parameters. Table 1 shows the six sets of structural parameters, Figs. 5, 6, 7, 8, 9 and 10 show the modal simulations of the six structures, we can choose the optimization parameters of the external frame by comparing them.

Fig. 3
figure 3

The structure of the external frame

Full size image
Fig. 4
figure 4

The width of external frame beam

Full size image
Table 1 Structural parameters of the external frame
Full size table
Fig. 5
figure 5

Structure 1 modes

Full size image
Fig. 6
figure 6

Structure 2 modes

Full size image
Fig. 7
figure 7

Structure 3 modes

Full size image
Fig. 8
figure 8

Structure 4 modes

Full size image
Fig. 9
figure 9

Structure 5 modes

Full size image
Fig. 10
figure 10

Structure 6 modes

Full size image

According to the simulation results, structures 3, 4 and 5 are the overall structure of the work with the frame beam width was 10 mm and the resonant beam width were 0.1, 0.2 and 0.3 mm. When the resonant beam width is gradually increased to 2 mm, its stiffness will increase gradually. At this time, the external frame and its stiffness ratio become smaller, resulting in the structure of the first ten modes did not appear working mode but the vibration of the external frame.

Structure 1, 2, 4, 6 are the overall structure of the work with the resonant beam size unchanged and the width of the frame beam were 1, 10 and 20 mm. Because the stiffness is smaller when the width of the external frame are 1 and 2.5 mm, the simulated figures show that the overall structure of the first order mode appears bending mode on each side of the frame, and the bending modes was similar to the beam bending mode, especially when the frame beam width was 1 mm, first ten order modes are not present work mode, at this time the system energy mainly concentrated in the vibration of the external frame. When the width of the frame becomes 20 mm, the first order mode of the whole structure shows that the frame is vibrating with the characteristics of the “board”. It can be seen, although the stiffness of the frame at this time increased, but the frame reflects the “board” characteristics. Therefore, the design of external frame, should ensure that the frame in line with the “beam” characteristics, and increase its stiffness under this condition.

3.2 Internal structure

Normally, the vertical vibration frequency of the system is much higher than the axial vibration frequency, so the effect of the system axial displacement is ignored when the system is modeled. When the internal structure of the resonant accelerometer is displaced in the axial direction of the resonator, the energy dissipates away from the inside of the resonator. Therefore, the appearance of the system vertical vibration should be avoided during the internal structure optimization.

Figure 11 shows the equivalent diagram of the internal structure, Figs. 12, 13, 14, 15, 16 and 17 show the simulations of the vertical vibration frequency from different internal structure parameters, and Table 2 shows the comparison between structural parameters and simulation results. From the results of structure 1–structure 3, it can be seen that the size of the equivalent resonant beam is constant. On the one hand, with the increase of the quality of the proof mass, the coupling from vertical vibration frequency to axial vibration frequency is enhanced, and the proof mass is displaced along the axial direction of the resonator. On the one hand, the increase in proof mass will boost the sensitivity of the system. Thus, the selection of proof mass must weigh the relationship between the resonant beam thickness and proof mass. From the simulated results of structure 4–structure 6, it can be seen that the coupling of the vertical vibration frequency to the axial vibration frequency increases with the decrease of the equivalent resonant beam thickness, that is, the decrease of the stiffness of the beam leads to the displacement of the mass along the axial direction of the resonator, which dissipates energy outwards. Therefore, we should try to ensure that the equivalent resonant beam stiffness is relatively large. The sensitivity formula shows that the smaller the thickness of the resonant beam, the higher of the sensitivity, but too small beam thickness will lead to the emergence of vertical vibration, and narrow the accelerometer range.

Fig. 11
figure 11

Equivalent diagram of the internal structure

Full size image
Fig. 12
figure 12

Structure 1 modes

Full size image
Fig. 13
figure 13

Structure 2 modes

Full size image
Fig. 14
figure 14

Structure 3 modes

Full size image
Fig. 15
figure 15

Structure 4 modes

Full size image
Fig. 16
figure 16

Structure 5 modes

Full size image
Fig. 17
figure 17

Structure 6 modes

Full size image
Table 2 The comparison between structural parameters and simulation results
Full size table

4 Performance simulations

From the above analysis, Table 3 shows the given internal structure parameters. From the analysis of the relationship between accelerometer and frequency, the equation of tension–frequency and pressure–frequency can be obtained, and the sensitivity curve of the whole structure can be obtained. As shown in Fig. 18, the blue line represents the tension–frequency curve and the red line represents the pressure–frequency curve.

Table 3 Internal structure parameters
Full size table
Fig. 18
figure 18

Tension–frequency and pressure–frequency curves

Full size image

In the tension–frequency and pressure–frequency equations, if \( F = \eta \frac{EJ}{{l^{2} }}, \) \( P = \zeta \frac{{\pi^{2} \sqrt {\frac{EJ}{\rho A}} }}{{l^{2} }} \), then the tension–frequency and pressure–frequency equations can be written as:

$$ \begin{aligned} H_{1} & = - \frac{1}{2}\sqrt { - 2\eta + 2\sqrt {\eta^{2} + 4\zeta^{2} \pi^{4} } } \sqrt {2\eta + 2\sqrt {\eta^{2} + 4\zeta^{2} \pi^{4} } } \\ & \quad - \sin \left( {\frac{1}{2}\sqrt { - 2\eta + 2\sqrt {\eta^{2} + 4\zeta^{2} \pi^{4} } } } \right)\sinh \left( {\frac{1}{2}\sqrt { - 2\eta + 2\sqrt {\eta^{2} + 4\zeta^{2} \pi^{4} } } } \right)\eta \\ & \quad + \frac{1}{2}\sqrt { - 2\eta + 2\sqrt {\eta^{2} + 4\zeta^{2} \pi^{4} } } \sqrt {2\eta + 2\sqrt {\eta^{2} + 4\zeta^{2} \pi^{4} } } \\ & \quad \cdot \cos \left( {\frac{1}{2}\sqrt { - 2\eta + 2\sqrt {\eta^{2} + 4\zeta^{2} \pi^{4} } } } \right) \cdot \cosh \left( {\frac{1}{2}\sqrt {2\eta + 2\sqrt {\eta^{2} + 4\zeta^{2} \pi^{4} } } } \right) = 0, \\ \end{aligned} $$
$$ \begin{aligned} H_{y} & = - \frac{1}{2}\sqrt { - 2\eta + 2\sqrt {\eta^{2} + 4\zeta^{2} \pi^{4} } } \sqrt {2\eta + 2\sqrt {\eta^{2} + 4\zeta^{2} \pi^{4} } } \\ & \quad - \sin \left( {\frac{1}{2}\sqrt {2\eta + 2\sqrt {\eta^{2} + 4\zeta^{2} \pi^{4} } } } \right)\sinh \left( {\frac{1}{2}\sqrt { - 2\eta + 2\sqrt {\eta^{2} + 4\zeta^{2} \pi^{4} } } } \right)\eta \\ & \quad + \frac{1}{2}\sqrt {2\eta + 2\sqrt {\eta^{2} + 4\zeta^{2} \pi^{4} } } \sqrt { - 2\eta + 2\sqrt {\eta^{2} + 4\zeta^{2} \pi^{4} } } \\ & \quad \cdot \cos \left( {\frac{1}{2}\sqrt {2\eta + 2\sqrt {\eta^{2} + 4\zeta^{2} \pi^{4} } } } \right) \cdot \cosh \left( {\frac{1}{2}\sqrt { - 2\eta + 2\sqrt {\eta^{2} + 4\zeta^{2} \pi^{4} } } } \right) = 0. \\ \end{aligned} $$

where E is the elastic modulus, J is the moment of inertia, l is the length of the beam, and A is the cross-sectional area of the beam, and \( \eta ,\zeta \) is arbitrary constants.

From \( F_{1} (\eta ,\zeta ) = 0 \), at \( \eta = 0 \), find the approximate solution of \( \zeta = \zeta (\eta ) \), that is, where the Taylor expansion is:

$$ F_{1} (\eta ,\zeta ) = 2.266887764 + 0.02785723822\eta - 0.0003764\eta^{2} + 0.00001441\eta^{3} . $$
(6)

From \( F_{y} (\eta ,\zeta ) = 0 \), at \( \eta = 0 \), find the approximate solution of \( \zeta = \zeta (\eta ) \), that is, where the Taylor expansion is:

$$ F_{y} (\eta ,\zeta ) = 2.266887764 + 0.02785723822\eta - 0.0003764\eta^{2} + 0.00001441\eta^{3} . $$
(7)

Therefore,

$$ F_{1} (\eta ,\zeta ) - F_{y} (\eta ,\zeta ) = 0.0557\eta + 0.0002882\eta^{3} . $$
(8)

Figure 19 shows the \( \zeta - \eta \) relationship curve. From \( \Delta \zeta = \Delta \zeta (\eta ) \), we can see \( \Delta p = \Delta p(F) \), therefore, the sensitivity curve of the overall structure is shown in Fig. 20. Where the solid line is the fitting curve, and its slope represents the sensitivity of the system. To further obtain the linear range of the resonant accelerometer, make the difference between the solid line and the dotted line in Figs. 20, and 21 is obtained. From Fig. 21, if |F| < 5 N, the system linearity is better, suitable for sensor measurement. Thus, the design of the resonant accelerometer range ±25 g and the sensitivity of 272.5 Hz/g can be introduced according to the quality of the proof mass.

Fig. 19
figure 19

The \( \zeta - \eta \) relationship curve

Full size image
Fig. 20
figure 20

The sensitivity curve of overall structure

Full size image
Fig. 21
figure 21

The linear range of the resonant accelerometer

Full size image

5 Conclusions

A resonant accelerometer is designed and analyzed. The device is mainly composed of the external frame and internal structure. The external frame mainly plays the role of supporting the internal structure, internal structure is mainly composed of a single proof mass and two resonators, which provides acceleration measurement using the decoupling resonators separately. The FEM simulations are performed by ANSYS software to verify the feasibility of the resonant accelerometer design. According to the simulation results, the design of external frame, should ensure that the frame in line with the “beam” characteristics and increase its stiffness. The design of internal structure, should ensure that the resonant beam stiffness, sensitivity, vertical vibration and range. The designed resonant accelerometer, if |F| < 5 N, the system linearity is better, suitable for sensor measurement, the range is ±25 g and the sensitivity is 272.5 Hz/g. Although, the above conditions are predicted for the resonant accelerometer, the predictions can be easily translated to other resonant sensors designs.