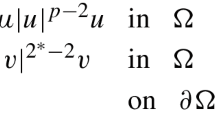Critical Stein–Weiss elliptic systems: symmetry, regularity and asymptotic properties of solutions

Abstract

In this paper, we study the following weighted nonlocal system with critical exponents related to the Stein–Weiss inequality

$$\begin{aligned} \left\{ \begin{aligned} -\Delta&u=\frac{1}{|x|^{\alpha }}\left( \int _{{\mathbb {R}}^N}\frac{v^{p}(y)}{|x-y|^{\mu }|y|^{\alpha }}dy\right) u^{q}, \\ -\Delta&v =\frac{1}{|x|^{\alpha }}\left( \int _{{\mathbb {R}}^N}\frac{u^{q}(y)}{|x-y|^{\mu }|y|^{\alpha }}dy\right) v^{p}, \end{aligned} \right. \end{aligned}$$

By using moving plane arguments in integral form, we obtain symmetry, regularity and asymptotic properties, as well as sufficient conditions for the nonexistence of solutions to the nonlocal Stein–Weiss system.

1 Introduction

Under suitable symmetry hypotheses, notably radial symmetry, classical estimates and embedding properties of function spaces admit substantial improvements. For instance, the following radial estimate of Strauss [32] establishes that all radial functions $u\in H^1({\mathbb {R}}^N)$ ($N\ge 2$) satisfy

$$\begin{aligned} |x|^{(N-1)/2}|u(x)|\le C\,\Vert \nabla u\Vert _{L^2},\quad |x|\ge 1. \end{aligned}$$

This inequality shows that a control on the $H^1$ norm of u gives a pointwise bound and decay of u, which are false in the general case. This phenomenon is quite natural, in the sense that symmetric functions can be regarded as functions defined on lower dimensional manifolds, hence satisfying stronger estimates, extended by the action of some group of symmetries. Radial functions are essentially functions on ${\mathbb {R}}^+$, while the norms on ${\mathbb {R}}^N$ introduce suitable dimensional weights connected to the volume form. Related weighted interpolation inequalities are due to Caffarelli et al. [4].

A central role in the analysis developed in this paper is played by the fractional integral

$$\begin{aligned} (T_\mu \phi )(x)=\int _{{\mathbb {R}}^N}\frac{\phi (y)}{|x-y|^\mu }\,dy,\ \ 0<\mu <N. \end{aligned}$$

Weighted $L^p$ estimates for $T_\mu$ is a fundamental problem of harmonic analysis, with a wide range of applications. Starting from the classical one-dimensional case studied by Hardy and Littlewood, an exhaustive analysis has been made on the admissible classes of weights and ranges of indices (see [30] and the references therein). In the special case of power weights the optimal result is due to Stein and Weiss [31], which established the following weighted Hardy–Littlewood–Sobolev inequality, which is now called the Stein–Weiss inequality.

Proposition 1.1

(Weighted HLS inequality [27]) Let $1<t,r<\infty$, $0<\mu <N$, $\alpha +\beta \ge 0$ and $0<\alpha +\beta +\mu \le N$, $f\in L^{t}({\mathbb {R}}^N)$, and $h\in L^{r}({\mathbb {R}}^N)$. There exists a sharp constant $C_{ t,r,\alpha , \beta ,\mu , N}$ such that

$$\begin{aligned} \int _{{\mathbb {R}}^{N}}\int _{{\mathbb {R}}^N}\frac{f(x)h(y)}{|x|^{\alpha }|x-y|^{\mu }|y|^{\beta }}dxdy\le C(t,r,N,\mu ,\alpha , \beta )\Vert f\Vert _{t}\Vert h\Vert _{r}, \end{aligned}$$

where

$$\begin{aligned} \frac{1}{t}+\frac{1}{r}+\frac{\alpha +\beta +\mu }{N}=2 \end{aligned}$$

and

$$\begin{aligned} 1-\frac{1}{t}-\frac{\mu }{N}<\frac{\alpha }{N}<1-\frac{1}{t}, \end{aligned}$$

where C is independent of f and h. Moreover, for any $h\in L^{r}({\mathbb {R}}^N)$, we have

$$\begin{aligned} \left\| \int _{{\mathbb {R}}^{N}}\frac{h(y)}{|x|^{\alpha }|x-y|^{\mu }|y|^{\beta }}dy\Vert _{s}\le C(s, N,\mu ,\alpha , \beta )\Vert h\right\| _{r}, \end{aligned}$$

where s satisfies $1+\frac{1}{s}=\frac{1}{r}+\frac{\alpha +\beta +\mu }{N}$ and $\frac{\alpha }{N}<\frac{1}{s}<\frac{\alpha +\mu }{N}$.

This inequality reduces to the classical Hardy–Littlewood–Sobolev inequality if $\alpha =\beta =0$. In this case, Lieb [28] applied the Riesz rearrangement inequalities to prove that the best constant for the classical Hardy–Littlewood–Sobolev inequality can be achieved by some extremals. Lieb also classified the solutions of the integral equation

$$\begin{aligned} u(x)=\int _{{\mathbb {R}}^{N}}\frac{u(y)^{\frac{N+\tau }{N-\tau }}}{|x-y|^{N-\tau }}dy,~~x\in {\mathbb {R}}^{N} \end{aligned}$$

(1.1)

as an open problem. Dou and Zhu [12] classified the extremal functions of the reversed HLS inequality and they computed the best constant. In fact, Eq. (1.1) arises as an Euler–Lagrange equation for a functional under a constraint in the context of the Hardy–Littlewood–Sobolev inequality and is closely related to the well-known fractional equation

$$\begin{aligned} (-\Delta )^{\frac{\tau }{2}}u=u^{\frac{N+\tau }{N-\tau }},~~x\in {\mathbb {R}}^{N}. \end{aligned}$$

(1.2)

When $N\ge 3$, $\tau =2$, Eq. (1.2) goes back to

$$\begin{aligned} -\Delta u=u^{\frac{N+2}{N-2}},~~x\in {\mathbb {R}}^{N}, \end{aligned}$$

(1.3)

which is a special case of the Lane–Emden equation

$$\begin{aligned} -\Delta u=u^{p},~~x\in {\mathbb {R}}^{N}. \end{aligned}$$

(1.4)

The classification of the solutions of Eq. (1.3) and the related best Sobolev constant play an important role in the Yamabe problem, which is the prescribed scalar curvature problem on Riemannian manifolds. It is well known that for $0<p<\frac{N+2}{N-2}$, Gidas and Spruck [16] proved that Eq. (1.4) has no positive solutions. This result is optimal in the sense that for any $p\ge \frac{N+2}{N-2}$, there are infinitely many positive solutions to (1.4). Gidas et al. [15], Caffarelli et al. [3] proved the symmetry and uniqueness of the positive solutions respectively. Chen and Li [6], Li [21] simplified the results above as an application of the moving plane method. Wei and Xu [33] generalized the classification of the solutions of the more general Eq. (1.2) with $\tau$ being any even number between 0 and N. Later on, Chen et al. [8] developed the method of moving planes in integral form in order to prove that any critical points of the functional is radially symmetric and they gave a positive answer to the Lieb open problem involving Eq. (1.1). Li [24] also studied the regularity of the locally integrable solution for problem (1.1) and used the moving sphere method to establish the classification of solutions.

For the doubly weighted case, Lieb [28] proved the existence of a sharp constant, provided that either one of r and t equals 2 or $r=t$. For $1<r,t<\infty$ with $\frac{1}{r}+\frac{1}{t}=1$, the sharp constant is given by Beckner in [1, 2]. It is well known that the corresponding Euler-Lagrange equations for the Stein–Weiss inequality are the system of integral equations

$$\begin{aligned} \left\{ \begin{aligned} u(x)&=\int _{{\mathbb {R}}^N}\frac{v^{q}(y)}{|x|^{\alpha }|x-y|^{\mu }|y|^{\beta }}dy,\\ v(x)&=\int _{{\mathbb {R}}^N}\frac{u^{p}(y)}{|x|^{\beta }|x-y|^{\mu }|y|^{\alpha }}dy, \end{aligned} \right. \end{aligned}$$

(1.5)

where $0<p,q<+\infty$, $0<\mu <N$, $\frac{\alpha }{N}<\frac{1}{p+1}<\frac{\mu +\alpha }{N}$ and $\frac{1}{p+1}+\frac{1}{q+1}=\frac{\mu +\alpha +\beta }{N}$. In [10] and [17], the authors obtained the symmetry, monotonicity and the optimal integrability of solutions to problem (1.5). In the special case when $\mu =N-2$, since the integral system (1.5) is equivalent to the nonlinear singular PDE system

$$\begin{aligned} \left\{ \begin{aligned} -\Delta (|x|^{\alpha }u(x))&=\frac{v^{q}(x)}{|x|^{\beta }},\\ -\Delta (|x|^{\beta }v(x))&=\frac{u^{p}(x)}{|x|^{\alpha }}, \end{aligned} \right. \end{aligned}$$

(1.6)

Chen and Li [11] proved the uniqueness of the solutions and classified solutions of problem (1.6) if $\alpha =\beta$ and $p=q$. Next, Lei et al. [20] studied the asymptotic radial symmetry and growth estimates of positive solutions for (1.5). Liu and Lei [26] discussed the nonexistence results for (1.5), and they also considered the existence of positive solutions for the following weighted system with double bounded coefficients

$$\begin{aligned} \left\{ \begin{aligned} u(x)&=c_{1}(x)\int _{{\mathbb {R}}^N}\frac{v^{q}(y)}{|x|^{\alpha }|x-y|^{\mu }|y|^{\beta }}dy,\\ v(x)&=c_{2}(x)\int _{{\mathbb {R}}^N}\frac{u^{p}(y)}{|x|^{\beta }|x-y|^{\mu }|y|^{\alpha }}dy, \end{aligned} \right. \end{aligned}$$

(1.7)

where $0<p,q<+\infty$, $0<\mu +\alpha +\beta <N$, $\frac{\alpha }{N}<\frac{1}{p+1}<\frac{\mu +\alpha }{N}$ and $\frac{\beta }{N}<\frac{1}{q+1}<\frac{\mu +\beta }{N}$.

More generally, Chen et al. [5] established the symmetry and regularity results related to the weighted Hardy–Sobolev type system

$$\begin{aligned} \left\{ \begin{aligned} u(x)&=\int _{{\mathbb {R}}^N}\frac{f_{1}(u(y), v(y))}{|x|^{\alpha }|x-y|^{\mu }|y|^{\beta }}dy,\\ v(x)&=\int _{{\mathbb {R}}^N}\frac{f_{2}(u(y), v(y))}{|x|^{\beta }|x-y|^{\mu }|y|^{\alpha }}dy, \end{aligned} \right. \end{aligned}$$

(1.8)

where

$$\begin{aligned} \begin{aligned} f_{1}(u(y),v(y))&=\lambda _{1}u^{p_{1}}(y)+\mu _{1}v^{q_{1}}(y)+\gamma _{1}u^{\alpha _{1}}(y)v^{\beta _{1}}(y), \\ f_{2}(u(y),v(y))&=\lambda _{2}u^{p_{2}}(y)+\mu _{2}v^{q_{2}}(y)+\gamma _{2}u^{\alpha _{2}}(y)v^{\beta _{2}}(y), \end{aligned} \end{aligned}$$

and nonnegative constants $\lambda _{i}$, $\mu _{i}$, $\gamma _{i}$ $(i=1,2)$ are not equal to zero simultaneously. For the special case of (1.8) corresponding to $\alpha =\beta =0$, there are some contributions on the system of integral equations

$$\begin{aligned} \left\{ \begin{aligned} u(x)&=\int _{{\mathbb {R}}^N}\frac{u^{p}(y) v^{q}(y)}{|x-y|^{N-\gamma }}dy,\\ v(x)&=\int _{{\mathbb {R}}^N}\frac{u^{q}(y) v^{p}(y)}{|x-y|^{N-\gamma }}dy, \end{aligned} \right. \end{aligned}$$

(1.9)

where $0<\gamma <N$, $1\le p,q\le \frac{N+\gamma }{N-\gamma }$ with $p+q\le \frac{N+\gamma }{N-\gamma }$. When $\gamma =2$, Li and Ma [22] proved the symmetry and uniqueness of the positive solutions for (1.9) with critical exponents $p+q=\frac{N+2}{N-2}$. Furthermore, Yu [34] studied the more general integral system

$$\begin{aligned} \left\{ \begin{aligned} u(x)&=\int _{{\mathbb {R}}^N}\frac{f(u(y), v(y))}{|x-y|^{N-\gamma }}dy,\\ v(x)&=\int _{{\mathbb {R}}^N}\frac{g(u(y), v(y))}{|x-y|^{N-\gamma }}dy, \end{aligned} \right. \end{aligned}$$

(1.10)

where f, g satisfy the following monotonicity conditions: $f(s_{1},s_{2})$ and $g(s_{1},s_{2})$ are nondecreasing in $s_{i}$ for fixed $s_{j}$ and, additionally, $\frac{f(s_{1},s_{2})}{s_{1}^{p_{1}}s_{2}^{q_{1}}}$ and $\frac{g(s_{1},s_{2})}{s_{1}^{p_{2}}s_{2}^{q_{2}}}$ are nondecreasing in $s_{i}$ for fixed $s_{j}$ with $p_{i},q_{i}\ge 0$ and $p_{i}+q_{i}=\frac{N+\gamma }{N-\gamma }$.

From the weighted Hardy–Littlewood–Sobolev inequality with $\alpha =\beta$ and $t=r$, assuming that $|u|^{p}\in L^{t}({\mathbb {R}}^N)$, we easily get the following inequality

$$\begin{aligned} \int _{{\mathbb {R}}^{N}}\int _{{\mathbb {R}}^N}\frac{|u(x)|^{p}|u(y)|^{p}}{|x|^{\alpha }|x-y|^{\mu }|y|^{\alpha }}dxdy\le C_{t, N,\mu ,\alpha }\Vert u\Vert _{pt}^{p}\Vert u\Vert _{pt}^{p}, \end{aligned}$$

where t satisfies

$$\begin{aligned} \frac{2}{t}+\frac{2\alpha +\mu }{N}=2. \end{aligned}$$

Furthermore, if $u\in H^{1}({\mathbb {R}}^N)$, from the Sobolev embedding theorems, we have

$$\begin{aligned} 2\le qt\le \frac{2N}{N-2}, \end{aligned}$$

and hence

$$\begin{aligned} 2-\frac{2\alpha +\mu }{N}\le p\le \frac{2N-2\alpha -\mu }{N-2}. \end{aligned}$$

Accordingly, the critical exponent $2_{\alpha ,\mu }^{*}:=\frac{2N-2\alpha -\mu }{N-2}$ ($2_{*\alpha ,\mu }:=2-\frac{2\alpha +\mu }{N}$) is called the upper (lower) critical exponent in the sense of the weighted Hardy–Littlewood–Sobolev inequality. It is obvious that

$$\begin{aligned} \int _{{\mathbb {R}}^{N}}\int _{{\mathbb {R}}^N}\frac{|u(x)|^{2_{\alpha ,\mu }^{*}}|u(y)|^{2_{\alpha ,\mu }^{*}}}{|x|^{\alpha }|x-y|^{\mu }|y|^{\alpha }}dxdy\le C( N,\mu ,\alpha )\Vert u\Vert _{\frac{2N}{N-2}}^{2\cdot 2_{\alpha ,\mu }^{*}}\le C(N,\mu ,\alpha )\Vert \nabla u\Vert _{2}^{2\cdot 2_{\alpha ,\mu }^{*}}.\nonumber \\ \end{aligned}$$

(1.11)

Therefore, we see that the best constant problem of (1.11) is related to the following critical nonlocal Hartree equation

$$\begin{aligned} -\Delta u=\frac{1}{|x|^{\alpha }}\left( \int _{{\mathbb {R}}^N}\frac{|u(y)|^{2_{\alpha ,\mu }^{*}}}{|x-y|^{\mu }|y|^{\alpha }}dy\right) |u|^{2_{\alpha ,\mu }^{*}-2}u,\quad x\in {\mathbb {R}}^N, \end{aligned}$$

(1.12)

which is a special case of the weighted Choquard equation

$$\begin{aligned} -\Delta u=\frac{1}{|x|^{\alpha }}\left( \int _{{\mathbb {R}}^N}\frac{|u(y)|^{p}(y)}{|x-y|^{\mu }|y|^{\alpha }}dy\right) |u|^{p-2}u,\quad x\in {\mathbb {R}}^N. \end{aligned}$$

(1.13)

The classification of solutions to problem (1.13) has attracted a lot of interest recently. If $\alpha =0$, Eq. (1.13) reduces to

$$\begin{aligned} -\Delta u=\left( \int _{{\mathbb {R}}^N}\frac{|u(y)|^{p}}{|x-y|^{\mu }}dy\right) |u|^{p-2}u,\quad x\in {\mathbb {R}}^N. \end{aligned}$$

(1.14)

Miao et al. [29] established the existence of solutions of (1.14) if $p=2$, $\mu =4$ and $N\ge 5$. For the symmetry and uniqueness of solutions for the nonlocal Hartree equation, by using the moving plane method introduced in [8, 9], Liu [25], Lei [19] and Du and Yang [14] classified the positive solutions of problem (1.14) with the critical exponent $\frac{2N-\mu }{N-2}$. Moreover, Du and Yang [14] also proved the nondegeneracy of the unique solutions for the equation when $\mu$ is close to N. As applications, Ding et al. [35] investigated the existence of semiclassical solutions of the critical Choquard equation with critical frequency.

The readers may turn to [18, 19] and the references therein for more backgrounds about the Hartree type equations. For (1.13) with $\alpha \ne 0$, the authors in [13] proved the existence of positive ground state solutions the critical equation by a nonlocal version of the concentration-compactness principle. They also established the regularity of positive solutions and proved the symmetry of these solutions by the moving plane method in integral form [7]. Finally, we recall that Li et al. [23] studied the equation without variational structure and classified the nonpositive solutions.

2 Main results

This paper is devoted to the study of some qualitative properties to the positive solutions of three nonlocal elliptic systems with weighted Stein–Weiss type convolution part. We first consider the following nonlocal system without a variational structure

$$\begin{aligned} \left\{ \begin{aligned} -\Delta&u=\frac{1}{|x|^{\alpha }}\left( \int _{{\mathbb {R}}^N}\frac{v^{p}(y)}{|x-y|^{\mu }|y|^{\alpha }}dy\right) u^{q}, \\ -\Delta&v =\frac{1}{|x|^{\alpha }}\left( \int _{{\mathbb {R}}^N}\frac{u^{q}(y)}{|x-y|^{\mu }|y|^{\alpha }}dy\right) v^{p}, \end{aligned} \right. \end{aligned}$$

(2.1)

where $N\ge 3$, $\alpha \ge 0$, $0<\mu <N$, p, $q>1$ and $0<2\alpha +\mu \le N$.

In Sect. 3, by investigating an equivalent integral system with Riesz potential, we are able to prove some qualitative properties of the positive solutions for problem (2.1). In fact, we obtain the symmetry result for the positive solutions of (2.1) via the moving plane arguments of integral form, which can be easily applied to more complicated equations without maximum principles.

Theorem 2.1

Suppose that $N\ge 3$, $\alpha \ge 0$, $0<\mu <N$, p, $q>1$ and $0<2\alpha +\mu \le N$. If $(u,v)\in L^{s_{0}}({\mathbb {R}}^N)\times L^{s_{0}}({\mathbb {R}}^N)$ is a pair of positive solutions of system (2.1) with $s_{0}=\frac{N(p+q-1)}{N+2-2\alpha -\mu }$, then u and v are radially symmetric and decreasing about the origin.

If $p+q=2\cdot 2_{\alpha ,\mu }^{*}-1$, then $s_{0}=\frac{2N}{N-2}$, and so $(u,v) \in L^{2^{*}}({\mathbb {R}}^N)\times L^{2^{*}}({\mathbb {R}}^N)$. Assuming that p, q lie in some suitable intervals depending on the parameters $\alpha$, $\mu$, then we can apply the regularity lifting lemma [9] to prove that the positive integral solutions possess better integral properties.

Theorem 2.2

Suppose that $N=3$, 4, 5, 6, $\alpha \ge 0$, $0<\mu <N$ and $N-2\le 2\alpha +\mu \le N$. Let $(u,v) \in L^{\frac{2N}{N-2}}({\mathbb {R}}^N)\times L^{\frac{2N}{N-2}}({\mathbb {R}}^N)$ be a pair of positive solutions of system (2.1), where p, q satisfy $\frac{2(N-2\alpha -\mu )}{N-2}\le p,q\le \min \left\{ \frac{4}{N-2},\frac{N+6-2(2\alpha +\mu )}{N-2}\right\}$ and $p+q=2\cdot 2_{\alpha ,\mu }^{*}-1$. Then $(u,v)\in L^{s}({\mathbb {R}}^{N})\times L^{s}({\mathbb {R}}^{N})$ with

$$\begin{aligned} s\in \left( \frac{N}{N-2},+\infty \right) . \end{aligned}$$

By using the symmetry and regularity results obtained above, we establish the asymptotic behaviour of solutions at infinity.

Theorem 2.3

Suppose that $N=3$, 4, 5, 6, $\alpha \ge 0$, $0<\mu <N$, p, $q>1$ and $N-2\le 2\alpha +\mu \le N$. Let $(u,v) \in L^{\frac{2N}{N-2}}({\mathbb {R}}^N)\times L^{\frac{2N}{N-2}}({\mathbb {R}}^N)$ be a pair of positive solutions of system (2.1). If p, q satisfy $p+q=2\cdot 2_{\alpha ,\mu }^{*}-1$ and $\frac{2(N-2\alpha -\mu )}{N-2}\le p,q\le \min \left\{ \frac{4}{N-2}, \frac{N+2+2(N+2-2\alpha -\mu )}{N-2}\right\}$, then the following properties hold.

• (1) If $0\le \alpha <2$, then both u(x) and v(x) are bounded and, moreover, we have u(x), $v(x)\in C^{\infty }({\mathbb {R}}^N-\{0\})$.

• (2) For large |x|, we have $u(x)\backsimeq \frac{C}{|x|^{N-2}}$ and $v(x)\backsimeq \frac{C}{|x|^{N-2}}$.

Next, we are interested in the following nonlocal system with variational structure

$$\begin{aligned} \left\{ \begin{aligned} -\Delta&u=\frac{1}{p|x|^{\alpha }}\left( \int _{{\mathbb {R}}^N}\frac{v^{p}(y)}{|x-y|^{\mu }|y|^{\alpha }}dy\right) u^{q-1}, \\ -\Delta&v =\frac{1}{q|x|^{\alpha }}\left( \int _{{\mathbb {R}}^N}\frac{u^{q}(y)}{|x-y|^{\mu }|y|^{\alpha }}dy\right) v^{p-1}, \end{aligned} \right. \end{aligned}$$

(2.2)

where $N\ge 3$, $\alpha \ge 0$, $0<\mu <N$, p, $q>1$ and $0<2\alpha +\mu \le N$. Notice that system (2.2) becomes (1.13) if $p=q$ and $u=v$, but problem (2.2) has not been well studied if $p\ne q$.

In Sect. 4, we are concerned with the nonexistence of positive solutions to system (2.2), provided that $p+q=2\cdot 2_{\alpha ,\mu }^{*}$, which is called a critical condition. We first prove that system (2.2) has no positive solutions in the subcritical case.

Theorem 2.4

Assume that $N\ge 3$, $\alpha \ge 0$, $0<\mu <N$, p, $q>1$ and $0<2\alpha +\mu \le N$. Let (u, v) $\in W_{loc}^{2,2}({\mathbb {R}}^N)\times W_{loc}^{2,2}({\mathbb {R}}^N)$ be a pair of solutions of (2.2). If $p+q<2\cdot 2_{\alpha ,\mu }^{*}$, then $u\equiv v\equiv 0$.

Analogously to the arguments for problem (2.1), we can also draw the conclusions for the system (2.2), such as symmetry, regularity and asymptotic behavior. Here we shall assume that u, v are integrable solutions belonging to $L^{s_{0}}({\mathbb {R}}^N)$ with $s_{0}=\frac{N(p+q-2)}{N+2-2\alpha -\mu }$.

We establish the following symmetry result.

Theorem 2.5

Suppose that $N\ge 3$, $\alpha \ge 0$, $0<\mu <N$, p, $q\ge 2$ and $0<2\alpha +\mu \le N$. Let $(u,v)\in L^{s_{0}}({\mathbb {R}}^N)\times L^{s_{0}}({\mathbb {R}}^N)$ be a pair of positive solutions of system (2.2) with $s_{0}=\frac{N(p+q-2)}{N+2-2\alpha -\mu }$. Then u and v are radially symmetric and decreasing about the origin.

As we can see, for the critical case $p+q=2\cdot 2_{\alpha ,\mu }^{*}$, we get $(u,v) \in L^{2^{*}}({\mathbb {R}}^N)\times L^{2^{*}}({\mathbb {R}}^N)$. Hence, arguing in the same way as Theorems 2.2 and 2.3, the regularity and decay properties are stated as follows.

Theorem 2.6

Suppose that $N=3$, 4, 5, 6, $\alpha \ge 0$, $0<\mu <N$, p, $q\ge 2$ and $N-2\le 2\alpha +\mu \le N$. Let $(u,v) \in L^{\frac{2N}{N-2}}({\mathbb {R}}^N)\times L^{\frac{2N}{N-2}}({\mathbb {R}}^N)$ be a pair of positive solutions of system (2.2). If p, q satisfy $p+q=2\cdot 2_{\alpha ,\mu }^{*}$ and $\frac{2(N-2\alpha -\mu )}{N-2}\le p-1,q-1\le \min \left\{ \frac{4}{N-2}, \frac{N+2+2(N+2-2\alpha -\mu )}{N-2}\right\}$, then $(u,v)\in L^{s}({\mathbb {R}}^N)\times L^{s}({\mathbb {R}}^N)$ with

$$\begin{aligned} s\in \left( \frac{N}{N-2},+\infty \right) . \end{aligned}$$

Theorem 2.7

Suppose that $N=3$, 4, 5, 6, $\alpha \ge 0$, $0<\mu <N$, p, $q\ge 2$ and $N-2\le 2\alpha +\mu \le N$. Let $(u,v) \in L^{\frac{2N}{N-2}}({\mathbb {R}}^N)\times L^{\frac{2N}{N-2}}({\mathbb {R}}^N)$ be a pair of positive solutions of system (2.2). If p, q satisfy $p+q=2\cdot 2_{\alpha ,\mu }^{*}$ and $\frac{2(N-2\alpha -\mu )}{N-2}\le p-1,q-1\le \min \left\{ \frac{4}{N-2}, \frac{N+2+2(N+2-2\alpha -\mu )}{N-2}\right\}$, then the following properties hold true.

• (1) If $0\le \alpha <2$, then both u(x) and v(x) are bounded and, moreover, we have u, $v\in C^{\infty }({\mathbb {R}}^N-\{0\})$.

• (2) For large |x|, we have $u(x)\backsimeq \frac{C}{|x|^{N-2}}$ and $v(x)\backsimeq \frac{C}{|x|^{N-2}}$.

Finally, we study the following Hamiltonian-type system

$$\begin{aligned} \left\{ \begin{aligned} -\Delta&u=\frac{1}{|x|^{\alpha _{1}}}\left( \int _{{\mathbb {R}}^N}\frac{v^{p}(y)}{|x-y|^{\mu _{1}}|y|^{\alpha _{1}}}dy\right) v^{p-1},\\ -\Delta&v =\frac{1}{|x|^{\alpha _{2}}}\left( \int _{{\mathbb {R}}^N}\frac{u^{q}(y)}{|x-y|^{\mu _{2}}|y|^{\alpha _{2}}}dy\right) u^{q-1}, \end{aligned} \right. \end{aligned}$$

(2.3)

where $N\ge 3$, $0<\mu _{1},\mu _{2}<N$, $\alpha _{1}$, $\alpha _{2}\ge 0$, $0<2\alpha _{1}+\mu _{1}\le N$, $0<2\alpha _{2}+\mu _{2}\le N$ and p, $q>1$.

In the last section, we verify the symmetry of positive solutions of the Hamiltonian system (2.3) with convolution part.

Theorem 2.8

Suppose that $N\ge 3$, $\alpha _{i}\ge 0$, $0<\mu _{i}<N$ and $0<2\alpha _{i}+\mu _{i}\le min\left\{ 4, N\right\}$, $i=1$, 2. If $(u,v)\in D^{1,2}({\mathbb {R}}^N)\times D^{1,2}({\mathbb {R}}^N)$ is a pair of positive solutions of (2.3) and $(p, q)=\left( \frac{2N-2\alpha _{1}-\mu _{1}}{N-2}, \frac{2N-2\alpha _{2}-\mu _{2}}{N-2}\right)$, then u and v are radially symmetric and decreasing about the origin.

An outline of the paper is as follows. In Sect. 3 we mainly focus on the nonlocal Hartree system (2.1). By translating the equation into an equivalent integral system, we apply a regularity lifting lemma to obtain the regularity of the solutions and the moving plane methods in integral form to study the symmetry of the positive solutions. Besides these, the decay at infinity is also shown by careful estimates. In Sect. 4 we will study system (2.2). Firstly, by establishing a Pohožaev identity, we prove a non-existence result. In this part we will also prove the regularity of the solutions by some iterative arguments and singular integral analysis. Finally, we prove the symmetry of solutions for the Hamiltonian system (2.3). This is done by using the moving plane method in integral form.

3 Qualitative properties for the nonlocal system (2.1)

In this section, we discuss the qualitative properties of system (2.1) with the critical condition $p+q=2\cdot 2_{\alpha ,\mu }^{*}-1$, including symmetry, regularity and asymptotic behavior at infinity. It is worth noting that system (2.1) is equivalent to the following integral system in ${\mathbb {R}}^{N}$,

$$\begin{aligned} \left\{ \begin{aligned} z(x)&=\int _{{\mathbb {R}}^N}\frac{v^{p}(y)}{|x|^{\alpha }|x-y|^{\mu }|y|^{\alpha }}dy,\\ h(x)&=\int _{{\mathbb {R}}^N}\frac{u^{q}(y)}{|x|^{\alpha }|x-y|^{\mu }|y|^{\alpha }}dy,\\ u(x)&=R_{N}\int _{{\mathbb {R}}^N}\frac{z(y)u^{q}(y)}{|x-y|^{N-2}}dy,\\ v(x)&=R_{N}\int _{{\mathbb {R}}^N}\frac{h(y)v^{p}(y)}{|x-y|^{N-2}}dy, \end{aligned} \right. \end{aligned}$$

(3.1)

where $R_{N}=\frac{\varGamma (\frac{N-2}{2})}{4\pi ^{\frac{N}{2}}}$.

3.1 Symmetry

In this subsection, we establish the symmetry of the positive solutions for (3.1) by means of the moving plane method in integral forms developed by Chen et al. [8]. We start this part with some basic definitions. For $\lambda \in {{\mathbb {R}}}$, define

$$\begin{aligned} \begin{aligned}&\Sigma _{\lambda }=\left\{ x=(x_{1},\ldots ,x_{n})\ |\ x_{1}<\lambda \right\} ,\quad x^{\lambda }=(2\lambda -x_{1},\ldots ,x_{n}),\\&u_{\lambda }(x)=u(x^{\lambda }),\quad v_{\lambda }(x)=v(x^{\lambda }), \quad z_{\lambda }(x)=z(x^{\lambda }),\quad h_{\lambda }(x)=h(x^{\lambda }), \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} \Sigma _{\lambda }^{u}&=\left\{ x\in \Sigma _{\lambda }\ |\ u(x)> u_{\lambda }(x) \right\} ,\quad \Sigma _{\lambda }^{v}=\left\{ x\in \Sigma _{\lambda }\ |\ v(x)> v_{\lambda }(x) \right\} ,\\ \Sigma _{\lambda }^{z}&=\left\{ x\in \Sigma _{\lambda }\ |\ z(x)> z_{\lambda }(x) \right\} ,\quad \Sigma _{\lambda }^{h}=\left\{ x\in \Sigma _{\lambda }\ |\ h(x)> h_{\lambda }(x) \right\} . \end{aligned} \end{aligned}$$

By straightforward computation we obtain

$$\begin{aligned} \begin{aligned} u(x)=&R_{N}\int _{\Sigma _{\lambda }}\frac{z(y)u^{q}(y)}{|x-y|^{N-2}}dy+R_{N}\int _{{\mathbb {R}}^N-\Sigma _{\lambda }}\frac{z(y)u^{q}(y)}{|x-y|^{N-2}}dy\\ =&R_{N}\int _{\Sigma _{\lambda }}\frac{z(y)u^{q}(y)}{|x-y|^{N-2}}dy+R_{N}\int _{\Sigma _{\lambda }}\frac{z(y^{\lambda })u^{q}(y^{\lambda })}{|x-y^{\lambda }|^{N-2}}dy, \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} u_{\lambda }(x)=&R_{N}\int _{\Sigma _{\lambda }}\frac{z(y)u^{q}(y)}{|x^{\lambda }-y|^{N-2}}dy+R_{N}\int _{{\mathbb {R}}^N-\Sigma _{\lambda }}\frac{z(y)u^{q}(y)}{|x^{\lambda }-y|^{N-2}}dy\\ =&R_{N}\int _{\Sigma _{\lambda }}\frac{z(y)u^{q}(y)}{|x^{\lambda }-y|^{N-2}}dy+R_{N}\int _{\Sigma _{\lambda }}\frac{z(y^{\lambda })u^{q}(y^{\lambda })}{|x^{\lambda }-y^{\lambda }|^{N-2}}dy. \end{aligned} \end{aligned}$$

Since $|x^{\lambda }-y^{\lambda }|=|x-y|$ and $|x^{\lambda }-y|=|x-y^{\lambda }|$, it follows that

$$\begin{aligned} u(x)-u_{\lambda }(x)=R_{N}\int _{\Sigma _{\lambda }}(\frac{1}{|x-y|^{N-2}}-\frac{1}{|x^{\lambda }-y|^{N-2}})(zu^{q}-z_{\lambda }u_{\lambda }^{q})dy, \end{aligned}$$

(3.2)

and

$$\begin{aligned} v(x)-v_{\lambda }(x)=R_{N}\int _{\Sigma _{\lambda }}(\frac{1}{|x-y|^{N-2}}-\frac{1}{|x^{\lambda }-y|^{N-2}})(hv^{p}-h_{\lambda }v_{\lambda }^{p})dy. \end{aligned}$$

(3.3)

For p, $q>1$, we have the following estimates.

Lemma 3.1

Under the assumption of Theorem 2.1, for any $\lambda <0$, there exists a constant $C>0$ such that

$$\begin{aligned}&\Vert u-u_{\lambda }\Vert _{L^{s_{0}}(\Sigma _{\lambda }^{u})}\le C \Vert v\Vert _{L^{s_{0}}(\Sigma _{\lambda }^{u})}^{p}\Vert u\Vert _{L^{s_{0}}(\Sigma _{\lambda }^u)}^{q-1}\Vert u-u_{\lambda }\Vert _{L^{s_{0}}(\Sigma _{\lambda }^{u})}\nonumber \\&\quad +\,C\Vert u\Vert _{L^{s_{0}}(\Sigma _{\lambda }^{u})}^{q}\Vert v\Vert _{L^{s_{0}}(\Sigma _{\lambda }^{v})}^{p-1}\Vert v-v_{\lambda }\Vert _{L^{s_{0}}(\Sigma _{\lambda }^{v})}, \end{aligned}$$

(3.4)

and

$$\begin{aligned}&\Vert v-v_{\lambda }\Vert _{L^{s_{0}}(\Sigma _{\lambda }^{v})}\le C \Vert u\Vert _{L^{s_{0}}(\Sigma _{\lambda }^{v})}^{q}\Vert v\Vert _{L^{s_{0}}(\Sigma _{\lambda }^v)}^{p-1}\Vert v-v_{\lambda }\Vert _{L^{s_{0}}(\Sigma _{\lambda }^{v})}\nonumber \\&\quad +\,C\Vert v\Vert _{L^{s_{0}}(\Sigma _{\lambda }^{v})}^{p}\Vert u\Vert _{L^{s_{0}}(\Sigma _{\lambda }^{u})}^{q-1} \Vert u-u_{\lambda }\Vert _{L^{s_{0}}(\Sigma _{\lambda }^{u})}. \end{aligned}$$

(3.5)

Proof

For any $x\in \Sigma _{\lambda }$, notice $|x^{\lambda }-y|\ge |x-y|$, by using the mean value theorem, from (3.2) and (3.3), we easily deduce

$$\begin{aligned} u(x)-u_{\lambda }(x)\le R_{N}q\int _{\Sigma _{\lambda }^u}\frac{zu^{q-1}(u-u_{\lambda })}{|x-y|^{N-2}}dy+R_{N}\int _{\Sigma _{\lambda }^z}\frac{u^{q}(z-z_{\lambda })}{|x-y|^{N-2}}dy, \end{aligned}$$

and

$$\begin{aligned} v(x)-v_{\lambda }(x)\le R_{N}p\int _{\Sigma _{\lambda }^v}\frac{hv^{p-1}(v-v_{\lambda })}{|x-y|^{N-2}}dy+R_{N}\int _{\Sigma _{\lambda }^h}\frac{v^{p}(h-h_{\lambda })}{|x-y|^{N-2}}dy. \end{aligned}$$

In virtue of $(u,v)\in L^{s_{0}}({\mathbb {R}}^N)\times L^{s_{0}}({\mathbb {R}}^N)$ with $s_{0}=\frac{N(p+q-1)}{N+2-2\alpha -\mu }$, we suppose that $z\in L^{k}({\mathbb {R}}^N)$, $h\in L^{t}({\mathbb {R}}^N)$, where k and t satisfy

$$\begin{aligned} \frac{1}{k}+\frac{q}{s_{0}}=\frac{N+2s_{0}}{Ns_{0}}\quad \text{ and } \quad \frac{1}{t}+\frac{p}{s_{0}}=\frac{N+2s_{0}}{Ns_{0}}. \end{aligned}$$

(3.6)

By applying the HLS inequality and the Hölder inequality, we have

$$\begin{aligned} \begin{aligned} \Vert u-u_{\lambda }\Vert _{{L^{s_{0}}}(\Sigma _{\lambda }^{u})}\le \,&C\Vert zu^{q-1}(u-u_{\lambda })\Vert _{L^{\frac{Ns_{0}}{N+2s_{0}}}(\Sigma _{\lambda }^{u})}+C\Vert u^{q}(z-z_{\lambda })\Vert _{L^{\frac{Ns_{0}}{N+2s_{0}}}(\Sigma _{\lambda }^{z})}\\ \le \,&C\Vert z\Vert _{L^{k}(\Sigma _{\lambda }^{u})}\Vert u\Vert _{L^{s_{0}}(\Sigma _{\lambda }^u)}^{q-1}\Vert u-u_{\lambda }\Vert _{L^{s_{0}}(\Sigma _{\lambda }^{u})}+C\Vert z-z_{\lambda }\Vert _{L^{k}(\Sigma _{\lambda }^z)}\Vert u\Vert _{L^{s_{0}}(\Sigma _{\lambda }^{u})}^{q}. \end{aligned} \end{aligned}$$

(3.7)

From (3.6), we obtain

$$\begin{aligned} \frac{pNk}{N+(N-2\alpha -\mu )k}=s_{0} \quad \text{ and } \quad \frac{qNt}{N+(N-2\alpha -\mu )t}=s_{0}. \end{aligned}$$

Analogously, we have

$$\begin{aligned} \begin{aligned} h(x)-h_{\lambda }(x)&=\int _{\Sigma _{\lambda }}\frac{1}{|x-y|^{\mu }}\left( \frac{u^{q}}{|x|^{\alpha }|y|^{\alpha }}-\frac{u_{\lambda }^{q}}{|x^{\lambda }|^{\alpha }|y^{\lambda }|^{\alpha }}\right) \\&\quad +\frac{1}{|x^{\lambda }-y|^{\mu }}\left( \frac{u_{\lambda }^{q}}{|x|^{\alpha }|y^{\lambda }|^{\alpha }}-\frac{u^{q}}{|x^{\lambda }|^{\alpha }|y|^{\alpha }}\right) dy\\&\le \,\int _{\Sigma _{\lambda }}\frac{1}{|x|^{\alpha }}\left( \frac{1}{|x-y|^{\mu }}-\frac{1}{|x^{\lambda }-y|^{\mu }}\right) \left( \frac{u^{q}}{|y|^{\alpha }}-\frac{u_{\lambda }^{q}}{|y^{\lambda }|^{\alpha }}\right) dy\\&\le \,\int _{\Sigma _{\lambda }^u}\frac{u^{q}-u_{\lambda }^{q}}{|x|^{\alpha }|x-y|^{\mu }|y|^{\alpha }}dy\\&\le \,q\int _{\Sigma _{\lambda }^u}\frac{u^{q-1}(u-u_{\lambda })}{|x|^{\alpha }|x-y|^{\mu }|y|^{\alpha }}dy, \end{aligned} \end{aligned}$$

(3.8)

and

$$\begin{aligned} \begin{aligned} z(x)-z_{\lambda }(x)&=\int _{\Sigma _{\lambda }}\frac{1}{|x-y|^{\mu }}\left( \frac{v^{p}}{|x|^{\alpha }|y|^{\alpha }}-\frac{v_{\lambda }^{p}}{|x^{\lambda }|^{\alpha }|y^{\lambda }|^{\alpha }}\right) \\&\quad +\frac{1}{|x^{\lambda }-y|^{\mu }}\left( \frac{v_{\lambda }^{p}}{|x|^{\alpha }|y^{\lambda }|^{\alpha }}-\frac{v^{p}}{|x^{\lambda }|^{\alpha }|y|^{\alpha }}\right) dy\\&\le \int _{\Sigma _{\lambda }}\frac{1}{|x|^{\alpha }}\left( \frac{1}{|x-y|^{\mu }}-\frac{1}{|x^{\lambda }-y|^{\mu }}\right) \left( \frac{v^{p}}{|y|^{\alpha }}-\frac{v_{\lambda }^{p}}{|y^{\lambda }|^{\alpha }}\right) dy\\&\le \int _{\Sigma _{\lambda }^v}\frac{v^{p}-v_{\lambda }^{p}}{|x|^{\alpha }|x-y|^{\mu }|y|^{\alpha }}dy\\&\le p\int _{\Sigma _{\lambda }^v}\frac{v^{p-1}(v-v_{\lambda })}{|x|^{\alpha }|x-y|^{\mu }|y|^{\alpha }}dy, \end{aligned} \end{aligned}$$

(3.9)

from which we can deduce that

$$\begin{aligned} \Vert h-h_{\lambda }\Vert _{L^{t}(\Sigma _{\lambda }^h)}\le C\Vert u\Vert _{L^{s_{0}}(\Sigma _{\lambda }^{u})}^{q-1}\Vert u-u_{\lambda }\Vert _{L^{s_{0}}(\Sigma _{\lambda }^{u})}, \end{aligned}$$

(3.10)

and

$$\begin{aligned} \Vert z-z_{\lambda }\Vert _{L^{k}(\Sigma _{\lambda }^z)}\le C\Vert v\Vert _{L^{s_{0}}(\Sigma _{\lambda }^{v})}^{p-1}\Vert v-v_{\lambda }\Vert _{L^{s_{0}}(\Sigma _{\lambda }^{v})}. \end{aligned}$$

(3.11)

Additionally, using the weighted HLS inequality again, we have

$$\begin{aligned} \Vert z(x)\Vert _{L^{k}(\Sigma _{\lambda }^{u})}\le C\Vert v^{p}\Vert _{L^{\frac{Nk}{N+(N-2\alpha -\mu )k}}(\Sigma _{\lambda }^{u})}\le C\Vert v\Vert _{L^{s_{0}}(\Sigma _{\lambda }^{u})}^{p}, \end{aligned}$$

(3.12)

and

$$\begin{aligned} \Vert h(x)\Vert _{L^{t}(\Sigma _{\lambda }^{v})}\le C\Vert u^{q}\Vert _{L^{\frac{Nt}{N+(N-2\alpha -\mu )t}}(\Sigma _{\lambda }^{v})}\le C\Vert u\Vert _{L^{s_{0}}(\Sigma _{\lambda }^{v})}^{q}. \end{aligned}$$

(3.13)

We deduce that $z\in L^{k}(\Sigma _{\lambda }^{u})$ and $h\in L^{t}(\Sigma _{\lambda }^{v})$.

Combining (3.11), (3.12) with (3.7), we see that (3.4) holds. Similarly, we obtain

$$\begin{aligned} \begin{aligned} \Vert v-v_{\lambda }\Vert _{{L^{s_{0}}}(\Sigma _{\lambda }^{v})}\le \,&C\Vert hv^{p-1}(v-v_{\lambda })\Vert _{L^{\frac{Ns_{0}}{N+2s_{0}}}(\Sigma _{\lambda }^{v})}+C\Vert v^{p}(h-h_{\lambda })\Vert _{L^{\frac{Ns_{0}}{N+2s_{0}}}(\Sigma _{\lambda }^{h})}\\ \le \,&C\Vert h\Vert _{L^{t}(\Sigma _{\lambda }^{v})}\Vert v\Vert _{L^{s_{0}}(\Sigma _{\lambda }^v)}^{p-1}\Vert v-v_{\lambda }\Vert _{L^{s_{0}}(\Sigma _{\lambda }^{v})}+C\Vert h-h_{\lambda }\Vert _{L^{t}(\Sigma _{\lambda }^h)}\Vert v\Vert _{L^{s_{0}}(\Sigma _{\lambda }^{v})}^{p}. \end{aligned} \end{aligned}$$

(3.14)

Thus, inserting (3.10) and (3.13) into (3.14), we complete the proof. $\square$

Lemma 3.2

Under the assumption of Theorem 2.1, there exists $M>0$ such that for any $\lambda <-M$, we have

$$\begin{aligned} u(x)\le u_{\lambda }(x),\ v(x)\le v_{\lambda }(x) \quad \forall x\in \Sigma _{\lambda }. \end{aligned}$$

(3.15)

Proof

Since u, v are integrable, letting $\lambda \rightarrow -\infty$, we have

$$\begin{aligned}&\Vert v\Vert _{L^{s_{0}}(\Sigma _{\lambda }^{u})}^{p}\Vert u\Vert _{L^{s_{0}}(\Sigma _{\lambda }^u)}^{q-1}\le \frac{1}{2C}, \\&\Vert u\Vert _{L^{s_{0}}(\Sigma _{\lambda }^{v})}^{q}\Vert v\Vert _{L^{s_{0}}(\Sigma _{\lambda }^v)}^{p-1}\le \frac{1}{2C},\\&\Vert u\Vert _{L^{s_{0}}(\Sigma _{\lambda }^{u})}^{q}\Vert v\Vert _{L^{s_{0}}(\Sigma _{\lambda }^{v})}^{p-1} \le \frac{1}{4C}, \end{aligned}$$

and

$$\begin{aligned} \Vert v\Vert _{L^{s_{0}}(\Sigma _{\lambda }^{v})}^{p}\Vert u\Vert _{L^{s_{0}}(\Sigma _{\lambda }^{u})}^{q-1}\le \frac{1}{4C}, \end{aligned}$$

where the constant C is the same as in Lemma 3.1. Hence, inserting those inequalities into (3.4) and (3.5), as $\lambda \rightarrow -\infty$, it follows that

$$\begin{aligned} \Vert u(x)-u_{\lambda }(x)\Vert _{L^{s}(\Sigma _{\lambda }^{u})}=0,\quad \Vert v(x)-v_{\lambda }(x)\Vert _{L^{r}(\Sigma _{\lambda }^{v})}=0, \end{aligned}$$

which shows that $\Sigma _{\lambda }^{u}=\Sigma _{\lambda }^{v}=\emptyset .$ Therefore, there exists $M>0$ such that for any $\lambda <-M$, relation (3.15) holds. $\square$

We now can move the plane $T_{\lambda }=\left\{ x\in {\mathbb {R}}^N|x_{1}=\lambda \right\}$ to the right as long as (3.15) is satisfied. Naturally, denote

$$\begin{aligned} \lambda _{0}=\sup \left\{ \lambda \ | \ u(x)\le u_{\rho }(x),\ v(x)\le v_{\rho }(x),\ x\in \Sigma _{\rho }, \ \rho \le \lambda \right\} . \end{aligned}$$

We observe that $\lambda _{0}<+\infty$.

Next, we deduce the following auxiliary property.

Lemma 3.3

Under the assumption of Theorem 2.1, then for any $\lambda _{0}<0$, we have

$$\begin{aligned} u(x)\equiv u_{\lambda _{0}}(x),\ v(x)\equiv v_{\lambda _{0}}(x) \quad \forall x\in \Sigma _{\lambda _{0}}. \end{aligned}$$

(3.16)

Proof

Suppose that at $\lambda _{0}<0$, there holds $u(x)\le u_{\lambda _{0}}(x)$ and $v(x)\le v_{\lambda _{0}}(x)$, but $u(x)\not \equiv u_{\lambda _{0}}(x)$ or $v(x)\not \equiv v_{\lambda _{0}}(x)$ on $\Sigma _{\lambda _{0}}$.

We claim that there exists $\varepsilon >0$ such that $u(x)\le u_{\lambda }(x)$ and $v(x)\le v_{\lambda }(x)$ on $\Sigma _{\lambda }$ for any $\lambda \in \left[ \lambda _{0},\lambda _{0}+\varepsilon \right)$.

Indeed, for any $\eta >0$, we can choose $R>0$ large enough such that

$$\begin{aligned} \Vert v\Vert _{L^{s_{0}}({\mathbb {R}}^N- B_{R}(0)))}^{p}\Vert u\Vert _{L^{s_{0}}({\mathbb {R}}^N- B_{R}(0)))}^{q-1}\le \frac{\eta }{2} \end{aligned}$$

(3.17)

and

$$\begin{aligned} \Vert u\Vert _{L^{s_{0}}({\mathbb {R}}^N- B_{R}(0)))}^{q}\Vert v\Vert _{L^{s_{0}}({\mathbb {R}}^N- B_{R}(0)))}^{p-1}\le \frac{\eta }{2}. \end{aligned}$$

(3.18)

For such $R>0$ and $\lambda >\lambda _{0}$, we show that the measures of the sets $\Sigma _{\lambda }^{u}\cap B_{R}(0)$ and $\Sigma _{\lambda }^{v}\cap B_{R}(0)$ go to 0 as $\lambda \rightarrow \lambda _{0}$.

Assume that

$$\begin{aligned} u(x)\not \equiv u_{\lambda _{0}}(x) \ \text{ on }\ \Sigma _{\lambda _{0}}. \end{aligned}$$

From (3.8), we obtain

$$\begin{aligned} h(x)-h_{\lambda _{0}}(x)<0 \ \text{ on }\ \Sigma _{\lambda _{0}}. \end{aligned}$$

Thus, by (3.3), we yield

$$\begin{aligned} v(x)- v_{\lambda _{0}}(x)<0\ \text{ on }\ \Sigma _{\lambda _{0}}. \end{aligned}$$

Combining with (3.9), it follows that

$$\begin{aligned} z(x)- z_{\lambda _{0}}(x)<0\ \text{ on }\ \Sigma _{\lambda _{0}}. \end{aligned}$$

From (3.2), we have

$$\begin{aligned} u(x)- u_{\lambda _{0}}(x)<0\ \text{ on }\ \Sigma _{\lambda _{0}}. \end{aligned}$$

Naturally, for any $\delta >0$, we define

$$\begin{aligned} D_{\delta }= & {} \left\{ x\in \Sigma _{\lambda _{0}}\cap B_{R}(0): u_{\lambda _{0}}(x)-u(x)>\delta \right\} , \nonumber \\ E_{\delta }= & {} \left\{ x\in \Sigma _{\lambda _{0}}\cap B_{R}(0): u_{\lambda _{0}}(x)-u(x)\le \delta \right\} , \end{aligned}$$

and

$$\begin{aligned} G_{\lambda }=(\Sigma _{\lambda }-\Sigma _{\lambda _{0}})\cap B_{R}(0). \end{aligned}$$

Obviously, we get

$$\begin{aligned} \lim \limits _{\delta \rightarrow 0}{\mathcal {L}}(E_{\delta })=0, \end{aligned}$$

(3.19)

and

$$\begin{aligned} \lim \limits _{\lambda \rightarrow \lambda _{0}}{\mathcal {L}}(G_{\lambda })=0, \end{aligned}$$

(3.20)

where ${\mathcal {L}}$ is the Lebesgue measure. For any $x \in \Sigma _{\lambda }^{u}\cap D_{\delta }$, since

$$\begin{aligned} u(x)-u_{\lambda }(x)=u(x)-u_{\lambda _{0}}(x)+u_{\lambda _{0}}(x)-u_{\lambda }(x)>0, \end{aligned}$$

we have

$$\begin{aligned} u_{\lambda _{0}}(x)-u_{\lambda }(x)>u_{\lambda _{0}}(x)-u(x)>\delta . \end{aligned}$$

Hence, by the Chebyshev inequality, for fixed $\delta >0$, we obtain that

$$\begin{aligned} {\mathcal {L}}(\Sigma _{\lambda }^{u}\cap D_{\delta })\le \frac{1}{\delta ^{s_{0}}}\int _{\Sigma _{\lambda }^{u}\cap D_{\delta }}|u_{\lambda _{0}}(x)-u_{\lambda }(x)|^{s_{0}}dx\le \frac{1}{\delta ^{s_{0}}}\int _{B_{R}(0)}|u_{\lambda _{0}}(x)-u_{\lambda }(x)|^{s_{0}}dx\rightarrow 0\nonumber \\ \end{aligned}$$

(3.21)

if $\lambda \rightarrow \lambda _{0}$. Notice that

$$\begin{aligned} \Sigma _{\lambda }^{u}\cap B_{R}(0)\subset (\Sigma _{\lambda }^{u}\cap D_{\delta })\cup E_{\delta }\cup G_{\lambda }, \end{aligned}$$

From (3.19)–(3.21), as $\lambda \rightarrow \lambda _{0}$ and $\delta \rightarrow 0$, we can easily get

$$\begin{aligned} {\mathcal {L}}(\Sigma _{\lambda }^{u}\cap B_{R}(0))\rightarrow 0. \end{aligned}$$

(3.22)

Analogously, we obtain

$$\begin{aligned} {\mathcal {L}}(\Sigma _{\lambda }^{v}\cap B_{R}(0))\rightarrow 0. \end{aligned}$$

(3.23)

Combining (3.22), (3.23), (3.17) with (3.18), there exists $\varepsilon >0$ such that for any $\lambda \in [ \lambda _{0},\lambda _{0}+\varepsilon )$,

$$\begin{aligned}&\Vert v\Vert _{L^{s_{0}}(\Sigma _{\lambda }^{u})}^{p}\Vert u\Vert _{L^{s}(\Sigma _{\lambda }^u)}^{q-1}\le \frac{1}{2C},\\&\Vert u\Vert _{L^{s_{0}}(\Sigma _{\lambda }^{v})}^{q}\Vert v\Vert _{L^{s_{0}}(\Sigma _{\lambda }^v)}^{p-1}\le \frac{1}{2C}, \\&\Vert u\Vert _{L^{s_{0}}(\Sigma _{\lambda }^{u})}^{q}\Vert v\Vert _{L^{s_{0}}(\Sigma _{\lambda }^{v})}^{p-1} \le \frac{1}{4C}, \end{aligned}$$

and

$$\begin{aligned} \Vert v\Vert _{L^{s_{0}}(\Sigma _{\lambda }^{v})}^{p}\Vert u\Vert _{L^{s_{0}}(\Sigma _{\lambda }^{u})}^{q-1}\le \frac{1}{4C}, \end{aligned}$$

where the constant C is the same as in Lemma 3.1. By the same arguments as above, we can conclude that $\Sigma _{\lambda }^{u}=\Sigma _{\lambda }^{v}=\emptyset$. Therefore, there exists $\varepsilon >0$ such that $u(x)\le u_{\lambda }(x)$ and $v(x)\le v_{\lambda }(x)$ on $\Sigma _{\lambda }$ for any $\lambda \in \left[ \lambda _{0},\lambda _{0}+\varepsilon \right)$. This contradicts the definition of $\lambda _{0}$, hence we obtain $u(x)\equiv u_{\lambda _{0}}(x)$ on $\Sigma _{\lambda _{0}}$.

Similarly, if $v(x)\not \equiv v_{\lambda _{0}}(x)$ on $\Sigma _{\lambda _{0}}$, which is also a contradiction. The proof is completed. $\square$

3.2 Proof of Theorem 2.1

Clearly, we can also move the plane from $+\infty$ to left, and define

$$\begin{aligned} \lambda _{1}=\inf \left\{ \lambda \ |\ u(x)\le u_{\rho }(x),\ v(x)\le v_{\rho }(x),\ x\in \Sigma _{\rho }^{'},\ \rho \ge \lambda \right\} , \end{aligned}$$

where $\Sigma _{\rho }^{'}=\left\{ x\in {\mathbb {R}}^N|x_{1}>\rho \right\}$.

If $\lambda _{0}=\lambda _{1}\ne 0$, then both u and v are radially symmetric and decreasing about the plane $x_{1}=\lambda _{0}$, which implies $u(x)\equiv u_{\lambda _{0}}(x)$ and $v(x)\equiv v_{\lambda _{0}}(x)$ on $\Sigma _{\lambda _{0}}$. Since $|x-y|<|x^{\lambda _{0}}-y|$ and $|y|>|y^{\lambda _{0}}|$, we deduce from (3.9) that

$$\begin{aligned} z(x)-z_{\lambda _{0}}(x)\le \int _{\Sigma _{\lambda _{0}}}\frac{1}{|x|^{\alpha }}\left( \frac{1}{|x-y|^{\mu }}-\frac{1}{|x^{\lambda _{0}}-y|^{\mu }}\right) \left( \frac{1}{|y|^{\alpha }}-\frac{1}{|y^{\lambda _{0}}|^{\alpha }}\right) v_{\lambda _{0}}^{p}dy<0. \end{aligned}$$

Therefore, we obtain that

$$\begin{aligned} 0=u(x)-u_{\lambda _{0}}(x)=R_{N}\int _{\Sigma _{\lambda _{0}}}(\frac{1}{|x-y|^{N-2}}-\frac{1}{|x^{\lambda _{0}}-y|^{N-2}})(z-z_{\lambda _{0}})u_{\lambda _{0}}^{q}dy<0, \end{aligned}$$

which is impossible. Hence, we get $\lambda _{0}=\lambda _{1}=0$. Notice that the direction of $x_{1}$ is arbitrary, hence u, v are radially symmetric and decreasing about origin. $\square$

3.3 Regularity

Since the integrability and the regularity play an essential role in estimating the decay rates of u(x) if $|x|\rightarrow \infty$, it is necessary for us to discuss the integrability of solutions to system (2.1) by applying the regularity lifting theorem (see in [9, Theorem 3.3.1]) to (2.1).

Lemma 3.4

Let X and Y be Banach spaces with norms $\Vert \cdot \Vert _{X}$ and $\Vert \cdot \Vert _{Y}$, respectively. The subspace $Z=X\cap Y$ of X and Y, is endowed with a new norm by

$$\begin{aligned} \Vert \cdot \Vert _{Z}=\root p \of {\Vert \cdot \Vert _{X}^{p}+\Vert \cdot \Vert _{Y}^{p}}, \quad p\in \left[ 1, \infty \right] . \end{aligned}$$

Suppose that ${\mathscr {T}}$ is a contraction map from Banach space X into itself and from Banach space Y into itself. If $f\in X$ and there exists a function $g\in Z=X\cap Y$ such that $f={\mathscr {T}}f+g$, then f also belongs to Z.

For some constant $A>0$, we define

$$\begin{aligned} u_A(x)=\left\{ \begin{aligned}&u(x),\quad u(x)>A \ or \ |x|>A;\\&0, \quad otherwise. \end{aligned} \right. \end{aligned}$$

and $u_{B}(x)=u(x)-u_{A}(x)$. Similarly, we can define $v_{A}(x)$ and $v_{B}(x)$. Then we define the functions

$$\begin{aligned} F_{u}(m)= & {} R_{N}\int _{{\mathbb {R}}^N}\frac{u^{q}(y)m(y) }{|x-y|^{N-2}}dy,\\ T_{v}(w)= & {} R_{N}\int _{{\mathbb {R}}^N}\frac{v^{p}(y) w(y)}{|x-y|^{N-2}}dy,\\ W_{u}(a)= & {} \int _{{\mathbb {R}}^N}\frac{u^{q-1}(y)a(y) }{|x|^{\alpha }|x-y|^{\mu }|y|^{\alpha }}dy,\\ G_{v}(b)= & {} \int _{{\mathbb {R}}^N}\frac{v^{p-1}(y)b(y) }{|x|^{\alpha }|x-y|^{\mu }|y|^{\alpha }}dy. \end{aligned}$$

Suppose a, $b \in L^{s}({\mathbb {R}}^{N})$, $m\in L^{k}({\mathbb {R}}^{N})$, and $h \in L^{t}({\mathbb {R}}^{N})$. We define the operator

$$\begin{aligned}&{\mathscr {T}}_{A}: L^{s}({\mathbb {R}}^{N})\times L^{s}({\mathbb {R}}^{N})\times L^{k}({\mathbb {R}}^{N})\times L^{t}({\mathbb {R}}^{N})\rightarrow L^{s}({\mathbb {R}}^{N})\times L^{s}({\mathbb {R}}^{N})\times L^{k}({\mathbb {R}}^{N})\times L^{t}({\mathbb {R}}^{N}), \\&{\mathscr {T}}_{A}(a,b,m,w)=(F_{u_{A}}(m),T_{v_{A}}(w),G_{v_{A}}(b),W_{u_{A}}(a)), \end{aligned}$$

with the norm

$$\begin{aligned}&\Vert (a,b,m,w)\Vert _{L^{s}({\mathbb {R}}^{N})\times L^{s}({\mathbb {R}}^{N})\times L^{k}({\mathbb {R}}^{N})\times L^{t}({\mathbb {R}}^{N})}\\&\quad =\Vert a\Vert _{L^{s}({\mathbb {R}}^{N})}+\Vert b\Vert _{L^{s}({\mathbb {R}}^{N})}+\Vert m\Vert _{L^{k}({\mathbb {R}}^{N})}+\Vert w\Vert _{L^{t}({\mathbb {R}}^{N})}. \end{aligned}$$

Hence, we deduce that (u, v, z, h) satisfies the operator equation

$$\begin{aligned} (u,v,z,h)={\mathscr {T}}_{A}(u,v,z,h)+(F_{u_{B}}(z),T_{v_{B}}(h),G_{v_{B}}(v),W_{u_{B}}(u)). \end{aligned}$$

Next, we will obtain the main result of Theorem 2.2 by proving the following two lemmas.

Lemma 3.5

Assume that $p+q=2\cdot 2_{\alpha ,\mu }^{*}-1$ and s, k, t satisfy

$$\begin{aligned} \left\{ \begin{aligned}&s>\frac{N}{N-2},\\&s>\frac{2N}{2N+p(N-2)-2(N+2-2\alpha -\mu )},\\&s>\frac{2N}{2N+q(N-2)-2(N+2-2\alpha -\mu )},\\&2N>[p(N-2)-4]s,\\&2N>[q(N-2)-4]s,\\&\frac{1}{s}-\frac{1}{k}=\frac{q(N-2)-4}{2N},\\&\frac{1}{s}-\frac{1}{t}=\frac{p(N-2)-4}{2N}. \end{aligned} \right. \end{aligned}$$

Then for A sufficiently large, ${\mathscr {T}}_{A}$ is a contraction map from $L^{s}({\mathbb {R}}^{N})\times L^{s}({\mathbb {R}}^{N})\times L^{k}({\mathbb {R}}^{N})\times L^{t}({\mathbb {R}}^{N})$ to itself.

Proof

Since $s>\frac{N}{N-2}$, $2N>[q(N-2)-4]s$ and $\frac{1}{s}-\frac{1}{k}=\frac{q(N-2)-4}{2N}$, by the Hardy–Littlewood–Sobolev inequality and the Hölder inequality, we have

$$\begin{aligned} \begin{aligned} \Vert F_{u_{A}}(m)\Vert _{L^{s}({\mathbb {R}}^N)}\le C\Vert u_{A}^{q}m\Vert _{L^{\frac{Ns}{N+2s}}({\mathbb {R}}^N)} \le C\Vert u_{A}\Vert _{L^{2^{*}}({\mathbb {R}}^N)}^{q}\Vert m\Vert _{L^{k}({\mathbb {R}}^N)}, \end{aligned} \end{aligned}$$

Similarly, from $2N>[p(N-2)-4]s$ and $\frac{1}{s}-\frac{1}{t}=\frac{p(N-2)-4}{2N}$, we get

$$\begin{aligned} \begin{aligned} \Vert T_{v_{A}}(w)\Vert _{L^{s}({\mathbb {R}}^N)}\le C\Vert v_{A}^{p}w\Vert _{L^{\frac{Ns}{N+2s}}({\mathbb {R}}^N)} \le C\Vert v_{A}\Vert _{L^{2^{*}}({\mathbb {R}}^N)}^{p}\Vert w\Vert _{L^{t}({\mathbb {R}}^N)}. \end{aligned} \end{aligned}$$

In addition, notice that $s>\frac{2N}{2N+p(N-2)-2(N+2-2\alpha -\mu )}$ and $s>\frac{2N}{2N+q(N-2)-2(N+2-2\alpha -\mu )}$. Using the weighted HLS inequality and the Hölder inequality, we obtain

$$\begin{aligned} \begin{aligned} \Vert W_{u_{A}}(a)\Vert _{L^{t}({\mathbb {R}}^N)}&\le C\Vert u_{A}^{q-1}a\Vert _{L^{\frac{Nt}{N+(N-2\alpha -\mu )t}}({\mathbb {R}}^N)}\\&\le C\Vert u_{A}^{q-1}a\Vert _{L^{\frac{2Ns}{2N+[2(N+2-2\alpha -\mu )-p(N-2)]s}}({\mathbb {R}}^N)}\\&\le C\Vert u_{A}\Vert _{L^{2^{*}}({\mathbb {R}}^N)}^{q-1}\Vert a\Vert _{L^{s}({\mathbb {R}}^N)}, \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} \Vert G_{v_{A}}(b)\Vert _{L^{k}({\mathbb {R}}^N)}&\le C\Vert v_{A}^{p-1}b\Vert _{L^{\frac{Nk}{N+(N-2\alpha -\mu )k}}({\mathbb {R}}^N)}\\&\le C\Vert v_{A}^{p-1}b\Vert _{L^{\frac{2Ns}{2N+[2(N+2-2\alpha -\mu )-q(N-2)]s}}({\mathbb {R}}^N)}\\&\le C\Vert v_{A}\Vert _{L^{2^{*}}({\mathbb {R}}^N)}^{p-1}\Vert b\Vert _{L^{s}({\mathbb {R}}^N)}. \end{aligned} \end{aligned}$$

By virtue of $u,v\in L^{\frac{2N}{N-2}}({\mathbb {R}}^N)$, we can choose A large enough such that

$$\begin{aligned} C\Vert u_{A}\Vert _{L^{2^{*}}({\mathbb {R}}^N)}^{q-1}<\frac{1}{4}\quad \text{ and }\quad C\Vert v_{A}\Vert _{L^{2^{*}}({\mathbb {R}}^N)}^{p-1}<\frac{1}{4}. \end{aligned}$$

Thus, ${\mathscr {T}}_{A}$ is a contraction map from $L^{s}({\mathbb {R}}^{N})\times L^{s}({\mathbb {R}}^{N})\times L^{k}({\mathbb {R}}^{N})\times L^{t}({\mathbb {R}}^{N})$ to itself. $\square$

Lemma 3.6

Suppose that $3\le N\le 6$, $\alpha \ge 0$, $0<\mu <N$ and $N-2\le 2\alpha +\mu \le N$. Let $(u,v,z,h) \in L^{\frac{2N}{N-2}}({\mathbb {R}}^N)\times L^{\frac{2N}{N-2}}({\mathbb {R}}^N)\times L^{k_{0}}({\mathbb {R}}^N)\times L^{t_{0}}({\mathbb {R}}^N)$ be a set of positive solutions of system (3.1) with $k_{0}=\frac{2N}{4-(q-1)(N-2)}$ and $t_{0}=\frac{2N}{4-(p-1)(N-2)}$, where p, q satisfying $\frac{2(N-2\alpha -\mu )}{N-2}\le p,q\le \min \left\{ \frac{4}{N-2},\frac{N+6-2(2\alpha +\mu )}{N-2}\right\}$ and $p+q=2\cdot 2_{\alpha ,\mu }^{*}-1$. Then $(u,v,z,h)\in L^{s}({\mathbb {R}}^{N})\times L^{s}({\mathbb {R}}^{N})\times L^{k}({\mathbb {R}}^{N})\times L^{t}({\mathbb {R}}^{N})$ with

$$\begin{aligned}&s\in \left( \frac{N}{N-2},+\infty \right) ,\ k\in \left( \frac{2N}{4-(q-2)(N-2)},\frac{2N}{4-q(N-2)}\right) \\&\quad \text{ and } \ t\in \left( \frac{2N}{4-(p-2)(N-2)},\frac{2N}{4-p(N-2)}\right) . \end{aligned}$$

Proof

Firstly, under the assumption of Lemma 3.5, we claim that

$$\begin{aligned} (F_{u_{B}}(z),T_{v_{B}}(h),G_{v_{B}}(v),W_{u_{B}}(u))\in L^{s}({\mathbb {R}}^{N})\times L^{s}({\mathbb {R}}^{N})\times L^{k}({\mathbb {R}}^{N})\times L^{t}({\mathbb {R}}^{N}). \end{aligned}$$

In fact, we know that $|u_{B}|\le A$ and $u_{B}=0$ for $|x|>A$. Following the same estimates as in the proof of the above Lemma, we easily have

$$\begin{aligned} \begin{aligned} \Vert F_{u_{B}}(z)\Vert _{L^{s}({\mathbb {R}}^N)}\le C\Vert u_{B}^{q}z\Vert _{L^{\frac{Ns}{N+2s}}({\mathbb {R}}^N)} \le C\Vert u_{B}^{q}\Vert _{L^{A_{1}}({\mathbb {R}}^N)} \Vert z\Vert _{L^{k_{0}}({\mathbb {R}}^N)}, \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} \Vert T_{v_{B}}(h)\Vert _{L^{s}({\mathbb {R}}^N)}\le C\Vert v_{B}^{p}h\Vert _{L^{\frac{Ns}{N+2s}}({\mathbb {R}}^N)} \le C\Vert v_{B}^{p}\Vert _{L^{A_{2}}({\mathbb {R}}^N)} \Vert h\Vert _{L^{t_{0}}({\mathbb {R}}^N)}, \end{aligned} \end{aligned}$$

where $A_{1}=\frac{2Nsq}{2N+[2(N+2-2\alpha -\mu )-p(N-2)]s}$, $A_{2}=\frac{2Nsp}{2N+[2(N+2-2\alpha -\mu )-q(N-2)]s}$, $k_{0}=\frac{2N}{4-(q-1)(N-2)}$ and $t_{0}=\frac{2N}{4-(p-1)(N-2)}$ satisfy $2N+[2(N+2-2\alpha -\mu )-p(N-2)]s>0$, $2N+[2(N+2-2\alpha -\mu )-q(N-2)]s>0$, $4-(q-1)(N-2)>0$ and $4-(p-1)(N-2)>0$. Moreover, we can get

$$\begin{aligned} \begin{aligned} \Vert W_{u_{B}}(u)\Vert _{L^{t}({\mathbb {R}}^N)}&\le C\Vert u_{B}^{q-1}u\Vert _{L^{\frac{Nt}{N+(N-2\alpha -\mu )t}}({\mathbb {R}}^N)}\\&\le C\Vert u_{B}^{q-1}u\Vert _{L^{\frac{2Ns}{2N+[2(N+2-2\alpha -\mu )-p(N-2)]s}}({\mathbb {R}}^N)}\\&\le C\Vert u_{B}^{q-1}\Vert _{L^{A_{3}}({\mathbb {R}}^N)}\Vert u\Vert _{L^{2^{*}}({\mathbb {R}}^N)}, \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} \Vert G_{v_{B}}(v)\Vert _{L^{k}({\mathbb {R}}^N)}&\le C\Vert v_{B}^{p-1}v\Vert _{L^{\frac{Nk}{N+(N-2\alpha -\mu )k}}({\mathbb {R}}^N)}\\&\le C\Vert v_{B}^{p-1}v\Vert _{L^{\frac{2Ns}{2N+[2(N+2-2\alpha -\mu )-q(N-2)]s}}({\mathbb {R}}^N)}\\&\le C\Vert v_{B}^{p-1}\Vert _{A_{4}}\Vert v\Vert _{L^{2^{*}}({\mathbb {R}}^N)}, \end{aligned} \end{aligned}$$

where $A_{3}=\frac{2Ns(q-1)}{2N+[2(N+2-2\alpha -\mu )-(p+1)(N-2)]s}$, $A_{4}=\frac{2Ns(p-1)}{2N+[2(N+2-2\alpha -\mu )-(q+1)(N-2)]s}$, and we require $2N+[2(N+2-2\alpha -\mu )-(p+1)(N-2)]s>0$ and $2N+[2(N+2-2\alpha -\mu )-(q+1)(N-2)]s>0$. Hence, we have

$$\begin{aligned} (F_{u_{B}}(z),T_{v_{B}}(h),G_{v_{B}}(v),W_{u_{B}}(u))\in L^{s}({\mathbb {R}}^{N})\times L^{s}({\mathbb {R}}^{N})\times L^{k}({\mathbb {R}}^{N})\times L^{t}({\mathbb {R}}^{N}), \end{aligned}$$

which implies ${\mathscr {T}}_{A}$ is also a contraction map from $L^{\frac{2N}{N-2}}({\mathbb {R}}^N)\times L^{\frac{2N}{N-2}}({\mathbb {R}}^N)\times L^{k_{0}}({\mathbb {R}}^N)\times L^{t_{0}}({\mathbb {R}}^N)$ to itself. Write

$$\begin{aligned} X=L^{\frac{2N}{N-2}}({\mathbb {R}}^N)\times L^{\frac{2N}{N-2}}({\mathbb {R}}^N)\times L^{k_{0}}({\mathbb {R}}^N)\times L^{t_{0}}({\mathbb {R}}^N) \end{aligned}$$

and

$$\begin{aligned} Y=L^{s}({\mathbb {R}}^{N})\times L^{s}({\mathbb {R}}^{N})\times L^{k}({\mathbb {R}}^{N})\times L^{t}({\mathbb {R}}^{N}). \end{aligned}$$

Evidently, if s, k and t satisfy

$$\begin{aligned} \left\{ \begin{aligned}&s>\frac{N}{N-2},\\&s>\frac{2N}{2N+p(N-2)-2(N+2-2\alpha -\mu )},\\&s>\frac{2N}{2N+q(N-2)-2(N+2-2\alpha -\mu )},\\&2N>[p(N-2)-4]s,\\&2N>[q(N-2)-4]s,\\&2N+[2(N+2-2\alpha -\mu )-p(N-2)]s>0,\\&2N+[2(N+2-2\alpha -\mu )-q(N-2)]s>0,\\&2N+[2(N+2-2\alpha -\mu )-(p+1)(N-2)]s>0,\\&2N+[2(N+2-2\alpha -\mu )-(q+1)(N-2)]s>0,\\&\frac{1}{s}-\frac{1}{k}=\frac{q(N-2)-4}{2N},\\&\frac{1}{s}-\frac{1}{t}=\frac{p(N-2)-4}{2N}, \end{aligned} \right. \end{aligned}$$

(3.24)

we deduce that $(u,v,z,h)\in L^{s}({\mathbb {R}}^{N})\times L^{s}({\mathbb {R}}^{N})\times L^{k}({\mathbb {R}}^{N})\times L^{t}({\mathbb {R}}^{N})$ by the regularity lifting theorem. From (3.24), if $\frac{1}{s}-\frac{1}{k}=\frac{q(N-2)-4}{2N}$ , $\frac{1}{s}-\frac{1}{t}=\frac{p(N-2)-4}{2N}$, then s, k, t should satisfy

$$\begin{aligned} \left\{ \begin{aligned}&\frac{N}{N-2}\ge \frac{2N}{2N+p(N-2)-2(N+2-2\alpha -\mu )},\\&\frac{N}{N-2}\ge \frac{2N}{2N+q(N-2)-2(N+2-2\alpha -\mu )},\\&p(N-2)-4\le 0,\\&q(N-2)-4\le 0,\\&2(N+2-2\alpha -\mu )-p(N-2)\ge 0,\\&2(N+2-2\alpha -\mu )-q(N-2)\ge 0,\\&2(N+2-2\alpha -\mu )-(p+1)(N-2)\ge 0,\\&2(N+2-2\alpha -\mu )-(q+1)(N-2)\ge 0. \end{aligned} \right. \end{aligned}$$

More accurately, we deduce that if p, q satisfy $\frac{2(N-2\alpha -\mu )}{N-2}<p,q\le min\left\{ \frac{4}{N-2},\right. \left. \frac{N+6-2(2\alpha +\mu )}{N-2}\right\}$, then $(u,v,z,h)\in L^{s}({\mathbb {R}}^{N})\times L^{s}({\mathbb {R}}^{N})\times L^{k}({\mathbb {R}}^{N})\times L^{t}({\mathbb {R}}^{N})$ with

$$\begin{aligned}&s\in \left( \frac{N}{N-2},+\infty \right) ,\ k\in \left( \frac{2N}{4-(q-2)(N-2)},\frac{2N}{4-q(N-2)}\right) \\&\quad \text{ and } \ t\in \left( \frac{2N}{4-(p-2)(N-2)},\frac{2N}{4-p(N-2)}\right) . \end{aligned}$$

The proof is now complete. $\square$

3.4 Decay

In this part, we will show the decay rate of the solutions of the critical weighted Hartree system (2.1).

3.5 Proof of Theorem 2.3

We first prove that $|x|^{\alpha }h(x)\in L^{\infty }({\mathbb {R}}^{N})$. It is obvious that

$$\begin{aligned} |x|^{\alpha }h(x)=\int _{{\mathbb {R}}^{N}}\frac{u^{q}(y)}{|x-y|^{\mu }|y|^{\alpha }}dy. \end{aligned}$$

Thus, for any $r>0$, we obtain

$$\begin{aligned} ||x|^{\alpha }h(x)|\le \int _{B_{r}(0)}\frac{|u(y)|^{q}}{|x-y|^{\mu }|y|^{\alpha }}dy+\int _{{\mathbb {R}}^{N}-B_{r}(0)}\frac{|u(y)|^{q}}{|x-y|^{\mu }|y|^{\alpha }}dy. \end{aligned}$$

(3.25)

On the one hand, for $x\in {\mathbb {R}}^{N}-B_{2r}(0)$, we have $|x-y|>|y|$, we have

$$\begin{aligned} \begin{aligned} \int _{B_{r}(0)}\frac{|u(y)|^{q}}{|x-y|^{\mu }|y|^{\alpha }}dy&<\int _{B_{r}(0)}\frac{|u(y)|^{q}}{|y|^{\mu +\alpha }}dy\\&\le \Vert u\Vert ^{q}_{L^{\frac{qk}{k-1}}(B_{r}(0))} \left\| \frac{1}{|y|^{\mu +\alpha }}\right\| _{L^{k}(B_{r}(0))}<\infty , \end{aligned} \end{aligned}$$

where $1<k<min\left\{ \frac{N}{N-q(N-2)}, \frac{N}{\mu +\alpha }\right\}$ if $N-q(N-2)>0$, while $1<k< \frac{N}{\mu +\alpha }$ if $N-q(N-2)\le 0$. For $x\in B_{2r}(0)$, we have

$$\begin{aligned} \begin{aligned} \int _{B_{r}(0)}\frac{|u(y)|^{q}}{|x-y|^{\mu }|y|^{\alpha }}dy&\le \int _{B_{r}(0)}\frac{|u(y)|^{q}}{|y|^{\mu +\alpha }}dy +\int _{B_{3r}(x)}\frac{|u(y)|^{q}}{|x-y|^{\mu +\alpha }}dy<\infty . \end{aligned} \end{aligned}$$

Thus, we can obtain that

$$\begin{aligned} \int _{B_{r}(0)}\frac{|u(y)|^{q}}{|x-y|^{\mu }|y|^{\alpha }}dy<\infty . \end{aligned}$$

(3.26)

On the other hand,

$$\begin{aligned}&\int _{{\mathbb {R}}^{N}-B_{r}(0)}\frac{|u(y)|^{q}}{|x-y|^{\mu }|y|^{\alpha }}dy \\&\quad =\int _{({\mathbb {R}}^{N}-B_{r}(0))\cap B_{r}(x)}\frac{|u(y)|^{q}}{|x-y|^{\mu }|y|^{\alpha }}dy +\int _{({\mathbb {R}}^{N}-B_{r}(0))\cap ({\mathbb {R}}^{N}-B_{r}(x))}\frac{|u(y)|^{q}}{|x-y|^{\mu }|y|^{\alpha }}dy\\&\quad :=Q_{1}+Q_{2}. \end{aligned}$$

As in the preceding estimates, we have

$$\begin{aligned} \begin{aligned} Q_{1}=\int _{({\mathbb {R}}^{N}-B_{r}(0))\cap B_{r}(x)}\frac{|u(y)|^{q}}{|x-y|^{\mu }|y|^{\alpha }}dy&\le \frac{1}{r^{\alpha }}\int _{({\mathbb {R}}^{N}-B_{r}(0))\cap B_{r}(x)}\frac{|u(y)|^{q}}{|x-y|^{\mu }}dy\\&\le \frac{1}{r^{\alpha }}\int _{B_{r}(x)}\frac{|u(y)|^{q}}{|x-y|^{\mu }}dy\\&\le \frac{1}{r^{\alpha }}\Vert u\Vert ^{q}_{L^{\frac{qk}{k-1}}(B_{r}(x))} \left\| \frac{1}{|y|^{\mu }}\right\| _{L^{k}(B_{r}(0))}<\infty , \end{aligned} \end{aligned}$$

where $1<k<\min \left\{ \frac{N}{N-q(N-2)}, \frac{N}{\mu }\right\}$ if $N-q(N-2)>0$, while $1<k< \frac{N}{\mu }$ if $N-q(N-2)\le 0$.

We observe that

$$\begin{aligned} \begin{aligned} Q_{2}=\int _{({\mathbb {R}}^{N}-B_{r}(0))\cap ({\mathbb {R}}^{N}-B_{r}(x))}\frac{|u(y)|^{q}}{|x-y|^{\mu }|y|^{\alpha }}dy&\le \frac{1}{r^{\mu }}\int _{{\mathbb {R}}^{N}-B_{r}(0)}\frac{|u(y)|^{q}}{|y|^{\alpha }}dy\\&\le \frac{1}{r^{\mu }}\Vert u\Vert ^{q}_{L^\frac{qk}{k-1}({\mathbb {R}}^{N}-B_{r}(0))} \left\| \frac{1}{|y|^{\alpha }}\right\| _{L^{k}({\mathbb {R}}^{N}-B_{r}(0))}<\infty , \end{aligned} \end{aligned}$$

where $\frac{N}{\alpha }\le k< \frac{N}{N-q(N-2)}$ if $N-q(N-2)>0$, while $k\ge \frac{N}{\alpha }$ if $N-q(N-2)\le 0$. Therefore, we get

$$\begin{aligned} \int _{{\mathbb {R}}^{N}-B_{r}(0)}\frac{|u(y)|^{q}}{|x-y|^{\mu }|y|^{\alpha }}dy<\infty . \end{aligned}$$

(3.27)

By (3.25), (3.26), (3.27), we can conclude that

$$\begin{aligned} |x|^{\alpha }h(x)\in L^{\infty }({\mathbb {R}}^{N}). \end{aligned}$$

(3.28)

Secondly, we claim that $v(x)\in L^{\infty }({\mathbb {R}}^{N})$. From (3.1) and (3.28), we have

$$\begin{aligned} |v(x)|\le \int _{{\mathbb {R}}^{N}}\frac{|y|^{\alpha }|h(y)||v(y)|^{p}}{|x-y|^{N-2}|y|^{\alpha }}dy \le |||x|^{\alpha }h(x)||_{L^{\infty }({\mathbb {R}}^{N})}\int _{{\mathbb {R}}^{N}}\frac{|v(y)|^{p}}{|x-y|^{N-2}|y|^{\alpha }}dy.\nonumber \\ \end{aligned}$$

(3.29)

For any $r>0$, we decompose as follows

$$\begin{aligned} \int _{{\mathbb {R}}^{N}}\frac{|v(y)|^{p}}{|x-y|^{N-2}|y|^{\alpha }}dy =\int _{B_{r}(0)}\frac{|v(y)|^{p}}{|x-y|^{N-2}|y|^{\alpha }}dy +\int _{{\mathbb {R}}^{N}-B_{r}(0)}\frac{|v(y)|^{p}}{|x-y|^{N-2}|y|^{\alpha }}dy.\nonumber \\ \end{aligned}$$

(3.30)

On the one hand, for $x\in {\mathbb {R}}^{N}-B_{2r}(0)$,

$$\begin{aligned} \begin{aligned} \int _{B_{r}(0)}\frac{|v(y)|^{p}}{|x-y|^{N-2}|y|^{\alpha }}dy&<\int _{B_{r}(0)}\frac{|v(y)|^{p}}{|y|^{N-2+\alpha }}dy\\&\le \Vert v\Vert ^{p}_{L^{\frac{pk}{k-1}}(B_{r}(0))} \left\| \frac{1}{|y|^{N-2+\alpha }}\right\| _{L^{k}(B_{r}(0))}<\infty , \end{aligned} \end{aligned}$$

where $1<k<\min \left\{ \frac{N}{N-p(N-2)}, \frac{N}{N-2+\alpha }\right\}$ if $N-p(N-2)>0$, while $1<k< \frac{N}{N-2+\alpha }$ if $N-p(N-2)\le 0$. However, for $x\in B_{2r}(0)$,

$$\begin{aligned} \begin{aligned} \int _{B_{r}(0)}\frac{|v(y)|^{p}}{|x-y|^{N-2}|y|^{\alpha }}dy&\le \int _{B_{r}(0)}\frac{|v(y)|^{p}}{|y|^{N-2+\alpha }}dy +\int _{B_{3r}(x)}\frac{|v(y)|^{p}}{|x-y|^{N-2+\alpha }}dy<\infty . \end{aligned} \end{aligned}$$

Consequently, we have

$$\begin{aligned} \int _{B_{r}(0)}\frac{|v(y)|^{p}}{|x-y|^{N-2}|y|^{\alpha }}dy<\infty . \end{aligned}$$

(3.31)

On the other hand,

$$\begin{aligned} \begin{aligned}&\int _{{\mathbb {R}}^{N}-B_{r}(0)}\frac{|v(y)|^{p}}{|x-y|^{N-2}|y|^{\alpha }}dy\\&\quad =\int _{({\mathbb {R}}^{N}-B_{r}(0))\cap B_{r}(x)}\frac{|v(y)|^{p}}{|x-y|^{N-2}|y|^{\alpha }}dy\\&\qquad +\int _{({\mathbb {R}}^{N}-B_{r}(0))\cap ({\mathbb {R}}^{N}-B_{r}(x))}\frac{|v(y)|^{p}}{|x-y|^{N-2}|y|^{\alpha }}dy:=P_{1}+P_{2}. \end{aligned} \end{aligned}$$

(3.32)

Clearly,

$$\begin{aligned} \begin{aligned} P_{1}=\int _{({\mathbb {R}}^{N}-B_{r}(0))\cap B_{r}(x)}\frac{|v(y)|^{p}}{|x-y|^{N-2}|y|^{\alpha }}dy&\le \frac{1}{r^{\alpha }}\int _{B_{r}(x)}\frac{|v(y)|^{p}}{|x-y|^{N-2}}dy<\infty . \end{aligned} \end{aligned}$$

(3.33)

In addition, we also have

$$\begin{aligned} \begin{aligned} P_{2}&=\int _{({\mathbb {R}}^{N}-B_{r}(0))\cap ({\mathbb {R}}^{N}-B_{r}(x))}\frac{|v(y)|^{p}}{|x-y|^{N-2}|y|^{\alpha }}dy\\&\le \int _{{\mathbb {R}}^{N}-B_{r}(0)}\frac{|v(y)|^{p}}{|y|^{N-2+\alpha }}dy +\int _{{\mathbb {R}}^{N}-B_{r}(x)}\frac{|v(y)|^{p}}{|x-y|^{N-2+\alpha }}dy. \end{aligned} \end{aligned}$$

Since

$$\begin{aligned} \begin{aligned} \int _{{\mathbb {R}}^{N}-B_{r}(0)}\frac{|v(y)|^{p}}{|y|^{N-2+\alpha }}dy&\le \Vert v\Vert ^{p}_{L^{\frac{pk}{k-1}}({\mathbb {R}}^{N}-B_{r}(0))} \left\| \frac{1}{|y|^{N-2+\alpha }}\right\| _{L^{k}({\mathbb {R}}^{N}-B_{r}(0))}<\infty , \end{aligned} \end{aligned}$$

where $\frac{N}{N-2+\alpha }<k<\frac{N}{N-p(N-2)}$ if $N-p(N-2)>0$, while $k>\frac{N}{N-2+\alpha }$ if $N-p(N-2)\le 0$, from which we conclude that

$$\begin{aligned} P_{2}=\int _{({\mathbb {R}}^{N}-B_{r}(0))\cap ({\mathbb {R}}^{N}-B_{r}(x))}\frac{|v(y)|^{p}}{|x-y|^{N-2}|y|^{\alpha }}dy<\infty . \end{aligned}$$

(3.34)

Combining with (3.32)–(3.34), we obtain

$$\begin{aligned} \int _{{\mathbb {R}}^{N}-B_{r}(0)}\frac{|v(y)|^{p}}{|x-y|^{N-2}|y|^{\alpha }}dy<\infty . \end{aligned}$$

(3.35)

Through (3.29), (3.30), (3.31), (3.35), we deduce that

$$\begin{aligned} v(x)\in L^{\infty }({\mathbb {R}}^{N}). \end{aligned}$$

Finally, we prove that u(x), $v(x)\in C^{\infty }({\mathbb {R}}^N-\{0\})$. For any $x\in {\mathbb {R}}^{N}-\{0\}$, we decompose v(x) as follows

$$\begin{aligned} v(x)=\int _{B_{2r}(x)}\frac{h(y)v^{p}(y)}{|x-y|^{N-2}}dy+\int _{{\mathbb {R}}^{N}-B_{2r}(x)}\frac{h(y)v^{p}(y)}{|x-y|^{N-2}}dy:=K_{1}+K_{2}, \end{aligned}$$

where $r<\frac{|x|}{2}$. It has been established in [27, Chapter 10] that for any $\delta <2$,

$$\begin{aligned} K_{1}=\int _{B_{2r}(x)}\frac{h(y)v^{p}(y)}{|x-y|^{N-2}}dy\in C^{\delta }({\mathbb {R}}^{N}-\{0\}). \end{aligned}$$

(3.36)

If we can obtain

$$\begin{aligned} K_{2}=\int _{{\mathbb {R}}^{N}-B_{2r}(x)}\frac{h(y)v^{p}(y)}{|x-y|^{N-2}}dy\in C^{\infty }({\mathbb {R}}^{N}-\{0\}), \end{aligned}$$

then together with (3.36) we can conclude that $v(x)\in C^{\delta }({\mathbb {R}}^{N}-\{0\})$. Thus, combining the classical bootstrap technique [27, Chapter 10], we prove that $v(x)\in C^{\infty }({\mathbb {R}}^{N}-\{0\})$.

In the following we will show that

$$\begin{aligned} K_{2}\in C^{\infty }({\mathbb {R}}^{N}-\{0\}). \end{aligned}$$

Define

$$\begin{aligned} \psi (x)=\int _{{\mathbb {R}}^{N}}\frac{h(y)v^{p}(y)}{|x-y|^{N-2}}\chi _{\{{\mathbb {R}}^{N}-B_{2r}(x)\}}dy. \end{aligned}$$

We claim that

$$\begin{aligned} \psi (x)\in C^{1}({\mathbb {R}}^{N}-\{0\}). \end{aligned}$$

Indeed, for any small $t<r$, $0<\theta <1$ and if $e_{i}$ is the unit ith vector, then

$$\begin{aligned} \begin{aligned} \left| \frac{\psi (x+te_{i})-\psi (x)}{t}\right|&\le \frac{1}{|t|}\int _{{\mathbb {R}}^{N}}\left| \frac{h(y)v^{p}(y)}{|x+te_{i}-y|^{N-2}}\chi _{\{{\mathbb {R}}^{N}-B_{2r}(x+te_{i})\}} -\frac{h(y)v^{p}(y)}{|x-y|^{N-2}}\chi _{\{{\mathbb {R}}^{N}-B_{2r}(x)\}}\right| dy\\&\le C\int _{{\mathbb {R}}^{N}}\frac{|h(y)||v(y)|^{p}}{|x+\theta te_{i}-y|^{N-1}}\chi _{\{{\mathbb {R}}^{N}-B_{2r}(x+\theta te_{i})\}}dy\\&\le C\int _{B_{r}(0)}\frac{|h(y)||v(y)|^{p}}{|x-y|^{N-1}}dy +C\int _{{\mathbb {R}}^{N}-B_{r}(x)- B_{r}(0)}\frac{|h(y)||v(y)|^{p}}{|x-y|^{N-1}}dy.\\ \end{aligned} \end{aligned}$$

Since $|x|^{\alpha }h(x)$, $v(x)\in L^{\infty }({\mathbb {R}}^N)$, it follows that

$$\begin{aligned} \begin{aligned} \int _{B_{r}(0)}\frac{|h(y)||v(y)|^{p}}{|x-y|^{N-1}}dy&\le \frac{1}{r^{N-1}}|||x|^{\alpha }h||_{L^{\infty }({\mathbb {R}}^{N})}||v||^{p}_{L^{\infty }({\mathbb {R}}^{N})}\int _{B_{r}(0)}\frac{1}{|y|^{\alpha }}dy<\infty . \end{aligned} \end{aligned}$$

(3.37)

Clearly, we also see that

$$\begin{aligned} \begin{aligned}&\int _{{\mathbb {R}}^{N}-B_{r}(x)- B_{r}(0)}\frac{|h(y)||v(y)|^{p}}{|x-y|^{N-1}}dy\\&\quad \le |||x|^{\alpha }h||_{L^{\infty }({\mathbb {R}}^{N})} \int _{{\mathbb {R}}^{N}-B_{r}(0)}\frac{|v(y)|^{p}}{|y|^{N-1+\alpha }}dy +|||x|^{\alpha }h||_{L^{\infty }({\mathbb {R}}^{N})} \int _{{\mathbb {R}}^{N}-B_{r}(x)}\frac{|v(y)|^{p}}{|x-y|^{N-1+\alpha }}dy. \end{aligned} \end{aligned}$$

Then by the regularity result we have

$$\begin{aligned} \begin{aligned} \int _{{\mathbb {R}}^{N}-B_{r}(0)}\frac{|v(y)|^{p}}{|y|^{N-1+\alpha }}dy&\le \Vert v(y)\Vert ^{p}_{L^{\frac{pk}{k-1}}({\mathbb {R}}^{N}-B_{r}(0))} \left\| \frac{1}{|y|^{N-1+\alpha }}\right\| _{L^{k}({\mathbb {R}}^{N}-B_{r}(0))}<\infty , \end{aligned} \end{aligned}$$

where the parameters $\alpha$, $\mu$, k satisfy one of following four cases:

• (1) if $N-p(N-2)>0$, $\alpha \le 1$, then $\frac{N}{N-1+\alpha }<k<\frac{N}{N-p(N-2)}$;

• (2) if $N-p(N-2)>0$, $1<\alpha <2$, then $1<k<\frac{N}{N-p(N-2)}$;

• (3) if $N-p(N-2)\le 0$, $\alpha \le 1$, then $k>\frac{N}{N-1+\alpha }$;

• (4) if $N-p(N-2)\le 0$, $1<\alpha <2$, then $k>1$.

Therefore we can deduce that

$$\begin{aligned} \int _{{\mathbb {R}}^{N}-B_{r}(x)- B_{r}(0)}\frac{|h(y)||v(y)|^{p}}{|x-y|^{N-1}}dy<\infty . \end{aligned}$$

(3.38)

Thus, from (3.37), (3.38) and the Lebesgue dominated convergence theorem, we can conclude that $\psi (x)\in C^{1}({\mathbb {R}}^{N}-\{0\})$. Repeating the above process, we can deduce $\psi (x)\in C^{\infty }({\mathbb {R}}^{N}-\{0\})$, which implies $K_{2}\in C^{\infty }({\mathbb {R}}^{N}-\{0\})$, so that $v(x)\in C^{\infty }({\mathbb {R}}^N-\{0\})$. Similarly, we have $|x|^{\alpha }z(x)\in L^{\infty }({\mathbb {R}}^N)$. Therefore, we can also obtain $u(x)\in L^{\infty }({\mathbb {R}}^N)$ and $u(x)\in C^{\infty }({\mathbb {R}}^N-\{0\})$.

Write $A=R_{N}\int _{{\mathbb {R}}^{N}} z(y)u^{q}(y)dy$. From Lemma 3.6, we have $(u,v,z,h)\in L^{s}({\mathbb {R}}^N)\times L^{s}({\mathbb {R}}^N)\times L^{k}({\mathbb {R}}^N)\times L^{t}({\mathbb {R}}^N)$, where s, k and t satisfy

$$\begin{aligned}&\frac{1}{s}\in \left( 0, \frac{N-2}{N}\right) , \ \frac{1}{k}\in \left( \frac{4-q(N-2)}{2N},\frac{2N-q(N-2)}{2N}\right) \\&\quad \text{ and } \ \frac{1}{t}\in \left( \frac{4-p(N-2)}{2N},\frac{2N-p(N-2)}{2N}\right) . \end{aligned}$$

We can take

$$\begin{aligned} \frac{1}{s}=\frac{N-2}{2N}+\frac{\varepsilon }{2Nq}\ \text{ and }\ \frac{1}{k}=\frac{2N-q(N-2)-\varepsilon }{2N}\ \text{ such } \text{ that }\ \frac{q}{s}+\frac{1}{k}=1, \end{aligned}$$

where $\varepsilon >0$ sufficiently small. Applying the Hölder inequality, we have

$$\begin{aligned} A\le R_{N}\Vert u\Vert _{s}^{q}\Vert z\Vert _{k}<\infty . \end{aligned}$$

For fixed $R>0$,

$$\begin{aligned} \begin{aligned} |x|^{N-2}u(x)-A=&R_{N}\int _{{\mathbb {R}}^{N}}\left( \frac{|x|^{N-2}}{|x-y|^{N-2}}-1\right) z(y)u^{q}(y)dy\\ =&R_{N}\int _{B_{R}(0)}\left( \frac{|x|^{N-2}}{|x-y|^{N-2}}-1\right) z(y)u^{q}(y)dy\\&+R_{N}\int _{{\mathbb {R}}^N - B_{R}(0)}\left( \frac{|x|^{N-2}}{|x-y|^{N-2}}-1\right) z(y)u^{q}(y)dy\\ :=&M_{1}+M_{2}. \end{aligned} \end{aligned}$$

For large |x|, by the Lebesgue dominated convergence theorem and

$$\begin{aligned} |M_{1}|\le R_{N} \int _{B_{R}(0)}|\frac{|x|^{N-2}}{|x-y|^{N-2}}-1|z(y)u^{q}(y)dy\le C\int _{B_{R}(0)}z(y)u^{q}(y)dy<\infty , \end{aligned}$$

we can see that $\lim \limits _{|x|\rightarrow \infty }|M_{1}|=0$.

Decompose $M_{2}$ into two parts by

$$\begin{aligned} M_{21}=R_{N}\int _{({\mathbb {R}}^N - B_{R}(0))- B_{\frac{|x|}{2}}(x)}\frac{|x|^{N-2}}{|x-y|^{N-2}}z(y)u^{q}(y)dy \end{aligned}$$

and

$$\begin{aligned} M_{22}=R_{N}\int _{B_{\frac{|x|}{2}}(x)}\frac{|x|^{N-2}}{|x-y|^{N-2}}z(y)u^{q}(y)dy. \end{aligned}$$

Since $|x-y|\ge \frac{|x|}{2}$ when $y\in ({\mathbb {R}}^N - B_{R}(0))- B_{\frac{|x|}{2}}(x)$, we have

$$\begin{aligned} M_{21}\le C\int _{{\mathbb {R}}^N - B_{R}(0)}z(y)u^{q}(y)dy, \end{aligned}$$

which implies $M_{21}\rightarrow 0$ as $R\rightarrow +\infty$.

In the following, we estimate $M_{22}$ as $|x|\rightarrow +\infty$. Clearly, from Theorem 2.1 we know u, v, z, h are radially symmetric and decreasing about $x_{0}=0$. Then we can write

$$\begin{aligned} U(r)=U(|x|)=u(x), \quad V(r)=V(|x|)=v(x), \end{aligned}$$

and

$$\begin{aligned} Z(r)=Z(|x|)=z(x), \quad H(r)=H(|x|)=h(x). \end{aligned}$$

Notice that $\frac{|x|}{2}<|y|<\frac{3|x|}{2}$ for $y\in B_{\frac{|x|}{2}}(x)$, we deduce that

$$\begin{aligned} u(y)\le u\left( \frac{x}{2}\right) =U\left( \frac{|x|}{2}\right) ,\quad v(y)\le v\left( \frac{x}{2}\right) =V\left( \frac{|x|}{2}\right) , \end{aligned}$$

and

$$\begin{aligned} z(y)\le z\left( \frac{x}{2}\right) =Z\left( \frac{|x|}{2}\right) , \quad h(y)\le h\left( \frac{x}{2}\right) =H\left( \frac{|x|}{2}\right) . \end{aligned}$$

Therefore,

$$\begin{aligned} \begin{aligned} M_{22}\le \,&|x|^{N-2} R_{N}Z\left( \frac{|x|}{2}\right) U^{q}\left( \frac{|x|}{2}\right) \int _{B_{\frac{|x|}{2}}(x)}\frac{dy}{|x-y|^{N-2}}\\ \le \,&C|x|^{N-2} Z\left( \frac{|x|}{2}\right) U^{q}\left( \frac{|x|}{2}\right) \int _{0}^{\frac{|x|}{2}}r^{2}\frac{dr}{r}\\ \le \,&C|x|^{N} Z\left( \frac{|x|}{2}\right) U^{q}\left( \frac{|x|}{2}\right) . \end{aligned} \end{aligned}$$

(3.39)

By choosing $\frac{1}{s}=\frac{N-2}{2N}+\frac{2\varepsilon }{2Nq}$ and $\frac{1}{k}=\frac{2N-q(N-2)-\varepsilon }{2N}$ with sufficiently small $\varepsilon >0$ such that $\frac{q}{s}+\frac{1}{k}>1$, together with the integrability results, we get $(u,z)\in L^{s}({\mathbb {R}}^N)\times L^{k}({\mathbb {R}}^N)$.

Since u, z are decreasing about $x_{0}=0$, we have

$$\begin{aligned} U^{s}\left( \frac{|x|}{2}\right) |x|^{N}\le C\int _{B_{\frac{|x|}{2}}(0)- {B_{\rho }(0)}}u^{s}(y)dy\le C, \end{aligned}$$

and

$$\begin{aligned} Z^{k}\left( \frac{|x|}{2}\right) |x|^{N}\le C, \end{aligned}$$

from which we conclude that

$$\begin{aligned} U\left( \frac{|x|}{2}\right) \le C|x|^{-\frac{N}{s}},\quad Z\left( \frac{|x|}{2}\right) \le C|x|^{-\frac{N}{k}}. \end{aligned}$$

(3.40)

Inserting (3.40) into (3.39), as $|x|\rightarrow +\infty$, we have

$$\begin{aligned} M_{22}\le C|x|^{N(1-\frac{q}{s}-\frac{1}{k})}\rightarrow 0. \end{aligned}$$

Therefore, we conclude that

$$\begin{aligned} \lim \limits _{|x|\rightarrow \infty }|x|^{N-2}u(x)-A=\lim _{|x|\rightarrow \infty }(M_{1}+M_{21}+M_{22})=0, \end{aligned}$$

which implies $u(x)\backsimeq \frac{C}{|x|^{N-2}}$ as $|x|\rightarrow +\infty$. Similarly, we have $v(x)\backsimeq \frac{C}{|x|^{N-2}}$ as $|x|\rightarrow +\infty$. The proof is completed. $\square$

4 Conclusions for the variational system (2.2)

In this section, we are going to study the nonlocal variational system (2.2). By using similar arguments as for the system (2.1), we can also prove symmetry and regularity properties, as well as the decay of the positive solutions to system (2.2). Furthermore, we establish the nonexistence results under the subcritical condition.

4.1 Nonexistence results for the subcritical case

We first obtain the corresponding Poho${\check{z}}$aev type identity for the subcritical case of system (2.2).

Lemma 4.1

Assume that $N\ge 3$, $0<\mu <N$, $\alpha \ge 0$ and $0<2\alpha +\mu \le N$. Let (u, v) $\in W_{loc}^{2,2}({\mathbb {R}}^N)\times W_{loc}^{2,2}({\mathbb {R}}^N)$ be a pair of solutions of (2.2), then there holds

$$\begin{aligned}&\frac{(N-2)}{2}\int _{{\mathbb {R}}^N}|\nabla u|^{2}dx+\frac{(N-2)}{2}\int _{{\mathbb {R}}^N}|\nabla v|^{2}dx\\&\quad =\frac{2N-2\alpha -\mu }{pq} \int _{{\mathbb {R}}^N}\int _{{\mathbb {R}}^N}\frac{v^{p}(x)u^{q}(y)}{|x|^{\alpha }|x-y|^{\mu }|y|^{\alpha }}dxdy. \end{aligned}$$

Proof

We define a cut-off function $\varphi \in C_{0}^{\infty }({\mathbb {R}}^N)$ with $0\le \varphi \le 1$, satisfying $\varphi =1$ in $B_{1}(0)$ and $\varphi =0$ outside $B_{1}(0)$. For $0<\lambda <\infty$ and $x\in {\mathbb {R}}^N$, we denote

$$\begin{aligned} \psi _{u,\lambda }(x)=\varphi (\lambda x)x\cdot \nabla u(x)\ \text{ and }\ \psi _{v,\lambda }(x)=\varphi (\lambda x)x\cdot \nabla v(x). \end{aligned}$$

Multiplying the first and the second equation of (2.2) by $\psi _{u,\lambda }(x)$ and $\psi _{v,\lambda }(x)$ respectively, and integrating by part, we get

$$\begin{aligned} \int _{{\mathbb {R}}^N}\nabla u\nabla \psi _{u,\lambda }dx=\frac{1}{p}\int _{{\mathbb {R}}^N}\left( \int _{{\mathbb {R}}^N}\frac{v^{p}(y)}{|x|^{\alpha }|x-y|^{\mu }|y|^{\alpha }}dy\right) u^{q-1}(x)\psi _{u,\lambda }(x)dx, \end{aligned}$$

and

$$\begin{aligned} \int _{{\mathbb {R}}^N}\nabla v\nabla \psi _{v,\lambda }dx=\frac{1}{q}\int _{{\mathbb {R}}^N}\left( \int _{{\mathbb {R}}^N}\frac{u^{q}(y)}{|x|^{\alpha }|x-y|^{\mu }|y|^{\alpha }}dy\right) v^{p-1}(x)\psi _{v,\lambda }(x)dx. \end{aligned}$$

But

$$\begin{aligned} \lim \limits _{\lambda \rightarrow 0}\int _{{\mathbb {R}}^N}\nabla u\nabla \psi _{u,\lambda }dx=-\frac{N-2}{2}\int _{{\mathbb {R}}^N}|\nabla u|^{2}dx, \end{aligned}$$

(4.1)

and

$$\begin{aligned} \lim \limits _{\lambda \rightarrow 0}\int _{{\mathbb {R}}^N}\nabla v\nabla \psi _{v,\lambda }dx=-\frac{N-2}{2}\int _{{\mathbb {R}}^N}|\nabla v|^{2}dx. \end{aligned}$$

(4.2)

Next, we claim that

$$\begin{aligned} \begin{aligned}&\frac{1}{p}\lim \limits _{\lambda \rightarrow 0}\int _{{\mathbb {R}}^N}\left( \int _{{\mathbb {R}}^N}\frac{v^{p}(y)}{|x|^{\alpha }|x-y|^{\mu }|y|^{\alpha }}dy\right) u^{q-1}(x)\psi _{u,\lambda }(x)dx \\&\qquad + \frac{1}{q}\lim \limits _{\lambda \rightarrow 0}\int _{{\mathbb {R}}^N}\left( \int _{{\mathbb {R}}^N}\frac{u^{q}(y)}{|x|^{\alpha }|x-y|^{\mu }|y|^{\alpha }}dy\right) v^{p-1}(x)\psi _{v,\lambda }(x)dx \\&\quad =-\frac{2N-2\alpha -\mu }{pq}\left( \int _{{\mathbb {R}}^N}\frac{u^{q}(y)}{|x|^{\alpha }|x-y|^{\mu }|y|^{\alpha }}dy\right) v^{p}(x)dx. \end{aligned} \end{aligned}$$

(4.3)

Indeed, letting

$$\begin{aligned} {\bar{u}}(x)=\frac{u(x)}{|x|^{\frac{\alpha }{q}}} \quad \text{ and }\quad {\bar{v}}(x)=\frac{v(x)}{|x|^{\frac{\alpha }{p}}}, \end{aligned}$$

we have

$$\begin{aligned} \frac{x\cdot \nabla u(x)}{|x|^{\frac{\alpha }{q}}}=x\cdot \nabla {\bar{u}}(x)+\frac{\alpha }{q}{\bar{u}}(x)\quad \text{ and }\quad \frac{x\cdot \nabla v(x)}{|x|^{\frac{\alpha }{p}}}=x\cdot \nabla {\bar{v}}(x)+\frac{\alpha }{p}{\bar{v}}(x). \end{aligned}$$

Then we have

$$\begin{aligned} \begin{aligned}&\frac{1}{q}\int _{{\mathbb {R}}^N}\left( \int _{{\mathbb {R}}^N}\frac{u^{q}(y)}{|x|^{\alpha }|x-y|^{\mu }|y|^{\alpha }}dy\right) v^{p-1}(x)\psi _{v,\lambda }(x)dx\\&\quad =\frac{\alpha }{pq}\int _{{\mathbb {R}}^N}\left( \int _{{\mathbb {R}}^N}\frac{{\bar{u}}^{q}(y)}{|x-y|^{\mu }}dy\right) {\bar{v}}^{p}(x)\varphi (\lambda x)dx \\&\qquad +\frac{1}{q}\int _{{\mathbb {R}}^N}\left( \int _{{\mathbb {R}}^N}\frac{{\bar{u}}^{q}(y)}{|x-y|^{\mu }}dy\right) {\bar{v}}^{p-1}(x)x\cdot \nabla {\bar{v}}(x)\varphi (\lambda x)dx, \end{aligned} \end{aligned}$$

(4.4)

and

$$\begin{aligned} \begin{aligned}&\frac{1}{p}\int _{{\mathbb {R}}^N}\left( \int _{{\mathbb {R}}^N}\frac{v^{p}(y)}{|x|^{\alpha }|x-y|^{\mu }|y|^{\alpha }}dy\right) u^{q-1}(x)\psi _{u,\lambda }(x)dx\\&\quad =\frac{\alpha }{pq}\int _{{\mathbb {R}}^N}\left( \int _{{\mathbb {R}}^N}\frac{{\bar{v}}^{p}(y)}{|x-y|^{\mu }}dy\right) {\bar{u}}^{q}(x)\varphi (\lambda x)dx \\&\qquad +\frac{1}{p}\int _{{\mathbb {R}}^N}\left( \int _{{\mathbb {R}}^N}\frac{{\bar{v}}^{p}(y)}{|x-y|^{\mu }}dy\right) {\bar{u}}^{q-1}(x)x\cdot \nabla {\bar{u}}(x)\varphi (\lambda x)dx. \end{aligned} \end{aligned}$$

(4.5)

A direct calculation shows that

$$\begin{aligned} \begin{aligned}&\int _{{\mathbb {R}}^N}\left( \int _{{\mathbb {R}}^N}\frac{{\bar{u}}^{q}(y)}{|x-y|^{\mu }}dy\right) {\bar{v}}^{p-1}(x)x\cdot \nabla {\bar{v}}(x)\varphi (\lambda x)dx\\&\quad =\int _{{\mathbb {R}}^N}\left( \int _{{\mathbb {R}}^N}\frac{{\bar{u}}^{q}(y)}{|x-y|^{\mu }}dy\right) x\cdot \nabla \left( \frac{{\bar{v}}^{p}(x)}{p}\right) \varphi (\lambda x)dx\\&\quad =-\int _{{\mathbb {R}}^N}\left( \int _{{\mathbb {R}}^N}\frac{{\bar{u}}^{q}(y)}{|x-y|^{\mu }}dy\right) \left[ \lambda x\cdot \nabla \varphi (\lambda x)+N\varphi (\lambda x)\right] \frac{{\bar{v}}^{p}(x)}{p}dx\\&\qquad +\mu \int _{{\mathbb {R}}^N}\int _{{\mathbb {R}}^N}\left( \frac{{\bar{u}}^{q}(y)}{|x-y|^{\mu }}\right) \frac{1}{|x-y|^{2}}x\cdot (x-y)\varphi (\lambda x)\frac{{\bar{v}}^{p}(x)}{p}dxdy. \end{aligned} \end{aligned}$$

(4.6)

We can also deduce that

$$\begin{aligned} \begin{aligned}&\int _{{\mathbb {R}}^N}\left( \int _{{\mathbb {R}}^N}\frac{{\bar{v}}^{p}(y)}{|x-y|^{\mu }}dy\right) {\bar{u}}^{q-1}(x)x\cdot \nabla {\bar{u}}(x)\varphi (\lambda x)dx\\&\quad =-\int _{{\mathbb {R}}^N}\left( \int _{{\mathbb {R}}^N}\frac{{\bar{v}}^{p}(y)}{|x-y|^{\mu }}dy\right) \left[ \lambda x\cdot \nabla \varphi (\lambda x)+N\varphi (\lambda x)\right] \frac{{\bar{u}}^{q}(x)}{q}dx\\&\qquad +\mu \int _{{\mathbb {R}}^N}\left( \int _{{\mathbb {R}}^N}\frac{{\bar{v}}^{p}(y)}{|x-y|^{\mu }}\right) \frac{1}{|x-y|^{2}}x\cdot (x-y)\varphi (\lambda x)\frac{{\bar{u}}^{q}(x)}{q}dxdy\\&\quad =-\int _{{\mathbb {R}}^N}\left( \int _{{\mathbb {R}}^N}\frac{{\bar{v}}^{p}(y)}{|x-y|^{\mu }}dy\right) \left[ \lambda x\cdot \nabla \varphi (\lambda x)+N\varphi (\lambda x)\right] \frac{{\bar{u}}^{q}(x)}{q}dx\\&\qquad -\mu \int _{{\mathbb {R}}^N}\int _{{\mathbb {R}}^N}\left( \frac{{\bar{u}}^{q}(y)}{|x-y|^{\mu }}\right) \frac{1}{|x-y|^{2}}y\cdot (x-y)\varphi (\lambda y)\frac{{\bar{v}}^{p}(x)}{q}dxdy. \end{aligned} \end{aligned}$$

(4.7)

Combining (4.4) with (4.5) and adding (4.6) to (4.7), we conclude from the dominated convergence Theorem that

$$\begin{aligned} \begin{aligned}&\frac{1}{p}\lim \limits _{\lambda \rightarrow 0}\int _{{\mathbb {R}}^N}\left( \int _{{\mathbb {R}}^N}\frac{v^{p}(y)}{|x|^{\alpha }|x-y|^{\mu }|y|^{\alpha }}dy\right) u^{q-1}(x)\psi _{u,\lambda }(x)dx\\&\quad +\frac{1}{q}\lim \limits _{\lambda \rightarrow 0}\int _{{\mathbb {R}}^N}\left( \int _{{\mathbb {R}}^N}\frac{u^{q}(y)}{|x|^{\alpha }|x-y|^{\mu }|y|^{\alpha }}dy\right) v^{p-1}(x)\psi _{v,\lambda }(x)dx=\\&\quad -\frac{2N-2\alpha -\mu }{pq}\left( \int _{{\mathbb {R}}^N}\frac{u^{q}(y)}{|x|^{\alpha }|x-y|^{\mu }|y|^{\alpha }}dy\right) v^{p}(x)dx. \end{aligned} \end{aligned}$$

(4.8)

Therefore, taking (4.1)–(4.3) into account, we infer that

$$\begin{aligned}&\frac{N-2}{2}\int _{{\mathbb {R}}^N}|\nabla u|^{2}dx+\frac{N-2}{2}\int _{{\mathbb {R}}^N}|\nabla v|^{2}dx\\&\quad =\frac{2N-2\alpha -\mu }{pq} \int _{{\mathbb {R}}^N}\int _{{\mathbb {R}}^N}\frac{v^{p}(x)u^{q}(y)}{|x|^{\alpha }|x-y|^{\mu }|y|^{\alpha }}dxdy. \end{aligned}$$

The proof is now complete. $\square$

4.2 Proof of Theorem 2.4

We first multiply the first equation of (2.2) by u and multiply the second equation of (2.2) by v, then it follows that

$$\begin{aligned} \int _{{\mathbb {R}}^N}|\nabla u|^{2}dx =\frac{1}{p}\int _{{\mathbb {R}}^N}\int _{{\mathbb {R}}^N}\frac{v^{p}(x)u^{q}(y)}{|x|^{\alpha }|x-y|^{\mu }|y|^{\alpha }}dxdy, \end{aligned}$$

and

$$\begin{aligned} \int _{{\mathbb {R}}^N}|\nabla v|^{2}dx=\frac{1}{q}\int _{{\mathbb {R}}^N}\int _{{\mathbb {R}}^N}\frac{v^{p}(x)u^{q}(y)}{|x|^{\alpha }|x-y|^{\mu }|y|^{\alpha }}dxdy. \end{aligned}$$

Together with the identity in Lemma 4.1, we deduce

$$\begin{aligned} \left( \frac{N-2}{2}-\frac{2N-2\alpha -\mu }{pq}\right) \int _{{\mathbb {R}}^N}\int _{{\mathbb {R}}^N}\frac{v^{p}(x)u^{q}(y)}{|x|^{\alpha }|x-y|^{\mu }|y|^{\alpha }}dxdy=0. \end{aligned}$$

If $p+q<\frac{2(2N-2\alpha -\mu )}{N-2}$, we get

$$\begin{aligned} u\equiv v\equiv 0. \end{aligned}$$

The proof is complete. ${} \Box$

4.3 Qualitative properties for the critical case

Next we focus on the qualitative results of system (2.2) with critical condition $p+q=\frac{2(2N-2\alpha -\mu )}{N-2}=2\cdot 2_{\alpha ,\mu }^{*}$, including symmetry, regularity and asymptotic behavior at infinity.

4.3.1 Symmetry

Analogously, we consider the following equivalent integral system in ${\mathbb {R}}^{N}$

$$\begin{aligned} \left\{ \begin{aligned} z(x)&=\int _{{\mathbb {R}}^N}\frac{v^{p}(y)}{|x|^{\alpha }|x-y|^{\mu }|y|^{\alpha }}dy,\\ h(x)&=\int _{{\mathbb {R}}^N}\frac{u^{q}(y)}{|x|^{\alpha }|x-y|^{\mu }|y|^{\alpha }}dy,\\ u(x)&=R_{N}\int _{{\mathbb {R}}^N}\frac{z(y)u^{q-1}(y)}{|x-y|^{N-2}}dy,\\ v(x)&=R_{N}\int _{{\mathbb {R}}^N}\frac{h(y)v^{p-1}(y)}{|x-y|^{N-2}}dy. \end{aligned} \right. \end{aligned}$$

(4.9)

For $\lambda \in {{\mathbb {R}}}$, define

$$\begin{aligned} \begin{aligned}&\Sigma _{\lambda }=\left\{ x=(x_{1},\ldots ,x_{n})\ |\ x_{1}<\lambda \right\} ,\quad x^{\lambda }=(2\lambda -x_{1},\ldots ,x_{n}),\\&u_{\lambda }(x)=u(x^{\lambda }),\quad v_{\lambda }(x)=v(x^{\lambda }), \quad z_{\lambda }(x)=z(x^{\lambda }),\quad h_{\lambda }(x)=h(x^{\lambda }), \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} \Sigma _{\lambda }^{u}&=\left\{ x\in \Sigma _{\lambda }\ |\ u(x)> u_{\lambda }(x) \right\} ,\quad \Sigma _{\lambda }^{v}=\left\{ x\in \Sigma _{\lambda }\ |\ v(x)> v_{\lambda }(x) \right\} ,\\ \Sigma _{\lambda }^{z}&=\left\{ x\in \Sigma _{\lambda }\ |\ z(x)> z_{\lambda }(x) \right\} ,\quad \Sigma _{\lambda }^{h}=\left\{ x\in \Sigma _{\lambda }\ |\ h(x)> h_{\lambda }(x) \right\} . \end{aligned} \end{aligned}$$

We rewrite u(x) and $u_{\lambda }(x)$ as

$$\begin{aligned} \begin{aligned} u(x)=&R_{N}\int _{\Sigma _{\lambda }}\frac{z(y)u^{q-1}(y)}{|x-y|^{N-2}}dy+R_{N}\int _{{\mathbb {R}}^N-\Sigma _{\lambda }}\frac{z(y)u^{q-1}(y)}{|x-y|^{N-2}}dy\\ =&R_{N}\int _{\Sigma _{\lambda }}\frac{z(y)u^{q-1}(y)}{|x-y|^{N-2}}dy+R_{N}\int _{\Sigma _{\lambda }}\frac{z(y^{\lambda })u^{q-1}(y^{\lambda })}{|x-y^{\lambda }|^{N-2}}dy \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} u_{\lambda }(x)=&R_{N}\int _{\Sigma _{\lambda }}\frac{z(y)u^{q-1}(y)}{|x^{\lambda }-y|^{N-2}}dy+R_{N}\int _{{\mathbb {R}}^N-\Sigma _{\lambda }}\frac{z(y)u^{q-1}(y)}{|x^{\lambda }-y|^{N-2}}dy\\ =&R_{N}\int _{\Sigma _{\lambda }}\frac{z(y)u^{q-1}(y)}{|x^{\lambda }-y|^{N-2}}dy+R_{N}\int _{\Sigma _{\lambda }}\frac{z(y^{\lambda })u^{q-1}(y^{\lambda })}{|x^{\lambda }-y^{\lambda }|^{N-2}}dy. \end{aligned} \end{aligned}$$

Since $|x^{\lambda }-y^{\lambda }|=|x-y|$ and $|x^{\lambda }-y|=|x-y^{\lambda }|$, it follows that

$$\begin{aligned} u(x)-u_{\lambda }(x)=R_{N}\int _{\Sigma _{\lambda }}\left( \frac{1}{|x-y|^{N-2}}-\frac{1}{|x^{\lambda }-y|^{N-2}}\right) (zu^{q-1}-z_{\lambda }u_{\lambda }^{q-1})dy,\nonumber \\ \end{aligned}$$

(4.10)

and

$$\begin{aligned} v(x)-v_{\lambda }(x)=R_{N}\int _{\Sigma _{\lambda }}\left( \frac{1}{|x-y|^{N-2}}-\frac{1}{|x^{\lambda }-y|^{N-2}}\right) (hv^{p-1}-h_{\lambda }v_{\lambda }^{p-1})dy.\nonumber \\ \end{aligned}$$

(4.11)

For the case p, $q>2$, we have the following property.

Lemma 4.2

Under the assumption of Theorem 2.5, for any $\lambda <0$, there exists a constant $C>0$ such that

$$\begin{aligned}&\Vert u-u_{\lambda }\Vert _{L^{s_{0}}(\Sigma _{\lambda }^{u})}\le C \Vert v\Vert _{L^{s_{0}}(\Sigma _{\lambda }^{u})}^{p}\Vert u\Vert _{L^{s_{0}}(\Sigma _{\lambda }^u)}^{q-2}\Vert u-u_{\lambda }\Vert _{L^{s_{0}}(\Sigma _{\lambda }^{u})} \nonumber \\&\quad +\,C\Vert u\Vert _{L^{s_{0}}(\Sigma _{\lambda }^{u})}^{q-1}\Vert v\Vert _{L^{s_{0}}(\Sigma _{\lambda }^{v})}^{p-1}\Vert v-v_{\lambda }\Vert _{L^{s_{0}}(\Sigma _{\lambda }^{v})}, \end{aligned}$$

(4.12)

and

$$\begin{aligned}&\Vert v-v_{\lambda }\Vert _{L^{s_{0}}(\Sigma _{\lambda }^{v})}\le C \Vert u\Vert _{L^{s_{0}}(\Sigma _{\lambda }^{v})}^{q}\Vert v\Vert _{L^{s_{0}}(\Sigma _{\lambda }^v)}^{p-2}\Vert v-v_{\lambda }\Vert _{L^{s_{0}}(\Sigma _{\lambda }^{v})} \nonumber \\&\quad +\,C\Vert v\Vert _{L^{s_{0}}(\Sigma _{\lambda }^{v})}^{p-1}\Vert u\Vert _{L^{s_{0}}(\Sigma _{\lambda }^{u})}^{q-1} \Vert u-u_{\lambda }\Vert _{L^{s_{0}}(\Sigma _{\lambda }^{u})}. \end{aligned}$$

(4.13)

Proof

For any $x\in \Sigma _{\lambda }$, notice $|x^{\lambda }-y|\ge |x-y|$, using the mean value theorem, from (4.10) and (4.11), we easily deduce

$$\begin{aligned} u(x)-u_{\lambda }(x)\le R_{N}(q-1)\int _{\Sigma _{\lambda }^u}\frac{zu^{q-2}(u-u_{\lambda })}{|x-y|^{N-2}}dy+R_{N}\int _{\Sigma _{\lambda }^z}\frac{u^{q-1}(z-z_{\lambda })}{|x-y|^{N-2}}dy, \end{aligned}$$

and

$$\begin{aligned} v(x)-v_{\lambda }(x)\le R_{N}(p-1)\int _{\Sigma _{\lambda }^v}\frac{hv^{p-2}(v-v_{\lambda })}{|x-y|^{N-2}}dy+R_{N}\int _{\Sigma _{\lambda }^h}\frac{v^{p-1}(h-h_{\lambda })}{|x-y|^{N-2}}dy. \end{aligned}$$

In virtue of $(u,v)\in L^{s_{0}}({\mathbb {R}}^N)\times L^{s_{0}}({\mathbb {R}}^N)$ with $s_{0}=\frac{N(p+q-2)}{N+2-2\alpha -\mu }$, assume that $z\in L^{k}({\mathbb {R}}^N)$, $h\in L^{t}({\mathbb {R}}^N)$, where $k,\ t$ such that

$$\begin{aligned} \frac{1}{k}+\frac{q-1}{s_{0}}=\frac{N+2s_{0}}{Ns_{0}}\ \text{ and } \ \frac{1}{t}+\frac{p-1}{s_{0}}=\frac{N+2s_{0}}{Ns_{0}}. \end{aligned}$$

(4.14)

Then we have

$$\begin{aligned} \frac{pNk}{N+(N-2\alpha -\mu )k}=s_{0} \ \text{ and } \ \frac{qNt}{N+(N-2\alpha -\mu )t}=s_{0}. \end{aligned}$$

By applying the HLS inequality and the Hölder inequality, we lead

$$\begin{aligned} \begin{aligned} \Vert u-u_{\lambda }\Vert _{{L^{s_{0}}}(\Sigma _{\lambda }^{u})}\le \,&C\Vert zu^{q-2}(u-u_{\lambda })\Vert _{L^{\frac{Ns_{0}}{N+2s_{0}}}(\Sigma _{\lambda }^{u})}+C\Vert u^{q-1}(z-z_{\lambda })\Vert _{L^{\frac{Ns_{0}}{N+2s_{0}}}(\Sigma _{\lambda }^{z})}\\ \le \,&C\Vert z\Vert _{L^{k}(\Sigma _{\lambda }^{u})}\Vert u\Vert _{L^{s_{0}}(\Sigma _{\lambda }^u)}^{q-2}\Vert u-u_{\lambda }\Vert _{L^{s_{0}}(\Sigma _{\lambda }^{u})}+C\Vert z-z_{\lambda }\Vert _{L^{k}(\Sigma _{\lambda }^z)}\Vert u\Vert _{L^{s_{0}}(\Sigma _{\lambda }^{u})}^{q-1}. \end{aligned} \end{aligned}$$

(4.15)

Similarly, we obtain

$$\begin{aligned} \begin{aligned} \Vert v-v_{\lambda }\Vert _{{L^{s_{0}}}(\Sigma _{\lambda }^{v})}\le \,&C\Vert hv^{p-2}(v-v_{\lambda })\Vert _{L^{\frac{Ns_{0}}{N+2s_{0}}}(\Sigma _{\lambda }^{v})}+C\Vert v^{p-1}(h-h_{\lambda })\Vert _{L^{\frac{Ns_{0}}{N+2s_{0}}}(\Sigma _{\lambda }^{h})}\\ \le \,&C\Vert h\Vert _{L^{t}(\Sigma _{\lambda }^{v})}\Vert v\Vert _{L^{s_{0}}(\Sigma _{\lambda }^v)}^{p-2}\Vert v-v_{\lambda }\Vert _{L^{s_{0}}(\Sigma _{\lambda }^{v})}+C\Vert h-h_{\lambda }\Vert _{L^{t}(\Sigma _{\lambda }^h)}\Vert v\Vert _{L^{s_{0}}(\Sigma _{\lambda }^{v})}^{p-1}. \end{aligned} \end{aligned}$$

(4.16)

Combining with relations (3.10)–(3.13), we easily obtain (4.12) and (4.13). We complete the proof. $\square$

For the case $p=q=2$ or $p>2$ and $q=2$, Lemma 4.2 can be replaced by the following lemmas.

Lemma 4.3

Under the assumption of Theorem 2.5, if $p=q=2$, for any $\lambda <0$, there exists a constant $C>0$ such that

$$\begin{aligned} \Vert u-u_{\lambda }\Vert _{L^{s_{0}}(\Sigma _{\lambda }^{u})}\le C\Vert u\Vert _{L^{s_{0}}(\Sigma _{\lambda }^{u})}\Vert v\Vert _{L^{s_{0}}(\Sigma _{\lambda }^{v})}\Vert v-v_{\lambda }\Vert _{L^{s_{0}}(\Sigma _{\lambda }^{v})}, \end{aligned}$$

and

$$\begin{aligned} \Vert v-v_{\lambda }\Vert _{L^{s_{0}}(\Sigma _{\lambda }^{v})}\le C\Vert v\Vert _{L^{s_{0}}(\Sigma _{\lambda }^{v})}\Vert u\Vert _{L^{s_{0}}(\Sigma _{\lambda }^{u})} \Vert u-u_{\lambda }\Vert _{L^{s_{0}}(\Sigma _{\lambda }^{u})}. \end{aligned}$$

Lemma 4.4

Under the assumption of Theorem 2.5, if $p>2$ and $q=2$, for any $\lambda <0$, there exists a constant $C>0$ such that

$$\begin{aligned} \Vert u-u_{\lambda }\Vert _{L^{s_{0}}(\Sigma _{\lambda }^{u})}\le C\Vert u\Vert _{L^{s_{0}}(\Sigma _{\lambda }^{u})}\Vert v\Vert _{L^{s_{0}}(\Sigma _{\lambda }^{v})}^{p-1}\Vert v-v_{\lambda }\Vert _{L^{s_{0}}(\Sigma _{\lambda }^{v})}, \end{aligned}$$

(4.17)

and

$$\begin{aligned}&\Vert v-v_{\lambda }\Vert _{L^{s_{0}}(\Sigma _{\lambda }^{v})}\le C \Vert u\Vert _{L^{s_{0}}(\Sigma _{\lambda }^{v})}^{2}\Vert v\Vert _{L^{s_{0}}(\Sigma _{\lambda }^v)}^{p-2}\Vert v-v_{\lambda }\Vert _{L^{s_{0}}(\Sigma _{\lambda }^{v})}\nonumber \\&\quad +\,C\Vert v\Vert _{L^{s_{0}}(\Sigma _{\lambda }^{v})}^{p-1}\Vert u\Vert _{L^{s_{0}}(\Sigma _{\lambda }^{u})} \Vert u-u_{\lambda }\Vert _{L^{s_{0}}(\Sigma _{\lambda }^{u})}. \end{aligned}$$

(4.18)

In the following, we provide the starting of the moving plane methods by using the $L^{s_{0}}$ estimates proved above.

Lemma 4.5

Under the assumption of Theorem 2.5, there exists $M>0$ such that for any $\lambda <-M$, we have

$$\begin{aligned} u(x)\le u_{\lambda }(x),\ v(x)\le v_{\lambda }(x) \quad \forall x\in \Sigma _{\lambda }. \end{aligned}$$

(4.19)

Proof

Since u, v are integrable, if $\lambda \rightarrow -\infty$, we have

$$\begin{aligned}&\Vert v\Vert _{L^{s_{0}}(\Sigma _{\lambda }^{u})}^{p}\Vert u\Vert _{L^{s}(\Sigma _{\lambda }^u)}^{q-2}\le \frac{1}{2C},\\&\Vert u\Vert _{L^{s_{0}}(\Sigma _{\lambda }^{v})}^{q}\Vert v\Vert _{L^{s_{0}}(\Sigma _{\lambda }^v)}^{p-2}\le \frac{1}{2C}, \end{aligned}$$

and

$$\begin{aligned} \Vert v\Vert _{L^{s_{0}}(\Sigma _{\lambda }^{v})}^{p-1}\Vert u\Vert _{L^{s_{0}}(\Sigma _{\lambda }^{u})}^{q-1} \le \frac{1}{4C}, \end{aligned}$$

where the constant C is the same as in Lemma 4.2. Hence, inserting those inequalities into (4.12) and (4.13), as $\lambda \rightarrow -\infty$, it follows

$$\begin{aligned} \Vert u(x)-u_{\lambda }(x)\Vert _{L^{s}(\Sigma _{\lambda }^{u})}=0,\quad \Vert v(x)-v_{\lambda }(x)\Vert _{L^{r}(\Sigma _{\lambda }^{v})}=0, \end{aligned}$$

which shows that $\Sigma _{\lambda }^{u}=\Sigma _{\lambda }^{v}=\emptyset .$ Therefore, there exists $M>0$ such that for any $\lambda <-M$, relation (4.19) holds. $\square$

We now can move the plane $T_{\lambda }=\left\{ x\in {\mathbb {R}}^N|x_{1}=\lambda \right\}$ to the right as long as (4.19) is satisfied. Setting

$$\begin{aligned} \lambda _{0}=\sup \left\{ \lambda \ | \ u(x)\le u_{\rho }(x),\ v(x)\le v_{\rho }(x),\ x\in \Sigma _{\rho }, \ \rho \le \lambda \right\} , \end{aligned}$$

we observe that $\lambda _{0}<+\infty$.

Next, we deduce the following property.

Lemma 4.6

Under the assumption of Theorem 2.5, then for any $\lambda _{0}<0$, we have

$$\begin{aligned} u(x)\equiv u_{\lambda _{0}}(x),\ v(x)\equiv v_{\lambda _{0}}(x) \quad \forall x\in \Sigma _{\lambda _{0}}. \end{aligned}$$

(4.20)

Proof

Suppose that at $\lambda _{0}<0$, there holds $u(x)\le u_{\lambda _{0}}(x)$ and $v(x)\le v_{\lambda _{0}}(x)$, but $u(x)\not \equiv u_{\lambda _{0}}(x)$ or $v(x)\not \equiv v_{\lambda _{0}}(x)$ on $\Sigma _{\lambda _{0}}$.

We claim that there exists $\varepsilon >0$ such that $u(x)\le u_{\lambda }(x)$ and $v(x)\le v_{\lambda }(x)$ on $\Sigma _{\lambda }$ for any $\lambda \in \left[ \lambda _{0},\lambda _{0}+\varepsilon \right)$.

Actually, for any $\eta >0$, there exists a suitable $R>0$ large enough such that

$$\begin{aligned}&\Vert v\Vert _{L^{s_{0}}({\mathbb {R}}^N- B_{R}(0)))}^{p}\Vert u\Vert _{L^{s}({\mathbb {R}}^N- B_{R}(0)))}^{q-2}\le \frac{\eta }{2}, \\&\Vert u\Vert _{L^{s_{0}}({\mathbb {R}}^N- B_{R}(0)))}^{q}\Vert v\Vert _{L^{s_{0}}({\mathbb {R}}^N- B_{R}(0)))}^{p-2}\le \frac{\eta }{2}, \end{aligned}$$

and

$$\begin{aligned} \Vert v\Vert _{L^{s_{0}}({\mathbb {R}}^N- B_{R}(0)))}^{p-1}\Vert u\Vert _{L^{s_{0}}({\mathbb {R}}^N- B_{R}(0)))}^{q-1} \le \frac{\eta }{4}. \end{aligned}$$

For such $R>0$ and $\lambda >\lambda _{0}$, we can verify that the measure of the set $\Sigma _{\lambda }\cap B_{R}(0)$ goes to 0 as $\lambda \rightarrow \lambda _{0}$.

By contradiction, we assume that

$$\begin{aligned} u(x)\not \equiv u_{\lambda _{0}}(x) \ \text{ in }\ \Sigma _{\lambda _{0}}. \end{aligned}$$

From (3.8), we obtain

$$\begin{aligned} h(x)-h_{\lambda _{0}}(x)<0 \ \text{ on }\ \Sigma _{\lambda _{0}}.. \end{aligned}$$

Thus, by (4.11), we yield

$$\begin{aligned} v(x)- v_{\lambda _{0}}(x)<0\ \text{ on }\ \Sigma _{\lambda _{0}}. \end{aligned}$$

Combining with (3.9), it follows that

$$\begin{aligned} z(x)- z_{\lambda _{0}}(x)<0\ \text{ on }\ \Sigma _{\lambda _{0}}, \end{aligned}$$

together with (4.10), we have

$$\begin{aligned} u(x)- u_{\lambda _{0}}(x)<0\ \text{ on }\ \Sigma _{\lambda _{0}}. \end{aligned}$$

Therefore, we can apply a similar argument as in Lemma 3.3 to conclude that $u(x)\equiv u_{\lambda _{0}}(x)$ and $v(x)\equiv v_{\lambda _{0}}(x)$ for any $x\in \Sigma _{\lambda _{0}}.$ $\square$

4.4 Proof of Theorem 2.5

Similarly, we can move the plane from $+\infty$ to left, and define

$$\begin{aligned} \lambda _{1}=\inf \left\{ \lambda \ |\ u(x)\le u_{\rho }(x),\ v(x)\le v_{\rho }(x),\ x\in \Sigma _{\rho }^{'},\ \rho \ge \lambda \right\} , \end{aligned}$$

where $\Sigma _{\rho }^{'}=\left\{ x\in {\mathbb {R}}^N|x_{1}>\rho \right\}$. If $\lambda _{0}=\lambda _{1}\ne 0$, then both u and v are radially symmetric and decreasing about the plane $x_{1}=\lambda _{0}$, which implies $u(x)\equiv u_{\lambda _{0}}(x)$ and $v(x)\equiv v_{\lambda _{0}}(x)$ on $\Sigma _{\lambda _{0}}$. Since $|x-y|<|x^{\lambda _{0}}-y|$ and $|y|>|y^{\lambda _{0}}|$, it is easy to deduce from (3.9) that

$$\begin{aligned} z(x)-z_{\lambda _{0}}(x)\le \int _{\Sigma _{\lambda _{0}}}\frac{1}{|x|^{\alpha }}\left( \frac{1}{|x-y|^{\mu }}-\frac{1}{|x^{\lambda _{0}}-y|^{\mu }}\right) \left( \frac{1}{|y|^{\alpha }}-\frac{1}{|y^{\lambda _{0}}|^{\alpha }}\right) v_{\lambda _{0}}^{p}dy<0. \end{aligned}$$

Therefore, we obtain that

$$\begin{aligned} 0=u(x)-u_{\lambda _{0}}(x)=R_{N}\int _{\Sigma _{\lambda _{0}}}\left( \frac{1}{|x-y|^{N-2}}-\frac{1}{|x^{\lambda _{0}}-y|^{N-2}}\right) (z-z_{\lambda _{0}})u_{\lambda _{0}}^{q-1}dy<0, \end{aligned}$$

which is impossible. Hence, we get $\lambda _{0}=\lambda _{1}=0$. Notice that the direction of $x_{1}$ is arbitrary, hence u, v are radially symmetric and decreasing about the origin. ${} \Box$

4.4.1 Regularity

Taking similar derivations as Theorem 2.2, we need to define the functions

$$\begin{aligned} F_{u}(m)= & {} R_{N}\int _{{\mathbb {R}}^N}\frac{u^{q-1}(y)m(y) }{|x-y|^{N-2}}dy,\\ T_{v}(w)= & {} R_{N}\int _{{\mathbb {R}}^N}\frac{v^{p-1}(y) w(y)}{|x-y|^{N-2}}dy, \\ W_{u}(a)= & {} \int _{{\mathbb {R}}^N}\frac{u^{q-1}(y)a(y)}{|x|^{\alpha }|x-y|^{\mu }|y|^{\alpha }}dy,\\ G_{v}(b)= & {} \int _{{\mathbb {R}}^N}\frac{v^{p-1}(y)b(y) }{|x|^{\alpha }|x-y|^{\mu }|y|^{\alpha }}dy. \end{aligned}$$

Suppose a, $b \in L^{s}({\mathbb {R}}^{N})$, $m\in L^{k}({\mathbb {R}}^{N})$, and $h \in L^{t}({\mathbb {R}}^{N})$, we also define the operator

$$\begin{aligned}&{\mathscr {T}}_{A}: L^{s}({\mathbb {R}}^{N})\times L^{s}({\mathbb {R}}^{N})\times L^{k}({\mathbb {R}}^{N})\times L^{t}({\mathbb {R}}^{N})\rightarrow L^{s}({\mathbb {R}}^{N})\times L^{s}({\mathbb {R}}^{N})\times L^{k}({\mathbb {R}}^{N})\times L^{t}({\mathbb {R}}^{N}), \\&{\mathscr {T}}_{A}(a,b,m,w)=(F_{u_{A}}(m),T_{v_{A}}(w),G_{v_{A}}(b),W_{u_{A}}(a)). \end{aligned}$$

Then (u, v, z, h) satisfies the operator equation

$$\begin{aligned} (u,v,z,h)={\mathscr {T}}_{A}(u,v,z,h)+(F_{u_{B}}(z),T_{v_{B}}(h),G_{v_{B}}(v),W_{u_{B}}(u)). \end{aligned}$$

In order to prove the main result of Theorem 2.6, we shall establish the following two lemmas.

Lemma 4.7

Assume that $p+q=2\cdot 2_{\alpha ,\mu }^{*}$ and s, k, t satisfy

$$\begin{aligned} \left\{ \begin{aligned}&s>\frac{N}{N-2},\\&s>\frac{2N}{2N+(p-1)(N-2)-2(N+2-2\alpha -\mu )},\\&s>\frac{2N}{2N+(q-1)(N-2)-2(N+2-2\alpha -\mu )},\\&2N>[(p-1)(N-2)-4]s,\\&2N>[(q-1)(N-2)-4]s,\\&\frac{1}{s}-\frac{1}{k}=\frac{(q-1)(N-2)-4}{2N},\\&\frac{1}{s}-\frac{1}{t}=\frac{(p-1)(N-2)-4}{2N}. \end{aligned} \right. \end{aligned}$$

Then for A sufficiently large, ${\mathscr {T}}_{A}$ is a contraction map from $L^{s}({\mathbb {R}}^{N})\times L^{s}({\mathbb {R}}^{N})\times L^{k}({\mathbb {R}}^{N})\times L^{t}({\mathbb {R}}^{N})$ to itself.

Lemma 4.8

Suppose that $3\le N\le 6$, $\alpha \ge 0$, $0<\mu <N$ and $N-2\le 2\alpha +\mu \le N$. Let $(u,v,z,h) \in L^{\frac{2N}{N-2}}({\mathbb {R}}^N)\times L^{\frac{2N}{N-2}}({\mathbb {R}}^N)\times L^{k_{0}}({\mathbb {R}}^N)\times L^{t_{0}}({\mathbb {R}}^N)$ be a set of positive solutions of system (4.9) with $k_{0}=\frac{2N}{4-(q-2)(N-2)}$ and $t_{0}=\frac{2N}{4-(p-2)(N-2)}$, where p, q satisfying $p+q=2\cdot 2_{\alpha ,\mu }^{*}$ and $\frac{2(N-2\alpha -\mu )}{N-2}\le p-1,q-1\le min\left\{ \frac{4}{N-2}, \frac{N+2+2(N+2-2\alpha -\mu )}{N-2}\right\}$. Then $(u,v,z,h)\in L^{s}({\mathbb {R}}^{N})\times L^{s}({\mathbb {R}}^{N})\times L^{k}({\mathbb {R}}^{N})\times L^{t}({\mathbb {R}}^{N})$ with

$$\begin{aligned} s\in \left( \frac{N}{N-2},+\infty \right) ,\quad k\in \left( \frac{2N}{4-(q-3)(N-2)},\frac{2N}{4-(q-1)(N-2)}\right) \end{aligned}$$

and

$$\begin{aligned} \quad t\in \left( \frac{2N}{4-(p-3)(N-2)},\frac{2N}{4-(p-1)(N-2)}\right) . \end{aligned}$$

4.4.2 Decay

The proof of this part is the same as the Theorem 2.3, here we omit for convenience.

5 Symmetry for the Hamiltonian system (2.3)

In this section, we shall prove the symmetry of (2.3) by discussing the following equivalent integral system in ${\mathbb {R}}^{N}$

$$\begin{aligned} \left\{ \begin{aligned} z(x)&=\int _{{\mathbb {R}}^N}\frac{v^{p}(y)}{|x|^{\alpha _{1}}|x-y|^{\mu _{1}}|y|^{\alpha _{1}}}dy,\\ h(x)&=\int _{{\mathbb {R}}^N}\frac{u^{q}(y)}{|x|^{\alpha _{2}}|x-y|^{\mu _{2}}|y|^{\alpha _{2}}}dy,\\ u(x)&=R_{N}\int _{{\mathbb {R}}^N}\frac{z(y)v^{p-1}(y)}{|x-y|^{N-2}}dy,\\ v(x)&=R_{N}\int _{{\mathbb {R}}^N}\frac{h(y)u^{q-1}(y)}{|x-y|^{N-2}}dy, \end{aligned} \right. \end{aligned}$$

(5.1)

where $p=2_{\alpha _{1},\mu _{1}}^{*}=\frac{2N-2\alpha _{1}-\mu _{1}}{N-2}$ and $q=2_{\alpha _{2},\mu _{2}}^{*}=\frac{2N-2\alpha _{2}-\mu _{2}}{N-2}$.

For $\lambda \in {{\mathbb {R}}}$, define

$$\begin{aligned} \begin{aligned}&\Sigma _{\lambda }=\left\{ x=(x_{1},\ldots ,x_{n})|x_{1}<\lambda \right\} ,\quad x^{\lambda }=(2\lambda -x_{1},\ldots ,x_{n}),\\&u_{\lambda }(x)=u(x^{\lambda }), \quad v_{\lambda }(x)=v(x^{\lambda }),\quad w_{\lambda }(x)=w(x^{\lambda }), \quad g_{\lambda }(x)=g(x^{\lambda }), \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} \Sigma _{\lambda }^{u}&=\left\{ x\in \Sigma _{\lambda }|u(x)> u_{\lambda }(x) \right\} ,\quad \Sigma _{\lambda }^{v}=\left\{ x\in \Sigma _{\lambda }|v(x)> v_{\lambda }(x) \right\} ,\\ \Sigma _{\lambda }^{w}&=\left\{ x\in \Sigma _{\lambda }|w(x)> w_{\lambda }(x) \right\} ,\quad \Sigma _{\lambda }^{g}=\left\{ x\in \Sigma _{\lambda }|g(x)> g_{\lambda }(x) \right\} . \end{aligned} \end{aligned}$$

We easily get

$$\begin{aligned} \begin{aligned} u(x)=&R_{N}\int _{\Sigma _{\lambda }}\frac{z(y)v^{p-1}(y)}{|x-y|^{N-2}}dy+R_{N}\int _{{\mathbb {R}}^N-\Sigma _{\lambda }}\frac{z(y)v^{p-1}(y)}{|x-y|^{N-2}}dy\\ =&R_{N}\int _{\Sigma _{\lambda }}\frac{z(y)v^{p-1}(y)}{|x-y|^{N-2}}dy+R_{N}\int _{\Sigma _{\lambda }}\frac{z(y^{\lambda })v^{p-1}(y^{\lambda })}{|x-y^{\lambda }|^{N-2}}dy, \end{aligned} \end{aligned}$$

and

$$\begin{aligned} u_{\lambda }(x)=R_{N}\int _{\Sigma _{\lambda }}\frac{z(y)v^{p-1}(y)}{|x^{\lambda }-y|^{N-2}}dy+R_{N}\int _{\Sigma _{\lambda }}\frac{z(y^{\lambda })v^{p-1}(y^{\lambda })}{|x^{\lambda }-y^{\lambda }|^{N-2}}dy. \end{aligned}$$

Since $|x^{\lambda }-y^{\lambda }|=|x-y|$ and $|x^{\lambda }-y|=|x-y^{\lambda }|$, then it follows that

$$\begin{aligned} u(x)-u_{\lambda }(x)=R_{N}\int _{\Sigma _{\lambda }}\left( \frac{1}{|x-y|^{N-2}}-\frac{1}{|x^{\lambda }-y|^{N-2}}\right) (zv^{p-1}-z_{\lambda }v_{\lambda }^{p-1})dy. \end{aligned}$$

(5.2)

Similarly, we obtain

$$\begin{aligned} v(x)-v_{\lambda }(x)=R_{N}\int _{\Sigma _{\lambda }}\left( \frac{1}{|x-y|^{N-2}}-\frac{1}{|x^{\lambda }-y|^{N-2}}\right) (hu^{q-1}-h_{\lambda }u_{\lambda }^{q-1})dy. \end{aligned}$$

(5.3)

First, we consider the case where $2\alpha _{1}+\mu _{1}\ne 4$ and $2\alpha _{2}+\mu _{2}\ne 4$. We have the following property.

Lemma 5.1

Suppose that $\alpha _{i}\ge 0$, $0<\mu _{i}<N$, $2\alpha _{i}+\mu _{i}\le 3$ if $N=3$ while $2\alpha _{i}+\mu _{i}<4$ if $N\ge 4$ $(i=1,2)$. For any $\lambda <0$, there exists a constant $C>0$ such that

$$\begin{aligned} \begin{aligned} \Vert u-u_{\lambda }\Vert _{L^{2^{*}}(\Sigma _{\lambda }^{u})} \le \,&C\left( \Vert v\Vert _{L^{2^{*}}(\Sigma _{\lambda }^{u})}^{p}\Vert v\Vert _{L^{2^{*}}(\Sigma _{\lambda }^u)}^{p-2}+ \Vert v\Vert _{L^{2^{*}}(\Sigma _{\lambda }^{u})}^{p-1}\Vert v\Vert _{L^{2^{*}}(\Sigma _{\lambda }^{v})}^{p-1} \right) \Vert v-v_{\lambda }\Vert _{L^{2^{*}}(\Sigma _{\lambda }^{v})}, \end{aligned}\nonumber \\ \end{aligned}$$

(5.4)

and

$$\begin{aligned} \begin{aligned} \Vert v-v_{\lambda }\Vert _{L^{2^{*}}(\Sigma _{\lambda }^{v})} \le \,&C\left( \Vert u\Vert _{L^{2^{*}}(\Sigma _{\lambda }^{v})}^{q}\Vert u\Vert _{L^{2^{*}}(\Sigma _{\lambda }^v)}^{q-2}+ \Vert u\Vert _{L^{2^{*}}(\Sigma _{\lambda }^{u})}^{q-1}\Vert u\Vert _{L^{2^{*}}(\Sigma _{\lambda }^{v})}^{q-1} \right) \Vert u-u_{\lambda }\Vert _{L^{2^{*}}(\Sigma _{\lambda }^{u})}. \end{aligned}\nonumber \\ \end{aligned}$$

(5.5)

Proof

For any $x\in \Sigma _{\lambda }$, notice $|x^{\lambda }-y|\ge |x-y|$, using the mean value theorem, from (5.2) we know that

$$\begin{aligned} u(x)-u_{\lambda }(x)\le R_{N}(p-1)\int _{\Sigma _{\lambda }^u}\frac{zv^{p-2}(v-v_{\lambda })}{|x-y|^{N-2}}dy+R_{N}\int _{\Sigma _{\lambda }^z}\frac{v^{p-1}(z-z_{\lambda })}{|x-y|^{N-2}}dy. \end{aligned}$$

By applying the HLS inequality and the Hölder inequality, we obtain

$$\begin{aligned} \begin{aligned} \Vert u-u_{\lambda }\Vert _{L^{2^{*}}(\Sigma _{\lambda }^{u})}\le \,&C\Vert zv^{p-2}(v-v_{\lambda })\Vert _{L^{\frac{2N}{N+2}}(\Sigma _{\lambda }^{u})}+C\Vert v^{p-1}(z-z_{\lambda })\Vert _{L^{\frac{2N}{N+2}}(\Sigma _{\lambda }^{u})}\\ \le \,&C\Vert zv^{p-2}\Vert _{L^{\frac{N}{2}}(\Sigma _{\lambda }^{u})}\Vert (v-v_{\lambda })\Vert _{L^{2^{*}}(\Sigma _{\lambda }^{v})}\\&+C\Vert v^{p-1}\Vert _{L^{\frac{2N}{N+2-2\alpha _{1}-\mu _{1}}}(\Sigma _{\lambda }^{u})}\Vert (z-z_{\lambda })\Vert _{L^{\frac{2N}{2\alpha _{1}+\mu _{1}}}(\Sigma _{\lambda }^{z})}\\ \le \,&C\Vert z\Vert _{L^{\frac{2N}{2\alpha _{1}+\mu _{1}}}(\Sigma _{\lambda }^{u})}\Vert v\Vert _{L^{2^{*}}(\Sigma _{\lambda }^u)}^{p-2}\Vert v-v_{\lambda }\Vert _{L^{2^{*}}(\Sigma _{\lambda }^{v})}\\&+C\Vert z-z_{\lambda }\Vert _{L^{\frac{2N}{2\alpha _{1}+\mu _{1}}}(\Sigma _{\lambda }^z)}\Vert v\Vert _{L^{2^{*}}(\Sigma _{\lambda }^{u})}^{p-1}. \end{aligned} \end{aligned}$$

(5.6)

Analogously, we also have

$$\begin{aligned} \begin{aligned} \Vert v-v_{\lambda }\Vert _{L^{2^{*}}(\Sigma _{\lambda }^{v})} \le \,&C\Vert hu^{q-2}(u-u_{\lambda })\Vert _{L^{\frac{2N}{N+2}}(\Sigma _{\lambda }^{v})}+C\Vert u^{q-1}(h-h_{\lambda })\Vert _{L^{\frac{2N}{N+2}}(\Sigma _{\lambda }^{v})}\\ \le \,&C\Vert hu^{q-2}\Vert _{L^{\frac{N}{2}}(\Sigma _{\lambda }^{v})}\Vert (u-u_{\lambda })\Vert _{L^{2^{*}}(\Sigma _{\lambda }^{u})}\\&+C\Vert u^{q-1}\Vert _{L^{\frac{2N}{N+2-2\alpha _{2}-\mu _{2}}}(\Sigma _{\lambda }^{v})}\Vert (h-h_{\lambda })\Vert _{L^{\frac{2N}{2\alpha _{2}+\mu _{2}}}(\Sigma _{\lambda }^{h})}\\ \le \,&C\Vert h\Vert _{L^{\frac{2N}{2\alpha _{2}+\mu _{2}}}(\Sigma _{\lambda }^{v})}\Vert u\Vert _{L^{2^{*}}(\Sigma _{\lambda }^v)}^{q-2}\Vert u-u_{\lambda }\Vert _{L^{2^{*}}(\Sigma _{\lambda }^{u})}\\&+C\Vert h-h_{\lambda }\Vert _{L^{\frac{2N}{2\alpha _{2}+\mu _{2}}}(\Sigma _{\lambda }^h)}\Vert u\Vert _{L^{2^{*}}(\Sigma _{\lambda }^{v})}^{q-1}. \end{aligned} \end{aligned}$$

(5.7)

From (3.8) and (3.9), we can deduce that

$$\begin{aligned} \Vert h-h_{\lambda }\Vert _{L^{\frac{2N}{2\alpha _{2}+\mu _{2}}}(\Sigma _{\lambda }^h)}\le & {} C\Vert u^{q-1}(u-u_{\lambda })\Vert _{L^{\frac{2N}{2N-2\alpha _{2}-\mu _{2}}}(\Sigma _{\lambda }^h\cap \Sigma _{\lambda }^u)}\nonumber \\\le & {} C\Vert u\Vert _{L^{2^{*}}(\Sigma _{\lambda }^{u})}^{q-1}\Vert u-u_{\lambda }\Vert _{L^{2^{*}}(\Sigma _{\lambda }^{u})}. \end{aligned}$$

(5.8)

and

$$\begin{aligned} \Vert z-z_{\lambda }\Vert _{L^{\frac{2N}{2\alpha _{1}+\mu _{1}}}(\Sigma _{\lambda }^z)}\le & {} C\Vert v^{p-1}(v-v_{\lambda })\Vert _{L^{\frac{2N}{2N-2\alpha _{1}-\mu _{1}}}(\Sigma _{\lambda }^z\cap \Sigma _{\lambda }^v)}\nonumber \\\le & {} C\Vert v\Vert _{L^{2^{*}}(\Sigma _{\lambda }^{v})}^{p-1}\Vert v-v_{\lambda }\Vert _{L^{2^{*}}(\Sigma _{\lambda }^{v})}. \end{aligned}$$

(5.9)

Additionally, using the weighted HLS inequality again, we have

$$\begin{aligned} \Vert z(x)\Vert _{L^{\frac{2N}{2\alpha _{1}+\mu _{1}}}(\Sigma _{\lambda }^{u})}\le C\Vert v^{p}\Vert _{L^{\frac{2N}{2N-2\alpha _{1}-\mu _{1}}}(\Sigma _{\lambda }^{u})}\le C\Vert v\Vert _{L^{2^{*}}(\Sigma _{\lambda }^{u})}^{p}, \end{aligned}$$

(5.10)

and

$$\begin{aligned} \Vert h(x)\Vert _{L^{\frac{2N}{2\alpha _{2}+\mu _{2}}}(\Sigma _{\lambda }^{v})}\le C\Vert u^{q}\Vert _{L^{\frac{2N}{2N-2\alpha _{2}-\mu _{2}}}(\Sigma _{\lambda }^{v})}\le C\Vert u\Vert _{L^{2^{*}}(\Sigma _{\lambda }^{v})}^{q}. \end{aligned}$$

(5.11)

Inserting (5.8)–(5.11) to (5.6) and (5.7), we can obtain (5.4) and (5.5). The proof is completed. $\square$

For the case $2\alpha _{i}+\mu _{i}=4$ $(i=1,2)$ or $2\alpha _{1}+\mu _{1}=4$ and $2\alpha _{2}+\mu _{2} \ne 4$, by the same derivation of the above, it is not difficult to find that the Lemma 5.1 would be replaced by the following lemmas.

Lemma 5.2

Suppose that $N\ge 4$, $\alpha _{i}\ge 0$, $0<\mu _{i}<N$ and $2\alpha _{i}+\mu _{i}=4(i=1,2)$. For any $\lambda <0$, there exists a constant $C>0$ such that

$$\begin{aligned} \begin{aligned} \Vert u-u_{\lambda }\Vert _{L^{2^{*}}(\Sigma _{\lambda }^{u})} \le \,&C\left( \Vert v\Vert _{L^{2^{*}}(\Sigma _{\lambda }^{u})}\Vert v\Vert _{L^{2^{*}}(\Sigma _{\lambda }^{v})} \right) \Vert v-v_{\lambda }\Vert _{L^{2^{*}}(\Sigma _{\lambda }^{v})}, \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} \Vert v-v_{\lambda }\Vert _{L^{2^{*}}(\Sigma _{\lambda }^{v})} \le&C\left( \Vert u\Vert _{L^{2^{*}}(\Sigma _{\lambda }^{u})}\Vert u\Vert _{L^{2^{*}}(\Sigma _{\lambda }^{v})} \right) \Vert u-u_{\lambda }\Vert _{L^{2^{*}}(\Sigma _{\lambda }^{u})}. \end{aligned} \end{aligned}$$

Lemma 5.3

Suppose that $N\ge 4$, $\alpha _{i}\ge 0$, $0<\mu _{i}<N$, $2\alpha _{1}+\mu _{1}=4$ and $2\alpha _{2}+\mu _{2}<4$. For any $\lambda <0$, there exists a constant $C>0$ such that

$$\begin{aligned} \begin{aligned} \Vert u-u_{\lambda }\Vert _{L^{2^{*}}(\Sigma _{\lambda }^{u})} \le&C\left( \Vert v\Vert _{L^{2^{*}}(\Sigma _{\lambda }^{u})}\Vert v\Vert _{L^{2^{*}}(\Sigma _{\lambda }^{v})}\right) \Vert v-v_{\lambda }\Vert _{L^{2^{*}}(\Sigma _{\lambda }^{v})}, \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} \Vert v-v_{\lambda }\Vert _{L^{2^{*}}(\Sigma _{\lambda }^{v})} \le&C\left( \Vert u\Vert _{L^{2^{*}}(\Sigma _{\lambda }^{v})}^{q}\Vert u\Vert _{L^{2^{*}}(\Sigma _{\lambda }^v)}^{q-2}+ \Vert u\Vert _{L^{2^{*}}(\Sigma _{\lambda }^{u})}^{q-1}\Vert u\Vert _{L^{2^{*}}(\Sigma _{\lambda }^{v})}^{q-1} \right) \Vert u-u_{\lambda }\Vert _{L^{2^{*}}(\Sigma _{\lambda }^{u})}. \end{aligned} \end{aligned}$$

The integral inequalities in Lemmas 5.1–5.3 can provide a beginning of the procedure of moving plane methods in integral forms. Thus, we are going to prove that for sufficiently small $\lambda$, there holds $u(x)\le u_{\lambda }(x)$ and $v(x)\le v_{\lambda }(x)$ for any $x\in \Sigma _{\lambda }$, which implies that we can start to move the plane from $-\infty$ to the right.

Lemma 5.4

Suppose that $N\ge 3$, $\alpha _{i}\ge 0$, $0<\mu _{i}<N$ and $0<2\alpha _{i}+\mu _{i}\le min\left\{ 4, N\right\}$. Let $(u,v) \in L^{\frac{2N}{N-2}}({\mathbb {R}}^N)\times L^{\frac{2N}{N-2}}({\mathbb {R}}^N)$ be a pair of positive solutions of system (5.1), then there exists $M>0$ such that for any $\lambda <-M$, we have

$$\begin{aligned} u(x)\le u_{\lambda }(x),\ v(x)\le v_{\lambda }(x) \quad \forall x\in \Sigma _{\lambda }. \end{aligned}$$

(5.12)

Proof

Since u, v are integrable, letting $\lambda \rightarrow -\infty$, we have

$$\begin{aligned} \Vert v\Vert _{L^{2^{*}}(\Sigma _{\lambda }^{u})}^{p}\Vert v\Vert _{L^{2^{*}}(\Sigma _{\lambda }^u)}^{p-2}+ \Vert v\Vert _{L^{2^{*}}(\Sigma _{\lambda }^{u})}^{p-1}\Vert v\Vert _{L^{2^{*}}(\Sigma _{\lambda }^{v})}^{p-1}\le \frac{1}{2C}, \end{aligned}$$

(5.13)

and

$$\begin{aligned} \Vert u\Vert _{L^{2^{*}}(\Sigma _{\lambda }^{v})}^{q}\Vert u\Vert _{L^{2^{*}}(\Sigma _{\lambda }^v)}^{q-2}+ \Vert u\Vert _{L^{2^{*}}(\Sigma _{\lambda }^{u})}^{q-1}\Vert u\Vert _{L^{2^{*}}(\Sigma _{\lambda }^{v})}^{q-1}\le \frac{1}{2C}, \end{aligned}$$

(5.14)

where the constant C is the same as in Lemma 5.1. Hence, as $\lambda \rightarrow -\infty$ in (5.4) and (5.5), we easily get

$$\begin{aligned} \Vert u(x)-u_{\lambda }(x)\Vert _{L^{2^{*}}(\Sigma _{\lambda }^{u})}=0,\quad \Vert v(x)-v_{\lambda }(x)\Vert _{L^{2^{*}}(\Sigma _{\lambda }^{v})}=0, \end{aligned}$$

which shows that $\Sigma _{\lambda }^{u}=\Sigma _{\lambda }^{v}=\emptyset .$ Therefore, there exists $M>0$ such that for any $\lambda <-M$, relation (5.12) holds. $\square$

Consequently, we now move the plane $T_{\lambda }=\left\{ x\in {\mathbb {R}}^N|x_{1}=\lambda \right\}$ to the right as long as (5.12) is satisfied. We can certainly define

$$\begin{aligned} \lambda _{0}=\sup \left\{ \lambda \ | \ u(x)\le u_{\rho }(x), v(x)\le v_{\rho }(x), x\in \Sigma _{\rho }, \rho \le \lambda \right\} , \end{aligned}$$

hence $\lambda _{0}<+\infty$. This can be seen by applying a similar argument as in the above lemmas from $\lambda$ near $+\infty$.

Next, we deduce that u, v are symmetric about the critical plane $x_{1}=\lambda _{0}$ in the $x_{1}$ direction.

Lemma 5.5

Under the assumption of Lemma 5.4, for any $\lambda _{0}<0$, we have

$$\begin{aligned} u(x)\equiv u_{\lambda _{0}}(x),\ v(x)\equiv v_{\lambda _{0}}(x) \quad \forall x\in \Sigma _{\lambda _{0}}. \end{aligned}$$

(5.15)

Proof

Suppose on the contrary that at $\lambda _{0}<0$, there hold $u(x)\le u_{\lambda _{0}}(x)$ and $v(x)\le v_{\lambda _{0}}(x)$, but $u(x)\not \equiv u_{\lambda _{0}}(x)$ or $v(x)\not \equiv v_{\lambda _{0}}(x)$ on $\Sigma _{\lambda _{0}}$. It is sufficient to claim that there exists an $\varepsilon >0$ such that $u(x)\le u_{\lambda }(x)$ and $v(x)\le v_{\lambda }(x)$ on $\Sigma _{\lambda }$ for any $\lambda \in \left[ \lambda _{0},\lambda _{0}+\varepsilon \right)$.

Indeed, for any $\eta >0$, we can choose suitable $R>0$ large enough such that

$$\begin{aligned} \Vert v\Vert _{L^{2^{*}}({\mathbb {R}}^N- B_{R}(0))}^{p}\Vert v\Vert _{L^{2^{*}}({\mathbb {R}}^N- B_{R}(0))}^{p-2}+ \Vert v\Vert _{L^{2^{*}}({\mathbb {R}}^N- B_{R}(0)))}^{p-1}\Vert v\Vert _{L^{2^{*}}({\mathbb {R}}^N- B_{R}(0)))}^{p-1}\le \eta ,\nonumber \\ \end{aligned}$$

(5.16)

and

$$\begin{aligned} \Vert u\Vert _{L^{2^{*}}({\mathbb {R}}^N- B_{R}(0)))}^{q}\Vert u\Vert _{L^{2^{*}}({\mathbb {R}}^N- B_{R}(0)))}^{q-2}+ \Vert u\Vert _{L^{2^{*}}({\mathbb {R}}^N- B_{R}(0)))}^{q-1}\Vert u\Vert _{L^{2^{*}}({\mathbb {R}}^N- B_{R}(0)))}^{q-1}\le \eta .\nonumber \\ \end{aligned}$$

(5.17)

For such $R>0$ and $\lambda >\lambda _{0}$, we can also show that the measures of the sets $\Sigma _{\lambda }^{u}\cap B_{R}(0)$ and $\Sigma _{\lambda }^{v}\cap B_{R}(0)$ go to 0 as $\lambda \rightarrow \lambda _{0}$.

By contradiction, we assume that

$$\begin{aligned} u(x)\not \equiv u_{\lambda _{0}}(x) \ \text{ on }\ \Sigma _{\lambda _{0}}. \end{aligned}$$

From (3.8) and (3.9), we obtain

$$\begin{aligned} h(x)-h_{\lambda _{0}}(x)<0,\quad z(x)-z_{\lambda _{0}}(x)\le 0. \end{aligned}$$

Thus, by (5.2) and (5.3), we yield

$$\begin{aligned} \begin{aligned} v(x)&- v_{\lambda _{0}}(x)<0\ \text{ on }\ \Sigma _{\lambda _{0}},\\ u(x)&- u_{\lambda _{0}}(x)<0\ \text{ on }\ \Sigma _{\lambda _{0}}. \end{aligned} \end{aligned}$$

Naturally, take the same derivations as in Lemma 3.3, we obtain that

$$\begin{aligned} {\mathcal {L}}(\Sigma _{\lambda }^{u}\cap B_{R}(0))\rightarrow 0, \end{aligned}$$

(5.18)

and

$$\begin{aligned} {\mathcal {L}}(\Sigma _{\lambda }^{v}\cap B_{R}(0))\rightarrow 0, \end{aligned}$$

(5.19)

where ${\mathcal {L}}$ is the Lebesgue measure.

Combining (5.16)–(5.19), there exists an $\varepsilon >0$ such that for any $\lambda \in [ \lambda _{0},\lambda _{0}+\varepsilon )$,

$$\begin{aligned} \Vert v\Vert _{L^{2^{*}}(\Sigma _{\lambda }^{u})}^{p}\Vert v\Vert _{L^{2^{*}}(\Sigma _{\lambda }^u)}^{p-2}+ \Vert v\Vert _{L^{2^{*}}(\Sigma _{\lambda }^{u})}^{p-1}\Vert v\Vert _{L^{2^{*}}(\Sigma _{\lambda }^{v})}^{p-1}\le \frac{1}{2C}, \end{aligned}$$

(5.20)

and

$$\begin{aligned} \Vert u\Vert _{L^{2^{*}}(\Sigma _{\lambda }^{v})}^{q}\Vert u\Vert _{L^{2^{*}}(\Sigma _{\lambda }^v)}^{q-2}+ \Vert u\Vert _{L^{2^{*}}(\Sigma _{\lambda }^{u})}^{q-1}\Vert u\Vert _{L^{2^{*}}(\Sigma _{\lambda }^{v})}^{q-1}\le \frac{1}{2C}, \end{aligned}$$

(5.21)

where the constant C is the same as in Lemma 5.1. By the same arguments as above, we can conclude that $\Sigma _{\lambda }^{u}=\Sigma _{\lambda }^{v}=\emptyset$. Therefore, there exists an $\varepsilon >0$ such that $u(x)\le u_{\lambda }(x)$ and $v(x)\le v_{\lambda }(x)$ on $\Sigma _{\lambda }$ for any $\lambda \in \left[ \lambda _{0},\lambda _{0}+\varepsilon \right)$. This contradicts the definition of $\lambda _{0}$, then we have $u(x)\equiv u_{\lambda _{0}}(x)$ on $\Sigma _{\lambda _{0}}$.

Similarly, if $v(x)\not \equiv v_{\lambda _{0}}$ on $\Sigma _{\lambda _{0}}$, we obtain a contradiction. The proof is completed. $\square$

5.1 Proof of Theorem 2.8

Similarly, we can also move the plane from $+\infty$ to left, and define

$$\begin{aligned} \lambda _{1}=\inf \left\{ \lambda \ |\ u(x)\le u_{\rho }(x),\ v(x)\le v_{\rho }(x),\ x\in \Sigma _{\rho }^{'},\ \rho \ge \lambda \right\} , \end{aligned}$$

where $\Sigma _{\rho }^{'}=\left\{ x\in {\mathbb {R}}^N|x_{1}>\rho \right\}$.

If $\lambda _{0}=\lambda _{1}\ne 0$, then both u and v are radially symmetric and decreasing about the plane $x_{1}=\lambda _{0}$, which implies $u(x)\equiv u_{\lambda _{0}}(x)$ and $v(x)\equiv v_{\lambda _{0}}(x)$ on $\Sigma _{\lambda _{0}}$. Thus, we also get

$$\begin{aligned} z(x)-z_{\lambda _{0}}(x)<0\quad \text{ and }\quad h(x)-h_{\lambda _{0}}(x)<0, \end{aligned}$$

from which we can deduce that

$$\begin{aligned} \begin{aligned} 0=u(x)-u_{\lambda _{0}}(x)=&R_{N}\int _{\Sigma _{\lambda _{0}}}\left( \frac{1}{|x-y|^{N-2}}-\frac{1}{|x^{\lambda _{0}}-y|^{N-2}}\right) (z-z_{\lambda _{0}})v_{\lambda _{0}}^{p-1}dy\\ \le&R_{N}\int _{\Sigma _{\lambda _{0}}}\frac{1}{|x-y|^{N-2}}(z-z_{\lambda _{0}})v_{\lambda _{0}}^{p-1}dy<0. \end{aligned} \end{aligned}$$

This contradiction shows that $\lambda _{0}=\lambda _{1}=0$. Since the direction of $x_{1}$ is arbitrary, we conclude that u and v are radially symmetric and decreasing about the origin. ${} \Box$