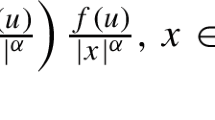Non-linear Schrödinger equation with non-local regional diffusion

Abstract

In this article we are interested in the nonlinear Schrödinger equation with non-local regional difussion

$$\begin{aligned}&\epsilon ^{2\alpha } (-\Delta )_{\rho }^{\alpha }u + u = f(u) \hbox { in } \mathbb {R}^{n}, \\&u \in H^{\alpha }(\mathbb {R}^{n}), \end{aligned}$$

where $f$ is a super-linear sub-critical function and $(-\Delta )_{\rho }^{\alpha }$ is a variational version of the regional laplacian, whose range of scope is a ball with radius $\rho (x)>0$. We study the existence of a ground state and we analyze the behavior of semi-classical solutions as $\varepsilon \rightarrow 0$.

1 Introduction

The aim of this article is to study the non-linear Schrödinger equation with non-local regional difussion

$$\begin{aligned} \epsilon ^{2\alpha } (-\Delta )_{\rho }^{\alpha }u + u = f(u) \quad \text{ in }\quad \mathbb {R}^{n},\quad u \in H^{\alpha }(\mathbb {R}^{n}), \end{aligned}$$

(1.1)

where $0< \alpha <1$, $\epsilon >0$, $n\ge 2$ and $f:\mathbb {R} \rightarrow \mathbb {R}$ is super-linear and has a sub-critical growth. The operator $(-\Delta )_{\rho }^{\alpha }$ is a variational version of the non-local regional laplacian, with range of scope determined by the positive function $\rho \in C(\mathbb {R}^{n}, \mathbb {R}^{+})$.

Recently, a great attention has been focused on the study of problems involving the fractional Laplacian, from a pure mathematical point of view as well as from concrete applications, since this operator naturally arises in many different contexts, such as, obstacle problems, financial mathematics, phase transitions, anomalous diffusions, crystal dislocations, soft thin films, semipermeable membranes, flame propagations, conservation laws, ultra relativistic limits of quantum mechanics, quasi-geostrophic flows, minimal surfaces, materials science and water waves. The literature is too wide to attempt a reasonable list of references here, so we refer the reader to the work by Di Nezza, Patalluci and Valdinoci [4], where a more extensive bibliography and an introduction to the subject are given.

In the context of fractional quantum mechanics, the non-linear fractional Schrödinger equation has been proposed by Laskin [13, 14] as a result of expanding the Feynman path integral, from the Brownian-like to the Lévy-like quantum mechanical paths. In the last 10 years, there has been a lot of interest in the study of the fractional Schrödinger equation, see the works in [2, 5, 8, 11] and [16]. In a recent paper Felmer et al. [8] considered positive solutions of nonlinear fractional Schrödinger equation

$$\begin{aligned} (-\Delta )^{\alpha }u + u = f(x,u)\;\;\text{ in }\;\; \mathbb {R}^{n}. \end{aligned}$$

(1.2)

They obtained the existence of a ground state by mountain pass argument and a comparison method devised by Rabinowitz [18] for $\alpha = 1$. They analyzed regularity, decay and symmetry properties of these solutions. At this point it is worth mentioning that the uniqueness of the ground state with power non-linearity was proved by Frank and Lenzmann [7] in the one dimensional case, and advances in the multi-dimensional case were obtained recently by Fall and Valdinoci [6]. We also mention the work by Cheng [2], where the fractional Schrödinger equation with unbounded potential

$$\begin{aligned} (-\Delta )^{\alpha }u + V(x)u = u^{p}\;\;\text{ in }\;\; \mathbb {R}^{n} \end{aligned}$$

(1.3)

was studied. The existence of a ground state of (1.3) is obtained by a Lagrange multiplier method and the Nehari manifold method is used to obtain standing waves with prescribed frequency.

On the other hand, research has been done in recent years for the regional fractional laplacian, where the scope of the operator is restricted to a variable region near each point. We mention the work by Guan [9] and Guan and Ma [10] where they study these operators, their relation with stochastic processes and they develop an integration by parts formula, and the work by Ishii and Nakamura [12], where the authors studied the Dirichlet problem for regional fractional laplacian modeled on the $p$-laplacian. These regional operators present various interesting characteristics that make them very attractive from the point of view of mathematical theory of non-local operators.

In this article we are interested in studying the non-linear Schrödinger equation when a variational version of the regional fractional laplacian is considered. We are specially interested in understanding the role of the scope function $\rho$ on the existence of positive solution and concentration in the semi-classical limit for Eq. (1.1).

Now we make precise assumptions on $\rho$ and $f$. For the scope function $\rho$ we assume $\rho : \mathbb {R}^{n}\rightarrow \mathbb {R}^{+}$ is continuous and it satisfies the following hypotheses:

• $(\rho _{1})$ There are numbers $0<\rho _0<\rho _\infty \le \infty$ such that

  $$\begin{aligned} \rho _{0 } \le \rho (x) < \rho _{\infty }, \quad \forall x \in \mathbb {R}^{n} \quad \text{ and }\quad \lim _{|x| \rightarrow \infty } \rho (x) =\rho _\infty . \end{aligned}$$

• $(\rho _{2})$ In case $\rho _\infty =\infty$ we further assume that there exists $a\in (0,1)$ such that

  $$\begin{aligned} \limsup _{|x| \rightarrow \infty } \frac{\rho (x)}{|x|}\le a. \end{aligned}$$

• $(\rho _{3})$ For any $x_{0}\in \mathbb {R}^{n}$, the equation

  $$\begin{aligned} |x| = \rho (x+x_{0}),\quad x\in \mathbb {R}^n, \end{aligned}$$

  defines an $(n-1)$-dimensional surface of class $C^1$ in $\mathbb {R}^{n}$.

Regarding the non-linearity $f$ we assume that $f:\mathbb {R}\rightarrow \mathbb {R}$ is a continuous function that satisfies the following hypotheses:

• $(f_{1})$ $f(t) \ge 0$ if $t\ge 0$ and $f(t) = 0$ if $t \le 0$.

• $(f_{2})$ The function $t \rightarrow \frac{f(t)}{t}$ is increasing for $t > 0$ and $\lim _{t\rightarrow 0} \frac{f(t)}{t} = 0$.

• $(f_{3})$ $\exists \;\theta > 2$ such that $\forall t >0$

  $$\begin{aligned} 0< \theta F(t) \le tf(t),\quad \text{ where }\quad F(t) = \int _{0}^{t}f(\xi )d\xi . \end{aligned}$$

• $(f_{4})$ $\exists \; C>0$ such that

  $$\begin{aligned} |f(t)| \le C(1+ |t|^{p}),\;\;1 < p < \frac{n+2\alpha }{n-2\alpha }. \end{aligned}$$

Before stating our results let us introduce the main ingredients involved in our approach. We let $H^\alpha (\mathbb {R}^{n})$ be the usual Sobolev space (see Sect. 2) equipped with the norm

$$\begin{aligned} \Vert u\Vert ^2=\int _{\mathbb {R}^{n}}\int _{\mathbb {R}^{n}}\frac{|u(x) - u(z)|^{2}}{|x-z|^{n+2\alpha }}dzdx + \int _{\mathbb {R}^{n}}u(x)^{2}dx. \end{aligned}$$

(1.4)

Given a function $\rho$ as above, we define

$$\begin{aligned} \Vert u\Vert ^2_\rho =\int _{\mathbb {R}^{n}}\int _{B(0,\rho (x))}\frac{|u(x) - u(z)|^{2}}{|x-z|^{n+2\alpha }}dzdx + \int _{\mathbb {R}^{n}}u(x)^{2}dx \end{aligned}$$

(1.5)

and the space

$$\begin{aligned} H_{\rho }^{\alpha }(\mathbb {R}^{n})=\{u\in L^2(\mathbb {R}^{n})\,/\, \Vert u\Vert ^2_\rho <\infty \}. \end{aligned}$$

For $u\in H_{\rho }^{\alpha }$ and $f$ satisfying ($f_{1}$)–($f_{4}$), as we see in Sect. 2, we may define the functional

$$\begin{aligned} I_{\rho }(u) = \frac{1}{2}\Vert u\Vert ^2_\rho - \int _{\mathbb {R}^{n}}F(u(x))dx, \end{aligned}$$

(1.6)

which is of class $C^1$. We say that $u\in H^{\alpha }(\mathbb {R}^{n})$ is a weak solution of (1.1) if $u$ is a critical point of $I_\rho$.

Now we are in a position to state our main existence theorem

Theorem 1.1

Assume $0<\alpha <1$ and $n\ge 2$. If $f$ satisfies ($f_{1}$)–($f_{4}$) and $\rho$ satisfies ($\rho _{1}$)–($\rho _{2}$) then (1.1) possesses at least one non-trivial weak solution. Moreover this solution satisfies $u(x)\ge 0$ a.e. for all $x\in \mathbb {R}^{n}.$

We prove the existence of a weak solution of (1.1) by applying the mountain pass theorem [1] to the functional $I_{\rho }$ defined on $H_{\rho }^{\alpha }(\mathbb {R}^{n})$. However, since Palais-Smale sequences lose compactness in $\mathbb {R}^{n}$, we need extra arguments based on comparison of the mountain pass critical value of $I_{\rho }$ with that of the limiting functional $I_{\rho _\infty }$, as devised by Rabinowitz [18]. See the work in [8], where a similar argument is used in the context of the $\alpha$-Laplacian.

In our second main theorem we are interested in the concentration behavior of ground states for the equation

$$\begin{aligned} \epsilon ^{2\alpha } (-\Delta )_{\rho }^{\alpha }u + u = u^{p}, \quad \text{ in } \quad \mathbb {R}^{n},\quad u \in H^{\alpha }(\mathbb {R}^{n}), \end{aligned}$$

(1.7)

when the positive parameter $\epsilon$ approaches zero. The scope function $\rho$, that describes the size of the ball of the influential region of the non-local operator, plays a key role in deciding the concentration point of ground states of the equation. Even though, at a first sight, the minimum point of $\rho$ seems to be the concentration point, there is a non-local effect that needs to be taken in account. We define the concentration function

$$\begin{aligned} \mathcal {H}(x) = - \frac{|S^{n-1}|}{2\alpha }\left( \frac{1}{\rho (x)^{2\alpha }} - \frac{1}{\rho _{\infty }^{2\alpha }}\right) +\frac{1}{2} \int _{\mathcal {C}^{+}(x)} \frac{dy}{|y|^{n+2\alpha }} - \frac{1}{2} \int _{\mathcal {C}^{-}(x)} \frac{dy}{|y|^{n+2\alpha }}, \end{aligned}$$

where the sets $\mathcal {C}^{+}({x})$ and $\mathcal {C}^{-}({x})$ are defined as follows

$$\begin{aligned} \mathcal {C}^{-}({x}) = \{ y\in \mathbb {R}^n : \;\; \rho (x+ y ) < |y| < \rho ({x})\} \end{aligned}$$

and

$$\begin{aligned} \mathcal {C}^{+}({x}) = \{y\in \mathbb {R}^n :\;\; \rho ({x}) < |y| < \rho (x + y )\}. \end{aligned}$$

Here we interpret the quotient $1/\rho _\infty ^{2\alpha }$ as zero, when $\rho _\infty =\infty$. Now we state our second theorem

Theorem 1.2

Let $0<\alpha <1$, $n\ge 2$. Suppose that $\rho$ satisfies ($\rho _{1}$)–($\rho _{3}$) and $1 < p < \frac{n+2\alpha }{n-2\alpha }$. Then for each sequence $\epsilon _{m} \rightarrow 0$, there exists a subsequence such that for every $m$, there is a non-negative solution $u_m=u_{\epsilon _m}$ of (1.7) that concentrates around a global minimum point $x_{0}$ of $\mathcal {H}$, as $\epsilon _m\rightarrow 0$. In more precise terms, for every $\delta >0$ there exists $R>0$ and $\epsilon _{0} >0$ such that if $\epsilon < \epsilon _{0}$ we have

$$\begin{aligned} \int _{B^c(x_0,\epsilon _m R)}u_{m}^2(x)dx \le \epsilon _m^n\delta ,\;\;\text{ and }\;\; \int _{ B(x_0,\epsilon _m R)}u_{m}^2(x)dx \ge \epsilon _m^n C,\qquad \forall \epsilon _m\le \epsilon _0, \end{aligned}$$

with $C$ a constant independent of $\delta$ and $m$.

The proof of this theorem again uses a comparison arguments in order to obtain the concentration, but here the estimates are more delicate, see Theorem 4.1. At this point we would like to comment that regularity of weak solutions to (1.1) is not considered in this article. In [8] the authors obtained regularity, up to Hölder continuity, by a bootstrap argument together with localization technique. We think that these arguments could be adapted to this problem, but that may require a considerable amount of additional work. Regularity of the solution could, in particular, help to obtain decay estimates for the solutions and then we could study further concentration properties of Eq. (1.7).

This article is organized as follows. In Sect. 2 we present preliminaries with the main tools and the functional setting of the problem and we discuss the definition of $(-\Delta )_{\rho }^{\alpha }$ and its regional character. In Sect. 3 we prove Theorem 1.1. In Sect. 4 we provide some properties of the concentration function $\mathcal {H}$ and we compute asymptotic values of the functional. In Sect. 5 we complete the study of the semi-classical limit, proving Theorem 1.2.

2 Preliminaries

In this section we recall some basic facts about the Sobolev space $H^\alpha (\mathbb {R}^n)$, its relations with the space $H^\alpha _\rho (\mathbb {R}^n)$, embeddings and compactness properties. We also discuss about the variational version of the regional fractional laplacian we consider in this paper.

Regarding the space $H^\alpha (\mathbb {R}^n)$ we recall the following embedding theorem.

Theorem 2.1

[4] Let $\alpha \in (0,1)$, then there exists a positive constant $C = C(n,\alpha )$ such that

$$\begin{aligned} \Vert u\Vert _{L^{2_{\alpha }^{*}}(\mathbb {R}^{n})}^{2} \le C \int _{\mathbb {R}^{n}} \int _{\mathbb {R}^{n}} \frac{|u(x) - u(y)|^{2}}{|x-y|^{n+2\alpha }}dydx \end{aligned}$$

(2.1)

and then $H^{\alpha }(\mathbb {R}^{n}) \hookrightarrow L^{q}(\mathbb {R}^{n})$ is continuous for all $q \in [2, 2_{\alpha }^{*}]$. Moreover, $H^{\alpha }(\mathbb {R}^{n}) \hookrightarrow L^{q}(\Omega )$ is compact for any bounded set $\Omega \subset \mathbb {R}^{n}$ and for all $q \in [2, 2_{\alpha }^{*})$, where $2_{\alpha }^{*} = \frac{2n}{n-2\alpha }$ is the critical exponent.

For the spaces $H^{\alpha }(\mathbb {R}^{n})$ and $H_{\rho }^{\alpha }(\mathbb {R}^{n})$ defined in the introduction, we consider the norms $\Vert \cdot \Vert$ and $\Vert \cdot \Vert _{\rho }$, respectively, as defined in (1.4) and (1.5). The following result is very important in our study.

Proposition 2.1

If $\rho$ satisfies ($\rho _{1}$) there exists a constant $C = C(n, \alpha , \rho _{0})> 0$ such that

$$\begin{aligned} \Vert u\Vert \le C \Vert u\Vert _{\rho } \end{aligned}$$

Proof

From the definition of $\Vert \cdot \Vert$, given $u \in H_{\rho }^{\alpha }(\mathbb {R}^{n})$ and for $\rho _0>0$, we have

$$\begin{aligned} \Vert u\Vert ^2&= \int _{\mathbb {R}^{n}} |u(x)|^{2}dx + \int _{\mathbb {R}^{n}}\int _{B(x,\rho _{0})} \frac{|u(x) - u(z)|^{2}}{|x-z|^{n+2\alpha }}dzdx\nonumber \\&+ \int _{\mathbb {R}^{n}}\int _{B^c(x,\rho _{0})} \frac{|u(x) - u(z)|^{2}}{|x-z|^{n+2\alpha }}dzdx. \end{aligned}$$

(2.2)

Using Fubini’s Theorem, we see that

$$\begin{aligned} \int _{\mathbb {R}^{n}}\int _{ B^c(x,\rho _{0})} \frac{|u(x) - u(z)|^{2}}{|x-z|^{n+2\alpha }}dzdx&= \int _{B^c (0,\rho _{0})} \int _{\mathbb {R}^{n}}\frac{|u(x+z) - u(x)|^2}{|z|^{n+2\alpha }}dxdz\nonumber \\&\le \frac{2|S^{n-1}|}{\alpha \rho _{0}^{2\alpha }}\Vert u\Vert _{L^{2}}^{2}. \end{aligned}$$

(2.3)

Then, from hypothesis ($\rho _1$), (2.2) and (2.3) it follows that

$$\begin{aligned} \Vert u\Vert ^{2}&\le C \left( \int _{\mathbb {R}^{n}}|u(x)|^{2}dx + \int _{\mathbb {R}^{n}}\int _{B(0,\rho (x))} \frac{|u(x+z) - u(x)|^{2}}{|z|^{n+2\alpha }}dzdx \right) , \end{aligned}$$

where $C= C(n,\alpha ,\rho _{0})$. This completes the proof. $\square$

Remark 2.1

By Proposition 2.1 we have that $H_{\rho }^{\alpha }(\mathbb {R}^{n}) \hookrightarrow H^{\alpha }(\mathbb {R}^{n})$ is continuous and then, by Theorem 2.1, we have that $H_{\rho }^{\alpha }(\mathbb {R}^{n}) \hookrightarrow L^{q}(\mathbb {R}^{n})$ is continuous for any $q\in [2,2_{\alpha }^{*}]$ and $H_{\rho }^{\alpha }(\mathbb {R}^{n}) \hookrightarrow L_{loc}^{q}(\mathbb {R}^{n})$ is compact for any $q\in [2,2_{\alpha }^{*})$.

Remark 2.2

Since $\Vert u\Vert _{\rho } \le \Vert u\Vert$, under the condition $(\rho _{1})$ Proposition 2.1 implies $\Vert \cdot \Vert _{\rho }$ and $\Vert \cdot \Vert$ are equivalent norms in $H^{\alpha } (\mathbb {R}^{n})$.

The following lemma is a version of the concentration compactness principle proved by Coti Zelati and Rabinowitz [3].

Lemma 2.1

Let $n\ge 2$. Assume that $\{u_{k}\}$ is bounded in $H_{\rho }^{\alpha }(\mathbb {R}^{n})$ and it satisfies

$$\begin{aligned} \lim _{k\rightarrow \infty } \sup _{y\in \mathbb {R}^{n}}\int _{B(y,R)}|u_{k}(x)|^{2}dx = 0, \end{aligned}$$

(2.4)

where $R>0$. Then $u_{k} \rightarrow 0$ in $L^{q}(\mathbb {R}^{n})$ for $2 < q < 2_{\alpha }^{*}$.

Proof

Let $2 < q < 2_{\alpha }^{*}$ and consider $\theta \in (0,1)$ such that

$$\begin{aligned} \frac{1}{q} = \frac{1-\theta }{2} + \frac{\theta }{2_{\alpha }^{*}}. \end{aligned}$$

Then by Hölder inequality and Theorem 2.1, for every $k$ we have

$$\begin{aligned} \Vert u_{k}\Vert _{L^{q}(B(y,R))}&\le \Vert u_{k}\Vert _{L^{2}(B(y,R))}^{1-\theta } \Vert u_{k}\Vert _{L^{2_{\alpha }^{*}}(B(y,R))}^{\theta }\\&\le C^{\theta } \Vert u_{k}\Vert _{L^{2}(B(y,R))}^{1-\theta } \Vert u_{k}\Vert _{\rho }^{\theta } \end{aligned}$$

so

$$\begin{aligned} \int _{B(y,R)}|u_{k}(x)|^{q}dx \le C^{\theta q} \Vert u_{k}\Vert _{L^{2}(B(y,R))}^{(1-\theta )q} \Vert u_{k}\Vert _{\rho }^{q\theta }. \end{aligned}$$

Taking $\theta = \frac{2}{q}$ and covering $\mathbb {R}^{n}$ with balls of radius $R$, in such a way that each point of $\mathbb {R}^{n}$ is contained in at most $n+1$ balls, we deduce that

$$\begin{aligned} \int _{\mathbb {R}^{n}} |u_{k}(x)|^{q}dx \le (n+1)C^{q\theta } \sup _{y\in \mathbb {R}^{n}} \left( \int _{B(y,R)}|u_{k}(x)|^{2} \right) ^{\frac{q-2}{2}}\Vert u_{k}\Vert _{\rho }^{2}. \end{aligned}$$

Then, by hypothesis, $u_{k} \rightarrow 0,$ in $L^{q}(\mathbb {R}^{n}).$ $\square$

The spaces ${H}^{\alpha }(\mathbb {R}^{n})$ and ${H}_\rho ^{\alpha }(\mathbb {R}^{n})$ are Hilbert spaces endowed with the inner products

$$\begin{aligned} \langle u,v \rangle = \int _{\mathbb {R}^{n}} u(x)v(x)dx + \int _{\mathbb {R}^{n}}\int _{\mathbb {R}^{n}} \frac{[u(x+z) - u(x)][v(x+z) - v(x)]}{|z|^{n+2\alpha }}dzdx \end{aligned}$$

and

$$\begin{aligned} \langle u,v \rangle _{\rho }= \int _{\mathbb {R}^{n}} u(x)v(x)dx + \int _{\mathbb {R}^{n}}\int _{B(0,\rho (x))} \frac{[u(x+z) - u(x)][v(x+z) - v(x)]}{|z|^{n+2\alpha }}dzdx, \end{aligned}$$

respectively. Using the equivalence of the norms $\Vert \cdot \Vert$ and $\Vert \cdot \Vert _\rho$ proved in Proposition 2.1, we can use the Lax-Milgram representation theorem to find a unique bijective linear map $\mathcal {M}_{\rho }: H^{\alpha }(\mathbb {R}^{n}) \rightarrow H^{\alpha }(\mathbb {R}^{n})$ such that

$$\begin{aligned} \langle u,v\rangle _\rho = \langle \mathcal {M}_{\rho }u , v \rangle \quad \text{ for } \text{ all }\quad u,v\in H^{\alpha }(\mathbb {R}^{n}). \end{aligned}$$

On the other hand, using Fourier transform we may consider an alternative way of defining the Sobolev space ${H}^{\alpha }(\mathbb {R}^{n})$ as

$$\begin{aligned} {H}^{\alpha }(\mathbb {R}^{n}) = \{ u\in L^{2}(\mathbb {R}^{n})/\;\;|\xi |^{\alpha }\widehat{u}(\xi ) \in L^{2}(\mathbb {R}^{n}) \} \end{aligned}$$

with inner product and norm given by

$$\begin{aligned} \langle u,v \rangle _{\widehat{H}^{\alpha }} = \int _{\mathbb {R}^{n}}(1 + |\xi |^{2{\alpha }})\widehat{u}(\xi ) \widehat{v}(\xi )d\xi \,\,\, \text{ and }\,\,\, \Vert u\Vert ^2_{\widehat{H}^{\alpha }} = \int _{\mathbb {R}^{n}} (1+|\xi |^{2{\alpha }})|\widehat{u}(\xi )|^{2}d\xi . \end{aligned}$$

If we define the fractional laplacian as

$$\begin{aligned} \widehat{(-\Delta )^{\alpha }u}(\xi ) = |\xi |^{2\alpha }\widehat{u}(\xi ), \end{aligned}$$

then it can be shown that for $0<\alpha < 1$ there exists a constant ${C}(n, \alpha )$ such that for all $u,v \in H^{\alpha }(\mathbb {R}^{n})$,

$$\begin{aligned} \int _{\mathbb {R}^{n}}(-\Delta )^{\alpha }u(x)v(x)dx&= \int _{\mathbb {R}^{n}} |\xi |^{2\alpha }\widehat{u}(\xi )\widehat{v}(\xi )d\xi \\&= {{C(n,\alpha )}}\int _{\mathbb {R}^{n}}\int _{\mathbb {R}^{n}} \frac{(u(x) - u(z))(v(x)-v(z))}{|x-z|^{n+2\alpha }}dzdx. \end{aligned}$$

See [4] Proposition 3.3. Then we have that

$$\begin{aligned} \langle u,v\rangle _\rho = \langle \mathcal {\mathcal {M}}_{\rho }u , v \rangle =\int _{\mathbb {R}^{n}} ((-\Delta )^\alpha {\mathcal {M}}_\rho u+{\mathcal {M}}_\rho u)(x)v(x)dx \end{aligned}$$

and if we define the operator $(-\Delta )_{\rho }^{\alpha }:H^{\alpha }(\mathbb {R}^{n})\rightarrow H^{-\alpha }(\mathbb {R}^{n})$ by

$$\begin{aligned} (-\Delta )_{\rho }^{\alpha } =(-\Delta )^\alpha \circ {\mathcal {M}}_\rho +{\mathcal {M}}_\rho - \mathcal {I}, \end{aligned}$$

(2.5)

where $\mathcal {I}$ is the natural injection from $H^{\alpha }(\mathbb {R}^{n})$ to $H^{-\alpha }(\mathbb {R}^{n})$ and $H^{-\alpha }(\mathbb {R}^{n})$ denotes the dual space of $H^{\alpha }(\mathbb {R}^{n})$. With these definitions we finally have that for all $u,v\in H^{\alpha }(\mathbb {R}^{n})$

$$\begin{aligned} \quad \int _{\mathbb {R}^{n}} \!\!\!\!(-\Delta )_{\rho }^{\alpha } uvdx = \int _{\mathbb {R}^{n}}\!\!\int _{B(0,\rho (x))} \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\frac{[u(x+z) - u(x)][v(x+z) - v(x)]}{|z|^{n+2\alpha }}dzdx. \end{aligned}$$

(2.6)

Proposition 2.2

If $\rho$ satisfies ($\rho _{1}$) and ($\rho _{2}$), then the operator $(-\Delta )_{\rho }^{\alpha }$ is regional, in the sense that given $u\in H^{\alpha }(\mathbb {R}^{n})$ with compact support, there exists $R>0$ so that for all $\varphi \in H^{\alpha }(\mathbb {R}^{n})$ such that

$$\begin{aligned} \mathrm{supp }(\varphi ) \cap B(0,R) = \phi \end{aligned}$$

then

$$\begin{aligned} \int _{\mathbb {R}^{n}} (-\Delta )_{\rho }^{\alpha } u(x)\varphi (x)dx =0. \end{aligned}$$

Proof

We assume that $\rho _\infty =\infty$ in ($\rho _1$) (the other case is similar). By ($\rho _2$) there exists $\bar{a}\in (0,1)$ and $R>0$ so that $|\rho (x)|\le \bar{a} |x|$ for all $|x|\ge R$.

If $\varphi \in H^{\alpha }(\mathbb {R}^{n})$ is such that $\mathrm{supp } \varphi \cap B(0, R)=\emptyset$ then

$$\begin{aligned} \cup _{x\in \mathrm{supp } \varphi } B(x,\rho (x))\subset \cup _{x\in \mathrm{supp } \varphi } B(x,\bar{a} |x|) \subset B(0, (1-\bar{a}) R)^c. \end{aligned}$$

On the other hand, given $u\in H^{\alpha }(\mathbb {R}^{n})$ with compact support, there exists $R_0$ such that

$$\begin{aligned} \cup _{x\in \mathrm{supp } u } B(x,\rho (x))\subset B(0,R_0). \end{aligned}$$

Then we make $R$ larger, if necessary, in order to get $R_0< (1-\bar{a}) R$ and thus we have that for any $(x,z)\in \mathbb {R}^{n}\times B(0,\rho (x))$ such that $x\in \mathrm{supp } \varphi$ or $x+z\in \mathrm{supp } \varphi$ we have $|x|\ge (1-\bar{a})R>R_0$ and then $u(x)=u(x+z)=0$. Consequently we have that

$$\begin{aligned}&\int _{\mathbb {R}^{n}} (-\Delta )_{\rho }^{\alpha } u(x)v(x)dx\\&\quad = \int _{\mathbb {R}^{n}}\int _{B(0,\rho (x))} \frac{[u(x+z) - u(x)][\varphi (x+z) - \varphi (x)]}{|z|^{n+2\alpha }}dzdx=0. \end{aligned}$$

$\square$

3 The ground state

In this section, our goal is to prove the existence of a ground state of Eq. (1.1), that is, a non-negative solution with lowest energy.

We start with a precise definition of the notion of solutions for Eq. (1.1).

Definition 3.1

We say that $u\in H_{\rho }^{\alpha }(\mathbb {R}^{n})$ is a weak solution of (1.1) if

$$\begin{aligned} \langle u,v \rangle _{\rho } = \int _{\mathbb {R}^{n}}f(x)v(x)dx,\quad \text{ for } \text{ all }\quad v\in H_{\rho }^{\alpha }(\mathbb {R}^{n}). \end{aligned}$$

We prove the existence of weak solution of (1.1) finding a critical point of the functional $I_{\rho }$ defined in (1.6). Using the properties of the Nemistky operators and the embeddings given in Remark 2.1, we can prove that the functional $I_{\rho }$ is of class $C^{1}(H_{\rho }^{\alpha }(\mathbb {R}^{n}), \mathbb {R})$ and we have

$$\begin{aligned} I'_{\rho }(u)v = \langle u,v \rangle _{\rho } - \int _{\mathbb {R}^{n}}f(u(x))v(x)dx,\;\;\forall \;v\in H_{\rho }^{\alpha }(\mathbb {R}^{n}). \end{aligned}$$

We define the Nehari manifold associated to the functional $I_{\rho }$ as

$$\begin{aligned} \mathcal {N}_{\rho } = \{u\in H_{\rho }^{\alpha }(\mathbb {R}^{n})\backslash \{0\}:\;\; I'_{\rho }(u)u=0\} \end{aligned}$$

and we observe that all non trivial solutions of (1.1) belong to $\mathcal {N}_{\rho }$. Next, from the growth assumptions $(f_{2})$ and $(f_{4})$ it is standard to prove that, for any $\epsilon >0$, there exists $C_{\epsilon }$ such that

$$\begin{aligned} |f(t)| \le \epsilon |t| + C_{\epsilon } |t|^{p},\;\;\forall t \in \mathbb {R}^{n} \end{aligned}$$

(3.1)

and consequently

$$\begin{aligned} |F(t)| \le \frac{\epsilon }{2} |t|^{2} + C_{\epsilon } |t|^{p+1},\;\;\forall t \in \mathbb {R}^{n}, \end{aligned}$$

(3.2)

where $1 < p <\frac{n+2\alpha }{n-2\alpha } = 2_{\alpha }^{*} - 1$. We start our analysis with

Lemma 3.1

Assume the hypotheses ($\rho _{1}$) and ($f_{1}$)–($f_{4}$) hold. Then for any $u\in H_{\rho }^{\alpha }(\mathbb {R}^{n})\setminus \{0\}$, there is a unique $t_{u} = t(u) > 0$ such that $t_{u}u \in \mathcal {N}_{\rho }$ and

$$\begin{aligned} I_{\rho }(t_{u}u) = \max _{t\ge 0} I_{\rho }(tu). \end{aligned}$$

Proof

Let $u\in H_{\rho }^{\alpha }(\mathbb {R}^{n})\setminus \{0\}$ and consider the function $\psi : \mathbb {R}^{+} \rightarrow \mathbb {R}$ defined as

$$\begin{aligned} \psi (t) = I_{\rho }(tu) = \frac{t^{2}}{2}\Vert u\Vert _{{\rho }}^{2} - \int _{\mathbb {R}^{n}}F(tu)dx. \end{aligned}$$

By (3.2) we have

$$\begin{aligned} \int _{\mathbb {R}^{n}}F(u)dx&\le C(\epsilon \Vert u\Vert _{{\rho }}^{2} + C_{\epsilon }\Vert u\Vert _{{\rho }}^{p+1}), \end{aligned}$$

then $\psi (t) > 0,\;\;\text{ for }\;\;t\;\;\text{ small }$. On the other hand, by ($f_{3}$) exists $A>0$ such that $F(t) \ge A|t|^{\theta },\;\;\forall t>0$. So

$$\begin{aligned} I_{\rho }(tu)&\le \frac{t^{2}}{2}\Vert u\Vert _{{\rho }}^{2} - At^{\theta }\int _{\mathbb {R}^{n}}|u|^{\theta }dx \end{aligned}$$

(3.3)

and since $\theta > 2$, we see that $\psi (t) < 0$ for $t$ large. By ($f_{2}$), $\psi (0) = 0$, therefore there is $t_{u} = t(u) > 0$ such that

$$\begin{aligned} \psi (t_{u}) = \max _{t\ge 0} \psi (t) = \max _{t\ge 0} I_{\rho }(tu) = I_{\rho }(t_{u}u). \end{aligned}$$

We see that $\psi '(t) = 0$ is equivalent to

$$\begin{aligned} \Vert u\Vert _{{\rho }}^{2} = \int _{\mathbb {R}^{n}}\frac{f(tu)u}{t}dx, \end{aligned}$$

(3.4)

from where, using ($f_{2}$) we see that $t_{u} >0$ such that $t_{u}u \in \mathcal {N}_{\rho }$ is unique. $\square$

Now we define two critical values as follows

$$\begin{aligned} c_{\rho }^{*} = \inf _{u\in \mathcal {N}_{\rho }} I_{\rho }(u)\quad \text{ and }\quad c_{\rho } = \inf _{\gamma \in \Gamma _{\rho }} \sup _{t\in [0,1]} I_{\rho }(\gamma (t)), \end{aligned}$$

(3.5)

where $\Gamma _{\rho }$ is given by

$$\begin{aligned} \Gamma _{\rho } = \{ \gamma \in C([0,1], H_{\rho }^{\alpha }(\mathbb {R}^{n})) /\;\;\gamma (0) = 0,\;I_{\rho }(\gamma (1)) < 0 \}. \end{aligned}$$

Under our assumptions, $\Gamma _{\rho }$ is not empty and $c_{\rho } >0$. We have

Lemma 3.2

$$\begin{aligned} c_{\rho }^{*} = \inf _{u\in H_{\rho }^{\alpha }(\mathbb {R}^{n})\setminus \{0\}} \sup _{t \ge 0} I_{\rho }(t u) = c_{\rho }. \end{aligned}$$

(3.6)

Proof

We notice that $I_{\rho }$ is bounded below on $\mathcal {N}_{\rho }$, since by ($f_{3}$), $I_{\rho }(u) >0$, for all $u\in \mathcal {N}_{\rho }$, so that $c_{\rho }^{*}$ is well defined. By Lemma 3.1 for any $u\in H_{\rho }^{\alpha }(\mathbb {R}^{n})\setminus \{0\}$ there is a unique $t_{u} = t(u) >0$ such that $t_{u}u \in \mathcal {N}_{\rho },$ then

$$\begin{aligned} c_{\rho }^{*} \le \inf _{u\in H_{\rho }^{\alpha }(\mathbb {R}^{n})\setminus \{0\}} \max _{t\ge 0} I_{\rho }(tu). \end{aligned}$$

On the other hand, for any $u\in \mathcal {N}_{\rho }$, we have

$$\begin{aligned} I_{\rho }(u)&= \max _{t\ge 0} I_{\rho }(tu) \ge \inf _{u\in H_{\rho }^{\alpha }(\mathbb {R}^{n})\setminus \{0\}} \max _{t\ge 0} I_{\rho }(tu) \end{aligned}$$

so

$$\begin{aligned} c_{\rho }^{*}=\inf _{\mathcal {N}_{\rho }} I_{\rho }(u) \ge \inf _{u\in H_{\rho }^{\alpha }(\mathbb {R}^{n})\setminus \{0\}} \max _{t\ge 0} I_{\rho }(tu), \end{aligned}$$

therefore the first equality in (3.2) holds. Next we prove the other equality. We claim that for every $\gamma \in \Gamma _{\rho }$ there exists $t_{0} \in [0,1]$ such that $\gamma (t_{0}) \in \mathcal {N}_{\rho }$.

In fact, by (3.1) and continuous embeddings we have

$$\begin{aligned} \int _{\mathbb {R}^{n}} f(u)udx \le C(\epsilon \Vert u\Vert _{{\rho }}^{2} + C_{\epsilon } \Vert u\Vert _{{\rho }}^{p+1}) \end{aligned}$$

(3.7)

and then, for $\gamma \in \Gamma _\rho$ we have

$$\begin{aligned} I'_{\rho }(\gamma (t))\gamma (t)&= \Vert \gamma (t) \Vert _{{\rho }}^{2} - \int _{\mathbb {R}^{n}} f(\gamma (t))\gamma (t)dx \\&\ge \left( 1 - C(\epsilon +C_{\epsilon } ) \Vert \gamma (t)\Vert _{{\rho }}^{p-1} \right) \Vert \gamma (t)\Vert _{{\rho }}^{2}. \end{aligned}$$

If we take $r = \left( \frac{1 - \epsilon C}{C_{\epsilon } C} \right) ^{\frac{1}{p-1}}$, then we see that

$$\begin{aligned} I'_{\rho } (\gamma (t)) \gamma (t) > 0 \quad \forall \; t\in [0,1], \;\;\text{ such } \text{ that, }\;\; \Vert \gamma (t)\Vert _{{\rho }} < r. \end{aligned}$$

On the other hand, using $(f_3)$ and since $I_{\rho }(\gamma (1)) <0$, we have

$$\begin{aligned} \Vert \gamma (1)\Vert _{H_{\rho }^{\alpha }}^{2}&< \int _{\mathbb {R}^{n}} 2F(\gamma (t))dx < \int _{\mathbb {R}^{n}} \theta F(\gamma (1))dx \le \int _{\mathbb {R}^{n}} f(\gamma (1)) \gamma (1)dx, \end{aligned}$$

that implies $I'_{\rho }(\gamma (1))\gamma (1) < 0.$ Thus, by the Intermediate Value Theorem, there exists $t_{0}\in (t_{*}, 1)$ such that $I'_{\rho }(\gamma (t_{0}))\gamma (t_{0}) = 0$ and so $\gamma (t_{0}) \in \mathcal {N}_{\rho }.$, completing the proof of the claim. From this result, $\max _{t\in [0,1]} I_{\rho }(\gamma (t)) \ge I_{\rho }(\gamma (t_{0})) \ge \inf _{\mathcal {N}_{\rho }} I_{\rho }$ and then

$$\begin{aligned} c_{\rho } \ge c_{\rho }^{*}. \end{aligned}$$

(3.8)

In order to prove the other inequality we see that from (3.3), there exists $t^{*}$ large enough such that $I_{\rho }(t^{*} u) <0$. Now we define the curve $\gamma _{u} : [0,1] \rightarrow H_{\rho }^{\alpha }(\mathbb {R}^{n})$ as $\gamma _{u}(t) = t(t^{*}u)$. Then $\gamma _{u} (0) = 0,$ $I_{\rho }(\gamma (1)) = I_{\rho }(t^{*}u) <0$ and $\gamma _u$ is continuous, so that $\gamma _{u} \in \Gamma _{\rho }$. Now, by definition of $\gamma _{u}$,

$$\begin{aligned} \max _{t\ge 0} I_{\rho }(tu) \ge \max _{\xi \in [0,1]}I_{\rho }(\gamma _{u}(\xi )),\;\;\forall \;H_{\rho }^{\alpha }(\mathbb {R}^{n})\setminus \{0\} \end{aligned}$$

then $c_{\rho }^{*} \ge c_{\rho }$, completing the proof. $\square$

Lemma 3.3

Suppose $\{u_{k}\} \subset H_{\rho }^{\alpha }(\mathbb {R}^{n})$ and there exists $b>0$ such that

$$\begin{aligned} I_{\rho }(u_{k}) \le b\;\;\text{ and }\;\;I'_{\rho }(u_{k}) \rightarrow 0\quad \text{ as }\quad k\rightarrow \infty . \end{aligned}$$

(3.9)

Then either

• (i) $u_{k} \rightarrow 0$ in $H_{\rho }^{\alpha }(\mathbb {R}^{n})$, or

• (ii) there is a sequence $(y_{k})\in \mathbb {R}^{n}$, and $R, \beta > 0$ such that

  $$\begin{aligned} \liminf _{k\rightarrow \infty } \int _{B(y_{k}, R)} |u_{k}(x)|^{2}dx > \beta . \end{aligned}$$

Proof

By (3.9) it is standard to check, for $k$ large enough

$$\begin{aligned} b + \Vert u_{k}\Vert _{{\rho }} \ge I_{\rho }(u_{k}) - \frac{1}{\theta }I'_{\rho }(u_{k})u_{k} \ge \left( \frac{1}{2} - \frac{1}{\theta } \right) \Vert u_{k}\Vert _{{\rho }}^{2} \end{aligned}$$

(3.10)

and then $\{u_{k}\}$ is bounded in $H_{\rho }^{\alpha }(\mathbb {R}^{n})$. Suppose ($ii$) is not satisfied, then for any $R>0$, (2.4) holds. Consequently by Lemma 2.1

$$\begin{aligned} \Vert u_{k}\Vert _{L^{p+1}} \rightarrow 0. \end{aligned}$$

(3.11)

Then, noticing that

$$\begin{aligned} I'_{\rho }(u_{k})u_{k} = \Vert u_{k} \Vert _{{\rho }}^{2} - \int _{\mathbb {R}^{n}}f(u_{k})u_{k}dx, \end{aligned}$$

(3.12)

by (3.1) and the continuous embedding we have

$$\begin{aligned} \int _{\mathbb {R}^{n}} f(u_{k})u_{k}dx \le \epsilon C\Vert u_{k} \Vert _{{\rho }}^{2} + C_{\epsilon }\Vert u_{k} \Vert _{L^{p+1}}^{p+1} \end{aligned}$$

where $1 < p < 2_{\alpha }^{*}-1$. So

$$\begin{aligned} I'_{\rho }(u_{k})u_{k} \ge (1-\epsilon C) \Vert u_{k} \Vert _{{\rho }}^{2} - C_{\epsilon } \Vert u_{k} \Vert _{L^{p+1}}^{p+1}. \end{aligned}$$

(3.13)

Choosing an appropriate $C$ and using (3.9) and (3.11), we find that $u_{k} \rightarrow 0\;\;\text{ in }\;\;H_{\rho }^{\alpha }(\mathbb {R}^{n})$, that is, ($i$) holds. $\square$

Continuing with our analysis, we consider the functional at infinity. When $\rho _{\infty } = \infty$ then the associated limiting functional is defined as

$$\begin{aligned} I(u) = \frac{1}{2}\Vert u\Vert ^2 - \int _{\mathbb {R}^{n}}F(u(x))dx \end{aligned}$$

(3.14)

and its Euler-Lagrange equations is given by

$$\begin{aligned} (-\Delta )^{\alpha }u + u = f(u), \quad \text{ in }\quad \mathbb {R}^{n}. \end{aligned}$$

(3.15)

This problem was studied by Felmer et al. [8] and they have proved the following theorem

Theorem 3.1

[8] Under ($f_{1}$)–($f_{4}$), the functional $I$ possesses at least one critical point with critical value $c$, where $c$ is defined by

$$\begin{aligned} c = \inf _{\gamma \in \Gamma } \max _{\theta \in [0,1]} I(\gamma (\theta )) \end{aligned}$$

(3.16)

and $\Gamma$ is given by

$$\begin{aligned} \Gamma = \{\gamma \in C([0,1], H^{\alpha }(\mathbb {R}^{n}))/\;\;\gamma (0)= 0,\;\;I(\gamma (1)) < 0\}. \end{aligned}$$

When $\rho _{\infty } < \infty$, then we define $I_{\rho _{\infty }}$ as in (1.6) with $\rho (x)\equiv \rho _\infty$. Following [8] and since the functional $I_{\rho _{\infty }}$ is invariant under translation, we can prove that $I_{\rho _{\infty }}$ has a critical point with critical value $c$, given by (3.16) with $I_{\rho _{\infty }}$ instead of $I$. Now we prove the existence of weak solution of (1.1).

Proof of Theorem 1.1

By Lemma 3.2, for every sequence $\{\epsilon _{k}\}$, there exists a sequence of $\{u_{k}\}$ in $H_{\rho }^{\alpha }(\mathbb {R}^{n})$ such that $\Vert u_{k} \Vert _{H_{\rho }^{\alpha }} = 1$ and

$$\begin{aligned} c_{\rho } \le \max _{t\ge 0} I_{\rho }(tu_{k}) \le c_{\rho } + \epsilon _{k}. \end{aligned}$$

(3.17)

As in the proof of Lemma 3.2, associated with each $u_{k}$, there is a function $\gamma _{k} \in \Gamma _{\rho }$ such that

$$\begin{aligned} \max _{\xi \in [0,1]} I_{\rho }(\gamma _{k}(\xi )) \le \max _{t\ge 0} I_{\rho }(tu_{k}) \le c_{\rho } + \epsilon _{k}. \end{aligned}$$

(3.18)

Now, considering $X = H_{\rho }^{\alpha }(\mathbb {R}^{n})$, $K = [0,1]$, $K_{0} = \{0,1\}$, $M = \Gamma _{\rho }$, $\varphi = \gamma _{k}$ and

$$\begin{aligned} c_{1} = \max _{\gamma _{k}(K_{0})}I_{\rho } = 0 < c_{\rho }, \end{aligned}$$

we can use Theorem $4.3$ of [15], to find a sequence $\{w_{k}\}$ in $H_{\rho }^{\alpha }(\mathbb {R}^{n})$ and $\{\xi _{k}\} \subset [0,1]$ such that $I_{\rho }(w_{k}) \in (c_{\rho } - \epsilon _{k}, c_{\rho } + \epsilon _{k})$,

$$\begin{aligned} \Vert w_{k} - \gamma _{k}(\xi _{k}) \Vert _{{\rho }} \le \epsilon _{k}^{1/2} \quad \text{ and }\quad \Vert I'_{\rho }(w_{k}) \Vert _{(H_{\rho }^{\alpha })'} \le \epsilon _{k}^{1/2}. \end{aligned}$$

(3.19)

Now, since

$$\begin{aligned} I_{\rho }(w_{k}) \rightarrow c_{\rho }\;\;\text{ in }\;\;\mathbb {R}\;\;\text{ and }\;\;I'_{\rho }(w_{k}) \rightarrow 0\;\;\text{ in }\;\;(H_{\rho }^{\alpha }(\mathbb {R}^{n}))', \end{aligned}$$

(3.20)

as in the proof of the Lemma 3.3, we show that $\{w_{k}\}$ is bounded in $H_{\rho }^{\alpha }(\mathbb {R}^{n})$. Moreover, up to a subsequence,

$$\begin{aligned} w_{k} \rightharpoonup w\;\;\text{ in }\;\;H_{\rho }^{\alpha }(\mathbb {R}^{n})\;\;\text{ and }\;\;w_{k} \rightarrow w\;\;\text{ in }\;\;L_{loc}^{q+1}(\mathbb {R}^{n}),\;\;1 \le q < 2_{\alpha }^{*}-1, \end{aligned}$$

(3.21)

where $w$ is weak solution of (1.1). By Lemma 3.3, there is a sequence $\{y_{k}\} \subset \mathbb {R}^{n}$, $\beta >0$ and $R>0$ such that

$$\begin{aligned} \liminf _{k\rightarrow \infty } \int _{B(y_{k}, R)} w_{k}^{2}dx \ge \beta . \end{aligned}$$

(3.22)

If $\{y_{k}\}$ contains a bounded subsequence, then (3.22) guarantees that $w \ne 0$ and the results follows. If $\{y_{k}\}$ is an unbounded sequence, first we prove that

$$\begin{aligned} c > c_{\rho }\quad \text{ or }\quad c_{\rho _{\infty }} > c_{\rho }, \end{aligned}$$

(3.23)

in case $\rho _{\infty } = \infty$ or $\rho _{\infty } < \infty$, respectively. When $\rho _\infty =\infty$ we let $u$ be a critical point $u$ with critical value $c$ and for any $y\in R^{n}$, we define $u_{y}(x) = u(x+y)$. Then for any $t>0$ we have

$$\begin{aligned} c&= I(u_{y}) \ge I(tu_{y}) > I_{\rho }(t u_{y}). \end{aligned}$$

Let $t^{*}>0$ such that $t^{*}u_{y} \in \mathcal {N}_{\rho }$ and

$$\begin{aligned} I_{\rho }(t^{*} u_{y}) = \sup _{t >0} I_{\rho }(t u_{y}), \end{aligned}$$

consequently $c > I_{\rho }(t^{*}u_{y}) \ge \inf _{\mathcal {N}_{\rho }} I_{\rho }(u) = c_{\rho },$ proving the first inequality in (3.23). When $\rho _\infty <\infty$, the other inequality is obtained similarly.

Now we may assume that, for given $R>0$,

$$\begin{aligned} \lim _{k\rightarrow \infty } \int _{B(0,R)} |u_{k}|^{2}dx =0, \end{aligned}$$

(3.24)

since the contrary implies that $w \ne 0$ and we finish the proof.

We analyze first the case $\rho _{\infty } = +\infty$. For this purpose we write

$$\begin{aligned} I_{\rho } (t u_{k}) = I(t u_{k}) - \frac{1}{2}\int _{\mathbb {R}^{n}} \int _{ B^c(0,\rho (x))} \frac{|t u_{k}(x+z) - t u_{k}(x)|^{2}}{|z|^{n+2\alpha }}dzdx, \end{aligned}$$

(3.25)

for $t\ge 0$, and we estimate the second term on the right. First we see that for any $\epsilon > 0$ and $\bar{t}>0$, there exists $R>0$ such that

$$\begin{aligned} \int _{ B^c(0,R)} \int _{ B^c(0,\rho (x))} \frac{|t u_{k}(x+z) - t u_{k}(x)|^{2}}{|z|^{n+2\alpha }} dzdx \le \epsilon , \end{aligned}$$

(3.26)

for all $t\in [0,\bar{t}]$. In fact, by our assumption, for any ${M} >0$, exists $R>0$ such that, for $|x| > R$ we have that $\rho (x)> {M}$. From here, interchanging the order of integration and using the continuous embedding, we have

$$\begin{aligned}&\int _{ B^c(0,R)} \int _{ B^c(0,\rho (x))} \frac{|t u_{k}(x+z) - t u_{k}(x)|^{2}}{|z|^{n+2\alpha }} dzdx \nonumber \\&\quad \le \int _{ B^c(0, {M})} \int _{ B^c(0,R)} \frac{|t u_{k}(x+z) - t u_{k}(x)|^{2}}{|z|^{n+2\alpha }} dxdz\nonumber \\&\quad \le \int _{ B^c(0, {M})} \int _{\mathbb {R}^{n}} \frac{|t u_{k}(x+z) - t u_{k}(x)|^{2}}{|z|^{n+2\alpha }} dxdz\nonumber \\&\quad \le \frac{2 {\bar{t}}^{2} |S^{n-1}|}{\alpha {M}^{2\alpha }} \Vert u_{k}\Vert _{L^{2}}^{2} \le \frac{2 {\bar{t}}^{2} C |S^{n-1}|}{\alpha {M}^{2\alpha }} \Vert u_{k}\Vert _{{\rho }}^{2}, \end{aligned}$$

(3.27)

from were we conclude (3.26) choosing $R>0$ large enough and recalling that $\Vert u_{k}\Vert _{{\rho }} = 1$. From now on we fix $R>0$ so that (3.24) and (3.26) hold. Next we prove that

$$\begin{aligned} \lim _{k\rightarrow \infty } \int _{B(0,R)} \int _{ B^c(0,\rho (x))} \frac{|t u_{k}(x+z) - t u_{k}(x)|^{2}}{|z|^{n+2\alpha }} dzdx = 0, \end{aligned}$$

(3.28)

for all $t\in [0,\bar{t}]$. In fact, by ($\rho _{1}$) there exists $\rho _{0} >0$ such that $\rho (x) \ge \rho _{0}$ for all $x\in \mathbb {R}^{n}$, so that

$$\begin{aligned}&\int _{B(0,R)} \int _{ B^c(0,\rho (x))} \frac{|t u_{k}(x+z) - t u_{k}(x)|^{2}}{|z|^{n+2\alpha }} dzdx \nonumber \\&\quad \le \int _{ B^c(0,\rho _{0})} \int _{B(0,R)} \frac{|t u_{k}(x+z) - t u_{k}(x)|^{2}}{|z|^{n+2\alpha }} dxdz \le \frac{2{\bar{t}}^{2}|S^{n-1}|}{\alpha \rho _{0}^{2\alpha }} \Vert u_{k}\Vert _{L^{2}(B(0,R))}^{2}\qquad \qquad \quad \end{aligned}$$

(3.29)

and we obtain (3.28) by (3.24). Thus, by 3.25, (3.26) and (3.28) we obtain

$$\begin{aligned} I_{\rho }(t u_{k})&\ge I(t u_{k}) - \epsilon - \int _{B(0,R)} \int _{ B^c(0,\rho (x))} \frac{|t u_{k}(x+z) - t u_{k}(x)|^{2}}{|z|^{n+2\alpha }} dzdx. \end{aligned}$$

If we choose $t = {t^*}$ such that $I({t^*} u_{k}) = \max _{t \ge 0} I(t u_{k})$ then we see that $c_{\rho } \ge c - \epsilon ,$ from were we get a contradiction with (3.23) if we take $\epsilon >0$ small enough.

Now we analyze the case $\rho _{\infty } < +\infty$. In this case we compare the functionals $I_{\rho }$ and $I_{\rho _{\infty }}$ writting

$$\begin{aligned} I_{\rho }(u) = I_{\rho _{\infty }}(u) - \frac{1}{2}\int _{\mathbb {R}^{n}}\int _{B(0, \rho _{\infty })\setminus B(0,\rho (x))} \frac{|u(x+z) - u(x)|^{2}}{|z|^{n+2\alpha }}dzdx. \end{aligned}$$

(3.30)

By hypothesis ($\rho _{1}$), for any $\epsilon >0$ there is $R>0$ such that

$$\begin{aligned} 0< \rho _{\infty } - \rho (x) < \epsilon ,\quad \text{ whenever }\quad |x|>R. \end{aligned}$$

Proceeding as before, for all $t\in [0,\bar{t}]$, we obtain the estimate

$$\begin{aligned}&\int _{ \mathbb {R}^n}\int _{B(0, \rho _{\infty })\setminus B(0,\rho (x))} \frac{|tu_k(x+z) - tu_k(x)|^{2}}{|z|^{n+2\alpha }}dzdx \nonumber \\&\quad \le C(\epsilon )\Vert u_k\Vert _{L^{2}}^{2}+C \Vert u_k\Vert _{L^{2}(B(0,R))}^{2}, \end{aligned}$$

(3.31)

where

$$\begin{aligned} C(\epsilon )=\frac{2|S^{n-1}|{\bar{t}}^2}{\alpha } \left( \frac{1}{(\rho _{\infty } - \epsilon )^{2\alpha }} - \frac{1}{\rho _{\infty }^{2\alpha }} \right) \,\,\,\text{ and }\,\,\, C= \frac{2|S^{n-1}|{\bar{t}}^2}{\alpha }\left( \frac{1}{\rho _{0}^{2\alpha }} - \frac{1}{\rho _{\infty }^{2\alpha }}\right) . \end{aligned}$$

Thus, we obtain

$$\begin{aligned} I_{\rho }(t u_{k}) \ge I_{\rho _{\infty }}(t u_{k}) - C(\epsilon )\Vert u_k\Vert _{L^{2}}^{2}+C \Vert u_k\Vert _{L^{2}(B(0,R))}^{2}. \end{aligned}$$

Choosing $t$ appropriately and $\epsilon$ small enough we conclude that $c_{\rho } > c_{\rho _{\infty }},$ contradicting (3.23). To complete the proof we only need to prove that $u$ is non-negative. Thanks to hypothesis ($f_1$) we see that $f(-u_-(x))=0$ for all $x\in \mathbb {R}^n$, so that it is enough to prove that

$$\begin{aligned} \langle u,u_-\rangle _\rho \le -\int _{\mathbb {R}^n}u_-^2dx. \end{aligned}$$

(3.32)

Here we consider $u_-=\max \{-u,0\}$ and $u_+=\max \{u,0\}$ so that $u=u_+-u_-$. An easy computation shows that for $x,z\in \mathbb {R}^n$ we have

$$\begin{aligned} (u(x+z)-u(x))(u_-(x+z)-u_-(x))&= -u_+(x+z)u_-(x)-u_+(x)u_-(x+z)\\&-(u_-(x+z)-u_-(x))^2\le 0, \end{aligned}$$

so that, by definition of the inner product $\langle \cdot ,\cdot \rangle _\rho$ given in Sect. 2, we obtain (3.32) that proves that $u_-=0$ a.e. in $\mathbb {R}^n$. $\square$

4 Asymptotic values of the functional when $\epsilon \rightarrow 0$

In this section we make a preliminary analysis of the asymptotic behavior of the functional associated to Eq. (1.7) when $\epsilon \rightarrow 0$. In this and next section we consider the power function $f(s)=s^p$ to prove Theorem 1.2. For simplicity, we prefer to treat only the power function, but all the arguments can be adapted to deal with a general $f$ satisfying the hypotheses ($f_1$)–($f_4$). We start with some basic properties of the function $\mathcal {H}$.

Lemma 4.1

Assuming $\rho$ satisfies $(\rho _1)$–$(\rho _3)$, the function $\mathcal {H}$ is continuous and

$$\begin{aligned} \lim _{|x|\rightarrow \infty }\mathcal {H}(x)=0. \end{aligned}$$

(4.1)

Moreover, there exists $x_{0}\in \mathbb {R}^{n}$ such that

$$\begin{aligned} \inf _{x\in \mathbb {R}^n}\mathcal {H}(x)=\mathcal {H}(x_{0}) < 0. \end{aligned}$$

(4.2)

Proof

Hypothesis $(\rho _3)$ implies that the function $\mathcal {H}$ is continuous in $\mathbb {R}^n$. By definition of the sets $\mathcal {C}^+(x)$ and $\mathcal {C}^-(x)$, when $\rho _\infty <\infty$, we see that

$$\begin{aligned} \lim _{|x|\rightarrow \infty }\text{ meas }(\mathcal {C}^+(x))=0\quad \text{ and }\quad \lim _{|x|\rightarrow \infty } \text{ meas }(\mathcal {C}^-(x))=0. \end{aligned}$$

In case $\rho _\infty =\infty$, we easily see that, for every $M>0$ we have that $\mathcal {C}^+(x)\subset B^c(0,M)$ if $|x|$ is large enough. For a similar statement with $\mathcal {C}^-(x)$, we use hypothesis $(\rho _2)$ to get that, for $|x|$ large enough,

$$\begin{aligned} |x+y|\ge \frac{1-a}{2}|x|, \quad \text{ for } \text{ all }\quad y\in \mathcal {C}^-(x). \end{aligned}$$

This implies that, for every $M>0$ we have that $\mathcal {C}^-(x)\subset B^c(0,M)$ if $|x|$ is large enough. Thus we conclude that (4.1) holds.

Next we see that

$$\begin{aligned} \mathcal {H}(x)&= -\frac{|S^{n-1}|}{2\alpha }\left( \frac{1}{\rho (x)^{2\alpha }}- \frac{1}{\rho _\infty ^{2\alpha }} \right) + \frac{1}{2} \int _{\mathcal {C}^{+}(x)} \frac{dy}{|y|^{n+2\alpha }} -\frac{1}{2} \int _{\mathcal {C}^{-}(x)} \frac{dy}{|y|^{n+2\alpha }}\\&\le -\frac{|S^{n-1}|}{2\alpha }\left( \frac{1}{\rho (x)^{2\alpha }}- \frac{1}{\rho _\infty ^{2\alpha }} \right) + \int _{\mathcal {C}^{+}(x)} \frac{dy}{|y|^{n+2\alpha }} < 0, \end{aligned}$$

where the last inequality follows from the fact that $\mathcal {C}^{+}(x) \subset B^c(0,\rho (x))$ and $\mathcal {C}^{+}(x)$ is a bounded set. From here and (4.1) the existence of a global minimum is a consequence of the continuity of $\mathcal {H}$. $\square$

In this section we will consider a sequence of functions $\{w_{m}\} \subset H^{\alpha }(\mathbb {R}^{n})$ such that $\Vert w_{m} - w\Vert _{L^{2}(\mathbb {R}^{2})} \rightarrow 0$, where $w\in H^{\alpha }(\mathbb {R}^{n})$. We will also consider sequences $\{z_m\}\subset \mathbb {R}^n$ and $\{\epsilon _m\}\subset \mathbb {R}$ and assume that $\epsilon _m\rightarrow 0$ as $m\rightarrow \infty$. We define $\overline{\rho }_{m}$ as

$$\begin{aligned} \overline{\rho }_{m}(x) = \frac{1}{\epsilon _m} \rho (\epsilon _m x + \epsilon _m z_m), \end{aligned}$$

(4.3)

and we consider the functional $I_\rho$ defined in (1.6), with $F(t)=|t|^{p+1}/({p+1})$ and for different scope functions $\rho$, in particular for ${\rho _\infty }/{\epsilon _m}$ constant and $\bar{\rho }_m$ defined in (4.3). In case $\epsilon _m z_m\rightarrow \bar{x}$ we will also consider the functional with ${\rho (\bar{x})}/{\epsilon _m}$. Thus, in this section we will be considering the functionals

$$\begin{aligned} I_{\frac{\rho _{\infty }}{\epsilon _{m}}}, I_{\frac{\rho (\bar{x})}{\epsilon _{m}}}\quad \text{ and }\quad I_{\bar{\rho }_m}. \end{aligned}$$

We will also consider the functional $I$ in $\mathbb {R}^n$ (with $\rho \equiv \infty$) defined in (3.14). The following theorem is a key to understand the concentration phenomenon for Eq. (1.7).

Theorem 4.1

Under hypotheses $(\rho _{1})$–$(\rho _{3})$, we assume as above that $w_{m}, w \in H^{\alpha }(\mathbb {R}^{n})$ are such that $\Vert w_{m} - w\Vert _{L^{2}(\mathbb {R}^{2})} \rightarrow 0$ and $\epsilon _m\rightarrow 0$, as $m\rightarrow \infty$. Then we have:

• (i) If $\epsilon _m z_m\rightarrow \bar{x}$ then

  $$\begin{aligned} \lim _{m \rightarrow \infty } \frac{I_{\overline{\rho }_{m}}(w_{m}) - I_{\frac{\rho _{\infty }}{\epsilon _{m}}}(w_{m})}{\epsilon _{m}^{2\alpha }} = \Vert w\Vert _{L^{2}}^{2} \mathcal {H}(\overline{x})\qquad \text{ and } \end{aligned}$$

  (4.4)

• (ii) If $|\epsilon _{m}|z_{{m}} \rightarrow \infty$ then

  $$\begin{aligned} \lim _{m \rightarrow \infty } \frac{I_{\overline{\rho }_{m}}(w_{m}) - I_{\frac{\rho _{\infty }}{\epsilon _{m}}}(w_{m})}{\epsilon _{m}^{2\alpha }} = 0. \end{aligned}$$

  (4.5)

In various stages of the proof of this theorem it will be convenient to replace the function $w_m$ by the truncated limit $w_{R}(x) = w(x)\chi _{B(0,R)}(x)$, where $R>0$. We clearly have

Lemma 4.2

For all $\delta >0$ there exist $m(\delta )>0$ and $R(\delta )>0$ such that

$$\begin{aligned} \int _{\mathbb {R}^{n}} |w_{m}(x) - w_{R}(x)|^{2}dx < \delta ,\;\;\text{ whenever }\;\;m > m(\delta ),\;\;R>R(\delta ). \end{aligned}$$

In order to prove Theorem 4.1 we first prove several lemmas under the hypotheses (i), that is

$$\begin{aligned} \epsilon _{m}z_{m} \rightarrow \overline{x}\;\;\text{ as }\;\;m\rightarrow \infty . \end{aligned}$$

We analyze the cases $\rho _{\infty } = +\infty$ and $\rho _{\infty } < +\infty$ separately. It will be convenient to decompose the problem considering

$$\begin{aligned} I_{\overline{\rho }_{m}} (w_{m}) - I_{\frac{\rho _{\infty }}{\epsilon _{m}}}(w_{m}) = I_{\overline{\rho }_{m}}(w_{m}) - I_{\frac{\rho (\overline{x})}{\epsilon _{m}}} (w_{m}) - \left( I_{\frac{\rho _{\infty }}{\epsilon _{m}}}(w_{m}) - I_{\frac{\rho (\overline{x})}{\epsilon _{m}}} (w_{m}) \right) . \end{aligned}$$

(4.6)

For the second term of the right hand side we have

Lemma 4.3

Under assumption of Theorem 4.1 and assuming (i)

$$\begin{aligned} \lim _{m \rightarrow \infty } \frac{ I_{\frac{\rho _{\infty }}{\epsilon _{m}}}(w_{m}) - I_{\frac{\rho (\overline{x})}{\epsilon _{m}}} (w_{m}) }{ \epsilon _{m}^{2\alpha } } = \frac{|S^{n-1}|}{2\alpha }\Vert w\Vert _{L^{2}}^{2}\left( \frac{1}{\rho (\overline{x})^{2\alpha }} - \frac{1}{\rho _{\infty }^{2\alpha }}\right) . \end{aligned}$$

(4.7)

In case $\rho _{\infty } = + \infty$, here we write $I_{\frac{\rho _{\infty }}{\epsilon _{m}}}=I$ and $1/\rho _\infty ^{2\alpha }=0$.

Proof

We first consider the case $\rho _{\infty } = + \infty$. We have

$$\begin{aligned}&I(w_{m}) - I_{\frac{\rho (\overline{x})}{\epsilon _{m}}}(w_{m})\\&\quad = \frac{1}{2}\int _{\mathbb {R}^{n}}\int _{B^c(0,\frac{\rho (\overline{x})}{\epsilon _{m}})} \frac{|w_{m}(x+z) - w_{m}(x)|^{2}}{|z|^{n+2\alpha }}dzdx\\&\quad = \frac{1}{2}\int _{B^c(0,\frac{\rho (\overline{x})}{\epsilon _{m}})} \int _{\mathbb {R}^{n}}\frac{w_{m}^{2}(x+z) - 2 w_{m}(x+z)w_{m}(z) + w_{m}^{2}(x)}{|z|^{n+2\alpha }}dxdz\\&\quad = \frac{|S^{n-1}|}{2\alpha }\Vert w_{m}\Vert _{L^{2}}^{2}\frac{\epsilon _{m}^{2\alpha }}{\rho (\overline{x})^{2\alpha }} - \int _{ B^c(0,\frac{\rho (\overline{x})}{\epsilon _{m}})} \int _{\mathbb {R}^{n}} w_{m}(x+z)w_{m}(x)dx\frac{dz}{|z|^{n+2\alpha }}. \end{aligned}$$

If we denote by $E_m$ the second term above and we consider $R>0$, we have

$$\begin{aligned}&|E_m-\int _{B^c(0,\frac{\rho (\overline{x})}{\epsilon _{m}})} \int _{\mathbb {R}^{n}} w_{R}(x+z)w_{R}(x)dx\frac{dz}{|z|^{n+2\alpha }}| \\&\quad \le (\Vert w_m\Vert _{L^2}+\Vert w_R\Vert _{L^2})\Vert w_m-w_R\Vert _{L^2} \int _{B^c(0,\frac{\rho (\overline{x})}{\epsilon _{m}})} \frac{dz}{|z|^{n+2\alpha }}\\&\quad =\frac{\epsilon _m^{2\alpha }}{\rho (\bar{x})^{2\alpha }} (\Vert w_m\Vert _{L^2}+\Vert w_R\Vert _{L^2})\Vert w_m-w_R\Vert _{L^2}. \end{aligned}$$

From here, using Lemma 4.2 and the fact that $w_R(\cdot )$ and $w_R(\cdot +z)$ have disjoint supports if $|z|>2R$, we obtain that $\lim _{m\rightarrow \infty }E_m=0$, which implies the result.

In case $\rho _{\infty } < +\infty$ we proceed similarly, noticing that we have to replace the integral over $B^c\left( 0,\frac{\rho (\overline{x})}{\epsilon _{m}}\right)$ by an integral over $B\left( 0,\frac{\rho _\infty }{\epsilon _{m}}\right) \setminus B\left( 0,\frac{\rho (\overline{x})}{\epsilon _{m}}\right)$ and compute accordingly. $\square$

Now we consider the first term in (4.6), for which it is convenient to write

$$\begin{aligned} \mathcal {I}&= \frac{I_{\overline{\rho }_{m}}(w_{m}) - I_{\rho (\overline{x})/\epsilon _{m}} (w_{m})}{\epsilon _{m}^{2\alpha }}\nonumber \\&= \frac{1}{2\epsilon _{m}^{2\alpha }} \int _{\mathbb {R}^n} \int _{A(\frac{\rho (\overline{x})}{\epsilon _m},\bar{\rho }_m (x ))} \frac{|w_{m}({x+z}) - w_{m}({x})|^{2}}{|z|^{n+2\alpha }}dzdx \nonumber \\&-\frac{1}{2\epsilon _{m}^{2\alpha }} \int _{\mathbb {R}^n}\int _{A(\bar{\rho }_m (x), \frac{\rho (\overline{x})}{\epsilon _m}) } \frac{|w_{m}({x+z}) - w_{m}({x})|^{2}}{|z|^{n+2\alpha }}dzdx \nonumber \\&= \mathcal {I}_1+ \mathcal {I}_2. \end{aligned}$$

(4.8)

Here, and in what follows, we denote by $A(a,b)$ the annulus $B(0,b)\setminus B(0,a)$ and we notice that $A(a,b)=\emptyset$ when $a\ge b$.

We start our analysis with $\mathcal {I}_1$ and for this purpose, we first consider the second and third term in the expansion of the quadratic expression $|w_{m}({x+z}) - w_{m}({x})|^{2}$.

Lemma 4.4

Under assumption of Theorem 4.1 and assuming (i) we have

$$\begin{aligned} \lim _{m\rightarrow \infty } \frac{1}{\epsilon _{m}^{2\alpha }}\int _{\mathbb {R}^n} \int _{A( \frac{\rho (\overline{x})}{\epsilon _m} ,\bar{\rho }_m(x))} \frac{w_{m}({x+z})w_{m}({x})}{|z|^{n+2\alpha }}dzdx = 0 \end{aligned}$$

and

$$\begin{aligned} \lim _{m\rightarrow \infty }\frac{1}{\epsilon _{m}^{2\alpha }}\int _{\mathbb {R}^n} \int _{A( \frac{\rho (\overline{x})}{\epsilon _m} ,\bar{\rho }_m (x) )} \frac{w_{m}^{2}({x})}{|z|^{n+2\alpha }}dzdx = 0. \end{aligned}$$

Proof

The first limit is obtained using the arguments given in the proof of Lemma 4.3. To study the second limit we see that

$$\begin{aligned}&\frac{1}{\epsilon _{m}^{2\alpha }}\int _{\mathbb {R}^n} \int _{ A( \frac{\rho (\overline{x})}{\epsilon _m} ,\bar{\rho }_m (x) ) } \frac{w_{m}^{2}({x})}{|z|^{n+2\alpha }}dzdx\\&\quad = \frac{|S^{n-1}|}{2\alpha } \int _{\mathbb {R}^n} w_{m}^{2}({x}) \left( \frac{1}{\rho (\overline{x})^{2\alpha }} - \frac{1}{\rho (\epsilon _m x+\epsilon _{m}z_{m})^{2\alpha }} \right) _+dx \\&\quad \le \frac{|S^{n-1}|}{2\alpha } \int _{\mathbb {R}^n} w_{R}^{2}({x}) \left( \frac{1}{\rho (\overline{x})^{2\alpha }} - \frac{1}{\rho (\epsilon _m x+\epsilon _{m}z_{m})^{2\alpha }} \right) _+dx \\&\qquad +\frac{|S^{n-1}|}{2\alpha \rho _0^{2\alpha }} (\Vert w_m\Vert _{L^2}+\Vert w_R\Vert _{L^2})\Vert w_m-w_R\Vert _{L^2}, \end{aligned}$$

where $R>0$. By the continuity of $\rho$ and the fact that $\epsilon _m z_m\rightarrow \bar{x}$ as $m\rightarrow \infty$, we see that

$$\begin{aligned} \lim _{m\rightarrow \infty }\left( \frac{1}{\rho (\overline{x})^{2\alpha }} - \frac{1}{\rho (\epsilon _m x+\epsilon _{m}z_{m})^{2\alpha }} \right) _+=0, \end{aligned}$$

uniformly in $B(0,R)$. From here, Lemma 4.2 and the inequality above, the result follows. $\square$

Next we consider the first term in the expansion of $|w_{m}(x+z) - w_{m}(x)|^{2}$.

Lemma 4.5

Under assumption of Theorem 4.1 and assuming (i)

$$\begin{aligned} \lim _{m\rightarrow \infty } \frac{1}{\epsilon _m^{2\alpha }} \int _{\mathbb {R}^n} \int _{ A( \frac{\rho (\overline{x})}{\epsilon _m} ,\bar{\rho }_m (x) ) } \frac{w_{m}({x+z})^{2}}{|z|^{n+2\alpha }}dzdx= \Vert w\Vert _{L^2} \int _{\mathcal {C}^+(\bar{x})}\frac{dz}{|z|^{n+2\alpha }}. \end{aligned}$$

Proof

To start we consider

$$\begin{aligned} \frac{1}{\epsilon _m^{2\alpha }} \int _{\mathbb {R}^n} \int _{ A( \frac{\rho (\overline{x})}{\epsilon _m} ,\bar{\rho }_m (x) ) } \frac{w_{m}({x+z})^{2}}{|z|^{n+2\alpha }}dzdx =E_m^1+E_m^2, \end{aligned}$$

where

$$\begin{aligned} E_m^1= \frac{1}{\epsilon _m^{2\alpha }} \int _{\mathbb {R}^n} \int _{A( \frac{\rho (\overline{x})}{\epsilon _m} ,\bar{\rho }_m (x) ) } \frac{w_{R}({x+z})^{2}}{|z|^{n+2\alpha }}dzdx, \end{aligned}$$

(4.9)

and $E_{m}^{2}$ is the error term. For $E_m^2$ we have

$$\begin{aligned} |{E_m^2}|&\le \dfrac{1}{\epsilon _m^{2\alpha }} \int _{\mathbb {R}^{n}}\int _{ B^c(0,\frac{\rho (\overline{x}}{\epsilon _m}))} \dfrac{|w_{m}({x+z}) ^{2} - w_{R}({x+z})^{2}|}{|z|^{n+2\alpha }}dzdx \nonumber \\&= \frac{1}{\epsilon _m^{2\alpha }} \int _{B^c(0,\dfrac{\rho (\overline{x}}{\epsilon _m}))}\int _{\mathbb {R}^{n}} {|w_{m}({x+z}) ^{2} - w_{R}({x+z})^{2}|}dx \dfrac{dz}{|z|^{n+2\alpha }}\nonumber \\&\le \dfrac{|S^{n-1}|}{2\alpha \rho (\bar{x})^{2\alpha }} (\Vert w_m\Vert _{L^2}+\Vert w_R\Vert _{L^2})\Vert w_m-w_R\Vert _{L^2}. \end{aligned}$$

(4.10)

Next we consider $E_m^1$ and we observe that

$$\begin{aligned} E_m^1&= \frac{1}{\epsilon _m^{2\alpha }}\int _{\mathbb {R}^n}\int _{B(-x,R) \cap A( \frac{\rho (\overline{x})}{\epsilon _m} ,\bar{\rho }_m (x) )} \frac{w({x+z})^{2}}{|z|^{n+2\alpha }}dzdx \nonumber \\&= \frac{1}{\epsilon _m^{2\alpha }}\int _{\Omega _m^+}\int _{B(-x,R) \cap A( \frac{\rho (\overline{x})}{\epsilon _m} ,\bar{\rho }_m (x) )} \frac{w({x+z})^{2}}{|z|^{n+2\alpha }}dzdx, \end{aligned}$$

(4.11)

where

$$\begin{aligned} \Omega _m^{+} = \left\{ x\in \mathbb {R}^n : \;\; \frac{\rho (\overline{x})}{\epsilon _m} - R < |x| < \frac{\rho (\epsilon _m x+\epsilon _{m}z_{m})}{\epsilon _m} + R\right\} . \end{aligned}$$

(4.12)

On the other hand we see that for any $(x,z)$ such that $|x+z| < R$ we have

$$\begin{aligned} \frac{1}{(|x| + R)^{n+2\alpha }} \le \frac{1}{|z|^{n+2\alpha }} \le \frac{1}{(|x| - R)^{n+2\alpha }}. \end{aligned}$$

(4.13)

Therefore

$$\begin{aligned} E_m^1&\le \frac{1}{\epsilon _m^{2\alpha }}\int _{\Omega _m^+} \frac{1}{(|x| - R)^{n+2\alpha }}\int _{B(-x,R) \cap A( \frac{\rho (\overline{x})}{\epsilon _m} ,\bar{\rho }_m (x) )} {w({x+z})^{2}}dzdx\nonumber \\&\le \frac{\Vert w_R\Vert _{L^2}}{\epsilon _m^{2\alpha }}\left( \int _{M_m} \frac{dx}{(|x| - R)^{n+2\alpha }}+ \int _{N_m} \frac{dx}{(|x| - R)^{n+2\alpha }}, \right) \end{aligned}$$

(4.14)

where the sets $M_m$ and $N_m$ are defined as follows

$$\begin{aligned} M_m&= \{x\in \Omega _m^+ :\,\, B(-x,R) \subset A( \frac{\rho (\overline{x})}{\epsilon _m} ,\bar{\rho }_m (x) ) \}\\&= \left\{ x\in \mathbb {R}^n :\,\, \frac{\rho (\overline{x})}{\epsilon _m} +R< |x| < \bar{\rho }_m (x) -R \right\} \end{aligned}$$

and

$$\begin{aligned} N_m&= \{ x\in \Omega _m^+\setminus M_m :\,\, B(-x,R) \cap A( \frac{\rho (\overline{x})}{\epsilon _m} ,\bar{\rho }_m (x) )\not = \emptyset \}\\&= \{ x\in \mathbb {R}^n :\,\, \frac{\rho (\overline{x})}{\epsilon _m} -R< |x| < \frac{\rho (\overline{x})}{\epsilon _m} +R\}\cup \\&\{ x\in \mathbb {R}^n :\,\, \bar{\rho }_m (x) -R<|x|<\bar{\rho }_m (x)+R \} =N_m^1\cup N_m^2. \end{aligned}$$

Similarly, from (4.11), (4.12) and (4.13) we find that

$$\begin{aligned} E_m^1&\ge \frac{1}{\epsilon _m^{2\alpha }}\int _{\Omega _m^+} \frac{1}{(|x| + R)^{n+2\alpha }}\int _{B(-x,R) \cap A( \frac{\rho (\overline{x})}{\epsilon _m} ,\bar{\rho }_m (x) )} {w({x+z})^{2}}dzdx\nonumber \\&\ge \frac{\Vert w_R\Vert _{L^2}}{\epsilon _m^{2\alpha }} \int _{M_m} \frac{dx}{(|x| + R)^{n+2\alpha }}. \end{aligned}$$

(4.15)

In order to complete the analysis of $E_m^1$ we just need to look at the limit of the integrals. We recall that, by hypothesis ($\rho _3$), the set defined by the equation

$$\begin{aligned} \rho (y+\bar{x})=|y|, \end{aligned}$$

is an ($n-1$)-dimensional surface and that we are assuming that $\lim _{m\rightarrow \infty } \epsilon _m z_{m}=\bar{x}.$ So we have

$$\begin{aligned}&\lim _{m\rightarrow \infty }\frac{1}{\epsilon _m^{2\alpha }}\int _{N_m^1}\frac{dx}{(|x|-R)^{n+2\alpha }}\\&\quad =\lim _{m\rightarrow \infty } \int _{\{ |\rho (y+\epsilon _mz_m)-|y||< \epsilon _m R\} }\frac{dy}{(|y|-\epsilon _m R)^{n+2\alpha }}=0. \end{aligned}$$

Using similar arguments we obtain

$$\begin{aligned} \lim _{m\rightarrow \infty }\frac{1}{\epsilon _m^{2\alpha }}\int _{N_m^2}\frac{dx}{(|x|-R)^{n+2\alpha }}=0 \end{aligned}$$

and

$$\begin{aligned} \lim _{m\rightarrow \infty }\frac{1}{\epsilon _m^{2\alpha }} \int _{M_m} \frac{dx}{(|x| \pm R)^{n+2\alpha }}= \int _{\mathcal {C}^+}\frac{dy}{(|y|)^{n+2\alpha }}, \end{aligned}$$

completing the proof of the lemma. $\square$

Using Lemmas 4.4 and 4.5 we conclude that

$$\begin{aligned} \lim _{m\rightarrow 0}\mathcal {I}_1&= \lim _{m\rightarrow 0} \frac{1}{2\epsilon _{m}^{2\alpha }} \int _{\mathbb {R}^n} \int _{A(\frac{\rho (\overline{x})}{\epsilon _m},\bar{\rho }_m (x ))} \frac{|w_{m}({x+z}) - w_{m}({x})|^{2}}{|z|^{n+2\alpha }}dzdx\nonumber \\&= \frac{\Vert w\Vert _{L^2}}{2} \int _{\mathcal {C}^+(\bar{x})}\frac{dz}{|z|^{n+2\alpha }}. \end{aligned}$$

(4.16)

In a complete analogous way we can prove that

$$\begin{aligned} \lim _{m\rightarrow 0}\mathcal {I}_2&= \lim _{m\rightarrow 0} \frac{1}{2\epsilon _{m}^{2\alpha }} \int _{\mathbb {R}^n} \int _{A(\bar{\rho }_m (x ),\frac{\rho (\overline{x})}{\epsilon _m})} \frac{|w_{m}({x+z}) - w_{m}({x})|^{2}}{|z|^{n+2\alpha }}dzdx\nonumber \\&= -\frac{\Vert w\Vert _{L^2}}{2} \int _{\mathcal {C}^-(\bar{x})}\frac{dz}{|z|^{n+2\alpha }}. \end{aligned}$$

(4.17)

Proof of Theorem 4.1

The proof of (i) is a consequence of (4.6), (4.8), (4.16), (4.17) and Lemma 4.3. Now we consider (ii) in case $\rho _{\infty } = \infty$. We have

$$\begin{aligned} \frac{|I(w_{m}) - I_{\overline{\rho }_{m}}(w_{m})|}{\epsilon _{m}^{2\alpha }}&= \frac{1}{2\epsilon _{m}^{2\alpha }}\int _{B(-z_m,\frac{R}{\epsilon _m})} \int _{B^{c}(0, \bar{\rho }_m(x))} \frac{|w_{m}(x+z) - w_{m}(x)|^{2}}{|z|^{n+2\alpha }}dzdx\\&+\frac{1}{2\epsilon _{m}^{2\alpha }}\int _{B^c(-z_m,\frac{R}{\epsilon _m})} \int _{B^{c}(0, \bar{\rho }_m(x))} \frac{|w_{m}(x+z) - w_{m}(x)|^{2}}{|z|^{n+2\alpha }}dzdx\\&= E^1_m+E^2_m, \end{aligned}$$

where $R>0$. By hypothesis $(\rho _{1})$ and since $\rho _\infty =\infty$, we have that for any $M>0$ there is $R>0$ and $m_0$ large enough such that

$$\begin{aligned} \rho (\epsilon _mx+\epsilon _m z_m)\ge \rho _0\quad \text{ if }\quad |x+z_m|\le \frac{R}{\epsilon _m} \end{aligned}$$

and

$$\begin{aligned} \rho (\epsilon _mx+\epsilon _m z_m)\ge M \quad \text{ if }\quad |x+z_m|> \frac{R}{\epsilon _m}, \quad \text{ for } \text{ all }\quad m\ge m_0. \end{aligned}$$

Consequently

$$\begin{aligned} E_m^1&\le \frac{1}{\epsilon _{m}^{2\alpha }}\int _{B(-z_m, \frac{R}{\epsilon _{m}})} \int _{B^{c}(0, \frac{\rho _{0}}{\epsilon _{m}})} \frac{w^2_{m}(x+z ) + w^2_{m}(x)}{|z|^{n+2\alpha }}dzdx \nonumber \\&\le \frac{|S^{n-1}|}{\alpha \rho _0^{2\alpha }} (\Vert w_m\Vert _{L^2}+\Vert w_R\Vert _{L^2})\Vert w_m-w_R\Vert _{L^2}\nonumber \\&+ \frac{1}{\epsilon _{m}^{2\alpha }}\int _{B(-z_m, \frac{R}{\epsilon _{m}})} \int _{B^{c}(0, \frac{\rho _{0}}{\epsilon _{m}})} \frac{w^2_{R}(x+z ) }{|z|^{n+2\alpha }}dzdx \nonumber \\&\quad + \frac{|S^{n-1}|}{\alpha \rho _{0}^{2\alpha }} \Vert w_{R}(.-z_{m})\Vert _{L^{2}(B(0, \frac{R}{\epsilon _{m}}))}^{2}. \end{aligned}$$

(4.18)

We observe that if $|x+z|<R$ and $|x+z_m|<R/\epsilon _m$ then $|z|>|z_m|/2$, where we may need to make $m$ larger. Then we further look at the integral above

$$\begin{aligned} \int _{B(-z_m, \frac{R}{\epsilon _{m}})} \int _{B^{c}(0, \frac{\rho _{0}}{\epsilon _{m}})} \frac{w^2_{R}(x+z ) }{|z|^{n+2\alpha }}dzdx&= \int _{B(-z_m, \frac{R}{\epsilon _{m}})} \int _{B(-x,R)} \frac{w^2(x+z ) }{|z|^{n+2\alpha }}dzdx \nonumber \\&\le \epsilon _m^{2\alpha }2^{n+2\alpha }R^n\Vert w\Vert ^2\frac{|S^{n-1}|}{n}\frac{1}{|\epsilon _m z_m|^{n+2\alpha }}.\qquad \quad \qquad \end{aligned}$$

(4.19)

On the other hand

$$\begin{aligned} E_m^2&\le \frac{1}{2\epsilon _{m}^{2\alpha }}\int _{B^{c}(-z_m, \frac{R}{\epsilon _{m}})} \int _{B^{c}(0, \frac{M}{\epsilon _{m}})} \frac{|w_{m}(x+z ) - w_{m}(x)|^{2}}{|z|^{n+2\alpha }}dzdx \nonumber \\&\le \frac{|S^{n-1}|}{2\alpha M^{2\alpha }} \Vert w_{m}\Vert _{L^{2}(\mathbb {R}^{n})}^{2}. \end{aligned}$$

(4.20)

From Lemma 4.2, (4.18)–(4.20) we can argue that (4.4) holds.

In the case $\rho _{\infty } < \infty$, by hypothesis $(\rho _{1})$ we have that, for any $\delta >0$ there is $R>0$ and $m$ large enough such that

$$\begin{aligned} \rho (\epsilon _mx+\epsilon _m z_m)\ge \rho _\infty -\delta \quad \text{ if }\quad |x+z_m|> \frac{R}{\epsilon _m}. \end{aligned}$$

Consequently

$$\begin{aligned} \frac{|I_{\frac{\rho _{\infty }}{\epsilon _{m}}}(w_{m}) - I_{\overline{\rho }_{m}}(w_{m})|}{\epsilon _{m}^{2\alpha }}&\le \frac{1}{2\epsilon _{m}^{2\alpha }}\int _{B(-z_m, \frac{R}{\epsilon _{m})}} \int _{ B^c(0, \frac{\rho _{0}}{\epsilon _{m}})} \frac{|w_{m}(x+z ) - w_{m}(x)|^{2}}{|z|^{n+2\alpha }}dzdx \nonumber \\&\quad + E_m^3, \end{aligned}$$

(4.21)

where

$$\begin{aligned} E_m^3&= \frac{1}{2\epsilon _{m}^{2\alpha }}\int _{B^{c}(-z_m, \frac{R}{\epsilon _{m}})} \int _{B(0, \frac{\rho _{\infty }}{\epsilon _{m}}) \setminus B(0, \frac{\rho _{\infty } - \delta }{\epsilon _{m}})} \frac{|w_{m}(x+z) - w_{m}(x)|^{2}}{|z|^{n+2\alpha }}dzdx \nonumber \\&\le \frac{|S^{n-1}|}{2\alpha } \Vert w_{m}\Vert _{L^{2}(\mathbb {R}^{n})}^{2}\left( \frac{1}{(\rho _{\infty } - \delta )^{2\alpha }} - \frac{1}{\rho _{\infty }^{2\alpha }} \right) . \end{aligned}$$

(4.22)

The integral in (4.21) is estimated exactly as $E_m^1$. From here and (4.21) we can argue that (4.4) holds, completing the proof. $\square$

Before leaving this section we prove a lemma that will be useful later. We recall that, by Lemma 3.1, for any $w_{m} \in H_{\rho _{m}}^{\alpha }(\mathbb {R}^{n})$, there is a unique $t_{m} = t(w_{m}) >0$ such that $t_{m}w_{m} \in \mathcal {N}_{\rho _{m}}$ and

$$\begin{aligned} I_{\rho _{m}}(t_{m}w_{m}) = \max _{t \ge 0} I_{\rho _{m}} (tw_{m}). \end{aligned}$$

(4.23)

Let $\mathcal {N}$ the Nehari manifold associated to the limit problem, that is

$$\begin{aligned} \mathcal {N} = \{u\in H^{\alpha }(\mathbb {R}^{n}) \setminus \{0\}/\;\;I'(u)u = 0\}. \end{aligned}$$

Lemma 4.6

Assume $w_{m} \rightarrow w$ in $H^{\alpha }(\mathbb {R}^{n})$ and $w \in \mathcal {N}$, then

$$\begin{aligned} \lim _{m\rightarrow \infty } t_{m} = 1. \end{aligned}$$

Proof

In fact, by definition of $t_{m}$ we have

$$\begin{aligned} t_{m}^{1-p}\Vert u_{m}\Vert ^{2} = \int _{\mathbb {R}^{n}} |u_{m}|^{p+1}dx. \end{aligned}$$

(4.24)

Since $w_{m} \rightarrow w\in \mathcal {N}$ we have that $\Vert w_{m}\Vert ^{2} \rightarrow \Vert w\Vert ^{2}$, $\int _{\mathbb {R}^{n}} u_{m}^{p+1}dx \rightarrow \int _{\mathbb {R}^{n}}u^{p+1}dx$ and $w$ is non-zero. Thus $t_{m}$ converges to $\bar{t}$ and $\bar{t}=1.$ $\square$

5 Concentration behaviour

In this section we complete our study on the concentration behavior for ground states of Eq. (1.7) and we prove Theorem 1.2. We start rescaling Eq. (1.7), for this purpose we define $\rho _{\epsilon }(x) = \frac{1}{\epsilon } \rho (\epsilon x)$ and $(-\Delta )_{\rho _{\epsilon }}^{\alpha }$ the operator defined by (2.5) changing $\rho$ by $\rho _{\epsilon }$. We then consider the rescaled equation

$$\begin{aligned} (-\Delta )_{\rho _{\epsilon }}^{\alpha } v(x) + v(x) = v^{p}(x), \quad \text{ in } \quad \mathbb {R}^{n} \end{aligned}$$

(5.1)

and we see that $u$ is a weak solution of (1.7) if and only if $v_{\epsilon }(x) = u(\epsilon x)$ is a weak solution of (5.1). In fact, by definition (2.6) and changing variables it is easy to see that for every test function $\varphi$

$$\begin{aligned}&\int _{\mathbb {R}^{n}} (-\Delta )_{\rho _{\epsilon }}^{\alpha } v_{\epsilon }(x)\varphi (x)dx= \epsilon ^{2\alpha }\int _{\mathbb {R}^{n}} (-\Delta )_{\rho }^{\alpha } u(\epsilon x)\varphi (x)dx. \end{aligned}$$

In order to study Eqs. (1.7) and (5.1), we consider the functional $I_{\rho _{\epsilon }}$ on the $\epsilon$-dependent Hilbert space $H_{\rho _\epsilon }^{\alpha }(\mathbb {R}^{n})$ with inner product $\langle \cdot ,\cdot \rangle _{\rho _\epsilon }$.

The functional $I_{\rho _{\epsilon }}$ is of class $C^1$ in $H_{\rho _{\epsilon }}^{\alpha }(\mathbb {R}^{n})$ and the critical points of $I_{\rho _{\epsilon }}$ are the weak solutions of (5.1). We further introduce

$$\begin{aligned} \mathcal {N}_{\rho _{\epsilon }} = \{v \in H_{\rho _{\epsilon }}^{\alpha }(\mathbb {R}^{n})\setminus \{0\}:\;\; I'_{\rho _{\epsilon }}(v)v =0\},\\ \Gamma _{\rho _{\epsilon }} = \{ \gamma \in C([0,1] , H_{\rho _{\epsilon }}^{\alpha }(\mathbb {R}^{n})):\;\; \gamma (0) = 0, \;\;I_{\rho _{\epsilon }}(\gamma (1)) <0 \} \end{aligned}$$

and the mountain pass minimax value

$$\begin{aligned} c_{\rho _{\epsilon }} = \inf _{\gamma \in \Gamma _{\rho _{\epsilon }}} \max _{t \in [0,1]} I_{\rho _{\epsilon }}(\gamma (t)). \end{aligned}$$

From Lemma 3.2 we also have

$$\begin{aligned} 0 < c_{\rho _{\epsilon }} = \inf _{v\in \mathcal {N}_{\rho _{\epsilon }}} I_{\rho _{\epsilon }}(v)= \inf _{v\in H_{\rho _{\epsilon }}^{\alpha }(\mathbb {R}^{n})\setminus \{0\}} \max _{t \ge 0} I_{\rho _{\epsilon }}(t v). \end{aligned}$$

(5.2)

For comparison purposes we consider the functional $I$ defined in 3.14, whose critical points are the solutions of 3.15, where $f(u)=u^p$. We also consider the critical value 3.16 that satisfies

$$\begin{aligned} c=\inf _{u\in H^{\alpha }(\mathbb {R}^{n})\setminus \{0\}} \max _{t \ge 0} I(t u). \end{aligned}$$

Now we start the proof of Theorem 1.2 with some preliminary lemmas.

Lemma 5.1

Suppose ($\rho _{1}$) holds. Then

$$\begin{aligned} \lim _{\epsilon \rightarrow 0^{+}} c_{\rho _{\epsilon }} = c. \end{aligned}$$

(5.3)

Proof

Since we obviously have

$$\begin{aligned} \int _{\mathbb {R}^{n}}\int _{B(0,\rho _\epsilon (x))} \frac{|u(x+z) - u(x)|^{2}}{|z|^{n+2\alpha }}dzdx \le \int _{\mathbb {R}^{n}}\int _{\mathbb {R}^{n}} \frac{|u(x+z) - u(x)|^{2}}{|z|^{n+2\alpha }}dzdx, \end{aligned}$$

for all $u\in H_{\rho _{\epsilon }}^{\alpha }(\mathbb {R}^{n})$, then we have $I_{\rho _{\epsilon }} (u) \le I(u)$ and therefore

$$\begin{aligned} \limsup _{\epsilon \rightarrow 0^{+}} c_{\rho _{\epsilon }} \le c. \end{aligned}$$

(5.4)

Now consider $v_\epsilon \in H^\alpha _{\rho _\epsilon }$ a solution of Eq. (5.1) with critical value $c_{\rho _\epsilon }$, then $c_{\rho _\epsilon }=I_{\rho _{\epsilon }} ( u_\epsilon )=\max _{t \ge 0} I_{\rho _{\epsilon }} (t u_\epsilon )$ and $I'_{\rho _{\epsilon }}(v_{\epsilon }) v_{\epsilon } = 0$, so that

$$\begin{aligned} \int _{\mathbb {R}^{n}}\int _{B(0,\rho _\epsilon (x))} \frac{|v_{\epsilon }(x+z) - v_{\epsilon }(x)|^{2}}{|z|^{n+2\alpha }}dzdx + \int _{\mathbb {R}^{n}} v_{\epsilon }^{2}dx = \int _{\mathbb {R}^{n}}v_{\epsilon }^{p+1}dx \end{aligned}$$

(5.5)

and then

$$\begin{aligned} c_{\rho _{\epsilon }} = \frac{p-1}{2(p+1)} \left( \int _{\mathbb {R}^{n}}\int _{B(0,\rho _\epsilon (x))} \frac{|v_{\epsilon }(x+z) - v_{\epsilon }(x)|^{2}}{|z|^{n+2\alpha }}dzdx + \int _{\mathbb {R}^{n}}v_{\epsilon }^{2}dx \right) . \end{aligned}$$

(5.6)

From here and using that $c_{\rho _{\epsilon }}$ by (5.4), we see that $\Vert v_{\epsilon }\Vert _{\rho _\epsilon }$ is bounded when $\epsilon \rightarrow 0^{+}$. Next we see that for any $t >0$ we have

$$\begin{aligned} c_{\rho _{\epsilon }}&\ge I(t v_\epsilon ) - \frac{1}{2}\int _{\mathbb {R}^{n}}\int _{ B^c(0,\rho _\epsilon (x))} \frac{t^{2}|v_\epsilon (x+z) - v_\epsilon (x)|^{2}}{|z|^{n+2\alpha }}dzdx. \end{aligned}$$

Using hypothesis ($\rho _{1}$) and estimating the second term in the right side as in (3.27) and (3.29), we find

$$\begin{aligned} c_{\rho _{\epsilon }} \ge I(t v_\epsilon ) - \frac{C t^{2}|S^{n-1}|\Vert v_\epsilon \Vert _{H_{\rho _\epsilon }^{\alpha }}^{2}}{\alpha \rho _{0}^{2\alpha }}\epsilon ^{2\alpha }. \end{aligned}$$

Now choosing $t = t^{*}_\epsilon >0$, such that $I(t^{*}_\epsilon v_\epsilon ) = \max _{t \ge 0} I(t v_\epsilon )$ we find

$$\begin{aligned} c_{\rho _{\epsilon }} \ge c - \frac{C(t_\epsilon ^{*})^{2}|S^{n-1}|\Vert v_\epsilon \Vert _{H_{\rho _\epsilon }^{\alpha }}^{2}}{\alpha \rho _{0}^{2\alpha }} \epsilon ^{2\alpha }, \end{aligned}$$

from where $\liminf _{\epsilon \rightarrow 0^{+}} c_{\rho _{\epsilon }} \ge c.$ Combining with (5.4) we get (5.3). $\square$

Lemma 5.2

If $v_\epsilon$ is s family solutions of (5.1) with critical value $c_{\rho _\epsilon }$, then there exists a family $\{y_{\epsilon }\}$ and positive constants $R$ and $\beta$ such that

$$\begin{aligned} \liminf _{\epsilon \rightarrow 0^{+}} \int _{B(y_{\epsilon }, R)}v_{\epsilon }^{2}(x)dx \ge \beta >0. \end{aligned}$$

(5.7)

If not, there exists a sequence $v_{k} = v_{\epsilon _{k}}$ such that

$$\begin{aligned} \lim _{k\rightarrow \infty } \sup _{y \in \mathbb {R}^{n}} \int _{B(y ,R)} v_{k}^{2}(x)dx = 0, \end{aligned}$$

the by Lemma 2.1, we have $v_{k} \rightarrow 0$ in $L^{q}(\mathbb {R}^{n})$ for any $2 < q < 2_{\alpha }^{*}.$ However, this is impossible because by (5.5), (5.6) and Lemma 5.1

$$\begin{aligned} \frac{p-1}{2(p+1)}\int _{\mathbb {R}^{n}}v_{\epsilon }^{p+1}(x)dx = c_{\rho _{\epsilon }} \rightarrow c,\;\;\text{ as }\;\;\epsilon \rightarrow 0. \end{aligned}$$

$\square$

Now let

$$\begin{aligned} w_{\epsilon }(x) = v_{\epsilon }(x + y_{\epsilon }) = u_{\epsilon }(\epsilon x + \epsilon y_{\epsilon }), \end{aligned}$$

(5.8)

then by (5.10),

$$\begin{aligned} \liminf _{\epsilon \rightarrow 0^{+}}\int _{B(0,R)} w_{\epsilon }^{2}(x)dx \ge \beta > 0. \end{aligned}$$

(5.9)

To continue, we consider the rescaled scope function $\overline{\rho }_\epsilon$, as defined in (4.3),

$$\begin{aligned} \bar{\rho }_\epsilon (x)=\frac{1}{\epsilon }\rho (\epsilon x+\epsilon y_\epsilon ) \end{aligned}$$

and then $w_\epsilon$ satisfies the equation

$$\begin{aligned} (-\Delta )_{\overline{\rho }_{\epsilon }}^{\alpha }w_{\epsilon }(x) + w_{\epsilon }(x) = w_{\epsilon }^{p}(x), \;\;\text{ in }\;\;\mathbb {R}^{n}. \end{aligned}$$

(5.10)

Now we prove the convergence of $w_\epsilon$ as $\epsilon \rightarrow 0$.

Lemma 5.3

For every sequence $\{\epsilon _m\}$ there is a subsequence, which will also be denoted by $\{\epsilon _m\}$, so that $w_{\epsilon _m}=w_{m} \rightarrow w$ in $H^{\alpha }(\mathbb {R}^{n})$, when $m\rightarrow \infty$, where $w$ is a solution of (3.15).

Proof

From (5.6) we see that $\{w_\epsilon \}$ is bounded, and then, for every sequence $\{\epsilon _m\}$ there is a subsequence, we keep calling the same, so that $w_{\epsilon _m}=w_{m} \rightharpoonup w$, which satisfies Eq. (3.15). To prove the convergence of this sequence we use its weak convergence together with (5.6) and Lemma 5.1 to get

$$\begin{aligned} \Vert w\Vert&\le \liminf _{m\rightarrow \infty }\left( \int _{\mathbb {R}^{n}}\int _{\mathbb {R}^{n}}\frac{|w_{m}(x+z) - w_{m}(x)|^{2}}{|z|^{n+2\alpha }}dzdx + \int _{\mathbb {R}^{n}}w_{m}^{2}(x)dx \right) \\&\le \limsup _{m \rightarrow \infty } \left( \int _{\mathbb {R}^{n}}\int _{B(0,\overline{\rho }_{\epsilon _{m}}(x))}\frac{|w_{m}(x+z) - w_{m}(x)|^{2}}{|z|^{n+2\alpha }}dzdx + \int _{\mathbb {R}^{n}}w_{m}^{2}(x)dx \right) \\&+ \limsup _{m\rightarrow \infty } \int _{\mathbb {R}^{n}}\int _{B^c(0,\overline{\rho }_{\epsilon _{m}}(x)) }\frac{|w_{m}(x+z) - w_{m}(x)|^{2}}{|z|^{n+2\alpha }}dzdx\\&\le \limsup _{m \rightarrow \infty } \frac{2(p+1)}{p-1}c_{\rho _{\epsilon _{m}}} + \limsup _{m \rightarrow \infty } \frac{2K|S^{n-1}|}{\alpha \rho _{0}^{2\alpha }}\epsilon _{m}^{2\alpha }\\&= \frac{2(p+1)}{p-1}c = \Vert w\Vert . \end{aligned}$$

Here $K$ is an estimate for $\Vert w_m\Vert$. Thus $\Vert w_m\Vert ^2 \rightarrow \Vert w\Vert ^2$ and hence $w_{m} \rightarrow w$ in $H^{\alpha }(\mathbb {R}^{n})$. $\square$

We are now in a position to complete the proof of our second main theorem.

Proof of Theorem 1.2

We first obtain an upper bound for the critical values $c_{\rho _{\epsilon _m}}=c_m$, for the sequence $\{\epsilon _m\}$ given in Lemma 5.3. Next we consider the scope function

$$\begin{aligned} \tilde{\rho }_m(x)=\frac{1}{\epsilon _m}\rho (\epsilon _m x+x_0), \end{aligned}$$

where $x_0$ is a global minimum point of $\mathcal {H}$, see Lemma 4.1. To continue, we consider the function $w_m=w_{\epsilon _m}$ as given in (5.8) and let $t_m>0$ such that $t_m w_m\in \mathcal {N}_{\tilde{\rho }_m}$. According to Lemma 5.3, $\{w_m\}$ converges to $w\in \mathcal {N}$, then $t_m\rightarrow 1$ and $t_mw_m\rightarrow w$.

Now we apply Theorem 4.1 to obtain that

$$\begin{aligned} c_m\le I_{\tilde{\rho }_m}(t_m w_m)=I_{\frac{\rho _\infty }{\epsilon _m}}(t_{m}{w}_{m}) + \epsilon _{m}^{2\alpha }\left( \Vert {w}\Vert _{L^{2}}^{2}\mathcal {H}(x_{0}) + o(1)\right) . \end{aligned}$$

(5.11)

We have used part (i) of Theorem 4.1 with $z_m=x_0/{\epsilon _m}$.

On the other hand, since $w_{m} \in H^{\alpha }(\mathbb {R}^{n})$ is a critical point of $I_{\bar{\rho }_m}$, we have that

$$\begin{aligned} c_m=I_{\bar{\rho }_m}(w_m)\ge I_{\bar{\rho }_m}(t_mw_m). \end{aligned}$$

(5.12)

We write $y_m=y_{\epsilon _m}$. If $\epsilon _m|y_m|\rightarrow \infty$, then we may apply part (ii) of Theorem 4.1 with $z_m=y_m$ in 5.12 and obtain that

$$\begin{aligned} c_m\ge I_{\frac{\rho _\infty }{\epsilon _m}}(t_{m}{w}_{m}) + \epsilon _{m}^{2\alpha } o(1), \end{aligned}$$

which contradicts (5.11). We conclude then, that $\{\epsilon _my_m\}$ is bounded and that, for a subsequence, $\epsilon _my_m\rightarrow \bar{x}$, for some $\bar{x}\in \mathbb {R}^n$. Now we apply Theorem 4.1 again, but now part (i) with $z_m=y_m$ in 5.12, and we obtain that

$$\begin{aligned} c_m\ge I_{\frac{\rho _\infty }{\epsilon _m}}(t_{m}{w}_{m}) + \epsilon _{m}^{2\alpha }\left( \Vert {w}\Vert _{L^{2}}^{2}\mathcal {H}(\bar{x}) + o(1)\right) . \end{aligned}$$

(5.13)

From (5.11) and (5.13) we finally get that

$$\begin{aligned} \Vert w\Vert _{L^{2}}^{2}\mathcal {H}(\overline{x}) + o(1) \le \Vert w\Vert _{L^{2}}^{2} \mathcal {H}(x_{0}) + o(1) \end{aligned}$$

and taking the limit as $m\rightarrow \infty$, we get

$$\begin{aligned} \mathcal {H}(\overline{x}) \le \mathcal {H}(x_{0}) \end{aligned}$$

(5.14)

completing the proof of the theorem. $\square$