Computing brain networks with complex dynamics

Abstract

The interplay between neuronal network connectivity and neuron dynamics is known to drive global brain behavior; however, the exact relationship between network connectivity and node dynamics is complex and remains poorly understood. Previous theoretical and modeling work has shown that in small toy networks, when nodes are equipped with discrete quadratic dynamics, properties of the emergent behavior of the complex quadratic network (CQN) can give rise to features that relate to the underlying topology. Specifically, when the long-term behavior of CQNs is represented by asymptotic fractal sets, certain topological features of the fractal can be used to classify the network topology. However, the success of this approach has thus far not been tested on more complex real-world networks. Here, we apply a CQN modeling approach to capture individual differences in real-world brain networks derived from human connectome data. We show that CQNs are more sensitive than traditional graph theoretic measures at capturing individual differences in the topology of the human connectome, and that features of the associated equi-M sets can differentiate between male and female connectomes. This study, therefore, provides a basis upon which future work can build in order to better quantify individual differences in brain connectivity, and how these differences drive brain function and behavior.

1 Introduction

The function of many systems in the life sciences can be described as collective behavior of units that are part of a larger network [1]. To gain insight into how the ensemble behavior of these units operates in natural systems, dynamical systems modeling has been widely used to understand the associated nonlinear and chaotic phenomena [2]. Modeling each coupled unit in a fashion that captures natural dynamics with accuracy is important for applications. Unfortunately, accuracy in modeling comes with a price, and matching the complexity of real systems in a mathematical model leads to increased analytical and computational challenges. This often compromises tractability of the model behavior and comes back around to take away precisely from its potential applicability.

To complement the dynamical systems approach to understanding complex systems, network science has been focused on the graph theoretical aspect of networks, particularly on investigating the relationship between the network’s connectivity architecture and its function. By applying graph theoretical measures, one can investigate, for example, the sensitivity of a system’s temporal behavior to removing/adding nodes or edges at different places in the network structure. However, graph theoretical measures cannot in and of themselves explain the mechanisms by which connectivity patterns act to change systemic behavior. Therefore, a network model needs to incorporate both graph structure and node-wise dynamics in one unified framework, which can then be used to interpret empirical results and make predictions.

This is true in particular for the brain, which can be viewed as a “dynamic network,” self-interacting in a time-dependent fashion and at multiple spatial and temporal scales, to deliver an optimal range for biological functioning. Graph theoretical approaches have been applied to brain networks to understand organizational and functional neural principles [3,4,5], with results supporting certain architectural and topological properties, such as modularity, small-worldness, the existence of hubs, and “rich clubs” [6, 7]. Such measures have been used successfully on brain imaging data, tying pathological behavioral patterns to specific abnormalities in connectivity [8,9,10]. Additionally, much effort has been invested toward formal modeling approaches that would explain how network connectivity patterns may affect functional dynamics [11, 12] from biophysical models [13] to simplified systems [14].

Navigating the trade-off between faithful representation and mathematical simplicity can be difficult. In computational neuroscience in particular, models of brain dynamics often lie at either end of the spectrum: incorporating intractable complexities in favor of biological realism or sacrificing accuracy (and with it, practical impact) in favor of mathematical simplicity. Indeed, it has become increasingly clear that the construction of a realistic, data-compatible computational model presents many difficulties related to dimensionality, computational cost, addressing multiple scales, and even simple bookkeeping. These difficulties make it nearly impossible to deliver any useful general results relating brain connectivity patterns to brain dynamics and observed behavior.

To bridge this gap, we previously developed a simplified complex quadratic network (CQN) model that captures both connectivity and coupled dynamics in terms of discrete iteration in the complex frame, in a canonical framework [15,16,17]. The model relies on ideas from traditional complex quadratic dynamics to address questions which are notoriously difficult in realistic models of natural networks. Rephrasing these questions in terms of complex map iterations presents an approachable way that can lead to novel results and to progress on applications.

Complex quadratic iterations of individual functions in the family $f_c = z^2+c$ deliver rich dynamics and provide textbook recipes for creating fractal asymptotic sets, with history going back more than a century [18, 19]. For a parameter value $c \in {\mathbb {C}}$, the Julia set of the corresponding map $f_c$ is defined as the boundary between initial points $z_0$ whose orbits remain bounded under iterations of $f_c$ (prisoners) and those which escape to infinity under repeated iterations of the map (escapees). One interesting result refers to the existence of an escape radius for these iterations: Once the orbit transcends the radius $R=2$, the orbit is guaranteed to escape.

The geometry of prisoner set for single quadratic maps is notoriously tied to the properties of the critical orbit of the function, starting at $z_0=0$ [20,21,22]. A famous theorem in discrete dynamics guarantees that prisoner sets for quadratic functions are either connected, if the orbit of the critical point $z=0$ is bounded, or totally disconnected, if the orbit of the critical point is unbounded [23]. The parameter locus c for which the map $f_c$ is postcritically bounded is then the same as the parameter locus for which the prisoner set is connected, and is known as the Mandelbrot set [24]. The Mandelbrot set has been extensively studied as a topological object in the complex plane, and since the critical orbit of $z_0=0$ governs the potential behaviors of all the other orbits, the Mandelbrot set can be seen as an atlas of information on global system dynamics, going beyond simply describing the evolution of the system from the resting state $z_0=0$. Because of this, the Mandelbrot set can be viewed as a key object in discrete dynamics that captures, in a canonical and efficient way, the long-term dynamic behavior of all functions in the quadratic family simultaneously.

In prior work, we have focused on tying connectivity to dynamic patterns using simple, low-dimensional networks, which are both analytically tractable and allow easier visualization and interpretation of the results. By defining and computing the equi-M set (see Sect. “Methods”), we observed visually a collection of universal, unifying features: For example, all equi-M sets appear to exhibit a main cardioid, and some reminiscent bulb-like structure (although the traditional hyperbolic bulbs no longer exist, since network combinatorics must track behavior of many nodes simultaneously). Hence, properties such as connectedness, size, position of the cusp, and tail present with a lot of variability, based on the architecture of the underlying network.

Fig. 1

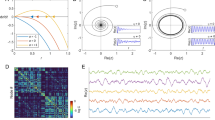
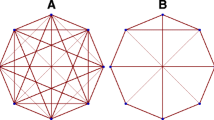
Illustration of how perturbations in the network placement and weights affect the shape of equi-M sets. The traditional Mandelbrot set for single-map iterations is shown for reference. For each c in the complex plane, the color represents how fast the critical orbit of $f(z)=z^2+c$ escapes the disk of radius two (with black representing no escape). All simulations used 100 iterations and a spatial resolution of $400 \times 400$ in the complex square $[-2,1] \times [-1.5,1.5]$. Four networks are show in the top panels, with direction, sign, and weight specified on each edge. The evolution equations for each network are shown in the second row. The corresponding equi-M sets are shown in the bottom panels. Changing to edge weights and adding negative feedback to the network induce quantifiable changes in the topology of the equi-M sets, altering the number of connected components, as well as the position and shape of the cusp. The same resolution and color coding were used as for the traditional M set

We further identified a few global network effects, associating larger connection weights with significantly smaller equi-M sets [16], and tying sparser networks to decreased node synchronization [17]. We found that the presence of even weak inhibitory coupling is efficient in breaking down sets into connected components when introduced in a network formed of purely excitation connections [15]. More interestingly, we also identified finer and less intuitive local effects, showing that changing the weight of one edge may lead to significant changes in the topology of the equi-M set (Fig. 1). This effect depends tightly on the position of the inserted/deleted edge in the network and is strongly related to the contribution of the edge to graph theoretical properties of the network, as well as to the weight of the edge.

Thus, while CQN modeling has shown great promise to quantify the effects of changes in the underlying connectivity of the network, its success thus far has been limited to simple toy models. However, it forms a critical basis upon which future plans to develop a theoretical correspondence between properties of more complex systems, and geometric properties of the equi-M set can be grounded. For example, it raises the possibility of using equi-M set topology toward an assessment and classification toolbox for brain functional dynamics. In this paper, we explore for the first time this practical possibility, by computing equi-M sets for a tractography-derived data set. We illustrate the ability of the equi-M set to differentiate between individuals and groups of individuals with different physiological profiles. We show that equi-M topological measures can outperform graph theoretical measures, by illustrating dynamic properties that connectome measures fail to capture.

2 Methods

2.1 Complex quadratic network (CQN) modeling

In our work, we use quadratic iterations to understand the principles of how dynamic behavior emerges in large networks of nodes, and how it depends on the network structure. Each node is viewed symbolically as an integrator of internal and external inputs. We use the asymptotic behavior of multi-dimensional orbits (via the topological and fractal structure of Julia and Mandelbrot sets) to quantify dynamic behavior under perturbations of the network architecture. Topological landmarks of Mandelbrot sets provide valuable means of classification and comparison between different systems’ behavior, as will be further summarized in the following section.

In our complex quadratic network (CQN) model, the node-wise dynamics are set to be complex quadratic dynamics, within the family $f_c :{\mathbb {C}} \rightarrow {\mathbb {C}}$, $f_c(z) = z^2+c$. More specifically, in this framework, each network node adds all weighted inputs from adjacent nodes and integrates the sum of inputs, in discrete time, as a complex quadratic map. If all the nodes use the same map $f(z) = z^2+c$, the system takes the form of an iteration in ${\mathbb {C}}^n$:

$$\begin{aligned} z_j(t) \longrightarrow z_j (t+1) = \left( \sum _{k=1}^{n}{g_{jk} A_{jk} z_k(t)} \right) ^2+c \end{aligned}$$

where n is the size of the network, $\displaystyle A=(A_{jk})_{j,k =1}^n$ is the binary adjacency matrix of the oriented underlying graph, that is, $A_{jk}=1$ if there is an edge from the node k to the node j, and $A_{jk}=0$ otherwise. The coefficients $g_{jk}$ are the signed weights along the adjacency edges (in particular, $g_{jk}=0$, if there is no edge connecting k to j, that is, if $A_{jk}=0$). In isolation, each node $z_j(t) \rightarrow z_j(t+1)$, $1 \le j \le n$, iterates as the quadratic function $f(z) = z^2 + c$. When coupled as a network with adjacency A, each node will act as a quadratic modulation on the sum of the inputs received along the incoming edges (as specified by the values of $A_{jk}$, for $1 \le k \le n$).

This “network environment” preserves, often in a weaker form, some of the properties and results determined in the traditional case of a single iterated quadratic map (e.g., the existence of an escape radius is guaranteed in some types of networks, but may fail in others). We used this to our advantage and proceeded to study theoretically the effects of network architecture on its long-term dynamics. To do this, we needed to extend the definitions of asymptotic sets from the traditional context of single-map iterations to the context of networks. Below, we will only provide the definitions and interpretations that lie within the scope of this paper. The broader context and construction can be found in [15,16,17].

Definition 1

We call the equi-Mandelbrot set (or the equi-M set) of the network, the locus of $c \in {\mathbb {C}}$ such that the multi-orbit of the critical point (0, ..., 0) is bounded for the equi-parameter $\textbf{c} =(c,c,...c) \in {\mathbb {C}}^n$.

Broadly speaking, one can interpret iterated orbits as describing temporal trajectories of an evolving system. Along these lines, we view a parameter $\textbf{c}$ in the equi-M set (for which the critical orbit escapes to $\infty$) as representing a system with unsustainable long-term dynamics when initiated from rest, while the $\textbf{c}$ range for which the critical orbit remains bounded can be viewed as the “sustainable dynamics locus.” We quantify the properties and shape of equi-M sets through the following metrics:

The positions of the cusp ($\gamma$) and of the tail ($\tau$). The presence of the cusp is a robust, network-independent feature of the equi-M sets throughout our data set—unlike the tail structure, which is very fragile to network modifications. However, the position $\gamma$ of the cusp along the real axis varies with the network properties, as illustrated in Fig. 3. For a fixed equi-M set, $\gamma$ is easy to compute (as the largest coordinate reached by the boundary of the equi-M set along the real axis) and relatively robust to choosing the spatial resolution. The accuracy of the tail position $\tau$, computed as the leftmost point of the equi-M set along the real axis, is more resolution-dependent, since the tail is connected by thin filaments.

The area ${{\mathcal {A}}}$ of the set in the complex plane. Our computation algorithm provides an overestimate of the exact value of ${{\mathcal {A}}}$, due to the finite iteration-based approximation of the asymptotic equi-M set (some of the equi-M points retained in our set representation may in reality escape upon further iteration). Note that spatial resolution of the computation may limit detection of thin filaments; these, however, have negligible area, hence, they are not expected to have a major contribution to the value of ${{\mathcal {A}}}$.

The horizontal diameter $d_h$ is the distance between the cusp and the tail along the real axis.

The vertical diameter $d_v$ is the largest vertical distance between two points of the set. Our computational algorithm provides us with slight underestimates of this measure; more exact computations are problematic, due to the presence of thin filaments around the boundary.

2.2 Subjects and DTI data

Our analysis is based on tractography-derived, neural connectivity data obtained from the S1200 Q4 release of the Human Connectome Project [25]. The project released to the public domain extensive MRI, behavioral, and demographic data from a large cohort of individuals ($>1000$). For our own study, we considered the Q4 subject subgroup (the latest available at the time the data analysis was performed), consisting of $N=197$ individuals, age 22–36 years (107 males, mean age $\mu \sim 25.8$ years, and 90 females, mean age $\mu \sim 28$ years).

2.3 Structural network construction

Preprocessed diffusion-weighted images, part of the Human Connectome Project, were used to construct structural connectomes for the subjects. Fiber tracking was done using DSI Studio with a modified FACT algorithm [26]. As a first step, data were reconstructed using generalized q-sampling imaging (GQI) [27]. Diffusion-weighted images were reconstructed in native space, and the quantitative anisotropy (QA) for each voxel was computed. Fiber tracking was performed until 250,000 streamlines were reconstructed with angular threshold of 50o, step size of 1.25 mm, minimum length of 10 mm, and maximum length of 400 mm. Streamline counts were estimated for the parcellations schemes based on the AAL [28] atlas version-1 containing 116 brain regions. The AAL atlas was registered to the isotropic diffusion component (ISO) image, an output of GQI. Registering directly to the ISO image minimizes any registration issues that could arise by first registering to an individual’s T1w image. Atlas registration was conducted using FSL FLIRT [29] with default parameters. The transformation matrix obtained from the registration was applied to all regions in the AAL atlas. In case, two regions were registered to the same voxel, the voxel was assigned to the region with the highest probability. In order to fully sample the fiber orientations within a voxel, tracking was repeated 250x with initiation at a random sub-voxel position generating 250 connectivity matrices per subject.

For each subject, a symmetric, non-negative, weighted structural connectivity matrix, A, was constructed from the connection strength based on the number of streamlines connecting two regions. The final connectivity matrix included edges which were present in at least 10% (or 25) of the 250 matrices. This connectivity matrix was normalized by dividing the number of streamlines between each two coupled regions by the combined volumes of the two regions. For each connectome, we computed a set of graph theoretical measures, consisting of node degree centrality, eigenspectrum, clustering coefficient, betweenness centrality, eigenvalue centrality, local efficiency, and numbers of 3-motifs and 4-motifs, using the Brain Connectivity Toolbox [30].

2.4 Equi-M set construction and quantification

To generate numerically, using a computer code, the equi-M set for each connectome, one needs to choose two computational parameters: the number of iterations (or network updates) and the spatial resolution in the c-plane (the sampling resolution for c). For the exploration in this paper, the number of iteration steps was fixed to 100, and the figures were produced in $400 \times 400$ spatial resolution. The values of these parameters can be easily improved in the future analyses, at higher computational cost.

For each equi-M set, we computed the set of topological metrics described in Sect. 2.1, quantifying its position and size. The metrics are based on common topological landmarks (like the cusp and the tail), use the symmetry of the set with respect to the real axis, and the fact that all equi-M sets in our data set presented as one connected component. These represent a preliminary set of measures, illustrating broad topological relationships, and are generally robust with respect to the computational parameters. Potential candidates for more advanced measures, aimed to better capture finer topological detail, are proposed for future analyses in the “Discussion” section. Those are expected to depend more sensitively on the number of iterations and on spatial resolution, hence may require future analyses to be carried out for multiple options of computational parameters, in order to allow comprehensive comparisons.

2.5 Correlation analysis

We investigate how the graph structure of the connectome (representing fixed, hardwired connectivity information, as captured in the set of graph theoretical measures in Sect. 2.3) reflects into the shape of the equi-M set (which encompasses how information propagates in the CQN), as represented by the set of topological measures in Sect. 2.1.

We computed both Pearson and Spearman correlations between the graph theoretical and the topological measures. Since the topology of the M set can be viewed as a symbolic representation of the network’s long-term dynamics, and since the network architecture (underlying graph) is a factor in determining these dynamics, correlations between properties of one and the other may help understand which graph theoretical properties lead to which types of long-term dynamics. Understanding this relationship at the level of simple quadratic dynamics may provide crucial information that can be extrapolated to the more complex, neural dynamics that occurs in reality in these brain networks.

In addition, correlations computed within the set of topological measures may help identify to what extent these measures are inter-related. Similarly, correlations computed within the set of graph theoretical measures will quantify the degree of redundancy in the information provided by these measures.

2.6 Gender-based statistics

We test if the shape of the equi-M set can distinguish statistically between the subjects’ gender. In order to make the least assumptions on our distributions, we used a Mann–Whitney nonparametric rank test (as provided by the Matlab 2020a package) to assess if each measure differs significantly ($p<0.001$) between the male and female subjects (the null hypothesis being that they are extracted from the same overall distribution).

3 Results

Here, we use our previously established CQN model (Methods) to generate equi-M sets describing individual connectomes derived from diffusion-weighted images of human brains from the Human Connectome Project. We quantify features of the topology of the equi-M sets as described in the Methods and use these results to (1) establish whether there are correlations between graph theoretical measures of the connectomes and geometric measures of the equi-M sets and (2) test whether the topology of the equi-M set can effectively differentiate between the subjects’ gender (as a proof of principle, to be potentially extended in the future to other physiological or behavioral measures).

3.1 Between-subject differences

Our computation of equi-M sets across all 197 subjects revealed between-subject differences. Figure 2 illustrates these differences between three example individuals (with the top panels of the figure showing the subjects’ data-derived connectomes, while the bottom panels show the corresponding equi-M sets).

While differences in the shapes of these three sets are undeniable, they are also subtle, especially when set against the theoretical potential for variability in shape as observed between the examples in Fig. 1, in response to making only local changes to the network connectivity. This was true in general for the entire data set, with all the 197 equi-M sets showing unifying geometric features (a common “signature” to all connectomes): all equi-M sets we obtained have a cusp and a tail, and a structure reminiscent of the main cardioid of the traditional Mandelbrot set. At the same time, much like fingerprints, the sets exhibit extensive variations in detail, due to subtle differences in the connectome.

Fig. 2

Examples of M sets for three connectomes in our data set. The connectomes are sparse; that is, many entries are zero, marking node pairs not directly connected by an edge. In addition, many nonzero entries are very small, corresponding to weak connections. Subtle differences in the connectomes reflect into noticeable, quantifiable differences in the topology of the equi-M sets, so that each individual has a unique, distinctive equi-M set, like a personal signature, or a fingerprint encoding the CQN dynamic flow through their brain connectome

To formally test these impressions, a quantifiable assessment of equi-M set topology is needed. However, this is difficult, because the dynamics no longer capture the simple combinatorics of a single iterated map. The hyperbolic bulb structure of the traditional Mandelbrot set, which could have been helpful for classifications, no longer exists in that form for network equi-M sets. Instead, we used position and shape landmarks (see “Methods” section), which allow us to quantify subtle versus significant geometric differences and to distinguish between shapes.

Figure 3 illustrates these landmarks for the same three equi-M sets as those in Fig. 2. Only the contours of the sets are shown here, to avoid overcrowding the panels. The set in the right panel is the “largest,” with the leftmost position for tip of the tail, the rightmost cusp, and the largest diameters and area. Beyond the differences in size, the set on the left has a “pinch point” on the real axis, at $x=-4.04$, which, if removed, breaks the set into two connected components, reminiscent of the original bulbs. In turn, the set in the middle panel has a “narrow bridge” at $x=-3.5$, with very small diameter $2y = 0.12$ across, connecting the main body and the tail region reminiscent of the traditional hyperbolic components. For the set on the right, the smallest vertical diameter between the body and the tail occurs at $x=-2.96$ and is $2y = 0.36$, with a less significant separation.

Fig. 3

Landmarks for equi-M sets. The panels show the contours of the equi-M sets for the same three connectomes as in Fig. 2, with labels marking in each case the position of the tail, the cusp, and other distinguishing points on the boundary

Pinch points and narrow bridges show future promise toward assembling a finer and more complete geometric assessment of the equi-M set signature. For the current study, we will strictly focus on using the collection of measures described in the “Methods” section, for all of our assessments. Based on these assessments, we investigated the graph theoretical source of the similarities and differences between sets.

3.2 Inter-correlations between graph and topological measures

We want to establish if there is a well-defined correspondence between graph teoretical properties of the connectomes in the data set and geometric properties of the corresponding equi-M sets.

For each subject, we computed the set of topological measures consisting of $(\gamma , \tau , {{\mathcal {A}}}, d_h, d_v)$ (as described in the “Methods” section). The mean and standard deviation of all five  measures are described in Fig. 4. The correlation analysis confirmed that these measures are not independent in the context of our data. Figure 5 suggests that they are strongly correlated with each other (e.g., a position of the cusp more to the right also corresponds to a tail shifted to the left, larger diameters, and a larger area).

Fig. 4

Topological measures statistics (means $\mu$ and standard deviations $\sigma$). Cusp position $\gamma$: $\mu = 0.77$; $\sigma = 0.36$. Tail position $\tau$: $\mu =-4.88$; $\sigma =1.87$. Area ${{\mathcal {A}}}$: $\mu =18.52$; $\sigma =15.29$. Horizontal diameter $d_h$: $\mu =5.65$; $\sigma =2.22$. Vertical diameter $d_v$: $\mu =5.10$; $\sigma =2.45$

For each connectome, the set of graph theoretical measures described in the “Methods” section were also computed: node degree centrality, eigenspectrum, clustering coefficient, betweenness centrality, eigenvalue centrality, local efficiency, and numbers of 3-motifs and 4-motifs. We performed correlation analyses, investigating the inter-relationship between the topological and the graph theoretical measures. The results of both Pearson and Searman correlation analyses are shown in Fig. 5. In both analyses, we found strong correlations between most pairs (overall average p-value $p=5.9088 \times 10^{-4}$). Higher degree centrality, eigenspectrum, and local efficiency correlated significantly with smaller equi-M sets. Specifically, the cusp and tail landmarks were closer to the origin, and the area and diameters were smaller. In contrast, the eigencentrality measure correlated positively with the size of the equi-M set (i.e., higher eigencentrality values corresponded to larger equi-M sets). Betweenness centrality did not show significant correlations. Interestingly, the number of motifs showed consistent significant negative correlations with the size of the equi-M set: the stronger the motifs, the smaller the topological measures. A potential explanation to this correlation between motif strength and size of the equi-M set is proposed in our previous work [17], but a complete proof is nontrivial and still under way.

Fig. 5

Correlations within and between graph theoretical and topological measures. The left panel presents the results of the Pearson correlation analysis, and the right panel shows the results of the Spearman correlation analysis. Each panel represents in color the correlation values for all pairs of measures for which the correlation value was significant (with a p-value threshold $\alpha =0.05$). The color coding for sign and strength of correlations is specified by the color bar. The pairs for which correlations were not significant are shown in white. On both axes, topological measures are labeled 1–5 (representing the following order: 1 = cusp position $\gamma$, 2 = absolute value of the tail position $\tau$, 3 = area ${{\mathcal {A}}}$, 4 = diameter along real axis $d_h$, and 5 = vertical diameter); then graph theoretical measures are labeled 1–13 (representing the following sequence: 1 = degree centrality; 2 = eigenspectrum; 3 = clustering coefficient; 4 = betweenness centrality; 5 = eigenvalue centrality; 6 = local efficiency; 7–8 = numbers of 3-motifs; and 9–13 = numbers of 4-motifs

This analysis confirms that there is a tight correspondence between connectome patterns and geometric patterns of the equi-M set. This approach can be refined with developing and using finer topological measures for the equi-M sets, as further considered in the “Discussion” section.

3.3 Gender-based statistics

Recent imaging research has been consistently reporting differences in structural and functional networking between the male and female connectomes. A tractography-based analysis of a large population of young subjects [31] found male brains to be optimized for intrahemispheric projections (interpreted as facilitating connectivity between perception and coordinated actions), while female brains appeared to emphasize interhemispheric communication (hence facilitating communication between analytical and intuitive processing modes). Another structural study exploring the biological basis of intelligence [32] suggested that these rely on neural mechanisms engaging an interacting network of regions, the patterns of which were also found to differ between genders. In turn, functional MRI studies also revealed a gender dimorphism in the functional organization of the brain, with a different balance between strongly and weakly connected brain nodes between genders [33]. Despite such widely reported structural and functional gender differences, few studies examine the relationship between the two. Among these, a recent study on a large subject group including both structural and funcional imaging measures [34] concluded that gender differences are encoded in both brain structure and brain function, but in different manners.

This hints to the complexity of the mechanisms that link hardwiring to function and that may underlie gender-based behavioral differences. However, no study to date has been able to successfully investigate these mechanisms and capture in a mathematically tractable way how gender differences in wiring paterns may lead to differences in the dynamics information flow through the connectome. In our work, we constructed the CQN model precisely as a tool to help us understand the emerging network dynamics, encoded in the form of a topological object entirely based on the structural connectome. To test the utility of our analytical approach, we investigated if our framework is able to identify gender differences in our subject population (consisting of healthy young adult male and females).

We found that our model is able to capture previously unidetified and nuanced differences between the male and female groups in our sample. Specifically, the shapes of the equi-M sets correlated with the sex of the subjects. These gender differences for the topology measures are described in Fig. 6. The equi-M sets corresponding to the male subgroup have significantly larger cusp coordinates, longer tails, larger areas, and horizontal and vertical diameters than the female counterparts. Figure 7 provides an illustration of the between-gender differences in topology stemming from differences in connectivity. Each figure panel presents a stochastic representation of the equi-M sets in each subject group (“frequency plot”), constructed as follows: To each point in the complex plane, we associated the number of subjects in the group for which that point is in the equi-M set. Then, we used a color map to represent this as a two-dimensional plot (with darker colors corresponding to more subjects and lighter colors to fewer subjects, as specified in the color bar). This conveys visual patterns such as, for example, the idea that the sets are smaller within the female group (the colored region is smaller than the corresponding one in the male group), and have less variability (the halo of transitional colors is thinner than that for males).

Fig. 6

Comparison of topological measures statistics by gender. Male statistics. Cusp position $\gamma$: $\mu = 0.88$; $\sigma = 0.36$. Tail position $\tau$: $\mu =-5.52$; $\sigma =1.76$. Area ${{\mathcal {A}}}$: $\mu =23.08$; $\sigma =16.19$. Horizontal diameter $d_h$: $\mu =6.40$; $\sigma =2.10$. Vertical diameter $d_v$: $\mu =5.85$; $\sigma =2.42$. Female statistics. Cusp position $\gamma$: $\mu = 0.63$; $\sigma = 0.33$. Tail position $\tau$: $\mu =-4.12$; $\sigma =1.73$. Area ${{\mathcal {A}}}$: $\mu =13.10$; $\sigma =12.26$. Horizontal diameter $d_h$: $\mu =4.76$; $\sigma =2.04$. Vertical diameter $d_v$: $\mu =4.21$; $\sigma =2.20$. The p-values of the male/female between-group comparison (Wilcoxon rank-sum test) can be found below the box corresponding to each measure

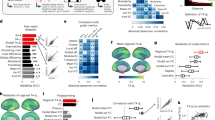
Further, in Fig. 8, we highlight how topology outperforms graph theory in identifying gender differences. We computed two group “mean” (or “prototypical”) connectomes, by averaging the individual connectomes over each subject group (males and females, respectively). The male and female prototype connectomes are shown in the top row of Fig. 8. We then computed the prototypical male and, respectively, female equi-M sets from these two connectomes, as illustrated in the bottom row of Fig. 8. The two prototypical connectomes are hardly distinguishable from each other with the naked eye; significant individual detail in connectivity patterns was mostly  eliminated  through averaging, resulting in two almost identical connectomes. However, these seemingly unnoticeable differences were enough to produce visibly different equi-M prototypical sets for males and females (with a deeper cusp, and wider and more pronounced detail around the cusp in the set corresponding to the female group than in the set corresponding to males).

Fig. 7

Stochastic versions of the equi-M set for the male group (left panel) and for the female group (right panel). The color for each point in these parameter squares represents for how many subjects the c value corresponding to the point is in the equi-M set of the subject’ network. The color map used (with lighter colors for lower numbers and darker colors for higher numbers) is indicated for each group in the color bar (color figure online)

Fig. 8

Prototypical connectomes and equi-M sets for the male and female groups. Top. Prototypical connectomes for male subjects (left) and female subjects (right), obtained by averaging the individual connectomes for the respective subject groups. Bottom. Prototypical equi-M sets for male (left) and female subjects (right), obtained from the prototypical connectomes for the respective groups

4 Discussion

Here we showed, for the first time, how the theory of complex quadratic networks (CQNs) can be applied to improve our understanding of natural networks, specifically tractography-derived brain networks (connectomes). We did so by using the equi-M set, a topological object describing the asymptotic dynamics of the network. We found that, as one might expect, the geometry of the equi-M set is to a large extent encoded in measurable graph theoretical properties of the connectome. Information on the size and the distribution of the weights in the network is crucial to producing the topology of the connectomes observed empirically. Crucially, some of the unifying and the distinguishing features between the tractography-generated equi-M sets seem to be driven by features in the connectome that might not be captured by traditional graph theoretical measures (see, for example, the prototypical sets in Fig. 8).

In order to obtain a better understanding of how the structural and dynamic aspects are tied, future work will focus on refining the topological assessments of equi-M sets to better probe the relationship between traditional graph theoretical measures and fractal properties of the equi-M set. For example, the traditional Mandelbrot set has a hyperbolic bulb structure. In particular, the bulbs that are centered along the real axis are tangent to each other along the axis at what we will call “pinch points” (because their removal would break the set into connected components). While for equi-M sets, the bulb structure is not preserved, some of the pinch points persist—either in this form, or just as a narrowing of the set (which we call “narrow bridge”), delimiting “pseudo-bulbs.” Although beyond the scope of this work, in the future studies, we plan to compute the number of pinch points as a measure of bulb structure preservation. We expect these to be easier to compute than the maximal vertical diameter in general, since the narrowing points of the sets are not typically associated with filaments (similarly with the seahorse valley in the traditional Mandelbrot set). An alternative measure, related to the presence of narrow bridges, is the entropy around the equi-M boundary (since it captures the regularity of the vertical variations between high and low points along the top boundary of the set).

We also explored the possibility of using the equi-M set as a classification and prediction tool. This is an interesting and promising direction of investigation, since a classification instrument that uses brain dynamics is one step closer to capturing the subjects’ physiology and behavior than classifiers based entirely on the hardwired structure (i.e., the connectome). A very important step in this direction is to show that classifications based on equi-M set topology can, in fact, outperform classifications using graph theoretical measures. Here, we gave a simple illustration of this potential, by showing that the topology of the equi-M set can efficiently capture differences in dynamics between male vs. female prototypical connectomes with otherwise seemingly indistinguishable architecture. In the future work, we plan to further explore the ability of the equi-M set to capture physiological and behavioral markers and its potential as a predictor of these aspects. One weakness of the current work is that the structural connectome has the intrinsic limitation of only capturing the physical connections, but not to what extent these are effectively used, or contribute to the coupled dynamics at the moment of the scan. In fact, it is likely that some of the weak connections between nodes may be typically silent, without much cost for the brain. In a parallel study [17], we showed that weak connections contribute crucially to CQN dynamics and synchronization. Hence, access to the functional connectome seems to be of utmost importance when aiming to understand the network dynamics. Direction and signature of connections (excitatory versus inhibitory) were also found in our preliminary explorations to be crucial to the emerging dynamics and down the line to the brain’s function and observed behavior. Future work will, therefore, incorporate both structural and functional connectivity analyses, where the functional network can include effective, signed, and/or directed connections.

In the long term, this direction can be unified into a statistically comprehensive approach. In this framework, for a given set of connectome data, one would be able to select a collection of topological measures that optimally reflect the differences in the equi-M sets, as well as their relationship with the graph architecture. This could then be used as a topological profiling toolbox (TPT) for the data set at hand. The TPT could be used to produce a “dynamic brain signature” based on the connectome—encoding the efficiency in each individual’s brain regulation. Eventually, we would develop TPT-like lookup charts that could be used as a neurobiologically-based diagnostic instrument to be used clinically to assess the efficiency of brain regulation and information transfer.

Future work will also look to improve the theoretical bounds and computational tractability of the model. For example, at this point, we have only computed a network escape radius for certain network conditions, which are not necessarily satisfied by all our data-generated networks. Practically, this implies that orbits that get large over the first 100 computed iterations are not automatically guaranteed to escape; hence, our numerically-generated plots are not guaranteed to be the most reliable representations of the true equi-M sets. More general escape radius theoretical results, together with improved, higher-resolution numerical simulations, will permit better estimation of topological measures for equi-M sets.

Despite these limitations, overall, the results of this study support the intriguing idea that CQNs have very practical applications, and as we further develop our analysis of CQN dynamics an equi-M set topology, more potential applications are likely to come through. Our work on CQNs aligns in spirit with an emerging recent effort to use network models with simplified, tractable node dynamics (e.g., threshold linear networks [35, 36]) to mathematically tie complex network structure with coupled dynamics. While at the moment these models are still few and far between, especially in computational neuroscience, there is increasing evidence that they can be used successfully to understand and predict natural network dynamics, with sharper clarity than more complex models.

Taken together, this work, therefore, establishes that CQN modeling is a new and exciting methodology that can be applied to complex real work networks such as the brain, in order to better understand the complex relationship between network structure, dynamics, and function. CQN modeling is useful to amplify small individual differences in human brain connectiomes and outperformed traditional graph theoretic measures as a classifier of gender in our data set. We, therefore, urge that the use of CQN modeling and quantification of the resulting equi-M set be adopted by researchers in addition to traditional graph theoretic measures in order to better classify brain network data, identify biomarkers of disease progression, and make predictions about task performance and further the field of personalized medicine.