Neural networks with block diagonal inner product layers: a look at neural network architecture through the lens of random matrices

Abstract

Two difficulties continue to burden deep learning researchers and users: (1) neural networks are cumbersome tools, and (2) the activity of the fully connected (FC) layers remains mysterious. We make contributions to these two issues by considering a modified version of the FC layer we call a block diagonal inner product (BDIP) layer. These modified layers have weight matrices that are block diagonal, turning a single FC layer into a set of densely connected neuron groups; they can be achieved by either initializing a purely block diagonal weight matrix or by iteratively pruning off-diagonal block entries. This idea is a natural extension of group, or depthwise separable, convolutional layers. This method condenses network storage and speeds up the run time without significant adverse effect on the testing accuracy, addressing the first problem. Looking at the distribution of the weights through training when varying the number of blocks in a layer gives insight into the second problem. We observe that, even after thousands of training iterations, inner product layers have singular value distributions that resemble that of truly random matrices with iid entries and that each block in a BDIP layer behaves like a smaller copy. For network architectures differing only by the number of blocks in one inner product layer, the ratio of the variance of the weights remains approximately constant for thousands of iterations, that is, the relationship in structure is preserved in the parameter distribution.

1 Introduction

Fully connected (FC) layers are unwieldy and perplexing, yet they continue to be present in the most successful networks [16, 33, 40]. Ideally, efforts to reduce the memory requirements of neural networks would also lessen their computational demand, but often these competing interests force a trade-off. Our work addresses both memory and computational efficiency without compromise. Focusing our attention on the FC layers, we decrease network memory footprint, improve network runtime and begin to uncover the mechanism of inner product layers.

There are a variety of methods to condense large networks without much harm to their accuracy. One such technique that has gained popularity is pruning [6, 7, 30], but traditional pruning has disadvantages related to network runtime. Most existing pruning processes slow down network training, and the resulting condensed network is usually significantly slower to execute [6]. Sparse format operations require additional overhead that can greatly slow down performance unless one prunes nearly all weight entries, which can damage network accuracy.

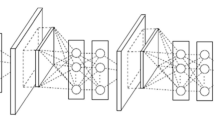
Localized memory access patterns can be computed faster than non-localized lookups. By implementing block diagonal inner product (BDIP) layers in place of FC layers, we condense neural networks in a structured manner that speeds up the final runtime and does little harm to the final accuracy. BDIP layers can be implemented by either initializing a purely block diagonal weight matrix or by initializing a fully connected layer and focusing pruning efforts off the diagonal blocks to coax the dense weight matrix into structured sparsity. The first method reduces the gradient computation time and hence the overall training time. The latter method retains higher accuracy and supports the robustness of networks to shaping, that is, pruning can be used as a mapping between architectures — in particular, a mapping to more convenient architectures. Depending on how many iterations the pruning process takes, this method may also speed up training.

We have converted a single fully connected layer into an ensemble of smaller inner product learners whose combined efforts form a stronger learner, in essence boosting the layer. These methods also bring artificial neural networks closer to the architecture of biological mammalian brains, which have more local connectivity [9].

Another link with our work and the mammalian brain is the relationship to random matrix theory. In neuroscience, synaptic connectivity is often represented by a matrix with entries drawn randomly from an appropriate distribution [28, 29]. The distribution of the singular values of a large, random matrix behaves predictably according to the Marchenko–Pastur law [21]. We show that this distribution also represents artificial neural activity matrices well after thousands of training iterations. This relationship allows us to compare the behavior of inner product layers in networks that have related structure, thereby uncovering a piece of the inner product layer “black box.” Specifically, we observe that when varying the number of blocks in a layer, the initial ratio of the variance of the weights is preserved to first order after thousands of training iterations.

2 Related work

There is an assortment of criteria by which one may choose which weights to prune. With any pruning method, the result is a sparse network that takes less storage space than its fully connected counterpart. Han et al. iteratively pruned a network using the penalty method by adding a mask that disregards pruned parameters for each weight tensor [7]. This means that the number of required floating point operations decreases, but the number performed stays the same. Furthermore, masking out updates takes additional time. Han et al. reported the average time spent on a forward propagation after pruning is completed and the resulting sparse layers have been converted to CSR format; for batch sizes larger than one, the sparse computations are significantly slower than the dense calculations [6].

More recently, there has been momentum in the direction of structured reduction in network architecture. Node pruning preserves some structure, but drastic node pruning can harm the network accuracy and requires additional weight fine-tuning [8, 36]. Other approaches include storing a low rank approximation for a layer’s weight matrix [31] and training smaller models on outputs of larger models (distillation) [10]. Group lasso expands the concept of node pruning to convolutional filters [18, 38, 39], that is, group lasso applies $L_1$-norm regularization to entire filters.

Structured efficient linear layers form linear layers as a composition of matrices [1, 3, 17, 24, 34]. Sidhawani et al. proposed structured parameter matrices characterized by low displacement rank that yield high compression rate as well as fast forward and gradient evaluation [34]. Their work focuses on Toeplitz-related transforms of the FC layer weight matrix. However, speedup is generally only seen for compression of large weight matrices. In [24], Moczulski et al. formed efficient linear layers, called ACDC layers, composed of diagonal matrices and the discrete cosine transform matrix.

Group, or depthwise separable, convolutions have been used in recent CNN architectures with great success [4, 11, 41]. In group convolutions, a particular filter does not see all of the channels of the previous layer. BDIP layers apply this idea of separable neuron groups to the FC layers. This method transforms a fully connected layer into an ensemble of smaller fully connected neuron groups that boost the layer.

There is less work considering the distribution of weights in artificial neural networks. Initialization distributions to combat vanishing gradients are supported by theoretical variances for back propagation gradients under the assumption that the weights are independent, which is not valid beyond the first iteration [5, 37]. Random weights have been looked at as good predictors of successful network architecture [32]. More recently, Tishby [27] has discussed the trend of the distribution of weight updates as they relate to the mutual information plane. To the best of our knowledge, the effects of architecture on the change in distribution of the weights through training and the connection between trained inner product layer weights and iid random matrices have not been explored. In theoretical neuroscience, random matrices are used to model synaptic connections and to study brain plasticity [28, 29, 35]. Knowing that inner product layers in artificial neural networks are well modeled by random matrices opens the field to a new range of analytical tools that may support a specific network’s robustness or plasticity.

3 Methodology

We consider two methods for implementing BDIP layers:

• 1. We initialize a layer with a purely block diagonal weight matrix and keep the number of connections constant throughout training.

• 2. We initialize a fully connected layer and iteratively prune entries off the diagonal blocks to achieve a block substructure.

When a BDIP layer is implemented using the second method, we will add the prefix “IP,” written IP-BDIP, to indicate it is an iteratively pruned BDIP layer. Within a layer, all blocks have the same size.¹ IP-BDIP layers are accomplished in three phases: a dense phase, an iterative pruning phase and a block diagonal phase. In the dense phase, a fully connected layer is initialized and trained in the standard way. During the iterative pruning phase, focused pruning is applied to entries off the diagonal blocks using the weight decay method with $L_1$-norm, that is, if W is the weight matrix for a fully connected layer we wish to push toward block diagonal, we add

$$\begin{aligned} \begin{aligned} D=\alpha \sum _{i,j}|{{\mathbb {1}}}_{i,j}W_{i,j}| \end{aligned} \end{aligned}$$

(1)

to the loss function during the iterative pruning phase, where $\alpha$ is a tuning parameter, $W_{i,j}$ is an entry in the layer’s weight matrix and ${\mathbb {1}}_{i,j}$ is an indicator function such that ${\mathbb {1}}_{i,j}=0$ when $W_{i,j}$ is off the diagonal blocks and ${\mathbb {1}}_{i,j}=1$ when $W_{i,j}$ is in a diagonal block. When pruning is completed, to maximize speedup it is best to reformat the weight matrix once such that the blocks are condensed and adjacent in memory.² Batched smaller dense calculations for the blocks use cuBLAS strided batched multiplication [26]. There is a lot of flexibility when using IP-BDIP layers that can be tuned for specific user needs. More pruning iterations may increase the total training time but can yield higher accuracy and reduce overfitting.

4 Experiments: speedup and accuracy

Our goal is to reduce memory storage of the inner product layers while maintaining or reducing the final execution time of the network with minimal loss in accuracy. We will also see reduction in the total training time in some cases. All experiments are run on the Bridges’ NVIDIA P100 GPUs through the Pittsburgh Supercomputing Center.

For speedup analysis, we timed block diagonal multiplications using $n\times n$ matrices with varying dimension sizes and varying numbers of blocks; we considered the forward pass and gradient updates. We also calculate an upper bound on the ratio of the number of pruning iterations to the number of pure block iterations that will yield speedup when using IP-BDIP layers.

For accuracy results, we ran experiments on three standard image classification datasets: MNIST [20], SVHN [25] and CIFAR10 [13]. MNIST and SVHN are both digit classification datasets; MNIST is handwritten in black and white, and SVHN contains colored pictures taken from the street of house numbers. The CIFAR10 dataset contains low resolution, colored images of objects in ten classes. We ran experiments on the MNIST dataset using a LeNet-5 [19] network, and the SVHN and CIFAR10 datasets using Krizhevsky’s cuda-convnet [14]. Cuda-convnet does not produce state-of-the-art accuracies for SVHN or CIFAR10, but demonstrates the performance differences between our methods and others. We also ran a few experiments on smaller, purely inner product layer networks without convolutional or other types of layers. With interest favoring deeper convolutional nets, we dedicate more space in this paper to exploring BDIP layers in convolutional nets to demonstrate their compatibility with modern networks. We implement our work in Caffe, which provides these architectures; Caffe’s MNIST example uses LeNet-5, and cuda-convnet can be found in Caffe’s CIFAR10 “quick” example.

For ease of transcription, let $(b_1, \ldots ,b_n)$-BD$_m$ denote a network architecture with m layers, not including the input layer, in which the last n layers are BDIP layers, where $b_i=j$ indicates that the ith BDIP layer has j blocks along the diagonal. If $b_i=1$, then the ith inner product layer is fully connected. In all cases in this paper, if $m>n$, then the first $m-n$ layers are convolutional.

4.1 Speedup

Figure 1 shows the speedup when performing matrix multiplication using an $n\times n$ weight matrix and batch size 100 when the weight matrix is purely block diagonal. In this section, speedup is always relative to the unaltered, fully connected calculation. The speedup when performing only the forward-pass matrix product is shown in the top pane, and the speedup when performing all gradient descent products is shown in the bottom pane. As the number of blocks increases, the overhead to perform cuBLAS strided batched multiplication can become noticeable; this library is not yet well optimized for performing many small matrix products [22]. However, with specialized batched multiplications for many small matrices, Jhurani et al. attained up to sixfold speedup [12]. Using cuBLAS strided batched multiplication, the maximum speedup is achieved when the number of blocks is $2^{-7}$ times the matrix dimension. When only timing the forward pass, the speedup is always greater than 1 when the number of blocks is at most $2^{-5}$ times the matrix dimension. When timing the forward and backward pass, the speedup is always greater than 1 when the number of blocks is at most $2^{-6}$ times the matrix dimension.

Fig. 1

Speedup when performing matrix multiplication using an $n\times n$ weight matrix and batch size 100. (Top) Speedup when performing only one forward matrix product. (Bottom) Speedup when performing all three matrix products involved in the forward and backward pass in gradient descent

On the other hand, using Toeplitz-related transforms, for displacement rank higher than approximately $2^{-9.5}$ times the matrix dimension the forward pass is slowed down, and backward pass is slowed down for displacement rank higher than approximately $2^{-10.4}$ times the matrix dimension [34]. From Fig. 3 in [34], speedup is generally only seen for compression of large weight matrices. From Fig. 2 in [24], we can see that ACDC layers do consistently provide speedup for multiple calls when compared to a dense linear layer. They achieve a maximum speedup of approximately 10 times for layers with dimension at most 8192, but in Fig. 1, we can see that BDIP layers exceed this maximum speedup by a small but clear margin for layers with dimension at most 8192.

For a given inner product layer, using IP-BDIP layers we would see speedup in that layer’s training time if

$$\begin{aligned} \frac{T({{\text {FC}}})-T({{\text {Block}}})}{T({{\text {Prune}}})}>\frac{y}{x} \end{aligned}$$

(2)

where $T(\cdot )$ is the combined time to perform the forward and backward passes of an inner product layer in the input state, x is the number of pure block iterations and y is the number of pruning iterations. $T({{\text {Prune}}})$ is the time to regularize and apply a mask to the off-diagonal block layer weights, which happens once in a training iteration. Figure 2 plots the upper bound in ratio 2 against the number of blocks for a layer with an $n\times n$ weight matrix and batch size 100.

Fig. 2

Using batch size 100, upper bound on the ratio of the number of pruning iterations to the number of pure block iterations that will result in an overall training speedup when using IP-BDIP layers

Fig. 3

For each inner product layer in LeNet-5 (top) and cuda-convnet (bottom): forward runtime speedup of block diagonal and CSR sparse formats, combined forward and backward runtime speedup of block diagonal format. LeNet-5 uses batch size 64, and cuda-convnet uses batch size 100

Figure 3 shows timing results for the inner product layers in LeNet-5 (top) and cuda-convnet (bottom), which both have two inner product layers. We plot the forward runtime speedup per inner product layer when the layers are purely block diagonal, the combined forward and backward runtime speedup to do the three matrix products involved in gradient descent training when the layers are purely block diagonal, and the runtime speedup of sparse matrix multiplication with random entries in CSR format using cuSPARSE [26]. The points at which the forward sparse and forward block curves meet in each plot in Fig. 3 indicate the FC dense forward runtime speedups for each layer; these are made clearer with dotted, black, vertical lines. Note that the block forward and combined forward/backward curves almost perfectly overlap in Fig. 3 (bottom).

In LeNet-5, the first inner product layer, ip1, has a $500 \times 800$ weight matrix, and the second inner product layer, ip2, has a $10 \times 500$ weight matrix, so the $(b_1,b_2)$-BD$_4$ LeNet-5 architecture has $(800\times 500)/b_1+(500\times 10)/b_2$ nonzero weights across both inner product layers. Figure 3 (top) shows there is greater than 1.4 times speedup for greater than or equal to 8000 nonzero entries in ip1, which happens for $b_1\le 50$, when timing both forward and backward matrix products in $(b_1,b_2)$-BD$_4$ LeNet-5, and 1.6 times speedup when $b_1=100$, or 4000 nonzero entries, when only timing the forward matrix product in $(b_1,b_2)$-BD$_4$ LeNet-5.

In cuda-convnet, the first inner product layer, ip1, has a $64 \times 1024$ weight matrix, and the second inner product layer, ip2, has a $10 \times 64$ weight matrix. The $(b_1,b_2)$-BD$_5$ cuda-convnet architecture has $(1024 \times 64)/b_1+(64 \times 10)/b_2$ nonzero entries across both inner product layers. Figure 3 (bottom) shows there is greater than 1.26 times speedup for greater than or equal to 2048 nonzero entries in ip1, which happens for $b_1\le 32$, when timing both forward and backward matrix products in $(b_1,b_2)$-BD$_5$ cuda-convnet, and 1.65 times speedup for greater than or equal to 1024 nonzero entries in ip1, which happens for $b_1\le 64$, when only timing the forward matrix product in $(b_1,b_2)$-BD$_5$ cuda-convnet.

In both plots of Fig. 3, we see sparse format performs poorly. Sparse format can be more than 8 times slower than dense calculations.

4.2 Accuracy results

All hyperparameters and initialization distributions provided by Caffe’s example architectures are left unchanged. Training is carried out with batched gradient descent using the cross-entropy loss function on the softmax of the output layer. In our experiments, we performed only manual tuning of the new hyperparameter introduced by IP-BDIP layers (see Eq. 1).

In ShuffleNet, Zhang et al. noted that when multiple group convolutions are stacked together, this can block information flow between channel groups and weaken representation [41]. To correct for this, they suggest dividing the channels in each group into subgroups and shuffling the outputs of the subgroups in this layer before feeding them to the next layer. Applying this approach to block inner product layers requires either moving entries in memory or doing more, smaller matrix products. Both of these options would hurt efficiency.

Using IP-BDIP layers also addresses information flow. Pruning does add some work to the training iterations, but, unlike the ShuffleNet method, does not add work to the final execution of the trained network. After pruning is completed, the learned weights are the result of a more complete picture; while the information flow has been constrained, it is preserved as an artifact in the remaining weights. Another alternative is to randomly shuffle whole blocks each pass like in the “ random sparse convolution” layer in the CNN library cuda-convnet [15]. We found that for the inner product layers in LeNet-5 and Krizhevsky’s cuda-convnet, the ShuffleNet method did not show as much improvement in accuracy as randomly shuffling the whole blocks, so we do not include results using the ShuffleNet method.

Table 1 shows the accuracy results for BDIP layers, BDIP layers with random block shuffling, IP-BDIP layers and layers with traditional iterative pruning using the penalty method to prune weight entries not subject to any confinement or organization. The baseline accuracy without using any parameter-efficient layers can be found in parenthesis next to the dataset name in Table 1.³ We show accuracy results for the most condensed net with BDIP layers and the net with the fastest speedup in the inner product layers.

Table 1 Accuracy results on MNIST dataset with the LeNet-5 network, and the SVHN and CIFAR10 datasets with the cuda-convnet network

4.2.1 MNIST

We experimented on the MNIST dataset with the LeNet-5 framework [19] using a training batch size of 64 for 10,000 iterations. LeNet-5 has two convolutional layers with pooling followed by two inner product layers with ReLU activation. LeNet-5 (1,1)-BD$_4$ achieves a final accuracy of 99.11%. In all cases, testing accuracy remains within 1% of this (1,1)-BD$_4$ accuracy.

Using traditional iterative pruning with $L_2$ regularization, as suggested in [7], pruning until 4000 and 500 nonzero entries survived in ip1 and ip2, respectively, gave an accuracy of 98.55%, but the forward multiplication was more than 8 times slower than the dense FC case (see Fig. 3, top). On the other hand, implementing the LeNet-5 (100,10)-BD$_4$ architecture with IP-BDIP layers using 15 dense iterations and 350 pruning iterations gave a final accuracy of 98.65%. (10,1)-BD$_4$ yielded approximately 1.4 times speedup for all gradient descent matrix products in both inner product layers after any pruning is completed, and (100,10)-BD$_4$ condensed the inner product layers in LeNet-5 approximately 81 fold.

In [34], Toeplitz (3) has error rate 2.09% using a single hidden layer net with 1000 hidden nodes on MNIST. This method yields 63.32-fold compression over the FC setting. However, from Fig. 3, this slows down the forward pass by around 1.5 times and the backward pass by around 5.5 times. A (49,1)-BD$_2$ net with one hidden layer that has 980 hidden nodes has 29.43 fold compression and error rate 4.37% using IP-BDIP layers on MNIST. Our speedup with this net is 1.53 for forward only and 1.04 when combining the forward and backward runtime. Our net achieves less than a $5\%$ error rate even though the blocks of neurons in the hidden layer can only see a portion of the test input images.⁴ What Toeplitz (3) gains in compression and accuracy, it sacrifices in execution time.

4.2.2 SVHN

We experimented on the SVHN dataset with Krizhevsky’s cuda-convnet [14] using batch size 100 for 9000 iterations. Cuda-convnet has three convolutional layers with ReLu activation and pooling, followed by two FC layers with no activation. Cuda-convnet (8,1)-BD$_5$ yielded approximately 1.5 times speedup for all gradient descent matrix products in both inner product layers when purely block diagonal, and cuda-convnet (64,2)-BD$_5$ condensed the inner product layers in cuda-convnet approximately 47-fold.

Using cuda-convnet (1,1)-BD$_5$ we obtained a final accuracy of 91.96%. Table 1 shows all methods stayed under a $2.5\%$ drop in accuracy. Using traditional iterative pruning with $L_2$ regularization until 1024 and 320 nonzero entries survived in the final two inner product layers, respectively, gave an accuracy of 90.93%, but the forward multiplication was more than 8 times slower than the dense FC computation. On the other hand, implementing cuda-convnet (64, 2)-BD$_5$ with IP-BDIP layers, which has corresponding numbers of nonzero entries, with 500 dense iterations and less than 1000 pruning iterations gave a final accuracy of 90.02%. This is approximately 47-fold compression of the inner product layer parameters with only a 2% drop in accuracy when compared to (1,1)-BD$_5$.

4.2.3 CIFAR10

We experimented on the CIFAR10 dataset with Krizhevsky’s cuda-convnet [14] using batch size 100 for 9000 iterations. Using cuda-convnet (1,1)-BD$_5$, we obtained a final accuracy of 76.29%. Table 1 shows all methods stayed within a $4\%$ drop in accuracy. Using traditional iterative pruning with $L_2$ regularization until 1024 and 320 nonzero entries survived in the final two inner product layers gave an accuracy of 75.18%, but again the forward multiplication was more than 8 times slower than the dense FC computation. On the other hand, implementing cuda-convnet (64, 2)-BD$_5$ with IP-BDIP layers, which has corresponding numbers of nonzero entries, with 500 dense iterations and less than 1000 pruning iterations gave a final accuracy of 74.81%. This is approximately 47 fold compression of the inner product layer parameters with only a 1.5% drop in accuracy. The total forward runtime of ip1 and ip2 in cuda-convnet (64, 2)-BD$_5$ is 1.6 times faster than in (1,1)-BD$_5$. To achieve comparable speed with sparse format, we used traditional iterative pruning to leave 37 and 40 nonzero entries in the final inner product layers giving an accuracy of 73.01%. Thus, implementing BDIP layers with pruning yields comparable accuracy and memory condensation to traditional iterative pruning with faster final execution time.

Whole node pruning decreases the accuracy more than corresponding reductions in the block diagonal setting. Node pruning until ip1 had only 2 outputs, i.e., a $1024\times 2$ weight matrix, and ip2 had a $2\times 10$ weight matrix for a total of 2068 weights between the two layers gave a final accuracy of 59.67%. On the other hand, using IP-BDIP layers, cuda-convnet (64,2)-BD$_5$ has a total of 1344 weights between the two inner product layers and had a final accuracy 74.81%.

The final accuracy on an independent test set was 76.29% on CIFAR10 using the cuda-convnet (1,1)-BD$_5$ net while the final accuracy on the training set itself was 83.32%. Using the cuda-convnet (64,2)-BD$_5$ net without pruning, the accuracy on an independent test set was 72.49%, but on the training set was 75.63%. Figure 4 graphs the difference between the accuracy on the training set and the accuracy on an independent test set when training Krizhevsky’s cuda-convnet [14] on the CIFAR10 dataset using BDIP layers; we plot $(b_1{,}1)$-BD$_5$ for various values of $b_1$. Figure 5 plots the ratio of the accuracy over the curves in Fig. 4; we can see that more blocks yield a higher accuracy to overfit ratio. With IP-BDIP layers, the accuracy of (64,2)-BD$_5$ on an independent test set was 74.81%, but on the training set was 76.85%. Both block diagonal methods decrease overfitting, but IP-BDIP layers decrease overfitting slightly more.

Fig. 4

Difference between the accuracy on the training set and the accuracy on an independent test set when training Krizhevsky’s cuda-convnet [14] on the CIFAR10 dataset

Fig. 5

Accuracy over the difference between the accuracy on the training set and the accuracy on an independent test set when training Krizhevsky’s cuda-convnet [14] on the CIFAR10 dataset

5 Random matrix theory observations

The Marchenko–Pastur distribution describes the asymptotic behavior of the singular values of large random matrices with iid entries [21]. Let X be an $m\times n$ matrix with iid entries $x_{ij}$ such that $\mathrm {E}[x_{ij}]=0$ and $\mathrm {Var}[x_{ij}]=\sigma ^2$. The Marchenko–Pastur theorem states that as $n,m\rightarrow \infty$ such that $m/n\rightarrow y>0$, with probability 1 the empirical spectral distribution of $\frac{1}{n}XX^\top$ converges in distribution to the density

$$\begin{aligned} \mu _{y}(x)={\left\{ \begin{array}{ll} \frac{1}{2\pi \sigma ^2y x}\sqrt{(b-x)(x-a)}&{} \text{ if } a\le x \le b\\ 0&{}\text{ otherwise } \end{array}\right. } \end{aligned}$$

(3)

with point mass $1-1/y$ at the origin if $y>1$ where $a = \sigma ^2(1-y^2)$ and $b = \sigma ^2(1+y^2)$.

Network weights do not remain independent through training. Without momentum, weight parameter W receives the update $W\leftarrow W-\frac{\lambda }{b}\sum _{i=1}^b\frac{\partial L(x_i)}{\partial W}$ in an iteration, where $\lambda$ is the learning rate, b is the batch size, L is the loss function and $x_i$ is sampled from the data distribution. One can easily verify

$$\begin{aligned} \Delta \mathrm {Var}(W)=\lambda ^2\mathrm {Var}\left( \frac{1}{b}\sum _{i=1}^b\frac{\partial L(x_i)}{\partial W}\right) -2\lambda \mathrm {Cov}\left( W, \frac{1}{b}\sum _{i=1}^b\frac{\partial L(x_i)}{\partial W}\right) \end{aligned}$$

(4)

using estimators for the right side of the equation. In our experience, the covariance quickly became the dominating term. However, for a large enough weight matrix, the singular values of an inner product layer weight matrix behave according to the Marchenko–Pastur distribution even after thousands of training iterations, that is, after thousands of correlated updates, the weight matrix behaves like a matrix with random iid entries. The assumption of independence fails at the microlevel when calculating the change in variance of the weights, but is accurate at the macrolevel when considering the behavior of the weight matrix as an operator.

In this section, we discuss only the first method for implementing BDIP layers without pruning. Networks that differ only by the number of blocks in one layer are referred to as sister networks. While a relationship between FC layer weights and the corresponding BDIP layer weights in trained sister networks is not evident from Eq. (4), indeed a relationship can be seen in the singular values of the weight matrices and, in particular, in the change in the variance of the weight matrix entries throughout training. The initialization ratio of variances in corresponding layer weight matrices of sister networks persists through thousands of training iterations. This finding may provide a good mechanism for examining related network architectures and may support claims about a network’s malleability or fitness.

5.1 MNIST

In our experiments on the MNIST dataset with the LeNet-5 framework [19], the inner product layer weights are initialized using the Xavier algorithm [5]. Thus, the initialization variance of the weights in ip1 is $b_1/800$ if ip1 is a BDIP layer, where $b_1$ is the number of blocks, and the ratio of the ip1 initialization variance in $(b_1{,}1)$-BD$_4$ LeNet-5 over the ip1 initialization variance (1,1)-BD$_4$ LeNet-5 is just $b_1$. Figure 6 (top) shows that this ratio is a good first-order estimate for the final ip1 variance ratio after 10,000 iterations in sister $(b_1{,}1)$-BD$_4$ LeNet-5 networks. We have written $(b_1{,}1)$-BD$_4$/(1,1)-BD$_4$ in the figure legend, but by this we mean the ratio of the ip1 weight matrix variance in $(b_1{,}1)$-BD$_4$ LeNet-5 over that of (1,1)-BD$_4$ LeNet-5. The final ip1 variance ratios are 5.03, 9.97, 19.96, 49.32 and 96.99 for $b_1=5,10,20,50,$ and 100, respectively. We can see that the relationship deteriorates as the number of blocks increases. This phenomenon persists when the sigmoid activation function is used for layer ip1, keeping the activation function consistent across sister networks. When using the sigmoid activation function, the ratio seemed to deteriorate less quickly, e.g., the final ip1 variance ratio was 101.00 for $b_1=100$.

Fig. 6

10,000 training iterations using LeNet-5 net on MNIST. (Top) The ratio of the ip1 weight matrix variance in $(b_1{,}1)$-BD$_4$ over the ip1 weight matrix variance in (1,1)-BD$_4$. (Bottom) Ratio of trained ip1 weight matrix singular values over singular values of a truly random matrix with the same dimensions

Figure 6 (bottom) compares the singular values of the ip1 layer weight matrix in sister $(b_1{,}1)$-BD$_4$ networks after 10,000 training iterations to the singular values of a truly random $800\times 500$ matrix whose entries were initialized with variance $6.6 \times 10^{-4}$, the final variance of the (1,1)-BD$_4$ LeNet-5 ip1 layer weights. We denote the random matrix R. To make this comparison, we aggregate the singular values of each block along the diagonal in ip1 of $(b_1{,}1)$-BD$_4$ LeNet-5 and sort them, but we note that the individual block spectral distributions appear identical to each other. For an array of singular values arranged by order, division is done entry-wise. We have written $(b_1{,}1)$-BD$_4/R$ in the figure legend, but by this we mean entry-wise division of the ordered singular values of the ip1 weight matrix in $(b_1{,}1)$-BD$_4$ LeNet-5 over the ordered singular values of R. By convention, the lowest order singular values are the largest.

The individual curves in Fig. 6 (bottom) are difficult to distinguish. In fact, for each curve in Fig. 6 (bottom) the average distance from one, when averaging over order, is bounded above by $4\times 10^{-2}$ (see Fig. 7). This behavior aligns with what the Marchenko–Pastur theorem dictates would happen to the ratio of the spectral distributions if the ip1 layer weight matrix had random iid entries, but in fact the ip1 layer weight matrices hold knowledge and are the product of 10,000 correlated updates. By the Marchenko–Pastur theorem, increasing the variance of the entries in a random matrix and simultaneously decreasing the matrix dimension by the same factor will not affect the singular value distribution; the decrease in matrix size would cancel with the increase in variance by the same factor [see Eq. (3)]. Figure 6 (top) shows that the ratio of the ip1 initialization variance in $(b_1{,}1)$-BD$_4$ LeNet-5 over the ip1 initialization variance (1,1)-BD$_4$ LeNet-5 is still $b_1$ after 10,000 training iterations, and for $b_1$ blocks the ip1 layer weight matrix decreases in dimension by a factor of $b_1$. Figure 6 (bottom) shows that these factors canceled for the trained ip1 matrices like they would for random matrices since the ratio of the singular values is just one, that is, the learned ip1 layer weight matrices behave like random operators.

The singular values of the trained ip1 layer weight matrices from $(b_1{,}1)$-BD$_4$ LeNet-5 follow the curve that the singular values of the truly random matrix create with some error in the largest and smallest singular values. The disparity in the extreme singular values will be the focus of future work; it may be the first place where network learning become evident, or it may be the result of overfitting. Using (1,1)-BD$_4$ LeNet-5, the accuracy reaches 98.28% by iteration 1000. After 1000 iterations, the ratio of the largest singular value of the trained weight matrix in layer ip1 over the largest singular value of a truly random matrix with the same dimensions and variance is 1.16. Figure 6 (bottom) shows that this ratio is 1.44 after the full 10,000 iterations. Figure 7 shows the expected value, taken over singular value order, of the distance between 1 and the ratio of sorted, aggregated singular values of ip1 weight matrices for sister $(b_1{,}1)$-BD$_4$ LeNet-5 networks and the singular values of R, a random matrix with iid entries of equal dimension; this is plotted over training iterations for varying values of $b_1$. In Fig. 7, we can see that at iteration zero smaller $b_1$ values correspond to expected ratios closer to one, which can be explained by the necessity of the limit in the Marchenko–Pastur theorem. On the other hand, after 10,000 training iterations, smaller $b_1$ values correspond to expected ratios farther away from one, indicating that larger values of $b_1$ maintain a final distribution that is more similar to that of a random matrix. In Figs. 4 and 5, we learned that larger values of $b_1$ also correspond to reduced overfit.

The ratios in Fig. 6 best highlight the relationship to random matrix theory and the relationship between ip1 layer weight matrix distributions in sister $(b_1{,}1)$-BD$_4$ networks, but we also include the ip1 layer weight matrix variances and their singular values without taking a ratio in Fig. 8. Figure 8 (top) shows that the variances did change through training, and so the fact that they maintained their original variance ratios is nontrivial. The curves in Fig. 8 (bottom) are again difficult to distinguish, but one can more clearly see the classic Marchenko–Pastur distribution.

Fig. 7

10,000 training iterations using LeNet-5 net on MNIST. Expected value taken over order of the distance between 1 and the ratio of sorted, aggregated singular values of ip1 weight matrices for sister $(b_1{,}1)$-BD$_4$ networks and the singular values of R, a random matrix with iid entries of equal dimension

Fig. 8

10,000 training iterations using LeNet-5 net on MNIST. (Top) Variance of weight matrix entries in layer ip1 in both the fully connected and block diagonal settings. (Bottom) Singular values of ip1 weight matrices for sister $(b_1{,}1)$-BD$_4$ networks and of R, a random matrix with iid entries of equal dimension

Figure 9 (top) compares the probability density function of the singular values of R, a truly random matrix with independent entries, to the measured distribution of the ip1 layer weight matrix singular values for the (1,1)-BD$_4$ LeNet-5 architecture after 10,000 training iterations. For a matrix M, $\lambda _M$ is the PDF of the eigenvalues of M. We use $W_{1}$ to denote the ip1 layer weight matrix in (1,1)-BD$_4$ after 10,000 training iterations and again R to denote a $800\times 500$ random matrix with iid entries that have the same variance as the entries in $W_{1}$. $\lambda _{(1/500)W_1W_1^\top }$ and $\lambda _{(1/500)RR^\top }$ align as we would expect from Fig. 6 (bottom).

Fig. 9

$\lambda _{\frac{1}{500}W_{b_1}W_{b_1}^\top }$ is the measured empirical spectral distribution of $\frac{1}{500}W_{b_1}W_{b_1}^\top$ where $W_{b_1}$ is the ip1 layer weight matrix in the $(b_1{,}1)$-BD architecture after 10,000 training iterations on MNIST using LeNet-5. Bar graph of $\lambda _{\frac{1}{500}W_{1}W_{1}^\top }$ with plot of $\lambda _{\frac{1}{500}RR^\top }$ for a random matrix R with the same variance

If we make ip2 a BDIP layer as well in the LeNet-5 framework, the change in variance in ip1 sees minimal effect. For $b_1=1,2,5,10,50,100$ and $b_2=1,2,5,10,$, the final variance in the ip1 layer weights using $(b_1,b_2)$-BD$_4$ over the final variance in the ip1 layer weights using $(b_1{,}1)$-BD$_4$ is approximately 1 with error $\le 0.05$.⁵

In our experiments, the relationship between inner product layers in sister networks is independent of network architecture. We ran experiments on purely inner product layer networks without convolutional or other types of layers with the same results, and we will discuss a small purely inner product layer network briefly here. In a three-layer network in which both hidden layers have 500 nodes and ReLu activation, we compare (1,1,1)-BD$_3$ to (1,100,1)-BD$_3$ on MNIST where in both cases ip2 is initialized with Xavier variance [5]. After 10,000 iterations, the ratio of the variance of the weight matrix entries in layer ip2 in block diagonal setting over the variance of the weight matrix entries in layer ip2 in the fully connected setting is 106.42.

Let $\sigma _{W_{b_2}}$ be the singular values of the ip2 layer weight matrix in the (1,$b_2$,1)-BD$_3$ architecture with only 3 inner product layers after 10,000 iterations. The final variance of the ip2 layer weights in (1,1,1)-BD$_3$ is 0.0012. If R is a $500\times 500$ truly random matrix with independent entries that have variance 0.0012, then $\mathrm {E}[|1-\sigma _{W_{1}}/\sigma _{R}|]=0.1162$. The final variance of the ip2 layer weights in (1,100,1)-BD$_3$ is 0.12. If R is a $500\times 500$ truly random matrix with independent entries that have variance 0.12, then $\mathrm {E}[|1-\sigma _{W_{100}}/\sigma _{R}|] = 0.0896$.

5.2 CIFAR10

In our experiments on CIFAR10 with Krizhevsky’s cuda-convnet [14], the first inner product layer weights are initialized using a Gaussian filler with standard deviation 0.1. Thus, the ratio of variance of the weights in ip1 in the block diagonal case over that of the fully connected case at initialization is 1. Figure 10 (top) indicates that this ratio is a good first-order estimate for the final ratio in sister $(b_1{,}1)$-BD$_5$ cuda-convnet networks after 9000 iterations at which time the ratios are 1.02, 1.02, 1.01, 1.11, 1.21 and 1.5 for $b_1=2,4,8,16,32,$ and 64, respectively. Like with our experiments on MNIST, the relationship deteriorates as the number of blocks grows.

Fig. 10

9000 training iterations using cuda-convnet on CIFAR10. (Top) Ratio of variance of ip1 weight matrix entries in block diagonal setting over variance of ip1 weight matrix entries in the fully connected setting. (Bottom) Ratio of trained ip1 weight matrix singular values over singular values of a truly random matrix with the same dimensions

We compared the singular values of the weight matrix in layer ip1 for sister $(b_1{,}1)$-BD$_5$ cuda-convnet networks after 9000 training iterations to the singular values of a truly random $1024 \times 64$ matrix initialized with variance $7\times 10^{-3}$, the final variance of the fully connected ip1 layer weights after training. We denote the random matrix R. As in the MNIST experiments, we aggregate the singular values of each block in the block diagonal method and sort them, and for an array of singular values arranged by order, division is done entry-wise. In Fig. 10 (bottom), we have written $(b_1{,}1)$-BD$_5/R$ in the figure legend, but by this we mean entry-wise division of the ordered singular values of the ip1 weight matrix in $(b_1{,}1)$-BD$_5$ cuda-convnet over the ordered singular values of R. By convention, the lowest order singular values are the largest.

By the Marchenko–Pastur theorem, maintaining the variance of the entries in a random matrix while decreasing the matrix dimension by the some factor $b_1$ will alter the singular value distribution by a factor of $1/\sqrt{b_1}$; see Eq. (3). Figure 10 (top) shows that the ratio of the ip1 initialization variance in $(b_1{,}1)$-BD$_5$ cuda-convnet over the ip1 initialization variance (1,1)-BD$_4$ cuda-convnet remains relatively constant after 9000 training iterations, and for $b_1$ blocks the ip1 layer weight matrix decreases in dimension by a factor of $b_1$. Figure 10 (bottom) shows that the ratio of the singular values of the trained layer ip1 weight matrix in $(b_1{,}1)$-BD$_5$ cuda-convnet networks over the singular values of R is approximately $1/\sqrt{b_1}$, suggesting that the trained layer ip1 weight matrix in $(b_1{,}1)$-BD$_5$ cuda-convnet networks behaves like a random matrix with deterioration as $b_1$ grows.

Again, the ratio of the variance and singular values of the ip1 layer weight matrix in block diagonal setting over that of the ip1 layer weight matrix in the fully connected setting after 9000 training iterations on CIFAR10 using cuda-convnet best highlight the relationship to random matrix theory, but we also include the variance and the singular values without taking a ratio in Fig. 11. The singular values of the fully connected ip1 layer weight matrix follow the curve that the singular values of the truly random matrix R create.

Fig. 11

9000 training iterations using cuda-convnet on CIFAR10. (Top) Variance of weight matrix entries in layer ip1 in both the fully connected and block diagonal settings. (Bottom) Singular values of ip1 weight matrices for sister $(b_1{,}1)$-BD$_5$ networks and of a random matrix with iid entries of equal dimension

Figure 12 compares the probability density function of the singular values of a truly random matrix with independent entries to the measured distribution of the ip1 layer weight matrix singular values using the (1,1)-BD$_5$ architecture after 9000 training iterations. We use $W_{1}$ to denote the ip1 layer weight matrix and R to denote a $1024\times 64$ random matrix with iid entries that have the same variance the entries in $W_{1}$.

Fig. 12

$\lambda _{\frac{1}{64}W_{b_1}W_{b_1}^\top }$ is the measured empirical spectral distribution of $\frac{1}{64}W_{b_1}W_{b_1}^\top$ where $W_{b_1}$ is the ip1 layer weight matrix in the $(b_1{,}1)$-BD$_5$ architecture after 9000 training iterations on the CIFAR10 dataset using cuda-convnet framework. Bar graph of $\lambda _{\frac{1}{64}W_{1}W_{1}^\top }$ with plot of $\lambda _{\frac{1}{64}RR^\top }$ for a random matrix R with the same variance

If in addition we make the ip2 a BDIP layer, again, the change in variance in ip1 sees minimal effect. For $b_1=1,2,4,8,16,32,64$, the final variance in the ip1 layer weights using the $(b_1,2)$-BD$_5$ cuda-convnet method over the final variance in the ip1 layer weights using the $(b_1{,}1)$-BD$_5$ cuda-convnet method is approximately 1 with error $\le 0.03$.

6 Conclusion

We have shown that BDIP layers can reduce network size, training time and final execution time without significant harm to the network performance. We have also shown that random matrix theory gives informative results about relationships in network structure that are preserved through thousands of training iterations.

While traditional iterative pruning can reduce storage, the scattered surviving weights make sparse computation inefficient, slowing down both training and final execution time. Our block diagonal methods address this inefficiency by confining dense regions to blocks along the diagonal. Without pruning, block diagonal method 1 allows for faster training time. IP-BDIP layers preserve the learning with focused, structured pruning that reduces computation for speedup during execution. In our experiments, IP-BDIP layers saw higher accuracy than the purely block diagonal method. The success of IP-BDIP layers supports the use of pruning as a mapping from large dense architectures to more efficient, smaller, dense architectures. Both methods make larger network architectures more feasible to train and use since they convert a fully connected layer into a collection of smaller inner product learners working jointly to form a stronger learner. In particular, GPU memory constraints become less constricting.

There is a lot of room for additional speedup with BDIP layers. Dependency between layers poses a noteworthy bottleneck in network parallelization. With structured sparsity like ours, one no longer needs a full barrier between layers. Additional speedup would be seen in software optimized to support weight matrices with organized sparse form, such as blocks, rather than being optimized for dense matrices. For example, for many small blocks, one can reach up to sixfold speedup with specialized batched matrix multiplication [12]. Hardware has been developing to better support sparse operations. Block format may be especially suitable for training on evolving architectures such as neuromorphic systems. These systems, which are far more efficient than GPUs at simulating mammalian brains, have a pronounced 2-D structure and are ill-suited to large dense matrix calculations [2, 23].

We have established a connection between random matrices with independent entries and trained inner product layers; the group behavior resembles that of a random matrix with independent entries, but the individual weight updates have complex dependencies. Similar random activity occurs in the mammalian brain and suggests looking at random matrix theory to support a network’s plasticity or robustness. This connection could help evaluate network fitness. We have also shown that the relationship in structure between sister networks is perpetuated in the ratio of the change in variance after thousands of training iterations. We emphasize that this is a nontrivial relationship surviving various datasets, network architectures and activation functions. Random matrix theory has been indispensable to the advancement of nuclear physics, quantum physics, neuroscience and ecology and has the potential to elevate artificial neural network analysis in the same manner.