A novel VIKOR method with an application to multiple criteria decision analysis for hospital-based post-acute care within a highly complex uncertain environment

Abstract

Post-acute care (PAC) is an interdisciplinary healthcare service used to assist in returning patients to their community after they receive acute medical services. To establish a fully developed PAC service model, the National Health Insurance Administration in Taiwan attempts to recruit professional medical service institutions (consisting of medical centers and regional and district hospitals) in a trial program for improving the rehabilitation quality of patients with cerebrovascular diseases (CVDs) and to reduce the re-hospitalization rate. The evaluation and selection of adequate medical service institutions are critical in the program for enhancing the effectiveness of hospital-based PAC in acute stroke management. However, because of the complexity of the national health insurance system and the healthcare system in Taiwan, the determination of pilot hospitals is a highly complicated and ambiguous multiple criteria decision analysis (MCDA) problem. Focusing on the requirement of generating a set of pilot hospitals for the PAC program and tackling imprecise and uncertain information associated with a complex medical circumstance, the purpose of this paper is to develop a novel compromising decision-making method based on the interval-valued Pythagorean fuzzy (IVPF) set theory and the VlseKriterijumska Optimizacija I Kompromisno Resenje (VIKOR) methodology to address the multiple criteria selection problem of pilot hospitals in assisting the establishment of a hospital-based PAC model. Considering the powerfulness of IVPF sets when handling vagueness and complex uncertainty in practical problems, this paper proposes a useful IVPF VIKOR method that is significantly different from the existing VIKOR methodology. The proposed methodology represents a comprehensive integration of high-order uncertainties within a decision environment into the basic VIKOR structure that is designed to lead to both better description and better applicability of MCDA. This paper presents some novel concepts such as remoteness indices and remoteness-based multiple criteria ranking indices and investigates their desirable properties in detail. With the theoretical support of these new concepts, this paper establishes useful remoteness-based group utility indices, individual regret indices, and compromise indices for the assessment of acceptable advantage and acceptable stability. Unlike the current VIKOR-based ranking process, this paper provides a systematic ranking procedure that is capable of improving the efficiency of determining ultimate compromise solutions. Overall, the present study provides several significant contributions, such as structuring the selection problem for hospital-based PAC, extending the IVPF theory and VIKOR to the medical and healthcare fields, simplifying the manipulation procedure in handling IVPF information, constructing valuable concepts of remoteness-based indices, and developing an effective IVPF VIKOR ranking procedure. A real-world example of selecting pilot hospitals in the PAC program for CVDs is provided to illustrate the application of the proposed method and to demonstrate its practicality and effectiveness. Furthermore, other valuable MCDA applications with a comparative analysis are conducted to validate the advantages of the proposed method in a variety of fields.

1 Introduction

Post-acute care (PAC) refers to the range of interdisciplinary healthcare services provided in a consistent, intensive manner within the optimal treatment period to patients who, after receiving acute care, stabilize without any life-threatening complications but exhibit short- or long-term disabilities. PAC is applied to promote their recovery from injuries in the shortest time possible and expedite their return to the normal functions of everyday life or alleviate their disability. A PAC program has recently been implemented in phases across Taiwan to target patients with cerebrovascular diseases (CVDs). The aim of this program was to establish a nationwide PAC model, which includes a vertically integrated transitional care system that delivers care services from acute and post-acute to chronic phases. The pilot hospitals selected for the program were required to develop a PAC model tailored to patients with CVDs to improve their PAC quality. Accordingly, the success of the program depended on these hospitals.

However, because of the complexity of the national health insurance (NHI) system and the healthcare system in Taiwan, the selection of pilot hospitals for the PAC program constitutes an intractable multiple criteria decision analysis (MCDA) problem. Selection criteria for the program may conflict with each other. Due to the ambiguity, inaccuracy, and uncertainty of this MCDA problem, the performances of candidate hospitals are difficult to quantify through these criteria. To address this complex problem, the concept of interval-valued Pythagorean fuzzy (IVPF) sets is applied to describe the fuzziness of decision making according to the degrees of membership and non-membership that are represented by flexible interval values that reflect the degree of hesitation. A novel IVPF MCDA method is proposed to address the ambiguity and multiple uncertainties of subjectively assessing candidate hospitals. The background, motivation, objective, and contributions of this study are detailed as follows.

1.1 Background of PAC for CVDs

PAC is a form of interdisciplinary care administered following acute care to facilitate the patients’ return to their community. PAC helps to reduce medical expenses, integrate healthcare services in different fields, and improve patient functions [40]. Depending on the country where it is used, PAC is also referred to intermediate care, subacute care, transitional care, and post-hospital care; all these care services have similar characteristics [21]. Moreover, an aging population produces a growing number of patients who become disabled following acute care, placing a burden on healthcare systems and family and social care [20]. This trend can be slowed by administering PAC, which entails the consistent and timely delivery of integrated care in line with the level of disability in individual patients to facilitate their recovery, thereby reducing their readmission expenditures [31], lightening the burden on family and social care [12], streamlining the allocation of acute care resources [20], and ensuring a seamless transition from acute to long-term care [51].

The National Health Insurance Administration (NHIA) piloted a PAC program for patients with CVDs because these patients have the highest rates of readmission and overstay [25] and spend a growing number of consecutive admission days in the acute phase [21], which involves severe comorbidity and requires cross-departmental cooperation. This program is officially named PAC-CVD and is aimed at enhancing PAC quality, facilitating the development of a vertically integrated transitional healthcare system and the recovery from disability in the post-acute phase, and reducing the risk of chronic disability and the burden on NHI resources and family and social care.

Hospital-based PAC-CVD requires its participating hospitals to organize a hierarchical interdisciplinary team including the medical center, community hospital, and regional hospital personnel. It is implemented in three phases: (1) the first pilot phase (recruiting institutional teams to develop a PAC model for patients with CVDs to improve PAC quality; establishing a vertically integrated transitional care system that delivers care to the patients from acute and post-acute to chronic phases; and ensuring the integrity and effectiveness of PAC to alleviate disability in patients); (2) the second pilot phase (institutional teams promote the PAC model; their experiences gained in the previous phase will be utilized to promote the application of the model in the treatment of other diseases); and (3) the promotion phase (providing the PAC model to more patients, recruiting more participating hospitals, and implementing the model as the transition from acute to long-term care). Thus, the program’s effectiveness depends largely on the pilot hospitals.

1.2 Motivation and focus of the study

Assessment of candidate hospitals for implementing the PAC-CVD program can be regarded as a complicated MCDA problem that requires consideration of multiple feasible alternatives and conflicting tangible and intangible criteria. In particular, NHIA intends to select one or more appropriate applicants to be the pilot hospitals for implementing the PAC-CVD program. That is, a set of compromise solutions needs to be identified in the multiple criteria evaluation and selection problem of pilot hospitals.

Generally, most existing MCDA methodology aims to find a unique solution that maximally achieves the overall criteria as much as possible. In contrast, the VlseKriterijumska Optimizacija I Kompromisno Resenje (i.e., multi-criteria optimization and compromise solution) (VIKOR) method is capable of determining a set of compromise solutions in the presence of conflicting criteria with respect to the preferences of the decision makers [16, 27, 33, 36, 37, 45]. Focusing on the requirement of determining a set of compromise solutions in the MCDA problem under study, this paper attempts to promote the VIKOR methodology to address the selection problem of pilot hospitals for facilitating implementation of hospital-based PAC-CVD.

The VIKOR method was introduced by Opricovic [34] and Opricovic and Tzeng [35]. To date, it is one of the famous MCDA approaches to address a discrete multiple criteria problem with non-commensurable and conflicting criteria [2, 3, 16, 18]. To achieve the purpose of ranking and selecting from a set of candidate alternatives, the VIKOR technique is established on the basis of the distance of an alternative to the ideal solution, in which aggregation, normalization, and preference are its fundamental procedures [16, 36, 37]. VIKOR focuses on the determination of a set of compromise solutions that are established by mutual concessions [2, 3, 27, 36, 37] to effectively aid MCDA and improve the quality of decision making [47, 59]. Over the past few years, VIKOR-related studies have gained popularity in various MCDA fields because of its great ability to compromise rank performance by comparing the measure of closeness to the ideal solution [16]. Many streams of the literature have reported studies involving the advancement and development of the VIKOR methodology within an uncertain environment, including the following: an extension of the crisp VIKOR method to the interval-valued neutrosophic set (IVNS) environment (named the VIKOR-IVNS method) [5], a fuzzy belief structure-based VIKOR method [19], an extended VIKOR method based on neutrosophic hesitant fuzzy information [29], a linguistic 2-tuple VIKOR method based on hybrid information (i.e., coexistence of real numbers and linguistic fuzzy variables) [41], a generalized distance-based VIKOR method based on heterogeneous information (consisting of crisp numbers, interval numbers, intuitionistic fuzzy (IF) numbers, and hesitant fuzzy linguistic values) [49], a remoteness index-based VIKOR method [10], an IF VIKOR method [44], and a dual hesitant fuzzy VIKOR method [43]. At present, the VIKOR methodology has been successfully utilized in a wide range of applications [18, 38, 56] and has been validated empirically in numerous real-world problems in business and management [23].

Although a great deal of effort has been made in VIKOR applications, current published findings supporting that VIKOR is an effective decision aiding method in the medical and healthcare fields are equivocal. Gul et al. [16] have conducted a state-of-the-art literature review to categorize, analyze, and interpret the existing research on VIKOR developments and applications. However, relatively little research has been conducted on the development of the VIKOR methodology in the fields of medicine and healthcare management. In the last few years, Lu et al. [30] combined the methods of decision-making trial and evaluation laboratory (DEMATEL), DEMATEL-based analytic network process (DANP), and VIKOR to evaluate the factors that influence the adoption of radio-frequency identification (RFID). Moreover, they applied their proposed hybrid method to the adoption of RFID in Taiwan’s healthcare industry. By introducing a new data normalization method, Zeng et al. [59] proposed an improved VIKOR approach with enhanced accuracy to make it suitable for medical data. In particular, the medical data adopted by Zeng et al. are normal reference ranges that are defined as the set of values that 95% of the normal population falls within. Liu et al. [28] presented a VIKOR-based fuzzy MCDA method to evaluate healthcare waste disposal methods. Chang [6] proposed a fuzzy VIKOR method and conducted a case study of the hospital service evaluation in Taiwan. Liu et al. [28] and Chang [6] published studies on the basis of fuzzy set theory and the VIKOR method and investigated data classed as ordinary fuzzy values. It is worth noting that Lu et al. [30] used crisp numbers as opposed to fuzzy numbers. The medical data were determined via the confidence intervals in the research of Zeng et al. [59]. This implies that Zeng et al. considered probabilities only and utilized crisp intervals to address numerical uncertainties in real-world applications. In brief, the data adopted by the aforementioned studies belong to crisp numbers/intervals or ordinary fuzzy numbers. Nevertheless, crisp or ordinary fuzzy numbers cannot sufficiently model the effects of high-order uncertainties associated with a complex environment, such as the context of the NHI system in Taiwan.

As is well known, uncertainty and vagueness are generally unavoidable due to the increasing complexity of down-to-earth decision-making problems in real-life situations [1, 48, 56, 57]. Although numerous fuzzy MCDA methods can handle uncertainty problems [32], most of them have some difficulty due to the lack of a powerful tool to tackle imprecise and ambiguous information and accommodate higher degrees of uncertainty in complex and varied circumstances. Furthermore, the multiple criteria evaluation problem of selecting appropriate pilot hospitals has become a challenging task for NHIA, especially when the highly complex landscape of the NHI system in Taiwan is taken into account. From this viewpoint, this paper attempts to propose a comprehensive and systematic VIKOR procedure that provides the ability to tackle more complex uncertain information contained in real-world situations for the selection of pilot hospitals in the PAC-CVD program.

To overcome the aforementioned difficulties, this paper would like to take the powerfulness of the theory of Pythagorean fuzziness into account to characterize uncertainty, imprecision, and vagueness in a more flexible way. Pythagorean fuzzy (PF) sets, which were initially introduced by Yager [52,53,54,55], are characterized by degrees of membership and non-membership, whose square sum is less than or equal to one but the sum is not required to be less than one [10, 14, 15, 42, 60]. It is worth noting that the main difference between PF sets and IF sets is their distinct constraint conditions. Figure 1a demonstrates the comparison of spaces of a PF value and an IF value. It is clear that the space of a PF value (i.e., the aqua blue and light green areas) is larger than the space of an IF value (i.e., the light green area). Thus, PF sets can not only depict uncertain information, which IF sets can capture, but also model more imprecise and ambiguous information, which the latter cannot describe [10, 26, 60].

Fig. 1

Geometrical interpretations of IF/IVIF and PF/IVPF values. a Comparison of spaces of IF and PF values. b Comparison of spaces of IVIF and IVPF values

The concept of IVPF sets is an extension of PF sets [26, 39, 60]. IVPF sets are three-dimensional and their membership, non-membership, and hesitation functions are defined by an interval value within [0, 1]. Meanwhile, the only requirement is that the square sum of respective upper bounds of the interval-valued membership and non-membership degrees is less than or equal to one. Figure 1b depicts the comparison of spaces of interval-valued intuitionistic fuzzy (IVIF) and IVPF values. Analogously, the space of an IVPF value is larger than the space of an IVIF value. Because of the relaxed constraint condition, IVPF sets are more precise in the modeling of vagueness and complex uncertainty in MCDA problems compared with IVIF sets. More importantly, the degrees of membership and non-membership within an IVPF value are represented by flexible interval values. Thus, compared with PF sets, IVPF sets can describe the degree of hesitation more precisely. Consider that the decision maker’s subjective judgment is often vague under many conditions. Moreover, the available information is often insufficient for the decision maker or analyst to determine exact degrees of membership and non-membership for certain evaluation items. From this perspective, IVPF sets with flexible interval membership/non-membership grades are appropriate for addressing such issues. Furthermore, incorporating an IVPF approach into the current VIKOR methods and techniques can enrich the existing VIKOR methodology. Therefore, this paper intends to develop a novel VIKOR method within the decision environment based on IVPF sets to solve the selection problem of pilot hospitals for hospital-based PAC-CVD.

1.3 Highlights of this paper

Aiming to address all crucial issues, i.e., to solve multiple criteria evaluation problems in the PAC-CVD program; to generate a set of compromise solutions for the selection of pilot hospitals; to treat high-order imprecise, vague, and uncertain information associated with a complex environment under Taiwan’s NHI system; and to enrich the VIKOR methodology via an important application in the medical and healthcare fields, this paper attempts to propose a novel VIKOR method in the IVPF context and apply it to the MCDA problem for hospital-based PAC-CVD. To be specific, the objective of this paper is to present a novel compromising decision-making technique by integrating the VIKOR methodology with the IVPF set theory to determine a set of compromise solutions as pilot hospitals for implementing the PAC-CVD program and further enhancing the effectiveness of hospital-based PAC in acute stroke management. As a whole, the main innovation and contributions of this work are highlighted as follows:

• (1) Structuring the selection problem for hospital-based PAC-CVD

Although numerous studies have explored PCA-related issues (e.g., criteria for selecting patients for PCA, PAC for different diseases, readmission and overstay before and after PAC administration and the relevant influential factors, core indicators of PAC effectiveness, and indicators of PAC quality), few studies have discussed the decision-making processes governing the selection of pilot hospitals during the establishment and implementation of PAC models. To address this limitation, this paper uses a multiple criteria model to structurally analyze the selection of pilot hospitals. Following the requirements of the PAC-CVD program, this paper also develops a novel compromising decision-making method to conduct the selection under uncertain conditions.

• (2) Extension of the IVPF set theory and VIKOR to the medical and healthcare fields

As a popular compromise approach, the VIKOR methodology continues to be applied productively across different application areas. However, comparatively few studies have focused on the application of the VIKOR methods and techniques in the fields of medicine and healthcare. Moreover, little attention has been given to the employment of VIKOR for MCDA in the IVPF context. From this perspective, this paper proposes a new VIKOR method based on IVPF set theory and enriches the VIKOR methodology to address an MCDA problem for hospital-based PAC-CVD in the medical and healthcare fields.

• (3) Simplification of the manipulation procedure in handling IVPF information

IVPF sets can depict more imprecise and ambiguous information and provide more degrees of flexibility because of their relaxed constraint conditions. Despite this advantage, one may confront heavy computations when IVPF sets are utilized for solving large-sized or complicated MCDA problems. To overcome this difficulty, this paper proposes an effective VIKOR-based decision-making procedure that provides the ability to represent and manipulate IVPF information contained in MCDA problems using simple and straightforward calculations.

• (4) Construction of remoteness indices based on the IVPF distance measure

In many practical MCDA problems, reference dependence and anchored judgment are common behavioral features for decision makers. To characterize the complexity and subjectivity of the decision-making mechanism and systematize the indefinite source of human judgments, this paper considers the positive- and negative-ideal IVPF evaluative ratings as points of reference and proposes a novel concept of remoteness indices based on the IVPF distance measure. Moreover, some important properties of the IVPF distance measure and the remoteness index are investigated for facilitating anchored judgments in a subjective decision-making process.

• (5) Development of remoteness-based multiple criteria ranking indices

The proposed remoteness indices are an effective tool to develop multiple criteria ranking indices for ranking candidate alternatives and determining compromise solutions. This paper introduces the concepts of remoteness-based group utility indices, individual regret indices, and compromise indices. Similar to current ranking indices in the VIKOR methodology, the proposed remoteness-based multiple criteria ranking indices can provide a mechanism to trade off a maximum group utility for the majority and a minimum individual regret for the opponent and can be employed as an aggregating function for a compromise ranking among alternatives. More importantly, these new indices are suitable in circumstances involving interval-valued Pythagorean fuzziness. They can fully reflect decision makers’ real preferences and describe more uncertainty, ambiguity, and inexactness in practical MCDA problems.

• (6) Establishment of an effective IVPF VIKOR ranking procedure

To provide a maximum group utility of the majority and a minimum of the individual regret of the opponent, the assessments of acceptable advantage and acceptable stability in decision making should be taken into consideration in the VIKOR-based ranking process. Furthermore, from a practical viewpoint, a final ranking procedure should be easily understandable by the decision makers if possible, which can improve the acceptability of the obtained results. To achieve the stated purposes, this paper constructs a systematized IVPF VIKOR ranking procedure using a composite mechanism that integrates the assessment of acceptable advantage with the assessment of acceptable stability. It is anticipated to enhance intuitive appeal and understandability of the obtained compromise solutions. Accordingly, the obtained pilot hospitals can be accepted and supported with confidence by NHIA, which will be beneficial for implementing the PAC-CVD program in practice.

The remainder of this paper is organized as follows. Section 2 briefly reviews the basic concepts and operations of IVPF sets. Section 3 first formulates an MCDA problem in the IVPF context. Additionally, it presents the IVPF distance measure between evaluative ratings and explores certain desirable properties. Next, this section constructs novel concepts of remoteness indices and remoteness-based multiple criteria ranking indices to develop an IVPF VIKOR method for MCDA involving IVPF information. Section 4 applies the proposed method to the selection of pilot hospitals in the PAC-CVD program under Taiwan’s NHI system to illustrate its feasibility and applicability. A comparative analysis in some practical MCDA problems is also conducted to examine the effectiveness and advantages of the proposed method in a variety of important application fields. Finally, Sect. 5 presents the conclusions.

2 Basic concepts and operations of IVPF sets

In this section, some basic concepts related to IVPF sets are briefly reviewed. Meanwhile, selected operations of IVPF values that are useful in this study are further presented.

Definition 1

([13, 26, 39, 60]) Let an ordinary finite non-empty set X be a universe of discourse. Let Int([0, 1]) denote the set of all closed subintervals of the unit interval [0, 1]. An IVPF set $\tilde{P}$ in X is defined as follows:

$$\tilde{P} = \{ {{\langle {x,\mu_{{\tilde{P}}} (x),\nu_{{\tilde{P}}} (x)} \rangle }|x \in X}\},$$

(1)

which is characterized by a membership function

$$\mu_{{\tilde{P}}} :X \to {\text{Int}}\left( {\left[ {0, \, 1} \right]} \right),\quad x \in X \to \mu_{{\tilde{P}}} (x) \, \left( { = \left[ {\mu_{{\tilde{P}}}^{ - } (x),\mu_{{\tilde{P}}}^{ + } (x)} \right]} \right) \subseteq [0,1]$$

(2)

and a non-membership function

$$\nu_{{\tilde{P}}} :X \to {\text{Int}}\left( {\left[ {0, \, 1} \right]} \right),\quad x \in X \to \nu_{{\tilde{P}}} (x){ (} = \left[ {\nu_{{\tilde{P}}}^{ - } (x),\nu_{{\tilde{P}}}^{ + } (x)} \right]) \subseteq [0,1]$$

(3)

with the following condition:

$$0 \le \left( {\mu_{{\tilde{P}}}^{ + } (x)} \right)^{ 2} + \left( {\nu_{{\tilde{P}}}^{ + } (x)} \right)^{ 2} \le 1\quad \forall x \in X,$$

(4)

where $\mu_{{\tilde{P}}}$ and $\nu_{{\tilde{P}}}$ represent the degree of membership and the degree of non-membership, respectively, of the element $x \in X$ to the set $\tilde{P}$. Additionally, the complement of $\tilde{P}$ is defined as

$$\tilde{P}^{c} = \left\{ {\left. {\left\langle {x,\nu_{{\tilde{P}}} (x),\mu_{{\tilde{P}}} (x)} \right\rangle } \right|x \in X} \right\}.$$

(5)

Definition 2

([13, 39, 60]) Let $\tilde{P}$ be an IVPF set in X. Let a function $\pi_{{\tilde{P}}} (x)$ denote the hesitation degree (or the degree of indeterminacy or the Pythagorean index) of the element $x \in X$ to the set $\tilde{P}$, shown as follows:

$$\pi_{{\tilde{P}}} (x) = \left[ {\pi_{{\tilde{P}}}^{ - } (x),\pi_{{\tilde{P}}}^{ + } (x)} \right]{ = }\left[ {\sqrt {1 - \left( {\mu_{{\tilde{P}}}^{ + } (x)} \right)^{2} - \left( {\nu_{{\tilde{P}}}^{ + } (x)} \right)^{2} } ,\sqrt {1 - \left( {\mu_{{\tilde{P}}}^{ - } (x)} \right)^{2} - \left( {\nu_{{\tilde{P}}}^{ - } (x)} \right)^{2} } } \right],$$

(6)

where the function $\pi_{{\tilde{P}}} (x)$ expresses a lack of knowledge regarding whether x belongs to $\tilde{P}$.

Definition 3

([13, 39, 60]) For an IVPF set $\tilde{P}$ in X, let the pair $(\mu_{{\tilde{P}}} (x),\nu_{{\tilde{P}}} (x) )$, denoted by $\tilde{p}$ for convenience, is called an IVPF value, where

$$\tilde{p} = \left( {\mu_{{\tilde{P}}} (x),\nu_{{\tilde{P}}} (x)} \right) = \left( {\left[ {\mu_{{\tilde{P}}}^{ - } (x),\mu_{{\tilde{P}}}^{ + } (x)} \right],\left[ {\nu_{{\tilde{P}}}^{ - } (x),\nu_{{\tilde{P}}}^{ + } (x)} \right]} \right).$$

(7)

Denote the set of all IVPF values in X by ${\tilde{\Phi}}$.

Definition 4

([13, 26, 39]) Let $\tilde{p}_{1}$ ($= (\mu_{{\tilde{P}_{1} }} (x),\nu_{{\tilde{P}_{1} }} (x))$), $\tilde{p}_{2}$ ($= (\mu_{{\tilde{P}_{2} }} (x),\nu_{{\tilde{P}_{2} }} (x))$), and $\tilde{p}$ ($= (\mu_{{\tilde{P}}} (x),\nu_{{\tilde{P}}} (x))$) be three IVPF values in ${\tilde{\Phi}}$. Let a real number $\alpha > 0$. Some basic operations are defined as follows:

$$\begin{aligned} \tilde{p}_{1} \vee \tilde{p}_{2} & = \left( {\left[ {{ \hbox{max} }\left\{ {\mu_{{\tilde{P}_{1} }}^{ - } (x),\mu_{{\tilde{P}_{2} }}^{ - } (x)} \right\},{ \hbox{max} }\left\{ {\mu_{{\tilde{P}_{1} }}^{ + } (x),\mu_{{\tilde{P}_{2} }}^{ + } (x)} \right\}} \right],} \right. \\ & \left. {\quad \left[ {{ \hbox{min} }\left\{ {\nu_{{\tilde{P}_{1} }}^{ - } (x),\nu_{{\tilde{P}_{2} }}^{ - } (x)} \right\},{ \hbox{min} }\left\{ {\nu_{{\tilde{P}_{1} }}^{ + } (x),\nu_{{\tilde{P}_{2} }}^{ + } (x)} \right\}} \right]} \right), \\ \end{aligned}$$

(8)

$$\begin{aligned} \tilde{p}_{1} \wedge \tilde{p}_{2} & = \left( {\left[ {\text{min}\left\{ {\mu_{{\tilde{P}_{1} }}^{ - } (x),\mu_{{\tilde{P}_{2} }}^{ - } (x)} \right\},\text{min}\left\{ {\mu_{{\tilde{P}_{1} }}^{ + } (x),\mu_{{\tilde{P}_{2} }}^{ + } (x)} \right\}} \right],} \right. \\ & \quad \left. {\left[ {\text{max}\left\{ {\nu_{{\tilde{P}_{1} }}^{ - } (x),\nu_{{\tilde{P}_{2} }}^{ - } (x)} \right\},\text{max}\left\{ {\nu_{{\tilde{P}_{1} }}^{ + } (x),\nu_{{\tilde{P}_{2} }}^{ + } (x)} \right\}} \right]} \right), \\ \end{aligned}$$

(9)

$$\begin{aligned} \tilde{p}_{1} \oplus \tilde{p}_{ 2} & = \left( {\left[ {\sqrt {\left( {\mu_{{\tilde{P}_{1} }}^{ - } (x)} \right)^{2} + \left( {\mu_{{\tilde{P}_{2} }}^{ - } (x)} \right)^{2} - \left( {\mu_{{\tilde{P}_{1} }}^{ - } (x)} \right)^{2} \cdot \left( {\mu_{{\tilde{P}_{2} }}^{ - } (x)} \right)^{2} } ,} \right.} \right. \\ & \left. {\sqrt {\left( {\mu_{{\tilde{P}_{1} }}^{ + } (x)} \right)^{2} + \left( {\mu_{{\tilde{P}_{2} }}^{ + } (x)} \right)^{2} - \left( {\mu_{{\tilde{P}_{1} }}^{ + } (x)} \right)^{2} \cdot \left( {\mu_{{\tilde{P}_{2} }}^{ + } (x)} \right)^{2} } } \right], \\ & \left. {\left[ {\nu_{{\tilde{P}_{1} }}^{ - } (x) \cdot \nu_{{\tilde{P}_{2} }}^{ - } (x),\nu_{{\tilde{P}_{1} }}^{ + } (x) \cdot \nu_{{\tilde{P}_{2} }}^{ + } (x)} \right]} \right), \\ \end{aligned}$$

(10)

$$\begin{aligned} \tilde{p}_{1} \otimes \tilde{p}_{ 2} & = \left( {\left[ {\mu_{{\tilde{P}_{1} }}^{ - } (x) \cdot \mu_{{\tilde{P}_{2} }}^{ - } (x),\mu_{{\tilde{P}_{1} }}^{ + } (x) \cdot \mu_{{\tilde{P}_{2} }}^{ + } (x)} \right],} \right. \\ & \left[ {\sqrt {\left( {\nu_{{\tilde{P}_{1} }}^{ - } (x)} \right)^{2} + \left( {\nu_{{\tilde{P}_{2} }}^{ - } (x)} \right)^{2} - \left( {\nu_{{\tilde{P}_{1} }}^{ - } (x)} \right)^{2} \cdot \left( {\nu_{{\tilde{P}_{2} }}^{ - } (x)} \right)^{2} } } \right., \\ & \left. {\left. {\sqrt {\left( {\nu_{{\tilde{P}_{1} }}^{ + } (x)} \right)^{2} + \left( {\nu_{{\tilde{P}_{2} }}^{ + } (x)} \right)^{2} - \left( {\nu_{{\tilde{P}_{1} }}^{ + } (x)} \right)^{2} \cdot \left( {\nu_{{\tilde{P}_{2} }}^{ + } (x)} \right)^{2} } } \right]} \right), \\ \end{aligned}$$

(11)

$$\tilde{p}^{c} = \left( {\left[ {\nu_{{\tilde{P}}}^{ - } (x),\nu_{{\tilde{P}}}^{ + } (x)} \right],\left[ {\mu_{{\tilde{P}}}^{ - } (x),\mu_{{\tilde{P}}}^{ + } (x)} \right]} \right),$$

(12)

$$\alpha \cdot \tilde{p} = \left( {\left[ {\sqrt {1 - \left( {1 - \left( {\mu_{{\tilde{P}}}^{ - } (x)} \right)^{2} } \right)^{\alpha } } ,\sqrt {1 - \left( {1 - \left( {\mu_{{\tilde{P}}}^{ + } (x)} \right)^{2} } \right)^{\alpha } } } \right],\left[ {\left( {\nu_{{\tilde{P}}}^{ - } (x)} \right)^{\alpha } ,\left( {\nu_{{\tilde{P}}}^{ + } (x)} \right)^{\alpha } } \right]} \right),$$

(13)

$$(\tilde{p})^{\alpha } = \left( {\left[ {\left( {\mu_{{\tilde{P}}}^{ - } (x)} \right)^{\alpha } ,\left( {\mu_{{\tilde{P}}}^{ + } (x)} \right)^{\alpha } } \right],\left[ {\sqrt {1 - \left( {1 - \left( {\nu_{{\tilde{P}}}^{ - } (x)} \right)^{2} } \right)^{\alpha } } ,\sqrt {1 - \left( {1 - \left( {\nu_{{\tilde{P}}}^{ + } (x)} \right)^{2} } \right)^{\alpha } } } \right]} \right).$$

(14)

Theorem 1

([13, 39, 60]) Let $\tilde{p}_{1}$, $\tilde{p}_{2}$, and $\tilde{p}$ be three IVPF values in ${\tilde{\Phi}}$. Let three real numbers $\alpha_{1} > 0$, $\alpha_{2} > 0$, and $\alpha > 0$. The following results are valid:

(T1.1):

$\tilde{p}_{1} \vee \tilde{p}_{2} = \tilde{p}_{2} \vee \tilde{p}_{1}$ and $\tilde{p}_{1} \wedge \tilde{p}_{2} = \tilde{p}_{2} \wedge \tilde{p}_{1}$;

(T1.2):

$\left( {\tilde{p}_{1} \vee \tilde{p}_{2} } \right) \wedge \tilde{p}_{2} = \tilde{p}_{2}$ and $\left( {\tilde{p}_{1} \wedge \tilde{p}_{2} } \right) \vee \tilde{p}_{2} = \tilde{p}_{2}$;

(T1.3):

$\tilde{p}_{1}^{c} \vee \tilde{p}_{2}^{c} = \left( {\tilde{p}_{1} \wedge \tilde{p}_{2} } \right)^{c}$ and $\tilde{p}_{1}^{c} \wedge \tilde{p}_{2}^{c} = \left( {\tilde{p}_{1} \vee \tilde{p}_{2} } \right)^{c}$;

(T1.4):

$\left( {\tilde{p}^{c} } \right)^{\alpha } = \left( {\alpha \cdot \tilde{p}} \right)^{c}$ and $\alpha \cdot \tilde{p}^{c} = \left( {\left( {\tilde{p}} \right)^{\alpha } } \right)^{c}$;

(T1.5):

$\alpha \cdot \left( {\tilde{p}_{1} \vee \tilde{p}_{2} } \right) = \alpha \cdot \tilde{p}_{1} \vee \alpha \cdot \tilde{p}_{2}$ and $\left( {\tilde{p}_{1} \vee \tilde{p}_{2} } \right)^{\alpha } = \left( {\tilde{p}_{1} } \right)^{\alpha } \vee \left( {\tilde{p}_{2} } \right)^{\alpha }$;

(T1.6):

$\tilde{p}_{1} \oplus \tilde{p}_{2} = \tilde{p}_{2} \oplus \tilde{p}_{1}$ and $\tilde{p}_{1} \otimes \tilde{p}_{2} = \tilde{p}_{2} \otimes \tilde{p}_{1}$;

(T1.7):

$\alpha \cdot \left( {\tilde{p}_{1} \oplus \tilde{p}_{2} } \right) = \alpha \cdot \tilde{p}_{1} \oplus \alpha \cdot \tilde{p}_{2}$ and $\alpha_{1} \cdot \tilde{p} \oplus \alpha_{2} \cdot \tilde{p} = \left( {\alpha_{1} + \alpha_{2} } \right) \cdot \tilde{p}$;

(T1.8):

$\left( {\tilde{p}_{1} \otimes \tilde{p}_{ 2} } \right)^{\alpha } = \left( {\tilde{p}_{1} } \right)^{\alpha } \otimes \left( {\tilde{p}_{2} } \right)^{\alpha }$ and $\left( {\tilde{p}} \right)^{{\alpha_{1} }} \otimes \left( {\tilde{p}} \right)^{{\alpha_{2} }} = \left( {\tilde{p}} \right)^{{(\alpha_{1} + \alpha_{2} )}}$;

(T1.9):

$\tilde{p}_{1}^{c} \oplus \tilde{p}_{2}^{c} = \left( {\tilde{p}_{1} \otimes \tilde{p}_{2} } \right)^{c}$ and $\tilde{p}_{1}^{c} \otimes \tilde{p}_{2}^{c} = \left( {\tilde{p}_{1} \oplus \tilde{p}_{2} } \right)^{c}$

3 Proposed methodology

This section first describes an MCDA problem within the IVPF environment. Because the development of the proposed IVPF VIKOR method starts with a helpful concept of IVPF distances, this section presents a distance measure between IVPF evaluative ratings and explores some related properties. Next, this section employs the distance measure to construct a novel concept of remoteness indices with respect to ideal IVPF evaluative ratings. Based on the proposed remoteness indices, this section establishes new multiple criteria ranking indices that consist of remoteness-based group utility indices, individual regret indices, and compromise indices, and develops an improved IVPF VIKOR ranking procedure for determining compromise priority orders among candidate alternatives over all criteria.

3.1 Problem statement

In a decision context based on IVPF sets, consider an MCDA problem that has limited numbers of candidate alternatives evaluated with multiple criteria. Mathematically, denote the alternative set by $Z = \{ z_{1} ,z_{2} , \ldots ,z_{m} \}$ that is a discrete set of m ($m \ge 2$) candidate alternatives. Denote the criterion set by $C = \{ c_{1} ,c_{2} , \ldots ,c_{n} \}$ that is a finite set of n ($n \ge 2$) criteria. In particular, the set C can be divided into two disjoint sets: C_I and C_II, where C_I denotes a collection of benefit criteria (i.e., the larger value means the better performance) and C_II denotes a collection of cost criteria (i.e., the larger value means the worse performance).

Let two intervals $\mu_{ij}$ (= $[\mu_{ij}^{ - } ,\mu_{ij}^{ + } ]$) and $\nu_{ij}$ (= $[\nu_{ij}^{ - } ,\nu_{ij}^{ + } ]$) in Int([0, 1]) express the degrees that alternative $z_{i} \in Z$ satisfies and dissatisfies, respectively, criterion $c_{j} \in C$. It is worth noting that $\mu_{ij}$ and $\nu_{ij}$ are more or less independent from each other. To be precise, the manifest requirement is that the square sum of upper bounds of the interval-valued degrees (i.e., $(\mu_{ij}^{ + } )^{2} + (\nu_{ij}^{ + } )^{2}$) is not greater than one. Let an IVPF value $\tilde{p}_{ij}$ (= $(\mu_{ij} ,\nu_{ij} )$) in ${\tilde{\Phi }}$ denote the evaluative rating of z_i with respect to c_j, expressed based on the following formula:

$$\tilde{p}_{ij} = \left( {\mu_{ij} ,\nu_{ij} } \right) = \left( {\left[ {\mu_{ij}^{ - } ,\mu_{ij}^{ + } } \right],\left[ {\nu_{ij}^{ - } ,\nu_{ij}^{ + } } \right]} \right),$$

(15)

where the expression is subject to the conditions of $0 \le \mu_{ij}^{ - } \le \mu_{ij}^{ + } \le 1$, $0 \le \nu_{ij}^{ - } \le \nu_{ij}^{ + } \le 1$, and $(\mu_{ij}^{ + } )^{2} + (\nu_{ij}^{ + } )^{2} \le 1$. Furthermore, the hesitation degree $\pi_{ij}$ that corresponds to each $\tilde{p}_{ij}$ is computed as follows:

$$\pi_{ij} = \left[ {\pi_{ij}^{ - } ,\pi_{ij}^{ + } } \right] = \left[ {\sqrt {1 - \left( {\mu_{ij}^{ + } } \right)^{2} - \left( {\nu_{ij}^{ + } } \right)^{2} } ,\sqrt {1 - \left( {\mu_{ij}^{ - } } \right)^{2} - \left( {\nu_{ij}^{ - } } \right)^{2} } } \right],$$

(16)

where $0 \le \pi_{ij}^{ - } \le \pi_{ij}^{ + } \le 1$.

The MCDA problem within the IVPF environment can be concisely represented in the following IVPF decision matrix:

$$\begin{aligned} \tilde{p} & = \left[ {\tilde{p}_{ij} } \right]_{m \times n} \\ & = \left[ {\begin{array}{*{20}c} {\left( {\left[ {\mu_{ 1 1}^{ - } ,\mu_{ 1 1}^{ + } } \right],\left[ {\nu_{ 1 1}^{ - } ,\nu_{ 1 1}^{ + } } \right]} \right)} & {\left( {\left[ {\mu_{ 1 2}^{ - } ,\mu_{ 1 2}^{ + } } \right],\left[ {\nu_{ 1 2}^{ - } ,\nu_{ 1 2}^{ + } } \right]} \right)} & \cdots & {\left( {\left[ {\mu_{ 1n}^{ - } ,\mu_{ 1n}^{ + } } \right],\left[ {\nu_{ 1n}^{ - } ,\nu_{ 1n}^{ + } } \right]} \right)} \\ {\left( {\left[ {\mu_{ 2 1}^{ - } ,\mu_{ 2 1}^{ + } } \right],\left[ {\nu_{ 2 1}^{ - } ,\nu_{ 2 1}^{ + } } \right]} \right)} & {\left( {\left[ {\mu_{ 2 2}^{ - } ,\mu_{ 2 2}^{ + } } \right],\left[ {\nu_{ 2 2}^{ - } ,\nu_{ 2 2}^{ + } } \right]} \right)} & \cdots & {\left( {\left[ {\mu_{ 2n}^{ - } ,\mu_{ 2n}^{ + } } \right],\left[ {\nu_{ 2n}^{ - } ,\nu_{ 2n}^{ + } } \right]} \right)} \\ \vdots & \vdots & \ddots & \vdots \\ {\left( {\left[ {\mu_{m 1}^{ - } ,\mu_{m 1}^{ + } } \right],\left[ {\nu_{m 1}^{ - } ,\nu_{m 1}^{ + } } \right]} \right)} & {\left( {\left[ {\mu_{m2}^{ - } ,\mu_{m2}^{ + } } \right],\left[ {\nu_{m2}^{ - } ,\nu_{m2}^{ + } } \right]} \right)} & \cdots & {\left( {\left[ {\mu_{mn}^{ - } ,\mu_{mn}^{ + } } \right],\left[ {\nu_{mn}^{ - } ,\nu_{mn}^{ + } } \right]} \right)} \\ \end{array} } \right]. \\ \end{aligned}$$

(17)

Additionally, let w_j denote the weight of criterion $c_{j} \in C$, which satisfies the following normalization conditions: $w_{j} \in [0,1]$ and $\sum\nolimits_{j = 1}^{n} {w_{j} } = 1$.

In the IVPF context, the MCDA problem addressed in this paper is how to assess the priority orders of candidate alternatives and to determine a set of compromise solutions from the alternative set Z according to the IVPF decision matrix $\tilde{p}$ and the weight vector $(w_{1} ,w_{2} , \ldots ,w_{n} )^{\text{T}}$ of the criteria.

3.2 Distance measure between IVPF evaluative ratings

Based on the Hamming distance (also referred to as the city block distance or Manhattan distance) model, Liang et al. [26], Peng and Yang [39], and Zhang [60] defined an IVPF distance measure for IVPF values. Motivated by their definition, this subsection presents the concept of a distance measure between IVPF evaluative ratings. Additionally, some essential properties are investigated to furnish a sound basis for subsequent developments of the proposed remoteness indices and remoteness-based multiple criteria ranking indices. Before describing the distance measure in detail, this subsection provides a fundamental concept of a lattice within the IVPF environment that is useful for developing relevant properties.

Let us define the lattice $(L_{\text{IVPF}} , \le_{{L_{\text{IVPF}} }} )$ of IVPF evaluative ratings on a universe X as follows:

$$L_{\text{IVPF}} = \left\{ {\left. {\left( {\mu_{ij} ,\nu_{ij} } \right)} \right|\mu_{ij} ,\nu_{ij} \subseteq [0,1],\left( {\mu_{ij}^{ + } } \right)^{2} + \left( {\nu_{ij}^{ + } } \right)^{2} \le 1} \right\}$$

(18)

with the partial order $\le_{{L_{\text{IVPF}} }}$, which is defined as, for any $\tilde{p}_{{i_{1} j}}$ ($= (\mu_{{i_{1} j}} ,\nu_{{i_{1} j}} ) = ([\mu_{{i_{1} j}}^{ - } ,\mu_{{i_{1} j}}^{ + } ],[\nu_{{i_{1} j}}^{ - } ,\nu_{{i_{1} j}}^{ + } ])$)$\in L_{\text{IVPF}}$ and $\tilde{p}_{{i_{2} j}}$ ($= (\mu_{{i_{2} j}} ,\nu_{{i_{2} j}} ) = ([\mu_{{i_{2} j}}^{ - } ,\mu_{{i_{2} j}}^{ + } ],[\nu_{{i_{2} j}}^{ - } ,\nu_{{i_{2} j}}^{ + } ])$)$\in L_{\text{IVPF}}$, $\tilde{p}_{{i_{1} j}} \le_{{L_{\text{IVPF}} }} \tilde{p}_{{i_{2} j}}$ if and only if $\mu_{{i_{1} j}}^{ - } \le \mu_{{i_{2} j}}^{ - }$, $\mu_{{i_{1} j}}^{ + } \le \mu_{{i_{2} j}}^{ + }$, $\nu_{{i_{1} j}}^{ - } \ge \nu_{{i_{2} j}}^{ - }$, and $\nu_{{i_{1} j}}^{ + } \ge \nu_{{i_{2} j}}^{ + }$. In particular, the top and bottom elements of the lattice $(L_{\text{IVPF}} , \le_{{L_{\text{IVPF}} }} )$ are ([1, 1], [0,0]) and ([0,0], [1, 1]), respectively.

Definition 5

Let $\tilde{p}_{{i_{1} j}}$ and $\tilde{p}_{{i_{2} j}}$ be two IVPF evaluative ratings with respect to each criterion $c_{j} \in C$ (= $C_{\text{I}} \cup C_{\text{II}}$, where $C_{\text{I}} \cap C_{\text{II}} = {\emptyset }$) in the IVPF decision matrix $\tilde{p}$. The distance measure between $\tilde{p}_{{i_{1} j}}$ and $\tilde{p}_{{i_{2} j}}$ is defined as follows:

$$\begin{aligned} d\left( {\tilde{p}_{{i_{1} j}} ,\tilde{p}_{{i_{2} j}} } \right) & = \frac{1}{4} \cdot \left( {\left| {\left( {\mu_{{i_{1} j}}^{ - } } \right)^{2} - \left( {\mu_{{i_{2} j}}^{ - } } \right)^{2} } \right| + \left| {\left( {\mu_{{i_{1} j}}^{ + } } \right)^{2} - \left( {\mu_{{i_{2} j}}^{ + } } \right)^{2} } \right| + \left| {\left( {\nu_{{i_{1} j}}^{ - } } \right)^{2} - \left( {\nu_{{i_{2} j}}^{ - } } \right)^{2} } \right|} \right. \\ & \quad + \,\left| {\left( {\nu_{{i_{1} j}}^{ + } } \right)^{2} - \left( {\nu_{{i_{2} j}}^{ + } } \right)^{2} } \right| + \left. {\left| {\left( {\pi_{{i_{1} j}}^{ - } } \right)^{2} - \left( {\pi_{{i_{2} j}}^{ - } } \right)^{2} } \right| + \left| {\left( {\pi_{{i_{1} j}}^{ + } } \right)^{2} - \left( {\pi_{{i_{2} j}}^{ + } } \right)^{2} } \right|} \right). \\ \end{aligned}$$

(19)

Theorem 2

Let $(L_{\text{IVPF}} , \le_{{L_{\text{IVPF}} }} )$ be a partially ordered set in X. Let $\tilde{p}_{{i_{1} j}}$, $\tilde{p}_{{i_{2} j}}$, and $\tilde{p}_{{i_{3} j}}$ be three IVPF evaluative ratings in $\tilde{p}$, where $\tilde{p}_{{i_{1} j}}$, $\tilde{p}_{{i_{2} j}}$, and $\tilde{p}_{{i_{3} j}}$ belong to $L_{\text{IVPF}}$ with the partial order $\le_{{L_{\text{IVPF}} }}$. The distance measure d is a metric and satisfies the following properties:

(T2.1):

$d(\tilde{p}_{{i_{1} j}} ,\tilde{p}_{{i_{1} j}} ) = 0$ (reflexivity);

(T2.2):

$d(\tilde{p}_{{i_{1} j}} ,\tilde{p}_{{i_{ 2} j}} ) = d(\tilde{p}_{{i_{2} j}} ,\tilde{p}_{{i_{1} j}} )$ (symmetry);

(T2.3):

$d(\tilde{p}_{{i_{1} j}} ,\tilde{p}_{{i_{ 2} j}} ) = 0$ if and only if $\tilde{p}_{{i_{1} j}} = \tilde{p}_{{i_{ 2} j}}$ (separability);

(T2.4):

$0 \le d(\tilde{p}_{{i_{1} j}} ,\tilde{p}_{{i_{ 2} j}} ) \le 1$ (boundedness);

(T2.5):

$d(\tilde{p}_{{i_{1} j}} ,\tilde{p}_{{i_{3} j}} ) \le d(\tilde{p}_{{i_{1} j}} ,\tilde{p}_{{i_{ 2} j}} ){ + }d(\tilde{p}_{{i_{2} j}} ,\tilde{p}_{{i_{3} j}} )$ (triangle inequality);

(T2.6):

$d(\tilde{p}_{{i_{1} j}} ,\tilde{p}_{{i_{ 2} j}} ) \le d(\tilde{p}_{{i_{1} j}} ,\tilde{p}_{{i_{3} j}} )$ and $d(\tilde{p}_{{i_{2} j}} ,\tilde{p}_{{i_{3} j}} ) \le d(\tilde{p}_{{i_{1} j}} ,\tilde{p}_{{i_{3} j}} )$ if $\tilde{p}_{{i_{1} j}} \le_{{L_{IVPF} }} \tilde{p}_{{i_{ 2} j}}$$\le_{{L_{IVPF} }} \tilde{p}_{{i_{3} j}}$

Proof

(T2.1) and (T2.2) are trivial.

(T2.3) For the necessity of separability, if $d(\tilde{p}_{{i_{1} j}} ,\tilde{p}_{{i_{ 2} j}} ) = 0$, then it implies that the conditions of $(\mu_{{i_{1} j}}^{ - } )^{2} = (\mu_{{i_{ 2} j}}^{ - } )^{2}$, $(\mu_{{i_{1} j}}^{ + } )^{2} = (\mu_{{i_{ 2} j}}^{ + } )^{2}$, $(\nu_{{i_{1} j}}^{ - } )^{2} = (\nu_{{i_{ 2} j}}^{ - } )^{2}$, $(\nu_{{i_{1} j}}^{ + } )^{2} = (\nu_{{i_{ 2} j}}^{ + } )^{2}$, $(\pi_{{i_{1} j}}^{ - } )^{2} = (\pi_{{i_{ 2} j}}^{ - } )^{2}$, and $(\pi_{{i_{1} j}}^{ + } )^{2} = (\pi_{{i_{ 2} j}}^{ + } )^{2}$ must be fulfilled. It follows that $\mu_{{i_{1} j}}^{ - } = \mu_{{i_{ 2} j}}^{ - }$, $\mu_{{i_{1} j}}^{ + } = \mu_{{i_{ 2} j}}^{ + }$, $\nu_{{i_{1} j}}^{ - } = \nu_{{i_{ 2} j}}^{ - }$, $\nu_{{i_{1} j}}^{ + } = \nu_{{i_{ 2} j}}^{ + }$, $\pi_{{i_{1} j}}^{ - } = \pi_{{i_{ 2} j}}^{ - }$, and $\pi_{{i_{1} j}}^{ + } = \pi_{{i_{ 2} j}}^{ + }$ because the lower and upper bounds of the interval-valued degrees $\mu_{{i_{1} j}}$, $\mu_{{i_{ 2} j}}$, $\nu_{{i_{1} j}}$, $\nu_{{i_{ 2} j}}$, $\pi_{{i_{1} j}}$, and $\pi_{{i_{ 2} j}}$ are not smaller than zero; thus, $\tilde{p}_{{i_{1} j}} = \tilde{p}_{{i_{ 2} j}}$. For the sufficiency of separability, if $\tilde{p}_{{i_{1} j}} = \tilde{p}_{{i_{ 2} j}}$, then it is obvious that $d(\tilde{p}_{{i_{1} j}} ,\tilde{p}_{{i_{ 2} j}} ) = 0$. Therefore, (T2.3) is valid

(T2.4) Applying (16), one can obtain $(\pi_{{i_{1} j}}^{ - } )^{2} = 1 - (\mu_{{i_{1} j}}^{ + } )^{2} - (\nu_{{i_{1} j}}^{ + } )^{2}$, $(\pi_{{i_{1} j}}^{ + } )^{2} = 1 - (\mu_{{i_{1} j}}^{ - } )^{2} - (\nu_{{i_{1} j}}^{ - } )^{2}$, $(\pi_{{i_{2} j}}^{ - } )^{2} = 1 - (\mu_{{i_{2} j}}^{ + } )^{2} - (\nu_{{i_{2} j}}^{ + } )^{2}$, and $(\pi_{{i_{2} j}}^{ + } )^{2} = 1 - (\mu_{{i_{2} j}}^{ - } )^{2} - (\nu_{{i_{2} j}}^{ - } )^{2}$. Because $0 \le \mu_{{i_{1} j}}^{ - } \le \mu_{{i_{1} j}}^{ + } \le 1$, $0 \le \mu_{{i_{2} j}}^{ - } \le \mu_{{i_{2} j}}^{ + } \le 1$, $0 \le \nu_{{i_{1} j}}^{ - } \le \nu_{{i_{1} j}}^{ + } \le 1$, $0 \le \nu_{{i_{2} j}}^{ - } \le \nu_{{i_{2} j}}^{ + } \le 1$, $(\mu_{{i_{1} j}}^{ + } )^{2} + (\nu_{{i_{1} j}}^{ + } )^{2} \le 1$, and $(\mu_{{i_{2} j}}^{ + } )^{2} + (\nu_{{i_{2} j}}^{ + } )^{2} \le 1$, it directly follows that:

$$\begin{aligned} d\left( {\tilde{p}_{{i_{1} j}} ,\tilde{p}_{{i_{2} j}} } \right) & = \frac{1}{4} \cdot \left( {\left| {\left( {\mu_{{i_{1} j}}^{ - } } \right)^{2} - \left( {\mu_{{i_{2} j}}^{ - } } \right)^{2} } \right| + \left| {\left( {\mu_{{i_{1} j}}^{ + } } \right)^{2} - \left( {\mu_{{i_{2} j}}^{ + } } \right)^{2} } \right| + \left| {\left( {\nu_{{i_{1} j}}^{ - } } \right)^{2} - \left( {\nu_{{i_{2} j}}^{ - } } \right)^{2} } \right| + \left| {\left( {\nu_{{i_{1} j}}^{ + } } \right)^{2} - \left( {\nu_{{i_{2} j}}^{ + } } \right)^{2} } \right|} \right. \\ & \quad + \left. {\left| {\left( {1 - \left( {\mu_{{i_{1} j}}^{ + } } \right)^{2} - \left( {\nu_{{i_{1} j}}^{ + } } \right)^{2} } \right) - \left( {1 - \left( {\mu_{{i_{2} j}}^{ + } } \right)^{2} - \left( {\nu_{{i_{2} j}}^{ + } } \right)^{2} } \right)} \right| + \left| {\left( {1 - \left( {\mu_{{i_{1} j}}^{ - } } \right)^{2} - \left( {\nu_{{i_{1} j}}^{ - } } \right)^{2} } \right) - \left( {1 - \left( {\mu_{{i_{2} j}}^{ - } } \right)^{2} - \left( {\nu_{{i_{2} j}}^{ - } } \right)^{2} } \right)} \right|} \right) \\ & = \frac{1}{4} \cdot \left( {\left| {\left( {\mu_{{i_{1} j}}^{ - } } \right)^{2} - \left( {\mu_{{i_{2} j}}^{ - } } \right)^{2} } \right| + \left| {\left( {\mu_{{i_{1} j}}^{ + } } \right)^{2} - \left( {\mu_{{i_{2} j}}^{ + } } \right)^{2} } \right| + \left| {\left( {\nu_{{i_{1} j}}^{ - } } \right)^{2} - \left( {\nu_{{i_{2} j}}^{ - } } \right)^{2} } \right| + \left| {\left( {\nu_{{i_{1} j}}^{ + } } \right)^{2} - \left( {\nu_{{i_{2} j}}^{ + } } \right)^{2} } \right|} \right. \\ & \quad + \left. {\left| {\left( {\left( {\mu_{{i_{2} j}}^{ + } } \right)^{2} - \left( {\mu_{{i_{1} j}}^{ + } } \right)^{2} } \right) + \left( {\left( {\nu_{{i_{2} j}}^{ + } } \right)^{2} - \left( {\nu_{{i_{1} j}}^{ + } } \right)^{2} } \right)} \right| + \left| {\left( {\left( {\mu_{{i_{2} j}}^{ - } } \right)^{2} - \left( {\mu_{{i_{1} j}}^{ - } } \right)^{2} } \right) + \left( {\left( {\nu_{{i_{2} j}}^{ - } } \right)^{2} - \left( {\nu_{{i_{1} j}}^{ - } } \right)^{2} } \right)} \right|} \right) \\ & \le \frac{1}{4} \cdot \left( {\left( {\mu_{{i_{1} j}}^{ - } } \right)^{2} + \left( {\nu_{{i_{1} j}}^{ - } } \right)^{2} + \left( {\mu_{{i_{1} j}}^{ + } } \right)^{2} + \left( {\nu_{{i_{1} j}}^{ + } } \right)^{2} + \left( {\mu_{{i_{2} j}}^{ - } } \right)^{2} + \left( {\nu_{{i_{2} j}}^{ - } } \right)^{2} + \left( {\mu_{{i_{2} j}}^{ + } } \right)^{2} + \left( {\nu_{{i_{2} j}}^{ + } } \right)^{2} } \right) \\ & \le \frac{1}{4} \cdot \left( {1 + 1 + 1 + 1} \right) = 1. \\ \end{aligned}$$

Additionally, it is easy to see that $d(\tilde{p}_{{i_{1} j}} ,\tilde{p}_{{i_{2} j}} ) \ge 0$ according to the definition in (19). Therefore, $0 \le d(\tilde{p}_{{i_{1} j}} ,\tilde{p}_{{i_{ 2} j}} ) \le 1$, i.e., (T2.4) is valid.

(T2.5) In view of the lower bounds of the interval-valued degrees, the following four assumptions will be examined: $(\mu_{{i_{1} j}}^{ - } )^{2} \le (\mu_{{i_{2} j}}^{ - } )^{2} \le (\mu_{{i_{3} j}}^{ - } )^{2}$, $(\mu_{{i_{3} j}}^{ - } )^{2} \le (\mu_{{i_{2} j}}^{ - } )^{2} \le (\mu_{{i_{1} j}}^{ - } )^{2}$, $(\mu_{{i_{2} j}}^{ - } )^{2} \le \hbox{min} \{ (\mu_{{i_{1} j}}^{ - } )^{2} ,(\mu_{{i_{3} j}}^{ - } )^{2} \}$, and $(\mu_{{i_{2} j}}^{ - } )^{2} \ge \hbox{max} \{ (\mu_{{i_{1} j}}^{ - } )^{2} ,(\mu_{{i_{3} j}}^{ - } )^{2} \}$. It is obvious that the inequality $|(\mu_{{i_{1} j}}^{ - } )^{2} - (\mu_{{i_{3} j}}^{ - } )^{2} |\le |(\mu_{{i_{1} j}}^{ - } )^{2} - (\mu_{{i_{2} j}}^{ - } )^{2} |+ |(\mu_{{i_{2} j}}^{ - } )^{2} - (\mu_{{i_{3} j}}^{ - } )^{2} |$ is fulfilled under the first two assumptions. It is known that $(\mu_{{i_{1} j}}^{ - } )^{2} - (\mu_{{i_{2} j}}^{ - } )^{2} \ge 0$ and $(\mu_{{i_{3} j}}^{ - } )^{2} - (\mu_{{i_{2} j}}^{ - } )^{2} \ge 0$ according to the third assumption. Thus,

$$\begin{aligned} & \left| {\left( {\mu_{{i_{1} j}}^{ - } } \right)^{2} - \left( {\mu_{{i_{ 2} j}}^{ - } } \right)^{2} } \right| + \left| {\left( {\mu_{{i_{2} j}}^{ - } } \right)^{2} - \left( {\mu_{{i_{3} j}}^{ - } } \right)^{2} } \right| - \left| {\left( {\mu_{{i_{1} j}}^{ - } } \right)^{2} - \left( {\mu_{{i_{3} j}}^{ - } } \right)^{2} } \right| \\ & = \left\{ {\begin{array}{*{20}c} {\left( {\mu_{{i_{1} j}}^{ - } } \right)^{2} - \left( {\mu_{{i_{ 2} j}}^{ - } } \right)^{2} + \left( {\mu_{{i_{3} j}}^{ - } } \right)^{2} - \left( {\mu_{{i_{ 2} j}}^{ - } } \right)^{2} - \left( {\mu_{{i_{1} j}}^{ - } } \right)^{2} + \left( {\mu_{{i_{3} j}}^{ - } } \right)^{2} } & {{\text{if }}\left( {\mu_{{i_{1} j}}^{ - } } \right)^{2} \ge \left( {\mu_{{i_{3} j}}^{ - } } \right)^{2} } \\ {\left( {\mu_{{i_{1} j}}^{ - } } \right)^{2} - \left( {\mu_{{i_{ 2} j}}^{ - } } \right)^{2} + \left( {\mu_{{i_{3} j}}^{ - } } \right)^{2} - \left( {\mu_{{i_{ 2} j}}^{ - } } \right)^{2} + \left( {\mu_{{i_{1} j}}^{ - } } \right)^{2} - \left( {\mu_{{i_{3} j}}^{ - } } \right)^{2} } & {{\text{if }}\left( {\mu_{{i_{1} j}}^{ - } } \right)^{2} \le \left( {\mu_{{i_{3} j}}^{ - } } \right)^{2} } \\ \end{array} } \right. \\ & = 2 \cdot \left( {\hbox{min} \left\{ {\left( {\mu_{{i_{1} j}}^{ - } } \right)^{2} ,\left( {\mu_{{i_{3} j}}^{ - } } \right)^{2} } \right\} - \left( {\mu_{{i_{2} j}}^{ - } } \right)^{2} } \right) \ge 0. \\ \end{aligned}$$

Analogously, the fourth assumption implies that

$$\begin{aligned} & \left| {\left( {\mu_{{i_{1} j}}^{ - } } \right)^{2} - \left( {\mu_{{i_{ 2} j}}^{ - } } \right)^{2} } \right| + \left| {\left( {\mu_{{i_{2} j}}^{ - } } \right)^{2} - \left( {\mu_{{i_{3} j}}^{ - } } \right)^{2} } \right| - \left| {\left( {\mu_{{i_{1} j}}^{ - } } \right)^{2} - \left( {\mu_{{i_{3} j}}^{ - } } \right)^{2} } \right| \\ & = \left\{ {\begin{array}{*{20}c} {\left( {\mu_{{i_{ 2} j}}^{ - } } \right)^{2} - \left( {\mu_{{i_{1} j}}^{ - } } \right)^{2} + \left( {\mu_{{i_{ 2} j}}^{ - } } \right)^{2} - \left( {\mu_{{i_{3} j}}^{ - } } \right)^{2} - \left( {\mu_{{i_{1} j}}^{ - } } \right)^{2} + \left( {\mu_{{i_{3} j}}^{ - } } \right)^{2} } & {{\text{if }}\left( {\mu_{{i_{1} j}}^{ - } } \right)^{2} \ge \left( {\mu_{{i_{3} j}}^{ - } } \right)^{2} } \\ {\left( {\mu_{{i_{ 2} j}}^{ - } } \right)^{2} - \left( {\mu_{{i_{1} j}}^{ - } } \right)^{2} + \left( {\mu_{{i_{ 2} j}}^{ - } } \right)^{2} - \left( {\mu_{{i_{3} j}}^{ - } } \right)^{2} + \left( {\mu_{{i_{1} j}}^{ - } } \right)^{2} - \left( {\mu_{{i_{3} j}}^{ - } } \right)^{2} } & {{\text{if }}\left( {\mu_{{i_{1} j}}^{ - } } \right)^{2} \le \left( {\mu_{{i_{3} j}}^{ - } } \right)^{2} } \\ \end{array} } \right. \\ & = 2 \cdot \left( {\left( {\mu_{{i_{ 2} j}}^{ - } } \right)^{2} - \hbox{max} \left\{ {\left( {\mu_{{i_{1} j}}^{ - } } \right)^{2} ,\left( {\mu_{{i_{3} j}}^{ - } } \right)^{2} } \right\}} \right) \ge 0. \\ \end{aligned}$$

Thus, $|(\mu_{{i_{1} j}}^{ - } )^{2} - (\mu_{{i_{3} j}}^{ - } )^{2} |\le |(\mu_{{i_{1} j}}^{ - } )^{2} - (\mu_{{i_{2} j}}^{ - } )^{2} |+ |(\mu_{{i_{2} j}}^{ - } )^{2} - (\mu_{{i_{3} j}}^{ - } )^{2} |$ is fulfilled under the last two assumptions. Analogously, it can be proven that $|(\nu_{{i_{1} j}}^{ - } )^{2} - (\nu_{{i_{3} j}}^{ - } )^{2} |\le |(\nu_{{i_{1} j}}^{ - } )^{2} - (\nu_{{i_{2} j}}^{ - } )^{2} |+$$|(\nu_{{i_{2} j}}^{ - } )^{2} - (\nu_{{i_{3} j}}^{ - } )^{2} |$ and $|(\pi_{{i_{1} j}}^{ - } )^{2} - (\pi_{{i_{3} j}}^{ - } )^{2} |\le |(\pi_{{i_{1} j}}^{ - } )^{2} - (\pi_{{i_{2} j}}^{ - } )^{2} |+ |(\pi_{{i_{2} j}}^{ - } )^{2} - (\pi_{{i_{3} j}}^{ - } )^{2} |$. Next, consider the upper bounds of the interval-valued degrees. In a similar manner, it is obtained that $|(\mu_{{i_{1} j}}^{ + } )^{2} - (\mu_{{i_{3} j}}^{ + } )^{2} |\le |(\mu_{{i_{1} j}}^{ + } )^{2} - (\mu_{{i_{2} j}}^{ + } )^{2} |+ |(\mu_{{i_{2} j}}^{ + } )^{2} - (\mu_{{i_{3} j}}^{ + } )^{2} |$, $|(\nu_{{i_{1} j}}^{ + } )^{2} - (\nu_{{i_{3} j}}^{ + } )^{2} |\le$$|(\nu_{{i_{1} j}}^{ + } )^{2} - (\nu_{{i_{2} j}}^{ + } )^{2} |+ |(\nu_{{i_{2} j}}^{ + } )^{2} - (\nu_{{i_{3} j}}^{ + } )^{2} |$ and $|(\pi_{{i_{1} j}}^{ + } )^{2} - (\pi_{{i_{3} j}}^{ + } )^{2} |\le |(\pi_{{i_{1} j}}^{ + } )^{2} - (\pi_{{i_{2} j}}^{ + } )^{2} |+ |(\pi_{{i_{2} j}}^{ + } )^{2} -$$(\pi_{{i_{3} j}}^{ + } )^{2} |$. Therefore, one can easily infer that the triangle inequality $d(\tilde{p}_{{i_{1} j}} ,\tilde{p}_{{i_{3} j}} ) \le$$d(\tilde{p}_{{i_{1} j}} ,\tilde{p}_{{i_{ 2} j}} ){ + }d(\tilde{p}_{{i_{2} j}} ,\tilde{p}_{{i_{3} j}} )$ is fulfilled, i.e., (T2.5) is valid. Accordingly, d is indeed a metric because it fulfills the requirements of reflexivity, symmetry, separability, and triangle inequality.

(T2.6) According to $\tilde{p}_{{i_{1} j}} \le_{{L_{\text{IVPF}} }} \tilde{p}_{{i_{ 2} j}} \le_{{L_{\text{IVPF}} }} \tilde{p}_{{i_{3} j}}$, one has $0 \le \mu_{{i_{1} j}}^{ - } \le \mu_{{i_{2} j}}^{ - } \le \mu_{{i_{3} j}}^{ - }$, $0 \le \mu_{{i_{1} j}}^{ + } \le \mu_{{i_{2} j}}^{ + } \le \mu_{{i_{3} j}}^{ + }$, $0 \le \nu_{{i_{3} j}}^{ - } \le \nu_{{i_{2} j}}^{ - } \le \nu_{{i_{1} j}}^{ - }$, and $0 \le \nu_{{i_{3} j}}^{ + } \le \nu_{{i_{2} j}}^{ + } \le \nu_{{i_{1} j}}^{ + }$. Correspondingly, the following results are valid: $0\le (\mu_{{i_{2} j}}^{ - } )^{2} - (\mu_{{i_{1} j}}^{ - } )^{2} \le (\mu_{{i_{3} j}}^{ - } )^{2} - (\mu_{{i_{1} j}}^{ - } )^{2}$, $0\le (\mu_{{i_{2} j}}^{ + } )^{2} - (\mu_{{i_{1} j}}^{ + } )^{2} \le (\mu_{{i_{3} j}}^{ + } )^{2} - (\mu_{{i_{1} j}}^{ + } )^{2}$, $0\le (\nu_{{i_{1} j}}^{ - } )^{2} - (\nu_{{i_{2} j}}^{ - } )^{2} \le (\nu_{{i_{1} j}}^{ - } )^{2} - (\nu_{{i_{3} j}}^{ - } )^{2}$, and $0\le (\nu_{{i_{1} j}}^{ + } )^{2} - (\nu_{{i_{2} j}}^{ + } )^{2} \le (\nu_{{i_{1} j}}^{ + } )^{2} - (\nu_{{i_{3} j}}^{ + } )^{2}$. With these results, one can then employ (16) and (19) to compute the distance measures $d(\tilde{p}_{{i_{1} j}} ,\tilde{p}_{{i_{2} j}} )$ and $d(\tilde{p}_{{i_{1} j}} ,\tilde{p}_{{i_{3} j}} )$ as follows:

$$\begin{aligned} d\left( {\tilde{p}_{{i_{1} j}} ,\tilde{p}_{{i_{2} j}} } \right) & = \frac{1}{4} \cdot \left( {\left( {\mu_{{i_{2} j}}^{ - } } \right)^{2} - \left( {\mu_{{i_{1} j}}^{ - } } \right)^{2} + \left( {\mu_{{i_{2} j}}^{ + } } \right)^{2} - \left( {\mu_{{i_{1} j}}^{ + } } \right)^{2} { + }\left( {\nu_{{i_{1} j}}^{ - } } \right)^{2} - \left( {\nu_{{i_{2} j}}^{ - } } \right)^{2} + \left( {\nu_{{i_{1} j}}^{ + } } \right)^{2} - \left( {\nu_{{i_{2} j}}^{ + } } \right)^{2} } \right. \\ & \left. {\quad + \left| {\left( {\mu_{{i_{2} j}}^{ - } } \right)^{2} + \left( {\nu_{{i_{2} j}}^{ - } } \right)^{2} - \left( {\mu_{{i_{1} j}}^{ - } } \right)^{2} - \left( {\nu_{{i_{1} j}}^{ - } } \right)^{2} } \right| + \left| {\left( {\mu_{{i_{2} j}}^{ + } } \right)^{2} + \left( {\nu_{{i_{2} j}}^{ + } } \right)^{2} - \left( {\mu_{{i_{1} j}}^{ + } } \right)^{2} - \left( {\nu_{{i_{1} j}}^{ + } } \right)^{2} } \right|} \right), \\ \end{aligned}$$

$$\begin{aligned} d\left( {\tilde{p}_{{i_{1} j}} ,\tilde{p}_{{i_{3} j}} } \right) & = \frac{1}{4} \cdot \left( {\left( {\mu_{{i_{3} j}}^{ - } } \right)^{2} - \left( {\mu_{{i_{1} j}}^{ - } } \right)^{2} + \left( {\mu_{{i_{3} j}}^{ + } } \right)^{2} - \left( {\mu_{{i_{1} j}}^{ + } } \right)^{2} { + }\left( {\nu_{{i_{1} j}}^{ - } } \right)^{2} - \left( {\nu_{{i_{3} j}}^{ - } } \right)^{2} + \left( {\nu_{{i_{1} j}}^{ + } } \right)^{2} - \left( {\nu_{{i_{3} j}}^{ + } } \right)^{2} } \right. \\ & \quad \left. { + \left| {\left( {\mu_{{i_{3} j}}^{ - } } \right)^{2} + \left( {\nu_{{i_{3} j}}^{ - } } \right)^{2} - \left( {\mu_{{i_{1} j}}^{ - } } \right)^{2} - \left( {\nu_{{i_{1} j}}^{ - } } \right)^{2} } \right| + \left| {\left( {\mu_{{i_{3} j}}^{ + } } \right)^{2} + \left( {\nu_{{i_{3} j}}^{ + } } \right)^{2} - \left( {\mu_{{i_{1} j}}^{ + } } \right)^{2} - \left( {\nu_{{i_{1} j}}^{ + } } \right)^{2} } \right|} \right). \\ \end{aligned}$$

It follows that

$$\begin{aligned} & d\left( {\tilde{p}_{{i_{1} j}} ,\tilde{p}_{{i_{3} j}} } \right) - d\left( {\tilde{p}_{{i_{1} j}} ,\tilde{p}_{{i_{ 2} j}} } \right) \\ & \quad = \frac{1}{4} \cdot \left( {\left( {\mu_{{i_{3} j}}^{ - } } \right)^{2} - \left( {\mu_{{i_{2} j}}^{ - } } \right)^{2} + \left( {\nu_{{i_{2} j}}^{ - } } \right)^{2} - \left( {\nu_{{i_{3} j}}^{ - } } \right)^{2} + \left| {\left( {\mu_{{i_{3} j}}^{ - } } \right)^{2} + \left( {\nu_{{i_{3} j}}^{ - } } \right)^{2} - \left( {\mu_{{i_{1} j}}^{ - } } \right)^{2} - \left( {\nu_{{i_{1} j}}^{ - } } \right)^{2} } \right|} \right. \\ & \left. {\quad \quad - \,\left| {\left( {\mu_{{i_{2} j}}^{ - } } \right)^{2} + \left( {\nu_{{i_{2} j}}^{ - } } \right)^{2} - \left( {\mu_{{i_{1} j}}^{ - } } \right)^{2} - \left( {\nu_{{i_{1} j}}^{ - } } \right)^{2} } \right|} \right) + \frac{1}{4} \cdot \left( {\left( {\mu_{{i_{3} j}}^{ + } } \right)^{2} - \left( {\mu_{{i_{2} j}}^{ + } } \right)^{2} + \left( {\nu_{{i_{2} j}}^{ + } } \right)^{2} - \left( {\nu_{{i_{3} j}}^{ + } } \right)^{2} } \right. \\ & \quad \left. {\quad + \,\left| {\left( {\mu_{{i_{3} j}}^{ + } } \right)^{2} + \left( {\nu_{{i_{3} j}}^{ + } } \right)^{2} - \left( {\mu_{{i_{1} j}}^{ + } } \right)^{2} - \left( {\nu_{{i_{1} j}}^{ + } } \right)^{2} } \right| - \left| {\left( {\mu_{{i_{2} j}}^{ + } } \right)^{2} + \left( {\nu_{{i_{2} j}}^{ + } } \right)^{2} - \left( {\mu_{{i_{1} j}}^{ + } } \right)^{2} - \left( {\nu_{{i_{1} j}}^{ + } } \right)^{2} } \right|} \right). \\ \end{aligned}$$

For notational convenience, let $\Upsilon = (1/4) \cdot ((\mu_{{i_{3} j}}^{ - } )^{2} - (\mu_{{i_{2} j}}^{ - } )^{2} + (\nu_{{i_{2} j}}^{ - } )^{2} - (\nu_{{i_{3} j}}^{ - } )^{2} + |(\mu_{{i_{3} j}}^{ - } )^{2} +$$(\nu_{{i_{3} j}}^{ - } )^{2} - (\mu_{{i_{1} j}}^{ - } )^{2} - (\nu_{{i_{1} j}}^{ - } )^{2} | - |(\mu_{{i_{2} j}}^{ - } )^{2} + (\nu_{{i_{2} j}}^{ - } )^{2} - (\mu_{{i_{1} j}}^{ - } )^{2} - (\nu_{{i_{1} j}}^{ - } )^{2} |)$. Let us examine the validity of $\Upsilon \ge 0$ under all of the possible situations defined by the relationships among $(\mu_{{i_{1} j}}^{ - } )^{2} { + (}\nu_{{i_{1} j}}^{ - } )^{2}$, $(\mu_{{i_{2} j}}^{ - } )^{2} + (\nu_{{i_{2} j}}^{ - } )^{2}$, and $(\mu_{{i_{3} j}}^{ - } )^{2} + (\nu_{{i_{3} j}}^{ - } )^{2}$. Consider the following four assumptions: (i) $(\mu_{{i_{1} j}}^{ - } )^{2} { + (}\nu_{{i_{1} j}}^{ - } )^{2} \le \hbox{min} \{ ((\mu_{{i_{2} j}}^{ - } )^{2} + (\nu_{{i_{2} j}}^{ - } )^{2} ,(\mu_{{i_{3} j}}^{ - } )^{2} + (\nu_{{i_{3} j}}^{ - } )^{2} \}$; (ii) $(\mu_{{i_{1} j}}^{ - } )^{2} { + (}\nu_{{i_{1} j}}^{ - } )^{2} \ge \hbox{max} \{ ((\mu_{{i_{2} j}}^{ - } )^{2} + (\nu_{{i_{2} j}}^{ - } )^{2} ,(\mu_{{i_{3} j}}^{ - } )^{2} + (\nu_{{i_{3} j}}^{ - } )^{2} \}$; (iii) $(\mu_{{i_{2} j}}^{ - } )^{2} + (\nu_{{i_{2} j}}^{ - } )^{2} \le (\mu_{{i_{1} j}}^{ - } )^{2} { + }$$(\nu_{{i_{1} j}}^{ - } )^{2} \le (\mu_{{i_{3} j}}^{ - } )^{2} + (\nu_{{i_{3} j}}^{ - } )^{2}$; and (iv) $(\mu_{{i_{3} j}}^{ - } )^{2} + (\nu_{{i_{3} j}}^{ - } )^{2} \le (\mu_{{i_{1} j}}^{ - } )^{2} { + (}\nu_{{i_{1} j}}^{ - } )^{2} \le (\mu_{{i_{2} j}}^{ - } )^{2} + (\nu_{{i_{2} j}}^{ - } )^{2}$. In regard to assumption (i), one can obtain

$$\begin{aligned}\Upsilon & = \frac{1}{4} \cdot \left[ {\left( {\mu_{{i_{3} j}}^{ - } } \right)^{2} - \left( {\mu_{{i_{2} j}}^{ - } } \right)^{2} + \left( {\nu_{{i_{2} j}}^{ - } } \right)^{2} - \left( {\nu_{{i_{3} j}}^{ - } } \right)^{2} + \left( {\mu_{{i_{3} j}}^{ - } } \right)^{2} + \left( {\nu_{{i_{3} j}}^{ - } } \right)^{2} - \left( {\mu_{{i_{1} j}}^{ - } } \right)^{2} - \left( {\nu_{{i_{1} j}}^{ - } } \right)^{2} } \right. \\ & \left. {\quad - \,\left( {\left( {\mu_{{i_{2} j}}^{ - } } \right)^{2} + \left( {\nu_{{i_{2} j}}^{ - } } \right)^{2} - \left( {\mu_{{i_{1} j}}^{ - } } \right)^{2} - \left( {\nu_{{i_{1} j}}^{ - } } \right)^{2} } \right)} \right] = \frac{1}{2} \cdot \left( {\left( {\mu_{{i_{3} j}}^{ - } } \right)^{2} - \left( {\mu_{{i_{2} j}}^{ - } } \right)^{2} } \right) \ge 0, \\ \end{aligned}$$

where $(\mu_{{i_{3} j}}^{ - } )^{2} \ge (\mu_{{i_{2} j}}^{ - } )^{2}$ can be known from $\mu_{{i_{3} j}}^{ - } \ge \mu_{{i_{2} j}}^{ - } \ge 0$ (based on $\tilde{p}_{{i_{ 2} j}} \le_{{L_{IVPF} }} \tilde{p}_{{i_{3} j}}$). Concerning assumption (ii), it is easy see that

$$\begin{aligned}\Upsilon & = \frac{1}{4} \cdot \left[ {\left( {\mu_{{i_{3} j}}^{ - } } \right)^{2} - \left( {\mu_{{i_{2} j}}^{ - } } \right)^{2} + \left( {\nu_{{i_{2} j}}^{ - } } \right)^{2} - \left( {\nu_{{i_{3} j}}^{ - } } \right)^{2} + \left( {\mu_{{i_{1} j}}^{ - } } \right)^{2} + \left( {\nu_{{i_{1} j}}^{ - } } \right)^{2} - \left( {\mu_{{i_{3} j}}^{ - } } \right)^{2} - \left( {\nu_{{i_{3} j}}^{ - } } \right)^{2} } \right. \\ & \quad \left. { - \,\left( {\left( {\mu_{{i_{1} j}}^{ - } } \right)^{2} + \left( {\nu_{{i_{1} j}}^{ - } } \right)^{2} - \left( {\mu_{{i_{2} j}}^{ - } } \right)^{2} - \left( {\nu_{{i_{2} j}}^{ - } } \right)^{2} } \right)} \right] = \frac{1}{2} \cdot \left( {\left( {\nu_{{i_{2} j}}^{ - } } \right)^{2} - \left( {\nu_{{i_{3} j}}^{ - } } \right)^{2} } \right) \ge 0, \\ \end{aligned}$$

where $(\nu_{{i_{2} j}}^{ - } )^{2} \ge (\nu_{{i_{3} j}}^{ - } )^{2}$ can be acquired from $\nu_{{i_{2} j}}^{ - } \ge \nu_{{i_{3} j}}^{ - } \ge 0$ (based on $\tilde{p}_{{i_{ 2} j}} \le_{{L_{IVPF} }} \tilde{p}_{{i_{3} j}}$). Regarding assumption (iii), the following result is valid:

$$\begin{aligned}\Upsilon & = \frac{1}{4} \cdot \left[ {\left( {\mu_{{i_{3} j}}^{ - } } \right)^{2} - \left( {\mu_{{i_{2} j}}^{ - } } \right)^{2} + \left( {\nu_{{i_{2} j}}^{ - } } \right)^{2} - \left( {\nu_{{i_{3} j}}^{ - } } \right)^{2} + \left( {\mu_{{i_{3} j}}^{ - } } \right)^{2} + \left( {\nu_{{i_{3} j}}^{ - } } \right)^{2} - \left( {\mu_{{i_{1} j}}^{ - } } \right)^{2} - \left( {\nu_{{i_{1} j}}^{ - } } \right)^{2} } \right. \\ & \left. {\quad - \left( {\left( {\mu_{{i_{1} j}}^{ - } } \right)^{2} + \left( {\nu_{{i_{1} j}}^{ - } } \right)^{2} - \left( {\mu_{{i_{2} j}}^{ - } } \right)^{2} - \left( {\nu_{{i_{2} j}}^{ - } } \right)^{2} } \right)} \right] = \frac{1}{2} \cdot \left( {\left( {\mu_{{i_{3} j}}^{ - } } \right)^{2} + \left( {\nu_{{i_{2} j}}^{ - } } \right)^{2} - \left( {\mu_{{i_{1} j}}^{ - } } \right)^{2} - \left( {\nu_{{i_{1} j}}^{ - } } \right)^{2} } \right) \\ & \ge \frac{1}{2} \cdot \left[ {\left( {\left( {\mu_{{i_{1} j}}^{ - } } \right)^{2} + \left( {\nu_{{i_{1} j}}^{ - } } \right)^{2} - \left( {\nu_{{i_{3} j}}^{ - } } \right)^{2} } \right) + \left( {\nu_{{i_{2} j}}^{ - } } \right)^{2} - \left( {\mu_{{i_{1} j}}^{ - } } \right)^{2} - \left( {\nu_{{i_{1} j}}^{ - } } \right)^{2} } \right] = \frac{1}{2} \cdot \left( {\left( {\nu_{{i_{2} j}}^{ - } } \right)^{2} - \left( {\nu_{{i_{3} j}}^{ - } } \right)^{2} } \right) \ge 0, \\ \end{aligned}$$

where $(\mu_{{i_{3} j}}^{ - } )^{2} \ge (\mu_{{i_{1} j}}^{ - } )^{2} { + (}\nu_{{i_{1} j}}^{ - } )^{2} - (\nu_{{i_{3} j}}^{ - } )^{2}$ and $(\nu_{{i_{2} j}}^{ - } )^{2} \ge (\nu_{{i_{3} j}}^{ - } )^{2}$ can be acquired according to assumption (iii) and $\nu_{{i_{2} j}}^{ - } \ge \nu_{{i_{3} j}}^{ - } \ge 0$ (based on $\tilde{p}_{{i_{ 2} j}} \le_{{L_{\text{IVPF}} }} \tilde{p}_{{i_{3} j}}$), respectively. With respect to assumption (iv), the following result is obtained:

$$\begin{aligned}\Upsilon & = \frac{1}{4} \cdot \left[ {\left( {\mu_{{i_{3} j}}^{ - } } \right)^{2} - \left( {\mu_{{i_{2} j}}^{ - } } \right)^{2} + \left( {\nu_{{i_{2} j}}^{ - } } \right)^{2} - \left( {\nu_{{i_{3} j}}^{ - } } \right)^{2} + \left( {\mu_{{i_{1} j}}^{ - } } \right)^{2} + \left( {\nu_{{i_{1} j}}^{ - } } \right)^{2} - \left( {\mu_{{i_{3} j}}^{ - } } \right)^{2} - \left( {\nu_{{i_{3} j}}^{ - } } \right)^{2} } \right. \\ & \quad \left. { - \left( {\left( {\mu_{{i_{2} j}}^{ - } } \right)^{2} + \left( {\nu_{{i_{2} j}}^{ - } } \right)^{2} - \left( {\mu_{{i_{1} j}}^{ - } } \right)^{2} - \left( {\nu_{{i_{1} j}}^{ - } } \right)^{2} } \right)} \right] = \frac{1}{2} \cdot \left( {\left( {\mu_{{i_{1} j}}^{ - } } \right)^{2} + \left( {\nu_{{i_{1} j}}^{ - } } \right)^{2} - \left( {\mu_{{i_{2} j}}^{ - } } \right)^{2} - \left( {\nu_{{i_{3} j}}^{ - } } \right)^{2} } \right) \\ & \ge \frac{1}{2} \cdot \left[ {\left( {\mu_{{i_{1} j}}^{ - } } \right)^{2} + \left( {\nu_{{i_{1} j}}^{ - } } \right)^{2} - \left( {\mu_{{i_{2} j}}^{ - } } \right)^{2} - \left( {\left( {\mu_{{i_{1} j}}^{ - } } \right)^{2} + \left( {\nu_{{i_{1} j}}^{ - } } \right)^{2} - \left( {\mu_{{i_{3} j}}^{ - } } \right)^{2} } \right)} \right] = \frac{1}{2} \cdot \left( {\left( {\mu_{{i_{3} j}}^{ - } } \right)^{2} - \left( {\mu_{{i_{2} j}}^{ - } } \right)^{2} } \right) \ge 0, \\ \end{aligned}$$

where $(\nu_{{i_{3} j}}^{ - } )^{2} \le (\mu_{{i_{1} j}}^{ - } )^{2} { + (}\nu_{{i_{1} j}}^{ - } )^{2} - (\mu_{{i_{3} j}}^{ - } )^{2}$ and $(\mu_{{i_{3} j}}^{ - } )^{2} \ge (\mu_{{i_{2} j}}^{ - } )^{2}$ can be derived according to assumption (iv) and $\mu_{{i_{3} j}}^{ - } \ge \mu_{{i_{2} j}}^{ - } \ge 0$ (based on $\tilde{p}_{{i_{ 2} j}} \le_{{L_{\text{IVPF}} }} \tilde{p}_{{i_{3} j}}$), respectively. Based on the above discussions, one can conclude that

$$\begin{aligned} & \frac{1}{4} \cdot \left( {\left( {\mu_{{i_{3} j}}^{ - } } \right)^{2} - \left( {\mu_{{i_{2} j}}^{ - } } \right)^{2} + \left( {\nu_{{i_{2} j}}^{ - } } \right)^{2} - \left( {\nu_{{i_{3} j}}^{ - } } \right)^{2} + \left| {\left( {\mu_{{i_{3} j}}^{ - } } \right)^{2} + \left( {\nu_{{i_{3} j}}^{ - } } \right)^{2} - \left( {\mu_{{i_{1} j}}^{ - } } \right)^{2} - \left( {\nu_{{i_{1} j}}^{ - } } \right)^{2} } \right|} \right. \\ & \left. {\quad - \,\left| {\left( {\mu_{{i_{2} j}}^{ - } } \right)^{2} + \left( {\nu_{{i_{2} j}}^{ - } } \right)^{2} - \left( {\mu_{{i_{1} j}}^{ - } } \right)^{2} - \left( {\nu_{{i_{1} j}}^{ - } } \right)^{2} } \right|} \right) \ge 0. \\ \end{aligned}$$

In a similar manner, one can prove that if $\tilde{p}_{{i_{1} j}} \le_{{L_{\text{IVPF}} }} \tilde{p}_{{i_{2} j}} \le_{{L_{\text{IVPF}} }} \tilde{p}_{{i_{3} j}}$,

$$\begin{aligned} & \frac{1}{4} \cdot \left( {\left( {\mu_{{i_{3} j}}^{ + } } \right)^{2} - \left( {\mu_{{i_{2} j}}^{ + } } \right)^{2} + \left( {\nu_{{i_{2} j}}^{ + } } \right)^{2} - \left( {\nu_{{i_{3} j}}^{ + } } \right)^{2} + \left| {\left( {\mu_{{i_{3} j}}^{ + } } \right)^{2} + \left( {\nu_{{i_{3} j}}^{ + } } \right)^{2} - \left( {\mu_{{i_{1} j}}^{ + } } \right)^{2} - \left( {\nu_{{i_{1} j}}^{ + } } \right)^{2} } \right|} \right. \\ & \left. {\quad - \,\left| {\left( {\mu_{{i_{2} j}}^{ + } } \right)^{2} + \left( {\nu_{{i_{2} j}}^{ + } } \right)^{2} - \left( {\mu_{{i_{1} j}}^{ + } } \right)^{2} - \left( {\nu_{{i_{1} j}}^{ + } } \right)^{2} } \right|} \right) \ge 0. \\ \end{aligned}$$

It follows that $d(\tilde{p}_{{i_{1} j}} ,\tilde{p}_{{i_{3} j}} ) - d(\tilde{p}_{{i_{1} j}} ,\tilde{p}_{{i_{ 2} j}} ) \ge 0$. That is, $d(\tilde{p}_{{i_{1} j}} ,\tilde{p}_{{i_{ 2} j}} ) \le d(\tilde{p}_{{i_{1} j}} ,\tilde{p}_{{i_{3} j}} )$ holds. Analogously, it can be shown that $d(\tilde{p}_{{i_{2} j}} ,\tilde{p}_{{i_{3} j}} ) \le d(\tilde{p}_{{i_{1} j}} ,\tilde{p}_{{i_{3} j}} )$ if $\tilde{p}_{{i_{1} j}} \le_{{L_{\text{IVPF}} }} \tilde{p}_{{i_{ 2} j}} \le_{{L_{\text{IVPF}} }}$$\tilde{p}_{{i_{3} j}}$. Therefore, (T2.6) is valid. This completes the proof.□

3.3 The proposed IVPF VIKOR methodology

This subsection attempts to develop a novel IVPF VIKOR method for addressing MCDA problems in the circumstances involving interval-valued Pythagorean fuzziness. First, this subsection constructs the concept of a remoteness index for serving as a basis of the proposed IVPF VIKOR method. As demonstrated in Theorem 2, the distance measure d possesses desirable and valuable properties that are beneficial for manipulating IVPF information and comparing IVPF values. Accordingly, this paper employs the distance measure d to construct the remoteness index for each IVPF evaluative rating.

It is worthwhile to mention that reference dependence is a common behavioral characteristic for decision makers when they have been confronted with practical MCDA problems [22]. Generally, the VIKOR methodology employs the positive- and negative-ideal solutions to serve as points of reference. Because decision makers usually tend to anchor their subjective judgments with certain points of reference when making an assessment [7,8,9, 47, 50], the positive- and negative-ideal solutions would affect the contrast between currently achievable performances among alternatives. In VIKOR, the specification of the positive- and negative-ideal solutions is directly generated from the evaluative ratings of all candidate alternatives with respect to various criteria [36, 37]. In a similar manner, this paper considers the evaluating ratings in the positive- and negative-ideal solutions as the points of reference to facilitate anchored judgments in a subjective decision-making process.

To state reference dependence and anchored judgments more concretely, this paper locates some appropriate points of reference, named the positive- and negative-ideal IVPF evaluative ratings, that are composed of all of the best and worst criterion values attainable, respectively. In particular, these ideal IVPF evaluative ratings are dependent on the IVPF decision matrix $\tilde{p}$. More precisely, this paper designates the positive-ideal IVPF evaluative rating as the largest and smallest IVPF values with all of the currently considered evaluative ratings with respect to benefit criteria and cost criteria, respectively. In contrast, the negative-ideal IVPF evaluative rating is designated the smallest and largest IVPF values with all of the currently considered evaluative ratings with respect to benefit criteria and cost criteria, respectively. These ideal IVPF evaluative ratings can be deemed points of reference that provide anchors for the decision maker’s subjective judgment of preferences. In this way, the positive- and negative-ideal IVPF evaluative ratings can serve as approachable and avoidable targets, respectively, in the decision-making process.

Definition 6

For an IVPF decision matrix $\tilde{p} = [\tilde{p}_{ij} ]_{m \times n}$, the positive-ideal IVPF evaluative rating $\tilde{p}_{*j}$ and the negative-ideal IVPF evaluative rating $\tilde{p}_{\# j}$ with respect to each criterion $c_{j} \in C$ (= $C_{\text{I}} \cup C_{\text{II}}$, where $C_{\text{I}} \cap C_{\text{II}} = {\emptyset }$) are defined as follows:

$$\begin{aligned} \tilde{p}_{*j} & = \left( {\mu_{*j} ,\nu_{*j} } \right) = \left( {\left[ {\mu_{*j}^{ - } ,\mu_{*j}^{ + } } \right],\left[ {\nu_{*j}^{ - } ,\nu_{*j}^{ + } } \right]} \right) \\ & = \left\{ {\begin{array}{*{20}l} {\left( {\left[ {\mathop {\hbox{max} }\limits_{i = 1}^{m} \mu_{ij}^{ - } ,\mathop {\hbox{max} }\limits_{i = 1}^{m} \mu_{ij}^{ + } } \right],\left[ {\mathop {\hbox{min} }\limits_{i = 1}^{m} \nu_{ij}^{ - } ,\mathop {\hbox{min} }\limits_{i = 1}^{m} \nu_{ij}^{ + } } \right]} \right)} \hfill & {{\text{if}}\quad c_{j} \in C_{\text{I}} ,} \hfill \\ {\left( {\left[ {\mathop {\hbox{min} }\limits_{i = 1}^{m} \mu_{ij}^{ - } ,\mathop {\hbox{min} }\limits_{i = 1}^{m} \mu_{ij}^{ + } } \right],\left[ {\mathop {\hbox{max} }\limits_{i = 1}^{m} \nu_{ij}^{ - } ,\mathop {\hbox{max} }\limits_{i = 1}^{m} \nu_{ij}^{ + } } \right]} \right)} \hfill & {{\text{if}}\quad c_{j} \in C_{\text{II}} ,} \hfill \\ \end{array} } \right. \\ \end{aligned}$$

(20)

$$\begin{aligned} \tilde{p}_{\# j} = \left( {\mu_{\# j} ,\nu_{\# j} } \right) = \left( {\left[ {\mu_{\# j}^{ - } ,\mu_{\# j}^{ + } } \right],\left[ {\nu_{\# j}^{ - } ,\nu_{\# j}^{ + } } \right]} \right) \hfill \\ \, = \left\{ {\begin{array}{*{20}l} {\left( {\left[ {\mathop {\hbox{min} }\limits_{i = 1}^{m} \mu_{ij}^{ - } ,\mathop {\hbox{min} }\limits_{i = 1}^{m} \mu_{ij}^{ + } } \right],\left[ {\mathop {\hbox{max} }\limits_{i = 1}^{m} \nu_{ij}^{ - } ,\mathop {\hbox{max} }\limits_{i = 1}^{m} \nu_{ij}^{ + } } \right]} \right)} \hfill & {{\text{if}}\quad c_{j} \in C_{\text{I}} ,} \hfill \\ {\left( {\left[ {\mathop {\hbox{max} }\limits_{i = 1}^{m} \mu_{ij}^{ - } ,\mathop {\hbox{max} }\limits_{i = 1}^{m} \mu_{ij}^{ + } } \right],\left[ {\mathop {\hbox{min} }\limits_{i = 1}^{m} \nu_{ij}^{ - } ,\mathop {\hbox{min} }\limits_{i = 1}^{m} \nu_{ij}^{ + } } \right]} \right)} \hfill & {{\text{if}}\quad c_{j} \in C_{\text{II}} .} \hfill \\ \end{array} } \right. \hfill \\ \end{aligned}$$

(21)

The hesitation degrees $\pi_{*j}$ and $\pi_{\# j}$ corresponding to $\tilde{p}_{ *j}$ and $\tilde{p}_{{{{\#}}j}}$, respectively, are defined as follows:

$$\pi_{*j} = \left[ {\pi_{*j}^{ - } ,\pi_{*j}^{ + } } \right] = \left[ {\sqrt {1 - \left( {\mu_{*j}^{ + } } \right)^{2} - \left( {\nu_{*j}^{ + } } \right)^{2} } ,\sqrt {1 - \left( {\mu_{*j}^{ - } } \right)^{2} - \left( {\nu_{*j}^{ - } } \right)^{2} } } \right],$$

(22)

$$\pi_{\# j} = \left[ {\pi_{\# j}^{ - } ,\pi_{\# j}^{ + } } \right] = \left[ {\sqrt {1 - \left( {\mu_{\# j}^{ + } } \right)^{2} - \left( {\nu_{\# j}^{ + } } \right)^{2} } ,\sqrt {1 - \left( {\mu_{\# j}^{ - } } \right)^{2} - \left( {\nu_{\# j}^{ - } } \right)^{2} } } \right].$$

(23)

Theorem 3

With respect to an IVPF decision matrix $\tilde{p}$, the IVPF evaluative rating $\tilde{p}_{ij}$, the positive-ideal IVPF evaluative rating $\tilde{p}_{ *j}$, and the negative-ideal IVPF evaluative rating $\tilde{p}_{{{{\#}}j}}$ satisfy the following properties:

(T3.1):

$\tilde{p}_{\# j} \le_{{L_{\text{IVPF}} }} \tilde{p}_{ij} \le_{{L_{\text{IVPF}} }} \tilde{p}_{*j}$ for all $c_{j} \in C_{\text{I}}$;

(T3.2):

$\tilde{p}_{*j} \le_{{L_{\text{IVPF}} }} \tilde{p}_{ij} \le_{{L_{\text{IVPF}} }} \tilde{p}_{\# j}$ for all $c_{j} \in C_{\text{II}}$

Proof

(T3.1) According to (20) and (21), it can be easily observed that $\mu_{\# j}^{ - } \le \mu_{ij}^{ - } \le \mu_{*j}^{ - }$, $\mu_{\# j}^{ + } \le \mu_{ij}^{ + } \le \mu_{*j}^{ + }$, $\nu_{\# j}^{ - } \ge \nu_{ij}^{ - } \ge \nu_{*j}^{ - }$ and $\nu_{\# j}^{ + } \ge \nu_{ij}^{ + } \ge \nu_{*j}^{ + }$ for each $c_{j} \in C_{\text{I}}$. Because the necessary and sufficient conditions of $\tilde{p}_{\# j} \le_{{L_{\text{IVPF}} }} \tilde{p}_{ij} \le_{{L_{\text{IVPF}} }} \tilde{p}_{*j}$ hold for all $c_{j} \in C_{\text{I}}$, (T3.1) is valid

(T3.2) In a similar manner, one can also prove that $\tilde{p}_{*j} \le_{{L_{\text{IVPF}} }} \tilde{p}_{ij} \le_{{L_{\text{IVPF}} }} \tilde{p}_{\# j}$ holds for all $c_{j} \in C_{\text{II}}$, because it can be obtained that $\mu_{\# j}^{ - } \ge \mu_{ij}^{ - } \ge \mu_{*j}^{ - }$, $\mu_{\# j}^{ + } \ge \mu_{ij}^{ + } \ge \mu_{*j}^{ + }$, $\nu_{\# j}^{ - } \le \nu_{ij}^{ - } \le \nu_{*j}^{ - }$ and $\nu_{\# j}^{ + } \le \nu_{ij}^{ + } \le \nu_{*j}^{ + }$ according to (20) and (21). Therefore, (T3.2) is valid, which completes the proof.□

Next, the distance measure d can be utilized to establish the remoteness index of each IVPF evaluative rating $\tilde{p}_{ij}$ with respect to the corresponding ideal IVPF evaluative ratings $\tilde{p}_{ *j}$ and $\tilde{p}_{{{{\# }}j}}$. Generally, the larger and the smaller $\tilde{p}_{ij}$ is, the greater the preference is for criteria $c_{j} \in C_{\text{I}}$ and $c_{j} \in C_{\text{II}}$, respectively. Accordingly, $\tilde{p}_{ *j}$ can be viewed as the most favorable value for c_j. Moreover, the specification of the proposed remoteness index can be reasonably designated via d.

The smaller the $d(\tilde{p}_{ij} ,\tilde{p}_{*j} )$ value is, the closer to $\tilde{p}_{ *j}$ it is, and the greater the preference is for $\tilde{p}_{ij}$. Nevertheless, it is worth noting that the $d(\tilde{p}_{ij} ,\tilde{p}_{*j} )$ values for all $c_{j} \in C$ do not have a consistent upper bound in most situations. The main reason is that the positive-ideal IVPF evaluative ratings are the most favorable IVPF values with all of the currently considered evaluative ratings with respect to each criterion; thus, they are frequently different among criteria. This implies that the maximal possible value of $d(\tilde{p}_{ij} ,\tilde{p}_{*j} )$ may be inconsistent among n criteria. A lack of consistent upper bounds would result in confusing judgments because the decision maker may not find any true meaning in comparing the $d(\tilde{p}_{ij} ,\tilde{p}_{*j} )$ values over all the criteria. Therefore, this paper attempts to employ a standardized value instead of the original distance to define the remoteness index. Note that the $d(\tilde{p}_{\# j} ,\tilde{p}_{*j} )$ value can be regarded as the upper bounds of the $d(\tilde{p}_{ij} ,\tilde{p}_{*j} )$ values for all $c_{j} \in C$. Thus, the standardized value is defined as the ratio of $d(\tilde{p}_{ij} ,\tilde{p}_{*j} )$ to $d(\tilde{p}_{\# j} ,\tilde{p}_{*j} )$. In this way, the concept of remoteness indices and their desirable properties are developed as follows.

Definition 7

Let $\tilde{p}_{ij}$, $\tilde{p}_{ *j}$, and $\tilde{p}_{{{{\# }}j}}$ denote an IVPF evaluative rating, the positive-ideal IVPF evaluative rating, and the negative-ideal IVPF evaluative rating, respectively, in the IVPF decision matrix $\tilde{p} = [\tilde{p}_{ij} ]_{m \times n}$. Moreover, without loss of generality, assume that $\tilde{p}_{\# j} \ne \tilde{p}_{ *j}$ for all $c_{j} \in C$. The remoteness index $I(\tilde{p}_{ij} )$ of $\tilde{p}_{ij}$ is defined as follows:

$$I\left( {\tilde{p}_{ij} } \right) = \frac{{d\left( {\tilde{p}_{ij} ,\tilde{p}_{*j} } \right)}}{{d\left( {\tilde{p}_{\# j} ,\tilde{p}_{*j} } \right)}} .$$

(24)

Theorem 4

Let $\tilde{p}_{ij}$, $\tilde{p}_{{i_{1} j}}$, and $\tilde{p}_{{i_{2} j}}$ be three evaluative ratings in the IVPF decision matrix $\tilde{p}$. The remoteness index $I(\tilde{p}_{ij} )$ satisfies the following properties:

(T4.1):

$I(\tilde{p}_{ij} ) = 0$ if and only if $\tilde{p}_{ij} = \tilde{p}_{ *j}$;

(T4.2):

$I(\tilde{p}_{ij} ) = 1$ if and only if $\tilde{p}_{ij} = \tilde{p}_{\# j}$;

(T4.3):

$0 \le I(\tilde{p}_{ij} ) \le 1$;

(T4.4):

For each $c_{j} \in C_{\text{I}}$, $I(\tilde{p}_{{i_{2} j}} ) \le I(\tilde{p}_{{i_{1} j}} )$ if $\tilde{p}_{{i_{1} j}} \le_{{L_{\text{IVPF}} }} \tilde{p}_{{i_{2} j}}$;

(T4.5):

For each $c_{j} \in C_{\text{II}}$, $I(\tilde{p}_{{i_{1} j}} ) \le I(\tilde{p}_{{i_{2} j}} )$ if $\tilde{p}_{{i_{1} j}} \le_{{L_{\text{IVPF}} }} \tilde{p}_{{i_{2} j}}$

Proof

(T4.1) For the necessity property, if $I(\tilde{p}_{ij} ) = 0$, then it implies that $d(\tilde{p}_{ij} ,\tilde{p}_{*j} ) = 0$. According to the separability property in (T2.3), it is obtained that $\tilde{p}_{ij} = \tilde{p}_{ *j}$. For the sufficiency property, if $\tilde{p}_{ij} = \tilde{p}_{ *j}$, it is obvious that $I(\tilde{p}_{ij} ) = 0$ because of the reflexivity property in (T2.1). Therefore, (T4.1) is valid

(T4.2) For the necessity property, if $I(\tilde{p}_{ij} ) = 1$, it implies that $d(\tilde{p}_{ij} ,\tilde{p}_{*j} ) = d(\tilde{p}_{\# j} ,\tilde{p}_{*j} )$. It follows that $\tilde{p}_{ij} = \tilde{p}_{\# j}$. For the sufficiency property, if $\tilde{p}_{ij} = \tilde{p}_{\# j}$, it is trivial to obtain that $I(\tilde{p}_{ij} ) = 1$ by employing (24). Thus, (T4.2) is valid

(T4.3) According to Theorem 3, it is known that $\tilde{p}_{\# j} \le_{{L_{\text{IVPF}} }} \tilde{p}_{ij} \le_{{L_{\text{IVPF}} }} \tilde{p}_{*j}$ and $\tilde{p}_{*j} \le_{{L_{\text{IVPF}} }} \tilde{p}_{ij} \le_{{L_{\text{IVPF}} }} \tilde{p}_{\# j}$ for $c_{j} \in C_{\text{I}}$ and $c_{j} \in C_{\text{II}}$, respectively. Next, applying (T2.6), one can obtain $d(\tilde{p}_{ij} ,\tilde{p}_{*j} ) \le d(\tilde{p}_{\# j} ,\tilde{p}_{*j} )$ and $d(\tilde{p}_{*j} ,\tilde{p}_{ij} ) \le d(\tilde{p}_{*j} ,\tilde{p}_{\# j} )$ (or, equivalently, $d(\tilde{p}_{ij} ,\tilde{p}_{ *j} ) \le d(\tilde{p}_{\# j} ,\tilde{p}_{ *j} )$ according to the symmetry property in (T2.2)) for $c_{j} \in C_{\text{I}}$ and $c_{j} \in C_{\text{II}}$, respectively. Furthermore, combining the condition $d(\tilde{p}_{ij} ,\tilde{p}_{ *j} ) \le d(\tilde{p}_{\# j} ,\tilde{p}_{ *j} )$ for $c_{j} \in C$ and the boundedness property in (T2.4), one can easily conclude that $0 \le I(\tilde{p}_{ij} ) \le 1$. Therefore, (T4.3) is valid

(T4.4) According to the premise condition and (T3.1), it is obvious to see that $\tilde{p}_{{i_{1} j}} \le_{{L_{\text{IVPF}} }} \tilde{p}_{{i_{2} j}} \le_{{L_{\text{IVPF}} }} \tilde{p}_{*j}$ for each $c_{j} \in C_{\text{I}}$. According to (T2.6), the condition $\tilde{p}_{{i_{1} j}} \le_{{L_{\text{IVPF}} }} \tilde{p}_{{i_{2} j}} \le_{{L_{\text{IVPF}} }} \tilde{p}_{*j}$ implies $d(\tilde{p}_{{i_{2} j}} ,\tilde{p}_{ *j} ) \le d(\tilde{p}_{{i_{1} j}} ,\tilde{p}_{ *j} )$. Note that in the denominator of (24), one has $d(\tilde{p}_{\# j} ,\tilde{p}_{*j} ) > 0$ because of the assumption of $\tilde{p}_{\# j} \ne \tilde{p}_{ *j}$ for all $c_{j} \in C$. Thus, it is easily proven that $I(\tilde{p}_{{i_{2} j}} ) \le I(\tilde{p}_{{i_{1} j}} )$ for $c_{j} \in C_{\text{I}}$; that is, (T4.4) is valid

(T4.5) Similar to the proof of (T4.4), it can be observed that $\tilde{p}_{*j} \le_{{L_{\text{IVPF}} }} \tilde{p}_{{i_{1} j}} \le_{{L_{\text{IVPF}} }} \tilde{p}_{{i_{2} j}}$ for each $c_{j} \in C_{\text{II}}$ by combining to the premise condition and (T3.2). The condition $\tilde{p}_{*j} \le_{{L_{\text{IVPF}} }} \tilde{p}_{{i_{1} j}} \le_{{L_{\text{IVPF}} }} \tilde{p}_{{i_{2} j}}$ implies $d(\tilde{p}_{{i_{1} j}} ,\tilde{p}_{ *j} ) \le d(\tilde{p}_{{i_{2} j}} ,\tilde{p}_{ *j} )$. Because $d(\tilde{p}_{\# j} ,\tilde{p}_{*j} ) > 0$ for all $c_{j} \in C$, one can infer that $I(\tilde{p}_{{i_{1} j}} ) \le I(\tilde{p}_{{i_{2} j}} )$ for $c_{j} \in C_{\text{II}}$, i.e., (T4.5) is valid. This completes the proof.□

Based on the concept of remoteness indices, this paper introduces new multiple criteria ranking indices that are useful for developing a compromise ranking procedure in the proposed IVPF VIKOR method. These remoteness-based multiple criteria ranking indices consist of remoteness-based group utility indices, individual regret indices, and compromise indices. In particular, the employment of remoteness-based compromise indices can assist decision makers in trading off the maximum group utility of the majority and the minimum individual regret of the opponent.

It is worth mentioning that the proposed $I(\tilde{p}_{ij} )$ index can not only measure the standardized degree of remoteness with respect to the positive-ideal IVPF evaluative rating but also satisfy several important properties, as shown in Theorem 4. Consider all of the evaluative ratings belong to $L_{\text{IVPF}}$ with the partial order $\le_{{L_{\text{IVPF}} }}$. The property in (T4.4) implies a monotonically increasing preference with respect to benefit criteria. That is, the larger the IVPF evaluative rating, the less the remoteness from the positive-ideal IVPF evaluative rating and the greater the preference for benefit criteria. In contrast, the property in (T4.5) implies monotonically decreasing preference with respect to cost criteria. That is, the smaller the IVPF evaluative rating, the less the remoteness from the positive-ideal IVPF evaluative rating and the greater the preference for cost criteria. Therefore, when the ideal IVPF evaluative ratings are employed for facilitating anchored judgments, the smaller the remoteness index $I(\tilde{p}_{ij} )$ is, the more prior the evaluative rating $\tilde{p}_{ij}$ is. It follows that the criterion-wise precedence relationship among alternatives can be determined according to ascending order of each $I(\tilde{p}_{ij} )$ value.

However, to synthesize all of the criterion-wise precedence relationships for acquiring a compromise ranking over all criteria, this paper needs to define the remoteness-based group utility index (i.e., the average group score) $S(z_{i} )$ and the remoteness-based individual regret index (i.e., the worst score in a particular criterion) $R(z_{i} )$. Afterward, the remoteness-based compromise index $Q(z_{i} )$ can be determined by combining $S(z_{i} )$ and $R(z_{i} )$ via a parameter $\upsilon$. It is worth noting that the parameter $\upsilon$ is a coefficient of decision mechanism [17]. When the $\upsilon$ value is large (more precisely, $\upsilon > 0.5$ is needed), the compromise solutions based on the $Q(z_{i} )$ values would tend toward majority agreement, i.e., the selection with “voting by majority.” When the $\upsilon$ value is small ($\upsilon < 0.5$), the compromise solutions based on the $Q(z_{i} )$ values would tend toward majority disagreement or negative attitude, i.e., the selection with “veto.” The particular case of $\upsilon \approx 0.5$ represents the consensus or a compromise attitude of the decision maker. In this way, the employment of the proposed $S(z_{i} )$, $R(z_{i} )$, and $Q(z_{i} )$ with parameter $\upsilon$ can reflect the decision maker’s trade-off strategy between “the maximum of the group utility for the majority” and “the minimum of the individual regret for the opponent.” The definitions and properties of remoteness-based multiple criteria ranking indices are presented below.

Definition 8

For an IVPF decision matrix $\tilde{p} = [\tilde{p}_{ij} ]_{m \times n}$ and a set of importance weights w_j for all $c_{j} \in C$, the remoteness-based group utility index $S(z_{i} )$, the remoteness-based individual regret index $R(z_{i} )$, and the remoteness-based compromise index $Q(z_{i} )$ of alternative $z_{i} \in Z$ are, respectively, defined as follows:

$$S(z_{i} ) = \sum\limits_{j = 1}^{n} {\left( {I(\tilde{p}_{ij} ) \cdot w_{j} } \right)} ,$$

(25)

$$R(z_{i} ) = \mathop {\hbox{max} }\limits_{j = 1}^{n} \left\{ {I(\tilde{p}_{ij} ) \cdot w_{j} } \right\},$$

(26)

$$Q(z_{i} ) = \upsilon \cdot \frac{{S(z_{i} ) - \mathop {\hbox{min} }\nolimits_{i' = 1}^{m} S(z_{i'} )}}{{\mathop {\hbox{max} }\nolimits_{i' = 1}^{m} S(z_{i'} ) - \mathop {\hbox{min} }\nolimits_{i' = 1}^{m} S(z_{i'} )}} + \left( {1 - \upsilon } \right) \cdot \frac{{R(z_{i} ) - \mathop {\hbox{min} }\nolimits_{i' = 1}^{m} R(z_{i'} )}}{{\mathop {\hbox{max} }\nolimits_{i' = 1}^{m} R(z_{i'} ) - \mathop {\hbox{min} }\nolimits_{i' = 1}^{m} R(z_{i'} )}},$$

(27)

where $\upsilon \in [0,1]$.

Theorem 5

The remoteness-based multiple criteria ranking indices $S(z_{i} )$, $R(z_{i} )$, and $Q(z_{i} )$, defined as in Definition 8, satisfy the following properties:

(T5.1):

$0 \le S(z_{i} ) \le 1$, $0 \le R(z_{i} ) \le 1$, and $0 \le Q(z_{i} ) \le 1$ for all $z_{i} \in Z$;

(T5.2):

$S(z_{{i_{1} }} ) \le S(z_{{i_{ 2} }} )$, $R(z_{{i_{1} }} ) \le R(z_{{i_{ 2} }} )$, and $Q(z_{{i_{1} }} ) \le Q(z_{{i_{ 2} }} )$ if $\tilde{p}_{{i_{2} j}} \le_{{L_{\text{IVPF}} }} \tilde{p}_{{i_{1} j}}$ and $\tilde{p}_{{i_{1} j}} \le_{{L_{\text{IVPF}} }} \tilde{p}_{{i_{2} j}}$ for all $c_{j} \in C_{\text{I}}$ and $c_{j} \in C_{\text{II}}$, respectively

Proof

(T5.1) For each $z_{i} \in Z$, it is obvious that $0 \le S(z_{i} ) \le 1$ and $0 \le R(z_{i} ) \le 1$ are fulfilled according to (T4.3) (i.e., $0 \le I(\tilde{p}_{ij} ) \le 1$) and the normalization condition of criterion weights (i.e., $0 \le w_{j} \le 1$ and $\sum\nolimits_{j = 1}^{n} {w_{j} } = 1$). Referring to (27), $Q(z_{i} )$ is defined as a linear combination of the normalized values of $S(z_{i} )$ and $R(z_{i} )$ for each $z_{i} \in Z$. Therefore, it can be easily concluded that $0 \le Q(z_{i} ) \le 1$ for all $z_{i} \in Z$, i.e., (T5.1) is valid.

(T5.2) According to (T4.4), it is known that $I(\tilde{p}_{{i_{1} j}} ) \le I(\tilde{p}_{{i_{2} j}} )$ because $\tilde{p}_{{i_{2} j}} \le_{{L_{\text{IVPF}} }} \tilde{p}_{{i_{1} j}}$ for each $c_{j} \in C_{\text{I}}$. Referring to (T4.5), one has $I(\tilde{p}_{{i_{1} j}} ) \le I(\tilde{p}_{{i_{2} j}} )$ because $\tilde{p}_{{i_{1} j}} \le_{{L_{\text{IVPF}} }} \tilde{p}_{{i_{2} j}}$ for each $c_{j} \in C_{\text{II}}$. Therefore, it can be obtained that $I(\tilde{p}_{{i_{1} j}} ) \le I(\tilde{p}_{{i_{2} j}} )$ for all $c_{j} \in C$ because $C = C_{\text{I}} \cup C_{\text{II}}$. Next, one can easily infer that the inequalities $S(z_{{i_{1} }} ) \le S(z_{{i_{ 2} }} )$, $R(z_{{i_{1} }} ) \le R(z_{{i_{ 2} }} )$, and $Q(z_{{i_{1} }} ) \le Q(z_{{i_{ 2} }} )$ hold. Thus, (T5.2) is valid, which completes the proof. □

Because the IVPF VIKOR method provides a maximum group utility that is represented by $\hbox{min} S(z_{i} )$ of the “majority” and a minimum of the individual regret that is represented by $\hbox{min} R(z_{i} )$ of the “opponent,” it is anticipated that the obtained compromise solutions can be understood, accepted, supported, and implemented with confidence by decision makers. For this purpose, the IVPF VIKOR ranking procedure must involve the assessments of acceptable advantage and acceptable stability in decision making; thus, it is capable of obtaining compromise solutions to support decision makers to conduct a negotiation and make a decision with confidence.

Assessing acceptable advantage and acceptable stability is a key feature of the compromise ranking procedure in the VIKOR methodology. Nevertheless, sometimes the assessment mechanism of acceptable advantage and acceptable stability is not easily understandable for decision makers. To enhance intuitive appeal and understandability of the VIKOR-based ranking assessments, this paper provides a simple and systematic framework for interpretations of compromise rankings that the IVPF VIKOR ranking procedure produces. The framework builds on the determination results of remoteness-based multiple criteria ranking indices.

First, the proposed IVPF VIKOR ranking procedure requires that the m alternatives be ranked in ascending order of the remoteness-based compromise index $Q(z_{i} )$. Let $\iota$ be a positive integer, where $\iota \in \{ 1,2, \ldots ,m\}$. Let $Z^{(\iota )}$ denote a subset of the alternative set Z, i.e., $Z^{(\iota )} \subseteq Z$. Note that the superscript $\iota$ in the parentheses of $Z^{(\iota )}$ indicates not only the component of the alternative subset but also the priority of the corresponding alternatives. For example, the alternatives in $Z^{(1)}$ are ranked the best by $Q(z_{i} )$, the alternatives in $Z^{(2)}$ are ranked the second best by $Q(z_{i} )$, etc. Let $Z^{(0)} = \emptyset$; then, $Z^{(\iota )}$ is defined as follows:

$$Z^{(\iota )} = \left\{ {z_{i} \left| {\mathop {\hbox{min} }\limits_{i = 1}^{m} } \right.Q(z_{i} ), \, z_{i} \in Z\backslash \mathop \cup \limits_{{\iota^{\prime} = 0}}^{\iota - 1} Z^{{(\iota^{\prime})}} } \right\}.$$

(28)

Furthermore, let $Z_{S}^{(1)}$ and $Z_{R}^{(1)}$ be two subsets of the alternative set Z, i.e., $Z_{S}^{(1)} \subseteq Z$ and $Z_{R}^{(1)} \subseteq Z$. Rank the m alternatives by sorting each $S(z_{i} )$ and $R(z_{i} )$ value in ascending order. More precisely, $Z_{S}^{(1)}$ and $Z_{R}^{(1)}$ denote the collections of the alternatives that are best ranked by $S(z_{i} )$ and $R(z_{i} )$, respectively, as shown in the following definitions:

$$Z_{S}^{(1)} = \left\{ {z_{i} \left| {\mathop {\hbox{min} }\limits_{i = 1}^{m} } \right.S(z_{i} ), \, z_{i} \in Z} \right\},$$

(29)

$$Z_{R}^{(1)} = \left\{ {z_{i} \left| {\mathop {\hbox{min} }\limits_{i = 1}^{m} } \right.R(z_{i} ), \, z_{i} \in Z} \right\}.$$

(30)

Let the alternative(s) $z^{*} \in Z^{*}$ that is (are) the ultimate compromise solution(s), where $Z^{*}$ is a subset of Z (i.e., $Z^{*} \subseteq Z$) and is defined as follows:

$$Z^{*} = \left\{ {\begin{array}{*{20}l} {Z^{(1)} } \hfill & {{\text{if}}\quad Q\left( {z^{(2)} } \right) - Q\left( {z^{(1)} } \right) \ge \frac{1}{m - 1}\,{\text{and}}\, \, z^{(1)} \in Z_{S}^{(1)} \cup Z_{R}^{(1)} ;} \hfill \\ {Z^{(1)} \cup Z^{(2)} } \hfill & {{\text{if}}\quad Q\left( {z^{(2)} } \right) - Q\left( {z^{(1)} } \right) \ge \frac{1}{m - 1}\,{\text{and}}\,z^{(1)} \notin Z_{S}^{(1)} \cup Z_{R}^{(1)} ;} \hfill \\ {Z^{(1)} \cup Z^{(2)} \cup \cdots \cup Z^{(\kappa )} } \hfill & {{\text{if}}\quad Q\left( {z^{(2)} } \right) - Q\left( {z^{(1)} } \right) < \frac{1}{m - 1}\,{\text{and}}\,\kappa \,{\text{is the largest }}\iota } \hfill \\ {} \hfill & {{\text{such that}}\,Q\left( {z^{(\kappa )} } \right) - Q\left( {z^{(1)} } \right) < \frac{1}{m - 1},} \hfill \\ \end{array} } \right.$$

(31)

where $z^{(\iota )} \in Z^{(\iota )}$ for $\iota = 1,2, \ldots ,m$.

It is worthwhile to mention that the assessment of acceptable advantage is in accordance with the condition $Q(z^{(2)} ) - Q(z^{(1)} ) \ge {1 \mathord{\left/ {\vphantom {1 {(m - 1)}}} \right. \kern-0pt} {(m - 1)}}$. Moreover, the assessment of acceptable stability in decision making indicates that alternative z⁽¹⁾ must be the best ranked by $S(z_{i} )$ and/or $R(z_{i} )$. As indicated in (31), one can conclude the alternatives in $Z^{(1)}$ as the ultimate compromise solutions if the conditions $Q(z^{(2)} ) - Q(z^{(1)} ) \ge$${1 \mathord{\left/ {\vphantom {1 {(m - 1)}}} \right. \kern-0pt} {(m - 1)}}$ and $z^{(1)} \in Z_{S}^{(1)} \cup Z_{R}^{(1)}$ are both fulfilled. In contrast, if the condition regarding acceptable stability is not satisfied, i.e., $z^{(1)} \notin Z_{S}^{(1)} \cup Z_{R}^{(1)}$, the set of ultimate compromise solutions $Z^{*}$ consists of the alternatives in $Z^{(1)} \cup Z^{(2)}$ under the premise condition $Q(z^{(2)} ) - Q(z^{(1)} ) \ge {1 \mathord{\left/ {\vphantom {1 {(m - 1)}}} \right. \kern-0pt} {(m - 1)}}$. If the condition regarding acceptable advantage is not satisfied, then denote a positive integer $\kappa$ as the largest $\iota$ such that $Q(z^{(\kappa )} ) - Q(z^{(1)} ) < 1/(m - 1)$. Accordingly, the set $Z^{*}$ consists of the alternatives in $Z^{(1)} \cup Z^{(2)} \cup \cdots \cup Z^{(\kappa )}$ because the positions of alternatives $z^{(1)} ,z^{(2)} , \ldots ,$ and $z^{(\kappa )}$ are in closeness.

According to the above compromise ranking process, the ultimate compromise solutions can be easily determined by comparing remoteness-based multiple criteria ranking indices and assessing acceptable advantage and acceptable stability. The proposed IVPF VIKOR ranking procedure in (31) can not only improve the implementation efficiency of the VIKOR-based ranking process but also enhance the understandability and acceptability of the obtained results.

The algorithmic procedure of the proposed IVPF VIKOR method is summarized as follows:

Step 1:

Formulate an MCDA problem with the set of alternatives $Z = \{ z_{1} ,z_{2} , \ldots ,z_{m} \}$ and the set of criteria $C = \{ c_{1} ,c_{2} , \ldots ,c_{n} \}$, which is divided into C_I and C_II

Step 2:

Construct the IVPF decision matrix $\tilde{p} = [\tilde{p}_{ij} ]_{m \times n}$ with the IVPF evaluative rating $\tilde{p}_{ij}$ for each alternative $z_{i} \in Z$ with respect to criterion $c_{j} \in C$ and the weight w_j of each $c_{j} \in C$

Step 3:

Identify the positive-ideal IVPF evaluative rating $\tilde{p}_{ *j}$ using (20) and the negative-ideal IVPF evaluative rating $\tilde{p}_{{{{\# }}j}}$ using (21) with respect to each $c_{j} \in C$

Step 4:

Apply (19) to compute the distance $d(\tilde{p}_{ij} ,\tilde{p}_{*j} )$ for each $z_{i} \in Z$ with respect to $c_{j} \in C$ and $d(\tilde{p}_{\# j} ,\tilde{p}_{*j} )$ for each $c_{j} \in C$, and then derive the remoteness index $I(\tilde{p}_{ij} )$ using (24) for each $\tilde{p}_{ij}$ in $\tilde{p}$

Step 5:

Employ (25) and (26) to, respectively, compute the remoteness-based group utility index $S(z_{i} )$ and the remoteness-based individual regret index $R(z_{i} )$ of each $z_{i} \in Z$

Step 6:

Set the parameter $\upsilon$ ($0 \le \upsilon \le 1$) as a coefficient of decision mechanism, and then calculate the remoteness-based compromise index $Q(z_{i} )$ using (27) of each $z_{i} \in Z$

Step 7:

Determine the subsets $Z_{S}^{(1)}$, $Z_{R}^{(1)}$, and $Z^{(\iota )}$ ($\iota \in \{ 1,2, \ldots ,m\}$) using (29), (30), and (28), respectively, and then obtain the set of ultimate compromise solutions $Z^{*}$ using (31)

4 Practical applications with a comparative analysis

This section first utilizes a case study concerning the selection of pilot hospitals in the PAC-CVD program to demonstrate the implementation process and practicality of the proposed IVPF VIKOR method. Furthermore, a sensitivity analysis is implemented to examine the obtained results in the PAC-CVD case. More discussions are provided to investigate the application effects of the developed approach to address IVIF information in the context of intuitionistic fuzziness. Finally, this section applies the proposed method to various application areas and conducts a comparative analysis with respect to other relevant MCDA methods to examine its effectiveness and advantages.

4.1 A case study for hospital-based PAC-CVD

In this subsection, an illustrative case concerning the selection of pilot hospitals in the PAC-CVD program is provided to demonstrate the feasibility and applicability of the proposed IVPF VIKOR method in the medical and healthcare fields.

Participants eligible for PAC-CVD must comprise a team of different levels of healthcare institutions led by a primary institution. The primary institution is responsible for preparing a submission for the program, synergizing the healthcare resources of members, delivering healthcare services, and allocating medical expenses. A pilot hospital must provide rehabilitation care services (including physical therapy, occupational therapy, and speech therapy) and establish a PAC team composed of physicians whose practices involve PAC-CVD, such as neurologists, neurosurgeons, internists, family physicians, or physiatrists. This interdisciplinary team must be led by a managing physician. Moreover, the pilot hospital must appoint full-time nurses, physiotherapists, speech-language pathologists, pharmacists, nutritionists, dietitians, and social workers.

The NHIA determined the edibility of candidate hospitals for PAC-CVD according to the requirements, integrity, and rationality of program as well as the background information, care models, and transitional care systems of the hospitals. The criteria considered for the selection of pilot hospitals are specified as follows:

• (1) Rationality of the transitional care system (c₁): the vertically integrated transitional care system’s delivery of care services from acute and post-acute to chronic phases.

• (2) Integration of healthcare institutions (c₂): the organization and operation of a team of different healthcare institutions, concerning the coherent delivery of services and ensuring the transition from acute to long-term care.

• (3) Adequacy of manpower allocation (c₃): the organization of the PAC team, concerning the areas of specialization, number, and employment status (full-time or part-time) of all healthcare professionals; the doctor-to-patient ratio in each branch of medicine; the quality of the professionals; and the consistency of scale-based measurements conducted by team members.

• (4) Completeness of care-related equipment (c₄): the completeness of PAC-related equipment, concerning the number of hospital beds in the PAC department, the intended use of PAC facilities, and the type of equipment that can be applied for PAC.

• (5) Assurance of healthcare quality (c₅): the healthcare quality assurance provided by each member institution, and its capability to treat comorbidities and complications.

• (6) Uniqueness and potential of PAC (c₆): the characteristics of the PAC model and possible improvements.

The PAC-CVD program received a consistent and adequate budget. Patients with CVDs who entered PAC were categorized according to their initial functional status and potential for active rehabilitation. Five post-acute function-related groups (FRGs) were planned according to the patients’ possible care pathways. The program drew on the annual NHI medical payment for hospitals to fund FRG 1 (i.e., PAC and high-intensity rehabilitation) and FRG 2 (i.e., PAC and medium-intensity rehabilitation). Moreover, the costs of eligibility determination, rewards, and outpatient diagnosis and treatment surcharges were covered by another NHI project aimed at promoting healthcare system integration. FRG 3 (institutional care and supportive rehabilitation), FRG 4 (outpatient medical care and rehabilitative model), and FRG 5 (home-based healthcare) were funded in accordance with NHI regulations.

All participating hospitals were entitled to financial rewards, outpatient diagnosis and treatment surcharges, and claims for the reimbursement of other categories of medical expenses. Their professional image and reputation could be reinforced through PAC, which is based on holistic care principles. Thus, many hospitals across Taiwan have submitted applications to their regional NHIA offices and 39 hospitals were approved. As an illustrative example, this study applied the developed IVPF VIKOR method to examine the selection for PAC-CVD of five candidate hospitals operating in eastern Taiwan.

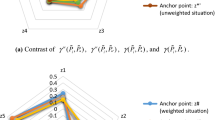
The proposed method was employed to help NHIA to select a set of ultimate compromise solutions from five candidate hospitals in eastern Taiwan using six criteria. In Step 1, the set of alternatives is denoted by $Z = \{ z_{1} ,z_{2} , \ldots ,z_{5} \}$ and the set of criteria $C = \{ c_{1} ,c_{2} , \ldots ,c_{6} \}$, where $C_{I} = \{ c_{1} ,c_{2} , \ldots ,c_{6} \}$ and $C_{\text{II}} = \emptyset$. In Step 2, the linguistic assessment values of the five alternatives with respect to six criteria provided by NHIA were designated to be represented by IVPF values. This paper adopted a seven-point rating scale, which originates from the IVPF linguistic scale developed by Peng and Yang [39]. The IVPF evaluative rating $\tilde{p}_{ij}$ in the IVPF decision matrix $\tilde{p} = [\tilde{p}_{ij} ]_{5 \times 6}$ is shown in Table 1. Moreover, the weight vector of the criteria was given in advance as (0.18, 0.22, 0.16, 0.14, 0.20, 0.10)^T.

Table 1 The IVPF evaluative rating $\tilde{p}_{ij}$ in the PAC-CVD case

In Step 3, the positive- and negative-ideal IVPF evaluative ratings were determined as follows: $\tilde{p}_{ * 1} = \tilde{p}_{ * 2} = \tilde{p}_{ * 5} = \tilde{p}_{ * 6} =$ ([0.8, 0.9], [0.1, 0.2]), $\tilde{p}_{*3} = \tilde{p}_{*4} =$ ([0.7, 0.8], [0.2, 0.3]), $\tilde{p}_{\# 1} = \tilde{p}_{\# 5} =$ ([0.5, 0.6], [0.4, 0.5]), $\tilde{p}_{\# 2} = \tilde{p}_{\# 4} = \tilde{p}_{\# 6} =$ ([0.2, 0.3], [0.7, 0.8]), and $\tilde{p}_{\# 3} =$ ([0.3, 0.4], [0.6, 0.7]). In Step 4, the computation results of the distances $d(\tilde{p}_{\# j} ,\tilde{p}_{*j} )$ and $d(\tilde{p}_{ij} ,\tilde{p}_{*j} )$ with respect to $c_{j} \in C$ and the remoteness index $I(\tilde{p}_{ij} )$ for each $\tilde{p}_{ij}$ are listed in Table 2. In Step 5, combining the obtained remoteness indices with the weight vector, one can determine the remoteness-based group utility index $S(z_{i} )$ and the remoteness-based individual regret index $R(z_{i} )$ of each $z_{i} \in Z$, as shown in Table 3. In Step 6, set $\upsilon$ = 0.5 because NHIA would tend toward a consensus or compromise attitude. The calculation results of the remoteness-based compromise index $Q(z_{i} )$ for each z_i are included in Table 3. Additionally, this table depicts three priority orders based on an ascending order of $S(z_{i} )$, $R(z_{i} )$, and $Q(z_{i} )$ for comparison.

Table 2 Results of $d\left( {\tilde{p}_{\# j} ,\tilde{p}_{*j} } \right)$, $d\left( {\tilde{p}_{ij} ,\tilde{p}_{*j} } \right)$, and $I\left( {\tilde{p}_{ij} } \right)$ in the PAC-CVD case

Table 3 Three sets of priority rankings in the PAC-CVD case ($\upsilon$ = 0.5)

In Step 7, it is obvious to see that $Z_{S}^{(1)} = \{ z_{2} \}$, $Z_{R}^{(1)} = \{ z_{5} \}$, $Z^{(1)} = \{ z_{5} \}$, $Z^{(2)} = \{ z_{3} \}$, $Z^{(3)} = \{ z_{2} \}$, $Z^{(4)} = \{ z_{4} \}$, and $Z^{(5)} = \{ z_{1} \}$ according to the priority ranking results in Table 3. It directly follows that $\, z^{(1)} \, (i.e., \, z_{5} ) \in Z_{S}^{(1)} \cup Z_{R}^{(1)} \, (i.e., \, \{ z_{2} ,z_{5} \} )$. However, $Z^{*} \ne Z^{(1)}$ because the condition of acceptable advantage was not fulfilled, i.e., $Q(z^{(2)} ) - Q(z^{(1)} ){ = }Q(z_{3} ) - Q(z_{5} ) = 0.3443 - 0.1516 = 0.1927 < {1 \mathord{\left/ {\vphantom {1 {(5 - 1)}}} \right. \kern-0pt} {(5 - 1)}}$. Next, it is easy to obtain that $\kappa = 2$ because $Q(z^{(3)} ) - Q(z^{(1)} ){ = }Q(z_{2} ) - Q(z_{5} ) = 0.5000 - 0.1516$$= 0.3484 \ge {1 \mathord{\left/ {\vphantom {1 {(5 - 1)}}} \right. \kern-0pt} {(5 - 1)}}$. It implies that the positions of alternatives $z^{(1)}$ and $z^{(2)}$ are in closeness. Therefore, one can conclude that $Z^{*} = Z^{(1)} \cup Z^{(2)} = \{ z_{3} ,z_{5} \}$. That is, when considering the consensus or a compromise attitude of NHIA, the third and fifth candidate hospitals (i.e., z₃ and z₅) are the compromise solutions for the PAC-CVD program. Furthermore, let the alternatives in curly brackets represent the ultimate compromise solutions using the proposed IVPF VIKOR ranking procedure in (31). Accordingly, the ultimate ranking result in this PAC-CVD case is denoted by $\{ z_{5} \succ z_{3} \} \succ z_{2} \succ z_{4} \succ z_{1}$.

4.2 Sensitivity analysis

This subsection attempts to conduct two sensitivity analyses to validate the obtained results in the PAC-CVD case. The aim of the first sensitivity analysis is to investigate the impact of various settings of the parameter $\upsilon$. For different values of the parameter $\upsilon$, Table 4 reveals the corresponding results of the remoteness-based compromise index $Q(z_{i} )$, the set of ultimate compromise solutions $Z^{*}$, and the ultimate rankings of the five candidate hospitals. Additionally, the results of the sensitivity analysis for various $\upsilon$ values are presented graphically in Fig. 2. More specifically, Fig. 2a depicts the comparison results of the remoteness-based compromise indices among five candidate hospitals under different settings of the parameter $\upsilon$. Figure 2b reveals the linear rankings of the five hospitals based on an ascending order of the $Q(z_{i} )$ values with respect to each $\upsilon$ value.

Table 4 Sensitivity analysis of the obtained results in the PAC-CVD case

Fig. 2

Sensitivity analysis within the IVPF environment. a Results of the $Q(z_{i} )$ values under different settings of the parameter $\upsilon$. b Results of the linear rankings with respective to different $\upsilon$ values

As indicated in Table 4 and Fig. 2a, the values of Q(z₁), Q(z₂), and Q(z₃) decrease but the values of Q(z₄) and Q(z₅) increase when the $\upsilon$ value increases from 0 to 1. In particular, eight ultimate ranking results were determined: $\{ z_{5} \succ z_{4} \} \succ z_{3}$$\succ z_{1} \succ z_{2}$, $\{ z_{5} \} \succ z_{4} \succ z_{3} \succ z_{1} \succ z_{2}$, $\{ z_{5} \} \succ z_{3} \succ z_{4} \succ z_{2} \succ z_{1}$, $\{ z_{5} \succ z_{3} \} \succ z_{2} \succ z_{4} \succ z_{1}$, $\{ z_{5} \succ z_{3} \succ z_{2} \} \succ z_{1} \succ z_{4}$, $\{ z_{2} \succ z_{5} \succ z_{3} \} \succ z_{1} \succ z_{4}$, $\{ z_{2} \succ z_{3} \succ z_{5} \} \succ z_{1} \succ z_{4}$, and $\{ z_{2} \succ$$z_{3} \} \succ z_{5} \succ z_{1} \succ z_{4}$ in the cases of $\upsilon = 0$, $\upsilon = 0.1,0.2$, $\upsilon = 0.3,0.4$, $\upsilon = 0.5$, $\upsilon = 0.6,0.7$, $\upsilon = 0.8$, $\upsilon = 0.9$, and $\upsilon = 1$, respectively. Moreover, five sets of ultimate compromise solutions were obtained: $\{ z_{4} ,z_{5} \}$, $\{ z_{5} \}$, $\{ z_{3} ,z_{5} \}$, $\{ z_{2} ,z_{3} ,z_{5} \}$, and $\{ z_{2} ,z_{3} \}$ for $\upsilon = 0$, $\upsilon = 0.1,0.2, \ldots ,0.4$, $\upsilon = 0.5$, $\upsilon = 0.6,0.7, \ldots ,0.9$, and $\upsilon = 1$, respectively. It is worthwhile to mention that the candidate hospitals z₄ and z₅ were selected with “veto” because they would tend toward majority disagreement. In contrast, z₂ and z₃ were selected with “voting by majority” because they would tend toward majority agreement. In the illustrative case of $\upsilon = 0.5$, z₃ and z₅ were selected with “consensus” because they would tend toward a compromise attitude. Furthermore, according to the sensitivity analysis in Fig. 2b, the candidate hospitals z₅ and z₂ were the best ranked in the linear ranking results for $\upsilon \le 0.7$ and $\upsilon \ge 0.8$, respectively. Based on the comparison results in Table 4 and the sensitivity analysis in Fig. 2, it appears clearly that the proposed method has the capability of producing flexible and reasonable ranking results that can reflect the decision maker’s trade-off strategy.

Next, the second sensitivity analysis was implemented to validate the advantages of the proposed approach using distance measures between IVPF evaluative ratings. In general, to deal successfully with imperfect information, one needs to have a proper model to represent the information, and adequate measures making it possible to process this information. The concept of distance measures plays a leading role among such measures [46]. As is well known, the concept of distance measures can be employed to identify measurements corresponding to similarity measures. Distance measures can be also used in developing classification methods and conducting a cluster analysis. Moreover, for numerous MCDA methods, distance measures have a pivotal role in defining relevant comparison indices or constructing the main structure of MCDA models. Consider three widely used methodologies for example. The technique for order preference by similarity to ideal solution (TOPSIS) considers the distances to both the ideal and the negative-deal solutions simultaneously to determine the closeness coefficient. The method of elimination and choice translating reality (ELECTRE) establishes the discordance index based on a distance measure. To identify goodness and poorness of fit, the linear programming technique for multidimensional analysis of preference (LINMAP) employs the concept of distances to measure consistency and inconsistency among the ranking orders of alternatives. From the previous discussion, it can be seen that the approach using distance measures plays a crucial role in any efforts to produce the effectiveness of MCDA methods. It is also worth noting that the approach using distance measures has several advantages over other techniques in handling uncertain information, especially within a highly complicated and ambiguous environment. To maximize the usefulness of systematic MCDA models under highly uncertain IVPF conditions, the concept of distance measures between IVPF evaluative ratings can be utilized to address this issue.

Furthermore, the following sensitivity analysis attempts to investigate the effect of various distance measures on the obtained results in the PAC-CVD case. As pointed out in Definition 5, the distance measure between IVPF evaluative ratings is based on the Hamming distance model. Turning now to the sensitivity analysis, this paper provides a generalized definition for the measured distance between the two IVPF evaluative ratings $\tilde{p}_{{i_{1} j}}$ and $\tilde{p}_{{i_{2} j}}$ as follows:

$$\begin{aligned} d^{\rho } \left( {\tilde{p}_{{i_{1} j}} ,\tilde{p}_{{i_{2} j}} } \right) & = \left[ {\frac{1}{4} \cdot \left( {\left| {\left( {\mu_{{i_{1} j}}^{ - } } \right)^{2} - \left( {\mu_{{i_{2} j}}^{ - } } \right)^{2} } \right|^{\rho } + \left| {\left( {\mu_{{i_{1} j}}^{ + } } \right)^{2} - \left( {\mu_{{i_{2} j}}^{ + } } \right)^{2} } \right|^{\rho } + \left| {\left( {\nu_{{i_{1} j}}^{ - } } \right)^{2} - \left( {\nu_{{i_{2} j}}^{ - } } \right)^{2} } \right|^{\rho } } \right.} \right. \\ & \quad \left. { + \,\left| {\left( {\nu_{{i_{1} j}}^{ + } } \right)^{2} - \left( {\nu_{{i_{2} j}}^{ + } } \right)^{2} } \right|^{\rho } + \left. {\left| {\left( {\pi_{{i_{1} j}}^{ - } } \right)^{2} - \left( {\pi_{{i_{2} j}}^{ - } } \right)^{2} } \right|^{\rho } + \left| {\left( {\pi_{{i_{1} j}}^{ + } } \right)^{2} - \left( {\pi_{{i_{2} j}}^{ + } } \right)^{2} } \right|^{\rho } } \right)} \right]^{{\frac{1}{\rho }}} , \\ \end{aligned}$$

(32)

where ρ is a distance parameter with $1 \le \rho < \infty$. When $\rho = 1$, (32) reduces to the Hamming distance in (19), and let $d^{1} (\tilde{p}_{{i_{1} j}} ,\tilde{p}_{{i_{ 2} j}} ) \equiv d(\tilde{p}_{{i_{1} j}} ,\tilde{p}_{{i_{ 2} j}} )$. When $\rho = 2$, (32) reduces to the Euclidean distance.

Several ρ values were designated when computing $d^{\rho } (\tilde{p}_{{i_{1} j}} ,\tilde{p}_{{i_{ 2} j}} )$: ρ = 2, 5, 10, 20, 50, and 100. With regard to the parameters ρ and $\upsilon$, the comparison results of the $Q(z_{i} )$ values and the corresponding linear rankings are highlighted in Figs. 3 and 4, respectively. Overall, the obtained $Q(z_{i} )$ values and the linear rankings are steady and reveal consistent patterns regardless of the ρ values. Despite this, a little difference in the linear ranking results has been found in the case of $\upsilon = 0.3$ when the Euclidean distance (i.e., ρ = 2) was employed. More specifically, the obtained linear ranking was $z_{5} \succ z_{3} \succ z_{4} \succ z_{1} \succ z_{2}$ in the case of ρ = 2. In contrast, the obtained linear ranking was $z_{5} \succ z_{3} \succ z_{4} \succ z_{2} \succ z_{1}$ with respect to the other ρ values.

Fig. 3

Sensitivity results of the $Q(z_{i} )$ values with respect to the parameter ρ. a The $Q(z_{i} )$ values when ρ = 2. b The $Q(z_{i} )$ values when ρ = 5. c The $Q(z_{i} )$ values when ρ = 10. d The $Q(z_{i} )$ values when ρ = 20. e The $Q(z_{i} )$ values when ρ = 50. f The $Q(z_{i} )$ values when ρ = 100

Fig. 4

Sensitivity results of the linear rankings with respect to the parameter ρ. a The linear rankings when ρ = 2. b The linear rankings when ρ = 5. c The linear rankings when ρ = 10. d The linear rankings when ρ = 20. e The linear rankings when ρ = 50. f The linear rankings when ρ = 100

Comparing the ultimate ranking results, except in the cases of $\upsilon =$ 0.3 and 0.4, the same outcomes were determined for all of the ρ values. To be precise, the following ultimate rankings were acquired: $\{ z_{5} \succ z_{4} \} \succ z_{3} \succ z_{1} \succ z_{2}$, $\{ z_{5} \} \succ z_{4} \succ z_{3} \succ z_{1} \succ z_{2}$, $\{ z_{5} \succ z_{3} \} \succ z_{2} \succ z_{4} \succ z_{1}$, $\{ z_{5} \succ z_{3} \succ z_{2} \} \succ z_{1} \succ z_{4}$, $\{ z_{2} \succ z_{5} \succ z_{3} \} \succ z_{1} \succ z_{4}$, $\{ z_{2} \succ z_{3} \succ$$z_{5} \} \succ z_{1} \succ z_{4}$, and $\{ z_{2} \succ z_{3} \} \succ z_{5} \succ z_{1} \succ z_{4}$ in the cases of $\upsilon = 0$, $\upsilon = 0.1,0.2$, $\upsilon = 0.5$, $\upsilon = 0.6,0.7$, $\upsilon = 0.8$, $\upsilon = 0.9$, and $\upsilon = 1$, respectively, regardless of the ρ values. Moreover, the following sets of ultimate compromise solutions were determined: $\{ z_{4} ,z_{5} \}$, $\{ z_{5} \}$, $\{ z_{3} ,z_{5} \}$, $\{ z_{2} ,z_{3} ,z_{5} \}$, and $\{ z_{2} ,z_{3} \}$ for $\upsilon = 0$, $\upsilon = 0.1,0.2$, $\upsilon = 0.5$, $\upsilon = 0.6,0.7, \ldots ,0.9$, and $\upsilon = 1$, respectively. With regard to $\upsilon =$ 0.3, the proposed method based on the Euclidean distance model (ρ = 2) produced the ultimate ranking $\{ z_{5} \} \succ z_{3} \succ z_{4} \succ z_{1} \succ z_{2}$ and $Z^{*} = \{ z_{5} \}$, while $\{ z_{5} \} \succ z_{3} \succ z_{4} \succ z_{2} \succ z_{1}$ (with $Z^{*} = \{ z_{5} \}$) was obtained with respect to the other ρ values. As regards $\upsilon =$ 0.4, the ultimate ranking $\{ z_{5} \succ z_{3} \} \succ z_{4} \succ z_{2} \succ z_{1}$ and $Z^{*} = \{ z_{3} ,z_{5} \}$ were yielded by the proposed method for ρ = 2, 5, and 10, while $\{ z_{5} \} \succ z_{3} \succ z_{4} \succ z_{2} \succ z_{1}$ (with $Z^{*} = \{ z_{5} \}$) was acquired in terms of the other ρ values. As a whole, compared with the other settings in $d^{\rho } (\tilde{p}_{{i_{1} j}} ,\tilde{p}_{{i_{ 2} j}} )$, $d(\tilde{p}_{{i_{1} j}} ,\tilde{p}_{{i_{ 2} j}} )$ based on the Hamming distance model and $d^{2} (\tilde{p}_{{i_{1} j}} ,\tilde{p}_{{i_{ 2} j}} )$ based on the Euclidean distance model yielded a common and typical result. Because of slightly different solution results between the two distance models, it can be inferred that the employment of $d(\tilde{p}_{{i_{1} j}} ,\tilde{p}_{{i_{ 2} j}} )$ or $d^{2} (\tilde{p}_{{i_{1} j}} ,\tilde{p}_{{i_{ 2} j}} )$ may possess a capability of adapting to the particularities in the real world. Thus, to capture the usual and variable practical situations, it is suggested that ρ = 1 and 2 when setting the distance parameter in $d^{\rho } (\tilde{p}_{{i_{1} j}} ,\tilde{p}_{{i_{ 2} j}} )$. In particular, as mentioned in Theorem 2, the $d(\tilde{p}_{{i_{1} j}} ,\tilde{p}_{{i_{ 2} j}} )$ measure retains several useful properties that can facilitate the manipulation of IVPF data and the comparison of IVPF information. Accordingly, it is appropriate to employ $d(\tilde{p}_{{i_{1} j}} ,\tilde{p}_{{i_{ 2} j}} )$ (or $d^{2} (\tilde{p}_{{i_{1} j}} ,\tilde{p}_{{i_{ 2} j}} )$) to establish the concept of remoteness indices for IVPF evaluative ratings. In brief, the conceptual discussion regarding the usefulness of distance measures and the sensitivity analysis with respect to different settings of the parameters $\upsilon$ and ρ have investigated the effect of various distance measures on the obtained results and demonstrated certain advantages of the developed approach based on distance measures between IVPF evaluative ratings.

4.3 More discussions in the context of intuitionistic fuzziness

In this subsection, the sensitivities of applying the developed approach over implementations of IVIF information have been investigated to examine the applicability and effectiveness of the proposed VIKOR methodology in the context of intuitionistic fuzziness. Consider the same selection problem of pilot hospitals in the PAC-CVD program. First, all of the IVPF evaluative ratings in the IVPF decision matrix $\tilde{p}$ must be converted into IVIF values to facilitate a sensitivity analysis of the proposed method within the IVIF environment. To adapt to the IVIF information, some formulas in the IVPF VIKOR method have to be replaced with appropriate IVIF operations. Accordingly, the developed VIKOR procedure can be employed to handle IVIF evaluative ratings and then to validate the feasibility and reasonability via the application outcomes.

Let an IVIF value $\tilde{p}_{ij}^{0}$ denote the evaluative rating of z_i with respect to c_j in the IVIF context. Based on the original IVPF evaluative rating $\tilde{p}_{ij}$, the $\tilde{p}_{ij}^{0}$ can be determined in the following manner:

$$\begin{aligned} \tilde{p}_{ij}^{0} & = \left( {\mu_{ij}^{0} ,\nu_{ij}^{0} } \right) = \left( {\left[ {\mu_{ij}^{0 - } ,\mu_{ij}^{0 + } } \right],\left[ {\nu_{ij}^{0 - } ,\nu_{ij}^{0 + } } \right]} \right) \\ & = \left( {\left[ {\frac{{\mu_{ij}^{ - } }}{{\mu_{ij}^{ - } + \nu_{ij}^{ - } + \pi_{ij}^{ + } }},\frac{{\mu_{ij}^{ + } }}{{\mu_{ij}^{ + } + \nu_{ij}^{ + } + \pi_{ij}^{ - } }}} \right],\left[ {\frac{{\nu_{ij}^{ - } }}{{\mu_{ij}^{ - } + \nu_{ij}^{ - } + \pi_{ij}^{ + } }},\frac{{\nu_{ij}^{ + } }}{{\mu_{ij}^{ + } + \nu_{ij}^{ + } + \pi_{ij}^{ - } }}} \right]} \right), \\ \end{aligned}$$

(33)

where $0 \le \mu_{ij}^{0 - } \le \mu_{ij}^{0 + } \le 1$, $0 \le \nu_{ij}^{0 - } \le \nu_{ij}^{0 + } \le 1$, and $\mu_{ij}^{0 + } + \nu_{ij}^{0 + } \le 1$. The hesitation degree $\pi_{ij}^{0}$ is calculated as follows:

$$\pi_{ij}^{0} = \left[ {\pi_{ij}^{0 - } ,\pi_{ij}^{0 + } } \right] = \left[ {\frac{{\pi_{ij}^{ - } }}{{\mu_{ij}^{ + } + \nu_{ij}^{ + } + \pi_{ij}^{ - } }},\frac{{\pi_{ij}^{ + } }}{{\mu_{ij}^{ - } + \nu_{ij}^{ - } + \pi_{ij}^{ + } }}} \right] ,$$

(34)

where $0 \le \pi_{ij}^{0 - } \le \pi_{ij}^{0 + } \le 1$. By use of the transformation outcomes in (33) and (34), the specification of the IVIF evaluative rating $\tilde{p}_{ij}^{0}$ will satisfy the necessary conditions of $\mu_{ij}^{0 - } + \nu_{ij}^{0 - } + \pi_{ij}^{0 + } = 1$ and $\mu_{ij}^{0 + } + \nu_{ij}^{0 + } + \pi_{ij}^{0 - } = 1$. Following the transformation procedure, the IVIF evaluative ratings in the PAC-CVD case were obtained, as shown in Table 5.

Table 5 The IVIF evaluative rating $\tilde{p}_{ij}^{0}$ in the PAC-CVD case

The distance measure between two IVIF evaluative ratings $\tilde{p}_{{i_{1} j}}^{0}$ and $\tilde{p}_{{i_{2} j}}^{0}$ is defined as follows:

$$\begin{aligned} d\left( {\tilde{p}_{{i_{1} j}}^{0} ,\tilde{p}_{{i_{2} j}}^{0} } \right) & = \frac{1}{4} \cdot \left( {\left| {\mu_{{i_{1} j}}^{0 - } - \mu_{{i_{2} j}}^{0 - } } \right| + \left| {\mu_{{i_{1} j}}^{0 + } - \mu_{{i_{2} j}}^{0 + } } \right| + \left| {\nu_{{i_{1} j}}^{0 - } - \nu_{{i_{2} j}}^{0 - } } \right| + \left| {\nu_{{i_{1} j}}^{0 + } - \nu_{{i_{2} j}}^{0 + } } \right|} \right. \\ & \left. {\quad + \,\left| {\pi_{{i_{1} j}}^{0 - } - \pi_{{i_{2} j}}^{0 - } } \right| + \left| {\pi_{{i_{1} j}}^{0 + } - \pi_{{i_{2} j}}^{0 + } } \right|} \right). \\ \end{aligned}$$

(35)

For an IVIF decision matrix $\tilde{p}^{0} = [\tilde{p}_{ij}^{0} ]_{m \times n}$, the positive-ideal IVIF evaluative rating $\tilde{p}_{*j}^{0}$ and the negative-ideal IVIF evaluative rating $\tilde{p}_{\# j}^{0}$ with respect to each criterion $c_{j} \in C$ are defined as follows:

$$\begin{aligned} \tilde{p}_{*j}^{0} & = \left( {\mu_{*j}^{0} ,\nu_{*j}^{0} } \right) = \left( {\left[ {\mu_{*j}^{0 - } ,\mu_{*j}^{0 + } } \right],\left[ {\nu_{*j}^{0 - } ,\nu_{*j}^{0 + } } \right]} \right) \\ & = \left\{ {\begin{array}{*{20}l} {\left( {\left[ {\mathop {\hbox{max} }\limits_{i = 1}^{m} \mu_{ij}^{0 - } ,\mathop {\hbox{max} }\limits_{i = 1}^{m} \mu_{ij}^{0 + } } \right],\left[ {\mathop {\hbox{min} }\limits_{i = 1}^{m} \nu_{ij}^{0 - } ,\mathop {\hbox{min} }\limits_{i = 1}^{m} \nu_{ij}^{0 + } } \right]} \right)} \hfill & {{\text{if}}\quad c_{j} \in C_{\text{I}} ,} \hfill \\ {\left( {\left[ {\mathop {\hbox{min} }\limits_{i = 1}^{m} \mu_{ij}^{0 - } ,\mathop {\hbox{min} }\limits_{i = 1}^{m} \mu_{ij}^{0 + } } \right],\left[ {\mathop {\hbox{max} }\limits_{i = 1}^{m} \nu_{ij}^{0 - } ,\mathop {\hbox{max} }\limits_{i = 1}^{m} \nu_{ij}^{0 + } } \right]} \right)} \hfill & {{\text{if}}\quad c_{j} \in C_{\text{II}} ,} \hfill \\ \end{array} } \right. \\ \end{aligned}$$

(36)

$$\begin{aligned} \tilde{p}_{\# j}^{0} & = \left( {\mu_{\# j}^{0} ,\nu_{\# j}^{0} } \right) = \left( {\left[ {\mu_{\# j}^{0 - } ,\mu_{\# j}^{0 + } } \right],\left[ {\nu_{\# j}^{0 - } ,\nu_{\# j}^{0 + } } \right]} \right) \\ & = \left\{ {\begin{array}{*{20}l} {\left( {\left[ {\mathop {\hbox{min} }\limits_{i = 1}^{m} \mu_{ij}^{0 - } ,\mathop {\hbox{min} }\limits_{i = 1}^{m} \mu_{ij}^{0 + } } \right],\left[ {\mathop {\hbox{max} }\limits_{i = 1}^{m} \nu_{ij}^{0 - } ,\mathop {\hbox{max} }\limits_{i = 1}^{m} \nu_{ij}^{0 + } } \right]} \right)} \hfill & {{\text{if}}\quad c_{j} \in C_{\text{I}} ,} \hfill \\ {\left( {\left[ {\mathop {\hbox{max} }\limits_{i = 1}^{m} \mu_{ij}^{0 - } ,\mathop {\hbox{max} }\limits_{i = 1}^{m} \mu_{ij}^{0 + } } \right],\left[ {\mathop {\hbox{min} }\limits_{i = 1}^{m} \nu_{ij}^{0 - } ,\mathop {\hbox{min} }\limits_{i = 1}^{m} \nu_{ij}^{0 + } } \right]} \right)} \hfill & {{\text{if}}\quad c_{j} \in C_{\text{II}} .} \hfill \\ \end{array} } \right. \\ \end{aligned}$$

(37)

The corresponding hesitation degrees are computed as follows:

$$\pi_{*j}^{0} = \left[ {\pi_{*j}^{0 - } ,\pi_{*j}^{0 + } } \right] = \left[ {1 - \mu_{*j}^{0 + } - \nu_{*j}^{0 + } ,1 - \mu_{*j}^{0 - } - \nu_{*j}^{0 - } } \right],$$

(38)

$$\pi_{\# j}^{0} = \left[ {\pi_{\# j}^{0 - } ,\pi_{\# j}^{0 + } } \right] = \left[ {1 - \mu_{\# j}^{0 + } - \nu_{\# j}^{0 + } ,1 - \mu_{\# j}^{0 - } - \nu_{\# j}^{0 - } } \right].$$

(39)

The proposed VIKOR procedure was then utilized to solve the selection problem of pilot hospitals within the IVIF environment. Analogously, a sensitivity analysis was conducted to observe the impact of different settings of the parameter $\upsilon$. The obtained results of $Q(z_{i} )$, $Z^{*}$, and the ultimate rankings are indicated in Table 6. Figure 5 presents the graphical outcomes of the sensitivity analysis, consisting of the comparative results of the remoteness-based compromise indices and the linear rankings among five candidate hospitals with respect to various $\upsilon$ values.

Table 6 Sensitivity analysis for the PAC-CVD case within the IVIF environment

Fig. 5

Sensitivity analysis within the IVIF environment. a Results of the $Q(z_{i} )$ values under different settings of the parameter $\upsilon$. b Results of the linear rankings with respective to different $\upsilon$ values

In regard to different settings of the parameter $\upsilon$ from 0 to 1, Figs. 2 and 5 demonstrate similar graphs about comparative patterns of the $Q(z_{i} )$ values and the linear rankings among the five candidate hospitals. The comparison results of the sensitivities within the IVPF and IVIF environments confirm that the obtained ranking orders are almost consistent except for the cases of $\upsilon =$ 0.1, 0.3, and 0.4. More precisely, the underlined parts in Table 6 indicate the difference between the application results of the developed approach in the IVPF and IVIF settings. As revealed in this table, the difference exists in the cases of $\upsilon =$ 0.1, 0.3, and 0.4. For $\upsilon =$ 0.1, the obtained ultimate ranking results were $\{ z_{5} \} \succ z_{4} \succ z_{3} \succ z_{1} \succ z_{2}$ (with $Z^{*} { = }\{ z_{5} \}$) and $\{ z_{5} \succ z_{4} \} \succ z_{3} \succ z_{1} \succ z_{2}$ (with $Z^{*} { = }\{ z_{4} ,z_{5} \}$) in the IVPF and IVIF contexts, respectively. For $\upsilon =$ 0.3, the ultimate ranking result based on the IVIF information was $\{ z_{5} \} \succ z_{3} \succ z_{4} \succ z_{1} \succ z_{2}$, which is slightly different from the obtained result $\{ z_{5} \} \succ z_{3} \succ z_{4} \succ z_{2} \succ z_{1}$ based on the IVPF information. For $\upsilon =$ 0.4, the obtained ultimate ranking results were $\{ z_{5} \} \succ z_{3} \succ z_{4} \succ z_{2} \succ z_{1}$ (with $Z^{*} { = }\{ z_{5} \}$) and $\{ z_{5} \succ z_{3} \} \succ z_{4} \succ z_{2} \succ z_{1}$ (with $Z^{*} { = }\{ z_{3} ,z_{5} \}$) in the IVPF and IVIF contexts, respectively. Concerning the remaining cases, the sets of ultimate compromise solutions and the ultimate ranking results of the alternatives using the proposed IVPF VIKOR method are in concordance with the results obtained by the IVIF version of the developed approach. Additionally, as depicted in Fig. 5b, the candidate hospitals z₅ and z₂ were the best ranked in the linear ranking results for $\upsilon \le 0.7$ and $\upsilon \ge 0.8$, respectively, which is in agreement with the results yielded by the IVPF VIKOR method. According to the sensitivity analysis, this paper found that the developed approach yields reasonable results and presents suitable outcomes to support decision makers in addressing MCDA problems within the IVIF environment.

4.4 Applications in other areas with a comparative discussion

It should be stressed that the IVPF VIKOR method is not only capable of solving the selection problem for hospital-based PAC-CVD in the medical and healthcare fields but can also be applied in other application areas. This subsection extends the proposed method to other fields to validate its empirical feasibility and effectiveness in potential areas. Additionally, a comparative analysis with some relevant MCDA methods within an ambiguous environment is conducted to demonstrate that the proposed method is a useful tool for fusing uncertain information and identifying a set of compromise solutions in face of a complex MCDA problem.

This paper utilizes three practical problems concerned with a risk evaluation of technological innovation in high-tech enterprises adopted from Liang et al. [26], an investment decision regarding software development projects adopted from Peng and Yang [39], and an evaluation decision of investment companies for a panel adopted from Garg [13] to conduct comparative studies. Detailed data of the weight vector $(w_{1} ,w_{2} , \ldots ,w_{n} )^{\text{T}}$ and the IVPF evaluative rating $\tilde{p}_{ij}$ in the IVPF decision matrix $\tilde{p}$ are listed in Table 7. For each application problem, the computation results of the remoteness-based multiple criteria ranking indices $S(z_{i} )$, $R(z_{i} )$, and $Q(z_{i} )$ in the case of $\upsilon$ = 0.5 (associated with a consensus or compromise attitude) are presented in Table 8. Moreover, three priority orders based on an ascending order of $S(z_{i} )$, $R(z_{i} )$, and $Q(z_{i} )$ are contrasted in this table. Taking the risk evaluation of technological innovation in high-tech enterprises for example, alternative z₁ is ranked first by $S(z_{i} )$ and fourth by $R(z_{i} )$. Conversely, alternative z₄ is ranked third by $S(z_{i} )$ and first by $R(z_{i} )$. Based on the increasing order of $Q(z_{i} )$, the priority ranking order is given as $z_{4} \succ z_{2} \succ z_{ 1} \succ z_{ 3}$, which suggests z₄ is the best choice. This result happens to be identical with that yielded by $R(z_{i} )$. It should be noted that the selection of alternative z₂ is also equitable because it is ranked second by $S(z_{i} )$, $R(z_{i} )$, and $Q(z_{i} )$. When employing the proposed IVPF VIKOR ranking procedure in Step 7, one can obtain $Z^{*} = \{ z_{2} ,z_{4} \}$ and the ultimate ranking result denoted by $\{ z_{4} \succ z_{2} \} \succ z_{1} \succ z_{3}$.

Table 7 The weight vector $(w_{1} ,w_{2} , \ldots ,w_{n} )^{\text{T}}$ and the IVPF evaluative rating $\tilde{p}_{ij}$ in the three comparative studies

Table 8 Results of the three sets of priority rankings in the three comparative studies ($\upsilon$ = 0.5)

Regarding the three application problems, Table 9 reveals the summary comparisons of the obtained results using the proposed IVPF VIKOR methodology with those yielded by the ranking method with IVPF weighted average aggregating operators [26], the IVPF TOPSIS method (i.e., an extension of Zhang and Xu’s [61] PF TOPSIS method) [26], the IVPF ELECTRE method [39], the MCDA method based on an improved accuracy function and IVPF aggregation operators [13], the MCDA method based on a classical accuracy function and IVPF aggregation operators [13], the MCDA method based on a novel accuracy function and IVIF aggregating operators [58], the MCDA method based on a new ranking method of IVIF values [11], and the IVIF TOPSIS method based on an improved score function [4]. As is well known, three broad categories of MCDA models have been widely researched: the scoring model, outranking model, and compromising model. The approaches proposed by Chen et al. [11], Garg [13, 26, 58] consider the scoring model. The IVPF ELECTRE method presented by Peng and Yang [39] belongs to the outranking model. The IVPF TOPSIS method [26], the IVIF TOPSIS method [4], and the proposed IVPF VIKOR method belong to the compromising model.

Table 9 Comparison analysis with the existing methods

For the risk evaluation problem of technological innovation in high-tech enterprises, it is easily seen from Table 9 that the ranking result of the four alternatives obtained by the proposed IVPF VIKOR method is quite similar to the results of Liang et al. [26] ranking method and the IVPF TOPSIS method. The outranking relationships among z₁, z₂, and z₃ and among z₁, z₃, and z₄ yielded by the three methods are the same; namely, $z_{2} \succ z_{ 1} \succ z_{ 3}$ and $z_{4} \succ z_{ 1} \succ z_{ 3}$. In particular, the difference is just the outranking relationship between z₂ and z₄; that is, $z_{ 2} \succ z_{ 4}$ for Liang et al.’s ranking method and $z_{4} \succ z_{2}$ for the IVPF TOPSIS method and the proposed method. The reason for this is not hard to see: Liang et al.’s ranking method is classified as the scoring model, while the IVPF TOPSIS method and the proposed method are classified as the compromising model. However, it may cause controversy because the best alternatives obtained by these methods are different. More specifically, it is confusing to conclude that z₂ is definitely superior to z₄ based on the ranking result using IVPF weighted average aggregating operators. Analogously, it is not easy to infer that z₄ is definitely superior to z₂ based on the IVPF TOPSIS method. Considering the controversial issue whether the best choice is z₂ or z₄, the proposed method suggested a set of ultimate compromise solutions, i.e., $Z^{*} = \{ z_{2} ,z_{4} \}$. Although $z_{4} \succ z_{2}$ was obtained according to an ascending order of $Q(z_{i} )$, the proposed IVPF VIKOR ranking procedure concluded that both z₂ and z₄ are the ultimate compromise solutions based on the assessment results of acceptable advantage and acceptable stability in decision making. Obviously, the conclusion of $\{ z_{4} \succ z_{2} \} \succ z_{1} \succ z_{3}$ is more reliable and reasonable than those obtained by Liang et al.’s ranking method and the IVPF TOPSIS method.

As the summary comparisons reveal in Table 9, the ultimate ranking results of the alternatives using the proposed IVPF VIKOR method are in concordance with the ranking results obtained by the comparative methods with respect to the applications to the investment decision regarding software development projects and the evaluation decision of investment companies for a panel. Concerning the application of the investment decision, the proposed method yielded the ultimate ranking result of $\{ z_{1} \} \succ z_{3} \succ z_{4} \succ z_{5} \succ z_{2}$, which is in agreement with the results of $z_{1} \succ z_{2}$, $z_{1} \succ z_{ 4}$, $z_{1} \succ z_{5}$, $z_{3} \succ z_{2}$, $z_{3} \succ z_{5}$, and $z_{4} \succ z_{2}$ obtained via Peng and Yang’s [39] IVPF ELECTRE method. Regarding the application of the evaluation decision, the ultimate ranking result of $\{ z_{2} \} \succ z_{4} \succ z_{3} \succ z_{1}$ determined by the proposed method is the same as the result of $z_{ 2} \succ z_{ 4} \succ z_{ 3} \succ z_{ 1}$ using the approaches developed by Bai [4], Chen et al. [11], Garg [13], and Ye [58]. Overall, the feasibility and effectiveness of the proposed IVPF VIKOR method have been validated through these practical applications.

It is worthwhile to mention that some outranking relationships between alternatives cannot be distinguished using the IVPF ELECTRE method. Peng and Yang [39] concluded that z₁ is superior to z₂, z₄, and z₅ according to the outranking relationships $z_{1} \succ z_{2}$, $z_{1} \succ z_{ 4}$, $z_{1} \succ z_{5}$, $z_{3} \succ z_{2}$, $z_{3} \succ z_{5}$, and $z_{4} \succ z_{2}$. However, the IVPF ELECTRE method cannot differentiate the outranking relationships between z₁ and z₃, z₂ and z₅, z₃ and z₄, and z₄ and z₅. Accordingly, the decision maker may be doubtful as to whether z₁ is the best choice because the priority orders of z₁ and z₃ cannot be confirmed via this method. In contrast, the proposed IVPF VIKOR method yielded the ultimate ranking result $\{ z_{1} \} \succ z_{3} \succ z_{4} \succ z_{5} \succ z_{2}$, which was not only in agreement with the outranking relationships obtained via the IVPF ELECTRE method but also concluded that z₁ is the ultimate compromise solution, i.e., $Z^{*} = \{ z_{1} \}$. Compared with the IVPF ELECTRE method, the proposed method can clarify the ultimate priority orders of all alternatives, which can overcome the difficulty in confusing discrimination between the outranking relationships of z₁ and z₃ and facilitate a final decision for the decision maker. Therefore, the proposed method has the capability of providing more persuasive ranking results among alternatives to aid and support decision making in practice.

Finally, this paper investigated the effect of different settings of the parameter $\upsilon$ on the ultimate ranking results among alternatives. In general, the ultimate compromise solutions yielded by the proposed IVPF VIKOR method would tend toward majority agreement and disagreement if the $\upsilon$ value increases from 0 to 1 and from 1 to 0, respectively. The sensitivity analysis of the obtained results under different settings of the $\upsilon$ value with respect to the three application problems is revealed in Table 10, which consists of the obtained results of $Q(z_{i} )$, the set of ultimate compromise solutions $Z^{*}$, and the ultimate ranking results. Concerning the comparisons among the three applications, the obtained results of $Q(z_{i} )$, $Z^{*}$, and the ultimate rankings in regard to the risk evaluation problem of technological innovation were relatively changeful. Conversely, the same results of $Z^{*}$ and steadier ultimate ranking results were acquired for the investment decision regarding software development projects and the evaluation decision of investment companies.

Table 10 Sensitivity analysis of the obtained results in other application areas

For the risk evaluation problem, when the $\upsilon$ value increases from 0 to 1, the values of Q(z₁) and Q(z₂) gradually decrease, whereas the values of Q(z₃) and Q(z₄) gradually increase. In particular, the magnitudes of the changes in Q(z₁) and Q(z₂) are significantly larger than those in Q(z₃) and Q(z₄). Six ultimate ranking results were drawn: $\{ z_{4} \} \succ z_{2} \succ z_{3} \succ z_{1}$, $\{ z_{4} \} \succ z_{2} \succ z_{1} \succ z_{3}$, $\{ z_{4} \succ z_{2} \} \succ z_{1} \succ z_{3}$, $\{ z_{2} \succ z_{1} \} \succ z_{4}$$\succ z_{3}$, $\{ z_{1} \succ z_{2} \} \succ z_{4} \succ z_{3}$, and $\{ z_{1} \} \succ z_{2} \succ z_{4} \succ z_{3}$ in the cases of $\upsilon = 0$, $\upsilon = 0.1,0.2,0.3,0.4$, $\upsilon = 0.5,0.6$, $\upsilon = 0.7$, $\upsilon = 0.8,0.9$, and $\upsilon = 1$, respectively. Moreover, four sets of ultimate compromise solutions were acquired: $\{ z_{4} \}$, $\{ z_{2} ,z_{4} \}$, $\{ z_{1} ,z_{2} \}$, and $\{ z_{1} \}$ for $\upsilon = 0,0.1, \ldots ,0.4$, $\upsilon = 0.5,0.6$, $\upsilon = 0.7,0.8,0.9$, and $\upsilon = 1$, respectively. For the investment decision problem, the values of Q(z₁) do not change and are steady at 0 regardless of the values of parameter $\upsilon$. There is a slight increase in Q(z₂) and Q(z₄) but an evident decrease in Q(z₃) and Q(z₅) in terms of increasing $\upsilon$ values. Four ultimate ranking results were derived: $\{ z_{1} \} \succ z_{4} \succ z_{3} \succ z_{2} \succ z_{5}$, ${\text{\{ }}z_{ 1} {\text{\} }} \succ z_{3} \succ z_{4} \succ z_{2} \succ z_{5}$, ${\text{\{ }}z_{ 1} {\text{\} }} \succ z_{ 3} \succ z_{4} \succ z_{ 5} \succ z_{2}$, and ${\text{\{ }}z_{ 1} {\text{\} }} \succ z_{ 3} \succ z_{5} \succ z_{4} \succ z_{2}$ in the cases of $\upsilon = 0$, $\upsilon = 0.1,0.2,0.3$, and $\upsilon = 0.4,0.5, \ldots ,0.9$, and $\upsilon = 1$, respectively. For each $\upsilon$ value, only one ultimate compromise solution was obtained, i.e., $Z^{*} = \{ z_{1} \}$. Concerning the evaluation decision problem, the values of Q(z₁) and Q(z₂) remain steady at 1 and 0, respectively, regardless of the values of $\upsilon$. The changes in Q(z₃) and Q(z₄) have common trends. To be precise, the values of Q(z₃) and Q(z₄) fall as the $\upsilon$ value increases from 0 to 1. One could obtain two ultimate ranking results consisting of $\{ z_{2} \} \succ z_{3} \succ z_{4} \succ z_{1}$ and $\{ z_{2} \} \succ z_{4} \succ z_{3} \succ z_{1}$ in the cases of $\upsilon = 0$ and $\upsilon = 0.1,0.2, \ldots ,1$, respectively. Additionally, only one ultimate compromise solution was acquired, i.e., $Z^{*} = \{ z_{2} \}$, for each $\upsilon$ value. In general, it is anticipated that a parameterized MCDA method possesses certain flexibility and adaptability by means of parameter settings to tackle diverse and varied real-world problems. As demonstrated in Table 10, the proposed IVPF VIKOR method has the capability of producing stable but flexible ranking results in different parameter values, which is essential for MCDA applications and decision-making reality.

5 Conclusions

This paper has proposed a novel VIKOR method within an uncertain environment based on IVPF sets and has applied it to MCDA for hospital-based PAC. Pilot hospitals for PAC-CVD, which is premised on holistic care, were required to develop a PAC model for patients with CVDs. The model will be implemented on the basis of their experiences treating other diseases. Additionally, because the program’s success depended on pilot hospitals, the IVPF VIKOR method has been proposed to solve problems with the selection of hospitals, and it has demonstrated the feasibility of the method through a case study. Most patients with CVDs exhibit sequelae of varying severity and therefore must undergo long-term, consistent rehabilitation to reduce the level of their disability. In summary, the findings of this study are expected to inform the development of the comprehensive and coherent care models required to facilitate rehabilitation following CVDs. More importantly, the IVPF VIKOR method can be used to select hospitals to develop PAC models for other diseases. In addition to hospital-based PAC, this paper has extended the proposed IVPF VIKOR method to a variety of fields to validate its empirical effectiveness in potential areas. Comparative discussions with other relevant MCDA methods within the uncertain environment have demonstrated the usefulness and advantages of the proposed method.

Overall, the feasibility and applicability of the proposed method have been demonstrated via the illustrative application to the selection problem of pilot hospitals in the PAC-CVD program. As opposed to the existing VIKOR methodology, the proposed method can sufficiently depict more uncertainty and ambiguity inherent in the decision-making process by utilizing the IVPF information. In addition to the IVPF environment, based on the implementation results of the sensitivities with IVIF information, the developed approach is also capable of effectively addressing IVIF evaluative ratings and producing reasonable and reliable outcomes to support decision making in the context of intuitionistic fuzziness.

It should be stressed that the developed methodology has been designed to lead to both better explanation and better applicability of MCDA because it represents a comprehensive integration of high-order uncertainties associated with a complicated real-world environment into the basic VIKOR structure. As is well known, the selection of alternatives to suit a particular MCDA objective has become more and more complicated due to increases in complexity, ambiguity, and uncertainty within the diverse and varied real-world environment. Decision makers usually confront imprecise and fuzzy circumstances in evaluating alternatives with respect to various criteria because of the subjective nature of human thinking in the practical decision-making process [24]. Based on the aforementioned applications and comparative results, it can be concluded that the proposed IVPF VIKOR method is very suitable and effective to handle an MCDA problem containing vague, uncertain, and incomplete information, especially a complicated problem involving risks and high-order uncertainties in nature. Furthermore, compared with the existing VIKOR methodology and most of the comparative approaches, the proposed method with an improved IVPF VIKOR ranking procedure is simple and easy to implement. According to the comparative discussions, it performs well with respect to ease of employment and computational efficiency but still produces reasonable and desirable results.