Self-tuned robust fractional order fuzzy PD controller for uncertain and nonlinear active suspension system

Abstract

In this paper, a self-tuned robust fractional order fuzzy proportional derivative (FO-FPD) controller is proposed for nonlinear active suspension system of a quarter car. Quarter car is a highly uncertain system as the number of riders or payload may vary. The control objective is to improve the level of ride comfort by minimizing the root mean square of vertical vibration acceleration (RMSVVA) of car body and maintaining hard constraints such as tracking force, ratio of tyre dynamic and static loads and suspension travel. The used FO-FPD controller is a nonlinear fuzzy logic controller having self-tuning capability, i.e. it changes its gains at runtime. The FO-FPD controller is realized using non-integer differentiator operator in FPD controller. The gains of FO-FPD and FPD controllers are tuned using Genetic Algorithm optimization method for a sinusoidal road surface. To evaluate the performances, extensive simulation studies were carried out and FO-FPD and FPD controllers were compared for different roads profiles such as sinusoidal, random and bump. It has been observed that FO-FPD and FPD controllers outperform passive suspension system in terms of RMSVVA and offer much better comfort ride while keeping all the hard constraint in the specified limits. Furthermore, FO-FPD controller demonstrated an excellent comfort ride, especially in uncertain environment, wherein it offered very robust behaviour as compared to FPD controller. Also, bonded-input and bounded-output stability conditions are established for overall closed loop control system by using small gain theorem.

1 Introduction

Automobile suspension system plays a vital role in providing the ride comfort to the driver along with the passengers by eliminating the undesired vibratory motion persuaded from the random road surfaces [1,2,3,4]. The classical passive suspension system (PSS) mainly consists of spring and a damper combination which fails to give appropriate corrective action under varying road conditions. It is able to improve the ride quality to a limited extent. On the other hand, active suspension system (ASS) provides additional control force for the road conditions and increases the ride comfort significantly [5]. Performance requirements for modern vehicle ASS usually comprise: (1) ride comforts, which means to isolate automobile body from road disturbances; (2) road holding capability, i.e. avoiding loss of contact between wheel and road; (3) suspension travel limitation, which is the constraint due to mechanical structure [6, 7]. It may be noted that PSS fails to achieve all these performance indices at the same time [8].

To enhance the capabilities of modern days ASS, many investigations based on adaptive control techniques, sliding mode control, H_∞ control, etc., have been reported [9, 10]. None of these methods have yielded a perfect control mechanism, thereby making the automobile system a green area of research. Scientist and engineers have used fuzzy logic controller (FLC) extensively in the field of control engineering in recent years, and a good success has been reported. It is due to its capability to establish a controller without the need of a mathematical model of process to be controlled [11,12,13]. This has been the main motivating force behind the use of FLC among the technical fraternity. FLC has been quite popular in process control, and it has also been used to control ASS [14,15,16,17]. However, if the system under consideration is nonlinear and possess highly uncertain nature FLC with adaptive and self-tuning capabilities is required. Generally, ASS possesses dynamic characteristics with nonlinearities due to spring stiffness, complexities and uncertainties which make it more difficult to design a FLC in order to manipulate such systems [10]. Therefore, this paper has been aimed to explore the application of adaptive and self-tuning FLC for the ASS.

2 Literature survey

Suspension systems significantly affect the ride quality of any vehicle. Being important they have always attracted both academia and industry researchers. Engineers and scientists have widely discussed the control issues of vehicle suspension system. Several research works have been reported in this regard and presented as follows.

In the last decade, Huang and Chao (2000) proposed FLC for a vehicle ASS to improve the ride comfort. They introduced a grey predictor to forecast the tyre deformation and filtered it from the feedback error signal. The control performance of this scheme was significantly improved [18]. Nizar et al. (2002) designed a sliding mode neural network inference FLC for a vehicle ASS to improve the ride and comfort. Simulation studies were accomplished on a quarter car model, and the results revealed that the proposed intelligent controller performed much better in comparison with conventional controllers with regard to body acceleration, tyre and suspension deflections [19]. Sharkawy (2005) presented fuzzy and adaptive fuzzy control strategies for automobiles’ ASS in order to provide effortless vertical motion of car body so as to attain the road holding and riding comfort over a wide range of road profiles. Simulation results showed the effectiveness of FLC over optimal linear quadratic regulator [20]. Cao et al. (2008) proposed a novel adaptive FLC based on interval type-2 fuzzy logic for nonlinear quarter car ASS. Numerical example clearly demonstrated that adaptive FLC based on type-2 fuzzy outperforms conventional FLC and PSS [21].

Recently, Lin and Lian (2011) studied a self-organizing fuzzy controller (SOFC) and found that it is difficult to select the learning rate and weighting distribution in the SOFC. In view of that they developed a hybrid self-organizing fuzzy and radial basis-function neural-network controller (HSFRBNC). It uses a radial basis-function neural network to regulate in real time the parameters of the SOFC so as to gain optimal values. Performances of the controllers were evaluated for an ASS. Simulation results revealed that the HSFRBNC outperformed SOFC in terms of ride comfort [22]. Chiou et al. (2012) presented a novel method for determining the gains of optimal fuzzy PID controller using the particle swarm optimization reinforcement evolutionary algorithm for ASS. Presented numerical results indicated that the fuzzy PID controller shows much better control performance as compared to conventional optimal linear feedback control method and provides a noticeable improvement in ride comfort and vehicle stability [23]. Further, Hacioglu and Yagiz (2013) presented a PD + PI type FLC with sliding surface to control an ASS. It consisted of two parts, i.e. fuzzy PD and fuzzy PI components. Inputs to these FLCs were the sliding surface functions and their derivatives. As per the simulation results, proposed FLC demonstrated better control performance as compared to conventional PID controller in terms of vibration isolation of vehicle body [24]. Lin and Lian (2013) developed a grey-prediction self-organizing fuzzy controller (GPSOFC) for ASS. They presented a grey-prediction procedure into an SOFC, to pre-correct its fuzzy rules for the control of ASS. It solved the problem of SOFCs with improperly selected parameters. Experimental results showed that GPSOFC outperformed SOFC and PSS [25]. Wang et al. (2015) proposed a fuzzy PID control scheme based on improved cultural algorithm to reduce the vertical vibration caused in a quarter car model by road disturbances from uneven road surfaces acting on tyre. The cultural algorithm is a two-level evolution mechanism and can be considered a Meta-Evolutionary Algorithm. Simulation results demonstrated that the ASS with fuzzy PID control scheme optimized by improved cultural algorithm considerably improved the ride comfort by suppressing the vertical vibration acceleration [26]. Bououden et al. (2016) proposed a novel technique for designing robust multivariable predictive control using the Takagi–Sugeno fuzzy approach for nonlinear ASS. Simulation outcomes demonstrated the effectiveness of proposed approach over model predictive control [27].

Control engineers always desire more tunable parameters in a controller in order to increase its degree of freedom. Large tunable parameters help them to further increase the robustness of controller so that it can track the reference set point tightly and do not deviate from it under uncertain environment or condition. Generally, FLC is realized using mathematical operators such as the differentiator and integrator. Recently, in the literature related to control engineering, a more malleable option of this operator, fractional order operator $d^{\mu } /{\text{d}}t^{\mu }$, where µ is non-integer, has been used. Using this mathematical operator, the control algorithm became quite famous and is known as a fractional order control among researchers and engineers [28, 29]. Recently, Das et al. (2012) presented a fractional order fuzzy PID controller without adaptive feature. Simulation studies were performed to control a delayed nonlinear system and an open loop unstable system with dead time. They observed that the proposed fractional order fuzzy PID controller demonstrated much superior performance as compared to other controllers [30]. Further, Mishra et al. (2015) proposed a Takagi–Sugeno model-based fractional order fuzzy PID controller with self-tuning features. The performance of proposed controller was assessed by controlling a nonlinear and uncertain binary distillation column. Simulation outcomes clearly showed that fractional order fuzzy PID controller outperformed integer order fuzzy PID controller in servo as well as regulatory mode in terms of integral of absolute error [31]. Various other recent applications of fractional order control systems have also been stated in the literature, such as control of two-link manipulator [32], control of automatic voltage regulator [33] and hybrid electric vehicle [34].

Literature survey presented above clearly indicates that an application of fractional order operators brings several advantages to the control scheme. Generally, it increases the robustness of a feedback control system. The performance of FLC can be further enhanced by using the fractional order operators. Furthermore, the strength of FLC with fractional order operators can be further enriched by incorporating adaptive or self-tuning features in it. In the present work, a robust fractional order fuzzy proportional derivative (FO-FPD) controller is proposed to control the ASS of quarter car model, wherein the main control objective is to minimize the root mean square of vertical vibration acceleration (RMSVVA) so as to achieve the road holding and riding comfort over a broad range of road surfaces. It is implemented in a position form. The FO-FPD controller is simply derived by swapping the integer order operators, i.e. differentiator with non-integer order operators from the fuzzy PD (FPD) controller presented in [35,36,37]. The gains of FO-FPD and FPD controllers are optimized using Genetic Algorithm (GA). The performances of fuzzy controllers are assessed in simulation for road disturbances such as sinusoidal, random and bump road surfaces under model uncertainties. Also, BIBO stability analysis is performed using small gain theorem, and adequate stability conditions are determined for FO-FPD and FPD controllers.

The paper is organized as follows. After an introduction in the first section, the brief literature survey of the related work is presented in Sect. 2, and the problem formulation, dynamic model of nonlinear ASS and problem statement is presented in Sect. 3. In Sect. 4, design and execution of FO-FPD and FPD controllers are presented along with their tuning criterion. Realization aspects of the fractional order operator have also been discussed in this section along with the controller gains optimized using GA for sinusoidal road input. In Sect. 5, performance comparison of FO-FPD and FPD controllers for road profiles, i.e. sinusoidal, random and bump road surfaces under model uncertainties, is carried out and presented. BIBO stability analysis of the closed loop control system is accomplished in Sect. 6. Finally, conclusions of the proposed work are drawn in Sect. 7.

3 Mathematical model and problem formulation

In this section, dynamic modelling of uncertain ASS is presented along with the problem statement and the performance requirements for vehicle ASS.

3.1 Dynamic model of a nonlinear active suspension system

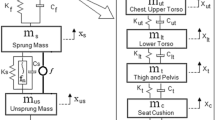
In the present work, the nonlinear quarter car suspension model shown in Fig. 1 is considered for study on the body vertical vibration caused by bumpy road [7, 10]. Here m _s is the sprung mass, which is the mass of car body; m _u is the unsprung mass, which denotes the mass of wheel assembly; Z _s , Z _u and Z _r are the displacement of car body, wheel and road, respectively; b _c and k _s are the damping and stiffness coefficients of the suspension system, respectively; b _t and k _t represents the damping and compressibility coefficients of the used pneumatic tyre, respectively; f _a is the control action for the suspension system.

Fig. 1

Quarter car model

According to Newton’s second law and free body diagram approach, the dynamic equations of the sprung and unsprung masses are as follows:

$$ m_{s} \ddot{Z}_{s} = - b_{c} \left( {\dot{Z}_{s} - \dot{Z}_{u} } \right) - k_{s} \left( {Z_{s} - Z_{u} } \right) + k_{sn} \left( {Z_{s} - Z_{u} } \right)^{3} + f_{a} $$

(1)

$$ m_{u} \ddot{Z}_{u} = b_{c} \left( {\dot{Z}_{s} - \dot{Z}_{u} } \right) + k_{s} \left( {Z_{s} - Z_{u} } \right) + k_{sn} \left( {Z_{s} - Z_{u} } \right)^{3} + b_{t} \left( {\dot{Z}_{r} - \dot{Z}_{u} } \right) + k_{t} \left( {Z_{r} - Z_{u} } \right) - f_{a} $$

(2)

where k _sn is the stiffness coefficient of nonlinear term in suspension system, $\ddot{Z}_{s}$ and $\dot{Z}_{s}$ are the vertical acceleration and speed of sprung mass or car body, respectively; $\ddot{Z}_{u}$ and $\dot{Z}_{u}$ are the vertical acceleration and velocity of unsprung mass or wheel assembly, respectively; ($Z_{s} - Z_{u}$) is the suspension deflection; and $\left( {Z_{u} - Z_{r} } \right)$ is the tyre deflection.

Generally, mass of car body $m_{s}$ varies as the number of passengers changes, leading to the variation in payload. It may also be noted that the variations in the sprung mass $m_{s}$ introduce the uncertainty in the system.

3.2 Problem statement

The following aspects are considered in terms of performance requirement for ASS while designing the controller [7, 10].

3.2.1 Ride comfort

While designing ASS, the main task for the researchers and engineers has always been to improve the level of ride comfort for the passenger in the car. This means that one has to design a controller which can successfully stabilize vertical motion of car body and to segregate the vibrations pass on to the passenger as well, in the presence of parametric uncertainty and nonlinearity.

3.2.2 Road holding

Car safety is another most important aspect for the design engineer. It needs to make sure that there is a firm uninterrupted contact of wheels to road, and also the dynamic tyre load should be as small as possible, i.e.

$$ \left| {F_{t} + F_{b} } \right| < \left( {m_{s} + m_{u} } \right)g\quad {\text{or}}\quad \frac{{\left| {F_{t} + F_{b} } \right|}}{{\left( {m_{s} + m_{u} } \right)g}} < 1 $$

(3)

where $F_{t}$ and $F_{b}$ are the elasticity and damping forces of the tyre. Also, the ratio of tyre dynamic load and static load must be less then unity. These forces are defined as

$$ F_{t} = k_{t} \left( {Z_{u} - Z_{r} } \right) $$

(4)

$$ F_{b} = b_{t} \left( {\dot{Z}_{u} - \dot{Z}_{r} } \right) $$

(5)

3.2.3 Suspension movement limitation

Since ASS is a mechanical structure one cannot exceed the suspension space beyond the allowable limit, which can be described as

$$ \left| {Z_{s} - Z_{u} } \right| \le Z_{\hbox{max} } , $$

(6)

3.2.4 Actuator saturation

Generally, an actuator will have an upper limit on the amplitude of force it can provide, i.e.

$$ f_{a} \le f_{a,\hbox{max} } $$

(7)

Based on the above defined ride comfort, road holding, suspension movement limitation and the actuator saturation, the control problem is formulated as described in next subsection.

3.2.5 Problem formulation

For ASS, described by the dynamic model, Eqs. (1) and (2), one should synthesize the control action $f_{a}$ in order to stabilize the vertical motion of sprung mass, i.e. car body in closed loop in the presence of parameter uncertainty, nonlinearity, external disturbance and noise. The essential performance requirement is the minimization of RMS of vertical vibration acceleration (m/s²) in view of ride comfort, while maintaining the other three features as hard constraints. The quarter car parameters and corresponding extreme limits of the hard constraints are given in Table 1 along with the used solver details.

Table 1 Model and simulation parameters of active suspension system

4 Design and implementation of FO-FPD and FPD controllers

FO-FPD controller is an improved form of the FPD controller as presented in [35,36,37]. In the present work, FPD controller is realized by discretizing its counterpart conventional PD controller using backward difference method in contrast to bilinear transformation in [35,36,37]. Therefore, in this work, FPD is realized in the position form as compared to velocity form in [35,36,37]. It is a nonlinear fuzzy PD controller with variable gains having adaptive or self-tuning capability. It may be noted that FO-FPD is obtained using non-integer order differentiator operator while FPD is achieved using integer order differentiator operator. The FPD controller is discussed in more detail in [35,36,37]. In the subsequent sections, design and implementation of FO-FPD and FPD controllers are presented.

4.1 Fractional order fuzzy PD controller

In this section, design of FO-FPD controller is presented. The backward difference method is used to transform the conventional PD controller from s-domain to z-domain. The structure of FO-FPD is shown in Fig. 2. Inputs to the FO-FPD controller are error e and rate of the change of error r, while $u_{{{\text{FO}} - {\text{FPD}}}}$ is a direct output obtained from FO-FPD. Also, $K_{e}$, $K_{r}$, $K_{u}$ are the scaling factors of FO-FPD controller, and $\mu$ is the fractional power of fractional order differentiator operator ($d^{\mu } /{\text{d}}t^{\mu }$) required to get the rate of the change of error r as shown in Fig. 2. The linguistic variables, i.e. e and r are described by two membership functions (MF), viz. ‘Positive (p)’ and ‘Negative (n)’. The two MFs are characterized by an adjustable parameter ‘L’ and are evenly described in the universe of discourse as shown in Fig. 3. Singleton MFs namely ‘Positive (op)’, ‘Zero (oz)’ and ‘Negative (on)’are considered for output variable, i.e. $u_{{{\text{FO}} - {\text{FPD}}}}$, as shown in Fig. 4. Parameter L is an adjustable constant. Further, four control rules, max–min inference mechanism and for defuzzification centre of mass technique has been considered [35,36,37]. The fuzzy control rules are as follows:

$$ R^{1} :IF\;K_{e} e\left( {nT} \right)is\;\varvec{n}\;AND\;K_{r} r\left( {nT} \right)\;{\text{is}}\;\varvec{n}\;{\text{THEN}}\;u_{{{\text{FO}} - {\text{FPD}}}} / u_{\text{FPD}} \;{\text{is}}\;\varvec{on} $$

$$ R^{2} :IF\;K_{e} e\left( {nT} \right)\;is\;\varvec{n}\;AND\;K_{r} r\left( {nT} \right)\;{\text{is}}\;\varvec{p}\;{\text{THEN}}\;u_{{{\text{FO}} - {\text{FPD}}}} / u_{\text{FPD}} \;{\text{is}}\;\varvec{oz} $$

$$ R^{3} :IF\;K_{e} e\left( {nT} \right)\;is\;\varvec{p}\;AND\;K_{r} r\left( {nT} \right)\;{\text{is}}\;\varvec{n}\;{\text{THEN}}\;u_{{{\text{FO}} - {\text{FPD}}}} / u_{\text{FPD}} \;{\text{is}}\;\varvec{oz} $$

$$ R^{4} :IF\;K_{e} e\left( {nT} \right)\;is\;\varvec{p}\;AND\;K_{r} r\left( {nT} \right)\;{\text{is}}\;\varvec{p}\;{\text{THEN}}\;u_{{{\text{FO}} - {\text{FPD}}}} / u_{\text{FPD}} \;{\text{is}}\;\varvec{op} $$

Fig. 2

FO-FPD control system

Fig. 3

Input membership functions

Fig. 4

Output membership functions

Also, the entire two-dimensional input space formed by input linguistic variables, i.e. e and r is divided in 20 input combinations (IC) regions as shown in Fig. 5. The formula applicable for each IC region is listed in Table 2. Based upon the input point position, i.e. (e, r) in input space, the formulae assigned for each IC regions, as tabulated in Table 2, calculates the control signal for FO-FPD. The control surface graph between inputs and output is depicted in Fig. 6. The output of FO-FPD is defined as:

$$ u_{{{\text{FO}} - {\text{FPD}}}}^{'} = K_{u} u_{{{\text{FO}} - {\text{FPD}}}} $$

(8)

From Table 2, output of FO-FPD controller is

$$ u_{{{\text{FO}} - {\text{FPD}}}} = \frac{{LK_{e} }}{{2\left[ {2L - \left| {K_{e} e} \right|} \right]}}e + \frac{{LK_{r} }}{{2\left[ {2L - \left| {K_{e} e} \right|} \right]}}r $$

(9)

Fig. 5

Input combination regions

Table 2 Analytical formulae for $u_{{{\text{FO}} - {\text{FPD}}}}$/$u_{\text{FPD}}$ for the 20 IC regions [35,36,37]

Fig. 6

FO-FPD/FPD controller surface

From Eq. (9), it is clear that FO-FPD controller shows a self-tuning behaviour, i.e. when the error ‘e’ increases, the controller gains $\frac{{LK_{e} }}{{2\left[ {2L - \left| {K_{e} e} \right|} \right]}}$ and $\frac{{LK_{r} }}{{2\left[ {2L - \left| {K_{e} e} \right|} \right]}}$ also increases automatically. Table 2 also reveals that the coefficients of input signal of FO-FPD controller change with e and r, respectively, and demonstrate variable nature. Therefore, FO-FPD controller is a nonlinear and adaptive controller with variable gains.

4.2 Fuzzy PD controller

The structural design of FPD controller is similar to the FO-FPD controller, and the configuration of FPD controller was realized by substituting the values of fractional power of fractional order differentiator operator ‘$\mu$’ as unity in FO-FPD controller. Thus, the control action of FPD controller is defined as:

$$ u_{\text{FPD}}^{'} = K_{u} u_{\text{FPD}} $$

(10)

4.3 Fractional order operators

Traditional PID controller has been the most popular controller in process industry. It uses integer order differentiator and integrator for its realization. Fractional order control is an emerging area in the field of control engineering, and many potential research works have been reported in the literature in this regard. To some extent, one can enhance the capability of conventional PID controller by using the non-integer order differentiator and integrator operators. Also, a differentiator is required to realize the FLC in position form, and its robustness can be further increased by utilizing the non-integer order differentiator.

Several approaches of fractional order integration and differentiation have been reported in the literature [28, 29, 38, 39]. In the present work, fraction order differentiator ($d^{\mu } /{\text{d}}t^{\mu }$) was implemented using Grünwald–Letnikov (G–L) fractional derivative definition which is briefly given as follows:

$$ {}_{a}^{ } D_{t}^{\mu } f\left( t \right) = \mathop {\lim }\limits_{h \to 0} \frac{1}{{h^{\mu } }}\mathop \sum \limits_{i = 0}^{{\left[ {\left( {t - a} \right)/h} \right]}} \left( { - 1} \right)^{i} \left( {\begin{array}{*{20}c} \mu \\ i \\ \end{array} } \right)f\left( {t - ih} \right) $$

(11)

where D is the mathematical operator (differentiator/integrator), t and a are the limits, $\mu$ is the order of the operation, h is the step size assumed to be very small, and $\left( {\begin{array}{*{20}c} \mu \\ i \\ \end{array} } \right) = \frac{{\left( \mu \right)\left( {\mu - 1} \right)\left( {\mu - 2} \right) \ldots \left( {\mu - i + 1} \right)}}{{\Gamma \left( {i - 1} \right)}}.$

The fractional order operators were implemented in discrete form. The derivative operator ‘s’ is transformed in z-domain by backward difference method, i.e. $s = \left( {1 - z^{ - 1} } \right)/T$; where $T$ is the sampling time. Further, expanding the backward difference equation binomially for fractional order operator ($s^{\mu }$).

$$ s^{\mu } = \left( {\frac{{1 - z^{ - 1} }}{T}} \right)^{\mu } = T^{ - \mu } \mathop \sum \limits_{i = 0}^{\infty } \left( { - 1} \right)^{i} \frac{{\left( \mu \right)\left( {\mu - 1} \right)\left( {\mu - 2} \right) \ldots \left( {\mu - i + 1} \right)}}{{\Gamma \left( {i - 1} \right)}}z^{ - i} $$

(12)

Therefore, the differentiator operator ‘$D$’ in discrete time can be expressed as

$$ D^{\mu } = T^{ - \mu } \mathop \sum \limits_{i = 0}^{\infty } \left( { - 1} \right)^{i} \left( {\begin{array}{*{20}c} \mu \\ i \\ \end{array} } \right)z^{ - i} $$

(13)

or

$$ D^{\mu } = T^{ - \mu } \mathop \sum \limits_{i = 0}^{\infty } b_{i} z^{ - i} ;\quad {\text{where}}\quad b_{i} = \left( { - 1} \right)^{i} \left( {\begin{array}{*{20}c} \mu \\ i \\ \end{array} } \right) $$

(14)

Binomial coefficient ‘$b_{i}$’ can be further simplified to subsequent recursive algorithm.

$$ b_{i} = \left( {1 - \frac{1 + \mu }{i}} \right)b_{i - 1} ;\quad i = 1,2,3, \ldots \quad {\text{and }}b_{0} = 1 $$

(15)

Therefore, the fractional order differentiator/integrator of a sequence $f\left[ n \right]$ is defined as

$$ D^{\mu } \left( {f\left[ n \right]} \right) = T^{ - \mu } \mathop \sum \limits_{i = 0}^{\infty } b_{i} f\left[ {n - i} \right] $$

(16)

From above equation, it is clear that in order to implement the fractional order operator, one has to calculate and store infinite number of coefficients. Therefore, short memory concept was introduced to realize these fractional order mathematical operators. Now, one has to calculate and store in memory only last few values. In the present study, a short memory of 100 was considered. Eq. 16 can be further simplified as:

$$ D^{\mu } \left( {f\left[ n \right]} \right) = T^{ - \mu } \mathop \sum \limits_{i = 0}^{100} b_{i} f\left[ {n - i} \right] $$

(17)

4.4 Optimization of FO–FPD and FPD controller gains

Tuning of gains of a controller plays significant role in its performance. Conventional controllers have several popular methods for tuning of their gains, but there is no such specified method available in the literature for tuning of intelligent controllers. Therefore, researchers are using various optimizing techniques to achieve this goal with a customized performance index. With the help of optimizing techniques, one can effectively tune any linear, nonlinear and intelligent controllers with large number of gains and for any combinations of performance indices.

In the present work, GA, developed by Goldberg [40], is used to optimize the gains of FO-FPD and FPD controllers in closed loop. GA is a heuristic search-based optimization method that mimics the procedure of natural evolution. GA is a specific class of evolutionary algorithms that use methods motivated by evolutionary biology such as inheritance, mutation, selection and crossover. For optimization, 20 is considered the size of population; 100 is kept as the maximum number of iterations, and 10⁻⁶ is retained as the tolerance level. The flow chart of GA is shown in Fig. 7.

Fig. 7

Genetic Algorithm—flow chart

4.4.1 Objective function and fitness function

The RMSVVA value defined below is selected as the cost function to be minimized. For better ride comfort of the car, one would require a small value of the RMSVVA (m/s²).

$$ J = \sqrt {\frac{1}{N}\mathop \sum \limits_{t = 1}^{N} \left| {\ddot{Z}_{s} } \right|^{2} } $$

(18)

where N is the number of sampling points.

In the present study, for tuning of fuzzy controllers, a sinusoidal road disturbance, i.e. $Z_{r} = 0.005\sin \left( {2\pi t} \right)$ in metres, is considered. It is a commonly used road surface in the literature. The cost function versus generation curve of FO-FPD and FPD controllers for sinusoidal road profile is shown in Fig. 8, and the corresponding cost functions, i.e. RMSVVA, are compared in Fig. 9. The optimized gains of fuzzy controllers are tabulated in Table 3.

Fig. 8

Cost function versus generation curve

Fig. 9

Comparison of RMS of vertical vibration acceleration

Table 3 Optimized gains of FO-FPD and FPD controllers

Further, in the following section, the performance of FO-FPD and FPD controllers is assessed for different road profiles. Also, the optimized controllers have been subjected to robust testing under model uncertainty.

5 Results and discussions

The objective of this work is to better the ride quality of the vehicle. Since the ride comfort is related to the vertical vibration acceleration felt in the automobile, therefore, an ultimate goal has been to decrease the vertical acceleration while maintaining the hard constraint within their prescribed limits. Extensive simulations were carried out to critically evaluate the performances of ASS having fuzzy controllers with PSS. The controllers were tested for various road surface profiles, such as sinusoidal, bump and random, and their impact on model uncertainties was also investigated. The optimized gains of FO-FPD and FPD controllers for sinusoidal road input were kept unchanged throughout the simulation studies, i.e. for other road profiles under consideration. The constraints for force and maximum suspension travel are taken as 5000 N and 0.15 m, respectively. Simulations are carried out using National Instrument^® software, LabVIEW™ 8.6 and its add-ons “Simulation and Control Design Toolkit”. Simulation configuration parameters are tabulated in Table 1. In the present work, ordinary differential equation solver, Runge–Kutta 4 with a fixed step size of 1 ms, is used.

5.1 Sinusoidal road profile

This kind of road surface is quite common in our day-to-day life, and therefore, for ride comfort study, it is a perfect road input. That is why it was considered to tune the gains of FO-FPD and FPD controllers. For sinusoid profile, the variation in body vertical displacement, vertical vibration acceleration and tyre deflection is plotted in Fig. 10a–c. It can be observed that FO-FPD and FPD controllers demonstrate very good performance as compared to PSS by significantly reducing the vertical vibration acceleration along with body vertical displacement and thus providing much superior ride comfort. Out of the fuzzy controllers, FO-FPD controller is able to further reduce RMSVVA by 5.4 times than FPD controller as shown in Fig. 9. Thus, FO-FPD controller shows much better performance as compared to FPD controller. It may be noted that both FO-FPD and FPD controllers are able to retain the three constraints, i.e. tracking force, ratio of tyre dynamic load and static load and suspension travel within specified limits, as depicted in Figs 10d–f.

Fig. 10

Performance for sinusoidal road surface: a vehicle body vertical displacement; b vehicle body vertical vibration acceleration; c tyre deflection; d tracking force; e ratio between tyre dynamic load and static load; f suspension travel

Further, it has been observed that during sinusoidal road profile, input point location, i.e. (e, r) lies in IC region 1–8. The variations of coefficients of e and r for FO-FPD and FPD controllers in the course of sinusoidal road surface are presented in Fig. 11. From Fig. 11, it is clear that FO-FPD and FPD controllers possess adaptive nature.

Fig. 11

Variation of coefficients of e and r for sinusoidal road surface: a coefficient of e; b coefficient of r

5.1.1 Model uncertainty

In automobiles, uncertainties in ASS and/or modelling errors generally are unavoidable. These may worsen the performance of ASS when the uncertainties are not particularly taken into account. Usually, uncertainty may arise in ASS due to variations in number of passenger. Also, sensor noise may be another source of uncertainty. Effects of these uncertainties on quarter car ASS are presented in detail in the subsequent sections.

5.1.1.1 Sprung mass uncertainty

Change in payloads leads to variations in sprung mass of vehicle. This unavoidable uncertainty carries substantial difficulties for the controller intended to provide a comfort ride under various hard constraints. Thus, overall the ASS will act as an uncertain nonlinear system. In the present work, sprung mass was varied from 400 to 800 kg for sinusoidal road profile and the corresponding variation in RMSVVA against the sprung mass variation is shown in Fig. 12. It has been observed that once the sprung mass increases or decreases from its normal value, i.e. 600 kg, and the significant growth in RMSVVA is noted in the performance of FPD in comparison with FO-FPD controller which shows negligible variations in RMSVVA and thus provides much better ride comfort in the presence of uncertainty. The variations in vertical acceleration for sprung mass of 400 and 800 kg are shown in Fig. 13a, b.

Fig. 12

RMS of vertical acceleration for variation in sprung mass from 400 to 800 kg for sinusoidal road surface

Fig. 13

Vehicle body vertical acceleration for sinusoidal road surface: a for sprung mass of 400 kg; b for sprung mass 800 kg

5.1.1.2 Sensor noise uncertainty

Noise is an integral part of every control and measurement system. It disturbs the decision-making ability of any controller in the plant as it embodies uncertainty in the controlled variable and control action. In the present work, to test the sensor noise suppression capability of the fuzzy controllers under study, sensor noise (in %) was included in the sprung mass displacement as follows:

$$ Z_{s} = Z_{s} + \left( {noise\,in\, \% } \right)*Z_{r} *random\left( { - 1,1} \right) $$

(19)

Noise amplitude was varied from $10^{ - 4}$ to $10^{ - 2}$% in the sprung mass displacement ($Z_{s}$). The variation in RMSVVA against the sensor noise is plotted in Fig. 14. It has been revealed that as the noise increases, RMSVVA significantly increases in FPD controller as compared to FO-FPD controller, where nominal changes were detected. Thus, FO-FPD controller outperformed FPD controller and offered superior ride comfort to the passengers in the vehicle. Hence, again FO-FPD controller demonstrated robust behaviour under uncertainty and strongly recommends its candidature as a robust controller. The variation in vertical acceleration for 0.005% sensor noise is depicted in Fig. 15.

Fig. 14

RMS of vertical acceleration for variation in sensor noise amplitude from 0.0001 to 0.01% for sinusoidal road profile

Fig. 15

Vertical acceleration for 0.005% sensor noise for sinusoidal road profile

5.2 Random road surface

Generally road surface has a random nature. Mathematically, this profile can be assumed as random profiles, which is represented by power spectrum density (PSD) [26]. The road roughness can be observed as a stationary process in space domain and the PSD of the road roughness disturbance input can be stated as

$$ G_{q} \left( n \right) = \frac{1}{v}G_{q} \left( {n_{0} } \right)\left( {\frac{n}{{n_{0} }}} \right)^{ - W} $$

(20)

where $n$ is the spatial frequency, $n_{0}$ is the reference spatial frequency which is defined by $n_{0} = 0.1$ (1/m), $G_{q} \left( {n_{0} } \right)$ represents the road roughness coefficient, and $W = 2$ is the road roughness constant. Associated to the frequency f, one can have $f = nv$ with $v$ for car forward velocity. Based on Eq. (20), one can attain the PSD of ground displacement as

$$ G_{q} \left( f \right) = G_{q} \left( {n_{0} } \right)n_{0}^{2} \left( {\frac{v}{{f^{2} }}} \right) $$

(21)

Accordingly, the PSD of ground velocity is specified by

$$ G_{{\dot{q}}} \left( f \right) = \left( {2\pi f} \right)^{2} G_{q} \left( f \right) $$

(22)

Substituting $G_{q} \left( f \right)$ from Eq. (21) in Eq. (22), one get

$$ \begin{aligned} G_{{\dot{q}}} \left( f \right) & = \left( {2\pi f} \right)^{2} G_{q} \left( {n_{0} } \right)n_{0}^{2} \left( {\frac{v}{{f^{2} }}} \right)\quad {\text{or}} \\ G_{{\dot{q}}} \left( f \right) & = 4\pi^{2} G_{q} \left( {n_{0} } \right)n_{0}^{2} v \\ \end{aligned} $$

(23)

Assuming the car velocity is constant, the PSD function $G_{{\dot{q}}} \left( f \right)$ can be calculated, and it is represent by $D_{n}$. Therefore, the road contour can be stated as follows:

$$ x\left( t \right) = D_{n}^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} \smallint w\left( t \right){\text{d}}t $$

(24)

where $w\left( t \right)$ is the white noise.

To generate the random road profile constant, car forward velocity of $v = 20$ m/s and the grade of road as D, which corresponds to a poor grade of road surface according to ISO2361 standard, was considered. The corresponding road roughness coefficient $G_{q} \left( {n_{0} } \right)$ is 64 × 10⁻⁶ and $D_{n}$ is 5.05 × 10⁻⁴. The road roughness for grade D can be given by

$$ x\left( t \right) = 0.022\smallint w\left( t \right){\text{d}}t $$

(25)

By calculation, the road profile of grade D in time domain is shown in Fig. 16.

Fig. 16

Random road grade D in time domain

Now, for further assessing the performance of fuzzy controllers tuned for sinusoidal road input, a random road surface of poor road grade as shown in Fig. 16 is introduced in closed loop. The variation in vehicle body vertical displacement, vertical acceleration and tyre deflection is depicted in Fig. 17a–c. Again, it can be noted that fuzzy controllers outperform PSS in suppressing the vertical displacement and acceleration considerably and offer a ride of greater comfort. The values of RMSVVA for random road input are compared in Fig. 18. The RMSVVA of FO-FPD controller is 0.105863, in contrast to 0.165509 in case of FPD controller and 0.485473 in case of PSS. Thus, FO-FPD controller will offer a better comfort ride. Further, it has been revealed that both the fuzzy controllers are able to maintain the hard constraints such as tracking force, ratio of tyre dynamic load and static load and suspension travel well within the prescribed limit as shown in Fig. 17d–f.

Fig. 17

Performance for random road profile: a vehicle body vertical displacement; b vehicle body vertical vibration acceleration; c tyre deflection; d tracking force; e ratio between tyre dynamic load and static load; f suspension travel

Fig. 18

Comparison of RMS vertical vibration acceleration for random road profile

5.2.1 Model uncertainty

As mentioned earlier, variation in the number of passengers in the vehicle leads to uncertainty in the sprung mass. Also, measurement noise can act as a source of uncertainty in the system. In the following sections, to assess the capability of fuzzy controllers tuned for sinusoidal road input, a random road input was tested in the closed loop and effect of model uncertainty on ride comfort was investigated.

5.2.1.1 Sprung mass uncertainty

In order to study the effect of model uncertainty on the ride comfort of passengers in the car, the sprung mass was varied from 400 to 800 kg for random road input and corresponding RMSVVA was recorded. RMSVVA for sprung mass varying from 400 to 800 kg is shown in Fig. 19. It has been revealed from Fig. 19 that as one would move away from the normal value of sprung mass, i.e. 600 kg, and the RMSVVA considerably increases in case of FPD controller, while for FO-FPD controller, a negligible change was observed. Thus, FO-FPD controller provides a much better comfort ride as compared to FPD controller under model uncertainty in sprung mass. Figure 20a, b presents the variations in vertical acceleration for sprung mass 400 and 800 kg. Also, fuzzy controllers are able to restrict the hard constraints well within their prescribed limits.

Fig. 19

RMS of vertical acceleration for variation in sprung mass from 400 to 800 kg for random road surface

Fig. 20

Vehicle body vertical acceleration for random road profile: a for sprung mass of 400 kg; b for sprung mass 800 kg

5.2.1.2 Sensor noise

Again, sensor noise (in %) was introduced in the sprung mass displacement as described by Eq. 19. The amplitude of measurement noise was varied from $10^{ - 4}$ to $10^{ - 2}$% in the vehicle body vertical displacement and the corresponding variation in RMSVVA against the measurement noise is shown in Fig. 21. It can be observed from the Fig. 21 that once the amplitude of sensor noise increases, the corresponding RMSVVA increases rapidly for FPD controller as compared to FO-FPD controller. Therefore, FO-FPD controller demonstrated quite robust behaviour and will provide an excellent comfortable ride under measurement noise uncertainty. The variation in vertical acceleration for 0.005% measurement noise is shown in Fig. 22.

Fig. 21

RMS of vertical acceleration for variation in sensor noise amplitude from 0.0001 to 0.01% for random road profile

Fig. 22

Vertical acceleration for 0.005% sensor noise for random road profile

5.3 Bump road surface

A very common bumpy road surface given by

$$ Z_{r} \left( t \right) = \left\{ {\begin{array}{*{20}l} {\frac{A}{2}\left( {1 - { \cos }\left( {\frac{2\pi v}{L}} \right)t} \right)},& {0 \le t \le \frac{L}{v},} \\ 0,& t > \frac{L}{v}, \\ \end{array} } \right. $$

(26)

where L and A are the length and the height of the bump, respectively, and $v$ is the car forward velocity. In the current work, $A = 0.1$ m, $L = 5$ m and $v = 20$ m/s are considered.

Now, again the gains of fuzzy controllers were kept unchanged and bump road profile as disturbance is introduced in the closed loop control system. The variations in car body vertical displacement, vertical acceleration and tyre deflection are shown in Fig. 23a–c, and their RMS value of vertical acceleration is compared in Fig. 24. Once again, in this case also FO-FPD and FPD controllers offer excellent comfort ride as compared to PSS and maintained the hard constraints such as tracking force, ratio of tyre dynamic load and static load and suspension travel well within the given limit as shown in Fig. 23d–f. FO-FPD controller showed RMSVVA of 0.0142981 and in case of FPD controller and PSS, it is 0.602041 and 1.01185, respectively. Also, here too FO-FPD controller demonstrated better comfort ride between both fuzzy controllers.

Fig. 23

Performance for bump road surface: a vehicle body vertical displacement; b vehicle body vertical vibration acceleration; c tyre deflection; d tracking force; e ratio between tyre dynamic load and static load; f suspension travel

Fig. 24

Comparison of RMS of vertical vibration acceleration for bump road profile

5.3.1 Model uncertainty

In order to study the robustness of FO-FPD and FPD controllers on a bump road, the performance of these controllers against model uncertainties was investigated in terms of variation in number of passengers in car and measurement noise.

5.3.1.1 Sprung mass uncertainty

The sprung mass was varied from its normal value, i.e. 600–400 and 800 kg, respectively, and the corresponding RMSVVA is plotted in Fig. 25. The significant changes of RMSVVA in case of FPD controller are observed as the sprung mass is decreased and increased from its normal value, while for FO-FPD controller, a very small change was noted. Therefore, FO-FPD controller delivers much superior comfort ride as compared to FPD controller, under model uncertainty due to the variation in number of passengers. The fluctuation in vertical acceleration for sprung mass 400 and 800 kg is depicted in Fig. 26a, b, respectively.

Fig. 25

RMS of vertical acceleration for variation in sprung mass from 400 to 800 kg for bump road surface

Fig. 26

Vehicle body vertical acceleration for bump road surface: a for sprung mass of 400 kg; b for sprung mass 800 kg

5.3.1.2 Sensor noise uncertainty

Once again, measurement noise (in %) was injected in the sprung mass vertical displacement ‘$Z_{s}$’ as defined in Eq. 19. Amplitude of sensor noise was varied from $10^{ - 4}$ to $10^{ - 2}$% in the sprung mass vertical displacement, and the corresponding changes in RMSVVA are shown in Fig. 27. It can be noted that as the amplitude of noise increases from $10^{ - 4}$%, initially RMSVVA of FPD controller increases slowly, but beyond 0.002%, it increases rapidly. While in case of FO-FPD controller, nominal change in RMSVVA was observed, as shown in Fig. 27. The changes in vertical acceleration for 0.005% sensor noise are depicted in Fig. 28.

Fig. 27

RMS of vertical acceleration for variation in sensor noise amplitude from 0.0001 to 0.01% for bump road profile

Fig. 28

Vertical acceleration for 0.005% sensor noise for bump road profile

6 Stability

Small gain theorem is used to establish the BIBO stability conditions for closed loop control system having FO-FPD/FPD controllers [35,36,37, 41,42,43,44]. It is an analytical method for defining BIBO stability of nonlinear systems.

6.1 Small gain theorem

The essence of the small gain theorem is given as follows. Consider a nonlinear dynamic system ${\mathbb{R}}$ and a nonlinear fuzzy logic controller ${\mathbf{\mathcal{F}\mathcal{L}}}{\mathbb{C}}$. The block diagram of nonlinear control system is shown in Fig. 29.

Fig. 29

Block diagram of nonlinear control system [37]

Assuming that for a nonlinear fuzzy controller ${\mathbf{\mathcal{F}\mathcal{L}}}{\mathbb{C}}$ and nonlinear system ${\mathbb{R}}$,

$$ \left\|{\mathbf{\mathcal{F}\mathcal{L}}}{\mathbb{C}}\left( {e\left( {nT} \right)} \right) \right\| \le \alpha_{1} \left\|e\left( {nT} \right) \right\|+ \gamma_{1} ,\quad \alpha_{1} , \gamma_{1} \ge 0 $$

(27)

and

$$ \left\|{\mathbb{R}}\left( {u\left( {nT} \right)} \right) \right\|\le \alpha_{2} \left\|u\left( {nT} \right) \right\|+ \gamma_{2} ,\quad \alpha_{2} , \gamma_{2} \ge 0 $$

(28)

where $\alpha_{1}$ is the gain of nonlinear fuzzy controller ${\mathbf{\mathcal{F}\mathcal{L}}}{\mathbb{C}}$, and $\alpha_{2}$ is the gain of nonlinear system ${\mathbb{R}}$; $\gamma_{1}$ and $\gamma_{2}$ are constants. Under the two above mention conditions, i.e. Eqs. (27) and (28), the nonlinear fuzzy control system is BIBO stable if

$$ \alpha_{1} \cdot \alpha_{2} < 1 $$

(29)

Also, for any plant or system, it is always true:

$$ \left\| {{\mathbb{R}}\left( {u\left( {nT} \right)} \right)} \right\| \le \left\| {\mathbb{R}} \right\| \cdot \left| {u\left( {nT} \right)} \right| $$

(30)

It means $\alpha_{2}=\left\|{\mathbb{R}} \right\|$, the operator norm of given nonlinear system ${\mathbb{R}}$ which is defined as $\left\| {\mathbb{R}} \right\| = \begin{array}{*{20}c} {\sup } \\ {u_{1} \ne u_{2} ;n \ge 0} \\ \end{array} \frac{{\left| {{\mathbb{R}}\left( {u_{1} \left( {nT} \right)} \right) - {\mathbb{R}}\left( {u_{2} \left( {nT} \right)} \right)} \right|}}{{u_{1} \left( {nT} \right) - u_{2} \left( {nT} \right)}} .$ Therefore, one would only require to find $\alpha_{1}$ for BIBO stability assessment.

6.2 Stability analysis of FO-FPD and FPD controllers

The FO-FPD and FPD controllers only differ by the use of differentiator operator. The FO-FPD controller use non-integer order differentiator operators while FPD controller use integer order differentiator operators. From Fig. 2, it is clear that input to the FO-FPD controller may alter due to non-integer order differentiator and its internal structure remains same as FPD controller. Therefore, the BIBO stability conditions will remain same for FO-FPD and FPD controllers. Also, the whole input space formed by error and rate of change of error is divided in 20 IC regions as shown in Fig. 5. BIBO stability conditions can be evolved for each IC regions, i.e. IC 1–IC 20 for FO-FPD/FPD control systems. The conditions established for BIBO stability are presented as follows.

Theorem 1

If the nonlinear system under control denoted by ${\mathbb{R}}$ , the sufficient conditions for FO-FPD/FPD control systems to be stable are:

• (1) the nonlinear system under control has a bounded norm (gain), i.e. $\left\| {\mathbb{R}} \right\| < \infty$; and

• (2) the parameters of FO-FPD/FPD controllers satisfy Eq. ( 31 ),

  $$ \varvec{\alpha}_{1} {\mathbb{R}} < \infty $$

  (31)

  where $\varvec{\alpha}_{1}$ is different for different IC regions and given in Table 4. More details about the BIBO stability analysis of nonlinear fuzzy controller are presented in [35,36, – 37, 41].

Table 4 $\varvec{\alpha}_{1}$ for all 20 IC regions of FO-FPD/FPD controllers

7 Conclusions

In the present work, a self-tuned robust fractional order fuzzy proportional derivative (FO-FPD) controller is successfully implemented in position form, in closed loop, to effectively control the automobile active suspension system. The considered system is a nonlinear and highly uncertain due to deviation in number of passengers (payload) and sensor noise. The main motive of closed loop control system is to enhance the level of ride comfort in the car. It is achieved by minimizing the RMS of vertical vibrational acceleration of vehicle body and keeping some hard constraints such as tracking force, ratio of tyre dynamic load and static load and suspension travel within the prescribed limits. The proposed FO-FPD controller is a nonlinear and adaptive controller which changes its gains according to variation in error or rate of changes in error. Non-integer differentiator operator is used in FPD Controller in order to realize the FO-FPD controller. The parameters of FO-FPD and FPD controllers are optimized using Genetic Algorithm for sinusoidal road surface. The performances of FO-FPD and FPD controllers are assessed in closed loop for different roads profiles such as sinusoidal, random and bump road surfaces, and a comparative study is carried out. Simulation study revealed that FO-FPD and FPD controllers offered considerably much better performance as compared to passive suspension system by providing excellent comfort ride while maintaining all hard constraints. Furthermore, FO-FPD controller offers much superior comfort ride, particularly in uncertain environment and exhibit very strong robust behaviour as compared to FPD controller. Also, sufficient BIBO stability conditions were established by using small gain theorem, for closed loop control system.

For future work, recent optimization techniques can be explored to tune the parameters of controllers. Also, the simulated outcomes can be verified experimentally.