1 Introduction

As a generalization of classical sets, fuzzy set [51] and intuitionistic fuzzy set [3], neutrosophic set was presented by Smarandache [32, 33] to capture the incomplete, indeterminate and inconsistent information. The neutrosophic set has three completely independent parts, which are truth-membership degree, indeterminacy-membership degree and falsity-membership degree; therefore, it is applied to many different areas, such as decision-making problems [1, 2, 4, 7–11, 19, 23, 31, 37–39, 42, 52]. In additionally, since the neutrosophic sets are hard to be applied in some real problems because of the truth-membership degree, indeterminacy-membership degree and falsity-membership degree lie in \({]}^-0,1^+{[}\), single-valued neutrosophic sets introduced by Wang et al. [40].

Recently, Lee [21, 22] proposed notation of bipolar fuzzy set and their operations based on fuzzy sets. A bipolar fuzzy set has two completely independent parts, which are positive membership degree \(T^+\rightarrow [0,1]\) and negative membership degree \(T^-\rightarrow [-1,0]\). Also the bipolar fuzzy models have been studied by many authors including theory and applications in [12, 17, 25, 34, 35, 50]. After the definition of Smarandache’s neutrosophic set, neutrosophic sets and neutrosophic logic have been applied in many real applications to handle uncertainty. The neutrosophic set uses one single value in \({]}^-0,1^+{[}\) to represent the truth-membership degree, indeterminacy-membership degree and falsity-membership degree of an element in the universe X. Then, Deli et al. [18] introduced the concept of bipolar neutrosophic sets, as an extension of neutrosophic sets. In the bipolar neutrosophic sets, the positive membership degree \(T^{+}(x),\,I^{+}(x),\,F^{+}(x)\) denotes the truth membership, indeterminate membership and false membership of an element \(x\in X\) corresponding to a bipolar neutrosophic set A and the negative membership degree \(T^{-}(x),\,I^{-}(x),\,F^{-}(x)\) denotes the truth membership, indeterminate membership and false membership of an element \(x\in X\) to some implicit counter-property corresponding to a bipolar neutrosophic set A.

Similarity measure is an important tool in constructing multi-criteria decision-making methods in many areas such as medical diagnosis, pattern recognition, clustering analysis, decision making and so on. Similarity measures under all sorts of fuzzy environments including single-valued neutrosophic environments have been studied by many researchers in [5, 6, 13, 14, 15, 20–24, 26–30, 43–49]. Also, Deli and Şubas’s [16] and Şahin et al. [36] presented some similarity measures on bipolar neutrosophic sets based on correlation coefficient similarity measure and Jaccard vector similarity measure of neutrosophic set and applied to a decision-making problem, respectively. This paper is constructed as follows. In Sect. 2, some basic definitions of neutrosophic sets and bipolar neutrosophic sets are introduced. In Sect. 3, we propose some similarity measures for bipolar neutrosophic sets such as; Dice similarity measure, weighted Dice similarity measure, Hybrid vector similarity measure and weighted Hybrid vector similarity measure and investigate their several properties. In Sect. 4, a multi-criteria decision-making method for bipolar neutrosophic set is developed based on these given similarity measures and a practical example is given. In Sect. 5, we compare the proposed method with the existing methods in order to demonstrate the practicality and effectiveness of the developed method in this paper. In Sect. 6, the conclusions are summarized.

2 Preliminary

In the section, we give some concepts related to neutrosophic sets and bipolar neutrosophic sets.

Definition 1

[32] Let E be a universe. A neutrosophic set A over E is defined by

$$\begin{aligned} A=\{\langle x,(T_A(x),I_A(x),F_A(x))\rangle :x\in E\}. \end{aligned}$$

where \(T_A(x)\), \(I_A(x)\) and \(F_A(x)\) are called truth-membership function, indeterminacy-membership function and falsity-membership function, respectively. They are, respectively, defined by

$$\begin{aligned} T_A:E\rightarrow ]^-0,1^+[,\quad I_A:E\rightarrow ]^-0,1^+[,\quad F_A:E\rightarrow ]^-0,1^+[ \end{aligned}$$

such that \(0^-\le T_A(x) + I_A(x) + F_A(x)\le 3^+\).

Definition 2

[40] Let E be a universe. A single-valued neutrosophic set (SVN-set) A over E is defined by

$$\begin{aligned} A=\{\langle x,(T_A(x),I_A(x),F_A(x))\rangle :x\in E\}. \end{aligned}$$

where \(T_A(x)\), \(I_A(x)\) and \(F_A(x)\) are called truth-membership function, indeterminacy-membership function and falsity-membership function, respectively. They are respectively defined by

$$\begin{aligned} T_A:E\rightarrow [0,1],\quad I_A:E\rightarrow [0,1],\quad F_A:E\rightarrow [0,1] \end{aligned}$$

such that \(0\le T_A(x) + I_A(x) + F_A(x)\le 3\).

Definition 3

[18] A bipolar neutrosophic set(BNS) A in X is defined as an object of the form

$$\begin{aligned} A=\{\langle x,T^{+}(x),I^{+}(x),F^{+}(x),T^{-}(x),I^{-}(x),F^{-}(x)\rangle :x\in X\}. \end{aligned}$$

where

$$\begin{aligned} T^{+},I^{+},F^{+}:E\rightarrow [0,1],T^{-},I^{-},F^{-}:X\rightarrow [-1,0]. \end{aligned}$$

The positive membership degree \(T^{+}(x),\,I^{+}(x),\,F^{+}(x)\) denotes the truth membership, indeterminate membership and false membership of an element \(x\in X\) corresponding to a bipolar neutrosophic set A and the negative membership degree \(T^{-}(x),\,I^{-}(x),\,F^{-}(x)\) denotes the truth membership, indeterminate membership and false membership of an element \(x\in X\) to some implicit counter-property corresponding to a bipolar neutrosophic set A.

Definition 4

[18] Let \(A_{1}=\langle x,T_{1}^{+}(x),I_{1}^{+}(x),F_{1}^{+}(x), T_{1}^{-}(x),I_{1}^{-}(x),F_{1}^{-}(x)\rangle\) and \(A_{2}=\langle x,T_{2}^{+}(x),I_{2}^{+}(x),F_{2}^{+}(x), T_{2}^{-}(x),I_{2}^{-}(x),F_{2}^{-}(x)\rangle\) be two BNSs in a universe of discourse X. Then the following operations are defined as follows:

  1. 1.

    \(A_{1}=A_{2}\) if and only if \(T_{1}^{+}(x)=T_{2}^{+}(x),I_{1}^{+} (x)=I_{2}^{+}(x),F_{1}^{+}(x)=F_{2}^{+}(x)\) and \(T_{1}^{-}(x)=T_{2}^{-}(x),I_{1}^{-}(x) =I_{2}^{-}(x),F_{1}^{-}(x)=F_{2}^{-}(x).\)

  2. 2.

    \(\begin{aligned} A_{1}\cup A_{2}= &{} \{\langle x,max(T_{1}^{+}(x),T_{2}^{+}(x)), \frac{I_{1}^{+}(x)+I_{2}^{+}(x)}{2},min(F_{1}^{+}(x),F_{2}^{+}(x)), \\ &{} min(T_{1}^{-}(x),T_{2}^{-}(x)),\frac{I_{1}^{-}(x)+I_{2}^{-}(x)}{2},max(F_{1}^{-}(x),F_{2}^{-}(x))\rangle \} \end{aligned}\) \(\forall x\in X.\)

  3. 3.

    \(\begin{aligned} A_{1}\cap A_{2}=&{} \{\langle x,min(T_{1}^{+}(x),T_{2}^{+}(x)),\frac{I_{1}^{+}(x)+I_{2}^{+}(x)}{2},max(F_{1}^{+}(x),F_{2}^{+}(x)), \\ &{}max(T_{1}^{-}(x),T_{2}^{-}(x)),\frac{I_{1}^{-}(x)+I_{2}^{-}(x)}{2},min(F_{1}^{-}(x),F_{2}^{-}(x))\rangle \} \end{aligned}\) \(\forall x\in X.\)

  4. 4.

    \(A^c= \{\langle x, 1-T_{A}^{+}(x),1-I_{A}^{+}(x), 1-F_{A}^{+}(x), 1-T_{A}^{-}(x),1-I_{A}^{-}(x), 1-F_{A}^{-}(x)\rangle \}\)

  5. 5.

    \(A_{1}\subseteq A_{2}\) if and only if \(T_{1}^{+}(x)\le T_{2}^{+}(x), I_{1}^{+}(x)\le I_{2}^{+}(x),F_{1}^{+}(x)\ge F_{2}^{+}(x)\) and \(T_{1}^{-}(x)\ge T_{2}^{-}(x),I_{1}^{-}(x)\ge I_{2}^{-}(x),F_{1}^{-}(x)\le F_{2}^{-}(x).\)

Definition 5

[45] Let \(A=\langle T_{A}(x_{i}),I_{A}(x_{i}),F_{A}(x_{i})\rangle\) and \(B=\langle T_{B}(x_{i}),I_{B}(x_{i}),F_{B}(x_{i})\rangle\) be two SVNSs in a universe of discourse \(X=(x_{1},x_{2},\ldots,x_{n}).\) Then Dice similarity measure between SVNSs A and B in the vector space is defined as follows:

$$\begin{aligned} D(A,B) =\frac{1}{n}\sum _{i=1}^{n}\times \begin{array}{c} \left( \begin{array}{r} \frac{\begin{array}{l} 2(T_{A}(x_{i})T_{B}(x_{i})+I_{A}(x_{i})I_{B}(x_{i})+F_{A}(x_{i})F_{B}(x_{i})) \end{array}}{\begin{array}{l} [((T_{A})^{2}(x_{i})+(I_{A})^{2}(x_{i})+(F_{A})^{2}(x_{i}))+((T_{B})^{2}(x_{i})+(I_{B})^{2}(x_{i})+(F_{B})^{2}(x_{i}))] \end{array}} \\ \end{array} \right) \\ \end{array} \end{aligned}$$

It satisfies the following properties:

  1. 1.

    \(0\le D(A,B)\le 1;\)

  2. 2.

    \(D(A,B)=D(B,A);\)

  3. 3.

    \(D(A,B)=1\) for \(A=B\) i.e.\(T_{A}(x_{i})=T_{B}(x_{i}), I_{A}(x_{i})=I_{B}(x_{i}),F_{A}(x_{i})=F_{B}(x_{i})(i=1,2\ldots ,n)\ \ \forall \ x_{i} (i=1,2,\ldots ,n)\in X.\)

Definition 6

[29] Let \(A=\langle T_{A}(x_{i}),I_{A}(x_{i}),F_{A}(x_{i})\rangle\) and \(B=\langle T_{B}(x_{i}),I_{B}(x_{i}),F_{B}(x_{i})\rangle\) be two SVN-sets in a universe of discourse \(X=(x_{1},x_{2},\ldots ,x_{n}).\) Then

$$\begin{aligned} E(X,Y)&=\lambda \left( \begin{array}{r} \frac{\begin{array}{l} 2(T_{A}(x_{i})T_{B}(x_{i})+I_{A}(x_{i})I_{B}(x_{i})+F_{A}(x_{i})F_{B}(x_{i})) \end{array}}{\begin{array}{l} [((T_{A})^{2}(x_{i})+(I_{A})^{2}(x_{i})+(F_{A})^{2}(x_{i}))+((T_{B})^{2}(x_{i})+ (I_{B})^{2}(x_{i})+(F_{B})^{2}(x_{i}))] \end{array}} \\ \end{array} \right) \\ &\quad +\,(1-\lambda )\left( \begin{array}{r} \frac{\begin{array}{l} T_{A}(x_{i})T_{B}(x_{i})+I_{A}(x_{i})I_{B}(x_{i})+F_{A}(x_{i})F_{B}(x_{i}) \end{array}}{\begin{array}{l} [\sqrt{((T_{A})^{2}(x_{i})+(I_{A})^{2}(x_{i})+(F_{A})^{2}(x_{i}))}.\sqrt{((T_{B})^{2}(x_{i})+(I_{B})^{2}(x_{i})+(F_{B})^{2}(x_{i}))}] \end{array}} \\ \end{array} \right) . \end{aligned}$$

It satisfies the following properties:

  1. 1.

    \(0\le E(X,Y)\le 1;\)

  2. 2.

    \(E(X,Y)=E(Y,X);\)

  3. 3.

    \(E(X,Y)=1\) for \(X=Y\) i.e.,\(x_{i}=y_{i}(i=1,2\ldots ,n)\forall x_{i} \in X\ and\ y_{i}\in Y.\)

3 Similarity measures of bipolar neutrosophic sets

In this section, we introduce some similarity measures for bipolar neutrosophic sets including Dice similarity measure, weighted Dice similarity measure, Hybrid vector similarity measure and weighted Hybrid vector similarity measure by extending the studies in [29, 45].

Definition 7

Let \(A=\langle T_{A}^{+}(x_{i}),I_{A}^{+}(x_{i}),F_{A}^{+}(x_{i}),T_{A}^{-}(x_{i}), I_{A}^{-}(x_{i}),F_{A}^{-}(x_{i})\rangle\) and \(B=\langle T_{B}^{+}(x_{i}),I_{B}^{+}(x_{i}),F_{B}^{+}(x_{i}),T_{B}^{-}(x_{i}),I_{B}^{-}(x_{i}),F_{B}^{-}(x_{i})\rangle\) be two BNSs in the set \(X=\{x_{1},x_{2},\ldots ,x_{n}\}.\) Then, Dice similarity measure between BNS A and B, denoted D(A, B), is defined as;

$$\begin{aligned} D(A,B) &=\frac{1}{n}\sum _{i=1}^{n} \\&\quad\,{ \times \begin{array}{c} \left( \begin{array}{r} \frac{\begin{array}{l} [(T_{A}^{+}(x_{i})T_{B}^{+}(x_{i})+I_{A}^{+}(x_{i})I_{B}^{+}(x_{i}) +F_{A}^{+}(x_{i})F_{B}^{+}(x_{i})){-}(T_{A}^{-}(x_{i})T_{B}^{-}(x_{i}) +I_{A}^{-}(x_{i})I_{B}^{-}(x_{i})+F_{A}^{-}(x_{i})F_{B}^{-}(x_{i}))] \end{array}}{\begin{array}{l} [((T_{A}^{+})^{2}(x_{i})+(I_{A}^{+})^{2}(x_{i})+(F_{A}^{+})^{2}(x_{i})) +((T_{B}^{+})^{2}(x_{i})+(I_{B}^{+})^{2}(x_{i})+(F_{B}^{+})^{2}(x_{i}))\\ -((T_{A}^{-})^{2}(x_{i})+(I_{A}^{-})^{2}(x_{i})+(F_{A}^{-})^{2}(x_{i})) -((T_{B}^{-})^{2}(x_{i})+(I_{B}^{-})^{2}(x_{i})+(F_{B}^{-})^{2}(x_{i}))] \end{array}} \\ \end{array} \right) \\ \end{array} } \end{aligned}$$

Example 1

Suppose that \(A=\langle 0.5,0.2,0.6,-0.4,-0.3,-0.7\rangle\), \(B=\langle 0.7,0.1,0.3,-0.2,-0.2,-0.1\rangle\) be two BNSs in the set. Then,

$$\begin{aligned} {D(A,B) = \frac{1}{6}\,\times\, \begin{array}{c} \left( \begin{array}{r} \frac{\begin{array}{l} [((0.5)(0.7)+(0.2)(0.1)+(0.6)(0.3)){-}((-0.4)(-0.2)+(-0.3)(-0.2)+(-0.7)(-0.1))] \end{array}}{\begin{array}{l} [((0.5)^{2}+(0.2)^{2}+(0.6)^{2})+((0.7)^{2}+(0.1)^{2}+(0.3)^{2})\\ -((-0.4)^{2}+(-0.3)^{2}+(-0.7)^{2})-((-0.2)^{2}+(-0.2)^{2}+(-0.1)^{2})] \end{array}} \\ \end{array} \right) \\ \end{array} }\\ =0.1382 \end{aligned}$$

Definition 8

Let \(A=\langle T_{A}^{+}(x_{i}),I_{A}^{+}(x_{i}),F_{A}^{+}(x_{i}),T_{A}^{-}(x_{i}), I_{A}^{-}(x_{i}),F_{A}^{-}(x_{i})\rangle\) and \(B=\langle T_{B}^{+}(x_{i}),I_{B}^{+}(x_{i}),F_{B}^{+}(x_{i}),T_{B}^{-}(x_{i}), I_{B}^{-}(x_{i}),F_{B}^{-}(x_{i})\rangle\) be two BNSs in the set \(X=\{x_{1},x_{2},\ldots ,x_{n}\}\) and \(w_{i}\in [0,1]\) be the weight of each element \(x_{i}\) for \(i=1,2,\ldots ,n\) such that \(\sum _{i=1}^{n}w_{i}=1\). Then, weighted Dice similarity measure between BNS A and B, denoted \(D_{w}(A,B)\), is defined as;

$$\begin{aligned}D_{w}(A,B) &=\sum _{i=1}^{n}w_{i}\\& \quad\, { \times \begin{array}{c} \left( \begin{array}{r} \frac{\begin{array}{l} [(T_{A}^{+}(x_{i})T_{B}^{+}(x_{i})+I_{A}^{+}(x_{i})I_{B}^{+}(x_{i})+F_{A}^{+}(x_{i})F_{B}^{+}(x_{i})){-}(T_{A}^{-}(x_{i})T_{B}^{-}(x_{i})+I_{A}^{-}(x_{i})I_{B}^{-}(x_{i})+F_{A}^{-}(x_{i})F_{B}^{-}(x_{i}))] \end{array}}{\begin{array}{l} [((T_{A}^{+})^{2}(x_{i})+(I_{A}^{+})^{2}(x_{i})+(F_{A}^{+})^{2}(x_{i}))+((T_{B}^{+})^{2}(x_{i})+(I_{B}^{+})^{2}(x_{i})+(F_{B}^{+})^{2}(x_{i}))\\ -((T_{A}^{-})^{2}(x_{i})+(I_{A}^{-})^{2}(x_{i})+(F_{A}^{-})^{2}(x_{i}))-((T_{B}^{-})^{2}(x_{i})+(I_{B}^{-})^{2}(x_{i})+(F_{B}^{-})^{2}(x_{i}))] \end{array}} \\ \end{array} \right) \\ \end{array} }. \end{aligned}$$

Example 2

Suppose that \(A=\langle 0.8,0.2,0.5,-0.2,-0.3,-0.4\rangle\), \(B=\langle 0.6,0.4,0.3,-0.1,-0.2,-0.3\rangle\) be two BNSs in the set and \(w=0.3\). Then,

$$\begin{aligned} {D_{w}(A,B)= 0.3\times \begin{array}{c} \left( \begin{array}{r} \frac{\begin{array}{l} [((0.8)(0.6)+(0.2)(0.4)+(0.5)(0.3)){-}((-0.2)(-0.1)+(-0.3)(-0.2)+(-0.4)(-0.3))] \end{array}}{\begin{array}{l} [((0.8)^{2}+(0.2)^{2}+(0.5)^{2})+((0.6)^{2}+(0.4)^{2}+(0.3)^{2})\\ -((-0.2)^{2}+(-0.3)^{2}+(-0.4)^{2})-((-0.1)^{2}+(-0.2)^{2}+(-0.3)^{2})] \end{array}} \\ \end{array} \right) \\ \end{array} } \\ =0.1378\\ \end{aligned}$$

Proposition 1

Let \(D_{w}(A,B)\) be a weighted Dice similarity measure between BNSs A and B. Then, we have

  1. 1.

    \(0\le D_{w}(A,B)\le 1;\)

  2. 2.

    \(D_{w}(A,B)=D_{w}(B,A);\)

  3. 3.

    \(D_{w}(A,B)=1\) for \(A=B\) i.e.,\(T_{A}^{+}(x_{i})=T_{B}^{+}(x_{i}),I_{A}^{+}(x_{i})=I_{B}^{+}(x_{i}), F_{A}^{+}(x_{i})=F_{B}^{+}(x_{i}),T_{A}^{-}(x_{i})=T_{B}^{-}(x_{i}), I_{A}^{-}(x_{i})=I_{B}^{-}(x_{i}),F_{A}^{-}(x_{i})=F_{B}^{-}(x_{i})(i=1,2\ldots ,n)\ \ \forall \ x_{i} (i=1,2,\ldots ,n)\in X.\)

Proof

  1. 1.

    It is clear from Definition 8.

  2. 2.
    $$\begin{aligned} D_{w}(A,B)& =\sum _{i=1}^{n}w_{i}\\& \quad \, { \times \begin{array}{c} \left( \begin{array}{r} \frac{\begin{array}{l} [(T_{A}^{+}(x_{i})T_{B}^{+}(x_{i})+I_{A}^{+}(x_{i})I_{B}^{+}(x_{i})+F_{A}^{+}(x_{i})F_{B}^{+}(x_{i})){-}(T_{A}^{-}(x_{i})T_{B}^{-}(x_{i})+I_{A}^{-}(x_{i})I_{B}^{-}(x_{i})+F_{A}^{-}(x_{i})F_{B}^{-}(x_{i}))] \end{array}}{\begin{array}{l} [((T_{A}^{+})^{2}(x_{i})+(I_{A}^{+})^{2}(x_{i})+(F_{A}^{+})^{2}(x_{i}))+((T_{B}^{+})^{2}(x_{i})+(I_{B}^{+})^{2}(x_{i})+(F_{B}^{+})^{2}(x_{i}))\\ -((T_{A}^{-})^{2}(x_{i})+(I_{A}^{-})^{2}(x_{i})+(F_{A}^{-})^{2}(x_{i}))-((T_{B}^{-})^{2}(x_{i})+(I_{B}^{-})^{2}(x_{i})+(F_{B}^{-})^{2}(x_{i}))] \end{array}} \\ \end{array} \right) \\ \end{array} }\\ &=\sum\limits _{i=1}^{n}w_{i} \\ & \quad \,{ \times \begin{array}{c} \left( \begin{array}{r} \frac{\begin{array}{l} [(T_{B}^{+}(x_{i})T_{A}^{+}(x_{i})+I_{B}^{+}(x_{i})I_{A}^{+}(x_{i})+F_{B}^{+}(x_{i})F_{A}^{+}(x_{i})){-}(T_{B}^{-}(x_{i})T_{A}^{-}(x_{i})+I_{B}^{-}(x_{i})I_{A}^{-}(x_{i})+F_{B}^{-}(x_{i})F_{A}^{-}(x_{i}))] \end{array}}{\begin{array}{l} [((T_{B}^{+})^{2}(x_{i})+(I_{B}^{+})^{2}(x_{i})+(F_{B}^{+})^{2}(x_{i}))+((T_{A}^{+})^{2}(x_{i})+(I_{A}^{+})^{2}(x_{i})+(F_{A}^{+})^{2}(x_{i}))\\ -((T_{B}^{-})^{2}(x_{i})+(I_{B}^{-})^{2}(x_{i})+(F_{B}^{-})^{2}(x_{i}))-((T_{A}^{-})^{2}(x_{i})+(I_{A}^{-})^{2}(x_{i})+(F_{A}^{-})^{2}(x_{i}))] \end{array}} \\ \end{array} \right) \\ \end{array} }.\\&=D_{w}(B,A) \end{aligned}$$
  3. 3.

    Since \(T_{A}^{+}(x_{i})=T_{B}^{+}(x_{i}),I_{A}^{+}(x_{i})=I_{B}^{+}(x_{i}),F_{A}^{+}(x_{i})=F_{B}^{+}(x_{i}),T_{A}^{-}(x_{i})=T_{B}^{-}(x_{i}),I_{A}^{-}(x_{i})=I_{B}^{-}(x_{i}),F_{A}^{-}(x_{i})=F_{B}^{-}(x_{i})(i=1,2\ldots ,n)\ \ \forall \ x_{i} (i=1,2,\ldots ,n)\in X\), we have \(D_{w}(A,B)=1\).

The proof is completed. \(\square\)

Definition 9

Let \(A=\langle T_{A}^{+}(x_{i}),I_{A}^{+}(x_{i}),F_{A}^{+}(x_{i}), T_{A}^{-}(x_{i}),I_{A}^{-}(x_{i}),F_{A}^{-}(x_{i})\rangle\) and \(B=\langle T_{B}^{+}(x_{i}),I_{B}^{+}(x_{i}),F_{B}^{+}(x_{i}),T_{B}^{-}(x_{i}),I_{B}^{-}(x_{i}),F_{B}^{-}(x_{i})\rangle\) be two BNSs in the set \(X=\{x_{1},x_{2},\ldots ,x_{n}\}\). Then, hybrid vector similarity measure between BNS A and B, denoted HybV(A, B), is defined as;

$$\begin{aligned} HybV(A,B) & = \lambda \frac{1}{n}\mathop \sum \limits_{{i = 1}}^{n} \\ & \quad \times \left( {\begin{array}{*{20}r} \hfill {\frac{{\begin{array}{*{20}l} {[(T_{A}^{ + } (x_{i} )T_{B}^{ + } (x_{i} ) + I_{A}^{ + } (x_{i} )I_{B}^{ + } (x_{i} ) + F_{A}^{ + } (x_{i} )F_{B}^{ + } (x_{i} )){-}(T_{A}^{ - } (x_{i} )T_{B}^{ - } (x_{i} ) + I_{A}^{ - } (x_{i} )I_{B}^{ - } (x_{i} ) + F_{A}^{ - } (x_{i} )F_{B}^{ - } (x_{i} ))]} \hfill \\ \end{array} }}{{\begin{array}{*{20}l} {2[((T_{A}^{ + } )^{2} (x_{i} ) + (I_{A}^{ + } )^{2} (x_{i} ) + (F_{A}^{ + } )^{2} (x_{i} )) + ((T_{B}^{ + } )^{2} (x_{i} ) + (I_{B}^{ + } )^{2} (x_{i} ) + (F_{B}^{ + } )^{2} (x_{i} ))} \hfill \\ { - ((T_{A}^{ - } )^{2} (x_{i} ) + (I_{A}^{ - } )^{2} (x_{i} ) + (F_{A}^{ - } )^{2} (x_{i} )) - ((T_{B}^{ - } )^{2} (x_{i} ) + (I_{B}^{ - } )^{2} (x_{i} ) + (F_{B}^{ - } )^{2} (x_{i} ))]} \hfill \\ \end{array} }}} \\ \end{array} } \right) \\ & \quad + (1 - \lambda )\frac{1}{n}\sum _{{i = 1}}^{n} \\ {\mkern 1mu} & \quad \quad \times \begin{array}{*{20}c} {\left( {\begin{array}{*{20}r} \hfill {\frac{{\begin{array}{*{20}l} {[(T_{A}^{ + } (x_{i} )T_{B}^{ + } (x_{i} ) + I_{A}^{ + } (x_{i} )I_{B}^{ + } (x_{i} ) + F_{A}^{ + } (x_{i} )F_{B}^{ + } (x_{i} )){-}(T_{A}^{ - } (x_{i} )T_{B}^{ - } (x_{i} ) + I_{A}^{ - } (x_{i} )I_{B}^{ - } (x_{i} ) + F_{A}^{ - } (x_{i} )F_{B}^{ - } (x_{i} ))]} \hfill \\ \end{array} }}{{\begin{array}{*{20}l} {2[\sqrt {(T_{A}^{ + } )^{2} (x_{i} ) + (I_{A}^{ + } )^{2} (x_{i} ) + (F_{A}^{ + } )^{2} (x_{i} )} \times \sqrt {(T_{B}^{ + } )^{2} (x_{i} ) + (I_{B}^{ + } )^{2} (x_{i} ) + (F_{B}^{ + } )^{2} (x_{i} )} } \hfill \\ { - \sqrt {(T_{A}^{ - } )^{2} (x_{i} ) + (I_{A}^{ - } )^{2} (x_{i} ) + (F_{A}^{ - } )^{2} (x_{i} )} \times \sqrt {(T_{B}^{ - } )^{2} (x_{i} ) + (I_{B}^{ - } )^{2} (x_{i} ) + (F_{B}^{ - } )^{2} (x_{i} )} ]} \hfill \\ \end{array} }}} \\ \end{array} } \right)} \\ \end{array} \\ \end{aligned}$$

Example 3

Suppose that \(A=\langle 0.6,0.3,0.4,-0.1,-0.3,-0.4\rangle\), \(B=\langle 0.5,0.2,0.3,-0.4,-0.2,-0.5\rangle\) be two BNSs in the set. Then,

$$\begin{aligned} HybV(A,B) & = (0.4)\, \times \,\frac{1}{6} \,\times\, \begin{array}{*{20}c} {\left( {\begin{array}{*{20}r} \hfill {\frac{{\begin{array}{*{20}l} {[((0.6)(0.5) + (0.3)(0.2) + (0.4)(0.3)){-}(( - 0.1)( - 0.4) + ( - 0.3)( - 0.2) + ( - 0.4)( - 0.5))]} \hfill \\ \end{array} }}{{\begin{array}{*{20}l} {2[((0.6)^{2} + (0.3)^{2} + (0.4)^{2} ) + ((0.5)^{2} + (0.2)^{2} + (0.3)^{2} )} \hfill \\ { - (( - 0.1)^{2} + ( - 0.3)^{2} + ( - 0.4)^{2} ) - (( - 0.4)^{2} + ( - 0.2)^{2} + ( - 0.5)^{2} )]} \hfill \\ \end{array} }}} \\ \end{array} } \right)} \\ \end{array} \\ & \quad + (1 - (0.4)) \,\times\, \frac{1}{6} \,\times \,\begin{array}{*{20}c} {\left( {\begin{array}{*{20}r} \hfill {\frac{{\begin{array}{*{20}l} {[((0.6)(0.5) + (0.3)(0.2) + (0.4)(0.3)){-}(( - 0.1)( - 0.4) + ( - 0.3)( - 0.2) + ( - 0.4)( - 0.5))]} \hfill \\ \end{array} }}{{\begin{array}{*{20}l} {2[\sqrt {((0.6)^{2} + (0.3)^{2} + (0.4)^{2} )} \,\times \,\sqrt {((0.5)^{2} + (0.2)^{2} + (0.3)^{2} )} } \hfill \\ { - \sqrt {(( - 0.1)^{2} + ( - 0.3)^{2} + ( - 0.4)^{2} )} \,\times\, \sqrt {(( - 0.4)^{2} + ( - 0.2)^{2} + ( - 0.5)^{2} )} ]} \hfill \\ \end{array} }}} \\ \end{array} } \right)} \\ \end{array} \\ & {\text{ = 0}}{\text{.1421}} \\ \end{aligned}$$

Definition 10

Let \(A=\langle T_{A}^{+}(x_{i}),I_{A}^{+}(x_{i}),F_{A}^{+}(x_{i}), T_{A}^{-}(x_{i}),I_{A}^{-}(x_{i}),F_{A}^{-}(x_{i})\rangle\) and \(B=\langle T_{B}^{+}(x_{i}),I_{B}^{+}(x_{i}),F_{B}^{+}(x_{i}), T_{B}^{-}(x_{i}),I_{B}^{-}(x_{i}),F_{B}^{-}(x_{i})\rangle\) be two BNSs in the set \(X=\{x_{1},x_{2},\ldots ,x_{n}\}\) and \(w_{i}\in [0,1]\) be the weight of each element \(x_{i}\) for \(i=1,2,\ldots ,n\) such that \(\sum _{i=1}^{n}w_{i}=1\). Then, weighted hybrid vector similarity measure between BNS A and B, denoted \(HybV_{w}(A,B)\), is defined as;

$$\begin{aligned} HybV_{w} (A,B) & = \lambda \sum\limits_{{i = 1}}^{n} {w_{i} } \\ & \quad \times \begin{array}{*{20}c} {\left( {\begin{array}{*{20}r} \hfill {\frac{{\begin{array}{*{20}l} {[(T_{A}^{ + } (x_{i} )T_{B}^{ + } (x_{i} ) + I_{A}^{ + } (x_{i} )I_{B}^{ + } (x_{i} ) + F_{A}^{ + } (x_{i} )F_{B}^{ + } (x_{i} )) - (T_{A}^{ - } (x_{i} )T_{B}^{ - } (x_{i} ) + I_{A}^{ - } (x_{i} )I_{B}^{ - } (x_{i} ) + F_{A}^{ - } (x_{i} )F_{B}^{ - } (x_{i} ))]} \hfill \\ \end{array} }}{{\begin{array}{*{20}l} {2[((T_{A}^{ + } )^{2} (x_{i} ) + (I_{A}^{ + } )^{2} (x_{i} ) + (F_{A}^{ + } )^{2} (x_{i} )) + ((T_{B}^{ + } )^{2} (x_{i} ) + (I_{B}^{ + } )^{2} (x_{i} ) + (F_{B}^{ + } )^{2} (x_{i} ))} \hfill \\ { - ((T_{A}^{ - } )^{2} (x_{i} ) + (I_{A}^{ - } )^{2} (x_{i} ) + (F_{A}^{ - } )^{2} (x_{i} )) - ((T_{B}^{ - } )^{2} (x_{i} ) + (I_{B}^{ - } )^{2} (x_{i} ) + (F_{B}^{ - } )^{2} (x_{i} ))]} \hfill \\ \end{array} }}} \\ \end{array} } \right)} \\ \end{array} \\ & \quad + (1 - \lambda )\sum\limits_{{i = 1}}^{n} {w_{i} } \\ & \quad \times \begin{array}{*{20}c} {\left( {\begin{array}{*{20}r} \hfill {\frac{{\begin{array}{*{20}l} {[(T_{A}^{ + } (x_{i} )T_{B}^{ + } (x_{i} ) + I_{A}^{ + } (x_{i} )I_{B}^{ + } (x_{i} ) + F_{A}^{ + } (x_{i} )F_{B}^{ + } (x_{i} )) - (T_{A}^{ - } (x_{i} )T_{B}^{ - } (x_{i} ) + I_{A}^{ - } (x_{i} )I_{B}^{ - } (x_{i} ) + F_{A}^{ - } (x_{i} )F_{B}^{ - } (x_{i} ))]} \hfill \\ \end{array} }}{{\begin{array}{*{20}l} {2[\sqrt {(T_{A}^{ + } )^{2} (x_{i} ) + (I_{A}^{ + } )^{2} (x_{i} ) + (F_{A}^{ + } )^{2} (x_{i} )} \times \sqrt {(T_{B}^{ + } )^{2} (x_{i} ) + (I_{B}^{ + } )^{2} (x_{i} ) + (F_{B}^{ + } )^{2} (x_{i} )} } \hfill \\ { - \sqrt {(T_{A}^{ - } )^{2} (x_{i} ) + (I_{A}^{ - } )^{2} (x_{i} ) + (F_{A}^{ - } )^{2} (x_{i} )} \times \sqrt {(T_{B}^{ - } )^{2} (x_{i} ) + (I_{B}^{ - } )^{2} (x_{i} ) + (F_{B}^{ - } )^{2} (x_{i} )} ]} \hfill \\ \end{array} }}} \\ \end{array} } \right)} \\ \end{array} \\ \end{aligned}$$

Proposition 2

Let \(HybV_{w}(A,B)\) be a weighted hybrid vector similarity measure between bipolar neutrosophic sets A and B. Then, we have

  1. 1.

    \(0\le HybV_{w}(A,B)\le 1;\)

  2. 2.

    \(HybV_{w}(A,B)=HybV_{w}(B,A);\)

  3. 3.

    \(HybV_{w}(A,B)=1\) for \(A=B\) i.e.,\(T_{A}^{+}(x_{i})=T_{B}^{+}(x_{i}), I_{A}^{+}(x_{i})=I_{B}^{+}(x_{i}), F_{A}^{+}(x_{i})=F_{B}^{+}(x_{i}), T_{A}^{-}(x_{i})=T_{B}^{-}(x_{i}), I_{A}^{-}(x_{i})=I_{B}^{-}(x_{i}), F_{A}^{-}(x_{i})=F_{B}^{-}(x_{i})(i=1,2\ldots ,n)\ \ \forall \ x_{i} (i=1,2,\ldots,n)\in X.\)

4 BN-multi-criteria decision-making methods

In this section, we introduce applications of weighted similarity measures in multi-criteria decision making problems under bipolar neutrosophic environment.

Definition 11

[36] Let \(U=(u_{1},u_{2},\ldots ,u_{n})\) be a set of alternatives, \(A=(a_{1},a_{2},\ldots , a_{m})\) be the set of attributes, \(w=(w_{1},w_{2},\ldots ,w_{n})^{T}\) be the weight vector of the attributes \(C_{j}(j=1,2,\ldots ,n)\) such that \(w_{j}\ge 0\) and \(\sum _{j=1}^{n}=1\) and \(b_{ij}=\langle T_{ij}^{+}, I_{ij}^{+}, F_{ij}^{+}, T_{ij}^{-}, I_{ij}^{-}, F_{ij}^{-}\rangle\) be the decision matrix whose entries are the rating values of the alternatives. Then,

figure a

is called an NB-multi-attribute decision-making matrix of the decision maker.

Also; positive ideal bipolar neutrosophic solution \(u^{*}=(b_{1}^{*},b_{2}^{*},\ldots ,b_{n}^{*})\) is the solution of decision matrix \([b_{ij}]_{m \times n}\) where every component of has the following form:

$$\begin{aligned} b_{j}^{*}= \langle max_{i}\{T_{ij}^{+}\}, min_{i} \{I_{ij}^{+}\}, min_{i}\{F_{ij}^{+}\}, min_{i}\{T_{ij}^{-}\}, max_{i} \{I_{ij}^{-}\},max_{i} \{F_{ij}^{-}\}\rangle (j=1,2\ldots ,n) \end{aligned}$$
(1)

and negative ideal bipolar neutrosophic solution \(\overline{u}^{*}=(\overline{b}_{1}^{*},\overline{{b}}_{2}^{*},\ldots,\overline{b}_{n}^{*})\) is the solution of decision matrix \([b_{ij}]_{m \times n}\) where every component of has the following form:

$$\begin{aligned} \overline{{b}}_{j}^{*}= \langle min_{i}\{T_{ij}^{+}\}, max_{i} \{I_{ij}^{+}\}, max_{i}\{F_{ij}^{+}\}, max_{i}\{T_{ij}^{-}\}, min_{i} \{I_{ij}^{-}\},min_{i} \{F_{ij}^{-}\}\rangle \end{aligned}$$
(2)

Now we give an algorithm as;

Algorithm

  • Step 1 Give the decision–making matrix \([b_{ij}]_{m \times n};\) for decision;

  • Step 2 Compute the positive ideal (or negative ideal) bipolar neutrosophic solution for \([b_{ij}]_{m \times n};\);

  • Step 3 Calculate the weighted hybrid vector (or Dice) similarity measure between positive ideal (or negative ideal) bipolar neutrosophic solution \(b_{j}^{*}\) and \(b_i=[b_{ij}]_{1 \times n}\) for all \(i=1,2\ldots ,m\) and \(j=1,2\ldots ,n\) as;

    $$\begin{aligned} HybV_{w} (b_{j}^{*} ,b_{i} ) & = \lambda \sum\limits_{{j = 1}}^{n} {w_{j} } \\ & \quad \times \begin{array}{*{20}c} {\left( {\begin{array}{*{20}r} \hfill {\frac{{\begin{array}{*{20}l} {[((T_{j}^{*} )^{ + } (T_{{ij}} )^{ + } + (I_{j}^{*} )^{ + } (I_{{ij}} )^{ + } + (F_{j}^{*} )^{ + } (F_{{ij}} )^{ + } ){-}((T_{j}^{*} )^{ - } (T_{{ij}} )^{ - } + (I_{j}^{*} )^{ - } (I_{{ij}} )^{ - } + (F_{j}^{*} )^{ - } (F_{{ij}} )^{ - } )]} \hfill \\ \end{array} }}{{\begin{array}{*{20}l} {2[(((T_{j}^{*} )^{ + } )^{2} + ((I_{j}^{*} )^{ + } )^{2} + ((F_{j}^{*} )^{ + } )^{2} ) + ((T_{{ij}}^{ + } )^{2} + (I_{{ij}}^{ + } )^{2} + (F_{{ij}}^{ + } )^{2} )} \hfill \\ { - (((T_{j}^{*} )^{ - } )^{2} + ((I_{j}^{*} )^{ - } )^{2} + ((F_{j}^{*} )^{ - } )^{2} ) - ((T_{{ij}}^{ - } )^{2} + (I_{{ij}}^{ - } )^{2} + (F_{{ij}}^{ - } )^{2} )]} \hfill \\ \end{array} }}} \\ \end{array} } \right)} \\ \end{array} \\ & \quad + (1 - \lambda )\sum\limits_{{j = 1}}^{n} {w_{j} } \\ \end{aligned}$$
    $$\begin{aligned} { \times \begin{array}{c} \left( \begin{array}{r} \frac{\begin{array}{l} [((T_{j}^{*})^{+}(T_{ij})^{+}+(I_{j}^{*})^{+}(I_{ij})^{+}+(F_{j}^{*})^{+}(F_{ij})^{+}){-}(T_{j}^{*})^{-}(T_{ij})^{-}+(I_{j}^{*})^{-}(I_{ij})^{-}+(F_{j}^{*})^{-}(F_{ij})^{-})] \end{array}}{\begin{array}{l} 2[\sqrt{((T_{j}^{*})^{+})^{2}+((I_{j}^{*})^{+})^{2}+((F_{j}^{*})^{+})^{2}}\times \sqrt{(T_{ij}^{+})^{2}+(I_{ij}^{+})^{2}+(F_{ij}^{+})^{2}}\\ -\sqrt{((T_{j}^{*})^{-})^{2}+((I_{j}^{*})^{-})^{2}+((F_{j}^{*})^{-})^{2}}\times \sqrt{(T_{ij}^{-})^{2}+(I_{ij}^{-})^{2}+(F_{ij}^{-})^{2}}] \end{array}} \\ \end{array} \right) \\ \end{array}} \end{aligned}$$
    (3)

  • Step 4. Determine the nonincreasing order of \(s_i=HybV_{w}(b_{j}^{*},b_{i})\) and select the best alternative.

Example 4

Let us consider the decision-making problem given in [41] for bipolar neutrosophic set. “Global environmental concern is a reality, and an increasing attention is focusing on the green production in various industries. A car company is desirable to select the most appropriate green supplier for one of the key elements in its manufacturing process.” [41]. After pre-evaluation, four suppliers(alternatives) are taken into consideration, which are denoted by \(u_1\), \(u_2\), \(u_3\) and \(u_4\). Three criteria are considered including \(a_{1}\) is product quality; \(a_{2}\) is technology capability; \(a_{3}\) is pollution control. Assume the weight vector of the three criteria is \(W=\{w_{1},w_{2},w_{3}\}^{T}=\{0.2,0.5,0.3\}^{T}\). In order to determine the decision information, an expert has gathered the criteria values for the four possible alternatives under bipolar neutrosophic environment. Then

Algorithm

  • Step 1 The decision–making matrix \([b_{ij}]_{m \times n}\) is given by a expert as;

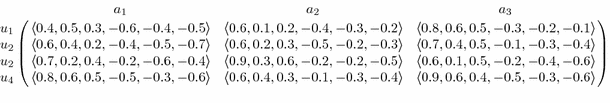
    figure b

  • Step 2 The positive ideal bipolar neutrosophic solutions for are computed as; \(u^{*}=[\langle 0.8,0.2,0.2,-0.6,-0.3,-0.4\rangle ,\langle 0.9,0.1,0.2,-0.5,-0.2,-0.2\rangle , \langle 0.9,0.1,0.4,-0.5,-0.2,-0.1\rangle ].\)

  • Step 3 The weighted hybrid vector similarity measure between positive ideal (or negative ideal) bipolar neutrosophic solution for alternative \(u_j\in U\) are computed and selected the best alternative.

  • Step 4 Ranking the alternatives (Table 1).

Table 1 Results for different values of \(\lambda\)
Full size table

5 Comparative analysis and discussion

In this subsection, a comparative study is presented to show the flexibility and feasibility of the introduced NB-multi-attribute decision-making method. Therefore, different methods are used to solve the same NB-multi-attribute decision-making problem with the bipolar neutrosophic information given by Şahin et al. [36], Deli et al. [18], Deli and Şubaş [16]. Şahin et al. [36] present a method by using Jaccard vector similarity and weighted Jaccard vector similarity measure and Deli and Şubaş [16] present a method by using correlation measure based on multi-criteria decision making for bipolar neutrosophic sets. Also, Deli et al. [18] contains two major phrases. The method firstly use score, certainty and accuracy functions to compare the bipolar neutrosophic sets. Secondly, he use bipolar neutrosophic weighted average operator and bipolar neutrosophic weighted geometric operator to aggregate the bipolar neutrosophic information. The ranking results obtained by different methods are summarized in Table 2.

Table 2 The ranking results of different methods
Full size table

In Table 2, there are some differences between the ranking results obtained by the methods. The optimal alternative is \(u_{3}\) obtained by the proposed methods except the result obtained by the method of Deli et al.’s method [18] and the proposed method \(HybV_{w}\) with \(\lambda =0.9\). The reason may be score, certainty and accuracy functions and weighted average operator and bipolar neutrosophic weighted geometric operator in Deli et al.’s method [18] and parameter \(\lambda\) in the proposed method \(HybV_{w}\). Generally, the proposed methods can effectively overcome the decision-making problems which contain bipolar neutrosophic information. So, we think the proposed methods developed in this paper is more suitable to handle this application example.

6 Conclusion

This paper developed a multi-criteria decision-making method for bipolar neutrosophic set is developed based on these given similarity measures. To get the comprehensive values, some similarity measures for bipolar neutrosophic sets such as; Dice similarity measure, weighted Dice similarity measure, Hybrid vector similarity measure and weighted Hybrid vector similarity measure are introduced. In the future, it shall be significant to research some special kinds of bipolar neutrosophic measures.