1 Introduction

Over the course of the last years, Additive Manufacturing (AM), especially the Laser Powder Bed Fusion process (L-PBF), has secured its place in the manufacturing industry. The advantages of AM include fast production-design cycles, rapid prototyping, function integration, and a vast freedom of design regarding the complexity and finesse of small features.

Current challenges in the research field of AM are the qualification of new materials (for example high entropy alloy development by mixing elemental powders) and AM specific alloy design. The rapid cooling rate causes changes in the microstructure, and the layer-wise manufacturing causes anisotropy in the build direction, thus changing the mechanical properties of an additively manufactured product in comparison to conventional manufacturing. For an increased material development speed, it would be a large advantage if the properties could be calculated beforehand.

The scientific goal, pursued in this paper, is to calculate the microstructure and the resulting mechanical properties starting only with the process parameters (like laser power, scanning velocity, and more). In the presented approach, three consecutive simulations are coupled to obtain the final mechanical properties. The first is a model of the L‑PBF process that simulates the melt pool behaviour regarding energy absorption and the solidification process. The outputs of this simulation are the solidification conditions of the process. The second model describes the resulting microstructure (starting from the solidification conditions) by solving the interface evolution during the solidification near the solid-liquid phase front. The phase field model has proven its efficiency in reproducing the evolution of the solid liquid interface during solidification conditions in weakly out-of-equilibrium conditions. In this case, linear kinetic effects are present at the interface, with fluxes and driving forces being proportional through the Onsager relations. Within the sharp-interface approach (transport equations in the bulk supplemented by boundary conditions at the interface), this proportionality is defined by the kinetic coefficients. A formal link between the latter and the parameters of the phase field model may be found using the so-called thin-interface limit. In L‑PBF the thermal conditions during solidification are in general far from the local equilibrium (\(\dot{T}/\mathrm{G}>\sim 100\,\mathrm{mm}/\mathrm{s}\)). For this regime, the reduction of the phase field equations to a sharp interface description is insufficient [10, 11]. In our former work, we already showed that the strongly-out-of-equilibrium conditions can be described by the model [3]. It was shown that the microstructure features, such as interdendritic spacing, compare well to experimental data.

The third model determines the effective material properties from the heterogeneous phases of the calculated microstructure. The asymptotic homogenization method [4] is adopted here to predict the effective elastic properties of the superalloy IN718, produced by L‑PBF.

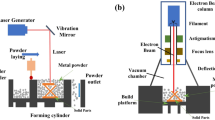
2 Melt Pool Model

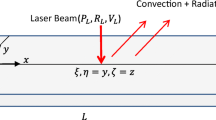
For the calculation of the solidification conditions, the heat Eq. 1 and the energy input by the laser radiation (2) have to be taken into account.

$$\rho \left(T\right)c_{p}\left(T\right)\frac{\partial T\left(t\right)}{\partial t}=\lambda \left(T\right)\left(\frac{\partial ^{2}T}{\partial x^{2}}+\frac{\partial ^{2}T}{\partial y^{2}}+\frac{\partial ^{2}T}{\partial z^{2}}\right)$$
(1)

Where \(\rho ,c_{p},\lambda\) are the temperature dependent material properties: density, heat capacity. and heat conductivity.

The measured beam profile of the EOSM 290 is fitted to a super Gaussian distribution to obtain the laser radiation intensity distribution in the working plane \((x,y)\).

$$I(x,y\rightarrow r)=I_{0}\cdot \Bigg(exp\left(-f\left(n\right)\cdot \left(\frac{r}{r_{0}}\right)^{n}\right)-exp\left(-f\left(n\right)\cdot \left(\frac{r_{\text{Limit}}}{r_{0}}\right)^{n}\right)\Bigg)$$
(2)

Where \(I_{0},f\left(n\right),r_{\text{Limit}}\) and \(r_{0}\) are the fitting parameters to describe the laser irradiation. In this work the parameters fitted are: \(n=2,r_{0}=42\mathrm{\mu}m,r_{\text{Limit}}=100\mathrm{\mu}m\) (\(I_{0},f(n)\) are normalization factors calculated in a way to ensure \(1\,W\) of laser beam power). The base absorption for the IN718 value is taken from literature (\(\alpha _{0}=35\%\)). The increased absorption with an increased meltpool depth (\(d_{mp}\)) keyhole formation is taken into account. With an increasing melt depth, the effective absorption is increased up to a factor (\(\alpha _{\mathrm{key}}\)) of ~2 caused by multiple reflections in the keyhole [1].

The energy absorption model coupled to the simulation as a Dirichlet boundary condition on the materials surface (3):

$$-\lambda \left(T\right)\frac{\partial T}{\partial z}\cdot \hat{n}=I_{0}\left(\overset{\rightarrow }{r}\right)\cdot P_{L}\cdot \alpha _{0}\cdot \alpha _{\mathrm{key}}\left(d_{mp}\right)$$
(3)

To model the keyhole behaviour, the material that reaches evaporation temperature \((T_{\mathrm{eva}}=3200^{\circ}C)\) is assumed to be transparent for the laser radiation. This leads to the formation of the keyhole in the simulations. A similar model was proposed by Philo [2].

The model has been verified for single track experiments with IN718 for different parameter settings of \(P_{L}\) and \(v_{S}\) and powder layer heights \(h_{L}\) (for \(h_{L}=0\mathrm{\mu}m\) see Fig. 1).

Fig. 1
figure 1

a Different combinations of \(P_{L}\) and \(v_{S}\) investigated and their respective line energy; b Comparison of calculated melt pool depth with melt pool depth from experiments

Full size image

For the microstructure calculation, only the EOS IN718 default parameter is used (\(P_{L}=285\,W,v_{S}=960\frac{mm}{s}\)). The solidification conditions are extracted in the lower third of the melt pool (see Fig. 2).

Fig. 2
figure 2

Calculated temperature distribution for the quasi-stationary L‑PBF process with the EOS default parameters for the material IN718, the solidification conditions are extracted from the orange encircled area

Full size image

The solidification conditions extracted for the EOS default parameter are \(\Updelta T\approx 46000\frac{K}{mm},\dot{T}\approx 10^{8}\,K/s\). Those values vary strongly along the solidification front, especially with the depth at which they are taken (measure point see Fig. 2).

3 Microstructure Simulation

In [3], we have presented phase field simulations of IN718 directional solidification under LPBF conditions. During our investigations, we varied the solidification speed over a wide range, i.e. from \(V_{g}=100\frac{mm}{s}\) to \(V_{g}=1200\frac{mm}{s}\). The latter value is still about ¼ of the solidification speed that may be extracted from the finite-element calculations where, as seen in Fig. 2, the slope of the isotherms dz/dx is approximately uniform in the orange encircled area. Our phase field simulations are, however, useful to apprehend the type of solidification microstructure corresponding to such conditions, and especially to such large solidification speeds. We recall that solidification experiments that are explained using commonly accepted solidification theories are performed at sub- \(\frac{mm}{s}\) solidification speeds.

The phase field simulations are performed using the MICRESS software, based on a multi-component phase field model [13] that is coupled to the TCNI8 ThermoCalc database. The composition of the alloy was chosen as follows, in wt%: 17.64 Fe, 19.00 Cr, 5.13 Nb, 3.05 Mo with Ni as balance. We simulate only the primary solidification, without precipitation of additional solid phases from the primary γ phase at a low temperature. The discretization grid spacing is 20 nm. The thermal gradient G is considered homogeneous in space and constant in time (so-called frozen temperature approximation), and diffusion is neglected in the solid phase. Fig. 3 shows a top view (thermal gradient pointing towards the reader) of a three-dimensional simulation where the growth velocity is \(V_{g}\) = 40 mm/s and G = \(10^{4}\) K/mm. Here, the crystalline axis of the superalloy form Euler angles (φ = 5°, θ = 5°, ψ = 5°) with respect to the thermal gradient.

Fig. 3
figure 3

Top view (thermal gradient pointing towards the reader) of the three-dimensional simulation of IN718 solidification under LPBF conditions

Full size image

We identify fingers with their tip in red colour. The morphology of the growing phase has been investigated in [3], and corresponds to a hybrid structure resulting from a solidification regime denoted as Strongly Out-of-Equilibrium (SOE). The fingers are unbranched dendrites, to which it is tempting to associate a cellular nature. Yet, they grow along a cubic direction of the crystal, in virtue of a selected growth direction determined by the anisotropy of solid-liquid interface energy, which is then contradictory with the cellular nature (let us note that here in Fig. 3 the dendrites therefore grow with a slight misorientation with respect to the thermal gradient). This hybrid feature, i.e. dendritic/cellular, of the microstructure pertains to the particular relations in the SOE regime between the different length scales, i.e. the dendrite tip radius, the diffusion length, and the distance between tips (tips spacing). On the theoretical level, these three length scales are of the same order. The main characteristics of the growth morphology may then be understood as follows: since the tip radius is not much smaller than the tips spacing, no side arms develop, and since the diffusion length is not much larger than the tips spacing, the interaction between tips is strongly reduced, yielding a poor organization of the finger array and a growth direction prescribed by the crystallography and not by the thermal gradient direction.

The three-dimensional calculation presented in Fig. 3 is performed until completion of the solidification. The final microstructure with fingers and interstice regions present, within the γ phase, strong micro-segregations of chemical elements like Nb, as shown in Fig. 4a. Eventually, the predicted solidified microstructure is transferred to the homogenization tool HOMAT [4, 5] via the standardized VTK exchange format.

Fig. 4
figure 4

a two-dimensional cut perpendicular to the thermal gradient of the Nb concentration field; b binarized image with a 4 wt% Nb threshold

Full size image

4 Homogenization of the Solidified Microstructure

4.1 Definition of the Homogenization Model

In order to derive effective elastic properties of the solidified microstructure, presenting strong micro-segregation of chemical elements, we have developed the homogenization scheme presented in this chapter. As Nobium (Nb) is the chemical element which partitions mostly at the solid-liquid interface, we select this element and perform a concentration threshold for it in order to binarize the microstructure and to produce a pseudo two-phase microstructure for the homogenization runs. Then, for each of these two phases, the specific elastic properties are assigned and the effective properties are calculated of the binarized microstructure using HOMAT. Fig. 4a illustrates a two-dimensional cut perpendicular to the thermal gradient of the Nb concentration. In Fig. 4b, the corresponding binarized microstructure, with a Nb threshold of a 4wt%, is shown. The dendrites appear in white, while the inter-dendritic region appears in blue.

To assign specific elastic properties for each pseudo-phase, it is essential to determine at first the average concentration of Nb in each of these phases. An average of 2.75 wt% within the dendrites and 7.8 wt% in the inter-dendritic region was found. These values correspond to a dendritic fraction of 53% and to an inter-dendritic region fraction of 47%, yielding the nominal Nb concentration in IN718, i.e. 5.13 wt%.

Single crystal elastic constants of the γ phase of nominal IN718 at room temperature are taken from the literature [6, 7]: C11 = 245.4 GPa; C12 = 162.05 GPa; C44 = 113.4 GPa. They present a pronounced Zener anisotropy: \(A^{Z}=\frac{2C_{44}}{C_{11}-C_{12}}=2.72\). The specification of the Nb concentration dependence of these SX crystal elastic properties is delicate. In the literature, only the first principles simulations of different Nb doped Ni systems have been performed recently in order to determine the effect of the Nb concentration on the elastic properties of these systems [7]. But, for industrial superalloys like IN718, no study has been found. Song et al. [8] show that the shear modulus C44 decreases quasi linearly with the Nb content with a slope of −6.08 GPa per wt% Nb. Adopting this slope the following values are obtained: C44 = 127.08 GPa for the finger phase and C44 = 96.32 GPa for the interstice. Assuming the same stiffness ratio C12/C44 and Zener anisotropy for the nominal IN718 single crystal, both variants produce the elastic constants at RT outlined in Table 1.

TABLE 1 Elastic constants of the pseudo-phases with 2.75 wt% and 7.81 wt% Nb content respectively at RT and 700 °C
Full size table

Moreover, the effective elastic properties of the solidified microstructure are predicted not only at room temperature but also at a service temperature, namely 700 °C. Taking the same stiffness reduction factors (sT_C11 = 0.829; sT_C12 = 0.859; sT_C44 = 0.816) as Hermann et al. [9] have measured experimentally for SX IN738LC, the elastic constants at 700 °C for both pseudo-phases (see Table 1) are obtained.

4.2 Homogenization Results

The predicted effective Hooke matrices of the IN718 microstructure at 700 °C (see expression (4)) is full anisotropic with noticeable extension-shear coupling terms (Hij with i = 1, 2, 3 and j = 4, 5, 6). These extension-shear couplings are induced by the small Euler angles between temperature gradient and crystal orientation of the finger network. It should be noted that, at room temperature, a similar full anisotropic equivalent behaviour is predicted, with, of course, higher stiffness terms.

$$H_{700^{\circ}C}=\left[\begin{array}{cc} \begin{array}{ccc} \mathbf{214.2} & \mathbf{130.7} & \mathbf{137.3}\\ & \mathbf{217.0} & \mathbf{135.3}\\ S & & \mathbf{210.8} \end{array} & \begin{array}{ccc} -15.4 & -1.1 & 0.8\\ 18.2 & 1.6 & -6.4\\ -1.0 & -1.1 & 8.6 \end{array}\\ \begin{array}{ccc} & Y & \\ & & M\\ & & \end{array} & \begin{array}{ccc} \mathbf{84.8} & -0.02 & 1.6\\ & \mathbf{91.8} & -2.0\\ & & \mathbf{89.2} \end{array} \end{array}\right]$$
(4)

The elastic engineering constants are determined by inverting the Hooke matrices at both temperatures (outlined in Table 2). The effective Young modules are rather isotropic: only a maximum deviation of −2.73% from the mean value 105.14 GPa is noted for Young modulus in finger direction Z at 700 °C. The effective shear modules present a more pronounced orthotropy with GXY <GYZ <GXZ. Mainly the shear modulus in the plane perpendicular to the finger structure is reduced: ∆GXY,m = −9.%. As expected, this tendency is the same at RT: ∆GXY,m = −8.4%. Eventually, the effective Poisson coefficients present the same orthotropy tendency as the shear modulus: νXY < νYZ < νXZ, and we observe a reduction of νXY by nearly ∆νXY,m = −8.% at both temperatures. Yet, the values are slightly larger at 700 °C than at 20 °C. Moreover, the Zener anisotropy coefficient of the homogenized microstructure, expressed by the mean value of the elastic constants, reduces compared to SX value 2.72: Az = 2.14 at RT and Az = 2.22 at 700 °C.

TABLE 2 Effective Young modules, shear modules (in [GPa]) and Poisson coefficients at 20 and 700 °C
Full size table

It should be noted that, in the present homogenization runs, the generated implicit forces, induced by the jump of the Hooke matrix at the finger-interstice interfaces, are rather small. Therefore, HOMAT applies only small corrections to the volume averaging expressions, which are accurate enough for this case. This behaviour differs strongly from the homogenization of partially solidified microstructures, where huge jumps exist at the finger/melt interfaces, leading to large corrections of the volume averaged Hooke matrix.

5 Conclusions and Outlook

In this paper three coupled simulations are used to calculate the mechanical properties of L‑PBF processed IN718.

The melt pool shape, the resulting microstructure, and the mechanical properties have been calculated (the latter at room temperature and at an estimated operating temperature (700 °C)).

The melt pool shape is within the reasonable range of the experimental values (less than 10% deviation). The microstructure, with the solidification conditions from the meltpool simulation as an input, reproduces the patterns observed in experiments (readers interested in additional details may be referred to [3]).

Then the resulting microstructure is reduced to two single crystalline phases, and for the homogenized microstructure, the mechanical properties are calculated. The Young’s Modulus for L‑PBF manufactured IN718 samples is around 200 GPa (varying in a small margin in dependence of the build direction) [12]. Our calculated Young’s Modulus is roughly 105 GPa. The wide gap between these results originates in our single crystalline approach to calculate the properties. L‑PBF samples normally are polycrystalline. This significant difference dictates the next step: extend the model to handle polycrystalline phases.