Modeling and combined application of MOEA/D and TOPSIS to optimize WEDM performances of A286 superalloy

Abstract

Superalloys are categorized as difficult to process materials with a broad spectrum of applications in industries. Process modeling and optimization of WEDM performances on nickel- and titanium-based superalloys are widely investigated. However, such investigations on iron-based superalloy are still lacking and hence probed in the present article. Thus, the paper targets modeling the correlation between the performance parameters and the control parameters with two popular techniques: response surface methodology (RSM) and artificial neural network (ANN) for WEDM of a typical iron-based superalloy, i.e., A286 superalloy. A comparison between the model estimates and the experimental values is made to check ANN and RSM's prediction accuracy. The estimates by the ANN model are exact and consistent with the experimental results. An analysis of variance (ANOVA) test is performed to perceive the degree of statistical significance of parameters. Moreover, a novel two-stage procedure, i.e., MOEA/D in collaboration with TOPSIS method, is implemented to search the optimal condition for process performances. The quality of Pareto-optimal solutions acquired using MOEA/D is compared to that of Pareto-optimal solutions obtained using NSGA II, PESA II, and MMOPSO through the use of a hypervolume (HV) parameter. Wilcoxon’s test is performed to identify the statistical difference between MOEA/D and competing algorithms. The optimal parametric combination recommended by the proposed optimization approach is T_on = 130 µs, T_off = 52 µs, I_peak = 12 A, W_f = 5 m/min and SV = 30 V. The proposed optimization technique can also be exploited in other manufacturing processes.

1 Introduction

Superalloys (nickel-, iron-, and titanium-based alloys) are the most exploited material in sectors like medical, automotive, aerospace, and nuclear reactors on account of their appealing properties at elevated temperatures (Khalid et al. 1999; Pollock and Tin 2006). On account of such characteristics, machining of superalloys by conventional machining practices frequently poses challenges like the evolution of high cutting forces during machining, the formation of burrs, the shortening of tool life, etc. To evade such challenges, machining such alloys is successfully exploited by advanced machining processes like electrochemical machining; spark erosion machining (EDM, wire-EDM), laser beam machining, etc. Yet, among the advanced machining processes, wire-EDM has gained lots of popularity and attention for the last couple of decades as it has more potential and flexibility in generating complex contours due to its embedded technology (Sharma et al. 2015). Moreover, wire-EDM profiles are highly accurate and precise, making the machined components eligible for critical applications. Regardless of its application potentials, wire-EDM has its problems because of the process anisotropy, instabilities, and participation of several process variables during the process. Thus, modeling the process is of utmost importance to understand the process behavior. Furthermore, it is equally important to perform the machining at optimal operating conditions to balance the quality and productivity parameters.

In consideration of the above, researchers have explored various approaches for modeling and predicting the responses (Majumder and Maity 2018; Saha and Mondal 2017). Furthermore, researchers also adopted different optimization procedures for determining the optimal combination of parameters (Saha and Mondal 2016; Saha et al. 2013).

Mandal et al. (2016) modeled four performance attributes with the process parameters during WEDM cutting of Nimonic C-263 superalloy. The desirability function determines the optimal operating conditions. In a recent investigation, the ANN model predicted important performance variables of the WEDM process of Inconel 718. Furthermore, the performance variables are optimized concurrently, exploiting a multi-response signal-to-noise (MRSN) ratio in conjunction with the Taguchi method (Ramakrishnan and Karunamoorthy 2008). Tonday and Tigga (2019) performed the optimization of machining time and surface roughness using RSM in WEDM of Inconel 718. Khan et al. (2014) reported the implementation of grey relational analysis to optimize surface roughness and microhardness simultaneously during the WEDM process. Tarng et al. (1995) exploited the simple weighting strategy to aggregate the two objectives (cutting velocity and surface roughness) into a single objective and then implemented simulated annealing to identify the optimal parameters. Similarly, a research group adopted the Tabu-search algorithm to minimize the objective function (derived from the weighted sum of the performance parameters) and then presented the optimal parametric conditions based on preferences (Sadeghi et al. 2011). Another investigation connected with the WEDM of Inconel-690 is mapping the performance parameters with the process parameters by employing RSM. Furthermore, the authors proposed a modified cuckoo search algorithm to determine the optimal responses (Rao and Venkaiah 2017). Nayak and Mahapatra (2016) proposed an ANN model to establish the relationship between the input parameters and the performance parameters during taper cutting operation of a deep-cryo-treated Inconel 718 in the WEDM process. Furthermore, the bat algorithm is employed to carry out the Optimization. In a different attempt, Kuriakose and Shunmugam (2005) proposed a non-dominated sorted genetic algorithm technique to determine the multiple varieties of optimal parameters for two performance parameters (Pareto set) during wire-EDM of Ti6Al4V. Similarly, Garg et al. (2012) reported a group of Pareto-optimal solutions for the conflicting objectives (CR and SR) in wire-EDM of Ti 6-2-4-2 alloy by exploiting the NSGA II algorithm. The observations from the reported literature direct the research gaps, which are stated as follows:

Most of the investigated works on wire-EDM have been carried out on nickel- and titanium-based alloys. However, sparse literature exists on the WEDM of Iron-based superalloys. Therefore, the present investigation focuses on WEDM of an iron-based superalloy, namely A286 superalloy, emphasizing the modeling and optimization of WEDM performances. This material is considered in the current work as it is categorized as hard-to-cut superalloy, which is extensively used for high-temperature applications (Musavi et al. 2018). Besides, this material is also deployed in frames, after-burner parts, fasteners, casings, rotors, and in other applications due to its attractive mechanical properties and good thermal resistivity (Alphonsa et al. 2015).

Furthermore, it is observed from the reported literatures that ANN and RSM have been quite effective in WEDM modeling; thus, we target the use of these two techniques in the present article in WEDM modeling for A286 superalloy. Predictions made by the two techniques are juxtaposed with the experimental observations to check the two models' prediction accuracy. Again, it is noticed that literature lacks the use of MOEA based on decomposition method in deriving the Pareto-optimal operating conditions for the WEDM responses. Furthermore, the literature also lacks the incorporation of any suitable strategy to derive the best optimal operation condition out of the Pareto sets of optimal operating conditions. Therefore, the present article employs a novel MOEA, i.e., MOEA/D, for multi-objective optimization followed by the implementation of a popular decision-making tool, i.e., TOPSIS, for procuring the best optimal solution. The overall workflow of the present article is demonstrated in Fig. 1. Since the significant contribution of the present paper is conceptualizing a novel methodology for optimization, it is elaborated in detail in the following section.

Fig. 1

Workflow of the present study

2 Optimization

Manufacturing process design, industrial design, structural design, and other fields have all benefited from optimization. We use optimization techniques to solve problems intelligently by selecting the best answer from a larger pool of options. In tackling optimization issues, metaheuristics have become more popular than exact approaches. These methods have been utilized to solve various problems, from single to multi-objective, continuous to discrete, constrained to unconstrained (Boussaïd et al 2013; Dokeroglu et al 2019; Hussain et al. 2019). Metaheuristics are classified into two types, i.e., single solution-based metaheuristic and population-based metaheuristic. Over the last two decades, population-based metaheuristics have got a lot of attention from academics and industry in a wide range of domains. Two factors prompt this: first, the growing need to increase searching efficiency, quality, and lower computational costs; second, the increasing difficulty of engineering optimization problems. Evolutionary algorithms (EAs) are a population-based metaheuristic that simulates natural processes to solve NP-hard and high-complexity problems. Some of the popular EAs are the genetic algorithm (GA) (Mirjalili 2019), cuckoo search (CS) (Abed-alguni and Paul 2020; Abed-alguni and Alkhateeb 2020; Abed-alguni 2019), grey wolf optimization (Abed-alguni and Alawad 2021; Abed-alguni and Barhoush 2018), whale optimization (Abed-alguni et al. 2019), and so on. Single-objective EAs, on the other hand, are unreliable in real-world situations where several objectives conflict, necessitating the use of MOEAs.

The traditional way of tackling multi-objective problems is by converting all objectives into a single-objective function and then employing the single-objective EAs to derive the optimal solution. Converting multiple objectives into a single-objective function is commonly accomplished by aggregating them into a weighted function. This method of handling multi-objective (MO) optimization problems has several drawbacks: the inability to handle discontinuous functions, having a priori information on the relative preferences of the objectives, problems related to non-convexity, delivering only one solution, and trade-offs between objectives are difficult to assess (Ngatchou et al. 2005). As a result, multi-objective evolutionary algorithms (MOEAs) have become popular because they remove these restrictions and provide a set of Pareto-optimal solutions (trade-off solutions).

NSGA II is one of the MOEAs that has been used in the WEDM process multiple times. However, decomposition-based MOEA, such as MOEA/D, has never been employed in any machining process, including the WEDM process. Besides, MOEA/D provides well-diversified Pareto optimum solutions for multi-objective problems. Its computing overhead is lower than other prominent algorithms such as multi-objective genetic local search (MOGLS) and non-dominated sorting genetic algorithm II (NSGA II). MOEA/D also outperforms other algorithms in terms of solution quality (Zhang and Li 2007). Thus, we intend to use MOEA/D for multi-objective optimization in the present work.

MOEAs generally produce a set of non-dominated solutions (Pareto-optimal solutions). The use of MOEA to create Pareto-optimal solutions for any conflicting objectives was also reported in the literature for multi-objective optimization in WEDM process in the preceding section. However, limitation lies in choosing the best optimal solution among the non-dominated optimal group, which creates ambiguity among decision-makers. Thus, a suitable decision-making strategy, i.e., a technique for order preference by similarity to ideal solution (TOPSIS), is adopted in this paper to account for such ambiguity and therefore aids in identifying the best optimal point.

3 Materials and experimental details

3.1 Material composition

In the current investigation, the material is an A286 alloy. The composition of this alloy is: C (0.05 wt.%), Mn (2 wt.%), S (0.025 wt.%), Al (0.35 wt.%), Cr (14 wt.%), Ni (25 wt.%), V (0.2 wt.%), Si (1wt.%), Mo (1.21 wt.%), Ti (2.1 wt.%) and Fe (balance).

3.2 Experimental details

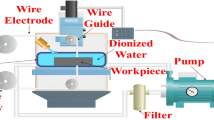
The machining runs have been performed on the Ultra cut F-1 model of wire-EDM machine tool. A view of the WEDM machining setup is displayed in Fig. 2. The longitudinal (Y-axis) and lateral (X-axis) travel ranges are 300 and 400 mm, respectively, and the z-direction travel range is 250 mm. The maximum workpiece size that can be mounted on the machine is (600 × 780 × 250) mm. The workpiece used for this study is of dimensions (200 × 150 × 5) mm, and the geometry proposed for the WEDM cut is a square of size (12 mm × 12 mm). Brass wire overlaid with a zinc layer (250 µm diameter) is deployed as the tool as it provides better flushing conditions in the spark gap (Dauw and Albert 1992). The dielectric fluid used in this study is deionized water.

Fig. 2

WEDM machining setup

In this research, the five process parameters, namely pulse on time (T_on), peak current (I_peak), pulse off time (T_off), servo voltage (SV), and wire feed rate (W_f), are controlled based on earlier works. Three levels for each parameter are considered based on preliminary experiments. During the selection, the bounds of the process parameters indicate fewer chances of wire breakage. The parameters to be controlled and their respective levels are furnished in tabular form, as shown in Table 1.

Table 1 Control parameters and their levels

The experimental layout is designed based on the L₂₇ orthogonal array because Taguchi's L₂₇ orthogonal array intends to exploit only 27 different combinations of parameter levels to extract similar information by conducting 243 (3⁵) experiments. Thus, 27 experiments run with each experiment replicated thrice for assessing the averaged values of responses such as MRR and SR. Table 2 portrays the different process parametric conditions along with the experimental outcomes.

Table 2 Experimental datasets

During the measurement of MRR, the kerf width is eliminated as the variation in kerf width is assumed to have a negligible impact on MRR as compared to the variation in the cutting speed and thickness of the workpiece. Therefore, MRR is evaluated by the following Eq. (1). Similar assumptions and methodology are seen in some of the previous works (Ramakrishnan and Karunamooorthy et al. 2006; Chalisgaonkar and Kumar 2015).

$$ MRR\left( {{\text{mm}}^{2} /\min } \right) = {\text{Cutting}}\;{\text{speed}}\left( {{\text{Cs}}} \right) \times {\text{plate}}\;{\text{thickness}}\left( L \right) $$

(1)

SR is calculated by measuring the arithmetic mean roughness (Ra) of the machined surface using Surtronic S-128 S-Series roughness tester. The measurement of Ra is carried out by traversing the probe along a length of 10 mm (cut-off length ($\lambda_{c}$) = 0.8 mm) in a direction perpendicular to the wire movement direction. For each SR evaluation, Ra is measured thrice from three different positions and averaged out.

4 MOEA/D optimization

MOEA/D, an evolutionary-based multi-objective optimization technique that fundamentally disintegrates a multi-objective optimization problem (MOP) into scalar subproblems, which are thereafter optimized concurrently (Zhang and Li 2007). Optimization of any subproblem is carried out only by exploiting information from its nearest subproblems. Meanwhile, the population of solutions is evolved using an evolutionary algorithm. Distances of nearest subproblems are between the weight vectors. Decomposition in MOEA/D ventured by three approaches is the weighted sum approach, Tchebycheff approach, and penalty-based boundary interactions (PBI) approach (Wang et al. 2015). The flow diagram of the MOEA/D algorithm is provided below (see Fig. 3):

Fig. 3

MOEA/D flow diagram

5 Identification of the best optimal solution by TOPSIS

TOPSIS, a competent MCDM technique initiated by Hwang and Yoon (1981), is employed to endorse the best alternative solution from a collection of Pareto-optimal solutions. The underlying concept is that if any solution is at the shortest geometric distance from a positive ideal solution and simultaneously be at the longest geometric distance from a negative ideal solution, then the solution is said to be the best compromise solution. The computational steps of TOPSIS are presented below:

Step 1 Frame the normalized decision matrix, each element $r_{ij}$ is evaluated by:

$$ r_{uv} = \frac{{x_{uv} }}{{\sqrt {\sum\limits_{u = 1}^{m} {x_{uv}^{2} } } }} $$

(2)

where $x_{uv} =$ response of $u^{th}$ alternative with respect to $v^{{{\text{th}}}}$ criterion.

Step 2 Calculate the weighted normalized decision matrix, the elements are specified by $n_{uv}$

$$ n_{uv} = w_{v} * r_{uv} \;u = 1,2, \ldots m,\;v = 1,2 $$

(3)

Step 3 Determine the positive ideal solution $S^{ + }$ and the negative ideal solution $S^{ - }$

$$ S_{{}}^{ + } = \left( {\max \left[ {n_{11} ,....n_{m1} } \right],\min \left[ {n_{12} ,....n_{m2} } \right]} \right) $$

(4)

$$ S_{{}}^{ - } = \left( {\min \left[ {n_{11} ,....n_{m1} } \right],\max \left[ {n_{12} ,....n_{m2} } \right]} \right) $$

(5)

Step 4 Compute the separation from the positive ideal solution $E_{i}^{ + }$ and the separation from the negative ideal solution $E_{i}^{ - }$ based on n-dimensional Euclidean distance.

$$ E_{u}^{ + } = \sqrt {\sum\limits_{v = 1}^{2} {\left( {\nu_{uv} - s_{v}^{ + } } \right)^{2} } } \;u = 1,2,3, \ldots m\;v = 1,2 $$

(6)

$$ E_{u}^{ - } = \sqrt {\sum\limits_{j = 1}^{2} {\left( {\nu_{ij} - s_{j}^{ - } } \right)^{2} } } \;u = 1,2,3, \ldots m\;v = 1,2 $$

(7)

Step 5 Compute the relative closeness ($CC_{u}$) to the ideal solution as given below:

$$ CC_{u} = \frac{{E_{u}^{ - } }}{{E_{u}^{ + } + E_{u}^{ - } }},\;u = 1,2,3, \ldots m $$

(8)

6 Modelling using RSM

Response surface methodology (RSM) is entirely a statistically based tool for developing, improving, and optimization processes. This includes three steps which are: (a) design an experimental layout to explore the domain of the process or predictor variables, (b) build an empirical model that maps the responses with the predictor variables, (c) optimize the process response. A first-order or a second-order polynomial is used to build an empirical model. The following equation gives the first-order model:

$$ \eta = \underbrace {{\beta_{0} }}_{{{\text{Intercept}}}} + \underbrace {{\beta_{1} x_{1} + \beta_{2} x_{2} + \beta_{3} x_{3} }}_{{{\text{MainEffects}}}} + \underbrace {{\beta_{12} x_{1} x_{2} + \beta_{13} x_{1} x_{3} + \beta_{23} x_{2} x_{3} }}_{{{\text{Interactions}}}} + \cdots $$

(9)

This is the first-order model inclusive of main effects and interactions. Interaction terms are incorporated to capture the curvature if present on the response surface. However, in many instances, the curvature in the actual response surface is so prominent that the first-order model is found to be inadequate. In such cases, a second-order model becomes an appropriate alternative. The second-order model is displayed in the following equation:

$$ \eta = \beta_{0} + \beta_{1} x_{1} + \beta_{2} x_{2} + \beta_{3} x_{3} + \beta_{11} x_{1}^{2} + \beta_{22} x_{2}^{2} + \beta_{3} x_{3}^{2} + \beta_{12} x_{1} x_{2} + \beta_{13} x_{1} x_{3} + \beta_{23} x_{2} x_{3} + \cdots $$

(10)

In the present investigation, having acquainted with the complexity of the machining process, full second-order quadratic models are considered to frame the objective functions for predictions as well as for optimization. The empirical models are displayed below:

$$ \begin{aligned} MRR& = 567 - 20.39T_{{{\text{on}}}} - 2.91T_{{{\text{off}}}} + 102.8I_{{{\text{peak}}}} + 28.4W_{f} + 2.83SV + 0.0497T_{{{\text{on}}}}^{2} + 0.0354T_{{{\text{off}}}}^{2} \\ & \quad - 8.192I_{{{\text{peak}}}}^{2} - 0.037W_{f}^{2} - 0.0302SV^{2} + 0.0117T_{{{\text{on}}}} *T_{{{\text{off}}}} + 0.858T_{{{\text{on}}}} *I_{{{\text{peak}}}} - 0.1511T_{{{\text{on}}}} *W_{f} \\ & \quad - 0.0034T_{{{\text{on}}}} *SV - 0.244T_{{{\text{off}}}} *I_{{{\text{peak}}}} - 0.1140T_{{{\text{off}}}} *W_{f} + 0.0196T_{{{\text{off}}}} *SV - 0.326I_{{{\text{peak}}}} *W_{f} \\ & \quad - 0.145I_{{{\text{peak}}}} *SV \\ \end{aligned} $$

(11)

$$ \begin{aligned} SR = & - 177.3 + 0.59T_{{{\text{on}}}} - 0.889T_{{{\text{off}}}} + 27.26I_{{{\text{peak}}}} + 1.82W_{f} + 0.110SV - 0.00276T_{{{\text{on}}}}^{2} + 0.00934T_{{{\text{off}}}}^{2} \\ & \quad - 1.2656I_{{{\text{peak}}}}^{2} - 0.0323W_{f}^{2} - 0.00642SV^{2} + 0.00014T_{{{\text{on}}}} *T_{{{\text{off}}}} + 0.0177T_{{{\text{on}}}} *I_{{{\text{peak}}}} - 0.0157T_{{{\text{on}}}} *W_{f} \\ & \quad - 0.0034T_{{{\text{on}}}} *SV - 0.244T_{{{\text{off}}}} *I_{{{\text{peak}}}} - 0.1140T_{{{\text{off}}}} *W_{{\text{f}}} + 0.0196T_{{{\text{off}}}} *SV - 0.326I_{{{\text{peak}}}} *W_{f} \\ & \quad - 0.145I_{{{\text{peak}}}} *SV \\ \end{aligned} $$

(12)

In addition, an ANOVA test is carried out on statistical software (MINITAB 17 version) to analyze the significant parameters (individual and interacting parameters) affecting the two response parameters, i.e., MRR and SR (see Tables 3 and 4). The models (Eq. 11 & Eq. 12) are found to fit the experimental data adequately for a confidence level of 95% (user-defined criteria) since from the ANOVA analysis (Tables 3 and 4) for both the models (MRR and SR), P values obtained are less than 0.05. To assess the statistical significance of individual parameters and the statistical significance of interacting parameters on performance parameters, we observe the values of two parameters, i.e., F-value and P-value. Any statistically significant parameter is likely to have a higher F-value (more than 1) and a lower P-value (less than 0.05).

From the ANOVA analysis for MRR (Table 3), it is evident that T_on, T_off, and Wf are influential parameters affecting the MRR. Apart from that, (T_on*I_peak) and (T_on*Wf) is the momentous two-way interaction parameters affecting the MRR. In the same manner, it can be depicted from the ANOVA analysis for SR (Table 4) that I_peak is the only influential parameter affecting the surface roughness, and there are no two-way interaction parameters that affect the SR.

Table 3 ANOVA analysis for MRR

Table 4 ANOVA analysis for SR

7 Modelling using ANN

Artificial neural networks (ANN) are data-driven algorithms that are used extensively to study different aspects of the machining domain (Imani et al. 2020; Saha et al. 2020). In this paper, ANN is deployed to predict responses in the WEDM process for A286 alloy. The ANN model's construction comprises necessary steps: normalization of datasets, selection of training algorithm, network topology determination, network training, testing, and model validation.

7.1 Normalization of datasets

Data normalization is a process of scaling the range of input and output variables to either [− 1, 1] or [0, 1]. In this paper, we carried out normalization to the input/output data by employing Eq. (13) as discussed in the article by Sanjay and Jyothi (2006).

$$ x_{i} = \frac{0.8}{{d_{\max } - d_{\min } }}(d_{i} - d_{\min } ) + 0.1 $$

(13)

where $d_{\max }$ is the maximum value of the response parameter,$d_{\min }$ is the minimum value of the response parameter, and $d_{i}$ is the nominal value of the response parameter.

7.2 Selection of training algorithm, network topology, network training, testing, and validation

The training algorithm proposed for developing the ANN model is a feedforward backpropagation algorithm. The network architecture which commonly executes this algorithm is a multilayer perceptron (MLP). In the present work, the input layer of the MLP has five neurons that correspond to five input features (T_on, T_off, I_peak, Wf, and SV). The next layer is the intermediate (hidden) layer, for which the number of neurons is to be specified by trial and error procedure. The last layer is the extreme (output) layer with two neurons corresponding to dual responses (MRR and SR). Hyperbolic tangent sigmoid transfer function and linear transfer function are incorporated in the intermediate and extreme layer, respectively, to map suitably the correlation between the responses and the input features. A Levenberg–Marquardt algorithm, i.e., trainlm, is proposed to train the network on account of its faster convergence rate. Gradient descent learning function, i.e., LEARNGD, is chosen to update the weights and biases associated with the network.

To ensure an optimal network structure for maximum performance, it is crucial to quantify the exact number of hidden neurons in the intermediate layer. After comprehensive trial and error, it is identified that the network topology which is most eligible in correlating the responses with the input features must have 9 hidden neurons in the intermediate layer. Hence, the network topology which is considered in this paper is 5-9-2. The strategy adopted during the process of identification of the network is discussed below.

For establishing the ANN models based on a different number of hidden neurons, a total of 81 samples are fragmented into 70% (training), 15% (testing), and 15% (validation) set. In this work, the performances of the different configured networks' performances (networks with variable hidden neurons in the intermediate layer) are assessed by the scatter plots. For the sake of brevity, scatter plots are provided here only for the selected network topology (5-9-2).

Scatter plots intuitively estimate the quality of model fitment by illustrating the degree of connection between the targets and network outputs. Figure 4 delivers scatter plots associated with training, testing, validation, and the overall dataset of the selected network. It is observed from the plots that the regression line almost inclines at an angle of 45⁰ with the network output and the target and exhibits a high correlation coefficient value, R = 0.99 for the training, testing, validation, and overall datasets. Such behavior ensures that the network topology 5-9-2 is proficient in mapping the MRR and SR with the input features. Moreover, it can also be ensured that the model is least overfitted and at the same time has maximum generalization capability.

Fig. 4

Training, testing, validation, and overall scatter plots for 5-9-2 network

8 Comparisons between ANN and RSM

To perform a comparison amid ANN and RSM model predictions, the predictions carried out by the ANN model and RSM-based polynomial regression models are compared with the experimentally obtained averaged responses for 27 experimental runs. It is evident from the plots portrayed in figures (Figs. 5 and 6) that the green dots representing the observed responses and the purple dots representing the ANN predicted responses completely coalesce with each other, thereby demonstrating the accuracy of the ANN model. On the other hand, RSM-based predictions represented by purple dots are slightly deviating from the green dots for almost all the observations except few cases, which depict that the accuracy of RSM-based models is less than the ANN model.

Fig. 5

Plots showing comparison between ANN and RSM predictions for MRR

Fig. 6

Plots showing a comparison between ANN and RSM predictions for SR

9 Multi-objective optimization using MOEA/D coupled with TOPSIS

The WEDM process often shows that when the MRR is high, the SR also increases due to the process's inherent nature. Nonetheless, stringent industrial requirements seek to yield high MRR and low SR to augment productivity and product quality, respectively. Thus, the contemporary problem is a multi-objective optimization problem (MOP) wherein it is targeted to maximize the MRR and minimize the SR simultaneously subjected to a list of parameter bounds. The MOP is stated as below:

$$ \begin{aligned} & {\text{Maximize}}\;MRR\left( {T_{{{\text{on}}}} ,{\text{T}}_{{{\text{off}}}} ,I_{{{\text{peak}}}} ,W_{f} ,SV} \right) \\ & {\text{Minimize}}\;SR\left( {T_{{{\text{on}}}} ,T_{{{\text{off}}}} ,I_{{{\text{peak}}}} ,W_{f} ,SV} \right) \\ \end{aligned} $$

$$ {\text{Subjected}}\;{\text{to}}:\begin{array}{*{20}l} {120 \le T_{{{\text{on}}}} \le 130} \hfill \\ {48 \le T_{{{\text{off}}}} \le 56} \hfill \\ {10 \le I_{{{\text{peak}}}} \le 12} \hfill \\ {5 \le W_{f} \le 9} \hfill \\ {30 \le SV \le 40} \hfill \\ \end{array} $$

To solve the MOP, we offer a metaheuristic optimization technique called the multi-objective evolutionary algorithm based on decomposition (MOEA/D). A vast number of optimal solutions are generated using MOEAs (non-dominated solutions). However, due to practical limits and to avoid information overload, it is best to adhere to a single solution that can achieve both goals to some extent. However, subjective ranking of solutions can be an option, although it is difficult and imprecise. As a result, we used the TOPSIS method to rank the non-dominated solution thoroughly in this paper.

To carry out the multi-objective optimization, response surface models, as referred to in Sect. 6, correlate the process parameters with the response parameters. The empirical models of MRR and SR (Eq. (11) & Eq. (12)) are used as the objective functions. The optimization code is framed for the minimization of objective functions. Thus, MRR in Eq. (11) is changed to (-MRR) during the optimization, while on the contrary, SR in Eq. (12) remains the same.

The optimization is implemented by developing a MATLAB code. The important tuning parameters of MOEA/D and their corresponding values are displayed below:

• (a) Maximum number of generations = 250.

• (b) Population size = 100.

• (c) Distribution index = 20.

• (d) Crossover probability = 1.

• (e) Mutation probability = 1/dimension of problem.

• (f) Mutation index = 20.

After optimizing the dual objectives (MRR & SR) with parameter boundaries as constraints, the Pareto front (PF) is retrieved, which indicates the set of non-dominated optimal solutions. Then, we intend to check the efficacy of MOEA/D by comparing its performance with the performances of prominent algorithms such as the non-dominated sorting genetic algorithm (NSGA II) (Deb et al. 2002), Pareto-envelope-based selection algorithm (PESA II) (Corne et al. 2001), and multi-objective particle swarm optimization (MMOPSO) (Lin et al. 2015). In the present paper, hypervolume (HV) (While et al. 2006) is considered the performance metric to evaluate the performances of the representative algorithms. For this goal, statistical data such as the mean and standard deviation of HV for all algorithms are retrieved (shown in Table 5) by running each algorithm 30 times. Table 5 shows that MOEA/D has the highest mean value of HV and the lowest standard deviation of HV, implying that MOEA/D outperforms other competing algorithms. In addition, a statistical test, namely Wilcoxon's test (presented in Table 5), was used to determine whether the mean HV produced by MOEA/D and the other algorithms differed significantly. MOEA/D is statistically superior to PESA II (shown by the-symbol) but statistically comparable to NSGA II and MMOPSO (represented by the = symbol). Besides, Fig. 7 depicts that MOEA/D provides more uniformly, well-diversified, and equally spread solutions. The above comprehensive analysis proves that MOEA/D has produced the best results.

Table 5 HV metric and Wilcoxon’s test

Fig. 7

PF of a MOEA/D, b NSGA II, c PESA II, and d MMOPSO

Since each solution in the PF of MOEA/D can be accepted as the candidate solution based on the operator's requirement. Thus, pointing out the best solution is a bit complicated task. To tackle such an ambiguous situation, a decision-making technique, i.e., TOPSIS, is intervened in this work to select the best optimal solution. In the TOPSIS algorithm's execution, weights are allotted to MRR and SR based on relative preferences. This paper allocates equal weights to the two performance parameters to establish the weighted normalized decision matrix. Then the positive ideal solution and negative ideal solution are identified according to the TOPSIS algorithm. Finally, each solution's relative closeness coefficient ($CC_{i}$) of the Pareto front is calculated based on the two distant measures (separation from a positive ideal solution,$E_{i}^{ + }$ and separation from a negative ideal solution, $E_{i}^{ - }$). The measurement of relative closeness coefficient plays a pivotal role in assigning the ranks of the Pareto solutions. To claim for top rank, it is essential that the solution should have the maximum relative closeness coefficient value.

Table 8 (see Appendix) reports all the 100 Pareto-optimal solutions along with the vital TOPSIS parameters and their rankings. It is evident that solution number 91 achieves the maximum relative closeness coefficient of 0.540115634 and holds the first rank (Table 8). Thus, solution number 91 draws the most priority to be the best optimal solution. Furthermore, for the sake of visualization, this particular solution is also indicated by a rectangular block on the Pareto front, as illustrated in Fig. 8. The values of the response parameters corresponding to the optimal solution are MRR = 36.04 and SR = 3.49, respectively.

Fig. 8

Pareto front with TOPSIS selection

Furthermore, a confirmatory experiment has been conducted to validate the responses at the optimal input parametric setting. The deviations between the optimal responses and the affirmative experimental responses are less than 1%, as shown in Table 6. Finally, it is intended to check the robustness of the proposed approach. Because of the above, optimization of dual responses is carried out with the proposed optimization approach and then compared with the optimization results put forth by the other technique in the paper by Devarasiddappa and Chandrasekaran (2020). In both methods, the computational procedure is carried out by allotting equal weightage for both the responses. It is observed that the proposed method is far more effective and robust in optimizing the dual responses. The results are reported in Table 7.

Table 6 Validation of the proposed optimization approach with experimental results

Table 7 Validation of the proposed optimization approach with other technique (Devarasiddappa and Chandrasekaran 2020)

10 Conclusions

Prior research works on wire-EDM have been investigated on nickel- and titanium-based alloys. However, there is a paucity of research on the WEDM of iron-based superalloys. Thus, in the present paper, we first targeted to model the two WEDM performance attributes: MRR and SR with the process parameters by two well-known techniques: ANN and RSM. Besides, we compared the predictions made by the two techniques with experimental observations to determine the best predictive model. It is noted that ANN model is relatively more accurate than RSM in predicting the responses. ANOVA analysis is performed to depict the significant parameters affecting the responses. From ANOVA analysis, we identified that I_peak is the most momentous individual parameter that affects the MRR followed by T_on and W_f. The interacting parameters found to be momentous for MRR are (T_on*I_peak) and (T_on*W_f). Again, from the ANOVA analysis for SR, I_peak is the sole parameter that is found to be momentous. However, there is no evidence of any momentous interacting parameters affecting the SR. Secondly, we targeted to optimize the WEDM performance attributes, i.e., MRR and SR simultaneously. To this end, we propose a novel decomposition-based evolutionary approach, i.e., MOEA/D as the optimizer to derive the Pareto-optimal solutions. To verify the quality of Pareto-optimal solutions, we compared the Pareto-optimal solutions of MOEA/D with the Pareto-optimal solutions obtained using the popular MOEAs such as NSGA II, PESA II, and MMOPSO. The performances are compared using hypervolume (HV) as the performance parameter. It is noted that MOEA/D outperforms the other competing algorithms. However, the major limitations of the proposed MOEA approach is that it may violate the essential assumption of MOEA/D if the PF is complex (i.e., discontinuous, degenerate, etc.) as the uniform weight vectors may be unable to produce the solutions in the feasible region which eventually results in diversity issues in the solution set (Qi et al. 2014). But such problem does not arise if the PF is continuous. Again, it is worth mentioning that other researchers in the WEDM have not mentioned any suitable procedure to identify the best optimal point out of the Pareto-optimal solutions obtained by evolutionary algorithms. Thus, the present paper is novel in the sense that it incorporates a multi-objective evolutionary algorithm based on decomposition (MOEA/D) in conjunction with an MCDM technique, namely a technique for order preference by similarity to ideal solution (TOPSIS) to identify the optimal machining condition from the set of Pareto-optimal solutions. The best parametric combination recommended by the combined approach is T_on = 130 µs, T_off = 52 µs, I_peak = 12 A, W_f = 5 m/min and SV = 30 V. Finally, a confirmatory experiment has been conducted to validate the responses at the optimal input parametric setting. The deviations among the optimal responses and the confirmatory experimental responses are found to be less than 1%. To validate the robustness of the proposed optimization methodology, optimization problem from published literature (Devarasiddappa and Chandrasekaran 2020) is solved with the proposed optimization methodology and the results are compared with the results furnished in the paper. The result obtained by the proposed approach is found to be more optimal than the results provided in the paper.

Future research might analyze other performance parameters such as microhardness, recast layer thickness, residual stress, etc. Moreover, modeling the different performance parameters can also be carried out by other advanced modeling techniques. The proposed optimization technique can be used to optimize other WEDM performance parameters. In addition, the proposed optimization technique can also be exploited in other manufacturing processes.

Appendix

See Table 8.

Table 8 Allocation of ranks to non-dominated optimal solutions exploiting TOPSIS method