1 Introduction

Forecasting techniques continue to be largely used in the time series analysis at present. One of the most popular forecasting techniques is the autoregressive integrated moving average (ARIMA) (Kadılar 2005). The approach of Box-Jenkins (1976) is also frequently used as a basic approach in time series literature to obtain the best ARIMA model. In addition, exponential smoothing methods have also been used in the literature for time series forecasting. Indeed, exponential smoothing models are special cases of ARIMA models. In classical time series, exponential smoothing methods are generally described under three headings as the simple exponential smoothing, Holt’s exponential smoothing and Winter’s exponential smoothing (Kadılar 2005). However, there are also new exponential smoothing methods proposed in the literature. One of these methods is ATA exponential smoothing method proposed by Yapar (2016). ATA exponential smoothing method (Yapar 2016; Yapar et al. 2017a, b) is an updated and effective time series analysis method proposed as an alternative to exponential smoothing methods in the literature.

Conventional forecasting techniques need assumptions like normality, stability and linearity because these methods are based on probability theory. However, many time series in real life do not satisfy any assumptions, and so these time series need to be solved via using some non-probabilistic methods in the literature. In the literature, non-probabilistic time series forecasting methods are generally separated into three parts as fuzzy time series, artificial neural networks and other computational methods. Additionally, these non-probabilistic methods could be used together. For instance, the analysis of a fuzzy time series method includes an artificial neural network or a computational method. In this regard, the content of this study is generally about a new non-probabilistic method. The first fuzzy time series approach was proposed by Song and Chissom (1993a). In Song and Chissom (1993a), the analysis of a fuzzy time series consists generally of three phases. These phases are fuzzification, the determination of fuzzy relations and defuzzification, respectively. In the fuzzification phase, dividing the universe of discourse proposed by Song and Chissom (1993a, b), was used largely in literature. Additionally, there are some studies about being selected for the optimal interval length in the literature because determining the interval lengths affects the forecasting performance significantly in the fuzzification phase. In the literature, the first study of these studies was proposed by Huarng (2001) to determine the optimal interval length. Huarng (2001) proposed two different approaches based on distribution and average. Huarng and Yu (2006) also proposed a ratio-based method to determine the optimal interval length. The other studies to determine the optimal intervals were given by Yolcu et al. (2009), Egrioglu et al. (2010) and Egrioglu et al. (2011). In fuzzy time series literature, the centralization technique is mainly used in the defuzzification phase that is the final phase to solve the fuzzy time series. The determining of fuzzy relations is very important in the fuzzy time series methods. Therefore, this stage is effective to improve the forecasting performance of any fuzzy time series method. Song and Chissom (1993b) used the complex matrix operations to determine fuzzy relations as being based on the fuzzy set theory of Zadeh (1965). Then, Chen (1996) proposed a new method based on fuzzy relation tables instead of the complex matrix operations of Song and Chissom (1993b). Thereby, many fuzzy time series methods based on fuzzy relation tables have been proposed so far. In fuzzy time series literature, some methods that use fuzzy relation tables to determine fuzzy relations were given by Chen (2002), Chen and Chen (2011), Chen and Tanuwijaya (2011), Kocak (2013), Cheng et al. (2016) and Kocak (2017). Artificial neural networks (ANNs) are intensely used in fuzzy time series. Aladag et al. (2009) used the ANNs to determine fuzzy relations for the high-order fuzzy time series model in the fuzzy time series literature. Egrioglu et al. (2009a) also used the ANNs for the high-order multivariate time series method. Yu and Huarng (2010) proposed a new method based on the artificial neural network to define fuzzy relations. In fuzzy time series literature, some methods that use ANNs to determine fuzzy relations were given by Egrioglu et al. (2009b), Aladag et al. (2010), Aladag (2013), Kocak (2015), Bas et al. (2015), Kocak (2013) and Bas et al. (2018). Also, many fuzzy time series methods have been proposed based on particle swarm optimization (PSO). In the fuzzy time series literature, Kuo et al. (2009) developed a new method named hybrid particle swarm optimization (MPSO) for solving the historical data of enrollments of the University of Alabama. Similarly, Hsu et al. (2010) used the modified PSO method and proposed a new method named modified turbulent particle swarm optimization (MTPSO) for forecasting temperature. Some methods that use PSO were also given by Kuo et al. (2010), Park et al. (2010), Huang et al. (2011), Aladag et al. (2012), Chen and Kao (2013), Singh and Borah (2014) and Cagcag Yolcu and Lam (2017). Besides, some studies use fuzzy c-means (FCM) to obtain membership values. Egrioglu et al. (2013) and Cagcag Yolcu and Alpaslan (2018) proposed different models based on FCM and PSO. There are also non-probabilistic and non-parametric time series forecasting methods based on the methods of machine learning, fuzzy inference system, artificial neural network, artificial intelligence, besides fuzzy time series methods. Some of these studies were given by Yolcu et al. (2013), Aladag et al. (2014), Zhou et al. (2016), Egrioğlu et al. (2017) and Tak (2021). Yolcu et al. (2013) proposed a new artificial neural network based on PSO for solving linear and nonlinear time series. Aladag et al. (2014) proposed a new artificial neural network time series forecasting method based on the median neuron model. Zhou et al. (2016) predicted some financial time series by using a dendritic neuron model. Tak (2018) proposed a meta fuzzy functions approach for time series forecasting. Tak et al. (2018) proposed a recurrent type-1 fuzzy functions approach for time series forecasting. Egrioglu et al. (2019a) proposed a median-Pi ANN model for time series analysis. Tak (2020a) proposed a type-1 possibilistic fuzzy forecasting functions method for time series forecasting. Fuzzy time series uses only membership values for solving fuzzy time series. However, intuitionistic fuzzy time series based on intuitionistic fuzzy sets use both membership and non-membership values. Therefore, more information is used for the forecasting process. The first article about intuitionistic fuzzy time series (IFTS) was proposed by Zheng et al. (2013a). For this reason, the subject of IFTS can be thought a new and an updated field for time series literature. Fundamental definitions of IFTS were initially given by Zheng et al. (2013a). Furthermore, Zheng et al. (2013b) used the intuitionistic fuzzy c-means algorithm proposed by Chaira (2011) to determine membership and non-membership values. Lei et al. (2016) proposed a high-order intuitionistic fuzzy time series model by using an unequal partition of the universe of discourse based on the fuzzy clustering algorithm. Kumar and Gangwar (2016) proposed a method to determine intuitionistic fuzzy relations. Fan et al. (2016) proposed a long-term intuitionistic fuzzy time series forecasting model. Egrioglu et al. (2019b) proposed an intuitionistic fuzzy time series forecasting method. Also, some other studies about intuitionistic fuzzy time series were proposed by Zheng et al. (2014), Wang et al. (2014), Joshi et al. (2016), Hu et al. (2017), Fan et al. (2017), Abhishekh et al. (2018) and Tak (2020b). A novel, explainable, robust

2 New definitions for intuitionistic fuzzy time series

Many definitions of fuzzy time series are based on Song and Chissom’s definition that is the first definition of fuzzy time series in the literature. However, in recent years, new definitions of fuzzy time series have been made, and many researchers have preferred to use new definitions in their studies. New definitions were explained in the study of Egrioglu et al. (2019b). The following new definitions are introduced below.

Definition 1

(New Definition: High-Order Single-Variable Intuitionistic Fuzzy Time Series Forecasting Model)

Let \({\mathrm{IF}}_{t}\) be an intuitionistic fuzzy time series. \({A}_{1},{A}_{2},\ldots ,{A}_{c}\) are intuitionistic fuzzy sets on a universal set. \({\mu }_{{A}_{j}}\left(t\right)\), \({\nu }_{{A}_{j}}\left(t\right)\) are membership and non-membership values of tth observation to jth intuitionistic fuzzy set. The high-order single-variable intuitionistic fuzzy time series model is given in Eq. (1).

$$ \begin{aligned} & X_{t} = G\left( {\mu_{{A_{1} }} \left( {t - 1} \right),\mu_{{A_{2} }} \left( {t - 1} \right) \ldots ,\mu_{{A_{c} }} \left( {t - 1} \right), \ldots ,{ }\mu_{{A_{1} }} \left( {t - p} \right),\mu_{{A_{2} }} \left( {t - p} \right), \ldots ,\mu_{{A_{c} }} \left( {t - p} \right),} \right. \\ & \quad \left. {\nu_{{A_{1} }} \left( {t - 1} \right),\nu_{{A_{2} }} \left( {t - 1} \right), \ldots ,\nu_{{A_{c} }} \left( {t - 1} \right), \ldots ,\nu_{{A_{1} }} \left( {t - p} \right),\nu_{{A_{2} }} \left( {t - p} \right), \ldots ,\nu_{{A_{c} }} \left( {t - p} \right)} \right) + \varepsilon_{t} \\ \end{aligned} $$
(1)

In Eq. (1), \(G\) is a linear or nonlinear function, \({\varepsilon }_{t}\) is an error term with zero mean, \({\mu }_{{A}_{1}}\left(t-1\right),\ldots ,{\mu }_{{A}_{c}}\left(t-p\right)\) and \({\nu }_{{A}_{2}}\left(t-1\right),\ldots ,{\nu }_{{A}_{c}}\left(t-p\right)\) are lagged membership values and non-membership values, respectively, obtained from \({X}_{t-1},\ldots ,{X}_{t-p}\). Equation (1) expresses that any time series are affected by lagged membership values and non-membership values.

Definition 2

(New Definition: High-Order Single-Variable Intuitionistic Fuzzy Time Series Forecasting Model based on the principal components analysis and the robust regression analysis)

Let \({\mathrm{IF}}_{t}\) be an intuitionistic fuzzy time series. \({A}_{1},{A}_{2},\ldots ,{A}_{c}\) are intuitionistic fuzzy sets on a universal set. \({\mu }_{{A}_{j}}\left(t\right)\), \({\nu }_{{A}_{j}}\left(t\right)\) are membership and non-membership values of tth observation to jth intuitionistic fuzzy set for \(j=1,2,\ldots ,c\). The high-order single-variable intuitionistic fuzzy time series model based on the principal components analysis is given in Eq. (2).

$$ X_{t} = \beta_{0} + \beta_{1} z_{1} + \beta_{2} z_{2} + \cdots \beta_{q} z_{q} { } + \varepsilon_{t} \quad {\text{for}}\quad q \le cp{ } $$
(2)

where \({z}_{i},i=1,2,\ldots ,q\) are principal components and are given in Eq. (3).

$$ \begin{aligned} & z_{i} = f_{i} \left( {\mu_{{A_{1} }} \left( {t - 1} \right),\mu_{{A_{2} }} \left( {t - 1} \right) \ldots ,\mu_{{A_{c} }} \left( {t - 1} \right), \ldots ,{ }\mu_{{A_{1} }} \left( {t - p} \right),\mu_{{A_{2} }} \left( {t - p} \right), \ldots ,\mu_{{A_{c} }} \left( {t - p} \right),} \right. \\ & \quad \left. {\nu_{{A_{1} }} \left( {t - 1} \right),\nu_{{A_{2} }} \left( {t - 1} \right), \ldots ,\nu_{{A_{c} }} \left( {t - 1} \right), \ldots ,\nu_{{A_{1} }} \left( {t - p} \right),\nu_{{A_{2} }} \left( {t - p} \right), \ldots ,\nu_{{A_{c} }} \left( {t - p} \right){ }} \right){ }\quad = 1,2,,\ldots ,q \\ \end{aligned} $$
(3)

In Eq. (3), \(p\) is the number of lagged variables, \({\mu }_{{A}_{1}}\left(t-1\right),\ldots ,{\mu }_{{A}_{c}}\left(t-p\right)\) and \({\nu }_{{A}_{1}}\left(t-1\right),\ldots ,{\nu }_{{A}_{c}}\left(t-p\right)\) are lagged membership values and non-membership values obtained from \({X}_{t-1},\ldots ,{X}_{t-p}\), q is the number of the important principal component for \(q\le cp\), \({f}_{i}\) is ith linear function obtained by using the correlation matrix of the principal component analysis,\({z}_{i}\) is the ith z-score calculated via the principal component analysis, \({\beta }_{0},{\beta }_{1},{\beta }_{2}\ldots {\beta }_{q}\) are regression coefficients obtained via the robust regression method and \({\varepsilon }_{t}\) is the error term with zero means.

3 Intuitionistic fuzzy C-means algorithm

Chaira (2011) proposed a clustering algorithm (IFCM) for intuitionistic fuzzy sets. The algorithms have been commonly used in intuitionistic fuzzy time-series studies (Zheng 2013a, b; Egrioglu et al. 2019b) in the literature. The algorithm of intuitionistic fuzzy c-means clustering was given in Algorithm 1.

Algorithm 1

The intuitionistic fuzzy c-means clustering algorithm.

Step 1. Calculate the membership values (\({u}_{ik}, i=1,2,\ldots ,c;k=1,2,\ldots ,n\)) by using Eq. (6).

$${u}_{ik}=\frac{{r}_{ik} }{\sum\nolimits_{i=1}^{c}{r}_{ik}}$$
(4)

Suppose \({x}_{k} (k=1,2,\ldots , n)\) is a time series with n observations. In Eq. (4), \(c\) is the number of clusters determined by the researcher, and \({r}_{ik} (i=1,2,\ldots ,c;k=1,2,\ldots ,n)\) are random values generated from the uniform distribution that has the parameters \(\left(0,1\right).\)

Step 2. Calculate the hesitation degrees (\({\pi }_{ik}, i=1,2,\ldots ,c;k=1,2,\ldots ,n\)) and intuitionistic fuzzy membership values (\({u}_{ik}^{*}, i=1,2,\ldots ,c;k=1,2,\ldots ,n)\) by using Eqs. (5) and (6), respectively. Thereafter, save the intuitionistic membership values \(({u}_{ik}^{*})\) into a matrix named \({U}_{\mathrm{old}}\).

$${\pi }_{ik} =1-{u}_{ik}-{\left(1-{{u}_{ik}}^{\alpha }\right)}^{1/\alpha }, \alpha >0$$
(5)
$${u}_{ik}^{*}={u}_{ik}+{\pi }_{ik}$$
(6)

Step 3. Calculate centres of the clusters (\({v}_{i}^{*}, i=1,2,\ldots ,c)\) of the intuitionistic membership values (\({u}_{ik}^{*})\) by using Eq. (7).

$${v}_{i}^{*}=\frac{\sum\nolimits_{k=1}^{n}{\left({u}_{ik}^{*}\right)}^{f}{x}_{k}}{\sum\nolimits_{k=1}^{n}{\left({u}_{ik}^{*}\right)}^{f}} ;i=1,2,\ldots ,c$$
(7)

In Eq. (7), \({x}_{k} \left(k=1,2,\ldots , n\right)\) are observations of the time series the and \(f\) is the fuzziness index.

Step 4. Update the membership values (\({u}_{ik}, i=1,2,\ldots ,c;k=1,2,\ldots ,n\)) by using Eqs. (8)–(9).

$${u}_{ik}=\frac{1}{{\sum \nolimits}_{j=1}^{c}{\left(\frac{{d}_{ik}}{{d}_{jk}}\right)}^{2/(f-1)}} i=1,2,\ldots ,c;k=1,2,\ldots ,n$$
(8)
$${d}_{ik}=\sqrt{{({x}_{k}-{v}_{i}^{*})}^{2}}$$
(9)

In Eq. (8), \({d}_{ik}\) (\(i=1,2,\ldots ,c;k=1,2,\ldots ,n\)) is the Euclidean distance measure between ith cluster centre and kth observation.

Step 5. Go to Step 2 and update the hesitation degrees (\({\pi }_{ik}, i=1,2,\ldots ,c;k=1,2,\ldots ,n\)) and fuzzy membership values (\({u}_{ik}^{*}, i=1,2,\ldots ,c;k=1,2,\ldots ,n)\) by using \({u}_{ik}\) values obtained in Step 4. Thereafter, save the new intuitionistic membership values (\({u}_{ik}^{*})\) into a matrix named \({U}_{\mathrm{new}}\).

Step 6. Calculate non-membership values \(({v}_{ik}, i=1,2,\ldots ,c;k=1,2,\ldots ,n)\) by using Eq. (10). Thereafter, save the new intuitionistic membership values \(({u}_{ik}^{*})\) into a matrix named \(V\).

$${u}_{ik}^{*}+{\pi }_{ik}+{v}_{ik}=1$$
(10)

In Eq. (10), \({u}_{ik}^{*}\) and \({\pi }_{ik}\) are intuitionistic membership values and hesitation degrees obtained in Step 5.

Step 7. Check the stopping criteria given in Eq. (11). If the condition is satisfied, stop the algorithm, otherwise make \({U}_{\mathrm{old}}={U}_{\mathrm{new}}\) and go to Step 3. \(\varepsilon \) is a small positive number and \({\Vert .\Vert }_{2}\) is the \({L}_{2}\) norm.

$${\Vert {U}_{\mathrm{new}}-{U}_{\mathrm{old}}\Vert }_{2}<\varepsilon $$
(11)

In Eq. (11), \(\varepsilon \) is a small positive number and \({\Vert .\Vert }_{2}\) is the \({L}_{2}\) norm.

4 The robust regression

The robust regression is commonly used instead of the least-square method in the literature because robust estimators are not affected by outliers too much. Robust regression techniques can be given as the L1 technique of Edgeworth (1887), M-Estimates of Mallows (1975), and S-Estimates of Rousseeuw (1984). Robust regression algorithms based on these fundamental robust techniques have been proposed in the literature. One of these algorithms is the iteratively reweighted least-squares technique (James et al. 1988). In this study, robust regression estimates were used iteratively reweighted the least-squares technique in defining the fuzzy relation phase. Accordingly, the algorithm of the iteratively reweighted least squares is given in Algorithm 2.

Algorithm 2

Iteratively reweighted least-squares algorithm.

Step 1. Calculate initial regression coefficient estimates \(\widehat{\beta }\) of β via the least-square method for linear regression model given in Eq. (12) and calculate standard deviation estimate \(\widehat{\sigma }\) of σ by using Eq. (13).

$$Y = X_{{n{*}\left( {p + 1} \right)}} \beta_{{\left( {p + 1} \right){*}1}} +\upvarepsilon _{{n{*}1}} $$
(12)
$$\hat{\sigma } = \frac{{{\text{Median}} \left( {\left| {e_{i} } \right|} \right)}}{0.6745} ;\quad i = 1,2, \ldots ,n$$
(13)

In Eq. (12), \(n\) is the observation number, \(p\) is the independent variable number, \(Y\) is the dependent variable vector, and \(X\) is the independent variable matrix that values of its first column are 1, \(\upvarepsilon \) is an error parameter vector, \({e}_{i}\) is an estimate of \(\upvarepsilon _{i}\) for ith observation obtained via the least and 0.6745 is the constant used to make estimates for normal distribution.

Step 2. Calculate residuals (\({e}_{i}\); \(i=1,2,\ldots ,n)\) by using Eq. (14).

$${e}_{i}={y}_{i}-{x}_{i}^{{{\prime}}}\widehat{\beta }$$
(14)

In Eq. (14), \({y}_{i}\) is ith observation value of the dependent variable and \({x}_{i}^{{{\prime}}}\) is a row vector that is the transpose of the first column of \(X\) matrix.

Step 3. Calculate weight values \({(w}_{i};i=1,2,\ldots n)\) via Eq. (15) by using bisquare weight function \((W)\) given in Eq. (16).

$${w}_{i}=W\left(\frac{{e}_{i}}{\widehat{\sigma }}\right)$$
(15)
$$W\left(e\right)=\left\{\begin{array}{l}{\left[1-{\left(\frac{e}{4.685}\right)}^{2}\right]}^{2},\quad \mathrm{for}\,\, \left|e\right|\le 4.685\\ 0 ,\quad \mathrm{for}\,\, \left|e\right|>4.685\end{array}\right\}$$
(16)

In Eq. (15), \(\widehat{\sigma }\) is standard deviation estimates and 4.685 is the tuning constant for the bisquare distribution.

Step 4. Calculate \({\widehat{\beta }}_{\mathrm{new}}\) by using Eq. (17).

$$\sum_{i=1}^{n}{w}_{i}{{x}_{i}(y}_{i}-{x}_{i}^{{{\prime}}}{\widehat{\beta }}_{\mathrm{new}})=0$$
(17)

Step 5. Calculate \({e}_{i({\mathrm{new}})} (i=1,2,\ldots n)\) by using Eq. (18).

$${e}_{i({\mathrm{new}})}={y}_{i}-{x}_{i}^{{{\prime}}}{\widehat{\beta }}_{\mathrm{new}}$$
(18)

Step 6. Check the stopping criteria given in Eq. (19). If the condition is satisfied, stop the algorithm, otherwise make \(\widehat{\beta }={\widehat{\beta }}_{\mathrm{new}}\) and go to Step 2.

$$\mathrm{max}_{i}\left(\left|{e}_{i}-{e}_{i({\mathrm{new}})}\right|\right)<\varepsilon $$
(19)

In Eq. (19), \(\varepsilon \) is a small positive number and \(\left|.\right|\) is the absolute value.

5 The proposed method

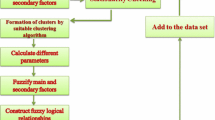
In this study, a new intuitionistic, high-order fuzzy time series forecasting method was proposed. The proposed method generally uses Eq. (3) given in Definition 1 and completely uses Eqs. (4)–(5) given in Definition 2. Thereby, both membership and non-membership are used in the intuitionistic fuzzy time series approach, unlike the fuzzy time series approach that uses only non-membership values. In the proposed method, the intuitionistic fuzzy c-means clustering method is used in the fuzzification phase. Furthermore, the principal component analysis is used to eliminate the multicollinearity problem and reduce dimension because there are many inputs before the phase of determining fuzzy relationships of the proposed method. The proposed method is based on the robust regression. For this reason, the iteratively reweighted least-squares technique is a robust regression method that is used to define functional relationships in the stage of determining the fuzzy relationships. Also, the proposed method does not need the defuzzification step because the outputs of the proposed method are real forecasts. The flowchart and algorithm of the proposed method is given in Fig. 1 and Algorithm 3, respectively.

Fig. 1
figure 1

Flowchart of the proposed method

Full size image

Algorithm 3

Algorithm of the proposed method.

Step 1. Determine \({X}_{t}\), \({X}_{t}^{\mathrm{{test}}}, {X}_{t}^{\mathrm{train}}\), \(n, {n}_{\mathrm{test}}\), \({n}_{\mathrm{train}}, c\) and \(m\) \((1,2,3,\ldots )\) are data and parameters used in the application of the proposed method. Here, \({X}_{t}\) is the time series, \({X}_{t}^{\mathrm{{test}}}\) is the test set of\({X}_{t}\), \({X}_{t}^{\mathrm{train}}\) is the training test of\({X}_{t}\), \(n\) is the length of \({X}_{t}\), \({n}_{\mathrm{test}}\) (the last part of %5, %10 or %15 of \(n\)) is the length of \({X}_{t}^{\mathrm{{test}}}\), \({n}_{\mathrm{train}}\) is the length of \({X}_{t}^{\mathrm{train}}\), \(c\) (2,3,…) is the number of fuzzy sets and \(m\) (1,2,3,…) is the order of the model.

Step 2. Calculate membership and non-membership for the training time series (\({X}_{t}^{\mathrm{train}})\) by using the intuitionistic fuzzy c-means (IFCM) clustering method via Algorithm 1 given in Sect. 3.

Here, the matrix of memberships named \(U({U}_{ij};i=1,2,\ldots ,{n}_{\mathrm{train}}; j=1,2,\ldots ,c)\), the matrix of non-membership named \(V \left({V}_{ij}; i=1,2,\ldots ,{n}_{\mathrm{train}}; j=1,2,\ldots ,c\right)\) and the vector of centres of clusters named \({v}^{*}\)(\({v}_{i}^{*};i=1,2,\ldots ,c))\) are obtained. Also, the intuitionistic fuzzy time series matrix \({(\mathrm{IF}}_{t}; i=1,2,\ldots ,c;j=1,2,\ldots ,(2c+1))\) is constituted by combining of \({X}_{t}^{\mathrm{train}}, U\) and \(V\), respectively.

For example, Let \({X}_{t}=\{{8,10,11,12,16,13,14}\}\), \({X}_{t}^{\mathrm{{test}}}=\) \(\{14\}\), \({X}_{t}^{\mathrm{train}}=\) \(\{{8,10,11,12,16,13}\}\), \(c=3\), \(m=2\) and \({n}_{\mathrm{test}}=1\) and \({n}_{\mathrm{train}}=6\). Also, let \({\mu }_{{A}_{i}}\left(t\right)\), \({\nu }_{{A}_{i}}\left(t\right)\) are membership and non-membership values of tth observation to ith intuitionistic fuzzy set. \(U\), \(V\), \({v}^{*}\) and \({\mathrm{IF}}_{t}\) calculated via Algorithm 1 are given below for \({X}_{t}^{\mathrm{train}}=\) \(\{{8,10,11,12,16,13}\}\).

$$U=\left\{ {\mu }_{{A}_{1}}\left(t\right),{ \mu }_{{A}_{2}}\left(t\right),{ \mu }_{{A}_{3}}\left(t\right)\right\}=\left[\begin{array}{lll}0.0314& 0.9630& 0.1021\\ 0.0482& 0.8408& 0.3144\\ 0.0574& 0.2494& 0.8778\\ 0.0017& 0.0025& 0.9988\\ 0.9985& 0.0015& 0.0037\\ 0.1878& 0.1056& 0.8907\end{array}\right]$$
(20)
$$V=\left\{ {v}_{{A}_{1}}\left(t\right),{ v}_{{A}_{2}}\left(t\right),{ v}_{{A}_{3}}\left(t\right)\right\}=\left[\begin{array}{lll}0.9513& 0.0030& 0.8527\\ 0.9270& 0.0765& 0.5897\\ 0.9139& 0.6664& 0.0504\\ 0.9971& 0.9957& 0.0012\\ 0.0015& 0.9974& 0.9937\\ 0.7420& 0.8480& 0.0419\end{array}\right]$$
(21)
$${v}^{*}=\left[\begin{array}{l}15.8612\\ 8.9699\\ 11.9189\end{array}\right]$$
(22)
$${\mathrm{IF}}_{t}=\left\{U, V\right\}=\left[\begin{array}{ll}\begin{array}{lll}0.0314& 0.9630& 0.1021\\ 0.0482& 0.8408& 0.3144\\ 0.0574& 0.2494& 0.8778\\ 0.0017& 0.0025& 0.9988\\ 0.9985& 0.0015& 0.0037\\ 0.1878& 0.1056& 0.8907\end{array}& \begin{array}{lll}0.9513& 0.0030& 0.8527\\ 0.9270& 0.0765& 0.5897\\ 0.9139& 0.6664& 0.0504\\ 0.9971& 0.9957& 0.0012\\ 0.0015& 0.9974& 0.9937\\ 0.7420& 0.8480& 0.0419\end{array}\end{array}\right]$$
(23)

Step 3. Apply lag process for \(U\) and \(V\) separately. And so, obtain input matrix ( \({X}_{\mathrm{input}}\)) that includes lagged variables of membership and non-membership under Eq. (5) given in Definition 2.

For example, \({X}_{\mathrm{input}}\) matrix obtained by using \(U\) and \(V\) in Eqs. (20) and (21) is given in Eq. (24).

$${X}_{\mathrm{input}}=\left[\begin{array}{l}\begin{array}{ll}\begin{array}{lll}0.0482& 0.8408& 0.3144\\ 0.0574& 0.2494& 0.8778\\ 0.0017& 0.0025& 0.9988\\ 0.9985& 0.0015& 0.0037\end{array}& \begin{array}{lllllllll}0.0314& 0.9630& 0.1021& 0.9270& 0.0765& 0.5897& 0.9513& 0.0030& 0.8527\\ 0.0482& 0.8408& 0.3144& 0.9139& 0.6664& 0.0504& 0.9270& 0.0765& 0.5897\\ 0.0574& 0.2494& 0.8778& 0.9971& 0.9957& 0.0012& 0.9139& 0.6664& 0.0504\\ 0.0017& 0.0025& 0.9988& 0.0015& 0.9974& 0.9937& 0.9971& 0.9957& 0.0012\end{array}\end{array}\end{array}\right]$$
(24)

Step 4. Principal component analysis (PCA) is applied to \({X}_{\mathrm{input}}\) matrix obtained in Step 3. And so, obtain the matrix of principal component coefficients (PCC), the matrix of principal component (PC), the matrix of important principal component (IPC) and the new input matrix \(({P}_{\mathrm{input}}),\) respectively.

Firstly, elements of \({X}_{\mathrm{input}}\) matrix are transformed to the standard normal matrix named \({Z}_{\mathrm{input}}\) that means and standard deviations of each column of \({Z}_{\mathrm{input}}\) are 0 and 1. Then, PCA is applied to \({Z}_{\mathrm{input}}\). And so, PCC and PC matrix are calculated. Also, important principal components are selected from principal components by taking into consideration the criterion that the explained variance ratio needs to be at least 0.85. In this way, IPC matrix is obtained. Lastly, the new input matrix named \({P}_{\mathrm{input}}\) is obtained by putting a vector that consists of 1 value to the first column of IPC.

For example, PCC, PC, IPC and \({P}_{\mathrm{input}}\) matrices obtained by applying PCA to \({X}_{\mathrm{input}}\) in Eq. (25) are given below.

$${\mathrm{PCC}}^{T}=\left[\begin{array}{ll}\begin{array}{lll}0.3408& -0.2341& -0.2191\\ -0.1459& -0.3597& 0.3900\\ -0.3145& 0.4443& -0.1921\end{array}& \begin{array}{lllllllll}-0.2722& -0.3262& 0.3051& -0.3375& 0.2447& 0.2465& 0.2765& 0.3362& -0.2889\\ 0.3239& -0.1962& 0.2564& 0.1551& 0.3544& -0.3568& -0.3169& 0.1599& -0.2918\\ 0.1181& -0.3364& 0.2708& 0.3473& -0.3256& 0.2305& -0.1198& 0.3505& -0.2223\end{array}\end{array}\right]$$
(25)
$$\mathrm{PC}=\left[\begin{array}{lll}-2.0114& -2.2301& 0.3612\\ -1.7560& 0.4749& -0.6783\\ -0.2017& 2.5459& 0.4131\\ 3.9691& -0.7907& -0.0960\end{array}\right]$$
(26)
$$\mathrm{IPC}=\left[\begin{array}{ll}-2.0114& -2.2301\\ -1.7560& 0.4749\\ -0.2017& 2.5459\\ 3.9691& -0.7907\end{array}\right]$$
(27)
$${P}_{\mathrm{input}}=\left[\begin{array}{ll}\begin{array}{c}1\\ 1\\ 1\\ 1\end{array}& \begin{array}{ll}-2.0114& -2.2301\\ -1.7560& 0.4749\\ -0.2017& 2.5459\\ 3.9691& -0.7907\end{array}\end{array}\right]$$
(28)

In Eq. (25), “T” indicates transpose operation. The explained variance ratio of two important principal components is %97.86. So, it can be said that the aims of dimension reduction and obtaining orthogonal inputs are accomplished via PCA.

Step 5. Define fuzzy relations by using robust Regression.

Robust regression coefficient estimates (\(\widehat{\beta }\)) is calculated via iteratively reweighted least-squares algorithm given in Algorithm 2 by taking \(X={P}_{\mathrm{input}}\) and \(Y={X}_{t}^{\mathrm{train}}\) in step 1 of Algorithm 2. Then, predictions of the training set ( \({\widehat{X}}_{t}^{\mathrm{train}})\) can be calculated by using Eq. (29), if any researcher aims to predict.

$${\widehat{X}}_{t}^{\mathrm{train}}={P}_{\mathrm{input}}\widehat{\beta }$$
(29)

For example, \(\widehat{\beta }\) obtained via Algorithm 2 by taking \(X={P}_{\mathrm{input}}\) in (29) and \(Y={X}_{t}^{\mathrm{train}}=\left[-,-,11,12,16,13\right]\) is given below.

$$\widehat{\beta }=\left[\begin{array}{l}13.000\\ 0.2257\\ 0.9445\end{array}\right]$$
(30)

Step 6. Apply determining membership values for time series (\({X}_{t})\) to obtain new memberships (\({U}_{\mathrm{new}})\) and new non-membership \(({V}_{\mathrm{new}})\) of \({X}_{t}\) by using centres of clusters (\({v}^{*})\) obtained in Step 1.

For example, \({U}_{\mathrm{new}}\) and \({V}_{new }\) for \({X}_{t}=\{{8,10,11,12,16,13,14}\}\) by using \({v}^{*}\) calculated for \({X}_{t}^{\mathrm{train}}=\{{8,10,11,12,16,13}\}\) are given below.

$${U}_{\mathrm{new}}=\left[\begin{array}{lll}0.0314& 0.9630& 0.1021\\ 0.0482& 0.8408& 0.3144\\ 0.0574& 0.2494& 0.8778\\ 0.0017& 0.0025& 0.9988\\ 0.9985& 0.0015& 0.0037\\ 0.1878& 0.1056& 0.8907\\ 0.6269& 0.1226& 0.5278\end{array}\right]$$
(31)
$${V}_{\mathrm{new}}=\left[\begin{array}{lll}0.9513& 0.0030& 0.8527\\ 0.9270& 0.0765& 0.5897\\ 0.9139& 0.6664& 0.0504\\ 0.9971& 0.9957& 0.0012\\ 0.0015& 0.9974& 0.9937\\ 0.7420& 0.8480& 0.0419\\ 0.2570& 0.8256& 0.3573\end{array}\right]$$
(32)

Step 7. Apply lag process for \({U}_{\mathrm{new}}\) and \({V}_{\mathrm{new}}\) obtained in Step 6 and obtain new input matrix \({(X}_{\mathrm{input}}^{\mathrm{new}}),\) the new standardized input matrix \({(Z}_{\mathrm{input}}^{\mathrm{new}})\) and standardized input matrix of the test set (\({Z}_{\mathrm{input}}^{\mathrm{{test}}}\)) that includes z scores of lagged variables of memberships and non-memberships.

Firstly, the new input matrix \(({X}_{\mathrm{input}}^{\mathrm{new}}\)) that includes lagged variables of memberships and non-memberships is obtained by using \({U}_{\mathrm{new}}\) and \({V}_{\mathrm{new}}.\) Then, elements of \({X}_{\mathrm{input}}^{\mathrm{new}}\) matrix is transformed to standard normal values, and so, \({Z}_{\mathrm{input}}^{\mathrm{new}}\) matrix has obtained that means and standard deviations of each column of \({Z}_{\mathrm{input}}^{\mathrm{new}}\) are 0 and 1. Lastly, \({Z}_{\mathrm{input}}^{\mathrm{{test}}}\) that includes the

last some rows of \({Z}_{\mathrm{input}}^{\mathrm{new}}\) is obtained.

For example, \({X}_{\mathrm{input}}^{\mathrm{new}}\) and matrix obtained by using \({U}_{\mathrm{new}}\) and \({V }_{\mathrm{new}}\) obtained for \({X}_{t}=\{{8,10,11,12,16,13,14}\}\), \(c=3\,\,\mathrm{and}\,\,m=2\) is given below:

$${X}_{\mathrm{input}}^{\mathrm{new}}=\left[\begin{array}{l}\begin{array}{ll}\begin{array}{lll}0.0482& 0.8408& 0.3144\\ 0.0574& 0.2494& 0.8778\\ 0.0017& 0.0025& 0.9988\\ 0.9985& 0.0015& 0.0037\\ 0.1878& 0.1056& 0.8907\end{array}& \begin{array}{lllllllll}0.0314& 0.9630& 0.1021& 0.9270& 0.0765& 0.5897& 0.9513& 0.0030& 0.8527\\ 0.0482& 0.8408& 0.3144& 0.9139& 0.6664& 0.0504& 0.9270& 0.0765& 0.5897\\ 0.0574& 0.2494& 0.8778& 0.9971& 0.9957& 0.0012& 0.9139& 0.6664& 0.0504\\ 0.0017& 0.0025& 0.9988& 0.0015& 0.9974& 0.9937& 0.9971& 0.9957& 0.0012\\ 0.9985& 0.0015& 0.0037& 0.7420& 0.8480& 0.0419& 0.0015& 0.9974& 0.9937\end{array}\end{array}\end{array}\right]$$
(33)
$${Z}_{\rm input}^{\rm new}=\left[\begin{array}{c}\begin{array}{cc}\begin{array}{ccc}-0.502& 1.712& -0.696\\ -0.480& 0.027& 0.600\\ -0.613& -0.677& 0.878\\ 1.764& -0.680& -1.411\\ -0.169& -0.383& 0.629\end{array}& \begin{array}{ccccccccc}-0.454& 1.196& -0.788& 0.513& -1.673& 0.577& 0.455& -1.126& 0.781\\ -0.415& 0.931& -0.320& 0.482& -0.132& -0.674& 0.398& -0.974& 0.203\\ -0.394& -0.352& 0.923& 0.684& 0.729& -0.758& 0.367& 0.245& -0.983\\ -0.523& -0.887& 1.190& -1.742& 0.733& 1.494& 0.563& 0.926& -1.092\\ 1.787& -0.889& -1.005& 0.063& 0.343& -0.666& -1.784& 0.930& 1.091\end{array}\end{array}\end{array}\right]$$
(34)
$${Z}_{\mathrm{input}}^{\mathrm{{test}}}=\left[\begin{array}{l}\begin{array}{ll}\begin{array}{lll}-0.169& -0.383& 0.629\end{array}& \begin{array}{lllllllll}1.787& -0.889& -1.005& 0.063& 0.343& -0.666& -1.784& 0.930& 1.091\end{array}\end{array}\end{array}\right]$$
(35)

In Eq. (35), \({\mathrm{Z}}_{\mathrm{input}}^{\mathrm{{test}}}\) is the last row of \({Z}_{\mathrm{input}}^{\mathrm{new}}\) given in Eq. (34) because \({n}_{\mathrm{test}}=1\).

Step 8. Calculate the matrix of principal component (\(\mathrm{PC}_{\mathrm{test}}\)), the matrix of important principal component (\(\mathrm{IPC}_{\mathrm{test}}\)) and the new input matrix (\({P}_{\mathrm{input}}^{\mathrm{{test}}}\)) for \({X}_{t}^{\mathrm{{test}}}\) by using \({\mathrm{Z}}_{\mathrm{input}}^{\mathrm{{test}}}\) obtained in Step 7.

Firstly, \(\mathrm{PC}_{\mathrm{test}}\) is calculated by using Eq. (36). In Eq. (36), PCC is the matrix of principal component coefficients calculated in Step 4. Also, important principal components are selected from principal components by taking into consideration the criterion that the explained variance ratio needs to be at least 0.85. In this way, \(\mathrm{IPC}_{\mathrm{test}}\) matrix is obtained. Lastly, the new input matrix \({(P}_{\mathrm{input}}^{\mathrm{{test}}})\) is obtained by putting a vector that consists of 1 value to the first column of IPC.

$$\mathrm{PC}_{\mathrm{test}}={Z}_{\mathrm{input}}^{\mathrm{{test}}}*\mathrm{PCC}$$
(36)

For example, \(\mathrm{PC}_{\mathrm{test}}\), \(\mathrm{IPC}_{\mathrm{test}}\) and \({P}_{\mathrm{input}}^{\mathrm{{test}}}\) calculated by using PCC and \({Z}_{\mathrm{input}}^{\mathrm{{test}}}\) are given below for \({X}_{t}^{\mathrm{{test}}}=\{14\}\).

$$\mathrm{PC}_{\mathrm{test}}=\left[\begin{array}{lll}-1.2061& 1.6675& 0.0540\end{array}\right]$$
(37)
$$\mathrm{IPC}_{\mathrm{test}}=\left[\begin{array}{ll}-1.2061& 1.6675\end{array}\right]$$
(38)
$${P}_{\mathrm{input}}^{\mathrm{{test}}}=\left[\begin{array}{lll}1& -1.2061& 1.6675\end{array}\right]$$
(39)

Step 9. Calculate the forecasts of \({X}_{t}^{\mathrm{{test}}} ({\widehat{X}}_{t}^{\mathrm{{test}}})\) by using \(\widehat{\beta }\) and \({P}_{\mathrm{input}}^{\mathrm{{test}}}\) obtained Step 5 and Step 8 via Eq. (40).

$${\widehat{X}}_{t}^{\mathrm{{test}}}={P}_{\mathrm{input}}^{\mathrm{{test}}}*\widehat{\beta }$$
(40)

For example, \({\widehat{X}}_{t}^{\mathrm{{test}}}\) calculated by using \(\widehat{\beta }\) and \({P}_{\mathrm{input}}^{\mathrm{{test}}}\) obtained in Eqs. (30) and (39) are given below for \({X}_{t}^{\mathrm{{test}}}=\{14\}\).

$${\widehat{X}}_{t}^{\mathrm{{test}}}=\left[14.3028\right]$$
(41)

Step 10. The root of mean square error (RMSE) and mean absolute percentage error (MAPE) values are calculated by using \({\widehat{X}}_{t}^{\mathrm{{test}}}\) obtained in Step 9 via Eqs. (42) and (43).

$$\mathrm{RMSE}=\sqrt{\frac{1}{\mathrm{ntest}}\sum_{t=1}^{\mathrm{ntest}}{\left({X}_{t}^{\mathrm{{test}}}-{\widehat{X}}_{t}^{\mathrm{{test}}}\right)}^{2}}$$
(42)
$$\mathrm{MAPE}=\frac{1}{\mathrm{ntest}}\sum_{t=1}^{\mathrm{ntest}}\left|\frac{{X}_{t}^{\mathrm{{test}}}-{\widehat{X}}_{t}^{\mathrm{{test}}}}{{X}_{t}^{\mathrm{{test}}}}\right|$$
(43)

For example, RMSE and MAPE calculated for \({X}_{t}^{\mathrm{{test}}}=\left\{14\right\}\) by using \({\widehat{X}}_{t}^{\mathrm{{test}}}\) are given in Eq. (43).

$$\mathrm{RMSE}=0.3028\,\mathrm{and\,MAPE}=0.0216$$
(44)

6 Applications

Energy data taken from the ministry of energy and natural resources of Turkey consists of 69 variables of primary energy consumption (PEC). Each of 69 PEC time series has 52 yearly observations between the years 1965 and 2016 for each country in the world. These 69 countries are universally divided into six continents called North America, South-Central America, Europe-Eurasia, Middle East, Africa, and the Asia Pacific, respectively.

Initially, the energy data of the Europe-Eurasia continent that consists of PEC variables of 32 countries were selected to make applications. However, 23 variables of these 32 variables have complete data that includes 52 observations because PEC variables of the other nine countries have some missing observations. For this reason, the proposed method and some other forecasting methods in the literature are applied to the 24 PEC variables that include PEC variables of 24 countries in Europe-Eurasia and the PEC variable of the total Europe-Eurasia continent. So, it is aimed to compare the forecasting performances of the proposed method with some alternative forecasting methods for the entire Europe-Eurasia continent. The names of 24 countries are Austria, Belgium, Bulgaria, Czech Republic, Denmark, Finland, France, Germany, Greece, Hungary, Ireland, Italy, Netherlands, Norway, Poland, Portugal, Romania, Slovakia, Spain, Sweden, Switzerland, Turkey, United Kingdom and another Europe-Eurasia.

Some of the distributions of the 25 PEC time series used in the application are similar and the others are different. When the 24-time series graphs are viewed in general, it can be seen that the 24-time series may have characteristics such as linear increasing trend, curvilinear increasing trend, and stationary or random fluctuations. Some graphs of 24 PEC time series that differ from each other are given in Fig. 2.

Fig. 2
figure 2

Yearly PEC observations of some countries in the million tonnes of oil equivalent

Full size image

The proposed method is compared with the following benchmarks.

DN-PSO Method: The Dendritic neuron (DN) method is an artificial intelligence model proposed by Zhou et al. (2016) to predict financial time series. Particle swarm optimization (PSO) is used in the training algorithm of the DN model and a Matlab m-file” is prepared for solving PEC time series with DN-PSO method.

ANN-PSO Method: This method is a multilayer perceptron artificial neural network (ANN) model trained by PSO used in Yolcu et al. (2013) for time series forecasting. A Matlab m-file” is prepared for solving PEC time series with the ANN-PSO method.

Median ANN Method: This method is a multilayer artificial neural network (ANN) model based on Median Neuron Model proposed by Aladag et al. (2014) for time series forecasting. A Matlab m-file” is prepared for solving PEC time series with the Median ANN method.

Median-Pi-ANN Method: The Median-Pi artificial neural network (Median-Pi-ANN) is a time series forecasting method proposed by Egrioglu et al. (2017). A Matlab m-file” is prepared for solving PEC time series with the Median-Pi-ANN method.

FTS-N: This method is a fuzzy time series network (FTS-N) model proposed by Bas et al. (2015) to forecast the linear and nonlinear time series. A Matlab m-file” is prepared for solving PEC time series with the FTS-N method.

SC-FTS: Song and Chissom (SC) (1993a) method is the first fuzzy time series (FTS) forecasting model in the fuzzy time series literature. A Matlab m-file” is prepared for solving PEC time series with the SC-FTS method.

C-FTS: This method is a fundamental fuzzy time series (FTS) model based on fuzzy logic relations proposed by Chen (2002) (C). A Matlab m-file” is prepared for solving PEC time series with the C-FTS method.

ARIMA Method: Autoregressive integrated moving average (ARIMA) method is a classic time series model that is often preferred by many researchers for time series analysis Kadılar (2005). Box-Jenkins’s (1976) approach is an effective method that provides to be obtained the best ARIMA model. A Matlab m-file” is prepared for solving PEC time series with Box-Jenkins’s (1976) approach.

H-ES Method: Holt’s exponential smoothing (H-ES) method is one of the exponential smoothing methods for time series analysis Kadılar (2005). A Matlab m-file” is prepared for solving PEC time series with the H-ES method.

A-ES Method: Ata’s exponential smoothing (A-ES) method proposed by Yapar (2016) is a new exponential smoothing method in the time series literature. A Matlab m-file” is prepared for solving PEC time series with the A-ES method.

How applications are made with the proposed method is given below.

  • Each of the 24 PEC time series has 52 observations. The first 47 and the last five observations of the time series are used for the training set and the test set, respectively. In other words, the length of the test set is determined as 5 for all applications.

  • The number of fuzzy sets (c) is tried between 3 and 10 increasing 1 unit.

  • The degree of the model (m) is tried between 2 and 5 increasing 1 unit.

  • The architecture that has minimum RMSE value is selected as the best architecture, and so, the best forecasts are obtained for the test set.

  • 30 runs are executed using random values (rn), and so, some statistics are calculated for RMSE and MAPE values.

How applications are made with alternative method is given below.

  • The methods of DN-PSO Zhou et al. (2016), ANN-PSO proposed by Yolcu et al. (2013), Median ANN proposed by Aladag et al. (2014), Median-Pi-ANN proposed by Egrioğlu et al. (2017) and FTS-N proposed by Bas et al. (2015) were applied like those applications of the proposed method above-mentioned.

  • In applications of the SC-FTS proposed by Song and Chissom (1993a) method and C-FTS method proposed by Chen (2002), the number of fuzzy sets is tried between 3 and 10 increasing 1 unit.

  • The methods of the ARIMA method Box-Jenkins’s (1976), Holt’s exponential smoothing (Kadılar (2005)) and ATA method proposed by Yapar (2016) method were applied as classic time series methods.

In the applications, DN-PSO method proposed by Zhou et al. (2016), ANN-PSO method proposed by Yolcu et al. (2013), Median ANN method proposed by Aladag et al. (2014), Median-Pi-ANN method, FTS-N method and the proposed method were the methods that can be solved by trying different random initial parameters. For this reason, for each PEC time series, these methods were tried 30 times by using 30 different random seed values, and so, 30 different RMSE and MAPE values were obtained for each time series in the applications of this study. The mean and median of these RMSE values are given in Table 1. When Table 1 is examined, it is seen that the RMSE statistics of the proposed method are smaller than the RMSE statistics of the other methods for the vast majority of 25 PEC time series solved. Therefore, it can be said that the proposed method is largely better than other methods in forecasting the future.

Table 1 Means and medians of RMSE values of the methods for PEC variables of the countries in the Europe & Eurasia continent
Full size table

In the applications, for each of 25 PEC time series, minimum RMSE values of all methods used in this study are given in Table 2. When Table 2 is examined, it is seen that minimum RMSE values of the proposed method are smaller than minimum RMSE values of the other methods for the vast majority of 25 PEC time series solved. Therefore, it can be said that the proposed method has a largely better forecasting performance than other methods.

Table 2 Minimum RMSE values of the methods for PEC variables of the countries in the Europe & Eurasia continent
Full size table

In addition, success rates obtained by examining Tables 1 and 2 were given in Table 3. When Table 3 is examined, it is seen that the proposed method has the highest success rates with 56%, 64% and 44% for minimum RMSE means minimum RMSE medians and minimum RMSE values, respectively. For instance, according to Table 3, 16 RMSE medians (16/25 = 64%) of 25 RMSE medians of the proposed method are smaller than RMSE medians of the other methods. Other methods have quite lower success rates than the success rates of the proposed method. Therefore, it can be said that the proposed method has a largely better forecasting performance than other methods according to RMSE measurement. Similarly, the proposed method has also the highest success rates with 44%, 44% and 32% for minimum MAPE means, minimum MAPE medians and minimum MAPE values, respectively. So, it can be said that the proposed method has a largely better forecasting performance than other methods according to MAPE measurement. However, the success rates with scores of 36% and 32% of ANN-PSO method proposed by Yolcu et al. (2013) for MAPE means and median means, respectively, and the success rate 24% of FTS-N method proposed by Bas et al. (2015) for minimum MAPE values are remarkable high values. Thereby, as a result, it can be said that the proposed method is the best, ANN-PSO method Yolcu et al. (2013) is the second-best method and the FTS-N method Bas et al. (2015) is the third-best method according to MAPE in forecasting the future.

Table 3 Success rates of the methods
Full size table

The optimal parameter values of the best method for each series are given in a Table in the supplementary file.

7 Explainable results of the proposed method

The inputs in the model can be tested and commented on. The inputs of the models are scores that are obtained from the principal component analysis. The contribution of each score to the forecasting model can be tested and commented on. An example for the Turkey time series is given below by using tables and graphs.

In the forecasting model of the Turkey time series, six PCA score variables are employed as inputs. It is seen that all inputs are significant in the model in Table 4. The importance of the inputs can be determined according to coefficients. The importance graph is given in Fig. 3.

Table 4 Explainable results for Turkey time series
Full size table
Fig. 3
figure 3

The importance graph of model inputs

Full size image

8 Conclusions and discussion

The high-order definition of intuitionistic fuzzy time series definition of Egrioglu et al. (2019b) means that any time series is affected by lagged time series, lagged membership values and non-membership values. However, indeed, membership and non-membership values are obtained from the lagged time series. So, it can be thought that membership and non-membership values include, largely, the information of lagged time series. From this viewpoint, in this study, a new high-order fuzzy intuitionistic time series definition given Definition 1 is introduced. It is explained that any time series is affected by lagged membership values and non-membership values in Definition 1. For this reason, it can be said that the advantage of the proposed method that uses Definition 1 is simplifying the model, since the number of inputs in the model is reduced. In the literature, intuitionistic fuzzy time series models have been proposed in recent years, since the definitions of classical fuzzy time series in literature can be insufficient for many real-life series. The reason for this is fuzzy time series approaches use only membership values for forecasting any time series. However, both membership and non-membership values are used in the intuitionistic fuzzy time series methods. Thus, the intuitionistic fuzzy time series methods are the approaches to increase the forecasting performance because of being used of more information. Also in this study, similarly, it has been shown that the forecasting performance of the proposed method that has a new intuitionistic fuzzy time series approach has much better forecasting performance than the classical time series and the classical fuzzy time series methods. Therefore, in future studies, it could be suggested that researchers prefer to use the intuitionistic fuzzy time series approaches instead of the classical time series and the classical fuzzy time series approaches.

In this study, a new forecasting algorithm is proposed, and it is shown that the proposed method has better forecasting performance with the best success rates between 32 and 64% than many time series models in the literature. In the proposed method, the principal component analysis method was used to make the dimension reduction. Then, the robust regression is used in the stage of determination relationships of the proposed method. Therefore, it can be suggested that some regression methods or statistical methods are used in the stage of determination relationships of the intuitionistic fuzzy time series that will be made in the future. In this study, the forecasting performances of 11 different time series forecasting methods are compared with each other. Then, for each PEC time series in the Europe-Eurasia continent, the best methods and the parameters of the best methods are given in Table 2. So, researchers that have worked in the energy fields could decide which methods they will select by looking at Table 2, when they would like to solve any PEC time series in the Europe-Eurasia continent.

In fuzzy time series methods, inputs of the models cannot be tested or commented on. The proposed method is an explainable artificial intelligence method. The proposed method is the first explainable fuzzy time series method in the literature. It is possible to test, order and comment on all inputs in the model because the fuzzy relations are modeled by using robust regression analysis. As a result of this study, it can be said that explainable artificial intelligence methods can be produced by combining statistical and machine learning methods. It can be expected that the studies about explainable fuzzy time series methods will be increased soon.