Solving multi-objective optimization problems using self-adaptive harmony search algorithms

Abstract

In recent years, there have been many multi-objective evolutionary algorithms proposed to solve multi-objective optimization problems. These evolutionary algorithms generate many solutions for iterations and move to the true Pareto optimal region gradually. As expected, since the harmony search algorithm can also iterate over a large number of solutions (in HM memory) and moves to the true Pareto optimal region, we use it to solve multi-objective optimization problems. In this paper, the proposed system architecture can be divided into two phases. In the first phase, we aim to search feasible solution regions as widely as possible in the entire process. In the second phase, we focus on searching optimized solutions stepwise in the feasible solution regions. Since the proposed algorithm uses many parameters, we adjust some of them in a self-adaptive way and call the algorithm self-adaptive. In the experiments, we use the eleven well-known multi-objective problems and three many-objective problems to examine the proposed algorithm and other existing algorithms, based on five performance indicators. As a result, our algorithm achieves better performances than the others in inverted generational distance, hypervolume, and spread indicators.

1 Introduction

In our lives, multi-objective optimization problems are ubiquitous. For a factory director, he must consider production speed, yield rates, cost reduction, quality improvement, etc., but these problems often conflict with each other. Increasing production speed may lost yield rates, and reducing costs may sacrifice product quality. Thus, it is a multi-objective problem. In general, an optimal solution of one objective function may not necessarily be the best solution to another objective function. Therefore, when the solutions to a multi-objective problem cannot satisfy all functions at the same time, different solutions must be balanced among these objective functions, thereby producing a set of optimal solutions, called a Pareto optimal set.

In recent years, there have been many multi-objective evolutionary algorithms (MOEAs) proposed such as NSGA-II (Deb et al. 2000, 2002), SPEA2 (Zitzler et al. 2001), MOEA/D (Zhang and Li 2007), NSGA-III (Deb and Jain 2014), NSLS (Chen et al. 2015), HMOGA (Zhang et al. 2015), BCE-IBEA (Li et al. 2016), MOEA/IGD-NS (Tian et al. 2016), and SOMEA (Zhang et al. 2016). The focus of these algorithms is that Pareto solutions can be generated for each iteration. Evolutionary algorithms (EAs) are inspired by natural evolution and rely on the concepts of survival of the fittest. Evolutionary algorithms imitate the evolution of the nature principle to achieve the best solutions. In general, all evolutionary algorithms begin with initial population randomization and then update each generation of population, based on the fitness function by using three operators: selection, crossover, and mutation. Since evolutionary algorithms can have many solutions for iterations, they can move to the true Pareto optimal region.

Besides, the harmony search (HS) algorithm proposed by Geem et al. (2001) is also an evolutionary algorithm. Inspired by the improvisation of music, a group of musicians improvise the pitch of their instruments to find a wonderful melody in a firm aesthetic evaluation and after practice. Similarly, after iterations, the HS algorithm seeks good enough solutions by evaluating a set of decision variables using fitness functions. In the past, the HS algorithm had good results on many application issues such as fuzzy logic control scheme (Mahto and Mukherjee 2017), path planning problem (Wu et al. 2017), combined heat and power economic dispatch (CHPED) problem (Feng et al. 2017), multi-machine power system stabilizer (PSS) (Chitara et al. 2016). As expected, since the HS algorithm can also iterate over a large number of solutions (in HM memory) and moves to the true Pareto optimal region, we use it to solve multi-objective optimization problems.

In this paper, we use the self-adaptive harmony search algorithm to solve multi-objective optimization problems. The proposed system architecture can be divided into two phases. In the first phase, we aim to search feasible solution regions as widely as possible in the entire process. In the second phase, we focus on searching optimized solutions stepwise in the feasible solution regions. Since the proposed algorithm uses many parameters, we adjust some of them in a self-adaptive way and call the algorithm self-adaptive.

In summary, we identify the originality and novelty in this paper as follows:

• (1) In this study, we use the two-phase self-adaptive harmony search algorithm to solve multi-objective optimization problems. In the first phase, we aim to search feasible solution regions as widely as possible in the entire process. In the second phase, we focus on searching optimized solutions stepwise in the feasible solution regions.

• (2) In the first phase, we modify the original harmony search algorithm using the standard deviation of parameter values in the harmony memory, instead of using predefined bandwidth (i.e., bw). When the number of non-dominated solutions is less than a predefined threshold (or the system is thought to enter a convergence stage), the system switches to Phase 2.

• (3) In the second phase, in order to get more non-dominated solutions in the feasible solution regions, reference points in a hyperplane are generated based on the extreme points derived from the harmony memory. These reference points are used to check whether a new solution generated by the variant HM2 mechanism is close to any of them. If not close enough, another new solution is generated based on the previous solution and checked again. Besides, parameter values are also adjusted for the next iteration, based on new harmony memory, until all iterations are finished.

• (4) In the comprehensive experiments, we use the eleven well-known multi-objective problems and three many-objective problems to examine the proposed algorithm and other existing algorithms, based on five performance indicators ever proposed.

The remainder of this paper is organized as follows: In Sect. 2, we review the related work done in recent years. In Sect. 3, we introduce the basic methods used in our work. In Sect. 4, we propose the system architecture consisting of two phases. In Sect. 5, Phase 1 describes searching feasible solution regions as widely as possible in the entire process. In Sect. 6, Phase 2 focuses on searching optimized solutions stepwise in the feasible solution regions. In Sect. 7, we use the eleven well-known multi-objective problems and three many-objective problems to examine the proposed algorithm and other existing algorithms, based on five performance indicators. Finally, we make conclusions and mention the future issues to be investigated in Sect. 8.

2 Related work

Mentioned in the introduction, many multi-objective evolutionary algorithms (MOEAs) have been proposed in the past, such as NSGA-II, SPEA2, MOEA/D, NSGA-III, NSLS, HMOGA, BCE-IBEA, MOEA/IGD-NS, and SOMEA. They are reviewed briefly as follows.

Deb et al. (2000, 2002) proposed a non-dominated sorting-based MOEA, called NSGA-II, which alleviates three difficulties of (1) the computational complexity, (2) the non-elitism approach, and (3) the need to specify a sharing parameter in earlier multi-objective evolutionary algorithms. Zitzler et al. (2001) proposed an improved version, namely SPEA2, which incorporates in contrast to its predecessor SPEA a fine-grained fitness assignment strategy, a density estimation technique, and an enhanced archive truncation method. Zhang and Li (2007) proposed a multi-objective evolutionary algorithm based on decomposition (MOEA/D). It decomposes a multi-objective optimization problem into a number of scalar optimization subproblems and optimizes them simultaneously. This makes MOEA/D have lower computational complexity at each generation than NSGA-II. Deb and Jain (2014) recognized a few recent efforts and discussed a number of viable directions for developing a potential EMO algorithm for solving many-objective optimization problems. Then, a reference-point-based many-objective evolutionary algorithm NSGA-III was proposed, following NSGA-II framework that emphasizes population members that are non-dominated, yet close to a set of supplied reference points.

Chen et al. (2015) proposed a new multi-objective optimization framework based on non-dominated sorting and local search (i.e., NSLS). At each iteration, given a population P, a simple local search method is used to get a better population P′, and then, the non-dominated sorting is adopted on P ∪ P′ to obtain a new population for the next iteration. To address the problem of exploitation lacking in the search process of NSGA-II, Zhang et al. (2015) proposed a hybrid multi-objective genetic algorithm (i.e., HMOGA) where a local search strategy is led into NSGA-II efficiently. Li et al. (2016) proposed a bi-criterion evolution (i.e., BCE) framework of the Pareto criterion (i.e., PC) and non-Pareto criterion (i.e., NPC), which attempts to make use of their strengths and compensates for each other’s weaknesses. The two evolution parts work collaboratively, with an abundant exchange of information to facilitate each other’s evolution. Finally, the BCE-IBEA (i.e., BCE with Indicator-Based EA embedded into the NPC evolution part) achieves better performances in the experiments. Tian et al. (2016) proposed an MOEA (i.e., MOEA/IGD-NS) whose environmental selection is based on an enhanced inverted generational distance metric that is able to detect non-contributing solutions (i.e., IGD-NS), thereby considerably accelerating the convergence of the evolutionary search. Under mild conditions, the Pareto front (Pareto set) of a continuous m-objective optimization problem forms an (m − 1)-dimensional piecewise continuous manifold. Based on this property, Zhang et al. (2016) proposed a self-organizing multi-objective evolutionary algorithm (i.e., SOMEA). At each generation, a self-organizing mapping method with (m − 1) latent variables is applied to establish the neighborhood relationship among current solutions. A solution is only allowed to mate with its neighboring solutions to generate a new solution.

Besides, HS algorithms were ever combined with non-dominated sorting-based or decomposition-based MOEAs to solve multi-objective optimization problems. Doush and Bataineh (2015) applied the HS algorithm to NSGA-II and MOEA/D, called harmony NSGA-II and harmony MOEA/D. This method modifies the population-generated part in NSGA-II and MOEA/D into HS memory and shows it useful for multi-objective problems. Dai et al. (2015) proposed a self-adaptive multi-objective harmony search (i.e., SAMOHS) algorithm to solve multi-objective optimization problems. In the SAMOHS algorithm, a modified self-adaptive bandwidth (bw) is employed and the self-adaptive parameter setting is proposed for harmony memory considering rate (HMCR) and pitch adjusting rate (PAR).

3 Backgrounds

In this section, we introduce the backgrounds related to our work, which involve multi-objective optimization problems (Zhang and Li 2007), non-dominated sort (Deb et al. 2000, 2002), harmony search algorithm (Geem et al. 2001; Huang and Wang 2014), and truncation (Zitzler et al. 2001).

3.1 Multi-objective optimization problems

Multi-objective optimization problems can be defined by the following formula:

$$ {\text{minimize}}\;\;F\left( \varvec{x} \right) \, = \left( {f_{1} \left( \varvec{x} \right), \ldots , f_{m} \left( \varvec{x} \right)} \right)^{\text{T}} ,\;\;{\text{subject}}\;{\text{to}}\;\varvec{x} \in\Omega ,\;m \ge 2 $$

(1)

where Ω is the decision variable space, R_m is called the objective space, and F: Ω → R_m consists of m real-valued objective functions.

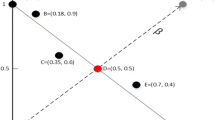
For two vectors u = (u₁, u₂,…, u_m) and v = (v₁, v₂,…, v_m) in the objective space R_m, if u_i≤ v_i for every i = 1,…, m and u_j< v_j for at least one j ∈ {1,…, m}, then we call u dominates v, as shown in Fig. 1a. On the other hand, if u_i> v_i for at least one i ∈ {1,…, m} and u_j < v_j for at least one j ∈ {1,…, m}, then we call u and v are non-dominated over each other, as shown in Fig. 1b.

Fig. 1

Domination between u and v

Finally, given x* ∈ Ω, if there is no point x ∈ Ω such that F(x) dominates F(x*), then F(x*) is called a true Pareto front vector, as shown in Fig. 2.

Fig. 2

Pareto front

3.2 Non-dominated sort

The non-dominated sorting used in NSGA-II is introduced here. For a set of solutions, the first-level Pareto front is found based on the non-domination mentioned above. Next, all the solutions on the first-level Pareto front are removed, and the remained solutions are used to find the second-level Pareto front if it exists. This process continues until all fronts are identified, as shown in Fig. 3.

Fig. 3

Set of solutions (left) and after sorting (right)

3.3 Harmony search algorithm

The general harmony search algorithm (i.e., HS) (Geem et al. 2001) is a meta-heuristic algorithm that imitates the improvisation process of musicians. First, a harmony memory (i.e., HM) with size HMS is created and randomly initialized. In order to find the better harmony (i.e., a better solution), each musician (i.e., a decision variable) plays a note (i.e., a given value in the range of the variable) to improvise a new harmony. As shown in Fig. 4, the new harmony improvisation process consists of three parts: random selection, memory consideration, and pitch adjustment. Once a new harmony is generated, its performance must be evaluated through multi-objective functions. If the new harmony is better than the worst harmony in the HM, the worst harmony is replaced with the new harmony. Then, keep on improvising a new harmony until the maximum number of iterations is reached.

Fig. 4

New harmony improvisation process

As shown in Fig. 4, the trial means the indicated pitch on the note played by a musician. Harmony memory consideration rate (i.e., HMCR) controls the random selection and memory consideration by adjusting the value between 0 and 1 which symbolizes exploration or exploitation. If HMCR is close to 0, the pitch tends to be randomly selected from all the possible range of variables; in other words, it is a purely random search. On the contrary, the pitch tends to be selected from the HM because the HM preserves the superior harmony of all. Besides, the pitch adjustment rate (i.e., PAR) determines whether the pitch should be further adjusted according to a variable distance bandwidth (i.e., bw) which symbolizes the range of a local search.

3.4 Truncation

The truncation procedure used in our work is borrowed from two parts of SPEA2 (i.e., fitness assignment and environmental selection). The fitness assignment defines the computational fitness function for the environmental selection, and then, the environmental selection filters the solution size and removes unwanted solutions.

3.4.1 Fitness Assignment

There are two functions S($i$) and R($i$) related to the fitness assignment of the truncation procedure as follows.

$$ S(i) = \left| {\left\{ {j|j \in P_{t} + \bar{P}_{t} \wedge i \prec j} \right\}} \right| $$

(2)

where |·| is the number of a set, + stands for multiset union, and ≺ is dominance relation. On the basis of the S values, the raw fitness R($i$) of solution i can be calculated as follows.

$$ R(i) = \mathop \sum \limits_{{ j \in P_{t} + \bar{P}_{t} , j \prec i}} S(j) $$

(3)

R($i$) = 0 corresponds to a non-dominated solution, while a high R($i$) value means that solution i is dominated by many solutions.

Besides, density information is incorporated to discriminate solutions with the same raw fitness values. Here, the inverse of the distance to the k-th nearest neighbor is regarded as the density estimate, denoted as $\sigma_{i}^{k}$. Usually, k is set to $\sqrt {\bar{N} {\text{ + N}}}$ where $\bar{N}$ is the archive size and N is the population size. Then, the density D($i$) is defined as follows.

$$ D(i) = \frac{1}{{\sigma_{i}^{k} + 2}} $$

(4)

In the denominator, two is added to ensure D($i$) < 1. Finally, adding D($i$) to the raw fitness R($i$) yields the fitness F($i$) as follows.

$$ F(i) = R(i) + D(i) $$

(5)

3.4.2 Environmental selection

During the environmental selection, the first step is to copy all non-dominated solutions (i.e., those which have a fitness value lower than one) from the archive and population to the archive of the next generation as follows.

$$ \bar{P}_{t + 1} = \left\{ {i|i \in P_{t} + \bar{P}_{t} \wedge F(i) < 1} \right\} $$

(6)

If the non-dominated front fits exactly into the archive (i.e., $\left| {\bar{P}_{t + 1} } \right|$ = $\bar{N}$), the environmental selection is completed; otherwise, two situations are considered: either the archive is too small (i.e., $\left| {\bar{P}_{t + 1} } \right|$ < $\bar{N}$) or too large (i.e., $\left| {\bar{P}_{t + 1} } \right|$ > $\bar{N}$). In the first case, the best $\bar{N}$ − $\left| {\bar{P}_{t + 1} } \right|$ dominated solutions in the previous archive and population are copied to the new archive. This can be accomplished by sorting the multiset $P_{t}$ + $\bar{P}_{t}$ according to the fitness values and copy the first $\bar{N}$ − $\left| {\bar{P}_{t + 1} } \right|$ solutions with F(i) ≥ 1 to $\bar{P}_{t + 1}$. In the second case, when the size of the current non-dominated multiset exceeds $\bar{N}$, the archive truncation procedure is invoked which iteratively removes solutions from $\bar{P}_{t + 1}$ until $\left| {\bar{P}_{t + 1} } \right|$ = $\bar{N}$. At each iteration, solution i is chosen for removal when $i$ ≤ $_{d} j$ for all $j$ ∈ $\bar{P}_{t + 1}$. The condition $i$ ≤ $_{d} j$ is defined as follows.

$$ \begin{aligned} & i \le_{d} j:\forall \;0 < k < \left| {\bar{P}_{t + 1} } \right|,\;\;\sigma_{i}^{k} = \sigma_{j}^{k} \\ & \quad \vee \exists 0 < k < \left| {\bar{P}_{t + 1} } \right|,\left[ {\left( {\forall \;0 < l < k < \sigma_{i}^{l} = \sigma_{j}^{l} } \right) \wedge \sigma_{i}^{k} < \sigma_{j}^{k} } \right] \\ \end{aligned} $$

(7)

where $\sigma_{i}^{k}$ denotes the distance of solution i to its k-th nearest neighbor in $\bar{P}_{t + 1}$. In other words, the solution which has the minimum distance to another solution is chosen for removal; if there are several solutions with the same minimum distance, the tie is broken by considering the second smallest distances and so forth.

4 System overviews

In this section, we briefly describe how to use the self-adaptive harmony search algorithm to solve multi-objective optimization problems. As shown in Fig. 5, the system architecture can be divided into two phases. In the first phase, we aim to search feasible solution regions as widely as possible in the entire process. In the second phase, we focus on searching optimized solutions stepwise in the feasible solution regions.

Fig. 5

System architecture

In Phase 1, we modify the original harmony search algorithm using the standard deviation of parameter values in the harmony memory, instead of using predefined bandwidth (i.e., bw). After all solutions are generated by the variant HM1 algorithm, non-dominated sorting and truncating procedure are applied to pick out feasible solutions from the harmony memory for the next iteration. When the number of non-dominated solutions is less than a predefined threshold (or the system is thought to enter a convergence stage), the system switches to Phase 2 for searching optimized solutions stepwise in the feasible solution regions. Otherwise, the system still stays in Phase 1 until all iterations are finished.

In Phase 2, in order to get more non-dominated solutions in the feasible solution regions, reference points in a hyperplane are generated based on the extreme points derived from the harmony memory. These reference points are used to assess whether a new solution generated by the variant HM2 algorithm is close to any of them. If not close enough, another new solution is generated based on the previous solution and checked again. After all solutions are generated by the variant HM2 algorithm, non-dominated sorting and truncating procedure are applied to pick out feasible solutions from the harmony memory for the next iteration. Finally, parameter values are adjusted for the next iteration, based on the harmony memory, until all iterations are finished.

5 Phase-1 process

In the first phase, we aim to search feasible solution regions as widely as possible in the entire process. Here, we modify the original harmony search algorithm using the standard deviation of parameter values in the harmony memory, instead of using predefined bandwidth (i.e., bw).

5.1 Phase-1 algorithm

In the phase-1 algorithm as shown in Fig. 6, we initialize the algorithm parameters first, including HMCR, PAR, hms, conv, T, and randomly generate the initial harmony memory HM. Then, the modified harmony search algorithm (i.e., the variant HM1 mechanism described later) is used to generate solutions which are stored in another harmony memory HM′. Next, the union of the current solutions in HM and new generated solutions in HM′ (i.e., 2 × hms solutions) is filtered using non-dominated sorting and truncating procedure which take only half of them (i.e., new HM with also hms solutions) for the next iteration. Finally, if the number of the intersection of HM′ and new HM is less than the predefined convergence threshold, the system switches to Phase 2 for searching optimized solutions stepwise in the feasible solution regions. Otherwise, the system still stays in Phase 1 until all iterations are finished.

Fig. 6

Phase-1 algorithm

5.2 Variant HM1 mechanism

In the variant HM1 mechanism as shown in Fig. 7, we modify the original harmony search algorithm using the standard deviation of parameter values in the harmony memory, instead of using predefined bandwidth (i.e., bw). This intention for the harmony search algorithm is to achieve the self-adaptive effect when each generated solution is fine-tuned using a dynamic range, but not a fixed range. The standard deviation of parameter values is defined as follows.

$$ {\text{std}}_{j} = \sqrt {\frac{1}{\text{hms}}\mathop \sum \limits_{i = 1}^{\text{hms}} \left( { x_{i,j} - u_{j} } \right)^{2} } $$

(8)

$$ u_{j} = \frac{1}{\text{hms}}\mathop \sum \limits_{i = 1}^{\text{hms}} x_{i,j} $$

(9)

where u_j is the mean value of the jth variable, hms is the size of the harmony memory, and x_i,j represents the jth variable value of the ith harmony memory as shown in Fig. 8.

Fig. 7

Variant HM1 mechanism

Fig. 8

Harmony memory

5.3 Filtering the harmony memory

After the variant HM1 mechanism generates hms solutions and stores them in the harmony memory HM′, then all the solutions in HM and HM′ (i.e., 2 × hms solutions) are filtered using non-dominated sorting and truncating procedure. The non-dominated sorting is used to sort these solutions based on different non-dominated levels. Then, the truncating procedure is applied to reduce some solutions in the last non-dominated level in order to make new HM with exactly hms solutions for the next iteration. In other words, we only keep the best hms solutions for the next iteration.

5.4 Convergence

In the process of generating new solutions for each iteration, the number of non-dominated solutions could be decreased iteration-by-iteration. It means the variant HM1 mechanism cannot find more non-dominated solutions in a wide way. For this situation, the system should switch to Phase 2 for finding more non-dominated solutions. In other words, the system has entered a convergence stage and should search optimized solutions stepwise in the feasible solution regions. Here, the convergence situation is defined as when the number of the intersection of HM′ and new HM is less than the predefined threshold.

6 Phase-2 process

In the second phase, we focus on searching optimized solutions stepwise in the feasible solution regions. Here, in order to get more non-dominated solutions in the feasible solution regions, reference points in a hyperplane are generated based on the extreme points derived from the harmony memory. These reference points are used to check whether a new solution generated by the variant HM2 mechanism is close to any of them. If not close enough, another new solution is generated based on the previous solution and checked again. Finally, parameter values are adjusted for the next iteration, based on new harmony memory, until all iterations are finished.

6.1 Phase-2 algorithm

In the phase-2 algorithm as shown in Fig. 9, we use the parameter values left in the phase-1 algorithm, including HM_t+1, HMCR, PAR, hms, t+ 1, and T. First, we take the generated solutions in the harmony memory to solve M objective functions and get M extreme points which constitute a hyperplane. Then, reference points in the hyperplane (described in Sect. 6.2) are generated to check whether a new solution generated by the variant HM2 mechanism (described in Sect. 6.3) is close to any of them. Before checking the closeness degree, two parameters should be calculated and marked first, i.e., (1) the nearest reference point of each solution in the harmony memory and (2) the average minimum Euclidean distance between reference points in the hyperplane. These two parameters are used to check the closeness degree between new solutions generated by the variant HM2 mechanism and their corresponding reference points. Similar to the process done in the phase-1 algorithm, the variant HM2 mechanism generates new solutions which are stored in another harmony memory HM′. Next, the union of the current solutions in HM and new generated solutions in HM′ (i.e., 2 × hms solutions) is filtered using non-dominated sorting and truncating procedure which take only half of them (i.e., new HM with also hms solutions) for the next iteration. Finally, HMCR and PAR are dynamically adjusted for the next iteration (described in Sect. 6.4), based on new harmony memory, until all iterations are finished.

Fig. 9

Phase-2 algorithm

6.2 Generating reference points

In the subsection, we present how the reference points are generated in the hyperplane as shown in Fig. 10. The generation of reference points is similar to that in NSGA-III (Deb and Jain 2014), but different from NSGA-III, the amount of reference points is determined by the number of non-dominated solutions in the harmony memory and the hyperplane size. Besides, the reference points are evenly distributed in the hyperplane.

Fig. 10

Generation of reference points

Here, we take three-objective functions (i.e., M = 3) as an example. As shown in Fig. 11, 21 reference points are evenly distributed in the standard hyperplane where the coordinates of the vertices are (1, 0, 0), (0, 1, 0), and (0, 0, 1). The amount of the reference points (i.e., 21) is calculated using Eq. (10) with M = 3 and p = 5, also based on Table 1 (Deb and Jain 2014).

Fig. 11

Twenty-one reference points on the hyperplane

Table 1 Amount of reference points for M = 3 and p = 1–13

$$ H \, = \, C\left( {\begin{array}{*{20}c} {M + p - 1} \\ p \\ \end{array} } \right) $$

(10)

However, as mentioned above, the actual amount of reference points is also determined by the number of non-dominated solutions in the harmony memory and the hyperplane size as follows.

• (1) The number of non-dominated solutions As more non-dominated solutions are required, more reference points should be used. However, since there is no obvious association between them, the indirect connection is built through p values, as shown in Fig. 12. Here, p values can be dynamically determined by the number of non-dominated solutions in the harmony memory as follows.

  Fig. 12

  

  Indirect connection through p

  $$ p = \frac{\text{num-non-dom}}{\text{hms}}*p_{\hbox{max} } $$

  (11)

  where num-non-dom is the number of non-dominated solutions, hms is the size of the harmony memory, and p_max is the corresponding p value with Ref-Pt more than and near to hms; for example, as shown in Table 1, Ref-Pt more than and near to hms (= 100) is 105, so p_max is 13.

• (2) The hyperplane size As more the hyperplane size is, more reference points are needed. Thus, the actual amount of reference points is the value [calculated using Eq. (10)] multiplied by the ratio of the actual hyperplane size to the standard hyperplane size as follows.

  $$ {\text{Num}}\left( {\text{Ref-Pt}} \right) = \frac{{{\text{Size}}\left( {\text{actual-hyperplane}} \right)}}{{{\text{Size}}\left( {\text{standard-hyperplane}} \right)}}*C\left( {\begin{array}{*{20}c} {M + p - 1} \\ p \\ \end{array} } \right) $$

  (12)

  where size(actual-hyperplane) is the actual hyperplane size and size(standard-hyperplane) is the standard hyperplane size.

6.3 Variant HM2 mechanism

In the variant HM2 mechanism as shown in Fig. 13, new solutions are generated and then checked whether they are close to any reference points. However, the generation way of new solutions could be different as shown in Fig. 14. For Case 1, a fixed solution is randomly selected from the harmony memory, and then, each parameter of this solution will be tuned one by one. Finally, the tuned solution becomes a new solution to be checked later. For Case 2, a new solution is generated in the same way as the variant HM1 mechanism; in other words, each parameter of a new solution could be tuned from the parameters of different solutions in the harmony memory or be randomly generated.

Fig. 13

Variant HM2 mechanism

Fig. 14

Tuning parameters

In checking whether new solutions are close to reference points, they must be within the Euclidean distance (or radius) of the nearest reference point, as shown in Fig. 15. Here, in fact, a so-called new solution x′_i has been mapped into F(x′_i) in the same space of reference points where F is the multi-objective function. For Case 1, it is no problem since the nearest reference point of the pretuned solution has been calculated and marked as mentioned in Sect. 6.2. But, for Case 2, a new solution is tuned from different solutions in the harmony memory or be randomly generated, so there is no corresponding nearest reference point. Here, the reference point nearest to the new solution F(x′_i) is regarded as the compared target. If the new solution is not close enough to any reference points, new solutions are continuously generated in the variant HM2 mechanism and then checked again till the closeness condition is satisfied. However, every 10-time failure, the radius of the nearest reference point will be increased by one-fourth of the radius till a new satisfied solution is found.

Fig. 15

Checking the closeness

6.4 Adjusting parameter values

In the variant HM2 mechanism, two key parameters related to the generation of new solutions are HMCR and PAR. In the variant HM1 mechanism mentioned in Sect. 5, they are fixed (or cannot be changed) for generating new solutions. However, for accelerating to search optimized solutions in the variant HM2 mechanism, we dynamically adjust HMCR and PAR for each iteration based on the change of new harmony memory. Here, we use the intersection of HM′ and new HM as the basis for dynamic adjustment; in other words, for the new solutions of HM′ appearing in the new HM of the next iteration (or called relevant solutions), we can use them, according to their generation way, to adjust HMCR and PAR for the next iteration.

First, HMCR is considered. Relevant solutions could be generated using Case 1 and Case 2 mentioned in Sect. 6.3. If relevant solutions generated using Case 1 are more than those using Case 2, HMCR should be increased for the next iteration; in other words, more solutions should be generated from the harmony memory. On the other hand, if relevant solutions generated using Case 2 are more than those using Case 1, HMCR should be decreased for the next iteration; in other words, more solutions should be generated randomly. Next, PAR is considered. If relevant solutions with more parameter tuning are more than those with less parameter tuning, PAR should be increased for the next iteration; otherwise, PAR should be decreased for the next iteration.

7 Experimental results

In this paper, we use the eleven well-known problem functions for multi-objective optimization; i.e., five 2-objective problem functions ZDT1–ZDT4, ZDT6 (Zitzler et al. 2000) and six 3-objective problem functions DTLZ1, DTLZ2, DTLZ4–DTLZ7 (Deb et al. 2001), and also choose the three problem functions from the benchmark functions for CEC’2018 competition on many-objective optimization; i.e., MaF1, MaF2, and MaF3 with M = 5, 10, and 15 (Cheng et al. 2018). Furthermore, five performance indicators are used to measure the proposed algorithm and other existing algorithms.

7.1 Performance indicators

In this subsection, five performance indicators used to measure all the algorithms are described in detail. These indicators include inverted generational distance (IGD) (Van Veldhuizen and Lamont 1998; Zhang et al. 2008), generational distance (GD) (Van Veldhuizen and Lamont 2000), hypervolume (HV) (Wang et al. 2010), coverage (Zhou et al. 2006), and spread (Wang et al. 2010) as follows.

• (1) Inverted generational distance (IGD)

The IGD metric provides combined information about the convergence and diversity of obtained solutions. This metric calculates the average minimum Euclidean distance between ${\text{PF}}_{\text{true}}$ and ${\text{PF}}_{\text{known}}$ in the objective space, which can be defined as follows.

$$ {\text{IGD}}\left( {{\text{PF}}_{\text{true}} ,\;{\text{PF}}_{\text{known}} } \right) = \frac{1}{{\left| {{\text{PF}}_{\text{true}} } \right|}}\mathop \sum \limits_{i = 1}^{{\left| {{\text{PF}}_{\text{true}} } \right|}} \min_{j = 1}^{{\left| {{\text{PF}}_{\text{known}} } \right|}} d\left( {{\text{PFT}}_{i} ,{\text{PFK}}_{j} } \right) $$

(13)

where ${\text{PF}}_{\text{true}}$ is the set of true Pareto front solutions of objective functions, ${\text{PF}}_{\text{known}}$ is the set of Pareto front solutions of the last iteration, ${\text{PFT}}_{i}$ is the ith ${\text{PF}}_{\text{true}}$ solution, and ${\text{PFK}}_{j}$ is the jth ${\text{PF}}_{\text{known}}$ solution.

• (2) Generational distance (GD)

The GD metric is a value representing how “far” ${\text{PF}}_{\text{known}}$ is from ${\text{PF}}_{\text{true}}$. This metric evaluates the distance error between ${\text{PF}}_{\text{known}}$ and ${\text{PF}}_{\text{true}}$; that is, when the GD value is equal to 0, it represents that ${\text{PF}}_{\text{known}}$ is ${\text{PF}}_{\text{true}}$. It calculates the average nearest distance between ${\text{PF}}_{\text{known}}$ solutions and ${\text{PF}}_{\text{true}}$ solutions, which can be defined as follows.

$$ {\text{GD}} = \frac{{\left( {\mathop \sum \nolimits_{i = 1}^{n} d_{i}^{p} } \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 p}}\right.\kern-0pt} \!\lower0.7ex\hbox{$p$}}}} }}{n} $$

(14)

where $n$ is the number of ${\text{PF}}_{\text{known}}$ solutions, $p$ = 2, and $d_{i}^{ }$ is the Euclidean distance in the objective space between each ${\text{PF}}_{\text{known}}$ solution and the nearest member of ${\text{PF}}_{\text{true}}$.

For example, as shown in Fig. 16, the GD value of three ${\text{PF}}_{\text{known}}$ solutions with $d_{1 }^{ }$ = $\sqrt {\left( {2.5 - 2} \right)^{2} + \left( {4.5 - 4} \right)^{2} }$, $d_{2}^{ }$ = $\sqrt {\left( {3 - 3} \right)^{2} + \left( {3 - 3} \right)^{2} }$, and $d_{3}^{ }$ = $\sqrt {\left( {6 - 5} \right)^{2} + \left( {1 - 1} \right)^{2} }$ is $\frac{{\sqrt {0.707^{2} + 0^{2} + 1^{2} } }}{3}$ = 0.408.

Fig. 16

${\text{PF}}_{\text{known}}$ and ${\text{PF}}_{\text{true}}$ for GD

• (3) Hypervolume (HV)

The HV metric provides combined information about the diversity of obtained solutions, and a larger HV value is desirable. A nadir point is dominated by all true Pareto front solutions. This HV metric calculates the volume in the objective space between ${\text{PF}}_{\text{known}}$ and the nadir point as shown in Fig. 17, which can be defined as follows.

$$ {\text{HV}}\left( {{\text{PF}}_{\text{known}} } \right) = \bigcup\nolimits_{j = 1}^{{\left| {{\text{PF}}_{\text{known}} } \right|}} {{\text{PFK}}_{j} } $$

(15)

where ${\text{PF}}_{\text{known}}$ is the set of Pareto front solutions of the last iteration and ${\text{PFK}}_{j}$ is the jth ${\text{PF}}_{\text{known}}$ solution.

Fig. 17

${\text{PF}}_{\text{known}}$ and ${\text{PF}}_{\text{true}}$ for HV

The HV value of ${\text{PF}}_{\text{known}}$ solutions is normalized by ${\text{PF}}_{\text{true}}$ also using the same nadir point. Thus, after the normalization, the HV value is confined in [0, 1].

• (4) Coverage

The coverage metric provides combined information about the convergence of obtained solutions. When the coverage value is 1, it represents that all ${\text{PF}}_{\text{known}}$ solutions are dominated by ${\text{PF}}_{\text{true}}$ solutions. This coverage metric investigates the relationship between domination and non-domination. The number of ${\text{PF}}_{\text{known}}$ solutions dominated by ${\text{PF}}_{\text{true}}$ solutions is divided by the total number of ${\text{PF}}_{\text{known}}$ solutions, and it can be defined as follows.

$$ {\text{Coverage}}\left( {{\text{PF}}_{\text{true}} ,{\text{PF}}_{\text{known}} } \right) = \frac{{\left| {\left\{ {b \in {\text{PF}}_{\text{known}} | \exists a \in {\text{PF}}_{\text{true}} , a \prec b} \right\}} \right|}}{{\left| {{\text{PF}}_{\text{known}} } \right|}} $$

(16)

where ${\text{PF}}_{\text{true}}$ is the set of true Pareto front solutions of objective functions, ${\text{PF}}_{\text{known}}$ is the set of Pareto front solutions of the last iteration, $a$ is one ${\text{PF}}_{\text{true}}$ solution, $b$ is one ${\text{PF}}_{\text{known}}$ solution, and $\prec$ is a domination operator.

• (5) Spread

The spread metric measures the extent of spread achieved among obtained solutions, and a smaller spread value is desirable. For the spread metric, not only the Euclidean distances between ${\text{PF}}_{\text{true}}$ extreme solutions as shown in Fig. 18 and their nearest ${\text{PF}}_{\text{known}}$ solutions are calculated, but also the Euclidean distances between ${\text{PF}}_{\text{known}}$ solutions are done. Finally, the spread can be defined as follows.

$$ {\text{Spread}} = \frac{{\mathop \sum \nolimits_{i = 1}^{m} d\left( {E_{i} ,{\text{PF}}_{\text{known}} } \right) + \mathop \sum \nolimits_{{X \in {\text{PF}}_{\text{known}} }} \left| {d\left( {X,{\text{PF}}_{\text{known}} } \right) - \bar{d}} \right|}}{{\mathop \sum \nolimits_{i = 1}^{m} d\left( {E_{i} ,{\text{PF}}_{\text{known}} } \right) + \left( {\left| {{\text{PF}}_{\text{known}} } \right| - m} \right)\bar{d}}} $$

(17)

$$ d\left( {X,{\text{PF}}_{\text{known}} } \right) = \mathop {\hbox{min} }\limits_{{Y \in {\text{PF}}_{\text{known}} , Y \ne X}} F\left( X \right) - F\left( Y \right) $$

(18)

$$ \bar{d} = \frac{1}{{\left| {{\text{PF}}_{\text{known}} } \right|}}\mathop \sum \limits_{{X \in {\text{PF}}_{\text{known}} }} d\left( {X,{\text{PF}}_{\text{known}} } \right) $$

(19)

where ($E_{1}$,…, $E_{m}$) are m${\text{PF}}_{\text{true}}$ extreme solutions, ${\text{PF}}_{\text{known}}$ is the set of Pareto front solutions of the last iteration, and $m$ is the size of objectives.

Fig. 18

${\text{PF}}_{\text{known}}$ and ${\text{PF}}_{\text{true}}$ for spread

7.2 Experimental environments

The experiments were implemented in MATLAB (version R2016b) and conducted on an Intel Core 3.60 GHz, 48 GB RAM with Windows 10. For the proposed algorithm, the parameters HMCR, PAR, and conv in Phase 1 are set to 0.99, 0.2, and 10, respectively. To be fair to all the compared algorithms, the population parameter (hms in our algorithm) is set to 100. The total number of iterations in all the algorithms is 250 for 2-objective problem functions, 500 for 3-objective problem functions, and 500 for many-objective problem functions. Each algorithm was run independently for 10 times.

7.3 Comparisons

• (1) Comparisons with algorithms on the PlatEMO platform

SPEA2 (Zitzler et al. 2001), MOEA/D (Zhang and Li 2007), NSGA-III (Deb and Jain 2014), NSLS (Chen et al. 2015), BCE-IBEA (Li et al. 2016), and MOEA/IGD-NS (Tian et al. 2016) algorithms on the PlatEMO platform (Tian et al. 2017) were used in the first experiments. Besides, the parameters used in these algorithms are shown in Table 2. The means and standard deviation of IGD, GD, HV, coverage, and spread obtained from all the algorithms (including ours) on the eleven problem functions are shown in Tables 3, 4, 5, 6, and 7.

Table 2 Parameters used in SPEA2, MOEA/D, NSGA-III, NSLS, BCE-IBEA, and MOEA/IGD-NS

Table 3 Inverted generational distance (IGD)

Table 4 Generational distance (GD)

Table 5 Hypervolume (HV)

Table 6 Coverage

Table 7 Spread

As shown in Table 3, our algorithm achieves better IGD values than the other algorithms on five problem functions, i.e., ZDT1–ZDT3 and DTLZ4–DTLZ5. It means that the solutions obtained by our algorithm are closer to the optimal Pareto front than the other algorithms. Besides, we also find that our algorithm can get better results for higher dimension problems (e.g., 2-objective problem ZDT1–ZDT3 n = 30), in general. As shown in Table 4, no algorithm has the overwhelming performances in GD values. Our algorithm only achieves better GD values than the other algorithms on ZDT1 and ZDT3. MOEA/D algorithm as the first place has better GD values than the other algorithms on three problem functions, i.e., DTLZ2 and DTLZ4–DTLZ5. As shown in Table 5, our algorithm achieves better HV values than the other algorithms on six problem functions, i.e., ZDT1–ZDT3, DTLZ2, DTLZ5, and DTLZ7.

As shown in Table 6, our algorithm only achieves better coverage values than the other algorithms on ZDT3. For ZDT4, ZDT6, and DTLZ6, our obtained solutions are completely dominated by the true Pareto front solutions, and this means more iterations are needed to find out better solutions. Besides, BCE-IBEA algorithm as the first place has better coverage values than the other algorithms on four problem functions, i.e., ZDT1–ZDT2, ZDT4, and DTLZ7. As shown in Table 7, our algorithm achieves better spread values than the other algorithms on six problem functions, i.e., ZDT2–ZDT3, DTLZ2, DTLZ4–DTLZ5, and DTLZ7. This means that the diversity of our algorithm is reachable on these problem functions.

In summary, our algorithm has the first place on three performance indicators IGD, HV, and Spread.

• (2) Comparisons with harmony-related algorithms

The second experiments are to compare our algorithm with three harmony-related algorithms, i.e., harmony NSGA-II and harmony MOEA/D proposed by Doush and Bataineh (2015), and SAMOHS proposed by Dai et al. (2015). Since the open sources of these three harmony-related algorithms are not available on the Internet, we implemented them from scratch. Besides, the parameters used in these algorithms are shown in Table 8. The means and standard deviation of IGD, GD, HV, coverage, and spread obtained from these algorithms (including ours) on the eleven problem functions are shown in Tables 9, 10, 11, 12, and 13.

Table 8 Parameters used in harm. NSGA-II, harm. MOEA/D, and SAMOHS

Table 9 Inverted generational distance (IGD)

Table 10 Generational distance (GD)

Table 11 Hypervolume (HV)

Table 12 Coverage

Table 13 Spread

As shown in Table 9, our algorithm achieves better IGD values than the other algorithms on six problem functions, i.e., ZDT1–ZDT3, DTLZ2, DTLZ4, and DTLZ6. As shown in Table 10, our algorithm also achieves better GD values than the other algorithms on five problem functions, i.e., ZDT1–ZDT3, DTLZ1, and DTLZ6. As shown in Table 11, our algorithm achieves the overwhelming HV values on eight problem functions, i.e., ZDT1–ZDT3, ZDT6, DTLZ2, and DTLZ4–DTLZ6. As shown in Table 12, our algorithm also achieves the overwhelming coverage values on seven problem functions, i.e., ZDT1–ZDT3, ZDT6, and DTLZ4–DTLZ6. Finally, as shown in Table 13, our algorithm achieves better spread values than the other algorithms on six problem functions, i.e., ZDT1–ZDT3, ZDT6, DTLZ1, and DTLZ6.

In summary, our algorithm has the first place on all performance indicators.

• (3) Comparisons with itself with fixed HMCR, PAR, and bw values

The third experiments are to verify whether the proposed algorithm can improve the performances by using the self-adaptive way or by dynamically adjusting parameters. Here, the proposed algorithm is compared with itself with fixed HMCR, PAR, and bw values where they are set to 0.99, 0.2, and 0.5, respectively. The means and standard deviation of IGD, GD, HV, coverage, and spread obtained from both our algorithms on the eleven problem functions are shown in Tables 14, 15, 16, 17, and 18. The results show the proposed algorithm with the self-adaptive way can always improve the performances, except ZDT4 and DTLZ1.

Table 14 Inverted generational distance (IGD)

Table 15 Generational distance (GD)

Table 16 Hypervolume (HV)

Table 17 Coverage

Table 18 Spread

• (4) Comparisons with algorithms on many-objective problems

The last experiments are to evaluate our algorithm and other algorithms such as NSGA-III (Deb and Jain 2014), SPEA2 + SDE (Li et al. 2014), and MOEA/DD (Li et al. 2015), on many-objective problems. Here, we modified our algorithm as the different version for many-objective problems. The means and standard deviation of IGD, GD, HV, coverage, and spread obtained from our algorithm and other algorithms on MaF1, MaF2, and MaF3 with M = 5, 10, and 15 are shown in Tables 19, 20, 21, 22, and 23.

Table 19 Inverted generational distance (IGD)

Table 20 Generational distance (GD)

Table 21 Hypervolume (HV)

Table 22 Coverage

Table 23 Spread

As shown in Table 19, our algorithm and SPEA2 + SDE achieve better IGD values than the other algorithms. As shown in Table 20, SPEA2 + SDE has the overwhelming performances in GD values. As shown in Table 21, SPEA2 + SDE has also the overwhelming performances in HV values. As shown in Table 22, NSGA-III and SPEA2 + SDE achieve better coverage values than the other algorithms. As shown in Table 23, our algorithm has the overwhelming performances in spread values.

In summary, although SPEA2 + SDE achieves the overwhelming performances in GD and HV values and has better IGD and coverage values than some algorithms, our algorithm has the overwhelming performances in spread values. Thus, no algorithm can be always the best one on different performance indicators for many-objective optimization problems. In this paper, we highlight that the proposed algorithm is also a competitive one for many-objective problems, on performance indicators IGD and spread. For the forthcoming research aiming at many-objective optimization problems, they can take our proposed algorithm as a compared one, especially on performance indicator spread.

• (5) Comparisons with true Pareto front solutions

For contrasting, the true Pareto front solutions and the solutions obtained by our algorithm on the eleven problem functions are plotted as shown in Figs. 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, and 29. For 2-objective problem functions, our solutions on ZDT1, ZDT2, ZDT3, and ZDT6 are fairly close to the true Pareto front solutions, except ZDT4. For 3-objective problem functions, our solutions on DTLZ1, DTLZ2, DTLZ4-DTLZ5, and DTLZ7 are quite close to the true Pareto front solutions, except ZDLZ6 where our solutions are not convergent enough.

Fig. 19

True Pareto front solutions (left) and our solutions (right) on ZDT1

Fig. 20

True Pareto front solutions (left) and our solutions (right) on ZDT2

Fig. 21

True Pareto front solutions (left) and our solutions (right) on ZDT3

Fig. 22

True Pareto front solutions (left) and our solutions (right) on ZDT4

Fig. 23

True Pareto front solutions (left) and our solutions (right) on ZDT6

Fig. 24

True Pareto front solutions (left) and our solutions (right) on DTLZ1

Fig. 25

True Pareto front solutions (left) and our solutions (right) on DTLZ2

Fig. 26

True Pareto front solutions (left) and our solutions (right) on DTLZ4

Fig. 27

True Pareto front solutions (left) and our solutions (right) on DTLZ5

Fig. 28

True Pareto front solutions (left) and our solutions (right) on DTLZ6

Fig. 29

True Pareto front solutions (left) and our solutions (right) on DTLZ7

8 Conclusions

In this paper, we propose the self-adaptive harmony search algorithm to solve multi-objective optimization problems. The system is divided into two phases. In Phase 1, we modify the original harmony search algorithm using the standard deviation of parameter values in the harmony memory (i.e., the variant HM1 algorithm), instead of using predefined bandwidth. In Phase 2, in order to get more non-dominated solutions in the feasible solution regions, reference points in a hyperplane are generated based on the extreme points derived from the harmony memory. These reference points are used to assess whether a new solution generated by the variant HM2 algorithm is close to any of them. If not close enough, another new solution is generated based on the previous solution and checked again. Finally, parameter values are adjusted for the next iteration, based on the harmony memory, until all iterations are finished.

In the experiments, we use the eleven well-known multi-objective problems and three many-objective problems to examine the proposed algorithm and other existing algorithms, based on five performance indicators. As a result, our algorithm achieves better performances than the others in IGD, HV, and spread indicators.

In the future, two issues observed in this study can be further investigated. First, when is the true convergence point for the system to switch from Phase 1 to Phase 2? Second, why can our algorithm not get better IGD performances than the other algorithms on less dimension problems? If these two issues could be solved, our algorithm will outperform the other algorithms drastically.