1 Introduction

The classic transportation problem consists of decision on how much product to send from each source to each destination in order to minimize the total transportation cost which is affected by the unit transportation cost between each source and each destination. In this classic problem the capacities (availabilities) of each source and each destination are given. For the cases that the sum of capacities of the sources equals the sum of capacities of the destinations, the problem is balanced. On the other hand, it can be converted to a balanced problem using dummy source or destination.

Fuzzy theory which was first introduced by Zadeh (1965) has been employed to formulate many real-life engineering and non-engineering problems. The fuzzy theory became more popular in the case of optimization problems by the excellent study of Bellman and Zadeh (1970). One of the main properties of the fuzzy numbers is that the non-membership degree of the elements is obtained by one minus the membership degree. But, in real-world situations as the information may have vagueness or insufficiency, the sum of membership and non-membership degrees can be a value less than one. In such cases fuzzy numbers are not suitable as in these numbers the sum of membership and non-membership degrees is exactly equal to one. To overcome such difficulty, Atanassov (1986) introduced the theory of intuitionistic fuzzy set (IFS) that is an extension of fuzzy theory and is highly useful for real-life problems to deal with vague information. The most important advantage of IFS compared to fuzzy set is that it isolates the membership and non-membership degrees of a number of the set in a way that for an element the sum of these degrees is less than or equal to one. Therefore, this theory seems to be very applicable when considering vagueness in estimation of parameters by decision maker. In the case of transportation problem some available information of the transportation costs, availabilities and demand values may be vague or insufficient in estimation procedure. Therefore, estimating exact membership functions and also exact non-membership functions may not be possible, where some hesitations still remain. For this reason, use of IFS to show the values of imprecise parameters may be more realistic than fuzzy set. For more applications of intuitionistic fuzzy numbers the studies of Nayagam et al. (2016), Kumar and Hussain (2014), Singh and Yadav (2016), He et al. (2017), etc., can be referred.

The literature of optimization problems is full of the works applying fuzzy and intuitionistic fuzzy set theory for formulating and tackling real-world optimization problems like production planning and scheduling problems, transportation problem (see Xu 1988; Cascetta et al. 2006; Ganesan and Veeramani 2006; Asunción et al. 2007; Hosseinzadeh Lotfi et al. 2009; Kaur and Kumar 2012; De and Sana 2013; Mahmoodirad et al. 2014; Mahmoodi-Rad et al. 2014; Niroomand et al. 2016a, b; Liu 2016; Taassori et al. 2016; Das et al. 2017). In transportation problems considered for real cases, in many situations parameters like transportation costs, supply values, demand values may be of uncertainty because of some reasons (see Dempe and Starostina 2006). To cope with the parameters having uncertainty in a transportation problem many studies have been done. Nagoorgani and Razak (2006) focused on a transportation problem with two stages in fuzzy environment for supply and demand values. Dinager and Palanivel (2009) proposed an approach for solving fuzzy transportation problem with trapezoidal fuzzy parameters. Pandian and Natarajan (2010) proposed a procedure to obtain optimal solution of a transportation problem in fuzzy environment. Mohideen and Kumar (2010) performed a comparative study on fuzzy transportation problems. Basirzadeh (2011) proposed a solution approach for a transportation problem of fuzzy environment. Kaur and Kumar (2012) tackled a transportation problem with parameters of trapezoidal fuzzy numbers. Aggarwal and Gupta (2017) studied the sensitivity analysis of intuitionistic fuzzy solid transportation problem. For the case of single-objective and multi-objective general linear programming under intuitionistic fuzzy values, the recent studies of Ramík and Vlach (2016), Razmi et al. (2016), Singh and Yadav (2017a), Singh and Yadav (2017b) may be interesting.

As for determining the unit transportation costs, availability values and demand values in a transportation problem the decision maker may hesitate, it would be more realistic to consider them as intuitionistic fuzzy numbers to consider both the uncertainty and the hesitation in the cost determination procedure. In addition to the parameters, considering intuitionistic fuzzy variables, fully intuitionistic fuzzy transportation problem where all variables and parameters are of intuitionistic fuzzy numbers can be defined. The studies of Kumar and Hussain (2014) and Singh and Yadav (2016) can be exampled for this problem. In this study, we consider a fully intuitionistic fuzzy transportation problem (FIFTP) with triangular intuitionistic fuzzy numbers (TIFN). The source of motivation is to propose a new solution approach to overcome the shortcomings of the approaches of the literature like obtaining negative objective function value, obtaining solutions dissatisfying the constraints. The results obtained by the proposed approach show a superior performance compared to the approaches of the literature.

The remainder of this paper is organized by the following sections. Section 2 presents some initial definitions of intuitionistic fuzzy numbers. Section 3 describes the mathematical formulation of the fully intuitionistic fuzzy transportation problem (FIFTP). The proposed solution approach and its comparison with the existing approaches of the literature are presented in Sect. 4. Computational experiments are done in Sect. 5. Finally, conclusions are drawn in Sect. 6.

2 Preliminaries

Some preliminaries of fuzzy theory, especially intuitionistic fuzzy numbers, are mentioned in this section.

Fig. 1
figure 1

Membership and non-membership functions for a TIFN

Full size image

2.1 Basic definitions

Some basic definitions from fuzzy theory which will be applied later in this paper are explained in this subsection.

Definition 1

(Singh and Yadav 2016) If X is a universe of discourse, then the following set of ordered triples defines an intuitionistic fuzzy set (IFS) \(\tilde{A}^{I}\),

$$\begin{aligned} \tilde{A}^{I}=\left\{ {\left\langle {x,\mu _{\tilde{A}^{I}} \left( x \right) ,\upsilon _{\tilde{A}^{I}} \left( x \right) } \right\rangle :x\in X} \right\} \end{aligned}$$
(1)

where \(\mu _{\tilde{A}^{I}} ,\upsilon _{\tilde{A}^{I}} :X\rightarrow \left[ {0,1} \right] \) and \(0\le \mu _{\tilde{A}^{I}} \left( x \right) +\upsilon _{\tilde{A}^{I}} \left( x \right) \le 1 (x\in X)\) are held. In this definition \(\mu _{\tilde{A}^{I}} \left( x \right) ,\upsilon _{\tilde{A}^{I}} \left( x \right) (x\in X)\) are called degree of membership and degree of non-membership, respectively. Also for \(x\in X\) the following relation calculates degree of hesitation \((h\left( x \right) )\).

$$\begin{aligned} h\left( x \right) =1-\mu _{\tilde{A}^{I}} \left( x \right) -\upsilon _{\tilde{A}^{I}} \left( x \right) \end{aligned}$$
(2)

Definition 2

(Singh and Yadav 2016) An intuitionistic fuzzy set (IFS) \(\tilde{A}^{I}=\left\{ {\left\langle {x,\mu _{\tilde{A}^{I}} \left( x \right) ,\upsilon _{\tilde{A}^{I}} \left( x \right) } \right\rangle :x\in X} \right\} \) must have the following two conditions,

  1. (i)

    There should be a real number r such that \(\mu _{\tilde{A}^{I}} \left( r \right) =1\) and \(\upsilon _{\tilde{A}^{I}} \left( r \right) =0\),

  2. (ii)

    \(\mu _{\tilde{A}^{I}} \left( x \right) \) and \(\upsilon _{\tilde{A}^{I}} \left( x \right) \) are piecewise continuous mapping from the set of real numbers to the interval \(\left[ {0,1} \right] \) where \(0\le \mu _{\tilde{A}^{I}} \left( x \right) +\upsilon _{\tilde{A}^{I}} \left( x \right) \le 1\).

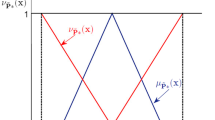
The membership and non-membership functions of the triangular intuitionistic fuzzy number (TIFN) \(\tilde{A}^{I}=( a_1 ,a_2 ,a_3 ;{a}'_1 ,a_2 ,{a}'_3 )\) are defined as follows,

$$\begin{aligned} \mu _{\tilde{A}^{I}} \left( x \right)= & {} \left\{ {\begin{array}{l@{\quad }l} \frac{x-a_1 }{a_2 -a_1 } &{} a_1<x\le a_2 \\ \frac{a_3 -x}{a_3 -a_2 } &{} a_2 \le x<a_3\\ 0&{} \hbox {otherwise} \\ \end{array}} \right. \end{aligned}$$
(3)
$$\begin{aligned} \upsilon _{\tilde{A}^{I}} \left( x \right)= & {} \left\{ {\begin{array}{l@{\quad }l} \frac{a_2 -x}{a_2 -{a}'_1 } &{} a_1<x\le a_2\\ \frac{x-a_2 }{{a}'_3 -a_2 } &{} a_2 \le x<a_3\\ 1&{} \hbox {otherwise} \\ \end{array}} \right. \end{aligned}$$
(4)

where \({a}'_1 \le a_1<a_2 <a_3 \le {a}'_3 \). These functions are schematically shown in Fig. 1.

Definition 3

(Singh and Yadav 2016) The following operations can be done on TIFNs \(\tilde{A}^{I}=\left( {a_1 ,a_2 ,a_3 ;{a}^{\prime }_1 ,a_2 ,{a}^{\prime }_3 } \right) \) and \(\tilde{B}^{I}=\left( {b_1 ,b_2 ,b_3 ;{b}^{\prime }_1 ,b_2 ,{b}^{\prime }_3 } \right) \),

$$\begin{aligned} \tilde{A}^{I}\oplus \tilde{B}^{I}= & {} \left( a_1 +b_1 ,a_2 +b_2 ,a_3 +b_3 ;{a}^{\prime }_1 \right. \nonumber \\&\quad \left. +\,{b}^{\prime }_1 ,a_2 +b_2 ,{a}^{\prime }_3 +{b}^{\prime }_3 \right) \end{aligned}$$
(5)
$$\begin{aligned} \tilde{A}^{I}\Theta \tilde{B}^{I}= & {} \left( a_1 +b_3 ,a_2 +b_2 ,a_3 +b_1 ;{a}^{\prime }_1 \right. \nonumber \\&\quad \left. +\,{b}^{\prime }_3 ,a_2 +b_2 ,{a}^{\prime }_3 +{b}^{\prime }_1 \right) \end{aligned}$$
(6)
$$\begin{aligned} \tilde{A}^{I}\otimes \tilde{B}^{I}= & {} \left( {l_1 ,l_2 ,l_3 ;{l}^{\prime }_1 ,l_2 ,{l}^{\prime }_3 } \right) \end{aligned}$$
(7)
$$\begin{aligned} k\tilde{A}^{I}= & {} \left( {ka_1 ,ka_2 ,ka_3 ;k{a}^{\prime }_1 ,ka_2 ,k{a}^{\prime }_3 } \right) \quad k\ge 0 \end{aligned}$$
(8)
$$\begin{aligned} k\tilde{A}^{I}= & {} \left( {ka_3 ,ka_2 ,ka_1 ;k{a}^{\prime }_3 ,ka_2 ,k{a}^{\prime }_1 } \right) \quad k<0 \end{aligned}$$
(9)

where \(l_1 =\min \left\{ {a_1 b_1 ,a_1 b_3 ,a_3 b_1 ,a_3 b_3 } \right\} , l_2 =a_2 b_2 , l_3 =\max \left\{ {a_1 b_1 ,a_1 b_3 ,a_3 b_1 ,a_3 b_3 } \right\} , {l}^{\prime }_1 =\min \big \{ {a}^{\prime }_1 {b}^{\prime }_1 ,{a}^{\prime }_1 {b}^{\prime }_3 ,{a}^{\prime }_3 {b}^{\prime }_1 , {a}^{\prime }_3 {b}^{\prime }_3 \big \}, {l}^{\prime }_3 =\max \left\{ {{a}^{\prime }_1 {b}^{\prime }_1 ,{a}^{\prime }_1 {b}^{\prime }_3 ,{a}^{\prime }_3 {b}^{\prime }_1 ,{a}^{\prime }_3 {b}^{\prime }_3 } \right\} \).

Definition 4

(Singh and Yadav 2016) Considering \(\tilde{A}^{I}=\left( {a_1 ,a_2 ,a_3 ;{a}^{\prime }_1 ,a_2 ,{a}^{\prime }_3 } \right) \), the score function of the membership and non-membership functions \(\mu _{\tilde{A}^{I}} \) and \(\upsilon _{\tilde{A}^{I}} \), is calculated as \(S\left( {\mu _{\tilde{A}^{I}} } \right) =\frac{a_1 +2a_2 +a_3 }{4}\) and \(S\left( {\upsilon _{\tilde{A}^{I}} } \right) =\frac{{a}^{\prime }_1 +2a_2 +{a}^{\prime }_3 }{4}\), respectively. Now, the accuracy ranking function of \(\tilde{A}^{I}=\left( {a_1 ,a_2 ,a_3 ;{a}^{\prime }_1 ,a_2 ,{a}^{\prime }_3 } \right) \) is calculated by the formula \(\mathfrak {R}\left( \! {\tilde{A}^{I}} \right) \!=\frac{S\left( {\mu _{\tilde{A}^{I}} } \right) +S\left( {\upsilon _{\tilde{A}^{I}} } \right) }{2}\).

Definition 5

(Singh and Yadav 2016) The following comparisons can be done on TIFNs \(\tilde{A}^{I}=\left( {a_1 ,a_2 ,a_3 ;{a}^{\prime }_1 ,a_2 ,{a}^{\prime }_3 } \right) \) and \(\tilde{B}^{I}=\left( {b_1 ,b_2 ,b_3 ;{b}^{\prime }_1 ,b_2 ,{b}^{\prime }_3 } \right) \),

  • \(\tilde{A}^{I}\ge \tilde{B}^{I}\) if \(\mathfrak {R}\left( {\tilde{A}^{I}} \right) \ge \mathfrak {R}\left( {\tilde{B}^{I}} \right) \),

  • \(\tilde{A}^{I}\le \tilde{B}^{I}\) if \(\mathfrak {R}\left( {\tilde{A}^{I}} \right) \le \mathfrak {R}\left( {\tilde{B}^{I}} \right) \),

  • \(\tilde{A}^{I}=\tilde{B}^{I}\) if \(\mathfrak {R}\left( {\tilde{A}^{I}} \right) =\mathfrak {R}\left( {\tilde{B}^{I}} \right) \),

  • \(\min \left\{ {\tilde{A}^{I},\tilde{B}^{I}} \right\} =\tilde{A}^{I}\) if \(\tilde{A}^{I}\le \tilde{B}^{I}\) or \(\tilde{B}^{I}\ge \tilde{A}^{I}\),

  • \(\max \left\{ {\tilde{A}^{I},\tilde{B}^{I}} \right\} =\tilde{A}^{I}\) if \(\tilde{A}^{I}\ge \tilde{B}^{I}\) or \(\tilde{B}^{I}\ les \tilde{A}^{I}\).

Theorem 1

\(\mathfrak {R}\left( \! {k_1 \tilde{A}^{I1}\!+\!k_2 \tilde{A}^{I2}+\cdots +k_n \tilde{A}^{In}} \!\right) \!=\!k_1 \mathfrak {R}\left( \! {\tilde{A}^{I1}} \right) +k_2 \mathfrak {R}\left( {\tilde{A}^{I2}} \right) +\cdots +k_n \mathfrak {R}\left( {\tilde{A}^{In}} \right) .\)

Proof

Let \(\tilde{A}^{I i}=\left( {a_1^i ,a_2^i ,a_3^i ;{a}_1 ^{{\prime }i},a_2^i ,{a}_3 ^{{\prime }i}} \right) \) for \(i=1,\ldots ,n\) be n TIFNs. Then for \(k_i >0, i=1,\ldots ,n\), we have,

Theorem 2

The TIFNs \(\tilde{A}^{I}=\left( {a_1 ,a_2 ,a_3 ;{a}^{\prime }_1 ,a_2 ,{a}^{\prime }_3 } \right) \) and \(\tilde{B}^{I}=\left( {b_1 ,b_2 ,b_3 ;{b}^{\prime }_1 ,b_2 ,{b}^{\prime }_3 } \right) \) are equal if and only if \(a_1 =b_1 , a_2 =b_2 , a_3 =b_3 , {a}^{\prime }_1 ={b}^{\prime }_1 \), and \({a}^{\prime }_3 ={b}^{\prime }_3 \).

Proof

The proof is straightforward. \(\square \)

2.2 Some particular cases (Kumar and Hussain 2014)

Considering \(\tilde{A}^{I}=\left( {a_1 ,a_2 ,a_3 ;{a}^{\prime }_1 ,a_2 ,{a}^{\prime }_3 } \right) \) as a TIFN, the following cases arise,

  • If \(a_1 ={a}^{\prime }_1 \) and \(a_3 ={a}^{\prime }_3 \), then \(\tilde{A}^{I}\) is a triangular fuzzy number represented by \(\tilde{A}=\left( {a_1 ,a_2 ,a_3 } \right) \).

  • If \(a_1 =a_2 =a_3 ={a}^{\prime }_1 ={a}^{\prime }_3 =q\), then \(\tilde{A}^{I}\) is a real number equal to q.

3 Fully intuitionistic fuzzy transportation problem (FIFTP)

In a primal transportation problem (TP) some products are to be sent from some sources to some destinations in a way that the supplying amount of the sources and the demand values of the destinations are respected. Each route from the sources to the destinations has a transportation cost for each unit of transported product. In this problem the aim is to minimize the total transportation cost. In most of real cases of these problems, it is almost impossible to determine an exact value for the unit transportation cost of each route. Therefore, use of interval or fuzzy values can be of interest to model the real cases of this problem. As for determining the unit transportation costs the decision maker may hesitate, it would be more realistic to consider the cost as IFN to consider both the uncertainty and the hesitation of the cost determination procedure. In this study, the costs of the above-mentioned transportation problem are TIFNs. To model such problem the following notations are defined.

  • m is the number of sources being indexed by i.

  • n is the number of destinations being indexed by j.

  • \(\tilde{a}_i^I =\left( {a_{i,1} ,a_{i,2} ,a_{i,3} ;{a}^{\prime }_{i,1} ,{a}^{\prime }_{i,2} ,{a}^{\prime }_{i,3} } \right) \) is the TIFN for the amount of product supplied by source i.

  • \(\tilde{b}_j^I =\left( {b_{j,1} ,b_{j,2} ,b_{j,3} ;{b}^{\prime }_{j,1} ,{b}^{\prime }_{j,2} ,{b}^{\prime }_{j,3} } \right) \) is the TIFN for the amount of product demanded by destination j.

  • \(\tilde{c}_{ij}^I =\left( {c_{ij,1} ,c_{ij,2} ,c_{ij,3} ;{c}^{\prime }_{ij,1} ,{c}^{\prime }_{ij,2} ,{c}^{\prime }_{ij,3} } \right) \) is the TIFN for the cost of sending one unit of product from source i to destination j.

  • \(\tilde{X}_{ij}^I =\left( {X_{ij,1} ,X_{ij,2} ,X_{ij,3} ;{X}^{\prime }_{ij,1} ,{X}^{\prime }_{ij,2} ,{X}^{\prime }_{ij,3} } \right) \) is a continuous intuitionistic fuzzy variable showing the amount of product sent from source i to destination j.

Now the mathematical formulation of the FIFTP is given as (see also Singh and Yadav (2016)),

$$\begin{aligned} \min \tilde{Z}^{I}=\sum _{i=1}^m {\sum _{j=1}^n {\tilde{c}_{ij}^I \otimes \tilde{X}_{ij}^I } } \end{aligned}$$
(10)

subject to

$$\begin{aligned} \sum _{j=1}^n {\tilde{X}_{ij}^I }= & {} \tilde{a}_i^I \quad \forall i \end{aligned}$$
(11)
$$\begin{aligned} \sum _{i=1}^m {\tilde{X}_{ij}^I }= & {} \tilde{b}_j^I \quad \forall j \end{aligned}$$
(12)
$$\begin{aligned} \tilde{X}_{ij}^I\ge & {} 0 \quad \forall i,j \end{aligned}$$
(13)

The same as the assumptions of the primal TP, here, it is assumed that all parameters including supply values, demand values and costs are of nonnegative TIFNs. Notably, negative values for the parameters of transportation problems have no physical justification.

Formulation (10)–(13) is called a mixed intuitionistic fuzzy transportation problem, if its parameters are of either crisp or fuzzy (fuzzy or intuitionistic fuzzy) values. On the other hand, it is classified to balanced and unbalanced intuitionistic fuzzy transportation problems if \(\sum \nolimits _{i=1}^m {\tilde{a}_i^I } =\sum \nolimits _{j=1}^n {\tilde{b}_j^I } \) and \(\sum \nolimits _{i=1}^m {\tilde{a}_i^I } \ne \sum \nolimits _{j=1}^n {\tilde{b}_j^I } \), respectively. For the case of unbalanced intuitionistic fuzzy transportation problem with \(\sum \nolimits _{i=1}^m {\tilde{a}_i^I } >\sum \nolimits _{j=1}^n {\tilde{b}_j^I } \), a dummy destination with demand of \(\sum \nolimits _{i=1}^m {\tilde{a}_i^I } -\sum \nolimits _{j=1}^n {\tilde{b}_j^I } \) and cost of zero is added to the problem. For the case of unbalanced intuitionistic fuzzy transportation problem with \(\sum \nolimits _{i=1}^m {\tilde{a}_i^I } <\sum \nolimits _{j=1}^n {\tilde{b}_j^I } \), a dummy source with availability of \(\sum \nolimits _{j=1}^n {\tilde{b}_j^I } -\sum \nolimits _{i=1}^m {\tilde{a}_i^I } \) and cost of zero is added to the problem.

In the next section of this paper we introduce a solution approach to the balanced FIFTP where all of the parameters and variables are of TIFNs.

4 Solution methodology

In this section, a simple solution approach for the balanced FIFTP is introduced which has many advantages compared to the existing approaches of the literature. Therefore, first the shortcomings of the approaches of the literature are reported; then, the proposed approach is explained.

4.1 Shortcomings of the existing studies

The studies of Kumar and Hussain (2014) and Singh and Yadav (2016) introduce approaches for solving fully intuitionistic fuzzy transportation problem. In the numerical examples and case studies solved in these studies, all unit transportation cost, supply and demand values are positive intuitionistic fuzzy values. But, some of the values obtained for intuitionistic fuzzy variables and also objective function values are negative where this is in contradiction with the general assumptions of transportation problem (nonnegative variables and nonnegative objective function value for the case of positive unit transportation costs). Interestingly, exactly the same shortcomings exist in the study of Singh and Yadav (2015) where an intuitionistic fuzzy transportation problem with crisp unit transportation costs was considered.

4.2 The proposed solution approach

The main purpose of proposing the solution approach of this subsection is to avoid the shortcomings of the previous studies mentioned in the previous subsection. The proposed approach is as follows:

Step 1. Considering triangular fuzzy intuitionistic parameters and variables, the balanced FIFTP is expanded as,

$$\begin{aligned} \min \tilde{Z}^{I}= & {} \sum _{i=1}^m \sum _{j=1}^n \left( {c_{ij}^1 ,c_{ij}^2 ,c_{ij}^3 ;c_{ij}^4 ,c_{ij}^2 ,c_{ij}^5 } \right) \nonumber \\&\quad \otimes \left( {X_{ij}^1 ,X_{ij}^2 ,X_{ij}^3 ;X_{ij}^4 ,X_{ij}^2 ,X_{ij}^5 } \right) \end{aligned}$$
(14)

subject to

$$\begin{aligned}&\sum _{j=1}^n {\left( {X_{ij}^1 ,X_{ij}^2 ,X_{ij}^3 ;X_{ij}^4 ,X_{ij}^2 ,X_{ij}^5 } \right) } \nonumber \\&\quad =\left( {a_i^1 ,a_i^2 ,a_i^3 ;a_i^4 ,a_i^2 ,a_i^5 } \right) \quad \forall i \end{aligned}$$
(15)
$$\begin{aligned}&\sum _{i=1}^m {\left( {X_{ij}^1 ,X_{ij}^2 ,X_{ij}^3 ;X_{ij}^4 ,X_{ij}^2 ,X_{ij}^5 } \right) } \nonumber \\&\quad =\left( {b_j^1 ,b_j^2 ,b_j^3 ;b_j^4 ,b_j^2 ,b_j^5 } \right) \quad \forall j \end{aligned}$$
(16)
$$\begin{aligned}&\left( {X_{ij}^1 ,X_{ij}^2 ,X_{ij}^3 ;X_{ij}^4 ,X_{ij}^2 ,X_{ij}^5 } \right) \ge 0 \quad \forall i,j \end{aligned}$$
(17)

Step 2. Using the accuracy function \(\mathfrak {R}\) of intuitionistic fuzzy numbers (other ranking functions also may be used if necessary), the following model is obtained.

$$\begin{aligned}&\min \tilde{Z}^{I}=\mathfrak {R}\left( \sum _{i=1}^m \sum _{j=1}^n \left( {c_{ij}^1 ,c_{ij}^2 ,c_{ij}^3 ;c_{ij}^4 ,c_{ij}^2 ,c_{ij}^5 } \right) \right. \nonumber \\&\quad \otimes \,\left. \left( {X_{ij}^1 ,X_{ij}^2 ,X_{ij}^3 ;X_{ij}^4 ,X_{ij}^2 ,X_{ij}^5 } \right) \right) \end{aligned}$$
(18)
$$\begin{aligned}&\hbox {subject to} \nonumber \\&\hbox {Constraints } (15){-}(17) \end{aligned}$$
(19)

Step 3. Convert the model of Step 2 to the following crisp model and solve it to find its optimal solution (\(X_{ij}^{k*} \) values).

$$\begin{aligned} \min \tilde{Z}^{I}= & {} \sum _{i=1}^m \sum _{j=1}^n \mathfrak {R}\left( \left( {c_{ij}^1 ,c_{ij}^2 ,c_{ij}^3 ;c_{ij}^4 ,c_{ij}^2 ,c_{ij}^5 } \right) \right. \nonumber \\&\left. \otimes \,\left( {X_{ij}^1 ,X_{ij}^2 ,X_{ij}^3 ;X_{ij}^4 ,X_{ij}^2 ,X_{ij}^5 } \right) \right) \end{aligned}$$
(20)

subject to

$$\begin{aligned}&\sum _{j=1}^n {X_{ij}^k } =a_i^k \quad \forall i,k|k\in \left\{ {1,\ldots ,5} \right\} \end{aligned}$$
(21)
$$\begin{aligned}&\sum _{i=1}^m {X_{ij}^k } =b_j^k \quad \forall j,k|k\in \left\{ {1,\ldots ,5} \right\} \end{aligned}$$
(22)
$$\begin{aligned}&X_{ij}^4 \ge 0 \quad \forall i,j \end{aligned}$$
(23)
$$\begin{aligned}&X_{ij}^2 -X_{ij}^1 \ge 0 \quad \forall i,j \end{aligned}$$
(24)
$$\begin{aligned}&X_{ij}^3 -X_{ij}^2 \ge 0 \quad \forall i,j \end{aligned}$$
(25)
$$\begin{aligned}&X_{ij}^1 -X_{ij}^4 \ge 0 \quad \forall i,j \end{aligned}$$
(26)
$$\begin{aligned}&X_{ij}^5 -X_{ij}^3 \ge 0 \quad \forall i,j \end{aligned}$$
(27)

Constraints (15) and (16) are converted to constraints (21) and (22), respectively, using the definitions mentioned in Sect. 2. On the other hand, constraint (17) is converted to constraints (23)–(27) to guarantee the nonnegativity condition of the problem and with respect to the conditions of intuitionistic fuzzy numbers.

Step 4. Calculate the intuitionistic fuzzy objective function value using the solution of Step 3 as follows,

$$\begin{aligned} \tilde{Z}^{I}= & {} \sum _{i=1}^m \sum _{j=1}^n \left( {c_{ij}^1 ,c_{ij}^2 ,c_{ij}^3 ;c_{ij}^4 ,c_{ij}^2 ,c_{ij}^5 } \right) \nonumber \\&\otimes \,\left( {X_{ij}^{1*} ,X_{ij}^{2*} ,X_{ij}^{3*} ;X_{ij}^{4*} ,X_{ij}^{2*} ,X_{ij}^{5*} } \right) \end{aligned}$$
(28)

In order to show the equivalency of proposed crisp problem (20)–(27) and FIFTP (10)–(13) [or formulation (14)–(17)], the following theorem is introduced.

Theorem 3

Formulations (10)–(13) and (20)–(27) are equivalent.

Proof

This equivalency is proved from feasibility and optimality point of views by defining the feasible solution sets \(S_f \) and \(S_c \) for formulations (10)–(13) and (20)–(27), respectively.

\(X=\left\{ {\tilde{X}_{ij}^I } \right\} \) is a solution for problem (10)–(13) (meaning that \(X\in S_f )\) if and only if it satisfies constraint set (11)–(13) and consequently set (15)–(17). Applying Definition 3 to set (15)–(17), the following set of constraints is obtained,

$$\begin{aligned}&\left( {\sum _{j=1}^n {X_{ij}^1 } ,\sum _{j=1}^n {X_{ij}^2 } ,\sum _{j=1}^n {X_{ij}^3 } ;\sum _{j=1}^n {X_{ij}^4 } ,\sum _{j=1}^n {X_{ij}^2 } ,\sum _{j=1}^n {X_{ij}^5 } } \right) \nonumber \\&\quad =\left( {a_i^1 ,a_i^2 ,a_i^3 ;a_i^4 ,a_i^2 ,a_i^5 } \right) \quad \forall i \end{aligned}$$
(29)
$$\begin{aligned}&\left( {\sum _{i=1}^m {X_{ij}^1 } ,\sum _{i=1}^m {X_{ij}^2 } ,\sum _{i=1}^m {X_{ij}^3 } ;\sum _{i=1}^m {X_{ij}^4 } ,\sum _{i=1}^m {X_{ij}^2 } ,\sum _{i=1}^m {X_{ij}^5 } } \right) \nonumber \\&\quad =\left( {b_j^1 ,b_j^2 ,b_j^3 ;b_j^4 ,b_j^2 ,b_j^5 } \right) \quad \forall j \end{aligned}$$
(30)
$$\begin{aligned}&\left( {X_{ij}^1 ,X_{ij}^2 ,X_{ij}^3 ;X_{ij}^4 ,X_{ij}^2 ,X_{ij}^5 } \right) \ge 0 \quad \forall i,j \end{aligned}$$
(31)

According to Theorem 2 and nonnegativity constraint (31), set (29)–(31) is converted to constraint set (21)–(27). This means that the solution \(X=\left\{ {\tilde{X}_{ij}^I } \right\} \) also satisfies constraint set (21)–(27), meaning that \(X\in S_c \). Therefore, \(S_f =S_c \).

From optimality point of view, we prove that the optimal solutions of formulations (10)–(13) and (20)–(27) are the same. For this aim, consider \(X^{*}=\left\{ {\tilde{X}_{ij}^{I*} } \right\} \) as optimal solution of problem (10)–(13) (meaning that \(X^{*}\in S_f )\). Then for any \(X\in S_c \), the relation \(\sum _{i=1}^m {\sum _{j=1}^n {\tilde{c}_{ij}^I \otimes \tilde{X}_{ij}^{I*} } } \le \sum _{i=1}^m {\sum _{j=1}^n {\tilde{c}_{ij}^I \otimes \tilde{X}_{ij}^I } } \) is correct if and only if,

$$\begin{aligned}&\sum _{i=1}^m \sum _{j=1}^n \left( {c_{ij}^1 ,c_{ij}^2 ,c_{ij}^3 ;c_{ij}^4 ,c_{ij}^2 ,c_{ij}^5 } \right) \nonumber \\&\quad \otimes \,\left( {X_{ij}^{1*} ,X_{ij}^{2*} ,X_{ij}^{3*} ;X_{ij}^{4*} ,X_{ij}^{2*} ,X_{ij}^{5*} } \right) \nonumber \\&\le \sum _{i=1}^m \sum _{j=1}^n \left( {c_{ij}^1 ,c_{ij}^2 ,c_{ij}^3 ;c_{ij}^4 ,c_{ij}^2 ,c_{ij}^5 } \right) \nonumber \\&\quad \otimes \,\left( {X_{ij}^1 ,X_{ij}^2 ,X_{ij}^3 ;X_{ij}^4 ,X_{ij}^2 ,X_{ij}^5 } \right) \end{aligned}$$
(32)

if and only if (according to Definition 5),

$$\begin{aligned}&\mathfrak {R}\left( \sum _{i=1}^m \sum _{j=1}^n \left( {c_{ij}^1 ,c_{ij}^2 ,c_{ij}^3 ;c_{ij}^4 ,c_{ij}^2 ,c_{ij}^5 } \right) \right. \nonumber \\&\quad \left. \otimes \,\left( {X_{ij}^{1*} ,X_{ij}^{2*} ,X_{ij}^{3*} ;X_{ij}^{4*} ,X_{ij}^{2*} ,X_{ij}^{5*} } \right) \right) \nonumber \\&\le \mathfrak {R}\left( \sum _{i=1}^m \sum _{j=1}^n \left( {c_{ij}^1 ,c_{ij}^2 ,c_{ij}^3 ;c_{ij}^4 ,c_{ij}^2 ,c_{ij}^5 } \right) \right. \nonumber \\&\left. \quad \otimes \, \left( {X_{ij}^1 ,X_{ij}^2 ,X_{ij}^3 ;X_{ij}^4 ,X_{ij}^2 ,X_{ij}^5 } \right) \right) \end{aligned}$$
(33)

if and only if,

$$\begin{aligned}&\sum _{i=1}^m \sum _{j=1}^n \mathfrak {R}\left( \left( {c_{ij}^1 ,c_{ij}^2 ,c_{ij}^3 ;c_{ij}^4 ,c_{ij}^2 ,c_{ij}^5 } \right) \right. \nonumber \\&\quad \left. \otimes \,\left( {X_{ij}^{1*} ,X_{ij}^{2*} ,X_{ij}^{3*} ;X_{ij}^{4*} ,X_{ij}^{2*} ,X_{ij}^{5*} } \right) \right) \nonumber \\&\le \sum _{i=1}^m \sum _{j=1}^n \mathfrak {R}\left( \left( {c_{ij}^1 ,c_{ij}^2 ,c_{ij}^3 ;c_{ij}^4 ,c_{ij}^2 ,c_{ij}^5 } \right) \right. \nonumber \\&\quad \left. \otimes \, \left( {X_{ij}^1 ,X_{ij}^2 ,X_{ij}^3 ;X_{ij}^4 ,X_{ij}^2 ,X_{ij}^5 } \right) \right) \end{aligned}$$
(34)

Inequality (34) indicates that \(X^{*}=\left\{ {\tilde{X}_{ij}^{I*} } \right\} \) is optimal solution of problem (20)–(27) too, and the theorem is proved. \(\square \)

It is notable to mention that for the case of trapezoidal intuitionistic fuzzy parameters and variables, the model of Step 1 is changed to the following model,

$$\begin{aligned} \min \tilde{Z}^{I}= & {} \sum _{i=1}^m \sum _{j=1}^n \left( {c_{ij}^1 ,c_{ij}^2 ,c_{ij}^3 ,c_{ij}^4 ;c_{ij}^5 ,c_{ij}^2 ,c_{ij}^3 ,c_{ij}^6 } \right) \nonumber \\&\otimes \,\left( {X_{ij}^1 ,X_{ij}^2 ,X_{ij}^3 ,X_{ij}^4 ;X_{ij}^5 ,X_{ij}^2 ,X_{ij}^3 ,X_{ij}^6 } \right) \nonumber \\ \end{aligned}$$
(35)

subject to

$$\begin{aligned}&\sum _{j=1}^n {\left( {X_{ij}^1 ,X_{ij}^2 ,X_{ij}^3 ,X_{ij}^4 ;X_{ij}^5 ,X_{ij}^2 ,X_{ij}^3 ,X_{ij}^6 } \right) } \nonumber \\&\quad =\left( {a_i^1 ,a_i^2 ,a_i^3 ,a_i^4 ;a_i^5 ,a_i^2 ,a_i^3 ,a_i^6 } \right) \quad \forall i \end{aligned}$$
(36)
$$\begin{aligned}&\sum _{i=1}^m {\left( {X_{ij}^1 ,X_{ij}^2 ,X_{ij}^3 ,X_{ij}^4 ;X_{ij}^5 ,X_{ij}^2 ,X_{ij}^3 ,X_{ij}^6 } \right) } \nonumber \\&\quad =\left( {b_j^1 ,b_j^2 ,b_j^3 ,b_j^4 ;b_j^5 ,b_j^2 ,b_j^3 ,b_j^6 } \right) \quad \forall j \end{aligned}$$
(37)
$$\begin{aligned}&\left( {X_{ij}^1 ,X_{ij}^2 ,X_{ij}^3 ,X_{ij}^4 ;X_{ij}^5 ,X_{ij}^2 ,X_{ij}^3 ,X_{ij}^6 } \right) \ge 0 \quad \forall i,j \end{aligned}$$
(38)
Table 1 The triangular intuitionistic parameters of Example 1 (the inside values are \(\tilde{c}_{ij}^I \)s)
Full size table
Table 2 The intuitionistic fuzzy solution (\(\tilde{X}_{ij}^{I*} \) values) and objective function values obtained for Example 1 by the proposed approach and Kumar and Hussain (2014)
Full size table

where the model of Step 3 is changed to the following model,

(39)

subject to

$$\begin{aligned}&\sum _{j=1}^n {X_{ij}^k } =a_i^k \quad \forall i,k|k\in \left\{ {1,\ldots ,6} \right\} \end{aligned}$$
(40)
$$\begin{aligned}&\sum _{i=1}^m {X_{ij}^k } =b_j^k \quad \forall j,k|k\in \left\{ {1,\ldots ,6} \right\} \end{aligned}$$
(41)
$$\begin{aligned}&X_{ij}^5 \ge 0 \quad \forall i,j \end{aligned}$$
(42)
$$\begin{aligned}&X_{ij}^2 -X_{ij}^1 \ge 0 \quad \forall i,j \end{aligned}$$
(43)
$$\begin{aligned}&X_{ij}^3 -X_{ij}^2 \ge 0 \quad \forall i,j \end{aligned}$$
(44)
$$\begin{aligned}&X_{ij}^4 -X_{ij}^3 \ge 0 \quad \forall i,j \end{aligned}$$
(45)
$$\begin{aligned}&X_{ij}^1 -X_{ij}^5 \ge 0 \quad \forall i,j \end{aligned}$$
(46)
$$\begin{aligned}&X_{ij}^6 -X_{ij}^4 \ge 0 \quad \forall i,j \end{aligned}$$
(47)

The other steps are changed accordingly.

5 Illustrative examples

To study the performance of the proposed approach of this study, the same numerical examples considered by Kumar and Hussain (2014), Singh and Yadav (2015) and Singh and Yadav (2016) are solved in this section. These benchmark examples make us able to compare the approaches in a correct way. Notably, in the procedure of the proposed approach and the above-mentioned approaches (except Example 1) and also in the comparisons, the accuracy ranking function \(\mathfrak {R}\) is used.

Example 1

This example is a real-life problem given by Kumar and Hussain (2014). A company has three factories for producing umbrella. The umbrellas should be moved to three retail stores under triangular intuitionistic fuzzy parameters [transportation costs \((\tilde{c}_{ij}^I )\), availabilities \((\tilde{a}_i^I )\) and demands \((\tilde{b}_j^I )\)] presented in Table 1. The example is solved by the proposed approach, and the obtained solution and the solution of Kumar and Hussain (2014) are represented in Table 2. It is noted that in this example different ranking functions are used in the procedure of the solution approaches. Therefore, no comparison is made on the objective function values.

Table 3 The triangular intuitionistic parameters of Example 2 (the inside values are \(\tilde{c}_{ij}^I \)s)
Full size table
Table 4 The intuitionistic fuzzy solution (\(\tilde{X}_{ij}^{I*} \) values) and objective function values obtained for Example 2 by the proposed approach and Singh and Yadav (2016)
Full size table
Table 5 The crisp and triangular intuitionistic parameters of Example 3 (the inside values are \(c_{ij} \)s)
Full size table
Table 6 The intuitionistic fuzzy solution (\(\tilde{X}_{ij}^{I*} \) values) and objective function values obtained for Example 3 by the proposed approach and Singh and Yadav (2015)
Full size table
Table 7 The crisp and triangular intuitionistic parameters of Example 4 (the inside values are \(c_{ij} \)s)
Full size table
Table 8 The intuitionistic fuzzy objective function values obtained for Example 4 by the proposed approach and Singh and Yadav (2015)
Full size table

Referring to the results of Table 2, the shortcomings of the approach of Kumar and Hussain (2014) can be realized as some obtained solutions are negative, and some of the demand values are not respected. On the other hand, all of these shortcomings are fixed in the results obtained by the proposed approach.

Example 2

This example was proposed by Singh and Yadav (2016). Its parameters are shown in Table 3. The example is solved by the proposed approach, and the obtained solution and the solution of Singh and Yadav (2016) are represented in Table 4.

Referring to the results of Table 4, the shortcomings of the approach of Singh and Yadav (2016) can be realized as some obtained solutions are negative, some of the demand values are not respected, and the objective function value is negative. On the other hand, all of these shortcomings are fixed in the results obtained by the proposed approach and a better rank for the intuitionistic cost is obtained (considering negative solutions obtained by Singh and Yadav (2016), this rank value is a superior result). Notably, the objective function value obtained by the proposed approach has a negative value which is because of a negative cost of Table 3.

Example 3

This example was proposed by Singh and Yadav (2015). Its parameters are shown in Table 5. The example is solved by the proposed approach, and the obtained solution and the solution of Singh and Yadav (2015) are represented in Table 6. In the procedure of the proposed approach, the crisp cost values of Table 5 are considered as intuitionistic fuzzy numbers with the same elements [for example \(c_{11} =16\) is considered as \(c_{11}^I =\left( {16,16,16;16,16,16} \right) \)].

Referring to the results of Table 6, the shortcomings of the approach of Singh and Yadav (2015) can be realized as some obtained solutions are negative, some of the demand values are not respected, and the objective function value is negative. On the other hand, all of these shortcomings are fixed in the results obtained by the proposed approach. The obtained rank for the intuitionistic cost of the proposed approach is not better than of Singh and Yadav (2015) as there are some negative values in the intuitionistic cost of Singh and Yadav (2015).

Example 4

This example was proposed by Singh and Yadav (2015). Its parameters are shown in Table 7. The example is solved by the proposed approach, and the obtained solution and the solution of Singh and Yadav (2015) are represented in Table 8. In the procedure of the proposed approach, the crisp cost values of Table 7 are considered as intuitionistic fuzzy numbers with the same elements [for example \(c_{11} =2\) is considered as \(c_{11}^I =\left( {2,2,2;2,2,2} \right) \)].

Referring to the results of Table 8, the shortcomings of the approach of Singh and Yadav (2015) can be realized as the objective function value is negative. On the other hand, this shortcomings are fixed in the results obtained by the proposed approach. The rank for the intuitionistic cost of the proposed approach is not better, as in the solution obtained by Singh and Yadav (2015) there are some negative values.

6 Concluding remarks

A transportation problem in its balanced form with triangular intuitionistic fuzzy parameters and variables was solved in this study. In the literature of the field, the proposed approaches have many shortcoming, e.g., obtaining negative solutions for the variables and obtaining negative objective function value in existence of positive unit transportation costs. In this study a novel approach was proposed to overcome such shortcomings. The performed computational experiments showed the superiority of the proposed approach over those of the literature from the results’ quality.

As future study, the intuitionistic fuzzy transportation problem can be solved in existence of other ranking functions than the accuracy function. On the other hand, trying to propose the methods free of ranking function may be interesting. Finally, a transportation problem with type-2 fuzzy numbers may be focused.