1 Introduction

One of the most famous and productive problems in graph theory is the vertex coloring problem. The problem requires the assignment of a color to each vertex in such a way that two vertices linked by an edge get different colors and the number of colors used is minimized (Demange et al. 2016; Jin et al. 2014). The vertex coloring problem can be employed to model many issues in various real-world applications, including matching (Carrabs et al. 2009) and register allocation (Chow and Hennessy 1990). A detailed survey can be found in Malaguti and Toth (2010). Over the past several decades, the vertex coloring problem has been studied by numerous researchers. Appel and Haken (1976) first solved the problem with the help of a computer. The method proposed by Appel and Haken (1976) was simplified by Robertson et al. (1997), but the simplified method still required a large number of computer validations. The readers can also consult Lü and Hao (2010) and Malaguti et al. (2008) for the latest work on the vertex coloring problem.

In classical graph theory, vertices and edges are deterministic. However, as the system becomes more complex, different types of indeterminacy exist in the applications of graph theory. Sometimes whether two vertices are joined by an edge cannot be completely determined in advance. Then, the question arises of how to address the indeterminacy phenomenon. In the relevant literature, researchers have depicted the indeterminacy factors in graph theory as random variables. Under such considerations, random graphs were first investigated by Erdős and Rényi (1959), leading to the E-R model of random graphs. In the E-R model, any two vertices were joined by an edge independently with fixed probability. At nearly the same time, Gilbert (1959) investigated the probability that two specific vertices were connected. After that, many researchers, such as Bollobás (1988), Mann and Szajkó (2013) and Sommer (2009), have worked on the vertex coloring problem in random graphs.

After the introduction of fuzzy set theory by Zadeh (1965), some scholars have used fuzzy set theory to address fuzziness in graphs. Rosenfeld (1975) introduced the concept of the fuzzy graph and some of its properties. Since then, several researchers have investigated the vertex coloring problem in fuzzy graphs. For instance, Muñoz et al. (2005) extended the concept of incompatibility among the nodes of a graph to include vagueness and graduation, and they studied the coloring of a fuzzy graph in two different ways. The first way was in the light of the successive coloring functions. The second way was based on an extension of the concept of coloring function by means of a distance defined between two colors (Pramanik et al. 2017). Based on the \(\delta \)-cut of a fuzzy graph, Rosyida et al. (2015) proposed a new approach to determine the fuzzy chromatic number of fuzzy graphs with a classic vertex set and fuzzy edge set. Keshavarz (2016) defined the total incompatibility degree of vertex coloring and introduced the fuzzy chromatic number of a fuzzy graph. Samanta et al. (2016) established the relation between the chromatic number of fuzzy graphs and its underlying graphs and the relation between the chromatic number of fuzzy graphs and its strength cut graphs. For more research on the vertex coloring problem in fuzzy graphs, we refer to Eisenbrand and Niemeier (2012) and Gómez et al. (2006).

When the uncertainty in real-life decisions is neither random nor fuzzy, we require a new tool to deal with it. Liu (2007) proposed uncertainty theory as a branch of axiomatic mathematics for modeling degrees of belief. In the field of graph theory, some researchers have employed uncertainty theory to address uncertainty in graphs. Gao and Gao (2013) proposed the concept of the uncertain graph, in which all vertices were deterministic and all edges were not deterministic and existed with some degree of belief described by uncertain measures. They also designed two algorithms to calculate the connectedness index of uncertain graphs. In addition, Gao et al. (2015) explored the uncertainty distribution of the diameter of an uncertain graph and presented an algorithm, which was similar to the Floyd algorithm (Floyd 1962), to calculate the distribution function of the diameter of an uncertain graph. Recently, Gao and Qin (2016) investigated how to calculate the uncertain measure that an uncertain graph was k-edge-connected and proposed an algorithm to numerically calculate the uncertain measure. Gao (2016) introduced uncertainty theory into the study of trees in graph theory and proposed the concepts of the tree index, path index, and star index of uncertain graphs. Rosyida et al. (2016a) colored a total uncertain graph by the classical coloring via \(\alpha \)-cut and investigated some properties of the \(\alpha \)-cut chromatic number of a total uncertain graph. Rosyida et al. (2016b) introduced a new approach for uncertain graph coloring based on an \(\alpha \)-cut of an uncertain graph.

To the best of our knowledge, no researchers have proposed the concept of the maximal uncertain independent vertex set or investigated the vertex coloring problem in uncertain graphs via maximal uncertain independent vertex sets before now. Hence, to address this research gap, the primary objective in this paper is to investigate the problem of vertex coloring in uncertain graphs. Our paper makes the following significant contributions. From the theoretical aspect, our contributions are threefold. First, based on uncertainty theory, the concepts of the maximal uncertain independent vertex set and uncertain chromatic set of an uncertain graph are proposed. Second, a degree of belief rule is presented to obtain the family of maximal uncertain independent vertex sets. Third, based on the maximal uncertain independent vertex set, the concept and some properties of the separation degree of an uncertain graph are proposed and discussed. From the practical aspect, our contributions are twofold. First, we design a maximum separation degree algorithm to obtain the uncertain chromatic set. Second, the problem of determining the minimum number of time slots k to complete certain jobs such that interfering jobs are not executed simultaneously is formulated and solved as a real-world application of the vertex coloring problem in uncertain graphs. The numerical results illustrate that using the maximal uncertain independent vertex set to investigate the vertex coloring problem in an uncertain graph is efficient and that the maximum separation degree algorithm is feasible and effective.

The remainder of this paper is organized as follows. In Sect. 2, we introduce some preliminaries of uncertainty theory and uncertain graph. In Sect. 3, the concepts of the uncertain independent vertex set and the maximal uncertain independent vertex set are proposed. A degree of belief rule is provided in Sect. 4 to obtain the maximal uncertain independent vertex set. In Sect. 5, the concept of the uncertain chromatic set is presented and the uncertainty distribution of the uncertain chromatic set is given. A maximum separation degree algorithm is also designed to obtain the uncertain chromatic set. To illustrate the application of the vertex coloring problem in uncertain graphs, numerical examples are given in Sect. 6. Concluding remarks are presented in Sect. 7.

2 Preliminary

2.1 Uncertainty theory

Uncertainty theory, founded by Liu (2007), was based on normality, duality, subadditivity, and product axioms. We recall some of the basic concepts of uncertainty theory.

Let \(\Gamma \) be a nonempty set and \(\mathcal{L}\) be a \(\sigma \)-algebra on \(\Gamma \). A set function M: \(\mathcal{L}\rightarrow [0,1]\) is called an uncertain measure if it satisfies the following axioms:

Axiom 1 :

(Normality) \(M\{\Gamma \}=1\) for the universal set \(\Gamma \).

Axiom 2 :

(Duality) \(M\{\Lambda \}+M\{\Lambda ^{c}\}=1\) for every event \(\Lambda \).

Axiom 3 :

(Subadditivity) For every countable sequence of events \(\Lambda _{1},\Lambda _{2},\ldots ,\) we have

$$\begin{aligned}&M\left\{ \bigcup _{i=1}^{\infty }\Lambda _{i}\right\} \le \sum _{i=1}^{\infty } M\{\Lambda _{i}\}. \end{aligned}$$

The triplet \((\Gamma ,\mathcal{L},M)\) is called an uncertainty space in uncertainty theory (Liu et al. 2016). To provide the operational law, Liu (2009) defined the product uncertain measure as follows.

Axiom 4 :

(Product) Let \((\Gamma _{k},\mathcal{L}_{k},M_{k})\) be uncertainty spaces for \(k=1, 2, \ldots .\) The product uncertain measure M is an uncertain measure satisfying

$$\begin{aligned}&M\left\{ \prod _{k=1}^{\infty }\Lambda _{k}\right\} = \bigwedge _{k=1}^{\infty }M_{k}\{\Lambda _{k}\}, \end{aligned}$$

where \(\Lambda _{k}\) are arbitrarily chosen events from \(\mathcal{L}_{k}\) for \(k=1, 2, \ldots \).

An uncertain variable (Liu 2007) \(\xi \) is a measurable function from an uncertainty space \((\Gamma ,\mathcal{L},M)\) to the set of real numbers, i.e., \(\{\xi \in B\}=\{\gamma \in \Gamma \bigm | \xi (\gamma )\in B\}\) is an event for any Borel set B.

The uncertainty distribution (Liu 2007) \(\Phi \) of an uncertain variable \(\xi \) is defined by

$$\begin{aligned} \Phi (x)=M\left\{ \xi \le x\right\} \end{aligned}$$

for every real number \(x\in \mathfrak {R}\).

2.2 Uncertain graph

When graph theory is applied to real-life decision-making problems, indeterminacy factors appear in the graphs due to the system complexity. Liu (2012) noted that to model indeterminacy, one could use probability theory as well as uncertainty theory. If there are sufficient historical data, then we can use probability theory to investigate the indeterminacy factors in graphs. However, we usually lack historical data. In such a case, we have to ask domain experts to evaluate the degree of belief that an edge exists. Gao and Gao (2013) proposed the concept of the uncertain graph in which all vertices were deterministic, while all edges were not deterministic and existed with some degrees of belief in uncertain measures. Throughout this paper, we refer to a graph in which the vertices and the edges are all deterministic as a classic graph. Following Gao et al. (2015) and Gao and Qin (2016), the graphs discussed in this paper are all undirected and simple. The definition of an uncertain graph, as proposed by Gao and Gao (2013), is as follows.

Definition 1

(Gao and Gao 2013) An uncertain graph G, denoted by \(G=(V,E,\xi )\), is a triplet consisting of a vertex set V(G), an edge set E(G), and a set of indicator functions \(\xi (G)\).

In this paper, we consider the uncertain graph \(G=(V,E,\xi )\) with n vertices and m edges. Following Gao and Gao (2013) and Zhang and Peng (2012), we define the vertex set as \(V(G)=(v_{1}, v_{2},\ldots , v_{n}),\) the edge set as \(E(G)=(e_{ij}\bigm |i,j=1,2,\ldots ,n),\) and the indicator function set as \(\xi (G)=(\xi _{ij}\bigm |i,j=1,2,\ldots ,n).\) In an uncertain graph G, the vertices \(v_{i}\) are all predetermined, whereas the edges \(e_{ij}\) (\(i,j=1,2,\ldots ,n\)) are uncertain and exist with some degree of belief described by uncertain measures.

For convenience, an indicator function \(\xi _{ij}\), which is a Boolean uncertain variable, is used to indicate the existence of the corresponding edge. Specifically, if the edge \(e_{ij}\) exists, then \(\xi _{ij}=1\), whereas if the edge \(e_{ij}\) does not exist, then \(\xi _{ij}=0\). Let \(M\{\xi _{ij}=1\}=\alpha _{ij}\) be the existence possibility of edge \(e_{ij}\). If \(\alpha _{ij}=1\), then edge \(e_{ij}\) always exists, or equivalently, \(e_{ij}\) is a deterministic edge. Gao and Gao (2013) also proposed the definition of an uncertain graph from another point of view.

Definition 2

(Gao and Gao 2013) A graph of order n is said to be uncertain if it has an uncertain adjacency matrix

$$\begin{aligned} A=\left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} 0&{}\alpha _{12}&{}\ldots &{}\alpha _{1n}\\ \alpha _{21}&{}0&{}\ldots &{}\alpha _{2n}\\ \vdots &{}\vdots &{}\ddots &{}\vdots \\ \alpha _{n1}&{}\alpha _{n2}&{}\ldots &{}0 \end{array}\right) , \end{aligned}$$

where \(\alpha _{ij}\) is the uncertain measure that edge \(e_{ij}\) between vertices \(v_{i}\) and \(v_{j}\) exists for \(i,j=1,2,\ldots ,n\).

Clearly, the uncertain adjacency matrix contains all the information of an uncertain graph. It is necessary to note that if the uncertain graph is undirected, then the uncertain adjacency matrix is symmetric, i.e., \(\alpha _{ij}=\alpha _{ji}\) for \(i,j=1,2,\ldots ,n.\)

Zhang and Peng (2013) proposed the underlying graph of an uncertain graph as follows. The underlying graph of an uncertain graph G, denoted by \(G^{*}\), was a graph obtained from uncertain graph G by replacing each edge by \(M\{\xi _{ij}=1\}=1.\)

3 Maximal uncertain independent vertex set of uncertain graph

In this section, we first present the concept of the maximal uncertain independent vertex set of an uncertain graph and then discuss how to find the maximal uncertain independent vertex set. To distinguish from the classical independent vertex set, we give the following formal definition of the uncertain independent vertex set of an uncertain graph.

Definition 3

Let \(G=(V,E,\xi )\) be an uncertain graph. A nonempty subset \(X\subseteq V\) is said to be an uncertain independent vertex set of uncertain graph G with the independence degree

$$\begin{aligned} I(X)=1-\max \{M\{\xi _{ij}=1\}\bigm |v_{i},v_{j}\in X, e_{ij}\in E\}, \end{aligned}$$

where M is an uncertain measure.

In a classic graph, a subset of V is called an independent set if no two adjacent vertices belong to it. That is to say, only some vertex sets meet the requirements to be an independent set in classical graph. However, all the edges of an uncertain graph are not deterministic. For a nonempty subset X of the vertex set V, the edges that link X exist with some degree of belief in uncertain measures. Motivated by the above considerations, we propose an approach, which is presented in Definition 3, to define the uncertain independent vertex set of an uncertain graph. For an uncertain graph, every nonempty subset X of the vertex set V can be an uncertain independent vertex set. Furthermore, the independence degrees of the independent vertex sets may be different.

It follows from the definition of an uncertain graph that if there is no edge linking vertices \(v_{i}\in V\) and \(v_{j}\in V\), then \(M\{\xi _{ij}=1\}=0.\) Therefore, \(I(X)=1.\) That is to say, every vertex set X whose elements are non-adjacent is an uncertain independent vertex set. Hence, the uncertain independent vertex set is consistent with the classical one from this point of view. When the uncertain variables disappear, the uncertain graph becomes the underlying graph \(\displaystyle G^{*}\). In this case, the independence degree I(X) for any subset X takes values of either 0 or 1. If \(I(X)=0\), then set X is not an independent vertex set of graph \(G^{*}.\) If \(I(X)=1\), then set X is in line with one of the independent vertex sets of graph \(G^{*}\).

For an uncertain graph, what is the independence degree of every uncertain independent vertex set? In general, Definition 3 provides a method to obtain the independence degree of every uncertain independent vertex set. We next present an example to illustrate how to find uncertain independent vertex sets and their corresponding independence degrees.

Example 1

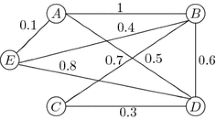
Assume that there are 5 vertices and 9 edges in uncertain graph \(G_{1}\) given in Fig. 1. Its uncertain adjacency matrix is

$$\begin{aligned} A_{1}=\left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 0&{}0.2&{}1&{}0&{}0.3\\ 0.2&{}0&{}0.5&{}0.1&{}0.9\\ 1&{}0.5&{}0&{}0.6&{}0.4\\ 0&{}0.1&{}0.6&{}0&{}0.8\\ 0.3&{}0.9&{}0.4&{}0.8&{}0 \end{array}\right) . \end{aligned}$$
Fig. 1
figure 1

Uncertain graph \(G_{1}\)

Full size image

In this example, there are 31 nonempty subsets \(X\subseteq V\). The 31 uncertain independent vertex sets’ independence degrees can be easily obtained using the method proposed in Definition 3. We summarize the independence degrees \(I(X_{i})\) of all the uncertain independent vertex sets \(X_{i} (i=1,2,\ldots , 31)\) in Table 1.

Table 1 List of the uncertain independent vertex sets of \(G_{1}\)
Full size table

A formal definition of the maximal uncertain independent vertex set of an uncertain graph is given in the following.

Definition 4

Let \(G=(V,E,\xi )\) be an uncertain graph. A nonempty subset \(X^{*}\subseteq V\) is said to be a maximal uncertain independent vertex set with independence degree \(I(X^{*})\) if \(I(X)\le I(X^{*})\) for any uncertain independent vertex set \(X\subseteq X^{*}.\)

According to Definition 4, there always exists a maximal uncertain independent vertex set for an uncertain graph. By comparing all the uncertain independent vertex sets, we can obtain the maximal uncertain independent vertex set. For example, we can compare the independence degree of the uncertain independent vertex set \(\left\{ A,C\right\} \) with the other uncertain independent vertex sets that contain the set \(\left\{ A,C\right\} \). The result shows that the independence degree of \(\left\{ A,C\right\} \) is not the largest among those sets that contain the set \(\left\{ A,C\right\} \). Therefore, \(\left\{ A,C\right\} \) is not the maximal uncertain independent vertex set. All the maximal uncertain independent vertex sets of uncertain graph G can be obtained by repeating the above procedure. These maximal uncertain independent vertex sets are summarized in Table 2.

Table 2 List of the maximal uncertain independent vertex sets of \(G_{1}\)
Full size table

4 Degree of belief rule to obtain the maximal uncertain independent vertex set

We can see that using Definition 4 to obtain all the maximal uncertain independent vertex sets is time consuming when the order of the uncertain graph is large. Therefore, we design an efficient method to obtain all the maximal uncertain independent vertex sets.

Let \(G=(V,E,\xi )\) be an uncertain graph and X be a maximal uncertain independent vertex set of graph G. We introduce a Boolean variable \(p_{i}\) for each vertex \(v_{i}\in V\). The variable \(p_{i}\) takes the value 1 if \(v_{i}\in X\), and 0 if \(v_{i}\notin X\). We denote the Boolean product that contains vertices \(v_{i}\) and \(v_{j}\) by \(p_{i}\wedge p_{j}.\) Similarly, \(p_{i}\vee p_{j}\) is the Boolean sum that contains only vertex \(v_{i}\), only vertex \(v_{j}\), or both vertices \(v_{i}\) and \(v_{j}.\)

Clearly, there exists a Boolean product corresponding to edge \(e_{ij}\) that links vertices \(v_{i}\) and \(v_{j}.\) For arbitrary vertices \(v_{i}, v_{j} \in V,\) the following cases are possible: (i) \(v_{i}\notin X\); (ii) \(v_{j}\notin X\); (iii) \(v_{i}\in X\) and \(v_{j}\in X\). This Boolean proposition can be expressed as the following proposition

$$\begin{aligned} \begin{array}{l@{\quad }l} P=\displaystyle \bigwedge _{(v_{i},v_{j})\in E}(\bar{p}_{i}\vee \bar{p}_{j}\vee \beta _{ij})=1, \end{array} \end{aligned}$$
(1)

where \(\beta _{ij}=1-\alpha _{ij}.\) We propose the following degree of belief rule to solve the above proposition.

Degree of belief rule\((\beta \wedge a) \vee (\beta ^{\prime }\wedge a\wedge b)=\beta \wedge a\) for all \(\beta \le \beta ^{\prime },\) where a and b are Boolean variables, and  \(\beta \) and \(\beta ^{\prime }\) are the degrees of belief, taking values from the interval [0, 1].

Next, we present an example to illustrate how to use the degree of belief rule to solve proposition (1) and to obtain all the maximal uncertain independent vertex sets for uncertain graphs.

Example 2

Assume that there are 4 vertices and 5 edges in uncertain graph \(G_{2}\) in Fig. 2. Its uncertain adjacency matrix is

$$\begin{aligned} A_{2}=\left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 0&{}0.5&{}0&{}0.2\\ 0.5&{}0&{}0.6&{}1\\ 0&{}0.6&{}0&{}0.3\\ 0.2&{}1&{}0.3&{}0 \end{array}\right) . \end{aligned}$$
Fig. 2
figure 2

Uncertain graph \(G_{2}\)

Full size image

Proposition P for uncertain graph \(G_{2}\) has the following form:

$$\begin{aligned} P= & {} (\bar{p}_{A}\vee \bar{p}_{B}\vee 0.5)\wedge (\bar{p}_{B}\vee \bar{p}_{C}\vee 0.4)\wedge (\bar{p}_{C}\vee \bar{p}_{D}\vee 0.7)\nonumber \\&\wedge (\bar{p}_{B}\vee \bar{p}_{D}\vee 0)\wedge (\bar{p}_{A}\vee \bar{p}_{D}\vee 0.8)=1. \end{aligned}$$
(2)

By using the degree of belief rule, we can transform proposition (2) into the following:

$$\begin{aligned} P= & {} (\bar{p}_{A}\wedge \bar{p}_{C}\wedge \bar{p}_{D}\wedge 1)\vee (\bar{p}_{A}\wedge \bar{p}_{B}\wedge \bar{p}_{C}\wedge 1)\nonumber \\&\vee (\bar{p}_{B}\wedge \bar{p}_{D}\wedge 1)\vee (\bar{p}_{B} \wedge \bar{p}_{C}\wedge 0.8)\vee (\bar{p}_{B}\wedge 0.7)\nonumber \\&\vee (\bar{p}_{C}\wedge \bar{p}_{D}\wedge 0.5) \vee (\bar{p}_{D}\wedge 0.4)=1. \end{aligned}$$
(3)

It follows from (3) that uncertain graph \(G_{2}\) has seven maximal uncertain independent vertex sets: \(\{B\}\), \(\{D\}\), and \(\{A,C\}\) with independence degree 1; \(\{A,D\}\) with independence degree 0.8; \(\{A,C,D\}\) with independence degree 0.7; \(\{A,B\}\) with independence degree 0.5; \(\{A,B,C\}\) with independence degree 0.4.

For Example 1, proposition P has the following form:

$$\begin{aligned} P= & {} (\bar{p}_{A}\vee \bar{p}_{B} \vee 0.8)\wedge (\bar{p}_{A}\vee \bar{p}_{C} \vee 0)\wedge (\bar{p}_{A}\vee \bar{p}_{E} \vee 0.7) \\&\wedge (\bar{p}_{B}\vee \bar{p}_{C} \vee 0.5)\wedge (\bar{p}_{B}\vee \bar{p}_{E} \vee 0.1)\\&\wedge (\bar{p}_{B}\vee \bar{p}_{D} \vee 0.9)\wedge (\bar{p}_{C}\vee \bar{p}_{E} \vee 0.6)\\&\wedge (\bar{p}_{C}\vee \bar{p}_{D} \vee 0.4)\wedge (\bar{p}_{D}\vee \bar{p}_{E} \vee 0.2)=1. \end{aligned}$$

By using the degree of belief rule, we obtain:

$$\begin{aligned} P= & {} (\bar{p}_{A}\wedge \bar{p}_{C}\wedge \bar{p}_{D}\wedge \bar{p}_{E}\wedge 1)\vee (\bar{p}_{A}\wedge \bar{p}_{B}\wedge \bar{p}_{D}\wedge \bar{p}_{E}\wedge 1)\\&\vee (\bar{p}_{A}\wedge \bar{p}_{B}\wedge \bar{p}_{C}\wedge \bar{p}_{D}\wedge 1)\vee (\bar{p}_{B}\wedge \bar{p}_{C}\wedge \bar{p}_{E}\wedge 1)\\&\vee (\bar{p}_{A}\wedge \bar{p}_{C}\wedge \bar{p}_{E}\wedge 0.9)\vee (\bar{p}_{C}\wedge \bar{p}_{E}\wedge 0.8)\\&\vee (\bar{p}_{B}\wedge \bar{p}_{C}\wedge \bar{p}_{D}\wedge 0.7)\vee (\bar{p}_{A}\wedge \bar{p}_{B}\wedge \bar{p}_{D}\wedge 0.6)\\&\vee (\bar{p}_{A}\wedge \bar{p}_{D}\wedge \bar{p}_{E}\wedge 0.5)\vee (\bar{p}_{A}\wedge \bar{p}_{E}\wedge 0.4)\\&\vee (\bar{p}_{A}\wedge \bar{p}_{B}\wedge 0.2)\vee (\bar{p}_{B}\wedge \bar{p}_{C}\wedge 0.2)\vee (\bar{p}_{A}\wedge 0.1)\\&\vee (\bar{p}_{C}\wedge 0.1)=1. \end{aligned}$$

Thus, uncertain graph \(G_{1}\) has 15 maximal uncertain independent vertex sets, as shown in Table 2.

5 Uncertain vertex coloring

5.1 Uncertain chromatic set

Generally, there are two approaches to define the vertex coloring of a graph. On the one hand, k-coloring of a graph G is defined as a mapping C: \(V\rightarrow \{1,2,\ldots ,k\}\) such that the colors on adjacent vertices are different. The minimum number k such that G admits k-coloring is called the chromatic number of G. On the other hand, k-coloring of a graph G is defined as a partition of V into k independent sets \(V_{1},V_{2},\ldots ,V_{k},\) such that the subsets \(V_{i}\) are nonempty, \(V_{i}\cap V_{j}=\emptyset \) (\(i\ne j\)), and \(\bigcup _{i=1}^{k}V_{i}=\displaystyle V\). Following Eisenbrand and Niemeier (2012) and Samanta et al. (2016), we consider the vertex coloring problem in an uncertain graph via the second approach. We next give the definition of the separation degree of an uncertain graph.

Definition 5

Let \(G=(V,E,\xi )\) be an uncertain graph with n vertices and \(\mathcal {A}\) be the family of all maximal uncertain independent vertex sets in G. For each \(k\in \{1,2,\ldots ,n\}\), the value

$$\begin{aligned} S(k)= & {} \text {min}\{I(X_{1}),\ldots , I(X_{i}),\ldots ,I(X_{k})\bigm |X_{i}\in \mathcal {A},\\&i=1,2,\ldots ,k\} \end{aligned}$$

is said to be the separation degree of an uncertain graph with k colors.

It is necessary to note that for an uncertain graph, we cannot precisely say that the graph can be colored by exact colors. For an uncertain graph G with n vertices, the chromatic number may be from 1 to n. In other words, the uncertain graph G can be colored by k colors, where \(k\in \{1,2,\ldots ,n\}.\) Hence, for the uncertain graph G, the chromatic number may not be uniquely determined; it may be a set consisting of several colors with some degrees of belief. For a classic graph, however, we can precisely say that the graph can be colored by exact colors. To distinguish from the classical chromatic number, we provide the following definition of the uncertain chromatic set for an uncertain graph.

Definition 6

Let \(G=(V,E,\xi )\) be an uncertain graph with n vertices. A set \(\chi (G)=\{(k,S_{\chi }(k))\bigm | k=1,2,\ldots ,n\}\) is said to be an uncertain chromatic set of the uncertain graph G if \(S_{\chi }(k)\) is the maximum separation degree of the uncertain graph G with k colors, i.e.,

$$\begin{aligned} S_{\chi }(k)\le S(k) \end{aligned}$$
(4)

for any separation degree S(k) of k-subsets of \(\mathcal {A}\) and for \(k=1,2,\ldots ,n\).

Some properties of the separation degree of an uncertain graph are investigated on the basis of Definitions 5 and 6. Let \(G=(V,E,\xi )\) be an uncertain graph with n vertices and \(X\subseteq V.\)

Property 1

(Normality) \(S(n)=1.\)

Property 2

(Nonnegativity) \(S(1)\ge 0.\) If \(S(1)=0\), then \(\exists v_{i}, v_{j}\in X\) such that \(M\{\xi _{ij}=1\}=1.\)

Proof

The nonnegativity property is obvious. Here \(S(1)=0\) means that we cannot use 1 color to make every adjacency vertices have a different color, so there must exist at least one edge with uncertain measure 1, that is, \(\exists v_{i}, v_{j}\in X\) such that \(M\{\xi _{ij}=1\}=1.\)

Property 3

(Monotonicity) If \(i>j\), \(i, j=1,2,\ldots ,n\), then \(S(i)\ge S(j).\)

This property means that the larger the number of colors used is, the grater the degree of belief that we can color the graph.

For an uncertain graph G, we can study the uncertain chromatic set \(\chi (G)\) from two points of view. One is to regard \(\chi (G)\) as a set that consists of several colors with degrees of belief; the other is to view \(\chi (G)\) as an uncertain variable. We mainly investigate the uncertain chromatic set \(\chi (G)\) from the second viewpoint in this paper.

From Definition 6, we can find that the degree of belief for an uncertain graph colored by k colors. An interesting question naturally arises: what is the degree of belief that an uncertain graph can be colored by k or less than k colors? In fact, the uncertain chromatic set \(\chi (G)=\{\left( k,S_{\chi }(k)\right) \bigm | k=1,2,\ldots ,n\}\) is a discrete function. We can obtain the uncertainty distribution of \(\chi (G)\) as follows:

$$\begin{aligned} \begin{array}{l@{\quad }l} \Phi (x)=\left\{ \begin{array}{l@{\quad }l} 0,&{}\quad \text{ if } x< 1\\ S_{\chi }(k),&{}\quad \text{ if } k\le x< k+1, 1\le k< n\\ 1,&{}\quad \text{ if } x\ge n. \end{array}\right. \end{array} \end{aligned}$$
(5)

We give the following necessary and sufficient conditions to determine the uncertain chromatic set of an uncertain graph \(G=(V,E,\xi )\).

Theorem 1

Let \(G=(V,E,\xi )\) be an uncertain graph with n vertices. The set \(\chi (G)=\{(k,S_{\chi }(k))\bigm | k=1,2,\ldots ,n\}\) is an uncertain chromatic set of G if and only if there are maximal uncertain independent vertex sets \(X_{1},X_{2},\ldots ,X_{k}\) with independence degrees \(I(X_{1}),I(X_{2}),\ldots ,I(X_{k})\), respectively, such that

  1. 1.

    \(\min \{I(X_{1}),I(X_{2}),\ldots ,I(X_{k})\}=S_{\chi }(k);\)

  2. 2.

    \(\bigcup _{i=1}^{k}X_{i}=\displaystyle V;\)

  3. 3.

    There is no other family \(\{X'_{1},X'_{2},\ldots ,X'_{k}\}\) in uncertain graph G such that \(X'_{1}\cup X'_{2}\cup \ldots \cup X'_{k}=V\) and

    $$\begin{aligned}&\min \{I(X'_{1}),I(X'_{2}),\ldots ,I(X'_{k})\}\\&\quad >\min \{I(X_{1}),I(X_{2}),\ldots ,I(X_{k})\}. \end{aligned}$$

Proof

Assume that the set

$$\begin{aligned} \chi (G)=\{\left( k,S_{\chi }(k)\right) \bigm | k=1,2,\ldots ,n\} \end{aligned}$$

is an uncertain chromatic set of G. It follows from Definition 6 that the inequality \(S(k)\le S_{\chi }(k)\) always holds for \(k=1,2,\ldots ,n.\) In other words, there exists a family \(\{X_{1},X_{2},\ldots ,X_{k}\}\subseteq \mathcal {A}\) such that

  1. 1.

    \(\min \{I(X_{1}),I(X_{2}),\ldots ,I(X_{k})\}=S_{\chi }(k);\)

  2. 2.

    \(\bigcup _{i=1}^{k}X_{i}=\displaystyle V;\)

  3. 3.

    There is no other family \(\{X_{1}^{\prime },X_{2}^{\prime },\ldots ,X_{k}^{\prime }\}\) in G such that

    $$\begin{aligned}&\text {min}\{I(X_{1}^{\prime }),I(X_{2}^{\prime }),\ldots ,I(X_{k}^{\prime })\}\\&\quad >\text {min}\{I(X_{1}),I(X_{2}),\ldots ,I(X_{k})\}. \end{aligned}$$

Otherwise, assume that there are k maximal uncertain independent vertex sets \(X_{1},X_{2},\ldots ,X_{k}\) with independence degrees \(I(X_{1})\), \(I(X_{2}), \ldots ,\)\(I(X_{k})\) that satisfy Properties 1–3. That is to say, \(S_{\chi }(k)\le S(k)\) for \(k=1,2,\ldots ,n.\) Thus, the theorem is verified.

5.2 Maximum separation degree algorithm

Given an uncertain graph \(G=(V,E,\xi )\) with n vertices and m edges. Based on the degree of belief rule and Theorem 1, we design the following maximum separation degree algorithm to find the uncertain chromatic set of an uncertain graph.

\(\textit{Step 1}\) :

Order the degrees of belief for the m edges of the uncertain graph such that \(\alpha _{1}\le \cdots \le \alpha _{l}\le \cdots \le \alpha _{m}\).

\(\textit{Step 2}\) :

Let \(e_{ij}\) be an edge such that its belief degree is \(\alpha _l\). Then, any set X such that \(v_i,v_j\in X\) satisfies \(I(X)=1-\alpha _l\).

\(\textit{Step 3}\) :

Let \(e_{rs}\) be an edge such that its belief degree is \(\alpha _{l-1}\). Then, any set X such that \(v_r,v_s\in X\) but \(v_i,v_j\notin X\) satisfies \(I(X)=1-\alpha _{l-1}\).

\(\textit{Step 4}\) :

Repeat Steps 2-3 for all \(l=1,\ldots ,m\) to obtain all the uncertain independent vertex sets.

\(\textit{Step 5}\) :

Use the degree of belief rule to obtain all the maximal uncertain independent vertex sets.

\(\textit{Step 6}\) :

Let \(\mathcal {A}\) be the family of all maximal uncertain independent vertex sets in an uncertain graph G.

\(\textit{Step 7}\) :

Determine the subfamily \(\{X^{\prime }_{1},X^{\prime }_{2},\ldots ,X^{\prime }_{k}\}\subseteq \mathcal {A}\) to meet \(\bigcup _{i=1}^{k}X^{\prime }_{i}=\displaystyle V,\) and \(\text {min}\{I(X^{\prime }_{1}),I(X^{\prime }_{2}),\ldots ,I(X^{\prime }_{k})\}\) taking largest value.

\(\textit{Step 8}\) :

Determine \(S_{\chi }(k)=\min \{I(X^{\prime }_{1}),I(X^{\prime }_{2}),\ldots ,I(X^{\prime }_{k})\}.\)

\(\textit{Step 9}\) :

Repeat Steps 6–8 for all \(k=1,2,\ldots ,n.\)

\(\textit{Step 10}\) :

Return \(\chi (G)=\{(k,S_{\chi }(k))\bigm | k=1,2,\ldots ,n\}.\)

In the next section, we present numerical experiments to illustrate the performance of the maximum separation degree algorithm and to demonstrate real-life applications of the vertex coloring problem in uncertain graphs with small and large sizes.

6 Numerical examples

In this section, we present some real-life decision-making problems to illustrate the applications of the vertex coloring problem in uncertain graphs by using the maximal uncertain independent vertex set and the maximum separation degree algorithm. The computational experiments are conducted on a personal computer [Dell with Intel(R) Core(TM)i5-2450M CPU 2.50 GHz and 2.50GB RAM].

Assume that there is a set of interfering jobs to be scheduled. We have to determine when to execute each job. Some jobs cannot be executed simultaneously due to the use of shared resources or some other interferences. Every job requires one time slot. Regard each vertex as a job, and two vertices are adjacent if their corresponding jobs cannot be executed simultaneously. Otherwise, two vertices are not adjacent. The minimum number of time slots k is regarded as the chromatic number k. We can model the interfering jobs as a graph, and the problem of determining the minimum number of time slots k is equivalent to the problem of determining the chromatic number of the graph.

So far in the literature, this problem has been modeled by using classical graphs in which the vertices and the edges are deterministic. However, the real-life situation may be more complex, so the adjacency between two vertices may not be completely determined. Therefore, we cannot model the problem by using classical graphs in that situation. As mentioned before, uncertainty theory is useful when we lack historical data to determine whether two vertices are joined by an edge. We perform several numerical experiments to show that the uncertain graph is a useful tool to handle the vertex coloring problem in such indeterminacy situations.

Example 3

Consider the uncertain graph \(G_{1}\) shown in Fig. 1. The five vertices are associated with five jobs. All the edges are associated with pairs of jobs that cannot be executed simultaneously. The problem of determining the minimum number of time slots k for the jobs with the maximum degree of belief that the interfering jobs are not executed simultaneously is solved by finding the uncertain chromatic set of \(G_{1}\).

According to Theorem 1, the method used to find the uncertain chromatic set of the uncertain graph can be divided into two steps. The first step is to find all the maximal uncertain independent vertex sets of graph \(G_{1}\), and the second step is to select the k maximal uncertain independent vertex sets that give the maximum value of separation degree \(S_{\chi }(k).\)

All the maximal uncertain independent vertex sets can be obtained using the belief of degree rule, as presented in Table 2. The next task is to select the k maximal uncertain independent vertex sets \(X_{1},X_{2},\ldots ,X_{k}\) that give the maximum separation degree \(S_{\chi }(k).\) By implementing the maximum separation degree algorithm, we obtain the following results.

Fig. 3
figure 3

Uncertainty distribution of \(\chi (G_{1})\)

Full size image

For \(k=1\), the coloring of \(G_{1}\) with 1 color is given by the set \(X_{8}\), where the maximum separation degree is \(S_{\chi }(1)=\min \{0\}=0.\)

For \(k=2\), the coloring of \(G_{1}\) with 2 colors is given by the sets \(X_{7},X_{10}\), where the maximum separation degree is \(S_{\chi }(2)=\min \{0.6,0.8\}=0.6.\)

For \(k=3\), the coloring of \(G_{1}\) with 3 colors is given by the sets \(X_{10},X_{13},X_{14}\), where the maximum separation degree is \(S_{\chi }(3)=\min \{0.8,1,1\}\)\(=0.8.\)

For \(k=4\), we can assign four different colors to the sets \(X_{12},X_{13},X_{14},X_{15}\) with the maximum separation degree \(S_{\chi }(4)=\min \{1,1,1,1\}=1.\)

Thus, the uncertain chromatic set of the uncertain graph \(G_{1}\) is \(\chi (G_{1})=\{(1,0),(2,0.6),(3,0.8),(4,1),(5,1)\}.\) The uncertainty distribution of the uncertain chromatic set is shown in Fig. 3.

The interpretation of this real-life problem of determining the minimum k time slots for the jobs is as follows: (1) If we use only 1 time slot, then the degree of belief that the 5 jobs can be executed simultaneously is 0; that is to say, we cannot execute the five jobs at one time slot. (2) If we use 2 time slots, then the degree of belief that the 5 jobs can be executed in 2 time slots is 0.6. (3) If we use 3 time slots, then the degree of belief that the 5 jobs can be executed in 3 time slots is 0.8. (4) If we use 4 or 5 time slots, then the degree of belief that the 5 jobs can be executed in 4 or 5 time slots is 1.

We can see from Example 3 that the maximum separation degree algorithm is an efficient algorithm to solve the vertex coloring problem in uncertain graphs. In the following, we further validate the performance of the algorithm by considering a large-scale uncertain graph.

Example 4

Consider the uncertain graph \(G_{3}\) with 8 vertices and 15 edges shown in Fig. 4. Its uncertain adjacency matrix is

$$\begin{aligned} A_{3}=\left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 0&{}0.8&{}1&{}0&{}0.3&{}0&{}0.2&{}0\\ 0.8&{}0&{}0&{}0.8&{}0&{}0.4&{}0&{}0\\ 1&{}0&{}0&{}0.4&{}0.1&{}0&{}0.9&{}0\\ 0&{}0.8&{}0.4&{}0&{}0&{}0.7&{}0&{}0.5\\ 0.3&{}0&{}0.1&{}0&{}0&{}0.5&{}0.3&{}0\\ 0&{}0.4&{}0&{}0.7&{}0.5&{}0&{}0&{}0.3\\ 0.2&{}0&{}0.9&{}0&{}0.3&{}0&{}0&{}0.5\\ 0&{}0&{}0&{}0.5&{}0&{}0.3&{}0.5&{}0 \end{array}\right) . \end{aligned}$$
Fig. 4
figure 4

Uncertain graph \(G_{3}\)

Full size image
Table 3 List of the maximal uncertain independent vertex sets of \(G_{3}\)
Full size table

Using the belief of degree rule, we obtain the 33 maximal uncertain independent vertex sets presented in Table 3. By implementing the maximum separation degree algorithm, we obtain the following results.

For \(k=1\), we can assign one color to the set \(\left\{ A,B,C,D,E,F,G,H\right\} \), with maximum separation degree \(S_{\chi }(1)=\min \{0\}=0.\)

For \(k=2\), the coloring of \(G_{3}\) with 2 colors is given by the sets \(\left\{ A,D,E,G\right\} \) and \(\left\{ B,C,F,H\right\} \), the maximum separation degree is \(S_{\chi }(2)=\min \{0.6,0.7\}=0.6.\)

For \(k=3\), the coloring of \(G_{3}\) with 3 colors is given by the sets \(\left\{ A,F\right\} \), \(\left\{ D,G\right\} \), and \(\left\{ B,C,E,H\right\} \), where the maximum separation degree is \(S_{\chi }(3)=\min \{0.9,1,1\}\)\(=0.9.\)

For \(k=4\), the coloring of \(G_{3}\) with 4 colors is given by the sets \(\left\{ A,F\right\} \), \(\left\{ D,G\right\} \), \(\left\{ B,C,H\right\} \), and \(\left\{ B,E,H\right\} \), where the maximum separation degree is \(S_{\chi }(4)=\min \{1,1,1,1\}=1.\)

Thus, the uncertain chromatic set of uncertain graph \(G_{3}\) is \(\chi (G_{3})=\{(1,0),(2,0.6),(3,0.9),(4,1),(5,1),(6,1),(7,1),(8,1)\}\).

7 Conclusions

To the best of our knowledge, no researchers have studied the vertex coloring problem in uncertain graphs via the maximal uncertain independent vertex set. The analysis in the paper aims to fill this void. We have introduced uncertainty theory into the study of the vertex coloring problem in an uncertain graph. Specifically, we considered the interesting research question: what was the degree of belief that an uncertain graph could be colored by k or less than k colors? To answer this question, the concepts of the maximal uncertain independent vertex set and the uncertain chromatic set of an uncertain graph were proposed. We then presented a maximum separation degree algorithm to obtain the uncertain chromatic set. Some real-life decision-making problems were presented to illustrate the applications of the vertex coloring problem in large and small uncertain graphs. The numerical results illustrated that using the maximal uncertain independent vertex set to investigate the vertex coloring problem in uncertain graphs was efficient. The numerical results also proved the feasibility and efficiency of the maximum separation degree algorithm for solving the vertex coloring problem in uncertain graphs.

There are several issues that should be discussed further. First, we focused on investigating the vertex coloring problem via an uncertain independent vertex set. Employing an \(\alpha \)-uncertain independent vertex set by using the \(\alpha \)-cut (Rosyida et al. 2016a) to obtain the uncertain chromatic set appears to be a promising future research direction. Second, the coloring problem in uncertain random graphs (Liu 2014) may become another topic in our future research. Finally, designing new metaheuristic algorithms (Cerulli et al. 2012; Furini et al. 2017; Morrison et al. 2016) to solve the vertex coloring problem in large-scale uncertain graphs is another potential research direction.