An improved NSGA-III algorithm based on objective space decomposition for many-objective optimization

Abstract

Maintaining balance between convergence and diversity is of great importance for many-objective evolutionary algorithms. The recently suggested non-dominated sorting genetic algorithm III could obtain a fair diversity but the convergence is unsatisfactory. For this purpose, an improved NSGA-III algorithm based on objective space decomposition (we call it NSGA-III-OSD) is proposed for enhancing the convergence of NSGA-III. Firstly, the objective space is decomposed into several subspaces by clustering the weight vectors uniformly distributed in the whole objective space and each subspace has its own population. Secondly, individual information is exchanged between subspaces in the mating selection phase. Finally, the convergence information is added in the environmental selection phase by the penalty-based boundary intersection distance. The proposed NSGA-III-OSD is tested on a number of many-objective optimization problems with three to fifteen objectives and compared with six state-of-the-art algorithms. Experimental results show that NSGA-III-OSD is competitive with the chosen state-of-the-art designs in convergence and diversity.

1 Introduction

Recently, many-objective optimization problems (MaOPs) mean that the optimization problems have more than three objectives, which have been the new research focus in evolutionary many-objective optimization (EMO) community (Khare et al. 2003; Purshouse and Fleming 2007; von Lücken et al. 2014). They not only bring a difficult challenge for many-objective evolutionary algorithms (MOEAs), but also are an urgent need for many real-world applications, such as engineering design (Fleming et al. 2005), radar waveform optimization (Hughes 2007) and engine calibration (Lygoe et al. 2013). And as we know, the popular multi-objective evolutionary algorithms, including non-dominated sorting genetic algorithm II (NSGA-II) (Deb et al. 2002), strength Pareto evolutionary algorithm 2 (SPEA2) (Zitzler et al. 2001) and Pareto envelope-based selection algorithm II (PESA-II) (Corne et al. 2001), could deal well with two or three objectives optimization problems. However, these Pareto dominance-based MOEAs all face great difficulties in many-objective optimization. On the one hand, with an increase in the number of objectives, almost all solutions in the population become non-dominated (Ishibuchi et al. 2008). That cannot produce enough selection pressure to make the population evolve. On the other hand, since most of these solutions are non-dominated, that makes the diversity maintenance operators play a leading role in the environmental selection. But this could cause a phenomenon named active diversity promotion (Purshouse and Fleming 2007). Such a phenomenon can make the population select dominance resistant solutions (DRSs) (Ikeda et al. 2001) which are bad for the search process.

Considering the aforementioned two difficulties in Pareto dominance-based MOEAs, there are two direct methods:

The one is the modified Pareto dominance. Modified Pareto dominance relaxes the form of Pareto dominance to enhance the selection pressure toward the PF. Köppen et al. (2005) introduced the fuzzy theory to define a fuzzy Pareto domination relation that can reflect the dominance degree between individuals. Deb et al. (2005a) proposed $\epsilon$-dominance that can divide the whole objective space into hyper-boxes and expand the domination area of individuals. Sato et al. (2007) used a novel method based on the Sine theorem to control dominance area of solutions, which can further change the dominance relation between individuals. Yang et al. (2013) presented the grid dominance that is similar to the $\epsilon$-dominance but the relaxing degree of grid dominance changed with the evolution of the population. In conclusion, this kind of method can well increase the selection pressure, but bring one or more parameters that need to be adjusted, and which is very hard before knowing the problem property.

The other one is the diversity promotion operator, and there is not too much work in this respect yet. Adra and Fleming (2011) presented two diversity management mechanisms by controlling the activation and deactivation of the crowding distance in NSGA-II (Deb et al. 2002). Deb and Jain (2014) proposed an improved NSGA-II procedure, named NSGA-III, whose diversity maintenance is aided by providing a set of well-distributed reference points and each solution is associated with a reference line. In addition, some papers not only focus on the diversity promotion but also consider the improvement in convergence. For example, Li et al. (2014) put forward a shift-based density estimation (SDE) strategy that can put the solutions with poor convergence into crowded regions by the coordinate transformation. However, since this kind of method still employs the Pareto dominance relation with low selection pressure, the convergence of those algorithms could be further improved.

Another framework is the decomposition-based method and is different from the above Pareto-based algorithms, which adopts the decomposition strategy and the neighborhood concept. And as the most popular algorithm among them, many-objective evolutionary algorithm based on decomposition (MOEA/D) was proposed by Zhang and Li (2007), which adopts aggregation functions to compare individuals and maintains the diversity of solutions by placing uniform distribution weight vectors. Although the modified versions of MOEA/D were continually proposed in Ke et al. (2014), Michalak (2015) and Zhao et al. (2012), all of them only show good performance on two and three objectives while they are not tested on many-objective optimization problems. Recent studies in Deb and Jain (2014) have shown that only MOEA/D-PBI is suited for many-objective optimization problems. However, it only uses the aggregation function to selection individuals that could obtain a good convergence, but in high-dimensional objective space, a solution with good aggregation function value does not mean it is closed to the corresponding weight vector. So although the weight vectors are uniformly distributed, it could also lead to the loss of diversity.

It is worth noting that MOEA/D-PBI adopts the neighborhood concept and the PBI aggregation function, which could obtain a good convergence, but the diversity is poor. While NSGA-III uses Pareto dominance relation and only considers the closest individual to the reference direction, which could obtain a desired diversity, but the convergence is unsatisfactory. Recently, Yuan et al. (2014) introduced the PBI aggregation function and proposed an improved version of the NSGA-III, called $\theta$-NSGA-III, which replaces the Pareto dominance relation by the $\theta$-dominance relation and could achieve balance between convergence and diversity for many-objective optimization. However, the rank of solutions is fully determined by $\theta$-dominance in the environmental selection phase, and its basic framework has been totally different from that of NSGA-III. So we aim to, under the basic framework of NSGA-III, improve the convergence of NSGA-III in many-objective optimization by introducing the neighborhood concept and the PBI aggregation function in MOEA/D, but still maintain the good diversity of NSGA-III.

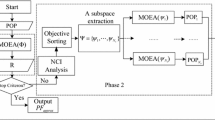
For this motivation, an improved NSGA-III based on objective space decomposition (we call it NSGA-III-OSD) is proposed. First, the objective space is decomposed into several subspaces by clustering the uniform distribution weight vectors that each of them can specify a unique subregion. Here, the definition of subspace is like the neighborhood in MOEA/D, which can be ready for mating restriction in the mating selection. Additionally, a smaller objective space can help to overcome the ineffectiveness of the Pareto dominance relation (He and Yen 2016). Then, each subspace has its own population, and for making the subpopulations evolve in a collaborative way, in the mating selection phase, the parents are selected not only from the subpopulation they belong to, but also from the whole population according to the individual exchange rate. Finally, the projector distance to the weight vector that represents the convergence information is added by the penalty-based boundary intersection (PBI) distance in the environmental selection phase.

The remainder of this paper is organized as follows. Section 2 provides some background knowledge of this paper. Section 3 is devoted to the description of our proposed algorithm for many-objective optimization. Experimental settings and comprehensive experiments are conducted and analyzed in Sect. 4. Finally, Sect. 5 concludes this paper and points out some future research issues.

2 Related backgrounds

2.1 Basic definitions

The many-objective optimization problem (MOP) can be defined as follows:

$$\begin{aligned}&\min \;{\varvec{F}}\left( {\varvec{x}} \right) =\left( {f_1 \left( {\varvec{x}} \right) , f_2 \left( {\varvec{x}} \right) ,\ldots ,f_M \left( {\varvec{x}} \right) } \right) ^{\hbox {T}}\nonumber \\&\qquad {\hbox {subject}}\;{\hbox {to}}\;{\varvec{x}}\in \varOmega \end{aligned}$$

(1)

where ${\varvec{x}}=\left( {x_1 ,x_2 ,\ldots ,x_n } \right) ^{\hbox {T}}$ is a n-dimensional decision variable vector from the decision space $\varOmega$ and M is the number of objectives.

Given two decision vectors ${\varvec{x}},{\varvec{y}}\in \varOmega$, we say ${\varvec{x}}$ is Pareto dominate ${\varvec{y}} ({\varvec{x}}\prec {\varvec{y}})$, if:

$$\begin{aligned}&\forall i\in \left\{ {1,2,\ldots ,M} \right\} :f_i \left( {\varvec{x}} \right) \le f_i \left( {\varvec{y}} \right) \nonumber \\&\exists i\in \left\{ {1,2,\ldots ,M} \right\} :f_i \left( {\varvec{x}} \right) <f_i \left( {\varvec{y}} \right) \end{aligned}$$

(2)

A solution ${\varvec{x}}^{*}\in \varOmega$ is Pareto optimal if there is no ${\varvec{x}}\in \varOmega$ making ${\varvec{x}}\prec {\varvec{x}}^{*}$. ${\varvec{F}}({\varvec{x}}^{{*}})$ is called a Pareto optimal objective vector. The set of all Pareto optimal solutions is called the Pareto optimal set (PS), and the set of all Pareto optimal objective vectors is called the Pareto front (PF), ${\hbox {PF}}=\left\{ {{\varvec{F}}\left( {\varvec{x}} \right) \in R^{m}|{\varvec{x}}\in {\hbox {PS}}} \right\}$.

2.2 NSGA-III

The basic framework of NSGA-III is similar to the original NSGA-II (Deb et al. 2002) with significant changes in its selection mechanism. NSGA-III first generates a set of reference points on a hyperplane. And suppose the parent population at the tth generation is $P_{{t}}$ and its size is N, the offspring population is $Q_{{t}}$, and the combined population is $U_{{t}} =P_{t} \cup Q_{t}$ (of size 2N). Then based on the non-dominated sorting, $U_{t}$ is divided into different non-domination levels ($F_1$, $F_2$ and so on). Then, a new population $S_{t}$ is constructed by selecting individuals of different non-domination levels one at a time, starting from $F_1$, until the size of $S_{t}$ is equal to N or for the first time becomes larger than N . Let us suppose that the last level included is the lth level. Individuals in $S_{t}{/}F_l$ are already chosen for $P_{t+1}$, and the remaining population individuals are chosen from $F_l$ by the diversity maintenance operator. But before that, objective values are first normalized by the ideal point and the extreme point. After normalization, the ideal point of the population $S_{t}$ is the zero vector and supplied reference points just lie on this normalized hyperplane. Then, the perpendicular distance between each individual in $S_{t}$ and each of the reference lines (joining the origin with a reference point) is calculated. Each individual in $S_{t}$ is then associated with a reference point having the minimum perpendicular distance.

Finally, the niche-preservation operation is used to select members from $F_l$. For the jth reference point, the niche count $\rho _j$ is the number of individuals from $S_{t}{/}F_l$ that are associated with the jth reference point. First, the reference point set $J_{\min } =\left\{ {j:\arg \min _j \rho _j } \right\}$ having the minimum $\rho _j$ value is identified. If $\left| {J_{\min } } \right| >1$, one ($\bar{j} \in J_{\mathrm{min}}$) is randomly chosen. Then there are two scenarios occurred:

• 1. If existing any member in the front $F_l$ is associated with the $\overline{j}$th reference point, this scenario includes two cases:

  • If $\rho _{\bar{j}} =0$, we choose the one having the shortest perpendicular distance to the $\overline{j}$th reference line in $F_l$ that are associated with the $\overline{j}$th reference point, and add it to $P_{t+1}$. The count of $\rho _{\bar{j}}$ is then increased by one.

  • If $\rho _{\bar{j}} >0$, a randomly chosen member from front $F_l$ that is associated with the $\overline{j}$th reference point is added to $P_{t+1}$, and the count of $\rho _{\bar{j}}$ is also increased by one.

• 2. If not, the reference point is excluded from further consideration for the current generation; meanwhile, $J_{\mathrm{min}}$ is recomputed and $\overline{j}$ is reselected.

The above procedure is repeated until the remaining population individuals of $P_{t+1}$ are filled.

3 The proposed NSGA-III-OSD

3.1 Framework of proposed algorithm

Algorithm 1 presents the general framework of NSGA-III-OSD. First, the initialization procedure generates N weight vectors, and then the K-means clustering algorithm (Hartigan and Wong 1979) is used to divide the weight vectors into a set of M clusters $\left\{ {CW^{1},CW^{2},\ldots ,CW^{M}} \right\}$, where the central clustering vectors are $\left\{ {{\varvec{c}}_1 ,{\varvec{c}}_2 ,\ldots ,{\varvec{c}}_M } \right\}$. Based on these central clustering vectors, the whole objective space is divided into M subspaces, denoted as $\left\{ {\varOmega ^{1},\varOmega ^{2},\ldots ,\varOmega ^{M}} \right\}$, the initial subpopulation is randomly produced, and the size is equal to the number of weight vectors in the subspace they belong to. For each subpopulation, the mating selection procedure chooses some parents for offspring generation. Then, the offspring are divided into different subspaces by allocation operator and finally update the associated parent subpopulations by environmental selection.

3.2 Initialization procedure

The initialization procedure of NSGA-III-OSD (line 1 of Algorithm 1), whose pseudo-code is given in Algorithm 2, contains three main steps: the generation of weight vectors, objective space decomposition and subpopulation initialization in subspace. To be specific, the initial subpopulation $S^{k}$ is randomly sampled from $\varOmega$.

3.2.1 Weight vectors generation

We employ the Das and Dennis’s systematic method (Das and Dennis 1998) to generate the set of weight vectors, $W=\left\{ {{\varvec{w}}^{1},{\varvec{w}}^{2},\ldots ,{\varvec{w}}^{N}} \right\}$. The size of W is $N=C_{H+M-1}^{M-1}$, where $H>0$ is the number of divisions in each objective coordinate. Like in the NSGA-III (Deb and Jain 2014), for more than five objectives, a two-layer weight vector generation method is adopted in our algorithm. At first, if $B=\left\{ {{\varvec{b}}^{1},{\varvec{b}}^{2}\ldots ,{\varvec{b}}^{N_1 }} \right\}$ and $I=\left\{ {{\varvec{i}}^{1},{\varvec{i}}^{2}\ldots ,{\varvec{i}}^{N_2 }} \right\}$ represent, respectively, the sets of weight vectors in the boundary and inside layers (where $N_1 +N_2 =N)$, which are initialized with different H settings. Suppose a weight vector A from inside layer I and the center weight vector O, $o_i =1/M,\,for\;i\in \left\{ {1,\ldots ,M} \right\}$, based on the formula of definite proportion, the weight vector A in the inside layer is transformed as:

$$\begin{aligned} {\varvec{A}}={\varvec{A}}+\lambda ({\varvec{O}}-{\varvec{A}})=(1-\lambda ){\varvec{A}}+\lambda {\varvec{O}} \end{aligned}$$

(3)

where $\lambda$ is a scaling factor and generally setting 0.5. At last, B and I compose the final weight vector set W. Figure 1 illustrates the two-layer weight vector generation method.

Fig. 1

Example the two-layer weight vector generation method, with $H_{1}=2$ for the boundary layer and $H_{2}=1$ for the inside layer

3.2.2 Objective space decomposition

Though the K-means clustering algorithm (Hartigan and Wong 1979), the weight vectors are divided into a set of M clusters, denoted as $\left\{ {CW^{1},CW^{2},\ldots ,CW^{M}} \right\}$. It is noted that the initial central clustering vectors are the weight vectors being the axis direction. Since the weight vectors uniformly distribute in the objective space, the number of weight vectors in every cluster is approximate to $\left\lfloor {N/M} \right\rfloor$. After that, the set of central clustering vectors $C=\{{\varvec{c}}^{1},{\varvec{c}}^{2},\ldots ,{\varvec{c}}^{M}\}$ can be obtained, especially the central clustering vector is also a weight vector, where $\sum \nolimits _{i=1}^M {c_i^k } =1$, whose pseudo-code is given in Algorithm 3, and Fig. 2 shows the illustration of objective space decomposition when $M=2$ and $M=3$. Each central clustering vector ${\varvec{c}}^{k}$ specifies a unique subspace, denoted as $\varOmega ^{k}$ in the objective space, where $\varOmega ^{k}$ is defined as:

$$\begin{aligned} \varOmega ^{k}= & {} \left\{ {\varvec{F}}({\varvec{x}})\in R_+^M |\left\langle {{\varvec{F}}({\varvec{x}}),{\varvec{c}}^{k}} \right\rangle \le \left\langle {{\varvec{F}}({\varvec{x}}),{\varvec{c}}^{j}} \right\rangle , \right\} \end{aligned}$$

(4)

where $j\in \left\{ {1,2,\ldots ,M} \right\} ,{\varvec{x}}\in \varOmega$ and $\left\langle {{\varvec{F}}({\varvec{x}}),{\varvec{c}}^{k}} \right\rangle$ is the acute angle between ${\varvec{F}}({\varvec{x}})$ and ${\varvec{c}}^{k}$. As we know, the weight vectors in the $CW^{k}$ uniformly distribute in each subspace $\varOmega ^{k}$, and each weight vector also specifies a unique subregion in the subspace as the same way.

Fig. 2

Illustration of objective space decomposition when a $M=2$ and b $M=3$

It is worth noting that NSGA-III-OSD employs a two-stage decomposition to divide the objective space. Similar to recently proposed EMO algorithm MOEA/D-M2M (Hai-lin et al. 2014), the first-stage decomposition is that different central clustering vectors are used to specify different subspaces, and the central clustering vectors are obtained by the K-means clustering algorithm (Hartigan and Wong 1979). Then, the second-stage decomposition is that different weight vectors in subspace is associated with a unique subregion. And the subregion is used for calculating the niche count in the niche-preservation operation. For being consistent with the idea of objective space decomposition, the angle between two vectors is used as the similarity metric in K-means clustering algorithm in Algorithm 3. Here, the definition of subspace is like the neighborhood in MOEA/D, and both of them are defined based on the relation between the weight vectors. The difference is that the neighborhood in MOEA/D is partially overlapping, but the subspace in NSGA-III-OSD is independent.

3.3 Reproduction operator

For each subpopulation, reproduction operator (line 5 and line 6 of Algorithm 1) is used to generate offspring solutions to update the subpopulation. First is mating selection, which chooses some mating parents for offspring generation, and second is genetic operator, including the simulated binary crossover (SBX) (Deb and Agrawal 1994) and polynomial mutation (Deb and Goyal 1996), which generates new offspring solutions based on the selected mating parents. Considering the exchange of individual information between subspaces, mating parents can be chosen randomly from the whole population according to the rate of individual exchange $\mu$, where $\mu \in [0,1]$. In fact, based on the definition of subspace, a mating restriction scheme is implemented in the mating selection, which can overcome the ineffective of recombination operator in many-objective optimization (Deb and Jain 2014). The pseudo-code of the mating selection procedure is given in Algorithm 4.

3.4 Allocation operator

Allocation operator (line 7 of Algorithm 1) is done to the offspring population R, which allocates the individual in R to the different subspaces according to the angles to central clustering vectors, and the pseudo-code of allocation operator is given in Algorithm 5.

3.5 Environmental selection

After the allocation operator, for each subpopulation, if there is new member added, the environmental selection is carried on this subpopulation, otherwise the subpopulation stays the same. First, in the subspace, the combined population $S^{k}$ is sorted into different non-domination levels ($F_1$, $F_2$ and so on). Then, starting from $F_1$, each non-domination level is selected one by one to construct a new population $S_t$, until the size of $S_t$ is equal to $\left| {{\hbox {CW}}^{k}} \right|$ or for the first time exceeds $\left| {{\hbox {CW}}^{k}} \right|$. And then the allocation operator is used again to allocate the individuals in subpopulation to the subregion in the subspace. Simultaneously, for each individual, the PBI distance to the associated weight vector is computed. Finally, like in NSGA-III, the same niche-preservation operation is employed on St, and only the perpendicular distance is replaced by the PBI distance. The pseudo-code of environmental selection is given in Algorithm 6.

3.6 PBI distance

The proposed PBI distance is defined for the niche-preservation operation. And each solution in $S^{k}$ is associated with the reference direction of a weight vector in ${\hbox {CW}}^{k}$. Let $d({\varvec{x}})=d_{j,1} ({\varvec{x}})+\theta d_{j,2} ({\varvec{x}}),j\in \left\{ {1,2,\ldots ,\left| {{\hbox {CW}}^{k}} \right| } \right\}$, where $\theta$ is a predefined penalty parameter and $d_{j,1} ({\varvec{x}})$ and $d_{j,2} ({\varvec{x}})$ are formulated as in Eqs. 5 and 6. The form of $d({\varvec{x}})$ is the same as the PBI aggregation function (Zhang and Li 2007). But here, the distances $d_{j,1} ({\varvec{x}})$ and $d_{j,2} ({\varvec{x}})$ are both computed in the original objective space. The first measure $d_{j,1} ({\varvec{x}})$ is the Euclidean distance between origin and the foot of the normal drawn from the solution to the j reference direction, while the second measure $d_{j,2} ({\varvec{x}})$ is the perpendicular distance of the solution from reference direction. These two measures are illustrated in Fig. 3. Mathematically, $d_{j,1} ({\varvec{x}})$ and $d_{j,2} ({\varvec{x}})$ are computed as follows:

$$\begin{aligned} d_{j,1} ({\varvec{x}})= & {} {\left\| {\left( {\varvec{F}}({\varvec{x}})\right) ^\mathrm{T}{\varvec{w}}_j } \right\| }\big /{\left\| {{\varvec{w}}_j } \right\| }\end{aligned}$$

(5)

$$\begin{aligned} d_{j,2} ({\varvec{x}})= & {} \left\| {{\varvec{F}}({\varvec{x}})-d_{j,1} ({\varvec{x}}) \left( {{{\varvec{w}}_j }\big /{\left\| {{\varvec{w}}_j } \right\| }} \right) } \right\| \end{aligned}$$

(6)

It is clear that a smaller value of $d_1$ indicates superior convergence, while a smaller value of $d_2$ ensures good diversity (Asafuddoula et al. 2013). In NSGA-III, on the one hand, Pareto dominance relation lacks enough selection pressure. On the other hand, the diversity operator only considers $d_2$ that can lead to stress diversity more than convergence. The PBI distance could introduce the convergence information in the environmental selection and better balance between convergence and diversity by adjusting the $\theta$ value. The influence of $\theta$ on the performance of NSGA-III-OSD is presented in Sect. 4.5.

Fig. 3

Illustration of PBI distance

3.7 Computational complexity of one generation of NSGA-III-OSD

In this section, we analyze the computational complexity of NSGA-III-OSD. For a population size N and an optimization problem of M objectives, the size of subpopulation in NSGA-III-OSD is approximately equal to $N_1 =\left\lfloor {N/M} \right\rfloor$. For one subpopulation, NSGA-III-OSD mainly performs the following four operations: (a) mating selection, (b) genetic operator, (c) allocation operator and (d) environmental selection. Genetic operator, here the simulated binary crossover (SBX) and polynomial mutation are performed on each decision variable of the parent solutions, which needs $O\left( {VN_1 } \right)$ computations to generate $N_1$ offspring, where V is the number of decision variables. Allocation operator (line 7 of Algorithm 1) requires $O\left( {M^{2}N_1 } \right)$ computations, $N_1$ offspring are allocated into M subspaces. The environmental selection involves four procedures: non-dominated sorting of the union population, allocation operator, PBI distance computing and niche-preservation operation. Non-dominated sorting needs $O\left( {MN_1 ^{2}} \right)$ computations in the worst case for the combined population of size $2N_1$ (this size is under the worst case, only when all offspring are allocated into one subspace, but not all subpopulation size can be $2N_1$ simultaneously); allocation operator requires $O\left( {MN_1 ^{2}} \right)$ computations; the computing of PBI distance needs $O\left( {MN_1} \right)$ computations. Thereafter, assuming that $L=\left| {F_l} \right|$ in the niche-preservation operation requires larger of $O\left( {L^{2}} \right)$ or $O\left( {LN_1 } \right)$ computations. So same to the NSGA-III, environmental selection needs a total $O\left( {MN_1 ^{2}} \right)$. Thus, in lines 5–13 of Algorithm 1, if all offspring are allocated into one subspace that is the best case, it requires $O\left( {M^{2}N_1 +MN_1 ^{2}} \right)$ computations, otherwise at most it requires $O\left( {M^{2}N_1 +M^{2}N_1 ^{2}} \right)$ computations. So, for M subpopulations, considering all the above considerations and computations, the overall worst-case complexity of one generation of NSGA-III-OSD is $O\left( {M^{2}N+MN^{2}} \right)$, and the best case is $O\left( {M^{2}N+N^{2}} \right)$.

3.8 Discussion

After describing the technical details of NSGA-III-OSD, this section discusses the similarities and differences between NSGA-III-OSD and $\theta$-NSGA-III, and both of them are the improved version of the NSGA-III.

• 1. Similarities between NSGA-III-OSD and $\theta$-NSGA-III:

  • Both of them adopt a set of weight vectors (or reference points) to guide the selection of individual.

  • In both algorithms, each solution is associated with a weight vector (or reference point). This procedure in NSGA-III-OSD is named the allocation operator but the clustering operator for $\theta$-NSGA-III.

  • Both of them employ the form of PBI aggregation function.

• 2. Differences between NSGA-III-OSD and $\theta$-NSGA-III:

  • NSGA-III-OSD employs the strategy of objective space decomposition that can help to overcome the ineffectiveness of the Pareto dominance relation (Zhenan and Yen 2016). Next mating restriction could be implemented, which can overcome the ineffective of recombination operator in many-objective optimization (Deb and Jain 2014).

  • $\theta$-NSGA-III uses the min–max normalization method to normalize the population, while in NSGA-III-OSD, since the several subpopulations evolve in a collaborative way, the normalization method used for the whole population is inappropriate.

  • $\theta$-NSGA-III abandons the Pareto dominance concept in selection, while the quality of a solution is fully determined by $\theta$-dominance. But in the environmental selection phase, NSGA-III-OSD still adopts the Pareto dominance relation and the PBI distance is applied to the niche-preservation operation.

4 Empirical analysis

This section presents the evaluation of the proposed NSGA-III-OSD. First, we describe the test problems and the quality indicators used in experiments (Sects. 4.1–4.2). Then, we briefly introduce six state-of-the-art algorithms used for comparison and the corresponding parameter settings in Sect. 4.3. Finally, the results are discussed in Sects. 4.4–4.5.

4.1 Test problems

For our empirical studies, two well-known test suites for many-objective optimization, the DTLZ test suite (Deb et al. 2005b) and the WFG test suite (Huband et al. 2006), are chosen. Like in NSGA-III, we only consider DTLZ1 to DTLZ4 problems for DTLZ test suite but all of WFG test suite. For each DTLZ instance and WFG instance, the number of objectives is considered from three to fifteen, i.e., $M\in \left\{ {3,5,8,10,15} \right\}$. According to (Deb et al. 2005b), the number of decision variables is set as $V=M+r-1$ for DTLZ test instances, where $r=5$ for DTLZ1 and $r=10$ for DTLZ2, DTLZ3 and DTLZ4. As suggested in (Huband et al. 2006), for WFG test instances, the number of decision variables is set as $V=k+l$, where the position-related variable $k=2{*}(M-1)$ and the distance-related variable $l=20$. In Table 1, the main characteristics of all test instances are listed.

Table 1 Characteristics of test instances

4.2 Quality indicators

In our empirical studies, the following three widely used quality indicators are considered. The first one can reflect the convergence of an algorithm. The latter two quality indicators can measure the convergence and diversity of solutions simultaneously.

• 1. Generational Distance (GD) indicator (Deb et al. 2005b).

For any algorithm, let P be the set of final non-dominated points obtained in the objective space and $P^*$ be a set of points uniformly spread over the true PF. Then GD is computed as:

$$\begin{aligned} {\hbox {GD}}(P,P^{{*}})=\frac{\sqrt{\sum _{u\in P} {d({\varvec{u}},P^{{*}})} }}{|P|} \end{aligned}$$

(7)

where $d({\varvec{u}},P^{{*}})$ is the Euclidean distance between a point ${\varvec{u}}\in P$ and its nearest neighbor in $P^*$ and $\left| P \right|$ is the cardinality of P. The smaller GD value indicates that the obtained solution set is more closed to the Pareto front.

• 2. Inverted Generational Distance (IGD) indicator (Zitzler et al. 2003).

For any algorithm, let P be the set of final non-dominated points obtained in the objective space and $P^*$ be a set of points uniformly spread over the true PF. Then IGD is computed as:

$$\begin{aligned} {\hbox {IGD}}\left( P,P^{{*}}\right) =\frac{\sum _{v\in P^{{*}}} {d({\varvec{v}},P)} }{\left| P^{{*}}\right| } \end{aligned}$$

(8)

where $d({\varvec{v}},P)$ is the Euclidean distance between a point ${\varvec{v}}\in P^*$ and its nearest neighbor in P and $\left| {P^*} \right|$ is the cardinality of $P^*$. The set P with smaller IGD value is better.

For calculating IGD, a reference set of the true Pareto front is required. Here, we provide two kinds of IGD calculations for the comparison of different types of algorithms: The first one is for MOEAs using reference directions, such as NSGA-III and MOEA/D, we employ a special way to calculate IGD as NSGA-III recommends, the intersecting points of weight vectors and the Pareto optimal surface compose $P^*$ over the true PF (Deb and Jain 2014). The second is for all MOEAs, we adopt a general way to calculate IGD that $P^*$ is composed by uniformly sampling 10,000 points over the true PF.

• 3. Hypervolume (HV) indicator (Zitzler and Thiele 1999)

Let P be the set of final non-dominated points obtained in the objective space by an algorithm, and ${\varvec{z}}{=}\left( {z_1 ,z_2 ,\ldots ,z_M } \right) ^\mathrm{T}$ be a reference point in the objective space which is dominated by all Pareto optimal points. Then the hypervolume indicator measures the volume of the region dominated by P and bounded by ${\varvec{z}}$.

$$\begin{aligned} {\hbox {HV}}\left( {P,{\varvec{z}}} \right) ={\hbox {Volume}}\left( {\bigcup _{{\varvec{F}}\in P} {\left[ {f_1 ,z_1 } \right] } \times \cdots \left[ {f_M ,z_M } \right] } \right) \end{aligned}$$

(9)

where M is the number of objectives. The larger is the HV value, the better is the solutions quality for approximating the whole PF. The HV indicator is used for WFG test suite, and we set reference points ${\varvec{z}}=\left( {3.0,\ldots ,1.0+2.0\times M} \right) ^{T}$. In addition, for three- to ten-objective test instances, we calculate HV value using the recently proposed WFG algorithm (While et al. 2012). And for fifteen-objective instances, we adopt the Monte Carlo simulation proposed in Bader and Zitzler (2011) to approximate the HV, and the number of sampling points is 1,000,000. And when we calculate the HV value, solutions dominated by the reference point are deleted. Additionally, for easy to compare, the obtained HV values in this paper are all normalized to [0, 1] by dividing $z=\prod _{i=1}^M {z_i }$.

4.3 Algorithms and parameters

In order to verify the proposed NSGA-III-OSD, we consider six state-of-the-art algorithms for comparisons, including $\theta$-NSGA-III (Yuan et al. 2014), NSGA-III (Deb and Jain 2014), MOEA/D (Zhang and Li 2007), GrEA (Yang et al. 2013), SPEA2 $+$ SDE (Li et al. 2014) and HypE (Bader and Zitzler 2011). NSGA-III is still based on the Pareto dominance relation, but the maintenance of population diversity is aided by using a set of well-distributed reference points. $\theta$-NSGA-III is an improved version of the NSGA-III, which replaces the Pareto dominance relation by the $\theta$-dominance relation. MOEA/D is a representative of the decomposition-based approach and uses a predefined set of weight vectors to maintain the solutions diversity. GrEA uses the basic framework of NSGA-II and introduces two concepts (i.e., grid dominance and grid difference), three grid-based criteria, (i.e., grid ranking, grid crowding distance and grid coordinate point distance) and a fitness adjustment strategy. SPEA2 $+$ SDE integrates a shift-based density estimation (SDE) strategy into SPEA2. HypE is a hypervolume-based evolutionary algorithm for many-objective optimization, which adopts Monte Carlo simulation to approximate the exact hypervolume values.

The seven MOEAs considered in this study need to set some parameters, and they are listed as follows:

• 1. Population size: The setting of population size N for NSGA-III, MOEA/D and NSGA-III-OSD cannot be arbitrarily specified, where N is controlled by a parameter H. Although $\theta$-NSGA-III adopts a simpler approach with any positive integer N, it adopts the Das and Dennis (1998) systematic method to generate the set of weight vectors for a fair comparison. Moreover, for eight-, ten- and fifteen-objective instances, we use the two-layer weight vector generation method in Sect. 3.2.1 for the above four algorithms. For the remaining three algorithms, although the population size can be set to any positive integer, the same population size is used for ensuring a fair comparison. The population size N used in this study for different number of objectives is summarized in Table 2. Maybe the setting of H for boundary and inside layers should be larger for fifteen-objective problems, but for a fair comparison, we make the weight vector size same to those in the original NSGA-III study. In addition, the population size of NSGA-III is slightly adjusted to the multiple of four just as in the original NSGA-III study (Deb and Jain 2014), i.e., 92, 212, 276 and 136 for three-, five-, ten- and fifteen-objective problems, respectively.

• 2. Number of runs and termination condition: Each algorithm is conducted 20 runs independently on each test instance. All the algorithms are executed on a desktop PC with 2.6 GHz CPU, 4 GB RAM and Windows 7 OS. The termination condition of an algorithm is the maximum number of fitness evaluations, as summarized in Table 3.

• 3. Settings for reproduction operator: The crossover probability is $p_c =1.0$ and its distribution index is $\eta _c =20$ ($\eta _c =30$ in NSGA-III-OSD, $\theta$-NSGA-III, and NSGA-III). The mutation probability is $p_m =1/V$ and its distribution index is $\eta _m =20$.

• 4. Significance test: To test the difference for statistical significance, the Conover–Inman procedure is applied with a 5 % significance level in the Kruskal–Wallis test (Conover 1999) for all pairwise comparisons.

• 5. Parameter setting in $\theta$-NSGA-III: The penalty parameter $\theta =5$ as suggested in (Yuan et al. 2014).

• 6. Parameter setting in MOEA/D: Neighborhood size $T=20$ and probability used to select in the neighborhood $\delta =0.9$. Since PBI function is involved in MOEA/D, the penalty parameter $\theta$ needs to be set for it. In this study, $\theta$ is just set to 5 for MOEA/D as suggested in (Zhang and Li 2007).

• 7. Parameter setting in NSGA-III-OSD: $\theta$ is set to 5, $\mu =0.2$ for three- and five-objective instances and $\mu =0.7$ for eight-, ten- and fifteen-objective instances. We will investigate the influence of $\theta$ and $\mu$ on the performance of the proposed NSGA-III-OSD in Sect. 4.5.

• 8. Grid division (div) in GrEA: The settings of div are according to (Yang et al. 2013) as shown in Table 4.

• 9. Parameter setting in SPEA2 $+$ SDE: The archive size is just set as the same as the population size.

• 10. Number of points in Monte Carlo sampling: It is set to 1,000,000 that ensures the precision.

Table 2 Number of population size

Table 3 Maximum number of fitness evaluations for different test instances

4.4 Results and discussion

In this section, for validating the performance of NSGA-III-OSD, our experiments can be divided into four parts. Firstly, for confirming our motivation of improving convergence, the first part is to compare NSGA-III-OSD with the original NSGA-III in the aspect of convergence. Secondly, to exhibit the overall performance as a reference-direction-based algorithm, the second part is to compare NSGA-III-OSD with $\theta$-NSGA-III, NSGA-III and MOEA/D. Then, to show the desired convergence and diversity as a general many-objective evolutionary algorithm, the third part is to compare NSGA-III-OSD with different types of many-objective evolutionary algorithms on two test suites. Finally, we investigate the influence of parameter $\mu$ and $\theta$ on the performance of NSGA-III-OSD.

4.4.1 Comparison with NSGA-III in convergence

In this subsection, the GD indicator is employed to compare the convergence capacity between the proposed NSGA-III-OSD and the original NSGA-III. Here, a reference set $P^*$ for calculating GD is composed by the intersecting points of weight vectors and the Pareto optimal surface. In addition, the best performance is shown in bold.

Table 5 shows the best, median and worst GD values obtained by NSGA-III-OSD and NSGA-III on DTLZ1 to DTLZ4 instances with different number of objectives. Table 5 shows that, compared with NSGA-III, NSGA-III-OSD has the obvious improvement in the aspect of convergence. This could illustrate that the mechanism of objective space decomposition and PBI distance indeed improve the convergence of original NSGA-III, which partly confirms the motivation of our study.

4.4.2 Comparison with NSGA-III, $\theta$-NSGA-III and MOEA/D

In this subsection, the first kind of IGD calculation is used to evaluate the algorithms. The DTLZ1 problem has a simple, linear PF $\left( \sum _{i=1}^M {f_i } \left( {{\varvec{x}}^{{*}}} \right) =0.5\right)$ but with $11^{5}-1$ local optima in the search space, which can measure the convergence capacity of algorithms. The DTLZ2 problem is a relatively easy test instance with a spherical PF $\left( \sum _{i=1}^M {f_i^2 } \left( {{\varvec{x}}^{{*}}} \right) =1\right)$. The PF of DTLZ3 is the same as DTLZ2, but whose search space contains $3^{10}-1$ local optima, which causes a tough challenge for algorithms to converge to the global PF. DTLZ4 also has the same PF shape as DTLZ2. However, in order to investigate an MOEA’s ability to maintain a good distribution of solutions, DTLZ4 introduces a variable density of solutions along the PF. This modification allows a biased density of points away from $f_M \left( {\varvec{x}} \right) =0$.

Table 4 Settings of grid division div in GrEA

Table 5 Best, median and worst GD values obtained by NSGA-III-OSD and NSGA-III on DTLZ1 to DTLZ4 instances with different number of objectives

Table 6 Best, median and worst IGD values obtained by NSGA-III-OSD, $\theta$-NSGA-III, NSGA-III and MOEA/D-PBI on DTLZ1 to DTLZ4 instances with different number of objectives

Table 6 shows the best, median and worst IGD values obtained by NSGA-III-OSD, $\theta$-NSGA-III, NSGA-III and MOEA/D-PBI on DTLZ1 to DTLZ4 instances with different number of objectives. Table 6 shows NSGA-III-OSD could perform well on all the instances, especially on DTLZ4 problem, and has obvious advantage than other three algorithms. This may owe to the mechanism of objective space decomposition. Compared with $\theta$-NSGA-III, NSGA-III-OSD significantly outperforms it on all the instances except eight-, ten- and fifteen-objective DTLZ2. And it is worth noting that, for three- and five-objective DTLZ1 and DTLZ3, $\theta$-NSGA-III is significantly worse than NSGA-III-OSD and NSGA-III. The reason may be that $\theta$-dominance only defines a partial order, the individuals from the same $\theta$-non-domination level may be on different Pareto non-domination levels, this may make the final solutions obtained by $\theta$-NSGA-III not Pareto non-dominated. Compared with NSGA-III, NSGA-III-OSD performs consistently better than it on all the instances except fifteen-objective DTLZ1. We guess the reason is that DTLZ1 is multimodal test problem containing a large number of local Pareto optimal fronts and the size of subpopulation $(N_1 ={135}/{15})$ in NSGA-III-OSD is a little small to overcome the local optima when $M=15$. But for fifteen-objective DTLZ3, it also has many local optima, and NSGA-III-OSD is better than NSGA-III. The reason may be that NSGA-III performs not well, which can be seen from the comparison with the best value of MOEA/D. Compared with MOEA/D, NSGA-III-OSD only loses the advantage on eight-, ten-, and fifteen-objective DTLZ2. For ten- and fifteen-objective DTLZ3, NSGA-III-OSD is worse than MOEA/D on the best value, but the best, median and worst value of NSGA-III-OSD are in the same order of magnitude. This illustrates that NSGA-III-OSD is more robust than MOEA/D.

4.4.3 Comparison with state-of-the-art algorithms

To show the validity of NSGA-III-OSD, we compare it with six state-of-the-art algorithms on DTLZ and WFG test suites. The average and standard deviation of the IGD (HV) indicator value over 20 independent runs are used in our experiment. In addition, to test the difference for significance, the performance score (Bader and Zitzler 2011) is adopted to reveal how many other algorithms significantly outperform the corresponding algorithm on the considered test instance, and the smaller the score, the better the algorithm.

Results on DTLZ Test Suite Comparison results of NSGA-III-OSD with other six MOEAs in terms of IGD values on DTLZ test suite are presented in Table 7. It shows both the average and standard deviation of the IGD values over 20 independent runs for the seven compared MOEAs, where the best average and standard deviation among the seven algorithms are highlighted in bold, and the numbers in the square brackets in Table 7 are their performance scores. Here, since the algorithms without reference directions might have a good distribution but with the solutions not located in the reference directions defined by the weight vectors, the second kind of IGD calculation is used for a fair comparison.

Table 7 Average and standard deviation of the IGD values obtained by the seven algorithms on DTLZ1 to DTLZ4 instances with different number of objectives

From the experimental results of DTLZ1, we find that NSGA-III-OSD shows better performance than the other six MOEAs on three-, eight- and ten-objective test instances. For five- and fifteen-objective instances, it obtains the second smallest IGD value. In addition, $\theta$-NSGA-III, NSGA-III and MOEA/D obtain better IGD values than GrEA and HypE on all DTLZ1 test instances, and NSGA-III achieves the best IGD value on fifteen-objective test instance. GrEA performs not well on all DTLZ1 instances, except the eight-objective case. SPEA2 $+$ SDE achieves a similar IGD value as MOEA/D and obtains the best value on five-objective test instance. HypE can deal well with three-objective instance but work worse on more than three objectives.

Figure 4 shows the parallel coordinates of non-dominated fronts obtained by NSGA-III-OSD and the other six MOEAs, respectively, for fifteen-objective DTLZ1 instance. This particular run is associated with the result closest to the average IGD value. From these seven plots, it is observed that the non-dominated front obtained by NSGA-III-OSD is promising in both convergence and diversity and slightly better than $\theta$-NSGA-III. But both of them are slightly worse than NSGA-III in the aspect of the solutions distribution. By contrast, MOEA/D cannot search well the extreme solutions and the diversity of solutions is not good. SPEA2 $+$ SDE can be well converged, but the objective values are much smaller than the maximum value of 0.5, which means that SPEA2 $+$ SDE obtains too many intermediate solutions. Both GrEA and HypE are far away from the PF because the maximum value of some objectives is much larger than 0.5.

Fig. 4

Parallel coordinates of non-dominated fronts obtained by seven algorithms on the fifteen-objective DTLZ1 instance. a NSGA-III-OSD, b $\theta$-NSGA-III, c NSGA-III, d MOEA/D, e GrEA, f SPEA2 $+$ SDE, g HypE

Fig. 5

Parallel coordinates of non-dominated fronts obtained by seven algorithms on the fifteen-objective DTLZ2 instance. a NSGA-III-OSD, b $\theta$-NSGA-III, c NSGA-III, d MOEA/D, e GrEA, f SPEA2 $+$ SDE, g HypE

Fig. 6

Parallel coordinates of non-dominated fronts obtained by seven algorithms on the fifteen-objective DTLZ3 instance. a NSGA-III-OSD, b $\theta$-NSGA-III, c NSGA-III, d MOEA/D, e GrEA, f SPEA2 $+$ SDE, g HypE

Fig. 7

Parallel coordinates of non-dominated fronts obtained by seven algorithms on the fifteen-objective DTLZ4 instance. a NSGA-III-OSD, b $\theta$-NSGA-III, c NSGA-III, d MOEA/D, e GrEA, f SPEA2 $+$ SDE, g HypE

From the experimental results of DTLZ2, we can find that the performance of NSGA-III-OSD, $\theta$-NSGA-III and MOEA/D is comparable in this problem, and all of them perform better than NSGA-III on all three- to fifteen-objective test instances. In particular, NSGA-III-OSD shows the best results on three- and eight-objective test instances, while MOEA/D obtains the best IGD values on ten-objective instance and $\theta$-NSGA-III on fifteen-objective instance. It is worth noting that, comparing DTLZ1 problem, GrEA performs much better this time and achieves the best IGD values on five-objective instance, which is better than SPEA2 $+$ SDE on almost all DTLZ2 instances, except the fifteen-objective instance. HypE can perform well with three- and five-objective instances but still work worse when the number of objectives increases.

Figure 5 presents the comparisons of the non-dominated fronts obtained by these seven MOEAs, respectively, for fifteen-objective DTLZ2 instance. It is clear that solutions achieved by NSGA-III-OSD, $\theta$-NSGA-III and MOEA/D are similar in terms of convergence and diversity. By contrast, the distribution of solutions achieved by NSGA-III is slightly worse than the above three algorithms. SPEA2 $+$ SDE can also obtain the good convergence, and the distribution is not so bad. The non-dominated front obtained by GrEA does not converge well on the eleventh objective, and the distribution is not satisfied. Note that the non-dominated front obtained by HypE only converges well on the twelfth and thirteenth objectives and the distribution of solutions is poor.

From the experimental results of DTLZ3, we find that the performance of NSGA-III-OSD is significantly better than the other six MOEAs on all test instances. $\theta$-NSGA-III and NSGA-III show the similar overall performance on DTLZ3. MOEA/D still obtains the closed to smallest IGD value on three- and five-objective test instances, but significantly worsen on more than five-objective test instances. SPEA2 $+$ SDE thoroughly defeats GrEA on all DTLZ3 test instances and is better than NSGA-III on fifteen-objective test instance. HypE is still helpless for more than three-objective instances.

Figure 6 plots the non-dominated fronts obtained by NSGA-III-OSD and the other six MOEAs, for fifteen-objective DTLZ3 instance. It is clear that the solutions obtained by NSGA-III-OSD, $\theta$-NSGA-III, NSGA-III and SPEA2 $+$ SDE converge well to the global PF, and the distribution of solutions achieved by NSGA-III-OSD is slightly better than the other three algorithms. By contrast, the solutions obtained by MOEA/D concentrate on several parts of the PF. Similar to the observations on fifteen-objective DTLZ1 instance, GrEA and HypE have significant difficulties in converging to the PF.

From the experimental results of DTLZ4, we find that NSGA-III-OSD performs significantly better than the other six MOEAs on almost all DTLZ4 instances, except the eight-objective case. It is worth mentioning that the standard deviation of IGD obtained by NSGA-III-OSD can reach ten to the negative five on three-objective test instance, which shows that NSGA-III-OSD is rather robust. $\theta$-NSGA-III shows the closest overall performance to NSGAIII-OSD. NSGA-III is significantly worse than NSGA-III-OSD, especially on the three-objective instance. MOEA/D performs significantly worse than the other six MOEAs on this problem. GrEA could obtain much better results this time and achieve the best value on eight-objective test instance. SPEA2 $+$ SDE is significantly worse than GrEA. HypE still has no advantage on DTLZ4 test problem.

Figure 7 shows the parallel coordinates of non-dominated fronts obtained by these seven algorithms. These plots clearly demonstrate that NSGA-III-OSD and $\theta$-NSGA-III are able to find a well-converged and wide-distributed solution set for fifteen-objective DTLZ4 instance. By contrast, the non-dominated front obtained by NSGA-III loses a little part on the twelfth objective and MOEA/D fails to cover most of intermediate solutions and some extreme solutions. Although the non-dominated fronts obtained by GrEA and SPEA2 $+$ SDE could well converge to the PF, the solution distribution is rather scattered. The solutions obtained by HypE seem to concentrate on the boundary of the PF.

Results on WFG Test Suite We compare the quality of the solution sets obtained by the seven algorithms on the nine WFG test problems in terms of hypervolume. Table 8 presents the average and standard deviation of the hypervolumes over 20 independent runs on WFG1 to WFG9, where the best average and standard deviation among the seven compared algorithms are highlighted in bold, and the numbers in the square brackets in Table 8 are their performance scores.

Table 8 Average and standard deviation of the HV values obtained by the seven algorithms on WFG1 to WFG9 instances with different number of objectives

Fig. 8

Average performance score over all test instances for different number of objectives. The smaller the score, the better the algorithm performance in the corresponding number of objectives

Fig. 9

Average performance score over all objective dimensions for different test problems, namely DTLZ(Dx) and WFG(Wx). The smaller the score, the better the algorithm performance in the corresponding test problem. The values of NSGA-III-OSD are connected by a solid line to easier assess the score

Fig. 10

Ranking in the average performance score over all test instances for the seven algorithms. The smaller the score, the better the overall performance of the algorithm

From the results in Table 8, we can find that NSGA-III-OSD can deal well with most the considered instances. Particularly, it obtains the best overall performance on five- and ten-objective WFG2–5 instances and ten- and fifteen-objective WFG6–8 instances. Moreover, it achieves the best performance on three-objective WFG8 and ten-objective WFG9. By contrast, it obtains the unsatisfactory results on WFG1 problem.

$\theta$-NSGA-III works well on five- and eight-objective WFG2–9 test instances, especially on WFG2, WFG5, WFG6 and WFG7 instances with eight objectives and WFG8 instance with five objectives. It is worth noting that $\theta$-NSGA-III performs significantly worse than NSGA-III-OSD and NSGA-III on fifteen-objective WFG1–3 instances.

NSGA-III obtains the best average HV values on almost fifteen-objective WFG test instances, except WFG3, WFG6, WFG7 and WFG8. It is noted that, for WFG1 problem, NSGA-III works poorly on three-, five- and eight-objective instances. But it can still perform very well on other objective numbers.

MOEA/D cannot produce satisfactory results on all the WFG test instances. And with the number of objectives increasing, the results gradually deteriorate.

GrEA can effectively work on most of WFG test instances, especially on five-objective WFG3, WFG6, WFG7 and WFG9 instances and eight-objective WFG3 and WFG9 instances.

SPEA2 $+$ SDE generally has the medium performance on most of the WFG problems and performs best on three-, five- and eight-objective WFG1 instances and three-objective WFG6 instance.

HypE can deal well with three-objective instances and obtain the best average HV values on WFG1, WFG2, WFG3, WFG4 and WFG9. However, it does not show any advantage with more than five objectives. But for WFG2 and WFG3 test problems, it performs very well on eight-, ten- and fifteen-objective instances.

Overall Performance Analysis In order to better visualize the performance score in Tables 7 and 8, we show figures where the score is summarized for different number of objectives and different test problems, respectively. Figure 8 shows the average performance over all test instances for different number of objectives. It shows that NSGA-III-OSD achieves the best score except for eight-objective test problem. Figure 9 shows the average performance over all objective dimensions for different test problems. For DTLZ2, MOEA/D outperforms NSGA-III-OSD, and for WFG1 and WFG3, GrEA is better than NSGA-III-OSD. Besides, for WFG5 and WFG6, NSGA-III is superior to NSGA-III-OSD, and both of them are comparable on WFG2, WFG4 and WFG7. For the remaining five test problems, NSGA-III-OSD obtains the best average performance score. Finally, we quantify how well each algorithm performs over all test suites. Figure 10 shows the average performance score over all 65 test instances for the seven algorithms, and according to the average performance score, the overall rank of each algorithm is given in the corresponding bracket.

4.5 Parameter sensitivity studies

There are two main parameters in NSGA-III-OSD: the rate of individual exchange $\mu$ in the mating selection and parameter $\theta$ in the PBI distance. To investigate the influence of these two parameters on the performance of NSGA-III-OSD, $\mu$ varies from 0.0 to 1.0 with a step size 0.1 and eight values are considered for $\theta$: 0, 0.1, 5, 10, 20, 30, 40, 50. We take DTLZ1 and DTLZ4 with five- and ten-objective, respectively, to compare the result of all 88 different parameter configurations. Each configuration on each test instance is conducted twenty runs independently. Note that the first kind of IGD calculation is used.

Figure 11 shows the average IGD values obtained by these 88 different configurations on different test instances. From these four plots, we can observe that different configurations can lead to different results. When $\mu =0.0$, it means that all mating parents are chosen from the corresponding subpopulation, and there is no individual information exchanging among subpopulations; when $\mu =1.0$, it means that all mating parents are chosen from the whole population. We find that the above two configurations are not a good choice. This is because too small $\mu$ setting makes the reproduction operator excessively exploit subspace, but too large $\mu$ setting is bad for local search. Besides, when setting $\theta =0$ and 0.1, the results are unsatisfactory and the IGD values can only reach ten to the negative one (for the clarity of graph, these results are not showed), and this is because too small $\theta$ can lead to converge excessively, while the diversity cannot be maintained. However, when $\theta =5$, the IGD values become better obviously and tend to be steady with the increase in $\theta$. In general, it is better to choose $\mu$ between 0.2 and 0.4 when the number of objectives is three or five and choose $\mu$ between 0.6 and 0.8 when the number of objectives is more than five. It can be clearly seen that $\theta =5$ generally achieves a better balance between convergence and diversity.

Fig. 11

Average IGD values obtained by NSGA-III-OSD with 66 different combinations of $\mu$ and $\theta$ on DTLZ1 and DTLZ4 with five and ten objectives, respectively

5 Conclusions

In this paper, we have presented an improved NSGA-III based on objective space decomposition, called NSGA-III-OSD, whose objective space is decomposed into several subspaces through the K-means clustering algorithm. By combining the advantages of NSGA-III and MOEA/D, NSGA-III-OSD is expected to enhance the convergence ability and maintain the good diversity of NSGA-III. To prove the validity, we have made an experimental comparison of NSGA-III-OSD with other six state-of-the-art algorithms on DTLZ test suite and the WFG test suite. The experiment results show that the proposed NSGA-III-OSD could perform well on almost all the instances in our study, and the obtained solution sets have good convergence and diversity.

In the future, we will further study the search behavior of NSGA-III-OSD with large populations for many-objective problems. And recently, we note that the constrained many-objective problems seem to be a new challenge for many-objective evolutionary algorithms (Jain and Deb 2014), and we will try to extend our NSGA-III-OSD to solve them by combining constraint handling techniques (Mezura-Montes and Coello Coello 2011).