Fairness in secure computing protocols based on incentives

Abstract

Cloud computing is based on utility and consumption of computer resources. To solve the security issues in cloud computing, secure computing protocols are often used. Recently, rational parties as a new kind of parties are proposed, who wish to maximize their utilities in secure computing protocols. The utility definitions in most previous rational secure computing protocols derive from prisoner’s dilemma game (PD game). In two-party rational computing protocols, parties decide to send their shares according to their utilities. Recently, we revisit the incentives for rational parties in secure computing protocols and give new utility definitions according to them. We find that the new utility definition is not similar to PD game any more. We discuss two-party and multi-party cases, respectively, and prove that parties have incentives to send their share to others. Furthermore, we also prove that parties can maximize their utilities in both cases.

1 Introduction

Cloud computing provides people and companies with various capabilities to process their data in the third centers. It tries to achieve economies of scale based on resources sharing Chen et al. (2014), Li et al. (2014). Cloud computing also focuses on maximizing the effectiveness of the shared resources Wang et al. (2015a). In this paper, we consider this effectiveness as utility, which is similar to the notion of payoff in game theory.

A cloud computing platform is a distributed set of machines in different locations, connected to a single network or hub service. In the scenario of secure multi-party computation Yao (1982, 1986), parties are assumed to be distributed and mutually distrustful. Meanwhile they also hope to complete the protocol with their private inputs. The basic properties of the protocol consist of privacy, correctness, input independence and fairness etc. Privacy means that parties can learn nothing other than the output of the protocols; that is, parties cannot learn any information about his opponent’s private inputs. Correctness means that the output is correct with respect to the private inputs. The property of input independence prevents parties from making their inputs dependent on his opponent’s inputs. Fairness means that both parties can get the output of the protocols in the end Chen et al. (2011, 2012). According to these security properties, it can be concluded that secure two-party computation can solve the security problems in cloud computing.

If both parties trust each other, the above properties are easily achieved Wang and Ma (2015); that is, parties compute the function with their true private inputs, get the correct result and then share the result with others. Unfortunately, the reality is far from it. In fact, parties in protocols cannot be assumed mutually trusted, although mutual trust does exist in reality. Traditionally, if parties honestly follow the steps of protocols, they are considered as honest parties. Otherwise, they will be considered as corrupted parties, which means they are corrupted by an adversary. The corrupted parties are divided into three types according to the ability of the adversary.

• 1. Semi-honest parties will follow the protocols as honest parties, while they may try to learn additional information other than the outputs by storing intermediate results.

• 2. Malicious parties may arbitrarily break the security of the protocols. For example, they may arbitrarily replace the private inputs or prematurely abort the protocol.

• 3. Covert parties are much like a combination of semi-honest parties and malicious parties. They behave like semi-honest parties in most time. However, sometimes they also have incentives to cheat as malicious parties.

Rational parties are proposed as a new kind of parties Halpern and Teague (2004), Halpern and Pass (2010) to solve secure issues in secure computation protocols.

1.1 Related works

Rational secret sharing and multi-party computing are cryptographic protocols for specific goals in the presence of rational parties, which are proposed by Halpern and Teague (2004). They proved that no constant-round protocols can reach Nash equilibrium. Then they proposed a random protocol including three rational parties and left the protocol in the presence of two rational parties as an open problem. Abraham et al. (2006) proposed a coalition-resistant protocol, which was fit for two rational parties. In addition, they gave the first fair solution for Yao’s classic millionaire’s problem in rational scenarios. Lysyanskaya and Triandopoulos (2006) considered the settings, where parties may take adversarial behaviors. They discussed the security of protocol under universal composition (UC) paradigm. Although their equilibrium ($\epsilon$-weakly dominated strategies) is stronger than Nash equilibrium, their protocol did not guarantee fairness. Asharov et al. (2011) proved that some game-theoretic notions were equivalent to those in cryptographic with respect to some utility assumptions. They also discussed security properties such as privacy, correctness and fairness using game-theoretic view. Consequently, Groce and Katz (2012) revisited this problem and reached a positive result about fairness under complete information with a computational Nash equilibrium.

The utility definitions of the above works were more or less inheriting the same definitions in game theory such as PD game. Consequently, most results conformed with or similar to those in game theory. A few of works seek the incentives for rational parties to participate in the protocol. Garay et al. (2013) discussed the problem of incentive-driven adversaries and tried to know why rational parties are willing to take part in the protocol. Wang et al. tried to find the incentives for rational parties in a practical view Wang et al. (2015b) by assuming rational parties have private types. However, there are still some insufficiencies. For example, parties only have prior probability on the private types. To choose optimal strategies, they have to judge which type his opponent belongs to.

1.2 Motivation and contribution

Traditionally, non-honest parties in two-party computation are corrupted by semi-honest, malicious or covert adversaries Aumann and Lindell (2007). Semi-honest adversaries almost follow the computation, while they may store some intermediate data such that they can learn some private information of the other party. Malicious adversaries may arbitrarily participate in the protocol for the computation and break the security of the protocol. For example, they may compute with wrong input or they may abort from the protocol ahead of time such that the other party cannot complete the protocol. Covert adversaries have incentive to cheat others if not being detected. The security level of protocol in the presence of semi-honest adversaries is too low. On the other hand, the security of protocol in the presence of malicious adversaries are too strong. Since it is hard to find corresponding parties for malicious parties in real world, we should define practical parties for two-party computation protocols. Covert adversaries are such practical ones and the security level in the presence of them is between semi-honest and malicious adversaries. Rational parties are also practical ones, whose properties derive from the real world.

Game theory are combined with two-party computation to find a new kind of parties with practical background. As mentioned in Halpern and Teague (2004), parties are rational, which means they hope to maximize their utilities in the computation. In fact, in most works like Abraham et al. (2006), Asharov et al. (2011), Groce and Katz (2012), two-party computation is divided into two stages. In the first stage, parties send their inputs to a third trusted parties (called TTP), who computes the result with their private inputs and randomly chooses some shares for the result. At the end of the first stage, TTP sends some shares to each party, respectively, such that each party cannot learn the result until they get enough shares. Then, parties enter into the second stage, where they exchange shares to learn the results. In this paper, parties are considered as rational. They should compute their utilities before they decide to exchange shares. In previous works, the second stage is considered as a prisoner’s dilemma game. Sending shares to the other party is similar to the action of cooperation and not sending shares is similar to the action of defect. So, the utility definition and existing results about PD game can be applied into rational two-party computation protocols. Since both parties cannot obtain the result without enough shares, the optimal result for rational two-party computation is mutual cooperation; that is, both parties have incentives to send his shares to the other. Finally, both of them can learn the results of the computation. Unfortunately, Nash equilibrium, a stable state for PD game, is mutual defect; that is, both parties have no incentives to send his shares to the other party. Consequently, the existing results about PD game cannot be directly applied to rational two-party computations. New methods should be found such that both parties have incentives to exchange their shares and finally obtain the results.

In this paper, we revisit the incentives for rational parties in the protocols and find that the utility definitions in PD game can no longer accurately reflect the incentives of rational parties. The main contributions of this paper are as follows.

• We detailed introduce the second stage of a rational two-party computation protocol. On the basis of parties’ incentives, we redefine the utilities for each party. Rational parties have enough incentives to send his share to his opponent.

• If one party receives one share from his opponent, he gets one utility; otherwise zero utility. Therefore, we find that the utility in this paper is different from PD game and other previous works.

• We prove that mutual cooperation is Nash equilibrium in the new game and we try to extend to multi-party computation using modular architecture. Finally, we also prove that all parties in computing protocols have incentives to their opponents based on the new utility and architecture.

1.3 Organization

The rest of paper is organized as follows. Section 2 presents some preliminaries such as rational parties, utility and Nash equilibrium. Section 3 presents the new utility definitions such that two rational parties have incentives to exchange their shares. We find that the utility definitions are different from PD game and previous protocols. Section 4 presents the construction of rational protocol under the new utility definitions. We prove Nash equilibrium under two-party case and multi-party case, respectively. The latter case is an extension of the former one by utilizing the idea of modularization. Finally, we conclude this paper and give some future works in Sect. 5.

2 Preliminaries

2.1 Rational parties

Rational parties, neither semi-honest nor malicious, are proposed in secret sharing and multi-party computation Halpern and Teague (2004). Rational parties hope to maximize their utilities. Note that previous works about secure multi-party computation concern parties’ abilities do not mention the notion of utilities, which denote the incentives for parties to participate in protocols; that is, what is the target for rational parties to complete secure protocols. The notion of utilities considers the practical background of secure protocols. Just like people in realities, rational parties will choose actions or strategies if they bring benefits to them. Some previous works connect utilities with security properties such as correctness, privacy and fairness. Furthermore, the strategies for rational parties can be affected by utility definitions.

The incentives of rational parties can be described by utility, which is important for them since the strategies they choose depend on utilities. The strategies help them to maximize their utilities. Here, we inherit the notions in game theory to define actions and utilities for parties who participate in the protocol. Let $\varGamma =(\{P_i\}_{i=1}^n,\{A_i\}_{i=1}^n,\{u_i\}_{i=1}^n)$ denote a protocol with n parties, where $\{ P_i\}_{i=1}^n$ denotes a set with n parities and $P_i$ denotes one party. Let $\{A_i\}_{i=1}^n$ denote an action set, where the possible actions for $P_i$ is $A_i$. Let $\{u_i\}_{i=1}^n$ denote utility function, which suffices $u_i:A_1\times \cdots \times A_n\mapsto R$ . Let $A\mathop {=}\limits ^\mathrm{def}A_1\times \cdots \times A_n$ such that $\mathbf a =(a_1,\ldots ,a_n)\in A$ is an outcome of a protocol. Here outcome describes the strategy for each party after one round. The utility function $u_i$ denotes the preference of $P_i$ for a certain outcome. For example, if $P_i$ prefers a with respect to a $'$, then it can be denoted as $u_i(\mathbf a )> u_i(\mathbf a ')$. If it suffices that $u_i(\mathbf a )\ge u_i(\mathbf a ')$, we call $P_i$ weakly prefers a. Note that in SMPC protocol, action sets and utility functions are common knowledge Osborne and Rubinstein (2004).

2.2 Nash equilibrium

Suppose utility function is common knowledge, if $P_1$ knows that other parties choose $a_2,\ldots ,a_n$ then $P_1$ is sure to adopt $a_1\in A_1$ to maximize his utility. $a_1$ is called best response of $P_1$ with respect to $a_2,\ldots ,a_n$. Given $a_1$, $P_2$ will choose $a'_2 \in A_2$ and so on such that each party will choose his best response. The tuple $\mathbf a$ is called self-enforcing if $a_i$ and only if is a best response with respect to $P_i$. If one action tuple is a self-enforcing, it is called Nash equilibrium. Definition 1 gives the formal definition of Nash equilibrium Axelrod (1990).

Definition 1

(Nash equilibrium of pure strategy) Let $\varGamma =(\{P_i\}_{i=1}^n,\{A_i\}_{i=1}^n, \{u_i\}_{i=1}^n)$ denote a normal game with n parties. An action tuple $\mathbf a$ is Nash equilibrium of pure strategy, if for every i and $a'_i \in A_i$ , we have,

$$\begin{aligned} u_i(a'_i,\mathbf a _{-i})\le u_i(\mathbf a ). \end{aligned}$$

The notions defined above are fit for multi-party case. For the two-party case, let n equal to 2.

2.3 The idea of modularization

In this paper, we try to extend the two-party case to the multi-party one. The latter case is more complex than the former one. For example, some parties may collude to deviate from the protocol. Consequently, the methods in two-party case do not necessarily fit for the multi-party case. Most works discuss these two cases, respectively. We try to relate these two cases using the idea of modularization which is widely used in software systems Mitchell and Mancoridis (2006), supply relationships Gunasekaran et al. (2007), etc. The basic idea of modularization is as follows: first separate some units with similar functions, where units are called modules, then form various kinds of products by combining different modules. The process of separation and combination is called modularization. There are three characters for each module: relative independentability, interchangeability and universality.

To the best of our knowledge, the notion of universally composable (UC) security Canetti (2000), proposed by Ran Canetti, is similar to the idea of modularization. The independently designed protocols can achieve security when they are concurrently running with other similar protocols.

In UC security frame, there are altogether three kernel models: ideal model, real model and $\mathcal {F}$-hybrid model. The main technology to prove UC security is “simulation”; that is, there is no UC secure without simulation. The most important notion in simulation is indistinguishability.

Definition 2

Suppose there is an indistinguishable distribution

$$\begin{aligned} X=\{X(k,a)\}_{k\in N, a\in \{0,1\}^*}. \end{aligned}$$

That is, the probability distribution X(k, a) is an infinite set with respect to $k\in N$ and $a\in \{0,1\}^*$. Here the distribution denotes the outputs of parties or attackers, where a denotes the inputs of parties or attackers and k is the secure parameter. If one probability only considers the distribution on $\{0,1\}$, it is binary distribution. Two binary distributions X and Y are indistinguishable (denoted as $X\thickapprox Y$), if for any $c\in N$, there exits $k_0\in N$ such that

$$\begin{aligned} |Pr(X(k,a)=1)-Pr(Y(k,a)=1)|<k^{-c}, \end{aligned}$$

for any $k>k_0$ and a.

2.4 Utility defintions based on PD game

Here, following the basic idea of Halpern and Teague (2004), the basic definitions in a two-party rational protocol $\varPi =({P_1,P_2},{A_1,A_2},{u_1,u_2})$ is given. $P_1$ and $P_2$ are two rational parties. Let $A_1=A_2=\{Send, Not\; Send\}$, where Send denotes the action that party sends share to the other and $Not\; Send$ denotes the action that party does not send share to the other. Let $u_1,u_2$ denote the utility of $P_1$ and $P_2$, respectively. There are altogether four outcomes in protocol $\varPi$ according to parties’ choices.

• 1. $\mathbf a ^1=(Not\; Send, Send)$. $P_1$ does not send share to $P_2$ while $P_2$ sends share to $P_1$. $P_1$ has two shares and can learn the secret while $P_2$ can not learn the secret for lack of the other share.

• 2. $\mathbf a ^2=(Send, Send)$. Both parties send shares to the other and all of them learn the secret.

• 3. $\mathbf a ^3=(Not\; Send,Not\; Send)$. No party sends shares to the other and no one will learn the secret.

• 4. $\mathbf a ^4=(Send,Not\;Send)$. $P_1$ sends shares to $P_2$ while $P_2$ does not send shares to $P_1$. $P_2$ have two shares and can learn the secret while $P_1$ cannot learn the secret for lack of the other share.

It suffices that $u_1(\mathbf a ^1)>u_1(\mathbf a ^2) >u_1(\mathbf a ^3)>u_1(\mathbf a ^4)$ according to the assumptions mentioned in most works of rational protocols. To better illustrate the relationships among the utilities, let $u_1(\mathbf a ^1)=U^+$, $u_1( \mathbf a ^2)=U$, $u_1(\mathbf a ^3)=U^-$, $u_1(\mathbf a ^4)=U^{-}$ such that $U^+>U>U^->U^{-}$. According to the result of PD game and Halpern and Teague (2004), rational parties have no incentives to send their shares to his opponent (ref. Table 1); that is, $(Not\; send,\; Not\; send)$ is Nash equilibrium in Table 1, which is similar to that of PD game. Consequently, both parties cannot get the result of the computation.

Table 1 The utility matrix of PD game

3 New utility definitions base on incentives

In this paper, we redefine utility definition considering the incentives for rational parties. We find that our definition is different from PD game since rational parties compute their utilities according to the number of shares they get.

Supposing there are two parties, they hope to exchange one share. If one party receives one share from his opponent, he has more chance to get the result. Since the main target is to learn the result, receiving shares from other can increase their utility. Therefore, party gets one utility if he receives one share from the other. Otherwise, he gets zero. Then we give the utility definitions for two-party case.

Let $\varGamma =({P_1,P_2},{A_1,A_2},{u_1,u_2})$ denote the second stage of a rational protocol in two-party case, where parties exchange their shares according to their utilities. $P_1$ and $P_2$ are two rational parties, who hope to exchange shares with his opponent. In $\varGamma$, $P_1$ and $P_2$ have two actions $A_1$ and $A_2$, where Send denotes the action that party sends share to the other and $Not\; Send$ denotes the action that party does not send share to the other. Let $u_1,u_2$ denote the utility of $P_1$ and $P_2$, respectively. Consequently, we give the definition of $u_1,u_2$ according to whether parties can receive shares. Let $\mathbf a$ denote the action profile of the game. Because each party has two choices, there are altogether four outcomes in $\varGamma$.

• 1. $\mathbf a ^1=(Not\; Send, Send)$. $P_1$ does not send share to $P_2$ while $P_2$ sends share to $P_1$. In this case, $P_1$ gets one share and $P_2$ gets no share. So $u_1(\mathbf a ^1)=1$ and $u_2(\mathbf a ^1)=0$.

• 2. $\mathbf a ^2=(Send, Send)$. Both parties send shares to the other and all of them learn the secret. In this case, $P_1$ gets one share and $P_2$ also gets one share. So $u_1(\mathbf a ^2)=1$ and $u_2(\mathbf a ^2)=1$.

• 3. $\mathbf a ^3=(Not\; Send,Not\; Send)$. No party sends shares to the other. In this case, $P_1$ gets no share and $P_2$ gets no share. So $u_1(\mathbf a ^3)=0$ and $u_2(\mathbf a ^3)=0$.

• 4. $\mathbf a ^4=(Send,Not\;Send)$. $P_1$ sends shares to $P_2$ while $P_2$ does not send shares to $P_1$. In this case, $P_1$ gets no share and $P_2$ gets one share. So $u_1(\mathbf a ^4)=0$ and $u_2(\mathbf a ^4)=1$.

In game theory, we use utility matrix (ref. Table 2) to denote the relationship between action and utility.

Table 2 The utility matrix of this paper

In the study by Asharov et al. (2011), Asharov and coworkers give parties’ symmetric utilities, shown in Table 3. Then Groce and Katz (2012) give a more general utility function, shown in Table 4, where $b_0>a_0\ge d_0 \ge c_0$. In the work by Asharov et al. (2011), $b_0=b_1=1,a_0=a_1=d_0=d_1=0,$ and $c_0=c_1=-1$. In this paper, if we use similar notations as in the study by Groce and Katz (2012), then $a_0=c_0=1,$ and $c_0=d_0=0$. It suffices that $a_0=c_0>b_0=d_0$.

Table 3 The utility matrix of Asharov et al. (2011)

Table 4 The utility matrix of Groce and Katz (2012)

From the relationships of these parameters, we can see that our utility definitions are different from those of Asharov et al. (2011) and Groce and Katz (2012). In the study by Asharov et al. (2011), $P_1$ has the same utility $a_0=d_0$ when they learn correct and incorrect results. Therefore, their conclusion about fairness is not desirable. Groce and Katz redefine the utility such that fairness can be achieved as long as the parties have a strict incentive to compute the function in the ideal world Groce and Katz (2012).

Groce and Katz (2012) in their study set $a_0\ge d_0$ and also get positive results about fairness by setting proper the geometric distribution $\alpha$. Most previous works compute the utility according to whether they can get correct results. Since it is hard to learn the correct results in one round, researchers design rational protocols with several rounds. Rational parties cannot learn the correct answer before a fixed round and learn it after the fixed round. However, the parties cannot learn which round is the fixed round. Otherwise, they have no incentives to exchange their shares before it. Therefore, most works choose the fixed round according to certain distribution like geometric distribution. The introduction of certain distribution can effectively circumvent premature aborting if parties hope to learn the correct answer. However, on the other hand, the certain distribution also leads to rational protocols with multiple rounds, which affect the round complexity. Consequently, new methods should be introduced to reduce the round complexity.

In this paper, we set $a_0$ strictly bigger than $d_0$ since the utility is defined according to the number of shares they get from others. In addition, it suffices that $c_0\ge d_0$, which means that party gets larger utility when he obtains more shares.

According to the definitions of Nash equilibrium and utilities in Table 2, (Send, Send) is Nash equilibrium in this paper. Note that in the study by Asharov et al. (2011) and Groce and Katz (2012), (Incorrect, Incorrect) is Nash equilibrium. The differences of equilibriums lead to different strategies in these works. In the work by Asharov et al. (2011) and Groce and Katz (2012), parties may choose strategies corresponding to Incorrect, while in our work, parties may choose strategies corresponding to Send. If both parties choose Send in one round, they will both get one share from the other party. Consequently, they will learn the correct result in this current round; that is, there is no need to set geometric distribution and multiple rounds for rational protocols since the exchanging can be completed in one round.

For a general secure computing protocol, we should also consider the achievements of privacy and correctness except for fairness. Recall that the protocol consists of two stages such as Asharov et al. (2011) and Groce and Katz (2012). The properties of privacy, correctness and fairness can be guaranteed in the first stage due to the existence of TTP. More specifically, parties send their private inputs to TTP, who computes the result. This guarantees privacy and correctness since TTP is a third trusted party. Then TTP assign shares to each party, which guarantees fairness. In the second stage, all these properties can still be guaranteed for reasons given below.

• 1. Privacy can be guaranteed since shares do not include any information about their inputs.

• 2. Correctness is guaranteed since the shares are computed and assigned by TTP. However, we follow the works of Groce and Katz (2012) to apply a message-authentication code (MAC) on each share such that fake shares can be detected. We omit the processes of addition and verification in our protocols for simplicity. Therefore, parties cannot send incorrect shares. Consequently they can learn correct result once they reconstruct the result.

• 3. Fairness means that both parties learn the result or not. In fact, we hope that both parties learn the result. Generally, fairness can be guaranteed by Nash equilibrium; that is, if (Send, Send) is Nash equilibrium, both parties get enough shares to reconstruct and learn the result.

4 Fairness in rational computing protocols

In this section, we present rational computing protocols in two-party case and multi-party case, respectively. The latter case is an extension of the former case. Note that we only consider the extension of Nash equilibrium from two-party case to multi-party case. However, it is not necessarily mean privacy and correctness are not considered in protocols. As mentioned in Sect. 3, privacy and correctness are guaranteed by TTP and MAC in both stages. So, we do not particularly mention the realization in this part and emphasis the realization of fairness.

4.1 Two-party case

In this paper, our rational two-party computation is a hybrid protocol, denoted as $\pi ^{fair}$. It consists of two stages, where the first stage is the functionality ShareGen and the second stage includes several iterations just like the protocol in Groce and Katz (2012). The first stage includes a TTP. The second stage is a protocol $\pi$ which consists of three phases: initial phase, exchange phase and output phase.

The first stage functionality ShareGen:

• 1. Inputs: ShareGen takes as input values $x_i$ from $P_i,i\in \{1,2\}$. If either input is of no vail, then ShareGen returns $\bot$ to parties.

• 2. Computation: TTP computes $f(x_1,x_2)$ and chooses random shares s and t such that $s\bigoplus t=f(x_1,x_2)$.

• 3. Outputs: Send s to $P_1$, and t to $P_2$.

The second stage protocol $\pi$:

• 1. Initial phase: Parties run the functionality ShareGen using their inputs $x_1$ and $x_2$. $P_1$ receives s and $P_2$ receives t.

• 2. Exchange phase: In exchange phase, two rational parties exchange their shares following definition of the second stage protocol (ref. Sect. 3) $\varGamma =({P_1,P_2},{A_1,A_2},{u_1,u_2})$. The strategies and their utility definitions are given in Table 2.

From the construction of the rational protocol, parties will send their shares to the other party since (Send,  Send) is Nash equilibrium in the exchange phase. Therefore, each party has incentives to send shares to his opponent. In the two-party case, both parties have incentives to exchange their shares with the other. Therefore, fairness can be guaranteed under this case. As mentioned in the last part in Sect. 3, privacy and correctness can also be guaranteed by TTP and MAC.

Fig. 1

The structure of protocol with multiple parties

Note that, in this paper, we only adopt a very simple share scheme, where each party only receive one share from TTP in the first stage. In fact, we can use more complex sharing scheme like Shamir secret sharing scheme Shamir (1979). We will consider more complex and secure sharing schemes in our future works to get perfect incentive-driving protocols.

4.2 Multi-party case

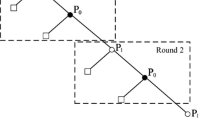
In this section, we mainly discuss the realization of fairness based on the conclusion of two-party case since we know that fairness can be achieved in two-party case. More specifically, we extend multi-party case based on two-party case by utilizing the basic idea of modularization. It is described as follows. The protocol with multiple parties firstly is divided into several sub-protocols, which consist of only two parties. Then design secure solutions for these two-party sub-protocols. Finally, discuss the strategy choices for multiple parties based on the existing result in two-party case. We give a simple example for multi-party case by modularization (shown in Fig. 1).

Suppose there are five parties $P_m$, $P_n$, $P_i$, $P_j$ and $P_k$. Two parties (like $P_m$, $P_n$ ) are connected by lines (either solid or dotted ones) if they execute two-party computing protocol. $\pi ^{fair}_{multi}$ can be divided into two sub-protocols $(\pi ^{fair}_{multi})_n$ and $(\pi ^{fair}_{multi})_i$. Since $P_n$ and $P_i$ have two neighbors $P_m$, $P_j$ and $P_k$, $P_j$, respectively, there are altogether four two-party computing protocols $\pi ^{fair}_{nm}$, $\pi ^{fair}_{nj}$, $\pi ^{fair}_{ij}$ and $\pi ^{fair}_{ik}$. In fact, here each of these two-party computing protocols are corresponding to $\pi ^{fair}$.

The security for rational two-party protocol $\pi ^{fair}$ is discussed in Sect. 4.1. In this section, we will continue to discuss the security for rational multi-party protocol. Here we borrow the notion of modularization. We assume that these parties in rational multi-party protocol construct one network. Two parties are connected, called neighbors, if they participate in two-party computing protocol. Each pair of neighbors run the two-party protocol $\pi ^{fair}$ (ref. Sect. 4.1). If $P_i$ and $P_j$ are neighbors, we denote $\pi ^{fair}_{ij}$ as the protocol $\pi ^{fair}$ between $P_i$ and $P_j$. Consequently, there are several $\pi ^{fair}_{ij}$ instances in the network. For the whole network, the rational multi-party protocol is denoted as $\pi ^{fair}_{multi}$. Each party $P_i$ in the network run an instance of this protocol denoted as $(\pi ^{fair}_{multi})_i$. Suppose each party $P_i$ has several neighbors denoted as $P_j$, then each pair of run $\pi ^{fair}_{ij}$. This process is presented in Fig. 2. Here there are altogether four levels.

• 1. In level one, each party may participate in a two-party protocol $\pi ^{fair}$.

• 2. In level two, each pair of neighbors (wlog. $P_i$ and $P_j$) may participate in the two-party protocol $\pi ^{fair}_{ij}$.

• 3. In level three, each party (wlog. $P_i$) runs $(\pi ^{fair}_{multi})_i$, which consists of several sub-protocols $\pi ^{fair}_{ij}$. Recall that $P_j$ is the neighbor of $P_i$.

• 4. In level four, $\pi ^{fair}_{multi}$ is executed by all parties in the network.

Fig. 2

Four levels of the protocol in multi-party case

From the structure of Fig. 2, it is clear that the protocol $\pi ^{fair}_{multi}$ can be divided into several sub-protocols $(\pi ^{fair}_{multi})_i$. These sub-protocols are two-party computing protocols, denoted as $\pi ^{fair}_{ij}$, where $P_i$ and $P_j$ are neighbors. As mentioned in Sect. 4.1 the two-party computing protocol is noted as $\pi ^{fair}$ for each party. So we decompose the multi-party protocol into several two-party protocols by utilizing the idea of modularization. Note that each sub-protocol has similar structures and properties except for the participants. Consequently, we will analyze the equilibrium of protocol $\pi ^{fair}_{multi}$ in a bottom-up way.

We prove that (Send, Send) is Nash equilibrium in $\pi ^{fair}$, which means that each party will take the action Send in $\pi ^{fair}$. So (Send, Send) is Nash equilibrium in $\pi ^{fair}_{ij}$ for $P_i$ and $P_j$. Since each party in the network takes Send, $(Send,\ldots , Send)$ is Nash equilibrium in $(\pi ^{fair}_{multi})_i$. Therefore, each party in the multi-party computing protocol will adopt Send. Consequently, we can achieve fairness in $\pi ^{fair}_{multi}$. The properties of privacy and correctness can be guaranteed by the existence of TTP and usage of MAC just like two-party case.

As we mentioned above, UC model discusses security of protocol according to the indistinguishability of ideal and real model. Generally, security level in UC model is higher than that in other formal models. However, we do not strictly follow the basic idea of UC model in this paper and leave it in the future works.

Note that in this paper, parties in the multi-party case still execute two-party computing protocol. The difference is that in two-party case, only one pair of parties execute the two-party protocol. While in multi-party case, several pairs execute the two-party protocols. Therefore, we do not discuss multi-party computing protocols, where each party contributes his private input and computes one functionality. Instead, we divide parties into several pairs, each of which run two-party computing protocol; that is, we discuss computing protocols in the presence of multiple parties, who compute binary function instead of multivariate function. In the future works, we will discuss how to achieve security properties in multivariate function like fairness in the presence of multiple parties.

5 Conclusions and future works

Rational parties are proposed to realize fairness in two-party computations. The main target is how to encourage both to send shares to the other. Previous works consider to use PD game describing the progress of exchanging shares and reach lots of positive results. However, little works consider the incentives for rational parties why they send shares to the other. This paper constructs a new incentive-driving game based on incentives and redefine their utilities accordingly. We prove that rational parties in our protocol both have incentives to send shares to their opponents. This opens a new way to study the achievements of fairness in rational protocols.

Although we mentioned UC model in Sect. 2, we do not prove the security under it. The reason is that, we only consider the extension of fairness from two-party case to multi-party case. In the future works, we will follow the traditional way to prove security under UC model, where exist an ideal world and real world. Furthermore, we will consider the realization of privacy, correctness and fairness at the same time in one rational computing protocol.