1 Introduction

The output feedback stabilization of single-input-single-output (SISO) one-dimensional linear hyperbolic systems is a subject that has been widely studied in the scientific literature since the nineties when both actuation and sensing are located at the boundaries. In the case where the control input and the measured output are co-located at the same boundary, the problem is now relatively well understood and has given rise to numerous publications, both in the linear case [1, 3] and in the nonlinear case [5, 13], in particular in fluid mechanics for Saint-Venant equations [5, 10, 16] or Euler equations [14], to name just a few of the many publications on the subject.

In contrast, when the actuator acts through one boundary, whereas the sensor is placed at the other boundary, the output feedback stabilization problem can become much more complicated and remains largely unexplored in the literature. As Krstic et al. pointed out in [18], the difficulty arises from the fact that “the input–output operator is no longer passive (...) which precludes the application of simple controllers”. Anti-located sensing and actuation requires to use dynamic compensators that include delayed values of the output (directly or through state observers). A meaningful example is the output feedback stabilization of a simple unstable wave equation addressed in [18] using a separation principle that combines a state feedback control with a state observer. This approach is extended to the adaptive stabilization of more general linear hyperbolic systems with unknown parameters in [2, 7]. Recently, an experimental application to the control of hydraulic waves is reported in [23], where the actuation is provided by a moving boundary, while the water level is measured at the other boundary.

We can also mention references [4, 17] which deal with MIMO systems with anti-located multivariable sensors and actuators for \(n \times n\) linear hyperbolic systems expressed in a characteristic form having a very specific input/output structure.

It is important to note that the use of control laws containing delayed output feedback or state observers can, however, prove to be problematic because it can be strongly sensitive to uncertainties on the characteristic velocities of the plant model [8, 12, 20]. This happens when the control design relies on a (supposed) exact knowledge of some characteristic velocities that must be exactly compensated in the control law such that the stability can be destroyed by arbitrarily small modelling uncertainties.

In this paper, our purpose is to highlight some features of this problem by addressing the feedback stabilization of an unstable open-loop system which is made up of two interconnected transport equations and provided with anti-located boundary sensing and actuation.

Our paper is organized as follows. The control problem is described in Sect. 2. It is first shown that the considered control system is open loop unstable and cannot be stabilized by a simple proportional output feedback. Then, it is shown that the system can be stabilized by a dynamic controller that involves a delayed output feedback. However, this control turns out not to be robust with respect to delay uncertainties precisely because the control requires a (utopian) exact knowledge of the transport velocity.

The main contribution of this paper is to show that the robustness of the control against delay uncertainties is recovered as soon as an arbitrary small diffusion is present in the system. For that purpose, in Sect. 3, it is first assumed that the considered plant is subject to a slight phenomenon of diffusion, interpreted as a viscosity and the corresponding (unstable) input–output transfer function is computed. Then, in Sects. 4 and 5, we show that the dynamic output (non-robust) feedback designed for the inviscid case also stabilizes exponentially the viscous system when the (unknown) diffusion is small, and that, in this case, the control proves to be perfectly robust, even if the diffusion is almost negligible. Interestingly, an upper bound on the decay rate appears when adding a small viscosity, and this upper bound is uniform with respect to the diffusion parameter \(\eta \) when it is small, while for the unperturbed system with \(\eta =0\) the decay rate is infinite (the system is finite-time stable).

Our analysis in Sects. 4 and 5 also reveals that the effect of diffusion on stability is far from being an obvious issue, contrary to what one might expect. It is indeed well known that, in hyperbolic systems, the presence of diffusion (or friction) can have a destabilizing as well as a stabilizing effect (see, for instance, the references [11, 22]). This issue is further discussed in Sect. 6 where we present an example of another simple hyperbolic system which simplifies the previous case and for which, however, the same diffusion term destroys the stability instead of strengthening it.

Some final conclusions are given in Sect. 7.

2 Description of the control problem

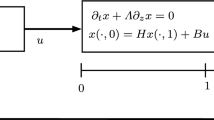
We consider the open-loop control system represented in Fig. 1. The system is made up of the positive feedback interconnection of two identical transport systems. The system dynamics are described in the time domain by the following equations:

$$\begin{aligned}{} & {} \partial _t y_1(t,x) + \upsilon \partial _x y_1(t,x) = 0, \end{aligned}$$
(1a)
$$\begin{aligned}{} & {} \partial _t y_2(t,x) + \upsilon \partial _x y_2(t,x) = 0, \end{aligned}$$
(1b)
$$\begin{aligned}{} & {} y_1(t,0) = y_2(t,1) + U(t), \end{aligned}$$
(1c)
$$\begin{aligned}{} & {} y_2(t,0) = y_1(t,1), \end{aligned}$$
(1d)
$$\begin{aligned}{} & {} Y(t) = y_1(t,1). \end{aligned}$$
(1e)

where U(t) is the control input and Y(t) is the measurable output. In the classical pure transport equations (1a) and (1b), the parameter \(\upsilon > 0\) denotes the transport velocity.

Fig. 1
figure 1

The structure of the open-loop control system considered in this paper

Full size image

In the frequency domain, it is well known that the transfer function of the transport systems (1a) and (1b) is

$$\begin{aligned} f_o(s) = e^{-s\tau } \qquad \text {with the time delay} \qquad \tau = \dfrac{1}{\upsilon }, \end{aligned}$$
(2)

where s denotes the Laplace complex variable.

It follows that the overall input–output transfer function of the open-loop system (1) is

$$\begin{aligned} G(s) = \dfrac{\text {Y}(s)}{\text {U}(s)} = \dfrac{f_o(s)}{1 - f_o^2(s)} = \dfrac{e^{s\tau }}{e^{2s\tau } - 1}, \end{aligned}$$
(3)

where \(\text {Y}(s)\) and \(\text {U}(s)\) denote the Laplace transforms of the output Y(t) and the input U(t), respectively.

The poles of the system are the roots of the characteristic equation

$$\begin{aligned} e^{2s\tau } - 1 = 0. \end{aligned}$$
(4)

This open-loop control system is clearly not asymptotically stable since all the poles are located on the imaginary axis.

In order to illustrate the challenge that arises when actuation and sensing are anti-located, we shall first show that, despite its apparent simplicity, this unstable system cannot be stabilized with a simple proportional output feedback, i.e. with a static proportional controller of the form

$$\begin{aligned} U(t) = - 2k_p Y(t) \end{aligned}$$
(5)

where \(k_p \ne 0\) is a control tuning parameter.

In the frequency domain, for the system (3) with the control law (5) the characteristic equation of the closed-loop system is:

$$\begin{aligned} e^{2s\tau } + 2k_pe^{s\tau } - 1 = 0. \end{aligned}$$
(6)

Solving this equation for \(e^{s\tau }\), we get

$$\begin{aligned} e^{s\tau } = -k_p \pm \sqrt{1 + k_p^2}. \end{aligned}$$
(7)

Then, for any \(k_p \ne 0\) there is an infinity of system poles \(\sigma + i\omega \) lying on two vertical lines with real parts:

$$\begin{aligned}{} & {} \sigma = \upsilon \ln \left( \sqrt{1 + k_p^2} + |k_p| \right) > 0 \nonumber \\{} & {} \quad \text {and} \quad \sigma = \upsilon \ln \left( \sqrt{1 + k_p^2} - |k_p| \right) < 0. \end{aligned}$$
(8)

It follows that the unstable system (3) cannot be stabilized with the static controller (5).

Let us now show that the system can actually be stabilized by a dynamic controller that involves a delayed output feedback.

From (3), it follows that the input–output dynamics of the system (1) in the time domain can alternatively be represented by the delay-difference equation

$$\begin{aligned} Y(t) - Y(t-2\tau ) = U(t-\tau ). \end{aligned}$$
(9)

A simple and natural candidate for a stabilizing feedback control law is then

$$\begin{aligned} U(t) = -2k_1 Y(t) - k_2Y(t-\tau ) \end{aligned}$$
(10)

where \(k_1\) and \(k_2\) are control tuning parameters. With this control law, the closed-loop dynamics are

$$\begin{aligned} Y(t) + 2k_1 Y(t-\tau ) + (k_2 - 1)Y(t-2\tau ) = 0. \end{aligned}$$
(11)

Clearly, we can conclude that the controller (10) exponentially stabilizes the system (1) if the tuning parameters \(k_1\) and \(k_2\) are selected such that the roots of the polynomial

$$\begin{aligned} w^2 + 2k_1 w + (k_2 - 1) \end{aligned}$$
(12)

are located inside the unit circle. However, this should be considered with caution because it is well known that boundary feedback stabilization of hyperbolic systems with delayed control may be sensitive to delay modelling errors (see e.g. [20]). To clarify this point we consider the time domain representation of the dynamical control law (10) defined as

$$\begin{aligned}{} & {} \partial _t {\hat{y}}_2(t,x) + \upsilon \partial _x {\hat{y}}_2(t,x) = 0,\nonumber \\{} & {} {\hat{y}}_{2}(t,0)= y_{1}(t,1), \end{aligned}$$
(13)
$$\begin{aligned}{} & {} U(t) = -2 k_1 y_1(t,1) - k_2 {\hat{y}}_2(t,1), \end{aligned}$$
(14)

where the transport equation (13) with transport velocity \(\upsilon = 1/\tau \) is equivalent to the time delay \(\tau \) of the control law (10). With this definition, the closed-loop system (1), (13), (14) is then represented as follows:

$$\begin{aligned}{} & {} \partial _t y_1(t,x) + \upsilon \partial _x y_1(t,x)= 0, \end{aligned}$$
(15a)
$$\begin{aligned}{} & {} \partial _t y_2(t,x) + \upsilon \partial _x y_2(t,x) = 0, \end{aligned}$$
(15b)
$$\begin{aligned}{} & {} \partial _t {\hat{y}}_2(t,x) + \upsilon \partial _x {\hat{y}}_2(t,x) = 0, \end{aligned}$$
(15c)
$$\begin{aligned}{} & {} \begin{pmatrix} y_1(t,0) \\ y_2(t,0) \\ {\hat{y}}_2(t,0) \end{pmatrix} = \underbrace{\begin{pmatrix} -2k_1 &{} 1 &{} - k_2 \\ 1 &{} 0 &{} 0 \\ \ 1 &{} 0 &{} 0 \end{pmatrix}}_{\displaystyle {\textbf{K}}}\begin{pmatrix} y_1(t,1) \\ y_2(t,1) \\ {\hat{y}}_2(t,1) \end{pmatrix}. \end{aligned}$$
(15d)

Now, as proved in Appendix A, for the matrix \({\textbf{K}}\) defined in (15d), it can be shown that

$$\begin{aligned} \bar{\rho }({\textbf{K}}) = |k_1| + \sqrt{1 + k_1^2 + |k_2|} \; \geqslant 1 \qquad \text {for all } (k_1, k_2)\in \mathbb {R}^{2}, \end{aligned}$$
(16)

where \(\bar{\rho }({\textbf{K}})\) is defined as follows:

$$\begin{aligned} \bar{\rho }({\textbf{K}}) :=\max \left\{ \rho (\text {diag}\!\left\{ e^{-i\theta _1}, e^{-i\theta _2}, e^{-i\theta _3}\right\} {\textbf{K}}) ; (\theta _1, \theta _2 , \theta _3)^{\! {\textsf{T}}} \in \mathbb {R}^3 \right\} , \end{aligned}$$
(17)

\(\rho (M)\) denoting the spectral radius of the matrix M. By [21] (see also [15, Chapter 9, Theorem 6.1] and [5, Chapter 3]), we know that \(\bar{\rho }({\textbf{K}}) < 1\) is a necessary (and sufficient) condition to have a stability which is robust against small uncertainties in the characteristic velocities. Although the ideal closed-loop system (15) is exponentially stable (with all the poles strictly located in the left half complex plane provided \(k_{1}\) and \(k_{2}\) are chosen accordingly), the stability can be destroyed by an arbitrarily small difference in characteristic velocities between the plant equations (15a), (15b) and the controller equation (15c). More precisely, if we assume that the physical transport velocities are \(\upsilon + \varepsilon _1\), \(\upsilon + \varepsilon _2\) with \(\varepsilon _1, \varepsilon _2\) representing uncertainties in the plant equations (15a), (15b) rewritten as follows:

$$\begin{aligned}{} & {} \partial _t y_1(t,x) + (\upsilon + \varepsilon _1) \partial _x y_1(t,x)= 0, \end{aligned}$$
(18a)
$$\begin{aligned}{} & {} \partial _t y_2(t,x) + (\upsilon + \varepsilon _2) \partial _x y_2(t,x) = 0, \end{aligned}$$
(18b)

then the closed-loop system (15) with (15a), (15b) replaced by (18a), (18b) may become unstable, with poles moving to the right half complex plane even for arbitrarily small \(\varepsilon _i\) perturbations.

Should this necessarily mean that the control law (10) with delayed feedback could not be applied in practice? Our objective, in this paper, is exactly to prove the opposite! Indeed, our main contribution will be to show that, even with the simple control law (10), the robustness of the output feedback stabilization against delay uncertainties can be recovered as soon as an arbitrary small diffusion is present in the system. Our analysis will also reveal, however, that the effect on stability of adding an arbitrarily small diffusion is far from obvious, contrary to what one might expect. Indeed, while diffusion strengthens the robustness of the exponential stability for the \(2\times 2\) problem (18), it can also destroy the stability of similar simpler systems as we will see in Sect. 6.

We shall consider the special case of a dead beat control where \(k_1 = 0\) and \(k_2 = 1\). In that case the characteristic equation of the closed-loop inviscid system reduces to \(e^{2s\tau } = 0\), meaning that all the poles of the system have negative real parts that are moved off to infinity. However, for that system we have

$$\begin{aligned} \bar{\rho }({\textbf{K}}) = \sqrt{2} \end{aligned}$$
(19)

showing a strict lack of robustness of the control w.r.t. delay inaccuracy.

3 The open-loop control system with diffusion

We consider again a control system as represented in Fig. 1. However, we assume here that the two transport systems are subject to a slight phenomenon of diffusion. The system is therefore made up of the feedback interconnection of two identical transport systems that are perturbed by a diffusion term which can be interpreted, for example, as a viscosity in the case of a fluid. For simplicity and without loss of generality, we assume a unit nominal transport velocity \(\upsilon = 1\). The dynamics of the open-loop control system are therefore described in the time domain by the following equations:

$$\begin{aligned}{} & {} \partial _t y_1(t,x) + \partial _x y_1(t,x) - \eta \partial ^2_{xx} y_1(t,x) = 0, \end{aligned}$$
(20a)
$$\begin{aligned}{} & {} \partial _t y_2(t,x) + \partial _x y_2(t,x) - \eta \partial ^2_{xx} y_2(t,x) = 0, \end{aligned}$$
(20b)
$$\begin{aligned}{} & {} y_1(t,0) = y_2(t,1) + U(t), \end{aligned}$$
(20c)
$$\begin{aligned}{} & {} y_2(t,0) = y_1(t,1), \end{aligned}$$
(20d)
$$\begin{aligned}{} & {} \partial _x y_1(t,1) = \partial _x y_2(t,1) = 0 \end{aligned}$$
(20e)
$$\begin{aligned}{} & {} Y(t) = y_1(t,1). \end{aligned}$$
(20f)

As above U(t) is the control input and Y(t) is the measurable output, while \(\eta > 0\) is the viscosity coefficient.

In the frequency domain, with \(\text {y}_{\!1}(s,x)\) and \(\text {y}_{2}(s,x)\) denoting the Laplace transforms of \(y_{1}(t,x)\) and \(y_{2}(t,x)\), the system is written

$$\begin{aligned}{} & {} s\text {y}_{\!1}(s,x) + \partial _x \text {y}_{\!1}(s,x) - \eta \partial ^2_{xx} \text {y}_{\!1}(s,x) = 0, \end{aligned}$$
(21a)
$$\begin{aligned}{} & {} s\text {y}_2(s,x) + \partial _x \text {y}_2(s,x) - \eta \partial ^2_{xx} \text {y}_2(s,x) = 0, \end{aligned}$$
(21b)
$$\begin{aligned}{} & {} \text {y}_{\!1}(s,0) = \text {y}_2(s,1) + \text {U}(s), \end{aligned}$$
(21c)
$$\begin{aligned}{} & {} \text {y}_2(s,0) = \text {y}_{\!1}(s,1), \end{aligned}$$
(21d)
$$\begin{aligned}{} & {} \partial _x \text {y}_{\!1}(s,1) = \partial _x \text {y}_2(s,1) = 0 \end{aligned}$$
(21e)
$$\begin{aligned}{} & {} \text {Y}(s) = \text {y}_{\!1}(s,1). \end{aligned}$$
(21f)

For any value of s, the solutions of the differential equations (21a), (21b) are written

$$\begin{aligned} \text {y}_i(s,x)= A_i(s) e^{\lambda _1(s)x} + B_i(s) e^{\lambda _2(s)x}, \qquad i= 1,2, \end{aligned}$$
(22)

where \(\lambda _1(s)\), \(\lambda _2(s)\) are the roots of the polynomial

$$\begin{aligned} \eta \lambda ^2 - \lambda - s = 0, \end{aligned}$$
(23)

which implies that

$$\begin{aligned} \lambda _1(s) = \dfrac{1 +\sqrt{1 + 4 \eta s}}{2\eta }, \qquad \lambda _2(s) = \dfrac{1 -\sqrt{1 + 4 \eta s}}{2\eta }. \end{aligned}$$
(24)

In (24) and in the following \(\sqrt{\cdot }\) denotes the principal value of the square root, which is well defined except when \(1 + 4 \eta s\in \mathbb {R}_{-}\); however this particular case implies that s is real and \(s\le -1/4\eta \) and therefore is negative and converges to \(-\infty \) when \(\eta \rightarrow 0^{+}\). We will see later on that this case can be considered separately. Using the solution (22) and the boundary condition (21e), we have for each \(i=1,2\),

$$\begin{aligned}{} & {} A_i(s) + B_i(s) = \text {y}_i(s,0), \end{aligned}$$
(25)
$$\begin{aligned}{} & {} \lambda _1(s)A_i(s)e^{\lambda _1(s)} + \lambda _2(s)B_i(s)e^{\lambda _2(s)} = 0, \end{aligned}$$
(26)
$$\begin{aligned}{} & {} \text {y}_i(s,1) = A_{i}(s)e^{\lambda _1(s)} + B_{i}(s)e^{\lambda _2(s)}. \end{aligned}$$
(27)

Eliminating \(A_i(s)\) and \(B_i(s)\) between these three equations, we get the transfer function \(f_\eta (s)\) of each viscous transport system:

$$\begin{aligned} f_\eta (s) = \dfrac{\text {y}_i(s,1)}{\text {y}_i(s,0)} = \dfrac{\lambda _1(s) - \lambda _2(s)}{\lambda _1(s) e^{-\lambda _2(s)} - \lambda _2(s) e^{-\lambda _1(s)}}. \end{aligned}$$
(28)

Remark that in the notation \(f_\eta \), we use a subscript to emphasize the dependency on the viscosity parameter \(\eta \). Remark also that in the limit, in the absence of a viscosity term (i.e. \(\eta =0\)), we recover the transfer function (2): \(f_o(s) = e^{-s\tau }\).

It follows that the system (21) is equivalent to:

$$\begin{aligned} \text {y}_{\!1}(s,1)= & {} f_\eta (s) \text {y}_{\!1}(s,0), \end{aligned}$$
(29a)
$$\begin{aligned} \text {y}_2(s,1)= & {} f_\eta (s) \text {y}_2(s,0), \end{aligned}$$
(29b)
$$\begin{aligned} \text {y}_{\!1}(s,0)= & {} \text {y}_2(s,1) + \text {U}(s), \end{aligned}$$
(29c)
$$\begin{aligned} \text {y}_2(s,0)= & {} \text {y}_{\!1}(s,1), \end{aligned}$$
(29d)
$$\begin{aligned} \text {Y}(s)= & {} \text {y}_{\!1}(s,1). \end{aligned}$$
(29e)

Eliminating \(\text {y}_i(s,0), \text {y}_i(s,1), (i=1,2),\) between these equations, we get that the overall input–output transfer function of the open-loop system (20) is

$$\begin{aligned} G(s) = \dfrac{\text {Y}(s)}{\text {U}(s)} = \dfrac{f_\eta (s)}{1 - f_\eta ^2(s)}. \end{aligned}$$
(30)

The poles of the system are the roots of the characteristic equation

$$\begin{aligned} f_\eta ^2(s) - 1 = 0. \end{aligned}$$
(31)

In particular, it can be checked that \(f_\eta (0) = 1\) for all \(\eta \ne 0\), which means that there is a pole at the origin. Therefore, as in the inviscid case, the open-loop system (20) is not asymptotically stable whatever the value of the viscosity \(\eta \). As a matter of illustration, in Fig. 2, we present the spectrum of the system for \(\eta = 0.1\).

Fig. 2
figure 2

The spectrum of the open-loop system with viscosity \(\eta = 0.1\)

Full size image

In the next section, we shall show that the system can be stabilized by output feedback when the (unknown) viscosity is small and even almost negligible.

4 Output feedback stabilization of the viscous system

We now assume that the open-loop control system (20) is closed with a dead beat output feedback controller

$$\begin{aligned} U(t) = - Y(t- 1). \end{aligned}$$
(32)

Note that this corresponds to the special case of the controller (10) where \(k_1=0\), \(k_2=1\) and \(\tau = 1/\upsilon = 1\). We know from Sect. 2 that, in this case, the inviscid system is exponentially stable, but the stability is not robust to small perturbations in the propagation speeds. We shall show here that the exponential stability remains in the viscous system, and we shall check in Sect. 5 that, in addition, the exponential stability is robust with small variations in the propagation speeds. In the frequency domain, the closed-loop system (20), (32) is then:

$$\begin{aligned}{} & {} \text {y}_{\!1}(s,1) = f_\eta (s) \text {y}_{\!1}(s,0), \end{aligned}$$
(33a)
$$\begin{aligned}{} & {} \text {y}_2(s,1) = f_\eta (s) \text {y}_2(s,0), \end{aligned}$$
(33b)
$$\begin{aligned}{} & {} {\hat{\text {y}}}_2(s,1) = e^{-s} {\hat{\text {y}}}_2(s,0) \end{aligned}$$
(33c)
$$\begin{aligned}{} & {} \text {y}_{\!1}(s,0) = \text {y}_2(s,1) - {\hat{\text {y}}}_2(s,1), \end{aligned}$$
(33d)
$$\begin{aligned}{} & {} \text {y}_2(s,0) = \text {y}_{\!1}(s,1), \end{aligned}$$
(33e)
$$\begin{aligned}{} & {} {\hat{\text {y}}}_2(s,0) = \text {y}_{\!1}(s,1), \end{aligned}$$
(33f)

From these equations, it follows that the characteristic equation of the closed-loop system is:

$$\begin{aligned} f_\eta ^2(s) - f_\eta (s)e^{-s} - 1 = 0. \end{aligned}$$
(34)

Our purpose is now to address the stability of this closed-loop system. For a given value of the viscosity \(\eta \), the spectrum \(\mathcal {S}_\eta \) of the closed-loop system is the set of the poles which are the roots of the characteristic equation (34):

$$\begin{aligned} \mathcal {S}_\eta = \{ s : f_\eta ^2(s) - f_\eta (s)e^{-s} - 1 = 0\}. \end{aligned}$$
(35)

Moreover, the maximal spectral abscissa is defined as the supremum of the real parts of the spectrum and denoted as follows:

$$\begin{aligned} \sigma _\eta = \sup \{\textrm{Re}(s) : s \in \mathcal {S}_\eta \}. \end{aligned}$$
(36)

As a matter of illustration, we present in Fig. 3 the spectrum of the closed-loop system for \(\eta = 0.1\).

Fig. 3
figure 3

The spectrum \(\mathcal {S}_\eta \) of the closed-loop system for \(\eta = 0.1\)

Full size image

The stability of the closed-loop system (33) can be deduced using the spectral mapping theorem. See [15, Chapter 9, Theorem 3.5] and [19] in the case \(\eta =0\), and reference [6] for the case \(\eta \ne 0\). In particular the system is exponentially stable if (and only if) \(\sigma _\eta < 0\).

Then, one of the main results of this paper is given in the following stability theorem.

Theorem 1

For any \(\delta > 0\), there exists \(\eta _{1}>0\) such that, for all \(\eta \in (0,\eta _{1})\), the maximal spectral abscissa satisfies

$$\begin{aligned} \sigma _\eta \leqslant -\ln (2) + \delta . \end{aligned}$$
(37)

\(\square \)

Conjecture 1

The bound \(\ln (2)\) on the decay rate is optimal. More precisely, for any \(\delta > 0\) and \(\eta _{1}>0\) there exists \(\eta \in (0,\eta _{1})\) such that the maximal abscissa satisfies

$$\begin{aligned} -\ln (2) - \delta \leqslant \sigma _\eta \leqslant -\ln (2) + \delta . \end{aligned}$$
(38)

\(\square \)

Remark 1

(Loss of continuity of the spectral abscissa) Conjecture 1 seems to be verified when looking at the spectrum numerically (see Fig. 4). This would imply a loss of continuity in the sense that any decay rate is achievable when \(\eta =0\). However, there is a bound \(\ln (2)\) as soon as \(\eta >0\), even if \(\eta \) is arbitrarily small.

In order to prove Theorem 1, it is useful to define the complex variable

$$\begin{aligned} z = \sqrt{1 + 4\eta s}, \end{aligned}$$
(39)

where we recall that \(\sqrt{\cdot }\) is the principal value of the square root. The functions \(\lambda _1\) and \(\lambda _2\) become

$$\begin{aligned} \lambda _1 = \dfrac{(1 + z)}{2\eta } \qquad \text {and} \qquad \lambda _2 = \dfrac{(1 - z)}{2\eta }. \end{aligned}$$
(40)

Then, defining the function

$$\begin{aligned} X_\eta (z) = \dfrac{1+z}{2} e^{-(1-z)/2\eta } - \dfrac{1-z}{2} e^{-(1+z)/2\eta }, \end{aligned}$$
(41)

we get, using (28), that the characteristic equation (34) is equivalent to

$$\begin{aligned} X^2_\eta (z) + ze^{-(z^2 - 1)/4\eta }X_\eta (z) - z^2 = 0. \end{aligned}$$
(42)

Let us now observe that \(X_\eta (0) = 0\). Consequently \(z = 0\) is a root of equation (42) for all \(\eta \). This implies obviously that \(s = -1/4\eta \in \mathcal {S}_\eta \) is a pole of the system (i.e. a root of the characteristic equation (34)). Note that this pole tends to \(-\infty \) as \(\eta \rightarrow 0^{+}\) so this is a very stable pole for small (positive) \(\eta \).

Let \(\mathcal {Z}_\eta \) denote the set of nonzero roots of equation (42). Then, using definition (41) and solving equation (42) with respect to \(X_\eta \), we have that every \(z \in \mathcal {Z}_\eta \) satisfies the equation

$$\begin{aligned} \dfrac{(1+z)}{z} e^{-(1-z)/2\eta } - \dfrac{(1-z)}{z} e^{-(1+z)/2\eta } = -e^{-(z^2-1)/4\eta } \pm \sqrt{e^{-(z^2-1)/2\eta } + 4}. \end{aligned}$$
(43)

We now consider a sequence

$$\begin{aligned} (\eta _n)_{n \in \mathbb {N}} \qquad \text {with} \qquad 0 < \eta _n \in \mathbb {R}, \; \forall n \in \mathbb {N}\qquad \text {and} \qquad \lim _{n \rightarrow +\infty } \eta _n = 0^+, \end{aligned}$$
(44)

and an associated sequence

$$\begin{aligned} (s_n)_{n \in \mathbb {N}} \qquad \text {such that} \qquad s_n \in \mathcal {S}_{\eta _n}, \forall n \in \mathbb {N}. \end{aligned}$$
(45)

In order to prove Theorem 1, we will look to the adherent points of the sequences \((s_n)_{n \in \mathbb {N}}\) when \(n \rightarrow +\infty \) (i.e. when \(\eta _n \rightarrow 0^+\)). By definition, we know that \({\bar{s}}\) is an adherent point of a sequence \((s_n)_{n \in \mathbb {N}}\) if and only if there exists a subsequence which converges to \( {{\bar{s}}}\). With a slight abuse of notation, we will write

$$\begin{aligned} s_n \longrightarrow {{\bar{s}}} \qquad \text {or} \qquad \lim _{n \rightarrow +\infty } s_n = {{\bar{s}}} \end{aligned}$$
(46)

to signify that \({{\bar{s}}}\) is an adherent point of a sequence \((s_n)_{n \in \mathbb {N}}\), but it is implied that the convergence in fact only relies on the adequate subsequence. This holds also for all other sequences that are introduced later in this article.

The proof of Theorem 1 is built from the two following lemmas.

Lemma 1

Let \((\eta _n)_{n \in \mathbb {N}}\) be a sequence of the form (44) and \((z_n)_{n \in \mathbb {N}}\) be any associated sequence of elements of \({\mathcal {Z}}_{\eta }\). Let \({{\bar{z}}}\) be an adherent point of the sequence \((z_n)_{n \in \mathbb {N}}\). Then,

$$\begin{aligned}&\text {a)} \;\; \textrm{Re}({{\bar{z}}}^2) \leqslant 1 \qquad \big (\text {precisely: } \textrm{Re}({{\bar{z}}}^2) \in [-\infty , 1]\; \big ); \end{aligned}$$
(47)
$$\begin{aligned}&\text {b)} \;\; \text {if } \textrm{Re}({{\bar{z}}}^2) = 1 \text { then } \left( \textrm{Re}({{\bar{z}}}) \right) ^{\! 2} = 1 \text { and } \textrm{Im}({{\bar{z}}}) = 0. \end{aligned}$$
(48)

Proof

The proof of this lemma is given in Appendix B. \(\square \)

Lemma 2

Let \((\eta _n)_{n \in \mathbb {N}}\) be a sequence of the form (44) and \((s_n)_{n \in \mathbb {N}}\) be any associated sequence of the form (45). Let \({{\bar{s}}}\) be an adherent point of \((s_n)_{n \in \mathbb {N}}\). Then,

$$\begin{aligned} \textrm{Re}({{\bar{s}}}) \leqslant - \ln (2) \qquad \big (\text {precisely: } \textrm{Re}({{\bar{s}}}) \in [-\infty , -\ln (2)]\; \big ). \end{aligned}$$
(49)

Proof

Let \({{\bar{s}}}\) be an adherence point of the considered sequence \((s_n)_{n \in \mathbb {N}}\). We restrict to a subsequence (still denoted \((s_n)_{n \in \mathbb {N}}\)) such that \((s_n)_{n \in \mathbb {N}}\) converges to \(\bar{s}\). Consider the sequence

$$\begin{aligned} (z_n)_{n \in \mathbb {N}} \qquad \text {such that} \qquad z_n = \sqrt{1+4\eta s_{n}}, \forall n \in \mathbb {N}. \end{aligned}$$
(50)

By definition \(z_{n}\in {\mathcal {Z}}_{\eta }\) for any \(n\in \mathbb {N}\). Let \({{\bar{z}}}\) be an adherence value of this sequence \((z_{n})_{n\in \mathbb {N}}\) and let us again restrict to a subsequence (still denoted \((z_{n})_{n\in \mathbb {N}}\)) that converges to \({{\bar{z}}}\). Note that since it is a subsequence, we still have \(s_{n}\rightarrow {{\bar{s}}}\). From Lemma 1, we know that necessarily \(\textrm{Re}({{\bar{z}}}^2) \in [-\infty , 1]\).

Let us first assume that \(\textrm{Re}({{\bar{z}}}^2)\) is strictly smaller than 1, i.e. \(\textrm{Re}({{\bar{z}}}^2) \in [-\infty , 1)\). In that case, from the definition of \(s_n\) in (45), we have

$$\begin{aligned} \textrm{Re}({{\bar{s}}})= & {} \lim _{n \rightarrow +\infty } \textrm{Re}(s_n) = \lim _{n \rightarrow +\infty } \dfrac{\textrm{Re}(z_n^2) - 1}{4 \eta _n}\nonumber \\= & {} \dfrac{\lim _{n \rightarrow +\infty } \textrm{Re}(z_n^2) - 1}{\lim _{n \rightarrow +\infty } 4 \eta _n} = \dfrac{\textrm{Re}({{\bar{z}}}^2) - 1}{\lim _{n \rightarrow +\infty } 4 \eta _n}. \end{aligned}$$
(51)

Since, by the definition (44), we know that \(\lim _{n \rightarrow +\infty } 4 \eta _n = 0^+\), we can conclude

$$\begin{aligned} \textrm{Re}({{\bar{s}}}) = - \infty \end{aligned}$$
(52)

and the lemma is proved.

Let us now assume that \(\textrm{Re}({{\bar{z}}}^2) = 1\). From Lemma 1 we know that, if \(\textrm{Re}({{\bar{z}}}^2) = 1\), then necessarily \(\textrm{Re}(\bar{z}) = \pm 1\) and \(\textrm{Im}({{\bar{z}}}) = 0\); hence, \({\bar{z}} = \pm 1\). We address the case where \({{\bar{z}}} = 1\) (the reader can easily handle the case \({{\bar{z}}} = -1\) by symmetry), and we introduce the notations

$$\begin{aligned} y_n = z_n -1, \qquad a_n = \textrm{Re}(y_n), \qquad b_n = \textrm{Im}(y_n). \end{aligned}$$
(53)

With these notations we have

$$\begin{aligned} \textrm{Re}(s_{n}) = \dfrac{\textrm{Re}(z_{n}^{2})-1}{4\eta _n} = \dfrac{\textrm{Re}((y_n+1)^{2})-1}{4\eta _n} = \dfrac{a^2_{n}-b_n^{2}}{4\eta _n} + \dfrac{a_n}{2\eta _{n}}. \end{aligned}$$
(54)

Here, the determination of adherent points of the sequence \((\textrm{Re}(s_n))_{n \in \mathbb {N}}\), induced by the limit \(\textrm{Re}(z_n) \rightarrow 1\), is clearly more delicate because it cannot be directly derived from formula (54) and requires a development which is detailed hereafter.

With the notation (53), the function \(X_\eta \) defined in (41) becomes

$$\begin{aligned} X_{\eta } = \left( 1+\frac{y_{n}}{2}\right) e^{y_{n}/2\eta _n}+ \frac{y_{n}}{2}e^{-1/\eta _n-y_{n}/2\eta _{n}}, \end{aligned}$$
(55)

such that the characteristic equation (42) is written

$$\begin{aligned}&\left( \left( 1+\frac{y_{n}}{2}\right) e^{y_{n}/2\eta _{n}}+ \frac{y_{n}}{2}e^{-1/\eta _{n}-y_{n}/2\eta _{n}}\right) ^{2} \nonumber \\&\quad +\,(1+y_{n})e^{-y_{n}/2\eta _{n}-y_{n}^{2}/4\eta _n}\left[ \left( 1+\frac{y_{n}}{2}\right) e^{y_{n}/2\eta _{n}}+ \frac{y_{n}}{2}e^{-1/4\eta _{n}-y_{n}/2\eta _{n}}\right] = (1+y_{n})^{2}. \end{aligned}$$
(56)

Now, because \(\eta _n \rightarrow 0^+\) and \(y_n \rightarrow 0\) (since \(z_{n}\rightarrow {\bar{z}}\)), we have

$$\begin{aligned}&\left( 1+\frac{y_{n}}{2}\right) ^{2}e^{y_{n}/\eta _{n}}+ o(e^{-1/\eta _{n}})\nonumber \\&\quad +\,(1+y_{n})\left( 1+\frac{y_{n}}{2}\right) e^{-y_{n}^{2}/4\eta _{n}}+o(e^{-1/4\eta _{n}-y_{n}/\eta _{n}-y_{n}^{2}/4\eta _{n}}) = (1+y_{n})^{2}. \end{aligned}$$
(57)

This implies that, for \(n \rightarrow +\infty \),

$$\begin{aligned} e^{y_{n}/\eta _{n}}+\frac{1+y_{n}}{1+\frac{y_{n}}{2}}e^{-y_{n}^{2}/4\eta _{n}} \longrightarrow 1. \end{aligned}$$
(58)

With (54), (58) becomes

$$\begin{aligned}{} & {} e^{a_n/\eta _{n}}e^{ib_n/\eta _{n}}\nonumber \\{} & {} \quad +\frac{(1+a_n+ib_n)(1+a_n/2-ib_n/2)}{|1+\frac{y_{n}}{2}|^{2}}e^{-a_n^{2}/4\eta _n}e^{b_n^{2}/4\eta _n}e^{-ia_nb_n/2\eta _{n}} \rightarrow 1, \end{aligned}$$
(59)

or, separating the real and imaginary parts,

$$\begin{aligned}{} & {} e^{a_n/\eta _{n}}\cos ({\textstyle \frac{b_n}{\eta _{n}}}) + e^{-a_n^{2}/4\eta _{n}}e^{b_n^{2}/4\eta _{n}}\nonumber \\{} & {} \quad \left[ \left( 1+{\textstyle \frac{3a_n +a_n^2 + b_n^2}{2}}\right) \cos \left( {\textstyle \frac{a_nb_n}{2\eta _{n}}}\right) +{\textstyle \frac{b_n}{2}}\sin ({\textstyle \frac{a_n b_n}{2\eta _{n}}})\right] \frac{1}{|1+\frac{y_{n}}{2}|^{2}}\rightarrow 1, \end{aligned}$$
(60)
$$\begin{aligned}{} & {} e^{a_n/\eta _{n}}\sin \left( {\textstyle \frac{b_n}{\eta _{n}}}\right) + e^{-a_n^{2}/4\eta _{n}}e^{b_n^{2}/4\eta _{n}}\nonumber \\{} & {} \quad \left[ -\left( 1+{\textstyle \frac{3a_n +a_n^2 + b_n^2}{2}}\right) \sin \left( {\textstyle \frac{a_nb_n}{2\eta _{n}}}\right) +{\textstyle \frac{b_n}{2}}\cos \left( {\textstyle \frac{a_n b_n}{2\eta _{n}}}\right) \right] \frac{1}{|1+\frac{y_{n}}{2}|^{2}}\rightarrow 0. \end{aligned}$$
(61)

Let us now denote \({{\bar{a}}}\) an adherence point of the sequence \((a_n/2\eta _n)_{n \in \mathbb {N}}\). We shall discuss successively the three cases : \({{\bar{a}}} = -\infty \), \({{\bar{a}}} \in (-\infty , +\infty )\) and \({{\bar{a}}} = +\infty \).

The case \(\bar{{{\textbf{a}}}} = - \infty .\) In this case, the lemma is trivial because, since \(a_n \rightarrow 0\) and \(a_n/2\eta _n \rightarrow {{\bar{a}}} = -\infty \), then \(a_n^2/4\eta _n + a_n/2\eta _n \rightarrow -\infty \) and therefore, from (54), \(\textrm{Re}({{\bar{s}}}) = - \infty \).

The case \(\bar{{{\textbf{a}}}} \in (- \infty , +\infty ).\)

In this case \(a_n^2/2\eta _n \rightarrow 0\) and \(a_n b_n/2\eta _n \rightarrow 0\) because \(a_n + i b_n = y_n \rightarrow 0\) while \(a_n/2\eta _n \rightarrow {{\bar{a}}}\in \mathbb {R}\). Then, from (60), we have

$$\begin{aligned} e^{a_n/\eta _{n}}\cos \left( {\textstyle \frac{b_n}{\eta _{n}}}\right) + e^{b_n^{2}/4\eta _{n}}(1 + o(1)) \longrightarrow 1. \end{aligned}$$
(62)

Let us now denote \({{\bar{c}}} \in [0,+\infty ]\) an adherence point of the sequence \((b_n^{2}/4\eta _{n})_{n \in \mathbb {N}}\) and \(\bar{\kappa }\in [-1,1]\) an adherent point of the sequence \((\cos ({\textstyle \frac{b_n}{\eta _{n}}}))_{n \in \mathbb {N}}\). Then, taking the limit,Footnote 1 we have from (62)

$$\begin{aligned} e^{2 {{\bar{a}}}} \bar{\kappa }+ e^{{{\bar{c}}}} = 1. \end{aligned}$$
(63)

Because \(e^{{{\bar{a}}}}\) is bounded and \(e^{{{\bar{a}}}} > 0\), and \(b_{n}^{2}/4\eta _{n}\ge 0\) for any \(n\in \mathbb {N}\), this implies necessarily that

$$\begin{aligned} {{\bar{c}}} \in [0, +\infty )\qquad \text {and}\qquad e^{{{\bar{c}}}} \geqslant 1 \qquad \text {and} \qquad \bar{\kappa }\in [-1, 0]. \end{aligned}$$
(64)

Then, it means in particular that \(b_n^2/\eta _n\) is bounded when \(\eta _n \rightarrow 0^+\), and from (61) we deduce that

$$\begin{aligned} e^{a_n/\eta _{n}}\sin \left( {\textstyle \frac{b_n}{\eta _{n}}}\right) + o(1) \longrightarrow 0 \end{aligned}$$
(65)

which implies that \(\sin ({\textstyle \frac{b_n}{\eta _{n}}}) \rightarrow 0\) and therefore that the only possible adherence points for \(\cos ({\textstyle \frac{b_n}{\eta _{n}}})\) are \(\bar{\kappa }= \pm 1\). Since \(\bar{\kappa }\in [-1,0]\), we deduce that \(\bar{\kappa }= -1\). Therefore, from (63),

$$\begin{aligned} e^{{{\bar{c}}}} = 1 + e^{2 {{\bar{a}}}}. \end{aligned}$$
(66)

Let us now consider the function \(e^{-\textrm{Re}(s_n)}\) with \(\textrm{Re}(s_n)\) given by (54):

$$\begin{aligned} e^{-\textrm{Re}(s_n)} = e^{(b_n^2 -a_n^2)/4\eta _n - a_n/2\eta _n} \longrightarrow e^{{{\bar{c}}}}e^{- {{\bar{a}}}} = e^{-{{\bar{a}}}} + e^{{{\bar{a}}}} = 2 \cosh ({{\bar{a}}}) \geqslant 2. \end{aligned}$$
(67)

It follows directly that

$$\begin{aligned} \textrm{Re}({{\bar{s}}}) \leqslant - \ln (2) \end{aligned}$$
(68)

and the lemma is proved.

The case \(\bar{{{\textbf{a}}}} = + \infty .\)

In this case, we first observe that \(e^{(a_n^2 - b_n^2)/4\eta _n - a_n/2\eta _n} \rightarrow 0\). Then, multiplying both sides of (60) by this quantity, we get:

$$\begin{aligned}&e^{(a_n^2 - b_n^2)/4\eta _n + a_n/2\eta _n}\cos \left( {\textstyle \frac{b_n}{\eta _n}}\right) +e^{-a_n/2\eta _n}\nonumber \\&\quad \times \, \left[ \left( 1+{\textstyle \frac{3a_n + a_n^2 + b_n^2}{2}}\right) \cos \left( {\textstyle \frac{a_nb_n}{2\eta _{n}}}\right) +{\textstyle \frac{b_{n}}{2}}\sin \left( {\textstyle \frac{a_nb_n}{2\eta _{n}}}\right) \right] \frac{1}{|1+\frac{y_{n}}{2}|^{2}} \nonumber \\&\quad -\,e^{(a_n^2 - b_n^2)/4\eta _n - a_n/2\eta _n}\rightarrow 0, \end{aligned}$$
(69)

From this expression, we deduce that

$$\begin{aligned} e^{(a_n^2 - b_n^2)/4\eta _n + a_n/2\eta _n}\cos ({\textstyle \frac{b_n}{\eta _n}}) \longrightarrow 0. \end{aligned}$$
(70)

A similar manipulation of (61) gives

$$\begin{aligned} e^{(a_n^2 - b_n^2)/4\eta _n + a_n/2\eta _n}\sin ({\textstyle \frac{b_n}{\eta _n}}) \longrightarrow 0. \end{aligned}$$
(71)

Combining (70) and (71) we obtain

$$\begin{aligned} e^{(a_n^2 - b_n^2)/2\eta _n + a_n/\eta _n} = e^{2\textrm{Re}(s_n)} \longrightarrow 0 \end{aligned}$$
(72)

which implies that \(\textrm{Re}(s_n) \rightarrow -\infty \) and the lemma is proved. \(\square \)

Based on Lemma 2, we can now give the following proof of Theorem 1.

Proof of Theorem 1

We assume by contradiction that the theorem does not hold:

$$\begin{aligned} \text { For any }\delta> 0, \not \exists \, \eta _1 > 0 \text { such that } \sigma _\eta \leqslant -\ln (2) + \delta \;\; \forall \eta \in (0, \eta _1). \end{aligned}$$
(73)

This implies that

$$\begin{aligned} \text{ For } \text{ all } \eta> 0, \; \exists \eta _{1}\in (0,\eta ) \text { such that } \exists s \in \mathcal {S}_{\eta _1} \text{ with } \textrm{Re}(s) \nonumber \\> -\ln (2) + \delta . \textrm{Re}(s) > -\ln (2) + \delta . \end{aligned}$$
(74)

It follows that we can build a sequence \((\eta _n)_{n \in \mathbb {N}}\) of the form (44) and an associated sequence \((s_n)_{n \in \mathbb {N}}\) with \(s_n \in \mathcal {S}_{\eta _n}\). For this sequence we deduce from (74) that necessarily \(\textrm{Re}({{\bar{s}}}) > - \ln (2) + \delta \), which is in contradiction with Lemma 2. \(\square \)

Fig. 4
figure 4

The spectrum \(\mathcal {S}_\eta \) of the closed-loop system for \(\eta = 0.02\) (red circle) and \(\eta = 0.2\) (green circle)

Full size image

The theorem is illustrated in Fig. 4 where the spectrum is represented for the values \(\eta \) = 0.02 and 0.2, and where the effectiveness of the stability margin \(-\ln (2)\) can be appreciated.

5 Robustness analysis

We consider again the control problem of the previous section. However, because we want to explicitly account for the sensitivity to delay uncertainties, we introduce an additional perturbation \(\varepsilon \) to the nominal transport velocity \(\upsilon = 1\). The open-loop system is therefore written in the time domain as follows:

$$\begin{aligned}{} & {} \partial _t y_1(t,x) + ( 1 + \varepsilon ) \partial _x y_1(t,x) - \eta \partial ^2_{xx} y_1(t,x) = 0, \end{aligned}$$
(75a)
$$\begin{aligned}{} & {} \partial _t y_2(t,x) + ( 1 + \varepsilon ) \partial _x y_2(t,x) - \eta \partial ^2_{xx} y_2(t,x) = 0, \end{aligned}$$
(75b)
$$\begin{aligned}{} & {} y_1(t,0) = y_2(t,1) + U(t), \end{aligned}$$
(75c)
$$\begin{aligned}{} & {} y_2(t,0) = y_1(t,1), \end{aligned}$$
(75d)
$$\begin{aligned}{} & {} \partial _x y_1(t,1) = \partial _x y_2(t,1) = 0 \end{aligned}$$
(75e)
$$\begin{aligned}{} & {} Y(t) = y_1(t,1), \end{aligned}$$
(75f)

We suppose, as before, that the system is closed with the dead beat output feedback controller

$$\begin{aligned} U(t) = - Y(t-1). \end{aligned}$$
(76)

Remark that this control law depends on the theoretical delay (\(\tau = 1\)), ignoring the uncertainty represented by \(\varepsilon \).

Remark also that for simplicity we assume here that we have the same uncertainty \(\varepsilon \) on both physical subsystems represented by transport equations (75a) and (75b). This may seem like a simplification, but, actually, it can be shown that this single perturbation, even if it is arbitrarily small, is sufficient to destroy the closed-loop stability when \(\eta = 0\) (see Fig. 5 hereafter).

In this case, the transfer functions of the two transport subsystems become

$$\begin{aligned} f_{\eta ,\varepsilon }(s) = \dfrac{\lambda _1(s) - \lambda _2(s)}{\lambda _1(s) e^{-\lambda _2(s)} - \lambda _2(s) e^{-\lambda _1(s)}}. \end{aligned}$$
(77)

with the function \(f_{\eta ,\varepsilon }\) now depending on both \(\eta \) and \(\varepsilon \) because the functions \(\lambda _1\) and \(\lambda _2\) are modified as follows:

$$\begin{aligned} \lambda _1(s)= & {} \dfrac{( 1 + \varepsilon ) +\sqrt{( 1 + \varepsilon )^2 +4\eta s}}{2\eta }, \nonumber \\ \lambda _2(s)= & {} \dfrac{( 1 + \varepsilon ) -\sqrt{( 1 + \varepsilon )^2 + 4\eta s}}{2\eta }. \end{aligned}$$
(78)

With this definition, the characteristic equation of the closed-loop system is now

$$\begin{aligned} f_{\eta ,\varepsilon }^2(s) - f_{\eta ,\varepsilon }(s)e^{-s} - 1 = 0. \end{aligned}$$
(79)

As in the previous section, we introduce the spectrum \({\mathcal {S}}_{\eta ,\varepsilon }\) and the maximal abscissa \(\sigma _{\eta ,\varepsilon }\) defined by

$$\begin{aligned}{} & {} \mathcal {S}_{\eta ,\varepsilon }=\{s\in \mathbb {C} : s\text { is solution of } (79)\}, \end{aligned}$$
(80)
$$\begin{aligned}{} & {} \sigma _{\eta ,\varepsilon } = \sup \{\textrm{Re}(s) : s \in \mathcal {S}_{\eta ,\varepsilon } \}. \end{aligned}$$
(81)

We remark that, by definition, we have

$$\begin{aligned} \mathcal {S}_{\eta ,0} = \mathcal {S}_\eta \qquad \text {and} \qquad \sigma _{\eta ,0} = \sigma _\eta . \end{aligned}$$
(82)

We then have the following robustness theorem.

Theorem 2

Let \(\delta >0\) and \(\eta >0\) be such that Theorem 1 holds, i.e.

$$\begin{aligned} \sigma _{\eta ,0}\leqslant - \text {ln}(2) + \delta . \end{aligned}$$
(83)

Then, there exists \(\varepsilon _{1}>0\) such that for any \(\varepsilon \in (-\varepsilon _{1},\varepsilon _{1})\) the maximal spectral abscissa \(\sigma _{\eta ,\varepsilon }\) satisfies

$$\begin{aligned} \sigma _{\eta ,\varepsilon }\leqslant - \text {ln}(2)+2\delta \end{aligned}$$
(84)

Proof

We proceed by contradiction, and we assume that Theorem 2 does not hold. This implies that for any \(\varepsilon _{1}>0\) there exists \(\varepsilon \in (-\varepsilon _{1}, \varepsilon _{1})\) such that

$$\begin{aligned} \sigma _{\eta ,\varepsilon }> - \text {ln}(2)+2\delta , \end{aligned}$$
(85)

and therefore that there exists \(s\in {\mathcal {S}}_{\eta ,\varepsilon }\) such that

$$\begin{aligned} \textrm{Re}(s)> - \text {ln}(2)+2\delta . \end{aligned}$$
(86)

Hence we can define a sequence

$$\begin{aligned} (\varepsilon _n)_{n \in \mathbb {N}} \qquad \text {with} \qquad \lim _{n \rightarrow +\infty } \varepsilon _n = 0, \end{aligned}$$
(87)

and an associated sequence \((s_n)_{n \in \mathbb {N}}\) such that

$$\begin{aligned} \textrm{Re}(s_n) > - \text {ln}(2)+2\delta , \;\; \text {with} \;\; s_n\in {\mathcal {S}}_{\eta ,\varepsilon _n} \; \forall n \in \mathbb {N}. \end{aligned}$$
(88)

  • If the sequence \((s_{n})_{n\in \mathbb {N}}\) is bounded, then we can extract a subsequence that converges to a limit \({\bar{s}}\in \mathbb {C}\). We still denote this subsequence by \((s_{n})_{n\in \mathbb {N}}\). As \(\varepsilon _{n}\rightarrow 0\), we can pass to the limit in (79) and deduce that \({\bar{s}}\in {\mathcal {S}}_{\eta ,0}={\mathcal {S}}_{\eta }\) and therefore, from the assumption on \(\delta \) and \(\eta \), that

    $$\begin{aligned} \textrm{Re}({\bar{s}})\leqslant - \text {ln}(2)+\delta . \end{aligned}$$
    (89)

    On the other hand, again passing to the limit, we deduce from (88) that

    $$\begin{aligned} \textrm{Re}({\bar{s}})\geqslant - \text {ln}(2)+2\delta >- \text {ln}(2)+\delta , \end{aligned}$$
    (90)

    which is in contradiction with (89).

  • If the sequence \((s_{n})_{n\in \mathbb {N}}\) is unbounded, then we can extract a subsequence such that \(|s_{n}|\rightarrow +\infty \). We still denote this subsequence by \((s_{n})_{n\in \mathbb {N}}\). We denote \(s_{n} = r_{n}e^{i\theta _{n}}\), with \(r_{n}\in \mathbb {R}_{+}\) and \(\theta _{n}\in [-\pi ,\pi )\), for \(n\in \mathbb {N}\). Since \(r_{n} =|s_{n}|\rightarrow +\infty \) and (88) holds, we deduce that for n sufficiently large \(\theta _{n}\in (-5\pi /8,5\pi /8)\). Denoting \((1+\varepsilon _{n})+4\eta s_{n} = r_{n}^{1}e^{i\theta _{n}^{1}}\) with \(r_{n}^{1}\in \mathbb {R}_{+}\) and \(\theta ^1_{n}\in [-\pi ,\pi )\) we deduce that for n sufficiently large (depending on \(\eta \)), \(r_{n}^{1}\rightarrow +\infty \) and \(\theta _{n}^{1}\in (-3\pi /4,3\pi /4)\). Thus,

    $$\begin{aligned} \sqrt{(1+\varepsilon _{n})+4\eta s_{n}}= \sqrt{r_{n}^{1}}e^{i\theta _{n}^{1}/2}, \end{aligned}$$
    (91)

    where \(\theta _{n}^{1}/2\in (-3\pi /8, 3\pi /8)\), which implies that \(\textrm{Re}(\sqrt{1+4\eta s_{n}})\rightarrow +\infty \). From the definition of \(\lambda _{1}\) and \(\lambda _{2}\), we deduce that

    $$\begin{aligned} \textrm{Re}(\lambda _{1}(s_{n}))\rightarrow +\infty ,\;\;\textrm{Re}(\lambda _{2}(s_{n}))\rightarrow -\infty , \end{aligned}$$
    (92)

    and

    $$\begin{aligned} \begin{aligned}&f_{\eta ,\varepsilon _{n}}\\&\quad =2\left[ \left( \frac{(1+\varepsilon _{n})}{\sqrt{(1+\varepsilon _{n})+4\eta s_{n}}}+1\right) e^{-\lambda _{2}(s_{n})}+\left( \frac{(1+\varepsilon _{n})}{\sqrt{(1+\varepsilon _{n})+4\eta s_{n}}}-1\right) e^{-\lambda _{1}(s_{n})}\right] ^{-1}. \end{aligned}\nonumber \\ \end{aligned}$$
    (93)

    Using (92) and observing that \((\frac{(1+\varepsilon _{n})}{\sqrt{(1+\varepsilon _{n})+4\eta s_{n}}}+1)\rightarrow 1\), we obtain that \(f_{\eta ,\varepsilon _{n}}\rightarrow 0\). Moreover, from (88), \(e^{-s_{n}}\) is bounded. Hence, we deduce that

    $$\begin{aligned} f_{\eta ,\varepsilon _n}^2(s_n) - f_{\eta ,\varepsilon _n}(s_n)e^{-s_n} - 1 \longrightarrow -1 \end{aligned}$$
    (94)

    and, from (79), we obtain again a contradiction.

In both cases, we obtain a contradiction, which means that there exists \(\varepsilon _{1}>0\) such that (84) holds for any \(\varepsilon \in (-\varepsilon _{1},\varepsilon _{1})\). This concludes the proof of Theorem 2. \(\square \)

Fig. 5
figure 5

The spectrum \(\mathcal {S}_{\eta , \varepsilon }\) of the closed-loop system: influence of viscosity on stability in case of delay uncertainty

Full size image

The theorem is illustrated in Fig. 5. In this figure, we can see what happens in the situation where there is no diffusion (\(\eta = 0\)) but a slight uncertainty (\(\varepsilon = 0.1\)) of the transport velocity: \(\upsilon = 1 + \varepsilon = 1.1\) instead of \(\upsilon = 1\). Although the ideal system (without modelling uncertainty) should be exponentially stable, it appears that it becomes unstable with poles (represented by green dots in Fig. 5) moving to the right-half complex plane.

In contrast, when there is some diffusion (\(\eta = 0.1\)) and no uncertainty (\(\varepsilon = 0\)), we know from Theorem 1 that the closed-loop system must be stable as it can be seen with the spectrum of blue dots (actually reprinted from Fig. 3) which is entirely strictly located in the left half plane.

Then, illustrating Theorem 2, the robustness of the control in presence of diffusion is clearly evidenced by the spectrum made up of red dots which results from a small shift of the initial blue spectrum but remains entirely in the left half plane.

6 Comparison with a simpler system

In this section, we consider the case of a system which is very close to the previous one but slightly simpler. Somewhat surprisingly, we will see that in this case the addition of a diffusion term does not seem to strengthen the system stability but instead destroys the stability.

We start with an ideal system without diffusion nor modelling uncertainty which is clearly a simplified form of the physical system (15) that we have considered in Sect. 2 and is written as follows:

$$\begin{aligned} \partial _t y(t,x) + \partial _x y(t,x) = 0, \end{aligned}$$
(95a)
$$\begin{aligned} \partial _t {\hat{y}}(t,x) + \partial _x {\hat{y}}(t,x) = 0, \end{aligned}$$
(95b)
$$\begin{aligned} \begin{pmatrix} y(t,0) \\ {\hat{y}}(t,0) \end{pmatrix} = \underbrace{\begin{pmatrix} 1 &{} -1 \\ 1 &{} -1 \end{pmatrix}}_{\displaystyle {\textbf{K}}} \begin{pmatrix} y(t,1)\\ {\hat{y}}(t,1) \end{pmatrix}. \end{aligned}$$
(95c)

In the frequency domain, the characteristic equation reduces to \(e^{2s} = 0\), meaning that the system is exponentially stable (for any decay rate). In fact, one can observe easily that the system is finite time stable: for any time \(t\ge 1\), \(\hat{y}(t,\cdot )=y(t,\cdot )\) on [0, 1], thus from the boundary condition at \(x=0\), \(y(t,0)=0\), which means that \(y(t,\cdot ) \equiv 0\) for \(t\ge 2\). However, in this case also, the exponential stability is not robust w.r.t. to delay inaccuracy because \(\bar{\rho }({\textbf{K}}) = \sqrt{2}\).

On the basis of our previous results in this paper, it seems natural to conjecture that the addition of a diffusion term in equation (95a) should allow to strengthen the system stability. To address this issue, the system dynamics (95) are modified with an additional diffusion parameter \(\eta \) as follows:

$$\begin{aligned}{} & {} \partial _t y(t,x) + \partial _x y(t,x) - \eta \partial _{xx} y(t,x)= 0, \end{aligned}$$
(96a)
$$\begin{aligned}{} & {} \partial _t {\hat{y}}(t,x) + \partial _x {\hat{y}}(t,x) = 0, \end{aligned}$$
(96b)
$$\begin{aligned}{} & {} y(t,0) = y(t,1) - {\hat{y}}(t,1), \end{aligned}$$
(96c)
$$\begin{aligned}{} & {} {\hat{y}}(t,0) = y(t,0), \end{aligned}$$
(96d)
$$\begin{aligned}{} & {} \partial _x y(t,1) = 0. \end{aligned}$$
(96e)

For this system in the frequency domain, after calculations similar to those in Sects. 3 and 4, it can be shown that the characteristic equation is

$$\begin{aligned} F_\eta (s) - 1 = 0 \qquad \text {with} \qquad F_\eta (s) = \dfrac{\left( \lambda _{1}(s)e^{\lambda _{1}(s)}-\lambda _{2}(s)e^{\lambda _{2}(s)}\right) (1+e^{-s})}{(\lambda _{1}(s)-\lambda _{2}(s))e^{\lambda _{1}(s)+\lambda _{2}(s)}}, \end{aligned}$$
(97)

where \(\lambda _1(s)\) and \(\lambda _2(s)\) are given by (24) and repeated here for convenience:

$$\begin{aligned} \lambda _1(s) = \dfrac{1 +\sqrt{1 + 4 \eta s}}{2\eta }, \qquad \lambda _2(s) = \dfrac{1 -\sqrt{1 + 4 \eta s}}{2\eta }. \end{aligned}$$
(98)

For a given value of \(\eta \), as in Sect. 4, we use the following notations for the spectrum and the maximal spectral abscissa:

$$\begin{aligned}{} & {} \mathcal {S}_\eta = \{ s\in \mathbb {C} : F_\eta (s) - 1 = 0\}, \end{aligned}$$
(99)
$$\begin{aligned}{} & {} \sigma _\eta = \sup \{\textrm{Re}(s) : s \in \mathcal {S}_\eta \}. \end{aligned}$$
(100)

We then have the surprising observation that a slight diffusion in the system has, in this case, a clear destabilizing effect. This is graphically illustrated in Fig. 6 and leads to the following conjecture.

Conjecture 2

For all \(\epsilon > 0\), there exists \(\eta _{1}>0\) such that for all \(\eta \in (0,\eta _{1})\) the maximal spectral abscissa satisfies the inequality \(\sigma _\eta > - \epsilon \). \(\square \)

Fig. 6
figure 6

The spectrum \(\mathcal {S}_{\eta }\) of the system (96) with \(\eta = 0.1\)

Full size image

7 Conclusion

We have discussed the output feedback stabilization of an unstable open-loop system which is made up of two interconnected transport equations and provided with anti-located boundary sensing and actuation. We have shown that the system can be stabilized by a dynamic controller that involves a delayed output feedback which turns out to be non-robust with respect to delay uncertainties. Then, we have shown that the designed control law can, however, stabilize the system in a robust way when there is a small unknown diffusion in the plant.

Our work in progress on this topic [6] will be focused on the output feedback stabilization of the motion of a viscous fluid represented by \(2\times 2\) hyperbolic PDEs when the control input is the flow rate at one boundary while the measurable output is the fluid density at the other boundary. There is, in this case, an important difference which lies in how viscosity affects the model, inducing a distributed internal coupling between the two partial differential equations. This implies that the system can no longer be considered as a feedback interconnection of two independent scalar transport equations which may lead to additional difficulties for the stability analysis.