1 Introduction

Due to numerous factors such as continuous population growth, economy development, climate change, water quality deterioration, agricultural water shortage has become more and more severe (Cameron and Damowski 2015; Amarasingha et al. 2015). The sustainable development of agricultural system depends on the stable and rational irrigation water management (Davijani et al. 2016). Agricultural water requirements could be met through carrying out effective water resources management schemes. However, it might be impossible with consideration of limited available water resources. Optimizing water-resources allocation is one of the commonly used approaches to increase the quantity of available water and improve water utilization efficiency in agriculture irrigation systems (Melkonyan 2015). For example, two-stage stochastic programming (TSP) is used for planning water allocation to identify the optimal irrigation scheme in agriculture irrigation systems (Hughes and Slaughter 2016). Nevertheless, the dynamic variations of irrigation system conditions, especially for sequential structure of large-scale agriculture problems, could not be adequately reflecting by TSP (Suinyuy et al. 2016).

As a result, many experts and scholars employed multistage stochastic programming (MSP) approach to manage water resource systems (Sirangelo et al. 2015; Agliardi et al. 2016; He 2016; Nematian 2016). Li et al. (2006) formulated an interval-parameter multistage stochastic linear programming method to allocate water resources; through using probability density functions and discrete intervals, the method can effectively express the uncertainties of the systems. Mohammed et al. (2007) developed a coupled hydrologic-economic spreadsheet water-allocation model which was used by both agriculture and environmental sectors for the Murray-Darling Basin (Australia) with various policy scenarios. Chen et al. (2015) developed an inexact multistage fuzzy-stochastic programming to tackle various uncertainties and their interrelationships under different α-cut levels at a plurality of periods; when the promised water allocation targets are violated after random events, recourse decisions can be made to minimize penalties with a maximized system benefit (Kouwenberg 2001; Gulpinar et al. 2002). MSP is effective for water resources management where the analysis of policy scenarios is desired (Casey and Sen 2005; Li et al. 2008a, b). However, MSP couldnot measure the potential economic loss caused by the lack of water resources. Besides, the agricultural systems are surrounded with a number of uncertain factors that would result in system risks, such as random inflow and water demand during growth cycle (Wang et al. 2016). Thus, a sound risk-averse method is desired for analyzing agricultural water management system. Value-at-risk (VaR), a measure of risk, can effectively quantify the potentially system risks within agricultural systems; however, VaR only can represent the average risk of a financial asset or portfolio value without considering the extreme occasion (Josh 2015; Wang et al. 2016). The conditional value at risk (CVaR) taking the impacts of all extreme values in the tail of the distribution into account is more effective in reflecting extreme occasions than that of VaR. It is desired to introduce the CVaR measure into agricultural water management and planning to generate water allocation scheme with a maximum system benefit and a minimum system risk.

Therefore, a risk aversion based interval stochastic programming (RAIS) method is proposed for supporting water resources management through integrating MSP and CVaR into a general framework. RAIS can deal with uncertainties expressed as probability distributions and interval numbers. Besides, it can reflect the dynamic processes of agricultural water management through setting a series of promised water targets with considering the uncertainties of crop water requirement. Dynamic risk analysis avoids the difficult adjustment of static risk analysis and is more realistic (Maryam et al. 2016). Then, the RAIS method will be demonstrated for agricultural water management and planning in Zhangweinan River Basin (China).

2 Methodology

Interval-parameter programming (IPP) can deal with intervals with known lower and upper bounds and one IPP model can be formulated as follows (Huang 1996):

$$ \hbox{max} \,f_{{}}^{ \pm } = C_{{}}^{ \pm } X_{{}}^{ \pm } $$
(1a)

subject to:

$$ A_{{}}^{ \pm } X_{{}}^{ \pm } \le B_{{}}^{ \pm } $$
(1b)
$$ X^{ \pm } \ge 0 $$
(1c)

where A ± ∊ {R ±}1×n, C ± ∊ {R ±}1×n, B ± ∊ {R ±}m×1, X ± ∊ {R ±}n×1;R ± denotes a set of interval numbers with deterministic lower and upper bounds; “−” and “+” represent the lower and upper bounds of the interval parameters (or variables), respectively. In agricultural water management, because of the spatial–temporal variability and inhomogeneity of natural factors and the uncertainty of human activities, water supplies during the planning horizon would have random features, and the promised water cannot always be satisfied. MSP can reflect dynamic features of water allocation processes. In MSP, recourse can be realized by taking corrective actions after a random event has taken place. The initial action is called the previous stage decision, and the corrective one is named the current stage decision. The previous stage decisions have to be made before further information of initial system uncertainties is revealed, whereas the current stage ones are allowed to adapt to this information (Li et al. 2008a, b). Uncertainties in MSP can be conceptualized into a multilayer scenario tree (as shown Fig. 1), with a one-to-one correspondence between the previous random variable and one of the nodes (states of the system) in each time stage (t). Based on techniques of IPP and MSP, the problem under consideration can be formulated as an interval MSP (IMSP) model:

$$ \hbox{max} \,f^{ \pm } = \sum\limits_{i = 1}^{I} {\sum\limits_{j = 1}^{J} {\sum\limits_{t = 1}^{T} {IB_{ijt}^{ \pm } IT_{ijt}^{ \pm } } } } - \sum\limits_{i = 1}^{I} {\sum\limits_{j = 1}^{J} {\sum\limits_{t = 1}^{T} {\sum\limits_{k = 1}^{K} {p_{tk} IP_{ijt}^{ \pm } ISD_{ijtk}^{ \pm } } } } } $$
(2a)

subject to:

$$ \sum\limits_{i = 1}^{I} {\sum\limits_{j = 1}^{J} {W_{ijt}^{ \pm } \left( {IT_{ijt}^{ \pm } - ISD_{ijtk}^{ \pm } } \right)} } \le IQ_{tk}^{ \pm } + \varepsilon_{(t - 1)k}^{ \pm } ,\quad \forall t, \, k $$
(2b)
$$ \varepsilon_{{\left( {t - 1} \right)k}}^{ \pm } = IQ_{{\left( {t - 1} \right)k}}^{ \pm } - \sum\limits_{i = 1}^{I} {\sum\limits_{j = 1}^{J} {W_{ij(t - 1)}^{ \pm } (IT_{ij(t - 1)}^{ \pm } - ISD_{ij(t - 1)k}^{ \pm } )} } + \varepsilon_{{\left( {t - 2} \right)k}}^{ \pm } ,\quad \forall t, \, k $$
(2c)
$$ IT_{ijt\hbox{max} }^{ \pm } \ge IT_{ijt}^{ \pm } \ge ISD_{ijtk}^{ \pm } \ge 0,\quad \forall i, \, j, \, t, \, k $$
(2d)
$$ W_{ijt}^{ \pm } \ge 0,\quad \forall i, \, j, \, t $$
(2e)
Fig. 1
figure 1

Multilayer scenario tree

Full size image

CVaR is a measure to deal with system risks caused by water shortage in agricultural water system and it can reflect the impacts of all extreme values in the tail of the distribution (available water resources). The CVaR risk-measure equation can be formulated as:

$$ CVaR_{\alpha } \left[ Z \right] = VaR_{\alpha } \left[ Z \right] + E\left[ {\hbox{max} \left\{ {0,Z - VaR_{\alpha } \left[ Z \right]} \right\}} \right] $$
(3)

where Z represents random variable, a (α ∊ (0, 1)) represents the expected value of the tail of the distribution of Z. However, only taking into account the impact of critical scenarios may lead to conservative and expensive policies (Rockafellar and Uryasev 2002). In this sense, the convex combination of expected value and CVaR has been considered in the objective function to express the loss function as shown below:

$$ \varphi_{t} \left( {X_{t - 1} ,\xi_{t} } \right) = \mathop {\text{Max}}\limits_{{X_{t} }} \left( {1 + \lambda } \right)E\left[ Z \right] + \lambda CVaR_{\alpha } \left[ Z \right] , $$
(4)

where Z = C t X t  + φ t+1(X t , ξ t+1), C ∊ R, X ∊ R, R represents the real number set, λ ∊ (0, 1). Application of formula (4) leads to a nested CVaR formulation, as illustrated in (5) for a 3-stage problem.

$$ \mathop {\text{Max}}\limits_{{X_{t} }} \left[ \begin{aligned} C_{1} X_{1} + \left( {1 + \lambda_{2} } \right) \cdot E\left[ {\mathop {\text{Max}}\limits_{{X_{2} }} C_{2} X_{2} + \left( {1 + \lambda_{3} } \right)} \right] \cdot E\left[ {Z_{3} } \right] + \,\left( {\lambda_{3} } \right)CVaR_{{\alpha_{2} }} \left[ {Z_{3} } \right] \hfill \\ + \left( {\lambda_{2} } \right)CVaR_{{\alpha_{1} }} \left[ {\mathop {\text{Max}}\limits_{{X_{2} }} C_{2} X_{2} + \left( {1 + \lambda_{3} } \right) \cdot E\left[ {Z_{3} } \right] + \left( {\lambda_{3} } \right)CVaR_{{\alpha_{2} }} \left[ {Z_{3} } \right]} \right] \hfill \\ \end{aligned}\right]$$
(5)

The use of the nested CVaR is necessary in order to ensure time consistency. Through introducing the CVaR measure into model (2), a risk aversion based interval stochastic programming (RAIS) model can be obtained:

$$ \begin{aligned} {\text{Max}}\, \, f^{ \pm } & = \sum\limits_{i = 1}^{I} {\sum\limits_{j = 1}^{J} {\sum\limits_{t = 1}^{T} {IB_{ijt}^{ \pm } IT_{ijt}^{ \pm } } } } - \sum\limits_{i = 1}^{I} {\sum\limits_{j = 1}^{J} {\sum\limits_{t = 1}^{T} {\sum\limits_{k = 1}^{K} {p_{tk} IP_{ijt}^{ \pm } ISD_{ijtk}^{ \pm } } } } } \\ & \quad - \lambda \left( {\xi + \frac{1}{1 - \alpha }\sum\limits_{t = 1}^{T} {\sum\limits_{k = 1}^{K} {p_{tk}^{{}} v_{tk}^{ \pm } } } } \right) \\ \end{aligned} $$
(6a)

subject to:

$$ \sum\limits_{i = 1}^{I} {\sum\limits_{j = 1}^{J} {W_{ijt}^{ \pm } \left( {IT_{ijt}^{ \pm } - ISD_{ijtk}^{ \pm } } \right)} } \le IQ_{tk}^{ \pm } + \varepsilon_{(t - 1)k}^{ \pm } ,\quad \forall t, \, k $$
(6b)
$$ \varepsilon_{{\left( {t - 1} \right)k}}^{ \pm } = IQ_{{\left( {t - 1} \right)k}}^{ \pm } - \sum\limits_{i = 1}^{I} {\sum\limits_{j = 1}^{J} {W_{ij(t - 1)}^{ \pm } (IT_{ij(t - 1)}^{ \pm } - ISD_{ij(t - 1)k}^{ \pm } )} } + \varepsilon_{{\left( {t - 2} \right)k}}^{ \pm } ,\quad \forall t, \, k $$
(6c)
$$ IT_{ijt\hbox{max} }^{ \pm } \ge IT_{ijt}^{ \pm } \ge ISD_{ijtk}^{ \pm } \ge 0,\quad \forall i, \, j, \, t, \, k $$
(6d)
$$ v_{tk}^{ \pm } \ge \sum\limits_{i = 1}^{I} {\sum\limits_{j = 1}^{J} {(ISD_{ijtk}^{ \pm } } } - \xi ),\quad \forall t, \, k $$
(6e)
$$ W_{ijt}^{ \pm } \ge 0,\quad \forall i, \, j, \, t $$
(6f)

The amount of water in this case study is the approximate to fall through statistical analysis, as shown Fig. 2, can be seen from the graph, the amount of water resources for data is not completely fall on the approximate normal distribution curve, therefore, compared with the VaR, using the advantage of CVaR can more accurately characterize the uncertainty of the water resources. α is used to calculate the value of CVaR tail risk, and λ represents the importance of risk value to the decision maker.

Fig. 2
figure 2

Statistical analysis of water resources

Full size image

In this study, an optimized set of target values is identified by having y ijt decision variables. Let IT ± ijt  = IT − ijt  + ΔIT ijt y ijt , where ΔIT ijt  = IT + ijt  − IT − ijt and y ijt ∈[0, 1]. When IT ± ijt approach their upper bounds (i.e. when y ijt  = 1), a relatively high benefit may be obtained if the water demands are satisfied; however, a high penalty may have to be paid when the promised water is not delivered. Conversely, when IT ± ijt reach their lower bounds (i.e. when y ijt  = 0), we may have a lower benefit but, at the same time, a lower risk of violating the promised targets (and thus lower penalty). Then, the RAIS model can be solved through transforming it into two deterministic submodels based on a two-step interactive algorithm to get the lower and upper bounds of f ±. When the system objective is to be maximized, the submodel corresponding to f + can be first formulated; the other submodel (corresponding to f −) can then be formulated based on the solution of the first submodel. The submodel corresponding to f + can be expressed as follows:

$$ \begin{aligned} {\text{Max}}\, \, f^{ + } & = \sum\limits_{i = 1}^{I} {\sum\limits_{j = 1}^{J} {\sum\limits_{t = 1}^{T} {IB_{ijt}^{ + } (IT_{ijt}^{ - } + \Delta IT_{ijt} y_{ijt} )} } } \,\,- \,\sum\limits_{i = 1}^{I} {\sum\limits_{j = 1}^{J} {\sum\limits_{t = 1}^{T} {\sum\limits_{k = 1}^{K} {p_{tk} IP_{ijt}^{ - } ISD_{ijtk}^{ - } } } } } \\ & \quad - \lambda \left( {\xi + \frac{1}{1 - \alpha }\sum\limits_{t = 1}^{T} {\sum\limits_{k = 1}^{K} {p_{tk}^{{}} v_{tk}^{ - } } } } \right) \\ \end{aligned} $$
(7a)

subject to

$$ \sum\limits_{i = 1}^{I} {\sum\limits_{j = 1}^{J} {W_{ijt}^{ - } \left( {IT_{ijt}^{ - } + \Delta IT_{ijt} y_{ijt} - ISD_{ijtk}^{ - } } \right)} } \le IQ_{tk}^{ + } + \varepsilon_{(t - 1)k}^{ + } ,\quad \forall t, \, k $$
(7b)
$$ \begin{aligned} \varepsilon_{{\left( {t - 1} \right)k}}^{ + } & = IQ_{{\left( {t - 1} \right)k}}^{ + } - \sum\limits_{i = 1}^{I} {\sum\limits_{j = 1}^{J} {W_{ij(t - 1)}^{ - } (IT_{ij(t - 1)}^{ - } + \Delta IT_{ij(t - 1)} y_{ijt} \,\,-\, ISD_{ij(t - 1)k}^{ - } )} } \, \\ & \quad + \varepsilon_{{\left( {t - 2} \right)k}}^{ + } ,\quad \forall t, \, k \\ \end{aligned} $$
(7c)
$$ v_{tk}^{ - } \ge \sum\limits_{i = 1}^{I} {\sum\limits_{j = 1}^{J} {(ISD_{ijtk}^{ - } } } - \xi ),\quad \forall t, \, k $$
(7d)
$$ 0 \le ID_{ijtk}^{ - } + IT_{ijt\hbox{min} }^{ + } \le IT_{ijt}^{ - } + \Delta IT_{ijt} y_{ijt} \le IT_{ijt\hbox{max} }^{ + } ,\quad \forall i, \, j, \, t, \, k $$
(7e)
$$ y_{ijt} = y_{{ij\left( {t - 1} \right)}}^{{}} ,\quad \forall i, \, j, \, t = 2, \, 3, \ldots , \, T $$
(7f)
$$ 0 < y_{ijt} < 1,\quad \forall i, \, j, \, t $$
(7g)

where ISD − ijtk and y ijt are decision variables. Solution for f + provides the extreme upper bound of system benefit under uncertain inputs of water-allocation targets. \( ISD_{ijt \, opt}^{ - } \) and y ijt can be obtained from submodel (7). Then the submodel corresponding to f − can be formulated as follows:

$$ \begin{aligned} {\text{Max}}\, \, f^{ - } & = \sum\limits_{i = 1}^{I} {\sum\limits_{j = 1}^{J} {\sum\limits_{t = 1}^{T} {IB_{ijt}^{ - } (IT_{ijt}^{ - } + \Delta IT_{ijt} y_{ijt \, opt} )} } } - \sum\limits_{i = 1}^{I} {\sum\limits_{j = 1}^{J} {\sum\limits_{t = 1}^{T} {\sum\limits_{k = 1}^{K} {p_{tk} IP_{ijt}^{ + } ISD_{ijtk}^{ + } } } } } \\ & \quad - \lambda \left( {\xi + \frac{1}{1 - \alpha }\sum\limits_{t = 1}^{T} {\sum\limits_{k = 1}^{K} {p_{tk}^{{}} v_{tk}^{ + } } } } \right) \\ \end{aligned} $$
(8a)

subject to

$$ \sum\limits_{i = 1}^{I} {\sum\limits_{j = 1}^{J} {W_{ijt}^{ + } \left( {IT_{ijt}^{ - } + \Delta IT_{ijt} y_{ijt \, opt} - ISD_{ijtk}^{ + } } \right)} } \le IQ_{tk}^{ - } + \varepsilon_{(t - 1)k}^{ - } ,\quad \forall t, \, k $$
(8b)
$$ \begin{aligned} \varepsilon_{{\left( {t - 1} \right)k}}^{ - } & = IQ_{{\left( {t - 1} \right)k}}^{ - } - \sum\limits_{i = 1}^{I} {\sum\limits_{j = 1}^{J} {W_{ij(t - 1)}^{ + } (IT_{ij(t - 1)}^{ - } + \Delta IT_{ij(t - 1)} y_{ij(t - 1) \, opt} - ISD_{ij(t - 1)k}^{ + } )} } \, \\ & \quad + \varepsilon_{{\left( {t - 2} \right)k}}^{ - } ,\quad \forall t, \, k \\ \end{aligned} $$
(8c)
$$ v_{tk}^{ + } \ge \sum\limits_{i = 1}^{I} {\sum\limits_{j = 1}^{J} {(ISD_{ijtk}^{ + } } } - \xi ),\quad \forall t, \, k $$
(8d)
$$ 0 \le ID_{ijtk}^{ + } + IT_{ijt\hbox{min} }^{ + } \le IT_{ijt}^{ - } + \Delta IT_{ijt} y_{ijt \, opt} \le IT_{ijt\hbox{max} }^{ - } ,\quad \forall i, \, j, \, t, \, k $$
(8e)
$$ y_{ijt \, opt} = y_{{ij\left( {t - 1} \right) \, opt}}^{{}} ,\quad \forall i, \, j, \, t = 2, \, 3, \ldots , \, T $$
(8f)
$$ 0 < y_{ijt} < 1,\quad \forall i, \, j, \, t $$
(8g)

where ISD + ijtk and y ijt are decision variables. Solution for f − provides the extreme lower bound of system benefit under uncertain inputs of water-allocation targets. Their solutions of ISD + ijt can be obtained through solving sub-model (8). By combining the solutions from sub-models (7) and (8), the final solution of model (6) can be obtained as follows:

$$ ISD_{ijtkopt}^{ \pm } = \left[ {ISD_{ijtkopt}^{ - } ,ISD_{ijtkopt}^{ + } } \right],\quad \forall i, \, j, \, t, \, k $$
(9)
$$ f^{ \pm } = \left[ {f_{opt}^{ - } ,f_{opt}^{ + } } \right] $$
(10)

The optimized water allocation schemes would be:

$$ Z_{ijtkopt}^{ \pm } = IT_{ijtopt}^{ \pm } - ISD_{ijtkopt}^{ \pm } ,\quad \forall i, \, j, \, t, \, k $$
(11)

where Z ± ijtk opt is the total water allocation to scenario k subarea j planting crop i. Figure 3 presents the framework of the RAIS method.

Fig. 3
figure 3

Framework of the RAIS method

Full size image

3 Case study

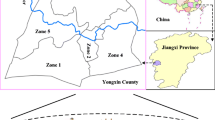
Zhangweinan River Basin is subordinate to Haihe River Basin and accounts for 11% of the total river basin. It stretches through Shanxi, Henan, Hebei, Shandong provinces and the municipality of Tianjin, with a basin area of 37,700 km2 (Xu et al. 2012). The topography of the basin consists of mountainous areas in the west and plain areas in the east. The basin is located in the semi-arid, semi-humid monsoon climate of temperate zone, with an average annual temperature of 14 °C and an average annual precipitation of 608.4 mm. Precipitation varies largely among different seasons. For example, precipitation in winter accounts for only 2% of annual precipitation, while that in summer, especially in July and August, accounts for more than half of annual precipitation (Li and Huang 2011). Zhangweinan River Basin is one of the main food and cotton producing regions in North China, and it faces serious water shortage.

The Yuecheng Reservoir lies in Ci County of Hebei Province and Anyang County of Henan Province. It is the largest reservoir in the Zhangweinan River Basin which is one of the two tributaries of the study river basin. This reservoir is also responsible for the water supply of municipal, industrial and agricultural sectors in two cities (i.e. Anyang and Handan). The total storage capacity of the reservoir is 11.3 billion m3, with a control basin area of 18,100 km2. Most of the area is cropland with cultivated crops, including wheat, maize, cotton, rice, bean, oilseed, and vegetables. Among them, wheat, maize, cotton and vegetable are the main crops and consume the majority of water from the reservoir. Double cropping maize and wheat is the dominating cropping system used on the study area (as shown Fig. 4). In this cropping system, maize is seeded in early June, immediately after the wheat harvest and harvested in the middle September; winter wheat is then seeded in early October and harvested in the following June.

Fig. 4
figure 4

The study area

Full size image

In agricultural irrigation system, uncertainties in water resources allocation processes may influence the stability of agricultural water management system. For example, the crop water requirement should be considered when the available water is under low level (Allen 2000). Moreover, many factors affect the crop water requirement such as evaporation, transpiration, evapotranspiration, weather parameters, crop factors, management and environmental conditions and so on. The determination of crop water demand has become an important limiting factor in such system. Many researchers tried to tackle these difficulties through reference evapotranspiration (Olivera-Guerra et al. 2014; Vipan et al. 2015; Wherley et al. 2015). Among them, actual crop evapotranspiration and single crop coefficients were considered in crop irrigation system. To better manage irrigation water inputs and improve water use efficiency for crop production, the actual crop evapotranspiration (ET) and the single crop coefficients (k cb ) were taken into account.

In double crop coefficients method, the reference standard crops were cited to reflect the uncertainties of crop water requirement when the types of crops are less than dual crop coefficient method. Evapotranspiration is an important part of the field water cycle and has significant influences on crop growth, development and yield (Alberto et al. 2014). Actual ET reflects the crop’s water need which consists of transpiration (T) and evaporation (E). Determination of k c under local climatic condition is the basis to improve planning and efficient irrigation management in many field crops. The crop coefficient (k c ) can be determined by dividing ET with ET 0 (reference crop evapotranspiration) (Allen 2000). However, previous studies mainly concentrated on Kc, and they paid little attention to its components, k cb (basal crop coefficient). In double crop coefficients approach, the different stages of crops’ growth cycle are taken into account, which is drawing more attention in view of potential future shortages of water needed for agricultural production.

$$ ET = \left( {k_{cb} + k_{r} } \right) \cdot ET_{0} $$
(12a)

According to the Penmen–Monteith equation, the standard crop evapotranspiration quantity computation formula is as follows:

$$ ET_{0} = \frac{{0.408\Delta (R_{n} - G) + \gamma \frac{900}{T + 273}u_{2} (e_{a} - e_{d} )}}{{\Delta + \gamma (1 + 0.34u_{2}^{{}} )}} $$
(12b)

Figure 5 presents the crop evapotranspiration coefficients of wheat, maize, cotton in the study area.

Fig. 5
figure 5

The crop evapotranspiration coefficient of wheat, maize, cotton

Full size image

In this study, the irrigation districts supplied by Yuecheng Reservoir are chosen as the study areas, and the districts are divided into fifteen subareas. Since wheat (which is cultivated from early October to early June), maize (which is grown from mid-June to late September) and cotton (which is sown in late April to early May and harvested in late October) are the three main crops that consume the majority of water from the reservoir, they are selected as the study crops. Moreover, five periods are chosen to cover the whole growth stages (which are divided on the basis of the water shortage response) of the three crops. These periods include October through December of last year, January through March, April through May, June through July, and August through September of current year (Liu et al. 2014). Four periods (i.e. winter of last year, spring, summer and autumn of current year) cover the growth stages of the three main crops. Available water for irrigation and water demand from crops both change along with different periods (i.e. growth period). Since the inflow of Yuecheng Reservoir varies significantly during four periods, it is divided into five discrete intervals with probability distributions to approximate the stochastic inflow value in each period. Five inflows are generated in each period with different probabilities, which are named as very-low (VL), low (L), medium (M), high (H) and very-high (VH), respectively. Table 1 provides the available water resources for irrigation under different reservoir inflows in each period. Tables 2, 3 and 4 present the irrigation targets, irrigation benefits, and penalties for different crops, respectively. The actual precipitation in each period is presented in Table 5.

Table 1 Available water resources for irrigation under different inflow scenarios in different periods
Full size table
Table 2 Irrigation targets for different crops in different subareas
Full size table
Table 3 Irrigation benefits for different crops
Full size table
Table 4 Penalty of each crop when water demand cannot be satisfied
Full size table
Table 5 The actual precipitation
Full size table

The proposed RAIS method is used for supporting agricultural water management in the study river basin under such uncertainties. The study problem can be formulated as follows:

$$ \begin{aligned} {\text{Max}}\, \, f^{ \pm } & = \sum\limits_{i = 1}^{I} {\sum\limits_{j = 1}^{J} {\sum\limits_{t = 1}^{T} {IB_{ijt}^{ \pm } IT_{ijt}^{ \pm } } } } - \sum\limits_{i = 1}^{I} {\sum\limits_{j = 1}^{J} {\sum\limits_{t = 1}^{T} {\sum\limits_{k = 1}^{K} {p_{tk} IP_{ijt}^{ \pm } ISD_{ijtk}^{ \pm } } } } } \\ & \quad - \lambda \left( {\xi + \frac{1}{1 - \alpha }\sum\limits_{t = 1}^{T} {\sum\limits_{k = 1}^{K} {p_{tk}^{{}} v_{tk}^{ \pm } } } } \right) \\ \end{aligned} $$
(10a)

subject to

$$ \sum\limits_{i = 1}^{I} {\sum\limits_{j = 1}^{J} {W_{ijt}^{ \pm } \left( {IT_{ijt}^{ \pm } - ISD_{ijtk}^{ \pm } } \right)} } \le IQ_{tk}^{ \pm } + \varepsilon_{(t - 1)k}^{ \pm } ,\quad \forall t, \, k $$
(10b)
$$ \varepsilon_{{\left( {t - 1} \right)k}}^{ \pm } = IQ_{{\left( {t - 1} \right)k}}^{ \pm } - \sum\limits_{i = 1}^{I} {\sum\limits_{j = 1}^{J} {W_{ij(t - 1)}^{ \pm } (IT_{ij(t - 1)}^{ \pm } - ISD_{ij(t - 1)k}^{ \pm } )} } + \varepsilon_{{\left( {t - 2} \right)k}}^{ \pm } ,\quad \forall t, \, k $$
(10c)
$$ W_{ijt}^{ \pm } = \frac{{CWR_{ijt}^{ \pm } - Ep_{ijt}^{ \pm } + \theta_{ij(t + 1)}^{ \pm } D_{ij(t + 1)}^{ \pm } - \theta_{ijt}^{ \pm } D_{ijt}^{ \pm } - \theta_{ijt\hbox{max} }^{ \pm } (D_{ij(t + 1)}^{ \pm } - D_{ijt}^{ \pm } )}}{\eta },\quad \forall i, \, j, \, t $$
(10d)
$$ v_{tk}^{ \pm } \ge \sum\limits_{i = 1}^{I} {\sum\limits_{j = 1}^{J} {(ISD_{ijtk}^{ \pm } } } - \xi ),\quad \forall t, \, k $$
(10e)
$$ CWR_{ijt}^{ \pm } = kc_{ijt}^{ \pm } \times E_{0ij}^{{}} ,\quad \forall i, \, j, \, t $$
(10f)
$$ Ep_{ijt}^{ \pm } = Ep_{0ijt}^{ \pm } - Ec_{ijt}^{ \pm } - SR_{ijt}^{ \pm } - UR_{ijt}^{ \pm } ,\quad \forall j, \, t $$
(10g)
$$ \sum\limits_{i = 1}^{I} {W_{ijt}^{ \pm } ISD_{ijtk}^{ \pm } } \le WAg_{jt}^{ \pm } ,\quad \forall j, \, t, \, k $$
(10h)
$$ 0 \le ISD_{ijtk}^{ \pm } + IT_{ijt\hbox{min} }^{ \pm } \le IT_{ijt}^{ \pm } \le IT_{ijt\hbox{max} }^{ \pm } ,\quad \forall i, \, j, \, t, \, k $$
(10i)
$$ \theta_{ijt\hbox{min} }^{ \pm } \le \theta_{ijt}^{ \pm } \le \theta_{ijt\hbox{max} }^{ \pm } ,\quad \forall i, \, j, \, t $$
(10j)
$$ IT_{ijt}^{ \pm } = IT_{{ij\left( {t - 1} \right)}}^{ \pm } ,\quad \forall i, \, j, \, t $$
(10k)
$$ D_{ijt}^{ \pm } \le D_{ij(t + 1)}^{ \pm } ,\quad \forall i, \, j, \, t $$
(10l)
$$ ISD_{ijtk}^{ \pm } \ge 0,\quad \forall i, \, j, \, t, \, k $$
(10m)

4 Result and discussion

Figure 6 compares the system benefits without and with consideration of system risks (λ = 0 and 1) under different α levels. When λ = 0, the system benefit would be [20.39, 245.93] × 106 RMB¥. When λ = 1, the sytem benefit would be [19.01, 244.71] × 106 RMB¥ (α = 0.90), [17.63, 243.50] × 106 RMB¥ (α = 0.95), [13.51, 239.86] × 106 RMB¥ (α = 0.98), which are lower those obtained without consideration of system risk. In addition, when sytem risk was taken into consideration, system benefit would decrease as α level is raised. A higher α level corresponding a higher degree of confidence would result in a lower system benefit but, at the same time, a waste of water available resources when the inflow is high; however, a lower α level related to a lower degree of confidence would lead to a higher system benefit (and thus a higher risk of water shortage when the inflow is low).

Fig. 6
figure 6

System benefits under different α levels (× 106 RMB¥)

Full size image

Figure 7 presents the system benefits under different λ levels, which shows that different λ levels lead to varied objective-function values. For example, when λ = 0, the system benefit would be [20.39, 245.93] × 106 RMB¥; when λ = 0.6, the system benefit would be [20.35, 245.80] × 106 RMB¥. Obviously, the system benefit would increase with λ level. Higher λ level corresponding higher proportion of risk loss in objective-function values would lead to lower system benefit with lower system risk; conversely, lower λ level corresponding lower proportion of risk loss in objective-function values, would result in higher system benefit with higher system risk.

Fig. 7
figure 7

System benifits under different λ levels

Full size image

Figure 8 presents the cumulative value of optimal cultivation area for wheat, maize and cotton in fifteen subareas. The inner circular rings present the lower bound of the irrigation areas, the outer circular rings present the upper bound. As shown in Fig. 8a–e, no water would be allocated to argriculture under the very-low (VL) inflow. On the contary, the irrigation area would be distributed the largest water when the availble water is very-high (VH). In comparison, argriculture would get some water even under VL inflow in period 3 (as shown in Fig. 8c).

Fig. 8
figure 8

Total irrigation area in different period

Full size image

Figure 9 presents the optimal irrigation areas of different crops in different subareas. Deficits would occur if the available water from the reservoir could not meet the irrigation demand. For example, when three crops (wheat, maize and cotton) were cultivated in period 4, the actual irrigated area for maize would be zero due to insufficient of surface water. In addition, due to their high irrigation benefits, wheat and cotton are more competitive than maize for irrigation water. Cotton would be fully irrigated under VL–VL–VL–VL inflow; wheat would be partly irrigated under L–L–L–L, M–M–M–M and H–H–H–H inflows and fully irrigrated under VH–VH–VH–VH inflow. This is mainly because cotton, as an economic crop with high irrigation benefit, can bring higher system benefit than wheat and maize. Figures 9, 10, 11, 12, 13, 14 and 15 present the irrigation areas in different subareas under different inflow scenrios in periods 1–5 (λ = 1). The results also indicate that different inflows correspond to varied available surface water and thus result in different water-allocation plans. For example, under M inflow, the irrigated area for wheat in DM would be [0, 106], [0, 750], [1214, 2277] and [1027.5, 1074.0] ha from period 1 to period 5.

Fig. 9
figure 9

Optimal irrigation area of each crop in different period

Full size image
Fig. 10
figure 10

Irrigation area in different subarea under t = 1 and λ = 1

Full size image
Fig. 11
figure 11

Irrigation area in different subarea under t = 2 and λ = 1

Full size image
Fig. 12
figure 12

Irrigation area in different subarea under t = 3 and λ = 1

Full size image
Fig. 13
figure 13

Irrigation area in different subarea under t = 4 and λ = 1

Full size image
Fig. 14
figure 14

Irrigation area in different subarea under t = 5 and λ = 1

Full size image
Fig. 15
figure 15

Irrigation area in different subarea under VL–VL–VL inflows (t = 3 and λ = 1)

Full size image

Figure 16 presents the optimal irrigation area of wheat under different λ levels in period 1. The irrigation area of wheat would be changed in different subareas under different λ levels. For example, when λ = 0.2, the irrigation area would be 1730, 2550, 1145 ha in QZ, FX, GP, respectively. In AY, the irrigation area of wheat would be 8420, 8356, 8258, 8245, 8239 ha under λ = 0.2, 0.4, 0.6, 0.8 and 1. Figure 16 presents the total irrigation area of wheat under M, H and VH inflows in period 1. Results indicate that different λ levels correspond to different proportion of risk loss in objective-function values and would result in different total irrigation area of wheat. Generally, the total irrigation area of wheat would increase with level λ increasing, apart from some special points (e.g., λ = 0.7). For example, under M inflow, the total irrigation area of wheat would be [32.23, 34.85] × 103, [33.48, 35.44] × 103, [32.14, 34.83] × 103 ha when λ = 0.7, 0.8, 0.9 respectively. Under H inflow, the total irrigation area would respectively be [33.30, 35.79] × 103, [33.32, 35.34] × 103, [33.42, 35.79] × 103 ha when λ = 0.7, 0.8 and 0.9. The abnormalities at λ = 0.8 demonstrate that values around 0.8 would have significant influence on the total irrigation area (Fig. 17).

Fig. 16
figure 16

Optimal irrigation area of wheat under different λ level when t = 1

Full size image
Fig. 17
figure 17

The total irrigation areas of wheat under M, H and VH inflows when t = 1 (103 ha)

Full size image

Figure 18 presents the irrigation area for wheat, maize and cotton of FX under different inflow scenarios. Due to the competition for water of industrial, there is no available for irrigation and irrigation area in FX would be zero under VL, VL–VL, VL–VL–VL and VL–VL–VL–VL–VL inflows. In period 2, irrigation area of wheat would increase with the inflow level changing from VL to VH. The irrigation target of wheat would be satisfied because of increased available water. In other words, the irrigation target of wheat cannot be satisfied under VL to H inflows due to lack of available water. Similarly, because there is no competition of cotton and maize (only wheat is planted in periods 1 and 2), the changing trends for irrigation area of wheat would be the same as that in period 1 (Fig. 18b). In period 3, cotton is cultivated. The irrigation area of wheat is more than those in periods 1 and 2 due to the increased precipitation in this period. In period 4, wheat, maize and cotton would be all planted. However, due to the weak competitive ability, the irrigation area of maize would be zero. In period 5, wheat has been harvested. Maize would be irrigated when the irrigation target of cotton is satisfied under L–L–L–L–L, M–M–M–M–M, H–H–H–H–H and VL–VL–VL–VL–VL inflows. This is mainly because the limited cotton area results in limited water requirement of cotton.

Fig. 18
figure 18

Optimal irrigation area of different crop in FX under λ = 1

Full size image

5 Conclusions

In this study, a risk aversion based interval stochastic programming (RAIS)method has been developed for planning agricultural water management. RAIS integrates interval-parameter programming (IPP), multistage stochastic programming (MSP), and conditional value-at-risk (CVaR) measure into a general framework. The developed RAIS can not only handle uncertainties expressed as probability distributions and interval numbers, but also reflect the system risk resulted from uncertain parameters within a multistage context. In its solution process, the RAIS model has been solved by a two-step interactive algorithm and transformed into two deterministic submodels that correspond to the lower and upper bounds of the desired objective-function value.

The proposed RAIS method has been applied to agricultural water management in the Zhangweinan River Basin. Through taking irrigation targets and limited available water resources into consideration, water allocation schemes for different crops in different periods under different scenarios have been obtained. Results indicate that a higher α level (corresponding a higher degree of confidence) would result in a lower system benefit; a lower α level (related to a lower degree of confidence) would lead to a higher system benefit (and thus a higher risk of water shortage when the inflow is low). Conversely, higher λ level (corresponding higher proportion of risk loss in objective-function values) would lead to lower system benefit with lower system risk; lower λ level (corresponding lower proportion of risk loss) would result in higher system benefit with higher system risk. Results can help decision-makers generate desired policies for agricultural water management with a maximized system payoff and a minimized risk loss.