Risk analysis for the downstream control section in the real-time flood control operation of a reservoir

Abstract

Many uncertainty factors are associated with the joint operation of a reservoir and its downstream river, which create risks in flood control decisions. Therefore, this paper proposes an analytical method for the estimation of the uncertainties and their risks in real-time flood control decisions. Three uncertainty factors, including reservoir discharge errors, forecasting errors of lateral inflows and river food routing errors are proposed and modeled as stochastic processes, and their internal transforming formulas are derived based on the theory of routing before combination. The definition and calculation formulas for the risks of each moment and the integrated risk of the entire flood process at the downstream flood control section are proposed by an analytical approach based on the combination theory of stochastic processes. The Dahuofang reservoir in northern China is selected as the study case. The results indicate that the risk of the flood peak is higher than that of other moments under the same controlled flood discharge and that the risk that arises from the uncertainties of the reservoir discharge and lateral inflow is decreased by the river storage function. Compared with the Monte Carlo method, the proposed method is effective and efficient for performing risk analysis of the downstream control section in the real-time flood control operation of a reservoir. The risk analysis results could provide important information regarding flood risks for the operators to implement flood control arrangements.

1 Introduction

Floods greatly influence people’s lives in China and are blamed for inflicting severe disasters, such as economic losses, social disruption, environmental/ecological destruction, or even human fatalities (Klein et al. 2010; Huang and Hsieh 2010). Approximately 66.7 % of the Chinese territory is impacted by floods. The economic loss caused by floods during the last 10 years is 2.2 % of the Chinese GDP, which is almost 22 times that of America’s and seven times that of Japan’s (Wang et al. 2004). Therefore, flood control operations to address flood hazards and disasters represent an important task for the Chinese government. However, there are many uncertainties associated with the flood control operations that create risks in flood control decisions (Turgeon 2005; Vorogushyn et al. 2010). Therefore, quantifying the uncertainties and their risks are recognized as one of the most pressing needs in flood control operations to allow the decision makers to make the most effective decision under conditions of uncertainty (Brekke et al. 2009; Bogner and Pappenberger 2011; Fayaed et al. 2013).

Generally speaking, the various updating methods that are adopted for flood risk analysis can be classified into four groups. The first is the return period method, which is brief and commonly used for the risk analysis and prediction of extreme events (Chebana et al. 2010; Chow et al. 1988; Yang et al. 2010). However, it is difficult to determine the integrated risk of a flood control system using the return period method. The second is the stochastic simulation method, which is known as the Monte Carlo (MC) method (Sun et al. 2012; Diao and Wang 2010). The MC method can solve many problems within complex systems, taking into account various uncertainties. However, the MC method cannot ensure the coherence between the numerical solutions and true values because the reliability and precision of the numerical results greatly depends on the sample size. The third conventional method is the first order second moment (FOSM) method and its advanced methods, which are advantageous for dealing with the lack of the distribution function of the uncertainty factors (Zhong et al. 2013; Ganji and Jowkarshorijeh 2012). However, these methods underestimate the flood risk because they neglect the high-order moments. The fourth method is the analytical method, which derives the flood risk of the system through integral or differential calculation on the basis of the established probability density function of the uncertainty factor (Delenne et al. 2012; Wu et al. 2011). The analytical method can calculate the risk of the system based on rigorous theories. With this in mind, the goal of this study is to develop risk analysis for the downstream flood control section in the real-time flood control operation of a reservoir through the analytical method.

A significant quantity of work has been published regarding the risk analysis of the uncertainties in flood control operations by analytical methods (Jiang 1995; Unami et al. 2010; Yan et al. 2014). Jiang conducted the risk assessment of flood releases in the operation of a reservoir based on stochastic differential equations (Jiang 1998). Three uncertainty factors, including the stochastic reservoir inflow, outflow and available storage capacity curve, were taken into account, and the probability density function of the reservoir water level was calculated using the Fokker–Planck equation. Zou et al. proposed a flood risk analysis with the improved interior-outer-set model (IIOSM) based on information diffusion theory, considering the uncertainties of a small sample size and incomplete information (Zou et al. 2012).

However, limited literature is available on the cascade of uncertainties along a river in the real-time flood control operation of a reservoir and the appropriate information that is given to decision makers. Therefore, the objective of this paper is to propose a risk analysis method for the downstream control section in the real-time flood control operation of a reservoir through the analytical method based on the combination theory of stochastic processes. The combination theory of stochastic processes has been widely used in the field of “load combination” (Wen 1977; Mori et al. 2003). The theory models the uncertainty factors of natural loads on a structure as stochastic processes because they are random in occurrence, duration and intensity (Pearce and Wen 1984). And then it combines the stochastic processes through probability combination methods to calculate the probability of a structural limit state being exceeded. Similarly, the uncertainty factors in a flood control system can be modeled as stochastic processes because they are random in occurrence, duration and intensity. When two or more uncertainty factors impact the flood control system at the same time, the combination problem of stochastic processes must be taken into consideration. Therefore, this paper considers the uncertainties of reservoir discharge errors, forecasting errors of lateral inflows and river flood routing errors, models them as stochastic processes, and then calculates their risks in flood control operations based on the combination theory of stochastic processes. The novel aspects and main contributions of this work include: (i) the mathematical descriptions of the proposed three uncertainty factors, with their internal transforming formulas based on the theory of routing before combination (RbC); (ii) the definition and calculation formulas of the risk of each moment and the integrated risk of the entire flood process at the downstream control section in the real-time flood control operation of a reservoir through the proposed analytical method based on the combination theory of stochastic processes; and (iii) the results of the risk analysis enable the operators to make effective decisions under uncertain conditions.

The remainder of this paper is organized as follows. Section 2 presents the generalized structure of the flood control system composed of a reservoir and its downstream river. The mathematical descriptions of the three uncertainty factors and the combined flow of the downstream control section in the real-time flood control operation of the system are defined in Sect. 3. The definition and calculation formulas of the flood risks at the downstream flood control section are proposed in Sect. 4. Section 5 presents the results of a case study using the proposed method, followed by discussions of the results and the potential applications of the proposed method in Sect. 6. Finally, the conclusions of this work are presented in Sect. 7.

2 The generalization of a flood control system composed of a reservoir and its downstream river

The flood control system composed of a reservoir and its downstream river is the basic unit of a river basin. The system is composed of the reservoir, its downstream river and the flood control section. The generalized structure of the system is shown in Fig. 1; the mathematical formula representing the system is expressed as:

Fig. 1

The generalized structure of the flood control system composed of a reservoir and its downstream river

$$ Z(t) = f[X(t),Y(t),C(t)] $$

(1)

where X(t) is the reservoir discharge at time t; Y(t) is the lateral inflow of the interval between the reservoir and its downstream flood control section at time t; C(t) represents the river food routing parameters at time t; and Z(t) is the combined flow of the downstream flood control section at time t.

In general, the theory of river flood routing involves two theories: RbC and routing after combination (RaC). The theory of RbC can be expressed as follows: the river flood routing of the inflows of the main and tributary rivers are conducted respectively, and then their routing results are combined. In the theory of RaC, the river flood routing of the combined flow comes after the combination of the main and tributary river inflows. Without consideration of the nonlinearity of river flood routing parameters, the results based on these two theories are nearly equal to each other, while X(t) and Y(t) are approximately independent from each other because X(t) is obtained from reservoir flood routing and Y(t) is acquired from flood forecast. Thus, the theory of RbC is adopted in this paper because it is more convenient for the description of the uncertainties of X(t) and Y(t). On the basis of the RbC theory, the generalized structure of the flood control system is simplified as:

$$ Z(t) = Z_{1} (t)\,+\,Z_{2} (t) = f_{1} [X(t),C(t)]\,+\,f_{2} [Y(t),C(t)] $$

(2)

where Z ₁(t) and Z ₂(t) are the response processes of X(t) and Y(t) at the downstream flood control section, respectively.

Figure 2 shows the transformed generalized structure of the flood control system.

Fig. 2

The transformed generalized structure of the flood control system

3 The mathematical description of the uncertainties

As shown in Eq. (2), the uncertainties of X(t), Y(t) and C(t) would inevitably lead to the random changes of Z ₁(t), Z ₂(t) and Z(t). Therefore, Z ₁(t), Z ₂(t) and Z(t) are modeled as stochastic processes considering the uncertainties of X(t), Y(t) and C(t). The characteristics of Z ₁(t), Z ₂(t) and Z(t) depend on the stochastic features of X(t), Y(t) and C(t), which are proposed in this section.

3.1 River flood routing errors

There are many uncertainty factors associated with the downstream flood control operations, such as channel morphology, roughness coefficient and local resistance, which lead to the modeling errors of the river flood routing model, i.e., river flood routing errors. Due to the river flood routing errors, the result of the river flood routing can be modeled as a stochastic process. The result of the deterministic river flood routing without consideration of the errors is the average process of the stochastic one. Therefore, the result of river flood routing considering the errors is expressed as:

$$ Z_{1} (t) = \bar{Z}_{1} (t) + \xi_{1} (t) $$

(3)

where $\bar{Z}_{1} (t)$ is the average of the stochastic response process of the reservoir discharge at the downstream flood control section and ξ ₁(t) is the river flood routing error of the response process of the reservoir discharge at the downstream flood control section.

In this paper, ξ ₁(t) is assumed to follow a normal distribution ($\xi_{1} (t)\sim N[0,\sigma_{{\xi_{1} }}^{2} (t)]$), mainly because the river flood routing parameters C(t) are acquired from the statistical methods that have optimal estimation techniques in the mean square error sense. Therefore, Z ₁(t) follows a normal distribution ($Z_{1} (t)\sim N[\bar{Z}_{1} (t),\sigma_{{\xi_{1} }}^{2} (t)]$) according to Eq. (3), and its probability density function is expressed as:

$$ s[z_{1} (t)] = \frac{1}{{\sqrt {2\pi } \sigma_{{\xi_{1} }} (t)}}\;\exp \left\{ { - \frac{{[z_{1} (t) - \bar{z}_{1} (t)]^{2} }}{{2\sigma_{{\xi_{1} }}^{2} (t)}}} \right\} $$

(4)

where $\bar{z}_{1} (t) = g[x(t)]$ and g[·] are the river flood routing function, such as the flow concentration curve, Muskingum formula and so on. When acquired from the flow concentration curve method, g[x(t)] can be expressed as follows:

$$g[x(t)] = \sum\limits_{i = 1}^{k} {q(i)} x(t - i) $$

(5)

where q(i) is the flow concentration coefficient and k is the time number of the unit hydrograph of flood concentration.

Therefore, s[z ₁(t)] can be treated as the converted formula of x(t) into z ₁(t), according to Eqs. (4) and (5). The conditional probability density function of z ₁(t) is expressed as follows:

$$ f[z_{1} (t)/g(x(t))] = \frac{1}{{\sqrt {2\pi } \sigma_{{\xi_{1} }} (t)}}\exp \left\{ { - \frac{{[z_{1} (t) - g(x(t))]^{2} }}{{2\sigma_{{\xi_{1} }}^{2} (t)}}} \right\} $$

(6)

Similarly, $Z_{2} (t) = \bar{Z}_{2} (t) + \xi_{2} (t)$ and the conditional probability density function of Z ₂(t) is expressed as follows:

$$ f[z_{2} (t)/g(y(t))] = \frac{1}{{\sqrt {2\pi } \sigma_{{\xi_{2} }} (t)}}\exp \left\{ - \frac{{[z_{2} (t) - g(y(t))]^{2} }}{{2\sigma_{{\xi_{2} }}^{2} (t)}}\right\} $$

(7)

where $g[y(t)] = \sum\limits_{i = 1}^{k} {q(i)} y(t - i).$

3.2 The reservoir discharge uncertainty

In the real-time operation of a reservoir, the discharge is determined by reservoir inflow, water storage capacity and operation rules (Li et al. 2010). When the operation rules are determinate, the uncertainty of reservoir discharge is mainly derived from the reservoir inflow-forecasting errors and the observation errors of the reservoir storage capacity curve. Therefore, this paper models x(t) as a stochastic process, considering the reservoir inflow-forecasting errors and the observation errors of the reservoir storage capacity curve. Chen et al. developed the relationship among the reservoir inflow-forecasting errors, observation errors of reservoir storage capacity curve, and reservoir discharge uncertainty based on stochastic differential equations (Chen et al. 2014). In that study, H(t) is assumed to follow a normal distribution, and the relation between X(t) and H(t) can be treated as a linear function when the variation range of the reservoir water level at time t is small. Thus, X(t) is expressed as follows:

$$ X(t) = \mu_{t} H(t) + \nu_{t} $$

(8)

where μ _t and ν _t are the linear fitting parameters for the reservoir discharge process at time t.

Therefore, X(t) is assumed to follow a normal distribution, and its probability density function is expressed as:

$$ f[x(t)] = \frac{1}{{\sqrt {2\pi } \sigma_{X} (t)}}\exp \left\{ - \frac{{[x(t) - \bar{x}(t)]^{2} }}{{2\sigma_{X}^{2} (t)}}\right\} $$

(9)

where $\bar{x}(t)$ and $\sigma_{X}^{2} (t)$ are derived as follows:

$$\begin{aligned} \bar{x}(t) &= \mu_{t} E[H(t)] + \nu_{t} \\ \sigma_{X}^{2} (t ) & = \mu_{t}^{2} D[H(t)]\end{aligned} $$

(10)

where E[H(t)] and D[H(t)] refer to the average and the variance of H(t), respectively, and their derivation details are given by Chen et al. (2014).

Therefore, based on Eq. (5), g[x(t)] follows a normal distribution ($g[x(t)]{\rm{\sim}}N({u_{gx}},\sigma_{gx}^2)$) because a linear combination of Gaussian processes remains Gaussian. u _gx and $\sigma_{gx}^{2}$ are estimated by:

$$ \begin{aligned} u_{gx} &= E\left[\sum\limits_{i = 1}^{k} {q(i)} x(t - i)\right] = \sum\limits_{i = 1}^{k} {q(i)} E[x(t - i)] = \sum\limits_{i = 1}^{k} {q(i)} \bar{x}(t - i) \hfill \\ \sigma_{gx}^{2} &= D\left[\sum\limits_{i = 1}^{k} {q(i)} x(t - i)\right] = \sum\limits_{i = 1}^{k} {q^{2} (i)} D[x(t - i)] = \sum\limits_{i = 1}^{k} {q^{2} (i)} \sigma_{X}^{2} (t - i) \end{aligned} $$

(11)

3.3 Lateral inflow forecasting errors

There are many uncertainties associated with real-time flood forecasting procedures, including hydrological observations, forecast model structure and parameter estimation, which lead to lateral inflow forecasting errors and make the lateral inflow a stochastic process (Zhong 2006). Thus, considering the forecasting errors, the lateral inflow is expressed as:

$$ Y(t) = \bar{Y}(t) + \xi_{3} (t) $$

(12)

where Y(t) is the lateral inflow considering the forecasting errors at time t; $\bar{Y}(t)$ is the average of the stochastic lateral inflow at time t, which can adopt the deterministic forecast results; and ξ ₃(t) is the lateral inflow forecasting errors at time t, which can be obtained from the statistical analysis of the forecasting errors of historical floods.

In this paper, ξ ₃(t) is assumed to follow a normal distribution ($\xi_{3} (t)\sim N[0,\sigma_{{\xi_{3} }}^{2} (t)]$)because the flood forecasting parameters are acquired from the statistical methods that have optimal estimation techniques in the mean square error sense (Li et al. 2010; Schaefli et al. 2006). Therefore, Y(t) follows a normal distribution, and its probability density function is expressed as:

$$ f[y(t)] = \frac{1}{{\sqrt {2\pi } \sigma_{{\xi_{3} }} (t)}}\exp \left\{ - \frac{{[y(t) - \bar{y}(t)]^{2} }}{{2\sigma_{{\xi_{3} }}^{2} (t)}}\right\} $$

(13)

Based on Eq. (7), g[y(t)] follows a normal distribution ($g [y(t)]\sim N(u_{gy} ,\sigma_{gy}^{2})$) because the linear combination of Gaussian processes is still Gaussian. u _gy and $\sigma_{gy}^{2}$ are estimated by:

$$ \begin{aligned} u_{gy} &= E\left[\sum\limits_{i = 1}^{k} {q(i)} y(t - i)\right] = \sum\limits_{i = 1}^{k} {q(i)} E[y(t - i)] = \sum\limits_{i = 1}^{k} {q(i)} \bar{y}(t - i) \hfill \\ \sigma_{gy}^{2} &= D\left[\sum\limits_{i = 1}^{k} {q(i)} y(t - i)\right] = \sum\limits_{i = 1}^{k} {q^{2} (i)} D[y(t - i)] = \sum\limits_{i = 1}^{k} {q^{2} (i)} \sigma_{{_{{\xi_{3} }} }}^{2} (t - i) \end{aligned} $$

(14)

3.4 The uncertainty of the combined flow at the downstream flood control section

As shown in Eq. (2), the uncertainties of Z ₁(t) and Z ₂(t) would inevitably lead to the random changes of Z(t). Therefore, Z(t) is modeled as a stochastic process. In general, Z ₁(t) and Z ₂(t) are assumed to be independent from each other, based on the theory of RbC. Therefore, the joint probability density function of g(X(t)), g(Y(t)) and Z(t) is expressed as

$$ f[z(t),g(x(t)),g(y(t))] = f[z(t)/g(x(t)),g(y(t))] \cdot f[g(x(t)),g(y(t))] = f[z(t)/g(x(t)),g(y(t))] \cdot f[g(x(t))] \cdot f[g(y(t))]$$

(15)

where $f[z(t)/g(x(t)),g(y(t))] = \int\limits_{ - \infty }^{ + \infty } {f_{{Z_{1} /g(X)}} [z_{1} (t)]f_{{Z_{2} /g(Y)}} [z(t) - z_{1} (t)]d[z_{1} (t)]}$ according to the convolution integral formula.

Substituting Eqs. (6) and (7) into the expression of $f[z(t)/g(x(t)),g(y(t))]\;$ yields:

$$\begin{aligned} f[z(t)/{\text{g}}(x(t)),g(y(t))] &= \frac{1}{{\sqrt {2\pi [\sigma_{{\xi_{1} }}^{2} (t) + \sigma_{{\xi_{2} }}^{2} (t)]} }}\\ &\quad \times \exp \left\{ { - \frac{{\{ z(t) - \{ g[x(t)] + g[y(t)]\} \}^{2} }}{{2[\sigma_{{\xi_{1} }}^{2} (t) + \sigma_{{\xi_{2} }}^{2} (t)]}}} \right\}\end{aligned} $$

(16)

The details of this derivation procedure are shown in Appendix 1.

Substituting Eq. (16) into Eq. (15) and rearranging yields:

$$ f[z(t),g(x(t)),g(y(t))] = \frac{1}{{2\pi \sigma_{gx} (t)\sigma_{gy} (t)\sqrt {2\pi [\sigma_{{\xi_{1} }}^{2} (t) + \sigma_{{\xi_{2} }}^{2} (t)]} }} \cdot \exp \left\{ - \frac{{[z(t) - g(x(t)) - g(y(t))]^{2} }}{{2[\sigma_{{\xi_{1} }}^{2} (t) + \sigma_{{\xi_{2} }}^{2} (t)]}} - \frac{{[g(x(t)) - u_{gx} (t)]^{2} }}{{2\sigma_{gx}^{2} (t)}} - \frac{{[g(y(t)) - u_{gy} (t)]^{2} }}{{2\sigma_{gy}^{2} (t)}}\right\} $$

(17)

Using the joint probability distribution of Z(t), g(x(t)) and g(y(t)) (i.e., Eq. (17)), risk analysis for the downstream flood control section can be conducted, as described in the next section.

4 The definition and calculation formulas of risks at the downstream flood control section

Define the flood risk of the downstream flood control section at time t as:

$$ P_{t,R} = P[Z(t) > Q_{R} ] $$

(18)

where P _t,R refers to the flood risk of the downstream flood control section at time t and Q _R refers to the controlled flood discharge or acceptable flood discharge at the downstream flood control section.

Figure 3 shows the schematic diagram of the flood risks of different moments during the entire flood at the downstream flood control section.

Fig. 3

The schematic diagram of the risks at the flood control section

As shown in Fig. 3, the stochastic combined flow at each moment may exceed the controlled flood discharge. Therefore, the integrated risk of the entire flood process is defined as:

$$ P_{R} = \hbox{max} (P_{t,R} ,t = 0,1,2, \cdot \cdot \cdot ,T) $$

(19)

where T refers to the time duration of the entire flood process.

According to Eq. (18), P _t,R is obtained from:

$$ \begin{aligned} P_{t,R} & = \int\limits_{ - \infty }^{ + \infty } {\int\limits_{ - \infty }^{ + \infty } {\int\limits_{ - \infty }^{{Q_{R} }} {f[z(t),g(x(t)),g(y(t))]d[z(t)]} } } \\ & \quad \times d[g(x(t))]d[g(y(t))]\end{aligned} $$

(20)

Substituting Eq. (17) into Eq. (20) yields:

$$ \begin{aligned} P_{t,R} = 0.5 + \frac{1}{{(\sqrt {2\pi } )^{3} }}\int\limits_{ - \infty }^{ + \infty } {\int\limits_{ - \infty }^{ + \infty } {\int\limits_{0}^{{Q^{\prime}_{R} }} {\exp\left[ - \frac{{h^{2} (t) + m^{2} (t) + n^{2} (t)}}{2}\right]} } } d[h(t)]d[m(t)]d[n(t)] \end{aligned}$$

(21)

where $Q^{\prime}_{R} = \frac{{Q_{R} - m(t)\sigma_{gx} (t) - u_{gx} (t) - n(t)\sigma_{gy} (t) - u_{gy} (t)}}{{\sqrt {\sigma_{{\xi_{1} }}^{2} (t) + \sigma_{{\xi_{2} }}^{2} (t)} }}$, $m(t) = \frac{{g(x(t)) - u_{gx} (t)}}{{\sigma_{gx} (t)}}$, and$n(t) = \frac{{g(y(t)) - u_{gy} (t)}}{{\sigma_{gy} (t)}}$.

The details of this derivation procedure are presented in Appendix 2.

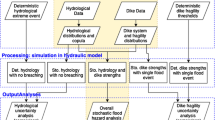
Therefore, the risk at each moment can be calculated using Eq. (21) along with the given controlled flood discharge Q _R . And then the integrated risk of the entire flood process can be derived from Eq. (19). The calculation flowchart for the risks described above is shown in Fig. 4.

Fig. 4

The flowchart for the calculation of the flood risks

5 Case study and results

5.1 Dahuofang reservoir

The case study is performed in the Dahuofang reservoir, which is a key flood control project located in the Hunhe River basin in China. The sketch map of the Hunhe River basin and the location of the Dahuofang Reservoir are shown in Fig. 5 (Chen et al. 2014). The reservoir is a multi-purpose reservoir that is built for flood control, irrigation, electricity generation, aquaculture and water supply. The total storage capacity, flood limited water level, and design flood water level of this reservoir are 2.268 billion m³, 126.40 m, and 136.63 m, respectively.

Fig. 5

Hunhe River basin and the Dahuofang reservoir

5.2 Parameters and data of the proposed model

As shown in Eq. (21), the calculation of the flood risk at each moment requires the information of $\sigma_{{\xi_{2} }}(t)$, u _gx (t), σ _gx (t), u _gy (t) and σ _gy (t), namely, the distribution parameters of $\sigma_{{\xi_{1} }}(t)$, $\sigma_{{\xi_{2} }}(t)$, g(X(t)) and g(Y(t)). According to the flowchart shown in Fig. 4, their specific derived procedures in real-time flood control operations of the Dahuofang reservoir are expressed as follows:

• (1) The distribution parameters of g(Y(t))

The flood control system adopts the rainfall-runoff model to perform flood forecasts. According to the model, the forecast simulation of the historical floods (1959–2005) is performed. Comparing the simulated results with the observed historical floods, the statistical analysis of their difference indicates that the relative errors of flood peak discharges follow a normal distribution of N(0, 0.2377²). There is no information regarding the error distribution of the forecasted inflows at other moments; therefore, it is assumed that the relative error is linearly increasing with the time and that the standard deviations of the relative errors of the forecasted inflows at other moments are obtained by

$$ \sigma^{{\prime }} (t) = \frac{t}{a} \times \sigma^{{\prime }} (a)\quad t = 0,1,2 \ldots ,T $$

(22)

where σ′(t) refers to the standard deviation of the relative error of the forecasted inflow at time t and a refers to the time of the flood peak.

Equation (22) is transformed into Eq. (23) because the absolute error of the forecasted lateral inflow is used in the calculation of flood risks:

$$ \sigma_{{\xi_{3} }} (t) = \sigma^{{\prime }} (t) \times \bar{y}(t), \quad t = 0,1,2 \ldots ,T $$

(23)

Figure 6 shows a forecasted lateral flood with the forecasting-error distributions, namely, the distribution information of y(t). The peak discharge, time interval (Δt) and time number (T) are 2,150 m³/s, 6 h and 22, respectively.

Fig. 6

The process of the forecasted lateral inflow and its forecasting errors

Therefore, the distribution parameters of g(y(t)) can be calculated with the distribution information of y(t) according to Eq. (14); the results are presented in Table 1.

Table 1 The distribution parameters of Y(t) and g(Y(t))

• (2) The distribution parameters of g(X(t))

The calculated procedures of x(t) and its distribution parameters are obtained as follows: (i) acquire a forecasted reservoir inflow; (ii) derive the stochastic reservoir water level and its error distribution at each moment according to the method proposed by Chen et al. (2014); and (iii) calculate the reservoir discharge and its distribution parameters according to Eq. (10).

Figure 7 shows the results of the reservoir discharge and its distribution parameters, namely, the distribution information of x(t).

Fig. 7

The process of the reservoir discharge and its error distribution

Therefore, the distribution parameters of g(x(t)) are calculated with the distribution information of x(t) according to Eq. (11); the results are presented in Table 2.

Table 2 The distribution parameters of X(t) and g(X(t))

• (3) The distribution parameters of river flood routing errors

The flood control system adopts the model of flow concentration curves to conduct river flood routing. According to the model, the river flood routing simulation of the historical floods (1959–2005) is performed. Comparing the simulated results with the observed historical floods, the statistical analysis of their difference indicates that the relative errors of peak discharges follow a normal distribution of N(0, 0.05²). There is no information regarding the distribution of the river flood routing errors at other moments; therefore, it is assumed that the relative error is linearly increasing with time and that the standard deviations of the relative errors of the river flood routing at other moments are obtained by

$$ \sigma^{\prime\prime}(t) = \frac{t}{b} \times \sigma^{\prime\prime}(b), \quad t = 0,1,2 \ldots ,T $$

(24)

where σ″(t) refers to the standard deviation of the relative river flood routing errors of the combined flow at time t and b refers to the time of the flood peak.

In this paper, the standard deviations of the relative river flood routing errors of X(t) and Y(t) are assumed to be equal to that of the combined flow as the flow concentration mechanisms are the same in the same river. Therefore,

$$ \begin{aligned} \sigma_{{\xi_{1} }} (t) &= \sigma^{{\prime \prime }} (t) \times u_{gx} (t) \hfill \\ \sigma_{{\xi_{2} }} (t) &= \sigma^{{\prime \prime }} (t) \times u_{gy} (t),\quad t = 0,1,2 \ldots ,T \end{aligned} $$

(25)

5.3 Results of the risk analysis for the downstream flood control section

Using the information of $\sigma_{{\xi_{1} }}(t)$, $\sigma_{{\xi_{2} }}(t)$, u _gx (t), σ _gx (t), u _gy (t) and σ _gy (t), the risks of the downstream flood control section at each moment are calculated according to Eq. (21) with the given controlled flood discharge Q _R . In this study, Matlab software is applied to implement the integral of Eq. (21) (Chapman 2003; Palm 2001). Generally, it only takes 1 s to calculate P _t,R under a given Q _R , which satisfies the real-time requirement of the flood control operation.

The risk results of the downstream flood control section at each moment are shown in Fig. 8.

Fig. 8

The risk of the downstream flood control section at each moment

Using the risk results of the downstream flood control section at each moment, the integrated risk of the entire flood process is calculated according to Eq. (19); the result is shown in Fig. 9.

Fig. 9

The integrated risk of the entire flood process at the flood control section

6 Discussion

As presented in Tables 1 and 2, the average processes of the reservoir discharge and lateral inflow exhibit transposition and attenuation as a result of the river storage function as well as the standard deviations of the reservoir discharge and lateral inflow. This result means the river storage function decreased the flood risk that arises from the uncertainties of reservoir discharge and lateral inflow.

As shown in Fig. 8, the solid black line on the top of the figure is the risk curve of the flood peak with the time sequence of 11, and the dotted black lines are the risk curves of the other moments. It is obvious that the risk of the flood peak is higher than that of other moments under the same controlled flood discharge. Therefore, the risk of the flood peak is equal to the integrated risk of the entire flood process according to Eq. (19). The risk curve of the flood peak in Fig. 8 is equal to the integrated risk curve of the entire flood process in Fig. 9. Thus, only the risks of the flood peak and its nearby moments must be calculated in real-time flood control operations to reduce the workload and meet the real-time requirement.

As shown in Fig. 9, the following important conclusions are obtained:

The integrated risk of the entire flood process increases while the controlled flood discharge decreases. Moreover, there is a limiting point in the risk curve. The controlled flood discharge of the point is 7,000 m³/s. On the right side of the point, the integrated risk of the entire flood process approximately remains constant at 0.

Figure 9 can estimate the impacts of the proposed uncertainties on the combined flow at the downstream flood control section and provide the probability that the stochastic flood discharge deviates from the controlled flood discharge. For example, the probability that the stochastic combined flow is larger than the controlled flood discharge of 6,400 m³/s is 1.61 %, which means that the integrated risk of the downstream flood control section is 1.61 % due to the uncertainties of the reservoir discharge, lateral inflow forecasting errors and river flood routing errors, as shown in Fig. 9.

The risk analysis results described above can provide important information about flood risks for the operators to conduct flood control arrangements in real-time flood control operations. For example, the risk values of some characteristic controlled flood discharges in the study area are derived based on Fig. 9, as presented in Table 3.

Table 3 Risk values of the characteristic controlled flood discharges in the study area

As presented in Table 3, the floods in the study area are divided into three categories, safe floods, warning floods and dangerous floods, according to the safety flood discharge, warning flood discharge and dangerous flood discharge.

The safety flood discharge is 7,000 m³/s, which means the floods with discharges that are less than 7,000 m³/s do not have flood risks without consideration of any uncertainties. However, the risk of the flood with the controlled flood discharge of 7,000 m³/s is 0.01 % due to the uncertainties, including reservoir discharge errors, forecasting errors of lateral inflows and river food routing errors, as presented in Table 3. If the flood risk is larger than the acceptable risk of the decision-makers, then the flood control operators are supposed to improve the operating programs. If the operating programs are optimal, then the decision-makers may implement emergency flood response options, such as opening emergency spillways or flood storage areas, evacuating people and goods, and placing sandbags on important flood control sections.

The warning flood discharge is 7,500 m³/s, which means the floods with discharges that are less than 7,500 m³/s do not need to start the flood warning system without consideration of any uncertainties. As presented in Table 3, the risk of the flood with the controlled flood discharge of 7,500 m³/s is 0, considering the proposed uncertainties. Therefore, the flood control operators do not need to start the flood warning system under the proposed uncertainties.

The dangerous flood discharge is 8,000 m³/s, the corresponding water level of which is equivalent to the levee crest elevation of the study area. The risk of the flood under the controlled flood discharge of 8,000 m³/s is 0, considering the proposed uncertainties. This means the study area does not have the risk of overtopping. Therefore, the operators do not need to conduct redundant flood control arrangements.

To evaluate the risk analysis results of the proposed method, the numerical simulation of the problem is performed using the MC method. Figure 10 shows the integrated risk curves of the entire flood process through the MC method compared with that obtained from the proposed method.

Fig. 10

Integrated risk curves of the entire flood process using the Monte Carlo and proposed methods

As shown in Fig. 10, the risk curve calculated by the MC method is similar to that obtained from the proposed method. The small difference between them is mainly because of the limited sample size of the MC method. However, the MC method is more time-consuming, which is a great barrier to real-time flood control operations. Therefore, the proposed method is more effective and efficient for performing risk analysis compared with the MC method.

Although the proposed method is effective for the risk analysis of the real-time operations of the flood control system, it has some limitations due to the adopted normal distribution assumptions. Moreover, the applied flood control system should have long-term data series for the hydrological variables to acquire the distribution parameters of the uncertainty factors.

7 Conclusions

In this paper, an analytical method that considers the uncertainties associated with the real-time operation of a reservoir and its downstream river was developed to estimate the flood control operation risks and was applied to the Dahuofang reservoir in northern China. The main conclusions are summarized as follows:

• (1) The mathematical descriptions of the uncertainties, including the reservoir discharge errors, lateral inflow forecasting errors, river flood routing errors and combined flow of the downstream flood control section, were proposed.

• (2) The risks of each moment and the integrated risk of the entire flood process at the downstream flood control section were proposed and calculated according to the proposed analytical method based on the combination theory of stochastic processes.

• (3) The average processes of reservoir discharge and lateral inflow exhibit transposition and attenuation as a result of the river storage function as well as the standard deviations of the reservoir discharge and the lateral inflow. The river storage function decreased the flood risk that arose from the uncertainties of the reservoir discharge and lateral inflow.

• (4) The risk of the flood peak is higher than that of other moments under the same controlled flood discharge, and the integrated risk increases while the controlled flood discharge decreases.

• (5) The integrated risk curve obtained from the proposed analytical method was compared with that obtained from the MC method. The result indicated that the proposed method is effective and efficient for risk analysis of the downstream flood control section in the real-time operation of a reservoir.

• (6) The risk analysis results can provide important information about flood risks for the operators to conduct flood control arrangements in real-time flood control operations. If the flood risk is greater than the acceptable risk of the decision-makers, then the flood control operators must improve the operating program. If the operating program is optimal, then the decision-makers can implement emergency flood response options, such as opening emergency spillways or flood storage and detention areas, evacuating people and goods, and placing sandbags on important flood control sections.

Appendices

Appendix 1

Subscript t is omitted in the derivation process to facilitate the description.

$$ f[z/g(x),g(y)] = \int\limits_{ - \infty }^{ + \infty } {\frac{1}{{2\pi \sigma_{{\xi_{1} }} \sigma_{{\xi_{2} }} }}\exp \left\{ - \frac{{[z_{1} - g(x)]^{2} }}{{2\sigma_{{\xi_{1} }}^{2} }} - \frac{{[z - z_{1} - g(y)]^{2} }}{{2\sigma_{{\xi_{2} }}^{2} }}\right\} d(z_{1} )} $$

(26)

If $\frac{{z_{1} - g(x)}}{{\sigma_{{\xi_{1} }} }} = m$ and $z - g(x) - g(y) = n$, then Eq. (26) is simplified as:

$$ f[z/g(x),g(y)] = \frac{1}{{2\pi \sigma_{{\xi_{2}}}}}\int_{- \infty}^{+ \infty} {\exp \left[- \frac{{m^{2}}}{2} - \frac{{(n - m\sigma_{{\xi_{1}}})^{2}}}{{2\sigma_{{\xi_{2}}}^{2}}}\right]} dm = \frac{1}{{2\pi \sigma_{{\xi_{2}}}}}\int_{- \infty}^{+ \infty} {\exp \left[- \frac{{m^{2} (\sigma_{{\xi_{1}}}^{2} + \sigma_{{\xi_{2}}}^{2}) - 2mn\sigma_{{\xi_{1}}} + n^{2}}}{{2\sigma_{{\xi_{2}}}^{2}}}\right]} dm = \frac{1}{{2\pi \sigma_{{\xi_{2}}}}}\int_{- \infty}^{+ \infty} {\exp \left[- \frac{{\sigma_{{\xi_{1}}}^{2} + \sigma_{{\xi_{2}}}^{2}}}{{2\sigma_{{\xi_{2}}}^{2}}}(m^{2} - \frac{{n\sigma_{{\xi_{1}}}}}{{\sigma_{{\xi_{2}}}^{2}}} \cdot m \cdot \frac{{2\sigma_{{\xi_{2}}}^{2}}}{{\sigma_{{\xi_{1}}}^{2} + \sigma_{{\xi_{2}}}^{2}}}) - \frac{{n^{2}}}{{2\sigma_{{\xi_{2}}}^{2}}}\right]} dm = \frac{1}{{2\pi \sigma_{{\xi_{2}}}}}\int_{- \infty}^{+ \infty} {\exp \left\{- \frac{{\sigma_{{\xi_{1}}}^{2} + \sigma_{{\xi_{2}}}^{2}}}{{2\sigma_{{\xi_{2}}}^{2}}}[m^{2} - \frac{{2n\sigma_{{\xi_{1}}}}}{{\sigma_{{\xi_{1}}}^{2} + \sigma_{{\xi_{2}}}^{2}}} \cdot m + \frac{{n^{2} \sigma_{{\xi_{1}}}^{2}}}{{(\sigma_{{\xi_{1}}}^{2} + \sigma_{{\xi_{2}}}^{2})^{2}}} - \frac{{n^{2} \sigma_{{\xi_{1}}}^{2}}}{{(\sigma_{{\xi_{1}}}^{2} + \sigma_{{\xi_{2}}}^{2})^{2}}}] - \frac{{n^{2}}}{{2\sigma_{{\xi_{2}}}^{2}}}\right\}} dm = \frac{1}{{2\pi \sigma_{{\xi_{2}}}}}\int_{- \infty}^{+ \infty} {\exp \left[- \frac{{\sigma_{{\xi_{1}}}^{2} + \sigma_{{\xi_{2}}}^{2}}}{{2\sigma_{{\xi_{2}}}^{2}}}(m - \frac{{n\sigma_{{\xi_{1}}}}}{{\sigma_{{\xi_{1}}}^{2} + \sigma_{{\xi_{2}}}^{2}}})^{2} + \frac{{n^{2} \sigma_{{\xi_{1}}}^{2}}}{{2\sigma_{{\xi_{2}}}^{2} (\sigma_{{\xi_{1}}}^{2} + \sigma_{{\xi_{2}}}^{2})}} - \frac{{n^{2}}}{{2\sigma_{{\xi_{2}}}^{2}}}\right]} dm = \frac{1}{{2\pi \sigma_{{\xi_{2}}}}}\int_{- \infty}^{+ \infty} {\exp \left[- (\sqrt {\frac{{\sigma_{{\xi_{1}}}^{2} + \sigma_{{\xi_{2}}}^{2}}}{2}} \frac{m}{{\sigma_{{\xi_{2}}}}} - \frac{{n\sigma_{{\xi_{1}}}}}{{\sqrt {\sigma_{{\xi_{1}}}^{2} + \sigma_{{\xi_{2}}}^{2}}}} \cdot \frac{1}{{\sqrt 2 \sigma_{{\xi_{2}}}}})^{2} - \frac{{n^{2}}}{{2(\sigma_{{\xi_{1}}}^{2} + \sigma_{{\xi_{2}}}^{2})}}\right]} dm $$

(27)

If $\sqrt {\frac{{\sigma_{{\xi_{1} }}^{2} + \sigma_{{\xi_{2} }}^{2} }}{2}} \frac{m}{{\sigma_{{\xi_{2} }} }} - \frac{{n\sigma_{{\xi_{1} }} }}{{\sqrt {\sigma_{{\xi_{1} }}^{2} + \sigma_{{\xi_{2} }}^{2} } }} \cdot \frac{1}{{\sqrt 2 \sigma_{{\xi_{2} }} }} = h$, then Eq. (27) is simplified as:

$$ f[z/g(x),g(y)] = \frac{1}{{2\pi \sigma_{{\xi_{2} }} }} \cdot \frac{{\sqrt 2 \sigma_{{\xi_{2} }} }}{{\sqrt {\sigma_{{\xi_{1} }}^{2} + \sigma_{{\xi_{2} }}^{2} } }} \cdot \exp \left[ - \frac{{n^{2} }}{{2(\sigma_{{\xi_{1} }}^{2} + \sigma_{{\xi_{2} }}^{2} )}}\right]\int_{ - \infty }^{ + \infty } {e^{{ - h^{2} }} } dh = \frac{1}{{\sqrt 2 \pi \cdot \sqrt {\sigma_{{\xi_{1} }}^{2} + \sigma_{{\xi_{2} }}^{2} } }}\exp \left[ - \frac{{n^{2} }}{{2(\sigma_{{\xi_{1} }}^{2} + \sigma_{{\xi_{2} }}^{2} )}}\right] \cdot \sqrt \pi = \frac{1}{{\sqrt {2\pi } \cdot \sqrt {\sigma_{{\xi_{1} }}^{2} + \sigma_{{\xi_{2} }}^{2} } }}\exp \left\{ - \frac{{\{ z - [g(x) + g(y)]\}^{2} }}{{2(\sigma_{{\xi_{1} }}^{2} + \sigma_{{\xi_{2} }}^{2} )}}\right\} $$

(28)

Therefore, $f[z/g(x),g(y)] = \frac{1}{{\sqrt {2\pi } \cdot \sqrt {\sigma_{{\xi_{1} }}^{2} + \sigma_{{\xi_{2} }}^{2} } }}\exp \{ - \frac{{\{ z - [g(x) + g(y)]\}^{2} }}{{2(\sigma_{{\xi_{1} }}^{2} + \sigma_{{\xi_{2} }}^{2} )}}\}$

Appendix 2

Subscript t is omitted in the derivation process to facilitate the description.

$$P_{t,R} = \int\limits_{ - \infty }^{ + \infty } {\int\limits_{ - \infty }^{ + \infty } {\int\limits_{ - \infty }^{{Q_{R} }} {f[z,g(x),g(y)]d(z)} } } d[g(x)]d[g(y)] = \int\limits_{ - \infty }^{ + \infty } {\int\limits_{ - \infty }^{ + \infty } {\int\limits_{ - \infty }^{{Q_{R} }} {\frac{1}{{2\pi \sigma_{gx} \sigma_{gy} \sqrt {2\pi (\sigma_{{\xi_{1} }}^{2} + \sigma_{{\xi_{2} }}^{2} )} }}\exp \left\{ - \frac{{[z - g(x) - g(y)]^{2} }}{{2(\sigma_{{\xi_{1} }}^{2} + \sigma_{{\xi_{2} }}^{2} )}} - \frac{{[g(x) - u_{gx} ]^{2} }}{{2\sigma_{gx}^{2} }} - \frac{{[g(y) - u_{gy} ]^{2} }}{{2\sigma_{gy}^{2} }}\right\} d(z)} } } d[g(x)]d[g(y)] = \int\limits_{ - \infty }^{ + \infty } {\int\limits_{ - \infty }^{ + \infty } {\frac{1}{{2\pi \sigma_{gx} \sigma_{gy} }}} } \exp \left\{ - \frac{{[g(x) - u_{gx} ]^{2} }}{{2\sigma_{gx}^{2} }} - \frac{{[g(y) - u_{gy} ]^{2} }}{{2\sigma_{gy}^{2} }}\right\} \int\limits_{ - \infty }^{{Q_{R} }} {\frac{1}{{\sqrt {2\pi (\sigma_{{\xi_{1} }}^{2} + \sigma_{{\xi_{2} }}^{2} )} }}} \exp \left\{ - \frac{{[z - g(x) - g(y)]^{2} }}{{2(\sigma_{{\xi_{1} }}^{2} + \sigma_{{\xi_{2} }}^{2} )}}\right\} d(z)d[g(x)]d[g(y)] $$

(29)

If $z = \sqrt {(\sigma_{{\xi_{1} }}^{2} + \sigma_{{\xi_{2} }}^{2} )} h + g(x) + g(y),$ then Eq. (29) is simplified as:

$$ P_{t,R} = \int\limits_{ - \infty }^{ + \infty } {\int\limits_{ - \infty }^{ + \infty } {\frac{1}{{2\pi \sigma_{gx} \sigma_{gy} }}} } \exp \{ - \frac{{[g(x) - u_{gx} ]^{2} }}{{2\sigma_{gx}^{2} }} - \frac{{[g(y) - u_{gy} ]^{2} }}{{2\sigma_{gy}^{2} }}\} \int\limits_{ - \infty }^{{\frac{{Q_{R} - g(x) - g(y)}}{{\sqrt {(\sigma_{{\xi_{1} }}^{2} + \sigma_{{\xi_{2} }}^{2} )} }}}} {\frac{1}{{\sqrt {2\pi } }}} \exp ( - \frac{{h^{2} }}{2})d(h)d[g(x)]d[g(y)] $$

(30)

If $\frac{{g(x) - u_{gx} }}{{\sigma_{gx} }} = m$ and$\frac{{g(y) - u_{gy} }}{{\sigma_{gy} }} = n,$ then Eq. (30) is simplified as:

$$ P_{t,R} = \int\limits_{ - \infty }^{ + \infty } {\int\limits_{ - \infty }^{ + \infty } {\frac{1}{2\pi }} } \exp \left\{ - \frac{{m^{2} }}{2} - \frac{{n^{2} }}{2}\right\} \int\limits_{ - \infty }^{{\frac{{Q_{R} - m\sigma_{gx} - u_{gx} - n\sigma_{gy} - u_{gy} }}{{\sqrt {(\sigma_{{\xi_{1} }}^{2} + \sigma_{{\xi_{2} }}^{2} )} }}}} {\frac{1}{{\sqrt {2\pi } }}} \exp \left( - \frac{{h^{2} }}{2}\right)dhdmdn = \int\limits_{ - \infty }^{ + \infty } {\int\limits_{ - \infty }^{ + \infty } {\frac{1}{2\pi }} } \exp\left \{ - \frac{{m^{2} }}{2} - \frac{{n^{2} }}{2}\right\} \{ \frac{1}{2} + \int\limits_{0}^{{\frac{{Q_{R} - m\sigma_{gx} - u_{gx} - n\sigma_{gy} - u_{gy} }}{{\sqrt {(\sigma_{{\xi_{1} }}^{2} + \sigma_{{\xi_{2} }}^{2} )} }}}} {\frac{1}{{\sqrt {2\pi } }}} \exp \left( - \frac{{h^{2} }}{2}\right)dh\} dmdn = 0.5 + \frac{1}{{(\sqrt {2\pi } )^{3} }}\int\limits_{ - \infty }^{ + \infty } {\int\limits_{ - \infty }^{ + \infty } {\int\limits_{0}^{{\frac{{Q_{R} - m\sigma_{gx} - u_{gx} - n\sigma_{gy} - u_{gy} }}{{\sqrt {(\sigma_{{\xi_{1} }}^{2} + \sigma_{{\xi_{2} }}^{2} )} }}}} {\exp ( - \frac{{h^{2} + m^{2} + n^{2} }}{2})} } } dhdmdn $$

(31)

If $Q^{\prime}_{R} = \frac{{Q_{R} - m(t)\sigma_{gx} (t) - u_{gx} (t) - n(t)\sigma_{gy} (t) - u_{gy} (t)}}{{\sqrt {\sigma_{{\xi_{1} }}^{2} (t) + \sigma_{{\xi_{2} }}^{2} (t)} }},$ then Eq. (31) is simplified as:

$$ P_{t,R} = 0.5 + \frac{1}{{(\sqrt {2\pi } )^{3} }}\int\limits_{ - \infty }^{ + \infty } {\int\limits_{ - \infty }^{ + \infty } {\int\limits_{0}^{{Q^{\prime}_{R} }} {\exp ( - \frac{{h^{2} + m^{2} + n^{2} }}{2})} } } dhdmdn $$

(32)