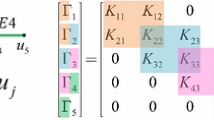Reduced-order modeling of nonlinear structural dynamical systems via element-wise stiffness evaluation procedure combined with hyper-reduction

Abstract

In nonlinear analysis, performing iterative inverse calculation and nonlinear system construction procedures incurs expensive computational costs. This paper presents an element-wise stiffness evaluation procedure combined with hyper-reduction reduced-order modeling (HE-STEP ROM) method. The proposed approach constructs a non-intrusive reduced-order model based on an element-wise stiffness evaluation procedure (E-STEP) and hyper-reduction methods. Because the E-STEP evaluates nonlinear stiffness coefficients element-by-element using cubic polynomial, numerous number of polynomial variables are required. The number of variables directly affects the computational efficiency of the online and offline stages. Therefore, to enhance efficiency of the online/offline stages, the proposed method employs hyper-reduction method. By applying hyper-reduction, the full stiffness coefficients are approximated from the stiffness coefficients evaluated at a few sampling points. Subsequently, the number of polynomial equations and variables is prominently reduced, and the efficiency of the reduced system increases. The efficiency and accuracy of the proposed approach are validated via several structural dynamic problems with geometric and material nonlinearities.

1 Introduction

The performance of computing devices has been increasing continuously, and thus it is possible to investigate various scientific and engineering problems with complex phenomena. Accordingly, the interest and need for a computer simulation-based approach has increased, and experiments have been replaced by computer simulations in several studies. In many industries, computer simulations have been performed on structural problems. However, problems with complex phenomena and numerous degrees of freedom remain difficult because they require expensive computational resources and time. To overcome these issues, reduced-order modeling (ROM) methods have been studied to efficiently simulate problems such as molecular system [1], computational fluid dynamics [2,3,4,5], vibration/acoustic system [6], weather prediction [7], and structure systems [8,9,10,11,12,13].

The model order reduction (MOR) method [14] and Krylov subspace method [15] are popular ROM methods and are used in commercial software. Proper orthogonal decomposition (POD) reduction method is the most widely used reduction method in the MOR method [16, 17]. In the POD method, proper orthogonal bases are obtained from sampled data by using the singular value decomposition (SVD) method. Among the sampling methods used in the POD method, the snapshot method is used when the degrees of freedom are higher than the number of sampled data [18]. The proper orthogonal bases project a high-dimensional full system into a low-dimensional space to construct a reduced system. Subsequently, in the online stage, the method exhibits computational advantage in the iterative inverse calculation procedure. However, the method still requires the repeated construction of a full-order nonlinear system, and this process requires considerable computation time. This bottleneck occurs in most MOR methods.

To alleviate the bottleneck, hyper-reduction methods have been explored for various fields. The hyper-reduction method reduces the cost of nonlinear system construction by using the interpolation method. First, a few sampling points are determined by employing point-selection algorithms. Then, the hyper-reduction constructs full-order nonlinear systems only at the selected sampling points, and approximates nonlinear system for residual degrees of freedom via interpolation. Hence, the computational cost for constructing the nonlinear system is significantly reduced by the aforementioned approximation procedure. Everson and Sirovich proposed a gappy POD method to estimate missing data and POD basis functions [19]. Astrid et al. recommended a missing point estimation method using the gappy POD [20]. Furthermore, randomized oversampling and QR decomposition were proposed to improve the performance of the gappy POD for noisy data [40]. The discrete empirical interpolation method (DEIM) was introduced by Chaturantabut and Sorensen [21, 22] to efficiently analyze nonlinear problems. The DEIM method was also applied to fluid problems [23] and strain-softening viscoplasticity nonlinear structural problems [24]. Carlberg et al. proposed the Gauss–Newton method with approximated tensors (GNAT) method. The GNAT method employs the gappy POD data reconstruction method [19] to approximate the nonlinear system through low-cost least squares problems in a low-dimensional subspace [26, 27]. Farhat et al. studied the energy-conserving sampling and weighting (ECSW) method for nonlinear structural dynamics [28, 29]. However, hyper-reduction methods require intrusive works such as writing the analysis code based on the governing equation or detailed formulation for problems. Intrusive works require considerable effort in constructing analytical models as well as reduced systems.

The non-intrusive reduced-order modeling methods generally construct a reduced system using data obtained from commercial software, and interpolation and machine-learning methods. The non-intrusive methods does not require a finite element analysis code with a full-order system, unlike classical MOR methods. In fluid fields, Xiao et al. proposed a non-intrusive POD-based ROM method with a radial basis function (RBF) for the Navier–Stokes problem [30] and the fluid-structural interaction (FSI) problem [31]. In welding simulation fields, Lu et al. presented a non-intrusive method with efficient sampling strategies [42,43,44]. Muravyov and Rizzi introduced the stiffness evaluation procedure (STEP) method [32]. The method evaluated a nonlinear system by using the cubic polynomial. In recent studies, nonintrusive reduced-order modeling methods have been recommended as evolutions of the STEP. The cubic polynomial-based approaches have been investigated in various applications such as nonlinear post-buckling analyses [33], prediction of fatigue life [34], and nonlinear stochastic computation analyses [35]. Kim and Cho proposed an element-wise stiffness evaluation procedure (E-STEP) reduced order modeling method for structural nonlinear dynamic systems [36, 37]. The boundary between sections of different thicknesses does not have a smooth relationship, but the E-STEP has successfully constructed a reduction system because the element-wise method is used [45]. This method is however difficult to apply to problems that cannot be approximated by the cubic polynomial, such as elasto-plastic or contact problems. This is because, in the elasto-plastic problem, additional variables related to plastic deformation as well as displacement are required.

The E-STEP constructs a non-intrusive reduced-order model for finite element structural model without access to finite element codes and formulation. The method evaluates the stiffness coefficients for the full-order system element-by-element using a displacement-based cubic polynomial, and data obtained from commercial software. Once the stiffness coefficients are evaluated and fixed, in the online stage, the internal forces and Jacobians can be efficiently reconstructed by updating polynomial variables. Then, the POD method is used to project evaluated system to a low-dimensional subspace to efficiently perform the inverse calculation. Therefore, the computation time of the online stage is saved, and high accuracy is exhibited because the stiffness coefficients are evaluated element-by-element. However, since the stiffness coefficients are evaluated for each element, numerous number of polynomial equations and variables are generated. These directly affects the computational costs of evaluating the stiffness coefficients and updating polynomial variables. Therefore, computational inefficiency and out-of-memory occur for a lot of degrees of freedom problems.

In this study, we present an element-wise stiffness evaluation procedure combined with hyper-reduction reduced-order modeling (HE-STEP ROM) method to overcome the fundamental issue, inefficiency resulting from an increasing number of polynomial variables, of the E-STEP ROM. The proposed method employs the hyper-reduction to reduce the computational costs of the offline and online stages by reducing the number of polynomial equations. Owing to a hyper-reduction technique, the stiffness coefficients are evaluated at only a few sampling points. Then, the stiffness coefficients for the residual degrees of freedom are approximated using the hyper-reduction technique. Therefore, the computing time in the offline stage is saved because the stiffness coefficients are evaluated only at a few sampling points; in the online stage, because the number of polynomial equations and variables decreases, the computational efficiency is significantly improved. Consequently, the HE-STEP ROM has higher efficiency than the E-STEP ROM over both the offline and online stages. In addition, the HE-STEP ROM can analyze problems with numerous degrees of freedom because fewer polynomial equations and variables exist.

The remainder of this paper is organized as follows. In Section 2, we introduce the element-wise stiffness evaluation procedure reduced-order modeling (E-STEP ROM) method for nonlinear structural analysis. Section 3 proposes the element-wise stiffness evaluation procedure combined with hyper-reduction reduced-order modeling (HE-STEP ROM) method for a nonlinear structural dynamic system. Numerical examples and results for the validation of the proposed approach are presented in Section 4. Three cases of structural dynamic analyses are executed for finite element problems with material and geometric nonlinearities. The conclusions of the study are provided in Section 5.

2 Element-wise stiffness evaluation procedure reduced-order modeling (E-STEP ROM)

The governing equations of motion for an N-dimensional structural finite element nonlinear system can be expressed as follows:

$$ {\mathbf{M\ddot{u}}} + {\mathbf{C\dot{u}}} + {\varvec{\Gamma}}\left( {{\mathbf{u}}_{0} } \right) + {\mathbf{K}}^{t} \left( {{\mathbf{u}}_{0} } \right)\Delta {\mathbf{u}} = {\mathbf{F}}^{ext} $$

(1)

where $\Delta {\mathbf{u}} = {\mathbf{u}} - {\mathbf{u}}_{0}$. ${\mathbf{M}} \in {\mathbb{R}}^{N \times N} ,{\mathbf{C}} \in {\mathbb{R}}^{N \times N}$, and ${\mathbf{K}}^{t} \in {\mathbb{R}}^{N \times N}$ denote the mass, linear proportional damping, and Jacobian matrices, respectively. Further, ${\mathbf{u}}_{0} \in {\mathbb{R}}^{N} ,{\mathbf{F}}^{ext} \in {\mathbb{R}}^{N}$, and ${\varvec{\Gamma}} \in {\mathbb{R}}^{N}$ denote the displacement in an iteration step, external force, and internal force vectors, respectively. After solving Equation (1) for Δu, the next step is generated with the updated displacement ${\mathbf{u}} \in {\mathbb{R}}^{N}$. Equation (1) is iteratively computed for the deformed states until a convergence solution is obtained. Therefore, the internal force and Jacobian are reconstructed in each element and reassembled in the global system whenever the displacement vector is updated. The Newmark’s time-integration scheme is commonly used to solve Equation (1) in time domain.

The E-STEP evaluates the stiffness coefficients of each element using the displacement-based cubic polynomial and data sampled from sampling analysis. The reason for the possibility of evaluating the nonlinear stiffness coefficients with the cubic polynomial is detailed in [45]. Then, the evaluated stiffness coefficients are assembled in the global system to construct full stiffness coefficients. The internal force for a ith component can be expressed by evaluated stiffness coefficients as follows:

$$ {\tilde\Gamma }_{i} \left( {\mathbf{u}} \right) = {\tilde\Gamma }_{i} \left( {\mathbf{u}} \right)_{1} + {\tilde\Gamma }_{i} \left( {\mathbf{u}} \right)_{2} \cdots + {\tilde\Gamma }_{i} \left( {\mathbf{u}} \right)_{{N_{e} }} = \mathop \sum \limits_{m = 1}^{{N_{e} }} \left[ {K_{ij}^{1} u_{j} + K_{ijk}^{2} u_{j} u_{k} + K_{ijkl}^{3} u_{j} u_{k} u_{l} } \right]_{m} $$

(2)

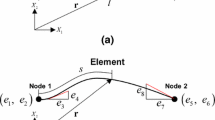
where ‘~’ is the cubic polynomial model, and N_e is the number of elements containing the node related to the ith degrees of freedom. For example, N_e at the black point in Figure 8 (a) is ‘4’. K¹, K², and K³ are linear, quadratic, and cubic stiffness coefficients, respectively. K¹ can be easily computed from a linear model and be also obtained from commercial software. Further, the nonlinear stiffness coefficients of each element are determined using the least squares method, and details of the determination stiffness coefficients are presented in Appendix A.

Equation (2) can be divided into ${\tilde{\mathbf{\Gamma }}}^{L}$ using the linear stiffness coefficient and ${\tilde{\mathbf{\Gamma }}}^{NL}$ using the nonlinear stiffness coefficients as follows:

$$ {\tilde\Gamma }_{i}^{L} \left( {\text{u}} \right) = \mathop \sum \limits_{m = 1}^{{N_{e} }} \left[ {K_{ij}^{1} u_{j} } \right]_{m} $$

(3)

$$ {\tilde\Gamma }_{i}^{NL} \left( {\text{u}} \right) = \mathop \sum \limits_{m = 1}^{{N_{e} }} \left[ {K_{ijk}^{2} u_{j} u_{k} + K_{ijkl}^{3} u_{j} u_{k} u_{l} } \right]_{m} $$

(4)

where L and NL indicate linear and nonlinear terms, respectively. The Jacobian for a ipth component can be computed from the u-derivative for the internal force as follows:

$$ \tilde{\text{K}}_{ip}^{t} = \frac{{\partial {\tilde\Gamma }_{i} \left( {\mathbf{u}} \right)}}{{\partial u_{p} }} = \mathop \sum \limits_{m = 1}^{{N_{e} }} \left[ {K_{ip}^{1} + K_{ijk}^{2} \left( {\delta_{jp} u_{k} + \delta_{kp} u_{j} } \right) + K_{ijkl}^{3} \left( {\delta_{jp} u_{k} u_{l} + \delta_{kp} u_{j} u_{l} + \delta_{lp} u_{j} u_{k} } \right)} \right]_{m} $$

(5)

The Jacobian can also be separated into ${\tilde{\mathbf{K}}}^{L}$ and ${\tilde{\mathbf{K}}}^{NL} \left( {\mathbf{u}} \right)$.

$$ \tilde{\text{K}}_{ip}^{L} = \mathop \sum \limits_{m = 1}^{{N_{e} }} \left[ {K_{ip}^{1} } \right]_{m} $$

(6)

$$ \tilde{\text{K}}_{ip}^{NL} \left( {\text{u}} \right) = \mathop \sum \limits_{m = 1}^{{N_{e} }} \left[ {K_{ijk}^{2} \left( {\delta_{jp} u_{k} + \delta_{kp} u_{j} } \right) + K_{ijkl}^{3} \left( {\delta_{jp} u_{k} u_{l} + \delta_{kp} u_{j} u_{l} + \delta_{lp} u_{j} u_{k} } \right)} \right]_{m} $$

(7)

Based on Equation (2) and (5), the internal forces and Jacobians for the full-order system can be constructed by updating the polynomial variables. In the present work, the indicial form of the vectors and matrices was introduced. In Equations (2)–(7), the subscripts, $i, j, k, l, p = 1, \ldots ,N$, and u_j is the displacement components corresponding to the jth global degree of freedom, only the degrees of freedom included in the mth element are used. δ_ij is the Kronecker delta in Equations (5)–(7)

$$ \delta_{ij} = \left\{ {\begin{array}{*{20}l} 0 \hfill & {\quad {\text{if}}\quad i \ne j,} \hfill \\ 1 \hfill & {\quad {\text{if}}\quad i = j.} \hfill \\ \end{array} } \right. $$

(8)

To increase the efficiency of the inverse calculation in the online stage, the E-STEP ROM employs the POD method. Proper orthogonal bases are extracted from the sampled displacement data using the singular value decomposition (SVD) method. The displacement vector can be expressed as follows:

$$ {\mathbf{u}} \approx {\mathbf{\Phi q}} $$

(9)

where ${\varvec{\Phi}} \in {\mathbb{R}}^{N \times r}$ and ${\mathbf{q}} \in {\mathbb{R}}^{r}$ are selected a few POD bases, $r \ll N$, and reduced displacement vector. The POD bases are used to project the high-dimensional full system into a low-dimensional subspace to construct a reduced system. By substituting Equations (2)–(7) into Equation (1) and applying the POD method, the reduced system can be constructed with the cubic polynomial model as

$$ {\varvec{\Phi}}^{\text{T}} {\mathbf{M\Phi \ddot{q}}} + {\varvec{\Phi}}^{\text{T}} {\mathbf{C\Phi \dot{q}}} + {\varvec{\Phi}}^{\text{T}} \left( {{\tilde{\mathbf{\Gamma }}}^{L} \left( {{\mathbf{u}}_{0} } \right) + {\tilde{\mathbf{\Gamma }}}^{NL} \left( {{\mathbf{u}}_{0} } \right)} \right) + {\varvec{\Phi}}^{\text{T}} \left( {{\tilde{\mathbf{K}}}^{L} + {\tilde{\mathbf{K}}}^{NL} \left( {{\mathbf{u}}_{0} } \right)} \right){\varvec{\Phi}}\Delta {\mathbf{q}} = {\varvec{\Phi}}^{\text{T}} {\mathbf{F}}^{ext} $$

(10)

Because the stiffness coefficients K¹, K², and K³ are predetermined and fixed in the offline stage, the nonlinear system can be constructed by updating only the polynomial variables. In addition, the inverse calculation can be efficiently performed in the low-dimensional reduced system.

However, the number of polynomial equations and variables directly affects the efficiency of the E-STEP ROM, and the numbers increase as the degrees of freedom in one element increases. The number of polynomial variables generated in one element is listed in Table 1 for several element types and dimensions. Table 1 shows that even if we consider overlapping adjacent elements, the number of polynomial variables increase rapidly depending on the degrees of freedom in the element. Therefore, we propose the HE-STEP ROM method to reduce the number of polynomial equations and variables. The proposed method achieve higher computational efficiency than the E-STEP ROM in the offline and online stages and reduce the computer storage requirement.

Table 1 Number of polynomial variables occurring in one element for various element types and dimensions

3 Element-wise stiffness evaluation procedure combined with hyper-reduction reduced-order modeling (HE-STEP ROM)

The hyper-reduction method constructs a nonlinear system only at a few selected sampling points, and approximates a full nonlinear system using interpolation techniques. Therefore, the proposed approach evaluates the stiffness coefficients only at the sampling points using the cubic polynomial, and approximates the stiffness coefficients for the other degrees of freedom using the hyper-reduction technique. This reduces the number of cubic polynomial equations and variables, which reduces the computational costs in the offline/online stages.

The most popular hyper-reduction method is the DEIM proposed by Chaturantabut and Sorensen [22]. The DEIM extracts a DEIM basis from the nonlinear internal force data by using the SVD method to construct the approximation model for the nonlinear internal forces. The nonlinear internal force can then be expressed using the DEIM bases, as follows:

$$ {\tilde{\mathbf{\Gamma }}}^{NL} = {\varvec{\Gamma}} - {\tilde{\mathbf{\Gamma }}}^{L} \approx {\mathbf{\Omega c}} $$

(11)

here ${\tilde{\mathbf{\Gamma }}}^{NL}$ is the nonlinear internal force term of the cubic polynomial model and can be obtained using the sampled internal force Γ and the linear internal force ${\tilde{\mathbf{\Gamma }}}^{L}$ of the cubic polynomial model. Further, ${\varvec{\Omega}} \in {\mathbb{R}}^{N \times p}$ and ${\mathbf{c}} \in {\mathbb{R}}^{p}$ denote the DEIM bases ($p \ll N$) and reduced nonlinear internal force terms, respectively.

Hereafter, we will use the shorthand ${\tilde{\mathbf{\Gamma }}}^{NL} = {\mathbf{\Omega c}}$ to simplify the notation. Let a Boolean matrix ${\mathbf{Z}} = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {{\mathbf{e}}_{1} } & {{\mathbf{e}}_{2} } \\ \end{array} } & {\begin{array}{*{20}c} \cdots & {{\mathbf{e}}_{p} } \\ \end{array} } \\ \end{array} } \right] \in {\mathbb{R}}^{N \times p}$ be the selected sampling point matrix, where ${\mathbf{e}}_{i} \in {\mathbb{R}}^{N}$ is the ith canonical unit vector. The nonlinear internal force vector can be approximated using the Boolean matrix Z and DEIM bases Ω as follows.

$$ {\mathbf{Z}}^{\text{T}} {\tilde{\mathbf{\Gamma }}}^{NL} = \left( {{\mathbf{Z}}^{\text{T}} {\varvec{\Omega}}} \right){\mathbf{c}} $$

(12)

$$ {\mathbf{c}} = \left( {{\mathbf{Z}}^{\text{T}} {\varvec{\Omega}}} \right)^{ - 1} {\mathbf{Z}}^{\text{T}} {\tilde{\mathbf{\Gamma }}}^{NL} $$

(13)

$$ {\tilde{\mathbf{\Gamma }}}^{NL} = {\mathbf{\Omega c}} = {\varvec{\Omega}}\left( {{\mathbf{Z}}^{\text{T}} {\varvec{\Omega}}} \right)^{ - 1} {\mathbf{Z}}^{\text{T}} {\tilde{\mathbf{\Gamma }}}^{NL} $$

(14)

The nonlinear internal force vector is approximated as ${\varvec{\Omega}}\left( {{\mathbf{Z}}^{\text{T}} {\varvec{\Omega}}} \right)^{ - 1} {\mathbf{Z}}^{\text{T}}$ and ${\tilde{\mathbf{\Gamma }}}^{NL} \varvec{ }$ calculated only at the sampling points p. Subsequently, applying Equation (14) to the internal force and Jacobian of the cubic polynomial model, these can be expressed as the following equations:

$$ {\tilde{\mathbf{\Gamma }}}^{L} \left( {\mathbf{u}} \right) + {\tilde{\mathbf{\Gamma }}}^{NL} \left( {\mathbf{u}} \right) \approx {\tilde{\mathbf{\Gamma }}}^{L} \left( {\mathbf{u}} \right) + {\varvec{\Omega}}\left( {{\mathbf{Z}}^{\text{T}} {\varvec{\Omega}}} \right)^{ - 1} {\mathbf{Z}}^{\text{T}} {\tilde{\mathbf{\Gamma }}}^{NL} \left( {\mathbf{u}} \right) $$

(15)

$$ {\tilde{\mathbf{K}}}^{L} + {\tilde{\mathbf{K}}}^{NL} \left( {\mathbf{u}} \right) \approx {\tilde{\mathbf{K}}}^{L} + {\varvec{\Omega}}\left( {{\mathbf{Z}}^{\text{T}} {\varvec{\Omega}}} \right)^{ - 1} {\mathbf{Z}}^{\text{T}} {\tilde{\mathbf{K}}}^{NL} \left( {\mathbf{u}} \right) $$

(16)

The linear terms are maintained, but the nonlinear terms are changed by the hyper-reduction technique. By substituting Equations (15–16) into Equation (10), the non-intrusive reduced-order model for the equilibrium can be expressed using precomputed matrix ${\mathbf{P}} = {\varvec{\Phi}}^{\text{T}} {\varvec{\Omega}}\left( {{\mathbf{Z}}^{\text{T}} {\varvec{\Omega}}} \right)^{ - 1} {\mathbf{Z}}^{\text{T}}$ as follows:

$$ {\varvec{\Phi}}^{\text{T}} {\mathbf{M\Phi \ddot{q}}} + {\varvec{\Phi}}^{\text{T}} {\mathbf{C\Phi \dot{q}}} + {\varvec{\Phi}}^{\text{T}} {\tilde{\mathbf{\Gamma }}}^{L} \left( {{\mathbf{u}}_{0} } \right) + {\mathbf{P\tilde{\Gamma }}}^{NL} \left( {{\mathbf{u}}_{0} } \right) + {\varvec{\Phi}}^{\text{T}} {\tilde{\mathbf{K}}}^{L} {\varvec{\Phi}}\Delta {\mathbf{q}} + {\mathbf{P\tilde{K}}}^{NL} \left( {{\mathbf{u}}_{0} } \right){\varvec{\Phi}}\Delta {\mathbf{q}} = {\varvec{\Phi}}^{\text{T}} {\mathbf{F}}^{ext} $$

(17)

For the nonlinear stiffness coefficients, the E-STEP method evaluates at the total degrees of freedom, but the proposed approach only needs to be evaluated at a few sampling points. Accordingly, the number of cubic polynomial equations and variables is reduced because the degree of freedom in which the stiffness coefficient has to be evaluated is reduced. The determining stiffness coefficients procedure via least square method in the offline stage and the number of polynomial variables that are updated in the online stage are reduced.

The sampling points and DEIM bases affect efficiency, robustness, and accuracy of the HE-STEP ROM. In the hyper-reduction methods, various sampling point selection strategies have been studied to select the optimal points [25, 38, 39]. In this study, the GappyPOD + E (where E is the eigenvector) deterministic sampling strategy proposed by Peherstorfer is used to select optimal sampling points [40]. The method can stably construct DEIM approximation model even for noisy data. The method is based on the lower bound for the smallest eigenvalues of the updated matrix [41], and takes more sampling points than the number of DEIM bases. Detailed explanations and derivation of formulation can be found in Refs. [40] and Appendix B.

The sampling point selection approach of the GappyPOD + E is summarized in Algorithm 1. Hence, the oversampling points matrix is expressed as ${\mathbf{Z}} \in {\mathbb{R}}^{{N \times \left( {p + o} \right)}}$, in the same way as the previous general sampling point matrix. Further, o is the number of oversampled points. Let $\uplambda_{1}^{\left( o \right)} , \ldots ,\uplambda_{N}^{\left( o \right)}$ be the eigenvalues of ${\varvec{\Sigma}}_{o}^{2}$, both arranged in descending order, ${\mathbf{Z}}^{\text{T}} {\varvec{\Omega}} = {\mathbf{V}}_{o} {\varvec{\Sigma}}_{o} {\mathbf{W}}_{o}^{\text{T}}$. In line 1 of Algorithm 1, the first p points are determined via QR factorization, using the column pivoting method. For each point, $i = p + 1 \,{\text{to}}\, o$, the right-singular vectors W_o are obtained by using the SVD of ${\mathbf{Z}}^{\text{T}} {\varvec{\Omega}}$ and the eigengap, g, is obtained on line 5. Then, ${\bar{\mathbf{\Omega }}} = {\mathbf{W}}_{o}^{\text{T}} {\varvec{\Omega}}^{\text{T}}$ is obtained on line 6. The bound Equation is computed from ${\bar{\mathbf{\Omega }}}$ for each column in line 7 and sorted in descending order on line 8. In bound equation, $\varvec{\omega}_{ + } \in {\mathbb{R}}^{1 \times N}$ is the row of Ω for the new sampling point and $\varvec{z}_{N}^{\left( p \right)} \in {\mathbb{R}}^{N}$ is the Nth canonical unit vector of dimension N. $( {\varvec{z}_{N}^{\left( o \right)} } )^{\text{T}} \bar{\varvec{\omega }}_{ + }$ for the column $\bar{\varvec{\omega }}_{ + }$ of ${\bar{\mathbf{\Omega }}}$ is obtained as $( {\varvec{z}_{N}^{\left( o \right)} } )^{\text{T}} \bar{\varvec{\omega }}_{ + } = \varvec{z}_{N}^{\left( o \right)} {\mathbf{W}}_{o}^{\text{T}}\varvec{\omega}_{ + }^{\text{T}} = ( {\varvec{w}_{o}^{end} } )\varvec{\omega}_{ + }^{\text{T}}$. $\varvec{w}_{o}^{end}$ is the right-singular vector related to the smallest singular value. In line 8, I is the array of indices of r, sorted in descending order. The sampling point corresponding to the column of ${\bar{\mathbf{\Omega }}}$ with the largest value is additionally determined and this process is repeated.

The appropriate number of sampling points and DEIM bases determine the accuracy and efficiency of the HE-STEP ROM. The numbers should be determined before the stiffness coefficients are evaluated. Therefore, the proposed method uses the averaged relative L₂ error for the nonlinear internal force term to determine the number of components.

$$ err_{DEIM} = \frac{1}{n}\mathop \sum \limits_{i = 1}^{n} \frac{{{\|\tilde{\mathbf{\Gamma }}}^{NL} \left( {:,n_{i} } \right) - {\varvec{\Omega}}\left( {{\mathbf{Z}}^{\text{T}} {\varvec{\Omega}}} \right)^{ - 1} {\mathbf{Z}}^{\text{T}} {\tilde{\mathbf{\Gamma }}}^{NL} \left( {:,n_{i} } \right)\|}}{{{\|\tilde{\mathbf{\Gamma }}}^{NL} \left( {:,n_{i} } \right)\|}} $$

(18)

The plot in Fig. 2 shows the averaged relative L₂ error between the sampled internal force data and approximated internal force for a plate problem. We can observe that the averaged relative L₂ error stabilizes when the number of DEIM bases and sampling points reach certain values. In the proposed method, we can determine the number of components by referring to the error plot.

4 Numerical results

This section demonstrates the performance of the HE-STEP ROM for several dynamic structural mechanical problems. We present three applications to verify the geometric and material nonlinearities and higher-order elements. The sampling analyses to construct the reduction system were performed using the ABAQUS. In this study, we set the ABAQUS integration scheme with the Newmark-β method to analyze the dynamic systems. The HE-STEP reduction systems were constructed and simulated in the MATLAB.

In other non-intrusive ROM papers [48,49,50,51], the ROM results were compared with those of a full system. In addition, E-STEP ROM is a suitable comparison object to verify the two main contributions of the proposed method (efficiency improvement, non-intrusive). Therefore, the efficiency and accuracy of the HE-STEP ROM method were compared with those of ABAQUS and E-STEP ROM solutions.

4.1 Plate with a hole

A 2-D plate with a hole is investigated to consider the effectiveness of the proposed method for the problem involving material nonlinearity, as depicted in Figure 1. The plate with a hole is modeled with a nearly incompressible Neo-Hooke material with parameters corresponding to C10 = 345000 and D1 = 0.00001. The size of the plate is 0.5 × 0.5 m with a thickness of 0.01 m. The density of the material is 1522 kg/m³. With respect to the FE model, the number of degrees of freedom corresponds to 5176. Furthermore, 4944 CPS3 (plane stress) elements are adapted in ABAQUS.

Fig. 1

Two-dimensional plane stress model consisting of a hyperelastic material. Analysis conditions for the plate (a), and distribution of nodes with the selected sampling points (b)

Figure 1 shows that the left edge is fixed for displacements in the x- and y-directions, and external forces are applied on the right edge. To construct the HE-STEP reduction system, we executed the sampling analyses for three cases with external forces via ABAQUS. The three force magnitude cases are simulated for $\left[ {F_{x} , F_{y} } \right] = \left[ {5, 0} \right], \left[ {3, - 2} \right], \left[ {3, 2} \right] \left( N \right)$ with the following equation:

$$ \vec{F}\left( t \right) = \left( {F_{x} sin\left( {2\pi t} \right)} \right) \cdot \hat{X} + \left( {F_{y} sin\left( {2\pi t} \right)} \right) \cdot \hat{Y} $$

(19)

Furthermore, 1300 data points with the displacement and internal force in each case are sampled during analysis time of $\left[ {0, 1.3s} \right]$ at a uniform time interval. The reduced system was simulated to validate the accuracy and efficiency by applying a complex external force as follows:

$$ \vec{F}_{test} \left( t \right) = \left( {sin\left( {2\pi t} \right) + sin\left( {3.85\pi t} \right)} \right) \cdot \hat{X} + \left( {sin\left( {2\pi t} \right) + sin\left( {3.85\pi t} \right)} \right) \cdot \hat{Y} $$

(20)

We use Algorithm 2 to obtain the sampling points and DEIM bases, and err_DEIM depicted in Figure 2 is calculated from Equation (18) to determine the number of DEIM bases and sampling points. Figure 2 shows that when the number of DEIM bases and sampling points reaches certain values, err_DEIM becomes stable. Additionally, the error values are more stable when oversampling is performed. Based on the err_DEIM values, we set the reasonable numbers to construct the reduction system. Subsequently, the reduced system for the plate model is constructed with 60 POD bases, 80 DEIM bases, and 100 sampling points. Thus, 100 cubic polynomial equations for sampling points are required to construct reduced system. The distribution of the sampling points is illustrated in Figure 1 (b) as red dots. We can observe that the sampling points are distributed in a structurally meaningful location. Sampling points are distributed at a specific locations and the number of elements including sampling points is 276 out of total of 4944. Since the number of sampling points as well as the number of elements including the sampling points affect the number of polynomial variables, it also affects computation efficiency.

Fig. 2

Averaged relative L₂ errors for the QDEIM and GappyPOD with oversampling

Figure 3 (a) shows the number of polynomial variables for nonzero coefficients when compared with the E-STEP ROM method. The number of variables decreased to 0.097% when compared with the E-STEP ROM method. This has a significant effect on the offline computation time, and online computation time for arbitrary force conditions. In Figure 3 (b), the offline computation time, i.e., stiffness coefficients evaluation procedure, is approximately 20.27 times faster because of the reduction in the number of polynomial variables. The CPU time is used to compare the online computation time with other analysis methods. Figure 3 (c) shows that the CPU time of the HE-STEP ROM is 28.35 times faster than that of ABAQUS and 8.68 times faster than that of the E-STEP ROM method.

Fig. 3

Number of polynomial variables (a) and offline computation time (b) for the E-STEP ROM and HE-STEP ROM. Online computation time (c) for the dynamic analysis of the plate with a hole

The solution responses of the ABAQUS, E-STEP ROM, and HE-STEP ROM are illustrated in Figure 4. The displacements are measured at the middle of the right edge, as indicated by the black point in Figure 1 (a). The ABAQUS solution is denoted with red lines, and the E-STEP ROM and HE-STEP ROM solutions are denoted with blue lines and green lines, respectively. To measure the accuracy of the proposed method, the mean relative error estimation method is used at an arbitrary single node.

$$ err_{SN} = \frac{{\mathop \sum \nolimits_{i = 1}^{{N_{s} }} \|{\mathbf{u}}_{i}^{refer} - {\mathbf{u}}_{i}^{ROM}\|_{2} }}{{\mathop \sum \nolimits_{i = 1}^{T} \|{\mathbf{u}}_{i}^{refer}\|_{2} }} \times 100\,(\% ) $$

(21)

where N_s denotes the number of solution responses with respect to the analysis time. Specifically, ${\mathbf{u}}_{i}^{refer}$ and ${\mathbf{u}}_{i}^{ROM}$ denote the ABAQUS displacement and HE-STEP ROM displacement solutions at the single node, respectively. Furthermore, err_SN in the x-direction and y-direction at the black point node are calculated, and they correspond to 0.198% and 0.1251%, respectively.

Fig. 4

x-displacement (a) and y-displacement (b) dynamic solution responses for the plate with a hole problem, as computed via the ABAQUS, E-STEP ROM, and HE-STEP ROM

The deformation shape and displacement difference (x- and y-direction) between the ABAQUS and HE-STEP ROM solutions are depicted in Figures 5 and 6. The red edges indicate the deformation shape of the ABAQUS, while the purple edges indicate the deformation shape of the HE-STEP ROM. The displacement difference at each node was calculated by $\left| {{\mathbf{u}}_{{}}^{refer} - {\mathbf{u}}_{{}}^{ROM} } \right|$, and these were drawn inside the mesh. The color bar indicates the difference in values. We can observe that the displacement solution of the HE-STEP ROM is approximately the same as that of ABAQUS. Figure 7 shows the von Mises stress distribution of the ABAQUS and HE-STEP ROM solutions. It was confirmed that similar values and distributions appeared in these as well. Hence, the HE-STEP ROM method exhibits superior performance to the ABAQUS and E-STEP ROM with satisfactory accuracy and high efficiency.

Fig. 5

Deformation shape and the x-displacement difference of the plate with a hole problem, as computed via the ABAQUS and HE-STEP ROM at 0.15 s (a), 0.93 s (b), and 1.5 s (c)

Fig. 6

Deformation shape and the y-displacement difference of the plate with a hole problem, as computed via the ABAQUS and HE-STEP ROM at 0.15 s (a), 0.93 s (b), and 1.5 s (c)

Fig. 7

von Mises stress fields of the plate with a hole problem, as computed via the ABAQUS (a–c) and HE-STEP ROM (d–f)

4.2 Corner brace

The corner brace model is examined to demonstrate the performance for geometric nonlinearities with large deformations, as depicted in Fig. 8. The material of the corner brace is set with a 2-D nearly incompressible Neo-Hooke hyperelastic material with C10 = 345000, D1 = 0.00001, and density corresponding to 1522 kg/m³. The corner brace is modeled with 2184 degrees of freedom and 990 CPS4 (plane stress) elements in ABAQUS. The lower edge of the model is constrained by zero-displacement boundary conditions, and the external force acts on the tip of the left edge to generate a large deformation.

Fig. 8

Two-dimensional corner brace model with a hyperelastic material. Configuration of corner brace model (a) and distribution of nodes with selected sampling points (b)

Furthermore, 900 data points for each case were sampled at uniform time distribution during [0, 0.9 s]. Sampling analyses are performed with the following external force equation for two magnitude cases: $\left[ {F_{x} , F_{y} } \right] = \left[ {0, 2} \right], \left[ {4, 0} \right] \left( N \right)$.

$$ \left\{ {\begin{array}{*{20}l} {\vec{F}\left( t \right) = \left( {F_{x} sin\left( {10\pi t} \right)} \right) \cdot \hat{X} + \left( {F_{y} sin\left( {10\pi t} \right)} \right) \cdot \hat{Y},} \hfill & {\quad t \le 0.1} \hfill \\ {\vec{F}\left( t \right) = 0,} \hfill & {\quad t > 0.1} \hfill \\ \end{array} } \right. $$

(22)

Validation simulation for the HE-STEP ROM is performed with the following force equation to evaluate the performance.

$$ \vec{F}_{test} \left( t \right) = \left( {sin\left( {5\pi t} \right) + sin\left( {20\pi t} \right)} \right) \cdot \hat{Y} $$

(23)

We select the number for DEIM bases and sampling points to construct a reasonable approximation model for the internal force term, as mentioned in Section 4.1. The number of components is determined based on the averaged relative L₂ error for the corner brace, as shown in Fig. 9. The figure shows that when oversampling is applied, the values of the errors are more stable than those of common QDEIM [40]. Therefore, we used 40 POD bases, 120 DEIM bases, and 140 sampling points to construct the reduction system. The distribution of nodes with 140 sampling points is illustrated at red points in Fig. 8. Furthermore, it is evident that the nodes are mainly distributed in the edges similar to that in the plate with a hole problem.

Fig. 9

Averaged relative L₂ error for the corner brace problem

The cubic polynomial equations decrease from total degrees of freedom (2184) to the number of sampling points (140) and the number of elements including sampling points is 244 out of a total of 990 elements. Figure 10a shows that the number of polynomial variables only decreases from 85144 to 25061. We found that the number of elements, including sampling points, is more important to the rate of reduction of polynomial variables. The offline computation time is reduced by approximately 23.37% when compared with that of E-STEP ROM, as shown in Fig. 10b. The CPU times with respect to online computation time are shown in Fig. 10c, and the CPU times for HE-STEP ROM are 5.65% and 22.6% of CPU time ratio for ABAQUS and E-STEP ROM, respectively.

Fig. 10

Number of polynomial variables (a) and offline computation time (b) for the E-STEP ROM and HE-STEP ROM. Online computation time (c) of the dynamic simulation for the corner brace problem

The solution responses for ABAQUS, E-STEP ROM, and HE-STEP ROM at the black point are plotted in Fig. 11. The err_SN of the proposed approach is 0.2415% in the x-direction and 0.4558% in the y-direction. The deformation shape of each solutions and displacement difference between the ABAQUS and HE-STEP ROM solutions were also drawn in Figs. 12 and 13. The red edges indicate the deformation shape of the ABAQUS, while the purple edges indicate the deformation shape of the HE-STEP ROM. The Von mises stress distributions of the ABAQUS and HE-STEP ROM are depicted in Fig. 14. As we can observe from the displacement difference or the stress distribution, the proposed method agrees well with the overall model results. Hence, the proposed approach shows excellent agreement with respect to the flexible structural dynamics problem involving large deformations.

Fig. 11

Dynamic solution response with x-displacement (a) and y-displacement (b) of the corner brace as computed from the ABAQUS, E-STEP ROM, and HE-STEP ROM

Fig. 12

Deformation shape and the x-displacement difference of the corner brace problem, as computed via the ABAQUS and HE-STEP ROM at 0.25 s (a), 0.5 s (b), and 0.9 s (c)

Fig. 13

Deformation shape and the y-displacement difference of the corner brace problem, as computed via the ABAQUS and HE-STEP ROM at 0.25 s (a), 0.5 s (b), and 0.9 s (c)

Fig. 14

von Mises stress fields of the corner brace problem, as computed via the ABAQUS (a–c) and HE-STEP ROM (d–f)

4.3 Plate Bending

The previous two numerical examples are examined with respect to material or geometrical nonlinearities with conventional solid elements. The plate bending problem considers the effectiveness of the high-order element model. We modeled the plate bending problem with a 6-degrees of freedom shell element and simply supported boundary condition on shortened edges, as depicted in Fig. 15. The model is constructed with 3366 degrees of freedom and 1024 S3 elements with a cross-section of 0.04 × 0.02 m, thickness of 0.0008 m, and density of 2700 kg/m³ in ABAQUS.

Fig. 15

Plate bending model with shell element. Configuration of plate model (a) and distributed nodes with sampling points (b)

We executed the sampling analyses with the following external force conditions on the red points in Fig. 15a. Unlike the previous problems, the external force points are distributed across the model.

$$ \left\{ {\begin{array}{*{20}l} {\vec{F}\left( t \right) = \left( {F_{x} \sin \left( {\omega t} \right)} \right) \cdot \hat{X} + \left( {F_{y} \sin \left( {\omega t} \right)} \right) \cdot \hat{Y},} \hfill & {\quad t \le \frac{\pi }{\omega }} \hfill \\ {\vec{F}\left( t \right) = 0,} \hfill & {\quad t > \frac{\pi }{\omega }} \hfill \\ \end{array} } \right. $$

(24)

We collected the sample data for the internal force and displacement at uniform time intervals of 5e⁻⁷ sec over a span of 0.001 s for the two loading cases, i.e., $\left[ {F_{x} , F_{y} , \omega } \right] = \left[ { - 6, - 6, 14825\,{\text{rad/s}}} \right], \left[ { - 8, - 8, 29650 \,{\text{rad/s}}} \right]$. We analyzed the following external force to measure the performance of the HE-STEP ROM for the plate model.

$$ \vec{F}_{test} \left( t \right) = \left( { - sin\left( {14825t} \right) - 3sin\left( {29650t} \right)} \right) \cdot \hat{Y} $$

(25)

Hence, before the stiffness coefficients are evaluated, we compute the averaged relative L₂ error to select the appropriate number of DEIM bases and sampling points. Based on the averaged relative L₂ error (Fig. 16), the HE-STEP reduced system is approximated with 80 POD bases, 100 DEIM bases, and 110 sampling points. The sampling points are scattered throughout the plate bending model, as illustrated in Fig. 15b. Then, the number of cubic polynomial equations decreases from 3366 to 110 and the number of elements including sampling points is 434 out of a total of 1024 elements. The polynomial variables did not decrease as much as shown in Fig. 17a because of the low rate of reduction of the elements including sampling points. Thus, as shown in Fig. 17b, the offline computation time is approximately twice as fast as that of the E-STEP ROM. Based on the previous examples, the efficiency of the online step is expected to be equal to the ratio of polynomial variables. Fig. 17c shows the CPU times, which are compared to those of ABAQUS and E-STEP ROM. The HE-STEP ROM is 1.74 times faster than ABAQUS and 1.63 times faster than E-STEP ROM. Through this example, we confirmed that the number of sampling points as well as the distribution affect the computational efficiency. Because the polynomial variables comprises the combination of all degrees of freedom belonging to an element, if at least one degree of freedom is selected as a sampling point, in element, the polynomial variables are almost maintained. Therefore, this problem shows lower efficiency than other examples.

Fig. 16

Averaged relative L₂ error for the plate bending problem

Fig. 17

Number of polynomial variables (a) and offline computation time (b) for the E-STEP ROM and HE-STEP ROM. Online computation time (c) of the simulation for the plate bending problem

The transient responses for the y-direction displacement and z-axis rotation on a black point on the surface are illustrated in Fig. 18. The err_SN of the proposed approach is 0.1678% for the y-direction displacement and 0.6312% for the z-axis rotation. The deformation shape of each solutions and y-direction displacement difference between the ABAQUS and HE-STEP ROM are illustrated in Fig. 19. The red edges indicate the deformation shape of the ABAQUS, while the purple edges indicate the deformation shape of the HE-STEP ROM. Figure 20 depicts the Von mises stress distributions of the ABAQUS and HE-STEP ROM solutions. Similar to other numerical examples, the proposed method results matched well with the ABAQUS results, and it was confirmed that the proposed method was accurate. The figures show that the solutions from ABAQUS and HE-STEP ROM are in good agreement with the ABAQUS solution.

Fig. 18

Transient responses with y-displacement (a) and rotation of z-axis (b) for the plate bending problem, as computed using the ABAQUS, E-STEP ROM, and HE-STEP ROM

Fig. 19

Deformation shape and the y-displacement difference of the plate bending problem, as computed via the ABAQUS and HE-STEP ROM at 0.32 ms (a), 0.52 ms (b), and 1 ms (c)

Fig. 20

von Mises stress fields of the plate bending problem, as computed via the ABAQUS (a–c) and HE-STEP ROM (d–f)

5 Conclusion

This study proposed the HE-STEP ROM to reduce the overall computational costs of E-STEP ROM. The hyper-reduction method was employed to reduce the number of cubic polynomial equations and variables required to construct stiffness coefficients, which significantly enhanced the efficiency of the offline and online computational efficiencies. The number of DEIM bases and sampling points that are the most important factors in determining the accuracy and efficiency of HE-STEP ROM must be determined as the averaged relative L₂ error in the offline stage.

The HE-STEP ROM is effective in the following procedures: In the offline stage, the stiffness coefficients for the internal force term are evaluated at only a few selected sampling points. The stiffness coefficients of the residual degrees of freedom are approximated via the hyper-reduction. As the number of cubic polynomial equations decreases, the computation time required to determine the stiffness coefficients also decreases; thus, it is efficient. Furthermore, in the online stage, the number of polynomial variables is reduced, then the nonlinear system is updated with a lower computational amount.

The numerical problems presented in Section 4 exhibit reasonable accuracy and efficiency for several nonlinear dynamic structural examples. The HE-STEP ROM was applied to problems with material and geometrical nonlinearities and high-order elements. Through these examples, it was confirmed that the number of elements, including sampling points, as well as the number of sampling points is important when determining the computational efficiency improvement of the HE-STEP ROM. Further, the efficiency improvement of the proposed method depends on how much it reduces polynomial variables. In particular, the number of sampling points affects the reduction of the polynomial variables. However, how the sampling points are distributed also affects the reduction of polynomial variables. The cubic polynomial equations consist of the combination of all degrees of freedom present in the element. Therefore, when at least one degree of freedom related to an element is selected as a sampling point, the polynomial variables generated from that element are almost maintained. If the sampling points are evenly distributed as in the plate bending example, the efficiency of the HE-STEP ROM decreases. However, we confirmed that the efficiency improvement is evident when the proposed method is compared to those of ABAQUS and E-STEP ROM methods.

Appendices

Appendix A : Stiffness evaluation procedure using the least squares method

To clarify the explanation, the displacement combination and stiffness coefficient matrices in Equation (2) are newly defined, as follows:

$$ \Gamma _{i} \left( {\mathbf{u}} \right) = \Gamma _{i} \left( {\mathbf{u}} \right)_{1} + \Gamma _{i} \left( {\mathbf{u}} \right)_{2} \cdots + \Gamma _{i} \left( {\mathbf{u}} \right)_{En} \approx \mathop \sum \limits_{m = 1}^{En} \left[ {K_{ijkl}^{{}} u_{j} u_{k} u_{l} } \right]_{m} $$

(A1)

where K_ijkl includes $K_{ij}^{1} ,K_{ijk}^{2}$, and $K_{ijkl}^{3}$ in Equation (A1). u_ju_ku_l is the displacement combination, which includes 1 as its value, and can also be expressed as u_j and u_ju_k ($u_{j} \cdot 1 \cdot 1$ and $u_{j} u_{k} \cdot 1$).

If the sample data sets, with internal force and displacement, are collected from the sampling analysis, the internal force model of Equation (A1) for the mth element can be represented as follows:

$$ \left[ {\begin{array}{*{20}c} {\Gamma _{11} } & \cdots & {\Gamma _{1S} } \\ \vdots & \ddots & \vdots \\ {\Gamma _{n1} } & \cdots & {\Gamma _{nS} } \\ \end{array} } \right]_{m} = \left[ {\begin{array}{*{20}c} {\tilde{K}_{11} } & \cdots & {\tilde{K}_{1p} } \\ \vdots & \ddots & \vdots \\ {\tilde{K}_{n1} } & \cdots & {\tilde{K}_{np} } \\ \end{array} } \right]_{m} \times \left[ {\begin{array}{*{20}c} {\tilde{u}_{11} } & \cdots & {\tilde{u}_{1S} } \\ \vdots & \ddots & \vdots \\ {\tilde{u}_{p1} } & \cdots & {\tilde{u}_{pS} } \\ \end{array} } \right]_{m} $$

(A2)

where m, n, p, and S are the element number, number of degrees of freedom for one element, number of displacement combinations for one element, and quantity of sample data, respectively. $\tilde{K}$ and $\tilde{u}$ indicate one combination of K_ijkl and u_ju_ku_l in Equation (A1), respectively. Γ_m and $\tilde{\varvec{u}}_{m}$ are the sampled internal force and displacement combination matrix in Equation (A2), respectively. Equation (A2) can be expressed as ${\varvec{\Gamma}}_{m} = \tilde{\varvec{K}}_{m} \tilde{\varvec{u}}_{m}$. The least squares method is used to evaluate the stiffness coefficient matrix, $\tilde{\varvec{K}}_{m}$, even if it is not a square matrix. Thus, the stiffness coefficient matrix can be solved for displacement combinations using the least squares method, as follows:

$$ \left[ {\begin{array}{*{20}c} {\Gamma _{11} } & \cdots & {\Gamma _{1S} } \\ \vdots & \ddots & \vdots \\ {\Gamma _{n1} } & \cdots & {\Gamma _{nS} } \\ \end{array} } \right]_{m} \left[ {\begin{array}{*{20}c} {\tilde{u}_{11} } & \cdots & {\tilde{u}_{1S} } \\ \vdots & \ddots & \vdots \\ {\tilde{u}_{p1} } & \cdots & {\tilde{u}_{pS} } \\ \end{array} } \right]_{m}^{ - 1} = \left[ {\begin{array}{*{20}c} {\tilde{K}_{11} } & \cdots & {\tilde{K}_{1p} } \\ \vdots & \ddots & \vdots \\ {\tilde{K}_{n1} } & \cdots & {\tilde{K}_{np} } \\ \end{array} } \right]_{m} $$

(A3)

The above process is performed for all elements and a stiffness coefficient suitable for each degree of freedom in the global system is assembled.

Appendix B: GappyPOD + E deterministic sampling strategy

The L₂ error of the approximation model satisfies the following equation:

$$ \|{\varvec{\Gamma}}^{nl} - {\tilde{\mathbf{\Gamma }}}^{nl}\|_{2} \le \|\left( {{\mathbf{Z}}^{\text{T}} {\varvec{\Omega}}} \right)^{\dag }\|_{2} \|{\varvec{\Gamma}}^{nl} - {\mathbf{\Omega \Omega }}^{\text{T}} {\varvec{\Gamma}}^{nl}\|_{2} $$

(B1)

Here, $\|{\varvec{\Gamma}}^{nl} - {\mathbf{\Omega \Omega }}^{\text{T}} {\varvec{\Gamma}}^{nl}\|_{2}$ affects the approximation quality of the subspace spanned by Ω, and $\|\left( {{\mathbf{Z}}^{\text{T}} {\varvec{\Omega}}} \right)^{\dag }\|_{2}$ quantifies the effectiveness of the sampling points.

To achieve robustness and minimize the quantity $\|\left( {{\mathbf{Z}}^{\text{T}} {\varvec{\Omega}}} \right)^{\dag }\|_{2}$ with a small number of sampling points, Refs. [40] proposed the GappyPOD + E (where E is the eigenvector) deterministic sampling strategy. The GappyPOD + E algorithm is based on the lower bound for the smallest eigenvalues of the updated matrix, which was introduced in [41]. The minimization problem is equal to maximizing the smallest eigenvalue of ${\mathbf{Z}}^{\text{T}} {\varvec{\Omega}}$.

$$ \|\left( {{\mathbf{Z}}^{\text{T}} {\varvec{\Omega}}} \right)^{\dag }\|_{2} = s_{max} \left( {\left( {{\mathbf{Z}}^{\text{T}} {\varvec{\Omega}}} \right)^{\dag } } \right) = \frac{1}{{s_{min} \left( {{\mathbf{Z}}^{\text{T}} {\varvec{\Omega}}} \right)}} $$

(B2)

where $s_{max} \left( {\mathbf{B}} \right)$ and $s_{min} \left( {\mathbf{B}} \right)$ indicate the largest and smallest singular values of B, respectively. The GappyPOD + E algorithm follows the lower bounds of the smallest eigenvalues to select the sampling points that maximize $s_{min} \left( {\mathbf{B}} \right)$; this is achieved by leveraging the eigenvector corresponding to the smallest eigenvalue. In this paper, the relevant summary is explained, and a detailed explanation and formulation can be found in Refs. [40]. If the authors add a sampling point, then ${\mathbf{Z}}_{p + 1}^{T} {\varvec{\Omega}} \in {\mathbb{R}}^{{\left( {p + 1} \right) \times N}}$ becomes

$$ {\mathbf{Z}}_{p + 1}^{T} {\varvec{\Omega}} = \left[ {\begin{array}{*{20}c} {{\mathbf{Z}}_{p}^{T} {\varvec{\Omega}} } \\ {\varvec{\omega}_{ + } } \\ \end{array} } \right], $$

(B3)

where $\varvec{\omega}_{ + } \in {\mathbb{R}}^{1 \times N}$ is the row of Ω for the new sampling point. Zimmermann et al. [46] demonstrated that the change in the singular values of ${\mathbf{Z}}_{p}^{T} {\varvec{\Omega}}$ to ${\mathbf{Z}}_{p + 1}^{T} {\varvec{\Omega}}$ can be computed using a symmetric rank-one update.

$$ {\mathbf{Z}}_{p + 1}^{T} {\varvec{\Omega}} = \left[ {\begin{array}{*{20}c} {\varvec{V}_{p} } & 0 \\ 0 & 1 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {{\varvec{\Sigma}}_{p} } \\ {\varvec{\omega}_{ + } \varvec{W}_{p} } \\ \end{array} } \right]\varvec{W}_{p}^{T} , $$

(B4)

where ${\mathbf{Z}}_{p}^{T} {\varvec{\Omega}} = \varvec{V}_{p} {\varvec{\Sigma}}_{p} \varvec{W}_{p}^{T}$ is computed using the SVD method. The singular values of ${\mathbf{Z}}_{p + 1}^{T} {\varvec{\Omega}}$ are calculated by the square roots of the eigenvalues of $\left( {{\mathbf{Z}}_{p + 1}^{T} {\varvec{\Omega}} } \right)^{T} {\mathbf{Z}}_{p + 1}^{T} {\varvec{\Omega}}$.

$$ \left( {{\mathbf{Z}}_{p + 1}^{T} {\varvec{\Omega}} } \right)^{T} {\mathbf{Z}}_{p + 1}^{T} {\varvec{\Omega}} = \varvec{W}_{p} \left( {{\varvec{\Sigma}}_{p}^{2} + \varvec{W}_{p}^{T}\varvec{\omega}_{ + }^{T}\varvec{\omega}_{ + } \varvec{W}_{p} } \right)\varvec{W}_{p}^{T} = \varvec{W}_{p} {\varvec{\Lambda}}_{p + 1} \varvec{W}_{p}^{T} , $$

(B5)

where the square roots of the eigenvalues of ${\varvec{\Lambda}}_{p + 1}$ are singular values of ${\mathbf{Z}}_{p + 1}^{T} {\varvec{\Omega}}$. Let $\uplambda_{1}^{{\left( {p + 1} \right)}} , \ldots ,\uplambda_{N}^{{\left( {p + 1} \right)}}$ be the eigenvalues of ${\varvec{\Lambda}}_{p + 1}$ and $\uplambda_{1}^{\left( p \right)} , \ldots ,\uplambda_{N}^{\left( p \right)}$ be the eigenvalues of ${\varvec{\Sigma}}_{p}^{2}$, both arranged in descending order. The GappyPOD + E algorithm aims to select a row Ω that maximizes the smallest eigenvalue $\uplambda_{N}^{{\left( {p + 1} \right)}}$. From Weyl’s theorem [47], we have $\uplambda_{N}^{{\left( {p + 1} \right)}} \ge \uplambda_{N}^{\left( p \right)}$, which shows that the additional sampling point will not increase the eigenvalues of $\|\left( {{\mathbf{Z}}_{p + 1}^{T} {\varvec{\Omega}}} \right)^{\dag }\|_{2}$, compared to the eigenvalues of $\|\left( {{\mathbf{Z}}_{p}^{T} {\varvec{\Omega}}} \right)^{\dag }\|_{2}$.

In Refs. [40], the lower bounds for the eigenvalues of the updated matrices, for selecting the sampling point to rapidly increase the smallest eigenvalue, are calculated using the following equation:

$$ {\text{g}} + \|\bar{\varvec{\omega }}_{ + }\|_{2}^{2} - \sqrt {\left( {{\text{g}} + \|\bar{\varvec{\omega }}_{ + }\|_{2}^{2} } \right)^{2} - 4{\text{g}}\left( {\varvec{z}_{N}^{\left( p \right)^{T}} \bar{\varvec{\omega }}_{ + } } \right)^{2} ,} $$

(B6)

where$\bar{\varvec{\omega }}_{ + } = \varvec{W}_{p}^{T}\varvec{\omega}_{ + }^{T}$. $g = \uplambda_{N - 1}^{\left( p \right)} - \uplambda_{N}^{\left( p \right)}$ indicates the eigengap and ${\varvec{\Sigma}}_{p}^{2}$ is the diagonal matrix, with diagonal elements sorted in descending order; thus, $\varvec{z}_{N}^{\left( p \right)} \in {\mathbb{R}}^{N}$ is the Nth canonical unit vector of dimension N. A detailed explanation and derivation of the bound equation can be found in Refs. [40].