1 Introduction

In conforming Galerkin finite element methods, the constitutive relations for the stress as well as the kinematic relations between strain and displacement gradient enter in a strong form, whereas the force balance is imposed only weakly. Depending on the material parameters, the mesh quality and the configuration of the boundary value problem, very fine meshes are required for a sufficiently accurate approximation of the stress, see, e.g., Arnold [1]; Babuška and Suri [4]. It is a well-known observation that more relaxed schemes may improve the convergence using discontinuous ansatz spaces for the displacement when an appropriate balance of both, the approximation of the constitutive relations and the balance laws, is ensured.

On the other hand, on a given mesh discontinuous Galerkin (DG) methods require far more degrees of freedom than conforming methods of the same approximation order. Here, we study two families of hybrid methods, where additional degrees of freedom on the skeleton of the discretization allow for static condensation of the element degrees of freedom resulting in a substantially smaller and sparser system matrix. The first hybrid method uses discontinuous ansatz functions on the faces and stability is achieved by extra degrees of freedom in the elements, whereas the second method uses conforming trace degrees of freedom, and stability is achieved using lower order polynomials in the elements. We compare efficiency and robustness of both approaches with various linear, quadratic conforming and other DG methods.

In general, DG methods for second-order elliptic problems require element boundary terms to achieve consistency and stability. The basic consistency term, see, e.g., Baumann and Oden [5] for convection–diffusion equations, is obtained by testing the force balance with discontinuous ansatz functions and integrating by parts, which results into integrals on the element faces with averages of the tractions and jumps of the test functions. One obtains a non-symmetric and singular variational setting which can be stabilized by an additional non-symmetric term or by penalty, see Arnold et al. [2, 3]. The symmetric version is applied to linear models in solid mechanics in Hansbo and Larson [20], Wihler [47], Liu et al. [29], Di Pietro and Nicaise [17], Grieshaber et al. [19]. Further formulations are applied to plasticity in Liu et al. [30], for finite elasticity in Ten Eyck and Lew [42], Kabaria et al. [23] and for failure in Mergheim et al. [31]. Hybrid methods for linear models are considered in Soon et al. [40], and divergence-free hybrid methods are analyzed in Lehrenfeld and Schöberl [27]. An extensive overview on existing DG methods is given in Di Pietro and Ern [15].

The recently introduced family of discontinuous Petrov–Galerkin (DPG) methods is applied to linear elasticity in various ways, see, e.g., Bramwell et al. [9], Carstensen et al. [11], Carstensen and Hellwig [12], Keith et al. [24]. Here, an ultra-weak multi-field formulation is used, which includes the displacement, the stress in the domain and as the respective trace variables. Hybridization to the trace variables can be performed locally as presented in Wieners and Wohlmuth [46]. The performance of the DPG method is based on an optimal choice of test-functions and highly depends on the choice of the considered spaces. Some choices allow for variants that are free of volume locking. The hybrid-mixed method presented in Harder et al. [21] also uses non-conforming spaces. Here the coupling degrees of freedom are restricted to the traces of the rigid body modes. Unlike the weakly conforming method considered here, the cell-wise spaces are discretized by a subdivision and not with higher order polynomials. The behavior of this approach with respect to volume locking is not studied. In Di Pietro and Ern [16], a locking-free primal formulation on general polyhedral meshes is considered. The absence of volumetric locking is achieved by solving local problems to reconstruct the strain tensor and the divergence using high-order polynomials. Static condensation eliminates interior degrees of freedom, leaving only face degrees of freedom. More traditional locking-free approaches can be based on the Hellinger–Reissner principle or on three-field Hu–Washizu based formulations (e.g., [37, 43]). Suitable choices of the spaces can then result in stable and locking-free formulations in the linear (see [26]) as well as non-linear elasticity setting (see [13]).

In our numerical study, we compare in particular different variants of hybrid DG methods first introduced in Wulfinghoff et al. [48], Reese et al. [34] and Krämer et al. [25] (see also  [45, 46] for the analysis of the hybridization process). The discretizations are defined in the next section in a uniform two-dimensional setting to highlight the different techniques which can be employed to achieve consistency and stability. The main contribution of this work is the numerical study in Sect. 3, where the convergence of these methods is investigated in detail with respect to the robustness in case of locking, nonlinearity and anisotropy. We test representative two- and three-dimensional configurations which can be investigated also by further methods so that one obtains a comprehensive overview and better understanding of stability and robustness issues.

2 The numerical setting

In this section we define different discretizations for hyperelastic materials, where we compute the displacement vector \({\varvec{ u}}\) and the first Piola–Kirchhoff stress tensor \({\varvec{ P}}\). For simplicity of the presentation, we consider the two-dimensional case, but note that the methods easily extend to the three-dimensional case as shown in some numerical examples. For given body forces \(\bar{{\varvec{ f}}}\) in the reference domain \(\Omega \) and traction forces \(\bar{{\varvec{ t}}}\) on the Neumann boundary \(\partial \Omega _t\subset \partial \Omega \) the force balance reads

$$\begin{aligned}&-\,\mathrm{Div }\left( {\varvec{ P}} \right) = \bar{{\varvec{ f}}} \quad \text { in } \Omega , \end{aligned}$$
(1a)
$$\begin{aligned}&{\varvec{ P}}{\varvec{ N}}= \bar{{\varvec{ t}}} \quad \text { on } \partial \Omega _t\,. \end{aligned}$$
(1b)

This is complemented by Dirichlet boundary conditions (\(\partial \Omega _u = \partial \Omega {\setminus }\partial \Omega _t\))

$$\begin{aligned} {\varvec{ u}}&= \bar{{\varvec{ u}}} \quad \text { on } \partial \Omega _u \,, \end{aligned}$$
(1c)

and the system is closed by a constitutive relation \({\varvec{ P}}({\varvec{ F}}) = \partial _{{\varvec{ F}}}\psi ({\varvec{ F}})\) for the strain-energy function \(\psi \) depending on the deformation gradient \({\varvec{ F}}= {\varvec{ I}}+ \mathrm{Grad}\left( {\varvec{ u}} \right) \). For simplicity of the presentation, we consider homogeneous data described by \(\bar{{\varvec{ f}}} = {\varvec{ 0}}\) and \(\bar{{\varvec{ u}}} = {\varvec{ 0}}\).

For conforming test functions \(\delta {\varvec{ u}}\) with \(\delta {\varvec{ u}}= {\varvec{ 0}}\) on \(\partial \Omega _u\) and \(\delta {\varvec{ F}}= \mathrm{Grad}\left( \delta {\varvec{ u}} \right) \) the force balance (1) is given in weak form (without body forces) by

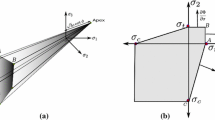
$$\begin{aligned} \int _{\Omega } {\varvec{ P}}: \delta {\varvec{ F}}\mathrm {d} \Omega = \int _{\partial \Omega _t} \bar{{\varvec{ t}}} \cdot \delta {\varvec{ u}}\, \mathrm {d} S \,. \end{aligned}$$

This is the starting point for discretizations on a family of triangulations \(\mathcal {T}_h\) with (open) quadrilaterals \(\Omega _e\) and with the skeleton \(\Gamma = \bigcup _{\Omega _e\in \mathcal {T}_h} \partial \Omega _e\) such that \(\overline{\Omega } = \bigcup _{\Omega _e\in \mathcal {T}_h} \Omega _e \cup \Gamma \). Integration by parts yields for the normal traction \({\varvec{ t}}_e = {\varvec{ P}}{\varvec{ N}}_e\)

$$\begin{aligned} \int _{\Omega _e} {\varvec{ P}}: \delta {\varvec{ F}}\mathrm {d} \Omega = \int _{\partial \Omega _e} {\varvec{ t}}_e \cdot \delta {\varvec{ u}}\, \mathrm {d} S \end{aligned}$$
(2)

on every quadrilateral \(\Omega _e\). Summing up (2) allows to combine the contributions on the inner faces. Therefore, we select an orientation of these faces and define the displacement jump

$$\begin{aligned}{}[{\varvec{ u}}] = {\left\{ \begin{array}{ll} {\varvec{ u}}_+- {\varvec{ u}}_{-} &{}\quad \text {on inner faces,}\\ {\varvec{ u}}&{}\quad \text {on boundary faces,}\\ \end{array}\right. } \end{aligned}$$

as well as the averaged normal traction

$$\begin{aligned} \{{\varvec{ t}}\}= {\left\{ \begin{array}{ll} ( {\varvec{ t}}_+ + {\varvec{ t}}_-)/2 &{}\quad \text {on inner faces,}\\ {\varvec{ t}}&{}\quad \text {on boundary faces,}\\ \end{array}\right. } \end{aligned}$$

see Fig. 1 for an illustration. This yields for \({\varvec{ H}}(\mathrm {div})\)-conforming stress and discontinuous test function the statement

$$\begin{aligned} \sum _e \int _{\Omega _e} {\varvec{ P}}: \mathrm{Grad}\left( \delta {\varvec{ u}}_h \right) \mathrm {d} \Omega= & {} \int _{\Gamma {\setminus }\partial \Omega _t} \{{\varvec{ P}}{\varvec{ N}}\} \cdot [\delta {\varvec{ u}}_h] \,\mathrm {d} S\nonumber \\&+ \int _{\partial \Omega _t} \bar{{\varvec{ t}}} \cdot \delta {\varvec{ u}}_h \,\mathrm {d} S \,. \end{aligned}$$
(3)
Fig. 1
figure 1

Illustration of the discrete setting

Full size image

2.1 The discontinuous Galerkin method

For DG methods we select local polynomial ansatz spaces \({\varvec{ V}}_{h,e}\), and we define the discontinuous ansatz and test space

$$\begin{aligned} {\varvec{ V}}_h^\mathrm{DG} = \big \{ {\varvec{ u}}_h\in {\varvec{ L}}_2(\Omega )^2:{\varvec{ u}}_h|_{\Omega _e}\in {\varvec{ V}}_{h,e} \big \} \,. \end{aligned}$$
(4)

Then, corresponding to (3), we define the consistent semi-linear DG form

$$\begin{aligned} a_h^\mathrm{DG}({\varvec{ u}},\delta {\varvec{ u}})= & {} \sum _e \int _{\Omega _e} {\varvec{ P}}({\varvec{ I}}+ \mathrm{Grad}\left( {\varvec{ u}} \right) ) : \mathrm{Grad}\left( \delta {\varvec{ u}} \right) \mathrm {d} \Omega \\&-\! \int _{\Gamma {\setminus }\partial \Omega _t} \{{\varvec{ P}}({\varvec{ I}}+ \mathrm{Grad}\left( {\varvec{ u}} \right) ){\varvec{ N}}\} \cdot [\delta {\varvec{ u}}]\, \mathrm {d} S \,, \end{aligned}$$

i.e., for the exact solution \({\varvec{ u}}\) we have

$$\begin{aligned} a_h^\mathrm{DG}({\varvec{ u}},\delta {\varvec{ u}}_h)=\int _{\partial \Omega _t} \bar{{\varvec{ t}}} \cdot \delta {\varvec{ u}}_h\, \mathrm {d} S \,,\qquad \delta {\varvec{ u}}_h \in {\varvec{ V}}_h^\mathrm{DG} \,. \end{aligned}$$

The linearization of the DG form is not coercive for discontinuous ansatz functions, so that some stabilization is required. Therefore, we now discuss several possibilities to achieve stability by choosing an additional semi-linear form \(s_h^{\mathrm{DG},k}(\cdot ,\cdot )\) so that

$$\begin{aligned} a_h^\mathrm{DG}({\varvec{ u}}_h,{\varvec{ u}}_h) + s_h^{\mathrm{DG},k}({\varvec{ u}}_h,{\varvec{ u}}_h) > 0\,,\qquad {\varvec{ u}}_h\in {\varvec{ V}}_h^\mathrm{DG}\,,\ {\varvec{ u}}_h\ne {\varvec{ 0}}\end{aligned}$$

in case of small strains. Then, for sufficiently small \(\bar{\varvec{ t}}\), a unique solution \({\varvec{ u}}_h\in {\varvec{ V}}_h^\mathrm{DG}\) exists satisfying

$$\begin{aligned}&a_h^\mathrm{DG}({\varvec{ u}}_h,\delta {\varvec{ u}}_h) + s_h^{\mathrm{DG},k}({\varvec{ u}}_h,\delta {\varvec{ u}}_h) \nonumber \\&\quad = \int _{\partial \Omega _t} \bar{{\varvec{ t}}} \cdot \delta {\varvec{ u}}_h\, \mathrm {d} S \,,\qquad \delta {\varvec{ u}}_h \in {\varvec{ V}}_h^\mathrm{DG} \,. \end{aligned}$$
(5)

In order to preserve asymptotic consistency, \(s_h^{\mathrm{DG},k}({\varvec{ u}},\delta {\varvec{ u}}_h) \rightarrow 0\) with \(h\rightarrow 0\) is required for the solution \({\varvec{ u}}\) of the continuous problem and for discontinuous test functions \(\delta {\varvec{ u}}_h\); in general for DG methods full consistency \(s_h^{\mathrm{DG},k}({\varvec{ u}},\delta {\varvec{ u}}_h) =0\) is achieved.

The convergence properties and the robustness of DG methods depend on the choice of the ansatz space and the stabilization. Elementary stabilizations are of Nitsche type penalty ([32])

$$\begin{aligned} s_h^{\mathrm{DG},1}({\varvec{ u}}_h,\delta {\varvec{ u}}_h) = \int _{\Gamma {\setminus }\partial \Omega _t} \theta [{\varvec{ u}}_h] \cdot [\delta {\varvec{ u}}_h]\, \mathrm {d} S \end{aligned}$$
(6)

with parameter \(\theta >0\). Note that in general this parameter depends on the local mesh size, the material parameters and the polynomial degree of the local ansatz spaces \({\varvec{ V}}_{h,e}\).

The DG method only with penalty, named the incomplete interior penalty method (IIPDG), is often used in nonlinear applications. The symmetric interior penalty method (SIPDG) introduced for linear elasticity in Arnold et al. [2, 3] extends to finite strains by minimizing the extended energy with consistency and stabilization terms, i.e.,

$$\begin{aligned} {\varvec{ u}}_h^{\mathrm{DG},2}&= \arg \min _{{\varvec{ u}}_h\in {\varvec{ V}}_h^\mathrm{DG}} \sum _e \int _{\Omega _e} \psi ({\varvec{ I}}+ \mathrm{Grad}\left( {\varvec{ u}}_h \right) ) \mathrm {d} \Omega \\&\quad - \int _{\Gamma {\setminus }\partial \Omega _t} \{{\varvec{ P}}({\varvec{ I}}+ \mathrm{Grad}\left( {\varvec{ u}}_h \right) ){\varvec{ N}}\} \cdot [{\varvec{ u}}_h]\, \mathrm {d} S\\&\quad + \frac{1}{2}\, s_h^{\mathrm{DG},1}({\varvec{ u}}_h,{\varvec{ u}}_h) -\int _{\partial \Omega _t} \bar{{\varvec{ t}}} \cdot {\varvec{ u}}_h\, \mathrm {d} S \,. \end{aligned}$$

In the variational form this additionally yields the adjoint consistency term

$$\begin{aligned} s_h^{\mathrm{DG},2}({\varvec{ u}}_h,\delta {\varvec{ u}}_h) = s_h^{\mathrm{DG},1}({\varvec{ u}}_h,\delta {\varvec{ u}}_h) - s_h^{\mathrm{DG},3}({\varvec{ u}}_h,\delta {\varvec{ u}}_h), \end{aligned}$$
(7)

where

$$\begin{aligned}&s_h^{\mathrm{DG},3}({\varvec{ u}}_h,\delta {\varvec{ u}}_h) \\&\quad = \int _{\Gamma {\setminus }\partial \Omega _t} [{\varvec{ u}}_h] \cdot \{(\partial _F {\varvec{ P}}({\varvec{ I}}+ \mathrm{Grad}\left( {\varvec{ u}}_h \right) ) \mathrm{Grad}\left( \delta {\varvec{ u}}_h \right) {\varvec{ N}}\}\, \mathrm {d} S. \end{aligned}$$

Using \(s_h^{\mathrm{DG},3}\) without any Nitsche type stabilization is considered in  [5], which yields a non-symmetric linearization in  (5).

In order to analyze robustness for linear materials in the nearly incompressible case, the expression

$$\begin{aligned} s_h^{\mathrm{DG},4}({\varvec{ u}}_h,\delta {\varvec{ u}}_h)= & {} s_h^{\mathrm{DG},2}({\varvec{ u}}_h,\delta {\varvec{ u}}_h) \\&+ \int _{\Gamma {\setminus }\partial \Omega _u} \frac{\lambda }{h} [{\varvec{ u}}_h\cdot {\varvec{ N}}] \ [\delta {\varvec{ u}}_h\cdot {\varvec{ N}}]\, \mathrm {d} S \end{aligned}$$

is considered in Hansbo and Larson [20], and the more relaxed scheme

$$\begin{aligned} s_h^{\mathrm{DG},5}({\varvec{ u}}_h,\delta {\varvec{ u}}_h)= & {} s_h^{\mathrm{DG},2}({\varvec{ u}}_h,\delta {\varvec{ u}}_h) \\&+ \int _{\Gamma {\setminus }\partial \Omega _u} \frac{\lambda }{h} [{\varvec{ u}}_h^\text {avg}\cdot {\varvec{ N}}] \ [\delta {\varvec{ u}}_h^\text {avg}\cdot {\varvec{ N}}]\, \mathrm {d} S \end{aligned}$$

with face averages \({\varvec{ u}}_h^\text {avg}\) is analyzed in Grieshaber et al.  [19]. A penalty term with face averages is also considered in Horger et al. [22] in a higher-order mortar domain decomposition context. Although presented in a mortar context, an application to higher-order nonconforming methods is possible within the same framework.

In case of bilinear ansatz spaces \({\varvec{ V}}_{e,h}\), reduced integration on the element faces together with a simple Nitsche penalty defines the semi-linear DG form

$$\begin{aligned} a_h^\mathrm{RD}({\varvec{ u}}_h,\delta {\varvec{ u}}_h)= & {} \sum _e \int _{\Omega _e} {\varvec{ P}}({\varvec{ I}}+ \mathrm{Grad}\left( {\varvec{ u}}_h \right) ) : \mathrm{Grad}\left( \delta {\varvec{ u}}_h \right) \mathrm {d} \Omega \nonumber \\&- \int _{\Gamma {\setminus }\partial \Omega _t}^\mathrm{RD} \{{\varvec{ P}}({\varvec{ I}}+ \mathrm{Grad}\left( {\varvec{ u}}_h \right) ){\varvec{ N}}\} \cdot [\delta {\varvec{ u}}_h] \nonumber \\&+ \int _{\Gamma {\setminus }\partial \Omega _u}^\mathrm{RD} \theta [{\varvec{ u}}_h] \cdot [\delta {\varvec{ u}}_h] \end{aligned}$$
(8)

which shows improved convergence in case of locking, see Bayat et al.  [6]. Here, \(\int _{\Gamma {\setminus }\partial \Omega _u}^\mathrm{RD}\) denotes the mid-point rule approximating the integral on every element face.

While robustness and even a full convergence analysis is provided for many different DG variants in the linear setting, it is still open to some extent, first of all how the computational cost can be reduced and secondly which method is more cost efficient taking into account computational time as well as memory efficiency. For all these methods the system matrix has the same structure with entries connecting all degrees of freedom of neighboring elements. It is the goal of hybrid methods to reduce the numerical expense while preserving the robustness properties.

Remark 1

Optimal \({\varvec{ L}}_2\) norm error estimates can be shown for sufficiently regular linear problems under the assumption of adjoint consistency, which follows from the symmetry of the methods, see, e.g., Chap. 4.2.4 in Di Pietro and Ern  [15]. While this works for SIPDG for the other methods, examples with suboptimal \({\varvec{ L}}_2\) convergence exists, see Chap. 2.8 in Rivière [38].

Also optimal \({\varvec{ L}}_\infty \)-norm error estimates are to the best of our knowledge currently only available for the symmetric interior penalty method, see Chen and Chen [14].

2.2 A low-order hybrid discontinuous Galerkin method with conforming traces

For hybrid methods with conforming traces we use a second discrete space

$$\begin{aligned} {\varvec{ V}}_{\Gamma ,h} \subset \left\{ {\varvec{ u}}_{\Gamma ,h} \in {\varvec{ C}}^0(\Gamma ) :{\varvec{ u}}_{\Gamma ,h} ={\varvec{ 0}}\text { on }\partial \Omega _u\right\} \end{aligned}$$

for the approximation of the displacement vector on the skeleton. The method proposed in Wulfinghoff et al. [48]; Reese et al. [34] uses traces of conforming bilinear ansatz functions, i.e. face-wise linear skeleton functions in \({\varvec{ V}}_{\Gamma ,h}\). In the elements, we use the discontinuous space \({\varvec{ V}}_h^\mathrm{DG}\) with linear ansatz functions \({\varvec{ V}}_{h,e}\), see  (4). For a given linear skeleton function \({\varvec{ u}}_{\Gamma ,h}\in {\varvec{ V}}_{\Gamma ,h}\), we consider the piecewise linear volume approximation \({\varvec{ u}}_h = \Pi ^\mathrm{lin}_h{\varvec{ u}}_{\Gamma ,h} \in {\varvec{ V}}_h^\mathrm{DG}\), defined in every element by the linear projection

$$\begin{aligned} \int _{\partial \Omega _e}^h \Pi ^\mathrm{lin}_h{\varvec{ u}}_{\Gamma ,h} \cdot \delta {\varvec{ u}}_h = \int _{\partial \Omega _e}^h {\varvec{ u}}_{\Gamma ,h}\cdot \delta {\varvec{ u}}_h \,,\qquad \delta {\varvec{ u}}_h \in {\varvec{ V}}_{h,e} \,, \end{aligned}$$

which is derived from the weak form proposed by  [48]. Here, the boundary integral on \(\partial \Omega _e\) is approximated by a trapezoidal quadrature rule

$$\begin{aligned} \int _{\partial \Omega _e}^h f = \sum _{j=1}^4 w_jf({\varvec{ X}}_{e,j}) \end{aligned}$$

using the element corners \({\varvec{ X}}_{e,1},{\varvec{ X}}_{e,2},{\varvec{ X}}_{e,3},{\varvec{ X}}_{e,4}\) and weights \(w_j>0\) (see the appendix in  [48] for an efficient realization). Since the strain approximation \({\varvec{ F}}_h = {\varvec{ I}}+ \mathrm{Grad}\left( {\varvec{ u}}_h \right) \) is constant in \(\Omega _e\), we obtain \(\mathrm{Div }\left( {\varvec{ P}}({\varvec{ F}}_h) \right) = {\varvec{ 0}}\) and

$$\begin{aligned} \int _{\Omega _e} {\varvec{ P}}({\varvec{ F}}_h) : \delta {\varvec{ F}}\mathrm {d} \Omega= & {} \int _{\partial \Omega _t} {\varvec{ P}}({\varvec{ F}}_h){\varvec{ N}}\cdot \delta {\varvec{ u}}\, \mathrm {d} S \\\approx & {} \int _{\partial \Omega _e}^h {\varvec{ P}}({\varvec{ F}}_h){\varvec{ N}}\cdot \delta {\varvec{ u}}\,. \end{aligned}$$

This defines the non-symmetric hybrid semi-linear form

$$\begin{aligned}&a_h^\mathrm{HDG}({\varvec{ u}}_{\Gamma ,h},\delta {\varvec{ u}}_{\Gamma ,h}) \\&= \sum _e \int _{\partial \Omega _e}^h {\varvec{ P}}\left( {\varvec{ I}}+ \mathrm{Grad}\left( \Pi ^\mathrm{lin}_h{\varvec{ u}}_{\Gamma ,h} \right) \right) {\varvec{ N}}\cdot \delta {\varvec{ u}}_{\Gamma ,h} \,. \end{aligned}$$

Adapting the standard Nitsche type penalty term (6) to the hybridization yields

$$\begin{aligned} s_h^{\mathrm{HDG}}({\varvec{ u}}_{\Gamma ,h},\delta {\varvec{ u}}_{\Gamma ,h}) =\sum _e \theta \int _{\partial \Omega _e}^h \left( {\varvec{ u}}_{\Gamma ,h}- \Pi ^\mathrm{lin}_h{\varvec{ u}}_{\Gamma ,h}\right) \cdot \delta {\varvec{ u}}_{\Gamma ,h} \,. \end{aligned}$$

Then, the skeleton solution \({\varvec{ u}}_{\Gamma ,h} \in {\varvec{ V}}_{\Gamma ,h}\) is computed by

$$\begin{aligned}&a_h^\mathrm{HDG}({\varvec{ u}}_{\Gamma ,h},\delta {\varvec{ u}}_{\Gamma ,h}) + s_h^{\mathrm{HDG}}({\varvec{ u}}_{\Gamma ,h},\delta {\varvec{ u}}_{\Gamma ,h}) \nonumber \\&\quad = \int _{\partial \Omega _t} \bar{{\varvec{ t}}} \cdot \delta {\varvec{ u}}_{\Gamma ,h} \mathrm {d} S \,,\qquad \delta {\varvec{ u}}_{\Gamma ,h} \in {\varvec{ V}}_{\Gamma ,h} \,. \end{aligned}$$

The system matrix is non-symmetric with the sparsity pattern of conforming bilinear elements, all modifications can be employed on element level which can be easily included within standard finite element codes.

We note that the hybrid DG method is based on the incomplete interior penalty method, hence straightforward \({\varvec{ L}}_2\) estimates based on an Aubin–Nitsche argument cannot be expected to hold, see Remark 1.

2.3 A hybridizable weakly conforming Galerkin method with nonconforming traces

On every element face \(\Gamma _f\subset \Gamma {\setminus }\partial \Omega _t\), we select a test space \({\varvec{ V}}_{f,h}\). This defines the weakly conforming ansatz space

$$\begin{aligned} {\varvec{ V}}_h^\mathrm{WC}&= \bigg \{ {\varvec{ u}}_h\in {\varvec{ V}}^\mathrm{DG}:\int _{\Gamma _f} [{\varvec{ u}}_h]\cdot \delta {\varvec{ t}}_{f,h}\, \mathrm dS =0\,, \\&\quad \delta {\varvec{ t}}_{f,h}\in {\varvec{ V}}_{f,h}\,,\ \Gamma _f\subset \Gamma {\setminus }\partial \Omega _t\Bigg \} \end{aligned}$$

and the weakly conforming finite element solution \({\varvec{ u}}_h\in {\varvec{ V}}_h^\mathrm{WC}\) solving

$$\begin{aligned} a_h({\varvec{ u}}_h,\delta {\varvec{ u}}_h):= & {} \sum _e \int _{\Omega _e} {\varvec{ P}}({\varvec{ I}}+ \mathrm{Grad}\left( {\varvec{ u}}_h \right) ):\mathrm{Grad}\left( \delta {\varvec{ u}}_h \right) \mathrm {d} \Omega \\= & {} \int _{\partial \Omega _t} \bar{{\varvec{ t}}} \cdot \delta {\varvec{ u}}_h\, \mathrm {d} S \,,\qquad \delta {\varvec{ u}}_h \in {\varvec{ V}}_h^\mathrm{WC} \,. \end{aligned}$$

If all linear polynomials are included in the test functions \({\varvec{ V}}_{f,h}\), in case of linear materials stability can be verified using Korn’s inequality on discontinuous spaces, see Brenner [10].

For the hybrid realization of this method, we introduce the discontinuous skeleton space

$$\begin{aligned}&{\varvec{ V}}_{\Gamma ,h}^\mathrm{WC} \\&\quad = \big \{ {\varvec{ u}}_{\Gamma ,h} \in {\varvec{ L}}_2(\Gamma ) :{\varvec{ u}}_{\Gamma ,h}|_{\Gamma _f}\in {\varvec{ V}}_{f,h}\,, \Gamma _f\subset \Gamma {\setminus }\partial \Omega _t\big \} \end{aligned}$$

and locally \( {\varvec{ V}}_{\partial \Omega _e,h}^\mathrm{WC} = \big \{ {\varvec{ t}}_{e,h} \in {\varvec{ L}}_2(\partial \Omega _e{\setminus }\partial \Omega _t) :{\varvec{ t}}_{e,h}|_{\Gamma _f}\in {\varvec{ V}}_{f,h}\,, \Gamma _f\subset \partial \Omega _e{\setminus }\partial \Omega _t\big \} \). Then, \({\varvec{ u}}_h\in {\varvec{ V}}_h^\mathrm{WC}\) is weakly conforming if and only if a skeleton function \({\varvec{ u}}_{\Gamma ,h} \in {\varvec{ V}}_{\Gamma ,h}^\mathrm{WC}\) exists such that

$$\begin{aligned} \int _{\partial \Omega _e{\setminus }\partial \Omega _t} {\varvec{ u}}_h \cdot \delta {\varvec{ t}}_{e,h}\, \mathrm {d} S&=\int _{\partial \Omega _e{\setminus }\partial \Omega _t} {\varvec{ u}}_{\Gamma ,h} \cdot \delta {\varvec{ t}}_{e,h}\, \mathrm {d} S \,, \qquad \\&\delta {\varvec{ t}}_{e,h} \in {\varvec{ V}}_{\partial \Omega _e,h}^\mathrm{WC} \,, \end{aligned}$$

and a saddle point \(({\varvec{ u}}_h,{\varvec{ t}}_h,{\varvec{ u}}_{\Gamma ,h}) \in {\varvec{ V}}_h^\mathrm{WC}\times \prod {\varvec{ V}}_{\partial \Omega _e,h}^\mathrm{WC} \times {\varvec{ V}}_{\Gamma ,h}^\mathrm{WC}\) of the Lagrange functional

$$\begin{aligned} L_h({\varvec{ u}}_h,{\varvec{ t}}_h,{\varvec{ u}}_{\Gamma ,h})&= \sum _e \int _{\Omega _e} \psi ({\varvec{ P}}({\varvec{ I}}+ \mathrm{Grad}\left( {\varvec{ u}}_h \right) ) \mathrm {d} \Omega \nonumber \\&\quad - \int _{\partial \Omega _t} \bar{{\varvec{ t}}} \cdot {\varvec{ u}}_h\, \mathrm {d} S\\&\quad +\sum _e \int _{\partial \Omega _e{\setminus }\partial \Omega _t} ({\varvec{ u}}_h - {\varvec{ u}}_{\Gamma ,h}) \cdot {\varvec{ t}}_{e,h}\, \mathrm {d} S \end{aligned}$$

characterizes the weakly conforming solution \({\varvec{ u}}_h\in {\varvec{ V}}_h^\mathrm{WC}\).

In case of linear materials and for suitable choices of \({\varvec{ V}}_{e,h}\) and \({\varvec{ V}}_{f,h}\) the bilinear form \(a_h(\cdot ,\cdot )\) is coercive and the saddle point problem is inf-sup stable, so that a unique solution exists. The inf-sup stability requires the primal space to be sufficiently large which excludes the local use of bilinear spaces and \(p\ge 0\) must be chosen for a stable method. The system can be reduced to a positive definite problem for the skeleton approximation \({\varvec{ u}}_{\Gamma ,h}\), see Wieners [45] for details.

As a nonconforming method, \({\varvec{ L}}_2\)-norm error estimates can be shown using standard techniques, see Chap. 3 of Braess [8].

2.4 Comparison of the hybrid approaches

We shortly discuss the similarities and differences of the presented hybrid discontinuous Galerkin method and the hybrid weakly conforming Galerkin method, see Table 1 for an overview. While both methods include parallelizable hybridization to degrees of freedom on the skeleton, the system structures are different. This is mainly based on the different skeleton spaces, which is a low order continuous space for the hybrid DG method, while it is a discontinuous one for the weakly conforming methods. The sparsity pattern of the hybrid DG method is the same as for conforming Q1 elements, having two degrees of freedom per node and a 9-point stencil structure on uniform grids. The structure for the weakly conforming method with degrees of freedom located at the faces results in a 7-point stencil on uniform grids. In order to be stable, at least three degrees of freedom are required on each face.

The local cell-wise spaces are linear for the hybrid DG methods, while it is of higher order for the weakly conforming space. The hybrid DG method achieves stability by a penalty term, while for the weakly conforming space the face degrees of freedom directly pose weak constraints to the discontinuous solution space so that no penalty term is required.

Table 1 Characteric features of the hybrid DG method with bilinear skeleton approximations and the hybrid weakly conforming method (with variable polynomial degrees)
Full size table

3 Numerical evaluation

We introduce five benchmark configurations for the investigation of the different discretization methods in 2D and 3D. The first test in Sect. 3.1 demonstrates the robustness of discontinuous discretizations for a thin beam with respect to anisotropy. The second one in Sect. 3.2 considers a ring with a soft and hard layer under surface loading. In that example we also examine small strain plasticity. The final two-dimensional benchmark in Sect. 3.3 tests large deformations of a nearly incompressible block. An extension of the compressed block to 3D is presented in Sect. 3.4 and a second three-dimensional example for a thin plate is given in Sect. 3.5. Here again the robustness with respect to anisotropic elements - elements with large aspect ratios - is illuminated.

We use only basic geometries, so that these configurations can be realized in different codes and with various methods. Here, we use the parallel finite element framework M++ introduced by Wieners [44] for the tests with conforming first order Q1 elements, conforming second order serendipity elements Q2, the IIPDG(Q1) method (5) with interior penalty  (6), the symmetric interior penalty DG method (7) with first order ansatz spaces SIPDG(Q1) and standard second order local space SIPDG(Q2), and the weakly conforming method with linear WCM(1) and quadratic WCM(2) test spaces \({\varvec{ V}}_{f,h}\), see Sect. 2.3. The reduced integration method RIDG defined by (8) and the hybrid DG method HDG described in Sect. 2.2 are realized as additional module in the finite element software FEAP, cf. Taylor [41]. In addition, a locking-free conforming finite element formulation, Q1SP with reduced integration and hourglass stabilization by Reese [33] and Reese et al. [35, 36] has been applied for a comparison in case of both volumetric and shear locking phenomena.

The computational cost in 2D of different methods is given in Table 2, where the number of degrees of freedom as well as the number of nonzero entries in the stiffness matrix are given. With these numbers, the advantage of hybrid methods becomes apparent. In comparison to bilinear DG, HDG requires only one fourth of the number of degrees of freedom per cell. The number of nonzero matrix entries reduces even more, which makes the global system more efficient to store and to solve. Also for the weakly conforming method, which is based on face degrees of freedom, a gain in efficiency can be seen in terms of size and sparsity of the system matrix, comparing to the DG methods. WCM(2), which is based on quadratic test spaces yields only a slightly larger number of degrees of freedom per cell than Q2 and slightly more nonzero entries. For many hybrid methods, the gain of efficiency with the global stiffness matrix comes at the cost of additional computations during the assembly. We remind that the cost of the hybridization is purely element-wise and can hence be efficiently performed in parallel with no extra need for communication. In Table 3 the DOF and nonzero matrix entries are given for the 3D setting. WCM and DG have a large amount of degrees of freedom compared to the other methods, but WCM only has twice as many nonzero entries in the stiffness matrix compared to a conforming method. DG on the other hand has nearly ten times the amount of entries in the system matrix which leads to a huge storage requirement in large 3D computations.

Table 2 Comparison of the numerical expense for different methods on uniform meshes
Full size table
Table 3 Comparison of number of degrees of freedom and and number of nonzero entries in the stiffness matrix for all methods in 3D
Full size table

3.1 A long thin elastic beam

For the test with respect to geometric anisotropy, we compare for different discretizations the vertical displacement \(u_2({\varvec{ A}})\) of a thin beam, which is fixed on the left side and loaded vertically on the right side. The geometry, the boundary conditions and the test point \({\varvec{ A}}\) are sketched in Fig. 2.

Fig. 2
figure 2

Configurations of the beam example. Geometry shown for a varying length l

Full size image

The height of the beam is kept constant, the length is chosen as 10 or \(5\,\hbox {mm}\). We test high element aspect ratios of \(h_x/h_y=10\) and \(h_x/h_y=2\) for the long beam, and \(h_x/h_y=10\) for the short beam. The long beam with high element ratio is compared in two situations; the same beam geometry is discretized by shorter elements, and a shorter beam geometry is considered with the same element geometry. In all cases, the initial mesh starts with only one cell in the vertical direction and \(N_x\) cells in the horizontal direction and we refine uniformly. The traction force \(\bar{t}\) is set to \(0.001\,\hbox {MPa}\) in all cases.

We use an isotropic linear elastic material where the Cauchy stress

$$\begin{aligned} {\varvec{\sigma }}({\varvec{ u}}) = 2\mu \varvec{\varepsilon } +\lambda \text { trace}(\varvec{\varepsilon }){\varvec{ I}}\end{aligned}$$

is determined from the infinitesimal strain tensor \(\varvec{\varepsilon } ({\varvec{ u}})=\text {sym}(\mathrm{grad}\left( {\varvec{ u}} \right) ) \) with \(\lambda = 24\,\hbox {GPa}\), \(\mu = 6\,\hbox {GPa}\) corresponding to Young’s modulus \(E = 16.8\,\hbox {GPa}\) and Poisson’s ratio \(\nu = 0.4\).

We compute all three configurations for the beam model with the discretization schemes listed in Table 2 (in all cases using \(\theta = \mu /h\) for SIPDG(Q1) and SIPDG(Q2), \(\theta = 10^2E/l\) for RIDG and \(\theta =2\bar{E} h/3l(h+l)\) for HDG, where \(\bar{E}=E/(1-\nu ^2)\), h is the element height and l is the element length, for more details refer to Wulfinghoff et al. [48]. The second order approximation schemes are locking free in this test. Severe locking is observed for the standard conforming and the standard DG methods of low order.

Fig. 3
figure 3

Convergence results for the beam example in Fig. 2: vertical displacement of the point A in Case 1 with respect to total degrees of freedom (left) and a close-up of the same setting (right)

Full size image

3.1.1 Discussion of Case 1

In Fig. 3, the results for Case 1 are depicted. The six first order methods show different convergence behavior. Q1 and SIPDG(Q1) are only producing viable results with a high number of degrees of freedom, in contrast to RIDG and HDG, which are close to the solution already on the coarse grids. It is well known, that standard bilinear conforming methods show severe locking problems [7, Ch. 8]. The bad performance of SIPDG(Q1) stems from the higher number of global degrees of freedom on the same grid. Due to the effect of a reduced integration scheme on the boundary, RIDG shows a significantly improved performance. Relaxing the continuity constraints for the discrete solution, no spurious shear stresses appear during the bending of the beam. WCM(1) shows no shear locking which is partially achieved by increasing the computational effort inside each cell. The hybridization reduces the problem to the skeleton, keeping the solution effort low. Also the HDG method reduces shear locking, using a twofold approach. In addition to a reduced integration, the local, discontinuous ansatz space is smaller. The bilinear ansatz, which introduces the main spurious stresses in conforming methods is removed. The reduced integration is tailored to the hybridization, which reduces the number of degrees of freedom on a fixed mesh.

A closer look on the higher order methods as shown in Fig. 3 (right) shows a better behavior for the DG methods compared to the conforming Q2. While for the first order approximations the error of SIPDG per degree of freedom is comparable to that of Q1, the second order approximations perform significantly better. The first order locking-free element Q1SP results in a similar error per degree of freedom as the second order element Q2. Both WCM methods are about as close to the exact solution as SIPDG(Q2).

We observe a monotone convergence behavior for all considered methods. While for the conforming methods (Q1 and Q2) the vertical tip displacement is an increasing function over the degrees of freedom, for most discontinuous methods it is decreasing. The exceptions are SIPDG(Q1) and WCM(2), which also show a monotonically increasing tip displacement.

3.1.2 The influence of the anisotropy of the geometry and the elements

Now we investigate the influence of the beam geometry and the element geometry in different methods. We restrict ourselves to the first-order methods for the sake of clearer comparison. In Case 2 the same beam geometry is considered as in Case 1, but the element geometry is more regular. As a consequence, more elements are required in the length direction of the beam. We compare with respect to the number of elements in the height direction (see Fig. 4 left), keeping in mind the different total number of elements. The methods which show locking effects, Q1 and SIPDG(Q1), clearly yield better results by improving the shape regularity of the elements. On the other hand, by introducing more elements in the length direction, the convergence of the RIDG, HDG as well as Q1SP do not improve as much as the latter elements do. This is due to the fact that these elements show already a good convergence on the coarse meshes of Case 1 in comparison to Case 2. This shows us a good efficiency of the RIDG, Q1SP and the HDG in terms of error per degrees of freedom.

In contrast to Case 2, Case 3 keeps the same element geometry as in Case 1 but the beam geometry is cut down to only half of its length. As a change of the beam geometry influences the analytical displacement, we consider a relative displacement for comparison. Here we see hardly any differences between the two cases. Only for RIDG a change of between both cases can be notices, but the approximation is on a similar level in both cases. The values of the HDG methods are almost the same, indicating a strong robustness with respect to the degenerated meshes and elements.

The missing methods in Fig. 4 show relative errors less than \(1\%\) starting from the initial mesh and they continue to maintain this good approximation in the other cases as well.

Fig. 4
figure 4

Comparison of convergence results of different cases for the beam example in Fig. 2: vertical displacement of the point A in Case 1 and 2 and Case 1 and 3 (right)

Full size image

3.2 Annulus under symmetric pressure

Next we consider an annulus which is deformed by applying symmetric pressure to its top and bottom, motivated by an example in Fuentes et al. [18]. We distinguish two settings, a bimaterial ring with large deformations and a single elasto-plastic material with small deformations.

The outer radius is given by \(r_o = 1.1\) mm and the inner radius is given by \(r_i = 0.5\) mm. We apply a symmetric load, so we can restrict ourselves to one quarter of the ring, see Fig. 5. A vertical traction \(\bar{{\varvec{ t}}}\) is applied on a part of the outer boundary for \(0 \le X_1 \le 1.1 \cos (0.3\pi )\) mm. Homogeneous Neumann boundary conditions are used on the remaining outer boundary and the inner boundary, i.e., \(\bar{{\varvec{ t}}} = \varvec{0}\) for \(\left| {\varvec{ X}}\right| = 0.5\,\hbox {mm}\) and for \(\left| {\varvec{ X}}\right| = 1.1\,\hbox {mm}\) with \(X_1 > 1.1 \cos (0.3\pi )\,\hbox {mm}\). Since we only compute one quarter of the whole ring, we use symmetry conditions \(({\varvec{ P}}{\varvec{ N}})\cdot {\varvec{ N}}= 0\) and \({\varvec{ u}}\cdot {\varvec{ N}}= 0\) for \(X_1 = 0\) and for \(X_2=0\) on the edges of the computed part.

Fig. 5
figure 5

Bimaterial annulus: sketch of the computational domain, exploiting the symmetric structure (left) and undeformed and deformed domain including stress distribution \(|\!|\sigma |\!|\) (right)

Full size image

The curved geometry is approximated by mapping the nodes of a uniformly refined mesh onto the quarter annulus, so that the boundaries and the interface are linearly interpolated. While this is optimal for linear DG methods, for higher order methods a better geometry approximation improves the approximation for sufficiently regular solutions, see Li et al. [28]. Since the example includes discontinuous Neumann data, we do not expect full regularity of the solution.

3.2.1 Bimaterial annulus

We consider a bimaterial of two Neo–Hooke materials with strain energy density

$$\begin{aligned} \psi ({\varvec{ F}}) = \frac{\mu }{2}\left( {\varvec{ F}}:{\varvec{ F}}-3-2\ln (J)\right) + \frac{\lambda }{4} \left( J^2-1-2 \ln (J)\right) ,\nonumber \\ \end{aligned}$$
(9)

where \(J=\mathrm{det }( {\varvec{ F}} )\) and \(\lambda = \nu E/\left( (1+\nu )(1-2\nu )\right) \), \(\mu = E/\left( 2(1+\nu )\right) \). The material for the outer part of the ring \(\left| {\varvec{ X}}\right| > 1\) mm is steel with \(E_\mathrm{S} = 200\,\hbox {GPa}\) and \(\nu _\mathrm{S} = 0.285\) whereas we consider rubber-like material with \(E_\mathrm{R} = 0.01\,\hbox {GPa}\) and \(\nu _\mathrm{R} = 0.499\) on the inner ring. The surface traction is given as \(\bar{t}_2 = 30\) MPa (thickness 1 mm).

We consider the vertical displacement on the top of the inter-material layer, i.e. \(u_2({\varvec{ A}})\) at point \({\varvec{ A}}=(0,1)\) mm. For SIPDG(Q2), we have to select a large penalty parameter \(\theta = 1000 \mu /h\) in order to achieve convergence on fine levels, whereas the penalty value for HDG is \(\theta =\mu /2h\). The displacement shown in the left part of Fig. 6 shows fast convergence for all considered methods with a significant larger error for Q1 due to volume locking in the nearly incompressible rubber layer and possible shear locking in the outer layer. Unlike Q1, the locking-free Q1SP is the only first order conforming element, which yields a smaller error per degree of freedom than the second order elements, namely Q2 and SIPDG(Q2) on the considered meshes of this example, see Fig. 6. A closer look at this figure shows that the approximation of the linear HDG method is quantitatively the same as the second order SIPDG(Q2) and Q2. This is due to the reduced locking of the HDG method, but also due to the low regularity induced by the discontinuous Neumann data, which reduces the convergence order for higher order discretizations.

Fig. 6
figure 6

Convergence for large deformation of the bimaterial annulus Fig. 5: vertical displacement of the solution at the point \({\varvec{ A}}\) for first order approximations HDG and conforming Q1 and Q1SP, second order approximations SIPDG(Q2) and conforming Q2 (left) and estimated relative error with respect to an extrapolated value for a reference solution on a fine mesh (right)

Full size image
Fig. 7
figure 7

Convergence test for the elasto-plastic model: vertical displacement of the point \({\varvec{ A}}\) (left) and plastic slip of the homogeneous steel ring (right)

Full size image
Fig. 8
figure 8

Geometric configuration of the nearly incompressible block compression test (left) and deformation of the block and the resulting stress component distribution \(\sigma _{22}\) (right)

Full size image

The discontinuous Neumann data implies \(\bar{{\varvec{ t}}}\not \in {\varvec{ H}}^{1/2}(\partial \Omega _t)\) and thus \({\varvec{ u}}\not \in {\varvec{ H}}^2(\Omega )\). Consequently, we cannot expect the higher order methods to converge of another order than the lowest order methods. Still an advantage of higher order methods is given, as they reduce the locking effects.

Fig. 9
figure 9

Vertical displacement of the point \({\varvec{ A}}\) for the block (left) and the estimated relative error (right), both with respect to the total number of degrees of freedom

Full size image

For highly nonlinear problems, an efficient parallelization of the assembly process is of special importance. In every iteration step, a reassembly of the nonlinear parts is required. This includes the computational cost of the hybridization, however this is done by a purely cell-wise operation. We note that the Nitsche-type penalty term (6) does not need to be reassembled during the nonlinear iteration. The adjoint consistency term (7) includes the linearization of the nonlinear stress and needs to be recomputed in each iteration step. Using an incomplete DG method the term is avoided, as it is for the hybrid DG. The parallel efficiency of the assembly process is mainly influenced by the amount of data that needs to be communicated between the processors. Since the elements are distributed among the processors, element-wise computations do not require any communication. The only necessary communication is the construction of the global system, which is only dependent on the position of the degrees of freedom. This makes hybrid methods efficient on parallel systems.

3.2.2 Small deformation elasto-plastic material behavior

For the elasto-plastic test, a single material of steel type, with \(E_\mathrm{S} = 200\,\hbox {GPa}\), \(\nu _\mathrm{S}=0.285\) is considered. The plastic deformation is modeled by \(J_2\) plasticity with isotropic hardening using the yield function

$$\begin{aligned} \Phi ({\varvec{\sigma }},p) = \Vert \mathrm{dev}( {\varvec{\sigma }} )\Vert -\sqrt{2/3}H_0p-\sqrt{2/3}K_0 \end{aligned}$$

with equivalent plastic strain rate \(\dot{p} = \sqrt{2/3}|\dot{\varvec{\varepsilon }}_\text {p}|\)  [39, Chap. 3.3].

We use the initial yield stress \(K_0 = 800\,\hbox {MPa}\) and the hardening modulus \(H_0 = 0.3\). The distribution of the plastic strain is shown in Fig. 7 (left). The relative displacement on the top of the ring, i.e. \(u_2({\varvec{ A}})\) with \({\varvec{ A}}=(0,1.1)\) mm is shown in Fig. 7 (right). It can be seen, that non-conforming methods achieve similar displacements with similar degrees of freedom. The largest error in the vertical displacement among all linear methods belongs to WCM(1) while HDG (using \(\theta =\mu /2h\)) and Q1 are about on the same level of accuracy. Similar to the observations on the bimaterial ring, the Q1SP element yields a smaller error per degree of freedom than that of the other two first order methods. In comparison to the second order methods, Q1SP converges almost as fast as the the quadratic schemes, namely Q2 and WCM(2).

3.3 2D compression test

We consider a rectangular block under a constant pressure load, an established and frequently used benchmark problem in finite elasticity (see, e.g, [35]). The block of \(20\times 10\) mm\(^2\) (thickness 1 mm) is punched in the middle on the length of 10 mm by a pressure of \(\bar{p} = 400\) MPa. The geometry, loading and deformed shape with stress distribution are illustrated in Fig. 8. We use the strain energy density (9) for an almost incompressible Neo–Hooke material with \(E = 240.565\) MPa and \(\nu = 0.4999\).

Fig. 10
figure 10

Compression test 3D: sketch of the full domain (left) and slice through the distribution of the vertical stress component \(\sigma _{33}\) (right). Only a quarter of the block was computed for symmetry reasons

Full size image
Fig. 11
figure 11

Vertical displacement of the point \({\varvec{ A}}\) for the block in 3D (left) and the estimated relative error (right), both with respect to the total number of degrees of freedom

Full size image

The horizontal degrees of freedom on the top of the block are restricted to zero, as well as the vertical degrees of freedom on the bottom of the block. The remaining boundary dofs are not restricted, i.e., homogeneous Neumann boundaries are applied. For symmetry reasons, we only calculate half of the block, beginning with four elements on the initial mesh and continuing with uniform refinements. We monitor the vertical displacement of the midpoint of the top of the block \(u_2({\varvec{ A}})\) over the mesh refinement for Q1, Q1SP, Q2, IIPDG (with penalty \(\theta = 200 \mu /h\)) and the hybrid DG method (with penalty \(\theta = \mu /2h\)) as depicted in Fig. 9 left. The error is estimated by comparing with the reference value on the finest mesh, see the right part of Fig. 9.

We observe severe volumetric locking for Q1 and IIPDG and only a moderate influence of the nearly incompressibility on the hybrid DG and the conforming biquadratic approach. Again, the Q1SP element converges faster than Q1. In comparison to Q2, it shows a smaller error on the first meshes, while on finer meshes the error is on a similar level. The hybrid DG method is of similar efficiency as that of biquadratic method. On the other hand, due to the hybridization, the HDG shows the same sparsity structure as Q1. Hence, compared to the biquadratic approach, the stiffness matrix is less dense, leading to a higher memory efficiency.

The three first order approaches Q1, IIPDG and HDG, show a large relative error on the initial mesh containing only four elements. For the HDG the error decays on a reasonable level already during the first refinement. The other first order element Q1SP as well as the serendipity element Q2 show a high order pre-asymptotic on the first two levels. On the finest considered levels, Q1SP, HDG and Q2 are almost equivalent in terms of error per degree of freedom, depicting the very good approximation of the first order locking-free HDG and Q1SP method. A closer look at the convergence rate reveals, that an error reduction rate of the order \(\mathcal {O}(h^2)\) can be observed on most meshes, which seems to be a pre-asymptotic rate. On the finest meshes the error reduction is rather of an order \(\mathcal {O}(h^{1.5})\), which is related to the regularity of the solution.

3.4 3D compression test

A compression test, similar to the one in Sect. 3.3, is now evaluated in 3D, see Fig. 10. For simplicity we apply only a small pressure load so that a linear elastic model is sufficient. The material parameters are set to \(\text {E}=4.82926\,\hbox {MPa}\) and \(\nu = 0.499\), which assures near incompressibility. The block in this example is \(100\,\hbox {mm}\) wide, 100 mm long and \(50\,\hbox {mm}\) high. Similar to the 2D block test, the vertical degrees of freedom at the bottom are fixed, i.e. \(u_3 = 0\). On the sides homogeneous Neumann boundary conditions are applied and on the entire top the conditions \(u_1 = u_2 = 0\) are enforced. Additionally, the block is punched in the middle segment of the top surface with a vertical distributed load \(q = 0.003\,\hbox {MPa}\). The computed vertical displacement at point \({\varvec{ A}}= (50,50,50)\,\hbox {mm}\) is used to compare the methods (Fig. 11).

Fig. 12
figure 12

Geometric configuration of the thin plate (left), deformation of the plate and the resulting stress distribution \(|\!|\sigma |\!|\) (right)

Full size image
Fig. 13
figure 13

Vertical displacement of the point \({\varvec{ A}}\) for the thin plate (left) and the estimated relative error (right), both with respect to the total number of degrees of freedom

Full size image

As in the 2D case, we observe severe volumetric locking for Q1 and IIPDG(Q1), while the other methods seem to be more robust with respect to incompressibility. For WCM(2) and Q1SP a few elements are sufficient to get a good approximation for \(u_3({\varvec{ A}})\). The high convergence efficiency in terms of degrees of freedom in case of WCM(2) can be explained by the structure of the scheme. In 3D, the global degrees of freedom for a standard method with degree q increase with order \(\mathcal {O}(q^3)\). Since in hybrid discretizations such as WCM(q) the inner degrees of freedom in each cell are condensed out, the number of global DOF only increases by the order of \(\mathcal {O}(q^2)\) , which benefits schemes with higher polynomial degrees. This is seen in the convergence of the RIDG, which lies between the Q1 and the Q1SP. However, RIDG still performs much better than the IIPDG(Q1).

3.5 Thin plate in 3D

As the second 3D example, we consider a thin plate \(\Omega = \omega \times (0,0.01)\,\hbox {mm}^3\) with \(\omega = (0,1)^2\) which is loaded by a pressure load on its entire top and fixed on each side, i.e., \(\partial \Omega _u = \partial \omega \times (0,0.01)\) and \(\partial \Omega _t = \omega \times \{0.01\}\). The material is compressible with \(E = 250\,\hbox {MPa}\) and \(\nu = 0.3\). The load is set to \(q = 2 \times 10^{-7}\,\hbox {MPa}\), which again results in small deformations so that linear elasticity is appropriate (Fig. 12).

In this example, we compute different mesh refinement schemes for linear and quadratic approximations. For an asymptotic convergence towards the estimated solution it is clear, that refinement in all three directions is necessary. However for the second order methods, convergence up to the observed accuracy can still be observed when we fix the vertical layer at 4 cells and only refine the two horizontal ones. This leads to a reduced number of degrees of freedom and a high efficiency, so we present the results of this two-dimensional refinement strategy (Fig. 13).

Due to shear locking effects on the thin geometry of the plate, Q1 does not reach the solution with the given number of degrees of freedom. On the other hand, Q1SP initially converges even faster than the Q2 element, but then shows a non-monotone convergence during the last two refinement steps. The best error per degree of freedom is obtained with WCM(2).

4 Conclusion

We presented several discontinuous and nonconforming methods and compared them with standard and locking-free conforming methods. In terms of error per degree of freedom, standard discontinuous Galerkin methods show a similar behavior as their conforming counterpart, including large errors due to locking effects for Q1. Due to more dense system matrices, standard DG methods were not competitive to conforming methods in terms of efficiency.

However with simple modifications DG methods can be improved significantly. A reduced integration of the face integrands yields a low-order method that is free of locking and improves the error per degree of freedom. Different hybridization techniques improve the efficiency in terms of the number of degrees of freedom and memory efficiency. The hybrid methods retain the locking-free approximation and the additional effort can be efficiently computed in parallel with minimal communication needed.

With HDG, the sparsity structure of Q1 is recovered, while WCM yields a sparsity structure different to standard methods. This is due to face degrees of freedom which was shown to be advantageous, in particular in the three-dimensional cases.