Progressive delamination analysis of composite materials using XFEM and a discrete damage zone model

Abstract

The modeling of progressive delamination by means of a discrete damage zone model within the extended finite element method is investigated. This framework allows for both bulk and interface damages to be conveniently traced, regardless of the underlying mesh alignment. For discrete interfaces, a new mixed-mode force–separation relation, which accounts for the coupled interaction between opening and sliding modes, is proposed. The model is based on the concept of Continuum Damage Mechanics and is shown to be thermodynamically consistent. An integral-type nonlocal damage is adopted in the bulk to regularize the softening material response. The resulting nonlinear equations are solved using a Newton scheme with a dissipation-based arc-length constraint, for which an analytical Jacobian is derived. Several benchmark delamination studies, as well as failure analyses of a fiber/epoxy unit cell, are presented and discussed in detail. The proposed model is validated against available analytical/experimental data and is found to be robust and mesh insensitive.

1 Introduction

In the design of engineering structures, it is often desired to understand and analyze the failure behavior of materials, which is often signified by damage and cracking. In contrast to brittle materials in the Griffith’s sense, most engineering materials exhibit some ductility after the strength limit is reached [1]. The failure process of these materials is preceded by the development of a nonlinear fracture process zone [2] ahead of the crack tip, in which initiation, growth and coalescence of micro-cracks and voids take place. When the size of the fracture process zone is negligible compared to the characteristic length scale of the problem, linear elastic fracture mechanics (LEFM) is applicable. LEFM theory is characterized by the propagation of traction-free cracks as the strain energy release rate exceeds the fracture energy of the material [3]. However, if the assumption of a “small” process zone ceases to hold, other models which take into account the nonlinear fracture process, must be employed.

A simple but powerful way to account for larger process zones is through the concept of cohesive zone models. These models date back to the well-known work of Barenblatt [4] and Dugdale [5] for elasto-plastic fracture in ductile materials, and Hillerborg et al. [6] for quasi-brittle materials. In cohesive zone models, the fracture process zone is lumped into a finite strip wherein a traction–separation or cohesive relation would represent the degrading mechanisms instead of typical stress–strain relations. A wide variety of traction–separation relations with linear, bilinear, trapezoidal and exponential shapes have been postulated and applied to investigate failure phenomena in many engineering applications with great success. A good overview on different cohesive relationships was recently reported in [7]. Some of the applications include static and dynamic failure in functionally graded materials [8, 9], delamination in fiber reinforced composites [10], and crack growth in brittle solids [11, 12]. Besides elastic bulk materials, cohesive zone models can be used in conjunction with other bulk constitutive relations to describe more complicated degrading phenomena, e.g. damage model for matrix cracking [13] and viscoelastic bulk for fracture of asphalt concrete [14], to mention only a few. The two most important parameters required in these models are the fracture strength and the fracture energy, which could determine the traction–separation relation. Some researchers have also shown that the shape of the traction–separation relation plays an important role in their numerical results [15, 16]. Note that cohesive zone models remove the singularity at the crack tip due to the action of these cohesive tractions on the internal fracture surface.

Due to the complexity of the nonlinear fracture process, numerical methods such as the finite element method (FEM), are very convenient and extensively used in the implementation of cohesive zone models. Typically, cohesive zones are treated within the framework of the FEM as continuous compliant layers, and therefore they are also referred to as continuous cohesive zone models (CCZMs) [17]. Among the widely used finite element techniques for the discretization of cohesive zones are interface elements [11, 18, 19] which are inserted at continuous inter-element boundaries along potential crack paths (e.g. laminate interfaces), and embedded discontinuities models [20], where the cohesive zone is incorporated at the element level.

During the past decade, the extended finite element method (XFEM), proposed by Belytschko and his co-workers [21, 22], has become a popular and elegant tool to address discontinuities. Several researchers have studied cohesive crack propagation based on CCZMs via the XFEM [23–26]. By enhancing the solution space of the standard FEM with discontinuous and asymptotic functions based on the local partition of unity, the XFEM avoids the need for meshes conforming to discontinuities and adaptive remeshing during the growth of discontinuities [27].

Apart from the aforementioned mesh-based methods, meshfree methods appear as an attractive approach to simulate cohesive cracks [28] and delamination [29]. These methods have been shown to alleviate difficulties associated with distorted or low quality meshes. Thus, they are especially suited for dynamic crack propagation in large deformation applications. The excellent review papers by Nguyen et al. [30] and Rabczuk [31] are recommended for more details on meshfree methods and their applications to fracture mechanics.

For continuous interface elements, a sufficiently high penalty stiffness needs to be enforced along the perfectly bonded interface to suppress the additional deformation caused by interface elements inserted before actual cracking occurs. When the penalty stiffness is combined with some specific numerical integration schemes, computational issues such as spurious oscillation in the stress field may appear [1, 19]. An alternatived implementation of cohesive zone models, which involves attachment of point-wise spring elements at FE node pairs of the interface, is shown to circumvent the above computational issue of CCZMs [17, 32, 33] in the sense that tractions distributed on the interface are explicitly lumped to point-wise spring elements in place of numerical integration methods. Hence, the material degrading in the process zone can be described in the so-called discrete cohesive zone model (DCZM) by a force–separation relation instead of traditional cohesive relations in CCZMs. A schematic comparison of continuous and point-wise interface elements is shown in Fig. 1.

Fig. 1

Schematic representation of continuous and discrete interface elements. Two continuous interface elements are represented by red lines (shown on the left) whereas three discrete spring elements are represented by blue lines (shown on the right). Gauss points in bulk elements are represented by multiplication signs. (Color figure online)

Based on the concept of nodal interfaces, Liu et al. [13] developed a discrete damage zone model from the perspective of Continuum Damage Mechanics (CDM) [34] to simulate pure mode I, II, and mixed-mode delamination of composites within the context of the FEM. The novelty of this model lies in that there is no need to assume a damage law and a cohesive relation separately since by a rigorous formulation one can derive the force–separation relation of point-wise springs according to a given evolution law for bulk material damage. Same or different damage laws could be used for bulk and interface elements depending upon the type of materials. For example, the same damage law may apply to both elements for a homogeneous solid while different damage laws in bulk and interface may be assumed for laminated composites with adhesive interfaces. The computational accuracy and efficiency of the model has been demonstrated through several benchmark problems [13].

In this work, the discrete damage zone model is enhanced further by developing an isotropic mixed-mode damage law and integrated with the XFEM framework. Thus, the behavior of nodal interfaces is described by enriched degrees of freedom rather than double nodes as used in standard FEM. This strategy offers significant flexibility in capturing discontinuities, irrespective of the underlying mesh alignment. In other words, within the XFEM framework, the crack geometry is decoupled from the mesh orientation, and hence fixed structured or unstructured meshes may be used for the analysis. Although adaptive crack propagation is not studied in this paper, we point out that cohesive cracks can be inserted or extended in arbitrary directions during the analysis, while in the FEM newly created cracks are restricted to element edges and mesh bias may be introduced.

Another distinct feature of our method is that an integral-type regularization technique [35] is adopted to prevent pathological mesh sensitivity induced by damage localization in the presence of strain softening. Since the model that we present benefits from both advantages of continuum damage theory and cohesive zone models, it can account simultaneously for the diffused damage in the bulk material and the highly localized deformation characterized by discrete interfaces.

The outline of this paper is as follows. Section 2 presents a brief review of the governing equations and the weak form. Section 3 discusses the nonlocal damage model of an integral-type for the bulk material. Then the discrete damage zone model is introduced and the force–separation relation of springs is derived by assuming Mazars damage law [36, 37]. Section 4 details the spatial discretization and consistent linearization of the governing equations, the corresponding computational algorithm and the implementation procedure. Section 5 investigates four numerical applications. A comparison with analytic solutions and available experimental data is presented to demonstrate the performance of the proposed method. Finally, Sect. 6 gives some concluding remarks.

2 Governing equations

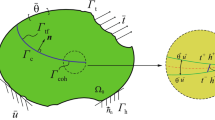
A solid $\Omega \subset \mathbb {R}^N$ (with $N \in \{ 1,2,3\}$) containing a crack $\Gamma _{\mathrm {c}}$ is considered, under the assumption of small deformations. The boundary $\Gamma$ is partitioned into three segments $\Gamma _{\mathrm {u}}$, $\Gamma _{\mathrm {t}}$, and $\Gamma _{\mathrm {c}}$, as shown in Fig. 2. Tractions imposed on $\Gamma _{\mathrm {t}}$ are prescribed as ${\bar{\varvec{t}}}$, while displacements imposed on $\Gamma _{\mathrm {u}}$ are prescribed as ${\bar{\varvec{u}}}$. The crack $\Gamma _{\mathrm {c}}$ is partitioned into a traction-free surface, denoted by $\Gamma _{\mathrm {tf}}$, and a fracture process zone, denoted by $\Gamma _{\mathrm {coh}}$ where a cohesive relation is active. The cohesive tractions acting on the lower and upper surfaces of $\Gamma _{\mathrm {coh}}$ are denoted by $\varvec{t}^+$ and $\varvec{t}^-$, respectively.

Fig. 2

Schematic illustration of a cracked domain subjected to prescribed tractions ${\bar{\varvec{t}}}$ and displacements ${\bar{\varvec{u}}}$. The crack is traction-free on $\Gamma _{\mathrm {tf}}$ (represented by black lines) while cohesive forces on $\Gamma _{\mathrm {coh}}$ (represented by red lines) indicate the fracture process zone. (Color figure online)

The equilibrium equation reads

$$\begin{aligned} \varvec{\nabla } \cdot \varvec{\sigma } + \varvec{b} = 0 \,\,\text{ in }\, \Omega \end{aligned}$$

(1)

where $\varvec{\nabla }$ is the gradient operator, $\varvec{\sigma }$ is the Cauchy stress tensor, and $\varvec{b}$ is the body force per unit volume. The associated natural boundary conditions are

$$\begin{aligned} \varvec{\sigma } \cdot \varvec{n}&= {\bar{\varvec{t}}} \,\,\text{ on }\, \Gamma _{\mathrm {t}},\nonumber \\ \varvec{\sigma } \cdot \varvec{n}^+&= -\varvec{\sigma } \cdot \varvec{n}^-=\varvec{t}({[\![}\varvec{u} {]\!]}) =\varvec{t}^+ = -\varvec{t}^- \,\,\text{ on }\, \Gamma _ {\mathrm {coh}} \end{aligned}$$

(2)

with $\varvec{n}$ the outward normal unit vector on the outer boundary, $\varvec{n}^+$ and $\varvec{n}^-$ the inward normal unit vectors on the upper and lower surfaces of $\Gamma _{\mathrm {coh}}$, respectively. The cohesive traction $\varvec{t}=\varvec{t}^+=-\varvec{t}^-$ is commonly related with the crack opening ${[\![}\varvec{u} {]\!]}=\varvec{u}^--\varvec{u}^+$ by a phenomenological cohesive relation.

The kinematic equation and the associated essential boundary conditions are expressed as

$$\begin{aligned} \varvec{\epsilon } = \varvec{\epsilon }(\varvec{u}) = \varvec{\nabla }^s \varvec{u} \,\,\text{ in }\, \Omega , \,\,\,\,\, \varvec{u}={\bar{\varvec{u}}} \,\,\text{ on }\, \Gamma _{\mathrm {u}} \end{aligned}$$

(3)

where $\varvec{\epsilon }$ is the strain tensor, $\varvec{u}$ is the displacement field, and $\varvec{\nabla }^s$ denotes the symmetric part of the gradient operator.

In this work, the degradation of the bulk material is described through an isotropic damage model with exponential softening. The constitutive law reads

$$\begin{aligned} \varvec{\sigma }=(1-D^{\Omega })\mathbf {C}:\varvec{\epsilon } = (1-D^{\Omega }) \varvec{\sigma }^e \end{aligned}$$

(4)

where $\mathbf {C}$ is the the Hooke’s tensor of the virgin material and $\varvec{\sigma }^e = \mathbf {C}:\varvec{\epsilon }$ is the effective stress. $D^{\Omega }$ is a scalar-valued damage variable of the bulk material whose value ranges from zero to unity: $D^{\Omega } = 0$ corresponds to an intact material whereas $D^{\Omega } = 1$ corresponds to a completely damaged material. A detailed damage evolution law is described in Sect. 3.1.

For the sake of finite element computations, the weak form of the problem is obtained from the strong form and then discretized using Galerkin’s method. The trial function space $\mathcal {U}$ and test function space $\mathcal {V}$ of the displacement field, are defined as

$$\begin{aligned}&\mathcal {U}=\{\varvec{u} | \varvec{u} \in H^1(\Omega ); \varvec{u} = {\bar{\varvec{u}}} \,\text{ on } \,\Gamma _{\mathrm {u}}; \varvec{u} \text{ is } \text{ discontinous } \text{ on } \Gamma _{\mathrm {c}} \}\end{aligned}$$

(5)

$$\begin{aligned}&\mathcal {V}=\{\varvec{v} | \varvec{v} \in H^1(\Omega ); \varvec{v} = 0 \,\text{ on } \,\Gamma _{\mathrm {u}}; \varvec{v} \text{ is } \text{ discontinous } \text{ on } \Gamma _{\mathrm {c}} \}\nonumber \\ \end{aligned}$$

(6)

with $H^1(\Omega )$ the first order Hilbert space.

By multiplying the equilibrium Equation (1) with a virtual displacement $\delta \varvec{u}$ and integrating over the problem domain $\Omega$, the weak form is obtained as:

Find $\varvec{u} \in \mathcal {U}$ such that

$$\begin{aligned}&\int _\Omega \varvec{\nabla }^s \delta \varvec{u} : \varvec{\sigma } \,d\Omega + \int _{\Gamma _{\mathrm {coh}}} \delta {[\![}\varvec{u} {]\!]}\cdot \varvec{t} \,d\Gamma \nonumber \\&\quad = \int _{\Gamma _{\mathrm {t}}} \delta \varvec{u} \cdot {\bar{\varvec{t}}} \,d\Gamma + \int _\Omega \delta \varvec{u} \cdot \varvec{b} \,d\Omega , \,\,\,\forall \delta \varvec{u} \in V \end{aligned}$$

(7)

Given the discrete damage zone model adopted in this work, the second integral term on the left-hand side of the above weak form is replaced by a summation of contributions collected from springs over $\Gamma _{\mathrm {coh}}$:

$$\begin{aligned} \int _{\Gamma _{\mathrm {coh}}} \delta {[\![}\varvec{u} {]\!]}\cdot \varvec{t} \,d\Gamma \approx \sum _{S=1}^{N_{SP}} \delta {[\![}\varvec{u}(\varvec{x}_S) {]\!]}\cdot \mathbf {F}_S \end{aligned}$$

(8)

with $N_{SP}$ the total number of point-wise springs located over $\Gamma _{\mathrm {coh}}$, $\varvec{x}_S$ the spatial coordinates of the $Sth$ spring, and $\mathbf {F}_S$ the force in that spring. The force–separation relation $\mathbf {F}_S = \mathbf {F}({{[\![}\varvec{u}(\varvec{x}_S) {]\!]})}$ is detailed in Sect. 3.2.

3 Constitutive relations

3.1 Nonlocal damage model for bulk degradation

The material behavior of the bulk is assumed to be linear elastic followed by a strain softening stage when damage occurs. The total stress–strain relation describing the material degradation is given in Eq. (4). It is complemented by a loading function defined in the strain space, which reads:

$$\begin{aligned} f(\varvec{\epsilon },\kappa )= \tilde{\epsilon }_{eq}(\varvec{\epsilon })-\kappa \end{aligned}$$

(9)

where $\kappa$ is an internal variable and $\tilde{\epsilon }_{eq}$ is the Mazars equivalent strain, for which the following definition is adopted [36]:

$$\begin{aligned} \tilde{\epsilon }_{eq}=\sqrt{\sum _{i=1}^3 \langle e_i \rangle ^2} \end{aligned}$$

(10)

with $e_i$ the principal strains and $\langle \cdot \rangle$ the Macaulay bracket defined such that $\langle e_i \rangle = (|e_i|+e_i)/2$. Mazars equivalent strain accounts for the fact that damage is driven mainly by tension in quasi-brittle materials.

The loading function obeys the loading–unloading conditions in the Kuhn–Tucker conditions, written as

$$\begin{aligned} \dot{\kappa } \ge 0,\,\,\,f(\varvec{\epsilon },\kappa ) \le 0,\,\,\,\dot{\kappa }f(\varvec{\epsilon },\kappa )=0 \end{aligned}$$

(11)

In this work, the damage evolution law proposed by Mazars [37] is used to determine the dependence of the damage variable $D^{\Omega }$ on the internal variable $\kappa$, which reads:

$$\begin{aligned} D^{\Omega }(\kappa ) = \left\{ \begin{array}{lll} 0 &{} \text{ if } &{} \kappa \le \epsilon ^{\mathrm {cr}} \\ 1-(1-A)\dfrac{\epsilon ^{\mathrm {cr}}}{\kappa }- \dfrac{A}{\exp (B(\kappa -\epsilon ^{\mathrm {cr}}))} &{} \text{ if } &{} \kappa > \epsilon ^{\mathrm {cr}} \end{array} \right. \end{aligned}$$

(12)

where $\epsilon ^{\mathrm {cr}}$ is the critical elastic strain under uniaxial tension, and $A$, $B$ are material damage parameters. For simplicity of the expressions, but without loss of generality, we assume that $A = 1.0$.

In the absence of an internal length scale, the presented strain-softening damage model suffers from inherent mesh size and alignment sensitivity that occurs once a certain damage level is reached. From a mathematical standpoint, this behavior is related to the loss of ellipticity of the governing equations under quasi-static conditions [38].

Herein, we employ an integral-type nonlocal formulation [35] to enhance the continuum model, which introduces a length scale to regularize the problem in the softening regime. This regularization technique is based on an integral averaging operator which replaces the damage variable $D^{\Omega }$ by its spatial weighted average $\bar{D}^{\Omega }$ over a predefined neighborhood, $V$. The nonlocal field $\bar{D}^{\Omega }(\varvec{x})$ is defined by

$$\begin{aligned} \bar{D}^{\Omega }(\varvec{x}) = \int _{V} \Phi ^{\prime }(\varvec{x},\varvec{\xi }) D^{\Omega }(\varvec{\xi }) \, d\varvec{\xi } \end{aligned}$$

(13)

with $\Phi ^{\prime }(\varvec{x},\varvec{\xi })$ a nonlocal weight function which is normalized to preserve a constant field, even in the vicinity of boundaries:

$$\begin{aligned} \Phi ^{\prime }(\varvec{x},\varvec{\xi }) = \dfrac{\Phi (\Vert \varvec{x}-\varvec{\xi } \Vert )}{\int _{V} \Phi (\Vert \varvec{x}-\varvec{\xi } \Vert ) \, d\varvec{\xi }} \end{aligned}$$

(14)

In the above equation, $\Phi$ is a monotonically decreasing function of the distance $r=\Vert \varvec{x}-\varvec{\xi } \Vert$. In this work, we choose $\Phi (r)$ to be a polynomial bell-shaped function with a bounded support $l_c$, given by

$$\begin{aligned} \Phi (r)=\left\langle 1- \dfrac{r^2}{l_c^2} \right\rangle ^2 \end{aligned}$$

(15)

$l_c$ is an internal length scale, which serves as a localization limiter to alleviate mesh sensitivity. The physical motivation for introducing a length scale is rooted in experimental observations in which quasi-brittle materials exhibit damage localization over a narrow region, whose size is characterized by the length parameter $l_c$. In this sense, the parameter $l_c$ represents an intrinsic material property. As pointed by Bažant and Pijaudier-Cabot [39], the length parameter $l_c$ can be determined either experimentally or by a micromechanics analysis. The bell-shaped function, decaying from 1 to 0 as $r \rightarrow l_c$, defines the influence of the damage at point $\varvec{\xi }$ on point $\varvec{x}$, as shown in Fig. 3a. The nonlocal integral (13) at a material point $\varvec{x}$ is approximated by the following Gauss quadrature

$$\begin{aligned} \begin{aligned} \bar{D}^{\Omega }&= \sum _{J=1}^{N_{J}} w_J \Phi _J D^{\Omega }(\varvec{x}_J) \\ \Phi _J&= \dfrac{\Phi (\Vert \varvec{x}-\varvec{x}_J\Vert )}{\sum _{M=1}^{N_J} w_M \Phi (\Vert \varvec{x}-\varvec{x}_M \Vert )} \end{aligned} \end{aligned}$$

(16)

where $N_J$ is the number of neighboring Gauss points, located within the circle centered at point $\varvec{x}$ with radius $l_c$. $w_J$ is the weight of Gauss point $J$ at the coordinate $\varvec{x}_J$, and $\Phi _J$ is the interaction coefficient.

Fig. 3

Nonlocal integral formulation within the XFEM: a bell-shaped weight function $\Phi (\Vert \varvec{x}-\varvec{\xi }) \Vert )$ centered at $\varvec{x}=(0,0)$ with $\varvec{\xi }=(x,y)$; b Subdomain quadrature for nonlocal damage over a designated neighborhood $V$ (shaded in gray). Gauss points appear as multiplication signs with only the blue and red ones being included in the nonlocal calculation. Crack surface $\Gamma _c$ is denoted by the red line. (Color figure online)

It is worth noting that the classical subdomain quadrature is also utilized for computing nonlocal damage fields within the context of the XFEM. In this scheme, elements crossed by a discontinuity are triangulated into multiple subdomains, as illustrated in Fig. 3b. The nonlocal integral at point $\varvec{x}$ has to account for the contributions of all subdomain Gauss points located within its neighborhood domain $V$, which is usually taken as a circle of radius $l_c$ centered at $\varvec{x}$. However, for a material point close to the discontinuity, only contributions from Gauss points located on the same side of the crack are accounted for when performing nonlocal averaging, as illustrated in Fig. 3b.

For efficient implementation, all searching and sorting of Gauss points and their nonlocal neighbors is done in the preprocessing step. Then, their weights and interaction coefficients are precomputed and stored for subsequent computational steps. Notice that this information needs to be updated for crack propagation problems because the adopted subdomain quadrature changes the position of Gauss points in those newly enriched elements.

3.2 Discrete damage zone model for material interfaces

The discrete damage zone model (DDZM), developed directly in the framework of damage mechanics and proposed in [13], is adopted. In the DDZM, the delamination progress is interpreted as the damage accumulation and evolution along material interfaces. The permanent reduction of material stiffness and strength is naturally accounted for by the irreversibility of damage if a discrete interface is previously loaded beyond its elastic limit. In this section, we show the procedure to go from the damage model to the force–separation relation under pure mode I and mode II conditions. Then the relationship between model parameters and experimentally measured fracture energy and cohesive strength is derived. For the mixed-mode delamination, a new formulation which is thermodynamically consistent is proposed. Finally, we provide a comprehensive comparison of the DDZM with other existing interface models.

3.2.1 Pure mode force–separation relation

In this work, the force–separation relation for the discrete interface is derived from Mazars damage law that governs the bulk behavior although any other damage law can equally be employed in this framework.

By adapting the bulk damage law (12), the irreversible damage evolution for the discrete interface is described in terms of interface separations as

$$\begin{aligned} D^{\Gamma }_{i} = \left\{ \begin{array}{ccc} 0 &{} \text{ if } &{} \delta _{i}^{*} \le \delta ^{\mathrm {cr}}_{i} \\ 1- \dfrac{1}{\exp (B_{i}(\delta _{i}^{*}-\delta ^{\mathrm {cr}}_{i}))} &{} \text{ if } &{} \delta _{i}^{*} > \delta ^{\mathrm {cr}}_{i} \end{array} \right. \,\,\,\,(i=n,t) \end{aligned}$$

(17)

where the subscripts $n$ and $t$ indicate the opening mode I and sliding mode II, respectively. $B_i$ is the damage coefficient and $\delta ^{\mathrm {cr}}_{i}$ is the critical interface separation corresponding to the damage initiation, whose identification is detailed later. The history variable $\delta ^{*}_{i}$, defined as the maximum converged value of effective separation that was reached, is characterized by the uncoupled loading functions

$$\begin{aligned} f_n({[\![}\varvec{u} {]\!]}, \delta _{n}^{*})=\langle {[\![}u_n {]\!]}\rangle - \delta ^{*}_{n},\,\,\,\, f_t({[\![}\varvec{u} {]\!]}, \delta _{t}^{*})=| {[\![}u_t {]\!]}| - \delta ^{*}_{t} \end{aligned}$$

(18)

which evolve according to the Kuhn–Tucker conditions

$$\begin{aligned} \dot{\delta }_{i}^{*} \ge 0,\,\,\,f_i({[\![}\varvec{u} {]\!]}, \delta _{i}^{*})\le 0,\,\,\,\dot{\delta }_{i}^{*} f_i({[\![}\varvec{u} {]\!]}, \delta _{i}^{*})=0 \,\,\,\,(i=n,t) \end{aligned}$$

(19)

In Eq. (18), the history variable $\delta _{n}^{*}$ is assumed to be frozen in the case of negative normal openings by introducing the Macaulay bracket. The absolute value operator in Eq. (18) implies that the tangential loading function is independent of the direction of sliding.

The force $F_i$ sustained by the spring is related to the current separation $\delta _{i}$ as follows:

$$\begin{aligned} F_{i}= K_{i}\delta _{i} =(1-D_{i}^{\Gamma })K_{i}^{0} \delta _{i} =(1-D_{i}^{\Gamma })F^{\mathrm {cr}}_i \dfrac{\delta _{i}}{\delta ^{\mathrm {cr}}_i} \,\,\,\,(i=n,t) \end{aligned}$$

(20)

where $K^{0}_{i}$ is the undamaged stiffness of the spring and $F^{\mathrm {cr}}_{i}=K_{i}^{\mathrm {cr}}\delta _{i}^{\mathrm {cr}}$ is the peak force in the spring.

Substitution of the damage evolution law (17) into Eq. (20) then yields the pure mode force–separation relation

$$\begin{aligned} F_{i}&= \left\{ \begin{array}{l@{\quad }ll} K^{0}_{i}\delta _{i}= F^{\mathrm {cr}}_i \dfrac{\delta _{i}}{\delta ^{\mathrm {cr}}_i} &{} \text{ if } &{} \delta ^{*}_{i} \le \delta ^\mathrm {cr}_{i} \\ \dfrac{K_{i}^{0}\delta _{i}}{\exp (B_{i}(\delta ^{*}_{i}-\delta ^\mathrm {cr}_{i}))}&{}&{}\\ \quad =F_{i}^\mathrm {cr}\dfrac{\delta _{i}}{\delta ^{\mathrm {cr}}_i \exp (B_{i}(\delta ^{*}_{i}-\delta ^\mathrm {cr}_{i}))} &{} \text{ if } &{} \delta ^{*}_{i} > \delta ^\mathrm {cr}_{i} \end{array} \right. \nonumber \\&\,\,\,\,(i=n,t) \end{aligned}$$

(21)

The force–separation relation is completed by replacing the normal stiffness $K_{n}$ with a penalty stiffness $K_p$ in the presence of negative value of $\delta _n$. This penalty parameter should be large enough to prevent interface penetration providing that no artificial computational issues such as oscillatory stress profile are introduced.

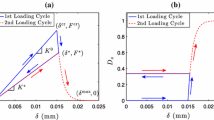
Figure 4a shows an interfacial deformation history involving loading, unloading, and reloading. Note that loading/reloading paths are indicated by solid arrows whereas unloading paths by dashed arrows. The corresponding constitutive behavior and damage variable evolution are plotted in Fig. 4b, c, respectively. As displacement jump $\delta$ initially increases, the interface behaves as a linear spring with an undamaged stiffness of $K^0$ until the critical separation $\delta ^{\mathrm {cr}}$ (point 1) is reached. Then a permanent reduction of stiffness is observed as more separation is applied from point 1 to 2. This will cause an irreversible response during the unloading and reloading stages. Namely, the constitutive model proceeds along a linear path to the origin upon unloading, and, the same path is followed in the case of reloading until it reaches point 2.

Fig. 4

Pure mode constitutive relation and damage evolution law for a discrete interface undergoing a specified deformation history. Loading and reloading paths are indicated by solid arrows whereas unloading paths are indicated by dashed arrows. a deformation history, b force–separation relation, c damage evolution relation

3.2.2 Parameter identification

Three sets of model parameters are introduced in the adopted force–separation relation: the damage coefficient $B_{i}$, the critical interface separation $\delta ^{\mathrm {cr}}_i$, and the initial stiffness $K_{i}^{0}$. Following the procedure detailed in [13], we can identify them once the fracture energies $G_{\mathrm {IC}}, G_{\mathrm {IIC}}$ and the cohesive strengths $\sigma _{\mathrm {max}}, \tau _{\mathrm {max}}$ of mode I (opening) and mode II (sliding) are experimentally measured:

• (i) The maximum force $F^{\mathrm {cr}}_{i}$, sustained by a spring, is achieved when $\delta _{i}=\delta _{i}^{\mathrm {cr}}$. This implicates that

  $$\begin{aligned} \dfrac{d{F^{\mathrm {cr}}_{i}}}{d{\delta _{i}}} \bigg |_{\delta _{i}=\delta _{i}^{\mathrm {cr}}} =0 \,\,\,\,(i=n,t) \end{aligned}$$

  (22)

  Applying the force–separation relation (21), the following simplifications can be made

  $$\begin{aligned} \dfrac{d{F^{\mathrm {cr}}_{i}}}{d{\delta _{i}}} \bigg |_{\delta _{i}=\delta _{i}^{\mathrm {cr}}} = (1-B_{i} \delta _{i}^{\mathrm {cr}})K^{0}_{i}=0 \Rightarrow B_i = \dfrac{1}{\delta ^\mathrm {cr}_{i}}\,\,\,\,(i=n,t) \end{aligned}$$

  (23)

• (ii) The force $F_i$ in the spring is obtained by lumping the traction $T_{i}$ acting on a characteristic area of $A_s$. For 2D problems, the characteristic area degrades to an effective length $l_s$ controlled by the spring and we have the following relationship:

  $$\begin{aligned} F^{\mathrm {cr}}_{n} = K_{n}^{0} \delta _{n}^{\mathrm {cr}}= \sigma _{\mathrm {max}}l_s, \,\,\,\, F^{\mathrm {cr}}_{t} = K_{t}^{0} \delta _{t}^{\mathrm {cr}}= \tau _{\mathrm {max}}l_s \end{aligned}$$

  (24)

  Notice that the effective length $l_s$ depends on the spacing between springs. That is to say, $l_s$ is equal to the element size along the delamination path for structured meshes, whereas for unstructured meshes, $l_s$ depends on mesh geometry and needs to be computed element by element. The spring force will be scaled by this parameter according to different mesh sizes.

• (iii) In order to relate these parameters to fracture energy of materials, one can use the fact that the area under the force–separation curve represents the energy dissipation which is needed to fully disconnect the crack surface controlled by the spring. That is

  $$\begin{aligned} \int _{0}^{\infty } F_{n}(\delta _{n}) \, d\delta _{n} / l_s&= \int _{0}^{\infty } T_{n}(\delta _{n}) \, d\delta _{n} = G_{\mathrm {IC}} \nonumber \\ \int _{0}^{\infty } F_{t}(\delta _{t}) \, d\delta _{t} / l_s&= \int _{0}^{\infty } T_{t}(\delta _{t}) \, d\delta _{t} = G_{\mathrm {IIC}} \end{aligned}$$

  (25)

  where the foregoing integral can be computed after applying Eqs. (21) and (23)

  $$\begin{aligned} \int _{0}^{\infty } F_{i}(\delta _{i}) \, d\delta _{i}&= \int _{0}^{\delta _{i}^{\mathrm {cr}}} K_{i}^{0} \delta _{i} \, d\delta _{i}\nonumber \\&+ \int _{\delta _{i}^{\mathrm {cr}}}^{\infty } \dfrac{K_{i}^{0}\delta _{i}}{\exp (B_{i}(\delta _{i}-\delta ^\mathrm {cr}_{i}))} \, d\delta _{i} \nonumber \\&= \dfrac{2.5K_{i}^{0}}{B_{i}^{2}}\,\,\,(i=n,t) \end{aligned}$$

  (26)

Combining Eqs. (23) through (26) yields that

$$\begin{aligned} \delta _{n}^{\mathrm {cr}}&= \dfrac{G_{\mathrm {IC}}}{2.5\sigma _{\mathrm {max}}},\,\,\, \delta _{t}^{\mathrm {cr}} = \dfrac{G_{\mathrm {IIC}}}{2.5\tau _{\mathrm {max}}}\end{aligned}$$

(27)

$$\begin{aligned} K_{n}^{0}&= \dfrac{B_{n}^{2} l_{s} G_{\mathrm {IC}}}{2.5}, \,\,\,K_{t}^{0} = \dfrac{B_{t}^{2} l_{s}G_{\mathrm {IIC}}}{2.5} \end{aligned}$$

(28)

It is noteworthy that the initial stiffnesses $K_i^0$ in the DDZM are determined by the critical energy release rates and cohesive strengths rather than arbitrarily selected high values in the typical bilinear cohesive models. This feature is also shared by the widely used Xu and Needleman (XN) exponential model [11].

3.2.3 Mixed-mode force–separation relation

In real structural components, delamination generally grows under mixed-mode conditions rather than a pure normal opening or pure transverse sliding. Therefore, a reliable cohesive model should be capable of predicting delamination onset and propagation under varying mode ratios. Herein a new mixed-mode exponential softening relation is presented in the context of Damage Mechanics. Compared with the one assumed in [13], in which two uncoupled anisotropic damage variables $D_n^{\Gamma }$ and $D_t^{\Gamma }$ were defined for each mode separately, the improved model accounts for the interaction between different modes by considering an isotropic damage $D^{\Gamma }$ in the interface.

Rather than defining an equivalent separation and determining its critical value corresponding to mixed-mode softening onset explicitly [25, 40, 41], a history ratio $\zeta$ is introduced as follows:

$$\begin{aligned} \zeta = \dfrac{\delta ^{*}_{\mathrm {eq}}}{\delta ^{\mathrm {cr}}_{\mathrm {eq}}}=\left[ \left( \dfrac{\delta ^{*}_{n}}{\delta ^{\mathrm {cr}}_n} \right) ^{\alpha } + \left( \dfrac{\delta ^{*}_{t}}{\delta ^{\mathrm {cr}}_t} \right) ^{\alpha } \right] ^{1/\alpha } \end{aligned}$$

(29)

where the constant $\alpha$ is a material parameter chosen to fit mixed mode fracture tests, $\delta ^{*}_{\mathrm {eq}}$ is the maximum converged value of the equivalent separation, and $\delta ^{\mathrm {cr}}_{\mathrm {eq}}$ is the critical equivalent separation. The nondimensional separation measure was originally proposed by Tvergaard and Hutchinson [42], and developed further by Alfano and Crisfield [43].

According to Eqs. (23) and (29), we extend the pure mode damage law (17) to mixed-mode cases through which the interface damage $D^{\Gamma }$ is related to the history ratio $\zeta$:

$$\begin{aligned} D^{\Gamma } = \left\{ \begin{array}{lcc} 0 &{} \text{ if } &{} \zeta \le 1 \\ 1- \dfrac{1}{\exp (\zeta -1)} &{} \text{ if } &{} \zeta > 1 \end{array} \right. \end{aligned}$$

(30)

Notice that the established mixed-mode damage law includes an interaction criterion (i.e. $\zeta =1$) for the prediction of damage initiation. It takes into account the fact that damage onset may occur before any of the interlaminar stress components reach their critical values under mixed-mode loadings [44], which is neglected in Liu’s formulation [13].

Figure 5a provides a visualization of the mixed-mode damage evolution for a specific value of $\alpha = 2$, which is plotted in the space $\left( \frac{\delta ^*_n}{\delta ^{\mathrm {cr}}_n},\frac{\delta ^*_t}{\delta ^{\mathrm {cr}}_t} \right)$ of normalized history separations. In order to get insight into the influence of parameter $\alpha$ on the mixed-mode damage evolution, the damage onset surfaces for $\alpha =2,3\,\text{ and }\,4$ are depicted in Fig. 5b. For comparison purposes, the damage initiation locus, determined by Liu’s anisotropic damage model [13], is also represented in Fig. 5b. It can be observed the interface damage is initialized more quickly for the new coupled damage formulation than that for Liu’s anisotropic model, when subjected to an identical mixed-mode deformation history.

Fig. 5

Mixed-mode damage variable $D^{\Gamma }$. a 3D contour plot of the isotropic interface damage variable $D^{\Gamma }$ for $\alpha =2$. b Comparison of damage onset surfaces for different mixed-mode interface models

The mixed-mode force–separation relation is then formulated in a local coordinate system with basis $\{ \varvec{t},\varvec{n} \}$ aligned with the tangential and normal directions to the crack, as follows:

$$\begin{aligned} \mathbf {F}^{L} = \mathbf {K}^L \varvec{\delta }^L = \left\{ \begin{array}{lcc} \mathbf {K}^0\varvec{\delta }^L &{} \text{ if } &{} \zeta \le 1 \\ \exp (1- \zeta )\mathbf {K}^0\varvec{\delta }^L &{} \text{ if } &{} \zeta > 1 \end{array} \right. \end{aligned}$$

(31)

where

$$\begin{aligned} \mathbf {F}^L=\begin{bmatrix} F_t \\ F_n \end{bmatrix},\,\,\, \varvec{\delta }^L=\begin{bmatrix} \delta _t\\ \delta _n \end{bmatrix},\,\,\, \mathbf {K}^0=\begin{bmatrix} K_t^0&0 \\ 0&K_n^0 \end{bmatrix} \end{aligned}$$

(32)

and the superscript $L$ denotes the quantities in the local coordinate system. Similarly, the penalty stiffness $K_p$ should be enforced in the normal direction to prevent penetration in case of crack closure. It is worth noting that the pure mode force–separation relation (21) is a particular case of the proposed mixed mode formulation.

Similar to the bilinear interface model [43], the proposed force–separation relation with exponential softening can also recover the power law criterion introduced in Reference [45, 46] if the spring is loaded under a fixed loading ratio $\beta =\delta _n/\delta _t$. The power law criterion, which is widely used to characterize mixed-mode interface failures, is established in terms of the individual components $G_{\mathrm {I}}$, $G_{\mathrm {II}}$ of energy release rate and pure mode fracture energies $G_{\mathrm {IC}}$, $G_{\mathrm {IIC}}$:

$$\begin{aligned} \left( \dfrac{G_{\mathrm {I}}}{G_{\mathrm {IC}}} \right) ^{\alpha /2} +\left( \dfrac{G_{\mathrm {II}}}{G_{\mathrm {IIC}}} \right) ^{\alpha /2} =1 \end{aligned}$$

(33)

with $\alpha$ the same parameter in the definition of history ratio (29). A good agreement with mixed-mode experimental data is typically obtained by setting $\alpha$ to be between 2 and 4. $\alpha =2 \,\text{ and }\, 4$ describe linear and quadratic interactions, respectively. The proof of the above statement, following Ref. [43], is reported in Appendix 1.

It bears emphasis that the complete decohesion of interfaces in the DDZM is only asymptotically reached when $\zeta \rightarrow \infty$, due to the exponential softening relation adopted. In practical applications, one could truncate the proposed force–separation relation by setting a damage threshold of 0.99, over which discrete springs are considered to fail completely. For convenience, we will refer to material points with $D^{\Gamma }=0.99$ and with zero crack opening, schematically illustrated in Fig. 6, as the physical and the mathematical crack tips, respectively. The physical crack tip, with its growth denoted by $\Delta a$, characterizes the boundary between the traction-free crack and cohesive zone. The cohesive zone length $L_{cz}$ is defined in the present study as the length of an irreversible damage zone ahead of the physical crack tip, with the damage variable $D^{\Gamma }$ ranging from 0 to 0.99.

Fig. 6

Schematic of a near crack-tip zone; Note that the cohesive forces are active across the shaded region

3.2.4 Thermodynamic consistency

The proposed discrete interface model can be recast in a rigorous thermodynamic framework. In analogy with continua, we first postulate a Helmholtz free energy per a single interface spring in terms of the separation configuration $(\delta _n,\delta _t)$ and the internal variable $D^{\Gamma }$, given by

$$\begin{aligned} \psi =(1-D^{\Gamma })\psi _{0}^{+} + \psi _{0}^{-} \end{aligned}$$

(34)

where $\psi _{0}^{+}$ and $\psi _{0}^{-}$ represent an additive decomposition of the stored energy $\psi _{0}$ of an undamaged spring, that is

$$\begin{aligned} \psi _{0}^{+} = \frac{1}{2}K_{n}^{0} \langle \delta _{n} \rangle ^2 + \frac{1}{2}K_{t}^{0} \delta _{t}^{2} \end{aligned}$$

(35)

and

$$\begin{aligned} \psi _{0}^{-} = \frac{1}{2}K_{p} (\delta _{n} - \langle \delta _{n} \rangle )^2 \end{aligned}$$

(36)

The aforementioned decomposition provides a distinction between energy contributions from the separation and closure of crack surfaces, respectively. The degradation acts only on the separation part $\psi _{0}^{+}$ by means of which the resistance to crack closure is maintained during interface failure.

In order to enforce thermodynamic consistency, the Clausius–Planck inequality requires the mechanical dissipation $\mathcal{{D}}_{\mathrm {mech}}$ to be non-negative. For isothermal conditions its local form reads:

$$\begin{aligned} \mathcal{{D}}_{\mathrm {mech}} = \mathbf {F}^{L} \cdot \dot{\varvec{\delta }^{L}} - \dot{\psi } \ge 0 \end{aligned}$$

(37)

where the time derivative of the stored free energy $\psi$ is computed as

$$\begin{aligned} \dot{\psi } = \dfrac{\partial {\psi }}{\partial {\varvec{\delta }^{L}}}\cdot \dot{\varvec{\delta }^{L}} + \dfrac{\partial {\psi }}{\partial {D^{\Gamma }}} \dot{D^{\Gamma }} = \dfrac{\partial {\psi }}{\partial {\varvec{\delta }^{L}}}\cdot \dot{\varvec{\delta }^{L}} - \psi _{0}^{+}\dot{D^{\Gamma }} \end{aligned}$$

(38)

Inserting the time derivative (38) into the Clausius–Planck inequality (37) yields

$$\begin{aligned} \left( \mathbf {F}^{L} - \dfrac{\partial {\psi }}{\partial {\varvec{\delta }^{L}}} \right) \cdot \dot{\varvec{\delta }^{L}} + \psi _{0}^{+} \dot{D^{\Gamma }} \ge 0 \end{aligned}$$

(39)

The above thermodynamic restriction has to be satisfied for any mechanical state. Following the Coleman and Noll procedure [47], one can rigorously obtain the mixed-mode force–separation relation given in (31) with negative normal separation penalized

$$\begin{aligned} F_{n} = (1-D^{\Gamma })K_{n}^{0} \langle \delta _n \rangle +K_{p}(\delta _n - \langle \delta _n \rangle ),\,\,\, F_{t}=(1-D^{\Gamma })K_{t}^{0} \delta _t \end{aligned}$$

(40)

And the mechanical dissipation reduces to

$$\begin{aligned} \mathcal{{D}_{\mathrm {mech}}} = \psi _{0}^{+} \dot{D^{\Gamma }} \ge 0 \end{aligned}$$

(41)

Considering that $\psi _{0}^{+}$ is a quadratic function, the rate $\dot{D^{\Gamma }}$ of the interface damage should be greater or equal to zero. However, this condition is satisfied automatically by the definitions in Eqs. (29) and (30)

$$\begin{aligned} \dot{D^{\Gamma }} = \left\{ \begin{array}{lll} 0 &{} \text{ if } &{} \zeta \le 1 \\ \exp (1-\zeta ) &{}&{}\\ \quad \times \zeta ^{1-\alpha } \left[ \dfrac{(\delta ^{*}_{n})^{\alpha -1}}{(\delta ^{\mathrm {cr}}_n)^{\alpha }} \dot{\delta ^{*}_{n}} + \dfrac{(\delta ^{*}_{t})^{\alpha -1}}{(\delta ^{\mathrm {cr}}_t)^{\alpha }} \dot{\delta ^{*}_{t}} \right] &{} \text{ if } &{} \zeta > 1 \end{array} \right. \end{aligned}$$

(42)

with $\dot{\delta }_{i}^{*} \ge 0,\,\delta _{i}^{*} \ge 0 \,(i=n,t)$ given in Eqs. (18) and (19). In other word, the proposed DDZM is thermodynamically consistent.

3.2.5 Comparison with existing interface models

The mixed-mode interface damage model proposed in this work is compared with other mixed-mode models reported in the literature. These models can be grouped into three main categories. The first is referred to as non-potential-based models (e.g. van den Bosch [48]). Such models define cohesive relations in an ad-hoc fashion and can not take all possible separation paths into account. As discussed in the work of McGarry et al. [49], this limitation may give rise to non-physical interface behavior under complex loading conditions. In addition, two different cohesive relations are needed to distinguish loading and unloading cases. The second are potential-based models, however are not necessarily thermodynamically consistent (e.g. Xu and Needleman [11] and Park et al. [50]). These models employ potential functions which are based on the work-of-separation performed by cohesive tractions. The traction–separation relations are obtained from the first derivatives of such potential functions. Analogously to non-potential-based models, additional cohesive relations are also needed to characterize unloading response for this class of models. Finally, the third category of models are potential-based methods which are also thermodynamically consistent (e.g. Alfano and Crisfield [43], Turon et al. [41], Mosler and Scheider [51]). These models are derivable from a stored Helmholtz free energy. In sharp contrast to the first two classes of interface models, both loading and unloading behaviors given by such thermodynamically consistent models follow a unique potential function. It bears emphasis that the proposed model in this work belongs to the third category as shown in Sect. 3.2.4, however, it differs from the other models in that it is developed for discrete interfaces rather than continuous ones.

The performance of the proposed DDZM is assessed under mixed-mode separations by comparison with other potential-based formulations, especially the well established Xu and Needleman (XN) model [11]. For completeness, the potential function of the XN model and material parameters (see Table 1) are provided

$$\begin{aligned} \phi _{\mathrm {XN}}&= G_{\mathrm {IC}} + G_{\mathrm {IC}} \exp \left( - \dfrac{\delta _{n}}{\delta _{n}^{\mathrm {cr}}}\right) \left[ \left\{ 1-r+\dfrac{\delta _{n}}{\delta _{n}^{\mathrm {cr}}} \right\} \left( \dfrac{1-q}{r-1}\right) \right. \nonumber \\&\left. - \left\{ q+\left( \dfrac{r-q}{r-1}\right) \dfrac{\delta _{n}}{\delta _{n}^{\mathrm {cr}}} \right\} \exp \left( -\dfrac{\delta _{t}^2}{{\delta _{t}^{\mathrm {cr}}}^2}\right) \right] \end{aligned}$$

(43)

with $q=G_{\mathrm {IIC}}/G_{\mathrm {IC}}$ and $r=2$.

Table 1 Material parameters for performance assessment

The individual components $W_n$, $W_t$ of the work performed by an interface following two non-proportional loading paths (paths 1 and 2), as well as the total amount $W_{\mathrm {total}}$, are evaluated according to

$$\begin{aligned} W_{n} = \int _{0}^{\delta _n} F_{n}(\delta _{n},\delta _{t}) \, d\delta _n /l_{s},\,\,\,\,\,W_{t} = \int _{0}^{\delta _t} F_{t}(\delta _{n},\delta _{t}) \, d\delta _t /l_{s} \end{aligned}$$

(44)

and

$$\begin{aligned} W_{\mathrm {total}}(\delta _{n},\delta _{t}) = W_{n} + W_{t} \end{aligned}$$

(45)

Path 1 denotes a normal opening $\delta _{n,max}$ followed by a tangential separation up to failure, whereas path 2 describes a tangential separation $\delta _{t,max}$ with a complete normal opening that follows. Both of the loading paths are schematically depicted in Fig. 7 and the mixed-mode ratio can be adjusted by gradually changing the value of $\delta _{n,max}$ or $\delta _{t,max}$. This type of analysis procedure, originally proposed by van den Bosch [48] and further developed by Park et al. [50], is of importance for the understanding of possible energy dissipation and failure responses predicted by interface models.

Fig. 7

Non-proportional loading paths

In Fig. 8, the work-of-separation as predicted by the DDZM and the XN model is plotted against the applied normal separation in the case of path 1 loading. $\delta _{n,max}=0\, \text{ and }\, \infty$ correspond to pure mode II and mode I failures, respectively. Between these two limiting cases, a smooth and monotonous variation of energy dissipation is expected, i.e. $W_{n}: 0 \rightarrow G_{\mathrm {IC}}, W_{t}: G_{\mathrm {IIC}} \rightarrow 0$, and $W_{\mathrm {total}}: G_{\mathrm {IIC}} \rightarrow G_{ \mathrm {IC}}$. As can be seen in Fig. 8, the DDZM presents a consistent prediction as expected, whereas the XN model gives a smooth but non-monotonous evolution of the total work $W_{\mathrm {total}}$.

Fig. 8

Variation of the normalized work-of-separation as a function of $\delta _{n,max}/\delta _{n}^{\mathrm {cr}}$ when the interface undergoes path 1 separation: a DDZM; b Xu and Needleman model ($q=r=2$)

A similar plot is shown for path 2 separation in Fig. 9, in which $\delta _{t,max}=0\, \text{ and }\, \infty$ represent pure mode I and mode II failures, respectively. It is clear that both models provide a monotonic increase ($0 \rightarrow G_{\mathrm {IIC}}$) of $W_{t}$ with increasing $\delta _{t,max}$. However, focusing on the total work $W_{\mathrm {total}}$ and the work $W_{n}$ of normal separation, the DDZM leads to a physically more realistic result than the XN model. First, the total work $W_{\mathrm {total}}$ is expected to increase monotonically from $G_{\mathrm {IC}}$ to $G_{\mathrm {IIC}}$ by increasing $\delta _{t,max}$ but the XN model gives a constant prediction. In addition, a negative energy dissipation up to $-G_{\mathrm {IC}}$ develops in the XN model for the normal separation. Figure 10 depicts the non-dimensional normal traction versus the normal separation $\delta _{n}$ and how it is affected by applied tangential separation $\delta _{t,max}$ for both models. According to Fig. 10b, the negative dissipation revealed in Fig. 9b can be attributed to the non-physical repulsive normal tractions given by the XN cohesive relation. Furthermore, for a physically sound interface model, it was stated in [49] that zero traction and consequently zero work for the normal separation should be enforced following a complete tangential failure and vice versa. As can be seen in Fig. 10, the DDZM fulfills such requirement while the XN model fails.

Fig. 9

Variation of the normalized work-of-separation as a function of $\delta _{t,max}/\delta _{t}^{\mathrm {cr}}$ when the interface undergoes path 2 separation: a DDZM; b Xu and Needleman model ($q=r=2$)

Fig. 10

Variation of the normal traction $T_{n}/\sigma _{\mathrm {max}}$ as a function of $\delta _{n}/\delta _{n}^{\mathrm {cr}}$ with different tangential separations $\delta _{t,max}/\delta _{t}^{\mathrm {cr}}$ previously applied (path 2): a DDZM; b Xu and Needleman model ($q=r=2$)

The aforementioned non-physical interface response associated with the XN model is due to the non-conservative and path-dependent nature of the interface failure. In other words, the work performed by cohesive tractions can not be appropriately represented through a potential function that is based on the work-of-separation and only depends on the current interface configuration. In contrast, past separation history is incorporated into the damage variable for the thermodynamically consistent DDZM.

Aside from the demonstrated advantages over the XN model, several other appealing features of the DDZM are illustrated by comparing it with two representative thermodynamically based interface models developed by Alfano and Crisfield (AC) [43] and Turon et al. (TCCD) [41], respectively. First, the DDZM is of exponential type whereas the AC and TCCD models are of bilinear type. From a computational point of view, the exponential DDZM is optimal since it provides a smoother softening regime. A more important advantage of the DDZM is that its formulation does not rely on a priori knowledge of the local mixed-mode ratio at each interface point, which is usually unknown in practical applications. Even though the global mixed-mode ratio is constant for some specific problems, the local mixed-mode ratio changes during the failure process. This is believed to be the main reason for anomalous sensitivity of mixed-mode energy dissipation on cohesive strengths arising in the TCCD model. Finally, in contrast to the AC model, the DDZM can automatically ensure the physical property that the complete delamination of an interface point is activated simultaneously for mode I and mode II without any additional constraint.

4 The XFEM implementation of DDZM

4.1 The XFEM discretization

Based on the partition of unity (PU) concept introduced by Babuška and Melenk [52], the extended finite element method locally enriches the standard FE displacement approximation using some pre-knowledge of the physics of problems at hand. For a comprehensive review on the XFEM, the reader is referred to Fries and Belyschko [53].

For strong discontinuities such as cracks, the displacement field in elements intersected by the crack is enhanced with a discontinuous Heaviside function, which results in a mesh that is independent of the crack. The classical branch functions which are typically used for modeling the near tip asymptotic fields in linear elasticity are not valid in cohesive zone models close to the tip as the stresses are now bounded and not singular. Hence only a Heaviside enrichment function is employed in this work.

In addition we take advantage of the shifted heaviside function [54] where postprocessing is simplified and blending elements are eliminated [55]. For shifted enrichment functions, the approximate function space is expressed in the following form:

$$\begin{aligned} \varvec{u}(\varvec{x})&= \sum _{i \in \mathcal {S}}N_i(\varvec{x})\varvec{u}_i + \sum _{i \in \mathcal {S}_H}N_i(\varvec{x})[H(\varvec{x})-H(\varvec{x}_i)]\varvec{a}_i, \nonumber \\&\quad \forall \varvec{x} \in \Omega \end{aligned}$$

(46)

where $\mathcal {S}$ is the total set of nodes in the domain, $\mathcal {S}_H \subset \mathcal {S}$ is the set of nodes (as shown in Fig. 11a as blue squares) that support elements crossed by the crack, $N_i(\varvec{x})$ are the standard FE shape functions, $\varvec{u}_i$ and $\varvec{a}_i$ are the nodal vectors of standard and enriched displacements, respectively. For two-dimensional problems, $\varvec{u}_i=\{u_{ix},u_{iy} \}^{\mathrm {T}}$ and $\varvec{a}_i=\{a_{ix},a_{iy}\}^{\mathrm {T}}$. $H(\varvec{x})$ is the Heaviside function defined by

$$\begin{aligned} H(\varvec{x})=\left\{ \begin{array}{ccc} +1 &{} \text{ above } &{}\Gamma _c \\ -1 &{} \text{ below } &{}\Gamma _c \end{array} \right. \end{aligned}$$

(47)

Fig. 11

A cohesive crack model using the XFEM and DDZM. a Enrichment visualization: red line denotes the crack $\Gamma _{c}$ and blue squares denote the enriched nodal set. b Schematic illustration of discrete interfaces embedded in an enriched element (zoom of the dashed line box). (Color figure online)

It follows that the displacement jump across the crack $\Gamma _c$ takes the form:

$$\begin{aligned} {[\![}\varvec{u} (\varvec{x}) {]\!]}= 2\sum _{i \in \mathcal {S}_H} N_i(\varvec{x})\varvec{a}_i,\,\,\,\,\forall \varvec{x} \in \Gamma _c \end{aligned}$$

(48)

Substituting the displacement approximations (46)–(48) into the weak forms (7) and (8) and using Voigt notation, leads to the discretized residual, which forms a system of nonlinear equations:

$$\begin{aligned} \mathbf {R}^u&=\mathbf {F}^{\mathrm {int}} -\mathbf {F}^{\mathrm {ext}} =0 \end{aligned}$$

(49)

$$\begin{aligned} \mathbf {R}^a&=\hat{\mathbf {F}}^{\mathrm {int}} + \hat{\mathbf {F}}^{\mathrm {coh}} -\hat{\mathbf {F}}^{\mathrm {ext}} =0 \end{aligned}$$

(50)

where $\mathbf {F}$ and $\hat{\mathbf {F}}$ are force vectors associated with the standard and enriched degrees of freedom, respectively, given by

$$\begin{aligned} \mathbf {F}^{\mathrm {int}}_i&= \int _{\Omega } (\mathbf {B}^u_i)^{\mathrm {T}} \varvec{\sigma } \, d\Omega , \quad i \in \mathcal {S}, \end{aligned}$$

(51)

$$\begin{aligned} \mathbf {F}^{\mathrm {ext}}_i&= \int _{\Omega } N_i \mathbf {b} \, d\Omega + \int _{\Gamma _t} N_i \bar{\mathbf {t}} \, d\Gamma , \quad i \in \mathcal {S}, \end{aligned}$$

(52)

$$\begin{aligned} \hat{\mathbf {F}}^{\mathrm {int}}_i&= \int _{\Omega } (\mathbf {B}^a_i)^{\mathrm {T}} \varvec{\sigma } \, d\Omega , \quad i \in \mathcal {S}_H, \end{aligned}$$

(53)

$$\begin{aligned} \hat{\mathbf {F}}^{\mathrm {ext}}_i&= \int _{\Omega } N_i H_i^{\mathrm {shift}}\ \mathbf {b} \, d\Omega + \int _{\Gamma _t} N_i H_i^{\mathrm {shift}} \bar{\mathbf {t}} \, d\Gamma , \quad i \in \mathcal {S}_H, \end{aligned}$$

(54)

$$\begin{aligned} \hat{\mathbf {F}}^{\mathrm {coh}}_i&= 2 \sum ^{N_{SP}}_{S=1} N_i(\varvec{x}_S) \mathbf {F}_S, \quad i \in \mathcal {S}_H. \end{aligned}$$

(55)

with $H_i^{\mathrm {shift}}$ the shifted-basis Heaviside function defined as

$$\begin{aligned} H_i^{\mathrm {shift}} =H(\varvec{x})-H(\varvec{x}_i) \end{aligned}$$

(56)

$\mathbf {B}^u_i$ and $\mathbf {B}^a_i$ are standard and enriched strain–displacement matrices, respectively. These matrices in two-dimensional cases are given by

$$\begin{aligned} \mathbf {B}_i^u&= \begin{bmatrix} N_{i,x}&0\\ 0&N_{i,y}\\ N_{i,y}&N_{i,x} \end{bmatrix}, \quad i \in \mathcal {S} \end{aligned}$$

(57)

$$\begin{aligned} \mathbf {B}_i^a&= \begin{bmatrix} (N_iH_i^{\mathrm {shift}})_{,x}&0\\ 0&(N_iH_i^{\mathrm {shift}})_{,y} \\ (N_iH_i^{\mathrm {shift}})_{,y}&(N_iH_i^{\mathrm {shift}})_{,x} \end{bmatrix}, \quad i \in \mathcal {S}_H \end{aligned}$$

(58)

Finally, the Cauchy stress $\varvec{\sigma }$ that appears in Eqs. (51) and (53) takes the form:

$$\begin{aligned} \varvec{\sigma }&= (1-\bar{D}^{\Omega }) \mathbf {C} \varvec{\epsilon }\nonumber \\&= (1-\bar{D}^{\Omega }) \mathbf {C} \left( \sum _{j \in \mathcal {S}} \mathbf {B}_j^u \varvec{u}_j +\sum _{j \in \mathcal {S}_H} \mathbf {B}_j^a \varvec{a}_j \right) \end{aligned}$$

(59)

and the force $\mathbf {F}_S$ sustained by the $S^{th}$ spring can be calculated by plugging the displacement jump (48) into the force–separation relation (31):

$$\begin{aligned} \mathbf {F}_S&= \mathbf {F}({[\![}\varvec{u} (\varvec{x}_S) {]\!]}) = \mathbf {\Lambda }^{\mathrm {T}} \mathbf {K}^L \varvec{\delta }^L \nonumber \\&= 2\mathbf {\Lambda }^{\mathrm {T}} \mathbf {K}^L \mathbf {\Lambda } \sum _{j \in \mathcal {S}_H} N_j(\varvec{x}_S)\varvec{a}_j \end{aligned}$$

(60)

In the above equation, the spring stiffness $\mathbf {K}^L$, formulated in the local coordinate system (as shown in Fig. 11b), is transformed to the global coordinate system by the rotation matrix $\mathbf {\Lambda }$, defined as

$$\begin{aligned} \mathbf {\Lambda }= \begin{bmatrix} \cos \theta&\sin \theta \\ -\sin \theta&\cos \theta \end{bmatrix} \end{aligned}$$

(61)

4.2 Consistent linearization

The nonlinear system introduced in Sect. 4.1 is solved using an incremental-iterative scheme wherein the total loading is divided into a sequence of incremental steps $[ t_n,t_{n+1}]$ and the Newton–Raphson method is invoked for the solution of each step. The linearized system at the equilibrium iteration $k$ within the incremental step $n+1$ is obtained by differentiating the discretized residual (49) and (50), as

$$\begin{aligned} {\varvec{J}} ^k _{n+1} \left\{ \begin{bmatrix} \Delta \varvec{u} \\ \Delta \varvec{a} \end{bmatrix} ^{k+1} _{n+1} - \begin{bmatrix} \Delta \varvec{u} \\ \Delta \varvec{a} \end{bmatrix} ^{k} _{n+1} \right\} +\begin{bmatrix} \mathbf {R}^u \\ \mathbf {R}^a \end{bmatrix} ^{k} _{n+1} =0 \end{aligned}$$

(62)

where ${\varvec{J}}$ is the Jacobian matrix (or consistent tangent stiffness matrix), given by

$$\begin{aligned} {\varvec{J}} = \begin{bmatrix} \mathbf {R}^u_{,\varvec{u}}&\mathbf {R}^u_{,\varvec{a}} \\ \mathbf {R}^a_{,\varvec{u}}&\mathbf {R}^a_{,\varvec{a}} \end{bmatrix} \end{aligned}$$

(63)

and the subscript comma denotes the differentiation with respect to the subscript quantity. The solution increments $\Delta \varvec{u}$ and $\Delta \varvec{a}$ are then obtained by solving the above system of equations.

For robustness and faster convergence of the scheme, the consistent tangent stiffness is derived analytically for the proposed nonlocal model in the framework of the XFEM. Following the method proposed in [56], Gauss integration is performed first to compute the integral-type internal forces $\mathbf {F}^{\mathrm {int}}$ and $\hat{\mathbf {F}}^{\mathrm {int}}$ given in Eqs. (51) and (53):

$$\begin{aligned} \mathbf {F}^{\mathrm {int}}=\sum _{I=1}^{N_I} w_I (\mathbf {B}^u_I)^{\mathrm {T}} \varvec{\sigma }_I,\,\,\,\, \hat{\mathbf {F}}^{\mathrm {int}}=\sum _{I=1}^{N_I} w_I (\mathbf {B}^a_I)^{\mathrm {T}} \varvec{\sigma }_I \end{aligned}$$

(64)

with

$$\begin{aligned} \varvec{\sigma }_I&= \left( 1-\bar{D}^{\Omega }_I \right) \varvec{\sigma }_I^e = \left( 1-\bar{D}^{\Omega }_I \right) \mathbf {C}\left( \mathbf {B}^u_I \mathbf {u}+ \mathbf {B}^a_I \mathbf {a} \right) \end{aligned}$$

(65)

$$\begin{aligned} \bar{D}^{\Omega }_I&=\sum _{J=1}^{N_J} w_J \Phi _{IJ} D^{\Omega }_J \end{aligned}$$

(66)

where upper case letters $I$ and $J$ are used to indicate indices of Gauss points. $N_I$ is the total number of Gauss points in the background mesh whereas $N_J$ is the number of the neighboring Gauss points within the influence window of point $\varvec{x}_I$. It is worth noting that a shorthand notation is adopted here to simplify derivations such that $w(\varvec{x}_I)=w_I$, $\mathbf {B}^u(\varvec{x}_I)=\mathbf {B}^u_I$, $\Phi _J(\varvec{x}_I)=\Phi _{IJ}$, $\bar{D}^{\Omega }(\varvec{x}_I)=\bar{D}^{\Omega }_I$, etc..

Differentiating the local damage $D^{\Omega }$ of the bulk material, with respect to the nodal vectors of standard and enriched displacements, leads to

$$\begin{aligned} \dfrac{\partial {D^{\Omega }}}{\partial {\varvec{u}}}&= \dfrac{\partial {D^{\Omega }}}{\partial {\kappa }} \dfrac{\partial {\kappa }}{\partial {\tilde{\epsilon }_{eq}}} \dfrac{\partial {\tilde{\epsilon }_{eq}}}{\partial {\varvec{\epsilon }}} \dfrac{\partial {\varvec{\epsilon }}}{\partial {\varvec{u}}} =d^{\prime }\kappa ^{\prime } \mathbf {g}\mathbf {B}^u \end{aligned}$$

(67)

$$\begin{aligned} \dfrac{\partial {D^{\Omega }}}{\partial {\varvec{a}}}&= \dfrac{\partial {D^{\Omega }}}{\partial {\kappa }} \dfrac{\partial {\kappa }}{\partial {\tilde{\epsilon }_{eq}}} \dfrac{\partial {\tilde{\epsilon }_{eq}}}{\partial {\varvec{\epsilon }}} \dfrac{\partial {\varvec{\epsilon }}}{\partial {\varvec{a}}} =d^{\prime }\kappa ^{\prime } \mathbf {g}\mathbf {B}^a \end{aligned}$$

(68)

with $d^{\prime } = \partial D^{\Omega } /\partial \kappa$, $\kappa ^{\prime } = \partial \kappa /\partial \tilde{\epsilon }_{eq}$, and $\mathbf {g}= \partial \tilde{\epsilon }_{eq} / \partial \varvec{\epsilon }$.

For the cohesive force $\hat{\mathbf {F}}^{\mathrm {coh}}$, which depends only on the enriched displacement vector $\varvec{a}$, no numerical integration needs to be performed due to the discrete interfaces adopted in this work. Thus, the partial derivative $\partial \hat{\mathbf {F}}^{\mathrm {coh}} / \partial \varvec{a}$ is explicated as follows:

$$\begin{aligned} \dfrac{\partial {\hat{\mathbf {F}}^{\mathrm {coh}}}}{\partial {\varvec{a}}}&= 2\sum _{S=1}^{N_{SP}} {\mathbf {N}}_S^{\mathrm {T}} \dfrac{\partial {\mathbf {F}_S}}{\partial {\varvec{a}}} =2\sum _{S=1}^{N_{SP}} {\mathbf {N}}_S^{\mathrm {T}} \varvec{\Lambda }_S^{\mathrm {T}} \dfrac{\partial {\mathbf {F}^L_S}}{\partial {\varvec{\delta }^L_S}} \dfrac{\partial {\varvec{\delta }^L_S}}{\partial {{[\![}\varvec{u} {]\!]}_S}} \dfrac{\partial {{[\![}\varvec{u} {]\!]}_S}}{\partial {\varvec{a}}} \nonumber \\&= 4\sum _{S=1}^{N_{SP}} \mathbf {N}_S^{\mathrm {T}} \varvec{\Lambda }^{\mathrm {T}}_S \mathbf {M}_S \varvec{\Lambda }_S \mathbf {N}_S \end{aligned}$$

(69)

with $\mathbf {M}_S=\partial \mathbf {F}^L_S/\partial \varvec{\delta }^L_S$.

Taking into account the expressions (64)–(69), the components of consistent tangent stiffness are obtained by differentiating the force vectors with respect to the nodal displacements

$$\begin{aligned} \mathbf {R}^{u}_{,\varvec{u}}&= \sum _{I=1}^{N_I} (1-\bar{D}^{\Omega }_I )w_I (\mathbf {B}^u_I)^{\mathrm {T}} \mathbf {C} \mathbf {B}^u_I\nonumber \\&-\sum _{I=1}^{N_I} \sum _{J=1}^{N_J} w_I w_J \Phi _{IJ} d^{\prime }_J \kappa ^{\prime }_J (\mathbf {B}^u_I)^{\mathrm {T}} \varvec{\sigma }_I^e \mathbf {g}_J \mathbf {B}^u_J \end{aligned}$$

(70)

$$\begin{aligned} \mathbf {R}^{u}_{,\varvec{a}}&= \sum _{I=1}^{N_I} (1-\bar{D}^{\Omega }_I )w_I (\mathbf {B}^u_I)^{\mathrm {T}} \mathbf {C} \mathbf {B}^a_I\nonumber \\&-\sum _{I=1}^{N_I} \sum _{J=1}^{N_J} w_I w_J \Phi _{IJ} d^{\prime }_J \kappa ^{\prime }_J (\mathbf {B}^u_I)^{\mathrm {T}} \varvec{\sigma }_I^e \mathbf {g}_J \mathbf {B}^a_J \end{aligned}$$

(71)

$$\begin{aligned} \mathbf {R}^{a}_{,\varvec{u}}&= \sum _{I=1}^{N_I} (1-\bar{D}^{\Omega }_I )w_I (\mathbf {B}^a_I)^{\mathrm {T}} \mathbf {C} \mathbf {B}^u_I\nonumber \\&-\sum _{I=1}^{N_I} \sum _{J=1}^{N_J} w_I w_J \Phi _{IJ} d^{\prime }_J \kappa ^{\prime }_J (\mathbf {B}^a_I)^{\mathrm {T}} \varvec{\sigma }_I^e \mathbf {g}_J \mathbf {B}^u_J \end{aligned}$$

(72)

$$\begin{aligned} \mathbf {R}^{a}_{,\varvec{a}}&= \sum _{I=1}^{N_I} (1-\bar{D}^{\Omega }_I )w_I (\mathbf {B}^a_I)^{\mathrm {T}} \mathbf {C} \mathbf {B}^a_I\nonumber \\&-\sum _{I=1}^{N_I} \sum _{J=1}^{N_J} w_I w_J \Phi _{IJ} d^{\prime }_J \kappa ^{\prime }_J (\mathbf {B}^a_I)^{\mathrm {T}} \varvec{\sigma }_I^e \mathbf {g}_J \mathbf {B}^a_J \nonumber \\&+4\sum _{S=1}^{N_{SP}} \mathbf {N}_S^{\mathrm {T}} \varvec{\Lambda }^{\mathrm {T}}_S \mathbf {M}_S \varvec{\Lambda }_S \mathbf {N}_S \end{aligned}$$

(73)

Details of those partial derivatives required to compute the above consistent tangent stiffness are given in Appendix 2. Note that the second terms on the right-hand side of Eqs. (70)–(73) represent the correction of the nonlocal interaction to the first terms which define the secant stiffness.

4.3 Solution methodology

Due to the presence of softening of material interfaces, limit points often appear in the structural equilibrium path, in which case the traditional incremental procedures may diverge. In order to handle such limit points, a path-following scheme, commonly known as the arc-length method, is adopted in this work to parameterize the equilibrium path by an arc-length parameter. Typically, the arc-length parameter is chosen to be the global norm of the incremental solution vector and loading factor [57, 58]. Nevertheless, as pointed out in Reference [59], this arc-length parameter often fails when limit points are mainly associated with localized failure process zones. A specific computational issue is that complex roots may be obtained for loading factors. As a remedy for this problem, a local control strategy was proposed by Alfano and Crisfield [60], where the arc-length parameter only depends on a limited set of degrees of freedom involved in the failure process. However, a priori knowledge of the position of the failure process zone required for this scheme is not always available in practice.

More recently, Verhoosel et al. [59] proposed a dissipation-based arc-length method where the released energy during failure, a global quantity directly related to the failure process, is coupled to the arc-length parameter. The robustness and convergence performance of the energy release control has been demonstrated by simulating a bending test on a single-edge notched beam. Following this idea, a path-following constraint $g$, which relates the incremental load factor $\Delta \lambda$ and the solution increments $\Delta \varvec{u}$ and $\Delta \varvec{a}$, is enforced at each load increment in this work. That is

$$\begin{aligned} g&= \dfrac{1}{2}( \mathbf {F}^{\mathrm {ext}} )^\mathrm {T} (\lambda _{0}\Delta \varvec{u} -\Delta \lambda \varvec{u}_0) \nonumber \\&+ \dfrac{1}{2}( \hat{\mathbf {F}}^{\mathrm {ext}} )^\mathrm {T} (\lambda _{0}\Delta \varvec{a} -\Delta \lambda \varvec{a}_0) -\Delta \ell =0 \end{aligned}$$

(74)

where the superscript $0$ indicates the converged values from the previous load increment and $\Delta \ell$ is the arc-length parameter that controls the size of each incremental step. See Reference [59] for more details.

The equilibrium state can thus be determined by solving the augmented system:

$$\begin{aligned} \mathbf {R}= \begin{bmatrix} \mathbf {F}^{\mathrm {int}}-\lambda \mathbf {F}^{\mathrm {ext}} \\ \hat{\mathbf {F}}^{\mathrm {int}} + \hat{\mathbf {F}}^{\mathrm {coh}}-\lambda \hat{\mathbf {F}}^{\mathrm {ext}} \\ g \end{bmatrix} = \begin{bmatrix} \mathbf{0} \\ \mathbf{0} \\ 0 \end{bmatrix} \end{aligned}$$

(75)

Correspondingly, the linearized system given in Eq. (62) needs to be augmented as follows

$$\begin{aligned}&\begin{bmatrix} \mathbf {R}^u_{,\varvec{u}}&\mathbf {R}^u_{,\varvec{a}}&-\mathbf {F}^{\mathrm {ext}} \\ \mathbf {R}^a_{,\varvec{u}}&\mathbf {R}^a_{,\varvec{a}}&-\hat{\mathbf {F}}^{\mathrm {ext}} \\ g_{,\varvec{u}}&g_{,\varvec{a}}&g_{,\lambda } \end{bmatrix} ^k _{n+1} \left\{ \begin{bmatrix} \Delta \varvec{u} \\ \Delta \varvec{a} \\ \Delta \lambda \end{bmatrix} ^{k+1} _{n+1} - \begin{bmatrix} \Delta \varvec{u} \\ \Delta \varvec{a} \\ \Delta \lambda \end{bmatrix} ^{k} _{n+1} \right\} + \mathbf {R} ^{k} _{n+1}\nonumber \\&=0 \end{aligned}$$

(76)

where the derivatives required to construct the above consistent tangent stiffness are defined as

$$\begin{aligned} \dfrac{\partial {g}}{\partial {\varvec{u}}}&= \dfrac{1}{2} \lambda _{0} (\mathbf {F}^{\mathrm {ext}})^{\mathrm {T}};\,\,\, \dfrac{\partial {g}}{\partial {\varvec{a}}}=\dfrac{1}{2} \lambda _{0} (\hat{\mathbf {F}}^{\mathrm {ext}})^{\mathrm {T}};\nonumber \\ \dfrac{\partial {g}}{\partial {\lambda }}&= - \dfrac{1}{2} \left( \varvec{u}_0^{\mathrm {T}}\mathbf {F}^{\mathrm {ext}}+ \varvec{a}_0^{\mathrm {T}} \hat{\mathbf {F}}^{\mathrm {ext}} \right) \end{aligned}$$

(77)

As evident from the above equations, the augmented part of the consistent tangent stiffness only needs to be updated at the beginning of each incremental step whereas the remainder part is recomputed in each iteration.

5 Numerical examples

The methodology proposed in the previous sections has been implemented in MATLAB®. In this section, its effectiveness to progressive delamination analyses is examined under pure mode I, pure mode II and mixed-mode loadings by using double cantilever beam (DCB), end notched flexure (ENF), and mixed-mode bending (MMB) test specimens. The model setup and boundary conditions for each test case are illustrated in Fig. 12, where the bulk behavior is taken to be linear elastic without damage. In addition, the failure process of a fiber/epoxy unit cell is also analyzed using the DDZM, in which case both the fiber/matrix debonding and matrix cracking are considered. Plane stress conditions are assumed for all numerical examples in this section. Bilinear quadrilateral elements are employed to discretize these specimen domains. Benefiting from the proposed XFEM formulation, the potential delamination and debonding paths can be arbitrarily positioned within elements rather than along element interfaces as in the FEM. In the following examples, mesh configurations are designed such that the discontinuity path cuts through the elements in order to test the XFEM-DDZM implementation.

Fig. 12

DCB, ENF, and MMB test specimens. a DCB test setup: pure mode I loading, b ENF and MMB test setup: pure mode II and mixed-mode loadings, respectively

5.1 Mode I: double cantilever beam (DCB) test

For DCB test specimens, a fixed boundary condition is applied at the right end. Pure mode I delamination is then driven by a load $P$ applied at the upper and lower surfaces of the left end (see Fig. 12a). The load point displacement $\Delta$ is recorded to obtain global force–displacement responses. In addition, the development of the cohesive zone length is also monitored for the following analysis.

5.1.1 Parametric study on mesh size and interface strength

In this example, we first investigate the effects of mesh size and interface strength on structural responses by conducting several groups of DCB simulations. As illustrated in Table 2, these DCB specimens share the same geometry and isotropic material properties, except for the interface strength $\sigma _{\mathrm {max}}$. Its values are varied as 5.7, 20, and 57 MPa. Accordingly, the parameter $B_{n}$ is computed to be 50.7, 177.9, and 507.1 $\mathrm {mm}^{-1}$. We consider a uniform structured mesh with 7 different element sizes: $3 \times 25$, $3 \times 40$, $3 \times 50$, $3 \times 100$, $3 \times 200$, $3 \times 400$, and $3 \times 800$, and analyze the problem for each of the interface strength values (total of 21 analyses). The mesh size is characterized by the element length $L_{el}$ along the direction of delamination growth.

Table 2 Material and geometry parameters for isotropic DCB specimens

The load–displacement curves, grouped by different values of interface strength, are plotted in Figs. 13, 14 and 15, against the analytical solution obtained using beam theory [61]. Note that some results for coarse meshes have not been displayed in Figs. 13 and 14 because they show extremely unreasonable oscillation and prediction of the peak load.

Fig. 13

Load–displacement curves obtained for different mesh sizes in a DCB test with interface strength $\sigma _{\mathrm {max}}=57$ MPa. a $P$–$\Delta$ curves, b zoomed $P$–$\Delta$ curves

Fig. 14

Load–displacement curves obtained for different mesh sizes in a DCB test with interface strength $\sigma _{\mathrm {max}}=20$ MPa. a $P$–$\Delta$ curves, b zoomed $P$–$\Delta$ curves

Fig. 15

Load–displacement curves obtained for different mesh sizes in a DCB test with interface strength $\sigma _{\mathrm {max}}=5.7$ MPa. a $P$–$\Delta$ curves, b zoomed $P$–$\Delta$ curves

For all values of interface strength adopted in simulations, it is evident that the numerical results are objective with respect to the mesh size. Furthermore, the converged results are found to be in very good agreement with the analytical solution, allowing the system response, determined using a mesh with $L_{el}=0.125$ mm, to serve as the reference solution. Conversely, results obtained using relatively coarse meshes overestimate significantly the peak load. Their smoothness in the softening regime, where steady state delamination occurs, also deteriorates with increasing mesh size $L_{el}$. The reason for this phenomenon is the number of discrete springs spanning the cohesive zone, defined as $N_{s}=1+L_{cz}/L_{el}$, is not enough to represent properly its softening traction profile. Hence, sufficient number of interface elements are needed to ensure accurate delamination analyses. On the other hand, excessive meshing results in high burden and poor computational efficiency. It should be noted that these considerations are also true for continuous type models and have been reported in the literature [62, 63]. To this end, meshing rules, considering adequate balance between accuracy and efficiency, can be estimated by the cohesive zone length $L_{cz}$ and the minimum number of discrete springs required to resolve it.

The former has been obtained in the foregoing simulation using a mesh with $L_{el}=0.125$ mm. Figure 16 shows the evolution process of cohesive zone lengths, together with loading forces, as functions of applied displacements for each case of interface strength values. It is found that the softening in the load–displacement curves is initiated once the cohesive zone is fully developed. One can also observe that specimens with $\sigma _{\mathrm {max}} = 5.7$ MPa tend to develop a longer cohesive zone, which indicates larger ductility. Apart from numerical simulations, several functional solutions have been proposed by researchers to estimate the length $L_{cz}^f$ of a fully developed cohesive zone. We have compared in Fig. 17 the numerical solutions with the predictions obtained using the following formulas suggested by Irwin [64] and Yang and Cox [65], respectively:

$$\begin{aligned} L_{cz,\mathrm {Irwin}}^{f}&= \dfrac{1}{\pi } E \dfrac{G_{\mathrm {IC}}}{(\sigma _{\mathrm {max}})^2} \end{aligned}$$

(78)

$$\begin{aligned} L_{cz,\mathrm {Yang}}^{f}&= \left( E \dfrac{G_{\mathrm {IC}}}{(\sigma _{\mathrm {max}})^2}\right) ^{\frac{1}{4}} h^{\frac{3}{4}} \end{aligned}$$

(79)

It can clearly be observed from Fig. 17 that the larger ductility present (when $\sigma _{\mathrm {max}}$ decreases), the larger deviation of the closed-form solutions from the true cohesive length scale. Therefore one has to resort to numerical techniques under such a condition.

Fig. 16

DCB test results with load, $P$ (dashed lines), and cohesive zone length, $L_{cz}$ (solid lines), plotted against the load point displacement, $\Delta$, using different interface strengths

Fig. 17

Numerical and closed-form estimations of the fully developed cohesive zone length for different interface strength $\sigma _{\mathrm {max}}$. (Color figure online)

In the case of $\sigma _{\mathrm {max}}=57$ MPa, the length of the fully developed cohesive zone is measured as 1.2 mm. As can be seen from Fig. 13, there is an apparent deterioration in the quality of results when the element size $L_{el}$ is increased from 0.5 to 1 mm. This indicates that the minimum value of $N_{s}$, required for a precise load–displacement response, lies between 2 and 3. The same analysis procedure is applied to the other cases of interface strength. For $\sigma _{\mathrm {max}}=20$ and 5.7 MPa, the minimum values of $N_{s}$ range from 2 to 3, and from 3 to 5, respectively. To be conservative, the minimum number of discrete springs in the DDZM for accurate resolution of the traction profile near the crack tip, is suggested to be 5 if convergence studies are not available.

It can be seen from Figs. 13, 14, 15 and 16 that lower interface strength leads to lower peak load, namely a more flexible elastic loading regime if the mesh size is fixed. However, there are no apparent differences in the delamination growth regime provided that converged solutions are obtained. The consistency between this finding and those observed by Turon et al. [63, 66] and Harper and Hallett [62] for conventional CCZMs indicates that the mesh optimization technique [63], namely, loosening the mesh size requirement by reducing the numerical interface strength, is also applicable to the DDZM.

5.1.2 Experimental validation

In order to further validate the proposed DDZM, another mode I DCB simulation, with the geometry and material parameters listed in Table 3, is performed. In this case, the specimen is fabricated using carbon fiber/epoxy HTA/6367C. A uniform structured mesh with $9 \times 1200$ elements is used to discretize the problem. As can be seen in Fig. 18a, the predicted load–displacement response matches well with experimental data available in [67, 68]. In the experiment, the mode I crack growth was also traced by using a traveling microscope. Figure 18b presents the crack growth as a function of the load point displacement for both numerical and experimental cases. It is observed that the onset of crack propagation is accurately captured by the DDZM while the following growth speed is slightly underestimated.

Fig. 18

Comparison with experimental data provided in Ref. [68] for the DCB setup. a Applied load versus load point displacement, b crack growth versus load point displacement

Table 3 Material and geometry parameters for HTA/6367C specimens [67, 68]

5.2 Mode II: end notched flexure (ENF) test

In this example, a simply supported ENF test specimen was loaded at its mid-span position (i.e. $c=0$) to activate a pure mode II delamination. The geometry and material parameters are taken from Table 3. In order to investigate the influence of mesh alignment on the numerical results, two types of finite element meshes are produced to discretize the domain. The first one is a $9 \times 1200$ structured mesh and the other one is an unstructured mesh consisting of 8,149 elements (see Fig. 19). Comparison of the load–displacement curves for the structured and unstructured meshes with the closed-form solution[61] are presented in Fig. 20, while comparison of the crack propagation processes is depicted in Fig. 21.

Fig. 19

Spatial discretizations of the ENF test specimen with enriched elements shaded in grey and laminate interfaces denoted by dashed lines. a ENF test specimen, b structured mesh, zoomed of the red box, c unstructured mesh, zoomed of the red box. (Color figure online)

Fig. 20

Comparison of load–displacement curves

Fig. 21

Comparison of crack growth processes

It is notable that the DDZM yields consistent load–displacement curves for both meshes and they are in close agreement with the analytical solution based on beam theory. Similarly, the predicted delamination growth processes, as reported in Fig. 21, also do not show any dependency on mesh alignment.

As revealed in Figs. 20 and 21, three different stages of the global response can be clearly identified: initial loading, delamination growth, and delamination arrest. Prior to the onset of delamination, no crack growth can be observed and thus the load–displacement response is linear upon initial loading. Following this stage, a sudden snap-back segment is traced by the adopted arc-length method, which corresponds to delamination propagation in a rapid, unstable manner. When the crack tip approaches the center of the specimen right beneath the loading position, the delamination propagation is suppressed and the sustained load increases again. These features captured by the DDZM are also consistent with experimental observations provided in Reference [69].

5.3 Mixed-mode: mixed-mode bending (MMB) test

The MMB delamination test was originally designed and developed by Reeder and Crews [70] as a measurement of fracture toughness of laminated composites under combined mode I and mode II loading conditions. A wide variety of mixed-mode ratios $\Psi =G_\mathrm {II}/(G_\mathrm {I}+G_\mathrm {II})$, ranging from pure mode I (0 %) to pure mode II (100 %), can be produced as desired by varying the lever arm length $c$ shown in Fig. 12b. In this subsection, the proposed mixed-mode DDZM will be applied to examine MMB specimens with material and geometrical parameters taken from Table 3. The parameter $\alpha$ is choose to be 2 in the following simulations since a good fit to experimental data is generally obtained by using this value.

First, the energy dissipation process of a single spring, subjected to a fixed loading ratio $\beta = \delta _n/\delta _t$, is carefully analyzed based on the novel mixed-mode formulation and the material parameters listed in Table 3. Figure 22 shows the variation of energy dissipation during a failure process for a wide range of loading ratios, from $\tan 0^{\circ }$ to $\tan 90^{\circ }$. For the sake of comparison, the results as computed by the original anisotropic model in [13] are presented in Fig. 23. As can been seen from these plots, both models give monotonously changed energy dissipation for varying failure modes. Nevertheless, the newly proposed isotropic damage model (Fig. 22) can guarantee a smoother energy dissipation process than Liu’s model where kink points arise.

Fig. 22

Work-of-separation as computed by the proposed mixed-mode formulation for a single spring: a normal component $W_{n}$; b shear component $W_{t}$; c total work $W_{\mathrm {total}}$

Fig. 23

Work-of-separation as computed by the anisotropoic damage model in [13] for a single spring: a normal component $W_{n}$; b shear component $W_{t}$; c total work $W_{\mathrm {total}}$

Moreover, the performance of the DDZM for delamination analyses in different mixed-mode ratios $\Psi$ is also investigated. Three test cases of $\Psi =25$, 50, and 75 % are considered. Computing the lever arm length $c$ given a mixed mode ratio has been standardized by ASTM and lately improved by Blanco et al. [71]. Following the procedure, the corresponding arm length $c$ to mixed-mode ratios of 25, 50, and 75 % are set to be 116.5, 63.1, and 43.9 mm, respectively. The left end loading versus displacement curves, as predicted by the new DDZM formulation, are plotted against beam theory solutions in Figs. 24, 25 and 26 for each value of mixed-mode ratios. Although the numerical results exhibit a slightly lower stiffness than analytical solutions in the elastic loading phase, an almost identical match can be observed after delamination is initiated for all simulation cases. In Figs. 24 and 25, our present results are also compared with those by Liu’s anisotropic damage model [13] in cases of $\Psi =25$ and 75 %, where the improvement resulted from the new isotropic interface model can be clearly seen.

Fig. 24

Comparison of load–displacement curves. The applied mixed-mode ratio $\Psi$ is taken as 25 %

Fig. 25

Comparison of load–displacement curves. The applied mixed-mode ratio $\Psi$ is taken as 75 %

Fig. 26

Load–displacement curves obtained for different interface strengths in an MMB test. The applied mixed-mode ratio $\Psi$ is taken as 50 %

Besides the original maximum interface stress combination ($\sigma _{\mathrm {max}}=$ 40 MPa and $\tau _{\mathrm {max}}=$ 60 MPa), we also applied three other cohesive strength combinations of 40:40, 40:80, and 40:120 in the case of $\Psi =50\,\%$. The corresponding parameter $B_{t}$ is varied as 99.8, 199.6, and 299.4 $\mathrm {mm}^{-1}$. The load–displacement curves are compared in Fig. 26, where they almost coincide with each other and agree well with the analytical solution. The illustrated insensitivity of the global response to the cohesive strength ratios is in sharp contrast to the sensitive results reported in [8, 66]. It indicates that the mixed-mode energy dissipation is characterized correctly by the proposed damage interface model in all cases.

5.4 Failure of a fiber/epoxy unit cell

As the last example, we study the failure process of a fiber/epoxy unit cell where the interaction between fiber debonding and matrix damage is considered. The problem configuration and boundary conditions are depicted in Fig. 27, where the specimen is subjected to a horizontal displacement $\Delta$ on its left and right edges. Considering the symmetry of the domain and the boundary conditions, only the top right quarter of the domain is modeled in the present study, with horizontal rollers deployed along the x-axis and vertical ones along the y-axis.

Fig. 27

A single circular fiber embedded in a square block of epoxy under a uniaxial tension. The dimensions are: $L=100$ mm and $R=50$ mm

The debonding behavior of the curved material interface is described by the DDZM, while the Mazars damage law is applied to capture the matrix degradation. Since the fiber inclusion is much stronger than the epoxy matrix, no damage is assumed in the fiber. The material properties of the fiber/epoxy specimen are listed in Table 4. Accordingly, the DDZM parameters $B_{n}$ and $B_{t}$ take values of 27.5 and 31.3 $\mathrm {mm}^{-1}$, respectively. Three different mesh resolutions of $19 \times 19$, $29 \times 29$, and $39 \times 39$ are adopted in the numerical analysis.

Table 4 Material properties of the fiber/epoxy unit cell

The overall response of the fiber/epoxy structure is measured in terms of the total resultant force $P$ acting along the right edge versus the applied displacement $\Delta$. Figure 28a depicts $P$ versus $\Delta$ curves for different mesh sizes using a local damage formulation. One can clearly observe reduced peak load upon mesh refinement. Furthermore, the local formulation tends to give different dissipated energies during the failure process and therefore it is unreliable. In order to alleviate mesh dependency, we apply the nonlocal formulation as discussed in Sect. 3. The characteristic length for the nonlocal continuum model is prescribed as $l_c = 6$ mm, which is larger than the coarsest element size, to insure mesh size insensitivity. The corresponding force–displacement curves are then obtained and shown in Fig. 28b for different meshes. It can be seen that the peak load and dissipated energy are nearly mesh insensitive.

Fig. 28

Mesh convergence studies for the fiber/epoxy unit cell using: a Local formulation, b nonlocal formulation

The numerical results obtained using the nonlocal damage formulation for mesh size $39 \times 39$ are used to visualize the simulated failure pathway in Fig. 29. We plot the distribution of both the nonlocal bulk damage $\bar{D}^{\Omega }$ and the interface damage $D^{\Gamma }$ within the fiber/epoxy specimen before it completely fails. In Fig. 29a, the red zone indicates the matrix damage path, where the elements have ruptured ($D^{\Gamma } \approx 1$). The figure is also linked with Fig. 29b, which illustrates the complete debonding of part of the matrix/fiber interface. Clearly, the coalescence of the matrix cracking and the interface debonding arises around a phase angle of $\varphi = 45 ^{\circ }$. Furthermore, the partially debonded interface is an intermediate state as compared with the damage distribution of both the perfectly bonded and completely debonded interfaces displayed in Fig. 29b.

Fig. 29

Damage state within the fiber/epoxy unit cell before it completely ruptures; $39\times 39$ mesh and $l_c=$ 6 mm are adopted here. a Contour plot showing the nonlocal bulk damage $\bar{D}^{\Omega }$, b interface damage $D^{\Gamma }$ along the curved debonding path

Through this study, we demonstrate the ability of the proposed damage-based method to reproduce a complex failure pattern (combination of interface debonding and matrix damage) in fiber reinforced composites.

6 Conclusion

In this paper, the extended finite element method, in combination with the discrete damage zone model [13], is proposed to model progressive delamination in composites. Owing to the damage-based XFEM formulation, both the diffused bulk damage and the interface delamination can be conveniently modeled, irrespective of the background mesh and the interface configuration.

With respect to discrete interfaces, we develop a new mixed-mode force–separation relation by introducing an isotropic interface damage variable, which takes into account the coupled interaction between failure modes. Furthermore, an integral-type nonlocal damage model is employed in the bulk to alleviate mesh size sensitivity. In this scheme, the weighted spatial averaging is applied to the damage variable. To insure robustness and fast convergence, a consistent tangent stiffness matrix is derived specifically for the XFEM formulation and the resulting system is solved using the dissipation-based arc-length method.

Benchmark examples carried out here clearly indicate that the proposed method is not biased by mesh size and alignment. Moreover, the results are in good agreement with the available analytical/experimental data for all cases of pure mode I, mode II, and mixed-mode with varying ratios, which demonstrates the excellent performance of our model. The influence of interface strengths on the load–displacement curves and the development of cohesive zones is also investigated in detail. To correctly capture the delamination behavior of composites, we conclude that at least five discrete springs should be used within the cohesive zone.

In addition, the energy dissipation of a single spring, subjected to a fixed loading ratio $\beta = \delta _n/\delta _t$, is carefully analyzed using the isotropic and anisotropic interface models. It is shown that the newly proposed isotropic damage model can guarantee a smoother energy dissipation process under mixed-mode loadings compared to the anisotropic one.

In the examples of fiber/epoxy unit cell, the proposed model is used to trace the failure process caused by fiber/epoxy debonding and matrix damage. It is shown that consistent global response and energy dissipation is obtained when applying the nonlocal damage formulation.

Appendices

Appendix 1

For completeness, we provide the proof in this appendix that the power law criterion given in (33) can be recovered by using the proposed mixed-mode force–separation relation (31), if the discrete interface is subjected to a deformation history with a constant ratio $\beta = \delta _n /\delta _t$.

Without loss of generality, we only consider a monotonic loading with $\delta _n \ge 0$. Then the history ratio (29) can be rewritten as

$$\begin{aligned} \zeta&= \left[ \left( \dfrac{\delta _{n}}{\delta ^{\mathrm {cr}}_n} \right) ^{\alpha } + \left( \dfrac{| \delta _{t} |}{\delta ^{\mathrm {cr}}_t} \right) ^{\alpha } \right] ^{1/\alpha }\nonumber \\&= \delta _{n} \left[ \left( \dfrac{1}{\delta ^{\mathrm {cr}}_n} \right) ^{\alpha } + \left( \dfrac{1}{|\beta |\delta ^{\mathrm {cr}}_t} \right) ^{\alpha } \right] ^{1/\alpha } \end{aligned}$$

(80)

Accoding to the mixed-mode damage law (30), the critical separation $\bar{\delta }_i$ corresponding to the damage initiation can be calculated as

$$\begin{aligned} \bar{\delta }_n=\frac{1}{\eta },\,\,\,\,\bar{\delta }_t=\frac{1}{\beta \eta } \end{aligned}$$

(81)

where

$$\begin{aligned} \eta =\left[ \left( \dfrac{1}{\delta ^{\mathrm {cr}}_n} \right) ^{\alpha } + \left( \dfrac{1}{|\beta |\delta ^{\mathrm {cr}}_t} \right) ^{\alpha } \right] ^{1/\alpha } \end{aligned}$$

(82)

Given the proposed mixed-mode force–separation relation (31), the energy release rate components of mode I and mode II due to the complete decohesion are obtained by splitting the integrals (44) into two parts:

$$\begin{aligned} G_{\mathrm {I}}&= \int _{0}^{\infty } F_{n}(\delta _n, \delta _t) \, d\delta _{n} /l_{s} \nonumber \\&= \left[ \int _{0}^{\frac{1}{\eta }} K_{n}^{0} \delta _n \, d\delta _n + \int ^{\infty }_{\frac{1}{\eta }} \dfrac{K_{n}^{0} \delta _n}{\exp (\eta \delta _n -1)} \, d\delta _n \right] \Bigg /l_s \nonumber \\&= \left( \dfrac{K_n^0}{2 \eta ^2} + \dfrac{2K_n^0}{\eta ^2} \right) /l_s = \dfrac{2.5K_n^0}{\eta ^2 l_s}\end{aligned}$$

(83)

$$\begin{aligned} G_{\mathrm {II}}&= \int _{0}^{\infty } F_{t}(\delta _n, \delta _t) \, d\delta _{t} /l_{s} \nonumber \\&= \left[ \int _{0}^{\frac{1}{\beta \eta }} K_{t}^{0} \delta _t \, d\delta _t + \int ^{\infty }_{\frac{1}{\beta \eta }} \dfrac{K_{t}^{0} \delta _t}{\exp (\beta \eta \delta _t -1)} \, d\delta _t \right] \Bigg /l_s \nonumber \\&= \left( \dfrac{K_t^0}{2 \beta ^2 \eta ^2} + \dfrac{2K_t^0}{\beta ^2 \eta ^2} \right) /l_s = \dfrac{2.5K_t^0}{\beta ^2 \eta ^2 l_s} \end{aligned}$$

(84)

Considering the expressions for the initial stiffnesses (28) and damage coefficient (23) results:

$$\begin{aligned} \dfrac{G_{\mathrm {I}}}{G_{\mathrm {IC}}} = \dfrac{1}{\eta ^2 {\delta ^{\mathrm {cr}}_n}^2},\,\,\,\, \dfrac{G_{\mathrm {II}}}{G_{\mathrm {IIC}}} = \dfrac{1}{|\beta |^2 \eta ^2 {\delta ^{\mathrm {cr}}_t}^2} \end{aligned}$$

(85)

Finally, the proof is completed:

$$\begin{aligned} \left( \dfrac{G_{\mathrm {I}}}{G_{\mathrm {IC}}} \right) ^{\alpha /2} +\left( \dfrac{G_{\mathrm {II}}}{G_{\mathrm {IIC}}} \right) ^{\alpha /2}&= \dfrac{1}{\eta ^{\alpha }} \left[ \left( \dfrac{1}{\delta ^{\mathrm {cr}}_n} \right) ^{\alpha } + \left( \dfrac{1}{|\beta |\delta ^{\mathrm {cr}}_t} \right) ^{\alpha } \right] \nonumber \\&= \dfrac{\eta ^{\alpha }}{\eta ^{\alpha }} = 1 \end{aligned}$$

(86)

Appendix 2

Considering the bulk damage law (12) and the mixed-mode force–separation relation (31) for discrete interfaces, the partial derivatives appear in Eqs. (70)–(73) are computed explicitly as follows:

$$\begin{aligned} d^{\prime }&=\dfrac{\partial {D^{\Omega }}}{\partial {\kappa }} =\left\{ \begin{array}{lcc} 0 &{} \text{ if } &{} \kappa \le \epsilon ^{\mathrm {cr}} \\ B \exp (-B(\kappa -\epsilon ^{\mathrm {cr}})) &{} \text{ if } &{} \kappa > \epsilon ^{\mathrm {cr}} \end{array} \right. \end{aligned}$$

(87)

$$\begin{aligned} \kappa ^{\prime }&=\dfrac{\partial {\kappa }}{\partial {\tilde{\epsilon }_{eq}}} =\left\{ \begin{array}{ccc} 0 &{} \text{ if } &{} \text{ unloading } \\ 1 &{} \text{ if } &{} \text{ loading } \end{array} \right. \end{aligned}$$

(88)

The partial derivative $\mathbf {g}$ is equal to

$$\begin{aligned} \mathbf {g}=\dfrac{\partial {\tilde{\epsilon }_{eq}}}{\partial {\varvec{\epsilon }}}= \dfrac{\partial {\tilde{\epsilon }_{eq}}}{\partial {\varvec{e}}} \dfrac{\partial {\varvec{e}}}{\partial {\varvec{I}}} \dfrac{\partial {\varvec{I}}}{\partial {\varvec{\epsilon }}} \end{aligned}$$

(89)

where $\varvec{e}$ and $\varvec{I}$ are arranged into column vectors as follows:

$$\begin{aligned} \varvec{I}&=\{I_1\,I_2 \}^{\mathrm {T}}\,\,\,\,\, \text{ with }\, I_1=\epsilon _{xx}+\epsilon _{yy},\, I_2=\epsilon _{xx} \epsilon _{yy}-\gamma ^2_{xy}/4 \end{aligned}$$

(90)

$$\begin{aligned} \varvec{e}&=\{e_1\,e_2\,e_3 \}^{\mathrm {T}}\,\,\text{ with }\, e_1=\dfrac{I_1}{2}+\dfrac{\sqrt{{I_1}^2-4I_2}}{2},\nonumber \\ e_2&=\dfrac{I_1}{2}-\dfrac{\sqrt{{I_1}^2-4I_2}}{2},\, e_3=h\dfrac{\nu }{\nu -1}I_1 \end{aligned}$$

(91)

In the above equations, $\nu$ is the Poisson ratio, $h=1$ for plane-stress cases, and $h=0$ for plane-strain cases. Then the partial derivative of the Eq. (89) are given by

$$\begin{aligned} \dfrac{\partial {\tilde{\epsilon }_{eq}}}{\partial {\varvec{e}}}&= \left\{ \dfrac{\langle e_1 \rangle }{\sqrt{\langle e_1 \rangle ^2 +\langle e_2 \rangle ^2+\langle e_3 \rangle ^2}}\, \dfrac{\langle e_2 \rangle }{\sqrt{\langle e_1 \rangle ^2 +\langle e_2 \rangle ^2+\langle e_3 \rangle ^2}}\,\right. \nonumber \\&\qquad \left. \dfrac{\langle e_3 \rangle }{\sqrt{\langle e_1 \rangle ^2 +\langle e_2 \rangle ^2+\langle e_3 \rangle ^2}} \right\} \end{aligned}$$

(92)

$$\begin{aligned} \dfrac{\partial {\varvec{e}}}{\partial {\varvec{I}}}&= \begin{bmatrix} \dfrac{1}{2}+\dfrac{I_1}{2\sqrt{{I_1}^2-4I_2}}&- \dfrac{1}{\sqrt{{I_1}^2-4I_2}} \\ \dfrac{1}{2}-\dfrac{I_1}{2\sqrt{{I_1}^2-4I_2}}&\dfrac{1}{\sqrt{{I_1}^2-4I_2}} \\ h\dfrac{\nu }{\nu -1}&0 \end{bmatrix} \end{aligned}$$

(93)

$$\begin{aligned} \dfrac{\partial {\varvec{I}}}{\partial {\varvec{\epsilon }}}&= \begin{bmatrix} 1&1&0 \\ \epsilon _{yy}&\epsilon _{xx}&-\dfrac{\gamma _{xy}}{2} \end{bmatrix} \end{aligned}$$

(94)

Finally, the partial derivative $\mathbf {M}$ for $\delta _n \ge 0$ is evaluated by differentiating the Eq. (31) as

$$\begin{aligned} \mathbf {M}=\dfrac{\partial {\mathbf {F}^L}}{\partial {\varvec{\delta }^L}}= \left\{ \begin{array}{lcc} \mathbf {K}^0 &{} \text{ if } &{} \zeta \le 1 \\ \dfrac{\mathbf {K}^0}{\exp (\zeta -1)} &{} \text{ if } &{} \zeta > 1\, \text{(unloading) } \\ \dfrac{\mathbf {K}^0}{\exp (\zeta -1)} \left\{ \mathbf {I}-\zeta ^{1-\alpha } \begin{bmatrix} \dfrac{|\delta _t|^{\alpha }}{(\delta ^{\mathrm {cr}}_t)^{\alpha }} &{} \dfrac{\delta _t \delta _n^{\alpha -1}}{(\delta ^{\mathrm {cr}}_n)^{\alpha }}\\ \dfrac{\mathrm {sign}(\delta _t)\delta _n|\delta _t|^{\alpha -1}}{(\delta ^{\mathrm {cr}}_t)^{\alpha }} &{} \dfrac{\delta _n^{\alpha }}{(\delta ^{\mathrm {cr}}_n)^{\alpha }} \end{bmatrix} \right\} &{} \text{ if } &{} \zeta > 1\, \text{(loading) } \end{array} \right. \end{aligned}$$

(95)

with $\mathbf {I}$ the identity matrix.