Delaunay and Regular Triangulations as Lexicographic Optimal Chains

Abstract

We introduce a total order on n-simplices in the n-Euclidean space for which the support of the lexicographic-minimal chain with the convex hull boundary as boundary constraint is precisely the n-dimensional Delaunay triangulation, or in a more general setting, the regular triangulation of a set of weighted points. This new characterization of regular and Delaunay triangulations is motivated by its possible generalization to submanifold triangulations as well as the recent development of polynomial-time triangulation algorithms taking advantage of this order.

1 Introduction

Besides their elegant mathematical properties [2, 11, 16], Delaunay triangulations, and more generally regular triangulations, are intensively used in the industry, being the basis of much of the meshing algorithms for geometry processing and engineering applications [8].

1.1 Related Work: Regular Triangulations and Their Optimality Properties

The usual definition of Delaunay triangulation considers a finite set of points ${{\textbf{P}}}\subset {\mathbb {R}}^n$ that is in general position, by which it is meant that no $n+1$ points of ${\textbf{P}}$ belong to a same hyperplane and no $n+2$ points of ${\textbf{P}}$ belong to a same sphere.

Given a finite set ${\textbf{P}}$ of at least $n+1$ points in ${\mathbb {R}}^n$ in general position, the Delaunay triangulation of ${\textbf{P}}$ is then defined as the set of n-simplices $\sigma \subset {{\textbf{P}}}$ whose circumscribed sphere contains no points in ${{\textbf{P}}}\setminus \sigma$. Equivalently, it can be defined as the dual of the Voronoi diagram of ${\textbf{P}}$. Associating a weight $\mu _i$ to each point $P_i$ in ${\textbf{P}}$, the Laguerre–Voronoi diagram of ${{\textbf{P}}}$, alternatively called power diagram, is a generalization of the Voronoi diagram. Its dual is called regular triangulation of the set of weighted points and coincides with the Delaunay triangulation when all weights $\mu _i$ are equal.

Delaunay triangulations satisfy several optimality criteria. It has been shown [16] and [4, Sect. 17.3.4] that “Among all triangulations of a set of points in ${\mathbb {R}}^2$, the Delaunay triangulation lexicographically maximizes the minimum angle, and also lexicographically minimizes the maximum circumradii”. We call bounding radius of a simplex the radius of the smallest ball containing it. In [4, Sect. 17.3.4], the grain of a triangulation T of points in the plane is defined as the maximum of the bounding radii of all triangles of T. Then [4, Thm. 17.3.9] asserts that, given a point set ${\textbf{P}}\subset {\mathbb {R}}^2$, the Delaunay triangulation minimizes the grain among all triangulations of ${\textbf{P}}$. This last fact is also a consequence of our main theorem when the dimension is 2.

The grain minimization property is a necessary but not sufficient condition for a triangulation to be Delaunay. Our result is a strengthening of this property into a necessary and sufficient condition, as well as a generalization to any dimension and to regular triangulations. Even for the significantly simpler situation of 2-dimensional Delaunay, we are not aware of any work giving the strengthening of the grain optimization required to get our sufficient condition.

Our work relies strongly on a variational characterization of Delaunay triangulations obtained in [6]. It is well known [4, 13] that the Delaunay triangulation in ${\mathbb {R}}^n$ is equivalent to the lower convex hull of points in ${\mathbb {R}}^{n}\times {\mathbb {R}}$ where each point $(x_1,\ldots ,x_n) \in {\textbf{P}} \subset {\mathbb {R}}^n$ is lifted to

$$\begin{aligned} \text {lift}{( x_1,\ldots ,x_n) } \underset{\text {def.}}{=} \left( x_1,\ldots ,x_n, \sum _{j=1}^n x_j^2 \right) \in {\mathcal {P}} \end{aligned}$$

where ${{\mathcal {P}}}\subset {\mathbb {R}}^{n+1}$ is the graph of the square norm function. Along this correspondence, an n-simplex $\{p_0,\dots ,p_n\}\subset {{\textbf{P}}}$ belongs to the Delaunay triangulation in ${\mathbb {R}}^n$ if and only if its lifted counterpart $\{\text {lift}( p_0),\dots ,\text {lift}( p_n)\}$ belongs to the boundary of the lower convex hull of $\text {lift}({{\textbf{P}}})\subset {{\mathcal {P}}}$, where “lower” refers to the negative direction on the last coordinate $x_{n+1}$. This equivalence extends to regular triangulations where the weighted point $((x_1,\ldots ,x_n),\mu )\in {\mathbb {R}}^n\times {\mathbb {R}}$ is now lifted to $\bigl (x_1,\ldots ,x_n, \sum _j x_j^2 - \mu \bigr )\in {\mathbb {R}}^{n+1}$ [4, 13].

Starting with this equivalence, Chen and coauthors [6] observed that Delaunay triangulations minimize, among all triangulations over a given vertex set ${\textbf{P}}$, the $L^p$ norm of the difference between the squared norm function and its piecewise-linear interpolation on the triangulation (see (10) below for a formal definition). This variational formulation has been successfully exploited [1, 5, 7] for the generation of Optimal Delaunay Triangulations obtained by optimizing the same functional with respect to the vertex positions in two and three dimensional Delaunay triangulations.

1.2 Result and Motivation in a Few Words

We introduce a new variational characterization of Delaunay and regular triangulations. Recall that a k-simplex is a set of $k+1$ points or vertices. Given a finite set of points ${\textbf{P}} \subset {\mathbb {R}}^n$, respectively a set of weighted points ${\textbf{P}} \subset {\mathbb {R}}^n\times {\mathbb {R}}$, in general position, we define a specific total order $\sigma _0< \ldots <\sigma _{N-1}$ on the set of n-simplices with vertices in ${\textbf{P}}$. This order allows to compare sets of simplices by comparing the sum of simplex weights, where the weight of simplex $\sigma _i$ is $2^i$. This total order on sets of n-simplices, induced by the total order on simplices, is called the lexicographic order.

A simplicial k-chain, whose formal definition is recalled in Sect. 2, is a set of k-simplices behaving as a vector over ${\mathbb {Z}}_2$, the field of integers modulo 2, when the addition is defined as the set-theoretic symmetric difference:

$$\begin{aligned}\varGamma _1+\varGamma _2 = (\varGamma _1 \cup \varGamma _2) \setminus (\varGamma _1 \cap \varGamma _2). \end{aligned}$$

The lexicographic comparison of two chains, or, merely, of two sets of simplices, can equivalently be defined as follows. We say that $\varGamma _1$ is less than $\varGamma _2$, in lexicographic order, and we write $\varGamma _1 \;{\sqsubseteq }_{lex }\;\varGamma _2$, if $\varGamma _1=\varGamma _2$ or if the maximal simplex in their symmetric difference is in $\varGamma _2$. In other words, for $\varGamma _1 \ne \varGamma _2$:

$$\begin{aligned} \varGamma _1 \;{\sqsubseteq }_{lex }\;\varGamma _2\ \iff \ \max {\{ \sigma \in (\varGamma _1 \cup \varGamma _2) \setminus (\varGamma _1 \cap \varGamma _2) \}} \in \varGamma _2. \end{aligned}$$

Fig. 1

The triangle bounding radius $\textrm{R}_B$ is the radius of the smallest enclosing circle. Triangles bounding radius $\textrm{R}_B$ and circumradius $\textrm{R}_C$ characterize the order among 2-simplices

The main result of this work (Theorem 1) asserts that the Delaunay, respectively regular, triangulation of ${\textbf{P}}$, is the minimal simplicial chain for the lexicographic order, among chains whose boundary coincides with the boundary of the convex hull of ${\textbf{P}}$. The formal statement of Theorem 1 is given in Sect. 3 after the exposition of some prerequisites.

The definition of the total order we use for comparing simplices might not seem very intuitive. It is introduced progressively, in Sect. 3.2 for 3-dimensional Delaunay, then in Sect. 3.5 for the general case of Delaunay or regular triangulation in any dimension $n \ge 1$. In the case of Delaunay triangulation in the plane, the comparison $\le$ between two triangles, $T_i$, $i=1,2$, is defined as follows.

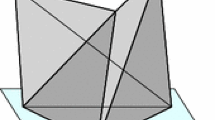
We denote by $\text {R}_\text {B}(T_i)$ the bounding radius of $T_i$, which is the radius of the smallest circle containing $T_i$ and by $\text {R}_\text {C}(T_i)$ the radius of the circumcircle of $T_i$, or circumradius (see Fig. 1). These two radii coincide when $T_i$ is acute. In order to compare $T_1$ and $T_2$ we first compare $\text {R}_\text {B}(T_1)$ and $\text {R}_\text {B}(T_2)$:

$$\begin{aligned}\text {R}_\text {B}(T_1) < \text {R}_\text {B}(T_2)\ \ \Longrightarrow \ \ T_1 \le T_2.\end{aligned}$$

In case of equality, which arises generically in case of two obtuse triangles sharing their longest edge, the tie is broken by comparing $\text {R}_\text {C}(T_1)$ and $\text {R}_\text {C}(T_2)$, in reverse order:

$$\begin{aligned} \text {R}_\text {B}(T_1) = \text {R}_\text {B}(T_2) \text { and } \text {R}_\text {C}(T_1) > \text {R}_\text {C}(T_2) \Longrightarrow T_1 \le T_2. \end{aligned}$$

In the particular case of dimension 2 and zero weights, using this particular total order on triangles, Theorem 1 asserts that the 2D Delaunay triangulation is the lexicographic minimum under boundary condition.

Our result characterizes regular triangulations as solutions of a particular linear programming problem over ${\mathbb {Z}}_2$ that can be computed in polynomial time, by simple matrix reduction algorithms [10, 18]. However, we do not expect such algorithms to compete with existing algorithms for the computation of Delaunay or regular triangulation in Euclidean space.

Instead, the characterization given by Theorem 1, being concise and linear by nature, enable generalizations beyond the situation of Delaunay or regular triangulation [10, 18]. This is illustrated by an example of application in Sect. 1.3. Also, we believe that our algebraic flavored characterization, by offering a novel perspective on a classical notion, may stimulate further theoretical research as well as applications.

1.3 Regular Triangulations on Curved Objects

Our initial motivation for this work was the design of meshing algorithms for manifolds or stratified sets, typically 2-submanifolds of the Euclidean 3-space [10, 18]. When the submanifold is known through a point set sampling, possibly with outliers, the computation of such a triangulation is known as surface reconstruction, or, when the ambient dimension is high, manifold learning.

In this context, we would like our triangulations to benefit from the same quality and optimality properties enjoyed by the Delaunay triangulation in Euclidean space and to be able to ignore outliers. A natural idea, in order to extend Delaunay or regular triangulations to this general situation, consists in using the same variational formulation of Theorem 1, but considering k-chains in ${\mathbb {R}}^n$ for $k<n$ instead of n-chains in ${\mathbb {R}}^n$.

The case $n=3$ and $k=2$ is illustrated on Fig. 2 which shows triangulated surfaces made of the triangles in $\varGamma _{\textrm{min}}$, the lexicographic minimal 2-chains in ${\mathbb {R}}^3$ under imposed boundary, where the total order $\le$ on triangles is the one given in Sect. 1.2:

$$\begin{aligned} \varGamma _{\textrm{min}}= \min _{{\sqsubseteq }_{lex }}{\{ \varGamma \in {\varvec{C}}_{2}(K):\partial \varGamma = \beta \}}. \end{aligned}$$

(1)

For ease of computation we can take K to be the 3D Delaunay triangulation of the data points rather than the full complex. We first see that the support of the minimal chain is a manifold. It has in fact been proved [9] that given a connected compact smooth 2-submanifold of Euclidean space, under good sampling conditions relatively to the reach of the manifold and starting from a well-chosen Čech or Rips simplicial complex over the points sample, the support of the lexicographic minimal cycle non-homologous to 0 has to be a triangulation of the manifold. We also see that the quality and arrangement of triangles in the obtained surface triangulation is, as expected, similar to that of planar Delaunay triangulations, making our approach a good candidate for extending the notion of Delaunay (or regular) triangulation to sampled curved objects.

Fig. 2

Our variational formulation, defining Delaunay triangulations when applied to n-chains in ambient ${\mathbb {R}}^n$, can be extended to k-chains in ${\mathbb {R}}^n$. This is illustrated here for $k=2$ and $n=3$. The boundary constraint $\beta$ of (1) is the set of edges connecting the red dots

1.4 Organization of the Paper

The paper is devoted to the proof of Theorem 1. Section  2 recalls standard definitions about simplicial complexes and chains, regular triangulations of weighted points, and states the formal definition of the lexicographic order. Section  3 states our main result.

Section 4 establishes geometric constructions of regular triangulations, with an emphasis on properties of their simplex links. A characterization of regular triangulations is given in terms of the support of a chain minimizing a weighted $L^1$ norm, denoted $\Vert \,{\cdot }\,\Vert _{(p)}$, under boundary constraints (Proposition 2). The weights in the norm $\Vert \,{\cdot }\,\Vert _{(p)}$ are parametrized by a real number $p\ge 1$. Lemmas 4 and 5 imply that, informally, for p large enough, a chain minimizing $\Vert \,{\cdot }\,\Vert _{(p)}$ under boundary constraints minimizes in particular a lexicographic preorder induced by the comparison of bounding radii ${\varvec{\mu }}_B$ of simplices.

Sections 4.2 and 4.3 describe a geometric construction that maps the link of a k-simplex $\tau$ in the regular triangulation to a polytope in ${\mathbb {R}}^{n-k}$. It establishes correspondences between properties of the link of $\tau$ with properties of the polytope, which are summarized in Lemma 7. In this section are defined several geometric objects used along the proof, such as the bisector $\textbf{bis}_\tau$ of a simplex $\tau$, the associated maps $\pi _{\textbf{bis}_\tau }$, $\pi _\tau$, $\varPhi _\tau$, and ${{\textbf{S}}}{{\textbf{h}}}_{\tau }$, and the notion of visible facet of a polytope.

Section 5 is self-contained and does not rely on previous constructions. It is devoted to the proof of Lemma 10, which establishes that convex hulls can be defined as minimal lexicographic chains under boundary constraints, for a particular lexicographic order denoted $\sqsubseteq _{{\textbf{0}}}$. This lemma is a crucial tool for the proof of the main theorem.

Finally, in Sect. 6, we are ready to give the proof of Theorem 1. The proof of the theorem requires many constructions, notations and intermediate results. In order to help the reader, we provide in Appendix A a proof outline, with two flowcharts and associated explanations. This proof outline is not self contained: it is meant to serve as a roadmap that, by giving a global view of the proof, may support the reader along Sects. 4, 5, and 6. It is completed by a glossary, Sect. A.4, of the main notions used in the proof outline.

2 Simplicial Complexes, Simplicial Chains, and Lexicographic Order

We recall here basic definitions of simplicial complexes and chains. A thorough exposition can be found in the first chapter of [15].

2.1 Simplicial Complexes

Simplicial complexes. For any $k\ge 0$, a simplex of dimension k, or k-simplex, is a set of $k+1$ vertices. If $\tau$ and $\sigma$ are simplices, we say that $\tau$ is a face of $\sigma$, or, equivalently, that $\sigma$ is a coface of $\tau$, when $\tau \subseteq \sigma$. A set K of simplices is called a simplicial complex if any $\sigma \in K$ has all its faces in K:

$$\begin{aligned} ( \sigma \in K\ \ \text {and} \ \ \emptyset \ne \tau \subseteq \sigma ) \quad \Longrightarrow \quad \tau \in K. \end{aligned}$$

We consider in this paper only finite sets K, i.e., only finite simplicial complexes. The dimension of a simplicial complex is the maximal dimension of its simplices. If any simplex in an n-dimensional simplicial complex K has at least one coface of dimension n, K is said to be a pure simplicial complex. Given a simplicial complex K, we denote by $K^{[k]}$ the subset of K containing all k-simplices of K.

Stars and link. For a simplex $\tau \in K$, the star of $\tau$ in K, denoted $\text {St}_{K}(\tau )$ is defined by $\text {St}_{K}(\tau ) = \{ \sigma \in K:\sigma \supseteq \tau \}$ and the link of $\tau$ in K, denoted $\text {Lk}_{K}(\tau )$ is defined by $\text {Lk}_{K}(\tau ) = \{ \sigma \in K: \sigma \cup \tau \in K,\,\sigma \cap \tau = \emptyset \}$. When, for $0\le k< n$, $\tau$ is a k-simplex in a pure n-dimensional simplicial complex K, the link $\text {Lk}_{K}(\tau )$ of $\tau$ in K is an $(n-k-1)$-dimensional pure simplicial complex.

Embedded simplicial complexes and geometric realization. Given a k-simplex $\sigma = \{v_0, \ldots , v_k \}$, where each vertex $v_i$, $0\le i\le k$, belongs to ${\mathbb {R}}^N$ for some $N\ge k$ such that the points $\{v_0,\dots ,v_k\}$ are affinely independent, the convex hull of $\sigma$, denoted ${{\mathcal {C}}}{{\mathcal {H}}}({ \sigma })$, is called a geometric k-simplex.

Given an n-dimensional simplicial complex K, an embedding of K consists in associating to each vertex in K a point in ${\mathbb {R}}^N$ such that¹:

• (1) For any k-simplex $\tau \in K$, the points associated to the vertices of $\tau$ are affinely independent.

• (2) For any pair of simplices $\sigma _1, \sigma _2 \in K$, one has

  $$\begin{aligned}{{\mathcal {C}}}{{\mathcal {H}}}({ \sigma _1})\cap {{\mathcal {C}}}{{\mathcal {H}}}({ \sigma _2})={{\mathcal {C}}}{{\mathcal {H}}}({\sigma _1\cap \sigma _2}).\end{aligned}$$

The geometric realization ${\mathcal {G}}(K) \subset {\mathbb {R}}^N$ of K is then defined as

$$\begin{aligned}{\mathcal {G}}(K) = \bigcup _{\sigma \in K}{{\mathcal {C}}}{{\mathcal {H}}}({ \sigma }).\end{aligned}$$

In the sequel of the paper, we consider several n-dimensional simplicial complexes whose vertices belong to ${\mathbb {R}}^n$. For example, given four points a, b, c, d in general position in ${\mathbb {R}}^2$, the simplicial complex made of the triangles in the Delaunay triangulation of $\{a,b,c,d\}$, together with all their faces, is a simplicial complex embedded in ${\mathbb {R}}^2$. By contrast, the full 2-dimensional simplicial complex over a, b, c, d, defined as the simplicial complex made of all possible triangles, $\{abc,abd, bcd, acd \}$ with all their faces, is not embedded in ${\mathbb {R}}^2$, regardless of the configurations of points a, b, c, d.

We mention that if K is a full simplicial complex, so is the link $\text {Lk}_{K}(\tau )$ of one of its simplex $\tau \in K$. If the geometric realization ${\mathcal {G}}(K)$ of K is an n-manifold, then the geometric realization of $\text {Lk}_{K}(\tau )$, ${\mathcal {G}}(\text {Lk}_{K}(\tau ))$, is an $(n-k-1)$-sphere.

2.2 Simplicial Chains

Let K be a simplicial complex of dimension at least k. The notion of chains can be defined with coefficients in any ring but we restrict here the definition to coefficients in the field ${\mathbb {Z}}_2 = {\mathbb {Z}}/2{\mathbb {Z}}$. Denoting by $K^{[k]}$ the set of k-simplices in K, a k-chain $\varGamma$ with coefficients in ${\mathbb {Z}}_2$ is a formal sum of k-simplices:

$$\begin{aligned} \varGamma = \sum _{i} x_i \sigma _i, \quad \text { with } x_i \in {\mathbb {Z}}_2 \ \text {and}\ \sigma _i \in K^{[k]}. \end{aligned}$$

(2)

Interpreting the coefficient $x_i\in {\mathbb {Z}}_2=\{0,1\}$ in front of simplex $\sigma _i$ as indicating the existing of $\sigma _i$ in the chain $\varGamma$, we can view the k-chain $\varGamma$ as a set of k-simplices: for a k-simplex $\sigma$ and a k-chain A, we write that $\sigma \in \varGamma$ if the coefficient for $\sigma$ in $\varGamma$ is 1. With this convention, the sum of two chains corresponds, when chains are seen as set of simplices, to their set-theoretic symmetric difference. For a k-chain $\varGamma$ and a k-simplex $\sigma$, we denote by $\varGamma (\sigma )\in {\mathbb {Z}}_2$ the coefficient of $\sigma$ in $\varGamma$, in other words:

$$\begin{aligned}\varGamma (\sigma ) = 1_{{\mathbb {Z}}_2}\ \iff \ \sigma \in \varGamma .\end{aligned}$$

We denote as ${\varvec{C}}_{k}(K)$ the vector space over the field ${\mathbb {Z}}_2$ of k-chains in the complex K. For a k-chain $\varGamma$ in ${\varvec{C}}_{k}(K)$, we denote by $|\varGamma |$ the support of $\varGamma$, which is the subcomplex of K made of all k-simplices in $\varGamma$ together with all their faces.

Boundary operator. In what follows, a k-simplex $\sigma$ can also be interpreted as the k-chain containing only the k-simplex $\sigma$, which is consistent with the notation in (2). Since the set of k-simplices $K^{[k]}$ is a basis for ${\varvec{C}}_{k}(K)$, a linear operator on ${\varvec{C}}_{k}(K)$ is entirely defined by its image on each simplex. For a k-simplex $\sigma =\{v_0,\dots ,v_k\}$, the boundary operator $\partial _k$ is the linear operator defined as:

$$\begin{aligned}\partial _k :{\varvec{C}}_{k}(K) \rightarrow {\varvec{C}}_{k-1}(K), \qquad \partial _k \sigma \underset{\text {def.}}{=}\sum _{i=0}^{k}\,[v_0, \ldots , \widehat{v_i},\dots ,v_k],\end{aligned}$$

where the symbol $\widehat{v_i}$ means the vertex is deleted from the set.

A k-cycle is a k-chain with null boundary. We say two k-chains $\varGamma$ and $\varGamma '$ are homologous if their difference (or equivalently their sum) is a boundary, in other words, if $\varGamma - \varGamma ' = \partial _{k+1} B$, for some ($k+1$)-chain B.

2.3 Regular Triangulations of Weighted Points

Definition 1 generalizes the square of Euclidean distance to weighted points.

Definition 1

[3, Sect. 4.4] Given two weighted points $(P_1,\mu _1), (P_2,\mu _2) \in {\mathbb {R}}^n\times {\mathbb {R}}$ their weighted distance is defined as

$$\begin{aligned} \text {D}( (P_1,\mu _1), (P_2,\mu _2) ) \underset{\text {def.}}{=} (P_1-P_2)^2 - \mu _1 - \mu _2. \end{aligned}$$

(3)

We recall now the definition of a regular triangulation over a set of weighted points. Regular triangulations can alternatively be defined as duals of the Laguerre (or power) diagrams of a set of weighted points. We use here a generalization of the empty sphere property of Delaunay triangulations.

Definition 2

[3, Lemma 4.5] A regular triangulation ${\mathcal {T}}$ of the set of weighted points ${{\textbf{P}}}=\{(P_1,\mu _1),\dots ,(P_N,\mu _N)\}\subset {\mathbb {R}}^n\times {\mathbb {R}}$, $N\ge n+1$, is a triangulation of the convex hull of $\{P_1,\dots ,P_N\}$ taking its vertices in $\{P_1,\dots ,P_N\}$ such that for any simplex $\sigma \in {{\mathcal {T}}}$, denoting $({{{\varvec{P}}}}_C (\sigma ),{\varvec{\mu }}_C (\sigma ))$ (Definition 7) the generalized circumsphere of $\sigma$, then

$$\begin{aligned} (P_i,\mu _i) \in {\textbf{P}} \setminus \sigma \ \quad \Longrightarrow \quad \ \text {D}(({{{\varvec{P}}}}_C (\sigma ), {\varvec{\mu }}_C (\sigma ) ), (P_i, \mu _i)) > 0. \end{aligned}$$

(4)

Definition 4 is equivalent to the definition of a Delaunay triangulation when all weights are equal. Notice the strict inequality in (4), where the usual definition would use a greater or equal inequality instead. However, the equality case will not occur under the generic condition assumed in Sect. 3.

2.4 Lexicographic Order

We assume now a total order on the k-simplices of K, $\sigma _1< \sigma _2<\ldots < \sigma _N$, where $N = \dim {\varvec{C}}_{k}(K)$. From this order, we define a lexicographic total order on k-chains. Recall that with coefficients in ${\mathbb {Z}}_2$ for k-chains $\varGamma _1, \varGamma _2 \in {\varvec{C}}_{k}(K)$, we can use interchangeably vector and set-theoretic operations: $\varGamma _1+ \varGamma _2 = \varGamma _1- \varGamma _2 = (\varGamma _1 \cup \varGamma _2) {\setminus } (\varGamma _1 \cap \varGamma _2)$.

Definition 3

(lexicographic order on chains) Assume there is a total order $\le$ on the set of k-simplices of K. For $\varGamma _1, \varGamma _2 \in {\varvec{C}}_{k}(K)$:

$$\begin{aligned} \varGamma _1 \;{\sqsubseteq }_{lex }\;\varGamma _2\ \underset{\text {def.}}{\iff }\ {\left\{ \begin{array}{ll}\varGamma _1 = \varGamma _2\qquad {\text {or}}\\ \max {\{ \sigma \in \varGamma _1 + \varGamma _2 \}} \in \varGamma _2.\end{array}\right. } \end{aligned}$$

The lexicographic order can equivalently be defined as a comparison of $L^1$ norm for a particular choice of simplices weights. For that, the d-simplices being totally ordered as $\sigma _0< \sigma _1< \ldots < \sigma _{N-1}$, we assign the weight $2^i$ to simplex $\sigma _i$. We can then define the norm of a d-chain $\varGamma = \sum _j c_j \sigma _j$ were $c_j \in {\mathbb {Z}}_2$ as

$$\begin{aligned} \Vert \varGamma \Vert _*= \left\| \sum _j c_j \sigma _j \right\| _*\!=\sum _j | c_j| 2^j, \end{aligned}$$

where $|\,{\cdot }\,|:{\mathbb {Z}}_2 \rightarrow \{0,1\} \subset {\mathbb {R}}$ assigns respective real numbers 0 and 1 to their corresponding elements in ${\mathbb {Z}}_2= \{0_{{\mathbb {Z}}_2}, 1_{{\mathbb {Z}}_2} \}$, i.e., $|0_{{\mathbb {Z}}_2}| = 0$ and $|1_{{\mathbb {Z}}_2}| = 1$. Another way of saying this is to associate to each k-chain $\varGamma \in {\varvec{C}}_{k}(K)$ the integer number whose $j^{\text {th}}$ bit in the binary expression, starting from the least significant bit, corresponds to the coefficients of $\sigma _j$ in $\varGamma$. Then $\Vert \varGamma \Vert _*$ is the value of the integer number. With this convention one has

$$\begin{aligned}\varGamma _1 \;{\sqsubseteq }_{lex }\;\varGamma _2 \ \iff \ \Vert \varGamma _1 \Vert _*\le \Vert \varGamma _2 \Vert _*.\end{aligned}$$

3 Main Result

This section gives the main result of the paper, Theorem 1, before entering into more technical matters. Both the generic condition and the total order on simplices inducing the lexicographic order are formally defined in Sect. 3.4. These formal definitions do not provide an easy visual intuition, being inductive by nature and expressed for the general case of weighted points. For this reason, we first provide an intuitive introduction in the case of zero weights, which corresponds to Delaunay triangulations.

3.1 Generic Configurations

In computational geometry, a property defined on a space of configuration parametrized by ${\mathbb {R}}^N$ is usually said generic when the set ${\mathcal {G}} \subseteq {\mathbb {R}}^N$ for which it holds is open and dense in ${\mathbb {R}}^N$. Another legitimate definition for a property to be generic is to hold almost everywhere, in other words such that ${\mathbb {R}}^N \setminus {\mathcal {G}}$ has Lebesgue measure zero.

Definition 4

(generic property)  We say that a property on a space of configuration parametrized by ${\mathbb {R}}^N$ satisfied on ${\mathcal {G}} \subseteq {\mathbb {R}}^N$ is generic, if ${\mathcal {G}}$ is an open dense subset whose complement has Lebesgues measure zero.

Note that the conjunction of finitely many generic conditions is generic. In the case of the Delaunay triangulation of m points in ${\mathbb {R}}^n$, the configuration space has dimension $N= mn$, and, for regular triangulations of m weighted points in ${\mathbb {R}}^n\times {\mathbb {R}}$, the dimension is $N=m(n+1)$.

In the context of applications, as a consequence of some symmetries in the input or from the finite representations by floating point numbers, the probability to encounter a non-generic configuration with real world data is not zero and practical implementations simulate generic configurations by breaking ties artificially, typically by symbolic perturbation (see Simulation Of Simplicity in [12]). Appendix I provides a more detailed discussion of Generic Condition 1 (Sect. 3.4) and 2 (Sect. 5), including the proofs that they are indeed generic.

3.2 Order $\le$ on Simplices for Delaunay Triangulations in ${\mathbb {R}}^2$ and ${\mathbb {R}}^3$.

The following definitions of total orders on simplices of two- and three-dimensional Delaunay triangulations should be seen as particular cases of definition (9) in Sect. 3.5.

3.2.1 2-Dimensional Delaunay Triangulations

For 2-dimensional Delaunay triangulations, the total order defined by (9) has already been introduced in Sect. 1.2. Denoting respectively $\text {R}_\text {B}(T)$ and $\text {R}_\text {C}(T)$ the bounding radius, radius of the smallest circle containing triangle T, and the circumradius of T (see Fig. 1), the order on triangles is defined as

$$\begin{aligned}T_1 \le T_2\ \iff \ {\left\{ \begin{array}{ll} T_1= T_2 \qquad \text {or} \\ \text {R}_\text {B}(T_1)^2 < \text {R}_\text {B}(T_2)^2 \qquad \text {or} \\ \text {R}_\text {B}(T_1)^2 = \text {R}_\text {B}(T_2)^2 \ \text {and} \ \text {R}_\text {C}(T_1)^2 > \text {R}_\text {C}(T_2)^2. \end{array}\right. }\end{aligned}$$

This preorder is a total order under our generic condition. Compared to Sect. 1.2, we have here used squared radii comparisons instead of radii comparisons. This obviously does not change the ordering, but makes the expression consistent with the general definition (9) since, for 2-dimensional Delaunay triangulations, one has $\mu _0(T) = \text {R}_\text {B}(T)^2$ and $\mu _1(T) = \text {R}_\text {C}(T)^2$.

3.2.2 3-Dimensional Delaunay Triangulations

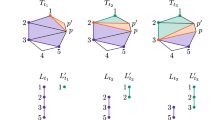
Given a non-degenerate tetrahedron $\sigma = abcd$ in ${\mathbb {R}}^3$, it must belong to one of the three categories illustrated on Fig. 3. This category depends on the dimension of $\varTheta (\sigma )$, which is, under generic condition, the unique lowest dimensional face of $\sigma$ with the same bounding radius as $\sigma$. Equivalently, $\varTheta (\sigma )$ is the unique face of $\sigma$ such that $\text {R}_\text {B}(\sigma ) = \text {R}_\text {C}(\varTheta (\sigma ))$.

For all three categories, we define $\mu _0 (\sigma )$ as the squared bounding radius of the simplex $\sigma$: $\mu _0(\sigma )=\text {R}_\text {B}(\sigma )^2$. For the second category, in the middle of Fig. 3, corresponding to $\varTheta (\sigma )=abc$, we define moreover $\mu _1(\sigma )=\text {R}_\text {C}(\sigma )^2$ which is the squared radius of the circumscribing sphere. For the third category, on the right of Fig. 3, corresponding to $\varTheta (\sigma ) = ab$, we define $\mu _1(\sigma )=\min {(\text {R}_\text {C}(abc),\text {R}_\text {C}(abd))^2}$ and $\mu _2(\sigma )= \text {R}_\text {C}(\sigma )^2$. The total order $\le$ on tetrahedra is then defined as

$$\begin{aligned} \sigma _1 \le \sigma _2\ \ \iff \ \ {\left\{ \begin{array}{ll}\sigma _1 = \sigma _2\quad \text {or} \\ \mu _0(\sigma _1) < \mu _0(\sigma _2)\quad \text {or} \\ \mu _0(\sigma _1) = \mu _0(\sigma _2)\ \text {and}\ \mu _1(\sigma _1)>\mu _1(\sigma _2)\quad \text {or} \\ \mu _0(\sigma _1)=\mu _0(\sigma _2)\ \text {and}\ \mu _1(\sigma _1)=\mu _1(\sigma _2)\ \text {and}\ \mu _2(\sigma _1)>\mu _2(\sigma _2). \end{array}\right. } \end{aligned}$$

Note that $\mu _1$ and $\mu _2$ are not defined for all kinds of tetrahedra. However, the equality configurations requiring the definitions of the quantities $\mu _1$ and $\mu _2$ only arise when the category of the triangles allows to define these quantities. As an example, if the tetrahedron $\sigma _1$ is from the first category ($\varTheta (\sigma ) = abcd$), then $\mu _0(\sigma _1)=\textrm{R}_B (\sigma _1)=\textrm{R}_C (\sigma _1)$. Under our generic condition, there cannot be another simplex with same circumradius as $\sigma _1$, and therefore, no tetrahedron with same bounding radius. It follows that in this case $\sigma _1$ is the only tetrahedron with bounding radius $\textrm{R}_B (\sigma _1)$: $\sigma _1\ne \sigma _2\ \Rightarrow \ \textrm{R}_B (\sigma _1) \ne \textrm{R}_B (\sigma _2)$.

Fig. 3

Illustration of the definition of $\varTheta (\sigma )$ for a tetrahedron $\sigma = abcd$ in the case of zero weights

3.3 The Theorem

We consider a set ${\textbf{P}}=\{(P_1,\mu _1), \ldots , (P_N,\mu _N)\}\subset {\mathbb {R}}^n\times {\mathbb {R}}$ of weighted points in n-dimensional Euclidean space. A weighted point (P, 0) is seen as a usual point $P\in {\mathbb {R}}^n$, while, when $\mu >0$, it is associated to the sphere centered at P with radius $r = \sqrt{\mu }$.

The aim of this paper is to prove Theorem 1 below, where the relation ${\sqsubseteq }_{lex }$ among n-chains is the lexicographic order defined according to Definition 3, the total order on n-simplices is given by (9) and the general position assumption is a generic condition formalized in Generic Condition 1 of Sect. 3.4.

Definition 5

(full simplicial complex)  Given a finite set ${\textbf{P}}$, the n-dimensional full simplicial complex over ${\textbf{P}}$, denoted $K_{{\textbf{P}}}$, is the simplicial complex made of all possible simplices up to dimension n with vertices in ${\textbf{P}}$.

Recall that, as explained in Sect. 2.2, a chain with coefficients in ${\mathbb {Z}}_2$ is identified to the set of simplices for which the coefficient is 1.

Theorem 1

Let ${\textbf{P}} = \{(P_1, \mu _1), \ldots , (P_N, \mu _N) \} \subset {\mathbb {R}}^n\times {\mathbb {R}}$, with $N \ge n+1$, be weighted points in general position and $K_{{\textbf{P}}}$ the n-dimensional full simplicial complex over ${\textbf{P}}$. Denote by $\beta _{{\textbf{P}}} \in {\varvec{C}}_{n-1}(K_{{\textbf{P}}})$ the $(n-1)$-chain, set of simplices belonging to the boundary of the convex hull ${{\mathcal {C}}}{{\mathcal {H}}}({ {{\textbf{P}}}})$. Then the simplicial complex $| \varGamma _{\textrm{min}}|$ support of

$$\begin{aligned}\varGamma _{\textrm{min}}= \min _{{\sqsubseteq }_{lex }}{ \{ \varGamma \in {\varvec{C}}_{n}(K_{{\textbf{P}}}): \partial \varGamma = \beta _{{\textbf{P}}} \}}\end{aligned}$$

is the regular triangulation of ${\textbf{P}}$.

When all the weights $\mu _i$ are equal, the regular triangulation (Definition 2) is the Delaunay triangulation. Obviously, replacing in Theorem 1 the full simplicial complex $K_{{\textbf{P}}}$ by any complex containing the regular triangulation would again give this triangulation as a minimum.

3.4 Generic Condition and Simplex Order, the Formal Definition

Definition 6

(degenerate simplex)  A k-simplex $\sigma = \{(P_0, \mu _0), \ldots , (P_k, \mu _k) \}$ is said to be degenerate if the set $\{P_0, \ldots , P_k\}$ is included in some $(k-1)$-dimensional affine space.

Note that if a k-simplex is non-degenerate, neither are any of its faces of dimension $k'<k$.

As Definition 1 generalizes the squared Euclidean distance to weighted points, we now define the respective generalizations of squares of both circumradius and smallest enclosing ball radius, to sets of weighted points.

Definition 7

Given a non-degenerate k-simplex $\sigma \subset {\textbf{P}}$ with $0\le k\le n$, the generalized circumsphere and smallest enclosing ball of $\sigma$ are the weighted points $({{{{\textbf {P}}}}}_C , {\varvec{\mu }}_C )(\sigma )$ and $({{{{\textbf {P}}}}}_B , {\varvec{\mu }}_B )(\sigma )$ respectively defined as:

$$\begin{aligned} {\varvec{\mu }}_C (\sigma )&{ \underset{\text {def.}}{=}} \min {\{ \mu \in {\mathbb {R}}:\exists \, P \in {\mathbb {R}}^n, \forall \, (P_i,\mu _i) \in \sigma , \, \text {D}( (P, \mu ), (P_i, \mu _i) ) = 0\}} \end{aligned}$$

(5)

$$\begin{aligned} {\varvec{\mu }}_B (\sigma )&{\underset{\text {def.}}{=}}\min {\{ \mu \in {\mathbb {R}}:\exists \, P \in {\mathbb {R}}^n, \forall \, (P_i,\mu _i) \in \sigma , \, \text {D}( (P, \mu ), (P_i, \mu _i) ) \le 0\}} \end{aligned}$$

(6)

${{{{\textbf {P}}}}}_C (\sigma )$ (respectively ${{{{\textbf {P}}}}}_B (\sigma )$) is the unique point P that realizes the minimum in (5) (respectively (6)).

Note that, since $\sigma$ is non-degenerate,

$$\begin{aligned}\{ (P, \mu ): \forall \, (P_i,\mu _i) \in \sigma , \text {D}( (P, \mu ), (P_i, \mu _i) ) = 0 \} \ne \emptyset ,\end{aligned}$$

so that the minimum in (5) is well defined and finite. The weights ${\varvec{\mu }}_C (\sigma )$ and ${\varvec{\mu }}_B (\sigma )$ are called respectively circumweight and bounding weight of $\sigma$. In the Delaunay case where weights are zero, ${\varvec{\mu }}_C (\sigma )$ and ${\varvec{\mu }}_B (\sigma )$ correspond respectively to the square of the circumradius and the square of the radius of the smallest ball enclosing $\sigma$, as depicted on Fig. 1, while ${{{{\textbf {P}}}}}_C (\sigma )$ and ${{{{\textbf {P}}}}}_B (\sigma )$ are the respective circles centers.

We give now the condition required in Theorem 1, for the general case, which, as explained in Sect. 3.1, is generic and can be handled by standard symbolic perturbation.

Generic Condition 1

We say that ${\textbf{P}} =\{(P_1, \mu _1), \ldots , (P_N, \mu _N) \} \subset {\mathbb {R}}^n\times {\mathbb {R}}$ is in general position if it does not contain any degenerate n-simplex, and if, for a k-simplex $\sigma$ and a $k'$-simplex $\sigma '$ in $K_{{\textbf{P}}}$ with $2\le k,k' \le n$, one has

$$\begin{aligned} {\varvec{\mu }}_C (\sigma ) = {\varvec{\mu }}_C (\sigma ')\ \ \Longrightarrow \ \ \sigma = \sigma '. \end{aligned}$$

(7)

We have the following observation deduced from Definitions 1 and 7:

Observation 2

If the weights of all points in ${\textbf{P}}$ are assumed non-positive, then, under Generic Condition 1, one has ${\varvec{\mu }}_C (\tau )>0$ and ${\varvec{\mu }}_B (\tau ) > 0$ for any simplex $\tau$.

From now on, we assume ${\textbf{P}}$ to be in general position, i.e., it satisfies Generic Condition 1.

The next lemma assigns to any simplex $\sigma$ a face $\varTheta (\sigma )$ which is inclusion minimal among the faces of $\sigma$ sharing the same generalized smallest enclosing ball as $\sigma$ (see Fig. 3).

Lemma 1

[proof in Appendix C] Under Generic Condition 1 on ${\textbf{P}}$, for any simplex $\sigma$, there exists a unique inclusion minimal face $\varTheta (\sigma )$ of $\sigma$ such that $({{{\textbf{P}}}}_B , {\varvec{\mu }}_B )(\sigma ) = ({{{\textbf{P}}}}_C , {\varvec{\mu }}_C )(\varTheta (\sigma ))$. Moreover, one has $({{{\textbf{P}}}}_C , {\varvec{\mu }}_C )(\varTheta (\sigma )) = ({{{\textbf{P}}}}_B , {\varvec{\mu }}_B )(\varTheta (\sigma ))$.

Figure 3 illustrates the possibilities for $\varTheta (\sigma )$ in the case $n=3$ and zero weights. In general, $\varTheta (\sigma )$ can even be of dimension 0 (a single vertex) but this cannot happen with zero weights. We will need the following lemma:

Lemma 2

For any k-simplex $\sigma \in K_{{\textbf{P}}}$, one has ${{{\textbf{P}}}}_B (\sigma ) \in {{\mathcal {C}}}{{\mathcal {H}}}({ \varTheta (\sigma )})$.

Proof

We claim first that, for any simplex $\sigma$, one has ${{{\textbf{P}}}}_B (\sigma ) \in {{\mathcal {C}}}{{\mathcal {H}}}({ \sigma })$. If $\sigma = \{ (P_0,\mu _0), \ldots ,(P_k,\mu _k)\}$, ${{\mathcal {C}}}{{\mathcal {H}}}({ \sigma })$ is the convex hull of $\{ P_0, \ldots , P_k \}$. If $P \notin {{\mathcal {C}}}{{\mathcal {H}}}({ \sigma })$ the projection of P on ${{\mathcal {C}}}{{\mathcal {H}}}({ \sigma })$ decreases the weighted distance from P to all the vertices of $\sigma$, which shows that $(P, \mu )$ cannot realize the ${{\,\mathrm{arg\,min}\,}}$ in (6). This proves the claim. Since by definition of $\varTheta (\sigma )$ (Lemma 1) one has ${{{\textbf{P}}}}_B (\sigma ) = {{{\textbf{P}}}}_B (\varTheta (\sigma ))$, the lemma follows by applying the claim to the simplex $\varTheta (\sigma )$. $\square$

3.5 Total Order on Simplices: The General Case

In this section, we provide the general definition of the total order on simplices that has been made explicit in Sect. 3.2 in the particular case of Delaunay triangulations in ${\mathbb {R}}^2$ and ${\mathbb {R}}^3$.

For an n-simplex $\sigma$ and k such that $0\le k \le \dim (\sigma ) - \dim (\varTheta (\sigma ))$ we define the $(k+\dim (\varTheta (\sigma )))$-dimensional face $\varTheta _{k} (\sigma )$ as follows. For $k=0$, $\varTheta _0(\sigma ) = \varTheta (\sigma )$, where $\varTheta (\sigma )$ is defined in Lemma 1. For $k>0$, $\varTheta _k(\sigma )$ is the $(\dim (\varTheta _{k-1} (\sigma ) )+1)$-dimensional coface of $\varTheta _{k-1} (\sigma )$ with minimal circumradius

$$\begin{aligned} \varTheta _k(\sigma ) \,\,=\!\! \mathop {\mathrm {arg\,min}}\limits _{\begin{array}{c} {\varTheta _{k-1}(\sigma ) \subset \tau \subseteq \sigma }\\ {\dim (\tau ) = \dim ( \varTheta _{k-1}(\sigma )) +1} \end{array}} \!\!\!\!{\varvec{\mu }}_C (\tau ) \end{aligned}$$

(8)

and $\mu _{k}(\sigma )$ is the circumweight of $\varTheta _k(\sigma )$: $\mu _{k}(\sigma ) = {\varvec{\mu }}_C (\varTheta _k(\sigma ))$. In particular, $\mu _{0}(\sigma ) = {\varvec{\mu }}_C (\varTheta (\sigma ) )= {\varvec{\mu }}_B (\sigma )$ (by Lemma 1) and if $k= \dim (\sigma ) - \dim (\varTheta (\sigma ))$ then $\mu _{k}(\sigma ) = {\varvec{\mu }}_C (\sigma )$.

Observe that, thanks to Generic Condition 1 and Lemma 1, one has, for two n-simplices $\sigma _1, \sigma _2$: ${\varvec{\mu }}_B (\sigma _1) = {\varvec{\mu }}_B (\sigma _2) \Rightarrow \varTheta (\sigma _1)= \varTheta (\sigma _2)$. Therefore, if ${\varvec{\mu }}_B (\sigma _1) = {\varvec{\mu }}_B (\sigma _2)$, $\mu _{k}(\sigma _1)$ and $\mu _{k}(\sigma _2)$ are defined for the same range of values of k. We define the following order relation on n-simplices (recall that $\mu _{0}(\sigma ) = {\varvec{\mu }}_B (\sigma )$):

$$\begin{aligned} \sigma _1 \le \sigma _2\ \ \underset{\text {def.}}{\iff }\ \ \sigma _1 = \sigma _2 \quad \ {\text {or}} \ \ {\left\{ \begin{array}{ll} \mu _{0}(\sigma _1)< \mu _{0}(\sigma _2) \quad \text {or}\\ \exists \, k\ge 1, \, \mu _{k}(\sigma _1) > \mu _{k}(\sigma _2)\\ \text {and} \ \forall j, \, 0\le j < k,\, \mu _{j}(\sigma _1) = \mu _{j}(\sigma _2). \end{array}\right. } \end{aligned}$$

(9)

One can check that when ${\textbf{P}}$ is in general position, the relation $\le$ is a total order. For example, when $n=2$ and the weights are zero, this order on triangles consists in first comparing the radii of the smallest circles enclosing the triangles $T_i$, $i=1,2$, whose squares are $\text {R}_\text {B}(T_i)^2 ={\varvec{\mu }}_B (T_i)= \mu _0(T_i)$. This is enough to induce, generically, an order on acute triangles. But obtuse triangles could generically share their longest edge and therefore have same bounding radius. In this case the tie is broken by comparing in reverse order the circumradii, whose squares are $\text {R}_\text {C}(T_i)^2 ={\varvec{\mu }}_C (T_i)= \mu _1(T_i)$.

By Definition 3, and under Generic Condition 1, the total order $\le$ on n-simplices induces a lexicographic total order ${\sqsubseteq }_{lex }$ on the n-chains of $K_{{\textbf{P}}}$.

Observation 3

From the definition of the order on simplices, the lexicographic minimum is invariant under a global translation of the weights by a common shift s: $\mu _i \leftarrow \mu _i+s$ for all i (as explicitly explained in Observation 8 in Appendix B). The same holds for regular triangulations. Therefore proving Theorem 1 for non-positive weights is enough to extend it to any weights.

4 Some Geometric Properties of Regular Triangulations

4.1 Lifts of Weighted Points and p-Norms

Given a weighted point $(P,\mu ) \in {\mathbb {R}}^n\times {\mathbb {R}}$, its lift with respect to the origin $O\in {\mathbb {R}}^n$, denoted by $\text {lift}(P,\mu )$, is a point in ${\mathbb {R}}^n\times {\mathbb {R}}$ given by:

$$\begin{aligned}\text {lift}(P,\mu ) \underset{\text {def.}}{=} ( (P-O), (P-O)^2 - \mu ),\end{aligned}$$

and, for a set of weighted points ${\textbf{P}} = \{(P_1, \mu _1), \ldots , (P_N, \mu _N) \} \subset {\mathbb {R}}^n\times {\mathbb {R}}$, $\text {lift}({\textbf{P}}) = \{\text {lift}(P_1, \mu _1), \ldots , \text {lift}(P_N, \mu _N)\} \subset {\mathbb {R}}^n\times {\mathbb {R}}$.

Similarly to Delaunay triangulations, it is a well-known fact that simplices of the regular triangulation of ${\textbf{P}}$ are in one-to-one correspondence with the lower convex hull of $\text {lift}({\textbf{P}})$:

Proposition 1

A simplex $\sigma$ is in the regular triangulation of ${\textbf{P}}$ if and only if $\textrm{lift}(\sigma )$ is a simplex on the lower convex hull of $\textrm{lift}({\textbf{P}})$.

Based on this lifted paraboloid formulation, the idea of variational formulation for Delaunay triangulations has emerged [6]. This idea has been exploited further in order to optimize triangulations in [1, 5]. We follow here the same idea but the variational formulation, while using the same criterion, is applied on the linear space of chains, which can be seen as a superset of the space of triangulations.

We define a function on the convex hull of a k-simplex $f_\sigma :{{\mathcal {C}}}{{\mathcal {H}}}({ \sigma })\rightarrow {\mathbb {R}}$ where $\sigma =\{(P_0, \mu _0),\dots , (P_k, \mu _k)\}$ as the difference between the linear interpolation of the height of the lifted vertices and the function $x \mapsto (x-O)^2$. More precisely, for a point $x\in {{\mathcal {C}}}{{\mathcal {H}}}({ \sigma })$ with barycentric coordinates $\lambda _i\ge 0$, $\sum _i \lambda _i = 1$, we have $x = \sum _i \lambda _i P_i$ and

$$\begin{aligned} f_\sigma :\, x \mapsto f_\sigma (x) \underset{\text {def.}}{=} \left( \sum _i \lambda _i ( (P_i-O)^2 - \mu _i) \right) - (x-O)^2. \end{aligned}$$

(10)

A short computation shows that the function $f_\sigma$, expressed in terms of barycentric coordinates, is invariant by isometry (translation, rotation, or symmetry on $\sigma$). In particular $f_\sigma (x)$ does not depend on the origin O of the lift.

It follows from Proposition 1 that, if $\sigma _{reg }$ is a simplex containing x in the regular triangulation of ${\textbf{P}}$, for any other simplex $\sigma$ containing x with vertices in ${\textbf{P}}$,

$$\begin{aligned} f_{\sigma _{reg }}(x) \le f_{\sigma }(x). \end{aligned}$$

(11)

In the particular case where all weights $\mu _i$ are non-positive, the convexity of $x \mapsto x^2$ says that the expression of $f_\sigma (x)$ in (10) is never negative and in this case (11) implies that defining the weight $w_p$ of an n-simplex $\sigma$ as

$$\begin{aligned} w_p(\sigma ) \underset{\text {def.}}{=} \Vert f_\sigma \Vert _{p} = \left( \int _{{{\mathcal {C}}}{{\mathcal {H}}}({ \sigma })}\! f_\sigma (x)^pdx \right) ^{\!{1}/{p}} \end{aligned}$$

(12)

allows to characterize the regular triangulation as the one induced by the chain $\varGamma _{\textrm{reg}}$ that, among all chains with boundary $\beta _{{\textbf{P}}}$, minimizes

$$\begin{aligned} \varGamma \mapsto \left\Vert \varGamma \right\Vert _{(p)} \underset{\text {def.}}{=} \sum _{\sigma } | \varGamma ( \sigma )|w_p(\sigma )^p \end{aligned}$$

(13)

In this last equation, the notation $|\varGamma (\sigma )|$ instead of $\varGamma (\sigma )$ is there since ${\varGamma (\sigma )\in {\mathbb {Z}}_2}$ and the sum is in ${\mathbb {R}}$. For this reason, we used the map $|\,{\cdot }\,|:{\mathbb {Z}}_2 \rightarrow \{0,1\} \subset {\mathbb {R}}$, that assigns respective real numbers 0 and 1 to their corresponding elements in ${\mathbb {Z}}_2= \{0_{{\mathbb {Z}}_2}, 1_{{\mathbb {Z}}_2} \}$, i.e., $|0_{{\mathbb {Z}}_2}| = 0$ and $|1_{{\mathbb {Z}}_2}| = 1$.

Formally, we have the following Proposition 2 which characterizes regular triangulations as a linear programming problem over ${\mathbb {Z}}_2$.

Proposition 2

Let ${\textbf{P}} = \{(P_1, \mu _1), \ldots , (P_N, \mu _N) \} \subset {\mathbb {R}}^n\times {\mathbb {R}}$, with $N \ge n+1$ be in general position with non-positive weights, and let $K_{{\textbf{P}}}$ be the n-dimensional full simplicial complex over ${\textbf{P}}$.

Denote by $\beta _{{\textbf{P}}} \in {\varvec{C}}_{n-1}(K_{{\textbf{P}}})$ the $(n-1)$-chain made of simplices belonging to the boundary of ${{\mathcal {C}}}{{\mathcal {H}}}({ {{\textbf{P}}}}))$ and by $\varGamma _{\textrm{reg}}$ the n-chain defined by the set of n-simplices in the regular triangulation of ${\textbf{P}}$. Then, for any $p\in [1, \infty )$, one has

$$\begin{aligned} \varGamma _{\textrm{reg}}= \mathop {\mathrm {arg\,min}}\limits _{\begin{array}{c} \varGamma \in {\varvec{C}}_{n}(K_{{\textbf{P}}})\\ \partial \varGamma = \beta _{{\textbf{P}}} \end{array} } \left\Vert \varGamma \right\Vert _{(p)} \end{aligned}$$

(14)

The proof of this proposition requires the next lemma. We consider points in the convex hull of ${\textbf{P}}$ that do not belong to the convex hull of any $(n-1)$-simplex in $K_{{\textbf{P}}}$, i.e., $x\in {{\mathcal {C}}}{{\mathcal {H}}}({ {{\textbf{P}}}})){\setminus } \bigcup _{\sigma \in K_{{\textbf{P}}}^{[n-1]}}{{\mathcal {C}}}{{\mathcal {H}}}({ \sigma })$. Note that $\bigcup _{\sigma \in K_{{\textbf{P}}}^{[n-1]}}{{\mathcal {C}}}{{\mathcal {H}}}({ \sigma })$, finite union of convex hulls of $(n-1)$-simplices in ${\mathbb {R}}^n$, has Lebesgue measure 0.

Lemma 3

[proof in Appendix D] Given ${\textbf{P}} = \{P_1, \ldots , P_N \} \subset {\mathbb {R}}^n$, with $N\ge n+1$, in general position, denote by $\beta _{{\textbf{P}}} \in C_{n-1}(K_{{\textbf{P}}})$ the $(n-1)$-chain made of simplices belonging to the boundary of ${{\mathcal {C}}}{{\mathcal {H}}}({ {{\textbf{P}}}})$. Let $\varGamma \in C_{n}(K_{{\textbf{P}}})$ be such that

$$\begin{aligned}\partial \varGamma = \beta _{{\textbf{P}}}.\end{aligned}$$

If $x\in {{\mathcal {C}}}{{\mathcal {H}}}({ {{\textbf{P}}}})$ does not belong to the convex hull of any $(n-1)$-simplex, then there is an odd number of n-simplices $\sigma \in \varGamma$ such that $x \in {{\mathcal {C}}}{{\mathcal {H}}}({ \sigma })$.

Proof of Proposition 2

Note that the minimum in the right hand side of (14) is unique under the assumed general position.

Since, in the regular triangulation, all $(n-1)$-simplices that are not on the boundary of ${{\mathcal {C}}}{{\mathcal {H}}}({ {{\textbf{P}}}})$ are shared by exactly two n-simplices, while only those in $\beta _{{\textbf{P}}}$ have a single n-coface, we have

$$\begin{aligned}\partial \varGamma _{\textrm{reg}}= \beta _{{\textbf{P}}}.\end{aligned}$$

We claim now that

$$\begin{aligned} \partial \varGamma = \beta _{{\textbf{P}}}\ \ \Longrightarrow \ \ \left\Vert \varGamma _{\textrm{reg}} \right\Vert _{(p)} \le \left\Vert \varGamma \right\Vert _{(p)}. \end{aligned}$$

(15)

Indeed, (12) and (13) give

$$\begin{aligned}\left\Vert \varGamma \right\Vert _{(p)} = \sum _{\sigma \in \varGamma } \int _{{{\mathcal {C}}}{{\mathcal {H}}}({ \sigma })} f_\sigma (x)^pdx = \int _{{{\mathcal {C}}}{{\mathcal {H}}}({ {{\textbf{P}}}})} \sum _{\begin{array}{c} \sigma \in \varGamma \\ {{\mathcal {C}}}{{\mathcal {H}}}({ \sigma }) \ni x \end{array}} f_\sigma (x)^pdx.\end{aligned}$$

We get

$$\begin{aligned} \left\Vert \varGamma \right\Vert _{(p)} = \int _{{{\mathcal {C}}}{{\mathcal {H}}}({ {\textbf{P}}}) \setminus \bigcup _{\sigma \in K_{{\textbf{P}}}^{[n-1]}} {{\mathcal {C}}}{{\mathcal {H}}}({ \sigma })} \sum _{\begin{array}{c} \sigma \in \varGamma \\ {{\mathcal {C}}}{{\mathcal {H}}}({ \sigma }) \ni x \end{array}} f_\sigma (x)^pdx. \end{aligned}$$

(16)

From the equivalence between regular triangulations and convex hull on lifted points we know that if $\sigma _{reg } \in \varGamma _{\textrm{reg}}$, then for any n-simplex in $\sigma \in K$,

$$\begin{aligned} x \in {{\mathcal {C}}}{{\mathcal {H}}}({ \sigma }) \cap {{\mathcal {C}}}{{\mathcal {H}}}({ \sigma _{reg }}) \ \ \Longrightarrow \ \ f_{\sigma _{reg }}(x) \le f_\sigma (x). \end{aligned}$$

(17)

According to Lemma 3, in (16), there is an odd number of simplex $\sigma \in \varGamma$ satisfying ${{\mathcal {C}}}{{\mathcal {H}}}({ \sigma }) \ni x$ in the condition. It follows that the condition has to hold for at least one simplex $\sigma$. Therefore (17) gives

$$\begin{aligned} x \in {{\mathcal {C}}}{{\mathcal {H}}}({ \sigma _{reg }}) \quad \Longrightarrow \quad f_{\sigma _{reg }}(x)^p\, \le \! \sum _{\begin{array}{c} \sigma \in \varGamma \\ {{\mathcal {C}}}{{\mathcal {H}}}({ \sigma }) \ni x \end{array}}\!\! f_\sigma (x)^p. \end{aligned}$$

(18)

Since for $x \in {{\mathcal {C}}}{{\mathcal {H}}}({ {\textbf{P}}}) {\setminus } \bigcup _{\sigma \in K_{{\textbf{P}}}^{[n-1]}} {{\mathcal {C}}}{{\mathcal {H}}}({ \sigma })$ there is exactly one simplex $\sigma _{reg }$ such that ${{\mathcal {C}}}{{\mathcal {H}}}({ \sigma _{reg }}) \ni x$, (18) can be rewritten as

$$\begin{aligned} \sum _{\begin{array}{c} \sigma \in \varGamma _{\textrm{reg}}\\ {{\mathcal {C}}}{{\mathcal {H}}}({ \sigma }) \ni x \end{array}} \!\! f_\sigma (x)^p\, \le \! \sum _{\begin{array}{c} \sigma \in \varGamma \\ {{\mathcal {C}}}{{\mathcal {H}}}({ \sigma }) \ni x \end{array}}\!\! f_\sigma (x)^p \end{aligned}$$

(19)

which, together with (16) gives the claim (15). Now, if some n-simplex $\sigma \in \varGamma$ with ${{\mathcal {C}}}{{\mathcal {H}}}({ \sigma }) \ni x$, for some $x \in {{\mathcal {C}}}{{\mathcal {H}}}({ {\textbf{P}}}) {\setminus } \bigcup _{\sigma \in K_{{\textbf{P}}}^{[n-1]}} {{\mathcal {C}}}{{\mathcal {H}}}({ \sigma })$, is not Delaunay, then

$$\begin{aligned}\sum _{\begin{array}{c} \sigma \in \varGamma _{\textrm{reg}}\\ {{\mathcal {C}}}{{\mathcal {H}}}({ \sigma }) \ni x \end{array}} \!\! f_\sigma (x)^p \,=\, f_{\sigma _{reg }}(x)^p \, < \! \sum _{ {{\mathcal {C}}}{{\mathcal {H}}}({ \sigma }) \ni x }\! f_\sigma (x)^p,\end{aligned}$$

and since the function is continuous, this implies $\left\Vert \varGamma \right\Vert _{(p)} > \left\Vert \varGamma _{\textrm{reg}} \right\Vert _{(p)}$. $\square$

Lemma 4

[proof in Appendix E] One has

$$\begin{aligned} \sup _{x\in {{\mathcal {C}}}{{\mathcal {H}}}({ \sigma })} f_\sigma (x) = {\varvec{\mu }}_B (\sigma ). \end{aligned}$$

(20)

The following is an immediate consequence used in the proof of Lemma 5:

$$\begin{aligned} \lim _{p\rightarrow \infty } w_p(\sigma ) = w_{\infty } (\sigma ) = \Vert f_\sigma \Vert _{\infty } = \sup _{x\in {{\mathcal {C}}}{{\mathcal {H}}}({ \sigma })} f_\sigma (x) = {\varvec{\mu }}_B (\sigma ). \end{aligned}$$

(21)

Lemma 5

Let ${\textbf{P}} = \{(P_1, \mu _1), \ldots , (P_N, \mu _N) \} \subset {\mathbb {R}}^n\times {\mathbb {R}}$, with $N \ge n+1$, be in general position with non-positive weights. Let $K_{{\textbf{P}}}$ be the corresponding n-dimensional full simplicial complex. For p large enough, the weight $w_p(\sigma )^p$ of any n-simplex $\sigma \in K_{{\textbf{P}}}$, is larger than the sum of the weights of all n-simplices in $K_{{\textbf{P}}}$ with smaller bounding weight ${\varvec{\mu }}_B$. In other words, denoting by $K_{{\textbf{P}}}^{[n]}$ the set of n-simplices in $K_{{\textbf{P}}}$,

$$\begin{aligned}\exists p^\star ,\, \forall \,p\ge p^\star , \, \forall \,\sigma \in K_{{\textbf{P}}}^{[n]}, \qquad w_p(\sigma )^p\; >\!\! \sum _{\begin{array}{c} \tau \in K_{{\textbf{P}}}^{[n]}\\ {\varvec{\mu }}_B (\tau ) < {\varvec{\mu }}_B (\sigma ) \end{array} } \!\!\!w_p(\tau )^p.\end{aligned}$$

Proof

Consider the smallest ratio between two bounding weights (respectively squared radii for the Delaunay case) of n-simplices in $K_{{\textbf{P}}}$:

$$\begin{aligned}\iota =\!\! \min _{\begin{array}{c} \sigma _1, \sigma _2 \in K_{\textbf{P}}^{[n]}\\ {\varvec{\mu }}_B (\sigma _1) < {\varvec{\mu }}_B (\sigma _2) \end{array} } \frac{{\varvec{\mu }}_B (\sigma _2)}{{\varvec{\mu }}_B (\sigma _1)}.\end{aligned}$$

One has $\iota >1$. Choose $\iota '$ such that $1< \iota ' < \iota$. For any n-simplex $\sigma \in K_{\textbf{P}}^{[n]}$ we have from (21) that

$$\begin{aligned}\lim _{p\rightarrow \infty } w_p(\sigma ) =\, {\varvec{\mu }}_B (\sigma ),\end{aligned}$$

it follows that, since there is only finitely many simplices in $K_{\textbf{P}}^{[n]}$, there exists some $p_0$ large enough such that for any $p> p_0$ one has

$$\begin{aligned}\forall \, \sigma _1, \sigma _2 \in K_{\textbf{P}}^{[n]}, \ \quad \ \ {\varvec{\mu }}_B (\sigma _1) < {\varvec{\mu }}_B (\sigma _2)\ \ \Longrightarrow \ \ \frac{w_p(\sigma _2)}{w_p(\sigma _1)} > \iota '.\end{aligned}$$

Let ${\mathcal {N}}$ be total number of n-simplices in $K_{\textbf{P}}$. Taking

realizes the statement of the lemma. $\square$

As explained in the proof of the main theorem of Sect. 6, Lemma 5 allows us to focus on the link of a single simplex $\tau$. However, before that, we need to introduce geometrical constructions that give an explicit representation of this link (Sects. 4.2 and 4.3).

4.2 Projection on the Bisector of a Simplex

In this section, we establish a condition for a simplex $\tau$ to belong to the regular triangulation and, when it is the case, give a characterization of its link in the regular triangulation.

Fig. 4

Illustration in dimension 2 and zero weights of the constructions of Sects. 4.2 and 4.3. The two triangles form a Delaunay triangulation of the four points a, b, c, d in the plane because the two red circumcircles are empty. Since both simplices abc and ab share the same blue circle as smallest enclosing disk, one has $\varTheta (abc) = ab$ and ${\varvec{\mu }}_B (abc) = {\varvec{\mu }}_B (ab)$

Fig. 5

Illustration in dimension 2 and zero weights of the constructions of Sects. 4.2 and 4.3. We are interested in the link of the edge $\tau = ab$. We start by projecting the points on the bisector $\textbf{bis}_\tau$ of $\tau$. The projection $\pi _{\textbf{bis}_\tau } (a) =\pi _{\textbf{bis}_\tau } (b) =\pi _{\textbf{bis}_\tau } (\tau )$ is the center $o_\tau$ of the circumcircle of $\tau$ which here is also the smallest enclosing circle of $\tau$ as $\varTheta (\tau )= \tau$

Fig. 6

Illustration in dimension 2 and zero weights of the constructions of Sects. 4.2 and 4.3. The horizontal axis is still the bisector $\textbf{bis}_\tau$ of $\tau$, but the vertical axis is now the weight axis. We represents the image by $\pi _\tau$ of $\tau =ab$, c, and d. Note that $\pi _\tau (\tau )=\pi _\tau (\{a,b\})=\pi _\tau (a)= \pi _\tau (b)$ is a single point

Fig. 7

Illustration in dimension 2 and zero weights of the constructions of Sects. 4.2 and 4.3. We represent the image by $\varPhi _\tau$ of $\tau =a,b$, c, and d

Fig. 8

Illustration in dimension 2 and zero weights of the constructions of Sects. 4.2 and 4.3. The red line between $\varPhi _\tau (\tau )$ and $\varPhi _\tau (d)$ (respectively $\varPhi _\tau (c)$) corresponds to the red circumcircle of triangle abd (respectively abc) on Fig. 4: A point is inside a circle if and only its image by $\varPhi$ is below the corresponding line. The horizontal blue line corresponds to the blue circle Fig. 4. The fact that $\tau$ belongs to the Delaunay triangulation of a, b, c, d is equivalent to the fact that $\varPhi _\tau (\tau )$ belongs to the lower convex hull of $\varPhi _\tau ( \{a,b,c,d\} )$. The fact that ${\varvec{\mu }}_B (abc) = {\varvec{\mu }}_B (ab)$ is equivalent to the fact that $\varPhi _\tau (c)$ is below $\varPhi _\tau (\tau )$. The half-line starting at $\varPhi _\tau (\tau )$ through $\varPhi _\tau (c)$ cuts the horizontal axis $\textbf{bis}_\tau$ at the shadow ${{\textbf{S}}}{{\textbf{h}}}_\tau (c, 0)$ of c

Given a k-simplex $\tau$, we denote by $\textbf{bis}_\tau$ the $(n-k)$-dimensional affine space bisector of $\tau$, formally defined as

$$\begin{aligned} \textbf{bis}_\tau \underset{\text {def.}}{=} \{ x \in {\mathbb {R}}^n: \forall \,v_1, v_2 \in \tau ,\, \text {D}( (x,0), v_1 )= \text {D}( (x,0), v_2 ) \}. \end{aligned}$$

(22)

In the particular case where $\tau$ is a vertex, i.e., $\dim (\tau )=0$, one has $\textbf{bis}_\tau = {\mathbb {R}}^n$.

Let $x\mapsto \pi _{\textbf{bis}_\tau } (x)$ and $x\mapsto d(x, \textbf{bis}_\tau )= d(x, \pi _{\textbf{bis}_\tau } (x))$ denote respectively the orthogonal projection on and the minimal distance to $\textbf{bis}_\tau$. We define a projection $\pi _\tau :{\textbf{P}} \rightarrow \textbf{bis}_\tau \times {\mathbb {R}}$ as follows:

$$\begin{aligned} \pi _\tau (P, \mu ) \underset{\text {def.}}{=} \bigl ( \pi _{\textbf{bis}_\tau } (P),\, \mu - d(P, \textbf{bis}_\tau )^2 \bigr ). \end{aligned}$$

(23)

Figures 4, 5, and 6 illustrate $\pi _\tau$ for ambient dimension 2 and $\dim (\tau )=1$. Figure 9 illustrates $\pi _\tau$ for ambient dimension 3 and $\dim (\tau )=1$.

Let $o_\tau = {{{{\textbf {P}}}}}_C (\tau ) \in \textbf{bis}_\tau$ denote the circumcenter of $\tau$ (or, for weighted points, the generalized circumcenter as defined in Definition 7). If $(P_i, \mu _i) \in \tau$, then $\text {D}( (o_\tau , {\varvec{\mu }}_C (\tau )), (P_i, \mu _i)) = 0$. Since $o_\tau = \pi _{\textbf{bis}_\tau } (P_i)$, we have:

$$\begin{aligned}(P_i -o_\tau )^2 - \mu _i - {\varvec{\mu }}_C (\tau ) = d(P, \textbf{bis}_\tau )^2 - \mu _i - {\varvec{\mu }}_C (\tau ) = 0.\end{aligned}$$

It follows that if we denote $\mu (\pi _\tau (P_i, \mu _i))$ the weight of $\pi _\tau (P_i, \mu _i)$, one has

$$\begin{aligned}\mu (\pi _\tau (P_i, \mu _i)) = \mu _i - d(P, \textbf{bis}_\tau )^2 = - {\varvec{\mu }}_C (\tau ).\end{aligned}$$

Therefore, $\pi _\tau$ sends all vertices of $\tau$ to a single weighted point:

$$\begin{aligned} (P_i, \mu _i) \in \tau \ \ \ \Longrightarrow \ \ \ \pi _\tau (P_i, \mu _i) = ( o_\tau , -{\varvec{\mu }}_C (\tau )). \end{aligned}$$

(24)

Fig. 9

Illustration in dimension 3 and zero weights for the definition of ${\textbf {bis}}_\tau$, $\pi _\tau$ (top left and right), and $\varPhi _\tau$ (bottom)

Lemma 6

Let ${\textbf{P}}$ be in general position, $\tau \in K_{{\textbf{P}}}$ a k-simplex and $\sigma \in K_{{\textbf{P}}}$ a coface of $\tau$. Then $\sigma$ is in the regular triangulation of ${\textbf{P}}$ if and only if $\pi _\tau (\sigma )$ is a coface of the vertex $\{ (o_\tau , -{\varvec{\mu }}_C (\tau )) \} = \pi _\tau (\tau )$ in the regular triangulation of $\pi _\tau ({\textbf{P}})$.

Proof

Under our generic condition, $\sigma$ is in the regular triangulation of ${\textbf{P}}$ if and only if there is a weighted point $({{{{\textbf {P}}}}}_C (\sigma ), {\varvec{\mu }}_C (\sigma ))$ such that:

$$\begin{aligned} \forall \, (P_i,\mu _i) \in \sigma , \quad \ \ \text {D}( ({{{{\textbf {P}}}}}_C (\sigma ), {\varvec{\mu }}_C (\sigma )), (P_i,\mu _i) )&= 0, \end{aligned}$$

(25)

$$\begin{aligned} \forall \, (P_i,\mu _i) \in {\textbf{P}} \setminus \sigma , \quad \ \ \text {D}( ({{{{\textbf {P}}}}}_C (\sigma ), {\varvec{\mu }}_C (\sigma )), (P_i,\mu _i) )&> 0. \end{aligned}$$

(26)

Observe that, since $\tau \subset \sigma$, (25) implies

$$\begin{aligned}\forall \,(P_i,\mu _i) \in \tau ,\quad \ \ \ \text {D}( ({{{{\textbf {P}}}}}_C (\sigma ), 0 ), (P_i,\mu _i) ) = {\varvec{\mu }}_C (\sigma ).\end{aligned}$$

This and the definition (22) of bisector show that ${{{{\textbf {P}}}}}_C (\sigma )$ must be on the bisector of $\tau$:

$$\begin{aligned} {{{{\textbf {P}}}}}_C (\sigma ) \in \textbf{bis}_\tau . \end{aligned}$$

(27)

We get, for $(P_i, \mu _i) \in {\textbf{P}}$,

$$\begin{aligned}&\text {D}( ({{{{\textbf {P}}}}}_C (\sigma ),{\varvec{\mu }}_C (\sigma )), (P_i,\mu _i)) \nonumber \\&\quad \quad = ({{{{\textbf {P}}}}}_C (\sigma ) - P_i)^2 - {\varvec{\mu }}_C (\sigma ) - \mu _i \nonumber \\&\quad \quad = ( \pi _{\textbf{bis}_\tau } ( P_i) - {{{{\textbf {P}}}}}_C (\sigma ))^2 + d(P_i, \textbf{bis}_\tau )^2 - {\varvec{\mu }}_C (\sigma ) - \mu _i \nonumber \\&\quad \quad = \text {D}_{\textbf{bis}_\tau } \bigl (({{{{\textbf {P}}}}}_C (\sigma ),{\varvec{\mu }}_C (\sigma )),( \pi _{\textbf{bis}_\tau } ( P_i) , \mu _i - d(P_i, \textbf{bis}_\tau )^2) \bigr ) \nonumber \\&\quad \quad = \text {D}_{\textbf{bis}_\tau } \bigl (( {{{{\textbf {P}}}}}_C (\sigma ), {\varvec{\mu }}_C (\sigma )),\pi _\tau (P_i, \mu _i) \bigr ) . \end{aligned}$$

(28)

In the last two lines, the weighted distance is denoted $\text {D}_{\textbf{bis}_\tau }$ instead of $\text {D}$ in order to stress that, thanks to (27), it occurs on weighted point of $\textbf{bis}_\tau \times {\mathbb {R}}$ rather than ${\mathbb {R}}^n \times {\mathbb {R}}$. Therefore (25) and (26) are equivalent to

$$\begin{aligned} \forall \, (P_i,\mu _i) \in \sigma , \quad \ \ \text {D}_{\textbf{bis}_\tau }( ({{{{\textbf {P}}}}}_C (\sigma ), {\varvec{\mu }}_C (\sigma )), \pi _\tau (P_i,\mu _i))&= 0, \\ \forall \,(P_i,\mu _i) \in {\textbf{P}} \setminus \sigma , \quad \ \ \text {D}_{\textbf{bis}_\tau }( ({{{{\textbf {P}}}}}_C (\sigma ), {\varvec{\mu }}_C (\sigma )), \pi _\tau (P_i,\mu _i) )&> 0, \end{aligned}$$

which precisely means that $\pi _\tau (\sigma )$ is a coface of the vertex $\pi _\tau (\tau ) = \{ (o_\tau , -{\varvec{\mu }}_C (\tau )) \}$ in the regular triangulation of $\pi _\tau ({\textbf{P}})$. $\square$

An immediate consequence of Lemma 6 is

Corollary 1

The projection $\pi _\tau$ preserves the structure of the regular triangulation around $\tau$, more precisely:

• (i) The simplex $\tau$ is in the regular triangulation of ${\textbf{P}}$ if and only if the vertex $\pi _\tau (\tau ) = \{ (o_\tau , -{\varvec{\mu }}_C (\tau )) \}$ is a vertex of the regular triangulation of $\pi _\tau ({\textbf{P}})$,

• (ii) If $\tau$ is in the regular triangulation of ${\textbf{P}}$, $\pi _\tau$ induces a simplicial isomorphism between the link of $\tau$ in the regular triangulation of ${\textbf{P}}$ and the link of vertex $\pi _\tau (\tau )$ in the regular triangulation of $\pi _\tau ({\textbf{P}})$.

4.3 Polytope and Shadow Associated to a Link in a Regular Triangulation

In this section, we study the link of a k-simplex $\tau$ in the regular triangulation of ${\textbf{P}}$ that satisfies:

$$\begin{aligned} ({{{{\textbf {P}}}}}_B , {\varvec{\mu }}_B ) ( \tau ) = ({{{{\textbf {P}}}}}_C , {\varvec{\mu }}_C ) (\tau ). \end{aligned}$$

(29)

Equivalently, we assume $\varTheta (\tau )=\tau$ and in this case both generalized smallest enclosing sphere and generalized circumsphere of $\tau$ coincide so that $o_\tau$ is also the center of the generalized smallest ball containing $\tau$.

We know, from Proposition 1 and Corollary 1(ii), that the link of $\tau$ in the regular triangulation is isomorphic to the link of $\text {lift}(\pi _\tau (\tau ))$ on the boundary of the lower convex hull of $\text {lift}(\pi _\tau ({\textbf{P}}))$. We consider the lift with the origin at $o_\tau$, in other words, the image of a vertex $(P,\mu ) \in {\textbf{P}}$ is

The construction of $\varPhi _\tau$ is illustrated on Fig. 7 in dimension 2 and Fig. 9, bottom, in dimension 3.

Observe that the image by $\varPhi _\tau$ of all vertices of simplex $\tau$ coincide. Therefore the image of $\tau$ is a single vertex:

$$\begin{aligned}\varPhi _\tau (\tau ) = \{ (0,{\varvec{\mu }}_C (\tau ) )\} \subset {\mathbb {R}}^{n-k} \times {\mathbb {R}}.\end{aligned}$$

Call $P_\tau$ the set of weighted points in $(P_i,\mu _i) \in {\textbf{P}}{\setminus } \tau$ such that $\tau \cup (P_i,\mu _i)$ has the same bounding weight as $\tau$. In the case of the Delaunay triangulation, $P_\tau$ corresponds to the set of points in ${\textbf{P}}$ (strictly) inside the smallest ball enclosing $\tau$. Formally, using the assumption (29), we introduce the following subset of vertices in the link of $\tau$:

$$\begin{aligned} P_\tau \underset{\text {def.}}{=} \{ (P_i,\mu _i) \in {\textbf{P}} \setminus \tau :\text {D}( ({{{{\textbf {P}}}}}_C (\tau ), {\varvec{\mu }}_C (\tau )), (P_i, \mu _i) ) < 0 \}. \end{aligned}$$

(30)

Denote by $K_\tau$ the $(n-k-1)$-dimensional simplicial complex made of all simplices over vertices in $P_\tau$ with dimension up to $n - k - 1$. Observe that, for any weighted point $(P, \mu )$, one has

$$\begin{aligned} \begin{aligned}&\text {D}( ({{{{\textbf {P}}}}}_C (\tau ), {\varvec{\mu }}_C (\tau )), (P, \mu ) )< 0 \\&\qquad \iff \ \ ( \pi _{\textbf{bis}_\tau } (P) - o_\tau )^2 - \mu + d (P, \textbf{bis}_\tau )^2 < {\varvec{\mu }}_C (\tau ). \end{aligned} \end{aligned}$$

(31)

Denote by ${\text {Height}}(\text {lift}(P, \mu ))$ the height of the lift of a point $(P, \mu )$, defined as the last coordinate of the lift, so that

$$\begin{aligned} {\text {Height}}( \varPhi _\tau (P,\mu ))= ( P - o_\tau )^2 - \mu . \end{aligned}$$

(32)

We have assumed the weights to be non-positive, $\mu \le 0$, and since under our generic conditions we have $\pi _{\textbf{bis}_\tau } (P) - o_\tau \ne 0$, (32) implies that $v\in P_\tau \Rightarrow {\text {Height}}(\varPhi _\tau (v,\mu ))> 0$ and, using Observation 2, (31) can be rephrased as

Observation 4

A vertex belongs to $P_\tau$ if and only if the height of its image by $\varPhi _\tau$ is strictly less than ${\varvec{\mu }}_C (\tau ) > 0$:

$$\begin{aligned}v\in P_\tau \ \ \iff \ \ 0<{\text {Height}}( \varPhi _\tau (v))< {\varvec{\mu }}_C (\tau ).\end{aligned}$$

This observation allows to define the following conical projection:

Definition 8

(shadow)  Let v be a vertex in $P_\tau$. The shadow ${{\textbf{S}}}{{\textbf{h}}}_{\tau }(v)$ of v is a point in the $(n-k)$-dimensional Euclidean space $\textbf{bis}_\tau$ defined as the intersection of the half-line starting at $(0, {\varvec{\mu }}_C (\tau ) )$ and going through $\varPhi _\tau (v)$ with the space $\textbf{bis}_\tau$.

$$\begin{aligned}{{\textbf{S}}}{{\textbf{h}}}_{\tau }( P, \mu ) \underset{\text {def.}}{=}\frac{{\varvec{\mu }}_C (\tau )}{ {\varvec{\mu }}_C (\tau ) -{\text {Height}}( \varPhi _\tau (P,\mu ))}( \pi _{\textbf{bis}_\tau } (P) - o_\tau ).\end{aligned}$$

The shadow of a simplex $\sigma \in K_\tau$ is a simplex in $\textbf{bis}_\tau$ whose vertices are the shadows of vertices of $\sigma$.

The construction of ${{\textbf{S}}}{{\textbf{h}}}_{\tau }$ is illustrated in Fig. 8 in dimension 2 and Fig. 9, bottom, in dimension 3.

Let $\varGamma _{\textrm{reg}}$ be the n-chain containing the n-simplices of the regular triangulation of ${\textbf{P}}$ and $| \varGamma _{\textrm{reg}}|$ the corresponding simplicial complex. Denote by $\text {X}(\tau ) \in {\varvec{C}}_{n-k-1}(K_\tau )$ the $(n-k-1)$-chain in the link of $\tau$ made of simplices $\sigma \in K_\tau$ such that $\tau \cup \sigma \in |\varGamma _{\textrm{reg}}|$:

(33)

${{\textbf{S}}}{{\textbf{h}}}_{\tau } (\text {X}(\tau ))$ will play a key role for the proof of Theorem 1 in Sect. 6.

Definition 9

(polytope and convex cone)  In the following, we call polytope a finite intersection of closed half spaces $\bigcap _i H_i$. The convex cone of a polytope at a point p on the boundary of the polytope is the intersection of all such $H_i$ whose boundary contains p.

Definition 10

(polytope facet visible from 0)  We say that a facet f of a polytope is visible from the point 0, or visible for short, if the closed half-space H containing the polytope and whose boundary is the supporting plane of f does not contain 0.

Definition 11

(shadow polytope)   The (possibly empty) intersection of the convex cone of the lower convex hull of $\varPhi _\tau ({\textbf{P}})$ at $\varPhi _\tau (\tau ) = ( 0, {\varvec{\mu }}_C (\tau ))$ with $\textbf{bis}_\tau = {\mathbb {R}}^{n-k} \times \{0\}$ is called shadow polytope of $\tau$.

Figure 10 depicts the shadow polytope corresponding to the example of Fig. 9 as the filled area and the bounded cells of its boundary by the two edges in blue.

Fig. 10

Illustration of the shadow polytope (grey area) of Definition 11 corresponding to the example of Fig. 9

For each upper half-space $H_j$ contributing to the convex cone of the lower convex hull of $\varPhi _\tau ({\textbf{P}})$ at $(0,{\varvec{\mu }}_C (\tau ))$, the intersection $H_j\cap \textbf{bis}_\tau$ is an $(n-k)$-dimensional half-space in $\textbf{bis}_\tau$. The shadow polytope is precisely defined as the intersection of all such half-spaces $H_j\cap \textbf{bis}_\tau$. Since each $H_j$ is a upper half-space and since by Observation 4 one has ${\varvec{\mu }}_C (\tau ) >0$, $H_j$ does not contain (0, 0), which implies that $H_j\cap \textbf{bis}_\tau$ does not contain the point $o_\tau$ in $\textbf{bis}_\tau$. It follows that

Observation 5

All facets of the shadow polytope are visible from 0.

Lemma 7

Let ${\textbf{P}}$ be in general position with non-positive weights.

• (i) $\tau$ is in the regular triangulation of ${\textbf{P}}$ if and only if $\varPhi _\tau (\tau ) = ( 0, {\varvec{\mu }}_C (\tau ))$ is an extremal point of the convex hull of $\varPhi _\tau ({\textbf{P}})$.

• (ii) When $\tau$ is in the regular triangulation of ${\textbf{P}}$, its link is isomorphic to the link of the vertex $\varPhi _\tau (\tau ) = ( 0, {\varvec{\mu }}_C (\tau ))$ in the simplicial complex corresponding to the boundary of the lower convex hull of $\varPhi _\tau ({\textbf{P}})$.

• (iii) When $\tau$ is in the regular triangulation of ${\textbf{P}}$, ${{\textbf{S}}}{{\textbf{h}}}_{\tau }$ induces a bijection between the simplices in $\text {X}(\tau )$ and the set of bounded facets of the boundary of the shadow polytope.

Proof

(i) follows from Corollary 1(i), together with Proposition 1. (ii) follows from Corollary 1(ii) together with Proposition 1.

For the claim (iii), observe that (ii) implies that the faces of the convex cone of the lower convex hull of $\varPhi _\tau ({\textbf{P}})$ at $\varPhi _\tau (\tau ) = ( 0, {\varvec{\mu }}_C (\tau ))$ are in one-to-one correspondence with the link of $\tau$ in the regular triangulation. If $\sigma$ is a simplex in the link of $\tau$ in the regular triangulation, denote by $CC _{\sigma }$ the convex cone in ${\mathbb {R}}^{n-k} \times {\mathbb {R}}$ with apex $\varPhi _\tau (\tau ) = ( 0, {\varvec{\mu }}_C (\tau ))$ and through ${{\mathcal {C}}}{{\mathcal {H}}}({\varPhi _\tau (\sigma )})$:

$$\begin{aligned}CC _{\sigma } \underset{\text {def.}}{=} \{ ( 0, {\varvec{\mu }}_C (\tau )) + \lambda x: x \in {{\mathcal {C}}}{{\mathcal {H}}}({\varPhi _\tau (\sigma )}),\,\lambda \ge 0 \}.\end{aligned}$$

Since ${\varvec{\mu }}_C (\tau ) > 0$, the intersection of $CC _{\sigma }$ with $\textbf{bis}_\tau = {\mathbb {R}}^{n-k} \times \{0\}$ is therefore (see Fig. 9 for an illustration):

• empty if all vertices of $\varPhi _\tau (\sigma )$ have height larger than ${\varvec{\mu }}_C (\tau )$,

• non-empty and unbounded if some vertices of $\varPhi _\tau (\sigma )$, but not all, have height larger than ${\varvec{\mu }}_C (\tau )$,

• non-empty and bounded, if and only if all vertices of $\varPhi _\tau (\sigma )$ have the height smaller than ${\varvec{\mu }}_C (\tau ) > 0$.

In Fig. 9, bottom, the cones corresponding to the third category are depicted, in blue, together with their non-empty, bounded, intersection (edge) with $\textbf{bis}_\tau$.

Therefore, since a simplex $\sigma$ in the link of $\tau$ of a regular triangulation belongs to $\text {X}(\tau )$ if and only all its vertices are in $P_\tau$, we get, with Observation 4, that $\sigma \in \text {X}(\tau )$ if and only if the intersection of $CC _{\sigma }$ with $\textbf{bis}_\tau = {\mathbb {R}}^{n-k} \times \{0\}$ is non-empty and bounded, as claimed. $\square$

5 Visible Convex Hulls as Lexicographic Minimal Chain

This section is self-contained and does not rely on previous constructions. Lemma 10 is a key ingredient for the proof of Theorem 1, but is also a result of independent interest: visible convex hulls can be characterized as lexicographic minimum chains under boundary constraints.

Remark 1

The result in Lemma 10 extends to lower convex hulls, since they are equivalent, up to a projective transformation. It extends also directly to regular triangulations, through the lift on paraboloid equivalence between regular triangulations and lower convex hulls. This is already a characterization of regular triangulations as lexicographic minimum chains under boundary constraints, but the total order on simplices given by this direct transposition is not invariant under isometry.

Lemmas 8 and 9 will be instrumental in the proof of Lemma 10. Recall (Sect. 2.1) that the link of a k-simplex in a pure n-dimensional simplicial complex is a pure $(n-k-1)$-simplicial complex.

Definition 12

(trace of a chain in a link) Given a k-simplex $\tau$ in a simplicial complex K and an n-chain $\varGamma$ on K, for $n > k$, we call trace of the n-chain $\varGamma$on the link of $\tau$ the $(n-k-1)$-chain ${\text {Tr}}_{\tau }(\varGamma )$, defined in the link $\text {Lk}_{K}(\tau )$ of $\tau$, as follows. For any $\sigma \in \text {Lk}_{K}(\tau )$,

$$\begin{aligned}{\text {Tr}}_{\tau }(\varGamma ) (\sigma ) \underset{\text {def.}}{=} \varGamma (\tau \cup \sigma ).\end{aligned}$$

The next lemma is used twice in what follows.

Lemma 8

Given a k-simplex $\tau$ in a simplical complex K and an n-chain $\varGamma$ on K for $n > k$, one has

$$\begin{aligned}\partial {\text {Tr}}_{\tau }(\varGamma )= {\text {Tr}}_{\tau } ( \partial \varGamma ).\end{aligned}$$

Proof

We need to prove that for any simplex $\sigma$ in the link of $\tau$, one has

$$\begin{aligned}\partial {\text {Tr}}_{\tau }(\varGamma ) (\sigma ) = {\text {Tr}}_{\tau } (\partial \varGamma ) (\sigma ).\end{aligned}$$

We have by definition that an $(n-k-2)$-simplex $\sigma$ is in ${\text {Tr}}_{\tau } (\partial \varGamma ) (\sigma )$ if and only if $\tau \cap \sigma =\emptyset$ and $\tau \cup \sigma$ is in $\partial \varGamma$. In other words, $\tau \cup \sigma$ has an odd number of n-cofaces in the chain $\varGamma$. This in turn means that $\sigma$ has an odd number of $(n-k)$-cofaces in the trace of $\varGamma$ in the link of $\tau$, i.e., $\sigma \in \partial {\text {Tr}}_{\tau }(\varGamma )$. $\square$

For a polytope C, we denote $\partial C$ the boundary of the set C.

Lemma 9

[proof in Appendix F] Let $C\subset {\mathbb {R}}^n$ be a polytope and $O\in {\mathbb {R}}^n \setminus C$. Let $X \subset \partial C$ be the union of a set of facets of C visible from O. If $x\in X$ maximizes the distance to O, then $x \in \partial X$, where $\partial X$ denotes the relative boundary of X in $\partial C$.

Note that, in the context of Lemma 9, there exists at least a point $x\in X$ that maximizes the distance to O, since X, union of facets, is a compact set.

We need to define another order on simplices together with the corresponding induced lexicographic order on chains, respectively denoted $\le _{{\textbf{0}}}$ and $\sqsubseteq _{{\textbf{0}}}$.

For that, we define the distance from a flat (an affine space) F to 0 as $d_{{\textbf{0}}}(F) = \inf _{p\in F} d(p, 0)$. If $\zeta$ is a non-degenerate k-simplex for some $k\ge 0$, define $d_{{\textbf{0}}}(\zeta ) = d_{{\textbf{0}}}(F(\zeta ))$ where $F(\zeta )$ is the k-dimensional flat support of $\zeta$. In order to compare two simplex for the order $\le _{{\textbf{0}}}$, we first compare the distances to 0 of their vertex farthest to 0. If they differ, the simplex whose farthest vertex is farther is greater for $\le _{{\textbf{0}}}$. If they share the same farthest vertex v, then the tie is broken by comparing, among the edges containing v in each simplex, the farthest one to 0, i.e., the one that maximizes $d_{{\textbf{0}}}$. Again, if the two simplices share also the same farthest edge, we consider the farthest 2-faces in each simplex containing this farthest edge, and so on. More formally:

We associate to an $(n-1)$-simplex $\sigma$ in ${\mathbb {R}}^n$ that does not contain 0 a dimension increasing sequence of faces $\emptyset = \tau _{-1}(\sigma ) \subset \tau _0(\sigma ) \subset \ldots \subset \tau _{n-1}(\sigma ) = \sigma$ with $\dim (\tau _i) = i$. Under a simple generic condition, it is defined as follows.

• $\tau _{-1}(\sigma )= \emptyset$ and $\tau _0(\sigma )$ is the vertex of $\sigma$ farthest from 0.

• For $i\ge 0$, $\tau _i(\sigma )$ is the coface of dimension i of $\tau _{i-1}(\sigma )$ whose supporting i-flat is farthest from 0:

  $$\begin{aligned} \tau _i(\sigma ) \,\underset{\text {def.}}{=}\,\arg \max _{\begin{array}{c} \zeta \supset \tau _{i-1}(\sigma )\\ \dim (\zeta ) = i \end{array}}d_{{\textbf{0}}}(\zeta ). \end{aligned}$$

  (34)

  For $i=0,\ldots ,n-1$ we set $\delta _i(\sigma ) = d_{{\textbf{0}}}(\tau _i(\sigma ))$ and we define the comparison $<_{{\textbf{0}}}$ between two $(n-1)$-simplices $\sigma _1$ and $\sigma _2$ as a lexicographic order on the sequences $(\delta _i(\sigma _1))_{i=0,\ldots , n-1}$ and $(\delta _i(\sigma _2))_{i=0,\ldots , n-1}$:

  $$\begin{aligned} \sigma _1<_{{\textbf{0}}} \sigma _2\underset{\text {def.}}{\iff } {\left\{ \begin{array}{ll} \exists \, k\ge 0, \ \ \delta _k(\sigma _1)< \delta _k(\sigma _2) \quad \text {and} \\ \forall j,\,0\le j < k,\ \ \delta _j(\sigma _1) = \delta _j(\sigma _2), \end{array}\right. } \end{aligned}$$

  (35)

  which defines an order relation:

  $$\begin{aligned} \sigma _1 \le _{{\textbf{0}}} \sigma _2\quad \underset{\text {def.}}{\iff }\quad \sigma _1= \sigma _2 \quad \text {or} \quad \sigma _1 <_{{\textbf{0}}} \sigma _2. \end{aligned}$$

  (36)

Generic Condition 2

Let K be an $(n-1)$-dimensional simplicial complex. For any pair of simplices $\sigma _1, \sigma _2 \in K$: $\dim (\sigma _1) = \dim (\sigma _2)= k$ and $d_{{\textbf{0}}}(\sigma _1) = d_{{\textbf{0}}}(\sigma _2)\ \Rightarrow \ \sigma _1=\sigma _2$.

Under Condition 2, $\le _{{\textbf{0}}}$ is a total order on simplices and, following Definition 3, the order $\le _{{\textbf{0}}}$ on simplices induces a lexicographic order $\sqsubseteq _{{\textbf{0}}}$ on k-chains of K.

Lemma 10

Let P be a set of points in ${\mathbb {R}}^n$ such that $0\in {\mathbb {R}}^n$ is not in the convex hull of P. Let K be the full $(n-1)$-dimensional simplicial complex over P, i.e., the simplicial complex made of all $(n-1)$-simplices whose vertices are points in P with all their faces. Assume that K satisfies Generic Condition 2.

Let X be an $(n-1)$-chain in K whose $(n-1)$-simplices are on the boundary of the convex hull of P and are all visible from $0\in {\mathbb {R}}^n$. Then

$$\begin{aligned} X = \min _{\sqsubseteq _{{\textbf{0}}}} {\{ \varGamma \in {\varvec{C}}_{n-1}(K):\partial \varGamma = \partial X\} }. \end{aligned}$$

(37)

If $n=1$, the boundary operator in (37) is meant as the boundary operator of reduced homology, i.e., the linear operator $\tilde{\partial _0}:{\varvec{C}}_{n-1}(K) \rightarrow {\mathbb {Z}}_2$ that counts the parity.

For $n=1$ (Fig. 11), we are given a set of real numbers for P and corresponding singletons for K, so that a 0-chain $\varGamma$ can be seen as a subsets of $P\subset {\mathbb {R}}$. Since 0 is not in the convex hull, numbers in P are either all positive, or either all negative. The minimal non-zero chain, for lexicographic order $\sqsubseteq _{{\textbf{0}}}$, is the chain containing only the vertex $x_1\in P$ with minimal absolute value in P. Replacing the constraint from being non-zero by the stronger constraint for $\varGamma$ to have odd cardinality, does not change this lexicographic minimum. Moreover, this parity constraint is a linear constraint (over the field ${\mathbb {Z}}_2$). This is why, for $n=1$, the boundary constraint $\partial \varGamma =\partial X$ is the linear operator $\tilde{\partial _0}:{\varvec{C}}_{n-1}(K) \rightarrow {\mathbb {Z}}_2$ that counts the parity.

Proof of Lemma 10

We first claim that the lemma holds for $n=1$. In this case (Fig. 11) the fact that 0 is not in the convex hull of P means that the 1-dimensional points in P are either all positive, or either all negative. The single simplex in the convex hull boundary visible from 0 is the point in P closest to 0, i.e., the one with the smallest absolute value, which corresponds to the minimum chain with odd parity in the $\sqsubseteq _{{\textbf{0}}}$ order, which proves the claim.

We assume then the theorem to be true for the dimension $n-1$ and proceed by induction. This recursion is illustrated in Fig. 12 for $n=2$ and Fig. 13 for $n=3$. Consider the minimum

$$\begin{aligned} \varGamma _{\textrm{min}}= \min _{\sqsubseteq _{{\textbf{0}}}}{\{ \varGamma \in {\varvec{C}}_{n-1}(K):\partial \varGamma = \partial X \}}. \end{aligned}$$

(38)

We need to prove that $\varGamma _{\textrm{min}}= X$.

There exists a unique vertex v in the simplices of $\partial X$ which is farthest from 0. Indeed, existence follows from compactness of $\partial X$, and unicity Generic Condition 2, which in the particular case of vertices says that no pair of vertices lie at the same distance from 0, since in this case, $d_0$ is merely the distance from the vertex to 0.

Let v be this unique vertex in the simplices of $\partial X$ which is farthest from 0. Since v is a vertex in at least one simplex in $\partial X = \partial \varGamma _{\textrm{min}}$, it must be a vertex in some simplex in $\varGamma _{\textrm{min}}$. Thanks to Lemma 9, if a point x is a local maximum in X of the distance to 0 one has $x \in \partial X$. It follows that v is also the vertex in the simplices of X which is farthest from 0. Since v is the vertex in X farthest from 0 and since by definition $\varGamma _{\textrm{min}}\sqsubseteq _{{\textbf{0}}} X$, we know that $\varGamma _{\textrm{min}}$ does not contain any vertex farther from the origin than v, therefore v is also the vertex in the simplices of $\varGamma _{\textrm{min}}$ farthest from 0.

Let us briefly give the principle of the induction. We show below that the trace of $\varGamma _{\textrm{min}}$ in the link of v is the solution of the same minimisation problem (37) with one dimension less, allowing to apply inductively Lemma 10 to show that X and $\varGamma _{\textrm{min}}$ coincide in the star of v. This allows to remove from X the star of v ((44) below) and iteratively apply the recursion on the remaining farthest vertex of X until X is empty. More formally:

Since $\partial \varGamma _{\textrm{min}}= \partial X$, Lemma 8 implies that

$$\begin{aligned} \partial {\text {Tr}}_v ( \varGamma _{\textrm{min}}) = {\text {Tr}}_v ( \partial \varGamma _{\textrm{min}}) = {\text {Tr}}_v ( \partial X). \end{aligned}$$

(39)

In order to define a lexicographic order on chains on the link of v in K, we consider the hyperplane $\varPi$ containing 0 and orthogonal to the line 0v. We associate to any $(n-2)$-simplex $\eta \in \text {Lk}_{K}(v)$ the $(n-2)$-simplex $\pi _{v\varPi }(\eta )$, conical projection of $\eta$ on $\varPi$ with center v. In other words, if u is a vertex of $\eta$,

$$\begin{aligned}\{ \pi _{v\varPi }(u) \} \underset{\text {def.}}{=} \varPi \cap uv,\end{aligned}$$

where uv denotes the line going through u and v. The map $\pi _{v\varPi }$ is a conical projection on vertices but it extends to a bijection on simplices and chains that does bot contain v that trivially commutes with the boundary operator.

By definition of the lexicographic order $\sqsubseteq _{{\textbf{0}}}$, the comparison of two chains whose farthest vertex is v starts by comparing their restrictions to the star of v. Therefore, since v is the farthest vertex in $\varGamma _{\textrm{min}}$, the restriction of $\varGamma _{\textrm{min}}$ to the star of v must be minimum under the constraint $\partial \varGamma = \partial X$. The constraint $\partial \varGamma = \partial X$ for the restriction of $\varGamma _{\textrm{min}}$ to the star of v is equivalent to the constraint given by (39) or equivalently by

$$\begin{aligned} \partial \pi _{v\varPi } ( {\text {Tr}}_v ( \varGamma _{\textrm{min}}) ) = \pi _{v\varPi } ( {\text {Tr}}_v (\partial X) ), \end{aligned}$$

(40)

and the minimization on the restriction of the $(n-1)$-chain $\varGamma _{\textrm{min}}$ to the star of v can equivalently be expressed as the minimization of the $(n-2)$-chain $\gamma _{\textrm{min}}= \pi _{v\varPi } ( {\text {Tr}}_v ( \varGamma _{\textrm{min}}))$ under the constraint $\partial \gamma _{\textrm{min}}=\pi _{v\varPi }( {\text {Tr}}_v (\partial X) )$, we have then:

$$\begin{aligned} \gamma _{\textrm{min}}&=\pi _{v\varPi } ( {\text {Tr}}_v ( \varGamma _{\textrm{min}}) ) \nonumber \\&=\pi _{v\varPi } \left( {\text {Tr}}_v \left( \min _{\sqsubseteq _{{\textbf{0}}}} {\{ \varGamma \in {\varvec{C}}_{n-1}(K): \partial \varGamma = \partial X \} } \right) \right) \nonumber \\&=\min _{\sqsubseteq _{{\textbf{0}}}} {\{ \gamma \in {\varvec{C}}_{n-2}( \pi _{v\varPi } ( \text {Lk}_{K}(v)) ):\partial \gamma = \pi _{v\varPi } ( {\text {Tr}}_v (\partial X) ) \} } \end{aligned}$$

(41)

$$\begin{aligned}&=\min _{\sqsubseteq _{{\textbf{0}}}} {\{ \gamma \in {\varvec{C}}_{n-2}( \pi _{v\varPi } ( \text {Lk}_{K}(v))):\partial \gamma = \partial \pi _{v\varPi } ( {\text {Tr}}_v ( X) ) \} }. \end{aligned}$$

(42)

In the third equality (41) we have used the fact that the orders on $(n-1)$-simplices in the star of v in K and the order on corresponding $(n-2)$-simplices in the image by $\pi _{v\varPi }$ of the link of v are compatible. The fourth equality (42) uses (40). Indeed, if F is a k-flat in ${\mathbb {R}}^n$ going through v, we have (see Fig. 14)

$$\begin{aligned} d_{{\textbf{0}}}(\pi _{v\varPi } (F) ) = d_{{\textbf{0}}}(F \cap \varPi ) = \frac{ d_{{\textbf{0}}}(F) \Vert v-0\Vert }{\sqrt{(v-0)^2 - d_{{\textbf{0}}}(F)^2} } \end{aligned}$$

(43)

with the convention $d_{{\textbf{0}}}(\pi _{v\varPi } (F))=+\infty$ in the non-generic case where $F\cap \varPi = \emptyset$ (the denominator vanishes in this case while since $v\in F$ one has $F\cap \varPi \ne \emptyset \Rightarrow d_{{\textbf{0}}}(F)<\Vert v-0\Vert$). As seen in (43), $d_{{\textbf{0}}}(F) \mapsto d_{{\textbf{0}}}(\pi _{v\varPi } (F) )$ is an increasing function and the orders are therefore consistent along the induction.

We claim that the minimization problem in (42) satisfies the condition of the theorem for $n'=n-1$ which is assumed true by induction. The recursion is as follows: Hyperplane $\varPi$ corresponds to ${\mathbb {R}}^{n'}$ with $n'=n-1$ and

$$\begin{aligned} n'&\leftarrow n-1, \\ P'&\leftarrow \pi _{v\varPi }(P\setminus \{v\}), \\ K'&\leftarrow \pi _{v\varPi }(\text {Lk}_{K} (v)) ,\\ X'&\leftarrow \pi _{v\varPi }( {\text {Tr}}_v (X)). \end{aligned}$$

Observe first that, in ${\mathbb {R}}^k$, a $(k-1)$-simplex with vertices in a point set P is in convex position (i.e., belongs to the convex hull boundary) and is visible from 0 if and only its supporting hyperplane separates P from 0.

Since $(n-1)$-simplices in X are in convex position and visible from 0, hyperplanes supporting these simplices separate all points of P from 0. Consider in particular such a simplex $\sigma$ in X which is moreover in the star of v and its associated supporting hyperplane $\varPi _\sigma \ni v$.

We have that since $\varPi _\sigma$ separate P from 0, $\varPi _\sigma \cap \varPi = \pi _{v\varPi } (\varPi _\sigma )$, separates $P' = \pi _{v\varPi } (P{\setminus } \{v\})$ from 0 in $\varPi$. It follows that the $(n'-1)$-simplices in $X' = \pi _{v\varPi }( {\text {Tr}}_v (X))$ are in convex position and are visible from 0. Therefore one can apply our lemma recursively, which gives us, using (42),

$$\begin{aligned}\gamma _{\textrm{min}}= \pi _{v\varPi } ( {\text {Tr}}_v(\varGamma _{\textrm{min}}))=\pi _{v\varPi }( {\text {Tr}}_v ( X)).\end{aligned}$$

It follows that the faces in the star of v corresponding to ${\text {Tr}}_v ( \varGamma _{\textrm{min}})$ belong to X. Call Y the $(n-1)$-chain made of these simplices in the star of v. We have both $Y\subset X$ and $Y \subset \varGamma _{\textrm{min}}$.

Since, seeing chains as set of simplices, one has $Y\subset X$, the chain $X \setminus Y$ can equivalently be noted as $X -Y$ when seeing them as vectors over ${\mathbb {Z}}_2$. We favor this linear formulation in the equations below. Since v is the vertex farthest from 0 in both X and in $\varGamma _{\textrm{min}}$ one has by definition of the lexicographic order:

$$\begin{aligned} \begin{aligned} \varGamma _{\textrm{min}}&=\min _{{\sqsubseteq }_{lex }}{\{ \varGamma \in {\varvec{C}}_{n-1}(K):\partial \varGamma = \partial X \}}\\&=Y+\min _{{\sqsubseteq }_{lex }}{\{ \varGamma \in {\varvec{C}}_{n-1}(K):\partial \varGamma = \partial (X-Y)\}}.\end{aligned} \end{aligned}$$

(44)

So, by considering the new problem $X \leftarrow (X-Y)$ and iterating as long as X is not empty, we get our final result $\varGamma _{\textrm{min}}= X$. $\square$

Fig. 11

Illustration of Lemma 10 for $n=1$. In this case X is a 0-chain, and has therefore no boundary

Fig. 12

Illustration of the recursion in the proof of Lemma 10 for $n=2$. In this case X is a 1-chain, and its boundary $\partial X$ is a zero chain made of two vertices. $X'$ is a 0-chain made of a single vertex, the red vertex nearest to O on the blue line representing $\varPi$

Fig. 13

Illustration of the recursion in the proof of Lemma 10 for $n=3$. In this case X is a 2-chain, and its boundary $\partial X$ is a 1-chain depicted as the red edges cycle. $X'$ is a 1-chain in $\varPi$ while $\partial X'$ is a 0-chain made of the two vertices framed by a little orange squares

Fig. 14

Illustration for (43)

6 Proof of Theorem 1

Recall the definitions of $P_\tau$ and $K_\tau$ introduced in Sect. 4.3, for a k-simplex $\tau \in K_{{\textbf{P}}}$ such that $\varTheta (\tau )=\tau$ (in other words such that ${\varvec{\mu }}_C (\tau )={\varvec{\mu }}_B (\tau )$):

• $P_\tau$ is the set of weighted points $(P_i,\mu _i) \in {\textbf{P}}{\setminus } \tau$ such that $\tau \cup (P_i,\mu _i)$ has the same bounding weight ${\varvec{\mu }}_B (\tau )$ as $\tau$,

• $K_\tau$, a subcomplex of the link of $\tau$, is made of all simplices over vertices in $P_\tau$ with dimension up to $n - k - 1$.

The next two lemmas establish the connection between the orders ${\sqsubseteq }_{lex }$ and $\sqsubseteq _{{\textbf{0}}}$ and introduce the notation ${\downarrow }_\rho \varGamma$ for an n-chain $\varGamma$ (46), used in the proof of Theorem 1.

Lemma 11

[proof in Appendix G]  For $\sigma _1,\sigma _2 \in K_\tau$, one has

$$\begin{aligned} {\varvec{\mu }}_C ( \tau \cup \sigma _1) \ge {\varvec{\mu }}_C ( \tau \cup \sigma _2)\ \ \iff \ \ d_{{\textbf{0}}}({{\textbf{S}}}{{\textbf{h}}}_{\tau }(\sigma _1)) \le d_{{\textbf{0}}}({{\textbf{S}}}{{\textbf{h}}}_{\tau }(\sigma _2)). \end{aligned}$$

(45)

For an n-chain $\varGamma$ denote by ${\downarrow }_{\rho } \varGamma$ the chain obtained by removing from $\varGamma$ all simplices with bounding weight strictly greater than $\rho$:

$$\begin{aligned} {\downarrow }_{\rho } \varGamma \underset{\text {def.}}{=} \{ \sigma \in \varGamma :{\varvec{\mu }}_B (\sigma ) \le \rho \}. \end{aligned}$$

(46)

Lemma 12

[proof in Appendix H] For two n-chains $\varGamma _1,\varGamma _2 \in {\varvec{C}}_{n}(K_{{\textbf{P}}})$ if $\varGamma _1 \ne \varGamma _2$ one has

$$\begin{aligned}{\downarrow }_{\rho }\varGamma _1\;{\sqsubseteq }_{lex }\;{\downarrow }_\rho \varGamma _2\quad \Longrightarrow \quad {{\textbf{S}}}{{\textbf{h}}}_{\tau _{\rho }}({\text {Tr}}_{\tau _{\rho }}( {\downarrow }_{\rho } \varGamma _1))\sqsubseteq _{{\textbf{0}}}{{\textbf{S}}}{{\textbf{h}}}_{\tau _{\rho }}({\text {Tr}}_{\tau _{\rho }}({\downarrow }_{\rho } \varGamma _2)),\end{aligned}$$

where $\tau _{\rho }$ is a simplex such that $\theta (\tau )=\tau$ and ${\varvec{\mu }}_B (\tau ) = \rho$.

Observation 6

(total orders equivalence)  Since both ${\sqsubseteq }_{lex }$ and $\sqsubseteq _{{\textbf{0}}}$ are total orders under our generic condition, the implication of Lemma 12 gives the equivalence

$$\begin{aligned}{\downarrow }_{\rho } \varGamma _1\;{\sqsubseteq }_{lex }\;{\downarrow }_{\rho } \varGamma _2\quad \Longleftrightarrow \quad {{\textbf{S}}}{{\textbf{h}}}_{\tau _{\rho }}({\text {Tr}}_{\tau _{\rho }}( {\downarrow }_{\rho } \varGamma _1))\sqsubseteq _{{\textbf{0}}}{{\textbf{S}}}{{\textbf{h}}}_{\tau _{\rho }}({\text {Tr}}_{\tau _{\rho }}({\downarrow }_{\rho } \varGamma _2)),\end{aligned}$$

where $\tau _{\rho }$ is a simplex such that $\theta (\tau ) = \tau$ and ${\varvec{\mu }}_B (\tau ) = \rho$.

We now have all the tools needed to prove our main theorem.

Proof of Theorem 1

We prove Theorem 1 in the case of non-positive weights which then extends to any weights thanks to Observations 3 and 8. As in Proposition 2, denote by $\varGamma _{\textrm{reg}}$ the chain that defines the regular triangulation of ${{\mathcal {C}}}{{\mathcal {H}}}({ {\textbf{P}}})$. As in Theorem 1 denote by $\beta _{{\textbf{P}}} \in {\varvec{C}}_{n-1}(K_{{\textbf{P}}})$ the $(n-1)$-chain made of simplices belonging to the boundary of ${{\mathcal {C}}}{{\mathcal {H}}}({ {\textbf{P}}})$.

According to Proposition 2, $\varGamma _{\textrm{reg}}$ minimizes $\varGamma \mapsto \left\Vert \varGamma \right\Vert _{(p)}$ among the chains with boundary $\beta _{{\textbf{P}}}$ for any $p\ge 1$. In particular, $\varGamma _{\textrm{reg}}$ minimizes $\varGamma \mapsto \left\Vert \varGamma \right\Vert _{p^\star }$ for the value $p^\star$ of Lemma 5.

Proposition 2 and Theorem 1 consider a minimum with respect to the same boundary condition while their objective differ. In order to prove Theorem 1, we have to show that both minimum still agree. By contradiction, we assume now that they differ, which means that $\varGamma _{\textrm{min}}\ne \varGamma _{\textrm{reg}}$ where $\varGamma _{\textrm{min}}$ is the minimal chain of Theorem 1. Consider ${\varvec{\mu }}_B ^{\ne }$ to be the largest bounding weight for which some simplex in $\varGamma _{\textrm{min}}$ and $\varGamma _{\textrm{reg}}$ differ:

$$\begin{aligned} {\varvec{\mu }}_B ^{\ne } \underset{\text {def.}}{=} \max {\{ {\varvec{\mu }}_B (\sigma ):\sigma \in \varGamma _{\textrm{min}}+ \varGamma _{\textrm{reg}}\}}. \end{aligned}$$

(47)

There must be at least one simplex with bounding weight ${\varvec{\mu }}_B ^{\ne }$ in $\varGamma _{\textrm{reg}}$ as otherwise, by definition of ${\varvec{\mu }}_B ^{\ne }$, there would be a simplex with radius ${\varvec{\mu }}_B ^{\ne }$ in $\varGamma _{\textrm{min}}$ and this would give $\varGamma _{\textrm{reg}}\;{\sqsubseteq }_{lex }\;\varGamma _{\textrm{min}}$ with $\varGamma _{\textrm{reg}}\ne \varGamma _{\textrm{min}}$ and since $\partial \varGamma _{\textrm{reg}}= \partial \varGamma _{\textrm{min}}= \beta _{{\textbf{P}}}$ this contradicts the definition of $\varGamma _{\textrm{min}}$.

Similarly, it follows from Lemma 5 that if there was no simplex with bounding weight ${\varvec{\mu }}_B ^{\ne }$ in $\varGamma _{\textrm{min}}$, one would have $\Vert \varGamma _{\textrm{min}}\Vert _{p^{\star }}<\Vert \varGamma _{\textrm{reg}}\Vert _{p^{\star }}$ and $\partial \varGamma _{\textrm{reg}}= \partial \varGamma _{\textrm{min}}$: a contradiction with the minimality of $\varGamma _{\textrm{reg}}$ for norm $\Vert \,{\cdot }\,\Vert _{p^{\star }}$ (Proposition 2). We have shown that if they differ, both $\varGamma _{\textrm{reg}}$ and $\varGamma _{\textrm{min}}$ must contain at least one simplex with bounding weight ${\varvec{\mu }}_B ^{\ne }$.

We know from Lemma 1 and Generic Condition 1 that the set of simplices with bounding weight ${\varvec{\mu }}_B ^{\ne }$ are all cofaces of some unique dimension minimal simplex $\tau _{{\varvec{\mu }}_B ^{\ne }}$. If $\dim \bigl ( \tau _{{\varvec{\mu }}_B ^{\ne }}\bigr )=n$, $\tau _{{\varvec{\mu }}_B ^{\ne }}$ is the unique simplex in $K_{{\textbf{P}}}$ whose bounding weight is ${\varvec{\mu }}_B ^{\ne }$. But then $\varGamma _{\textrm{reg}}$ and $\varGamma _{\textrm{min}}$ coincide on simplices with bounding weight ${\varvec{\mu }}_B ^{\ne }$, a contradiction with the definition of ${\varvec{\mu }}_B ^{\ne }$.

Assume now that $\dim \bigl (\tau _{{\varvec{\mu }}_B ^{\ne }}\bigr )=k<n$. By definition of ${\varvec{\mu }}_B ^{\ne }$ one has

$$\begin{aligned} {\downarrow }_{{\varvec{\mu }}_B ^{\ne }} \varGamma _{\textrm{reg}}- {\downarrow }_{{\varvec{\mu }}_B ^{\ne }}\varGamma _{\textrm{min}}= \varGamma _{\textrm{reg}}- \varGamma _{\textrm{min}}, \end{aligned}$$

(48)

where ${\downarrow }_{{\varvec{\mu }}_B ^{\ne }}$ is defined in (46). In order to simplify the notations, we allow ourselves to replace for the rest of the section $\downarrow _{{\varvec{\mu }}_B ^{\ne }}$ by $\downarrow$ and $\tau _{{\varvec{\mu }}_B ^{\ne }}$ by $\tau$. It follows from (48) that

$$\begin{aligned}\partial ( {\downarrow } \varGamma _{\textrm{reg}}- {\downarrow } \varGamma _{\textrm{min}})= \partial \varGamma _{\textrm{reg}}- \partial \varGamma _{\textrm{min}}= \beta _{{\textbf{P}}} - \beta _{{\textbf{P}}} = 0.\end{aligned}$$

${\downarrow }\varGamma _{\textrm{reg}}$ and ${\downarrow }\varGamma _{\textrm{min}}$ have therefore the same boundary and by Lemma 8, their trace also have the same boundary:

$$\begin{aligned} \partial {\text {Tr}}_{\tau }( {\downarrow } \varGamma _{\textrm{min}})= \partial {\text {Tr}}_{\tau }( {\downarrow }\varGamma _{\textrm{reg}}). \end{aligned}$$

(49)

Observe that the set of $(n-k-1)$-simplices in ${\text {Tr}}_{\tau }({\downarrow }\varGamma _{\textrm{reg}})$ coincides with the definition of $\text {X}(\tau )$ in (33). Also we have, from (iii) in Lemma 7, that the set of shadows of simplices in $\text {X}(\tau )$, is a chain in ${{\textbf{S}}}{{\textbf{h}}}_{\tau }( K_\tau )$ made of the faces of the convex hull of ${{\textbf{S}}}{{\textbf{h}}}_{\tau }(P_\tau )$ visible from the origin 0. We get the following characterization of ${{\textbf{S}}}{{\textbf{h}}}_{\tau }({\text {Tr}}_{\tau }({\downarrow }\varGamma _{\textrm{reg}}))$:

Observation 7

The chain ${{\textbf{S}}}{{\textbf{h}}}_{\tau }({\text {Tr}}_{\tau }({\downarrow }\varGamma _{\textrm{reg}}))$ is the set of $(n-k-1)$-faces of the convex hull of ${{\textbf{S}}}{{\textbf{h}}}_{\tau }(P_\tau )$ visible from the origin 0.

In the remainder of this proof we use the lexicographic order $\sqsubseteq _{{\textbf{0}}}$ on shadows of $(n-k-1)$-chains in $K_\tau$, defined at the beginning of Sect. 5. This order is equivalent to the order ${\sqsubseteq }_{lex }$ on corresponding n-chains restricted to the set of simplices with bounding weight ${\varvec{\mu }}_B ^{\ne }$ (Lemma 12 and Observation 6).

This correspondence allows to conclude the proof by applying Lemma 10 that says the chain defined by visible faces of a polytope minimizes the lexicographic order $\sqsubseteq _{{\textbf{0}}}$ among chains with same boundary. More formally, thanks to Lemma 12 we have

$$\begin{aligned}{\downarrow }\varGamma _1\;{\sqsubseteq }_{lex }\;{\downarrow }\varGamma _2\quad \Longrightarrow \quad {{\textbf{S}}}{{\textbf{h}}}_{\tau }({\text {Tr}}_{\tau }({\downarrow }\varGamma _1))\sqsubseteq _{{\textbf{0}}}{{\textbf{S}}}{{\textbf{h}}}_{\tau }({\text {Tr}}_{\tau }({\downarrow }\varGamma _2)).\end{aligned}$$

It follows that ${{\textbf{S}}}{{\textbf{h}}}_{\tau }({\text {Tr}}_{\tau }( { \downarrow }\varGamma _{\textrm{min}}))$ is the the minimum for order $\sqsubseteq _{{\textbf{0}}}$, among all chains in the complex ${{\textbf{S}}}{{\textbf{h}}}_{\tau }(K_\tau )$ that satisfy the constraint (49), or, equivalently:

$$\begin{aligned}{{\textbf{S}}}{{\textbf{h}}}_{\tau }({\text {Tr}}_{\tau }({\downarrow } \varGamma _{\textrm{min}})) = \min _{\sqsubseteq _{{\textbf{0}}}}{\{ \varGamma ' \in {\varvec{C}}_{n-k-1}({{\textbf{S}}}{{\textbf{h}}}_{\tau }( K_\tau )):\partial \varGamma '=\partial {{\textbf{S}}}{{\textbf{h}}}_{\tau }({\text {Tr}}_{\tau } ( {\downarrow }\varGamma _{\textrm{reg}}))\}}.\end{aligned}$$

Observation 7 allows us to apply Lemma 10 with

$$\begin{aligned} n&\leftarrow n-k,\\ X&\leftarrow {{\textbf{S}}}{{\textbf{h}}}_{\tau }({\text {Tr}}_{\tau }( { \downarrow } \varGamma _{\textrm{reg}}))= {{\textbf{S}}}{{\textbf{h}}}_{\tau }(\text {X}(\tau ) ) ,\\ P&\leftarrow {{\textbf{S}}}{{\textbf{h}}}_{\tau }(P_\tau ) , \\ K&\leftarrow {{\textbf{S}}}{{\textbf{h}}}_{\tau }(K_\tau ), \end{aligned}$$

implying

$$\begin{aligned}{{\textbf{S}}}{{\textbf{h}}}_{\tau }({\text {Tr}}_{\tau }({\downarrow }\varGamma _{\textrm{min}}))={{\textbf{S}}}{{\textbf{h}}}_{\tau }({\text {Tr}}_{\tau } ({\downarrow }\varGamma _{\textrm{reg}}) ).\end{aligned}$$

In other words, $\varGamma _{\textrm{min}}$ and $\varGamma _{\textrm{reg}}$ coincide on simplices with bounding weight ${\varvec{\mu }}_B ^{\ne }$, a contradiction with the definition (47) of ${\varvec{\mu }}_B ^{\ne }$. $\square$

Appendices

A Overview of the Proof

This section, designed as a complementary roadmap, summarizes the arguments in the proof’s main steps, and illustrates them in Figs. 15 and 16. It is completed by a glossary, Appendix A.4, which recalls most of the notions used in this overview. The theorem is proven for points with non-positive weights which, thanks to Observation 3, is enough to be true for any weights. The proof splits into two main steps, (A) and (B), summarized on the flowcharts of Figs. 15 and 16.

Fig. 15

Flow chart of the main steps of part (A) of the proof of Theorem 1

1.1 A.1 Step (A)

Step (A) corresponds to the beginning of the proof of Theorem 1 in Sect. 6 and relies on the definitions and lemmas given in Sect. 4.1. We denote by $\varGamma _{\textrm{reg}}$ the simplicial n-chain whose support coincides with the regular triangulation, and by $\varGamma _{\textrm{min}}$ the n-chain minimal for order ${\sqsubseteq }_{lex }$ under the boundary constraint $\partial \varGamma = \beta _{{\textbf{P}}}$. Proving Theorem 1 consists then in proving that $\varGamma _{\textrm{min}}= \varGamma _{\textrm{reg}}$.

We assume in step (A), for the sake of contradiction, that $\varGamma _{\textrm{min}}\ne \varGamma _{\textrm{reg}}$ (see Fig. 15). Proposition 2 is then established by reusing the observation first made in [6]: the Delaunay (or regular) triangulation in dimension ${\mathbb {R}}^n$ is equivalent to the convex hull of points in ${\mathbb {R}}^{n+1}$ where each point $(x_1,\ldots ,x_n) \in {\mathbb {R}}^n$ is lifted to a paraboloid as $\bigl (x_1,\ldots ,x_n, \sum _j x_j^2\bigr )\in {\mathbb {R}}^{n+1}$.

This implies that the Delaunay triangulation minimizes, among all triangulations, the $L^p$ norm of the difference of two functions: the one with the lifted triangulation’s simplices as graph and the one with the paraboloid as graph. This characterization as a minimum generalizes from a minimum among triangulations to a minimum among all chains with the convex hull of points as boundary (Proposition 2). It results that $\varGamma _{\textrm{reg}}$ can be characterized as the chain minimizing the norm $\Vert \,{\cdot }\,\Vert _{(p)}$ under the boundary constraint $\partial \varGamma = \beta _{{\textbf{P}}}$.

The statement of Proposition 2 is the same as Theorem 1 except for the order along which the minimum is taken: $\varGamma _{\textrm{reg}}$ minimizes $\Vert \,{\cdot }\,\Vert _{(p)}$ while $\varGamma _{\textrm{min}}$ is minimum for ${\sqsubseteq }_{lex }$ (in particular, both statements share the same boundary constraint).

The bounding weight ${\varvec{\mu }}_B (\sigma )$ is the dominant quantity in the definition of the order on simplices which induces the lexicographic order ${\sqsubseteq }_{lex }$ on chains. For p large enough, ${\varvec{\mu }}_B (\sigma )$ is also the dominant quantity in $\Vert \,{ \cdot }\,\Vert _{(p)}$, since ${\varvec{\mu }}_B (\sigma )=\lim _{p\rightarrow \infty } w_p(\sigma )$ and, for p large enough, the weight $w_p(\sigma )^p$ of any single simplex $\sigma$ in the $\Vert \,{\cdot }\,\Vert _{(p)}$ norm is larger than the sum of all weights of all simplices with smaller bounding weights (Lemma 5 in Sect. 4.1).

As detailed in the proof of Theorem 1 in Sect. 6, this fact allows us to focus on the link of a k-simplex $\tau _{{\varvec{\mu }}_B ^{\ne }}$, inclusion minimal among simplices whose bounding weight ${\varvec{\mu }}_B ^{\ne }$ is the largest bounding weight for which some simplex in $\varGamma _{\textrm{reg}}$ and $\varGamma _{\textrm{min}}$ differ.

At this point, it remains to compare the traces of $\varGamma _{\textrm{reg}}$ and $\varGamma _{\textrm{min}}$ in the link of $\tau _{{\varvec{\mu }}_B ^{\ne }}$, and prove that they are identical, to get the contradiction. This comparison is rather trivial for $n<3$, but requires the additional constructions of step (B) for $n\ge 3$.

1.2 A.2 Case $n < 3$

For $n=1$, for p large enough, the order ${\sqsubseteq }_{lex }$ and the order induced by comparing $\Vert \,{\cdot }\,\Vert _{(p)}$ coincide, so that the result follows immediately from Proposition 2.

For $n=2$, the proof is detailed in [18, Sect. 4.2.3]. In this case, the two orders differ even for large p. However it can be observed that chains minimum for either $\Vert \,{\cdot }\, \Vert _{(p)}$, for p large enough, or for ${\sqsubseteq }_{lex }$ (under boundary constraint) contain generically only one simplex $\sigma$ for each bounding weight ${\varvec{\mu }}_B (\sigma )$. It results that, in both triangulations, the set of simplices with a given bounding weight is made of a single simplex, acute triangle or longest edge of obtuse triangle, and therefore (with the generic condition) coincide. This with the definition of $\tau _{{\varvec{\mu }}_B ^{\ne }}$ in step (A) gives the contradiction.

Fig. 16

Flow chart of the main steps of part (B) of the proof of Theorem 1. In this part, one focuses on the subset of the link of the k-simplex $\tau _{{\varvec{\mu }}_B ^{\ne }}$ defined in step (A), with same bounding radius (or bounding weight) as $\tau _{{\varvec{\mu }}_B ^{\ne }}$

1.3 A.3 Step (B)

The proof for $n\ge 3$ needs to focus on sets of n-simplices with same bounding weight ${\varvec{\mu }}_B$. Formally, it includes the proof for $n=1$ and $n=2$ as limit trivial cases.

Under the generic condition, n-simplices sharing the same bounding weight ${\varvec{\mu }}_B$ are all cofaces of some simplex $\tau$ such that ${\varvec{\mu }}_B (\tau )= {\varvec{\mu }}_C (\tau ) = {\varvec{\mu }}_B$. For example, in the situation of Fig. 3, for a Delaunay triangulation in ${\mathbb {R}}^3$, the set of tetrahedra with the same bounding radius $\textrm{R}_B$, under generic condition, is not of the same nature in examples left, middle and right. On the left, since $\textrm{R}_B (\sigma ) = \textrm{R}_C (\sigma )$, there is, under generic condition, a single such tetrahedron abcd. In the middle, $\tau$ would be the triangle abc and, denoting by $\textrm{B}_B (\tau )$ the unique ball with radius $\textrm{R}_B$ enclosing $\tau$, there is exactly one tetrahedron abcq with bounding radius $\textrm{R}_B$, in the full simplicial complex $K_{{\textbf{P}}}$, for each point $q \in \textrm{B}_B (\tau ) \cap ({\textbf{P}} {\setminus } \{a,b,c\} )$. These vertices are in the link of $\tau$. On the right, $\tau$ would be the edge ab and there is a one-to-one correspondence between tetrahedra abpq with bounding radius $\textrm{R}_B$, in the full simplicial complex $K_{{\textbf{P}}}$, and edges $p,q \in \textrm{B}_B (\tau ) \cap ({\textbf{P}} {\setminus } \{a,b\} )$. These edges are in the link of $\tau$.

Understanding the structure of the set of simplices with same bounding radius and that belong to the regular triangulation requires additional geometric constructions, see Fig. 16. Extending the classical lifted paraboloid construction, we introduce, in Sects. 4.2 and 4.3, several definitions associated to a k-simplex $\tau$ in an n-dimensional regular triangulation. The bisector $\textbf{bis}_\tau$ together with the maps $\pi _\tau$, and $\varPhi _\tau$, are intermediary constructions allowing to define formally the shadow map ${{\textbf{S}}}{{\textbf{h}}}_\tau$,

$$\begin{aligned}{{\textbf{S}}}{{\textbf{h}}}_\tau :\{ \{v\} \in \text {Lk}_{K_{{\textbf{P}}}} \tau :\, {\varvec{\mu }}_B (\tau \cup \{v\}) = {\varvec{\mu }}_B (\tau ) \} \rightarrow {\mathbb {R}}^{n-k},\end{aligned}$$

and extend it as a simplicial map that send simplices in

$$\begin{aligned}\{ \sigma \in \text {Lk}_{K_{{\textbf{P}}}} \tau : {\varvec{\mu }}_B (\tau \cup \sigma ) = {\varvec{\mu }}_B (\tau )\}\end{aligned}$$

toward the full simplicial complex over the images of vertices by ${{\textbf{S}}}{{\textbf{h}}}_\tau$.

Noting $\tau$ for the k-simplex $\tau _{{\varvec{\mu }}_B ^{\ne }}$ defined in step (A), with ${\varvec{\mu }}_B (\tau ) = {\varvec{\mu }}_B ^{\ne }$, the map ${{\textbf{S}}}{{\textbf{h}}}_{\tau }$, allows to compare the traces of $\varGamma _{\textrm{reg}}$ and $\varGamma _{\textrm{min}}$ in the link of $\tau =\tau _{{\varvec{\mu }}_B ^{\ne }}$. Indeed, denoting $| \varGamma _{\textrm{reg}}| \subset K_{{\textbf{P}}}$ the simplicial complex containing the n-simplices of the regular triangulation of ${\textbf{P}}$, the simplicial map induced by ${{\textbf{S}}}{{\textbf{h}}}_\tau$ then defines a simplicial isomorphism (Lemma 7 in Sect. 4.3) between simplices in the link of $\tau$ in $| \varGamma _{\textrm{reg}}|$ whose union with $\tau$ does not increase the bounding weight of $\tau$:

$$\begin{aligned}\bigl \{ \sigma \in \text {Lk}_{| \varGamma _{\textrm{reg}}| } \tau : {\varvec{\mu }}_B (\tau \cup \sigma ) = {\varvec{\mu }}_B (\tau ) \bigr \},\end{aligned}$$

and the simplices in the visible convex hull, in ${\mathbb {R}}^{n-k}$, of the images of vertices by ${{\textbf{S}}}{{\textbf{h}}}_\tau$. This visible convex hull is a simplicial ball, and therefore

$$\begin{aligned}\bigl \{ \sigma \in \text {Lk}_{K_{| \varGamma _{\textrm{reg}}| }} \tau : {\varvec{\mu }}_B (\tau \cup \sigma ) = {\varvec{\mu }}_B ^{\ne } \bigr \}\end{aligned}$$

is a simplicial complex homeomorphic to an $(n-k-1)$-ball. This last fact may be of independent interest.

For example, in Fig. 9, there are six tetrahedra in the star of the edge $\tau$ in $| \varGamma _{\textrm{reg}}|$ but only two of them share the same bounding radius as $\tau$, and are therefore in $\{ \sigma \in | \varGamma _{\textrm{reg}}|:{\varvec{\mu }}_B (\sigma ) = {\varvec{\mu }}_B (\tau ) \}$ as seen in Fig. 9, top right, where only two tetrahedra, in blue, are included in the bounding sphere. In this case, the corresponding simplicial complex ${{\textbf{S}}}{{\textbf{h}}}_\tau \bigl ( \text {Lk}_{\{ \sigma \in |\varGamma _{\textrm{reg}}|:{\varvec{\mu }}_B (\sigma ) = {\varvec{\mu }}_B (\tau ) \} }\tau \bigr )$, topologically a 1-dimensional ball, is made of the two edges sharing a vertex, in blue, inside the plane $\textbf{bis}_\tau$ seen in Fig. 9, bottom.

By induction on the dimension of convex cones and convex polytopes, one shows that this bounded subcomplex of the boundary of a convex polytope visible from the origin can be expressed as the minimum under boundary constraint (Lemma 10 in Sect. 5) for another lexicographic order denoted $\sqsubseteq _{{\textbf{0}}}$.

The lexicographic order $\sqsubseteq _{{\textbf{0}}}$ on the images by ${{\textbf{S}}}{{\textbf{h}}}_\tau$ is shown (Lemmas 11 and 12 in Sect. 6) to be equivalent to the order induced by ${\sqsubseteq }_{lex }$ on the trace of chains in $\text {Lk}_{\{ \sigma \in K_{{\textbf{P}}}:{\varvec{\mu }}_B (\sigma ) = {\varvec{\mu }}_B (\tau ) \} } \tau$. This equivalence between orders allows then to conclude (proof of Theorem 1 in Sect. 6). Indeed, we have shown that the traces of $\varGamma _{\textrm{reg}}$ and $\varGamma _{\textrm{min}}$ in $\text {Lk}_{\{ \sigma \in K_{{\textbf{P}}}: {\varvec{\mu }}_B (\sigma ) = {\varvec{\mu }}_B (\tau ) \} } \tau$ minimizes the same order under the same boundary constraints. It follows that they coincide, establishing the contradiction with the assumption at the beginning of step (A).

1.4 A.4 Glossary

Bisector of a simplex. Given a k-simplex in ${\mathbb {R}}^n$, its bisector $\textbf{bis}_\tau$, defined by (22), is the $(n-k)$-dimensional affine space, set of points with same weighted distance to each vertex of $\tau$. In the case of zero weighs (that is in the case of Delaunay complex), it is the set of point equidistant from each vertex of $\tau$. When $\tau$ is a Delaunay (respectively regular triangulation) simplex, it is also the affine space supporting the Voronoi (respectively power diagram) cell dual to $\tau$. Figure 5 shows the line bisector $\textbf{bis}_\tau$ of an edge $\tau =ab$ in ${\mathbb {R}}^2$.

Bounding weight ${\varvec{\mu }}_B (\sigma )$ of a simplex $\sigma$. The bounding weight ${\varvec{\mu }}_B (\sigma )$ of a simplex $\sigma$ is a generalization, for weighted points, of the square of the radius of the smallest ball enclosing the simplex $\textrm{R}_B (\sigma )^2$. It is the dominant term in the definition of the order on simplices which induces the lexicographic order ${\sqsubseteq }_{lex }$ on chains. It is formally defined in Definition 7 and is related to the weights $w_p(\sigma )^p$ of simplex $\sigma$ in the norm $\Vert \cdot \Vert _{(p)}$ by Lemma 4:

$$\begin{aligned}{\varvec{\mu }}_B (\sigma ) = \lim _{p\rightarrow \infty } w_p(\sigma ).\end{aligned}$$

Full simplicial complex $K_{{\textbf{P}}}$ over a set of points. Given a set of points ${\textbf{P}} \subset {\mathbb {R}}^n$, the full simplicial complex $K_{{\textbf{P}}}$ is the simplicial complex made of all possible simplex of dimension less or equal to n with vertices in ${{\textbf{P}}}$. Unlike Delaunay or regular triangulation complexes, it is not embedded in general, as simplices convex hulls overlap as soon as $\sharp {\textbf{P}} > n+1$.

Lexicographic order induced by a total order. It is defined formally in Definition 3. A total order $\le$ on n-simplices induces a lexicographic order $\sqsubseteq$ on n-chains. Seeing the two n-chains $\varGamma _1 \ne \varGamma _2$ with coefficients in ${\mathbb {Z}}_2$ as sets of n-simplices, we write $\varGamma _1 \sqsubset \varGamma _2$ if the largest simplex which is in the symmetric difference $(\varGamma _1 \cup \varGamma _2) {\setminus } (\varGamma _1 \cap \varGamma _2)$, belongs to $\varGamma _2$.

Lexicographic order ${\sqsubseteq }_{lex }$. The lexicographic order ${\sqsubseteq }_{lex }$ of Theorem 1 is induced by the total order $\le$ on simplices. This total order $\le$ is given in Sect. 3.5 for the general case and Sect. 3.2 gives a more explicit expression for the particular cases of Delaunay triangulations in ${\mathbb {R}}^2$ and ${\mathbb {R}}^3$.

Lexicographic order $\sqsubseteq _{{\textbf{0}}}$. The lexicographic order $\sqsubseteq _{{\textbf{0}}}$ is induced by the total order $\le _{{\textbf{0}}}$ defined by (35) and (36) in Sect. 5. According to Lemma 10, visible convex hulls are minimum for order $\sqsubseteq _{{\textbf{0}}}$ under boundary constraint.

Norm $\Vert \,{\cdot }\,\Vert _{(p)}$. It is defined in Sect. 4.1 by (13) as

$$\begin{aligned}\left\Vert \varGamma \right\Vert _{(p)} \underset{\text {def.}}{=} \sum _{\sigma } | \varGamma ( \sigma )|w_p(\sigma )^p.\end{aligned}$$

It is a kind of $L^1$ norm on vector $\varGamma$ whose coefficient $w_p(\sigma )^p$, for simplex $\sigma$, is defined, by (12), as the $p^{\text {th}}$ power of the $L^p$ norm of function $f_\sigma :{{\mathcal {C}}}{{\mathcal {H}}}({ \sigma }) \rightarrow {\mathbb {R}}$ defined in (10).

Restriction ${\downarrow }_{\rho }\varGamma$ of a chain $\varGamma$. For a chain $\varGamma$, we denote by $\downarrow _{\rho } \varGamma$ the chain obtained by removing from $\varGamma$ all simplices with bounding weight strictly greater than $\rho$: ${\downarrow }_{\rho } \varGamma \underset{\text {def.}}{=} \{ \sigma \in \varGamma :{\varvec{\mu }}_B (\sigma ) \le \rho \}$.

Shadow map ${{\textbf{S}}}{{\textbf{h}}}_\tau$ (Definition8). Given a k-simplex $\tau \in K_{{\textbf{P}}}$, the shadow map ${{\textbf{S}}}{{\textbf{h}}}_{\tau }$ is a map that sends the vertices of the link of $\tau$ that belong to simplices with same bounding radius as $\tau$,

$$\begin{aligned}\bigl \{ \{ v\} \in \text {Lk}_{K_{{\textbf{P}}}} \tau : {\varvec{\mu }}_B (\tau \cup \{v\}) = {\varvec{\mu }}_B (\tau ) \bigr \},\end{aligned}$$

toward ${\mathbb {R}}^{n-k}$.

It is a conical projection applied to the images by $\varPhi _\tau$, as illustrated in Fig. 9, bottom. It follows a sequence of geometric constructions, notably the bisector $\textbf{bis}_\tau$, and the maps $\pi _\tau$ and $\varPhi _\tau$, detailed in Sects. 4.2 and 4.3.

The simplicial map induced by the shadow map ${{\textbf{S}}}{{\textbf{h}}}_\tau$ realizes a simplicial isomorphism between the full simplicial complex

$$\begin{aligned}\{\sigma \in \text {Lk}_{K_{{\textbf{P}}}} \tau :{\varvec{\mu }}_B (\tau \cup \sigma ) = {\varvec{\mu }}_B (\tau ) \}\end{aligned}$$

and the corresponding full complex over the vertices images. Moreover, its restriction to $\text {Lk}_{| \varGamma _{\textrm{reg}}|} \tau$, the support of the link of $\tau$ in the regular triangulation $| \varGamma _{\textrm{reg}}|$, is a simplicial isomorphism between

$$\begin{aligned}\bigl \{\sigma \in \text {Lk}_{| \varGamma _{\textrm{reg}}|} \tau :{\varvec{\mu }}_B (\tau \cup \sigma ) = {\varvec{\mu }}_B (\tau ) \bigr \}\end{aligned}$$

and the visible convex hull of the vertices images (Lemma 7 in Sect. 4.3). As a consequence, $\{\sigma \in \text {Lk}_{| \varGamma _{\textrm{reg}}|} \tau : {\varvec{\mu }}_B (\tau \cup \sigma ) = {\varvec{\mu }}_B (\tau ) \}$ is a simplicial $(n-k-1)$-ball (i.e., its geometric realization is a topological $(n-k-1)$-ball).

Simplex (Sect. 2.1 or [15, first chapter]). A k-simplex is a set of $k+1$ vertices. In particular, a vertex a is a 0-simplex, and edge $\{a,b\}$, sometimes denoted ab is a 1-simplex and a triangle $\{a,b,c\}$, sometimes denoted abc is a 2-simplex. For example, if $\tau _1=ab$ and $\tau _2 =cd$ are edges, then $\tau _1 \cup \tau _2$ is the 3-simplex, or tetrahedron, abcd. To each k-simplex is associated a realization as a topological space, namely the convex hull of $k+1$ affinely independent points. We denote by ${{\mathcal {C}}}{{\mathcal {H}}}({ \sigma })$ the convex hull of the vertices of $\sigma$.

Simplicial chain (Sect. 2.2 or [15, first chapter]). A k-simplicial chain $\varGamma$ over a simplicial complex K is a vector, over the field ${\mathbb {Z}}_2$, defined by associating a coefficient denoted $\varGamma (\sigma )\in \{0,1\}={\mathbb {Z}}_2$ to each k-simplex in K. It is sometimes convenient to see a k-chain also as the set of k-simplices $\varGamma =\{\sigma :\varGamma (\sigma )=1\}$. With this convention we allow ourselves to write for example $\varGamma _1+\varGamma _2=\varGamma _1-\varGamma _2=(\varGamma _1\cup \varGamma _2)\setminus (\varGamma _1\cap \varGamma _2)$.

Simplicial complexes (Sect. 2.1 or [15, first chapter]). A set K of simplices is called a simplicial complex if any $\sigma \in K$ has all its faces in K:

$$\begin{aligned}(\sigma \in K\ \text {and}\ \emptyset \ne \tau \subseteq \sigma ) \ \ \Longrightarrow \ \ \tau \in K.\end{aligned}$$

Given a simplicial complex K, we denote by $K^{[k]}$ the subset of K containing all k-simplices in K.

Support $|\varGamma |$ of a simplicial chain $\varGamma$. The support $|\varGamma |$ of a simplicial n-chain $\varGamma$ is the n-dimensional simplicial complex made of simplices in $\varGamma$ with all their faces.

Trace of a chain in the link of a simplex (Definition 12). Given a k-simplex $\tau \in K$ and an n-chain $\varGamma$ on K, the trace ${\text {Tr}}_{\tau }(\varGamma )$ of $\varGamma$ is an $(n-k-1)$-chain ${\text {Tr}}_{\tau }(\varGamma )$ defined in the link $\text {Lk}_{K}(\tau )$ of $\tau$. For any $(n-k-1)$-simplex $\sigma \in \text {Lk}_{K}(\tau )$, one has

$$\begin{aligned}{\text {Tr}}_{\tau }(\varGamma ) (\sigma ) \underset{\text {def.}}{=} \varGamma (\tau \cup \sigma ).\end{aligned}$$

This linear operator commutes with the boundary operator as stated by Lemma 8:

$$\begin{aligned}\partial {\text {Tr}}_{\tau }(\varGamma )={\text {Tr}}_{\tau } ( \partial \varGamma ).\end{aligned}$$

Visible convex hull. Definition 10 formally defines a polytope facet visible from the point 0. Given a finite set of points $P \in {\mathbb {R}}^m$ in general position (no $m+1$ points lie on the same affine $(m-1)$-space), whose convex hull ${{\mathcal {C}}}{{\mathcal {H}}}({ P})$ does not contain the point $0\in {\mathbb {R}}^m$. The visible convex hull is the $(m-1)$-simplicial complex embedded in ${\mathbb {R}}^m$ corresponding to the subset of the boundary $\partial \,{{\mathcal {C}}}{{\mathcal {H}}}({ P})$ of ${{\mathcal {C}}}{{\mathcal {H}}}({ P})$ “visible” from the point 0. In other word, its image by the embedding in ${\mathbb {R}}^m$ is the set of points $x \in \partial \, {{\mathcal {C}}}{{\mathcal {H}}}({ P})$ such that the segment [0, x) does not intersect ${{\mathcal {C}}}{{\mathcal {H}}}({ P})$. It is a simplicial ball, i.e., a simplicial complex homeomorphic to a closed $(d-1)$-ball.

Weighted distance. The weighted distance between two weighted points, given in Definition 1, generalizes the squared Euclidean distance between ordinary points:

$$\begin{aligned}\text {D}( (P_1,\mu _1), (P_2,\mu _2)) \underset{\text {def.}}{=} (P_1-P_2)^2 - \mu _1 - \mu _2.\end{aligned}$$

B Invariance by Global Weight Translation

Observation 8

Let $\psi _\lambda :{\mathbb {R}}^n\times {\mathbb {R}}\rightarrow {\mathbb {R}}^n\times {\mathbb {R}}$ be the transformation that shifts the weight by $\lambda$:

$$\begin{aligned}\psi _\lambda (P, \mu ) = (P, \mu + \lambda ).\end{aligned}$$

Let $\sigma \in K_{{\textbf{P}}}$ be a simplex, from Definitions 7 and 1 we have

$$\begin{aligned} {{{ {\textbf {P}}}}}_C ( \psi _\lambda (\sigma ))&= {{{ {\textbf {P}}}}}_C (\sigma )\,\, \text {and}\,\, {\varvec{\mu }}_C ( \psi _\lambda (\sigma )) = {\varvec{\mu }}_C (\sigma ) - \lambda ,\\ {{{ {\textbf {P}}}}}_B ( \psi _\lambda (\sigma ))&= {{{ {\textbf {P}}}}}_B ( \sigma ) \,\, \text {and}\,\, {\varvec{\mu }}_B ( \psi _\lambda (\sigma )) = {\varvec{\mu }}_B (\sigma )-\lambda . \end{aligned}$$

It follows that a global shift by a constant value $\lambda$ results in an opposite shift on the weights of generalized circumcenters. It therefore preserves the relative order between simplices weights ${\varvec{\mu }}_C$ and ${\varvec{\mu }}_B$:

$$\begin{aligned}{\varvec{\mu }}_C (\sigma _1) \le {\varvec{\mu }}_C (\sigma _2)\quad \iff \quad {\varvec{\mu }}_C (\psi _\lambda (\sigma _1)) \le {\varvec{\mu }}_C (\psi _\lambda (\sigma _2)),\end{aligned}$$

and the same relation holds for ${\varvec{\mu }}_B$. Since the order $\le$ between simplices (9) defined in Sect. 3.5 relies entirely on comparisons on ${\varvec{\mu }}_C$ and ${\varvec{\mu }}_B$, this total order is preserved by a global weight translation.

C Proof of Lemma 1

Figure 3 illustrates the possibilities for $\varTheta (\sigma )$ in the case $n=3$ and zero weights.

Recall relation (6) in Definition 7. Denote by $\tau \subset \sigma$ the set of vertices $(P_i, \mu _i) \in \sigma$ for which

$$\begin{aligned}\text {D}(({{{\textbf{P}}}}_B (\sigma ), {\varvec{\mu }}_B (\sigma ) ), (P_i, \mu _i)) =0.\end{aligned}$$

This set cannot be empty as, if all inequalities in (6) where strict, a strictly smaller value of $\mu$ would still match the inequality, which would contradict with the ${{\,\mathrm{arg\,min}\,}}$ in (6). One has then $\tau \ne \emptyset$ and

$$\begin{aligned} \forall \, (P_i, \mu _i) \in \tau ,\quad \text {D}( ({{{\textbf{P}}}}_B (\sigma ), {\varvec{\mu }}_B (\sigma ) ), (P_i, \mu _i) ) =0, \end{aligned}$$

(50)

and therefore $({{{\textbf{P}}}}_B (\sigma ), {\varvec{\mu }}_B (\sigma ) )$ also meet the condition required for $({{{\textbf{P}}}}_B (\tau ), {\varvec{\mu }}_B (\tau ) )$ in (6) of Definition 7:

$$\begin{aligned} \forall \,(P_i, \mu _i) \in \tau ,\quad \text {D}(({{{\textbf{P}}}}_B (\sigma ), {\varvec{\mu }}_B (\sigma ) ), (P_i, \mu _i)) \le 0. \end{aligned}$$

(51)

No point $(P, \mu )$ with $\mu <{\varvec{\mu }}_B (\sigma )$ can satisfy (50) or (51) as it would again similarly contradict the ${{\,\mathrm{arg\,min}\,}}$ in (6). It follows that

$$\begin{aligned}({{{\textbf{P}}}}_B , {\varvec{\mu }}_B )(\sigma ) = ({{{\textbf{P}}}}_B , {\varvec{\mu }}_B )(\tau ) = ({{{\textbf{P}}}}_C , {\varvec{\mu }}_C )(\tau ).\end{aligned}$$

D Proof of Lemma 3

The idea of the proof is to shoot a ray from a point $x\in {{\mathcal {C}}}{{\mathcal {H}}}({ {\textbf{P}}})$, that does not belong to the convex hull of any $(n-1)$-simplex, to the outside of the convex hull ${{\mathcal {C}}}{{\mathcal {H}}}({ {\textbf{P}}})$ and keep track of the number of covering n-simplices along the ray as it crosses $(n-1)$-simplices, where, by covering simplices of a point y we mean the n-simplices $\sigma \in \varGamma$ such that $y \in {{\mathcal {C}}}{{\mathcal {H}}}({ \sigma })$. We claim that since

$$\begin{aligned} x\in {{\mathcal {C}}}{{\mathcal {H}}}({ {\textbf{P}}})\, \setminus \!\! \bigcup _{\sigma \in K_{{\textbf{P}}}^{[n-1]}}\!\! {{\mathcal {C}}}{{\mathcal {H}}}({ \sigma }) \end{aligned}$$

there is $x_\star \in {\mathbb {R}}^n \setminus {{\mathcal {C}}}{{\mathcal {H}}}({ {\textbf{P}}})$ such that

$$\begin{aligned}{}[ x_\star \, x ] \,\cap \! \bigcup _{\sigma \in K_{{\textbf{P}}}^{[n-2]}}\!\! {{\mathcal {C}}}{{\mathcal {H}}}({ \sigma })=\emptyset , \end{aligned}$$

(52)

where $[ x_\star \, x]$ denotes the line segment in ${\mathbb {R}}^n$ between $x_\star$ and x. Indeed, we consider moving a point $x_t$ from $x_0$ to some $x_1$, picking $x_0, x_1$ far away enough to have $[ x_0 \, x_1] \cap {{\mathcal {C}}}{{\mathcal {H}}}({ {\textbf{P}}}) =\emptyset$ and in such a way that $[ x_0 \, x_1]$ belongs to none of the affine hyperplanes spanned by x and $(n-2)$-simplices in $K_{{\textbf{P}}}$, which occurs generically. Then, the negation of condition (52) with $x_\star =x_t$, occurs only as isolated values of t. We can pick a value $t^\star$ for which this does not occur: set $x_\star = x_{t^\star }$ and the claim is proved.

Next, we move a point $y(t) = (1-t)x_\star +t x$ along segment $[ x_\star \,x]$. This segment intersect transversally the $(n-1)$-faces ${{\mathcal {C}}}{{\mathcal {H}}}({ \tau })$, for $\tau \in K_{{\textbf{P}}}$. At each intersection point we can keep track of the change in the number of covering n-simplices of y(t). We know that this number is zero at $x_\star$ since $x_\star \notin {{\mathcal {C}}}{{\mathcal {H}}}({ {\textbf{P}}})$. Since ${{\mathcal {C}}}{{\mathcal {H}}}({ {\textbf{P}}})\cap [ x_\star \, x]$ is convex there is a single intersection point $y(t_b)$ between $[ x_\star \, x ]$ and the boundary of ${{\mathcal {C}}}{{\mathcal {H}}}({ {\textbf{P}}})$.

This point $y(t_b) \in (x_\star , x)$ hits the convex hull ${{\mathcal {C}}}{{\mathcal {H}}}({ \tau _b})$ of an $(n-1)$-simplex $\tau _b \in \beta _{{\textbf{P}}}$, face of the convex hull boundary. Since $\partial \varGamma =\beta _{{\textbf{P}}}$, we know that $\tau _b$ is shared by an odd number $n_b$ of n-simplices in $\varGamma$. By definition of the convex hull, and since ${\textbf{P}}$ is in general position, for each n-simplex $\sigma$ coface of $\tau _b$, ${{\mathcal {C}}}{{\mathcal {H}}}({ \sigma })$ is on the inner side of the convex hull supporting halfspace. It follows that, starting from the outer point $x_\star$, the number of covering simplices becomes the odd number $n_b$ just after the first crossing point $y(t_b)$.

Then, when crossing the convex hull ${{\mathcal {C}}}{{\mathcal {H}}}({ \tau _i})$ of any other $(n-1)$-simplex $\tau _i \notin \beta _{{\textbf{P}}}$, at some point $y(t_i)$, it follows from the condition $\partial \varGamma =\beta _{{\textbf{P}}}$ that the number $n_i$ of n-simplices in $\varGamma$ coface of $\tau _i$ has to be even. When crossing ${{\mathcal {C}}}{{\mathcal {H}}}({ \tau _i})$, along $[x_\star \,x]$, point $y(t_i)$ exits $k^-$, and enters $k^+$ n-simplices in $\varGamma$, with $k^- + k^+ = n_i$. The current number of covering n-simplices value is incremented by $k^+ - k^-$. Since $n_i$ is even and

$$\begin{aligned}k^+ - k^- = k^+ + k^- - 2 k^- = n_i - 2 k^-.\end{aligned}$$

$k^+ - k^-$ is therefore even and the number of covering simplices remains odd along the path and, in particular, is odd at point x.

E Proof of Lemma 4

Since the expression (10) does not depend on the origin O, let us choose this origin to be $O= {{{{\textbf {P}}}}}_B (\sigma )$. With barycentric coordinates based on the vertices $P_i$, $i=0,k$, of $\sigma$, i.e., $\lambda _i\ge 0$, $\sum _i \lambda _i = 1$, such that $x = \sum _i \lambda _i P_i$, the expression of $f_\sigma$ is

$$\begin{aligned}f_\sigma (x) = \left( \sum _i \lambda _i( (P_i -{{{{\textbf {P}}}}}_B (\sigma ) )^2-\mu _i)\right) - (x-{{{{\textbf {P}}}}}_B (\sigma ) ) ^2.\end{aligned}$$

One has $(P_i -{{{{\textbf {P}}}}}_B (\sigma ) )^2 -\mu _i - {\varvec{\mu }}_B (\sigma ) = \text {D}( ({{{{\textbf {P}}}}}_B (\sigma ), {\varvec{\mu }}_B (\sigma )), (P_i, \mu _i)) \le 0$ so that $(P_i -{{{{\textbf {P}}}}}_B (\sigma ) )^2- \mu _i \le {\varvec{\mu }}_B (\sigma )$ and it follows that

$$\begin{aligned} \forall \,x,\quad f_\sigma (x) \le {\varvec{\mu }}_B (\sigma ) - (x-{{{{\textbf {P}}}}}_B (\sigma ) ) ^2. \end{aligned}$$

(53)

We have from Lemma 2 that ${{{{\textbf {P}}}}}_B (\sigma ) \in | \varTheta (\sigma ) | \subset {{\mathcal {C}}}{{\mathcal {H}}}({ \sigma })$ so that, in the expression of ${{{{\textbf {P}}}}}_B (\sigma )$ as a barycenter of vertices of $\sigma$, only coefficients $\lambda _i$ corresponding to vertices of $\varTheta (\sigma ) \subset \sigma$ are non-zero:

$$\begin{aligned}{{{{\textbf {P}}}}}_B (\sigma )\, =\!\sum _{(P_i, \mu _i) \in \varTheta (\sigma )} \!\! \lambda _i P_i.\end{aligned}$$

One has, by the definition of (P$_C ,{\varvec{\mu }}_C )$, that

$$\begin{aligned}(P_i, \mu _i) \in \varTheta (\sigma )\quad \Longrightarrow \quad ( P_i - {{{{\textbf {P}}}}}_C (\varTheta (\sigma )) )^2 - \mu _i ={\varvec{\mu }}_C (\varTheta (\sigma ))\end{aligned}$$

and, since we know from Lemma 1 that

$$\begin{aligned}({{{{\textbf {P}}}}}_B , {\varvec{\mu }}_B )(\sigma ) = ({{{{\textbf {P}}}}}_B , {\varvec{\mu }}_B )(\varTheta (\sigma )) = ({{{{\textbf {P}}}}}_C , {\varvec{\mu }}_C )(\varTheta (\sigma )),\end{aligned}$$

one gets

$$\begin{aligned}(P_i, \mu _i) \in \varTheta (\sigma )\quad \Longrightarrow \quad (P_i - {{{{\textbf {P}}}}}_B (\sigma ) )^2 - \mu _i ={\varvec{\mu }}_B (\sigma )\end{aligned}$$

and

$$\begin{aligned}f_\sigma ({{{{\textbf {P}}}}}_B (\sigma ) ) = \left( \,\sum _{(P_i, \mu _i) \in \varTheta (\sigma )}\!\!\!\lambda _i ( (P_i - {{{{\textbf {P}}}}}_B (\sigma ) )^2 - \mu _i) \right) - 0^2 = {\varvec{\mu }}_B (\sigma ).\end{aligned}$$

This with (53) ends the proof.

F Proof of Lemma 9

Assume for a contradiction that x is in the relative interior of X, that is there is some $\rho >0$ such that ${\mathcal {B}} (2x)(x,\rho )\cap X={\mathcal {B}} (2x)(x,\rho )\cap \partial C$. Then all facets containing x are visible from O. If x is not a vertex of C, it belongs then to the relative interior of a convex face f in $\partial C$ with $\dim f \ge 1$. Then we have a contradiction since the function $y\mapsto d(O,y)$ is convex on f and cannot have an interior local maximum at x. We assume now that x is a vertex of C.

Following for example [14, 17], denote by ${\text {Tan}}_x C$ and ${\text {Nor}}_x C$ respectively the tangent and normal cone to C at x. In case of a closed polytope they can be expressed as

$$\begin{aligned}{\text {Tan}}_x C = \bigcap _{\rho >0}\,\{ \lambda (c-x):\lambda \ge 0,\, c \in {\mathcal {B}}(x, \rho )\},\end{aligned}$$

where ${\mathcal {B}}(x, \rho )$ denotes the ball centered at x with radius $\rho$, and

$$\begin{aligned} {\text {Nor}}_x C =( {\text {Tan}}_x C)^{\perp } \underset{\text {def.}}{=} \{ u:\forall \, v \in {\text {Tan}}_x C, \,\langle u, v \rangle \le 0\}. \end{aligned}$$

(54)

Since C is a convex polytope, ${\text {Tan}}_x C$ is a convex closed cone and one has [17]

$$\begin{aligned} {\text {Tan}}_x C = ( {\text {Nor}}_x C )^{\perp } \underset{\text {def.}}{=} \{ v:\forall \, u \in {\text {Nor}}_x C,\,\langle u, v \rangle \le 0\}. \end{aligned}$$

(55)

Each facet $F_i$ of C containing x is supported by a half-space $H_i = \{ y:\langle y-x,n_i \rangle \le 0 \}$ with outer normal $n_i$, and one has

$$\begin{aligned} {\text {Nor}}_x C = \left\{ \sum _i \lambda _i n_i: \forall i,\;\lambda _i \ge 0 \right\} \end{aligned}$$

(56)

and, since O belongs to none of the half-spaces $H_i$,

$$\begin{aligned}\forall i,\ \ \langle O-x, n_i \rangle > 0.\end{aligned}$$

This with (56) gives

$$\begin{aligned}\forall \, u \in {\text {Nor}}_x C,\ \ \langle O-x, u \rangle > 0.\end{aligned}$$

Using (55) we get that $O-x$ is in the interior of $-{\text {Tan}}_x C$, i.e.,

$$\begin{aligned} x-O \in ( {\text {Tan}}_x C)^\circ . \end{aligned}$$

(57)

Since x is a vertex of C, ${\text {Tan}}_x C$ is the convex hull of ${\text {Tan}}_x \partial C$, therefore (57) implies at there are $t_1,\dots ,t_{n+1}\in {\text {Tan}}_x\partial C$ and $\lambda _1,\ldots ,\lambda _{n+1} \ge 0$ such that

$$\begin{aligned}x-O = \sum _i \lambda _i t_i\end{aligned}$$

which gives, since $O \notin C$,

$$\begin{aligned}0 < \langle x-O, x- O\rangle = \left\langle x-O, \sum _i \lambda _i t_i \right\rangle = \sum _i \lambda _i \langle x-O, t_i \rangle .\end{aligned}$$

Since all the $\lambda _i$ are not negative, there must be at least one i for which

$$\begin{aligned}\langle x-O, t_i \rangle > 0. \end{aligned}$$

This precisely means that $y \mapsto d(O, y)$ is increasing in the direction $t_i$ in a neighborhood of x in $\partial C$, and, with the assumption that x is in the relative interior of X, we have that $y \mapsto d(O,y)$ is increasing in the direction $t_i$ in a neighborhood of x in X. This gives a contradiction since x is assumed to be a local maximum of $y \mapsto d(O, y)$ in X.

G Proof of Lemma 11

Using Definition 7 one has

$$\begin{aligned} ({{{{\textbf {P}}}}}_C , {\varvec{\mu }}_C )(\pi _\tau (\tau ) \cup \pi _\tau (\sigma ))\, =\!\!\!\!\!\!\mathop {\mathrm {arg\,min}}\limits _{\begin{array}{c} {(P, \mu ) \in {\mathbb {R}}^n \times {\mathbb {R}}:}\\ {\forall (P_i, \mu _i) \in \pi _\tau (\tau ) \cup \pi _\tau (\sigma ),}\\ {\text {D}( (P, \mu ), (P_i, \mu _i))=0} \end{array}}\!\!\!\mu . \end{aligned}$$

(58)

Looking at Definition 7 in light of (28), in the proof of Lemma 6, we get that

$$\begin{aligned} \sigma \supset \tau \quad \Longrightarrow \quad {\varvec{\mu }}_C (\sigma ) = {\varvec{\mu }}_C (\pi _\tau (\sigma )) \ \text {and}\ {{{{\textbf {P}}}}}_C (\sigma ) = {{{{\textbf {P}}}}}_C (\pi _\tau (\sigma )). \end{aligned}$$

(59)

Since both terms of (45) are invariant by a global translation, we can assume without loss of generality and in order to make the computations simpler that $o_\tau =0$. In this case, as seen in (24), the coordinates of $\pi _\tau (\tau )$ are $(0, -{\varvec{\mu }}_C (\pi _\tau (\tau ))=(0,-{\varvec{\mu }}_C ( \tau ))$ by (59). So that $\text {D}((P, \mu ), \pi _\tau (\tau )) =0$ gives us

$$\begin{aligned} \mu = P^2 + {\varvec{\mu }}_C ( \tau ). \end{aligned}$$

(60)

It follows that among the weighted points $(P, \mu )$ that satisfy $\text {D}((P,\mu ),\pi _\tau (\tau ))=0$, minimizing $\mu$ is equivalent to minimizing $P^2$.

One can reformulate the characterization (58) of $({{{{\textbf {P}}}}}_C ,{\varvec{\mu }}_C )(\pi _\tau (\tau \cup \sigma )) =({{{{\textbf {P}}}}}_C , {\varvec{\mu }}_C )(\pi _\tau (\tau ) \cup \pi _\tau (\sigma ))$ as

$$\begin{aligned} ({{{{\textbf {P}}}}}_C , {\varvec{\mu }}_C )(\pi _\tau (\tau ) \cup \pi _\tau (\sigma )\,=\!\mathop {\mathrm {arg\,min}}\limits _{\begin{array}{c} {(P, \mu ) \in {\mathbb {R}}^n \times {\mathbb {R}}}:\\ \forall (P_i, \mu _i) \in \pi _\tau (\tau ) \cup \pi _\tau (\sigma ),\\ \text {D}( (P, \mu ), (P_i, \mu _i)) = 0 \end{array}}\!\!\!P^2. \end{aligned}$$

(61)

For $(P, \mu ) \in {\mathbb {R}}^{n-k} \times {\mathbb {R}}$, define the hyperplane $\varPi _{(P, \mu )}$ in ${\mathbb {R}}^{n-k} \times {\mathbb {R}}$ as

$$\begin{aligned} (X,z) \in \varPi _{(P, \mu )}\ \ \underset{\text {def.}}{\iff }\ \ z = \mu - P^2 + 2\langle P, X \rangle . \end{aligned}$$

(62)

Observe that

$$\begin{aligned}\text {D}( (P, \mu ), (P_i, \mu _i)) = 0\quad \iff \quad \text {lift}(P_i, \mu _i) \in \varPi _{(P, \mu )}.\end{aligned}$$

So that the definition of $({{{{\textbf {P}}}}}_C , {\varvec{\mu }}_C )(\pi _\tau (\tau ) \cup \pi _\tau (\sigma ))$ given in (61) can be equivalently formulated as $\varPi _{ ({{{{\textbf {P}}}}}_C , {\varvec{\mu }}_C )}$ being the hyperplane in ${\mathbb {R}}^{n-k} \times {\mathbb {R}}$ that minimizes ${{{{\textbf {P}}}}}_C ^2$ among all hyperplanes containing both $\text {lift}(\pi _\tau (\tau ))$ and all the points in $\text {lift}(\pi _\tau (\sigma ))$.

But, as seen in (62), $2\Vert {{{{\textbf {P}}}}}_C \Vert$ is the slope of the hyperplane $\varPi _{({{{{\textbf {P}}}}}_C , {\varvec{\mu }}_C )}$ so that $\varPi _{(P, \mu )}$ is the hyperplane with minimal slope going through $\varPhi _\tau (\tau ) = \text {lift}(\pi _\tau (\tau ))$ and all the points in $\varPhi _\tau (\sigma ) = \text {lift}(\pi _\tau (\sigma ))$. This slope $2\Vert {{{{\textbf {P}}}}}_C \Vert$ is also the slope of the unique $(\dim (\sigma )+1)$-dimensional affine space F going through $\varPhi _\tau (\tau ) = \text {lift}(\pi _\tau (\tau ))= (0, {\varvec{\mu }}_C (\tau ))$ and all the points in $\varPhi _\tau (\sigma ) = \text {lift}(\pi _\tau (\sigma ))$. Since $F \cap {\mathbb {R}}^{n-k} \times \{0\}$ is the affine space supporting ${{\textbf{S}}}{{\textbf{h}}}_{\tau }(\sigma )$, one has

$$\begin{aligned}d_{{\textbf{0}}}({{\textbf{S}}}{{\textbf{h}}}_{\tau }(\sigma )) = \frac{{\varvec{\mu }}_C (\tau )}{ 2 \Vert {{{{\textbf {P}}}}}_C \left( \pi _\tau (\tau ) \cup \pi _\tau (\sigma ) \right) \Vert }\end{aligned}$$

so that, using (59) for the second equality,

$$\begin{aligned}d_{{\textbf{0}}}({{\textbf{S}}}{{\textbf{h}}}_{\tau }(\sigma )) = \dfrac{{\varvec{\mu }}_C (\tau )}{ 2 \sqrt{ {\varvec{\mu }}_C (\pi _\tau (\tau ) \cup \pi _\tau (\sigma )) - {\varvec{\mu }}_C (\tau ) }}=\dfrac{{\varvec{\mu }}_C (\tau )}{ 2 \sqrt{ {\varvec{\mu }}_C (\tau \cup \sigma ) - {\varvec{\mu }}_C (\tau )) }}.\end{aligned}$$

It follows that the map

$$\begin{aligned}{\varvec{\mu }}_C ( \tau \cup \sigma ) \mapsto d_{{\textbf{0}}}({{\textbf{S}}}{{\textbf{h}}}_{\tau }(\sigma ))\end{aligned}$$

is decreasing.

H Proof of Lemma 12

In this proof, we denote by ${\underset{\rho }{\rightarrow }}\varGamma$ the set of simplices in $\varGamma$ with bounding weight equal to $\rho$:

$$\begin{aligned}{\underset{\rho }{\rightarrow }}\varGamma \underset{\text {def.}}{=}\{ \sigma \in \varGamma : {\varvec{\mu }}_B (\sigma ) = \rho \}.\end{aligned}$$

We claim that

$$\begin{aligned} ( {\downarrow }_{\rho } \varGamma _1 \;{\sqsubseteq }_{lex }\;{\downarrow }_{\rho }\varGamma _2)\ \ \ \Longrightarrow \ \ \ \left( {\underset{\rho }{\rightarrow } }\varGamma _1 \;{\sqsubseteq }_{lex }\;{\underset{\rho }{\rightarrow }} \varGamma _2 \right) . \end{aligned}$$

(63)

Indeed, by definition of the lexicographic order, if this did not hold, it would imply ${\underset{\rho }{\rightarrow }}\varGamma _1\ne \underset{\rho }{\rightarrow }\varGamma _2$ and the largest simplex for which ${\underset{\rho }{\rightarrow }}\varGamma _1$ and ${\underset{\rho }{\rightarrow }}\varGamma _2$ differ would be in $\varGamma _1$ contradicting ${\downarrow }_{\rho }\varGamma _1\;{\sqsubseteq }_{lex }\;{\downarrow }_{\rho } \varGamma _2$ which proves the claim (63).

Note that, from Lemma 1 and Generic Condition 1, all the simplices in $\underset{\rho }{\rightarrow } \varGamma _1$ and ${\underset{\rho }{\rightarrow }} \varGamma _2$ are in the star of a single simplex $\tau = \tau _{\rho }$ such that ${\varvec{\mu }}_C (\tau ) = {\varvec{\mu }}_B (\tau ) = \rho$.

It remains to show that the order ${\sqsubseteq }_{lex }$ restricted to simplices $\tau \cup \sigma$ with ${\varvec{\mu }}_B (\tau \cup \sigma ) = \rho$ corresponds to the order $\sqsubseteq _{{\textbf{0}}}$ on the shadow of $\sigma$. By definition of ${\sqsubseteq }_{lex }$, since in (9) one has always $\mu _{0}(\tau \cup \sigma _1)= \mu _{0}(\tau \cup \sigma _2)= \rho$, it goes like this:

$$\begin{aligned} \sigma _1< \sigma _2\ \ \underset{\text {def.}}{\iff }\ \ {\left\{ \begin{array}{ll}\exists \,k\ge 1,\,\mu _{k}(\tau \cup \sigma _1) > \mu _{k}(\tau \cup \sigma _2)\quad \text {and}\\ \forall j,\, 0\le j < k,\ \ \mu _{j}(\tau \cup \sigma _1) = \mu _{j}(\tau \cup \sigma _2). \end{array}\right. } \end{aligned}$$

(64)

Observe that this expression is similar to (35).

For a 0-simplex $\{v\} \in K_{{\textbf{P}}}$, the circumweight ${\varvec{\mu }}_C (\tau \cup \{v\})$ is, according to Lemma 11, a decreasing function of the distance $d_{{\textbf{0}}}({{\textbf{S}}}{{\textbf{h}}}_{\tau }(\eta ))$ between its shadow and the origin. It follows that for an $(n-k-1)$-simplex $\sigma \in K_{{\textbf{P}}}$, the vertex v for which the circumweight ${\varvec{\mu }}_C (\tau \cup \{v\})$ is minimal has its shadow ${{\textbf{S}}}{{\textbf{h}}}_{\tau }(v)$ maximizing the distance to the origin. This minimal circumweight is $\mu _{1}(\tau \cup \{v\})$ while this maximal distance is $\delta _0(\sigma )$.

More generally, looking at (34) and (8), Lemma 11 allows to check that the simplex $\varTheta _k(\sigma )$ of (8) in the star of $\tau$ in $K_{{\textbf{P}}}$ corresponds to the simplex $\tau _{k-1}(\sigma )$ in (34) in the link of $\tau$:

$$\begin{aligned}\varTheta _k(\sigma )= \tau \cup \tau _{k-1}(\sigma ).\end{aligned}$$

So that for $\sigma _1, \sigma _2 \in K_{{\textbf{P}}}$ referring to (35) and (64):

$$\begin{aligned}\mu _{k}(\tau \cup \sigma _1) \le \mu _{k}(\tau \cup \sigma _2)\ \ \iff \ \ \delta _{k-1}(\sigma _1) \ge \delta _{k-1}(\sigma _2).\end{aligned}$$

It follows that, for $\varGamma _1,\varGamma _2 \in {\varvec{C}}_{n}(K_{{\textbf{P}}})$ and $\tau = \tau _{\rho }$:

$$\begin{aligned}{\underset{\rho }{\rightarrow }} \varGamma _1\;{\sqsubseteq }_{lex }\;\underset{\rho }{\rightarrow } \varGamma _2 \ \ \iff \ \ {{\textbf{S}}}{{\textbf{h}}}_{\tau }( {\text {Tr}}_{\tau _{\rho }}( {\downarrow }_{\rho } \varGamma _1))\sqsubseteq _{{\textbf{0}}}{{\textbf{S}}}{{\textbf{h}}}_{\tau _{\rho }}({\text {Tr}}_{\tau _{\rho }}(\downarrow _{\rho } \varGamma _2)),\end{aligned}$$

which, with claim (63), ends the proof.

I Generic Conditions

The generic condition required by the main theorem is Generic Condition 1 of Sect. 3.4. Because it applies to weighted points, it relies on the notion of circumweight of a simplex. In case of zero weight, it boils down to requiring that simplices are not degenerate, which means that the vertices are affinely independent, and that two distinct simplices have distinct circumradii.

Each forbidden event, either for a simplex to be degenerate, or for a given pair of distinct simplices to have same circumradius corresponds to the zero of a non-zero polynomial on ${\mathbb {R}}^N$, which has therefore measures 0, and whose complement is open and dense. It follows that Generic Condition 1, conjunction of finitely many generic conditions, is generic. Condition 2, in Sect. 5, corresponds to Generic Condition 1 after some geometric transformation and is generic for the same reason.

Looking in detail to Generic Condition 1, we see that it is stronger than the usual generic condition required for Delaunay or regular triangulations. For example, for a Delaunay triangulation in ${\mathbb {R}}^2$ to be a triangulation of the convex hull of the points, it is usually required that triples are non-degenerate (no triple of points on the same line) and that no set of four points lie on a same circle. This last condition corresponds to our condition that two distinct triangles cannot have the same circumradius, in the particular case of two triangles sharing two vertices.

In particular, our stronger condition, for two triangles that may not share any vertex to have same circumradius, is not really necessary for Theorem 1 to hold, at the price of a kind of theoretical symbolic perturbation for the definition of the simplices total order. Since, in practice, non-generic inputs can be managed by symbolic perturbation, relaxing our generic condition would obscure our result without much advantages.