Maximum Plane Trees in Multipartite Geometric Graphs

Abstract

A geometric graph is a graph whose vertices are points in the plane and whose edges are straight-line segments between the points. A plane spanning tree in a geometric graph is a spanning tree that is non-crossing. Let R and B be two disjoint sets of points in the plane such that $R\cup B$ is in general position, and let $n=|R\cup B|$. Assume that the points of R are colored red and the points of B are colored blue. A bichromatic plane spanning tree is a plane spanning tree in the complete bipartite geometric graph with bipartition (R, B). In this paper we consider the maximum bichromatic plane spanning tree problem, which is the problem of computing a bichromatic plane spanning tree of maximum total edge length.

• 1. For the maximum bichromatic plane spanning tree problem, we present an approximation algorithm with ratio 1 / 4 that runs in $O(n\log n)$ time.

• 2. We also consider the multicolored version of this problem where the input points are colored with $k>2$ colors. We present an approximation algorithm that computes a plane spanning tree in a complete k-partite geometric graph, and whose ratio is 1 / 6 if $k=3$, and 1 / 8 if $k\geqslant 4$.

• 3. We also revisit the special case of the problem where $k=n$, i.e., the problem of computing a maximum plane spanning tree in a complete geometric graph. For this problem, we present an approximation algorithm with ratio 0.503; this is an extension of the algorithm presented by Dumitrescu and Tóth (Discrete Comput Geom 44(4):727–752, 2010) whose ratio is 0.502.

• 4. For points that are in convex position, the maximum bichromatic plane spanning tree problem can be solved in $O(n^3)$ time. We present an $O(n^5)$-time algorithm that solves this problem for the case where the red points lie on a line and the blue points lie on one side of the line.

1 Introduction

Let P be a set of n points in the plane in general position, i.e., no three points are collinear. Let K(P) be the complete geometric graph with vertex set P. It is well known that the standard minimum spanning tree (MinST) problem in K(P) can be solved in $\varTheta (n\log n)$ time. Also, any minimum spanning tree in K(P) is plane, i.e., its edges do not cross each other. The maximum spanning tree (MaxST) problem is the problem of computing a spanning tree in K(P) whose total edge length is maximum. Monma et al. [5] showed that this problem can be solved in $\varTheta (n\log n)$ time. However, a MaxST is not necessarily plane. The maximum plane spanning tree (MaxPST) problem is to compute a plane spanning tree in K(P) whose total edge length is maximum. It is not known whether or not this problem is NP-hard. This problem is introduced by Alon et al. [1] where they presented an approximation algorithm with ratio 0.5. The approximation ratio was improved to 0.502 by Dumitrescu and Tóth [4].

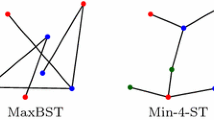
Let R and B be two disjoint sets of points in the plane such that $R\cup B$ is in general position, and let $n=|R\cup B|$. Suppose that the points of R are colored red and the points of B are colored blue. Let K(R, B) be the complete bipartite geometric graph with bipartition (R, B). The minimum bichromatic spanning tree (MinBST) problem is to compute a minimum spanning tree in K(R, B). The maximum bichromatic spanning tree (MaxBST) problem is to compute a spanning tree in K(R, B) whose total edge length is maximum. Recently, Biniaz et al. [2] showed that both the MinBST and the MaxBST problems can be solved in $\varTheta (n\log n)$ time. We note that none of MinBST and MaxBST is necessarily plane; they might have crossing edges as depicted in Fig. 1. Borgelt et al. [3] studied the problem of computing a minimum bichromatic plane spanning tree, which we refer to as the MinBPST problem. They showed that this problem is NP-hard, and also presented a polynomial-time approximation algorithm with approximation ratio of $O(\sqrt{n})$. In this paper we study the problem of computing a maximum bichromatic plane spanning tree, which we refer to as the MaxBPST problem. See Fig. 1.

Fig. 1

Minimum bichromatic spanning tree and maximum spanning trees

A natural extension of the MinBST and the MaxBST problems is to have more than two colors. In this multicolored version, the input points are colored by $k>2$ colors, and we are looking for a minimum (resp. maximum) spanning tree in which the two endpoints of every edge have distinct colors. In other words, we look for a minimum (resp. maximum) spanning tree in a complete k-partite geometric graph. We refer to these problems as the Min-k-ST and the Max-k-ST problems, respectively. Biniaz et al. [2] showed that both these problems can be solved in $O(n\log n \log k)$ time. Notice that the MinST and the MaxST problems are special cases of the Min-k-ST and the Max-k-ST problems in which every input point has a unique color, i.e., $k=n$. In this paper we also study the problem of computing a plane Max-k-ST, which we refer to as the Max-k-PST problem. See Fig. 1.

1.1 Our Contributions

In this paper we study the maximum plane spanning tree problems. In Sect. 3 we present an approximation algorithm with ratio 1 / 4 for the MaxBPST problem. We study the Max-k-PST problem in Sect. 4. For this problem, we present an approximation algorithm whose ratio is 1 / 6 if $k=3$, and 1 / 8 if $k\geqslant 4$. In Sect. 5 we consider the MaxPST problem, where we modify the algorithm presented by Dumitrescu and Tóth [4] for this problem; this modification improves the approximation ratio to 0.503. All the presented approximation algorithms run in $O(n\log n)$ time, where n is the number of input points.

We also study the MaxBPST problem in the special configurations of the input point set. One special configuration is convex position. The $O(n^3)$-time algorithm of Borgelt et al. [3] for the MinBPST problem for points in convex position, also solves the MaxBPST problem for points in convex position within the same time bound. The semi-collinear configuration is another special case in which the red points are on a line and the blue points are on one side of the line. In Sect. 6 we present an $O(n^5)$-time algorithm that solves the MaxBPST problem for semi-collinear point sets. The presented algorithm, can also solve the MinBPST problem for this configuration within the same time bound. Concluding remarks are given in Sect. 7.

2 Preliminaries

For any two points p and q in the plane, we refer to the line segment between p and q as pq, and to the Euclidean distance between p and q as |pq|. The lune between p and q, which we denote by $\mathrm {lune}(p,q)$, is the intersection of the two disks of radius |pq| that are centered at p and q.

For a point set P, the diameter of P is the maximum Euclidean distance between any two points of P. A pair of points that realizes the diameter of P is referred to as a diametral pair.

Let G be a geometric graph with colored vertices. We denote by $L(G)$ the total Euclidean length of the edges of G. A star is a tree with one internal node, which we refer to as the center of the star. For a color c, a c-star in G is a star whose center is colored c and the colors of its leaves are different from c.

3 The Maximum Bichromatic Plane Spanning Tree Problem

In this section we consider the MaxBPST problem: Given two sets R and B of red and blue points in the plane, respectively, such that $R\cup B$ is in general position, we are looking for a maximum plane spanning tree in K(R, B). First we verify the existence of a plane spanning tree in K(R, B) and then we present an approximation algorithm with ratio 1 / 4 for the MaxBPST problem that runs in $O(n\log n)$ time where $n=|R\cup B|$. A plane spanning tree in K(R, B) can be obtained as follows. Pick a red point $r\in R$ and connect it to every blue point in B. This gives a star in K(R, B) with center r. The edges of this star can be extended to partition the plane into cones, except possibly one cone; we split this cone into two cones by adding its bisector. Then, we connect all the red points in each cone to one of the blue points on the boundary of that cone. This gives a plane spanning tree in K(R, B).

In the rest of this section we will show that the length of the longest star in K(R, B) is at least 1 / 4 times the length of an optimal MaxBST. Moreover, we show that this estimate is the best possible for the length of a longest star. Our algorithm computes such a star and augments it to form a spanning tree. Note that, as described above, every star in K(R, B) can easily be augmented to form a spanning tree in K(R, B) in $O(n\log n)$ time.

If $|R|=1$ or $|B|=1$, then the problem is trivial. Assume $|R|\geqslant 2$ and $|B|\geqslant 2$. Our algorithm first computes a diametral pair (a, b) in R and a diametral pair (p, q) in B. Then, it returns the spanning tree obtained by augmenting the longest star $S_x$ in K(R, B) that is centered at a point $x\in \{a,b,p,q\}$. Since diametral pairs of R and B can be computed in $O(n\log n)$ time, the running time of the algorithm follows. In the rest of this section we will show that the longest of these stars satisfies the approximation ratio.

Let $T^*$ be an optimal MaxBST and let $L^*_{}$ denote the length of $T^*$. We make an arbitrary point the root of $T^*$ and partition the edges of $T^*$ into two sets as follows. Let $E^*_R$ be the set of edges (u, v) in $T^*$ where u is a red point and u is the parent of v. Let $E^*_B$ be the set of edges (u, v) where u is a blue point and u is the parent of v. The edges of $E^*_R$ (resp. $E^*_B$) form a forest in which each component is a red-star (resp. blue-star). Let $L^*_{R}$ and $L^*_{B}$ denote the total lengths of the edges of $E^*_R$ and $E^*_B$, respectively. Without loss of generality assume that $L^*_{R}\leqslant L^*_{B}$. Then,

$$\begin{aligned} L^*_{}=L^*_{B}+L^*_{R}\leqslant 2L^*_{B}. \end{aligned}$$

(1)

We will show that, in this case, the length of the longest of $S_p$ and $S_q$ is at least 1 / 4 times the length of an optimal MaxBST; as described at the beginning of this section, this star can be augmented to form a bichromatic plane spanning tree. To that end, let $F_{B}$ be the set of edges that is obtained by connecting every red point to its farthest blue point. Notice that the edges of $F_{B}$ form a forest in which every component is a blue-star. Moreover, observe that

$$\begin{aligned} L^*_{B}\leqslant L(F_{B}). \end{aligned}$$

(2)

Lemma 1

$L(F_{B})\leqslant L(S_p)+L(S_q)$.

Proof

Let $C_p$ and $C_q$ be the two disks of radius |pq| that are centered at p and q, respectively. Since (p, q) is a diameter of B, all blue points lie in $\mathrm {lune}(p,q)$; see Fig. 2a.

Fig. 2

Illustration of Lemma 1

For any red point $r\in R$, let f(r) denote its neighbor in $F_{B}$. Recall that f(r) is the farthest blue point to r, and note that f(r) is in $\mathrm {lune}(p,q)$. See Fig. 2a. We are going to show that $|rf(r)|\leqslant |rp|+|rq|$. Depending on whether or not $r\in \mathrm {lune}(p,q)$ we consider the following two cases.

• $r\notin \mathrm {lune}(p,q)$. Thus, we have that $r\notin C_p$ or $r\notin C_q$. Without loss of generality assume $r\notin C_p$; see Fig. 2a. By the triangle inequality we have $|rf(r)|\leqslant |rq|+|qf(r)|$. Since pq is a diameter of B, we have $|qf(r)|\leqslant |pq|$. In addition, since $r\notin C_p$, we have $|pq|\leqslant |rp|$. By combining these inequalities, we get

  $$\begin{aligned} |rf(r)|\leqslant |rq|+|qf(r)|\leqslant |rq|+|pq|\leqslant |rq|+|rp|. \end{aligned}$$

• $r\in \mathrm {lune}(p,q)$. Without loss of generality assume that pq has unit length, pq is horizontal, r is above pq, and r is closer to q than to p. If f(r) is on or above pq, then |rf(r)| is smaller than |pq|, and hence smaller than $|rp|+|rq|$. Assume f(r) is below pq. Let s be the intersection point of the boundaries of $C_p$ and $C_q$ that is below pq as in Fig. 2b.

Claim 1

$|rf(r)|\leqslant |rs|$.

Let $f'(r)$ be the intersection point of the ray that is emanating from r and passing through f(r) with the boundary of $\mathrm {lune}(p,q)$. Note that $|rf(r)|\leqslant |rf'(r)|$. If $f'(r)$ is on the boundary of $C_q$, then the perpendicular bisector of the segment $sf'(r)$ passes through q. In this case r is in the same side of this perpendicular as $f'(r)$, and thus, $|rf'(r)|\leqslant |rs|$; see Fig. 2b. Similarly, if $f'(r)$ is on the boundary of $C_p$, then both r and $f'(r)$ are on a same side of the perpendicular bisector of $sf'(r)$ which passes through p. This proves the claim.

Based on Claim 1, in order to show that $|rf(r)|\leqslant |rp|+|rq|$, it suffices to show that $|rs|\leqslant |rp|+|rq|$. Let $x=|rs|$ and $\alpha =\angle rsq$; see Fig. 2c. Note that $\sqrt{3}/2\leqslant x\leqslant \sqrt{3}$ and $0\leqslant \alpha \leqslant \frac{\pi }{6}$. By the cosine rule we have

$$\begin{aligned} |rp|=\sqrt{1+x^2-2x\cos (\pi /3-\alpha )} \quad \text {and}\quad |rq|=\sqrt{1+x^2-2x\cos \alpha }. \end{aligned}$$

Define

$$\begin{aligned} f(x,\alpha )=\sqrt{1+x^2-2x\cos (\pi /3- \alpha )}+\sqrt{1+x^2-2x\cos \alpha }-x. \end{aligned}$$

(3)

Then, $|rp|+|rq|-|rs| = f(x,\alpha )$. In “Appendix” we show that $f(x,\alpha )\geqslant 0$ for all $\sqrt{3}/2\leqslant x\leqslant \sqrt{3}$ and $0\leqslant \alpha \leqslant \frac{\pi }{6}$. This implies that $|rs|\leqslant |rp|+|rq|$.

Since in both previous cases $|rf(r)|\leqslant |rp|+|rq|$, we have

$$\begin{aligned} L(F_{B})=\sum _{r\in R}|rf(r)|\leqslant \sum _{r\in R}|rp|+\sum _{r\in R}|rq|=L(S_p)+L(S_q). \end{aligned}$$

$\square$

Combining Inequalities (1), (2), and Lemma 1, we get

$$\begin{aligned} L^*_{}\leqslant 2L^*_{B}\leqslant 2L(F_{B})\leqslant 2\cdot (L(S_p)+L(S_q)). \end{aligned}$$

Therefore, the length of the longest of $S_p$ and $S_q$ is at least 1 / 4 times $L^*_{}$. To this end, we have proved the following theorem:

Theorem 1

Let R and B be two disjoint sets of points in the plane such that $R\cup B$ is in general position, and let $n=|R\cup B|$. One can compute, in $O(n\log n)$ time, a plane spanning tree in K(R, B) whose length is at least 1 / 4 times the length of a maximum spanning tree in K(R, B).

3.1 A Matching Upper Bound

In this section we show that the above estimate is best possible for the length of the longest star in K(R, B). Consider the figure to the right which shows a set R of n / 2 red points and a set B of n / 2 blue points that are equally distributed on two circular arcs of arbitrary large radius and of arbitrary small length $\epsilon$ that are at distance 1 from each other. The bichromatic plane spanning tree/path that is shown in this figure has $n-2$ edges of length at least 1. Any bichromatic star on this point set has at most n / 4 edges each of length at most $1+\epsilon$ and at most n / 4 edges each of length at most $\epsilon$. Thus, the ratio of the length of a longest bichromatic star and the length of a MaxBST is at most $\frac{n/4+\epsilon n/2}{n-2}$, which approaches 1 / 4 from above when $\epsilon$ gets arbitrarily small and n gets arbitrarily large.

4 The Maximum k-Colored Plane Spanning Tree Problem

In the multicolored version of the maximum plane spanning tree problem, the input points are colored by more than two colors, and we want the two endpoints of every edge in the tree to have distinct colors. Formally, we are given a set P of n points in the plane in general position that is partitioned into subsets $P_1,\dots ,P_k$, with $k \geqslant 3$. For each $c\in \{1,\dots ,k\}$, assume the points of $P_c$ are colored c. Let $K(P_1,\dots ,P_k)$ be the complete multipartite geometric graph on P, which has edges between every point of each set in the partition to all points of the other sets. This graph contains a plane spanning tree; this can be verified by an argument similar to that of Sect. 3 for K(R, B). We pick a point p in $P_1$ and connect it to every point in $P{\setminus } P_1$ to obtain a star. Using this star, we partition the plane into cones with their apices at p. Then we connect all points of $P_1$ in every cone to a point of $P{\setminus } P_1$ on the boundary of that cone. This gives a plane spanning tree in $K(P_1,\dots ,P_k)$.

The Max-k-PST problem is the problem of computing a maximum plane spanning tree in $K(P_1,\dots ,P_k)$. The standard MaxPST problem can be interpreted as an instance of this multicolored version in which $k=n$, i.e., each point has a unique color. In this section, we present an approximation algorithm, for the Max-k-PST problem, whose ratio is 1 / 6 if $k=3$, and 1 / 8 if $k\geqslant 4$.

We will show that the length of the longest star in $K(P_1,\dots ,P_k)$ is at least 1 / 8 (resp. 1 / 6) times the length of an optimal Max-k-ST if $k\geqslant 4$ (resp. $k=3$). Our algorithm computes such a star and augments it to form a spanning tree in $O(n\log n)$ time. The algorithm is as follows. Compute a bichromatic diameter of P, i.e., two points of different colors that have the maximum distance. We show, by contradiction, that the MaxST in K(P), which can be computed in $O(n\log n)$ time [5], contains a bichromatic diameter of P. As for contrary, take a bichromatic diameter $(p_i,p_j)$ of P, and consider the path $\delta$ in MaxST with endpoints $p_i$ and $p_j$. Since $p_i$ and $p_j$ have distinct colors, $\delta$ contains a bichromatic edge e which is shorter than $(p_i,p_j)$. By replacing e with $(p_i,p_j)$ we obtain a larger spanning tree in K(P) which contradicts our first choice of MaxST. Therefore, MaxST contains a bichromatic diameter of P. Let (p, q) be such a bichromatic diameter. Notice that the length of any edge in $K(P_1,\dots ,P_k)$ is at most |pq|. Without loss of generality assume that $p\in P_i$ and $q\in P_j$. Notice that all points of $P{\setminus } (P_i\cup P_j)$ lie in $\mathrm {lune}(p,q)$, because, otherwise (p, q) cannot be a bichromatic diameter of P. To simplify the notation, we write R, B, and G, for $P_i$, $P_j$, and $P{\setminus } (P_i\cup P_j)$, respectively. Moreover, we assume that the points of R, B, and G are colored red, blue, and green, respectively. Compute a diametral pair $(r,r')$ in R, a diametral pair $(b,b')$ in B, and a diametral pair $(g,g')$ in G. Then, return the spanning tree obtained by augmenting the longest star $S_x$ in $K(P_1,\dots ,P_k)$ that is centered at a point $x\in \{p,q,r,r',b,b',g,g'\}$. We show that the length of $S_x$ is at least 1 / 8 times the length of an optimal tree. It might be that any of R, B, and G consists of a single point, in which case, $r=r'$, $b=b'$, or $g=g'$, respectively. Our following analysis of the lower bound holds even in these cases.

Let $T^*$ be an optimal Max-k-ST, and let $L^*_{}$ denote the length of $T^*$. We make an arbitrary point the root of $T^*$ and partition the edges of $T^*$ into four sets as follows. Let $E^*_R$ be the set of edges (u, v) in $T^*$ where u is a red point and u is the parent of v. Let $E^*_B$ be the set of edges (u, v) where u is a blue point and u is the parent of v. Let $E^*_G$ be the set of edges (u, v) where u is a green point, v is not a green point, and u is the parent of v. Let $E^*$ be the set of edges (u, v) where both u and v are green points. The edges of each of $E^*_R$, $E^*_B$, and $E^*_G$ form a forest in which each component is a red-star, a blue-star, and a green-star, respectively. Let $L^*_{R}$, $L^*_{B}$, and $L^*_{G}$ denote the total lengths of the edges of $E^*_R$, $E^*_B$, and $E^*_G$, respectively. Let $L^*_{E}$ denote the total length of the edges in $E^*$. Then,

$$\begin{aligned} L^*_{}=L^*_{R}+L^*_{B}+L^*_{G}+L^*_{E}. \end{aligned}$$

We consider two cases depending on where or not $L^*_{E}$ is larger than $\max \{L^*_{R},L^*_{B},L^*_{G}\}$.

• $L^*_{E}\geqslant \max \{L^*_{R},L^*_{B},L^*_{G}\}$. In this case $L^*_{E}\geqslant \frac{1}{4}L^*_{}$. The number of edges in $E^*$ is at most $n(G)-1$, where n(G) is the number of points in G. Recall that the length of every edge in $E^*$ is at most |pq|. Thus $L^*_{E}\leqslant (n(G)-1)\cdot |pq|$. Each of the stars $S_p$ and $S_q$ has an edge to every point of G. Thus $L(S_p)+L(S_q)\geqslant n(G)\cdot |pq|$. Therefore,

  $$\begin{aligned} \frac{_1}{^4}L^*_{} \leqslant L^*_{E}\leqslant (n(G)-1)\cdot |pq|< n(G)\cdot |pq|\leqslant L(S_p)+L(S_q), \end{aligned}$$

  which implies that the longest of $S_p$ and $S_q$ has length at least $\frac{1}{8}L^*_{}$.

• $L^*_{E} < \max \{L^*_{R},L^*_{B},L^*_{G}\}$. Without loss of generality assume that $L^*_{B}=\max \{L^*_{R},L^*_{B},L^*_{G}\}$. Thus, $L^*_{B}\geqslant \frac{1}{4}L^*_{}$. Let $F_{B}$ be the set of edges that is obtained by connecting every point of $R\cup G$ to its farthest blue point. Notice that the edges of $F_{B}$ form a forest in which every component is a blue-star. Observe that $L^*_{B}\leqslant L(F_{B})$. Moreover, by Lemma 1 we have $L(F_{B})\leqslant L(S_{b})+L(S_{b'})$. Therefore,

  $$\begin{aligned} \frac{_1}{^4}L^*_{} \leqslant L^*_{B}\leqslant L(F_{B})\leqslant L(S_b)+L(S_{b'}), \end{aligned}$$

  which implies that the longest of $S_{b}$ and $S_{b'}$ has length at least $\frac{1}{8}L^*_{}$.

The point set $\{p,q,r,r',b,b',g,g'\}$ can be computed in $O(n\log n)$ time, and thus, the running time of the algorithm follows.

Note 1

If $k=3$, then $E^*$ is empty, and thus, the longest star $S_x$ with $x\in \{r,r',b,b',g,g'\}$ has length at least $\frac{1}{6}L^*_{}$.

Note 2

If the diameter pair of P is monochromatic, then we get the ratio of 1 / 6. Assume both points of a diametral pair (p, q) of P belong to $P_i$. Let $R=P_i$ and $G=R{\setminus } P_i$. Then, B is empty and $L^*_{}=L^*_{R}+L^*_{G}+L^*_{E}$. Moreover, we have $r=p$ and $r'=q$. If $L^*_{G}\geqslant \frac{1}{3}L^*_{}$, then the longest of $S_{g}$ and $S_{g'}$ has length at least $\frac{1}{6}L^*_{}$. If $L^*_{G}< \frac{1}{3}L^*_{}$, then $L^*_{R}\leqslant L(S_r)+L(S_{r'})$ and $L^*_{E}\leqslant L(S_r)+L(S_{r'})$. Thus, the longest of $S_{r}$ and $S_{r'}$ has length at least $\frac{1}{6}L^*_{}$.

Theorem 2

Let P be a set of n points in the plane in general position that is partitioned into subsets $P_1,\dots ,P_k$, with $k\geqslant 3$. One can compute, in $O(n\log n)$ time, a plane spanning tree in $K(P_1,\dots ,P_k)$ whose length is at least 1 / 8 (resp. 1 / 6) times the length of a maximum spanning tree in $K(P_1,\dots ,P_k)$ if $k\geqslant 4$$(resp. k=3)$.

5 The Maximum Plane Spanning Tree Problem

In this section we study the MaxPST problem, which is a special case of the Max-k-PST problem where every input point has a unique color. Formally speaking, given a set P of points in the plane in general position, we want to compute a maximum plane spanning tree in K(P). We revisit this problem which was first studied by Alon, Rajagopalan and Suri (1993), and then by Dumitrescu and Tóth [4]. Alon et al. [1] presented an approximation algorithm with ratio 1 / 2 for this problem. In fact they proved that the length of the longest star in K(P) is at least 0.5 times the length of an optimal tree; this bound is tight for a longest star. Dumitrescu and Tóth [4] improved the approximation ratio to 0.502. They proved that the length of the longest double-star in K(P) (a double-star is a tree with two internal nodes) is at least 0.502 times the length of an optimal solution. They left as an open problem a more precise analysis of the approximation ratio of their algorithm. In this section we modify the algorithm of Dumitrescu and Tóth [4], and slightly improve the approximation ratio to 0.503. We will describe their algorithm briefly, and provide detail on the parts that we will modify. The algorithm outputs the longest of five plane trees $S_a$, $S_b$, $S_h$, $E_a$, $E_b$, that are describe below.

Fig. 3

a The plane tree $E_a$. The red, blue, and green edges belong to $E^1_a$, $E^2_a$, and $E^3_a$ respectively. b The distance between p and c is less than 0.948 (Color figure online)

Let $n=|P|$, and let $L^*_{}$ denote the length of an optimal MaxST in K(P). Compute a diametral pair (a, b) of P. Without loss of generality assume that ab is a horizontal, $|ab|=1$, $a=(0,0)$, and $b=(1,0)$. Since (a, b) is a diametral pair, the length of any edge in K(P) is at most 1. Thus, $L^*_{}\leqslant n-1$. Moreover, all points of P are in $\mathrm {lune}(a,b)$. See Fig. 3. Let $h = (x_h , y_h)$ be a point in P with the largest value of |y| (absolute value of the y-coordinate). Without loss of generality assume that $y_h\geqslant 0$. Define $S_a$, $S_b$, and $S_h$ as three spanning stars that are centered at a, b, and h respectively. We compute plane trees $E_a$ and $E_b$ as follows; this computation is different from the one that is presented in [4].

Set $w = 0.6$. Let $V_a$ be the vertical strip between the lines $x=0$ and $x=\frac{1-w}{2} = 0.2$, $V_m$ be the vertical strip between the lines $x=0.2$ and $x=\frac{1+w}{2}= 0.8$, and $V_b$ be the vertical strip between the lines $x=0.8$ and $x=1$. Note that $a\in V_a$ and $b\in V_b$. See Fig. 3a. We describe how to construct $E_a$; the construction of $E_b$ is analogous. Connect a to each point in $V_b$ and let $E^1_a$ denotes the set of edges of the resulting star (the red edges in Fig. 3a). The edge ab has length 1 and every other edge has length at least $\frac{1+w}{2}$. The edges of $E^1_a$ partition $V_a$ into convex regions. Each of these regions is bounded by at least one edge of $E^1_a$ from above or below. Take any region $\mathcal {A}$ of the partition of $V_a$. Let av be an edge of $E^1_a$ that bounds $\mathcal {A}$ either from above or blow. Note that $v\in V_b$. Connect all points that are in $\mathcal {A}$ (excluding a) to v. Let $E^2_a$ be the set of all such edges after considering all regions (the blue edges in Fig. 3a). Since any edge in $E^2_a$ connects a point in $V_a$ to a point in $V_b$, each edge in $E^2_a$ has length at least w. The edges of $E^1_a\cup E^2_a$ partition $V_m$ into convex regions. Each of these regions is bounded by at least one edge of $E^1_a\cup E^2_a$. Take any region $\mathcal {M}$ of the partition of $V_m$. Consider the following two cases: (a) If $\mathcal {M}$ is bounded by an edge uv of $E^2_a$, then connect all points that are in $\mathcal {M}$ to one of u and v that maximizes the total length of the new edges, and (b) if $\mathcal {M}$ is not bounded by any edge of $E^2_a$, then it is bounded by an edge av of $E^1_a$, connect all points that are in $\mathcal {M}$ to one of a and v that maximizes the total length of the new edges. Let $E^3_a$ be the set of all such edges after considering all regions of $V_m$ (the green edges in Fig. 3a). Let $E_a$ be the graph with vertex set P and edge set $E^1_a\cup E^2_b \cup E^3_a$.

The following is a restatement of Lemma 3 in [4].

Lemma 2

(Dumitrescu and Tóth [4]) Let a and b be two points in the plane that are at distance at least $\alpha$ from each other, for some real $\alpha >0$. Let S be a set of m points in the plane. Let $S_a$ and $S_b$ be two star that are centered at a and b, respectively, and connected to all points of S. Then, the length of the longest of $S_a$ and $S_b$ is at least $\frac{\alpha \cdot m}{2}$.

Recall that the length of each edge in $E^1_a$ is at least $\frac{1+w}{2}$ and the length of each edge in $E^2_{a}$ is at least w. By Lemma 2 the total length of the edges in $E^3_a$ is at least $\frac{w}{2}$ times the number of points in $V_m$.

Lemma 3

Let $n_a$ and $n_b$ denote the number of points in $V_a$ and $V_b$ respectively. Then

$$\begin{aligned} L(E_a)\geqslant \frac{_{n_b}}{^2}+\frac{_w}{^2}(n+n_a)+\frac{_{1-3w}}{^2},\quad L(E_b)\geqslant \frac{_{n_a}}{^2}+\frac{_w}{^2}(n+n_b)+\frac{_{1-3w}}{^2}, \end{aligned}$$

and consequently

$$\begin{aligned} L(E_a)+L(E_b)\geqslant \frac{_{n_a+n_b}}{^2}+\frac{_w}{^2}(2n+n_a+n_b)+1-3w. \end{aligned}$$

Proof

Since $E^1_a$, $E^2_a$, and $E^3_a$ are pairwise disjoint, we have $L(E_a)=L(E^1_a)+L(E^2_a)+L(E^3_a)$. $E^1_a$ contains $n_b$ edges (including ab) of length at least $\frac{1+w}{2}$ with the length of ab is 1. Thus, $L(E^1_a)\geqslant \frac{1+w}{2}(n_b-1)+1$. $E^2_a$ has $n_a-1$ edges of length at least w. Thus, $L(E^2_a)\geqslant w(n_a-1)$. $V_m$ contains $n-n_a-n_b$ points, and thus, the length of $E^3_a$ is at least $\frac{w}{2}(n-n_a-n_b)$. Therefore,

$$\begin{aligned} L(E_a)\geqslant & {} \frac{_{1+w}}{^2}(n_b-1)+1+ w(n_a-1) + \frac{_w}{^2}(n-n_a-n_b)\\&=\frac{_{n_b}}{^2}+\frac{_w}{^2}(n+n_a)+\frac{_{1-3w}}{^2}. \end{aligned}$$

The estimation of $L(E_b)$ is analogous. $\square$

The following lemma summarizes Lemmas 3, 4, 5, and 7 in [4]. Let $P = \{p_1,\dots ,p_n\}$, where $p_i = (x_i, y_i)$. Let $d_{max}(p_i)$ denote the maximum distance from $p_i$ to other points in P.

Lemma 4

(Dumitrescu and Tóth [4]) Let $\delta$ and t be two constants where $0\leqslant \delta \leqslant t\leqslant 1$. Then

• 1. $L(S_a)+L(S_b)\geqslant n$.

• 2. $L^*_{}\leqslant \sum _{i=1}^{n} d_{max}(p_i)$.

• 3. if $\sum _{i=1}^{n}|y_i|\geqslant \delta n$, then $L(S_a)+L(S_b)\geqslant 2n\sqrt{\frac{1}{4}+\delta ^2}$.

• 4. if $\sum _{i=1}^{n}|y_i|\leqslant \delta n$ and $y_h\geqslant t$, then $L(S_h)\geqslant (t-\delta )n$.

Set $\delta = 0.055$ and $t = 0.558$; these constants are different from the ones that are chosen in [4].

Lemma 5

Assume that $|y_h|\leqslant t$. Let $p_i=(x_i,y_i)$ be a point of P in $V_m$ with $|y_i| \leqslant 0.15$. Then $d_{max}(p_i) \leqslant 0.948$.

Proof

The maximum distance is attained when $p_i=(0.2, -0.15)$ or $p_i=(0.8, -0.15)$. Because of symmetry we assume that $p_i=(0.2, -0.15)$. Let $c = (x_c , y_c )$ be the rightmost intersection point of the line $y= t$ and $\mathrm {lune}(a,b)$. See Fig. 3b. The furthest point from $p_i$ in the allowed region is c. Note that $y_c=t$ and $x_c =\sqrt{1-t^2} < 0.83$. Thus, $x_c-x_i<0.63$. Therefore $d_{max}(p_i)\leqslant |p_ic|< \sqrt{0.63^2+(0.15+t)^2}< 0.948$. $\square$

To prove the approximation ratio, we show that the length of the longest of $S_a$, $S_b$, $S_h$, $E_a$, $E_b$ is at least 0.503 times $L^*_{}$. In order to do that, we recall the following four cases that are considered in [4].

• 1. If $\sum _{i=1}^{n}|y_i|\geqslant \delta n$, then the output of the algorithm is not shorter than the longest of $S_a$ and $S_b$. By Lemma 4, the approximation ratio is at least

  $$\begin{aligned} \frac{L(S_a)+L(S_b)}{2L^*_{}}\geqslant \sqrt{\frac{_1}{^4}+\delta ^2}\geqslant 0.503.\end{aligned}$$

• 2. If $\sum _{i=1}^{n}|y_i|< \delta n$ and $y_h\geqslant t$, then the output of the algorithm is not shorter than $S_h$. By Lemma 4, the approximation ratio is at least

  $$\begin{aligned} \frac{L(S_h)}{L^*_{}}\geqslant t-\delta =0.503. \end{aligned}$$

• 3. If $\sum _{i=1}^{n}|y_i|< \delta n$, $y_h < t$, and $n_a+n_b\geqslant (1-z)n$, for a constant $z = 0.49$, then the output of the algorithm is not shorter than the longest of $E_a$ and $E_b$. As a consequence of Lemma 3, the approximation ratio is at least

  $$\begin{aligned} \frac{L(E_a)+L(E_b)}{2L^*_{}}&\nonumber \geqslant \frac{n_a+n_b}{2\cdot 2n}+\frac{w(2n+n_a+n_b)}{2\cdot 2n}+\frac{1-3w}{2n}\\&\geqslant \frac{(1-z)(1+w)}{4}+\frac{w}{2}+\frac{1-3w}{2n}\geqslant 0.503, \end{aligned}$$

  where the last inequality is valid for all $n\geqslant 400$.

• 4. If $\sum _{i=1}^{n}|y_i|< \delta n$, $y_h < t$, and $n_a+n_b< (1-z)n$, then the output of the algorithm is not shorter than the longest of $S_a$ and $S_b$. There are at least $zn=.49 n$ points in $V_m$. At most $\frac{11{n}}{30}$ points have $|y_i|\geqslant 0.15$ because otherwise we have $\sum _{i=1}^{n}|y_i|\geqslant 0.15 \cdot \frac{11 n}{30}= 0.055n=\delta n$, which is a contradiction. Thus, at least $\frac{49 n}{100}-\frac{11 n}{30}=\frac{37n}{300}$ points in $V_m$ have $|y_i|\leqslant 0.15$. By Lemma 4 and Lemma 5 we have

  $$\begin{aligned}L^*_{}\leqslant \frac{263 n}{300}+0.948\cdot \frac{37n}{300}< 0.994 n.\end{aligned}$$

  The approximation ratio is at least

  $$\begin{aligned} \frac{L(S_a)+L(S_b)}{2L^*_{}}\geqslant \frac{n}{2\cdot 0.994 n}> 0.503. \end{aligned}$$

Theorem 3

Let P be a set of n points in the plane in general position. One can compute, in $O(n\log n)$ time, a plane spanning tree in K(P) whose length is at least 0.503 times the length of a maximum spanning tree.

6 The MaxBPST Problem on Special Point Sets

In this section we consider the MaxBPST problem on some restricted point sets, such as

(i):

Point sets that are in convex position,

(ii):

Point sets that are semi-collinear, and

(iii):

Point sets with only two red points.

6.1 Points in Convex Position

Assume $R\cup B$ is in convex position and let $|R|\leqslant |B|$. Borgelt et al. [3] presented a dynamic programming algorithm that solves the MinBPST problem, in K(R, B), in $O(|R|^2 |B|)$ time. Their algorithm can be adjusted to solve the MaxBPST within the same time bound; this can be done by replacing the minimization function—in their recursive computation of a MinBPST—with the maximization function.

6.2 Semi-collinear Point Sets

In this section we consider the special case where the input points are semi-collinear, i.e., the red points lie on a line $\ell$ and the blue points lie on one side of $\ell$. Without loss of generality, we assume that $\ell$ is horizontal and the blue points lie above $\ell$. Let R and B denote the non-empty sets of red and blue points, respectively, and let $n=|R\cup B|$. We present a top-down dynamic programming algorithm that solves the MaxBPST problem for semi-collinear points in $O(n^5)$ time. In a dynamic programming algorithm we maintain a table that stores the solutions of subproblems. In a top-down dynamic programming algorithm, when we encounter a subproblem, first we check the corresponding table-entry; if the subproblem is already solved, then we use that solution, otherwise, we solve the subproblem recursively.

6.2.1 Subproblems

Let $m=|R|$, then $|B|=n-m$. Let $r_1,\dots , r_m$ be the sequence of red points from left to right, and let $\{b_1,\dots , b_{n-m}\}$ be the set of blue points. We introduce $A(i,j,u,v,u',v',w)$ to be the problem of computing the weight of a MaxBPST that spans a red point set $R_A$ and a blue point set $B_A$ where

• i and j, with $i\leqslant j$, are the indices of two red points such that $R_A=\{r_i,\dots , r_j\}$.

• u and v are the indices of two blue points such that $B_A$ contains the blue points that are to the right side of $\ell (r_i,b_u)$, to the left side of $\ell (r_j,b_v)$, and lower than both $b_u$ and $b_v$.

• $u'$ (resp. $v'$) takes a value in the set $\{\mathrm {in}, \mathrm {ex}\}$ which indicates whether the blue point $b_u$ (resp. $b_v$) is included in $B_A$ or excluded.

• w takes a value in the set $\{\mathrm {con}, \mathrm {nco}\}$ where $\mathrm {con}$ stands for “connected” and $\mathrm {nco}$ stands for “not connected”.

Based on the definition of $B_A$, if $u'=\mathrm {in}$ and $v'=\mathrm {ex}$, then $b_u$ is the topmost point of $B_A$. The MaxBPST that is associated to $A(\cdot )$ satisfies the following two rules:

• Rule 1: If $u'=\mathrm {in}$ (resp. $v'=\mathrm {in}$), then we have a constrained version of $A(\cdot )$ where $b_ur_i$ (resp. $b_vr_j$) should be part of the tree, but $A(\cdot )$ returns the total weight of new edges, i.e., the weight of a MaxBPST minus $|b_ur_i|$ (resp. $|b_vr_j|$).

• Rule 2: If $u'=v'=\mathrm {in}$, then $u=v$, and consequently $b_u=b_v$. Thus, every time we call $A(\cdot )$ with $u'=v'=\mathrm {in}$, we ensure that $u=v$.

The parameter w will be used to guarantee that no cycle is created in the final solution, and thus, implies the correctness of our algorithm. While maintaining the above two rules, the output of $A(\cdot )$ is determined as follows:

• if $w=\mathrm {con}$, then the output is the weight of a MaxBPST tree on $R_A\cup B_A$.

• if $w=\mathrm {nco}$, then we find two vertex-disjoint bichromatic trees $T_i$ and $T_j$ that span $R_A\cup B_A$, where $T_i\cup T_j$ is plane, $r_i$ is a vertex of $T_i$, $r_j$ is a vertex of $T_j$, and the total weight of $T_i\cup T_j$ is maximized. Following Rule 1, if $u'=\mathrm {in}$, then $T_i$ should contain $r_ib_u$, and if $v'=\mathrm {in}$, then $T_j$ should contain $r_jb_v$. In addition, the output is the total weight of $T_i\cup T_j$ except the weight of the edges $r_ib_u$ and $r_jb_v$.

Depending on the values of $u',v'$, and w, we have eight different configurations for $A(\cdot )$. Our top-level call of $A(\cdot )$, that will be described in Sect. 6.2.2, is of the form $A(\cdot ,\cdot ,\cdot ,\cdot ,\mathrm {ex},\mathrm {ex},\mathrm {con})$. Based on this first call we will never call three cases $A(\cdot ,\cdot ,\cdot ,\cdot ,\mathrm {in},\mathrm {in},\mathrm {nco})$, $A(\cdot ,\cdot ,\cdot ,\cdot ,\mathrm {ex},\mathrm {in},\mathrm {con})$ and $A(\cdot ,\cdot ,\cdot ,\cdot ,\mathrm {ex},\mathrm {in},\mathrm {nco})$ during the recursive calls. So, we will describe how to handle each of the remaining five configurations (we will describe the first two configurations in detail and the remaining cases briefly). During recursive calls to $A(\cdot )$ we make sure that the size of input gets smaller, or we transfer from one configuration to another configuration which decreases the size of input. Therefore, the algorithm will terminate. In each of the configurations, if $|R_A|\leqslant 1$ or $|B_A|\leqslant 1$, then the solution is trivial. Thus, in the description of the following configurations we assume that $|R_A|\geqslant 2$ and $|B_A|\geqslant 2$.

1. Subproblem $A(i,j,u,v,\mathrm {ex},\mathrm {ex},\mathrm {con})$

Since $u'=\mathrm {ex}$ and $v'=\mathrm {ex}$, the set $B_A$ does not contain any of $b_u$ and $b_v$. Since $w=\mathrm {con}$, $A(\cdot )$ returns the wight of a maximum bichromatic plane tree that spans $R_A\cup B_A$. Let $b_t$ be a topmost point in $B_A$. In any solution of $A(\cdot )$, $b_t$ is connected to at least one red point; let $r_k$, with $k\in \{i,\dots ,j\}$, be the leftmost such point. Since $b_t$ is a topmost blue point, the solution does not contain an edge e that connects a blue point to the left (resp. right) of $\ell (b_t,r_k)$ to a red point to the right (resp. left) of $\ell (b_t,r_k)$, because, otherwise, e crosses $b_tr_k$. Thus, the edge $b_tr_k$ splits the problem into two subproblems, one to the left and one to to the right. See Fig. 4(left). Since $r_k$ is the leftmost red point that $b_t$ is connected to, $b_t$ is not an input point to the left subproblem ($b_t$ is excluded). However, $b_t$ might be connected to some red points to the right of $r_k$, and thus, $b_t$ is an input point to the right subproblem ($b_t$ is included). Therefore, we have

$$\begin{aligned} A(i,j,u,v,\mathrm {ex},\mathrm {ex},\mathrm {con})= & {} |b_tr_k|+A(i,k,u,t,\mathrm {ex},\mathrm {ex},\mathrm {con})\\&+A(k,j,t,v,\mathrm {in},\mathrm {ex},\mathrm {con}). \end{aligned}$$

By Rule 1, the value that is returned by $A(k,j,t,v,\mathrm {in},\mathrm {ex},\mathrm {con})$ does not include $|b_tr_k|$. This makes sure that, in $A(i,j,u,v,\mathrm {ex},\mathrm {ex},\mathrm {con})$, we do not count $|b_tr_k|$ twice. Since we do not know the value of k, we try all $j-i+1$ possible values for k, then pick the one that maximizes $A(i,j,u,v,\mathrm {ex},\mathrm {ex},\mathrm {con})$.

Fig. 4

Illustration for solving $A(i,j,u,v,\mathrm {ex},\mathrm {ex},\mathrm {con})$ and $A(i,j,u,v,\mathrm {in},\mathrm {ex},\mathrm {con})$

2. Subproblem $A(i,j,u,v,\mathrm {in},\mathrm {ex},\mathrm {con})$

In this subproblem the set $B_A$ contains $b_u$ but does not contain $b_v$. Moreover, the solution associated with this problem should contain the edge $b_ur_i$ while the value that is returned by $A(\cdot )$ does not contain $|b_ur_i|$. See Fig. 4(right). We consider two cases depending on whether or not $b_u$ is connected to any red point other than $r_i$. Then, we take the case that gives the maximum value. If $b_u$ is not connected to any other red point, then

$$\begin{aligned} A(i,j,u,v,\mathrm {in},\mathrm {ex},\mathrm {con})=A(i,j,u,v,\mathrm {ex},\mathrm {ex},\mathrm {con}). \end{aligned}$$

If $b_u$ is connected to some red points other than $r_i$, then let $r_k$, with $k\in \{i+1,\dots ,j\}$, be the rightmost one. Since $b_u$ is the topmost blue point in $B_A$, the edge $b_ur_k$ splits the problem into two subproblems, one to the left and one to the right. Since $r_k$ is the rightmost red point that $b_u$ is connected to, $b_u$ is not an input point to the right subproblem. The solution of the left subproblem is a tree that contains both edges $b_ur_i$ and $b_ur_k$. See Fig. 4(right). Therefore, we have

$$\begin{aligned} A(i,j,u,v,\mathrm {in},\mathrm {ex},\mathrm {con})= & {} |b_ur_k|+A(i,k,u,u,\mathrm {in},\mathrm {in},\mathrm {con})\\&+A(k,j,u,v,\mathrm {ex},\mathrm {ex},\mathrm {con}). \end{aligned}$$

Notice that Rule 2 is maintained here. Also, by Rule 1, the value that is returned by $A(i,k,u,u,\mathrm {in},\mathrm {in},\mathrm {con})$ does not include $|b_ur_i|$ nor $|b_ur_k|$. Since we do not know the value of k, we try all $j-i$ possible values of k, then pick the one that maximizes $A(\cdot )$.

3. Subproblem $A(i,j,u,u,\mathrm {in},\mathrm {in},\mathrm {con})$

In this case $u=v$, and $B_A$ contains $b_u$. Since $w = \mathrm {con}$, the output is the weight of a maximum bichromatic plane tree on $R_A\cup B_A$. Since $u'=v'=\mathrm {in}$, both edges $b_ur_i$ and $b_ur_j$ are in this tree, but, by Rule 1, $A(\cdot )$ returns the weight of this tree except these two edges. See Fig. 5(left). We consider two cases depending on whether or not $b_u$ is connected to any red point other than $r_i$ and $r_j$. Then, we take the case that gives the maximum value. If $b_u$ is not connected to any other red point, then we can exclude $b_u$ to obtain a smaller subproblem $A(i,j,u,u,\mathrm {ex},\mathrm {ex},w)$. Moreover, since $b_u$ is already connected to $r_i$ and $r_j$, the solution of $A(i,j,u,u,\mathrm {ex},\mathrm {ex},w)$ should not connect $r_i$ and $r_j$ because otherwise it creates a cycle. Thus, we set $w=\mathrm {nco}$. Therefore,

$$\begin{aligned} A(i,j,u,u,\mathrm {in},\mathrm {in},\mathrm {con})=A(i,j,u,u,\mathrm {ex},\mathrm {ex},\mathrm {nco}). \end{aligned}$$

Fig. 5

Illustration for solving $A(i,j,u,u,\mathrm {in},\mathrm {in},\mathrm {con})$ and $A(i,j,u,v,\mathrm {ex},\mathrm {ex},\mathrm {nco})$

If $b_u$ is connected to some red points other than $r_i$ and $r_j$, then let $r_k$, $k\in \{i+1,\dots ,j-1\}$, be the leftmost one; see Fig. 5(left). This splits the problem into two subproblems such that

$$\begin{aligned} A(i,j,u,u,\mathrm {in},\mathrm {in},\mathrm {con})= & {} |b_ur_k|+A(i,k,u,u,\mathrm {ex},\mathrm {ex},\mathrm {nco})\\&+A(k,j,u,u,\mathrm {in},\mathrm {in},\mathrm {con}). \end{aligned}$$

We try all $j-i-1$ possible values of k, then pick the one that maximizes $A(\cdot )$. Our choice of $r_k$ implies that $b_u$ is not connected to any red point between $r_i$ and $r_k$. Because of this and since $b_u$ is already connected to $r_i$ and $r_k$, the solution of $A(i,k,u,u,\mathrm {ex},\mathrm {ex},w)$ should not connect $r_i$ and $r_k$ because otherwise it creates a cycle. Thus, we set $w=\mathrm {nco}$.

4. Subproblem $A(i,j,u,v,\mathrm {ex},\mathrm {ex},\mathrm {nco})$

In this subproblem, $B_A$ does not contain any of $b_u$ and $b_v$. The solution to this subproblem consists of two vertex disjoint spanning trees that span $R_A\cup B_A$, their union is plane, and $r_i$ and $r_j$ are not in a same tree. Let $b_t$ be a topmost point in $B_A$. In any solution of $A(\cdot )$, $b_t$ is connected to at least one red point; let $r_k$, $k\in \{i,\dots ,j\}$, be the leftmost one. See Fig. 5(right). We consider two cases: (1) $k\in \{i,j\}$, and (2) $k\in \{i+1,{\ldots ,}j-1\}$. Then, we take the one that maximizes $A(\cdot )$. In case (1) if $k=i$ then

$$\begin{aligned} A(i,j,u,v,\mathrm {ex},\mathrm {ex},\mathrm {nco})= & {} |b_tr_i|+ A(i,i,u,t,\mathrm {ex},\mathrm {ex},\mathrm {con})\\&+A(i,j,t,v,\mathrm {in},\mathrm {ex},\mathrm {nco}), \end{aligned}$$

and if $k=j$ then

$$\begin{aligned} A(i,j,u,v,\mathrm {ex},\mathrm {ex},\mathrm {nco})= & {} |b_tr_j|+A(i,j,u,t,\mathrm {ex},\mathrm {ex},\mathrm {nco})\\&+ A(j,j,t,v,\mathrm {in},\mathrm {ex},\mathrm {con}). \end{aligned}$$

Notice that if $k=i$, then all the blue points to the left of $r_ib_t$ should get connected to $r_i$. Thus, the disconnectivity of the final solution should be maintained via $A(i,j,t,v,\mathrm {in},\mathrm {ex},w)$ where we set $w=\mathrm {nco}$.

In case (2) we have two subproblems, only in one of them $r_k$ should not be connected to the other extreme red point. This raises two cases, thus, we take the one that gives a larger value.

$$\begin{aligned} A(i,j,u,v,\mathrm {ex},\mathrm {ex},\mathrm {nco})&=|b_tr_k| +\max \{A(i,k,u,t,\mathrm {ex},\mathrm {ex}, \mathrm {con})\\&\quad +A(k,j,t,v,\mathrm {in},\mathrm {ex},\mathrm {nco}), A(i,k,u,t,\mathrm {ex},\mathrm {ex},\mathrm {nco}) \\&\quad +A(k,j,t,v,\mathrm {in},\mathrm {ex},\mathrm {con})\}. \end{aligned}$$

We try all possible values of k, then pick the one that maximizes $A(\cdot )$.

5. Subproblem $A(i,j,u,v,\mathrm {in},\mathrm {ex},\mathrm {nco})$

The optimal solution associated with this subproblem consists of two trees, one of them contains the edge $b_ur_i$. We consider two cases depending on whether or not $b_u$ is connected to any red point other than $r_i$, then take the one that maximizes $A(\cdot )$. If $b_u$ is not connected to any other red point, then

$$\begin{aligned} A(i,j,u,v,\mathrm {in},\mathrm {ex},\mathrm {nco})=A(i,j,u,v,\mathrm {ex},\mathrm {ex},\mathrm {nco}). \end{aligned}$$

If $b_u$ is connected to some red points other than $r_i$, then let $r_k$, $k\in \{i+1,\dots ,j-1\}$, be the rightmost one (note that k cannot be j, because, otherwise, the disconnectivity of $r_i$ and $r_j$ will not be maintained). This splits the problem into two subproblems. In the left subproblem, $r_k$ is connected to $r_i$ via $b_u$, thus, the disconnectivity of $r_i$ and $r_j$ should be maintained by the right subproblem. Therefore, we have

$$\begin{aligned} A(i,j,u,v,\mathrm {in},\mathrm {ex},\mathrm {nco})= & {} |b_ur_k|+A(i,k,u,u,\mathrm {in},\mathrm {in},\mathrm {con})\\&+A(k,j,u,v,\mathrm {ex},\mathrm {ex},\mathrm {nco}). \end{aligned}$$

Notice that both Rule 1 and Rule 2 are satisfied here. We try all $j-i-1$ possible values of k, then pick the one that maximizes $A(\cdot )$.

6.2.2 The Top-Level Problem

In this section we describe how to use problem $A(\cdot )$, that is defined in the previous section, to solve the original top level problem which is to compute a MaxBPST for semi-collinear points. Let $B=\{b_1,\dots , b_{n-m}\}$ be the set of blue points and $r_1,\dots , r_m$ be the sequence of red points from left to right. Add two (fake) blue points $b_0$ and $b_{n-m+1}$ such that all points of B are to the right side of $\ell (r_1,b_0)$, to the left side of $\ell (r_m,b_{n-m+1})$, and lower than both $b_0$ and $b_{n-m+1}$. We maintain a table A such that each entry $A[i,j,u,v,u',v',w]$ stores the weight of a MaxBPST associated with subproblem $A(i,j,u,v,u',v',w)$. To fill table A we use a top-down dynamic programming approach: we initialize all table entries by a negative value, and then call $A(1,m,0,n-m+1,\mathrm {ex},\mathrm {ex},\mathrm {con})$. After filling table A, the weight of an optimal MaxBPST is stored in $A[1,m,0,n-m+1,\mathrm {ex},\mathrm {ex},\mathrm {con}]$; the tree itself can also be retrieved from table A.

6.2.3 Running Time Analysis

The indices i and j go over the red points, while the indices u and v go over the blue points. Each of the indices $u',v'$, and w takes only two values. Thus, we have $O(|R|^2|B|^2)$ subproblems in total, and hence the table A has $O(|R|^2|B|^2)$ entries. The blue points associated with each subproblem, and a topmost one, can be computed in O(|B|) preprocessing time. Thus the total preprocessing time is $O(|R|^2|B|^3)$. After that, during the algorithm, to solve each subproblem, the index k goes over O(|R|) red points. Thus, after preprocessing, we spend $O(|R|^3|B|^2)$ to solve all the subproblems. Therefore, the total running time of our algorithm is $O(|R|^3|B|^2+|R|^2|B|^3)$.

Notice that to solve each subproblem we do not need all the blue points that are associated with that subproblem, but we do need a topmost one. Moreover, notice that we need to find a topmost blue point only for subproblems of type $A(\cdot ,\cdot ,\cdot ,\cdot ,\mathrm {ex},\mathrm {ex},\cdot )$. We describe how to compute topmost blue points for all such subproblems in $O(|R|^2|B|^2)$ preprocessing time. This will improve the running time of our algorithm to $O(|R|^3|B|^2)$.

For simplicity of description, we assume that no two blue points have a same y-coordinate, however, for the purpose of our algorithm we do not need this assumption. The topmost blue point for a subproblem $A(i,j,u,v,\mathrm {ex},\mathrm {ex},w)$ is uniquely defined by i, j, u, and v; it is independent of w. Let $B=\{b_1,\dots ,b_{|B|}\}$ denote the set of all blue points, including the two fake blue points that we add in the top level of the algorithm. Assume that points of R are on x-axis, and points of B lie above x-axis. Let $r_1,\dots , r_{|R|}$ be the red points from left to right. For each $i\in \{1,\dots ,|R|\}$, let $L_i^\mathrm {c}$ be the sorted list of points of B in clockwise order around $r_i$ by starting from x-axis. Similarly, let $L_i^\mathrm {cc}$ be the sorted list of points of B in counterclockwise order around $r_i$.

We maintain a table T whose entry T[i, j, u, v] (with $i,j\in \{1,\dots , |R|\}$ and $u,v\in \{1,\dots , |B|\}$) stores the topmost blue point for the subproblem $A(i,j,u,v,\mathrm {ex},\mathrm {ex},w)$. Recall that the blue input set to each subproblem $A(i,j,u,v,\mathrm {ex},\mathrm {ex},w)$ is to the right side of $\ell (b_u,r_i)$, to the left side of $\ell (b_v,r_j)$, and lower than both $b_u$ and $b_v$.

Fig. 6

Illustration of the first phase of filling table T where $b_u$ is above $b_v$ (left) and $b_u$ is below $b_v$ (right)

For each pair (i, j), with $i,j\in \{1,\dots , |R|\}$, we fill the entries $T[i,j,\cdot ,\cdot ]$, in two phases, as follows. In the first phase we fill the entries related to the cases where $b_u$ is above $b_v$, and in the second phase we fill the entries related to the cases where $b_u$ is below $b_v$. We describe the first phase; the second phase is analogous. We iterate over $v\in \{1,\dots ,|B|\}$. In the vth iteration we compute the topmost blue point for all $A(i,j,u,v,\mathrm {ex},\mathrm {ex},w)$ where $u\in \{1,\dots ,|B|\}$ and $b_u$ is above $b_v$. Let $b_t$ be the current topmost blue point that is to the left side of $\ell (b_v,r_j)$ and below $b_v$. Traverse the points of $L_i^\mathrm {cc}$ from the beginning, and let $b_u$ be the current point. We have two cases:

• $b_u$ is above $b_v$ [Fig. 6(left)]. Set $T[i,j,u,v]=b_t$, then proceed to the next point in $L_i^\mathrm {cc}$ .

• $b_u$ is below $b_v$ [Fig. 6(right)]. If $b_u$ is to the left of $\ell (b_v,r_j)$ and above $b_t$, then let $b_u$ be the current $b_t$ . Then proceed to the next point in $L_i^\mathrm {cc}$.

This is the end of the first phase. In the second phase we iterate over $u\in \{1,\dots ,|B|\}$, and in the uth iteration we traverse $L_j^\mathrm {c}$ and find T[i, j, u, v] for $b_v$’s that are above $b_u$. As for the running time, the lists $L_i^\mathrm {c}$ and $L_i^\mathrm {cc}$, for all $i\in \{1,\dots ,|R|\}$, can be computed in $O(|R||B|\log |B|)$ time. After that, we spend $O(|R|^2|B|^2)$ time to fill T. Therefore, our dynamic programming algorithm runs in $O(|R|^3|B|^2)$ time.

Theorem 4

Let R and B be two disjoint sets of points in the plane such that the points of R lie on a straight line, the points of B are on one side of this line, and no two points of B are collinear with any point of R. Then, a maximum plane spanning tree in K(R, B) can be computed in $O(|R|^3|B|^2)$ time.

Note The dynamic programming algorithm presented in this section can easily be adjusted to solve the MinBPST problem, and also the bottleneck versions of the bichromatic plane spanning tree problem (minimizing the length of the longest edge, or maximizing the length of the shortest edge) for semi-collinear points in $O(|R|^3|B|^2)$ time.

6.3 Two Red Points

Borgelt et al. [3] showed that a minimum bichromatic plane spanning tree of two red points and n blue points can be computed in $O(n\log n)$ time. In this section we show how to compute a maximum bichromatic plane spanning tree for such a point set in $O(n^2)$ time. Let $\ell$ be the line passing through the two red points, and assume $\ell$ is horizontal. This introduces two instances of the semi-collinear case: one instance below $\ell$ and one instance above $\ell$. In an optimal tree, either the two red points are connected by a blue point above $\ell$ and disconnected below $\ell$, or the two red points are connected by a blue point below $\ell$ and disconnected above $\ell$. Thus, we can compute an optimal tree by taking the longest of the two trees obtained from these two cases. Since $|R|=2$, the running time of our algorithm for this case is $O(|R|^3|B|^2)=O(n^2)$.

7 Concluding Remarks

In this paper we presented constant factor approximation algorithms for the problem of computing a maximum plane spanning tree in a multipartite geometric graph with $k\ge 2$ sets in the partition. It is not known whether or not this problem is NP-hard. A natural open problem is to improve any of the presented approximation ratios. For $k=2$, we showed that the length of the longest c-star is at least 1 / 4 times the length of a Max-k-ST; we showed that this bound is tight. When the number k of sets in the partition is 3 (resp. at least 4) we showed that the length of the longest c-star is at least 1 / 6 (resp. 1 / 8) times the length of a Max-k-ST. We believe that these bounds are not tight.

The figure to the right shows a set of n / 3 red, n / 3 green, and n / 3 blue points that are equally distributed on two circular arcs of arbitrary large radius and of arbitrary small length $\epsilon$ that are at distance 1 from each other. The plane spanning tree that is shown in this figure has $n-3$ edges of length at least 1. Any c-star on this point set has at most n / 3 edges each of length at most $1+\epsilon$ and at most n / 3 edges each of length at most $\epsilon$. Thus, the ratio of the length of a longest c-star and the length of a Max-3-ST is at most $\frac{n/3+2\epsilon n/3}{n-3}$ which approaches 1 / 3 from above when $\epsilon$ gets arbitrarily small and n gets arbitrarily large. We conjecture that when the number of sets in the partition is k, with $k\geqslant 3$, then the length of the longest c-star is at least 1 / 3 times the length of a Max-k-ST.

We also presented exact algorithms for some special bichromatic input point sets. Providing an $o(n^2)$ algorithm for the two red point case is open.

Appendix: Proof of \(f(x,\alpha ) \geqslant 0\)

We want to show that

$$\begin{aligned} f(x,\alpha ) = \sqrt{1 + x^2 - 2x\cos \left( \pi /3 - \alpha \right) } + \sqrt{1 + x^2 - 2x\cos \alpha } - x \geqslant 0 \end{aligned}$$

for all $\sqrt{3}/2\leqslant x \leqslant \sqrt{3}$ and $0\leqslant \alpha \leqslant \frac{\pi }{6}$. From elementary trigonometry, we have

$$\begin{aligned} \cos \left( \frac{\pi }{3} - \alpha \right) = \frac{1}{2}\cos \alpha + \frac{\sqrt{3}}{2}\sin \alpha , \end{aligned}$$

from which $f(x,\alpha )$ can be re-written as

$$\begin{aligned} f(x,\alpha ) = \sqrt{1 + x^2 - x\cos \alpha -\sqrt{3}\,x\sin \alpha } + \sqrt{1 + x^2 - 2x\cos \alpha } - x . \end{aligned}$$

Let us solve the equation $f(x,\alpha ) = 0$, which corresponds to

$$\begin{aligned} \sqrt{1 + x^2 - x\cos \alpha -\sqrt{3}\,x\sin \alpha } + \sqrt{1 + x^2 - 2x\cos \alpha } = x . \end{aligned}$$

By squaring on both sides, we find

$$\begin{aligned}&2 + 2x^2 - 3x\cos \alpha -\sqrt{3}\,x\sin \alpha \\&\quad +2\sqrt{1 + x^2 - x\cos \alpha -\sqrt{3}\,x\sin \alpha }\sqrt{1 + x^2 - 2x\cos \alpha } = x^2, \end{aligned}$$

which we write as

$$\begin{aligned}&2\sqrt{1 + x^2 - x\cos \alpha -\sqrt{3}\,x\sin \alpha }\sqrt{1 + x^2 - 2x\cos \alpha }\\&\quad = -2 -x^2 + 3x\cos \alpha +\sqrt{3}\,x\sin \alpha . \end{aligned}$$

Squaring once more, we find

$$\begin{aligned}&4\left( 1 + x^2 - x\cos \alpha -\sqrt{3}\,x\sin \alpha \right) \left( 1 + x^2 - 2x\cos \alpha \right) \\&\quad = \left( -2 -x^2 + 3x\cos \alpha +\sqrt{3}\,x\sin \alpha \right) ^2, \end{aligned}$$

which is equivalent to

$$\begin{aligned}&4\left( 1 + x^2 - x\cos \alpha -\sqrt{3}\,x\sin \alpha \right) \left( 1 + x^2 - 2x\cos \alpha \right) \\&\quad - \left( -2 -x^2 + 3x\cos \alpha +\sqrt{3}\,x\sin \alpha \right) ^2 = 0 , \end{aligned}$$

which can be factored into

$$\begin{aligned} 3x^2\left( x-\left( \cos \alpha +\frac{1}{\sqrt{3}}\sin \alpha \right) \right) ^2 = 0 . \end{aligned}$$

Since $x > 0$ and

$$\begin{aligned} f\left( \cos \alpha +\frac{1}{\sqrt{3}}\sin \alpha ,\alpha \right) = 0, \end{aligned}$$

we have that $f(x,\alpha ) = 0$ if and only if $x = \cos \alpha +\frac{1}{\sqrt{3}}\sin \alpha$. Therefore, on its domain, f is equal to 0 precisely on the curve $x = \cos \alpha +\frac{1}{\sqrt{3}}\sin \alpha$ and nowhere else. Thus, below this curve, f is everywhere positive or everywhere negative. Since $f\left( \frac{\sqrt{3}}{2},\frac{\pi }{6}\right) = 1-\frac{\sqrt{3}}{2} > 0$, f is everywhere positive below the curve. Similarly, since $f(\sqrt{3},0) = \sqrt{4-\sqrt{3}} - 1 > 0$, f is everywhere positive above the curve. Therefore, $f(x,\alpha ) \geqslant 0$ for all $\sqrt{3}/2\leqslant x \leqslant \sqrt{3}$ and $0\leqslant \alpha \leqslant \frac{\pi }{6}$.