On Group Feedback Vertex Set Parameterized by the Size of the Cutset

Abstract

We study parameterized complexity of a generalization of the classical Feedback Vertex Set problem, namely the Group Feedback Vertex Set problem: we are given a graph $G$ with edges labeled with group elements, and the goal is to compute the smallest set of vertices that hits all cycles of $G$ that evaluate to a non-null element of the group. This problem generalizes not only Feedback Vertex Set, but also Subset Feedback Vertex Set, Multiway Cut and Odd Cycle Transversal . Completing the results of Guillemot (Discrete Optim 8(1):61–71, 2011), we provide a fixed-parameter algorithm for the parameterization by the size of the cutset only. Our algorithm works even if the group is given as a blackbox performing group operations.

1 Introduction

The parameterized complexity is an approach for tackling NP-hard problems by designing algorithms that perform well, when the instance is in some sense simple; its difficulty is measured by an integer, called the parameter, additionally appended to the input. Formally, we say that a problem is fixed-parameter tractable (FPT), if it admits an algorithm that given input of length $n$ and parameter $k$, resolves the task in time $f(k)n^c$, where $f$ is some computable function and $c$ is a constant independent of the parameter.

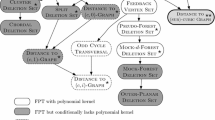
The search for fixed-parameter algorithms led to the development of a number of new techniques and gave valuable insight into structures of many classes of NP-hard problems. Among them, there is a family of so-called graph cut problems, where the goal is to delete as few as possible edges or vertices (depending on the variant) in order to make the graph satisfy a global separation requirement. This class is perhaps best represented by the classical Feedback Vertex Set problem (FVS) where, given an undirected graph $G$, we seek for a minimum set of vertices that hits all cycles of $G$. Other examples are Multiway Cut (MWC : separate each pair from a given set of terminals in a graph with a minimum cutset) or Odd Cycle Transversal (OCT : make a graph bipartite by a minimum number of vertex deletions).

The research on the aforementioned problems had a great impact on the development of parameterized complexity. The long line of research concerning parameterized algorithms for FVS contains [1–4, 11–13, 15, 18, 23], leading to an algorithm working in $O(3^k n^{O(1)})$ time [7]. The search for a polynomial kernel for FVS lead to surprising applications of deep combinatorial results such as Gallai’s theorem [26], which has also been found useful in designing FPT algorithms [10]. While investigating the graph cut problems such as MWC , Márx [21] introduced the important separator technique, which turned out to be very robust and is now the key ingredient in parameterized algorithms for various problems such as variants of FVS [5, 10] or Almost 2-SAT [24]. Moreover, the recent developments on MWC show applicability of linear programming in parameterized complexity, leading to the fastest currently known algorithms not only for MWC , but also Almost 2-SAT and OCT [9, 22]. Last but not least, the research on the OCT problem resulted in the introduction of iterative compression, a simple yet powerful technique for designing parameterized algorithms [25].

1.1 Considered Problem

In this paper we study a generalization of the FVS problem, namely Group Feedback Vertex Set .¹ Let $\varSigma$ be a finite (not necessarily abelian) group, with unit element $1_\varSigma$. We use the multiplicative convention for denoting the group operation.

Definition 1

For a finite group $\varSigma$, a directed graph $G=(V,A)$ and a labeling function $\varLambda :A \rightarrow \varSigma$, we call $(G,\varLambda )$ a $\varSigma$ -labeled graph iff for each arc $(u,v) \in A$ we have $(v,u) \in A$ and $\varLambda ((u,v)) = \varLambda ((v,u))^{-1}$.

We somehow abuse the notation and by $(G{\setminus } X, \varLambda )$ denote the $\varSigma$-labeled graph $(G {\setminus } X, \varLambda |_{A(G {\setminus } X)})$, even though formally $\varLambda$ has in its domain arcs that do not exist in $G{\setminus } X$ (i.e., we ignore that, to be completely formal, we need to restrict the domain of the labeling $\varLambda$).

For a path² $P=(v_1,\ldots ,v_{\ell })$ we denote $\varLambda (P)=\varLambda ((v_1,v_2)) \cdot \ldots \cdot \varLambda ((v_{\ell -1},v_{\ell }))$. Similarly, for a cycle $C=(v_1,\ldots ,v_{\ell },v_1)$ we denote $\varLambda (C)=\varLambda ((v_1,v_2)) \cdot \ldots \cdot \varLambda ((v_{\ell -1},v_{\ell })) \cdot \varLambda ((v_{\ell },v_1))$. We call a cycle $C$ a non-null cycle, iff $\varLambda (C)\not = 1_\varSigma$. Observe that if the group $\varSigma$ is non-abelian, then it may happen that cyclic shifts of the same cycle yield different elements of the group; nevertheless, the notion of a non-null cycle is well-defined, as either all of them are equal to $1_\varSigma$ or none of them.

Lemma 1

Assume that $(x_1,\ldots ,x_\ell ,x_1)$ is a cycle in a $\varSigma$-labeled graph $(G,\varLambda )$. If $\varLambda ((x_1,\ldots ,x_\ell ,x_1)) \not = 1_\varSigma$, then $\varLambda ((x_2,\ldots ,x_{\ell },x_1,x_2))\not = 1_\varSigma$.

Proof

Let $g_1 = \varLambda ((x_1,x_2))$ and $g_2=\varLambda ((x_2,\ldots ,x_{\ell },x_1))$. We have that $g_1 \cdot g_2 = 1_\varSigma$ iff $g_2 \cdot g_1 = 1_\varSigma$ and the lemma follows. $\square$

In the Group Feedback Vertex Set problem we want to hit all non-null cycles in a $\varSigma$-labeled graph using at most $k$ vertices.

As observed in [14], for a graph excluding a non-null cycle we can define a consistent labeling.

Definition 2

For a $\varSigma$-labeled graph $(G,\varLambda )$ we call $\lambda :V \rightarrow \varSigma$ a consistent labeling iff for each arc $(u,v) = a \in A(G)$ we have $\lambda (v) = \lambda (u) \cdot \varLambda (a)$.

Lemma 2

([14]) A $\varSigma$-labeled graph $(G,\varLambda )$ has a consistent labeling iff it does not contain a non-null cycle. Moreover, there is a polynomial-time algorithm which, given $(G,\varLambda )$, finds either a non-null cycle in $G$ or a consistent labeling of $G$.

Note that when analysing the complexity of the GFVS problem, it is important how the group $\varSigma$ is represented. In [14] it is assumed that $\varSigma$ is given via its multiplication table as a part of the input. In this paper we assume a more general model, where operations in $\varSigma$ are computed by a given blackbox. More precisely, we assume that we are given subroutines that can multiply two elements, return an inverse of an element, provide the neutral element $1_\varSigma$, or check whether two elements are equal. The running times of our algorithms are always measured in terms of basic operations and group operations, while space complexity is measured in the number of bits and group elements stored.

As noted in [20], GFVS subsumes not only the classical FVS problem, but also OCT (with $\varSigma = \mathbb {Z}_2$) and MWC (with $\varSigma$ being an arbitrary group of size not smaller than the number of terminals). We note that if $\varSigma$ is given in the blackbox, Group Feedback Vertex Set subsumes also Edge Subset Feedback Vertex Set, which is equivalent to Subset Feedback Vertex Set  [10].

Lemma 3

Given an ESFVS instance $(G,S,k)$, one can in polynomial time construct an equivalent GFVS instance $(G',\varLambda ,k)$ with group $\varSigma = \mathbb {Z}_2^{|S|}$.

Proof

To construct the new GFVS instance, create the graph $G'$ by replacing each edge of $G$ with arcs in both direction, keep the parameter $k$, take $\varSigma = \mathbb {Z}_2^{|S|}$ and construct a $\varSigma$-labeling $\varLambda$ by setting any $|S|$ linearly independent values of $\varLambda ((u,v))$ for $uv \in S$ and $\varLambda ((u,v)) = 1_\varSigma$ for $uv \notin S$. Clearly, this construction can be done in polynomial time and the operations on the group $\varSigma$ can be performed by a subroutine in time polynomial in $|S|$ by representing elements of $\varSigma$ as bit vectors of length $|S|$. $\square$

We note that the Group Feedback Vertex Set problem was also studied from the graph theoretical point of view, as, in addition to the aforementioned reductions, it also subsumes the setting of Mader’s $\mathcal {S}$-paths theorem [6, 19]. In particular, Kawarabayashi and Wollan proved the Erdős–Pósa property for non-null cycles in highly connected graphs, generalizing a list of previous results [19], while Wollan proved the Erdős–Pósa property for non-null cycles in general graphs labeled with an abelian group [28].

The study of parameterized complexity of GFVS was initiated by Guillemot [14], who presented a fixed-parameter algorithm for GFVS parameterized by $|\varSigma |+k$ running in time³ $O^*(2^{O(k\log |\varSigma |)})$. When parameterized by $k$, Guillemot showed a fixed-parameter algorithm for the easier edge-deletion variant of GFVS , running in time $O^*(2^{O(k \log k)})$. Recently, Kratsch and Wahlström presented a randomized kernelization algorithm that reduces the size of a GFVS instance to $O(k^{2|\varSigma |})$ [20].

Before we proceed to the description of our results, let us briefly sketch their motivation. The main purpose of studying the GFVS problem is to find the common points in the fixed-parameter algorithms for problems it generalizes. Precisely this approach has been presented by Guillemot in [14], where at the base of the algorithm lies a subroutine that solves a very general version of Multiway Cut . When reducing various graph cut problems to GFVS , usually the size of the group depends on the number of distinguished vertices or edges in the instance, as in Lemma 3. Hence, an application of the general $O^*(2^{O(k\log |\varSigma |)})$ algorithm of Guillemot unfortunately incorporates this parameter in the running time. It appears that by a more refined combinatorial analysis, usually one can get rid of this dependence; this is the case both in Subset Feedback Vertex Set  [10] and in Multiway Cut  [9, 22]. This suggested that the phenomenon can be, in fact, more general.

1.2 Our Result and Techniques

Our main result is a fixed-parameter algorithm for GFVS parameterized by the size of the cutset only. Recall that time and space complexities refer to basic and group operations performed, and bits and group elements stored, respectively.

Theorem 1

Group Feedback Vertex Set can be solved in $O^*(2^{O(k\log k)})$ time and polynomial space.

Our algorithm uses a similar approach as described by Kratsch and Wahlström in [20]: in each step of iterative compression, when we are given a solution $Z$ of size $k+1$, we guess the values of a consistent labeling on the vertices of $Z$, and reduce the problem to Multiway Cut . However, by a straightforward application of this approach we obtain $O^*(2^{O(k \log |\varSigma |)})$ time complexity. To reduce the dependency on $|\varSigma |$, we carefully analyse the structure of a solution, provide a few reduction rules in a spirit of the ones used in the recent algorithm for Subset Feedback Vertex Set [10] and, finally, for each vertex of $Z$ we reduce the number of choices for a value of a consistent labeling to polynomial in $k$. Therefore, the number of reasonable consistent labelings of $Z$ is bounded by $2^{O(k \log k)}$ and we can afford solving a Multiway Cut instance for each such labeling.

A comparison with the previous algorithm for Subset Feedback Vertex Set  [10] is in place; note that the bound on the running time of our algorithm matches the one for Subset Feedback Vertex Set  [10], while our algorithm works in a much more general framework. In our opinion, the group-labeled setting is a much more convenient and insightful way of looking at graph-separation problems as compared to the definition of Subset Feedback Vertex Set. To support this claim, let us briefly analyse how the algorithm of Theorem 1 solves an ESFVS instance $(G,S,k)$, via the reduction of Lemma 3. Every edge of $S$ translates to a different $\mathbb {Z}_2$ coordinate of the group $\varSigma = \mathbb {Z}_2^{|S|}$. The step where we guess the correct labeling of every vertex of the modulator $Z$ corresponds, in the language of ESFVS , to a guessing, between every pair $u,v$ of vertices of $Z$, which edges of $S$ lie on surviving paths between $u$ and $v$ — and the core of our argumentation is that there is only a limited number of reasonable choices. Such a branching step, while completely natural in the GFVS language, seems far-fetched and hard to guess in the ESFVS regime, in particular if one needs to argue about a limited number of subcases.

We would also like to mention that running time bound of both the algorithm of [10] and the algorithm of Theorem 1 have high polynomial dependency on the input size, due to the usage of iterative compression and multiple flow computations, and in this work we do not analyse this dependency in detail.

Finally, let us mention that after this work has been presented at WG 2012 [8], Wahlström [27] has shown how to generalize the LP-branching approach introduced in [9] to a number of graph separation problems and, among other results, he presented an $O^*(4^k)$-time algorithm for GFVS . At the same time, Iwata et al. [16] developed a way to perform several similar flow-based branching algorithms keeping only linear dependence on the input size in the running time bound. Their techniques turned out to be compatible with Wahlström’s approach [17], yielding a linear dependency on the input size in time bounds for all edge deletion problems considered in [27].

2 Preliminaries

2.1 Notation

We use standard graph notation. For a graph $G$, by $V(G)$ and $E(G)$ we denote its vertex and edge sets, respectively, and $uv$ denotes an edge between vertices $u$ and $v$. In case of a directed graph $G$, we denote the arc set of $G$ by $A(G)$, and $(u,v)$ denotes an arc pointed from $u$ to $v$. For $v \in V(G)$, its neighborhood $N_G(v)$ is defined as $N_G(v) = \{u: uv\in E(G)\}$, and $N_G[v] = N_G(v) \cup \{v\}$ is the closed neighborhood of $v$. We extend this notation to subsets of vertices: $N_G[X] = \bigcup _{v \in X} N_G[v]$ and $N_G(X) = N_G[X] {\setminus } X$. For a set $X \subseteq V(G)$ by $G[X]$ we denote the subgraph of $G$ induced by $X$. For a set $X$ of vertices or edges of $G$, by $G {\setminus } X$ we denote the graph with the vertices or edges of $X$ removed; in case of vertex removal, we remove also all the incident edges. By somehow abusing the notation, we often treat the (directed) $\varSigma$-labeled graph also as an undirected graph, as the neighborhood relation in the underlying undirected graph is the same.

In the Group Feedback Vertex Set problem definition in [14] a set of forbidden vertices $F \subseteq V(G)$ is additionally given as a part of the input. One can easily gadget such vertices by replacing each of them by a clique of size $k+1$ labeled with $1_\varSigma$; therefore, for the sake of simplicity we assume that all the vertices are allowed.

3 Algorithm

In this section we prove Theorem 1. We proceed with a standard application of the iterative compression technique in Sect. 3.1. In each step of the iterative compression, we solve a Compression Group Feedback Vertex Set problem, where we are given a solution $Z$ of size a bit too large — $k+1$ — and we are to find a new solution disjoint from it. We first prepare the Compression Group Feedback Vertex Set instance by untangling it in Sect. 3.2, in the same manner as it is done in the kernelization algorithm of [20]. The main step of the algorithm is done in Sect. 3.3, where we provide a set of reduction rules that enable us for each vertex $v \in Z$ to limit the number of choices for a value of a consistent labeling on $v$ to polynomial in $k$. Finally, we iterate over all $O^*(2^{O(k \log k)})$ remaining labelings of $Z$ and, for each labeling, reduce the instance to Multiway Cut (Sect. 3.4).

3.1 Iterative Compression

The first step in the proof of Theorem 1 is a standard technique in the design of parameterized algorithms, that is, iterative compression, introduced by Reed et al. [25]. Iterative compression was also the first step of the parameterized algorithm for Subset Feedback Vertex Set  [10].

We define a compression problem, where the input additionally contains a feasible solution $Z \subseteq V(G)$, and we are asked whether there exists a solution of size at most $k$ which is disjoint from $Z$.

In Sect. 3.2 we prove the following lemma providing a parameterized algorithm for Compression Group Feedback Vertex Set.

Lemma 4

The Compression Group Feedback Vertex Set problem can be solved in $O^*(2^{O(|Z|(\log k + \log |Z|))} \cdot 2^k)$ time and polynomial space.

Armed with the aforementioned result, we can easily prove Theorem 1.

Proof

(of Theorem 1) In the iterative compression approach we start with an empty solution for an empty graph, and in each of the $n$ steps we add a single vertex both to a feasible solution and to the graph; we use Lemma 4 to compress the feasible solution after guessing which vertices of the solution of size at most $k+1$ should not be removed.

Formally, for a given instance $(G=(V,A),\varLambda ,k)$ let $V = \{v_1, \ldots , v_n\}$. For $0 \le i \le n$ define $V_i = \{v_1,\ldots ,v_i\}$ (in particular, $V_0=\emptyset$) and let $\varLambda _i$ be the function $\varLambda$ restricted to the set of arcs $A_i=\{(u,v) \in A : u,v \in V_i\}$. Initially we set $X_0=\emptyset$, which is a solution to the graph $(G[V_0],\varLambda _0)$. For each $i=1,\ldots ,n$ we set $Z_i=X_{i-1} \cup \{v_i\}$, which is a feasible solution to $(G[V_i],\varLambda _i)$ of size at most $k+1$. If $|Z_i| \le k$, then we set $X_i=Z_i$ and continue the inductive process. Otherwise, if $|Z_i| = k+1$, we apply Lemma 4 to the instance $I_{Z_i'}=(G[V_i{\setminus } (Z_i {\setminus } Z_i')],\varLambda _i,k'=|Z_i'|-1,Z_i')$ for every choice of $Z_i' \subseteq Z_i$. If for each set $Z_i'$ the algorithm from Lemma 4 returns NO, then there is no solution for $(G[V_i],\varLambda _i)$ and, consequently, there is no solution for $(G,\varLambda )$. However, if for some $Z_i'$ the algorithm from Lemma 4 returns a set $X_i'$ of size smaller than $|Z_i'|$, then we set $X_i = (Z_i {\setminus } Z_i') \cup X_i'$. Since $|X_i| = |Z_i {\setminus } Z_i'| + |X_i'| < |Z_i| = k+1$, the set $X_i$ is a solution of size at most $k$ for the instance $(G_i,\varLambda _i)$.

Finally, we observe that since $(G_n,\varLambda _n)=(G,\varLambda )$, the set $X_n$ is a solution for the initial instance $(G=(V,A),\varLambda ,k)$ of Group Feedback Vertex Set. The claimed bound on the running time follows from the observation that $|Z_i|\le k+1$ for each of polynomially many steps. $\square$

At this point a reader might wonder why we do not add an assumption $|Z| \le k+1$ to the C-GFVS problem definition and parameterize the problem solely by $k$. The reason for this is that in Sect. 3.3 we will solve the C-GFVS problem recursively, sometimes decreasing the value of $k$ without decreasing the size of $Z$, and to always work with a feasible instance of the C-GFVS problem we avoid adding the $|Z| \le k+1$ assumption to the problem definition.

3.2 Untangling

In order to prove Lemma 4 we use the concept of untangling, previously used by Kratsch and Wahlström [20]. We transform an instance of C-GFVS to ensure that each arc $(u,v)$ with both endpoints in $V(G) {\setminus } Z$ is labeled $1_\varSigma$ by $\varLambda$.

Definition 3

We call an instance $(G=(V,A),\varLambda ,k,Z)$ of C-GFVS untangled, iff for each arc $(u,v) \in A$ such that $u,v \in V{\setminus } Z$ we have $\varLambda ((u,v))=1_\varSigma$.

Moreover, by untangling a labeling $\varLambda$ around vertex $x$ with a group element $g$ we mean changing the labeling to $\varLambda ':A \rightarrow \varSigma$, such that for $(u,v) = a \in A$, we have

$$\begin{aligned} \varLambda '(a)= \left\{ \begin{array}{ll} g \cdot \varLambda (a) &{} \mathrm{if } \,\, u = x;\\ \varLambda (a) \cdot g^{-1} &{} \mathrm{if } \,\, v = x; \\ \varLambda (a) &{} \mathrm{otherwise }. \end{array} \right. \end{aligned}$$

Lemma 5

Let $(G=(V,A),\varLambda )$ be a $\varSigma$-labeled graph, $x \in V$ be a vertex of $G$ and let $g \in \varSigma$ be a group element. For every subset of vertices $X \subseteq V$ the graph $(G{\setminus } X,\varLambda )$ contains a non-null cycle iff $(G{\setminus } X,\varLambda ')$ contains a non-null cycle, where $\varLambda '$ is the labeling $\varLambda$ untangled around the vertex $x$ with a group element $g$.

Proof

The lemma follows from the fact that for any cycle $C$ in $G$ we have $\varLambda (C)=1_\varSigma$ iff $\varLambda '(C)=1_\varSigma$. $\square$

In Sect. 3.3 we prove the following lemma.

Lemma 6

The Compression Group Feedback Vertex Set problem for untangled instances can be solved in $O^*(2^{O(|Z| (\log k + \log |Z|))} \cdot 2^k)$ time and polynomial space.

Having Lemmata 5 and 6 we can prove Lemma 4.

Proof

(of Lemma 4) Let $(G,\varLambda ,k,Z)$ be an instance of C-GFVS. Since $(G{\setminus } Z)$ has no non-null cycle, by Lemma 2 there is a consistent labeling $\lambda$ of $(G{\setminus } Z, \varLambda )$.

Let $\varLambda '$ be a result of untangling $\varLambda$ around each vertex $v \in V(G){\setminus } Z$ with $\lambda (v)$. Clearly, this operation can be done in polynomial time. Note that, by associativity of $\varSigma$, the order in which we untangle subsequent vertices does not matter. After all the untangling operations, for an arc $a=(u,v) \in A(G)$, such that $u,v \in V(G) {\setminus } Z$, we have $\varLambda '(a) = (\lambda (u) \cdot \varLambda (a)) \cdot \lambda (v)^{-1} = \lambda (v) \cdot \lambda (v)^{-1} = 1_\varSigma$. Therefore, by Lemma 5 the instance $(G,\varLambda ',k,Z)$ is an untangled instance of C-GFVS, which is a YES-instance iff $(G,\varLambda ,k,Z)$ is a YES-instance. Consequently, we can use Lemma 6 and the claim follows. $\square$

3.3 Fixing a Labeling on $Z$

In this section we prove Lemma 6 using the following lemma, which we prove in Sect. 3.4.

Lemma 7

Let $(G,\varLambda ,k,Z)$ be an untangled instances of C-GFVS. There is an algorithm which for a given function $\phi :Z\rightarrow \varSigma$, finds a set $X \subseteq V(G){\setminus } Z$ of size at most $k$, such that there exists a consistent labeling $\lambda :V(G){\setminus } X \rightarrow \varSigma$ of $(G{\setminus } X,\varLambda )$, where $\lambda |_{Z} = \phi$, or checks that such a set $X$ does not exist; the algorithm works in $O^*(2^k)$ time and uses polynomial space.

We could try all $(|\varSigma |+1)^{|Z|}$ possible assignments $\phi$ and use the algorithm from Lemma 7. Unfortunately, since $|\varSigma |$ is not our parameter we cannot iterate over all such assignments. Therefore, the goal of this section is to show that after some preprocessing, it is enough to consider only $2^{O(|Z|(\log k + \log |Z|))}$ assignments $\phi$; together with Lemma 2 and Lemma 7 this suffices to prove Lemma 6.

Definition 4

Let $(G,\varLambda ,k,Z)$ be an untangled instance of C-GFVS, let $z$ be a vertex in $Z$ and by $\varSigma _z$ denote the set $\varLambda (\{(z,v) \in A(G) : v \in V(G) {\setminus } Z\})$.

By a flow graph $F(G,\varLambda ,Z,z)$, we denote the undirected graph $(V',E')$, where $V' = (V(G) {\setminus } Z) \cup \varSigma _z$ and $E' = \{uv : (u,v) \in A(G[V(G) {\setminus } Z])\} \cup \{gv : (z,v) \in A(G), v \in V(G) {\setminus } Z, \varLambda ((z,v)) = g\}$.

Less formally, in the flow graph we take the underlying undirected graph of $G[V(G) {\setminus } Z]$ and add a vertex for each group element $g \in \varSigma _z$, that is a group element for which there exists an arc from $z$ to $V(G) {\setminus } Z$ labeled with $g$ by $\varLambda$. A vertex $g \in \varSigma _z$ is adjacent to all the vertices of $V(G) {\setminus } Z$ for which there exists an arc going from $z$, labeled with $g$ by $\varLambda$.

Lemma 8

Let $(G,\varLambda ,k,Z)$ be an untangled instance of C-GFVS. Let $H$ be the flow graph $F(G,\varLambda ,Z,z)$ for some $z \in Z$. If for some vertex $v \in V(H){\setminus } \varSigma _z$, there are at least $k+2$ paths in $H$ from $v$ to $\varSigma _z$ that are vertex disjoint apart from $v$, then $v$ belongs to every solution of C-GFVS.

Proof

Let us assume that $v$ is not a part of a solution $X \subseteq V(G){\setminus } Z$, where $|X| \le k$. Then at least $2$ out of the $k+2$ paths from $v$ to $\varSigma _z$ remain in $H {\setminus } X$. These two paths are vertex disjoint apart from $v$ and end in different elements of $\varSigma _z$, so they correspond to a non-null cycle in $G{\setminus } X$, a contradiction. $\square$

Definition 5

For an untangled instance $(G,\varLambda ,k,Z)$ of C-GFVS by an external path we denote any path $P$ beginning and ending in $Z$, but with all internal vertices belonging to $V(G){\setminus } Z$. Moreover, for two distinct vertices $z_1,z_2 \in Z$, by $\varSigma (z_1,z_2)$ we denote the set of all elements $g \in \varSigma$, for which there exists an external path $P$ from $z_1$ to $z_2$ with $\varLambda (P)=g$.

Note that an arc $(z_1,z_2)$ for $z_1,z_2\in Z$ also forms an external path from $z_1$ to $z_2$.

Lemma 9

Let $(G,\varLambda ,k,Z)$ be an untangled instance of C-GFVS. If for each $z \in Z$ and $v \in V(G) {\setminus } Z$ there are at most $k+1$ vertex disjoint paths from $v$ to $\varSigma _z$ in $F(G,\varLambda ,Z,z)$ and for some $z_1,z_2 \in Z$, $z_1 \ne z_2$, we have $|\varSigma (z_1,z_2)| \ge k^3(k+1)^2+2$, then there is no solution for $(G,\varLambda ,k,Z)$.

Proof

Let us assume that $X \subseteq V(G){\setminus } Z$ is a solution for $(G,\varLambda ,k,Z)$; in particular, $|X|\le k$. Let $\mathcal {P}$ be a set of external paths from $z_1$ to $z_2$, containing exactly one path $P$ for each $g \in \varSigma (z_1,z_2)$ with $\varLambda (P)=g$. Note that the only arcs with non-null labels in $P$ are possibly the first and the last arc.

By the pigeon-hole principle, there exists a vertex $w \in X$, which belongs to at least $k^2(k+1)^2+1$ paths in $\mathcal {P}$, since otherwise there would be at least two paths in $\mathcal {P}$ disjoint from $X$, creating a non-null closed walk disjoint from $X$. Note that existence of a non-null closed walk disjoint from $X$ is a sufficient proof that $X$ is not a solution to $(G,\varLambda ,k,Z)$, as it contradicts existence of a consistent labeling, guaranteed by Lemma 2.

Consider the connected component $C$ of $G[V(G) {\setminus } Z]$ to which $w$ belongs. Observe that there exists a vertex $z\in \{z_1,z_2\}$ that has at least $k(k+1)+1$ incident arcs going to $C$ with pairwise different labels in $\varLambda$, since otherwise $v$ would belong to at most $k^2(k+1)^2$ paths in $\mathcal {P}$.

Let $H$ be the flow graph $F(G,\varLambda ,Z,z)$ and let $T \subseteq \varSigma _z$ be the set of labels of arcs going from $z$ to $C$; recall that $|T| > k(k+1)$. Since there is no non-null cycle in $(G{\setminus } X,\varLambda )$, we infer that in $H_0 = H[C \cup T] {\setminus } (X\cap C)$, no two vertices of $T$ belong to the same connected component. Moreover, as $C$ is connected in $G$, for each $t \in T$ there exists a path $P_t$ with endpoints $w$ and $t$ in $H[C \cup T]$. Let $v_t$ be the closest to $t$ vertex from $X$ on the path $P_t$; note that such a vertex always exists, as $w\in X$. As $|X| \le k$ and $|T| > k(k+1)$, there exists $v \in X$ such that $v = v_t$ for at least $k+2$ elements $t \in T$. By the definition of the vertices $v_t$ and the fact that there are no two vertices of $T$ in the same connected component of $H_0$, the subpaths of $P_t$ from $t$ to $v_t$ for all $t$ with $v=v_t$ are vertex disjoint apart from $v$. As there are at least $k+2$ of them, we have a contradiction. $\square$

We are now ready to prove Lemma 6 given Lemma 7.

Proof

(of Lemma 6) If there exists a vertex $v$ satisfying the properties of Lemma 8, we can assume that it has to be a part of the solution; therefore, we can remove the vertex from the graph and solve the problem for decremented parameter value. Hence, we assume that for each $z \in Z$ and $v \in V(G) {\setminus } Z$, there are at most $k+1$ vertex disjoint paths from $v$ to $\varSigma _z$ in $F(G,\varLambda ,Z,z)$. We note that one can compute the number of such vertex disjoint paths in polynomial time, using a maximum flow algorithm.

Observe that one can easily compute the sets $\varSigma (z_1,z_2)$ for every $z_1,z_2 \in Z$, since the only non-null label arcs on paths contributing to $\varSigma (z_1,z_2)$ are the first and the last one, and we can iterate over all such arcs and check whether their endpoints are in the same connected component in $G[V(G) {\setminus } Z]$. Clearly, this can be done in polynomial time.

By Lemma 9, if there is a pair of vertices $z_1,z_2 \in Z$ with $|\varSigma (z_1,z_2)| \ge k^3(k+1)^2+2$, we know that there is no solution. Otherwise, we can enumerate all the reasonable labelings of $Z$ as follows. For the sake of analysis let $G'=(Z,E')$ be an auxiliary undirected graph, where two vertices of $Z$ are adjacent, when they are connected by an external path in $G{\setminus } X$, for some fixed solution $X \subseteq V(G) {\setminus } Z$. Let $F$ be any spanning forest of $G'$. Since $F$ has at most $|Z|-1$ edges, we can guess $F$, by trying at most

$$\begin{aligned} \sum _{i=0}^{|Z|-1} \left( {\begin{array}{c}\left( {\begin{array}{c}|Z|\\ 2\end{array}}\right) \\ i\end{array}}\right) = 2^{O(|Z| \log |Z|)} \end{aligned}$$

possibilities; in the above expression we iterate over all possible choices of $i = |E(F)|$, and then choose $i$ edges out of at most $\left( {\begin{array}{c}|Z|\\ 2\end{array}}\right)$ options.

Let us assume, that we have guessed $F$ correctly. Observe that for any two vertices $z_1, z_2 \in Z$, belonging to two different connected components of $F$, there is no path between $z_1$ and $z_2$ in $G {\setminus } X$. Therefore, there exists a consistent labeling of $G {\setminus } X$, which labels an arbitrary vertex from each connected component of $F$ with $1_\varSigma$. Having fixed the labeling on one vertex from each component of $F$, we can root the components in corresponding vertices and iteratively guess the labeling on the remaining vertices in a top-down manner. At each step we use the fact that if we have already fixed a value $\phi (z_1)$, then for each external path corresponding to an edge $z_1z_2$ of $F$, there are at most $k^3(k+1)^2+1$ possible values of $\phi (z_2)$, since $\phi ^{-1}(z_1) \cdot \phi (z_2) \in \varSigma (z_1,z_2)$; recall that we have already computed the sets $\varSigma (z_1,z_2)$ earlier in the process. Hence, having fixed $F$ there are at most $2^{O(|Z|\log k)}$ possible labelings $\phi$ of $Z$, as for each edge of the forest $F$ we choose one of at most $k^3(k+1)^2+1$ options. As the number of choices of $F$ is bounded by $2^{O(|Z|\log |Z|)}$, we obtain at most $2^{O(|Z|(\log k + \log |Z|))}$ labelings $\phi$ of $Z$ in total, and we can use Lemma 7 for each of them. $\square$

3.4 Reduction to Multiway Cut

In this section, we prove Lemma 7, by a reduction to Multiway Cut. A similar reduction was also used recently by Kratsch and Wahlström in the kernelization algorithm for Group Feedback Vertex Set parameterized by $k$ with constant $|\varSigma |$ [20]. Currently the fastest FPT algorithm for Multiway Cut is due to Cygan et al. [9], and it solves the problem in $O^*(2^k)$ time and polynomial space.

Proof

(of Lemma 7) Firstly, we check whether the given function $\phi$ satisfies $\phi (z_2) = \phi (z_1) \cdot \varLambda ((z_1,z_2))$, for each arc $(z_1,z_2) \in G[Z]$, since otherwise there is no set $X$ we are looking for.

Given a $\varSigma$-labeled graph $(G,\varLambda )$, a set $Z$, an integer $k$, and a function $\phi :Z \rightarrow \varSigma$, we create an undirected graph $G'=(V',E')$. As the vertex set, we set $V'=(V(G) {\setminus } Z) \cup T$ and $T=\{g : (u,v) \in A(G),\ u\in Z,\ v \in V(G) {\setminus } Z,\ \phi (u) \cdot \varLambda ((u,v)) = g\}$. Note that the set $T \cup \{1_\varSigma \}$ is exactly the set of potential labels for vertices in $V(G) {\setminus } Z$ of a consistent labeling of $(G,\varLambda )$ which extends $\phi$ on $Z$. Observe that we do not need to consider here arcs from $V(G) {\setminus } Z$ to $Z$, as in the definition of a $\varSigma$-labeled graph we have assumed that every arc $(u,v)$ with label $\varLambda ((u,v))$ is accompanied with an arc $(v,u)$ with label $\varLambda ((v,u)) = \varLambda ((u,v))^{-1}$. As the edge set, we set $E'=\{uv : (u,v) \in A(G[V(G) {\setminus } Z])\} \cup \{gv: (u,v) \in A(G),\ u\in Z,\ v\in V(G) {\setminus } Z,\ \phi (u) \cdot \varLambda ((u,v))=g\}$. We show that $(G',T,k)$ is a YES-instance of Multiway Cut iff there exists a set $X\subseteq V(G){\setminus } Z$, such that there exists a consistent labeling $\lambda$ of $(G{\setminus } X, \varLambda )$ with $\lambda |_Z=\phi$.

Let $X$ be a solution for $(G',T,k)$. We define a consistent labeling $\lambda$ of $(G{\setminus } X,\varLambda )$. For $v \in Z$ we set $\lambda (v) = \phi (v)$. For $v \in (V(G) {\setminus } Z) {\setminus } X$, if $v$ is reachable from a terminal $g \in T$ in $G'{\setminus } X$, we set $\lambda (v) = g$. If $v \in (V(G) {\setminus } Z) {\setminus } X$ is not reachable from any terminal in $G'$, we set $\lambda (v) = 1_\varSigma$. Since each arc in $A(G[V(G) {\setminus } Z])$ is labeled $1_\varSigma$ by $\varLambda$, and each vertex in $V(G) {\setminus } Z$ is reachable from at most one terminal in $G'{\setminus } X$, $\lambda$ is a consistent labeling of $(G{\setminus } X,\varLambda )$.

Let $X\subseteq V(G){\setminus } Z$ be a set of vertices of $G$, $|X| \le k$, such that there is a consistent labeling $\lambda$ of $(G{\setminus } X,\varLambda )$, where $\lambda |_Z=\phi$. By the definition of edges between $T$ and $V(G) {\setminus } Z$ in $G'$, each vertex of $V(G) {\setminus } Z$ is reachable from at most one terminal in $G'$, since otherwise $\lambda$ would not be a consistent labeling of $(G{\setminus } X,\lambda )$. Therefore, $X$ is a solution for $(G',T,k)$.

We can now apply the algorithm for Multiway Cut of [9] to the instance $(G',T,k)$ in order to conclude the proof. $\square$

4 Conclusions

We have shown a relatively simple fixed-parameter algorithm for Group Feedback Vertex Set running in time $O^*(2^{O(k \log k)})$. Our algorithm works even in a robust blackbox model, that allows us to generalize the recent algorithm for Subset Feedback Vertex Set [10] within the same complexity bound. In a subsequent work, Wahlström [27] improved the dependency on the parameter in the running time to $4^k$, using a significantly different approach.

We would like to note that if we represent group elements by strings consisting of $g$ and $g^{-1}$ for $g \in \varLambda (A(G))$ (formally, we perform the computations in the free group over generators corresponding to the arcs of the graph), then after slight modifications of our algorithm we can solve the Group Feedback Vertex Set problem even for infinite groups for which the word problem, i.e., the problem of checking whether results of two sequences of multiplications are equal, is polynomial-time solvable. The lengths of representations of group elements created during the computation can be bounded linearly in the size of the input graph. Therefore, if a group admits a polynomial-time algorithm solving the word problem, then we can use this algorithm as the blackbox.