Synthetic benchmarking of concentrated pyroclastic current models

Abstract

Validation and benchmarking of pyroclastic current (PC) models is required to evaluate their performance and their reliability for hazard assessment. Here, we present results of a benchmarking initiative built to evaluate four models commonly used to assess concentrated PC hazard: SHALTOP, TITAN2D, VolcFlow, and IMEX_SfloW2D. The benchmark focuses on the simulation of channelized flows with similar source conditions over five different synthetic channel geometries: (1) a flat incline plane, (2) a channel with a sharp 45° bend, (3) a straight channel with a break-in-slope, (4) a straight channel with an obstacle, and (5) a straight channel with a constriction. Several outputs from 60 simulations using three different initial volume fluxes were investigated to evaluate the performance of the four models when simulating valley-confined PC kinematics, including overflows induced by topographic changes. Quantification of the differences obtained between model outputs at t = 100 s allowed us to identify (1) issues with the Voellmy-Salm implementation of TITAN2D and (2) small discrepancies between the three other codes that are either due to various curvature and velocity formulations and/or numerical frameworks. Benchmark results were also in agreement with field observations of natural PCs: a sudden change in channel geometries combined with a high-volume flux is key to generate overflows. The synthetic benchmarks proved to be useful for evaluating model performance, needed for PC hazard assessment. The overarching goal is to provide an interpretation framework for volcanic mass flow hazard assessment studies to the geoscience community.

Résumé

La validation et l'analyse comparative des modèles numériques d’écoulements pyroclastiques sont nécessaires pour estimer leur performance et leur fiabilité lors de l'évaluation des risques naturels. Nous présentons ici les résultats d’une inter-comparaison de quatre modèles numériques couramment utilisés pour l’évaluation des risques causés par les écoulements pyroclastiques concentrés (EPC) : SHALTOP, TITAN2D, VolcFlow et IMEX_SfloW2D. L’analyse se concentre sur la simulation d'écoulements, ayant des conditions source similaires, sur cinq topographies numériques différentes : 1) un plan incliné plat, 2) un chenal avec un virage aigu à 45°, 3) un chenal droit avec une rupture de pente, 4) un chenal droit avec un obstacle, et 5) un chenal droit avec un rétrécissement. Afin d’évaluer précisément la capacité des quatre modèles à simuler la dynamique des EPC dans un chenal, ainsi que celle des débordements induits par les changements topographiques, trois flux volumiques différents à la source ont été utilisés. La quantification des différences obtenues entre les résultats des modèles à t = 100 s nous a permis d'identifier : 1) des problèmes d’implémentation de la rhéologie Voellmy-Salm dans TITAN2D, et 2) de légères divergences entre les trois autres codes, dues soit à des formulations différentes de la courbure de la topographie et/ou de la vitesse, soit à des schémas numériques différents. Les résultats de l’analyse sont également en accord avec les observations de terrain des EPC naturels : un changement soudain de la géométrie du chenal combiné à un flux volumique local élevé semble être les clés pour générer des débordements. Cette inter-comparaison synthétique s’est montrée très efficace pour évaluer la performance des modèles numériques. L'objectif global étant de proposer à la communauté des Géosciences un cadre d'étude pour l'évaluation des risques liés aux écoulements gravitaires d’origine volcanique.

Introduction

Motivation

Our current ability to simulate the behavior of pyroclastic currents (PCs) is limited by our incomplete knowledge of their internal dynamics. These fast-moving flows composed of hot volcanic particles and gas represent a threat for infrastructure and populations surrounding volcanoes (Neri et al. 2015; Brown et al. 2017). Advances in our knowledge have been hindered because of (i) the intrinsic dangers and costs of performing field studies on natural deposits just after their emplacement; (ii) the difficulties in investigating their internal structure and performing in situ measurements, and (iii) the complications of linking deposits with their unsteady and non-uniform flow behavior (Dufek et al. 2015). Both numerical modeling (Dartevelle 2004,b; Dufek and Bergantz 2007; Esposti Ongaro et al. 2008, 2012; Dufek et al. 2009; Benage et al. 2016; Kelfoun et al. 2017; Sweeney and Valentine 2017; Valentine and Sweeney 2018) and experimental modeling (Dellino et al. 2010; Roche et al. 2008, 2010; Roche 2012, 2015; Andrews 2014; Andrews and Manga 2011, 2012; Breard et al. 2016; Sulpizio et al. 2016; Breard and Lube 2017; Smith et al. 2018; Dellino et al. 2019; Brosch and Lube 2020) approaches have progressively emerged as one key alternative to study these hazardous flows and further enhancing the sedimentological and physical models of PCs, as summarized in recent review papers (Sulpizio et al. 2014; Dufek et al. 2015; Dufek 2016; Lube et al. 2020).

In this study, we adopt the term “pyroclastic current” in its most general sense as proposed by Palladino (2017). Pyroclastic currents display a strong vertical stratification of the volumetric particle concentration ranging from a concentrated regime (between 10 and 60vol.%) dominated by particle-particle interactions, to a dilute regime (less than a few vol.%; Weit et al. 2018) dominated by gas-particle interactions (Lube et al. 2020). When these two regimes coexist in a single PC, the flow is named concentrated pyroclastic current (CPC), which displays a concentrated basal zone and a dilute upper zone referred here as the “ash-cloud surge.” The interface between the two zones has intermediate and complex dynamics, dominated by exchanges of mass and momentum and by particle clustering (Breard and Lube 2017; Lube et al. 2020). Although it is recognized that both the concentrated and dilute systems coexist in most PCs, in some cases, no concentrated basal zone is observed (Valentine 2020), and the flow is named dilute pyroclastic current (DPC). While the study of the two endmembers, i.e., CPC and DPC, is essential to build a comprehensive PC model and to help in the interpretation of natural PC deposits, this study focuses on CPCs only.

A key process: PC overspilling

Small-volume CPCs, which display a volume inferior to 10⁸ m³ usually, are remarkably sensitive to the topography and stay mostly channelized into deep valleys (Cole et al. 2002; Tierz et al. 2016). Under specific circumstances, they can overspill from these valleys and inundate the surrounding slopes, often reaching inhabited areas away from the channelized flow paths. These inhabited areas may be unprepared for these hazards, and flow overspill events can cause damages and death. Here, two processes can be distinguished: (i) the “CPC overspill” for which the CPC, often accompanied by its upper ash-cloud surge but not always, escapes the volcanic valley, like at Merapi during the 2006 and 2010 eruptions (Charbonnier and Gertisser 2008; Lube et al. 2011; Gertisser et al. 2012; Charbonnier et al. 2013), at Volcán de Colima (Mexico) in 2015 (Macorps et al. 2018) or recently at Fuego volcano in 2018 (Charbonnier et al. 2019; Albino et al. 2020); (ii) the “ash-cloud surge detachment” for which only the dilute upper zone of the PC detaches and escapes the valley, like at Montserrat (Loughlin et al. 2002; Ogburn et al. 2014), Unzen (Nakada and Fujii 1993), or Merapi (Komorowski et al. 2013).

As we restricted our study to CPC only, we focus here on the CPC overspill process. Several field studies have shown that CPC overspill is likely to be controlled by two main parameters (Charbonnier and Gertisser 2008; Lube et al. 2011; Gertisser et al. 2012; Ogburn et al. 2014; Macorps et al. 2018):

(i) The morphology of the valley. Valleys in volcanic landscape display a wide range of morphologies, and CPC overspill events usually occur when the flow encounters a sudden topographical change (Gertisser et al. 2012; Ogburn et al. 2014). A modification of the channel geometry (both from natural causes and/or the result of human intervention) can potentially reduce the channel capacity (i.e., the maximum volume flux supported by a valley at a specific location), causing CPC to overspill. At least four main topographic features have been identified to have a significant impact on the CPC dynamics: a sharp valley bend (Ogburn et al. 2014; Macorps et al. 2018), a well-defined break in slope along the valley (Bourdier and Abdurackmann 2001; Charbonnier and Gertisser 2012), a sudden constriction of the valley width (Charbonnier and Gertisser 2008, 2011; Jenkins et al. 2013), and an obstacle obstructing the valley (i.e., sabo dam, lava ridges, bridges; Charbonnier and Gertisser 2008; Lube et al. 2011).

(ii) The CPC local volume flux into that valley at the overspill site. The capacity of a CPC to overspill channel confines is also controlled by how fast and how long it takes for the entire CPC mass to be transported down the channel slope. A large CPC volume flux, exacerbated by the pulsating behavior of CPCs in some eruptions, can locally exceed the channel capacity of a valley and allow the flow to overspill on the surrounding slopes. Previous studies at Soufriere Hills Volcano (Ogburn et al. 2014), Merapi (Charbonnier and Gertisser 2008; Cronin et al. 2013; Jenkins et al. 2013), or Volcán de Colima (Macorps et al. 2018) highlighted the direct link between the increase of the local CPC volume flux (calculated along the cross-sectional area of the channel) and the occurrence of CPC overspilling and/or ash-cloud surge detachment and decoupling phenomenon. A small-volume CPC generated by a short explosion or a small dome collapse may not generate any of these processes, but a voluminous and fast CPC generated by a large collapse of a fast-growing lava dome may generate flow overspilling and/or ash-cloud surge decoupling phenomenon, as its volume flux would be higher and exceeds the channel capacity in some areas.

Benchmarking of numerical models for concentrated pyroclastic currents

Because of the complex physics of PCs, various numerical codes have been developed throughout the years (more than 30 since Valentine and Wohletz (1989), see Table 1), while no rigorous PC model inter-comparison has been conducted yet. The urgent need for a community-wide PC model benchmark clearly arises today not only to better assess the applicability and performance of the various models available, but also to support and improve PC hazards assessment worldwide. A first attempt of a CPC model inter-comparison was conducted by Charbonnier and Gertisser (2012) using two of the most widely used mass flow models, i.e., VolcFlow and TITAN2D, based on the reproduction of the 2010 Merapi eruption. A second attempt was conducted recently by Ogburn and Calder (2017) who compared a larger variety of models (i.e., TITAN2D, VolcFlow, LAHARZ, and PFz) in their ability to reproduce a series of well-recorded block-and-ash flows from Soufrière Hills Volcano (Montserrat, West Indies, UK). Their approach was based on a best-fit procedure of field observations, using different sources, rheologies, and boundary conditions. Here, we present a benchmark study aiming at assessing model-related uncertainties by comparing flow simulations performed under similar source and boundary conditions, following the validation framework proposed by Esposti Ongaro et al. (2020) based upon a hierarchical procedure commonly adopted for complex engineering systems (Oberkampf et al. 2002).

Table 1 Compilation of the main modeling approaches and the related numerical models used to simulate concentrated pyroclastic currents. Italicized entries highlight models tested in this benchmark

Following Esposti Ongaro et al. (2020), we here distinguish between verification (i.e., the assessment of the mathematical correctness of a numerical model) and validation (i.e., the assessment of model reliability/performance with respect to the natural phenomenon). The validation procedure can be subdivided in four validation tiers, at an increasing level of complexity. At each level, the successful comparison of model results with reference datasets is a confirmation of model reliability (see Esposti Ongaro et al. 2020, section “Confirmation”). In this work, we have tested models that have already been verified and confirmed at the lowest validation Tier 3, against some reference Unit problems (i.e., simple experiments to test some fundamental physical behavior; see for example Mangeney et al. 2007; Gueugneau et al. 2017). We focus on Tier 2, Benchmarks, i.e., standardized problems having some degree of complexity, mainly concerning geometrical and scaling complications, for which full-scale experiments can be designed. In cases where experimental datasets are not (yet) available, synthetic benchmarks (also called inter-comparison studies) can be conceived to define the differences/similarities of the numerical models. In this framework, a benchmark is a preliminary step before the validation of models against a natural case. Numerous benchmark studies of this type have already been conducted in geosciences for volcanic plume models (Suzuki et al. 2016 in 3D and Costa et al. 2016, in 1D), lava flow models (Cordonnier et al. 2015; Dietterich et al. 2017), landslide/debris flow models (Landslide benchmarking initiative by the JTC1, Hungr et al. 2007 and Pastor et al. 2018), tsunamis (Horrillo et al. 2015), ocean processes (Martinec et al. 2018), or geothermal modeling (Wang et al. 2020).

We present here the results of the first synthetic benchmark of CPC models. Our inter-comparison is based on four commonly used geophysical mass flow models: VolcFlow (Kelfoun and Druitt 2005), TITAN2D (Patra et al. 2005), SHALTOP (Bouchut and Westdickenberg 2004; Mangeney-Castelnau et al. 2005; Mangeney et al. 2007), and IMEX_Sflow2D (De’Michieli Vitturi et al. 2019). An overview of PC modeling approaches and constitutive equations of each model is followed by the description of the source and boundary conditions used in our benchmarks. Flow simulation results are presented based upon several outputs, selected to accurately investigate numerical flow dynamics, and models are evaluated in their relative capacity to simulate natural-like equivalent: (i) CPC kinematics and (ii) CPC overspill processes induced by topographic changes. Models give consistent results for the four topographical cases but display noticeable differences in their degree of interaction with the topographic features. These differences are discussed and put into perspective for potential design of ad hoc validation experiments and current hazard assessment procedures for PCs.

Modeling concentrated pyroclastic currents

Overview of PC modeling approaches

The fluid dynamics of PCs is extremely complex, including a broad spectrum of phenomena, with a multi-scale interplay between inertial and dissipative processes occurring at a microscopic (e.g., particle-particle interactions), mesoscopic (e.g., turbulence, particle clustering), and macroscopic scale (e.g., bulk internal and basal friction, interaction with the topography, particle deposition; Freundt and Bursik 1998; Dartevelle 2004; Dufek et al. 2015; Dufek 2016; Lube et al. 2020; Esposti Ongaro et al. 2020). However, when limiting investigation to CPCs, some of the complexity can be reduced by neglecting the role of the multiphase processes (by adopting a mixture theory or neglecting the role of the interstitial fluids and the contribution of the kinetic stress to the bulk stress), heat exchange (assuming an isothermal approximation), turbulence (neglecting energy cascade in laminar flows), and the flow compressibility. Although such approximations can be questioned, it is common practice among volcanologists to consider CPCs to be controlled by inertial processes (pressure and gravity forces), topographic interaction, and frictional dissipation (Dufek et al. 2015).

To reproduce partially or entirely these fundamental elements of CPC dynamics, many codes have been developed, using different modeling techniques and approaches (Table 1). They can be divided into two main categories: (1) kinematic/empirical models based on statistical correlations or simple physical principles, preferentially used for uncertainty quantification and hazard inundation forecasting purposes (Iverson et al. 1998; Tierz et al. 2016, 2018; Aravena et al. 2020), and (2) models based on the fundamental laws of fluid dynamics, at different level of approximations, used for both hazard assessment and to study fundamental CPC processes and physical behavior. For the latter, two main sub-categories can be distinguished: multiphase flow models that consider the three-dimensional Navier Stokes equations for each constituent of the volcanic mixture, and depth-averaged models both for steady-state or transient dynamics, usually considering the eruptive mixture as a single (averaged) phase. For a comprehensive review of the different modeling approaches used to simulate PCs, we refer to Roche et al. (2013); Dufek (2016), and Esposti Ongaro et al. (2020).

Depth-averaged approach

In this study, we focus on two-dimensional, depth-averaged, transient mixture models because they constitute a good compromise between model reliability and computational requirements. Since the first mathematical formulation of the approach by Savage and Hutter (1989), depth-averaged models have been extensively used to model gravity-driven flows, especially for their ability to simulate some of their fundamental processes: flow sedimentation/deposition, sensitivity to the topography, and frictional behavior. Such gravity-driven flows include geophysical flows like landslides, debris flows, or rock avalanches (Denlinger and Iverson 2004; Iverson et al. 2004; Mangeney-Castelnau et al. 2003, Mangeney-Castelnau et al. 2005, Mangeney et al. 2007; Kelfoun and Druitt 2005; McDougall and Hungr 2004; Christen et al. 2010; George and Iverson 2014; Lucas et al. 2014; Brunet et al. 2017; Peruzzetto et al. 2019), as well as volcanic flows like CPCs (Sheridan et al. 2004; Kelfoun et al. 2009, 2017; Gueugneau et al. 2019, 2020; Salvatici et al. 2016) or lava flows (Bernabeu et al. 2014; Kelfoun and Vallejo Vargas 2015 ).

Introduced by de Saint-Venant (1871), the depth-averaged approach considers that for thin flows (i.e., flow length far exceeding flow thickness, which is the case for CPCs), reduction of model dimensionality can be obtained by formally integrating the incompressible fluid dynamics equations along the vertical dimension and by neglecting the vertical component of the acceleration. With this approximation, the pressure reduces to hydrostatic and the equation for the vertical component of momentum can be disregarded. In addition, the energy equation is often neglected, the flow being considered as isothermal.

On a flat surface, in a Cartesian coordinate system with x and y horizontal, z vertical, and where h(x, y, t) is the flow depth parallel to z, the Saint-Venant’s equations (also called shallow-water equations) can be simply derived and expressed as the balance equations of mass (Eq. 1) and momentum (Eqs. 2 and 3):

$$\frac{\partial h}{\partial t}+\frac{\partial }{\partial x}\left(h{u}_x\right)+\frac{\partial }{\partial y}\left(h{u}_y\right)=0$$

(1)

$$\frac{\partial }{\partial t}\left(h{u}_x\right)+\frac{\partial }{\partial x}\left(h{u}_x^2+\frac{1}{2}g{h}^2\right)+\frac{\partial }{\partial y}\left(h{u}_x{u}_y\right)=\frac{\tau_x}{\rho }$$

(2)

$$\frac{\partial }{\partial t}\left(h{u}_y\right)+\frac{\partial }{\partial x}\left(h{u}_x{u}_y\right)+\frac{\partial }{\partial y}\left(h{u}_y^2+\frac{1}{2}g{h}^2\right)=\frac{\tau_y}{\rho }$$

(3)

where u_x and u_y are the components of the velocity vector u, g is the gravitational acceleration along z, ρ the average flow density, and τ_x and τ_y are the components of the resistive stress, usually neglected for fluids such as water.

For thin flows over a non-planar surface, the formulation is less simple since longitudinal driving forces and non-hydrostatic terms can be non-negligible. Two main approaches are used in the scientific literature to formulate the mathematical problem in such case. Savage and Hutter (1989) first introduced the use of a local, boundary-fitted coordinate system (Fig. 1B). Its formulation is intuitive but entails complex geometric transformations involving curvature terms (Iverson and Denlinger 2001). The second uses universal Cartesian coordinates (Fig. 1A) and does not require a geometrical transformation but implies non-hydrostatic (and non-hyperbolic) terms in the depth-averaged equations (e.g., Denlinger and Iverson 2004; Juez et al. 2013). The transformation between the two coordinate systems can be difficult in the case of a realistic topography, but the two approaches are generally considered equivalent for simple geometries (i.e., for gentle slopes and small topographic variations), even though no rigorous comparison between the resulting models has been performed yet.

Fig. 1

The two different coordinate systems used for depth-averaged models: a absolute coordinate system using the cartesian reference frame (X,Y,Z); b local boundary-fitted coordinate system (x,y,z), tangent to the topography

Rheology

The resistive stresses τ_x and τ_y (or shear stresses) are non-negligible in geophysical flows, and rheological laws must be used to describe them. Due to the small number of parameters needed to reproduce first-order dynamics of gravity-driven flows (Gruber and Bartelt 2007; Hungr 2008; Fisher et al. 2012; Lucas et al. 2014; McDougall 2017), two rheological laws are commonly used in the literature: (i) The Coulomb rheology that links the normal stress σ applied by the flow on the ground to its tangential stress (friction) τ by a friction coefficient μ, after a certain threshold C (i.e., cohesive stresses):

$$\tau =\mu\ \sigma +C$$

(4)

and (ii) the Voellmy-Salm rheology, developed initially for snow avalanches (Voellmy 1955; Salm et al. 1990), based on the Coulomb rheology with a velocity-dependent dissipative term added to account for particle collisions and interparticle frictions:

$$\tau =\mu\ \sigma +\frac{\rho g{u}^2}{\xi }$$

(5)

where ξ is the empirical Voellmy coefficient, ρ the flow density, g the gravity, and u the flow velocity.

In these two rheologies, the friction and Voellmy coefficients are constant during the flow emplacement and friction stresses only varies with the normal stress (i.e., flow thickness and flow velocity). The choice of a correct value for each of these rheological parameters is then crucial. The friction coefficient is usually estimated using the ratio H/L (vertical drop over horizontal length of the flow). Recent studies have shown that the coefficient decreases as the flow volume or runout distance increases (Charbonnier and Gertisser 2012; Lucas et al. 2014). The Voellmy coefficient is known to vary with topographic roughness, i.e., the higher the roughness, the higher the dissipative term, so the lower the Voellmy coefficient (Gruber and Bartelt 2007; Fisher et al. 2012). In the case of CPCs, different studies have pointed out that a constant friction coefficient (i.e., Coulomb rheology) is too simplistic to accurately represent their complex behavior (Kelfoun et al. 2009; Kelfoun 2011; Moretti et al. 2012; Gueugneau et al. 2019). Other rheologies have been tested: some authors found that using a constant resistive stress allow to better model CPC emplacement dynamics (Kelfoun 2011; Gueugneau et al. 2017, 2019; Ogburn and Calder 2017) while recent studies pointed out that the Voellmy rheology, with a velocity-dependent dissipative term, can also model first-order CPC dynamics (Kelfoun 2011; Salvatici et al. 2016; De’Michieli Vitturi et al. 2019; Patra et al. 2020). Even though all four selected models have the capability of using more complex rheologies to further explore the physics of PCs (which is beyond the scope of this paper), the Voellmy-Salm rheology was chosen for this benchmarking exercise.

Models in local boundary-fitted coordinates

In local coordinates, the same approach used to derive Eqs. (1)–(3) can be adopted, in which (x, y) represent, in each point of the domain, the coordinate directions tangent to the 2D surface, while (h) is the flow thickness in the direction normal to the tangent plane (Fig. 1B). The depth-averaged balance equation can be written in this reference frame as:

$$\frac{\partial h}{\partial t}+\frac{\partial }{\partial x}\left(h{u}_x\right)+\frac{\partial }{\partial y}\left(h{u}_y\right)=0$$

(6)

$$\frac{\partial }{\partial t}\left(h{u}_x\right)+\frac{\partial }{\partial x}\left(h{u}_x^2\right)+\frac{\partial }{\partial y}\left(h{u}_x{u}_y\right)={S}_x$$

(7)

$$\frac{\partial }{\partial t}\left(h{u}_y\right)+\frac{\partial }{\partial x}\left(h{u}_x{u}_y\right)+\frac{\partial }{\partial y}\left(h{u}_y^2\right)={S}_y$$

(8)

The terms on the right side of the momentum balance Eqs. (7) and (8) are source terms which correspond to the sum of all forces applied to the fluid and can be expressed as:

$${S}_i=\underset{\left[1\right]}{\underbrace{g_ih}}-\underset{\left[2\right]}{\underbrace{\frac{1}{2}\frac{\partial }{\partial i}\left({g}_z{h}^2\right)}}-\underset{\left[3\right]}{\underbrace{\tau_i/\rho }}$$

(9)

with (1) the gravity acceleration component expressed along the x and y axis, (2) the hydrostatic pressure acceleration component, and (3) the resistive stress component. The gravity vector $\overrightarrow{g}$ is expressed with its three components in the local coordinate system $\overrightarrow{g}=\left({g}_x,{g}_y,{g}_z\right)$, as shown in Fig. 1B. The resistive stress τ, initially depth-averaged by Savage and Hutter (1991) in local coordinates for granular flows with a Coulomb rheology on an arbitrary topography, can be written as follows using the Voellmy rheology:

$${\tau}_i=\frac{u_i}{\left\Vert \boldsymbol{u}\right\Vert}\left(\mu \rho h\left( gcos\left(\theta \right)+\frac{{\left\Vert \boldsymbol{u}\right\Vert}^2}{r}\right)+\frac{\left\Vert \boldsymbol{g}\right\Vert }{\xi }{\left\Vert \boldsymbol{u}\right\Vert}^2\right)$$

(10)

where ρ is the flow density, h its thickness, and $\left\Vert \boldsymbol{u}\right\Vert =\sqrt{u_x^2+{u}_y^2}$ is the norm of the flow velocity in the topography-linked coordinate system. The topography is implemented by two different elements: (i) the ground slope angle θ to ensure that the normal stresses stay normal to the local topography, and (ii) centrifugal acceleration effects caused by terrain curvature that can be approximated by the term $\frac{{\left\Vert \boldsymbol{u}\right\Vert}^2}{r}$, with r the local curvature radius in the direction of the flow, according to the scale analysis of Savage and Hutter (1989). The computation of r is not straightforward, and several approximations have been suggested, as described further. The exact expression of the curvature involves the topography curvature tensor and not only a scalar r (Mangeney-Castelnau et al. 2005; Mangeney et al. 2007; Peruzzetto et al. 2021). Two of the models described below and tested in this benchmark are based on the local-coordinate formulation.

VolcFlow (Kelfoun and Druitt 2005) was developed to simulate volcanic mass flows like debris avalanches, lahars, lava flows, and CPCs but can also be applied to simulate other geophysical flows such as landslides and tsunamis (Giachetti et al. 2011). It relies on a finite-difference method that solves the hyperbolic part of partial differential Eqs. (6) to (8) using a first- or second-order upwind scheme. The model enables the choice of different rheologies from viscous rheologies like Newtonian and Bingham, plastic rheologies, or granular rheologies such as Coulomb or Voellmy. Hence, using the Voellmy rheology, the source terms can be written as:

$${S}_x={g}_xh-\frac{1}{2}\frac{\partial }{\partial x}\left({g}_z{h}^2\right)-\frac{u_x}{\left\Vert \boldsymbol{u}\right\Vert}\left( h\mu \left({g}_z+\frac{{\left\Vert \boldsymbol{u}\right\Vert}^2}{r}\right)+\varepsilon {\left\Vert \boldsymbol{u}\right\Vert}^2\right)$$

(11)

$${S}_y={g}_yh-\frac{1}{2}\frac{\partial }{\partial y}\left({g}_z{h}^2\right)-\frac{u_y}{\left\Vert \boldsymbol{u}\right\Vert}\left( h\mu \left({g}_z+\frac{{\left\Vert \boldsymbol{u}\right\Vert}^2}{r}\right)+\varepsilon {\left\Vert \boldsymbol{u}\right\Vert}^2\right)$$

(12)

where $\varepsilon =\frac{\left\Vert \boldsymbol{g}\right\Vert }{\xi }$, and g_x, g_y, g_z are the gravity components calculated following: g_z = gcos(α), g_x = gsin(α_x), and g_y = gsin(α_y), with α the ground slope angle, and α_x and α_y being the slope angles in the xz and yz planes respectively (see Fig. 1B). In this code, the curvature radius r is calculated using the approximated formulation:

$$r=\sin \left(\alpha \right){\gamma}_x+\cos \left(\alpha \right){\gamma}_y$$

(13)

where γ_x and γ_x are the topography curvature in the direction x and y, calculated following:

$${\gamma}_x=\frac{\partial^2z}{\partial {x}^2}+{\left(1+{\left(\frac{\partial z}{\partial x}\right)}^2\right)}^{-3/2}$$

(14)

$${\gamma}_y=\frac{\partial^2z}{\partial {y}^2}+{\left(1+{\left(\frac{\partial z}{\partial y}\right)}^2\right)}^{-3/2}$$

(15)

The code, written in Matlab, has been verified in Kelfoun and Druitt (2005) and Kelfoun (2017) and confirmed/validated for CPCs in Kelfoun et al. (2009), Charbonnier and Gertisser (2012), and Gueugneau et al. (2017) using an alternate version including pore pressure, and more recently in Kelfoun et al. (2017), Gueugneau et al. (2019, 2020), and Charbonnier et al. (2020) using the two-layer version of the code (Kelfoun 2017).

TITAN2D (Patra et al. 2005) was developed initially to model geophysical mass flows. It has been extensively used in volcanology to simulate CPCs. TITAN2D relies on a finite-volume method (i.e., fluxes are based on the centroid of each cells) and solves hyperbolic partial differential equations using a first- or second-order Gudonov scheme, for which a local grid refinement (adaptive mesh refinement — AMR) is used to increase the accuracy of the simulation, while reducing the computational cost. The friction forces are also expressed following the Savage and Hutter approach with the Coulomb rheology but can also integrate the Pouliquen and Voellmy rheologies as well (Simakov et al. 2019). For the latter, source terms can be written as:

$${S}_x={g}_xh-\frac{1}{2}\frac{\partial }{\partial x}\left({g}_z{h}^2\right)-\frac{u_x}{\left\Vert \boldsymbol{u}\right\Vert}\left( h\mu \left({g}_z+\frac{{\left\Vert \boldsymbol{u}\right\Vert}^2}{r_x}\right)+\frac{\left\Vert \boldsymbol{g}\right\Vert }{\xi }{\left\Vert \boldsymbol{u}\right\Vert}^2\right)$$

(17)

$${S}_y={g}_yh-\frac{1}{2}\frac{\partial }{\partial y}\left({g}_z{h}^2\right)-\frac{u_y}{\left\Vert \boldsymbol{u}\right\Vert}\left( h\mu \left({g}_z+\frac{{\left\Vert \boldsymbol{u}\right\Vert}^2}{r_y}\right)+\frac{\left\Vert \boldsymbol{g}\right\Vert }{\xi }{\left\Vert \boldsymbol{u}\right\Vert}^2\right)$$

(18)

where g_x, g_y,and g_z are the projections of the gravity vector g along x,y and z axis. Here, the curvature is also approximated, but in contrast to VolcFlow, two curvature terms are calculated in the x and y directions by a simplified formulation:

$$\frac{1}{r_x}=\frac{\partial^2z}{\partial {x}^2}$$

(19)

$$\frac{1}{r_y}=\frac{\partial^2z}{\partial {y}^2}$$

(20)

This code, written in C, has been verified in Patra et al. (2005) and confirmed/validated for CPCs in various studies, for example by Sheridan et al. (2004), Sulpizio et al. (2010), Capra et al. (2011), Charbonnier and Gertisser (2009, 2012), Stefanescu et al. (2012), Tierz et al. (2018), and Patra et al. (2020).

Models in absolute coordinates

Use of an absolute Cartesian system (such as, for example, the Universal Transverse Mercator — UTM — coordinate system) facilitates the incorporation of a georeferenced topography and the formulation of the transport equations. However, treatment of non-hydrostatic terms can be problematic in case of complex geometries since it gives rise to non-hyperbolic terms in the transport equations (Bouchut and Westdickenberg 2004; Denlinger and Iverson 2004; Castro-Orgaz et al. 2015).

Two of the models tested in this benchmark are based on the global-coordinate formulation.

IMEX-SfloW2D (de’Michieli Vitturi et al. 2019) was developed to simulate geophysical mass flow over 3D topographies. The model adopts an absolute Cartesian (X, Y, Z) reference frame (Fig. 1A), so that mass and momentum equations are integrated along the axis Z parallel to the gravity g. The present formulation of the code neglects non-hydrostatic terms associated with steep slopes and rugged topographies. Therefore, its formulation can be easily recast in a local coordinate system for gentle slopes. The model is based on the finite-volume method, and it is discretized in time with an explicit–implicit Runge-Kutta method, in which the hyperbolic part of the governing equations is solved explicitly with a second-order central-upwind scheme. The main novelty of this model is the implicit treatment of the source terms, which is a key feature to properly model flow stopping (when friction becomes dominant). The model integrates the topography as the function b = b(X, Y), which can be imported as a georeferenced digital elevation model.

$$\frac{\partial h}{\partial t}+\frac{\partial }{\partial X}\left(h{u}_X\right)+\frac{\partial }{\partial Y}\left(h{u}_Y\right)=0$$

(21)

$$\frac{\partial }{\partial t}\left(h{u}_X\right)+\frac{\partial }{\partial X}\left(h{u}_X^2\right)+\frac{\partial }{\partial Y}\left(h{u}_X{u}_Y\right)+ gh\frac{\partial \left(h+b\right)}{\partial X}={S}_X$$

(22)

$$\frac{\partial }{\partial t}\left(h{u}_Y\right)+\frac{\partial }{\partial X}\left(h{u}_X{u}_Y\right)+\frac{\partial }{\partial Y}\left(h{u}_Y^2\right)+ gh\frac{\partial \left(h+b\right)}{\partial Y}={S}_Y$$

(23)

In the first version of the model, the code only integrates the Coulomb and Voellmy rheologies and does not integrate non-hydrostatic corrections (i.e., curvature effect; will be added in the future). Therefore, source terms are written as:

$${S}_X=-\frac{u_X}{\left\Vert \boldsymbol{u}\right\Vert}\left( h\mu {g}_n+\frac{g}{\xi }{\left\Vert \boldsymbol{u}\right\Vert}^2\right)$$

(24)

$${S}_Y=-\frac{u_Y}{\left\Vert \boldsymbol{u}\right\Vert}\left( h\mu {g}_n+\frac{g}{\xi }{\left\Vert \boldsymbol{u}\right\Vert}^2\right)$$

(25)

where $\left\Vert \boldsymbol{u}\right\Vert =\sqrt{u_X^2+{u}_Y^2}$ and g_n is the component of the gravity acceleration g = (0; 0; −g) along the surface normal vector n, given by:

$${g}_n=\mathbf{g}\bullet \mathbf{n}=\frac{g}{\sqrt{1+{\left(\frac{\partial b}{\partial x}\right)}^2+{\left(\frac{\partial b}{\partial y}\right)}^2}}$$

(26)

The code, open source and written in FORTRAN90, has been verified and tested against standard unit problems and applied to the 2014 CPCs from Mount Etna in de’Michieli Vitturi et al. (2019) and to the 2008 Chaiten CPCs in Aravena et al. (2020).

SHALTOP was developed to simulate landslides and debris avalanches. The numerical method used to solve the hyperbolic equation system relies on a finite volume formulation (second-order upwind scheme) coupled with the apparent topography approach of Bouchut et al. (2003) to deal with friction (Mangeney et al. 2007). The detailed derivation of SHALTOP mass and momentum equations is given in Bouchut et al. (2003) for flows on 1D topographies, and in Bouchut and Westdickenberg (2004) for flows on complex topographies. A discussion on these derivations is provided in Peruzzetto et al. (2021). The integration of mass and momentum equations is performed in the direction normal to the topography, which requires the use of an appropriate frame linked to the topography (see Fig 1A and Peruzzetto et al. 2021). However, the final equations for the depth-averaged velocity $\overrightarrow{V}$ are given in the fixed Cartesian coordinate system (X, Y, Z) = (X, Z), with X = (X, Y). In the following, the notation $\overrightarrow{}$ is used for 3D vectors, and the bold notation is used for 2D vectors. The slope θ of the topography b = b(X, Y) = b(X) is given by:

$$\cos \left(\theta \right)={\left(1+{\left\Vert {\nabla}_{\mathbf{X}}b\right\Vert}^2\ \right)}^{{~}^{-1}\!\left/\!\!{~}_{2}\right.}$$

(27)

Then, s = cos(θ)∇_Xb such that the unit vector tangent to the topography is

$$\overrightarrow{n}=\left(-\mathbf{s},\cos \left(\theta \right)\right)$$

(28)

With these notations, $\overrightarrow{V}$ is parameterized with u = (u, u_t) following:

$$\overrightarrow{V}=\left(\cos \left(\theta \right)\mathbf{u},{\mathbf{s}}^t\mathbf{u}\right)$$

(29)

where the first two components are given by cos(θ)u, and the last component of $\overrightarrow{V}$ is deduced from the constraint that $\overrightarrow{V}$ is tangent to the topography (that is, ${\overrightarrow{V}}^t\overrightarrow{n}=0$). s^tu is the scalar product of s and u (^t is the transpose operator). With these notations, the norm of physical depth-average velocity is given by:

$$\left\Vert \overrightarrow{V}\right\Vert ={\left({\left(\cos \left(\theta \right)\left\Vert \mathbf{u}\right\Vert \right)}^2+{\left({\mathbf{s}}^t\mathbf{u}\right)}^2\right)}^{{~}^{1}\!\left/\!\!{~}_{2}\right.}$$

(30)

The formal derivation of the SHALTOP equations involves the topography curvature. The topography curvature tensor is given by:

$$\mathcal{H}={\cos}^3\left(\theta \right)\left(\begin{array}{cc}\frac{\partial^2b}{\partial {X}^2}& \frac{\partial^2b}{\partial X\partial Y}\\ {}\frac{\partial^2b}{\partial X\partial Y}& \frac{\partial^2b}{\partial {Y}^2}\end{array}\right)$$

(31)

With these equations, SHALTOP solves the mass and momentum equation for u and h, the thickness of the material layer in the direction normal to the topography, following:

$$\frac{\partial }{\partial t}\left(\frac{h}{\cos \left(\theta \right)}\right)+{\nabla}_{\mathbf{X}}\cdot \left(h\mathbf{u}\right)=0$$

(32)

$$\frac{\partial \left(h\mathbf{u}\right)}{\partial t}+\cos \left(\theta \right){\nabla}_{\mathbf{X}}\cdot \left(h\ \left(\mathbf{u}\otimes \mathbf{u}\right)\right)=\mathbf{S}$$

(33)

Hence, SHALTOP’s source term S is written:

$$\mathbf{S}={\mathbf{F}}_g+{\mathbf{F}}_{\gamma }+{\mathbf{F}}_{frictions}$$

(34)

with F_g the gravity and lateral pressure forces (corresponding to the terms [1] and [2] in Eq. (9)), and F_γ is the curvature force following:

$${\mathbf{F}}_g=-\frac{h}{\cos \left(\theta \right)}\left( Id-{\mathbf{ss}}^t\right){\nabla}_{\mathbf{X}}\ \left(g\left(h\ \cos \left(\theta \right)+b\right)\right)$$

(35)

$${\mathbf{F}}_{\gamma }=-\frac{h}{\cos \left(\theta \right)}\left({\mathbf{u}}^t\mathcal{H}\mathbf{u}\right)\mathbf{s}+\frac{h}{\cos \left(\theta \right)}\left({\mathbf{s}}^t\mathcal{H}\mathbf{u}\right)\mathbf{u}$$

(36)

With the Voellmy rheology, the friction forces of the flow are:

$${\mathbf{F}}_{friction}=-\frac{h\mu g\cos \left(\theta \right)\mathbf{u}}{\left\Vert \overrightarrow{V}\right\Vert}\left(1+\frac{{\mathbf{u}}^t\mathcal{H}\mathbf{u}}{g\cos \left(\theta \right)}\right)-g\frac{\mathbf{u}\left\Vert \overrightarrow{V}\right\Vert }{\xi }$$

(37)

Note that curvature effects influence two terms in SHALTOP: the friction forces F_frictions (as in the previous codes), but also the curvature force F_γ. SHALTOP also allows for the selection of other granular rheologies like Coulomb or Pouliquen, or viscous fluid rheologies like Newton or Bingham. SHALTOP, written in FORTRAN90, has been used successfully to reproduce both granular flows at the laboratory scale (Mangeney-Castelnau et al. 2005; Mangeney et al. 2007) as well as real landslides deposits (i.e., Lucas et al. 2014; Brunet et al. 2017; Peruzzetto et al. 2019) and dynamics inferred from seismic recordings (Favreau et al. 2010; Moretti et al. 2015, 2020; Yamada et al. 2016). It has also been proven efficient to study CPCs induced by partial dome collapse (Levy et al. 2015).

Building a synthetic benchmarking procedure

Because such overspill events represent one of the deadliest and most unpredictable characteristics of CPCs, the source and boundary conditions used in this benchmarking procedure consider both the volume flux in the valley and synthetic channel topographies as modular input parameters.

Synthetic topographies

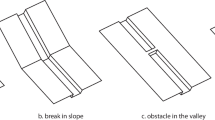
To investigate the role of various channel morphology on CPC models, five synthetic topographies were built for this benchmark (Fig. 2; Table 2): four of them contain a channel with a significant topographic feature (as described earlier) while the last one is an inclined plane, used as a control case for our four benchmarked models. These synthetic topographies are restricted to a rectangular domain of 5000 m long and 1500 m wide, enough to contain a valley and its surroundings, and with a scale similar to areas affected by small-volume CPCs, like block-and-ash flows (BAFs; Brown 2015). These topographies are generated numerically as digital elevation models (DEMs), with regular grids of 1000 × 300 cells of 5 m spatial resolution. The synthetic longitudinal profile was simplified into a constant slope of 20°, obtained by averaging the H/L (vertical drop over horizontal length) ratio of 80 BAFs as found in the database FlowDat (Ogburn 2012) and measured at Merapi, Unzen, Soufriere Hills, and Colima volcanoes. A single pseudo-sinusoidal valley (in cross-section) 80–120 m wide and 60 m deep is dug at the center of the domain. The synthetic topographies are:

• 1. Inclined plane case (Fig. 2a): rectangular and planar surface of 5000 by 1500 m with a 20° slope

• 2. Bend case (Fig. 2b): designed as a channel with two opposed 45° angles bends starting at 1500 m from the source, and distant of 500 m from each other. The channel depth (60 m) is not modified along the bends

• 3. Break in slope case (Fig. 2c): designed as a straight channel, but with a well-defined change of slope angle at 2500 m from the source, decreasing from 20° proximally to 10° distally

• 4. Obstacle case (Fig. 2d): designed as a straight channel composed of an obstacle located at 2500 m from the source, of 50 m long and 40 m high, corresponding to roughly two-thirds of the channel depth (60 m)

• 5. Valley constriction case (Fig. 2e): designed as a straight channel with a sharp narrowing of its width from 1500 to 3000 m from the source, switching from a 120- to 50-m wide channel cross section

Fig. 2

Representation of the five synthetic topographies with their key features: a the inclined plane case; b the bend case; c the break in slope case; d the obstacle case and e. the constriction case. The channel morphology is shown on the side of each topography, along with its dimensions. See text for explanations

Table 2 Summary of the selected dimensions for the four synthetic topographies

Modeled CPC volume flux

To accurately evaluate CPC models in their capacity to overspill from a volcanic valley, different volumetric rates are set as fixed source conditions in our benchmarks to generate flows with different initial volume fluxes. A total volume of V = 1 × 10⁶ m³ is selected, corresponding to the mean volume of 80 BAFs selected from the FlowDat database (Ogburn 2012), with values ranging from 10⁵ to 10⁷ m³. To input a volumetric rate in the models, the total volume is discretized into sub-volumes supplied at each time step, during a specific duration Δt. A decreasing volumetric rate at the source was chosen for all four models: the volume per time step decreases linearly from an initial volume V_ini to 0 during the duration Δt. Three different scenarios are defined, i.e., high, medium, and low, in which the total volume V = 1 × 10⁶ m³ is supplied at three different rates, represented in Fig. 3, and summarized in Table 3.

Fig. 3

Initial volumetric/mass fluxes set as fixed input parameters in all four models for the three scenarios considered in this benchmark (see also Table 3)

Table 3 Description of the source conditions for each of the scenarios selected for the synthetic benchmarks

Procedure and inputs/outputs parameters

Each of the four selected models was evaluated on all five synthetic topographies. Thus, for each topographic case, the three volumetric rate scenarios (i.e., low, medium-, and high-volume flux) were simulated independently, leading to a total number of 15 simulations per model, or 60 simulations for the entire benchmark exercise. For each simulation, the same input parameter values were used and kept constant to ensure each model run was performed under the exact same conditions. While a representative flow density is not required in these models (simplified in their system of equations), rheological parameter values, such as the friction coefficient μ and the Voellmy drag coefficient ξ, need to be defined. Since the Voellmy law uses empirical parameters, representative values of the two empirical coefficients were taken from a compilation of previous studies: Kelfoun (2011) used the values 0.08–0.19; 10 m s⁻² with VolcFlow for the friction coefficient μ and the Voellmy drag coefficient ξ, respectively, whereas de’Michieli Vitturi et al. (2019) used values of 0.1–0.4; 500 m s⁻² with IMEX_SfloW2D, Salvatici et al. (2016) used values of 0.19; 1000 m s⁻² with DAN3D, and Patra et al. (2020) used 0.5; 120 m s⁻² with TITAN2D. Combining values from these previous studies, the average couple 0.2; 750 m s⁻² was selected for this benchmark.

The source (as represented by black dots in Fig. 2) is approximated here as a circular spot with a 25-m radius set at the center of the valley (center of the domain for the inclined plane) and at 500 m from the domain top boundary (to avoid back flow issues). Simple boundary conditions are considered, with free inlet/outlet for flows at the borders and absence of surface roughness. All the input parameters and boundary conditions are summarized in Table 4.

Table 4 Summary of the selected input parameters and boundary conditions for each simulation

The ability of our simulations to reproduce natural cases cannot be quantified because we do not have a reference case for each scenario. However, results from each simulation can be compared and the differences observed can be quantified. For consistency and to facilitate post-processing analyses, all simulations are manually stopped at 100 s, and the following simulation outputs are used to evaluate the performance of each model:

• The maximum inundated area of the flow at t = 100 s

• The maximum runout of the flow at t = 100 s

• The evolution of the flow thickness through time at two locations of interest along the channel from t = 0 s to t = 100 s

• The evolution of the center of mass velocity through time from t = 0 s to t = 100 s

• The evolution of the front velocity through time from t = 0 s to t = 100 s

As all simulations are artificially stopped after 100 s (i.e., flows are still in movement), no stopping criterion was needed to be implemented. The computational setting (i.e., the real computational time on a desktop PC and size and format of the output files) is given in Table 5.

Table 5 Comparison of performances and outputs of the four codes used in the synthetic benchmarks. The detailed description of the conditions for which these data were obtained is given in the text

Benchmarking results

Inter-comparison procedure

Results of the model inter-comparison are presented for each topographic case in Figs. 4, 5, 6, 7 and 8. The maps of maximum flow extent (a–d) are generated by extracting information from each pixel inundated by the flow at the end of the simulation (after 100 s). As some depth-averaged models tend to produce unrealistic, thin flow edges (thickness < 10⁻⁶ m), a threshold of minimum flow depth is fixed here at 10⁻³ m. To quantify the differences between model results, two ratios are calculated and displayed in a table below each model’s map (Figs. 4, 5, 6, 7 and 8): the maximum area ratio A_X/R and the maximum runout ratio R_X/R. Both are calculated by comparing the outputs of a reference model (area A_Rand runout R_R) to those of the other models (A_X and R_X) following:

$${A}_{X/R}=\frac{A_X-{A}_R}{A_R}\times 100$$

(38)

$${R}_{X/R}=\frac{R_X-{R}_R}{R_R}\times 100$$

(39)

Fig. 4

Results of the model inter-comparison for the inclined plane case. Maps a to d show the inundated areas from each model (red colormap for the low volumetric rate, green colormap for the medium volumetric rate, and blue colormap for the high volumetric rate). Graphs 1 to 9 correspond to the time-varying parameters for each scenario and model, with the flow thickness (1 to 3) at location 1 (shown in the top left map), the center of mass velocity (4 to 6) and the front velocity (7 to 9)

Fig. 5

Results of the model inter-comparison for the bend case. See Fig. 4 caption for details

Fig. 6

Results of the model inter-comparison for the break in slope case. See Fig. 4 caption for details

Fig. 7

Results of the model inter-comparison for the obstacle case. See Fig. 4 caption for details

Fig. 8

Results of the model inter-comparison for the constriction case. See Fig. 4 caption for details

In order to reduce the amount of data displayed in each figure, percentages are only shown using the averaged area and flow runouts obtained for the three scenarios together. However, we invite the reader to refer to the supplementary material in which the complete data analysis for each model is provided (Supplementary Tables 1–4).

Inclined plane case

Simulations performed in the control case “inclined plane” (Fig. 4) show a similar lobate shape and aspect ratios for the 4 models. An increase of roughly 5 to 25 % (depending on the model considered) in the maximum extent area and 5 % in the runout can be seen between the medium- and the high-volume flux scenarios. Flow simulation results with VolcFlow, SHALTOP, and IMEX_Sflo2D show a good consistency: areas covered by the flows show only 17% maximum differences, and their runout only 10%. The velocity and thickness curves of these three models (Fig. 4) are almost superimposed, even though the IMEX_SfloW2D simulated flow is slightly faster than the other two, and consequently slightly more widespread and thinner. While velocities measured at the center of mass are very similar in the 3 codes, the front velocities are significantly different during the first 25 s (when the force balance dominates; see Fig. 13 in Mangeney-Castelnau et al. 2003), with much higher initial velocities obtained with SHALTOP and IMEX_SfloW2D. After ~ 25 s, SHALTOP and VolcFlow give very similar front velocities. However, TITAN2D simulation results strongly differ from those obtained with the three other codes: the simulated flows are much faster (up to two times in the high-volume flux scenario), causing a larger flow extent (up to 70%), and runout (41% to 45%), with lower thicknesses.

Bend case

Results of the topographic bend case (Fig. 5) highlight significant differences between models, especially for the maximum extent of the simulated flows. The four models overflow at the bend location, but at different scales. Differences are also visible between the 3 scenarios: the TITAN2D simulations easily overflow with the 3 different input volume fluxes, whereas the VolcFlow and IMEX_SfloW2D simulations only overflow in the high and moderate volume fluxes scenarios, while the SHALTOP simulations only do it in the high-volume flux scenario. If we arbitrarily consider the VolcFlow simulation as a reference for a comparison with an averaged maximum flow extent of 1.97 × 10⁵ m² (see supplementary materials Table 3), the TITAN2D simulations cover an averaged surface up to 617% larger (7 times, 14.1 × 10⁵ m²) partially due to the presence of a large overspill at the source in the high-volume flux scenario that produces an overbank flow outside of the channel, traveling 1400 m downstream (Fig. 5), whereas the SHALTOP and IMEX simulated flows inundate an averaged area of only 16% (2.29 × 10⁵ m²) and 52% larger (2.99 × 10⁵ m²) than the VolcFlow ones, respectively.

The evolution of simulated thicknesses and velocities with time (graphs in Fig. 5) follows almost the same general pattern, especially for VolcFlow, SHALTOP, and IMEX, with center of mass velocity curves that are almost superimposed (Fig. 5). Simulated flows accelerate until they reach the bend, and then decelerate until the end of the simulation. Similarly, flow thicknesses also increase sharply to reach values of 9 to 12 m at location 1, and then follow a linear decrease until the end of the simulation, as the mass in the channel is drained and accumulates at the front to build a lobe (not seen in locations 1 or 2). However, simulated flows reach location 1 at different times, with the IMEX ones always arriving first, then the SHALTOP ones always 5 s later, and finally the VolcFlow ones 8 s later. This trend is coherent with the observed variations in velocities (from the front or center of mass). Note that, on the contrary, SHALTOP flows were slower than the VolcFlow ones in the inclined plane case. TITAN2D simulated flows show the same general pattern than those from the three other codes, but its center of mass velocities is marked by a sudden acceleration during the first few seconds of the simulations in all three scenarios, leading to velocities 1.5 to 2 times higher. Consequently, TITAN2D generates large overflows (2 to 4 m thick) in all three scenarios, and its peak in flow thicknesses at location 1 occurs 20 to 25 s earlier than those from the three other models.

In summary, all simulated flows with the four models show some interactions with the synthetic bend and two trends emerge: (i) TITAN2D flows travel generally faster than the other ones and produce major overflows in all three scenarios, and (ii) VolcFlow, IMEX_SfloW2D, and SHALTOP flows all travel slower than the TITAN2D ones and produce overspills with a limited extent only in the high- or moderate-volume flux scenarios.

Break in slope case

Results of the break in slope case (Fig. 6) show more consistency between models than in the previous case. As an example, the runout differences between TITAN2D and the other codes are now only between 21 and 28% (41–50% previously), depending on the scenario considered. Differences obtained between scenarios are also limited to the simulation runouts (5–8%). No overflow occurs, and flows stay channelized, except for TITAN2D in the high-volumetric rate scenario where overflows occur at the source. When the slope angle is divided by two (from 20° to 10°) at 2500 m from the source, the flow front stops, and a frontal lobe starts to form (i.e., graphs 4 to 6: Fig. 6), attested by a sudden drop of both front and center of mass velocities, associated with an increase of the flow thickness in the three scenarios at location 2. We note that the 10° slope is close to the friction coefficient of the simulation flows (11°), potentially explaining formation of a frontal lobe. TITAN2D simulated flows show similar high initial accelerations as those already observed in the bend case, which shifts the center of mass velocity curves up by 20 m s⁻¹ compared to those from other models. As a result, VolcFlow, SHALTOP, and IMEX_SfloW2D simulations start to build a frontal lobe deposit immediately after the break in slope (front velocity drops; flow thickness at location 2 increases), whereas for TITAN2D simulations, such a frontal deposit does not build immediately after the break in slope but at least 1000 m further downstream (i.e., flow thickness at location 2 does not increase). Although no overflow is observed here, the break in slope did modify the flow dynamics in all four models. Similar to the bend case, TITAN2D simulated flows show again higher velocities, longer runouts compared to those from VolcFlow, SHALTOP, and IMEX_SfloW2D.

Obstacle case

In the obstacle case (Fig. 7), no overflow is observed, but the differences in runout between simulated flows from each different model are more important than in the two previous cases. Here, SHALTOP simulated flows show the shortest runouts, as they stop at the foot of the obstacle in the low and moderate volume flux scenarios and travel only 250 m after passing over the obstacle in the high-volume flux scenario. As a result, TITAN2D simulated flows have an averaged runout 81% longer than those from SHALTOP, with 17% and 38% longer runouts for those from VolcFlow and IMEX_SfloW2D, respectively. The TITAN2D flows also do not show any sign of flow accumulation prior to or after the obstacle, since both thicknesses and velocities remain constant or even decrease toward the end of the simulation (graphs 1 to 6 in Fig. 7). As a result, they reach the bottom edge of the DEM with runouts exceeding 4000 m in the 3 scenarios (note that for TITAN2D flows, cropping due to the AMR does not allow them to reach > 4500m). VolcFlow, SHALTOP, and IMEX_SfloW2D simulated flows show similar patterns but with larger differences than in the previous cases. Their flow thicknesses evolution at location 1 show two phases (graphs 1 to 3 in Fig. 7): (i) one peak when the flow front reaches the probed location 1 (roughly 8 to 10 m thick, similar to the TITAN2D flows), and (ii) a second peak a few tens of seconds later that reaches more than 40 m thick (similar to the obstacle height), corresponding to the accumulation of mass at the foot of the obstacle that fills the channel until they reach the top of the obstacle. Surprisingly, IMEX and VolcFlow flows reach location 2 (graphs 4 to 6 in Fig. 7) before the mass accumulation peak (second peak location 1), so that their flow fronts already passed the 40-m-high obstacle when the mass accumulation phase starts (note that the enlargement of the flow around the obstacle is not a sign of an overflowing around it but simply due to the filling of the channel before the obstacle). This is also confirmed by their front velocities that do not decrease significantly at the passage of the obstacle. It is not the case for the SHALTOP flows that reach location 2 a few tens of seconds after the mass accumulation peak (or never reach it, like in the case of the lower volume flux scenarios).

To summarize, the presence of a large bump/obstacle obstructing the channel, perpendicular to the greatest slope gradient, seems to affect the four models considered here differently: (i) TITAN2D flows do not really interact with the obstacle and do not show any sign of mass accumulation in its vicinity, (ii) VolcFlow and IMEX_SfloW2D flows seem to moderately interact with it and exhibit a delayed mass accumulation after their fronts already passed the obstacle, and (iii) SHALTOP flows highly interact with the obstacle and are unable to cross it if the mass accumulating at its foot does not exceed its top height.

Constriction case

In the constriction case (Fig. 8), TITAN2D simulations are not shown because they all ended unexpectedly with an error generated at the constriction point. VolcFlow is the only model that generates a small overflow in all three scenarios after the simulated flow encounters the constriction. The area inundated by this overflow is limited (5.85 × 10³ m² maximum, corresponding to only 3% of the maximum extent area; see supplementary material table 2) as the overbank flow does not spread much laterally away from the channel (< 40 m). However, such overflows of the Volcflow simulations cause a loss of flow momentum, as shown by a drop in both the front and center of mass velocities stronger than in the other models (see graphs 1 to 3 in Fig. 8), reducing the flow propagation into the constriction. In consequence, VolcFlow simulated flow runouts hardly exceed 2000 m, even in the high-volume flux scenario, which is 46% and 56% shorter than those of SHALTOP and IMEX_SfloW2D, respectively. SHALTOP simulated flows do not show any overflow at the constriction point (location 1 in Fig. 8) but exhibit a sudden mass accumulation when flows enter the constriction, as shown by the small deceleration of both front and center of mass velocities (graphs 7 to 12 in Fig. 8). Interestingly, this change in flow dynamics at the constriction point is followed by a strong re-acceleration (from 30 to 51 m/s in the next 20 s for the high-volume flux scenario) followed by a strong deceleration at the end of the constriction when the channel width increases (graphs 4 to 6 in Fig. 8). These complex flow dynamics result in long SHALTOP simulated flow runouts, exceeding 3000 m for the high-volume flux scenario. We also note that a gap in each SHALTOP simulated flow is visible inside the constriction part, and such gaps are interpreted here as mass flow separations, such processes being commonly observed with depth-averaged models simulating flow over complex topographies (Levy et al. 2015). Finally, while IMEX_SfloW2D simulated flows do not accumulate mass at the constriction point, its velocities slowly decrease, causing an increase of the flow thickness at the exit (graphs 4 to 6 in Fig. 8) and maximum flow runouts similar to the SHALTOP ones.

In conclusion, results of the model inter-comparison in the constriction case exhibit the most complicated results among the four topographical cases. Overall, the reduction of the cross-sectional area of the channel (by modifying only its width) seems to drastically modify the simulated flow dynamics with all three models, as well as to generate an overflow with VolcFlow.

Computational performances and usability

In order to give a representative computational time scale and performance comparison for all four models in our benchmark cases, all simulations with TITAN2D, SHALTOP, and VolcFlow were performed on the same computer (i.e., a desktop PC equipped with a quad-core (8 threads) i7-4770K 3.5 GHz CPU, 16 GB of RAM, and a 1TB SSD), while IMEX_SfloW2D simulations were performed on a laptop computer with similar specifications than the first PC. All simulations were run as scripts, and no visual representation was activated so that all the computer resources were fully dedicated to the modeling tasks. Simulation time steps are adjusted automatically by each code, and data are saved every second (except for TITAN2D for which every time step is saved automatically). For consistency, the computational time is given for simulations performed with a second-order scheme, except for TITAN2D. In addition to the computational time, output data size and format, as well as the visualization method used to analyze each model output, are given in Table 5. For the data size, only the data related to the flow thicknesses and velocities are recorded to minimize the calculation time. A short and qualitative comparison of the usability of each model, summarizing the key advantages and drawbacks of each code for a first-time user, is listed in Table 5. The benchmarks proposed here can be completed in the future by other models that might be used in CPC hazard and risk assessment. All the material needed for completing these synthetic benchmarks, including the procedure, the DEMs used, and the results from all four models are available upon request at: https://vhub.org/groups/benchmarking_models

Discussion and perspectives for hazard and risks

Results of the synthetic benchmarks performed with four depth-averaged models highlight their abilities to simulate the interaction of CPCs with various channel morphologies, but some discrepancies between the simulation results are noticeable. While all simulations were based upon the same (i) source conditions, (ii) digital topographies, and (iii) flow rheologies, output parameters obtained with the four different codes show important variability. It is worth mentioning that the magnitude of these differences is associated to a specific value of each of the two rheological parameters and cannot be generalized. Thus, only the causes of these differences will be discussed here. Two groups of models can be distinguished: (1) VolcFlow, IMEX, and SHALTOP simulations that highly interact with topographic features and give similar (but not identical) flow velocity, thickness, and aerial distribution, and (2) TITAN2D simulations with limited topographic interaction, higher velocities, greater inundated area, and longer runouts than the three other codes.

The curvature effects

Results of the four channelized cases (Figs. 5–8) display a similar trend for the first model group: IMEX_SfloW2D always reaches the channel topographic feature (location 1) first as its front and center of mass velocities are the highest, followed by SHALTOP with moderate velocities and then VolcFlow in third with the lowest velocities of the three. Interestingly, when simulations are performed on the inclined plane (Fig. 4), there is much less variability, and VolcFlow is slightly faster than SHALTOP. The presence of a terrain curvature (i.e., the channel) and rapid topographic changes seems to impact each model differently, with SHALTOP interacting much more with the topography.

With depth-averaged models, Patra et al. (2020) and Peruzzetto et al. (2021) have demonstrated that curvature effects have a limited influence on the flow dynamics when the Voellmy rheology is used, as the velocity-dependent stresses represent a significant contribution of the total resistive stresses with such slope (20°). However, in our four benchmark cases (Figs. 5 to 8), the channel is narrow and curved, and the simulated flows encounter sudden changes in channel morphology and/or slope during propagation. Such topographic changes increase the centrifugal acceleration and modify the associated resistive term in the basal friction force (see Eq. 10). The four models used in this study do not simulate these effects the same way: IMEX_SfloW2D does not consider any curvature effect, VolcFlow and TITAN2D consider an approximation of the terrain curvature in the directions parallel to the flow (friction term Eqs. 13–15 and 19–20 respectively), and SHALTOP considers the full curvature tensor in the friction term (Eq. 31) plus the curvature force in Eq. 36). Hence, the different formulation of the terrain curvature might be responsible for a non-negligible part of the observed differences in our modeling results. Nevertheless, since the TITAN2D simulations also show important discrepancies with the ones from the three other codes in the case of the inclined plane (that does not contain any terrain curvature), the analysis of TITAN2D results will be treated separately in the section “Numerical framework”.

Peruzzetto et al. (2021) demonstrated that expressing the terrain curvature for a channelized flow with an approximated formulation like VolcFlow (Eqs. 13–15) breaks the rotational invariance of the equations and generally leads to higher resistive stresses, in comparison to models using the full curvature tensor, as SHALTOP. Hence, this could explain why VolcFlow simulated flows have the slowest front velocity, the shortest runouts, and the smallest inundated areas. To verify this hypothesis, additional simulations were performed only with VolcFlow and SHALTOP and presented in Fig. 9: (i) simulations without any curvature effects, similar to IMEX_SfloW2D (i.e., curvature in the friction force is null for both models, and in SHALTOP), (ii) simulations with the approximated curvature formulation Eq. (13) in the friction force (the curvature force F_γ in SHALTOP is still kept null). To better highlight the differences, simulations were performed only for the two benchmarks with the sharpest curvature variations, i.e., the bend case and obstacle case, using the highest volume flux scenario (S3).

Fig. 9

Results of the complementary benchmark between VolcFlow and SHALTOP for the bend case (top half) and the obstacle case (bottom half). The left part of the figure shows the results of simulations without any curvature effects implemented in the models, whereas the right part shows the results of simulations with an approximated curvature implemented in VolcFlow and SHALTOP. The colormap of each simulation refers to the thickness distribution of the flow after 100 s of simulation time. White dash lines show the flow outlines with the curvature effects, as shown in Figs. 5 and 7

Results from the simulations performed with the “no curvature” condition (Fig. 9 left side) show that for the bend case, removing curvature effects increases runout and inundated area compared to simulations with the “exact” curvature condition in Fig. 5 (also reported in Fig. 9 as white dashed lines). In SHALTOP specifically, this could be explained by the fact that the curvature force maintains the flow in the central channel by reducing the bouncing effect, and thus reduces overflow (see Fig. 7b, c; Peruzzetto et al. 2021). The differences between these two models (VolcFlow, SHALTOP) and IMEX-SfloW2D are then reduced by 30% for the inundated area and 50% for the flow runout, respectively. Simulation results obtained in the obstacle case with the no curvature condition does not seem to significantly modify the runout of the two models. However, it seems to affect the overspill of SHALTOP’s simulated flow at the obstacle location by increasing its inundated area by 19%. In the latter case, the presence of a straight channel parallel to the flow propagation direction most likely reduces the role of curvature effects during flow emplacement, even though the curvature force increases both the front and center of mass velocities, as discussed above (Peruzzetto et al. 2021).

Using the “approximated curvature” condition (i.e., in the friction force) in the bend case (Fig. 9 right side), the SHALTOP simulated flow has a shorter runout than simulations with the exact curvature condition (white dashed lines), providing results closer to the VolcFlow simulations (only 1–5% differences). Such a condition also does not really modify the SHALTOP results in the obstacle case. This can be related to the orientation of the channel. In the obstacle case, the channel is aligned with the y axis, such that the approximated expression of the curvature in Eq. (13) in the friction term is consistent with the exact expression. This shows that the overflow observed at the obstacle in SHALTOP simulations results from the lack of the curvature force and not from the lack of curvature in the friction term. In the bend case, the channel is rotated by a 45° angle. At the bottom of the channel, the curvature in the flow direction is zero, but γ_x and γ_y in Eqs. (14 and 15) are positive. In turn, the approximated curvature in Eq. (8) is also positive, which artificially increases friction. Consequently, the approximation of the curvature can indeed reduce the runout and inundated area of the simulated flow in a channel not aligned with the referential axis, which is consistent with the results of Peruzzetto et al. (2021).

In summary, results of our benchmark confirmed the conclusions of Patra et al. (2020) and Peruzzetto et al. (2021) that the impact of the curvature effects with a Voellmy rheology on channelized flow propagation is limited on smooth topographies but can be non-negligible in case of sudden topographic changes. Even though our simulations were performed on simplified topographies, results highlight the importance of considering such centrifugal acceleration effects when dealing with CPCs. Such curvature conditions for CPCs should be non-approximated and invariant in rotation, as these flows are usually emplaced in sharp and tortuous valleys.

Differences in flow velocity calculation

Even when curvature effects are disabled, SHALTOP flows do not interact the same way with the obstacle as those of VolcFlow and IMEX_SfloW2D (see Figs. 7 and 9). Difference in the mathematical models could be one explanation. Indeed, in VolcFlow, the projection of the gravity terms is not performed in an orthonormal system and in IMEX_SfloW2D, the shallow approximation and the depth-averaging are performed in the vertical direction, which significantly increases the runout distance (see Figure 6a in Delgado-Sanchez et al. 2020). This results in differences in how the source terms are solved in each code. Because of the different integration methods used for the momentum and mass balance equations (Eqs. 1–3) in each code, the resulting flow velocity is not equivalent for all four models: (i) VolcFlow and TITAN2D use a two-component velocity in the plane x,y tangent to the slope (see Eqs. 11–12, 17–18 and Fig. 1B), (ii) IMEX_SfloW2D uses a two-component velocity in the horizontal plane X,Y perpendicular to $\overrightarrow{g}$ (see Eqs. 24 and 25, and Fig 1A), and (iii) SHALTOP uses the physical flow velocity, which has three components in the X,Y,Z coordinate system (see Eq. 30). As detailed in Savage and Hutter (1989, 1991), in the depth-averaged approach, the resistive stresses τ_x and τ_y are tangent to the slope. This implies that the flow velocity must remain tangent to the topography, collinear to τ_x and τ_y. For cases (i) and (ii), the tangentiality is easily achieved over planar or smooth topography but not over complex, rough topographies where non-hydrostatic forces like the “curvature force” arise (Bouchut and Westdickenberg 2004; Iverson et al. 2004; Peruzzetto et al. 2021). A result of this is that resistive stresses calculated in cases (i) and (ii) can be underestimated when flows encounter rapid topographic changes. In case (iii), the use of the physical velocity enables the calculation of the curvature force F_γ, which ensures that the flow velocity stays tangent to the topography. This could potentially explain why SHALTOP simulations barely cross the obstacle in Figs. 7 and 9: when the flows reach the obstacle, the curvature force F_γ becomes high, and the frictions increase. This causes the flows to abruptly decelerate (see front velocities graphs 10 to 12 in Fig. 7), while the curvature force helps the flows to stay confined in the channel and accumulate at the foot of the obstacle before eventually overtopping it. In summary, the use of a two-component slope-tangent velocity to calculate the friction terms in depth-averaged models seems coherent for smooth or planar topographies (i.e., the break in slope and inclined plane cases in our benchmarks), but can lead to important discrepancies with models using a three-component velocity over more complex topographies (i.e., the obstacle and bend cases). In particular, the curvature effects in SHALTOP (case (iii)) make it much more sensitive to topography variations.

Numerical framework

While terrain curvature and the flow velocity treatment explain some of the differences observed in the benchmark results, some discrepancies remain unexplained. For instance, IMEX_SfloW2D flows are always 5 to 15% faster than VolcFlow and SHALTOP flows (center of mass velocity), even in the inclined plane case. These limited residual differences can be attributed to the different numerical framework used by each code. However, terrain curvature and the flow velocity calculation do not explain why TITAN2D flows behave so differently than the others. The most remarkable characteristic of TITAN2D flows is the fast acceleration during the first computational steps, shifting up velocity curves by 20 m s⁻¹ or more compared to those from the other three models, regardless of the scenario chosen. Without such a large initial acceleration, TITAN2D simulation results could be comparable to those from the three other codes, at least for the evolution of flow velocities (see graphs 7 to 12 in Figs. 5–8). After verification of the TITAN2D source code used for this study (4.1.0), the cause of this rapid acceleration was identified and attributed to an error in the numerical implementation of the Voellmy-Salm rheology. A new version of the source code (4.2.0) is currently under development and was tested here for the bend case with the low-volume flux scenario (see Supplementary Material Fig. S1). The new simulated flow velocity and resulting inundated area seem to be closer to those obtained with the three other codes, but some instabilities remain (see velocity curve) and must be improved. The corrected version of the code will be released soon after undergoing further confirmation and validation tests.

Model performance and usability for hazard assessment

Performance and usability of models play an important role in the user’s model choice for a particular case study. This choice also strongly depends on the type of the hazard assessment performed. Regarding the choice of the four selected models for CPC hazard assessment, time is an important variable, and a balance must be stricken in terms of the total computational time required to couple the physical model and the uncertainty quantification (UQ) technique chosen (e.g., Marzocchi and Bebbington 2012; Calder et al. 2015; Bevilacqua et al. 2019; Tierz et al. 2021). For rapid crisis management, when a few simulations must be run in a limited amount of time for risk mitigation, the computational time (Table 5) is the most crucial metric. It is worth remarking, however, that such a comparison might be incomplete, because the models might have a different convergence rate to the solution (at decreasing grid size). Nevertheless, our benchmark results show that the four selected models have reasonable computational times (minutes to < 2 h) when used with moderately large topographies like our synthetic ones (grids of 300,000 cells, see Table 2) with a standard computer configuration (see Table 5 and Supplementary Material for detail of the computational setup). Models that give results within a few minutes such as VolcFlow and IMEX_SfloW2D seem more suitable for this specific task. Note that the values of computational time given here are dependent on the computational resources used and can significantly change from one computer configuration to another. For other hazard assessment purposes, the quality of the assessment is dependent on both the diversity of models and the UQ technique selected. For example, using an ensemble run of simulations from a single PC model only but with a sophisticated UQ solution (i.e., dominance factors or expected contributions) is not enough to fully assess the epistemic uncertainty of the system. However, a probabilistic assessment using an ensemble of PC models coupled with a standard UQ technique (i.e., inversions or emulators) will allow a modeler to capture the values and variability in some relevant variables for PC hazard assessment (e.g., Bayarri et al. 2009; Stefanescu et al. 2012; Spiller et al. 2014; Tierz et al. 2016; Patra et al. 2020). The strong variability obtained in the benchmarking results presented in this study highlights the importance of using an ensemble of different models for the same phenomena to directly compare outputs and internal variables in all the models while controlling other factors like numerical solution procedures, input ranges, and computer hardware.

Model accessibility is also an important aspect in a user’s decision to choose a particular code for their purposes. VolcFlow and TITAN2D are freely available on their respective websites and can be used through a graphical user interface (GUI) and/or cyberinfrastructure (i.e., TITAN2D on VHub), which does increase their accessibility (note that VolcFlow needs Matlab, which requires a paid license). Moreover, the availability of proper documentation (i.e., user guide and website) allows any user to run these models without any prior training. In contrast, SHALTOP and IMEX_SfloW2D lack some of these resources, even though the last one is available through GitHub. Accessibility improvement for these two codes should be considered in the future.

Model performance and usability metrics should also include both pre- and post-processing analyses (Table 5) that can drastically increase the total time needed to display a final simulation result. A harmonization of the input data implementation and a standardization of output formats (i.e., georeferenced ASCII files for the final state and a compressed binary format for kinematic data) could help potential users to process data more efficiently and speed up the hazard assessment process, while also significantly decreasing the time spent for future similar inter-comparison of these models.

Volcanological implications

Results from these benchmarks highlight the ability of the four selected depth-averaged models to simulate first-order CPC dynamics: (i) flow velocities and flow thickness distribution inside the synthetic channels are similar to those from natural CPCs like block-and-ash flows (Calder et al. 1999; Brown 2015), and (ii) simulated flows stay confined within the synthetic valleys and overflow only at specific locations. Overflows occurred in the bend case with all models, and for the constriction cases with VolcFlow only (TITAN2D overbanks near the source are not considered here due to errors found in the code). Even though no overflow occurred in the break in slope and obstacle cases (Figs. 6 and 7), some processes associated with deposition, linked to both a sudden decrease in flow velocities and increase of flow thickness, were observed both before the obstacle and after the break in slope, drastically reducing the channel capacity and promoting late flow overspills. Hence, the first-order dynamics of CPC overspill processes seem to be successfully reproduced by the models during these synthetic benchmarks.

Simulation results support field observations that a sudden change in channel geometries (shape, slope, dimensions, sinuosity), combined with a high-volume flux, are keys to generate overflows. To illustrate the relationship between flow overspill processes and channel geometry, the overbank width of VolcFlow simulated flows measured along the synthetic channels for both the “bend” and the “constriction” cases with the high-volume flux scenario (Fig. 10a) are compared to the channel cross-sectional area and the channel sinuosity extracted from the synthetic topographies of the bend and the constriction cases, respectively. Results show that overspill processes occur either after a drop in the channel capacity (constriction) or a peak in channel sinuosity (bend). The same observations were made for several past natural BAFs: the June 14, 2006 BAFs (Charbonnier and Gertisser 2008, 2011; Lube et al. 2011) and the November 5, 2010 BAFs at Merapi (Charbonnier et al. 2013; Cronin et al. 2013) and the July 11, 2015 BAFs at Colima (Macorps et al. 2018). To highlight the similarities between these natural cases and the benchmark results, the same set of data (channel cross-sectional area, channel sinuosity, overbank width) as for the synthetic topographies were extracted from these three natural case studies (Fig. 10b–d). Similar correlations are obtained where a sharp decrease of channel capacity, or a sudden increase of channel sinuosity, is linked to an increase of the overbank width (Fig. 10b–d).

Fig. 10

Morphometric data extracted from the benchmark results compared to a set of field data compiled from three recent eruptions associated with block-and-ash flows (BAFs): a Channel sinuosity and cross-sectional area measured along the synthetic channel in the bend” and the “constriction” benchmark cases respectively, as well as the corresponding overbank width extracted from two VolcFlow simulations. b Cross-sectional area measured along the Gendol channel at Merapi, and the corresponding overbank width measured before and after the emplacement of the 2006 and 2010 BAFs, respectively. c Sinuosity gradient measured along the Gendol river at Merapi in 2010 before the eruption. d Cross-sectional area measured along the Montegrande channel at Colima in 2005, and the corresponding overbank width measured after the emplacement of the 2015 BAFs (from Macorps et al. 2018)

In addition, the flow discharge rate seems to be as important as the channel geometry for triggering overspill processes. Fig. 11 shows that such a relationship was indeed obtained in our synthetic benchmarks by the VolcFlow, IMEX_SfloW2D, and TITAN2D simulations in the bend and constriction cases: the cumulative overbank area measured from these simulated flows increases proportionally with the averaged flow discharge rate at the source. This also corroborates with field observations at Merapi for both the 2006 and 2010 BAFs: using Charbonnier and Gertisser (2008) data, the discharge rate of the June 14, 2006 BAF can be estimated at 2.5 × 10³ m³ s⁻¹, whereas the averaged discharge rate of the November 5, 2010 BAF was estimated by Kelfoun et al. (2017) at 43 × 10³ m³ s⁻¹. While the channel capacity of the Gendol river did not change significantly between 2006 and 2010 (see Fig.10b), a much higher volumetric rate in 2010 (by twenty times) allowed the occurrence of significantly larger overflows than in 2006 (cumulated overbank areas increased by almost twenty times, see Fig. 10b). Similar trends are observed in the synthetic benchmarks for both VolcFlow and TITAN2D simulated flows, although no predictive pattern is found.

Fig. 11

Cumulated overbank area versus averaged discharge rate of at the source extracted from VolcFlow and IMEX_SfloW2D simulation results in the constriction and bend benchmark cases, compared to those estimated from field observations after the 2006 and 2010 BAFs at Merapi

Outcomes and perspectives

The main outcome of this CPC model benchmarking exercise is that, except for TITAN2D, all selected models coherently reproduce similar emplacement dynamics (depth-averaged velocity, thickness) and interactions with topographic artifacts as those observed with natural CPCs, even though a first-order rheological law was used (Voellmy). With TITAN2D, large discrepancies in flow simulation outputs compared to the ones obtained with the other three models allowed us to detect issues with the Voellmy-Salm implementation in the code. Our benchmarks also highlighted noticeable differences both between simulations performed with different models for the same benchmark case and those performed with the same model between different benchmark cases. In contrast to the previous inter-comparison exercise of Ogburn and Calder (2017), the use of similar source conditions and flow rheology in all our simulations enable us to better interpret those differences: most discrepancies arise from (i) the various velocities resulting from the gravity projection or from the direction of the shallow approximation and curvature formulations implemented in the source terms of each model, and (ii) the diverse numerical frameworks implemented in each model, an inherent characteristic of each code that cannot be altered by the benchmark procedure itself (in contrast to input parameters). As the computational performance of such models increases year after year, allowing the use of more accurate DEMs with higher spatial and vertical resolution and rougher channel topographies, the divergence of such model benchmarking results is likely to become more important in the future, and the most accurate (i.e., realistic) models must be prioritized. It is important to stress that this exercise was based on a synthetic dataset, and model accuracy cannot be quantified but simply estimated. The need of a reference framework to better quantify such CPC model inter-comparison and benchmarking efforts is crucial. To respond to that specific need, a new large-scale experimental facility has been developed at USF (Tampa, FL, USA) to serve as a reference framework for future experimental CPC benchmarks. Finally, due to the large variability in the results obtained here, the use of a single model for hazard and risk assessment purposes is not recommended, and a compilation of output data from different models with a robust UQ solution, without significantly increasing the pre- and post-processing time, seems to be more appropriate. For such UQ modeling purposes, one would need to quantify the aleatory uncertainty via one or more models (and/or, e.g., the structural — epistemic — uncertainty of each model), and then, for instance, use an ensemble of models to further characterize the epistemic uncertainty (e.g., Tierz et al. 2016, 2018). This method is already used in routine in other geosciences; for example, hurricane tracking in meteorology is assessed by compiling simulations of several different codes using a well-established workflow in near real-time.

Conclusions

We present the results of the first synthetic benchmarks for CPC numerical models. Except for TITAN2D, for which issues with the Voellmy-Salm implementation were detected thanks to the benchmarks, the three other codes, VolcFlow, SHALTOP, and IMEX_SfloW2D, satisfactorily produce similar first-order CPC dynamics over four simplified volcanic-like valleys with various topographic changes (channel bend and constriction, break-in-slope and obstacle). Results, specific to the Voellmy rheology, are coherent among the various models and were obtained in a short amount of time, from a few minutes to an hour depending on the model and topographic setting, which demonstrated the usefulness and ability of such model benchmarking efforts to correctly evaluate and select appropriate models for hazard assessment purposes. The benchmarks also highlight some discrepancies in the results obtained both between models and benchmark cases, especially regarding their ability to reproduce CPC overspill processes, which have been proven to be the most deadly and unpredictable phenomenon associated with CPC during recent eruptions at Merapi, Colima, and Fuego volcanoes. It is shown that incorporating curvature effects into such models is a key component to accurately simulate CPC overspill processes related to topography variations, even on a mean slope of 20°. Except for TITAN2D, these discrepancies in the simulation results can be partly compensated by implementing the same curvature and velocity formulations in all models. The remaining differences come from the various numerical frameworks used, intrinsic to each code and which cannot be altered by the benchmarking procedure itself.

Nevertheless, even with the lack of a reference framework, results obtained here show that such a synthetic benchmark procedure seems to be adapted to qualitatively evaluate the performance of CPC numerical models over natural-like volcanic terrains and should be complemented in the future with new large-scale experimental designs, more realistic volcanic digital topographies, and a more diverse set of numerical models with robust UQ techniques.