The importance of pore throats in controlling the permeability of magmatic foams

Abstract

Vesiculation of hydrous melts at 1 atm was studied in situ by synchrotron X-ray tomographic microscopy at the TOMCAT beamline of the Swiss Light Source (Villigen, Switzerland). Water-undersaturated basaltic, andesitic, trachyandesitic, and dacitic glasses were synthesized at high pressures and then laser heated at 1 atm. on the beamline, causing vesiculation. The porosity, bubble number density, size distributions of bubbles, and pore throats, as well as their tortuosity and connectivity, were measured in three-dimensional tomographic reconstructions of sample volumes, which were also used for lattice Boltzmann simulations of viscous permeabilities. Connectivity of bubbles by pore throats varied from ~ 100 to 10⁵ mm⁻³, and for each sample correlated with porosity and permeability. Consideration of the results of this and previous studies of the viscous permeabilities of aphyric and crystal-poor magmatic samples demonstrated that at similar porosities permeability can vary by orders of magnitude, even for similar compositions. Comparison of the permeability relationships from this study with previous models (Degruyter et al., Bull Vulcanol 72:63–74, 2010; Burgisser et al., Earth Planet Sci Lett 470:37–47, 2017) relating porosity, characteristic pore-throat diameters, and tortuosity demonstrated good agreement. Modifying the Burgisser et al. model by using the maximum pore-throat diameter, instead of the average diameter, as the characteristic diameter reproduced the lattice Boltzmann permeabilities to within 1 order of magnitude. Correlations between average bubble diameters and maximum pore-throat diameters, and between porosity and tortuosity, in our experiments produced relationships that allow application of the modified Burgisser et al. model to predict permeability based only upon the average bubble diameter and porosity. These experimental results are consistent with previous studies suggesting that increasing bubble growth rates result in decreasing permeability of equivalent porosity foams. This effect of growth rate substantially contributes to the multiple orders of magnitude variations in the permeabilities of vesicular magmas at similar porosities.

Introduction

Competition between magma inflation due to gas exsolution and expansion, and the escape of gas, exerts a significant control on the explosivity of volcanic eruptions (e.g., Sparks 2003; Spieler et al. 2004; Mueller et al. 2005, 2008). This competition is profoundly influenced by the permeability of the vesiculating magma. Relatively, impermeable magmas can lead to violent eruptions, whereas permeable ones may not (Sparks 2003; Mueller et al. 2005, 2008). Understanding the development of porosity, Φ, and permeability, k, during magma vesiculation is one of the keys to modeling volcanic processes and improving our knowledge of volcanic eruptions and their precursors (Fagents et al. 2013). Due to the significance of permeability, many studies characterized the porosities and permeabilities of natural and experimental samples and demonstrated orders of magnitude differences in permeability at similar porosities (e.g., Klug and Cashman 1996; Saar and Manga 1999; Blower 2001; Rust and Cashman 2004; Mueller et al. 2005, 2008; Bouvet de Maisonneuve et al. 2008; Wright et al. 2009; Degruyter et al. 2010; Bai et al. 2010; Polacci et al. 2014; Farquharson et al. 2015; Kushnir et al. 2016; Lindoo et al. 2016; Burgisser et al. 2017).

The structural details of porous media, such as tortousity and the size of the bubbles and connecting pore throats, have long been known to significantly influence permeability (Carman 1937; Archie 1942). Polacci et al. (2008) suggested that “a few large vesicles, exhibiting mostly irregular, tortuous, channel-like textures” in scoria from Stromboli volcano (Italy) were preferential pathways for gas escape from the magma. Degruyter et al. (2010) and Burgisser et al. (2017) demonstrated that sample tortuosity and the pore-throat characteristic diameter play significant roles in controlling magmatic permeability.

Here, we report high-temperature, in situ X-ray tomographic microscopy experiments studying the vesiculation of four, crystal-free, silicate melts at 1 atm. Tomographic reconstructions were used to measure the development of bubble- and pore-throat size distributions, the interconnections between bubbles, and the relationship between these properties and viscous permeability. We concentrated on the viscous permeability, k₁, and the applicability of the Carman-Kozeny equation to magmatic foams (Carman 1937). We did not investigate the inertial permeabilities, k₂, in our samples, but relationships between viscous and inertial permeability have been previously determined (Rust and Cashman 2004; Yokoyama and Takeuchi 2009; Bai et al. 2010; Polacci et al. 2014; Burgisser et al. 2017). Zhou et al. (2019) proposed a universal power-law equation relating viscous and inertial permeabilities for all geologic porous media with parameters equivalent to those Polacci et al. (2014) found for volcanic samples. Thus, knowledge of the viscous permeability allows calculation of the inertial permeability using the relationships in Polacci et al. (2014) and Zhou et al. (2019).

Methods

Hydrous glass preparation

Samples of MORB, trachyandesite, andesite, and dacite were studied (Table 1). The MORB is a dredge haul sample donated by C. Langmuir; the trachyandesite is a scoria from the 2010 eruption of Eyjafjallajökull, Iceland, and the andesite and dacite compositions were from Atka Island, Alaska, USA. Each sample was ground to less than 50 μm in diameter and dried at 110 °C. Approximately 70 mg of powder plus distilled water was loaded into 3-mm-diameter Pt capsules and welded closed in a water bath without volatile loss. Water concentrations are based upon the added water and was 3 wt% in experiments with MORB, trachyandesite and dacite. The only successful experiment with andesite contained 5 wt% water. The rock-plus-water mixtures were melted above their liquidi in a piston-cylinder apparatus at a temperature of 1250 °C or 1200 °C (trachyandesite only), and a pressure of 1.0 GPa for a duration of 2 h or of 1 h (trachyandesite only) in 19.1 mm NaCl-pyrex assemblies (Baker 2004) and isobarically quenched. Subsamples with volumes of approximately ~ 1 to 2 mm³ of these crystal-free glasses were used for the synchrotron X-ray tomographic microscopy experiments.

Table 1 Starting glass compositions

In situ synchrotron X-ray tomographic microscopy

In situ synchrotron X-ray tomographic microscopy was performed at the TOMCAT beamline of the Swiss Light Source of the Paul Scherrer Institut (Villigen, Switzerland) using a laser-based heating system (Fife et al. 2012) and the ultra-fast endstation (Mokso et al. 2010; Mokso et al. 2017). The laser system comprises two, class four diode lasers of 980 nm wavelength on opposite sides of, and 40 mm away from, the sample; these each provide up to 150 W of power. A pyrometer was used to measure the temperature. The ultra-fast endstation incorporated a pco. DIMAX camera for rapid imaging (Mokso et al. 2010, 2017).

The temperature was increased until approximately 600 °C and then heated at either 1 °C s⁻¹ or 6 °C s⁻¹ to the maximum temperature of the experiment, resulting in sample vesiculation and creation of a silicate foam under open-system conditions such that the sample was free to expand and exsolved gas escaped the system. Initially, a programmed heating rate of ~ 6 °C s⁻¹ was chosen as the best compromise between instantaneous heating of the sample and the need for bubbles to grow slowly enough to be successfully imaged. Due to many experimental failures, a slower programmed heating rate of ~ 1 °C s⁻¹ was found to produce more successful experiments (Table 2). Measurement of the time-temperature histories of the experiments demonstrated that heating rates were often ~ 20% slower than the programmed ones (Table 2).

Table 2 Results of bubble growth experiments

Data acquisition commenced at the first visible onset of vesiculation, such as bubble formation and sample expansion. During data acquisition, samples reached a maximum temperature between ~ 950 and ~ 1200 °C. Polychromatic X-rays were filtered to 5% power, generating 3 ms exposure times, and 701 projections were captured over an angular range of 180 degrees during continuous rotation. The microscope-camera imaging system had a 2.89 μm × 2.89 μm pixel size and a 5.83 mm × 5.83 mm field of view. Reconstructions were performed using a modified GRIDREC algorithm (Dowd et al. 1999; Rivers and Wang 2006; Marone and Stampanoni 2012) coupled with Parzen filtering of the sinograms.

Many bubble growth experiments were performed, but few were successful. The most significant problem was image blurring due to sample motion caused by rapid vesiculation that rendered the tomographic reconstructions useless. Other problems were samples that failed to heat to temperatures high enough to vesiculate (which included all rhyolitic samples investigated) and samples that cracked into small pieces during heating.

Of the 62 experiments performed, only one dynamic experiment on the andesitic composition, one on the trachyandesitic composition, and one on the dacitic composition yielded 3D reconstructions useful for quantitative measurements. Due to rapid bubble growth, only the final steps of 4 experiments on the MORB composition were successfully imaged. Even successful experiments contained some image artifacts due to sample movement during bubble growth. These artifacts were avoided during the sample analysis.

Image analysis and quantification

Bubble distributions in the samples were not homogeneous because of thermal gradients in the laser furnace. Thus, only representative central portions of the samples, far from their edges and the capsule walls, were analyzed, and the measurements reported are not representative of the entire sample, but only of the volume investigated. The tomographic reconstructions were inspected with ImageJ and subvolumes of the samples were chosen; in most cases, they were 256 × 256 × 256 voxels in volume (Fig. 1a–c). Because these volumes were too large for lattice Boltzmann determination of their permeability (discussed below), representative subvolumes of 370 × 370 × 370 μm³ (128 × 128 × 128 voxels, trachyandesite EFJ-8a) or 462 × 462 × 462 μm³ (160 × 160 × 160 voxels, andesite DRB2012-2a, dacite DRB2012-6e-8, -9, -10, MORB DRB2012-7a-2, -3, -cf) or 578 × 578 × 578 μm³ (200 × 200 × 200 voxels, dacite DRB2012-6e-07, MORB DRB2012-7f-10) were used for all quantitative analyses with the Pore3D software library (Brun et al. 2010; Zandomeneghi et al. 2010). Details of the image analysis techniques are provided in the Supplementary Materials.

Fig. 1

a Slice of complete sample DRB2012-6e-10. The 256 × 256 pixel region in this slice sampled for analysis is shown by the dashed lines. b Detailed image of the portion of the 256 × 256 slice sampled from the larger image. c Thresholded image of b with a smaller 160 × 160 pixel region used for quantitative measurements shown enclosed by the solid lines

Lattice Boltzmann modeling of permeabilities

Because of the dynamic nature of the experiments and the collapse of the samples with loss of vesicularity near, or at, their termination, sample permeabilities could not be measured directly. Instead, lattice Boltzmann modeling of permeabilities was performed using an established lattice Boltzmann code (Hill et al. 2001; Hill and Koch 2002), as previously done in Bai et al. (2010). Details of the lattice Boltzmann modeling are found in the Supplementary Materials.

Bubble growth during isobaric heating versus isothermal decompression

Experiments were performed by isobaric heating at atmospheric pressure because a high-pressure furnace was not available on the TOMCAT beamline. The time-temperature-pressure path in these experiments is different from bubble formation during near-isothermal decompression in natural systems and in many experiments (Burgisser and Gardner 2004; Lindoo et al. 2016, 2017; Mueller et al. 2005; Spieler et al. 2004; Takeuchi et al. 2009).

Although bubble nucleation and growth during isothermal decompression and isobaric heating experiments are both driven by supersaturation of the melt with a volatile, the viscosity of the melt increases during isothermal decompression (due to water loss to the bubbles) and may either increase (due to water loss) or decrease (due to increasing temperature) during isobaric heating. For example, in these experiments, the andesitic melt begins vesiculation at 900 °C with a water concentration of 5 wt% and a viscosity of ~ 750 Pa s (calculated following Giordano et al. 2008). If this melt lost all its water by the end of the experiment at 1100 °C, the viscosity would be ~ 6700 Pa s. Estimating that approximately 1 wt% water remains in the melt at ~ 1000 °C yields a melt viscosity ~ 3100 Pa s at the middle of this experiment. The diffusivity of water in the melt also is controlled by a combination of heating and dehydration. Using Ni and Zhang (2018), the water diffusivity at the start of vesiculation is ~ 3 × 10⁻¹³ m² s⁻¹ and decreases to ~ 1 × 10⁻¹⁴ m² s⁻¹ when water is lost. On the contrary, for isothermal decompression at 1100 °C of the same melt composition, the viscosity would increase from 32 Pa s at the start of vesiculation to ~ 6700 Pa s if all of the water is exsolved from the melt, and the water diffusivity would decrease from ~ 3 × 10⁻¹² to ~ 1 × 10⁻¹⁴ m² s⁻¹.

These differences in the history of the melt viscosity and diffusivity influence the rates of bubble growth and coalescence of neighboring bubbles. Following Navon and Lyakhovsky (1998), the radius of a bubble during initial stages of growth will be significantly affected by the melt viscosity:

$$ r\propto \mathit{\exp}\left[\frac{\varDelta P}{4\eta }t\right], $$

(1)

where r is the bubble radius, ΔP is the supersaturation pressure, η is the melt viscosity, and t is the time. As the bubble grows and supersaturation decreases, the bubble radius is a function of the square root of the product of the volatile diffusivity in the melt and time (Eq. 36 of Navon and Lyakhovsky 1998). Melt viscosity also exerts control on the time necessary for interacting bubble walls to fail and coalescence to begin, τ_df:

$$ {\tau}_{df}\approx \frac{3\eta {r}^2}{4\varDelta P{h}_{min}^2}, $$

(2)

where h_min is the critical thickness at which the walls fail (Navon and Lyakhovsky 1998). Equations 1 and 2 demonstrate that rates of bubble growth and coalescence during the early stages of isobaric heating experiments should be slower than those in isothermal decompression experiments because of the higher viscosities and lower water diffusivities in the melt early in the isobaric heating experiments. However, as both types of experiments reach the end of bubble growth and water loss, the rates at which bubble growth and coalescence occur should converge.

Both isothermal decompression and isobaric heating experiments are expected to produce random bubble structures, due to the stochasticity in both the location and timing of bubble nucleation in the melts. Because of the higher viscosities and lower diffusivities of isobaric heating experiments, the vesicularity and interconnectivity of bubbles are expected to be smaller than in isothermal decompression experiments of similar, short durations (Eqs. 1 and 2). Because of these differences between isothermal decompression and isobaric heating experiments, bubble growth and coalescence rates were not studied, but instead we concentrated on the development of porosity and permeability of the foams, while fully recognizing that the determined values may be minimal ones.

Despite the differences between isothermal decompression and isobaric heating experiments, we can compare rates of magma ascent and the rates of degassing during isobaric heating experiments by dividing the melt supersaturation pressure (Table 2) by the duration of the isobaric heating (Table 2) to yield equivalent decompression rates of approximately 0.1 to 2 MPa s⁻¹. Although these equivalent decompression rates are only rough approximations, the low values are similar to decompression rates found by Ferguson et al. (2016) for eruptive products of Kilauea volcano and the high values to decompression rates found by Humphreys et al. (2008) for the May 18, 1980 plinian eruption of Mt. St. Helens.

Results

Visual observations

Bubble growth occurred rapidly at temperatures above 600 °C. Typical bubble nucleation and growth can be seen in Fig. 2 and Supplemental Movie 1 of andesitic sample DRB2012-2a (Table 2).

Fig. 2

a, b, c Selected 3D renderings of andesitic experiment DRB2012-2a during vesiculation. In the earliest image, the sample is approximately 1 × 1 × 2 mm in size. Due to the perspective projections of these renderings, the scale bars are only approximate. Representative interior sections of these samples were chosen for quantitative analysis. d, e, f Corresponding thresholded tomographic slices (axial slice number 128 near the center of the reconstruction) from each of the renderings shown in panels a, b, and c, in which black is the melt and white is either the bubbles in the samples or the air around samples (seen in panels e and f). The 500 μm scale bar in panel d also applies to panels e and f. Melt viscosities are calculated using Giordano et al. (2008) with 5 wt% H₂O in the melt at 900 °C and an estimated 1 wt% H₂O at 994 °C; at 1089 °C, near the end of bubble growth, the melt is assumed to be anhydrous for the viscosity calculation. See Supplementary Materials for a movie of this sample during bubble growth

In the absence of nucleation delay, bubble growth is presumed to occur once the sample temperature exceeds that of the glass transition (Giordano et al. 2005), as discussed in the Supplementary Materials. Bubble growth was initially observed as a dense cloud of small bubbles that grew into larger, easily discernible, bubbles that rapidly became interconnected (Fig. 2). Typically, these early growth rates were so rapid that they were blurred in the tomographic images, so meaningful quantitative measurements could not be made.

Early bubbles vary from ellipsoidal to sub-spherical, but within seconds all evolve into sub-spherical to spherical shapes. Bubbles coalesced and typically grew to a maximum size, creating a foam with thin-walled bubbles. If the sample was not immediately quenched, the foam contracted and underwent partial collapse, and in some cases collapse occurred before the termination of the experiment. This behavior is attributed to the loss of volatiles, either through failure of the bubble walls or diffusion through them.

Not every tomographic reconstruction set could be used for all the quantitative analyses presented in the “Methods” section. In some cases, permeabilities could not be determined (DRB2012-6e-07) because of the large computer memory required to resolve the surface area of the interconnected bubbles.

Summary of the bubble number density (BND), bubble size distribution (BSD), and pore-throat size distribution (PTD)

Table 2 presents a summary of our quantitative measurements, and the sizes of all bubbles and pore throats measured in the studied samples are provided as Supplementary Material (Table S1). Figures 3 and 4 graphically portray the measured bubble- and pore-size distributions. Immediately below is a summary of these quantitative measurements; a more detailed description for each sample is found in the Supplementary Material.

Fig. 3

Bubble size distributions in experimental samples. In each panel, a volume-normalized histogram of the sizes of the bubbles (the bar graphs) is presented together with the cumulative distribution of the bubble sizes (solid black line). The porosity is given in the upper right corner of each subpanel. The mean bubble diameter, d, and one-standard deviation about the mean is given in each subpanel. Bin sizes are 5 μm. All panels for each composition are plotted in order of increasing experimental duration and temperature. a Basaltic results. Note that in this figure the sample with a porosity 0.50 was made by re-heating the sample with 0.52 porosity (Table 2). b–d Andesitic results. e Trachyandesitic results. f Dacitic results

Fig. 4

Pore-throat size distributions in experimental samples. In each panel, a volume-normalized histogram of the sizes of the pore throats (the bar graphs) is presented together with the cumulative distribution of the pore throat sizes (solid black line). The porosity is given in the upper right corner of each subpanel. The mean pore throat diameter, d, and one-standard deviation about the mean is given in each subpanel. Bin sizes are 5 μm. All panels for each composition are plotted in order of increasing experimental duration and temperature. a Basaltic results. b–d Andesitic results. e Trachyandesitic results. f Dacitic results

In general, bubble number densities tend to increase with porosity up to a maximum and decrease at higher porosity (Fig. 3, Table 2), although between any two steps the BND can decrease (Table 2). Increasing BNDs are attributed to continuous nucleation and decreasing BNDs to bubble coalescence. The measured bubble and pore-throat size distributions are not Gaussian, but instead often display “long tails” to large bubble and throat sizes, a characteristic indicative of power-law distributions (Newman 2005).

Bubble diameters typically varied from the spatial resolution of the imaging to a maximums of a few hundred microns, with the largest bubbles, near 460 mm, in the high-porosity basaltic sample (Figs. 3 and 4). With the exception of the basaltic composition, there is a trend of increasing bubble diameter with increasing porosity. Pore throats often reached 60 to 70 mm in diameter, although most were less than 20 mm (Fig. 4); the pore-throat densities and diameters, at porosities above ~ 0.33, also increase with porosity.

Connectivity, coordination number, and tortuosity

In all cases, connected and total porosity are similar (Table 2). The connectivity, β, is a standard topological property that measures the number of interconnections (in this study pore throats) between objects (in this case bubbles). β is calculated by (Odgaard and Gundersen 1993; Thovert et al. 1993):

$$ \beta =\frac{\#\mathrm{pore}\ \mathrm{throats}-\#\mathrm{bubbles}+1}{\kern2.25em \mathrm{sample}\ \mathrm{volume}}. $$

(3)

The β values increase from hundreds to thousands per cubic millimeter with increasing porosity to maximums in the tens to hundreds of thousands per cubic millimeter and then, with the exception of the basaltic composition, decrease at higher porosities (Table 2). This trend is similar to those observed for the BNDs and the PTDs (Table 2, Figs. 3 and 4).

The average coordination number (or number of interconnected bubbles surrounding a bubble) for each porosity (Table 2) of each composition is similar and varies between ~ 4 and 6, with a few outliers reaching values near 7 or 8 (DRB2012-7c-f, DRB2012-2a-18, DRB2012-6e-10, DRB2012-2a-19). These averages are far below the maximum value of equal-volume, deformable bubbles surrounding a central bubble (the kissing number) of 32 (Cox and Graner 2004). However, the standard deviations for each sample are often as large as, or even larger than, the mean, and the maximum coordination numbers can reach almost 600 (Table 2, see Fig. 1 for a large bubble with a high kissing number). Such high values of the kissing number are not inconsistent with polydisperse foam simulations that display average coordination numbers between 11 and 14, but contain some polyhedra with coordinations approaching 100 (Kraynik et al. 2004).

The sample tortuosity, τ, varies from a low of 1.09 (dacites DRB2012-06e-8 and DRB2012-6e-9) to a high of 1.72 (andesite DRB2012-2a-9); however, most tortuosities are between 1.1 and 1.3 (Table 2). The relationship between increasing porosity and decreasing tortuosity in the studied samples can be described by, cf., Wright et al. (2009) and Degruyter et al. (2010):

$$ \uptau =\left(1.0487\pm 1.0201\right){\left(\varPhi \right)}^{-0.3192\pm 0.0252}, $$

(4a)

and a correlation between increasing connectivity and decreasing tortuosity was found:

$$ \uptau =\left(2.4376\pm 1.1044\right){\left(\beta \right)}^{-0.0687\pm 0.0102}. $$

(4b)

Permeability

The lattice Boltzmann (LB), viscous permeabilities, k₁, of the samples vary from 3 × 10⁻¹⁵ to greater than 5 × 10⁻¹¹ m² (Table 2, Fig. 5). The LB permeabilities were fit with a power law because both the Carman-Kozeny relation (Carman 1937) and percolation theory (Stauffer and Aharony 1994) predict a power-law relationship between porosity and permeability. Formally, percolation theory predicts k₁ ∼ (Φ − Φ_c)^μ, where, k₁ is the viscous permeability, Φ_c is the critical porosity threshold where the sample becomes permeable, and μ is an exponent that depends upon the system dimensionality (Stauffer and Aharony 1994). The critical porosity threshold for monodisperse spheres in three dimensions is ~ 0.29 (Domb 1972; Lorenz and Ziff 2001); however, as discussed below, the critical porosity threshold is a function of the size distribution and shape of the vesicles. Experimentally determined permeability thresholds in natural and experimental magmatic foams can vary from below ~ 0.03 (Saar and Manga 1999; Bai et al. 2010) to values in excess of 0.63 (Takeuchi et al. 2008, 2009; Lindoo et al. 2016). The critical porosity threshold for any given sample is unknown until measured, and therefore the porosity-permeability relationships in some magmatic foams have been empirically fit with a simpler power law: k₁ = AΦ^B, where A and B are fitting constants (Klug and Cashman 1996; Bai et al. 2010); some authors have estimated the critical porosity threshold (typically 0.3) and fit their data with the percolation theory relationship (Saar and Manga 1999; Blower 2001; Rust and Cashman 2004, 2011; Bai et al. 2010).

Fig. 5

Experimental foam permeabilities determined by lattice Boltzmann simulations plotted as a function of porosity. Uncertainties in the measured porosity and in the permeability are estimated at 20 relative percent and typically the same size as, or smaller than, the symbols. The solid blue line is the power-law fit to the lattice Boltzmann permeabilities of the andesitic composition. The proposed relationships between porosity and permeability for basaltic and for silicic compositions from Bai et al. (2010) are also plotted. (Color on line)

The andesitic sample’s relationship between porosity, Φ, and LB permeability is k₁ = 1.68x10⁻¹¹Φ⁵ (Fig. 5). Assuming a critical porosity of 0.010 below the minimum porosity at which the LB permeability was determined, or 0.15, produces a percolation theory fit of k₁ = 5.79x10⁻¹²(Φ − Φ_c)^2.1. Up to Φ ~ 0.60, the andesitic permeabilities are similar to the Bai et al. (2010) fit to silicic permeabilities measured by Klug and Cashman (1996), but at higher porosities the permeabilities diverge from Bai et al.’s (2010) fit, leading to an order of magnitude difference between the two at Φ ~ 0.90 (Fig. 5).

The LB permeabilities of two basaltic foams at Φ ~ 0.50 bracket the fit to andesitic experiments, but the LB permeability increases to an order of magnitude greater at Φ ~ 0.55. The permeability values at Φ ~ 0.50 (DRB2012-07a-3) may be artificially low because of bubble bursting at the end of previous experiment (DRB2012-07a-2), probably causing loss of porosity and pore throats. These measurements at Φ ~ 0.50 and ~ 0.55 were made on two different chips of basaltic melt; this complicates interpretation because the two samples have slightly different time-temperature histories (Table 2), which together with bubble popping in the sample at Φ ~ 0.50 may might create differences in porosity and permeability. LB permeabilities at Φ ~ 0.55 and ~ 0.73 are similar to those found by Bai et al. (2010) on a high-K basaltic foam from Stromboli (Fig. 5).

The trachyandesitic sample’s LB permeability at Φ ~ 0.30 is significantly above that of the andesitic sample, but at higher porosities the LB permeability falls to values similar to the andesitic composition (Fig. 5). The LB permeability of the dacitic composition at Φ ~ 0.79 cannot be distinguished from that of the similarly porous andesitic experiment, but the two higher porosity dacitic foams display significantly higher LB permeabilities than expected from the trend described by the lower porosity dacitic and andesitic experiments (Fig. 5).

Discussion

Permeability is not a simple function of porosity

Porosity is often considered the primary control of permeability; in most cases increasing porosity results in higher permeabilities (Fig. 5), but other variables such as bubble sizes, composition, connectivity, pore-throat diameter, tortuosity, etc. significantly influence permeability (e.g., Carman 1937; Archie 1942; Rust and Cashman 2004; Mueller et al. 2005; Bai et al. 2010; Degruyter et al. 2010; Polacci et al. 2012, 2014; Lindoo et al. 2016; Burgisser et al. 2017; Colombier et al. 2017).

A significant difference in the physical properties of the studied melt compositions is their viscosity (Table 1). However, a simple correlation between melt viscosity and permeability at a specific porosity does not exist. These crystal-free samples demonstrate that at Φ ~ 0.5 basalts can have LB permeabilities similar to andesites, and at porosities approaching 0.9, the lattice Boltzmann permeabilities of basalts and dacites are similar (Fig. 5), despite these melts displaying orders of magnitude differences in their viscosities (Table 1). Comparison of melt viscosities with the average pore-throat diameters (Fig. 4) does not provide evidence of a positive correlation between these two properties either (cf., Polacci et al. 2014).

Connectivity does not predict permeability, as evidenced by an order of magnitude difference in the LB permeability of samples with similar connectivity and porosity (Table 2, Fig. 5, Supplementary Fig. 2). Additionally, tortuosity also does not appear to directly correlate with porosity-permeability relations (Table 2). However, the bubble- and pore-throat size distributions (Figs. 3 and 4) suggest that larger bubbles and larger pore throats correlate with increasing permeability.

Porosity-permeability trends compared to previous determinations

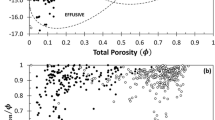
Figure 6 compares lattice Boltzmann permeability determinations with previous measurements of porosity and permeability from aphyric to low-crystallinity natural and experimental samples. The LB permeabilities of our experiments are consistent with previous measurements of similar composition samples (Fig. 6), even though in some cases experimental samples are orders of magnitude smaller than natural samples. At any given porosity, permeability can vary by orders of magnitude; nevertheless, trends are visible in the data as porosity increases from negligible values to near 1.0 (Fig. 6).

Fig. 6

Permeability measurements as a function of porosity for aphyric to low-crystallinity vesiculated samples of basaltic to rhyolitic composition from the literature and this study. (Color on line)

Most viscous permeabilities increase from ~ 10⁻¹⁷ m² at porosities near 0.01 to ~ 10⁻¹³ m² at 0.20 to 0.30 porosity, although some rhyolites at 0.30 porosity have permeabilities of only 10⁻¹⁵ m² (Fig. 6). At porosities above ~ 0.3, the permeabilities continue to increase but at a slower rate than at lower porosities (Fig. 6). For porosities between 0.5 and 0.9, the permeabilities in Fig. 6 range from values of ~ 10⁻¹⁴ m² (Lindoo et al. 2016) to 10⁻¹⁰ m² (Bai et al. 2010). The slow increase in permeability at porosities above the percolation threshold for interpenetrating spheres, ~ 0.29, suggests that once a permeable pathway is created, the addition of other gas transport pathways at higher porosities (as shown by higher values of β and lower values of tortuosity, Table 2) increases permeability less significantly than the first pathway.

In general, silicic foams have lower permeabilities and mafic foams higher permeabilities, but the dacitic foams with greater than 0.80 porosity (DRB2012-6e) have lattice Boltzmann permeabilities similar to basaltic foams with similar porosities (Fig. 6). Rust and Cashman's (2004) permeabilities of rhyolite, pumice, and obsidian as well as Farquharson et al.’s (2015) permeabilities of pumiceous andesite demonstrate almost a two order of magnitude variation at similar porosities (Fig. 6). Thus, any influence of composition on porosity-permeability relationships appears weak.

Because the critical porosity for each sample is unknown, the data were fit by empirical power laws without including a critical porosity, and all can be fit with a single power law, k₁ = 6.0x10⁻¹²Φ^4.0. But, the dispersion of permeabilities around this average fit is orders of magnitude at porosities from 0.15 to 0.90 (Fig. 6). The range of permeabilities displayed in Fig. 6 also can be bound by two power-law fits. The lower bound is k₁ = 1.5x10⁻¹⁴Φ^1.8 and the upper bound is k₁ = 1.5x10⁻¹⁰Φ^4.0. More than 90% of the viscous permeability determinations in Fig. 6 fall within the boundaries defined by these two power laws.

Figure 6 demonstrates that some samples are permeable at porosities below the percolation threshold of 0.29 and others remain impermeable at porosities as high as ~ 0.8 (e.g., Takeuchi et al. 2008, 2009; Lindoo et al. 2016; Burgisser et al. 2017). Permeabilities at low porosities may be due to bubbles acting as hard, rather than interpenetrable, spheres that have a percolation threshold of ~ 0.20 (Ogata et al. 2005; Ziff and Torquato 2017). Polydispersity of sphere sizes may lead to changes in the percolation threshold, as seen experimentally (Burgisser et al. 2017), but numerical simulations suggest that such effects are minor (Consiglio et al. 2003; Ogata et al. 2005). Non-spherical shapes have been shown to dramatically affect the percolation threshold. Garboczi et al. (1995) demonstrated that the percolation threshold for randomly oriented, interpenetrating, prolate ellipsoids decreased from the porosity value for spheres, 0.29, to 0.26 for an aspect ratio of 2, to 0.18 for an aspect ratio of 4, to 0.09 for an aspect ratio of 10, and to 0.007 for an aspect ratio of 100. Thus, even a small fraction of high-aspect ratio ellipsoidal bubbles could create a permeable magma.

The lack of permeability at porosities above the interpenetrating sphere threshold may reflect observations that the percolation threshold in finite systems does not necessarily occur at a specified porosity for a non-infinite system (Stauffer and Aharony 1994; Colombier et al. 2017). Additionally, the durations of the experiments may not be sufficiently long for interacting bubble walls to fail and coalescence to begin (Eq. 2).

Although percolation theory and the simple power-law relationships between porosity and permeability support the expected relationship between these two properties, permeability variations of up to 4 orders of magnitude at similar porosities (Fig. 6) indicate that, in addition to porosity, other properties of the foams, such as the size and shape distributions of bubbles and pore throats, significantly influence their permeability.

Both crystallinity and bubble anisotropy have been shown to influence the permeability of natural and experimental magmatic foams; however, these influences were not investigated in this study. Degruyter et al. (2010), Schneider et al. (2012), and Burgisser et al. (2017) provide multiple examples of the effects of preferred bubble orientation on magma permeability. The effect of crystals on permeability development in magmatic foams was investigated experimentally in Bai et al. (2011) and Lindoo et al. (2017). Nevertheless, the permeabilities of crystal-rich magmatic samples determined by Saar and Manga (1999), Mueller et al. (2008), Bai et al. (2011), Farquharson et al. (2015), Kushnir et al. (2016), and Lindoo et al. (2017) all plot in the same region as the aphyric to low-crystallinity samples, but are not shown in Fig. 6.

Comparison of measurements with the models of Degruyter et al. (2010) and Burgisser et al. (2017)

Many models for the calculation of permeability have been constructed and demonstrated to reproduce the results of the individual studies (e.g., Saar and Manga 1999; Mueller et al. 2005; Polacci et al. 2008; Bai et al. 2010; Degruyter et al. 2010; Lindoo et al. 2016; Burgisser et al. 2017; La Spina et al. 2017). Burgisser et al. (2017) developed a Carman-Kozeny-based model for permeability calculations based on modifications of Degruyter et al. (2010):

$$ {k}_1=\frac{\varPhi_c^n{d}_t^2}{16{\upchi \uptau}^2}, $$

(5)

where ${\phi}_c^n$ is the connected porosity raised to the nth power, d_t is the characteristic diameter of pore throats, and τ is the tortuosity. χ is the channel circularity:

$$ \chi =\left(\frac{r^2}{l^2}+\frac{l^2}{r^2}\right), $$

(6)

where r is the equivalent circle radius of the throat and l is its major axis (χ = 2 for circular pore throats). Degruyter et al. (2010) set n = 1, but Burgisser et al. (2017) fit their data with Eq. 5 and when n = 2.4 they found that 26 of their 28 viscous permeability measurements were reproduced to within one log unit.

Equation 6 was applied to our samples for which the appropriate variables were measured (Table 2) to predict permeabilities using both n = 1 and n = 2.49; in both applications, the value of χ was set to 2 (Degruyter et al. 2010). The quality of the model fit to the data was assessed by calculating chi-squared as defined by:

$$ \mathrm{chi}-\mathrm{squared}=\sum \frac{{\left(\log \left[\mathrm{calculated}\ \mathrm{permeability}\right]-\log \left[\mathrm{measured}\ \mathrm{permeability}\right]\right)}^2}{\left(\left(\log \left[\mathrm{measured}\ \mathrm{permeability}\right]\right)\right)}. $$

(7)

Application of the Degruyter et al. (2010) formulation of Eq. 6 with d_t equaling the average pore-throat diameter predicted the permeabilities of 17 out of 23 permeability determinations to within 1 log unit (all were within 1.6 log units) and produced a chi-squared value of 1.13 (Fig. 7a). With Burgisser et al.’s (2017) value of n, 19 permeability predictions were within 1 log unit of our determinations (all were within 1.4 log units), and the chi-squared value was 1.14 (Fig. 7a). The fit of these models to the measurements of this study is impressive when considering the almost 5 orders of magnitude spread in the lattice Boltzmann permeabilities; however, the trend between predicted and measured permeabilities is at high angles to the slope of the perfect 1:1 correlation line between model and measurement (Fig. 7a), indicating the need for further model refinement.

Fig. 7

a Application of the models for the prediction of permeability using the Carman-Kozeny equations of Degruyter et al. (2010) and of Burgisser et al. (2017). The line labeled 1:1 represents a perfect fit of a model to the data; the line labeled “5x” represents the modeled values multiplied by 5 and the line labeled “0.2x” represents the modeled values multiplied by 0.2. In these models, the average pore throat value (Table 2) was used as the characteristic diameter of pore throats. b Modification of the models of Degruyter et al. and of Burgisser et al. by using the maximum pore throat (Table 2) as the characteristic diameter and an empirical value of χ = 10. c Comparison of the modified Burgisser et al. model and measured permeabilities of samples from Bai et al. (2010) and of the isotropic samples from Burgisser et al. (2017) using relationships between the average bubble diameter and the largest throat diameter and between the porosity and the tortuosity, as determined in this study. The data from Bai et al. (2010) and from Burgisser et al. (2017) were not used to calibrate the model. (Color on line)

Toward a better model of viscous permeability

We developed a modified version of the models of Degruyter et al. (2010) and Burgisser et al. (2017) using the maximum pore-throat diameter. Three caveats that must be considered for this model are as follows: (1) The model is only calibrated for permeabilities between ~ 10⁻¹⁵ and 10⁻¹⁰ m²; (2) We have no technique to determine when an individual sample becomes permeable, although we can approximate the permeability threshold at Φ ~ 0.3 (the percolation threshold for interpenetrating spheres) or use the methods presented in Burgisser et al. (2017); (3) The model is probably only applicable to isotropic, or nearly isotropic, samples.

Fluid conductivity in porous media can be related to a random resistor network by application of percolation theory (Stauffer and Aharony 1994; Blower 2001). Applying this paradigm, the porous network is envisioned as resistors interconnected to one another that create a continuous circuit when the permeability threshold is exceeded. The connections between resistors in the network can be either in parallel or in series (Stauffer and Aharony 1994; Blower 2001). The conductivity of the network is related to the specifics of the pore-throat cross-sectional area, as expressed in the numerator of the Carman-Kozeny relationship as the square of the characteristic throat diameter, d_t² (Eq. 5). Given a complete description of the lengths and diameters of the pore throats, together with detailed information about their connections in either series or parallel sub-circuits, sample permeability should be calculable, but these data are not available. However, by making the simplifying assumption that the largest pore throat dominates the permeability (as the minimum-valued resistor in a parallel circuit dominates the current flow), the width of that throat, d_max, can be used as the characteristic pore-throat diameter in Eq. 5. Support for the idea of parallel connections between bubbles is provided by the high values of the connective density, ranging from 10³ to 10⁴ mm⁻³ (Table 2). Replacing the average throat diameter with the maximum throat diameter, and leaving χ = 2, in Eq. 5 did not significantly improve the fit of the Degruyter et al. (2010) or Burgisser et al. (2017) models; however, the Burgisser et al. (2017) model yielded calculated permeabilities consistently above the measured ones by a factor of 5. Based upon this observation, an empirical value of χ = 10 (or a fitting factor of 5 times the original value of χ = 2) was chosen, and the resulting fit of the Burgisser et al. model to the data is remarkable (Fig. 7b), with all but one of the measurements reproduced to within one log unit and a chi-squared value of 0.01.

The challenge in applying this model to predict permeability is that the tortuosity and the maximum throat diameter needed for the calculation typically are not known (cf. Burgisser et al. 2017). In most cases, published studies only provide average bubble diameters and porosities. However, the relationship found in this study between tortuosity and porosity (Eq. 4a) can be used to estimate the tortuosity. Additionally, we found that the maximum throat diameter is related to the average bubble size, d_avg^bubble (m), by

$$ {d}_{\mathrm{max}}=2.22251x{10}^{-5}\ln \left({d}_{\mathrm{avg}}^{\mathrm{bubble}}\right)+2.69501x{10}^{-4}. $$

(8)

To test this model, the permeabilities of samples within the range of our calibration, 10⁻¹⁵ to 10⁻¹⁰ m², from Bai et al. (2010) and the isotropic pumices of Burgisser et al. (2017) were estimated using the correlations between tortuosity and porosity and between the average bubble size and the maximum throat diameter (Fig. 7c). We did not apply the model to the non-isotropic samples of Burgisser et al. (2017) because we doubt our correlations would apply to these samples and lack the necessary data to test our model on non-isotropic samples.

Although there is clearly a degradation in the accuracy of the model when the correlations are used to estimate the tortuosity and maximum throat diameter rather than their measured values (cf. Figure 7c with Fig. 7b), the permeability of 11 of the 14 samples from Bai et al. (2010) are reproduced within 1 log unit. The maximum difference between estimated and measured permeabilities is 1.9 log units, and the chi-squared value is 0.77. The estimated permeabilities of Burgisser et al.’s (2017) 13 isotropic samples are within 0.9 of a log unit of the measured values, and the chi-squared value is 0.35. The accuracy of this model is similar to that reported by Burgisser et al. (2017), who found that they could reproduce 26 of the 28 (isotropic and anisotropic) samples investigated to within 1 log unit.

This test indicates the model’s utility for estimating sample permeability with knowledge of only the porosity and the average bubble diameter. However, as shown in Fig. 7c, the model has a tendency to overestimate the permeabilities by a factor of ~ 5. An ad hoc correction could be made for this overestimation, but even without such correction the test indicates that permeabilities can be calculated to within an order of magnitude with the model.

Role of bubble growth rate on permeability

Although we did not directly determine the effect of bubble growth rate on permeability, our results agree with previous studies indicating that bubble growth rates significantly influence permeability (e.g., Rust and Cashman 2004; Burgisser and Gardner 2004; Mueller al. 2005, 2008; Takeuchi et al. 2009; Castro et al. 2012; Lindoo et al. 2016). In particular, Lindoo et al. (2016) noted that increasing decompression rates, leading to increasing bubble growth rates, increased the percolation threshold. This hypothesis is consistent with two observations on the basaltic composition where the slowly heated experiment DRB2012-7f-10 (1 °C s⁻¹) with Φ ~ 0.55 has a permeability (1.5 × 10⁻¹¹ m²) similar to the rapidly heated (6 °C s⁻¹), Φ ~ 0.73, experiment DRB2012-7c-f (2.9 × 10⁻¹¹ m²), whereas the fit from Bai et al. (2010) predicts a permeability of at least 5 × 10⁻¹¹ m² at Φ = 0.73.

We note that there may be a correlation between the bubble growth rate and the size distribution of pore throats that significantly influences permeability. We propose this tentative hypothesis because of the often lower permeabilities of the rapidly heated (5 °C min⁻¹) andesitic foam in comparison to the more slowly heated (~ 1 °C min⁻¹) trachyandesitic and dacitic foams with similar porosities (Table 2, Fig. 5).

Despite the need for further experiments to constrain the effects of decompression and growth rate on the permeability of silicate foams, we suggest that the orders of magnitude variability seen in permeability at similar porosities in Fig. 6 is significantly controlled by the bubble growth rate. The formation of a pore throat between two bubbles requires them to partially coalesce; for coalescence to occur the interbubble melt film (IBF) must thin to the point where it fails, estimated to be a thickness of 0.5 μm in a rhyolitic melt by Castro et al. (2012). The rate at which the IBF thins is a function of the surface tension, melt viscosity, and bubble size; the timescales of thinning vary from less than a second in basaltic melts to thousands of seconds in dacitic melts (Castro et al. 2012; Nguyen et al. 2013). In the case where bubbles are growing on timescales shorter than that of IBF thinning, coalescence is not as effective in creating large pore throats as at slower growth rates, and permeabilities at equal porosities are lower than in the case where bubble growth is slower than IBF thinning. Consideration of the lubrication and drag forces during bubble growth also suggests the possibility of a bubble size dependence of connectivity (and therefore permeability), which are currently being explored.

Conclusions

A complete characterization of magmatic foams is required to model permeability because permeability-porosity relationships alone do not provide sufficient data for accurate modeling and prediction. Furthermore, average properties of the foam, in particular average pore-throat diameters, appear to be insufficient to fully characterize permeability. Complete measurements of porosity, bubble, and pore-throat size distributions, as well as tortuosity, are required to model the permeability of magmatic foams. We stress the apparent importance of the largest pore throat on the permeability of magmatic foams and propose a model for permeability calculation, which we consider a step in the right direction that can be used to benchmark future studies. The results of this study are consistent with previous work indicating the importance of the bubble growth rate on the permeability of magmatic foams. Higher growth rates appear to produce lower permeabilities, and the effect of growth rate on permeability may help explain the orders of magnitude spread in permeabilities at similar porosity.