1 Introduction

The study of hemodynamics in stenotic arteries has been a significant domain of research in recent decades because of its countless important applications in the field of cardiovascular disease. Stenosis, also known as atherosclerosis, is the narrowing of blood vessels as a consequence of the accumulation of fatty substances inside the artery wall. These substances impede the blood supply and can cause rupture, leading to blood clot formation, which increases resistance to flow; therefore blood flow will be less effective in fulfilling its function. A number of researchers have presented theoretical and experimental studies exploring the effects of stenosis on blood flow [1, 2]. The influence of stenosis height and hematocrit on wall resistance and shear stress through a catheterized stenotic artery was studied by Srivastava [3], who found that resistance increased with stenosis height and hematocrit. Ali et al. [4] used a method of finite difference to study the pulsatile flow of blood in a tapered artery with a single stenosis. They observed that the flow rate and wall shear stress are strongly influenced by the degree of the tapered artery.

Numerous researchers believe that to understand various cardiovascular diseases and their treatments, it is crucial to study the dynamic properties of blood flow [5,6,7,8].

The rheology of human blood exhibits a Newtonian nature at a high shear rate, even though the non-Newtonian nature is dominant at a low shear rate or when it circulates in small-diameter or diseased arteries. Misra and Shit [9] treated the blood as a fluid non-Newtonian in the circular cross-section artery using the Hershel–Bulkley model. A combination of analytical and numerical techniques has been used to solve this problem. They found that the skin friction and resistance to flow increased with the height of the stenosis. Likewise, Sankar and Lee [10] developed a mathematical model flow of blood assumed to be non-Newtonian through a narrowed artery. They treated blood as a Herschel–Bulkley model and used the perturbation method. Their findings show that with increasing yield strength and stenosis height, the core radius of the plug and wall shear stress increased. Recently, Shahzad et al. [11] examined the flow of blood considered Carreau fluid in artery with multiple stenoses.

The Sutterby fluid model belongs to a category of non-Newtonian fluids that have the ability to predict the flow domain for an appropriate shear rate range, as well as for the zero shear rate regions. By selecting different values of the power-law index, the rheological characteristics of Newtonian and non-Newtonian fluids can be predicted using this model. In the literature, the number of studies investigating the flow of Sutterby fluid in stenotic arteries is very limited. For instance, Abbass et al. [12] numerically explored the unsteady flow of blood in stenotic artery subjected to a magnetic field and external body acceleration using the finite difference method. The Sutterby model represents blood as a non-Newtonian fluid. Shabbir et al. [13] carried out a numerical study of heat and mass exchange on pulsatile blood flow of Sutterby fluid in a tapered stenosed artery under atherosclerotic conditions taking into account body acceleration. They found that there is a close relationship between the temperature distribution in the narrowed zone of the blood vessel and the viscoelastic properties of the blood.

Blood is presumed to be a magnetohydrodynamic fluid. Travel sickness, headache and joint pain, for example, are conditions that could be effectively treated with the application of a suitable magnetic field. In biomedical sciences, MHD has a vast domain of applications, including the treatment of tumor cancer, bleeding control, magnetic targeting of drugs, hyperthermal cell death and endoscopic magnetics [14]. The electromagnetic field was first used in biomathematics by Kolins [15]. Barnothy [16] discovered that the use of an external magnetic field affects the biological systems of living organisms. When external electric and magnetic fields are subjected simultaneously to the flow of a fluid, the flow field changes, leading to what is recognized as EMHD flow, i.e., electro-magneto hydrodynamics. A variety of theoretical, experimental and computational studies have been conducted on blood flow modulated by magnetohydrodynamics (MHD) or electrohydrodynamics (EHD). Electric and magnetic field impacts on the flow of fluids are represented by momentum equations with forces, the so-called, Coulomb force and the Lorentz force, respectively. The blood flow of Newtonian bio-magnetic fluid with effects of heat and mass exchange in a tapered porous artery with stenosis was investigated by Nadeem et al. [17]. In a study by Bali and Awasthi [18], the impact of an applied magnetic field on the resistance to blood flow velocity in a stenotic artery was investigated. They found that with increasing magnetic field, the results reveal a reduction in velocity and an increase in resistance to blood flow. Manchi and Ponalagusamy [19] studied the electromagnetohydrodynamics flow of the Sutterby model in an inclined tapered porous artery with stenosis. As a result, they concluded that an increase in the electro-osmosis parameter minimized hemodynamic factors. Karmakar et al. [20] studied the hemodynamics of an artery cross section under the influence of electro-osmosis. He computed and interpreted precise mathematical results for the study. Their findings showed that the electro-osmotic parameter and Helmholtz-Smoluchowski velocity had a significant impact on promoting blood circulation in the endoscopic environment. Karmakar and Das [21] conducted research to illustrate the electrokinetic double layer (EDL) characteristics of blood flow via an irregular artery with wall slip. Their investigation showed that increasing the values of the electro-osmotic parameter considerably reduces the rate of heat transmission. Ali et al. [22] recently performed research that utilized diverging/converging ciliated micro-vessels to illustrate the blood streaming under electro-osmotic and Lorentz forces. Some further important research papers on EMHD pumping simulation under diverse areas are given in Refs. [23,24,25,26,27,28,29].

In most existing studies, it was assumed that blood vessels have no inclination to the horizontal. However, in reality, the vessels within the human physiological system are not horizontal, but instead have an angle of inclination. Researchers were encouraged by this fact to consider blood flow in inclined arteries. Zaman et al. [30] examined the unsteady flow of non-Newtonian blood represented by power law fluid through an inclined overlapping stenotic artery with slip effect at the surface. They found that when increasing the slip velocity or inclination angle, the velocity profile will have higher magnitudes throughout the arterial segment. The effect of electromagnetic force on blood flow mixed with Cu nanoparticles within an inclined overlapping stenotic artery was investigated by Umadevi et al. [31]. They concluded that high buoyancy and electromagnetic forces are associated with higher velocity profiles than viscous forces.

The human body is exposed every day to body acceleration or vibration, for example, driving a vehicle or rapid body movements in sports or traveling, which causes symptoms such as headaches and accelerated heart rate. The amplitude and frequency of such vibrations also have a significant effect on blood flow in narrowed arteries and might play a vital role in the circulatory system. In this regard, Siddiqui et al. [32] used a non-Newtonian Bingham plastic fluid model to study blood flow. The model was applied to investigate the flow characteristics within a constricted artery while considering the slip velocity at the wall and body acceleration. Using the perturbation method, they found that body acceleration increases axial velocity and volumetric flow. Similarly, Haghighi and Chalak [33] explored the influence of body acceleration on the flow of blood in stenotic artery using the Sisko model with the numerical finite difference method. They found that body acceleration has the tendency to decrease resistance to flow of blood.

Nanofluid dynamics, a new field of fluid dynamics, has emerged and is now being applied in diverse fields such as energy, medical research and biology. Many applications for these fluids can be found in the fields of medical science and engineering. Currently, the greatest challenge facing engineers, doctors and scientists is to discover new applications for nanoparticles in the fields of life sciences and healthcare. In medical applications, nanoparticles are used as hyperthermia treatments, drug carriers and tracking agents. Changdar and Soumen [34] obtained analytical results of single-phase blood nanofluid flow through an inclined multiple stenosed artery under the action of a magnetic field. The findings showed that increasing the nanoparticle concentration reduced the hemodynamic effects of stenosis. Ahmed and Nadeem [35] studied the unsteady flow of Cu-nanoparticles through a curved stenosed artery. Different shapes of nanoparticles, such as bricks, cylindrical shapes, and platelets, were investigated. The distribution of nanofluid wall velocity, impedance, and shear stress was studied using the perturbation approximation method along with the varying curvature parameter. They concluded that the platelet shape offers minimal resistance compared to the brick and cylindrical shapes. Zaman et al. [36] developed a mathematical model to depict the effect of various types of nanoparticles (Cu, TiO2, Al2O3) on the unsteady flow of blood through a stenotic artery. They found that the blood flow velocity in the stenotic region is reduced by adding nanoparticles to the base fluid. Elnaqeeb [37] theoretically explored the potential benefits of gold nanoparticles in enhancing blood flow through an artery that contains multiple stenoses under a radial magnetic field. The findings indicated that the introduction of gold nanoparticles could enhance the velocity through the region of the stenosed artery. However, the flow can decelerate as the radial magnetic field increases.

The aim of this work is to discuss the coupled mechanism between electrohydrodynamics and magnetohydrodynamics of the flow of the pulsatile Sutterby nanofluid inside an inclined porous tapered artery with overlapping stenosis, considering the boundary condition of the slip effect and periodic body acceleration. The heat source and thermal radiation are also taken into account. Blood flow characteristics are simulated using gold (Au) nanoparticles in this study. Using the finite difference method (FDM), we obtain numerical solutions for the velocity profile, temperature profile, flow rate, wall shear stress and resistance to flow. The novelty of all the relevant physiological factors incorporated into the model is discussed and graphically represented.

The originality and novelty underlying this research are stated below. Furthermore, Table 1 presents a comparative literature review:

  • Mathematical and numerical simulations of blood flow in an inclined tapered porous artery having overlapping stenosis with gold nanoparticles are achieved.

  • To characterize the non-Newtonian rheological behavior of blood, the Sutterby fluid model was adapted.

  • The model equations integrate the various effects of the heat source, viscous dissipation, body acceleration, electro-osmosis, magnetic field, and nanoparticles.

  • Adopt of a numerical approach to obtain the solutions of the governing equations.

  • The outcomes of this model will be very helpful in the treatment of cardiovascular diseases and cancer.

Table 1 A literature comparative review to identify gaps in the study
Full size table

2 Mathematical formulation

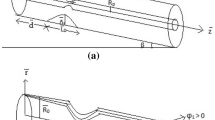
Consider that blood flow is axisymmetric, laminar, incompressible and naturally unsteady through a porous tapered artery with overlapping stenosis having an angle of inclination λ, under the simultaneous effects of magnetohydrodynamic (MHD), electrohydrodynamics (EHD) and body acceleration. The geometry is described in a cylindrical coordinate system (r, θ, z), where r is the radial coordinate, z is the axial coordinate and θ is the circumferential (tangential) coordinate, which is neglected here since the flow is axisymmetric, see Fig. 1. Gold nanoparticles (Au) are injected into the blood (base fluid) which is assumed to be a non-Newtonian fluid, using the Sutterby model to simulate its rheology. In the flow regime, the axial electrical field of force Ez and the transversal magnetic field of force B0 are included.

Fig. 1
figure 1

The geometry of the inclined stenotic artery makes an angle λ with the horizontal

Full size image

2.1 Geometry of the stenosis

The geometric structure of the tapered artery with overlapping stenosis is described mathematically as follows [40],

$$\overline{R}\left( z \right) = \left\{ {\begin{array}{*{20}l} {\left( {R_{0} + \chi^{*} \overline{z}} \right) - \frac{3}{2}\frac{\delta }{{l_{0}^{4} }}\left[ {11\left( {\overline{z} - \overline{d}} \right)l_{0}^{3} - 47\left( {\overline{z} - \overline{d}} \right)^{2} l_{0}^{2} + 72\left( {\overline{z} - \overline{d}} \right)^{3} l_{0} - 36\left( {\overline{z} - \overline{d}} \right)^{4} } \right],} \hfill & {\overline{d} \le \overline{z} \le \overline{d} + l_{0} } \hfill \\ {\left( {R_{0} + \chi^{*} \overline{z}} \right)} \hfill & {{\text{otherwise}} } \hfill \\ \end{array} } \right.$$
(1)

in which R(z) is the radius of artery in the stenotic region, R0 is the radius of the artery in the non-stenotic region assumed to be constant, d is the stenosis location, L0 is the stenosis length, and δ is the stenosis height. The parameter of tapering χ* is given by χ* = tan(Ψ), where Ψ is the angle of tapering, which takes the values Ψ < 0 for converging, Ψ > 0 for diverging artery, and Ψ = 0 for non-tapering artery as shown in Fig. 2.

Fig. 2
figure 2

Representation of the shape of the stenosis with different tapering angles

Full size image

2.2 Governing equations

The following is an outline of the adopting physical assumptions:

  • The Sutterby fluid model is utilized to characterize the rheology of blood.

  • The nanoparticles are distributed homogeneously in the blood (base fluid).

  • The induced magnetic field has a negligible effect on the formation of blood flow, given that the magnetic Reynolds number is negligible.

  • Thermal radiation, viscous dissipation and Heat source are taken into account.

  • For heat emission, the Rosseland hypothesis is considered.

  • The Debye-Hückel approximation is employed to simplify the complexity of the stream formulation.

  • No overlapping electrical double layer is considered.

The following are the velocity and temperature profiles for the present problem,

$$V = \left[ {\overline{u}\left( {r,z,t} \right),0,\overline{w}\left( {r,z,t} \right)} \right];\,T = T\left( {r,z,t} \right)$$
(2)

where u is the radial velocity and w the axial velocity. Taking all the above considerations into account, for an incompressible Sutterby nanofluid, the equations governing continuity, momentum and energy can be written as follows [12, 13, 30, 41],

$$\frac{{\partial \overline{u}}}{{\partial \overline{r}}} + \frac{{\overline{u}}}{{\overline{r}}} + \frac{{\partial \overline{w}}}{{\partial \overline{z}}} = 0$$
(3)
$$\rho_{{{\text{nf}}}} \left( {\frac{{\partial \overline{u}}}{{\partial \overline{t}}} + \overline{u}\frac{{\partial \overline{u}}}{{\partial \overline{r}}} + \overline{w}\frac{{\partial \overline{u}}}{{\partial \overline{z}}}} \right) = - \frac{{\partial \overline{p}}}{{\partial \overline{r}}} + \left( {\frac{1}{{\overline{r}}}\frac{\partial }{{\partial \overline{r}}}\left( {\overline{r}\overline{S}_{rr} } \right) + \frac{\partial }{{\partial \overline{z}}}\left( {\overline{S}_{rz} } \right)} \right) - \frac{{\overline{S}_{\theta \theta } }}{{\overline{r}}}$$
(4)
$$\begin{aligned} \rho_{{{\text{nf}}}} \left( {\frac{{\partial \overline{w}}}{{\partial \overline{t}}} + u\frac{{\partial \overline{w}}}{{\partial \overline{r}}} + w\frac{{\partial \overline{w}}}{{\partial \overline{z}}}} \right) = & - \frac{{\partial \overline{p}}}{{\partial \overline{z}}} + \left( {\frac{1}{{\overline{r}}}\frac{\partial }{{\partial \overline{r}}}\left( {\overline{r}\overline{S}_{rz} } \right) + \frac{\partial }{{\partial \overline{z}}}\left( {\overline{S}_{zz} } \right)} \right) \\ & \quad + \rho_{{{\text{nf}}}} \overline{G}\left( t \right) - \sigma_{{{\text{nf}}}} B_{0}^{2} \overline{w} - \frac{{\mu_{{{\text{nf}}}} }}{{k_{b} }}\overline{w} + \rho_{e} E_{z} + \left( {\rho \gamma } \right)_{{{\text{nf}}}} g\left( {T - T_{1} } \right)\sin \left( \lambda \right) \\ \end{aligned}$$
(5)
$$\begin{aligned} \left( {\rho Cp} \right)_{{{\text{nf}}}} \left( {\frac{\partial T}{{\partial \overline{t}}} + \overline{u}\frac{\partial T}{{\partial \overline{r}}} + \overline{w}\frac{\partial T}{{\partial \overline{z}}}} \right) &= \overline{S}_{rr} \frac{{\partial \overline{u}}}{{\partial \overline{r}}} + \overline{S}_{rz} \frac{{\partial \overline{w}}}{{\partial \overline{r}}} + \overline{S}_{zr} \frac{{\partial \overline{u}}}{{\partial \overline{z}}} \\ &\quad + \overline{S}_{zz} \frac{{\partial \overline{w}}}{{\partial \overline{z}}} + k_{{{\text{nf}}}} \left( {\frac{{\partial^{2} T}}{{\partial \overline{r}^{2} }} + \frac{1}{{\overline{r}}}\frac{\partial T}{{\partial \overline{r}}} + \frac{{\partial^{2} T}}{{\partial \overline{z}^{2} }}} \right) - \frac{1}{{\overline{r}}}\frac{{\partial \left( {\overline{r}q_{r} } \right)}}{{\partial \overline{r}}} + \beta_{0} \\ \end{aligned}$$
(6)

In the above series of equations, the physical parameters, ρnf, γnf, λ, Cpnf, knf, μnf and β0 are defined as the density of nanofluid, the coefficient of thermal expansion, the angle of inclination of the artery with respect to the horizontal plane, the specific heat, the thermal conductivity, the dynamic viscosity and the heat generation parameter, respectively.

Where \({q}_{{\text{r}}}\) is the thermal radiation and is stated as [42,43,44,45]

$$q_{{\text{r}}} = - \frac{{4\sigma^{*} }}{{3k^{*} }}\frac{{\partial T^{4} }}{{\partial \overline{r}}} = - \frac{{16\sigma^{*} }}{{3k^{*} }}T_{1}^{3} \frac{\partial T}{{\partial \overline{r}}}$$
(7)

The additional stress component is represented by the Srr, Srz and Szz terms in Eqs. (4) ,(5) and (6). The constituent equation of the Sutterby rheological model is as follows [13, 38],

$$S = \mu_{{{\text{nf}}}} \left[ {\frac{{\sinh^{ - 1} \left( {B\dot{\gamma }} \right)}}{{B\dot{\gamma }}}} \right]^{m} A_{1}$$
(8)
$$\overline{S}_{rr} = \mu_{{{\text{nf}}}} \left[ {1 - \frac{{mB^{2} }}{6}\left\{ {2\left( {\left( {\frac{{\partial \overline{u}}}{{\partial \overline{r}}}} \right)^{2} + \left( {\frac{{\overline{u}}}{{\overline{r}}}} \right)^{2} + \left( {\frac{{\partial \overline{w}}}{{\partial \overline{z}}}} \right)^{2} } \right) + \left( {\frac{{\partial \overline{u}}}{{\partial \overline{z}}} + \frac{{\partial \overline{w}}}{{\partial \overline{r}}}} \right)^{2} } \right\}} \right]2\left( {\frac{{\partial \overline{u}}}{{\partial \overline{r}}}} \right)$$
(9)
$$S_{rz} = \mu_{{{\text{nf}}}} \left[ {1 - \frac{{mB^{2} }}{6}\left\{ {2\left( {\left( {\frac{{\partial \overline{u}}}{{\partial \overline{r}}}} \right)^{2} + \left( {\frac{{\overline{u}}}{{\overline{r}}}} \right)^{2} + \left( {\frac{{\partial \overline{w}}}{{\partial \overline{z}}}} \right)^{2} } \right) + \left( {\frac{{\partial \overline{u}}}{{\partial \overline{z}}} + \frac{{\partial \overline{w}}}{{\partial \overline{r}}}} \right)^{2} } \right\}} \right]\left( {\frac{{\partial \overline{w}}}{{\partial \overline{r}}} + \frac{{\partial \overline{u}}}{{\partial \overline{z}}}} \right)$$
(10)
$$S_{\theta \theta } = \mu_{{{\text{nf}}}} \left[ {1 - \frac{{mB^{2} }}{6}\left\{ {2\left( {\left( {\frac{{\partial \overline{u}}}{{\partial \overline{r}}}} \right)^{2} + \left( {\frac{{\overline{u}}}{{\overline{r}}}} \right)^{2} + \left( {\frac{{\partial \overline{w}}}{{\partial \overline{z}}}} \right)^{2} } \right) + \left( {\frac{{\partial \overline{u}}}{{\partial \overline{z}}} + \frac{{\partial \overline{w}}}{{\partial \overline{r}}}} \right)^{2} } \right\}} \right]2\left( {\frac{{\overline{u}}}{{\overline{r}}}} \right)$$
(11)
$$S_{zz} = \mu_{{{\text{nf}}}} \left[ {1 - \frac{{mB^{2} }}{6}\left\{ {2\left( {\left( {\frac{{\partial \overline{u}}}{{\partial \overline{r}}}} \right)^{2} + \left( {\frac{{\overline{u}}}{{\overline{r}}}} \right)^{2} + \left( {\frac{{\partial \overline{w}}}{{\partial \overline{z}}}} \right)^{2} } \right) + \left( {\frac{{\partial \overline{u}}}{{\partial \overline{z}}} + \frac{{\partial \overline{w}}}{{\partial \overline{r}}}} \right)^{2} } \right\}} \right]2\left( {\frac{{\partial \overline{w}}}{{\partial \overline{z}}}} \right)$$
(12)

The boundary and initial conditions for the velocity profile and temperature field are at the wall (r = R) and at the center of the artery (r = 0). They also include an axial hydrodynamic slip velocity (ws) at the arterial wall [19],

$$\overline{w}\left( {r,0} \right) = 0;\;T\left( {r,0} \right) = 0\;{\text{at}}\;\overline{t} = 0$$
(13)
$$\frac{{\partial \overline{w}}}{{\partial \overline{r}}} = 0;\;\frac{\partial T}{{\partial \overline{r}}} = 0\;{\text{at}}\;\overline{r} = 0$$
(14)
$$\overline{w}\left( {r,t} \right) = w_{{\text{s}}} ;\;T = T_{w} \;{\text{at}}\;\overline{r} = \overline{R}$$
(15)

2.3 Dimensionless analysis

The dimensionless quantities below are defined in order to simplify the equations governing the problem by means of a non-dimensional analysis [19, 46],

$$\begin{aligned} r = & \frac{{\overline{r}}}{{R_{0} }},\; z = \frac{{\overline{z}}}{{l_{0} }},\;u = \frac{{l_{0} }}{{\delta u_{e} }}\overline{u},\;w = \frac{{\overline{w}}}{{u_{e} }},\; R = \frac{{\overline{R}}}{{R_{0} }},\;d = \frac{{\overline{d}}}{{R_{0} }} \\ p = & \frac{{R_{0}^{2} }}{{u_{e} l_{0} \mu_{f} }}\overline{p},\; t = \frac{{u_{e} }}{{R_{0} }}\overline{t},\;\beta = \frac{{\beta_{0} R_{0}^{2} }}{{k_{f} \left( {T_{{\text{w}}} - T_{1} } \right)}},\;\theta = \frac{{T - T_{1} }}{{T_{{\text{w}}} - T_{1} }},\;\chi = \frac{{l_{0} }}{{R_{0} }}\chi^{*} \\ u_{e} = & - \left( {\frac{{E_{z} \epsilon \psi_{\omega } }}{{\mu_{f} }}} \right),\;S_{rr} = \frac{{l_{0} }}{{u_{e} \mu_{f} }}\overline{S}_{rr} ,\;{\text{S}}_{{{\text{zz}}}} = \frac{{l_{0} }}{{u_{e} \mu_{f} }}\overline{S}_{zz} ,\;{\text{S}}_{{{\text{rz}}}} = \frac{{R_{0} }}{{u_{e} \mu_{f} }}\overline{S}_{rz} , \\ {\text{S}}_{\theta \theta } = & \frac{{l_{0} }}{{u_{e} \mu_{f} }}\overline{S}_{\theta \theta } ,\;\delta = \frac{{\overline{\delta }}}{{R_{0} }},\;\xi = \frac{{R_{0} }}{{l_{0} }}\overline{\xi },\;M = R_{0} B_{0} \sqrt {\frac{{\sigma_{f} }}{{\mu_{f} }}} ,\;B_{2} = \frac{{\rho_{f} R_{0}^{2} }}{{u_{e} \mu_{f} }}, \\ G\left( t \right) = & \frac{{\rho_{f} R_{0}^{2} }}{{u_{e} \mu_{f} }},\;{\text{Pr}} = \frac{{Cp_{f} \mu_{f} }}{{k_{f} }},\;{\text{Gr}} = \frac{{\left( {\rho \gamma } \right)_{f} gR_{0}^{2} \left( {T_{{\text{w}}} - T_{1} } \right)}}{{u_{e} \mu_{f} }},\;{\text{Re}} = \frac{{\rho_{f} u_{e} R_{0} }}{{\mu_{f} }}, \\ {\text{Da}} = & \frac{{k_{b} }}{{R_{0}^{2} }}\;\varepsilon = \frac{{B^{2} u_{e}^{2} }}{{6R_{0}^{2} }},\;{\text{Br}} = \frac{{u_{e}^{2} \mu_{f} }}{{k_{f} \Delta T}},\;R_{d} = \frac{{16\sigma^{*} T_{1}^{3} }}{{3k^{*} k_{f} }} \\ \end{aligned}$$
(16)

In the above, r is the dimensionless radial coordinate, z is the dimensionless axial coordinate, w is the dimensionless axial velocity, u is the dimensionless radial velocity component, R is the dimensionless radius, p is the dimensionless pressure, t is the dimensionless time, β is the dimensionless heat generation parameter, θ is the dimensionless blood temperature, and ws is the dimensionless slip velocity, The Helmholtz–Smoluchowski velocity is represented by ue and the wall temperature is Tw, the vessel aspect ratio \(\upxi\) and the stenosis height parameter δ are the dimensionless geometric parameters. In addition, Re is the Reynolds number, Pr is the Prandtl number, Gr is the local thermal Grashof number, Da is the Darcy number and Br is Brinkman number. After introducing the non-dimensional parameters of Eq. (16) into Eqs. (3–6), the non-dimensionalized form of governing Eqs. (3–6) are,

$$\delta \left( {\frac{\partial u}{{\partial r}} + \frac{u}{r}} \right) + \frac{\partial w}{{\partial z}} = 0$$
(17)
$$\frac{{\rho_{{{\text{nf}}}} }}{{\rho_{f} }}\left( {\frac{{R_{0} }}{{l_{0} }}} \right)^{2} \left( {{\text{Re}} \frac{\partial u}{{\partial t}} + {\text{Re}} \left( {\frac{{R_{0} }}{{l_{0} }}} \right)\left( {\delta u\frac{\partial u}{{\partial r}} + w\frac{\partial u}{{\partial z}}} \right)} \right) = - \frac{\partial p}{{\partial r}} + \left( {\frac{{R_{0} }}{{l_{0} }}} \right)^{2} \left( {\frac{1}{r}\frac{\partial }{\partial r}\left( {rS_{rr} } \right) + \frac{\partial }{\partial z}\left( {S_{rz} } \right) - \frac{{S_{\theta \theta } }}{r}} \right)$$
(18)
$$\begin{aligned} \frac{{\rho_{{{\text{nf}}}} }}{{\rho_{f} }}\left( {{\text{Re}} \frac{\partial w}{{\partial t}} + {\text{Re}} \left( {\frac{{R_{0} }}{{l_{0} }}} \right)\left( {\delta u\frac{\partial w}{{\partial r}} + w\frac{\partial w}{{\partial z}}} \right)} \right) = & - \frac{\partial p}{{\partial z}} + \left( {\frac{{\mu_{{{\text{nf}}}} }}{{\mu_{f} }}} \right)\frac{1}{r}\frac{\partial }{\partial r}\left( {rS_{rz} } \right) + \left( {\frac{{\mu_{{{\text{nf}}}} }}{{\mu_{f} }}} \right)\left( {\frac{{R_{0} }}{{l_{0} }}} \right)^{2} \frac{\partial }{\partial z}\left( {S_{zz} } \right)\\& + \frac{{\rho_{{{\text{nf}}}} }}{{\rho_{f} }}B_{2} \cos \left( {\omega_{b} t + \alpha } \right) \\ & \quad - \left( {\frac{{\sigma_{{{\text{nf}}}} }}{{\sigma_{f} }}M^{2} + \frac{{\mu_{{{\text{nf}}}} }}{{\mu_{f} }}\frac{1}{Da}} \right)w + {\text{Ke}}^{2} \psi \left( r \right) + \frac{{\left( {\rho \gamma } \right)_{{{\text{nf}}}} }}{{\left( {\rho \gamma } \right)_{f} }}{\text{Gr}}\theta \sin \left( \lambda \right) \\ \end{aligned}$$
(19)
$$\begin{aligned} \left( {\rho Cp} \right)_{{{\text{nf}}}} {\text{Re}} \Pr \left( {\frac{\partial \theta }{{\partial t}} + \left( {\frac{{R_{0} }}{{l_{0} }}} \right)\left( {\delta u\frac{\partial \theta }{{\partial r}} + w\frac{\partial \theta }{{\partial z}}} \right)} \right) = & \left( {\frac{{\mu_{{{\text{nf}}}} }}{{\mu_{f} }}} \right){\text{Br}}\left( {S_{rz} \frac{\partial w}{{\partial r}} + \left( {\frac{{R_{0} }}{{l_{0} }}} \right)^{2} \left( {\delta S_{rr} \frac{\partial u}{{\partial r}} + \delta S_{zr} \frac{\partial u}{{\partial z}} + S_{zz} \frac{\partial w}{{\partial z}}} \right)} \right) \\ & \quad + \frac{{k_{{{\text{nf}}}} }}{{k_{f} }}\left( {\frac{{\partial^{2} \theta }}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial \theta }{{\partial r}} + \left( {\frac{{R_{0} }}{{l_{0} }}} \right)^{2} \frac{{\partial^{2} \theta }}{{\partial z^{2} }}} \right) + \left( {\frac{{\partial^{2} \theta }}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial \theta }{{\partial r}}} \right)R_{d} + \beta \\ \end{aligned}$$
(20)

where

$$S_{rr} = 2\left[ {1 - m\varepsilon \left\{ {2\left( {\delta \left( {\frac{{R_{0} }}{{l_{0} }}} \right)^{2} \left( {\left( {\frac{\partial u}{{\partial r}}} \right)^{2} + \left( \frac{u}{r} \right)^{2} } \right) + \left( {\frac{{R_{0} }}{{l_{0} }}} \right)^{2} \left( {\frac{\partial w}{{\partial z}}} \right)^{2} } \right) + \left( {\delta \left( {\frac{{R_{0} }}{{l_{0} }}} \right)^{2} \frac{\partial u}{{\partial z}} + \frac{\partial w}{{\partial r}}} \right)^{2} } \right\}} \right]\left( {\delta \frac{\partial u}{{\partial r}}} \right)$$
(21)
$$\begin{aligned}S_{rz} &= \left[ {1 - m\varepsilon \left\{ {2\left( {\delta \left( {\frac{{R_{0} }}{{l_{0} }}} \right)^{2} \left( {\left( {\frac{\partial u}{{\partial r}}} \right)^{2} + \left( \frac{u}{r} \right)^{2} } \right) + \left( {\frac{{R_{0} }}{{l_{0} }}} \right)^{2} \left( {\frac{\partial w}{{\partial z}}} \right)^{2} } \right) + \left( {\delta \left( {\frac{{R_{0} }}{{l_{0} }}} \right)^{2} \frac{\partial u}{{\partial z}} + \frac{\partial w}{{\partial r}}} \right)^{2} } \right\}} \right]\\ & \quad \times \left( {\frac{\partial w}{{\partial r}} + \delta \left( {\frac{{R_{0} }}{{l_{0} }}} \right)^{2} \frac{\partial u}{{\partial z}}} \right) \end{aligned}$$
(22)
$$S_{\theta \theta } = 2\left[ {1 - m\varepsilon \left\{ {2\left( {\delta \left( {\frac{{R_{0} }}{{l_{0} }}} \right)^{2} \left( {\left( {\frac{\partial u}{{\partial r}}} \right)^{2} + \left( \frac{u}{r} \right)^{2} } \right) + \left( {\frac{{R_{0} }}{{l_{0} }}} \right)^{2} \left( {\frac{\partial w}{{\partial z}}} \right)^{2} } \right) + \left( {\delta \left( {\frac{{R_{0} }}{{l_{0} }}} \right)^{2} \frac{\partial u}{{\partial z}} + \frac{\partial w}{{\partial r}}} \right)^{2} } \right\}} \right]\left( {\delta \frac{u}{r}} \right)$$
(23)
$$S_{zz} = 2\left[ {1 - m\varepsilon \left\{ {2\left( {\delta \left( {\frac{{R_{0} }}{{l_{0} }}} \right)^{2} \left( {\left( {\frac{\partial u}{{\partial r}}} \right)^{2} + \left( \frac{u}{r} \right)^{2} } \right) + \left( {\frac{{R_{0} }}{{l_{0} }}} \right)^{2} \left( {\frac{\partial w}{{\partial z}}} \right)^{2} } \right) + \left( {\delta \left( {\frac{{R_{0} }}{{l_{0} }}} \right)^{2} \frac{\partial u}{{\partial z}} + \frac{\partial w}{{\partial r}}} \right)^{2} } \right\}} \right]\left( {\frac{\partial w}{{\partial z}}} \right)$$
(24)

2.4 Electroosmotic flow

The electric field applied axially to the nanofluid which electrically conductive, applies a net electrical body force (ρe Ez) and generates near the vessel walls an electric double layer (EDL). This result in an electric charge density (ρe) for an equilibrium electrolyte (z +  = z −  = z0) as follows [19, 27, 41],

$$\rho_{{\text{e}}} = z_{0} e_{0} \left( {n_{ + } - n_{ - } } \right)$$
(25)

where n+ is the cations, n− the anions, e0 is the electronic charge and z0 represents the charge balance, using the Boltzmann distribution we can determine \({n}_{+}\) and \({n}_{-}\) (supposing there is no overlap between the EDL) [19, 41, 47],

$$n_{ \pm } = n_{0} \exp \left( { \mp \frac{{z_{0} e_{0} \overline{\psi }}}{{T_{0} k_{{\text{B}}} }}} \right)$$
(26)

In which n0 the density of ions in the electrolyte, kB is Boltzmann’s constant and T0 is the mean temperature. A Poisson equation governs the relation that linking the electric potential distribution (ψ) and the net density charge (ρe),

$$\nabla^{2} \overline{\psi } = \frac{1}{{\overline{r}}}\frac{{\partial \overline{\psi }}}{{\partial \overline{r}}} + \frac{{\partial^{2} \overline{\psi }}}{{\partial \overline{r}^{2} }} = - \frac{{\rho_{{\text{e}}} }}{\epsilon }$$
(27)

with \(\epsilon\) representing the constant dielectric. Summarizing Eqs. (25–27) we obtain the non-linear Poisson–Boltzmann equation,

$$\frac{1}{{\overline{r}}}\frac{{\partial \overline{\psi }}}{{\partial \overline{r}}} + \frac{{\partial^{2} \psi }}{{\partial \overline{r}^{2} }} = \frac{{2z_{0} e_{0} n_{0} }}{\epsilon }\sinh \left( {\frac{{z_{0} e_{0} \overline{\psi }}}{{T_{0} k_{B} }}} \right)$$
(28)

The characteristic thickness of the EDL can be defined by the Debye length parameter,

$$\lambda_{D} = \sqrt {\frac{{\epsilon T_{0} k_{{\text{B}}} }}{{2z_{0}^{2} e_{0}^{2} n_{0} }}}$$
(29)

We can easily find the solution for the electric-osmotic potential distribution using the Poisson–Boltzmann equation,

$$\frac{1}{{\overline{r}}}\frac{{\partial \overline{\psi }}}{{\partial \overline{r}}} + \frac{{\partial^{2} \overline{\psi }}}{{\partial \overline{r}^{2} }} = k^{2} \overline{\psi }$$
(30)

For the potential electro-osmotic function, the boundary conditions are as follows,

$$\frac{{\partial \overline{\psi }}}{{\partial \overline{r}}} = 0\;{\text{at}}\;\overline{r} = 0\;{\text{and}}\;\overline{\psi } = \psi_{\omega } \;{\text{at}}\;\overline{r} = \overline{R}\left( z \right)$$
(31)

in which ψw is the zeta potential of the wall. Using the non-dimensional parameters \(r=\frac{\overline{r}}{{R }_{0}}\) and \(\psi =\frac{\overline{\psi }}{{\psi }_{\omega }}\), we obtain the dimensionless form of Eqs. (30) and (31) as follows,

$$\frac{1}{r}\frac{\partial \psi \left( r \right)}{{\partial r}} + \frac{{\partial^{2} \psi \left( r \right)}}{{\partial r^{2} }} = {\text{Ke}}^{2} \psi \left( r \right)$$
(32)
$$\frac{\partial \psi }{{\partial r}}\left( 0 \right) = 0\;{\text{and}}\;\psi \left( R \right) = 1$$
(33)

Applying the boundary conditions (33) to the analytical solution of Eq. (32) gives the electric potential distribution expression,

$$\psi \left( r \right) = \frac{{I_{0} \left( {{\text{Ke}} r} \right)}}{{I_{0} \left( {{\text{Ke}} R} \right)}}$$
(34)

The relationship between arterial radius and Debye length is represented by\({\text{Ke}} = \frac{{R_{0} }}{{\lambda_{D} }}\), which determines the relative intensity of electro-kinetic effects.

In addition, the dimensionless form of the represented shape in Eq. (1) is written as follows,

$$R\left( z \right) = \left\{ {\begin{array}{*{20}l} {\left( {1 + \chi z} \right) - \frac{3\delta }{2}\left[ {11\left( {z - d} \right) - 47\left( {z - d} \right)^{2} + 72\left( {z - d} \right)^{3} - 36\left( {z - d} \right)^{4} } \right],} \hfill & {d \le z \le d + 1} \hfill \\ {\left( {1 + \chi z} \right) } \hfill & {{\text{otherwise}}} \hfill \\ \end{array} } \right.$$
(35)

In the cardio-vascular system, blood flow is provoked by the action of pumping the heart, producing a pressure gradient through the vascular network. There are two components to the pressure gradient, a constant (non-fluctuating) component and a pulsatile (fluctuating) component, as shown below, see Burton [48],

$$- \frac{{\partial \overline{p}}}{{\partial \overline{z}}} = A_{0} + A_{1} \cos \left( {\omega_{{\text{f}}} t} \right)\;t > 0$$
(36)

where A0 and A1 are respectively the magnitudes of the constant and pulsatile components of the pressure gradient, and ωf = 2πf1 represents the angular frequency with f1 the frequency of the cardiac pulse. In the non-dimensional form, Eq. (36) can be written as,

$$- \frac{\partial p}{{\partial z}} = B_{1} \left( {1 + e\cos \left( {\omega_{{\text{f}}} t} \right)} \right)$$
(37)

where \(B_{1} = \frac{{A_{0} R_{0}^{2} }}{{u_{e} \mu_{f} }};\;e = \frac{{A_{1} }}{{A_{0} }}\).

In the axial direction, the blood flow containing the gold nanoparticles is subject to a periodic external body acceleration G (t) which is expressed by the following equation [49],

$$\overline{G}\left( t \right) = a_{0} \cos \left( {\omega_{r} t + \alpha } \right)\;t > 0$$
(38)

In which a0 represents the body’s acceleration amplitud α phase angle and ωr = 2π f2, f2 is the body’s acceleration frequency.

Two different assumptions were taken into account for the rest of the analysis; δ ≪ 1 and.

\(\xi =\frac{{R}_{0}}{{l}_{0}}\approx O(1)\), i.e. the parameter of stenosis height is well below unity and the aspect ratio of the vessel is of a magnitude comparable to unity. Following the imposition of these assumptions, Eqs. (17–20) will be simplified to a coupled system of differential equations,

$$\begin{aligned} \frac{{\rho_{{{\text{nf}}}} }}{{\rho_{f} }}{\text{Re}} \frac{\partial w}{{\partial t}} = & B_{1} \left( {1 + e\cos \left( {\omega_{f} t} \right)} \right) + \frac{{\rho_{{{\text{nf}}}} }}{{\rho_{f} }}B_{2} \left( {\cos \left( {\omega_{r} t + \alpha } \right)} \right) + \left( {\frac{{\mu_{{{\text{nf}}}} }}{{\mu_{f} }}} \right)\frac{1}{r}\frac{\partial }{\partial r}\left( {r\left( {\frac{\partial w}{{\partial r}} - m\varepsilon \left( {\frac{\partial w}{{\partial r}}} \right)^{3} } \right)} \right) \\ - & \quad \left( {\frac{{\sigma_{{{\text{nf}}}} }}{{\sigma_{f} }}M^{2} + \frac{{\mu_{{{\text{nf}}}} }}{{\mu_{f} }}\frac{1}{Da}} \right)w + {\text{Ke}}^{2} \psi \left( r \right) + \frac{{\left( {\rho \gamma } \right)_{{{\text{nf}}}} }}{{\left( {\rho \gamma } \right)_{f} }}{\text{Gr}}\theta \sin \left( \lambda \right) \\ \end{aligned}$$
(39)
$${\text{Re}} \Pr \frac{{\left( {\rho Cp} \right)_{{{\text{nf}}}} }}{{\left( {\rho Cp} \right)_{f} }}\left( {\frac{\partial \theta }{{\partial t}}} \right) = \left( {\frac{{\mu_{{{\text{nf}}}} }}{{\mu_{f} }}} \right){\text{Br}}\left( {\left( {\frac{\partial w}{{\partial r}} - m\varepsilon \left( {\frac{\partial w}{{\partial r}}} \right)^{3} } \right)\frac{\partial w}{{\partial r}}} \right) + \left( {\frac{{\partial^{2} \theta }}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial \theta }{{\partial r}}} \right)\left( {\frac{{k_{{{\text{nf}}}} }}{{k_{f} }} + R_{d} } \right) + \beta$$
(40)

The non-dimensional boundary conditions can be written as follows,

$$w\left( {r,0} \right) = 0;\;\theta \left( {r,0} \right) = 0\;{\text{at}}\;t = 0$$
(41)
$$\frac{\partial w}{{\partial r}} = 0;\;\frac{\partial \theta }{{\partial r}} = 0\;{\text{at}}\;r = 0$$
(42)
$$w\left( {r,t} \right) = w_{{\text{s}}} ;\;\theta = 1\;{\text{at}}\;r = R$$
(43)

The wall shear stress, the flow rate and the resistance to flow expressions take the form respectively,

$$S_{rz} = \frac{{\mu_{{{\text{nf}}}} }}{{\mu_{f} }}\left. {\left( {\left( {\frac{\partial w}{{\partial r}}} \right) - m\varepsilon \left( {\frac{\partial w}{{\partial r}}} \right)^{3} } \right)} \right|_{r = R}$$
(44)
$$Q = 2\pi \mathop \int \limits_{0}^{R} rw\left( {r,z,t} \right){\text{d}}r$$
(45)
$${\Lambda } = \frac{{\left| {L\left( {\frac{\partial p}{{\partial z}}} \right)} \right|}}{Q}$$
(46)

The thermo-physical properties for nanofluid are given as [50,51,52],

$$\begin{gathered} \mu_{{{\text{nf}}}} = \frac{{\mu_{f} }}{{\left( {1 - \phi } \right)^{2.5} }},\;\rho_{{{\text{nf}}}} = \left( {1 - \phi } \right)\rho_{f} + \phi \rho_{s} \hfill \\ \left( {\rho Cp} \right)_{{{\text{nf}}}} = \left( {1 - \phi } \right)\left( {\rho Cp} \right)_{f} + \phi \left( {\rho Cp} \right)_{s} ,\;\left( {\rho \gamma } \right)_{{{\text{nf}}}} = \left( {1 - \phi } \right)\left( {\rho \gamma } \right)_{f} + \phi \left( {\rho \gamma } \right)_{s} \hfill \\ \frac{{k_{{{\text{nf}}}} }}{{k_{f} }} = \frac{{k_{s} + \left( {n2 - 1} \right)k_{f} - \left( {n2 - 1} \right)\phi \left( {k_{f} - k_{s} } \right)}}{{k_{s} + \left( {n2 - 1} \right)k_{f} + \phi \left( {k_{f} - k_{s} } \right)}} , \hfill \\ \frac{{\sigma_{{{\text{nf}}}} }}{{\sigma_{f} }} = \frac{{\sigma_{s} + \left( {n2 - 1} \right)\sigma_{f} - \left( {n2 - 1} \right)\phi \left( {\sigma_{f} - \sigma_{s} } \right)}}{{\sigma_{s} + \left( {n2 - 1} \right)\sigma_{f} + \phi \left( {\sigma_{f} - \sigma_{s} } \right)}} \hfill \\ \end{gathered}$$
(47)

2.5 Radial coordinate transformation

The radial coordinate transformation \(x = \frac{r}{R\left( z \right)}\) was applied to the reduced governing equations in order to limit geometric effects. Therefore, Eqs. (39–40) take the following form,

$$\begin{aligned} C_{1} {\text{Re}} \frac{\partial w}{{\partial t}} = & B_{1} \left( {1 + e\cos \left( {\omega_{f} t} \right)} \right) + C_{1} B_{2} \left( {\cos \left( {\omega_{r} t + \alpha } \right)} \right) + C_{5} \frac{1}{{xR^{2} }}\frac{\partial }{\partial x}\left( {x\left( {\frac{\partial w}{{\partial x}} - \frac{m\varepsilon }{{R^{2} }}\left( {\frac{\partial w}{{\partial x}}} \right)^{3} } \right)} \right) \\ & \quad - \left( {C_{2} M^{2} + C_{5} \frac{1}{{{\text{Da}}}}} \right)w + {\text{Ke}}^{2} \frac{{I_{0} \left( {x {\text{Ke}} R} \right)}}{{I_{0} \left( {{\text{Ke}} R} \right)}} + C_{4} {\text{Gr}}\theta \sin \left( \lambda \right) \\ \end{aligned}$$
(48)
$${\text{Re}} \Pr C_{6} \left( {\frac{\partial \theta }{{\partial t}}} \right) = C_{5} \frac{{{\text{Br}}}}{{R^{2} }}\left( {\left( {\frac{\partial w}{{\partial x}} - \frac{m\varepsilon }{{R^{2} }}\left( {\frac{\partial w}{{\partial x}}} \right)^{3} } \right)\frac{\partial w}{{\partial x}}} \right) + \frac{1}{{R^{2} }}\left( {\frac{{\partial^{2} \theta }}{{\partial x^{2} }} + \frac{1}{x}\frac{\partial \theta }{{\partial x}}} \right)\left( {C_{3} + R_{d} } \right) + \beta$$
(49)

The non-dimensional boundary conditions associated,

$$w\left( {x,0} \right) = 0;\;\theta \left( {x,0} \right) = 0\;{\text{at}}\;t = 0$$
(50)
$$\frac{\partial w}{{\partial x}} = 0;\;\frac{\partial \theta }{{\partial x}} = 0\;{\text{at}}\;x = 0$$
(51)
$$w\left( {x,t} \right) = w_{{\text{s}}} ;\;\theta = 1\;{\text{at}}\;x = 1$$
(52)

Likewise, wall shear stress, the dimensionless flow rate and the resistance to flow are represented as follows,

$$S_{xz} = \frac{{C_{5} }}{R}\left. {\left( {\left( {\frac{\partial w}{{\partial x}}} \right) - \frac{m\varepsilon }{{R^{2} }}\left( {\frac{\partial w}{{\partial x}}} \right)^{3} } \right)} \right|_{x = 1}$$
(53)
$$Q = 2\pi R^{2} \mathop \int \limits_{0}^{1} xw\left( {x,z,t} \right){\text{d}}x$$
(54)
$$\Lambda = \frac{{\left| {L\left( {\frac{\partial p}{{\partial z}}} \right)} \right|}}{Q}$$
(55)

where \(C_{1} = \frac{{\rho_{{{\text{nf}}}} }}{{\rho_{f} }};\;C_{2} = \frac{{\sigma_{{{\text{nf}}}} }}{{\sigma_{f} }};\;C_{3} = \frac{{k_{{{\text{nf}}}} }}{{k_{f} }}\;;\;C_{4} = \frac{{\left( {\rho \gamma } \right)_{{{\text{nf}}}} }}{{\left( {\rho \gamma } \right)_{f} }}\;;\;C_{5} = \frac{{\mu_{{{\text{nf}}}} }}{{\mu_{f} }}\;;\;C_{6} = \frac{{\left( {\rho Cp} \right)_{{{\text{nf}}}} }}{{\left( {\rho Cp} \right)_{f} }}\).

3 Numerical method

Hoffmann’s book [53] presents a number of computational methods for solving PDEs (Partial Differential Equations). It also provides a comprehensive explanation of the distinctions between the parabolic, elliptical and hyperbolic shapes of these equations. The explicit finite difference methods are specifically recommended in the book to solve time-dependent problems. Consequently, the present reduced time-dependent equations, denoted by (48) and (49), are calculated using this method of explicit finite difference. To ensure stability and convergence, the simulation defines shorter temporal and spatial variables.

3.1 Numerical procedure

The following section describes the required steps to obtain the formulation of the finite difference for various partial derivatives,

$$\frac{\partial w}{{\partial t}} \cong \frac{{\left( w \right)_{i,j}^{k + 1} - \left( w \right)_{i,j}^{k} }}{\Delta t}$$
(56)
$$\frac{\partial w}{{\partial x}} \cong \frac{{\left( w \right)_{i,j + 1}^{k} - \left( w \right)_{i,j - 1}^{k} }}{2\Delta x} = w_{x}$$
(57)
$$\frac{{\partial^{2} w}}{{\partial x^{2} }} \cong \frac{{\left( w \right)_{i,j + 1}^{k} - 2\left( w \right)_{i,j}^{k} + \left( w \right)_{i,j - 1}^{k} }}{{\left( {\Delta x} \right)^{2} }} = w_{xx}$$
(58)

The approximations of finite differences above can be used to transform Eqs. (48–49) into the following finite difference equation,

$$\begin{aligned} \left( w \right)_{i,j}^{k + 1} = & \left( w \right)_{i,j}^{k} + \frac{\Delta t}{{C_{1} {\text{Re}} }}\left[ {\left( {B_{1} \left( {1 + e \cdot \cos \left( {\omega_{f} t^{k} } \right)} \right)} \right) + C_{1} B_{2} \left( {\cos \left( {\omega_{r} t + \alpha } \right)} \right)} \right. \\ & \quad + C_{5} \frac{1}{{R^{2} }}\frac{1}{x}\frac{\partial }{\partial x}\left( {x\left( {\left( {w_{x} } \right)_{i,j}^{k} - \left( {\frac{m\varepsilon }{{R^{2} }}} \right)\left( {\left( {w_{x} } \right)_{i,j}^{k} } \right)^{3} } \right)} \right) - \left( {C_{2} M^{2} + C_{5} \frac{1}{{{\text{Da}}}}} \right)w_{i,j}^{k} \\ & \quad \;\left. { + {\text{Ke}}^{2} \frac{{I_{0} \left( {x {\text{Ke}} R} \right)}}{{I_{0} \left( {{\text{Ke}} R} \right)}} + C_{4} {\text{Gr}}\theta_{i,j}^{k} \sin \left( \lambda \right)} \right] \\ \end{aligned}$$
(59)
$$\begin{aligned} \left( \theta \right)_{i,j}^{k + 1} = & \left( \theta \right)_{i,j}^{k} + \frac{\Delta t}{{C_{6} {\text{Re}} \Pr }}\left[ {\frac{1}{{R^{2} }}\left( {Br\left( {\left( {w_{x} } \right)_{i,j}^{k} - \frac{{m\varepsilon_{2} }}{{R^{2} }}\left( {\left( {w_{x} } \right)_{i,j}^{k} } \right)^{3} } \right)} \right)} \right. \\ & \quad \left. { + \frac{1}{{R^{2} }}\left( {\left( {\theta_{xx} } \right)_{i,j}^{k} + \frac{1}{{x_{i} }}\left( {\theta_{x} } \right)_{i,j}^{k} } \right)\left( {C_{3} + R_{d} } \right) + \beta } \right] \\ \end{aligned}$$
(60)

Once the temperature field has been numerically calculated, the Nusselt number Nu is computed using the finite difference formula below,

$${\text{Nu}} = \frac{1}{{R^{k} }}\left( {\frac{{T_{i,N}^{k} - T_{i,N - 1}^{k} }}{\Delta x}} \right)$$
(61)

The form of the finite difference of the imposed boundary conditions is as follows,

$$w_{i,j}^{1} = \theta_{i,j}^{1} = 0$$
(62)
$$w_{i,1}^{k} = w_{i,2}^{k} ;\;\theta_{i,1}^{k} = \theta_{i,2}^{k}$$
(63)
$$w_{i,N + 1}^{k} = w_{s} ;\;\theta_{i,N + 1}^{k} = 1$$
(64)

We define here

$$\left\{ {\begin{array}{*{20}l} {x_{j} = \left( {j - 1} \right)\Delta x;} \hfill & \quad {j = 1,2, \ldots ,N + 1} \hfill \\ {z_{i} = \left( {i - 1} \right)\Delta z;} \hfill &\quad {i = 1,2, \ldots ,M + 1} \hfill \\ {t^{k} = \left( {k - 1} \right)\Delta t;} \hfill &\quad {k = 1,2, \ldots ,k_{{\max }} } \hfill \\ \end{array} } \right.$$
(65)

where Δt, Δx and Δz are small increments in time, step sizes along the radial and axial directions, respectively. The stability of the explicit finite difference scheme depends on the selection of step-size along the temporal direction which is stated as [53],

$$\Delta t \le \frac{1}{{2{\text{Re}} }}\left( {\Delta x} \right)^{2}$$
(66)

This numerical scheme’s stability depends on both the step size and the time increment. According to the stability condition, Δx = 0.025 and Δt = 0.0001 are chosen to meet the condition of stability. Several researches [12, 46, 54] established that these values are adequate for the stability and convergence of the FTCS method. The investigations shown above have thoroughly confirmed that the FTCS technique is accurate for blood flow modeling in complicated geometries.

3.2 Code validation

To validate the FTCS numerical method of our research outcomes, a comparison of velocity and temperature profiles of blood against dimensionless radius was done with the results of Shabbir et al. [13] when stenosis height (δ = 0.1) and without nanoparticles (ϕ = 0.00), ignoring the Darcy number (Da), velocity slip (ws), heat source (β) and thermal radiation (Rd). A good agreement of our findings was found with the results of Shabbir et al. [13] as shown in Figs. 3.

Fig. 3
figure 3

Graph comparison for a non-dimensional temperature profile b non-dimensional velocity profile

Full size image
Fig. 4
figure 4

Flow chart illustrating the work plan schematically

Full size image

4 Results and discussion

The characteristics of hemodynamics of the stenosis artery with gold nanoparticles are calculated in this section. Given the emerging factors, graphical results for flow parameters like axial flow velocity, temperature distribution, wall shear stress, flow rate, flow resistance and heat transfer coefficient are shown in Figures.  Figure 4 depicts the schematic illustration of the work plan. These figures represent a comparative analysis of the hemodynamic characteristics in the region of the stenosis for three different situations of arterial narrowing (non-tapered, diverging and converging arteries). In Table 2, the thermophysical quantities for blood (base fluid) and gold nanoparticles (Au) are displayed. The default values for the main parameters used in the FTCS calculations are shown in Table 3, while Table 4 shows the range of parameters used in the calculations.

Fig. 5
figure 5

Effect of electro-kinetic parameter Ke on velocity profile

Full size image
Fig. 6
figure 6

Effect of body acceleration parameter B2 on velocity profile

Full size image
Fig. 7
figure 7

Effect of Darcy number Da on velocity profile

Full size image
Fig. 8
figure 8

Effect of stenosis height δ on velocity profile

Full size image
Fig. 9
figure 9

Effect of Sutterby fluid parameter ε on velocity profile

Full size image
Fig. 10
figure 10

Effect of magnetic parameter M on velocity profile

Full size image
Fig. 11
figure 11

Effect of shape of nanoparticles n2 on velocity profile

Full size image
Fig. 12
figure 12

Effect of slip velocity ws on velocity profile

Full size image
Fig. 13
figure 13

Effect of volume fraction of nanoparticles ϕ on velocity profile

Full size image
Fig. 14
figure 14

Effect of heat source parameter β on temperature profile

Full size image
Fig. 15
figure 15

Effect of stenosis height δ on temperature profile

Full size image
Fig. 16
figure 16

Effect of Sutterby fluid parameter ε on temperature profile

Full size image
Fig. 17
figure 17

Effect of magnetic parameter M on temperature profile

Full size image
Fig. 18
figure 18

Effect of thermal radiation parameter Rd on temperature profile

Full size image
Fig. 19
figure 19

Effect of shape of nanoparticles n2 on temperature profile

Full size image
Fig. 20
figure 20

Effect of volume fraction of nanoparticles ϕ on temperature profile

Full size image
Fig. 21
figure 21

Effect of slip velocity ws on flow rate

Full size image
Fig. 22
figure 22

Effect of pressure gradient parameter B1 on flow rate

Full size image
Fig. 23
figure 23

Effect of body acceleration parameter B2 on flow rate

Full size image
Fig. 24
figure 24

Effect of Grashof number Gr on wall shear stress

Full size image
Fig. 25
figure 25

Effect of Reynolds number Re on wall shear stress

Full size image
Fig. 26
figure 26

Effect of angle of inclination λ on resistance to flow

Full size image
Fig. 27
figure 27

Effect of electro-kinetic parameter Ke on resistance to flow

Full size image
Fig. 28
figure 28

Nusselt number for different Prandtl number Pr

Full size image
Fig. 29
figure 29

Nusselt number for different thermal radiation parameter Rd

Full size image
Fig. 30
figure 30

Nusselt number for different Brinkman number Br

Full size image
Table 2 Thermophysical properties of fluid and nanoparticles [50, 51]
Full size table
Table 3 Default values for emerging parameters
Full size table
Table 4 Various dimensionless parameter ranges
Full size table

4.1 Velocity profile

The impact of the electro-kinetic parameter (Ke) on the axial velocity is illustrated in Fig. 5–13, which shows that the axial velocity is strongly dependent on the electric field strength. This parameter (Ke) contributes to increasing the magnitude of the axial velocity caused by the electro-kinetic body force term, i.e., Ke2ψ, as given in Eq. (48). The parameter Ke has an inverse relationship with the thickness of the electrical double layer (EDL), since the electro-osmotic parameter (Ke) is defined as the ratio between the tube radius (R0) and the Debye length (λD). Therefore, decreasing the thickness of the EDL, i.e., raising the value of Ke, will result in an increase in the velocity profile. This can be explained by the fact that When the EDL width is reduced, the electro-osmotic forces are strengthened and fluid drag is reduced, allowing a large quantity of fluid to rapidly flow along the axis of the tube relative to the charged surface, under the effect of an applied electric field. The electro-osmotic forces contribute to blood movement in the arterial system by exploiting the ionic nature of blood and the negatively charged endothelial layer enveloping blood vessels. This phenomenon promotes the general circulation of blood throughout the body, potentially increasing blood velocity in the arterial system. There was also a significant difference between the effects of tapering, and the maximum amplitude was found in the diverging artery.

Figure 6 shows the response of the velocity profile across the artery cross section (i.e. in radial coordinates) to different values of body acceleration (B2) in the region of stenosis. As body acceleration increases, there is a marked increase in velocity amplitudes for the diverging, non-tapering and converging stenotic artery. The reason for the increase in velocity of blood is that the body acceleration increases the heartbeat and pulse. The heart speeds up to pump more blood, so that can reach the muscles. This allows more oxygen and other nutrients to be delivered to the various parts of the body. Depending on the situation, the body acceleration may cause an increase in blood velocity that can be advantageous or harmful to physiological function; it can also lead to inflammation, atherosclerosis, and tissue damage. However, velocity magnitudes are higher for the diverging artery than for the non-tapered and converging arteries.

The effect of different values of the Darcy number on the velocity profile is shown in Fig. 7. The figure shows the velocity distribution at the stenosis region for the tapered (diverging or converging) and non-tapered artery cases. It was observed that as the Darcy number changes, i.e., the permeability of the medium changes, Since, Da is directly proportional to the permeability of the porous medium, which offers a lower resistance to flow and lead to an increase in the velocity profile at the stenotic artery region. Increased permeability of the artery wall has been linked to several clinical diseases, such as tissue injury and inflammation. This may result in increased blood flow in certain areas, which may raise the risk of atherosclerosis, induce turbulence, and encourage endothelial damage. Higher permeability, however, may also help with waste product clearance and the supply of nutrients and oxygen. This is essential for preserving tissue health. As a result, the physiological circumstances that underlie permeability’s influence on blood velocity and any possible choices between nutrition delivery and tissue injury must be taken into account.

In Fig. 8, dimensionless velocity profile in the stenotic artery for different values of stenosis height δ for the diverging, non-tapered and converging artery are shown. From this figure, it can be seen that the velocity profile decreases as δ increases. As the stenosis becomes severe, the narrowing of the artery can be significant and considerably limits the amount of blood that can flow through it. This reduction in the cross-sectional area of the artery reduces the total volume of blood that can flow through it, leads to a decrease in blood flow velocity, which can also result other complications. In addition, the velocity profile is greater in a diverging than in a converging artery, while velocity profile of the non-tapered artery situated between these two profiles.

The impact of the Sutterby fluid parameter ε on the velocity profile is shown in Fig. 9. The graph shows that the velocity profile increases for higher values of the Sutterby fluid parameter. An increase in the Sutterby Fluid Parameter ε indicates more pronounced shear-thinning behavior, leading to a decrease in viscosity as the shear rate increases. This decrease in viscosity allows the fluid to flow more easily, particularly near solid boundaries where shear rates are higher. Also, the velocity profile is lowest for the converging tapered artery and highest for the diverging tapered artery.

Figure 10 shows the non-dimensional velocity profile for different values of magnetic parameter M. It can be seen that an increase in the intensity of the magnetic field leads to a reduction in the velocity of the blood. This is because a stronger magnetic field increases the Lorentz magnetic drag force, resulting in greater deceleration of blood flow. This force is created when charged particles rapidly move in a magnetic field with strong intensity, opposing the movement of blood. The dynamics of blood flow in the arteries therefore depend to a large extent on the magnetic field. It can therefore be a valuable aid in the diagnosis and treatment of a range of cardiovascular diseases. In MRI, the use of static magnetic fields reduces the time needed for healing fractures and regenerating nerves. Conversely, a reduction in blood velocity may also raise the risk of thrombosis because it makes it possible for platelets and other clotting components to accumulate. It is crucial to weigh the advantages and disadvantages of using magnetic fields to regulate blood flow in various medical situations. Comparing the different tapering arteries it was found that the diverging artery has the maximum velocity magnitude.

Figure 11 shows the distribution of axial velocity in the region of stenosis for the cases of diverging, converging and non-tapered artery. It can be seen from the graphs that by changing the shape of the nanoparticles from sphere to cylinders to blades, i.e., by increasing the shape parameter from 3.0 to 4.9 then 8.6, the velocity profile in the region of the stenotic artery is apparently improved. As the shape parameter increases, the thermal conductivity of the nanofluid increases, which promotes micro-convection near the nanoparticles, leading to increased thermal diffusion in the nanofluid and accelerating the velocity of the blood. In the case of the diverging artery, higher velocity amplitudes are obtained.

Figure 12 illustrates the variation in velocity profiles with a different wall slip velocity, the axial velocity increases as the slip parameter increases. The slip parameter is a boundary condition applied to the inside wall of the artery. The existence of a slip velocity results in an increase in the quantity of movement, which boosts the blood in the regime close to the wall and increases blood flow. If slip causes compression of an area of the wall, blood flow to that region will be diminished. This can encourage the formation of plaques, as the cells in the arterial wall need sufficient oxygen and nutrients to function properly. However, the velocity magnitude is higher for the diverging artery than for the non-tapering and converging arteries.

The variation in axial velocity as a function of time with different values of nanoparticle volume fraction for the diverging, non-tapered and converging artery is shown in Fig. 13. Initially, the addition of nanoparticles can lead to a reduction in the velocity of blood due to their tendency to aggregate and form clusters. These clusters can block the narrow passage created by the stenosis, thereby reducing blood flow. However, over time, the nanoparticles may begin to disperse and become more evenly distributed in the bloodstream. This can actually help to increase the velocity of blood by reducing the viscosity of the blood and improving its ability to flow through the narrowed artery. Through mechanical assistance and targeted drug delivery, nanomaterials have the potential to increase blood flow velocity in atherosclerotic arteries. They also improve blood flow to organs, which reduces the risk of blockages by increasing oxygen-rich blood circulation. Further, the maximum value is obtained with diverging arteries compared to converging and non-tapered arteries.

4.2 Temperature profile

Blood temperature has a crucial role in controlling physiological processes linked to coronary artery disease, such as blood viscosity, heart rate, inflammation, constriction of blood vessels, and the prevention of cardiovascular diseases (CVD). Therefore, it is crucial to maintain the temperature of the body at a regular level to avoid heart attacks and strokes as well as to keep the blood vessels healthy. This subsection provides a discussion on the impacts of different parameters in the temperature field for various tapering angle.

Figures 14–20 displays the influence of the heat generation parameter β on the temperature profile. The temperature profile is significantly increased by increasing this parameter from 0.1 to 1.0, since more heat is generated. As a result, the heat source parameter β can avoid rising blood pressure, clot formation and other problems by enhancing blood temperature, maintaining blood viscosity and facilitating blood flow through the vessels. Moreover, the tapering effect shows marked differences in temperature profile giving maximum magnitude to the converging artery. In medical applications, this effect may correspond, for instance, to punctual thermal therapy as part of a laser treatment.

Figure 15 represents the temperature profile with stenosis height for different tapered arteries. This graph reveals that the temperature profile increases for increasing values of stenosis height δ. The temperature amplitude for the converging artery is relatively higher than for the non-tapered and diverging arteries.

Figure 16 illustrates the dimensionless temperature with different values of Sutterby fluid parameter ε for converging, non-tapered and diverging arteries. It is observed that the dimensionless temperature enhance by increasing the value of Sutterby fluid parameter. There was a significant change in the tapering effect, where the converging artery showed the maximum magnitude.

The temperature distribution in the stenosis region for different values of the magnetic parameter is shown in Fig. 17. This figure clearly shows that the temperature rises as the magnetic parameter increases. This finding may be helpful in hyperthermia treatment of cancer cells/tumors. Energy dissipation caused by the application of a magnetic field can result in an elevation in blood temperature.

Figure 18 shows the temperature distribution for various values of the radiation parameter Rd. It was observed that the temperature of blood increased with increasing Rd. As the radiation parameter represents the rate between heat transfer by conduction and heat transfer by radiation. Increasing the radiation parameter is known to increase the transport of energy in the fluid and therefore affects the rate of heat transfer. The physical explanation governing this phenomenon is that the walls of blood vessels become heated as a result of the radiation effects generated during radiation therapy. As a result, the blood temperature is elevated in the vicinity of the blood vessels. Also, Vasodilation occurs during exercise, or when muscles are under continuous stress, to deliver more oxygen to muscles and tissues. Stretching of the muscles generates heat, which is subsequently transferred to the blood vessels via radiation. Hyperthermia treatment may, however, be aimed primarily at increasing the temperature of the blood, while avoiding affecting the tissues around the vessel. This figure also shows marked differences due to the tapering effect, with the converging artery with the maximum magnitude.

The changes in the temperature profile with increasing nanoparticle shape at the stenosis are shown in Fig. 19. Raising the shape parameter from 3.0 to 8.6 gives a marked temperature increase, i.e., sphere-shaped nanoparticles generate lowest temperatures while blade-shaped nanoparticles reach highest temperatures. Nanoparticles with higher shape parameters have a larger surface area, enabling more efficient heat transfer between the nanoparticles and the blood, promoting rapid heat exchange. In other words, nanoparticles with a larger surface area can absorb or dissipate heat more efficiently. For instance, in hyperthermia therapy, where heat is intentionally applied to target tissues, high surface area nanoparticles can efficiently transfer heat to the surrounding blood, helping to maintain a controlled body temperature. In addition, the amplitude is higher in the convergent artery case than in the divergent and non-tapered cases, which is entirely the contrary of the behavior calculated for the velocity profile.

Figure 20 shows the variation in temperature for different concentrations of nanoparticles. When the volume fraction increases from ϕ = 0 (without nanoparticles, i.e. pure blood) to ϕ = 0.05, the temperature increases in the same way, due to the increase in thermal conductivity of nanofluids. Similarly, when comparing the diverging and converging artery, it can be seen that greater increases are achieved for the converging artery than for the diverging artery.

4.3 Flow rate

Figure 21–23 illustrates the effects of the slip parameter ws on the dimensionless flow rate in the region of the stenotic artery. It is obvious that the flow rate rises with the increases in the slip parameter. The flow behavior is directly linked to the velocity behavior; if velocity is a decreasing (or increasing) function of a given variable, so is the flow rate. Consequently, the increase in flow with rise in slip parameter is a direct result of the increase in velocity as this parameter increases.

Figure 22 shows the effects of pressure gradient parameter B1 on dimensionless flow rate for various cases of the tapered artery. The B1 value varies for different sizes of artery. For example, for arterioles or the coronary artery, B1 has a value of 1.41. In the case of the femoral artery, B1 reaches a higher value of 6.6, for details see [48]. It is clear that by elevating the pressure parameter, the flow of blood accelerates considerably leading to an increase in the amount of blood passed through the artery which confirms that the femoral artery reaches its maximum value compared to the coronary artery. In Addition, the diverging artery has a higher value than the converging artery and the non-diverging artery.

Figure 23 shows the evolution of flow rate over the length of the arterial segment with overlapping stenosis for different body acceleration amplitudes. We can see from this figure that the periodic nature of the flow changes progressively as the amplitude of body acceleration increases. This means that in the vibratory environment, the velocity of the blood flow increases. It can be also observed that the diverging artery has the maximum amplitude, comparing to the converging and non-tapered arteries.

4.4 Wall shear stress

“Wall Shear Stress” refers to the magnitude of force per unit area that the artery’s internal wall, or endothelium, exerts on blood flow. This research suggests that vessel segments with low wall shear stress or variable wall shear stress are more likely to cause atherosclerotic plaques. Furthermore, these lesions may cause serious cardiovascular conditions like a heart attack or stroke.

In Figures. 24 and 25 the effect of the thermal buoyancy parameter, Grashof number Gr, on the wall shear stress profile for converging, non-tapered and diverging arteries is shown. Increasing the values of Gr improves the wall shear stress profiles because the thermal buoyancy force overcomes the viscous force. The effects of tapering also show a significant difference, with the diverging artery showing the maximum amplitude.

Figure 25 shows the variation in the non-dimensional velocity profile for different values of Re. An increase in Reynolds number from 3 to 5 leads to a decrease in wall shear stress, because the regime becomes viscous when the Reynolds number is low. However, the force of inertia increases with the Reynolds number, the slowing of the flow is the effect dominated due to stenotic occlusion. The Reynolds number is employed to categorize fluid systems where the impact of viscosity plays a vital role in determining fluid velocities or flow patterns.

4.5 Resistance to flow

Figures 26 and 27 shows the impact of the angle of inclination (λ) of the artery on resistance to flow. This graph shows that as the inclination angle increases from 0° to 90°, the resistance to flow decreases, meaning that the flow is significantly accelerated. As can be seen, for the horizontal artery (λ = 0°), the resistance to flow is maximum; although, with increasing angle of inclination until the vertical artery (λ = 90°), the resistance to flow reaches its minimum value. From the figure, it is clear that converging arteries achieve higher values than diverging and non-tapering arteries.

The resistance to flow for different electro-kinetic is shown in Fig. 27. It can be seen that increasing the values of Ke reduces the resistance to flow. Physically, with an assist electrical field (electrical field along the z-axis), the drag of the fluid decreases and the bulk fluid becomes proportional to the surface area charged, amplifying the flow rate and therefore reduces the resistance to flow.

4.6 Nusselt number

Figures 28, 29 and 30 shows the Nusselt number for different Prandtl numbers Pr (from 7 to 21). It is shown that the rate of heat transfer increases with increasing Pr values from 7 to 21 at the artery throat. An inverse relationship between the Prandtl number and heat exchange from the artery wall to the fluid is indicated, since the Prandtl number represents the ratio between momentum diffusivity and thermal diffusivity. With a very low value of Pr (Pr < 1), the rate of momentum diffusion is significantly lower in comparison to the rate of thermal diffusion. In the normal ambient temperature interval of 19 to 30.8 degrees Celsius, Mitvalsky [58] pointed out that blood in laminar flow has a Prandtl number of between 15 and 25. The doping of the metal nanoparticles obviously reduces these values, so the range covered by the current simulations, i.e., Pr from 7 to 21, is suitable for hemodynamics. The diffusivity of the quantity of movement in blood is therefore much higher than its thermal diffusivity. This property was explained by Diller [59] and Hensley et al. [60] as being required for thermoregulation and other bio-thermal functions. It is also observed that the Nusselt number increases with a rate of 141.3% for converging artery, 119.4% for non-tapered artery and 105.1% for diverging artery.

Figure 29 illustrates the variation of the Nusselt number with varying values of the thermal radiation parameter Rd. A remarkable observation shows that the Nusselt number decreases with increasing thermal radiation parameter. The rate of decreases in Nusselt number for the converging artery was 32.63%, while it was 29.54% and 27.59% for the non-tapering and diverging arteries, respectively. Furthermore, the diverging artery has higher amplitude than the converging artery and the non-tapering artery.

Figure 30 shows the variation of the Nusselt number with different values of the Brinkman number. A significant observation is that the Nusselt number increases with the Brinkman number. This indicates that the dissipation of energy caused by the viscosity of the blood enhanced the rate of heat transfer. The rate of increase in the Nusselt number for the converging artery was 3.80%, respectively, while it was 3.40% and 3.06% for the non-tapered and diverging artery, respectively. Also, the diverging artery has higher amplitude than the converging artery and the non-tapered artery.

5 Conclusions

In the current study, we have investigated the simultaneous impact of an axially aligned electrical field and a transversal magnetic field on the blood flow of Sutterby nanofluid in an inclined tapered porous artery with overlapping stenosis. Periodic body acceleration and Slip effects are also taken into account. The model investigates the effect of different factors on blood flow characteristics for the perfusion of Au (gold) nanoparticles in the blood (base fluid). Various nanoparticle shapes, i.e., sphere, cylinders and blades, are explored. Nonlinear governing equations transformed with initial and boundary conditions and solved using a method of finite difference.

The main aspects of this study are outlined below:

  • As the strength of the axial electric field increases, the velocity of the nanofluid (Au-blood) accelerates with increasing the electro-osmotic parameter values (Ke), while the magnetic field normally applied to the flow opposes the movement of the nanofluid, resulting in a declining trend for increasing values of the magnetic parameter (M).

  • The wall shear stress of the stenosis artery decreases with increasing Reynolds number (Re) and with decreasing Grashof number (Gr).

  • With decreasing concentration of nanoparticles, the non-dimensional temperature profiles decrease. On the other hand, velocity increases and starts to decrease over time.

  • The flow rate (Q), for each of the three arteries shapes (converging, diverging and non-tapered), is enriched in the presence of periodic body acceleration.

  • The temperature profile is inversely proportional to the Sutterby fluid parameter (ε), whereas the opposite is observed for the axial velocity of the nanofluid.

  • The resistance to flow (Λ) in the stenotic zone are remarkably accelerated by decreasing the angle of inclination (β) of the artery and the electro-osmotic parameter (Ke).

  • An increase in Nusselt number is found for increasing values of Brinkman number (Br) and Prandtl number (Pr), whereas the opposite is observed for the thermal radiation parameter (Rd).

  • The converging, diverging and non-tapering arterial blood vessel structure is capable of significantly modifying hemodynamic flow variables.

The current simulations have provided some intriguing insights into non-Newtonian nano-doped blood flow via inclined tapered porous artery with overlapping stenosis taken into account the several effects that may be affect the blood flow. Nevertheless, there are several limitations to this research. In reality, a more complex two- or three-dimensional study that does not use mild stenotic conditions may be more useful in obtaining accurate results. In addition, using a temperature-dependent viscosity also might be expanded. Future research will focus on these areas, and it is possible that artery wall deformability may be investigated.