Consistency, precision, and accuracy assessment of the collocation boundary element method for two-dimensional problems of potential and elasticity

Abstract

The collocation boundary element method, as developed and taught in the traditional books, suffers from severe inconsistencies, partly responsible for the method’s lack of clarity and broader applicability (not to mention the uncontrollable proliferation of misleading alternatives that only add to more confusion). This has been recently corrected, as summarized in this review paper, in which we report the proposition of a convergence theorem for the general, just consistent, three-dimensional isoparametric formulation of potential and elasticity problems (https://doi.org/10.1016/j.enganabound.2023.01.017), and also introduce the not interchangeable concepts of nodes and loci, for boundary displacements and tractions in elasticity, respectively, as well as of points, for domain sources. We have implemented, for both two-dimensional potential and elasticity problems, real-variable (https://doi.org/10.1016/j.enganabound.2023.01.015, https://doi.org/10.1016/j.enganabound.2023.03.026) and—still better—complex-variable (https://doi.org/10.1016/j.enganabound.2023.04.024) codes for generally high-order, curved elements, which effortlessly enable evaluations with numerical precision that is only machine-limited and only resorts to the problem’s mathematics—plus Gauss–Legendre quadrature of all integrals’ regular parts. (Ad hoc mechanical interpretations, “regularizations,” interval subdivisions, special quadrature formulas, or variable transformations are neither strictly speaking correct nor generally applicable nor required.) Despite the singular kernels that enter diverse forms of Somigliana’s identity (as for evaluating stress results at a domain point), problem-unrelated singularities do not come up in a mathematically consistent formulation and implementation: singularities are just man-made. A few examples of highly challenging topological issues are presented. We show that fracture mechanics problems may be dealt with seamlessly, and we manage to objectively assess a problem’s topological consistency, precision, accuracy, and round-off errors related to a given mesh discretization and software-conditioned computational digits.

1 Introduction

The collocation boundary element method (CBEM) was recently revised for general three-dimensional (3D) elasticity and potential problems [1], with the proposition of important conceptual improvements but also fixing some basic misconceptions that have been part of the formulation from the very beginning. The main feature of this revisit is probably the incorporation of the correct numerical treatment of quasi-singularities for two-dimensional (2D) problems, which had already been proposed in the 1990 s [2, 3]. The corresponding algorithms are given in [4], with numerical assessments for extremely challenging topology configurations published in [5] in terms of real-variable Cartesian coordinates (x, y). Shortly thereafter we realized that a much more efficient code is obtained using the complex variable $z=x+iy$ [6].

Although not conceptually relevant, we prefer, for 2D problems, to have the natural, integration variable $\xi$ spanning the interval [0, 1], as this in general leads to simpler expressions than with the $[-1,1]$ interval probably inherited from finite element developments.

As given in Fig. 1 (reproduced from [1, 4]), we have three cases of singularity or quasi-singularity to deal with:

• an actual singularity (point A for $0\le \xi _s \le 1$),

• a real quasi-singularity (point B for $\xi _s < 0\ \textrm{or}\ \xi _s > 1$),

• a complex quasi-singularity (point C for $\xi _s =a \pm ib$).

In the latter case, $\Re (\xi _s)=a$ is the real part. The indicated closest point $\xi _\perp \ne a$ (numerical data given in [1]) is just irrelevant and should not part be part of the treatment, a concept ignored in the traditional literature on the subject, as shown in [2, 3].

Fig. 1

Cubic, curved element with nodal points given by $\diamond$. The singularity cases are: actual singularity (point A for $0\le \xi _s \le 1$), real quasi-singularity (point B for $\xi _s < 0\ \textrm{or}\ \xi _s > 1$), and complex quasi-singularity (point C for $\xi _s =a \pm ib$). In the latter case, $\Re (\xi _s)=a$ is the real part, while the indicated closest point $\xi _\perp \ne a$ is just irrelevant [1,2,3,4]

Although this does not necessarily lead to relevant numerical improvements, we also revisit the formulation for the spectral consistency assessment of the single-layer potential matrix G [7,8,9].¹ Not least, we refer to a conceptually important convergence Theorem formulated in [1] for general 3D problems.

This contribution summarizes the main features of the above-outlined papers, discusses a few conceptual aspects that have not been explored before, and conveys some numerical comparisons of the real-variable formulation [4] and its complex-variable counterpart [6]. This is not a review paper per se but more a collection of reflections on the consistent conception of the collocation boundary element method.² References to other authors’ developments only take place when strictly necessary.³

We outline how general potential, flux, displacement and stress results may be precisely obtained at internal points. However, owing to space restrictions we only show numerical assessments of the constituent matrices and for stress results—the latter actually the most critical issues one may face particularly when dealing with extremely small source-to-field distances. Numerical problems of potential—as well as of displacement results in elasticity—are dealt with comprehensively in papers [1, 4,5,6]. Conditioning of the CBEM matrices is checked in [5] for a topologically challenging problem. This latter paper also shows how to obtain the threshold distance of a source point s to a boundary segment (element) $\Gamma _{seg}$ for the (mathematically exact) corrections to be demanded—given the problem’s overall precision requirement.

1.1 Paper outline

More than just reviewing papers [1, 4,5,6], we present and discuss anew and more in-depth some important conceptual aspects of Somigliana’s identity as applied to the collocation boundary element method. We summarize the main features of these papers, define the basic boundary parameters required in a problem simulation, and address the underlying propositions and assumptions. Then, we outline the basic equations for 2D problems of potential and elasticity in terms of the complex variable $z=x+iy$, which includes the evaluation of results in the domain. Our main concern is to lay down the main conceptual aspects of the proposed developments while demonstrating the ease of computational implementation for problems with topology issues to which continuous mechanics may no longer be applicable—but mathematics does.

It remains for the physicists and engineers to demonstrate that singularities exist in the real world, although they are—as a mathematical abstraction—useful when properly handled, as in the present case of applying Somigliana’s identity: mathematics and physics keep here too in harmony (Wigner [14]).

Two academic—although very challenging—numerical examples close this paper. We show that distances smaller than a proton size and crack openings smaller than possibly reproducible in a laboratory may be seamlessly considered in the formulation. Such extreme cases of numerical application are justified for scientific objectivity, according to Carl Sagan’s standard “extraordinary claims require extraordinary evidence” [15].

1.2 Summary from recently published papers

The following subjects are covered in [1, 4,5,6].

• All basic concepts are consistently laid down in [1] for general three-dimensional (3D) problems of potential and elasticity, which brings Appendices A (to illustrate the convergence Theorem 1 enunciated for 2D and 3D problems), B (for the illustrative application to the Timoshenko beam as an exact 2D elasticity problem, also showing how boundary conditions are to be consistently dealt with) and C (for the illustrative developments of a—one-dimensional—truss element with arbitrarily variable cross section while making explicit singularity issues that one might think pertaining exclusively to general 2D and 3D formulations).

• Paper [4] deals with the exact numerical corrections and the code implementation details for 2D problems of potential and elasticity with generally curved boundary, which includes Appendices A (for the Newton–Raphson evaluation of the complex source pole $\xi _s=a\pm ib$ corresponding to a general quasi-singularity), B (for the evaluation of integrals involving the logarithm of a generally complex argument $\xi _s=a\pm ib$ while only resorting to Gauss–Legendre quadrature), C (for the evaluation of integrals with algebraic real singularities and quasi-singularities $\xi _s=a$) and D (for complex quasi-singularities $\xi _s=a\pm ib$).

• Topologically challenging numerical evaluations are illustrated in [5] for 2D problems of potential and elasticity, with precision, accuracy, and convergence assessments. We objectively determine how close to a boundary segment (element) a source point should be to justify the special exact treatments proposed in [4]. We also investigate the conditioning of the matrices that constitute the CBEM.

• The complex-variable ($z=x+iy$) counterpart of the above developments is outlined in [6], which shows that drastic simplifications may be achieved, and where we no longer need to deal differently with real ($\xi _s=a$) and complex ($\xi _s=a\pm ib$) quasi-singularity cases, while arriving at a simpler and more robust code implementation—particularly for stress results at domain points that may be as close to the boundary as deemed necessary in an engineering application, provided that we have sufficient machine precision.

1.3 Basic consistent notation required in a problem simulation

The following boundary and domain entities must be well understood for the consistent problem outline, according to [1, 4,5,6].

• In an isoparametric formulation, the body’s boundary geometry is described—in terms of local parametric variables $(\xi ,\eta )$ for the 3D problem, or just $(\xi )$ for the 2D problem, in a similar way as potentials and displacements are described, here interpolated from nodal coordinates characterized by the subscript m. However, we might think of an exact geometric description (which may be called isogeometric [16], although this is not being dealt with presently [17]).

• Potential or displacements are interpolated along the boundary from attributed nodal parameters, which are indicated by the subscript n.

• Normal flux or tractions are interpolated along the boundary from parameters referred to surface-oriented loci, to which we attribute the subscript $\ell$. Thus, their definition depends on the boundary unit normal $\textbf{n}$. (The false, misleading dilemma continuous versus discontinuous elements is adequately dealt with in [1].)

• Potential, flux, displacement, or stress results are evaluated at domain points s, for source, which may be arbitrarily close to (but not at) the boundary.

These four entities must be understood as topologically distinct, although it is quite natural to have the same nodes for geometry as for potential or displacement in an isoparametric formulation (which includes the subparametric case). Boundary normal flux or traction loci are different from potential or displacement nodes in terms of topological concept, location, and amount eventually required in a model idealization. Source points s are domain entities, which may become arbitrarily close to nodes n in the frame of a collocation approach, as implemented presently, or when evaluating results at internal points, but they are geometrically different concepts.

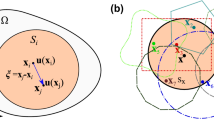
We illustrate on the left in Fig. 2—taken from a paper in preparation [17]—the case of two consecutive cubic boundary elements of a 2D problem, with ${{n}_{m}}={{n}_{n}}=4$ nodal parameters $n_m$ for geometry ($\circ$) and $n_n$ for potential or displacement ($\odot$), which in this case coincide (as usually proceeded in an isoparametric formulation), and ${{n}_{\ell }}=n_n=4$ parameter loci ($\times$) for normal flux or traction, which are not at the element extremities but at distances $\epsilon \rightarrow 0$ (we do not say “discontinuous” but rather “consistent,” as the whole formulation). We also indicate the points ($*$) for the collocation of the sources s in the domain but at distances $\rightarrow 0$ from the nodal points n, in the frame of the CBEM. There are $n^d=n^{el}(n_n-1)=3n^{el}$ nodes for a total of $n^{el}$ elements that comprise the complete problem we are simulating. For an elasticity problem implemented in terms of real variables, the double-layer potential matrix H is square of order $2 n^d=2 {{n}^{el}}({{n}_{n}}-1)=6{{n}^{el}}$, and the single-layer potential matrix G has the same number of rows but $2 n^t=2 {{n}^{el}}{{n}_{\ell }}=8{{n}^{el}}$ columns, where $n^t$ is the total number of traction loci.

The case on the right in this figure is almost similar, also with ${{n}_{m}}={{n}_{n}}=4$ nodal parameters for geometry and potential or displacement, but whose locations only coincide at the extremities (as just an implementation possibility using Radau–Lobatto abscissas for the nodes n). Most important, we have ${{n}_{\ell }}=n_n-1=3$ parameter loci for normal flux or traction along an element, which are at finite distances from the element extremities (such implementation still satisfies the convergence Theorem 1 [1]). There are in this case $n^d=n^t=n^{el}(n_n-1)=3n^{el}$ nodes and loci for a total of $n^{el}$ elements. For an elasticity problem implemented in terms of real variables, both matrices G and H are square of order $2n^d=2 {{n}^{el}}({{n}_{n}}-1)=6{{n}^{el}}$.

Fig. 2

Two consecutive cubic elements for a 2D problem, illustrated on the left for $n_m=n_n=n_\ell = 4$ nodes and loci per element, and on the right for $n_m=n_n = 4$ nodes and $n_\ell = 3$ loci [17]

1.4 Basic propositions and assumptions

The following propositions, assumptions, and definitions are dealt with comprehensively in [1].

• Proposition 1 Continuous patches of the whole $\Gamma$ are expressed in terms of a succession of boundary segments (elements) $\Gamma _{seg}$ as $\textbf{x}(\xi ,\eta )=N^g_m(\xi ,\eta )\textbf{x}_m$, where $N^g_m\equiv N^g_m(\xi ,\eta )$ are interpolating polynomials—with local support, for $\xi ,\eta \in [0,1]$, from nodal coordinates $\textbf{x}_m$ in an isoparametric formulation (we usually refer to the geometry coordinates (x, y, z), (x, y) or the complex $z=x+iy$), as for 3D or 2D problems. For the 2D problem, $N^g_m\equiv N^g_m(\xi )$ interpolate from $n_m$ nodes along $\Gamma _{seg}$ and are of degree $n_m-1$. The advantage of such an isoparametric formulation—see Ansatz 1, next, is that a convergence Theorem 1 is proposed and proved similarly to a convergence theorem proposed by Zienkiewicz and collaborators in the 1960 s for the displacement finite element method [18, 19]—although here needing more elaboration to be proved and with restrictions for the 3D case. The disadvantage of this formulation is that generally curved boundaries must have their geometry approximated. If $N^g_m(\xi ,\eta )$ is the exact boundary representation of a given problem, for $\textbf{x}_m$ considered as general parameters regardless of any nodal connotation, this is an isogeometric formulation [16], which is comprehended in the present developments, although in such a case we must give up the computational consistency provided by the convergence Theorem 1. This is dealt with in a paper in elaboration [17].

• Ansatz 1 The boundary potential or displacement is approximated along a boundary segment $\Gamma _{seg}$ in terms of $\textbf{u}(\xi ,\eta )=N^{o_e}_n(\xi ,\eta )\textbf{u}_n$, where $N^{o_e}_n\equiv N^{o_e}_n(\xi ,\eta )$ are interpolating polynomials—with local support—from nodal potential or displacements $\textbf{u}_n$. The superscript $o_e$ stands for element order (or, more generally in the 3D case, for element type). The present 2D code implementations are restricted to linear, quadratic, cubic, or quartic elements: just enter $o_e=1,2,3$ or 4, which rely on $n_n=o_e+1$ nodes along a segment $\Gamma _{seg}$.⁴ We also propose the Definition 1 of rigid-body displacements in terms of the columns of a matrix $\textbf{W}$ that, for computational convenience, constitute an orthonormal basis (the one-column case for constant potential included).

• Ansatz 2. The normal flux or traction force is approximated on a boundary segment $\Gamma _{seg}$ as $\textbf{t}(\xi ,\eta )=\left( |J|_{(\textrm{at}\ \ell )}/|J|\right) N^{o_e}_\ell (\xi ,\eta )\textbf{t}_\ell$, where $N^{o_e}_\ell \equiv N^{o_e}_\ell (\xi ,\eta )$ are interpolating polynomials—with local support—from the surface flux of traction parameters $\textbf{t}_\ell$, whose definition depends on the boundary unit normal $\textbf{n}$, and $|J| \equiv |J|(\xi ,\eta )$ is the Jacobian of the Cartesian to parametric coordinate transformation of the geometry. As proposed in [1, 8], the term $\left( |J|_{(\textrm{at}\ \ell )}/|J|\right)$ is paramount for the correct interpolation along generally curved boundaries. Moreover, as shown in [1] in the proof of Theorem 1 and illustrated in its Appendix A, the polynomial $N^{o_e}_\ell (\xi ,\eta )$ may be one order less than $N^{o_e}_n(\xi ,\eta )$ in an isoparametric formulation—as indicated in the previous Section and illustrated on the right in Fig. 2. Then, we may have for the 2D problem $N^{o_e}_\ell (\xi )$ defined in terms of $n_\ell$ nodes that are equal to either $n_n$ or $n_n-1$, as taken from Ansatz 1.

• Proposition 2. For the development of the CBEM [1], the source points are collocated in the open domain $\Omega$ at points s that are infinitesimally close to the displacement boundary nodes n of Ansatz 1.

2 A short review of the consistent, collocation boundary element method [1]

2.1 Basic problem outline

We basically summarize Section 2 of paper [1] while accruing some concepts. We consider a generally three-dimensional, finite elastic domain⁵ submitted to body forces $b_i$ in $\Omega$ and traction forces ${\overline{t}}_i$ on $\Gamma _{\sigma }\subset \Gamma$. Displacements ${\overline{u}}_i$ are known on $\Gamma _u = \Gamma {\setminus }\Gamma _{\sigma }$. Particularizations for potential problems and for 2D elasticity follow seamlessly. We shall later on restrict the implementation to 2D problems. Our task is—under the hypothesis of small displacements and linear elasticity for a homogeneous, isotropic medium—to find an approximation of the stress field $\sigma _{ij}$ such that $\sigma _{ji,j}+b_i=0$ and $\sigma _{ij}=\sigma _{ji}$ in $\Omega$, $\sigma _{ji}n_j={\overline{t}}_i$ on $\Gamma _{\sigma }$, and, for the corresponding displacements, $u_i={\overline{u}}_i$ on $\Gamma _u$. Indicial notation is used throughout the paper, although we eventually change to matrix notation. As already defined, $n_j$ are the Cartesian projections of the boundary unit normal $\textbf{n}$.

2.2 From weighted residuals to the Somigliana’s identity

2.2.1 From variational to weighted residuals

The following developments are both didactic and informative [1, 8]. The strong-form principle of stationary total potential energy [24] is, for a variation $\delta u_i$ of the displacements $u_i$:

$$\begin{aligned} \delta \Pi (u_i)=-\!\int _{\Omega }{(\sigma _{ji,j}+b_i)\ \delta u_i \ \textrm{d}\Omega } +\! \int _{\Gamma }{(\sigma _{ji}\ n_j-t_i)\ \delta u_i \ \textrm{d}\Gamma }=0 \end{aligned}$$

(1)

in which we have already extended the boundary integral from $\Gamma _{\sigma }$ to $\Gamma$, since $\delta u_i=0$ on $\Gamma _u$, while considering that Hooke’s law applies:

$$\begin{aligned} \sigma _{ij}=C_{ijkl}\ u_{k,l} \quad \Rightarrow \quad \sigma _{ij}=\sigma _{ji} \quad \textrm{in} \quad \Omega \end{aligned}$$

(2)

A less restrictive expression of the above equation is the weighted-residual statement

$$\begin{aligned} -\int _{\Omega }{(\sigma _{ji,j}+b_i)\ \delta u^{*}_i \ \textrm{d}\Omega } + \int _{\Gamma }{(\sigma _{ji}\ n_j-t_i)\ \delta u^{*}_i \ \textrm{d}\Gamma }=0 \end{aligned}$$

(3)

as it seems to have been first proposed by Brebbia [10, 25] as one of the possibilities of arriving at the boundary element method [12, 13]. We are for now just assuming (restricting) that the virtual weighting function $\delta u^{*}_i$ is a displacement field for which stresses $\delta \sigma ^{*}_{ij}=C_{ijkl}\ \delta u^{*}_{k,l}$ may be found, that is, according to the same material properties of the displacement field $u_i$, as in Eq. (2). However, $\delta u^{*}_i$ is not necessarily an increment of $u_i$, in general, that is, $\delta u^{*}_i\ne \delta u_i$, as they may refer to completely different problem setups and also be conditioned to different continuity/integrability requirements—see Sect. 2.4.

After twice integration by parts of the left-most term and application of Green’s theorem, this equation becomes

$$\begin{aligned} \int _{\Gamma }{\delta \sigma ^{*}_{ji}\ n_j u_i \ \textrm{d}\Gamma }- \int _{\Omega }{\delta \sigma ^{*}_{ji,j}\ u_i \ \textrm{d}\Omega } = \int _{\Gamma }{t_i\ \delta u^{*}_i \ \textrm{d}\Gamma }+ \int _{\Omega }{b_i\ \delta u^{*}_i \ \textrm{d}\Omega } \end{aligned}$$

(4)

where we considered that $\sigma _{ji}\ \delta u^{*}_{i,j}\equiv u_{k,l}\ C_{ijkl}\ \delta u^{*}_{i,j}\equiv u_{k,l}\ \delta \sigma ^{*}_{kl}$⁶.

2.2.2 The concept of fundamental solution

We start with the working hypothesis (Assumption 1 of [1]) that a fundamental solution of the problem stated above is known, characterized by a $(\ )^*$, such that

$$\begin{aligned} \delta \sigma ^*_{ji,j}=0 \quad \textrm{in} \quad \Omega \end{aligned}$$

(5)

that is, in the problem’s domain of interest. The only reason for this assumption is in principle to get rid of the domain integral on the left-hand side in Eq. (4).⁷. This is however more far-reaching, as developed in the next section.

The collocation boundary element method has been from the very beginning formulated with the more restrictive assumption of a fundamental solution $\sigma ^*_{ijs}$ that fulfills $\sigma ^*_{jis,j} =- \Delta _{is}$ in the open domain, where $\Delta _{is}$ is a Dirac function, with $\Delta _{is}=0$, in general, except if the indices i and s characterize the same geometric location and the same coordinate direction, when $\Delta _{is}=1$, then for a point force of unit value [10]⁸. The present developments seem to be more natural and general, if not more consistent than in the textbooks⁹.

2.2.3 Somigliana’s identity

Let $\delta \sigma ^{*}_{ij}\equiv \sigma ^{*}_{ij}(\textbf{x})$ and $\delta u^{*}_i\equiv \delta u^{*}_i(\textbf{x})$ be functions of global support with the argument $\textbf{x}=\textbf{x}_f-\textbf{x}_s$, where $\textbf{x}_s$ and $\textbf{x}_f$ are the coordinates of the source and field points, that is, where the virtual point force $\delta p^{*}_s\equiv \delta p^{*}(\textbf{x}_s)$ is applied and its effect is measured, respectively. Then,

$$\begin{aligned} \delta u^{*}_i \equiv (u^{*}_{is}+u^r_{ik}\ C_{ks})\ \delta p^{*}_s, \qquad \delta \sigma ^{*}_{ij} \equiv \sigma ^{*}_{ijs}\ \delta p^{*}_s \end{aligned}$$

(6)

where $u^r_{ik}$, for $k=1\dots n^r$, are $n^r$ rigid-body displacements (Definition 1 of [1]) multiplied by constants $C_{ks}$ that may be actually evaluated [1, 7]. This is a more consistent proposition than in the technical literature [10]. For the sake of completeness, we write down the expressions of $u^{*}_{is}$ and $\sigma ^{*}_{ijs}$, as developed by Kelvin and just in terms of the present notation, for the distance $r=|\textbf{x}_f-\textbf{x}_s|$, the generalized Kronecker delta $\delta _{is}$, material’s shear modulus G and Poisson’s ratio $\nu$:

$$\begin{aligned} u_{is}^{*}&=\frac{-1}{8\pi G(1-\nu )}\left[ (3-4\nu )\ln r{{\delta }_{i s}}-r{{,}_{i}}r{{,}_{s}} \right] \end{aligned}$$

(7)

$$\begin{aligned} \sigma _{ijs }^{*}&=\frac{-1}{4\pi (1-\nu )r}\left[ (1-2\nu )(r_{,i}{{\delta }_{js }}+r_{,j}{{\delta }_{is }}-r_{,s}{{\delta }_{ij}})+2r_{,i}r_{,j}r_{,s} \right] \end{aligned}$$

(8)

Both $\delta \sigma ^{*}_{ij}$ and $\delta u^{*}_i$ tend to infinity as $\textbf{x}_f\rightarrow \textbf{x}_s$, in general. However, the correct interpretation is that they are simply not defined at $\textbf{x}_f= \textbf{x}_s$, and, as shown in [4,5,6], the actual results of interest $(u_i,\sigma _{ij})$ turn out bounded everywhere in the domain, no matter how close we come to the boundary, provided only that we deal with the problem’s mathematics adequately¹⁰. The stress fundamental solution $\sigma ^{*}_{ijs}$ introduced above is already conveniently normalized: for a domain $\Omega _0 \notin \Omega$ that contains $\delta p^{*}_s$,

$$\begin{aligned} \int _{\Omega _0}{\sigma ^{*}_{jis,j}\ \textrm{d}\Omega }=\int _{\Gamma _0}{\sigma ^{*}_{jis}\ n_j\ \textrm{d}\Gamma }\equiv -\delta _{is} \end{aligned}$$

(9)

where $\Gamma _0$ is the enclosing boundary. According to the latter equation, the domain integral on the left-hand side of Eq. (4) simplifies to

$$\begin{aligned} \int _{\Omega }{\delta \sigma ^{*}_{ji,j}\ u_i \textrm{d}\Omega } =-\delta _{is}\ u_i \ \delta p^{*}_s\equiv -u_s\ \delta p^{*}_s \end{aligned}$$

(10)

Substituting for $\delta u^{*}_i$ and $\delta \sigma ^{*}_{ij}$ in Eq. (4) according to their expressions above, we obtain for arbitrary $\delta p^{*}_s$ the Somigliana’s identity [7, 38],

$$\begin{aligned} {{u}_s}=&\int _{\,\Gamma }{{{t}_{i}}u_{is}^{*}\text {d}\Gamma } -\int _{\,\Gamma }{\sigma _{jis}^{*}{{n }_{j}}{{u}_{i}}\text {d}\Gamma } +\int _{\,\Omega }{{{b}_{i}}u_{is}^{*}\text {d}\Omega }\nonumber \\&+{{C}_{ks}}\left( {{\int _{\,\Gamma }{{{t}_{i}}u_{ik}^{r}\text {d}\Gamma }}}+\int _{\,\Omega }{{{b}_{i}}u_{ik}^{r}\text {d}\Omega } \right) \end{aligned}$$

(11)

which enables the evaluation of displacements $u_s$ (and, subsequently, stresses) at a domain point s for prescribed domain and boundary data $b_i$, ${\overline{t}}_i$, ${\overline{u}}_i$. The term in brackets, which is not present in Somigliana’s original expression, is void only if $b_i$ and $t_i$ are in equilibrium. Then, numerical results are affected by $C_{ks}$, which turn out to be not arbitrary but problem-dependent [1, 5, 7]¹¹.

As already observed in Footnote 10 and developed next, Eq. (11) is also used to evaluate displacement $u_i$ and traction $t_i$ approximations along $\Gamma _{\sigma }$ and $\Gamma _u$, respectively, in the context of the conventional CBEM¹².

Remarks on the consistency of Eq. (11) and on a not-so-consistent way of arriving at it using Betti’s Reciprocal Theorem are presented in Sect. 2.4.

2.3 Basic matrix expressions of the CBEM

According to Proposition 1 (isoparametric geometry representation), Ansatz 1 (displacement approximation), Definition 1 (rigid-body displacements) and Ansatz 2 (traction force approximation) of [1], as briefly outlined in Sects. 1.3 and 1.4 and illustrated in Fig. 2, a Proposition 2—of collocating the source points s in Eq. (11) at domain points that are infinitesimally close to the boundary displacement nodes n—leads to the basic equation of the CBEM,

$$\begin{aligned}&\left[ \int _{\Gamma }{\sigma ^{*}_{jis}n_j u_{in} \textrm{d}\Gamma } +\delta _{sn} \right] \left\{ d_n\right\} \nonumber \\&=\left[ \int _{\Gamma }{u^{*}_{is} t_{i\ell } \textrm{d}\Gamma }\right] \left\{ t_{\ell }\right\} +\left\{ \int _{\Omega } u^{*}_{is} {b_i \textrm{d}\Omega } \right\} \nonumber \\&+\left[ C_{ks}\right] \left\{ \left[ \int _{\Gamma }{ u^r_{ik} t_{i\ell }\textrm{d}\Gamma }\right] \left\{ t_{\ell }\right\} +\int _{\Omega }{u^r_{ik} b_i \textrm{d}\Omega }\right\} \end{aligned}$$

(12)

in terms of real variables, where the brackets already indicate matrices and vectors for the matrix expression of the collocation boundary element method. This results into

$$\begin{aligned} \textbf{H}(\textbf{d}-\textbf{d}^p)=\textbf{G}(\textbf{t}-\textbf{t}^p)_{ad} \end{aligned}$$

(13)

(See Footnote 11.) As developed in Section 2.5.1 of [1], we are assuming rather for the sake of convenience that an either analytical or numerical particular solution $\sigma ^p_{ji,j}+b_i=0$ of the problem’s equilibrium equation is known (Assumption 1 of [1]), with corresponding boundary displacement $u_i^p$ and traction $t_i^p$ data approximated from nodal displacements $\textbf{d}^p$ and traction parameters $\textbf{t}^p$, according to Ansätze 1 and 2,¹³.

In this equation, as for 2D elasticity, H is the square, double-layer potential matrix of order $2n^d=2 {{n}^{el}}o_e$, and G is the single-layer potential matrix with $2n^d$ rows and $2(n^d+n^{el})$ columns, as we code for $n^{el}$ elements of a given order $o_e$ for both $N_n^{o_e}$ and $N_\ell ^{o_e}$ introduced in Sects. 1.3 and 1.4, in principle taking into account that the left and right tangents at a nodal point connecting two elements are different, according to the scheme on the left in Fig. 2, and so are the traction parameters. The problem’s primary boundary displacement and traction parameters are $\textbf{d}$ and $\textbf{t}$, which are in part known and in part to be obtained in the context of a general mixed-boundary formulation [1]. As comprehensively assessed in [1, 4, 5, 7], we write for consistency that the traction $(\textbf{t}-\textbf{t}^p)_{ad}$ is admissible, that is, in equilibrium with the applied domain forces: this follows the same mathematical/mechanical principle that, since, for a finite domain, rigid-body displacement amounts of $(\textbf{d}-\textbf{d}^p)$—in the space spanned by the columns of the orthonormal matrix W in Definition 1 of [1] referred to in Sect. 1.4—cannot be transformed into forces, also non-equilibrated forces can not be elastically transformed into displacements. This leads to attributing to the constants $C_{ks}$ in Eqs. (11) and (12) values related to a projector $\textbf{P}^{\perp }_R$ onto the admissible space of traction forces $(\textbf{t}-\textbf{t}^p)_{ad}$, as outlined in [1, 7, 8] for real variables and in [6] for complex variables—see Footnote 11.

2.3.1 Equivalent nodal force and stiffness-type matrix

As developed in Section 2.6.1 of [1], for instance, and is a usual procedure in the finite element methods, it may be necessary to express the boundary traction forces in terms of equivalent nodal forces $\textbf{p}=\left[ p_n\right] \in \Re ^{2n^d}$, which are obtained from the virtual work statement

$$\begin{aligned} \delta d_n\ p_n=\delta d_n\ \int _{\Gamma }{u_{in}\ t_{i\ell }\ \textrm{d}\Gamma }\ t_\ell \quad \Rightarrow \quad p_n = L_{\ell n}\ t_\ell \quad \textrm{or} \quad \textbf{p}=\textbf{L}^{\textrm{T}}{} \textbf{t} \end{aligned}$$

(14)

where $\textbf{L}^{\textrm{T}}$ carries out an equilibrium transformation.

Moreover, a stiffness-type matrix may be constructed from Eq. (13) and above:

$$\begin{aligned} \textbf{L}^{\textrm{T}}{} \textbf{G}_{ad}^{(-1)}{} \textbf{H}(\textbf{d}-\textbf{d}^p)=(\textbf{p}-\textbf{p}^p) \end{aligned}$$

(15)

where $\textbf{G}_{ad}^{(-1)}$ is to be obtained in the frame of generalized inverses [40, 41]. The stiffness-type matrix $\textbf{K} = \textbf{L}^{\textrm{T}}\textbf{G}_{ad}^{(-1)}{} \textbf{H}$ is by construction nonsymmetric. In fact, it becomes symmetric only for some very particular cases, as discussed in the following and illustrated in Appendix C of [1] for a truss element.

2.4 Consistency assessment

We make a few consistency considerations on the weak, strong, and inverse forms of Eqs. (1) and (3) to constructively arrive at some important conceptual aspects regarding the fundamentals of Somigliana’s equation (11).

2.4.1 On the weak form of Eq. (1)

The variational Eq. (1) is presented in its strong form. Its weak form—after adequate integration by parts and application of Green’s theorem—leads to the displacement finite element method, with a stiffness matrix that is symmetric by construction independently of mesh discretization while considering the test function $u_i$ and its variation $\delta u_i$ piece-wise approximated in the domain using the same functions—Galerkin’s approach, which is quite natural and convenient, as they turn out conditioned by the same continuity/integrability requirements. Bathe and Wilson’s [42] “finite difference energy method” is a rather academic application of this equation.

2.4.2 On the strong-form Eq. (3)

The strong-form, weighted-residual Eq. (3) is the basis for many numerical implementations [10], such as in the finite difference method, which does not lead to symmetric matrices, in general. The attempt to represent in the integral statement of Eq. (3) displacements $u_i$ (from which the stress field $\sigma _{ij}$ is to be obtained) and the weight functions $\delta u_i^*$ as increments of each other—original Galerkin’s approach—is not practical, in general, particularly because they must satisfy different continuity requirements and this may show no computational advantages. Since we only have displacements $\delta u_i^*$ in this equation (of which no derivatives are required), we may think of implementing Eq. (3) for the equilibrium equations in brackets locally approximated¹⁴ and just collocated at discrete points distributed in $\Omega$, thus considering $\delta u_i^*=1$ at given points and void elsewhere ($\delta u_i^*$ not necessarily to be interpreted as Dirac functions). As the number of collocation points increases (and the problem is well-posed), the numerical solution tends to be the exact solution (whether analytical or not) of the integral Eq. (3). Notice that this collocation procedure is a matter of mathematics only (no mechanical reasoning involved).

2.4.3 On the inverse-form counterpart of Eq. (3): Betti’s theorem is just out of place

Despite having the inverse-form Eq. (4) coming from the strong-form Eq. (3) by sheer mathematical transformations (twice integration by parts and application of Green’s theorem), it is largely proposed in the technical literature a questionable and unnecessary means to arrive at the Somigliana’s identity, Eq. (11), namely by resorting to Betti’s Reciprocity Theorem [44], whose roots and—-welcome—conceptual intricacies in the frame of the elasticity theory, in general, are outlined by Love [27]. Chen and Zhou [21], for instance, propose what they call the “Betti-Somigliana formula.” Brebbia et al. [10] (in a book to a great extent still up-to-date except for missing the paradigm-shifting propositions of [1, 4,5,6]) observed that Eq. (4), there similarly written as Eq. (5.47) and similarly obtained in terms of weighted residuals [25], “corresponds to Betti’s second reciprocal work theorem.” This would be adequate if followed by the caveat: provided $u_i$ and $\delta u^*_i$ may be demonstrably considered increments of each other. Such indiscriminate reference to Betti’s Theorem may not be harmful in its outcome—except for lacking the term in brackets multiplied by the constants $C_{ks}$, second line of Eq. (11)—but is just mistaken and the source of an important conceptual misinterpretation of the CBEM.

Betti’s theorem [44] relies on the principle of superposition of effects (rather intuitive for linear elastic problems and small displacements¹⁵), is quite often called Maxwell–Betti’s reciprocal theorem (its usefulness is shown in  Selvadurai and Dumont [46], for instance) and is resorted to proving that a stiffness matrix is symmetric—usually by construction and no matter how coarse or refined is a problem’s numerical discretization mesh.

Observe that $\sigma _{ij}$, with which we construct an ideally analytical solution $t_i=\sigma _{ji}n_j$ on the boundary $\Gamma$ for Eq. (11) (see Footnote 5)—and also introduce boundary approximations, as in next Section, and $\delta \sigma ^{*}_{kl}$ cannot be viewed as increments of the same problem’s solution (the latter is just a convenient, homogeneous solution), as required to prove Betti’s theorem in terms of a superposition of effects, which is achievable from Eq. (1) but not from Eq. (4), in general.

When this is the case, such as in the frame of a non-singular fundamental solution (as in the methods proposed by Trefftz [26] or Pian [47]), the symmetry of a stiffness matrix is demonstrated (although in a mixed variational framework, as the Hellinger–Reissner potential [48], for instance)—but the term on the left in Eq. (11) just vanishes, and so does the present beauty and usefulness of Somigliana’s identity, the basis of the CBEM and also to be applied in the evaluation of results at internal points, Sects. 3.2 and 4.2 for potential and elasticity problems.

2.4.4 The beauty of Somigliana’s identity

This beauty comes from Kelvin’s (as here, for elasticity) singular fundamental solution that enables to transform the symmetric differential operator on $\sigma _{ji}$ in Eq. (3) via twice integration by parts into the differential operator on $\delta \sigma ^*_{ji}$ in Eq. (4): Eqs. (9) and (10) do all the magic but this is just a mathematical convenience (in the present form only applicable to a homogeneous medium), in the same way as point-by-point collocation is a mathematical convenience in the more generally applicable finite difference method, as remarked above. We should pay tribute to Green, Somigliana, and Kelvin, but Betti’s theorem does not belong here (and Betti’s lore neither needs nor deserves this).

2.4.5 On the collocation boundary element implementation

We have arrived at the boundary element implementation of Sect. 2 by cutting out from the infinite, open domain the (also open) subset $\Omega$ of interest to numerically simulate a problem, for displacements $u_i$ and tractions $t_i$ of the sought solution given approximately (or exactly, as it may happen) along the boundary $\Gamma$ in terms of nodal values $d_n$ and surface parameters $t_\ell$, respectively, which are in part known and in part to be evaluated. Arbitrary, weighting point forces $\delta p^{*}_s$ are then applied (collocated) at points s in the open domain $\Omega$ that are infinitely close to the boundary nodal points n, to construct from Somigliana’s equation (11) a system that enables the evaluation of the subset of unknown parameters of $d_n$ and $t_\ell$, for a general, well-posed problem with mixed-boundary conditions. Nowhere in this procedure is assumed that $\delta \sigma ^{*}_{ijs}$ and $\sigma _{ij}$ are increments of each other: a solution $(u_i,\sigma _{ij})$ must satisfy the problem’s boundary conditions on $\Gamma _u$ and $\Gamma _\sigma$, which is not the case of $(\delta u^{*}_{is},\delta \sigma ^{*}_{ijs})$.

There is no way of representing smooth, analytical traction solutions $t_i$ along smooth patches of $\Gamma$ directly in terms of a function $\sigma ^{*}_{jis}n_j$ that tends to infinity as the domain source point s approaches the boundary—and vice versa. The same reasoning applies to $\sigma _{kl}$ and $\delta \sigma ^{*}_{kl}$ at a domain point.

There seems to be only a possibility for the above-mentioned (unnecessary, Betti’s reciprocity) incremental interpretation to be feasible, namely when the domain coalesces to a line and the boundary $\Gamma$ coalesces to points, as by dealing with the ideal, topologically degenerated, representation of a truss or a beam element in terms of the Somigliana’s identity of Eq. (11). An illustration is given in Appendix C of [1], where we arrive at a symmetric stiffness matrix—constructed as in Eq. (15)—for a truss element with arbitrarily variable cross section (just to make the problem more interesting) as well as at the analytical representation of results at internal points via Somigliana’s identity. The reason for the achieved symmetry is that both analytical and fundamental solutions lead to displacements and stresses that are constant along the degenerated (point) boundaries, that is, are equally, exactly represented on $\Gamma$. Moreover, since the problem’s closed-form analytical solution is obtained, we constate that a continuous displacement u(x) and a discontinuous $u^*(x,x_s)$ may be thought as increments of each other—except at $x=x_s$, where $u^*$ is undefined. However, it is still too forced to think of such a formulation as coming from Betti’s reciprocity theorem, as, for instance, u(x) has local support (is valid only in $\Omega$ and void outside), whereas $u^*(x,x_s)$ has global support, which is well explored in Appendix C of [1]: a coincidence does not build a case.

As given in the convergence Theorem 1 of [1] together with a Corollary and the illustrative Appendix A, as well as in the present paper’s numerical example of Sect. 5.2, some particular problems may be represented exactly within machine precision—but also, in this case, a stiffness matrix, whose construction is independent of actual boundary data (see, for instance, Section 2.6 of [8]), would not be symmetric.

The collocation boundary element method’s consistently inherent lack of symmetry has been the source of much misunderstanding in the technical literature, as brought to this author’s awareness by Prof. Herbert Mang (from the University of Vienna) during a technical visit to PUC-Rio in the year 1985 [49]. This ended up motivating the development of the variational, hybrid boundary element method [28] (1989), which uses Kelvin’s singular fundamental solution as the problem’s approximate solution (a subject per se, whose unfolding is still to be completely explored—see, for instance, [50]) and is symmetric by construction, since based on the Hellinger–Reissner potential. Applications coming from this method are, for instance, Dumont [29], Gaul et al. [30], Dumont [31], Dumont and Lopes [32], Dumont and Chaves [33], Dumont et al. [34], Wagner et al. [35], Dumont and Aguilar [36], Dumont and Mamani [37], as cite before.

It is worth quoting a few paragraphs from Dumont [28].

“The resultant equations of the conventional boundary element method cannot be accounted for using sound mechanical (variational) considerations, but are to be interpreted as a set of weighted expressions between forces and displacements which are similarly described over the boundary. The present success of the boundary element method itself speaks for such a solution which allies simplicity to ponderation (from Latin pondus = weight), despite the flagrant non-symmetry of the equations. By increasing the discretization of the boundary, the results converge to the correct solution and the non-symmetry tends to vanish.

But any energetically consistent formulation of problems for which the principle of superposition (and therefore Betti’s reciprocal theorem) is valid must yield symmetric matrices for any finite discretization, whether integral equations are used or not.

In the conventional boundary element method, the resulting nonsymmetric relations between forces and displacements cannot be made symmetric without the perpetration of conceptual mistakes and loss of accuracy [this loss of accuracy was reported, for instance, by  Li et al. [49], although they failed to explain the conceptual mistakes]. The numerical examples of the literature showing the good performance of a symmetrized formulation are mere evidence of a fine mesh refinement, in which case the original formulation would already yield nearly symmetric equations.”

2.4.6 The beauty of combining Somigliana’s identity and correct maths

Although based on a singular fundamental solution (which must satisfy Hölder condition¹⁶ [10, 20]), the integral statement of Eq. (11) does not lead to a singular domain displacement $u_s$ if the boundary and domain data—$u_i$, $t_i$, $b_i$, and the topology—do not imply a singularity and we just do the math correctly¹⁷. Moreover, if in the mesh discretization of Eq. (11) the boundary and domain data are just a coarse approximation of the actual problem, the internal results also turn out coarse approximations—but nowhere unduly tend to infinity [5, 6].

Given a (2D, as dealt with presently) problem’s mesh discretization, we can always in full control assess its topology consistency and numerical precision, and—for the entered data of actual interest—the accuracy of results. We can also objectively estimate the possibility of round-off errors, as illustrated in Sects. 5.1 and 5.2.

3 Complex-variable expressions for potential problems

We present in the following a brief outline of the developments proposed in [6] for 2D potential problems in terms of a complex variable $z=x+iy$. The reader is recommended to compare these developments with the real-variable ones of [4].

3.1 Basic CBEM equation for the 2D potential problem

In complex-variable notation, matrices $G_{s\ell }$ and $H_{sn}$ of Eq. (13) for the potential problem (with material property k, such as for conductivity in a steady-state heat conduction problem) are

$$\begin{aligned} G_{s\ell }\simeq -\frac{{\left| J \right| }_{(\text {at }\ell \text {)}}}{2\pi k}{G\!L}\!\!\int _\Gamma {\ln z\,N_{\ell }^{{{o}_{e}}}\,\text {d}\xi }-\left\{ \begin{array}{ll} \{\ \} &{} no\_sing \\ \dfrac{{\left| J \right| }_{(\text {at }\ell \text {)}}}{2\pi k}C_{Gr} &{} sing \\ \dfrac{{\left| J \right| }_{(\text {at }\ell \text {)}}}{2\pi k}C_{Gc} &{} quasi\_sing \end{array} \right. \end{aligned}$$

(16)

$$\begin{aligned} H_{sn}\simeq \frac{i}{2\pi }{G\!L}\!\!\int _{\Gamma }{\frac{z'}{z}N_n^{o_e}}\textrm{d}\xi + \delta _{sn}+ \left\{ \begin{array}{ll} \{\ \} &{} no\_sing,\ \textrm{real}\ quasi\_sing \\ 1- \dfrac{\theta ^+ - \theta ^-}{2\pi } &{} sing \\ \dfrac{i}{2\pi } N^{o_e}_n|_{\xi _s}C_1 &{} \textrm{complex}\ quasi\_sing \end{array} \right. \end{aligned}$$

(17)

for integration carried out along successive boundary segments $\Gamma _{seg}\equiv \Gamma _{seg}(z_f)$ of $\Gamma$. The whole development is outlined in [6].¹⁸ As proposed in [4, 6], use of the parametric/integration variable $\xi$ in the normalized unit interval [0, 1] leads to simpler implementations than for $\xi \in [-1,1]$. Both interpolation functions $t_\ell \equiv N^{o_e}_\ell |J|_{\textrm{at} \ell }/|J|$ and $u_n \equiv N^{o_e}_n$ of the parameter $\xi \in [0,1]$ have compact support—Ansätze 1 and 2 of [1]. The nodes and sources span $n,s=1,\dots ,n^d\equiv n^s$, and the loci span $\ell =1,\dots ,n^t$, according to Sect. 1.3 and illustrated in Fig. 2, so that we have the whole boundary automatically covered in Eqs. (16) and (17)—and no explicit indication of summation over boundary segments is required. Derivative $d(\,)/d\xi$ is indicated as $(\,)'$. We address all integration peculiarities in the following—mainly resorting to [6]. The notation “$G\!L$” before the integral signs means “Gauss–Legendre evaluation with $n_{g}$ abscissas $\xi _i \in [0,1]$”, and the symbol $\simeq$ indicates approximation that is due solely to the applied numerical quadrature, as the corrections indicated on the right are accurate within machine precision.

Correction terms are conditioned by three logical constants $< no\_sing,\ sing,\ quasi\_sing>$, which depend, according to Fig. 1, on the position of the source point s with respect to the boundary element [1,2,3,4, 6].

In Eq. (16), $C_{Gr} \equiv C_G(\ell ,\xi _s \rightarrow a)$ and $C_{Gc} \equiv C_G(\ell ,\xi _s \equiv a + bi)$ have the generic expression of Equation (B.4) of [6],

$$\begin{aligned} C_{G} \equiv C_{G}(\ell ,\xi _s)=\int _{0}^{1}{\ln (\xi -\xi _s )N_{\ell }^{{{o}_{e}}}\,\text {d}\xi }-\sum _{i=1}^{n_g}{\ln ( \xi _i -\xi _s )N_{\ell }^{o_e}(\xi _s)h_i } \end{aligned}$$

(18)

for either singularity or quasi-singularity of $G_{s\ell }$. They are obtained in Appendices B.2.1 and B.2.2 of [6], and should just be stored and made ready (as black boxes) for code implementation according to any software language.

We also evaluate and store a correction term required in Eq. (17) in case of a complex quasi-singularity:

$$\begin{aligned} C_{1}=\ln \frac{\xi _s-1}{\xi _s}-\sum \limits _{i=1}^{{{n}_{g}}}{\frac{{{h}_{i}}}{{{\xi }_{i}}-\xi _s}} \end{aligned}$$

(19)

Equation (17) also brings in the second row the discontinuous term for the case of a singularity of the matrix $\textbf{H}$ (source point infinitesimally close to the boundary segment), as obtained in [4] for integration along a general path around the singularity pole and illustrated in Fig. 3.

An expedited, code-independent means of evaluating the angle difference in Eq. (17) is given in [6].

Fig. 3

General path for the integration around a singularity in Eqs. (17) and (30) [4, 6]

3.2 Internal potential and flux results

3.2.1 Somigliana’s complex-variable expression for potential

We resort to Eqs. (16) and (17) and rewrite Eq. (11) for a given domain point s as [6]

$$\begin{aligned} u_s\simeq u^p+\Re \left( G_{G\!L}\!-\!\dfrac{{\left| J \right| }_{(\text {at }\ell \text {)}}}{2\pi k}C_{Gc}\right) (t_\ell -t^p_\ell )_{ad} -\Re \left( H_{G\!L}\!+\!\dfrac{i}{2\pi } N^{o_e}_n|_{\xi _s}C_1\right) (d_n-d^p_n) \end{aligned}$$

(20)

with sum implicit for $\ell$ and n spanning all loci and nodes of the boundary element implementation. All boundary data are real quantities, and we also assume that some particular solution is known. As given before, normal flux is supposed to be in balance.

3.2.2 Somigliana’s complex-variable expression for flux

As outlined in Appendices C.3 and C.4 of [6], the expression of the potential flux in the domain is

$$\begin{aligned} q_s&\equiv (q_x-iq_y)|_s=q_s^p-\frac{|J|_{(at \, \ell )}}{2\pi }\left( G\!L\!\!\int _{\Gamma }{\frac{ N^{o_e}_\ell }{z} \textrm{d}\xi }+G^q\right) (t_\ell -t^p_\ell )_{ad} \nonumber \\&+\frac{ik}{2\pi }\left( G\!L\!\!\int _{\Gamma }{\frac{z' N^{o_e}_n}{z^2}\ \textrm{d}\xi }+ H^q\right) (d_n\!-\!d^p_n) \end{aligned}$$

(21)

also with sum implicit for $\ell$ and n spanning all loci and nodes of the boundary element implementation. This expression accrues two simple—and exact—corrections to the Gauss–Legendre evaluations:

$$\begin{aligned} G^q= \left. \frac{N^{o_e}_\ell }{z'}C_1\right| _{\xi _s},\quad H^q=\left. \left( \frac{N^{o_e}_n}{z'}C_2\!+\!\frac{{N'}^{o_e}_n}{z'}C_1\right) \right| _{\xi _s} \end{aligned}$$

(22)

Besides $C_1$, there is in the evaluation of $H^q$ a correction term $C_2$, which we present together with a third $C_3$, required later on for the elasticity problem:

$$\begin{aligned} C_{2}=\frac{1}{(\xi _s-1)\xi _s}-\sum \limits _{i=1}^{{{n}_{g}}}{\frac{{{h}_{i}}}{{{\left( {{\xi }_{i}}-\xi _s \right) }^{2}}}},\quad C_{3}=\frac{1-2\xi _s}{2(\xi _s-1)^2\xi _s^2}-\sum \limits _{i=1}^{{{n}_{g}}}{\frac{{{h}_{i}}}{{{\left( {{\xi }_{i}}-\xi _s \right) }^3}}} \end{aligned}$$

(23)

We cannot help drawing the attention to the extraordinary feature that comes from properly dealing with the quasi-singularity problem in terms of the complex parametric variable $\xi _s-\xi =a + bi-\xi \rightarrow 0$ as $|z|\equiv |z_f-z_s|\rightarrow 0$, which was proposed already in the year 1994 [2]: although both $N_n^{o_e}(\xi )$ and $N_\ell ^{o_e}(\xi )$ are defined with compact support, $\xi \in [0,1]$, which also applies to the definition of the boundary geometry via the complex $z'(\xi )$, the correction terms of Eq. (22) are to be evaluated at $\xi _s=a+bi\notin [0,1]$. This is not an inconsistency, as with these corrections, also considering the correction term of Eq. (18), we are dealing with the problem’s mathematics—not its mechanical simulation. Any other treatment (variable transformation, series expansion, interval subdivision, increase in the number of quadrature points, etc.) is just an unnecessary approximation—which may be both computationally intensive and uncontrollably wrong.

What really matters is that in the end correct mathematics and mechanics are not in contradiction [14].

4 Complex-variable expressions for elasticity problems

4.1 Basic CBEM equation for the 2D elasticity problem

In complex-variable, 2D plane-strain elasticity, it is suggested in [6] after some literature survey and a thorough development to rework the matrices of Eq. (13) as

(24)

(25)

also using $n=-iz'/|J| \Leftrightarrow {\bar{n}}=i{\bar{z}}'/|J|$ for the unit normal, and considering $\textrm{d}\Gamma = |J| \textrm{d}\xi$.

In the above arrays, the rows refer to the source, complex point force $p^*_s$ = $(p^*_x+i\ p^*_y)|_{(at\ s)}$ and its conjugate ${\bar{p}}^*_s$ = $(p^*_x-i\ p^*_y)|_{( at\ s)}$. The first columns stand for either node n or locus $\ell$ on a boundary segment, to which either complex displacements $d_n$ = $(d_x+i\ d_y)|_{(at\ n)}$ or tractions $t_\ell$ = $(t_x+i\ t_y)|_{(at\ \ell )}$ are attached. The second columns give their conjugates.

Observe that, in a code implementation, we only need to evaluate the first rows of the above matrices [6].

As for the potential problem, we develop Eqs. (24) and (25) for evaluations in principle using Gauss–Legendre quadrature (with eventual approximations indicated by the symbol $\simeq$) and then eventually accruing mathematically exact corrections conditioned by three logical constants $< no\_sing,\ sing,\ quasi\_sing>$:

$$\begin{aligned} G_{s\ell }\simeq \textbf{G}_{G\!L}+\left\{ \!\! \begin{array}{ll} \{\ \} &{}no\_sing \\ -\dfrac{(3\!-\!4\nu ){\left| J \right| }_{(\text {at }\ell \text {)}}}{8\pi G(1\!-\!\nu )}C_{Gr}{} \textbf{I} &{}sing \\ \dfrac{{\left| J \right| }_{(\text {at }\ell \text {)}}}{16\pi G(1-\nu )}\left[ \begin{matrix} - C_{Gc}^{\Re } &{} {\bar{G}}_1 \\ G_1 &{} -C_{Gc}^{\Re }\\ \end{matrix} \right]&quasi\_sing\end{array} \right. \end{aligned}$$

(26)

$$\begin{aligned} H_{sn}\simeq \textbf{H}_{G\!L}+ \left\{ \begin{array}{ll} \{\ \} &{}no\_sing \\ \textbf{H}_{(f\!p)}+\textbf{H}_{disc} &{}sing \\ \dfrac{i}{8\pi (1-\nu )}\left[ \begin{matrix} H_1 &{} -{\bar{H}}_2 \\ H_2 &{} -{\bar{H}}_1 \end{matrix} \right]&quasi\_sing \end{array} \right. \end{aligned}$$

(27)

where $\textbf{I}$ is the identity matrix of order two. In the code implementation, the local $2\times 2$ arrays $G_{s\ell }$ and $H_{sn}$ above are adequately mapped onto the global numberings $s,n,\ell$.

4.1.1 Correction terms for matrix $\textbf{G}$

The terms $C_{Gr}$ and $C_{Gc}^{\Re }=(3--4\nu )(C_G+{\bar{C}}_G)$ of Eq. (26) are outlined in Appendix B.2 of [6] and similarly used as in Eq. (18), for potential problems. (The notation $C_{Gc}^{\Re }$ seems to be a slight writing improvement, as compared with Eq. (19) of [6].) Moreover, in Eq. (26)

$$\begin{aligned} G_1= \left. \dfrac{{{\bar{z}}}N^{o_e}_\ell }{z'}C_1 \right| _{\xi _s} \end{aligned}$$

(28)

for $C_1$ given in Eq. (19). Observe that $G_1=0$ for a real quasi-singularity.

4.1.2 Correction terms for the singular integral part of matrix $\textbf{H}$

In the case of an actual singularity (sing) of Eq. (27), the finite part $\textbf{H}_{f\!p}\equiv \textbf{H}_{G\!L}+\textbf{H}_{(f\!p)}$ has the interval normalization correction

$$\begin{aligned} \textbf{H}_{(f\!p)} = \left\{ \! \begin{array}{cl} \pm \dfrac{(1\!-\!2\nu )i}{4\pi (1\!-\!\nu )}\left( \ln |J|_{\xi =a}-\sum \limits _{i=1}^{n_g}{\dfrac{h_i}{\xi _i}} \right) \left[ \begin{matrix} 1 &{} 0 \\ 0 &{} -1 \\ \end{matrix} \right] &{} a=0\ \textrm{or}\ 1 \\ \dfrac{(1\!-\!2\nu )i}{4\pi (1\!-\!\nu )} \left( \ln \dfrac{1\!-\!a}{a}-\sum \limits _{i=1}^{n_g}{\dfrac{h_i}{\xi _i\!-\!a}} \right) \left[ \begin{matrix} 1 &{} \!0 \\ 0 &{} \!-1 \end{matrix} \right]&a \in (0,1) \end{array} \right. \end{aligned}$$

(29)

as given in Equations (C.5) and (C.4) of [6]. The discontinuous—also called jump—term is

$$\begin{aligned} \textbf{H}_{disc} = \left( 1\!-\! \dfrac{\theta ^+-\theta ^-}{2\pi }\right) \textbf{I}+\dfrac{i(z'+{\bar{z}}')}{8\pi (1\!-\!\nu )|J|^2}\left[ \begin{matrix} 0 &{} \!z' \\ -{\bar{z}}' &{} \!0 \\ \end{matrix} \right] _{\theta ^-}^{\theta ^+} +\frac{i(1\!-\!2\nu )}{4\pi \left( 1\!-\!\nu \right) }\left[ \begin{matrix}1&{}0\\ 0&{}-1\end{matrix}\right] \ln \frac{{\epsilon ^{+}}}{{\epsilon ^{-}}} \end{aligned}$$

(30)

according to Appendix A.5 of [6] and considering Equation (A.28) for a general path around the singularity point, as illustrated in Fig. 3. Compare the latter equation with the results in the second row of Eq. (17) for the potential problem—as well to Equations (25) and (26) of [4] for the real-variable outline.

As remarked for the potential problem, evaluating the angle difference in the first term on the right-hand side of Eq. (30) is a straightforward procedure [6].

The term involving $\epsilon ^+/\epsilon ^-$ on the right-hand side of the above equation is void only if the finite part $\textbf{H}_{f\!p}\equiv \textbf{H}_{G\!L}+\textbf{H}_{(f\!p)}$ is evaluated in the sense of a Cauchy principal value, which shows that the integration path around a singularity, as illustrated in Fig. 3 is almost—but not completely—general for the elasticity problem. Such a strict concept is not necessary for the potential problem, Eq. (17), which also does not require the special term brought in Eq. (29) for the interval normalization—before applying the Gauss–Legendre quadrature in the interval $\xi \in [0,1]$ of the finite-part integral.

We can never overestimate the geometric meaning of the evaluations carried out for the matrix H in the second row of Eq. (27), which holds for the evaluations of Eq. (17). We illustrate on the top of Fig. 4—as well as in Fig. 2—that the source point is collocated in the domain $\Omega$ but infinitesimally close to the boundary $\Gamma$, according to the terms of Eq. (25) (there is the Kronecker delta $\delta _{sn}$). This is geometrically the same as illustrated on the bottom left of the figure, with the source point becoming excluded from the domain of interest. No matter the geometric interpretation, the singular integral is ultimately evaluated as the sum of finite parts (whether or not in the strict sense of a Cauchy principal value) plus a discontinuous term, as given on the right. This interpretation holds whether real or complex variables are used, as reproduced from [1, 4, 6]. In [1], the illustration is applied also to a simple truss element, Appendix C. This hopefully contributes to demystifying the application of a singular (although for the truss element not going to infinity) fundamental solution to deal with a problem analytically (recall the consistency remarks in Sect. 2.4).

Fig. 4

Reproduction from [1, 4, 6] that shows, for a 2D problem, the scheme for a source point (on the top) in the domain $\Omega$—but in the limit of tending to $\Gamma$, that may be interpreted as having been excluded from the domain of interest (bottom left), also corresponding to the computational-ready pattern on the right of a finite part and a discontinuous term

4.1.3 Correction terms for the quasi-singular integral of matrix $\textbf{H}$

Whether real or complex, the quasi-singularity case ($quasi\_sing$) of Eq. (27) requires that corrections be accrued according to Appendices C.3 and C.4 of [6]:

$$\begin{aligned} H_1=\left. (3-4\nu )N^{o_e}_n C_1 \right| _{\xi _s} -\left. N^{o_e}_n C_1\right| _{{\bar{\xi }}_s},\quad H_2= \left. \dfrac{{\bar{z}}}{z'}\left( N^{o_e}_nC_2 + {N'}^{o_e}_nC_1 \right) \right| _{\xi _s} \end{aligned}$$

(31)

Observe that $H_1$ is evaluated at both $\xi _s$ and ${\bar{\xi }}_s$, and $H_2$ turns out void for a real singularity.

Section 3.1.3 of [6] outlines how the real- and complex-variable expressions of the matrices G and H are related.

4.2 Results at internal points

4.2.1 Somigliana’s complex-variable expression for displacements

According to the previous developments and as proceeded for the potential problem, the Somigliana’s identity for complex displacements in the domain is

$$\begin{aligned} \left\{ \begin{matrix} u \\ {\bar{u}} \end{matrix} \right\} _{\!s}&=\left\{ \begin{matrix} u^p \\ {\bar{u}}^p \end{matrix} \right\} _{\!s} +\left( {{\textbf{G}}_{G\!L}} + \dfrac{{\left| J \right| }_{(\text {at }\ell )}}{16\pi G(1\!-\!\nu )}\left[ \begin{matrix} -(3\!-\!4\nu )\, C_{Gc} &{} {\bar{G}}_1 \\ G_1 &{} \!-(3\!-\!4\nu )\,C_{Gc} \\ \end{matrix} \right] \right) \left\{ \begin{matrix} (t\!-\!t^p)_{ad} \\ ({\bar{t}}\!-\!{\bar{t}}^p)_{ad} \end{matrix} \right\} _{\!\ell } \nonumber \\&\quad -\left( {{\textbf{H}}_{G\!L}} +\dfrac{i}{8\pi (1-\nu )}\left[ \begin{matrix} H_1 &{} - {\bar{H}}_2 \\ H_2 &{} -{\bar{H}}_1 \end{matrix} \right] \right) \left\{ \begin{matrix} d-d^p \\ {\bar{d}}-{\bar{d}}^p \end{matrix} \right\} _n \end{aligned}$$

(32)

as already laid down in Sect. 4.1. Of course, we only need to evaluate the upper part, for $u_s=(u_x+i u_y)_s$.

4.2.2 Somigliana’s complex-variable expression for stresses

The real-variable formula for stress results in the domain, as conveniently expressed in [1], was adapted in Appendix A of [6] for the stress combination classically proposed in the literature [51]. Our only attempt was to arrive at simple expressions—and the outcome was proven successful:

(33)

The correction terms $G^q$ and $H^q$ are the same ones for potential flux results at internal points, Eq. (22). Additional corrections are, according to Equation (C.21) of [6],

$$\begin{aligned}&G^{\sigma }= \left. \left( \frac{{\bar{z}}'C_1\!+\!{\bar{z}}C_2}{{z'}^2}N_{\ell }^{o_e} + \frac{z'{N'}_{\ell }^{o_e}\!-\!z''N_{\ell }^{o_e}}{{z'}^3}{\bar{z}}C_1 \right) \right| _{\xi _s} \end{aligned}$$

(34)

$$\begin{aligned}&H^{\sigma }= \left( \dfrac{z''{\bar{z}}\!-\!z'{\bar{z}}'}{{z'}^3}\left( {N'}_n^{o_e}C_1 \!+\!N_n^{o_e}C_2\right) -\dfrac{{\bar{z}}}{{z'}^2}\left( C_1{N''}_n^{o_e}\!+\!2C_2{N'}_n^{o_e}\!+\!2C_3N_n^{o_e}\right) \biggr ) \right| _{\xi _s} \end{aligned}$$

(35)

with $C_1$, $C_{2}$ and $C_{3}$ given in Eqs. (19) and (23), as developed in Appendix C of [6].

5 Illustrative numerical applications

The following application to an infinite plate with a hole was prepared for presentation at a conference [52]. The second illustration is for a topologically extremely challenging problem, as proposed in [5], further elaborated in [6] and presently accrued by many conceptual assessments.

5.1 Application to an infinite plate with a circular hole

Figure 5 presents on the left the scheme of an infinite plate with a circular hole of unit radius $a=1$, as detailed next. The displacement and stress solutions for a uniform stress field ($\sigma _{xx}=1$, $\sigma _{yy}=\tau _{xy}=0$) at infinity are, in polar coordinates [53],

$$\begin{aligned}&{{u}_{r}}=\frac{1}{4G{{r}^{3}}}\left[ \cos 2\theta \left( 4(1-\nu ){{a}^{2}}{{r}^{2}}+{{r}^{4}}-{{a}^{4}} \right) +(1-2\nu ){{r}^{4}}+{{a}^{2}}{{r}^{2}} \right] \nonumber \\&{{u}_{\theta }}=\frac{1}{4G{{r}^{3}}}\sin 2\theta \left[ 4\nu {{a}^{2}}{{r}^{2}}-{{({{a}^{2}}+{{r}^{2}})}^{2}} \right] \end{aligned}$$

(36)

$$\begin{aligned} {{\sigma }_{rr}}&=\dfrac{1}{2}\left( 1-\dfrac{{{a}^{2}}}{{{r}^{2}}} \right) +\dfrac{1}{2}\left( 1-4\dfrac{{{a}^{2}}}{{{r}^{2}}}+3\dfrac{{{a}^{4}}}{{{r}^{4}}} \right) (2{{\cos }^{2}}\theta -1) \nonumber \\ {{\sigma }_{\theta \theta }}&=\dfrac{1}{2}\left( 1+\dfrac{{{a}^{2}}}{{{r}^{2}}} \right) -\frac{1}{2}\left( 1+3\dfrac{{{a}^{4}}}{{{r}^{4}}} \right) (2{{\cos }^{2}}\theta -1) \nonumber \\ {{\tau }_{r\theta }}&=\left( -1-2\dfrac{{{a}^{2}}}{{{r}^{2}}}+3\dfrac{{{a}^{4}}}{{{r}^{4}}} \right) \sin \theta \cos \theta \end{aligned}$$

(37)

It is worth noticing that these analytical results are valid for the set union $\Omega \cup \Gamma$. On the other hand, our numerical results, as evaluated in Sect. 4.2, are valid only at internal points, that is, in the open set $\Omega$, which excludes $\Gamma$, although we may get arbitrarily close to the boundary provided we have sufficient machine precision.

The maximum stress is $\sigma _{xx}(x=0,y=\pm a)={{\sigma }_{\theta \theta }}(r=a,\theta =\pm \pi /2)=3$, and the maximum $\sigma _{yy}$ stress is $\sigma _{yy}(x=\pm a,y=0)=-1$. On the right in the figure are the analytical stress results $(\sigma _{xx}, \ \sigma _{yy}, \ \tau _{xy})$ of Eq. (37) at the 18 internal points $5 \dots 10$, $15 \dots 20$, $25 \dots 30$ given on the left (lines just connecting points).

Fig. 5

Left: infinite plate with a circular hole of unit radius discretized with 40 equidistant nodes and 10 quartic elements, also indicating three series of 12 external and 18 internal points for stress evaluations. Right: analytical $(\sigma _{xx}, \ \sigma _{yy}, \ \tau _{xy})$ results evaluated at the 18 internal points [52]

The circular hole is discretized with 10 quartic elements and 40 equally spaced nodes, which are also equidistant from the center. On purpose, this discretization does not reflect the geometric polar symmetry (although all elements keep the same configuration in polar coordinates as we shift the angle $\theta$ by $\pi /5$), and we also do not take advantage of the double symmetry of expected results in our code implementation. Since this is an isoparametric—not isogeometric—formulation, the modeled surface is not smooth between elements: we measure for the left and right tangent angles at nodes 1, 5, 9, 13, 17, 21, 25, 29, 33, and 37 the value $(\theta ^+ - \theta ^-)/2\pi \approx 0.4999900076$, to be compared with 0.5. Then, numerical evaluations with relative accuracy errors smaller than about $10^{-6}$ are not to be expected, as a rule, and to be confirmed shortly. Since nodes 1 and 21 are affected by the angularity indicated above, results about them are expected to present the largest relative errors. The lack of polar symmetry leads to tangents at nodes 6, 16, 26, and 36 not exactly integer multiples of $\pi /4$. On the other hand, smoothness—and horizontal tangent—is preserved about nodes 11 and 31, where the problem’s stress concentration factor is to be measured.

We evaluate stress results at the indicated three series of 10 points, which are equally spaced from $0.6+10^{-10}$ through $1.5+10^{-10}$ distances from the center. Then, points 1 $\ldots$ 4, 11 $\ldots$ 14, and 21 $\ldots$ 24 are actually internal to the cavity, that is, external in relation to the open domain of interest. Points 5, 15, and 25 are inside the open domain but set just $10^{-10}$ distant from nodes 1, 31, and 36, respectively. Besides the geometry errors, we should expect round-off errors to occur for these extremely close points, as outlined next.

Eight Gauss–Legendre points per element are used for both real- and complex-variable evaluations, a total of 80 integration points. A precision of 25 digits is implemented in the Maple code (Maplesoft, a division of Waterloo Maple Inc., Waterloo, Ontario), which seems to be more than sufficient for the evaluation of the matrices G and H of Eq. (13). In fact, by comparing $|\textbf{H}{} \textbf{W}-\textbf{W}|$ with zero (as for a cavity), where W is the orthonormal matrix of rigid-body displacements (Definition 1 of [1], as outlined in Sect. 1.4), we obtain with both real- and complex-variable codes the global relative error of only $10^{-18}$. There is in principle no means of evaluating the precision errors related to the matrix G in the case of a cavity—we use zero rigid-body displacements, that is, $C_{ks}=0$ in Eq. (12). (We might have analyzed the complementary case of a finite domain with the same geometry of the cavity.) From the assessments for the numerical examples of Sect. 5.2, we estimate that the errors related to G are of about the same order of magnitude as the ones reported above for H.

We solve Eq. (13) for the displacement difference $(\textbf{d}-\textbf{d}^p)$ considering that $\textbf{t} = \textbf{0}$ and that there is a particular solution $(\textbf{d}^p,\textbf{t}^p)$ corresponding to the proposed far stress field $(\sigma _{xx}=1,\sigma _{yy}=\tau _{xy}=0)$. The stress results are evaluated according to Equations (39) of [4], for real variables, and (29) of [6], in terms of complex variables, here reproduced as Eq. (33). Although the simulated problem corresponds to an applied constant stress field, the analytical solution—Eq. (36)—is not a linear polynomial, to which Theorem 1 of [1] would be applicable within the adopted precision digits and numerical quadrature errors of the regular integrals involved. Then, our only precision estimate is the one related to the spectral norm of the matrix H, as checked above, and the remarks regarding the matrix G. The best we can do is to trust the above precision result ($10^{-18}$) for H and assert that accuracy errors come from geometry approximations (arc segments as a succession of quartic polynomials), displacement approximations of Eq. (36) also as a succession of quartic polynomials, and eventual round-off errors.

Figure 6 shows errors of the numerical stress results $(\sigma _{xx},\sigma _{yy},\tau _{xy})$ at the 30 external and internal points described above—as compared with the analytical values of Eq. (37). We display absolute, not relative, errors, since several zero or very small analytical values are involved. Dash, blue lines are for the real-variable evaluations of Equations (39) of [4], while solid, black lines refer to the complex-variable values from Eq. (33).

A first accuracy estimate is for results at the cavity points 1 $\ldots$ 4, 11 $\ldots$ 14 and 21 $\ldots$ 24 (then external to the domain of interest), which should be void for the solution to be exact. However, as the cavity is not exactly a circle, the actual exact, reference, solution is by far more involved than the one of Eq. (36)—and just ten quartic elements turn out to constitute a relatively coarse mesh: absolute errors—in general smaller than $10^{-6}$—are solely attributable to the geometry and displacement approximations, not to evaluation precision, which has been checked before ($\approx 10^{-18}$). The basic conclusion related to the geometry representation errors still holds: our accuracy threshold (independently of the problem’s actual solution) is about $10^{-6}$ (we should not expect smaller errors than that).

Real- and complex-variable simulations lead to approximately the same accuracy of results, in general. However, the real-variable round-off errors for the critical, close point 5 become excessively large, while just large at points 15 and 25: they are at the very small source-to-boundary distance $10^{-10}$, as described above. The largest complex variable, absolute errors of $(\sigma _{xx},\sigma _{yy},\tau _{xy})$ are at point 5, close to node 1, where there is an angularity: their magnitudes are $(2.19\times 10^{-4},4.92\times 10^{-4},2.08\times 10^{-4})$, for numerical values to be compared with the target ones $(0,-1,0)$. These errors are $(6.81\times 10^{-6},1.77\times 10^{-6},3.78\times 10^{-21})$ for point 15, which is close to node 31 on a smooth surface: the corresponding target, analytical values are (3, 0, 0). The stress results at the close point 25—target values $(0.5,0.5,-0.5)$—are evaluated with errors $(1.35\times 10^{-5},1.25\times 10^{-7},3.87\times 10^{-6})$.

Fig. 6

Absolute errors in the numerical evaluation of stress results $\sigma _{xx}$, $\sigma _{yy}$, $\tau _{xy}$ at 30 internal/external points for the infinite plate with a hole of Fig. 5, in terms of complex (solid, black lines) and real variables (dash, blue lines). (Color figure online)

The most important lesson to be drawn from the above developments concerns not the displayed numbers per se: it is how to carry out methodologically and objectively an investigation about how large is the precision error (how reliable are our mathematical evaluations) and how large is the accuracy error in a numerical modeling—to make sure that we have a better precision than the achievable accuracy.

5.2 Application to a topologically extremely challenging problem

5.2.1 Problem description

Figure 7 represents a two-dimensional domain (about 25 units across) with some challenging topological features, to be subjected to a series of elastic fields, as described in [6], which is the elaboration of a numerical model proposed in [5] by including the indicated curved, kinked crack. Readers are referred to these papers for a detailed description of the problem. On the other hand, the present text is more than a summarizing review, as some additional conceptual features are accrued.

The geometric data for the generation of this figure are given in Table 1 of [6] and reproduced here also as Table 1, for completeness. There are a total of 16 boundary patches, whose key nodes are given in the first column, numbered $1,\ldots ,93$, with corresponding (x, y) Cartesian coordinates in the next column. Nodes are generated along the curved boundary patches (such as nodes $2,\ldots ,16$, for the first patch) according to a local function (Shape)—with respect to the chord drawn between the key nodes—of the parametric variable $\xi \in [0,1]$ given in the third column and with their relative distances increasing (or decreasing) according to the geometric factor shown in the fourth column. If the shape function is entered as a constant, it is actually the radius of a circle’s arc for the generated patch, if geometrically feasible, and is otherwise just a straight line segment. The last key node of a closed subboundary (nodes 53, 69, and 93 for three subboundaries in the Table) is actually a dummy number, as it has the same coordinates as the first node (the curved, kinked crack is just a collapsed cavity). This generating Table would serve for an isogeometric formulation, which is not the present case [17]. This table has actually been generated for $o_e=2$ from a more primitive data set with a multiplication factor, $f_{ref} = 2$, for the relative number of nodes along a boundary patch (this is important for an h-convergence investigation, as more or less refined meshes are generated from the primitive data by just changing $f_{ref}$, while changing $o_e$ provides a p-refinement). We use in the numerical analysis the same primitive data and $o_e=4$, which doubles the total number of nodes, for 46 quartic elements, for instance.

Table 1 Key nodes, boundary patch shapes and distance amplification factor between nodes for the geometry generation of Fig. 7, according to [6]

It is worth remarking that the cusp at node 1 has an internal angle of about $10^{-8}$ rad, the reentrancy angle at node 17 is only $10^{-13}$ rad wide, when simulated with 46 quadratic elements, and the strip of material between the cavity and the external boundary is only about $10^{-4}$ unities wide. As given in Table 5 of [5] and, more comprehensively, in Table 2 of [6], the small angles above are by far larger for more refined meshes that use the same primitive boundary geometry (we are dealing with an isoparametric formulation, for the sinus-shaped and circular boundary geometries of Fig. 7 represented by polynomial segments). As a matter of fact, the small angle of about $10^{-13}$ at node 17 becomes negative for the same mesh with 46 quadratic elements but “just” double precision (then not precise enough) for the numerical processing of this topologically too challenging problem—which means boundary interpenetration is reproduced. In order to avoid that—while still being able to detect eventual round-off errors, we presently carry out evaluations using 25 and 50 digits of precision in our Maple code.

This elastic body is subjected to two rigid-body translations and a set of four linear, quadratic, cubic, quartic and quintic polynomial fields, thus a total of 22 fundamental (that is, homogeneous) solutions of the elastostatics problem for homogeneous, isotropic material ($G=80{,}000$, $\nu =0.2$), as given in Equations (15–19) of [5], in terms of real variables, and very compactly on the right in Equation (34) of [6], here reproduced:

$$\begin{aligned} \left[ \begin{matrix} 1\pm i &{} (3\!-\!4\nu )(z\pm {\bar{z}})\pm iz &{} (3\!-\!4\nu )(z^2\pm {\bar{z}}^2)\pm 2z{\bar{z}}\\ (3\!-\!4\nu )(z^3\pm {\bar{z}}^3)\pm 3z{\bar{z}}^2 &{} (3\!-\!4\nu )(z^4\pm {\bar{z}}^4)\pm 4z{\bar{z}}^3&{} (3\!-\!4\nu )(z^5\pm {\bar{z}}^5)\pm 5z{\bar{z}}^4 \end{matrix} \right] \end{aligned}$$

(38)

The domain of Fig. 7 is cut out from the open, infinite domain submitted to the proposed polynomial fields, with the corresponding displacement and traction fields applied to the boundary, which is a generalization of the patch tests introduced by Irons [43]. Applying closed-form analytical fields enables the numerical assessment of very complicated topologies, such as the present one, for which an exact solution is known irrespective of cut-out geometry (stress results are bounded at the simulated crack tips).

The indicated crosses in Fig. 7 are a total of 41—in part internal and in part external—equally spaced points $(x_{int},y_{int})$ of coordinates

$$\begin{aligned} (x_{int},y_{int})_{i+1}=(x,y)_{51}+\left[ (x,y)_{58}-(x,y)_{51}\right] (0.0001+i/40),\quad i=0,\ldots ,40 \end{aligned}$$

(39)

thus generated from boundary nodes $(x,y)_{51}$ and $(x,y)_{58}$ of Fig. 7 (which are on its turn obtained from Table 1), at which stress results are to be numerically evaluated for the applied stress field.

Some of these points are extremely close to the boundary, as described in [5, 6] and to be investigated next. Most important, we generate between internal point 30 and the crack-tip node 69, which are visually indistinguishable from each other in the figure, a series of 10 points that approach node 69 at geometrically decreasing distances, as indicated in the first row of Table 2, which is a reproduction from [6]. A similar series of 10 very close points to node 17 is also generated, with the distances indicated in the second row of this table. If we consider all geometric data given in meter, the smallest distances are actually about one thousandth of a typical proton size. As remarked in [6], continuum mechanics is here no longer applicable but so is mathematics.

Fig. 7

Two-dimensional elastic body with some very challenging topological features, to be submitted to a set of 22 elastic fields [6]. The indicated small angles are for a mesh discretization with 46 quadratic elements. This figure also corresponds to a discretization with 23 quartic elements, one of them is depicted

Table 2 Reproduction from [6] for internal points numbered 42–51 and 52–61, which are very close to nodes 69 and 17 of Fig. 7, respectively

5.2.2 Numerical simulations

Since this problem is the same one of [5] but with the inclusion of the indicated curved, kinked crack, we had to run it again in terms of real variables, to compare the results at internal points using Equations (42) of [4] with the ones in terms of complex variable obtained in [6] and given in Eq. (33). Papers [5, 6] also have complete problem formulation and numerical assessments for potential problems.

As schematized in Table 3, we run six different numerical models of the problem proposed above, for quadratic or quartic ($o_e=2\ \textrm{or}\ 4$) element orders, $n_g = 4\ \textrm{or}\ 8$ Gauss–Legendre quadrature abscissas along a boundary element, and precision digits $D= 25\ \textrm{or}\ 50$ for the numerical evaluations in the implemented Maple codes. Figure 7 corresponds to the simulations characterized as $46\_2\ldots$ (three cases), that is, 46 quadratic elements, whose (isoparametric) geometry is visually indistinguishable from the simulation $23\_4\_50\_8$, for 23 quartic elements run using $D=50$ digits of precision and $n_g=8$ Gauss–Legendre abscissas along a boundary element. The latter mesh simulation implies very large elements, as the one element depicted in Fig. 7. As given in this table, we also have two meshes with double the number of indicated nodes in Fig. 7: $92\_2\_50\_4$ and $46\_4\_50\_8$, for quadratic and quartic elements.

The data in parentheses in this table indicate for each numerical simulation the respective total numbers of displacement nodes, traction loci, and quadrature abscissas. The first number is then the total number $n^d$ (see Sect. 1.3) of rows we need in assembling matrices H and G in terms of complex variable—since, as mentioned before, we only evaluate the upper parts of the indicated expressions in Eqs. (24) and (25). The second number, for the total number $n^t$ of traction loci, is half the number of columns of the matrix G, in the present implementation using $N_n^{o_e}=N_\ell ^{o_e}$, as indicated in Sect. 1.4. With the third number of total quadrature abscissas and the number of precision digits D, we have an estimate of the involved computational costs. We do not present such cost comparisons, but the complex-variable code is by far smaller and simpler, and also runs by far faster than the code in terms of real variables (and is less likely to produce round-off errors, as we show for the evaluation of stress results at points that are very close to the boundary).

Table 3 Summary of six numerical examples for elasticity run in [6] for the complex-variable formulation and presently also in terms of real variables, for the problem of Fig. 7

5.2.3 Topology consistency, precision and accuracy of matrices $\textbf{H}$ and $\textbf{G}$ in the complex-variable implementation

We assess in this section topology consistency, precision, and accuracy of the matrices $\textbf{H}$ and $\textbf{G}$ for the elasticity problem only in terms of complex variables, according to Sect. 4.1, as we should not expect tangible numerical differences in terms of real variables. We only need to consider the first rows of terms of matrices $\textbf{H}$ and $\textbf{G}$ in Eqs. (24) and (25).

We first obtain the evaluation precision of $\textbf{H}$ using the array $\textbf{W}$ of rigid-body displacements, according to Definition 1 of [1] and given in Equation (A.12) of [6]. Observe once more that all numerical evaluations are precise within Gauss–Legendre quadrature errors of the regular parts of all integrals needed in our problems, as the introduced corrections are exact within machine precision (no round-off errors detected). This is given according to the norm

$$\begin{aligned} \left| \textbf{HW} \right| =\frac{1}{3}\sum \limits _{k=1}^{3}\left| \sqrt{{\sum \limits _{s=1}^{{{n}^d}}{{{\left( \sum \limits _{n=1}^{2{{n}^d}}{{{H}_{sn}}{{W}_{nk}}} \right) }^{2}}}}\bigg /{\sum \limits _{s=1}^{{{n}^d}}{{{\left( \sum \limits _{n=1}^{2{{n}^d}}{\left| {{H}_{sn}}{{W}_{nk}} \right| } \right) }^{2}}}}}\right| \end{aligned}$$

(40)

for a problem with $n^d$ nodes and $k=1,2,3$ rigid-body cases of elasticity, which are then averaged to evaluate as a single result.

We should ideally have $|\textbf{HW}|=0$ for a finite elastic body. Then, this condition also checks the problem’s topology consistency, since it cannot hold if there is some boundary interpenetration or if it is not closed.

The matrices $\textbf{H}$ and $\textbf{G}$ are checked for displacements $\textbf{d}_k$ and traction parameters $\textbf{t}_k$ of the linear, quadratic, cubic, quartic and quintic analytical solutions (precision for $k=3,4,5,6$ linear displacement fields and then satisfying Theorem 1 of [1], and accuracy for $k=7 \dots n_{as}=22$ higher-order solutions):

$$\begin{aligned} \left| \textbf{Hd}\!-\!\textbf{Gt} \right| _p\leftarrow \left| \!\sqrt{{\sum \limits _{s=1}^{{{n}^d}}{{{\left( \sum \limits _{\ell =1}^{2n^t}{{{G}_{s\ell }}{{t}_{\ell k}}}\!-\!\sum \limits _{n=1}^{2{{n}^d}}{{{H}_{sn}}{{d}_{nk}}} \right) }^{2}}}}\bigg /{\sum \limits _{s=1}^{{{n}^d}}{{{\left( \sum \limits _{n=1}^{2{{n}^d}}{{{H}_{sn}}{{d}_{nk}}} \right) }^{2}}}}\;}\right| \end{aligned}$$

(41)

which are then averaged as five solution groups $\left| \textbf{Hd}\!-\!\textbf{Gt} \right| _p$, for the polynomials in Eq. (38) of orders $p=1,\ldots ,5$.

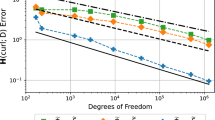
The logarithms of the error norms of Eqs. (40) and (41) are presented in the vertical axis of Fig. 8 for the six numerical examples of Table 3. “Rigid body” in the horizontal axis stands for the norm result of Eq. (40): topology and precision check. The label “1st” for the four-set of linear displacements ($p=1$ above) corresponds to checking convergence Theorem 1 of [1]: also topology and precision check. Labels “2nd”... “5th” refer to the averaged norms of Eq. (41) for the remaining four-set of test solutions in Eq. (38): accuracy checks.

There is an obvious remark concerning these results, namely that they all apply to the same matrices H and G, just multiplied by different boundary displacement and traction parameters. The following overview of the numerical results (which is not given in [6]) is paramount to appreciate the strongness of the present developments.

Topology consistency and precision assessments We draw in Fig. 8 a green, dashed, rectangle to enclose error results for topology and precision, which are related to the convergence Theorem 1 and are therefore independent of mesh discretization. The results for the six numerical simulations come out grouped as three cases intrinsically related to the Gauss–Legendre quadrature capacity, thus expressing the precision of evaluating the regular part of the integrals, as the singular and quasi-singular parts are all evaluated exactly.

Fig. 8

Error norms $|\textbf{HW}|$, Eq. (40), for rigid-body displacements, and $|\textbf{G}{} \textbf{t}-\textbf{Hd}|_p$, Eq. (41), for the sets of polynomial displacement fields of order $p=1 \ldots 5$, Eq. (38). The linear test fields also provide the means of checking the convergence theorem of [1]

The models $46\_2\_50\_8$ and $46\_4\_50\_8$, for quadratic and quartic elements, correspond to implementations with the same total of $n^{el}=46$ elements and have required $n_g=8$ Gauss–Legendre abscissas per element, with a total demand of $n^{el}\times n_g= 368$ quadrature abscissas. They both present about 12 digits of precision for the error norms $|\textbf{HW}|$ and $\left| \textbf{Hd}\!-\!\textbf{Gt} \right| _1$ (recall that 8 abscissas integrate exactly a polynomial of order 15). The results for the quartic element are slightly less accurate, as the integrals are more involved, since they comprehend a total of 184 nodes, double the number as for the model $46\_2\_50\_8$. Moreover, the error results for the norm $\left| \textbf{Hd}\!-\!\textbf{Gt} \right| _1$ are slightly larger, as more complex data are handled.

The results for the model $23\_4\_50\_8$, for $n_g=8$, which has the large quartic element depicted in Fig. 7 (just compare it with the doubly refined model $46\_4\_50\_8$) have errors of about $10^{-8}$, which are comparable in Fig. 8 with the results of $92\_2\_50\_4$—incredibly precise for just $n_g=4$ but with the large total of $n^{el}\times n_g=368$ quadrature abscissas.

The third group of results, for the models $46\_2\_25\_4$ and $46\_2\_50\_4$, show the just expected highest precision achievable for $n_g=4$ and—most important in the case—that the machine precision $D=25$ does not lead to round-off errors (see, however, Sect. 5.2.4).

Since the error norm $|\textbf{HW}|$ has not blown up, these models are topologically consistent—and round-off errors are evidently under control. We may sum up that precision is conditioned by the value of $n_g$ as well as by the total number $n^{el}\times n_g$ of quadrature abscissas along the problem’s whole boundary.

Accuracy assessments Once the models’ topology consistency and achievable precision are checked, we may proceed with a very simple h-p-refinement (and $n_g$) study for applications to higher-order displacement fields (recall that h stands for element size and p for polynomial order in the finite element literature). A blue, dash-dot, rectangle is drawn in Fig. 8 to enclose the cases related to the error norm of Eq. (41) for $p=2,3,4,5$.

We check that a model with quadratic elements is unnecessarily too precise for $n_g=8$ since its accuracy is indistinguishably the same as when using $n_g=4$. In terms of an h-refinement, duplicating the number of quadratic elements (from $n^{el}=46$ to $n^{el}=92$) leads to an accuracy increase of about one digit.

The use of $n_g=8$ for a quartic element is recommended, as it has the length of two quadratic elements (we have not tested $n_g=6$, which may not be impracticable). This turns out to be more than a sufficient number of quadrature abscissas, as the achieved accuracy—even for the simplest case of quadratic displacement fields (label “2nd” in the graph)—is several orders of magnitude lower than the achievable precision, as discussed in the latter Section. We see that an accuracy increase of about two orders of magnitude is obtained, in general, when we double the number of quartic elements (from $n^{el}=23$ to $n^{el}=46$, in this case).

Concerning a p-refinement, the results show—at least for the present numerical example—over one order of magnitude of accuracy increase when changing from quadratic to quartic elements (compare the models $23\_4\_50\_8$ with $46\_2\_50\_4$, and $46\_4\_50\_8$ with $92\_2\_50\_4$) for the same total number of nodes $n^d=o_e\times n^{el}$ and quadrature abscissas $n^{el}\times n_g$¹⁹.

According to [6], such a high number of precision digits is not needed in a practical implementation, as an accuracy of about four digits for the highest-order test polynomials is in reach for maybe just double precision digits and four quadrature points per quadratic element. However, this is not our present subject of interest.

5.2.4 Some comparative precision and accuracy assessments of stress results for real- and complex-variable implementations

We show in the following the stress error results at 61 internal/external points of Fig. 7 for just the numerical models $46\_2\_25\_4$ and $23\_4\_50\_8$ taken from [6], to compare the real- and complex-variable approaches directly—while considering the precision and accuracy issues already addressed in the previous Section. Displacement results are not shown (see, however, [6]), as evaluation errors are larger and round-off errors more critical for stresses. As given in Table 3, these models represent the coarsest meshes—for which the largest errors are expected to occur—and we choose $D=25$ evaluation digits in the first case to better explore eventual round-off errors. (It is worth repeating that the number of precision digits smaller than 20 would render the model $46\_2\_25\_4$ inconsistent, for interpenetration of the boundary faces adjacent to node 17.)

Stress results are obtained for the total of 61 domain points indicated in the horizontal axes of Figs. 9 and 10, for stress evaluations in terms of real (top) and complex variables (bottom), according to the chosen numerical models. There are 41 points marked as “$+$” in Fig. 7 (points 2... 8 and 40 are external), and we also consider the very close points numbered 42 through 61 referred to in Table 2. Vertical dash-dot lines mark the closest points 42 and 52.

We consider the Frobenius norm $\Vert \ \Vert$ at any of the $1,\dots ,61$ domain points [6]:

$$\begin{aligned} \epsilon _{stress}\leftarrow \left\{ \begin{array}{l} {\Vert {{\varvec{\sigma }}}_n-{{\varvec{\sigma }}}_a \Vert }/\max (1, \Vert {{\varvec{\sigma }}}_a\Vert ),\quad \text {for an internal point} \\ {\Vert {{\varvec{\sigma }}}_n \Vert }/\max (1, \Vert {{\varvec{\sigma }}}_a\Vert ),\quad \text {for an external point} \end{array} \right. \end{aligned}$$

(42)

where ${{\varvec{\sigma }}}_n$ is either the vector with the complex stress combination of Eq. (33) or the real vector $<\sigma _{xx}\ \sigma _{yy}\ \sigma _{xy}>^\textrm{T}$ [5] obtained numerically, and $\max \Vert {{\varvec{\sigma }}}_a\Vert$ is the maximum norm of the corresponding stress vector obtained analytically. We use the notation “$\leftarrow$” to indicate that $\epsilon _{stress}$ is the averaged results for each set of polynomial displacement fields in Eq. (38), as given in the vertical axes of Figs. 9 and 10 in log scale. These averaged results are connected by line segments: constant (“0th”, red, dot), linear (“1st”, red, solid), quadratic (“2nd”, blue, dash), cubic (“3rd”, blue, long dash), quartic (“4th”, black, dash-space), and quintic (“5th”, black, dash-dot).

According to Theorem 1 of [1] and pointed out above [5, 6], the numerical evaluations for constant and linear solutions correspond to analytical solutions of the problem—although within precision digits, number of Gauss–Legendre quadrature abscissas and eventual round-off errors. Then, these solutions provide the means to estimate the precision threshold of a numerical simulation for the demanded kind of results. As indicated, the error results for constant and linear displacement fields are multiplied by 10 in Fig. 9 and by $10^3$ in Fig. 10 to accommodate a better error resolution in the plots. In both figures, the top graphs are for evaluations using real variables and are to compare with the bottom results for the complex-variable formulation.

The real- and complex-variable results in each figure are comparable in terms of precision (results for 0th and 1st) and accuracy (for higher displacement fields), except for points that are too close to the boundary, as round-off errors take place and may become completely out of limits. We see in the top plot of Fig. 9 that real-variable stress results are reliable only for distances larger than about $10^{-7}$ (which, for unities in m, may be considered small enough), whereas for the complex-variable evaluations we obtain reliable results for subnanometer distances about $10^{-10}$. And that for “only” 25 digits of precision! It is worth remarking that complex-variable displacement results are reliably obtained for all points of Table 2, as shown in [6] but not here. The graphs of both Figs. 9 and 10 show that accuracy errors are always larger than the precision errors (Theorem 1) and in general (but not as a strict rule) increase as we consider higher nonlinear displacement fields.

Figure 10 presents—for about the same computational cost (evidently, computational cost increases when using 50 digits of precision) as for the previous evaluations—results that are several orders of magnitude more precise and one order of magnitude more accurate. This is related to the p-refinement from quadratic to quartic elements, as outlined above [5, 6]. Reliable results for the real-variable evaluations are achieved for distances that are orders of magnitude smaller than before, and this is to be credited to a large number of precision digits. Results for internal points in the neighborhood of the (locally badly discretized) reentrancy tend to be completely out of limits, in terms of real variables, and so do results for the external point 40, which are also related to the poor local mesh discretization. In the complex-variable implementation, as shown at the bottom of Fig. 10, results for constant and linear displacement fields—to check Theorem 1 of [1]—pass the test brilliantly. Then, as it should be, overall accuracy results are reliable for distances up to $10^{-18}$. Observe that here, too, results for the external point 40 are worse. Also, results at points 42 through 51 (piece-wise horizontal plots) are by orders of magnitude more accurate than at points 52 through 61, since the mesh adjacent to node 17 is coarser.

Fig. 9

Errors, according to Eq. (42), in the stress evaluation at 61 internal and external points of Fig. 7, generated for six groups of elasticity test fields for the mesh configuration $46\_2\_25\_4$, in terms of real (top) and complex (bottom) variables. The bottom plot is a reproduction from [6]

Fig. 10

Errors, according to Eq. (42), in the stress evaluation at 61 internal and external points of Fig. 7, generated for six groups of elasticity test fields for the mesh configuration $23\_4\_50\_8$, in terms of real (top) and complex (bottom) variables. The bottom plot is a reproduction from [6]

6 Concluding remarks

This paper’s brief outline and the simple, comparative numerical assessments for 2D elasticity show that the paradigm-shifting developments proposed in [1, 4, 5] could be further improved—in terms of code simplicity, computational cost, and overall robustness—by resorting to a complex-variable formulation [6]. With the numerical illustrations, we

• check a recently proposed Convergence Theorem [1] of the CBEM,

• check topology consistency and arrive at objective estimates for precision, accuracy, and eventual round-off errors,

• show that mesh refinement is required only to improve a mechanical simulation, not for mathematical evaluations,

• and also show that extremely challenging topology features are dealt with seamlessly.

A not lesser contribution is the proposition that three distinct geometric entities be properly handled: boundary nodes n (for displacements), boundary loci $\ell$ (for tractions), and domain points s, at which we collocate the singular sources and evaluate results. Since the previous developments were based on the isoparametric formulation (for the convergence theorem to hold), we have not considered a fourth geometric entity, namely the parameters by means of which a problem’s actual geometry might be described—eventually differently than displacement approximations. This would consist in an isogeometric approach (to which the convergence theorem is not generally applicable). Once we have a problem’s numerical precision and accuracy completely under control, an—application-oriented—comparison between isoparametric and isogeometric formulations has become possible, and is one of the subjects of a paper in preparation [17], which is surely going to revisit the numerical illustrations of Sects. 5.1 and 5.2.

Round-off errors may cause numerical results to blow up. Such (here controllable/avoidable) errors—and the (uncontrollable, mostly unperceived) ones occurring in the literature for unnecessarily proposed mathematical approximations—should be acknowledged as just “man-made.”

We reviewed the main features of papers [1, 4,5,6] to accrue concepts and draw attention to several numerical issues that were up to now unachievable in the general literature on the CBEM—in part for their lack of a proper mathematical language,²⁰ and to a great extent for the excessive proliferation of misleading alternatives (which we should better not review).²¹ On the other hand, we could not help explaining that Betti’s reciprocity theorem is just out of place in the CBEM.

The present illustrations considered distances smaller than a proton size, and cusps and crack openings that may be thinner than deemed reproducible in a laboratory. Addressing such extreme topological issues is in accordance with Carl Sagan’s standard “extraordinary claims require extraordinary evidence” [15]. We maintain that “singularity” does not exist in the real world: it is just a mathematical abstraction—although a powerful and useful one, as hopefully demonstrated. This corroborates Wigner’s postulate on the effectiveness of mathematics in natural sciences—whether reasonable or unreasonable [14].

The theoretical paper [1] applies to general 3D elasticity problems. The numerical implementations for the simulation of 2D problems of potential and elasticity consist of just applying Gauss–Legendre quadrature for curved isoparametric elements of any polynomial order, with eventual—mathematically exact—corrections accrued in terms of constants and built-in functions previously evaluated and stored. Extension to a hypersingular formulation is straightforward, as all we need are the Somigliana’s identities for flux and stress results in the domain [4, 6, 56], which are reproduced in Eqs. (21) and (33) in terms of complex variable.

The numerical issues related to the mathematically exact handling of the integrals for 3D problems (thus avoiding undue approximations) are overwhelming. We have successfully dealt with the cases for flat elements, basically for potential problems [57, 58], and also in applications that include the fast multipole method [59]. These developments still deserve improvements before they can be considered mature and eventually applicable (if ever possible) to curved boundaries.