1 Introduction

In beam-like structure analysis, the displacement field of various beam theories are generally defined through the specific assumption. Among them, the Euler–Bernoulli beam theory (EBBT) and Timoshenko beam theory are most widely used in continuum mechanics. Before and after bending, the Euler–Bernoulli beam theory assumed that the straight line perpendicular to the midplane is remain straight and perpendicular to midplane of the beam, and this theory is applicable to the mechanical study of slender beams. However, it is not accurate for thick beam because the shear deformation effect is not taken into account. The Timoshenko beam theory, also known as the first-order shear deformation beam theory (FSDBT), assumes that the straight line perpendicular to the center plane after bending is not perpendicular to the center plane. Thus, the shear deformable effect has been taken account and then the responses of thick beam can be accurately predicted. But, in Timoshenko beam theory, it is assumed that the distribution of transverse shear stress is constant along the thickness direction, and the selection of shear correction factor is essential to obtain an accurate solution since the free shear stresses on the top and bottom surfaces of the beam are not been satisfied in shear forces.

In order to account for the warping of the section as well as to satisfy the surface free traction condition, the various higher-order shear deformation beam theories (HOSDBT) have been proposed to better predict responses of beams without the need of a shear correction factor, such as the trigonometric shear deformation beam theory (TSDBT) [1], parabolic shear deformation beam theory (PSDBT) [2,3,4,5,6] and the hyperbolic shear deformation beam theory (HSDBT)[7], and of which the axial displacement varies along the beam depth in a higher order through the shear shape function [8,9,10,11,12,13].

Nowadays, micro-/nano-beam structures are commonly applied in micro- and nano-electro-mechanical systems (MEMS/NEMS) [14,15,16]. The aforementioned one-dimensional beam theories can be effectively used to predict the mechanical responses of the nano-structural units. However, it is well known that size-effect phenomenon has been observed in some experiments at the micro-/nano-scale, which cannot be captured by the classical continuum theory. To address the size-effect phenomenon, the higher-order continuum theories (e.g., the nonlocal elastic theory [17, 18], strain gradient theory [19] and couple stress theory [20]) are popular in analyzing the mechanical responses of nanostructures by introducing some length-scale parameters. Out of these, the nonlocal elasticity theory, originally presented by Kroner [21] and developed by Eringen et al. [17, 18, 22, 23], assumes that the stress state at any point is dependent not only on the strain field at the corresponding point, but also on others in the domain.

Owning to the difficulty of solving nonlocal integral equations, Eringen [18] proposed an equivalent differential form of the nonlocal elasticity theory, which is commonly applied to predict the mechanical behaviors of the nanostructures. Based on the nonlocal differential model, some pioneering studies can be viewed in [24,25,26]. Also, the nonlocal differential model is extended to the higher-order shear deformation beam theories to take account into the shear deformation effect of nanobeams. Sayyad and Ghugal [27] applied nonlocal differential model to develop a unified beam theories to analyze bending, buckling and vibration of functionally graded (FG) nanobeam. Jena et al. [28] analyzed vibration of single-walled carbon nanotube (SWCNT) by employing one variable shear deformation beam theory. Refaeinejad et al. [29] studied vibration of the FG nanobeam by employing nonlocal higher-order shear deformation beam theories. Thai and Vo [30] developed a nonlocal sinusoidal shear deformation beam theory to investigate the bending, buckling, and vibration of nanobeams. Ebrahimi and Barati [31] used third-order shear deformation beam theory to study free vibration of FG nanobeams by using Navier method. However, some paradoxes have been found in the nonlocal differential model. In particularly, the size-dependent behaviors are not been observed in the static bending analysis of cantilever Euler–Bernoulli beam when the beam end was subjected to a laterally concentrated force [32,33,34]. Furthermore, it is found that increasing nonlocal parameter lead to increasing in the vibration frequency under clamped-free boundary condition, which is inconsistent with the stiffness-softening phenomenon in other boundaries [35, 36]. Therefore, the nonlocal integral elasticity theory has got renewed attention by researchers. Tuna and Kirca [37, 38] studied static bending, buckling and vibration of nanobeams by utilizing analytical method. Alotta et al. [39] derived the finite element formulation for the axial deformation, bending deflection and rotation within framework of the nonlocal Timoshenko beam theory. Norouzzadeh and Ansari [40] performed a finite element analysis to investigate bending of Timoshenko nanobeams based on nonlocal integral model and compared the results with those in framework of nonlocal differential model. It is deduced that the well-posed solutions are obtained based on nonlocal integral model for the contradictory cantilever beam problems. Eptaimeros et al. [41] analyzed dynamical behaviors of Euler–Bernoulli nanobeam by employing the nonlocal integral model and eliminated paradoxes arising from the nonlocal differential model. Rajasekaran and Khaniki [42] applied nonlocal integral model to analyze static and dynamic mechanics of Euler–Bernoulli nanobeam. Taghizadeh et al. [43] performed buckling analysis of nanobeams and examine the buckling load influenced by the attenuation function type. However, Barretta et al. [44, 45] indicated that, owning to improper approximations, the boundary conditions of beam ends cannot be satisfied accurately in the nonlocal integral elasticity theory.

To break this ill-posedness of solutions, Eringen [46] proposed the two-phase local/nonlocal elasticity theory to address the size-dependent effect of nanobeams by combining the local elasticity part. Fakher et al. [47] applied the two-phase integral elasticity theory to examine buckling and vibration behaviors of nanobeams resting in size-dependent elastic foundation and under thermal load by employing exact solution, FEM and generalized differential quadrature method (GDQM). Fakher and Hosseini-Hashemi [48] proposed an efficient locking-free two-phase nonlocal finite element model to study free vibration of Timoshenko nanobeams. Based on nonlocal integral model, Danesh and Javanbakht [49] performed free vibration analysis of nonlocal Timoshenko beam theory and two-dimensional nonlocal elasticity theory with different kernels, which are compared to each other for different theories and kernels. Khodabakhsh and Reddy [50] proposed a general finite element formulation of Euler–Bernoulli beam for the two-phase integro-differential form of Eringen nonlocal model. Naghinejad and Ovesy [51] applied two-phase nonlocal integral model to study viscoelastic buckling and postbuckling problems of Euler–Bernoulli nanobeams.

Pinnola [52] applied the modified differential form of stress-driven nonlocal model to study the bending behaviors of systems of straight elastic beams. However, the determination of finite element shape function is complicated. To this motivation, the simple two-node beam element containing Lagrange and Hermite interpolation functions is applied in the finite element modeling of two-phase local/nonlocal integral model in this work. Based on the nonlocal integral model, most existing researches have adopted Euler–Bernoulli beam and Timoshenko nanobeam theories for evaluating the mechanical responses of nanostructures. Moreover, it is noted that the estimation of the shear correction factor is crucial because of the stipulation of energy equivalence between Timoshenko beams and the three-dimensional Cauchy continuum. The application of higher-order shear deformation beam theory can prevent the necessity of shear correction factor.

In this study, several higher-order shear deformation beam theories are developed to study the size-dependent static and dynamic mechanical behaviors of nanobeams using the two-phase local/nonlocal integral elasticity theory. The paper is arranged as follows. In Sect. 2, the kinematics and two-phase local/nonlocal constitutive equations of the various higher-order shear deformation beam theories in unified form are illustrated. In Sect. 3 the finite element formulation of high-order shear deformation nanobeams for bending, buckling and free vibration problems is constructed by utilizing the principle of minimum potential energy. In Sect. 4, by comparing the present calculation results with those of the Euler–Bernoulli beams, the influence of shear deformation on bending deflection, buckling load and vibration frequency is evaluated. A parametric study including the nonlocal parameter, nonlocal phase parameter and slenderness ratio is carried out to evaluate the mechanical responses of various high-order shear deformation theory nanobeams under different boundary conditions. Some main conclusions of the research are summarized in Sect. 5.

2 Mathematical formulation

2.1 Higher-order shear deformation beam theory

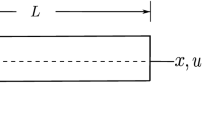
Figure 1 shows a straight nanobeam with length L, width b and thickness h.

Fig. 1
figure 1

Beam configuration and coordinate system

Full size image

The displacement field of higher-order shear deformation beam can be expressed as follows:

$$ \begin{gathered} u_{x} = - zw^{\prime}(x,t) + f(z)(w^{\prime}(x,t) + \phi (x,t)) \hfill \\ u_{z} = w(x,t) \hfill \\ \end{gathered} $$
(1)

where \(u_{x}\) and \(u_{z}\) denote the axial and transverse displacement components, respectively. \(w\) is the transverse displacement at the midplane. \(\phi\) is the rotation angle of cross section according to the vertical direction. The parameter \(t\) refers to the time. In this paper, superscript \(^{\prime}\) and overhead \(\cdot\) correspond to the derivative with respect to \(x\) and \(t\), respectively. \(f(z)\) is the shape function to determine the stress and the transverse shear strain distributions along the thickness of the beam (Fig. 2). The shape functions \(f(z)\) are chosen to satisfy the zero transverse shear stress condition of the upper and lower fibers of the cross section without a shear correction factor. The displacement fields of the commonly used higher-order shear deformation beam theories (HOSDBT) including parabolic shear deformation beam theory (PSDBT) based on Reddy [53], trigonometric shear deformation beam theory (TSDBT) based on Touratier [54], and hyperbolic shear deformation beam theory (HSDBT) based on Soldatos [55] can be obtained from Eq. (1) by using different shape functions \(f(z)\) given in

$$ f(z) = \left\{ {\begin{array}{*{20}c} 0 & {\text{(EBBT)}} \\ {z\left( {1 - \frac{{4z^{2} }}{{3h^{2} }}} \right)} & {\text{(PSDBT)}} \\ {\frac{h}{\pi }\sin \left( {\frac{\pi z}{h}} \right)} & {\text{(TSDBT)}} \\ {h\sinh \left( \frac{z}{h} \right) - z\cosh \left( \frac{1}{2} \right)} & {\text{(HSDBT)}} \\ \end{array} } \right. $$
(2)

in which, the EBBT is used for comparison purpose.

Fig. 2
figure 2

Beam element with six degrees of freedom

Full size image

The nonzero strain components are given by

$$ \begin{gathered} \varepsilon_{xx} = - zw^{\prime\prime} + f(z)(\phi^{\prime} + w^{\prime\prime}) \hfill \\ \gamma_{xz} = f^{\prime}(z)(w^{\prime} + \phi ) \hfill \\ \end{gathered} $$
(3)

The variation of the total strain energy with volume \(V\) is calculated as

$$ \begin{aligned} \delta U &= \int_{V} ( \sigma_{xx} \delta \varepsilon_{xx} + \sigma_{xz} \delta \gamma_{xz} ){\text{d}} V \hfill \\ &= \int_{V} ( \sigma_{xx} \delta ( - zw^{\prime\prime} + f(\phi^{\prime} + w^{\prime\prime})) + f^{\prime}\sigma_{xz} \delta (w^{\prime} + \phi )){\text{d}} V \hfill \\ &= \int_{0}^{L} {s\delta w^{\prime\prime} + m\delta \phi^{\prime} + r\delta (w^{\prime} + \phi ){\text{d}} x} \hfill \\ \end{aligned} $$
(4)

where

$$ {\text{\{ }}s,m,r{\text{\} }} = \int_{A} {{\text{\{ }} - z\sigma_{xx} ,f\sigma_{xx} ,f^{\prime}\sigma_{xz} {\text{\} d}}A} $$
(5)

The variation of kinetic energy of the beams is

$$ \begin{aligned} \delta T &= \rho \int_{V} {\dot{u}_{x} \delta \dot{u}_{x} {\text{d}} V} + \rho \int_{V} {\dot{u}_{z} \delta \dot{u}_{z} {\text{d}} V} \\ &= \rho \int_{V} {( - z\dot{w^{\prime}} + f(\dot{w^{\prime}} + \dot{\phi }))\delta ( - z\dot{w^{\prime}} + f(\dot{w^{\prime}} + \dot{\phi })){\text{d}} V} + \rho \int_{V} {\dot{w}\delta \dot{w}{\text{d}} V} \\ &= \rho \int_{V} {z^{2} \dot{w^{\prime}}\delta \dot{w^{\prime}} - zf\dot{w^{\prime}}\delta (\dot{w^{\prime}} + \dot{\phi }) - zf(\dot{w^{\prime}} + \dot{\phi })\delta \dot{w^{\prime}}} \\ &\quad + f^{2} (\dot{w^{\prime}} + \dot{\phi })\delta (\dot{w^{\prime}} + \dot{\phi }){\text{d}} V + \rho \int_{V} {\dot{w}\delta \dot{w}{\text{d}} V} \\ &= m_{0} \int_{0}^{L} {\dot{w^{\prime}}} \delta \dot{w^{\prime}}{\text{d}} x + m_{1} \int_{0}^{L} {\dot{w^{\prime}}} \delta (\dot{w^{\prime}} + \dot{\phi }){\text{d}} x + m_{1} \int_{0}^{L} {(\dot{w^{\prime}} + \dot{\phi })\delta \dot{w^{\prime}}} {\text{d}} x \\ &\quad + m_{2} \int_{0}^{L} {(\dot{w^{\prime}} + \dot{\phi })\delta (\dot{w^{\prime}} + \dot{\phi })} {\text{d}} x + m_{3} \int_{0}^{L} {\dot{w}\delta \dot{w}} {\text{d}} x \\ \end{aligned} $$
(6)

in which,\(\rho\) is the mass density and

$$ {\text{\{ }}m_{0} ,m_{1} ,m_{2} ,m_{3} {\text{\} }} = \rho \int_{A} {{\text{\{ }}z^{2} ,( - zf),f^{2} ,1{\text{\} }}dA} $$
(7)

The variation of work done by the action of the external loads is given by

$$ \delta W = \int_{0}^{L} {q(x)\delta w{\text{d}} x} + \int_{0}^{L} {Pw^{\prime}} \delta w^{\prime}{\text{d}} x $$
(8)

where \(q(x)\) and \(P\) refer to the externally applied transverse distributed force and the axial compressive force at the two beam ends, respectively.

For vibration analysis, it is assumed that displacement functions can be written as

$$ {\text{\{ }}w(x,t),\phi (x,t){\text{\} }} = {\text{\{ }}W(x),\Phi (x){\text{\} }}e^{ - i\omega t} $$
(9)

Accordingly, one obtains

$$ \{ s,m,r\} (x,t) = \{ S(x),M(x),R(x)\} e^{ - i\omega t} $$
(10)

According to minimum total potential energy and taking account into Eqs. (9) and (10), one can obtain that

$$ \delta \Pi = \delta (U - W + T){\mkern 1mu} = e^{{ - 2i\omega t}} \left\{ \begin{gathered} \int_{0}^{L} {S\delta W^{{\prime \prime }} + M\delta (\Phi ^{\prime } + W^{{\prime \prime }} ) + R\delta (W^{\prime } + \Phi )dx} \hfill \\ - \int_{0}^{L} {q\delta Wdx} - \int_{0}^{L} {PW^{\prime } } \delta W^{\prime } dx \hfill \\ - \omega ^{2} [m_{0} \int_{0}^{L} {W^{\prime } } \delta W^{\prime } dx + m_{1} \int_{0}^{L} {W^{\prime } } \delta (W^{\prime } + \Phi )dx + m_{1} \int_{0}^{L} {(W^{\prime } + \Phi )\delta W^{\prime } } dx \hfill \\ + m_{2} \int_{0}^{L} {(W^{\prime } + \Phi )\delta (W^{\prime } + \Phi )} dx + m_{3} \int_{0}^{L} {W\delta Wdx]} \hfill \\ \end{gathered} \right\} = 0 $$
(11)

2.2 The two-phase local/nonlocal integral model

According to [56], the two-phase local/nonlocal constitutive model takes the following form

$$ \sigma_{ij} (x) = (1 - \xi )\tau_{ij} (x) + \frac{\xi }{2\kappa }\int_{V} {{\text{e}}^{{ - \frac{{\left| {x - \eta } \right|}}{\kappa }}} } \tau_{ij} {(}\eta {)}{\text{d}} V(\eta ) $$
(12)

where \(\sigma_{ij}\) and \(\tau_{ij}\) refer to the pure nonlocal and local stress components. The volume fraction \(\xi\) represents the nonlocal properties which is called the nonlocal phase parameter, and \(\kappa\) is a nonlocal length-scale parameter. The two-phase local/nonlocal constitutive model is a combination of the nonlocal elasticity and local elasticity. \(\xi = 1\) and \(\xi = 0\) refer to the purely nonlocal integral and local theory, respectively.

According to the 1D Hooke’s law, the nonzero local stress component is given by

$$ \begin{gathered} \tau_{xx} = E\varepsilon_{xx} \hfill \\ \tau_{xz} = G\gamma_{xz} \hfill \\ \end{gathered} $$
(13)

in which, \(E\) and \(G\) correspond to the elastic and shear modulus.

By substituting Eqs. (3) and (13) into (12), one gets

$$ \begin{gathered} \sigma_{xx} = E[(1 - \xi )( - zw^{\prime\prime} + f(\phi^{\prime} + w^{\prime\prime})) + \frac{\xi }{2\kappa }\int_{0}^{L} {( - zw^{\prime\prime} + f(\phi^{\prime} + w^{\prime\prime})){\text{e}}^{{ - \frac{{\left| {x - \eta } \right|}}{\kappa }}} {\text{d}}\eta } ] \hfill \\ \sigma_{xz} = G[(1 - \xi )(f^{\prime}(w^{\prime} + \varphi )) + \frac{\xi }{2\kappa }\int_{0}^{L} {(f^{\prime}(w^{\prime} + \varphi )){\text{e}}^{{ - \frac{{\left| {x - \eta } \right|}}{\kappa }}} d\eta } ] \hfill \\ \end{gathered} $$
(14)

Combining Eqs. (5) and (14), integrating with respect to the cross section and taking account into Eqs. (9) and (10), the nonlocal constitutive equation can be described as follows:

$$ \begin{gathered} S = e^{ - i\omega t} \{ (1 - \xi )(I_{1} W^{\prime\prime} + I_{2} (\Phi^{\prime} + W^{\prime\prime})) + \frac{\xi }{2\kappa }\int_{0}^{L} {(I_{1} W^{\prime\prime} + I_{2} (\Phi^{\prime} + W^{\prime\prime})){\text{e}}^{{ - \frac{{\left| {x - \eta } \right|}}{\kappa }}} d\eta } \} \hfill \\ M = e^{ - i\omega t} \{ (1 - \xi )(I_{2} W^{\prime\prime} + I_{3} (\Phi^{\prime} + W^{\prime\prime})) + \frac{\xi }{2\kappa }\int_{0}^{L} {(I_{2} W^{\prime\prime} + I_{3} (\Phi^{\prime} + W^{\prime\prime})){\text{e}}^{{ - \frac{{\left| {x - \eta } \right|}}{\kappa }}} d\eta } \} \hfill \\ R = e^{ - i\omega t} \{ (1 - \xi )I_{4} (W^{\prime} + \Phi ) + \frac{\xi }{2\kappa }\int_{0}^{L} {I_{4} (W^{\prime} + \Phi ){\text{e}}^{{ - \frac{{\left| {x - \eta } \right|}}{\kappa }}} d\eta } \} \hfill \\ \end{gathered} $$
(15)

in which

$$ {\text{\{ }}I_{1} ,I_{2} ,I_{3} ,I_{4} {\text{\} }} = \int_{A} {{\text{\{ }}Ez^{2} ,Ef( - z),Ef^{2} ,Gf^{{\prime}{2}} {\text{\} }}dA} $$
(16)

3 Nonlocal finite element model

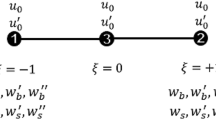
In this section, the bending, buckling and free vibration of the higher-order shear deformation nanobeam is studied by using finite element method (FEM). In order to use a lengthwise FEM, the nanobeam is divided into several two-node elements with equal lengths. Combining Eq. (11) and (15), it is noted that the transverse deflection \(W\) is differentiated twice with respect to x and the rotation angle \(\Phi\) is differentiated only once. The Hermite cubic and Lagrange interpolation functions for \(W\) and \(\Phi\) are applied in the finite element analysis, respectively. Each element has three degrees of freedom including the deflection \(W\), the derivative of deflection \(- W^{\prime}\) and the rotation angle \(\Phi^{\prime}\) at any nodes of the beam as follows.

Consequently, the displacement field of the i-th element is given by

$$ \begin{gathered} W^{i} = {\mathbf{N}}_{i} {\mathbf{d}}_{i} \hfill \\ \Phi^{i} = {\mathbf{M}}_{i} {\mathbf{d}}_{i} \hfill \\ \end{gathered} $$
(17)

in which

$$ \begin{gathered} {\mathbf{N}}_{i} = \left[ {\begin{array}{*{20}c} {N_{i1} (x)} & {N_{i2} (x)} & 0 & {N_{i3} (x)} & {N_{i4} (x)} & 0 \\ \end{array} } \right] \hfill \\ {\mathbf{M}}_{i} = \left[ {\begin{array}{*{20}c} 0 & 0 & {N_{i5} {(}x{)}} & 0 & 0 & {N_{i6} {(}x{)}} \\ \end{array} } \right] \hfill \\ {\mathbf{d}}_{i} = \left[ {\begin{array}{*{20}c} W & { - W^{\prime}_{i} } & {\Phi_{i} } & {W_{i + 1} } & { - W^{\prime}_{i + 1} } & {\Phi_{i + 1} } \\ \end{array} } \right]^{T} \hfill \\ l_{i} = x_{i + 1} - x_{i} \hfill \\ \end{gathered} $$
(18)

where \(x_{i}\) and \(x_{{i{ + }1}}\) refer to the coordinate values of the x-axis at the left and right nodes of the i-th element, respectively. \({\mathbf{d}}_{i}\) is the nodal displacement vector of the i-th element. \(l_{i} = x_{i + 1} - x_{i}\) denotes the length of the i-th element. \({\mathbf{N}}_{i}\) and \({\mathbf{M}}_{i}\) denote the shape function vector of the i-th element composed of linear Hermite cubic and Lagrange interpolation functions, respectively, which can be written as

$$ \begin{gathered} \{ N_{i1} {(}x{)},N_{i2} {(}x{)},N_{i3} {(}x{)},N_{i4} {(}x{)}] \hfill \\ { = }\left\{ \begin{gathered} {\text{\{ }}1 - \frac{{3(x - x_{i} )^{2} }}{{l_{i}^{2} }} + \frac{{2(x - x_{i} )^{3} }}{{l_{i}^{3} }},{(}x - x_{i} ) - \frac{{2(x - x_{i} )^{2} }}{{l_{i} }} + \frac{{(x - x_{i} )^{3} }}{{l_{i}^{2} }} \hfill \\ ,\frac{{3(x - x_{i} )^{2} }}{{l_{i}^{2} }} - \frac{{2(x - x_{i} )^{3} }}{{l_{i}^{3} }}, - \frac{{(x - x_{i} )^{2} }}{{l_{i} }} + \frac{{(x - x_{i} )^{3} }}{{l_{i}^{2} }} \hfill \\ \end{gathered} \right\} \hfill \\ \{ N_{i5} {(}x{)},N_{i6} {(}x{\text{)\} = }}\left\{ {1 - \frac{{x - x_{i} }}{{l_{i} }},\frac{{x - x_{i} }}{{l_{i} }}} \right\} \hfill \\ \end{gathered} $$
(19)

Therefore, the total potential energy can be rewritten as

$$ \delta \Pi = \sum\limits_{n = 0}^{N} {\delta \Pi_{n} ({\mathbf{d}}_{n`} )} = 0 $$
(20)

Combining Eqs. (17) and (20) and considering the linear property of variation, one gets

$$ \delta \Pi_{1} ({\mathbf{d}}_{1`} ) = \delta \Pi_{2} ({\mathbf{d}}_{2`} ) = ... = \delta \Pi_{N} ({\mathbf{d}}_{N`} ) = 0 $$
(21)

Substituting Eq. (17) into Eq. (11) and combining Eq. (21), the variation of the potential energy of the i-th element is expressed as

$$ \begin{aligned} \delta \Pi ({\mathbf{d}}_{i} ) & = e^{ - 2i\omega t} {{\{ }}(1 - \xi )\int_{{x_{i} }}^{{x_{i + 1} }} {\delta {\mathbf{d}}_{i}^{T} \left[ \begin{gathered} {\mathbf{N}}_{i}^{\prime \prime T} [I_{1} {\mathbf{N}}_{i}^{\prime \prime } + I_{2} ({\mathbf{M}}_{i}^{\prime } + {\mathbf{N}}_{i}^{\prime \prime } )] \hfill \\ + ({\mathbf{M}}_{i}^{\prime T} { + }{\mathbf{N}}_{i}^{\prime \prime T} )[I_{2} {\mathbf{N}}_{i}^{\prime \prime } + I_{3} ({\mathbf{M}}_{i}^{\prime } + {\mathbf{N}}_{i}^{\prime \prime } )] \hfill \\ + ({\mathbf{N}}_{i}^{\prime T} + {\mathbf{M}}_{i}^{T} )[I_{4} ({\mathbf{N}}_{i}^{\prime } + {\mathbf{M}}_{i} )]{\text{d}} x \hfill \\ \end{gathered} \right]} {\mathbf{d}}_{i} {\text{d}} x \\ &\quad + \int_{{x_{i} }}^{{x_{i + 1} }} {\delta {\mathbf{d}}_{i}^{T} \left[ \begin{gathered} {\mathbf{N}}_{i}^{\prime \prime T} [\frac{\xi }{2\kappa }\sum\limits_{j = 1}^{N} {\int_{{x_{j} }}^{{x_{j + 1} }} {(I_{1} {\mathbf{N}}_{j}^{\prime \prime } + I_{2} ({\mathbf{M}}_{j}^{\prime } + {\mathbf{N}}_{j}^{\prime \prime } )){\text{e}}^{{ - \frac{{\left| {x - \eta } \right|}}{\kappa }}} d\eta } } ] \hfill \\ + ({\mathbf{M}}_{i}^{\prime T} { + }{\mathbf{N}}_{i}^{\prime \prime T} )[\frac{\xi }{2\kappa }\sum\limits_{j = 1}^{N} {\int_{{x_{j} }}^{{x_{j + 1} }} {(I_{2} {\mathbf{N}}_{j}^{\prime \prime } + I_{3} ({\mathbf{M}}_{j}^{\prime } + {\mathbf{N}}_{j}^{\prime \prime } )){\text{e}}^{{ - \frac{{\left| {x - \eta } \right|}}{\kappa }}} d\eta } } ] \hfill \\ + ({\mathbf{N}}_{i}^{\prime T} + {\mathbf{M}}_{i}^{T} )[\frac{\xi }{2\kappa }\sum\limits_{j = 1}^{N} {\int_{{x_{j} }}^{{x_{j + 0} }} {I_{4} ({\mathbf{N}}_{j}^{\prime } + {\mathbf{M}}_{j} ){\text{e}}^{{ - \frac{{\left| {x - \eta } \right|}}{\kappa }}} d\eta } } ] \hfill \\ \end{gathered} \right]} {\mathbf{d}}_{j} {\text{d}} x \\ &\quad - \int_{{x_{i} }}^{{x_{i + 1} }} {\delta {\mathbf{d}}_{i}^{T} {\mathbf{N}}_{i}^{T} q{\text{d}} x} - P\int_{{x_{i} }}^{{x_{i + 1} }} {\delta {\mathbf{d}}_{i}^{T} {\mathbf{N}}_{i}^{\prime T} {\mathbf{N}}_{i}^{\prime } } {\mathbf{d}}_{i} {\text{d}} x \\ &\quad - \omega^{2} \int_{{x_{i} }}^{{x_{i + 1} }} {\delta {\mathbf{d}}_{i}^{T} \left[ \begin{gathered} m_{0} {\mathbf{N}}_{i}^{\prime T} {\mathbf{N}}_{i}^{\prime } + m_{1} ({\mathbf{N}}_{i}^{\prime T} + {\mathbf{M}}_{i} ){\mathbf{N}}_{i}^{\prime } + m_{1} {\mathbf{N}}_{i}^{\prime T} \delta ({\mathbf{N}}_{i}^{\prime } + {\mathbf{M}}_{i} ) \hfill \\ + m_{2} ({\mathbf{N}}_{i}^{\prime T} + {\mathbf{M}}_{i}^{T} )({\mathbf{N}}_{i}^{\prime } + {\mathbf{M}}_{i} ) + m_{3} {\mathbf{N}}_{i}^{T} {\mathbf{N}}_{i} \hfill \\ \end{gathered} \right]} {\mathbf{d}}_{i} {\text{d}} x{{\} }} = {0} \\ \end{aligned} $$
(22)

According to Eq. (22), the finite element formulation of the i-th element can be represented as

$$ (1 - \xi ){\mathbf{K}}_{i}^{l} {\mathbf{d}}_{i} + \xi \sum\limits_{j = 1}^{N} {{\mathbf{K}}_{ij}^{nl} } {\mathbf{d}}_{j} - P{\tilde{\mathbf{K}}}_{i} - \omega^{2} {\tilde{\mathbf{M}}}_{i} = {\mathbf{F}}_{i} $$
(23)

in which

$$ \begin{aligned} {\mathbf{K}}_{i}^{l} & = \int_{{x_{i} }}^{{x_{i + 1} }} {\left[ \begin{gathered} {\mathbf{N}}_{i}^{\prime \prime T} [I_{1} {\mathbf{N}}_{i}^{\prime \prime } + I_{2} ({\mathbf{M}}_{i}^{\prime } + {\mathbf{N}}_{i}^{\prime \prime } )] \hfill \\ + ({\mathbf{M}}_{i}^{\prime T} { + }{\mathbf{N}}_{i}^{\prime \prime T} )[I_{2} {\mathbf{N}}_{i}^{\prime \prime } + I_{3} ({\mathbf{M}}_{i}^{\prime } + {\mathbf{N}}_{i}^{\prime \prime } )] \hfill \\ + ({\mathbf{N}}_{i}^{\prime T} + {\mathbf{M}}_{i}^{T} )[I_{4} ({\mathbf{N}}_{i}^{\prime } + {\mathbf{M}}_{i} )]{\text{d}} x \hfill \\ \end{gathered} \right]} {\text{d}} x \\ {\mathbf{K}}_{ij}^{nl} & = \int_{{x_{i} }}^{{x_{i + 1} }} {\int_{{x_{j} }}^{{x_{j + 1} }} {\left[ \begin{gathered} {\mathbf{N}}_{i}^{\prime \prime T} [\frac{\xi }{2\kappa }(I_{1} {\mathbf{N}}_{j}^{\prime \prime } + I_{2} ({\mathbf{M}}_{j}^{\prime } + {\mathbf{N}}_{j}^{\prime \prime } )){\text{e}}^{{ - \frac{{\left| {x - \eta } \right|}}{\kappa }}} ] \hfill \\ + ({\mathbf{M}}_{i}^{\prime T} { + }{\mathbf{N}}_{i}^{\prime \prime T} )[\frac{\xi }{2\kappa }(I_{2} {\mathbf{N}}_{j}^{\prime \prime } + I_{3} ({\mathbf{M}}_{j}^{\prime } + {\mathbf{N}}_{j}^{\prime \prime } )){\text{e}}^{{ - \frac{{\left| {x - \eta } \right|}}{\kappa }}} ] \hfill \\ + ({\mathbf{N}}_{i}^{\prime T} + {\mathbf{M}}_{i}^{T} )[\frac{\xi }{2\kappa }I_{4} ({\mathbf{N}}_{j}^{\prime } + {\mathbf{M}}_{j} ){\text{e}}^{{ - \frac{{\left| {x - \eta } \right|}}{\kappa }}} ] \hfill \\ \end{gathered} \right]} } d\eta {\text{d}} x \hfill \\ {\tilde{\mathbf{K}}}_{i} & = \int_{{x_{i} }}^{{x_{i + 1} }} {{\mathbf{N}}_{i}^{\prime T} {\mathbf{N}}_{i}^{\prime } } {\text{d}} x \\ {\tilde{\mathbf{M}}}_{i} & = \int_{{x_{i} }}^{{x_{i + 1} }} {\left[ \begin{gathered} m_{0} {\mathbf{N}}_{i}^{\prime T} {\mathbf{N}}_{i}^{\prime } + m_{1} ({\mathbf{N}}_{i}^{\prime T} + {\mathbf{M}}_{i} ){\mathbf{N}}_{i}^{\prime } + m_{1} {\mathbf{N}}_{i}^{\prime T} \delta ({\mathbf{N}}_{i}^{\prime } + {\mathbf{M}}_{i} ) \hfill \\ + m_{2} ({\mathbf{N}}_{i}^{\prime T} + {\mathbf{M}}_{i}^{T} )({\mathbf{N}}_{i}^{\prime } + {\mathbf{M}}_{i} ) + m_{3} {\mathbf{N}}_{i}^{T} {\mathbf{N}}_{i} \hfill \\ \end{gathered} \right]} {\text{d}} x \\ {\mathbf{F}}_{i} & { = }\int_{{x_{i} }}^{{x_{i + 1} }} {{\mathbf{N}}_{i}^{T} q{\text{d}} x} \end{aligned} $$
(24)

where \({\mathbf{F}}_{i}\),\({\tilde{\mathbf{K}}}_{i}\) and \({\tilde{\mathbf{M}}}_{i}\) are the external force, the geometric stiffness and the mass stiffness matrix of the i-th element, respectively, which all are local properties because they are independent of constitutive relationship. Also, the first term and the second term given in Eq. (23) represent the influence of the local and nonlocal elasticity theories on the mechanical behaviors, respectively. \({\mathbf{K}}_{i}^{l}\) and \({\mathbf{K}}_{ij}^{nl}\) refer to the local and nonlocal stiffness matrixes of the i-th element, respectively. \({\mathbf{K}}_{i}^{l}\) indicates that the stress at the reference point depends only on the strain at the same point. \({\mathbf{K}}_{ij}^{nl}\) accounts for the influence exerted on the i-th element by the j-th elements, in which the integrals in Eq. (24) are computed analytically without using any numerical approximation method. Noticed that

$$ \int_{{x_{i} }}^{{x_{i + 1} }} {\int_{{x_{j} }}^{{x_{j + 1} }} {g(x,\eta )} } {\text{e}}^{{ - \frac{{\left| {x - \eta } \right|}}{\kappa }}} {\text{d}} \eta {\text{d}} x{ = }\left\{ {\begin{array}{*{20}llll} {\int_{{x_{i} }}^{{x_{i + 1} }} {[\int_{{x_{j} }}^{x} {g(x,\eta ){\text{e}}^{{\frac{\eta - x}{\kappa }}} {\text{d}} \eta + \int_{x}^{{x_{j + 1} }} {g(x,\eta ){\text{e}}^{{\frac{x - \eta }{\kappa }}} {\text{d}} \eta ]{\text{d}} x} } } } & {(i = j)} \\ {\int_{{x_{i} }}^{{x_{i + 1} }} {\int_{{x_{j} }}^{{x_{j + 1} }} {g(x,\eta ){\text{e}}^{{\frac{\eta - x}{\kappa }}} {\text{d}} \eta {\text{d}} x} } } & {(i > j)} \\ {\int_{{x_{i} }}^{{x_{i + 1} }} {\int_{{x_{j} }}^{{x_{j + 1} }} {g(x,\eta ){\text{e}}^{{\frac{x - \eta }{\kappa }}} {\text{d}} \eta {\text{d}} x} } } & {(i < j)} \\ \end{array} } \right. $$
(25)

in which,\(g(x,\eta )\) represents the integral function in Eq. (24).

Consequently, the finite element formulation can be constructed by assemblage of all elements. For static bending analysis, a transversal load \(q\) is considered in the finite element formulation and the following equation of motion is achieved as

$$ {\mathbf{Kd}} = {\mathbf{F}} $$
(26)

For free vibration analysis, by neglecting the influence of external forces, the finite element model can be obtained in the following form

$$ {(}{\mathbf{K}} - \omega^{2} {\tilde{\mathbf{M}}}{)}{\mathbf{d}} = {0} $$
(27)

Also, for buckling problem, by neglecting the transversal force and time dependent terms in Eq. (23), one can get the following eigenvalue problem

$$ {(}{\mathbf{K}} - P{\tilde{\mathbf{K}}}{)}{\mathbf{d}} = {0} $$
(28)

in which, \({\mathbf{K}}\), \({\tilde{\mathbf{K}}}\) and \({\tilde{\mathbf{M}}}\) is the global stiffness, geometric stiffness and mass stiffness matrix, respectively. \({\mathbf{d}}\) refers to the global displacement vector.

4 Results and discussion

The numerical analysis is performed to investigate the bending, buckling, and free vibration of the higher-order shear deformation theory nanobeams including the EBBT, PSDBT, HSDBT and TSDBT under clamped–clamped, simply-supported, clamped-simply and cantilever beam (C–C, S–S, C–S and C–F) are carried out by using finite element formulations. The geometric dimensions and material properties are assumed as: \(E = 69\,{\text{GPa}}\), \(\upsilon = 0.3\), \(h = 1\,{\mu m}\) and \(b = 2h\). In this paper, the non-dimensional forms of the maximum deflections under uniformly (U) distributed load \(q_{0}\) and lateral point (P) force \(F\) at beam end, buckling load and vibration frequency are introduced as:\(\overline{w} = {100}EIw/(q_{0} L^{4} )\), \(\overline{w} = {100}EIw/(FL^{3} )\), \(\overline{P} = PL^{2} /(EI)\), \(\overline{\omega } = \omega L^{2} \sqrt {\rho A/(EI)}\).

4.1 Assessment of the present formulation

At first, the efficiency and accuracy of the present FEM are validated in this subsection. A convergence study for bending, buckling and free vibration of various beam theories is illustrated in Figs. 3, 4, 5 for \(L = 10h\). It was inferred from these figures that 50 elements are sufficient to yield converged solutions. Therefore, 50 elements are applied to achieve the accurate evaluations in the following analysis. Meanwhile, it can be obvious that the convergence rate of EBBT is faster than that of higher-order shear deformation beam models. It is clearly observed that the results based on different high-order shear deformation beam models have well consistency for all boundary conditions considered. Furthermore, to validate the results of the present FEM, the numerical results of EBBT for various nonlocal parameter \(\kappa\) are compared with Refs [57,58,59]. and listed in Tables 1, 2, 3, in which the normalized vibration frequency is defined as the ratio between nonlocal model and the corresponding local ones. Still, a good agreement can be obtained.

Fig. 3
figure 3

Convergence of bending deflections of a CCU-, b SSU- c CFU- and d CFP-beams based on various high-order shear deformation beam theories for ξ = 0.5

Full size image
Fig. 4
figure 4

Convergence of buckling loads of a CC-, b SS-, c CS- and d CF-beams based on various high-order shear deformation beam theories for ξ = 0.5

Full size image
Fig. 5
figure 5

Convergence of vibration frequencies of a CC-, b SS-, c CS- and d CF-beams based on various high-order shear deformation beam theories for ξ = 0.5

Full size image
Table 1 Comparison of nondimensional maximum deflections of Euler–Bernoulli beams between the present FEM results and the exciting results
Full size table
Table 2 Comparison of nondimensional buckling loads of Euler–Bernoulli beams between the present FEM results and the exciting results
Full size table
Table 3 Comparison of normalized vibration frequencies of Euler–Bernoulli beams between the present FEM results and the exciting results under SS boundary condition
Full size table

4.2 Mechanical analysis of high-order shear deformation theory nanobeams

Figures 3, 4, 5 depict that the maximum bending deflections, critical buckling loads and vibration frequencies are almost same for different high-order shear deformation beam models for \(L/h = 10\). Therefore, this subsection conducts a detailed parametric study of CC-, SS-, CF- and CS-beams based on PSDBT for different nonlocal parameter \(\kappa\), nonlocal phase parameter \(\xi\) and slenderness ratio L/h. Figures 6, 7, 8 illustrate the influence of \(\kappa\) and \(\xi\) on the bending, buckling and vibration behaviors for various boundary conditions. Figures 6, 7, 8 show that the influence of the nonlocal parameter \(\kappa\) and nonlocal phase parameter \(\xi\) on the non-dimensional maximum deflections, critical buckling loads and vibration frequencies of EBBT and PSDBT is significant. The increase in the nonlocal parameter \(\kappa\) or nonlocal phase parameter \(\xi\) lead to increasing in the bending deflections, and the decreasing in the buckling loads and vibration frequencies. Meanwhile, the maximum deflections, buckling loads and vibration frequencies is most sensitive to \(\kappa\) with the increase of \(\xi\). It is found that, for different \(\kappa\) and \(\xi\), the non-dimensional maximum deflections of PSDBT is larger than that of EBBT, while the non-dimensional buckling loads and vibration frequencies of PSDBT are lower than that of EBBT.

Fig. 6
figure 6

The nondimensional maximum deflections of a CCU-, b SSU-, c CFU- and d CFP-beams versus \(\kappa /L\) for different \(\xi\) (solid and dash lines represent the data for PSDBT and EBBT)

Full size image
Fig. 7
figure 7

The nondimensional buckling loads of a CC-, b SS-, c CS- and d CF-beams versus \(\kappa /L\) for different \(\xi\)(solid and dash lines represent the data for PSDBT and EBBT)

Full size image
Fig. 8
figure 8

The nondimensional vibration frequencies of a CC-, b SS-, c CS- and d CF-beams versus \(\kappa /L\) for different \(\xi\)(solid and dash lines represent the data for PSDBT and EBBT)

Full size image

Figures 9, 10, 11 show the effect of slenderness ratio L/h on the bending, buckling and free vibration behaviors of EBBT and PSDBT for \(\xi = 0.5\). Compared with EBBT, the shear deformation effect is significant for the deep beam. With increasing in L/h, the values of the non-dimensional maximum deflections decrease, while the non-dimensional buckling loads and vibration frequencies increase for PSDBT. Moreover, the difference of non-dimensional maximum deflections, buckling loads and vibration frequencies between the two beam theories decrease as L/h increases. Furthermore, variations of non-dimensional maximum deflections, buckling loads and vibration frequencies for different \(\kappa\) and L/h get affected by the boundary conditions. It is observed that under CC, SS and CS boundary conditions, the influence of shear deformation effect on non-dimensional maximum deflections, buckling loads and vibration frequencies is not significant when L/h is greater than 40, while under CF boundary conditions, this influence is not significant when L/h = 20. It is also noticed from Figs. 9, 10, 11 that the difference between EBBT and PSDBT in the non-dimensional maximum deflections under CC, SS and CS boundary conditions increases with increasing in the nonlocal parameter \(\kappa\) for deep beam cases, while the opposite trend can be observed for the buckling loads and vibration frequencies. Furthermore, the difference of non-dimensional maximum deflections, buckling loads and vibration frequencies between EBBT and PSDBT caused by shear deformation effect remains almost unchanged for CF boundary condition. It is indicated that for harder boundary conditions, the influence of shear deformation on non-dimensional maximum deflections increases with increasing in \(\kappa\) for small L/h. However, this effect decreases in non-dimensional buckling loads and vibration frequencies with increasing in \(\kappa\).

Fig. 9
figure 9

The dimensionless maximum deflections of a CCU-, b SSU-, c CFU- and d CFP-beams versus \(L/h\) for different \(\kappa /L\) (solid and dash lines represent the data for PSDBT and EBBT)

Full size image
Fig. 10
figure 10

The dimensionless buckling loads of a CC-, b SS-, c CS- and d CF-beams versus \(L/h\) for different \(\kappa /L\) (solid and dash lines represent the data for PSDBT and EBBT)

Full size image
Fig. 11
figure 11

The dimensionless vibration frequencies of a CC-, b SS-, c CS- and d CF-beams versus \(L/h\) for different \(\kappa /L\) (solid and dash lines represent the data for PSDBT and EBBT)

Full size image

Figure 12 illustrates the effect of nonlocal parameter \(\kappa\) on the normalized maximum deflections, buckling loads and vibration frequencies of PSDBT for \(\xi = 0.5\) and \(L/h = 10\). It is shown in Fig. 12 that the arrangement from largest to least associated with the effect of \(\kappa\) on the normalized maximum deflection would be CC-, CS-, CF- and SS-beams, while the opposite trend is observed in normalized buckling loads and vibration frequencies. It is found that influence of \(\kappa\) on the normalized maximum deflections, buckling loads and vibration frequencies of PSDBT is smaller than that of EBBT for CC boundary condition, while the opposite trend is observed for SS boundary condition. Also, the difference of normalized maximum deflections, buckling loads and vibration frequencies between the two beam models is not obvious for CS and CF boundary conditions.

Fig. 12
figure 12

Normalized a maximum deflections, b buckling loads and c vibration frequencies of microbeams based on PSDBT versus \(\kappa /L\) (solid and dash lines represent the data for PSDBT and EBBT)

Full size image

Figures 13, 14 show the influence of the nonlocal phase parameter \(\xi\) on the first five orders of normalized buckling loads and vibration frequencies of the nanobeams for \(\kappa /L = 0.2\) and \(L/h = 10\). The normalized buckling loads and vibration frequencies decrease with increasing in nonlocal phase parameter \(\xi\), buckling and vibration orders. However, the decrease rates decrease with increasing in the buckling and vibration orders.

Fig. 13
figure 13

The high-order normalized buckling loads of a CC-, b SS-, c CS- and d CF-beams versus \(\xi\) (solid and dash lines represent the data for PSDBT and EBBT)

Full size image
Fig. 14
figure 14

The high-order normalized vibration frequencies of a CC-, b SS-, c CS- and d CF-beams versus \(\xi\) (solid and dash lines represent the data for PSDBT and EBBT)

Full size image

5 Conclusion

From the present numerical solutions, the main conclusions can be summarized as follows:

  1. 1.

    The bending deflections, critical buckling loads and vibration frequencies from finite element simulation are in well agreement with the existing solutions. The difference among PSDBT, TSDBT and HSDBT is not significant for all boundary conditions.

  2. 2.

    With increasing in \(\kappa\) or \(\xi\), the maximum deflection increases, while the buckling loads and vibration frequencies decrease. By conduct a comparation of numerical solutions between EBBT and PSDBT, it is found that the maximum deflections based on PSDBT are larger than those based on EBBT, while buckling loads and vibration frequencies based on EBBT are larger than those based on PSDBT.

  3. 3.

    The shear deformation effect is significant for the lower L/h. With the increase in L/h, the maximum deflections, buckling loads and vibration frequencies based on PSDBT approach to those based on EBBT. The difference of bending deflections between EBBT and PSDBT under CC, SS and CS boundary conditions increases with increasing in the nonlocal parameter \(\kappa\) for small L/h, while the difference of those under CF-beams trends to be smooth. The opposite trend can be observed in buckling loads and vibration frequencies.

  4. 4.

    The arrangement from largest to least associated with the influence of shear deformation effect on the normalized maximum deflections would be CC-, CS-, CF- and SS-beams with the increase in \(\kappa\), while the opposite trend can be observed in normalized buckling loads and vibration frequencies. The difference of normalized maximum deflections, buckling loads and vibration frequencies between EBBT and PSDBT is pronounced with a fixed \(\kappa\) for CC and SS boundary conditions.

  5. 5.

    The normalized buckling loads and vibration frequencies decrease with the increase in the buckling and vibration orders, while the decrease rates decrease.