1 Introduction

After several years of experience in the composite’s industry, the use of modern processing technology has led to the development of a special class of advanced composite materials with strong mechanical properties called functionally graded materials (FGMs), which are suitable for many applications in a highly efficient and lightweight design. FGMs typically consist of two or different phases of material constituents to ensure the best possible performance through a smooth and continuous change of mechanical properties from one surface to another according to a certain function along a desired direction of the structure, thus removing interface problems and mitigating thermal stress concentrations. The result is a heterogeneous and anisotropic structure whose properties are superior to those of each of its monolithic components taken separately. This special class of materials was first time used by Japanese scientists as structural elements in the aerospace and nuclear field, because of its high strength combined with high resistance to large temperature gradients and excellent durability as compared to conventional composite materials. Nowadays, these elements having different geometric shapes such as beams, plates and shells made of FGMs can form the essential feature of various structural designs in engineering applications. Moreover, curved advanced composite beams have been widely recognized as one of the most fundamental structural elements supporting the whole structure which can be successfully used in the construction of modern buildings, stadiums, airports, bridges and many other structures. In any event, curved beams are subjected to external loads including warping and distortion deformations with multiple combinations of their magnitudes depending on many factors, also for permanent loads. Owing to the importance of this subject, various computational methods recommended by different beams theories have been proposed to estimate the flexural strength and vibration response of laminated composite, sandwich and functionally graded straight and/or curved beams under varying conditions.

The classical beam theory (CBT) developed by Euler–Bernoulli remains the most common model due to its simplicity and provides acceptable approximations to many engineering problems. Since the transverse shear deformation effect is disregarded in this theory, it underestimates static response and overestimates buckling loads and natural frequencies for thick and/or deep beams and is mainly limited to the case of thin beams. A number of research papers have been published on the basis of this theory, for instance Wang et al. [1] presented an analytical method using kinematic assumptions of the Euler–Bernoulli theory to investigate the free vibration of two-directional functionally graded (FG) beams with a simple power-law gradation of the material properties along the beam length and an exponential gradation along the beam thickness. An additional analytical model based on the classical beam hypothesis was presented by Pydah and Sabale [2] for the bending analysis of bidirectional FG circular beams, in which the material properties were assumed to vary smoothly and continuously along the axial and radial directions of the beam. Much later, an extensive effort done by Mohamed et al. [3] in order to investigate numerically the nonlinear free and forced vibrations of curved beams around post-buckling configuration based on nonlinear elastic foundations with clamped–clamped boundary condition and the kinematic assumptions of Euler–Bernoulli theory. In 1921, Timoshenko [4] proposed the first-order shear deformation theory (FSDT) by making a major improvement to the Euler–Bernoulli model to examine thick beams in which the shear deformation and rotary inertia effects are considered via a constant transverse shear stress distribution through the thickness. Therefore, this theory requires a shear correction factor to satisfy the stress-free boundary conditions on the top and bottom surfaces of the beam and to adequately represent the strain energy resulting from the shear deformation effect. A number of studies have been carried out on composite curved beams in the framework of Timoshenko’s beam theory, for example Yousefi and Rastago [5] presented the free vibration analysis of FG spatial curved beams with circular cross sections for different boundary conditions by considering the effects of thickness-curvature based on FSDT and Ritz method. Nanda and Kapuria [6] proposed a spectral finite element method (SFEM) for wave propagation analysis of laminated composite curved beams using two beam models, namely, FSDT and CLT (i.e., Classical laminate theory). Jouneghani et al. [7] applied the FSDT combined with Hamilton’s principle to obtain the governing equations of the free vibration problem of FG porous doubly-curved shell structures. In another survey, Wan et al. [8] analyzed the geometrically nonlinear behaviors of FG curved beams with variable curvatures subjected to thermal and mechanical loads based on Timoshenko’s beam theory. Whereas Huang and Ouyang [9] applied a new approach based on the same theory previously used by Wan et al. [8] for analyzing the static behavior of two-dimensional FG beams with different boundary conditions, in which the material properties of the beam are assumed to vary smoothly both in the length and thickness directions. A simple analytical approach based on the FSDT formulations is presented by Hieu and Tung [10] for buckling analysis of moderately thick carbon nanotube-reinforced composite (CNTRC) cylindrical shells and toroidal shell segments subjected to thermal and thermomechanical loading conditions.

In order to obtain more accurate predictions of the bending response of thick beams without using a shear correction factor, higher-order shear deformation theories (HSDTs) have been suggested by many researchers based on different assumptions and kinematic models. For example, Surana and Nguyen [11] developed a new two-dimensional element formulation based on higher-order transverse shear deformation for linear static analysis of laminated composite curved beams using the principle of virtual work to derive the approximation functions and the hierarchical nodal variables. A higher-order shear deformation theory (HSDT) was successfully proposed by Li et al. [12] to study the static bending and dynamic behaviors of FG cantilever beams with power-law gradient variation subjected to a uniform pressure. Several numerical computations are displayed graphically in this investigation to show the effects of the gradient index on the deflection and stress distribution. Later in 2014, Jun and his co-authors [13] treated the free vibration problems of the laminated composite shallow curved beams based on the trigonometric shear deformation theory (TSDT) and the dynamic stiffness method in which the effect of different geometries, boundary conditions, loading and other shell parameters are evaluated. A refined parabolic shear deformation beam theory based on finite element model utilizing Hermite-cubic interpolation function was reported by Vo et al. [14] to examine the buckling and free vibration response of FG sandwich beam with homogeneous hardcore and soft core. In the next year, Nguyen et al. [15] presented the analytical solutions for natural frequencies and critical buckling loads for three types of FG sandwich beams with various boundary conditions by using hyperbolic shear deformation theory. To check the efficiency of this theory, the obtained numerical results have been compared with those obtained using the FSDT and HSDT theories existing in the literature. Moreover, Kurtaran [16] developed a large displacement static and transient analysis of FG deep curved beams having constant curvature with various ceramic and metal combinations by using generalized differential quadrature method. An equivalent single-layer trigonometric shear deformation theory has been proposed by Sayyad et al. [17] to study the bending analysis of laminated composite and sandwich beams, in which the governing differential equations and boundary conditions are achieved by employing the principle of virtual work. Tornabene et al. [18] used the generalized differential quadrature method (GDQM) in the basis of higher-order equivalent single-layer approach to investigate the static deformations of FG laminated free-form and doubly-curved shells with the emphasis on recovering precise values of strains and stresses through the thickness of the structure. Luu and Lee [19] proposed a geometric non-linearity formulation based on the shear deformable theory to investigate in detail the effects of different geometric parameters on the buckling and post-buckling behaviors of elliptical curved beams subjected to a central concentrated vertical load with various boundary conditions. A unified quasi-3D HSDT with 4-unknowns which includes the thickness stretching effect is presented by Mantari and Canales [20] to analyze the static response of laminated cross-ply beams. The generalized governing equations are solved using the Navier-type closed-form solution for several simply supported composite beams subjected to different kinds of loads. Furthermore, Guo et al. [21] developed an efficient domain decomposition approach for static and dynamic analysis, including free, force, and transient vibration response of isotropic and laminated composite curved beams with various combinations of classical and elastic boundary constraints.

In another study, Sayyad and Ghugal [22] developed a sinusoidal shear deformation theory (SSDT) considering the effects of both transverse shear and normal stresses for the bending analysis of simply supported FG sandwich curved beams in elevation subjected to uniform transverse loads. Tornabene [23] employed an accurate HSDT in conjunction with a numerical method to investigate the dynamic response of rotating doubly-curved shell structures made of FGMs. Therefore, this analysis is performed to assess the critical value of rotating speed, which defines the stiffness reduction of the structure. Karami et al. [24] studied the mechanical buckling behavior of functionally graded carbon nanotube-reinforced composite (FG-CNTRC) curved beams by using a nonlocal higher-order shear deformation beam theory in combination with the Eringen nonlocal differential model (ENDM). In this study, the Galerkin method was also applied to calculate the critical buckling load of FG-CNTRC curved beams for different boundary conditions. He et al. [25] presented a simplified theoretical model based on two-dimensional elasticity theory to obtain the analytical solutions for static bending stress of bimodular functionally graded curved beams and to determine the position of the unknown neutral layer. Katariya and Panda [26] developed a higher-order finite element model to study the static bending and free vibration responses of the skew sandwich composite shell panels with laminate facings and different types of core materials. A unified formulation for free vibration analysis of different types of curved laminated composite beams subjected to general boundary conditions has been suggested by Qin et al. [27]. In keeping with HSDT, an enhanced variational approach is exploited in this analysis for the numerical modeling. Allam et al. [28] applied a refined higher-order shear deformation theory (RHSDT) with only four independent unknowns to investigate the bending and free vibration behavior of laminated composite and sandwich plates and shells. Avhad and Sayyad [29] have presented a new higher-order shear and normal deformation theory for the static analysis of FG sandwich beams curved in elevation, in which the non-dimensional displacements and stresses are computed for simply supported FG sandwich straight and curved beams. Recently, an improved shear deformation beam theory is applied by Magnucki et al. [30] for bending response of simply supported beams with symmetrically varying mechanical properties in the depth direction, from which the differential equations of equilibrium are obtained using the principle of stationary total potential energy. Cuong-Le et al. [31] presented a three-dimensional isogeometric analysis (3D-IGA) numerical solution based on the non-uniform rational B-splines (NURBS) basis function for solving the free vibration and buckling problems of annular plate, conical, and cylindrical shells made of FG porous rock materials. Similar to these research activities, it is also found from the literature that many recent studies have been widely embraced by many researchers using different computational models based on elasticity theory, finite element solution, and integral transform techniques to examine the continuous and discontinuous contact problems between the functionally graded layers, as well as to investigate the bending, free vibration and post-buckling responses of plates, beams and shells made of porous and nonporous FG materials, having a complex geometry and arbitrary loading and boundary conditions (e.g., Yaylaci and Birinci [32], Öner et al. [33], Adiyaman et al. [34], Yaylaci [35], Uzun Yaylaci et al. [36], Pham et al. [37], Akbaş et al. [38], Shahmohammadi et al. [39], Ghannadpour and Mehrparvar [40], Milan and Ayatollahi [41], Yaylaci et al. [42,43,44], Karami et al. [45]).

Numerous theoretical research and analytical solutions on static analysis of FG straight beams using higher-order shear deformation theories have been conducted extensively over the past decades, but few researchers have examined the static analysis of FG curved beams because of their more complex behavior. In the present study, the static analysis of FG sandwich curved beams in elevation under uniform mechanical loads was investigated through the constitutive equations of the linear theory of elasticity concepts, with the use of a simple and efficient higher-order shear and normal deformation theory developed on the basis of a unified kinematic model in integral form, which includes the shear deformation and thickness stretching effects, and satisfies the stress-free boundary conditions on the upper and lower surfaces of the beam without any proper implementation of shear correction factor. Therefore, the governing equations of FG sandwich curved beams for three types of layer configurations are described by means of the principle of virtual work, which was given in a variational form, and they are solved numerically via Navier’s solution technique for simply supported boundary conditions. A convergence study and extensive comparisons with previous results were conducted to verify the accuracy and effectiveness of the proposed beam theory. Thus, we represent a large parametric investigation to assess the effects of the power-law index, length-to-thickness ratio and types of layer configurations (i.e., skin–core-skin thickness ratio) on the displacements and stresses, which is useful for the structural analysis and design of FG sandwich curved beams.

2 FG sandwich curved beam models

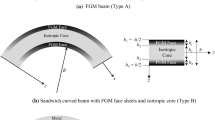
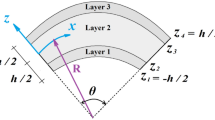
Consider a sandwich beam curved in elevation and composed in three layers. Top and bottom layers (skins) are made up of functionally graded materials and middle layer (core) is made up of homogeneous material. The beam has length L, width b, thickness h and radius of curvature R as shown in Fig. 1. The beam under examination occupies the region \(0 \le x \le L\);\(- b/2 \le y \le b/2\);\(- h/2 \le z \le h/2\) in Cartesian coordinate systems. The beam is subjected to a uniform transverse load and three types of symmetric sandwich curved beams with functionally graded skins are considered in this investigation (2–1–2, 1–1–1, 1–2–1).

Fig. 1
figure 1

The coordinate system of FG sandwich curved beam

Full size image
Fig. 2
figure 2

Variation of elasticity modulus through the thickness direction of the FG sandwich curved beams for three types of layer configurations and various values of the power-law index p

Full size image

The elastic properties of the material such as elasticity modulus in each layer of FG sandwich curved beams change gradually and continuously through the thickness direction according to the volume fractions of the constituents. For simplicity, it should be noted that the Poisson’s ratio is taken to be constant as its effect is less than that of elasticity modulus. Whereas the simple mixture rule used for the computation of elasticity modulus can be defined as follows [14, 24]:

$$ E^{{(n)}} (z) = \left( {E_{c} - E_{m} } \right)V^{{(n)}} (z) + E_{m} $$
(1)

where the subscripts \(c\) and \(m\) indicate the elastic properties of FG sandwich curved beam, ceramic and metal, respectively. While \(V^{{(n)}} (z)\) denotes the volume fraction function of ceramic phase (i.e., the three layers are arranged from top to bottom according to the numbers \(n = 1,2,3\)) expressed as follows [46]:

$$ \begin{aligned} &{\text{Top FG layer: }}V^{{(1)}} (z) = \left( {\frac{{z - h_{0} }}{{h_{1} - h_{0} }}} \right)^{p} {\text{ for }}z \in [h_{0} ,h_{1} ] \hfill \\ &{\text{Middle layer: }}V^{{(2)}} (z) = 1{\text{ for }}z \in [h_{1} ,h_{2} ] \hfill \\ & {\text{Bottom FG layer: }}V^{{(3)}} (z) = \left( {\frac{{z - h_{3} }}{{h_{2} - h_{3} }}} \right)^{p} {\text{ for }}z \in [h_{2} ,h_{3} ] \hfill \\ \end{aligned} $$
(2)

where \(p\) refers to the power-law index/parameter that controls the volume fraction gradation through the thickness of the skins. The variation of elasticity modulus through the thickness of the FG sandwich curved beams according to the type of layer configuration 1–0–1; 1–2–1; 1–1–1; 2–1–2 for various values of \(p\) is shown in Fig. 2a–d.

3 Assumptions and mathematical formulation

The proposed theory acknowledges that the shear and normal deformation have an important part in predicting the accurate structural behavior of straight and curved beams made of functionally graded materials. Therefore, the mathematical formulation of the present integral higher-order shear and normal deformation theory (IHSNDT) is based on the following kinematic assumptions.

  1. 1.

    The axial displacement in the x-direction is expressed in terms of extension, bending and integral shear components.

  2. 2.

    The transverse displacement in the z-direction consists of both bending and transverse normal deformation \((\varepsilon _{z} \ne 0)\) components.

  3. 3.

    The theory includes four independent unknown variables.

  4. 4.

    The theory provides the hyperbolic cosine distribution of transverse shear stress through the thickness of the beam curved in elevation with stretching effect, and satisfies the boundary conditions without the need for the shear correction factor.

  5. 5.

    The proposed beam theory is able of the analysis of both straight and curved beams by means of a unified kinematic model, which depends on the value of the radius of curvature.

3.1 Kinematic and constitutive relations

Based on the above assumptions of the present IHSNDT theory considering the effects of both transverse shear and normal deformations, the unified displacement field of any point of the curved beam may be written as follows:

$$ \begin{aligned} u\left( {x,z} \right) & = \left( {1 + \frac{z}{R}} \right)u_{0} \left( x \right) - z\frac{{\partial w_{0} \left( x \right)}}{{\partial x}} + k_{1} f\left( z \right)\int \theta \left( x \right)dx \hfill \\ w\left( {x,z} \right) &= w_{0} \left( x \right) + g\left( z \right)\varphi \left( x \right) \hfill \\ \end{aligned} $$
(3)

where \(u_{0} (x)\) and \(w_{0} (x)\) are the displacement components at an arbitrary point on the mid-plane of the FG sandwich curved beam in x and z-directions, respectively. Whereas \(\theta (x)\) is the rotation of a cross section of the beam at the mid-plane resulting from transverse shear and \(\varphi (x)\) is an unknown variable connected to the transverse displacement. The integral is held undetermined, and the constant \(k_{1}\) is selected with respect to the geometry. In this study, we adopt the non-polynomial hyperbolic shear shape function as the form given by Soldatos [47]

$$ f(z) = z\cosh \left( {\frac{1}{2}} \right) - h\sinh \left( {\frac{z}{h}} \right){\text{ , }}g(z) = f^{\prime}(z) $$
(4)

Using the linear strain–displacement relationships based on the definition of theory of elasticity, the normal and shear strain components can be written as

$$ \varepsilon _{x} = \frac{{\partial u}}{{\partial x}} + \frac{w}{R},{\text{ }}\varepsilon _{z} = \frac{{\partial w}}{{\partial z}},{\text{ }}\gamma _{{xz}} = {\text{ }}\frac{{\partial u}}{{\partial z}} + \frac{{\partial w}}{{\partial x}} - \frac{{u_{0} }}{R} $$
(5)

where \(\varepsilon _{x} ,{\text{ }}\varepsilon _{z}\) and \(\gamma _{{xz}}\) denote normal and transverse shear strain components. Substituting the formulas of the displacements considered by Eq. (3) into the relations given in Eq. (5), the following strain–displacement equations at any point of the curved beam system can be obtained as

$$ \begin{aligned} \varepsilon _{x} &= \varepsilon _{x}^{0} + z\varepsilon _{x}^{1} + f(z)\varepsilon _{x}^{2} + g(z)\varepsilon _{x}^{3} ,{\text{ }} \hfill \\ \varepsilon _{z} & = g^{\prime}(z)\varepsilon _{z}^{0} ,{\text{ }}\gamma _{{xz}} = g(z)\gamma _{{xz}}^{0} \hfill \\ \end{aligned} $$
(6)

where

$$ \begin{aligned} \varepsilon _{x}^{0} & = \frac{{\partial u_{0} }}{{\partial x}} + \frac{{w_{0} }}{R},{\text{ }}\varepsilon _{x}^{1} = - \frac{{\partial ^{2} w_{0} }}{{\partial x^{2} }},{\text{ }}\varepsilon _{x}^{2} = k_{1} \theta ,{\text{ }}\varepsilon _{x}^{3} = \frac{\varphi }{R},{\text{ }} \hfill \\ \gamma _{{xz}}^{0} & = k_{1} \int {\theta dx} + \frac{{\partial \varphi }}{{\partial x}} = k_{1} A'\frac{{\partial \theta }}{{\partial x}} + \frac{{\partial \varphi }}{{\partial x}},{\text{ }}\varepsilon _{z}^{0} = \varphi \hfill \\ \end{aligned} $$
(7)

in which \(A'\) is defined according to the type of solution utilized, in this instance via Navier method. Thus, the coefficients \(A'\) and \(k_{1}\) are represented by

$$ A' = - 1/\alpha ^{2} ,{\text{ }}k_{1} = \alpha ^{2} $$
(8)

where

$$ \alpha = m\pi /L $$
(9)

The constitutive relations linking the three components of stress to the three components of strain for each layer of FG sandwich curved beam can be determined by means of the generalized Hooke’s law

$$ \left\{ {\begin{array}{*{20}c} {\sigma _{x} } \\ {\sigma _{z} } \\ {\tau _{{xz}} } \\ \end{array} } \right\}^{{(n)}} = \left[ {\begin{array}{*{20}c} {Q_{{11}} (z)} & {Q_{{13}} (z)} & 0 \\ {Q_{{13}} (z)} & {Q_{{33}} (z)} & 0 \\ 0 & 0 & {Q_{{55}} (z)} \\ \end{array} } \right]^{{(n)}} \left\{ {\begin{array}{*{20}c} {\varepsilon _{x} } \\ {\varepsilon _{z} } \\ {\gamma _{{xz}} } \\ \end{array} } \right\}^{{(n)}} $$
(10)

in which \(Q_{{ij}} (z)\) are the elastic stiffness constants that can be expressed in the following standard terms

$$ Q_{{11}} (z) = Q_{{33}} (z) = \frac{{E(z)}}{{1 - \nu ^{2} }},{\text{ }}Q_{{13}} (z) = \frac{{\nu E(z)}}{{1 - \nu ^{2} }},{\text{ }}Q_{{55}} (z) = \frac{{E(z)}}{{2(1 + \nu )}} $$
(11)

3.2 Governing equations

The governing differential equations and associated boundary conditions of the proposed theory are derived by applying the variational form of the principle of virtual work, which can be expressed as follows [48,49,50,51]:

$$ \int\limits_{0}^{L} {\int\limits_{{ - b/2}}^{{b/2}} {\int\limits_{{ - h/2}}^{{h/2}} {\left( {\sigma _{x}^{{(n)}} \delta \varepsilon _{x} + \sigma _{z}^{{(n)}} \delta \varepsilon _{z} + \tau _{{xz}}^{{(n)}} \delta \gamma _{{xz}} } \right)} dzdydx} } - \int\limits_{0}^{L} {q\delta wdx} = 0 $$
(12)

where \(\delta\) is interpreted as a variational operator and \(q\) is the distributed transverse load. By substituting the values of strain components given in Eq. (6) into Eq. (12), the principle of virtual work can be rewritten according to the stress resultants as follows:

$$ \int\limits_{0}^{L} {\left( {N_{x} \delta \varepsilon _{x}^{0} + M_{x}^{b} \delta \varepsilon _{x}^{1} + M_{x}^{s} \delta \varepsilon _{x}^{2} + Q_{x} \delta \varepsilon _{x}^{3} + V_{z} \delta \varepsilon _{z}^{0} + S_{{xz}}^{s} \gamma _{{xz}}^{0} } \right)} dx - \int\limits_{0}^{L} {q\left( {\delta w_{0} + g(z)\delta \varphi } \right)dx} = 0 $$
(13)

The subscripts ''b'' and ''s'' are the moment resultants analogous to classical beam theory and the moment resultants due to shear deformation, respectively. While \(N_{x} ,{\text{ }}M_{x}^{b} ,{\text{ }}M_{x}^{s} ,{\text{ }}Q_{x} ,{\text{ }}V_{z}\) and \(S_{{xz}}^{s}\) are the six stress resultants related to the present hyperbolic beam theory which can be obtained by the following integrations

$$ \begin{aligned} N_{x} &= \sum\limits_{{n = 1}}^{3} {\int_{{h_{n} }}^{{h_{{n + 1}} }} {b\sigma _{x}^{{(n)}} } dz} ,{\text{ }}M_{x}^{b} = \sum\limits_{{n = 1}}^{3} {\int_{{h_{n} }}^{{h_{{n + 1}} }} {b\sigma _{x}^{{(n)}} z} dz} ,{\text{ }}M_{x}^{s} = \sum\limits_{{n = 1}}^{3} {\int_{{h_{n} }}^{{h_{{n + 1}} }} {b\sigma _{x}^{{(n)}} f(z)} dz} ,{\text{ }} \hfill \\ Q_{x} &= \sum\limits_{{n = 1}}^{3} {\int_{{h_{n} }}^{{h_{{n + 1}} }} {b\sigma _{x}^{{(n)}} g(z)} dz} ,{\text{ }}V_{z} = \sum\limits_{{n = 1}}^{3} {\int_{{h_{n} }}^{{h_{{n + 1}} }} {b\sigma _{z}^{{(n)}} g^{\prime}(z)} dz} ,{\text{ }}S_{{xz}}^{s} = \sum\limits_{{n = 1}}^{3} {\int_{{h_{n} }}^{{h_{{n + 1}} }} {b\tau _{{xz}}^{{(n)}} g(z)} dz} \hfill \\ \end{aligned} $$
(14)

By substituting strains and stresses terms from Eqs. (7) and (10) into Eq. (13) and integrating by parts and collecting the coefficients of \(\delta u_{0} ,\delta w_{0} ,\delta \theta\) and \(\delta \varphi\), the four governing differential equations are obtained

$$ \begin{aligned} & \delta {\text{ }}u_{0} :{\text{ }}\frac{{\partial N_{x} }}{{\partial x}} = 0, \hfill \\ &\delta {\text{ }}w_{0} :{\text{ }}\frac{{\partial ^{2} M_{x}^{b} }}{{\partial x^{2} }} - \frac{{N_{x} }}{R} + q = 0, \hfill \\ & \delta {\text{ }}\theta :{\text{ }} - k_{1} M_{x}^{s} + k_{1} A'\frac{{\partial S_{{xz}}^{s} }}{{\partial x}} = 0, \hfill \\ & \delta {\text{ }}\varphi :{\text{ }}\frac{{\partial S_{{xz}}^{s} }}{{\partial x}} - \frac{{Q_{x} }}{R} - V_{z} = 0 \hfill \\ \end{aligned} $$
(15)

By substituting Eq. (6) into Eq. (10) and the subsequent results into Eq. (14), the stress resultants of the present analytical model can be found in terms of virtual strains as follows:

$$ \begin{aligned} N_{x} &= A_{{11}} \varepsilon _{x}^{0} + B_{{11}} \varepsilon _{x}^{1} + A_{{11}}^{s} \varepsilon _{x}^{2} + E_{{11}} \varepsilon _{x}^{3} + E_{{13}}^{s} \varepsilon _{z}^{0} , \hfill \\ M_{x}^{b} &= B_{{11}} \varepsilon _{x}^{0} + D_{{11}} \varepsilon _{x}^{1} + B_{{11}}^{s} \varepsilon _{x}^{2} + F_{{11}} \varepsilon _{x}^{3} + F_{{13}}^{s} \varepsilon _{z}^{0} , \hfill \\ M_{x}^{s} & = A_{{11}}^{s} \varepsilon _{x}^{0} + B_{{11}}^{s} \varepsilon _{x}^{1} + D_{{11}}^{s} \varepsilon _{x}^{2} + H_{{11}}^{s} \varepsilon _{x}^{3} + I_{{13}}^{s} \varepsilon _{z}^{0} , \hfill \\ Q_{x} & = E_{{11}} \varepsilon _{x}^{0} + F_{{11}} \varepsilon _{x}^{1} + H_{{11}}^{s} \varepsilon _{x}^{2} + H_{{11}} \varepsilon _{x}^{3} + J_{{13}}^{s} \varepsilon _{z}^{0} , \hfill \\ V_{z} &= E_{{13}}^{s} \varepsilon _{x}^{0} + F_{{13}}^{s} \varepsilon _{x}^{1} + I_{{13}}^{s} \varepsilon _{x}^{2} + J_{{13}}^{s} \varepsilon _{x}^{3} + L_{{33}}^{s} \varepsilon _{z}^{0} , \hfill \\ S_{{xz}}^{s} &= K_{{55}}^{s} \gamma _{{xz}}^{0} \hfill \\ \end{aligned} $$
(16)

Next, by substituting Eq. (7) and Eq. (16) into Eq. (15), one can obtain the governing differential equations in terms of unknown displacement variables \((u_{0} ,w_{0} ,{\text{ }}\theta ,\varphi )\) as follows:

$$ \delta u_{0} :{\text{ }}A_{{11}} \frac{{\partial ^{2} u_{0} }}{{\partial x^{2} }} + \frac{{A_{{11}} }}{R}\frac{{\partial w_{0} }}{{\partial x}} - B_{{11}} \frac{{\partial ^{3} w_{0} }}{{\partial x^{3} }} + k_{1} A_{{11}}^{s} \frac{{\partial \theta }}{{\partial x}} + \left( {\frac{{E_{{11}} }}{R} + E_{{13}}^{s} } \right)\frac{{\partial \varphi }}{{\partial x}} = 0 $$
(17a)
$$ \begin{aligned}& \delta w_{0} :{\text{ }}B_{{11}} \frac{{\partial ^{3} u_{0} }}{{\partial x^{3} }} - \frac{{A_{{11}} }}{R}\frac{{\partial u_{0} }}{{\partial x}} + \frac{{2B_{{11}} }}{R}\frac{{\partial ^{2} w_{0} }}{{\partial x^{2} }} - D_{{11}} \frac{{\partial ^{4} w_{0} }}{{\partial x^{4} }} - \frac{{A_{{11}} }}{{R^{2} }}w_{0} + k_{1} B_{{11}}^{s} \frac{{\partial ^{2} \theta }}{{\partial x^{2} }} - \frac{{k_{1} A_{{11}}^{s} }}{R}\theta \hfill \\&\qquad + \left( {\frac{{F_{{11}} }}{R} + F_{{13}}^{s} } \right)\frac{{\partial ^{2} \varphi }}{{\partial x^{2} }} - \left( {\frac{{E_{{11}} }}{{R^{2} }} + \frac{{E_{{13}}^{s} }}{R}} \right)\varphi + q = 0 \hfill \\ \end{aligned} $$
(17b)
$$\begin{aligned} & \delta \theta :{k_1}A_{11}^s\frac{{\partial {u_0}}}{{\partial x}} - \frac{{{k_1}A_{11}^s}}{R}{w_0} + {k_1}B_{11}^s\frac{{{\partial ^2}{w_0}}}{{\partial {x^2}}} + k_1^2{{A'}^2}K_{55}^s\frac{{{\partial ^2}\theta }}{{\partial {x^2}}} - k_1^2D_{11}^s\theta + {k_1}A^\prime K_{55}^s\frac{{{\partial ^2}\varphi }}{{\partial {x^2}}}\\&\qquad - \left( {\frac{{{k_1}H_{11}^s}}{R} + {k_1}I_{13}^s} \right)\varphi = 0 \end{aligned}$$
(17c)
$$ \begin{aligned} & \delta \varphi :{\text{ }} - \left( {\frac{{E_{{11}} }}{R} + E_{{13}}^{s} } \right)\frac{{\partial u_{0} }}{{\partial x}} + \left( {\frac{{F_{{11}} }}{R} + F_{{13}}^{s} } \right)\frac{{\partial ^{2} w_{0} }}{{\partial x^{2} }} - \left( {\frac{{E_{{11}} }}{{R^{2} }} + \frac{{E_{{13}}^{s} }}{R}} \right)w_{0} + k_{1} A^{\prime}K_{{55}}^{s} \frac{{\partial ^{2} \theta }}{{\partial x^{2} }} + K_{{55}}^{s} \frac{{\partial ^{2} \varphi }}{{\partial x^{2} }} \hfill \\ &\qquad {\text{ }} - \left( {\frac{{k_{1} H_{{11}}^{s} }}{R} + k_{1} I_{{13}}^{s} } \right)\theta - \left( {\frac{{H_{{11}} }}{{R^{2} }} + \frac{{2J_{{13}}^{s} }}{R} + L_{{33}}^{s} } \right)\varphi = 0 \hfill \\ \end{aligned} $$
(17d)

where the FG sandwich beam stiffness components are given as follows:

$$\begin{array}{l} \left( {{A_{11}},{B_{11}},{D_{11}},A_{11}^s,B_{11}^s,D_{11}^s} \right) = \sum\limits_{n = 1}^3 {\int_{{h_n}}^{{h_{n + 1}}} {bQ_{11}^{(n)}(z)\left( {1,z,{z^2},f(z),zf(z),{f^2}(z)} \right)dz} } ,\\ \left( {{E_{11}},{F_{11}},{H_{11}},H_{11}^s} \right) = \sum\limits_{n = 1}^3 {\int_{{h_n}}^{{h_{n + 1}}} {bQ_{11}^{(n)}(z)\left( {g(z),zg(z),{g^2}(z),f(z)g(z)} \right)dz} } ,\\ \left( {E_{13}^s,F_{13}^s,I_{13}^s,J_{13}^s} \right) = \sum\limits_{n = 1}^3 {\int_{{h_n}}^{{h_{n + 1}}} {bQ_{13}^{(n)}(z)\left( {g^\prime(z),zg^\prime(z),f(z)g^\prime(z),g(z)g^\prime(z)} \right)dz,} } \\ K_{55}^s = \sum\limits_{n = 1}^3 {\int_{{h_n}}^{{h_{n + 1}}} {bQ_{55}^{(n)}(z){g^2}(z)dz} } ,\\ L_{33}^s = \sum\limits_{n = 1}^3 {\int_{{h_n}}^{{h_{n + 1}}} {bQ_{33}^{(n)}(z){{g'}^2}(z)dz} } \end{array}$$
(18)

3.3 Analytical solution procedure

The analytical solutions of Eq. (17) for simply supported FG sandwich curved beams under uniform distributed loads can be adopted, by using the well-known Navier’s solution technique. The boundary conditions along the edges at \(x = 0\) and \(x = L\) related to the present hyperbolic beam theory are expressed as follows:

$$ w_{0} = N_{x} = M_{x}^{b} = M_{x}^{s} = \varphi = 0 $$
(19)

For boundary conditions given in Eq. (19), the analytical solutions are assumed to be defined by the following single trigonometric series

$$ \left\{ {\begin{array}{*{20}c} {u_{0} } \\ {w_{0} } \\ \theta \\ \varphi \\ \end{array} } \right\} = \sum\limits_{{m = 1}}^{\infty } {\left\{ {\begin{array}{*{20}c} {U_{m} \cos (\alpha {\text{ }}x)} \\ {W_{m} \sin (\alpha {\text{ }}x)} \\ {\Theta _{m} \sin (\alpha {\text{ }}x)} \\ {\Phi _{m} \sin (\alpha {\text{ }}x)} \\ \end{array} } \right\}} $$
(20)

where \(U_{m} ,W_{m} ,\Theta _{m}\) and \(\Phi _{m}\) are unknown parameters of the FG sandwich curved beam. The transverse load \(q(x)\) applied on the top surface of the curved beam is presented as a single trigonometric series

$$ q(x) = \sum\limits_{{m = 1}}^{\infty } {q_{m} \sin (\alpha {\text{ }}x)} $$
(21)

in which the coefficient of Fourier expansion is fixed by \(q_{m} = 4q_{0} /m\pi\) for uniformly distributed loading with maximum intensity \(q_{0}\) and \(m\) is the positive integer that changes with odd numbers \((m = 1,3,5...\infty )\). The analytical solution is obtained by substituting Eqs. (18–21) into Eq. (17), leads to the following matrix form

$$ \left[ {\begin{array}{*{20}c} {K_{{11}} } & {K_{{12}} } & {K_{{13}} } & {K_{{14}} } \\ {K_{{12}} } & {K_{{22}} } & {K_{{23}} } & {K_{{24}} } \\ {K_{{13}} } & {K_{{23}} } & {K_{{33}} } & {K_{{34}} } \\ {K_{{14}} } & {K_{{24}} } & {K_{{34}} } & {K_{{44}} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {U_{m} } \\ {W_{m} } \\ {\Theta _{m} } \\ {\Phi _{m} } \\ \end{array} } \right\}{\text{ }} = \left\{ {\begin{array}{*{20}c} 0 \\ {q_{m} } \\ 0 \\ 0 \\ \end{array} } \right\} $$
(22)

where \([K_{{ij}} ]\) represents the components of the stiffness matrix, which can be expressed as follows:

$$\begin{array}{l} {K_{11}} = - {\alpha ^2}{A_{11}},{K_{12}} = \alpha \left( {\frac{{{A_{11}}}}{R} + {\alpha ^2}{B_{11}}} \right),\\ {K_{13}} = {k_1}\alpha A_{11}^s,{K_{14}} = \alpha \left( {\frac{{{E_{11}}}}{R} + E_{13}^s} \right),\\ {K_{22}} = - \frac{{{A_{11}}}}{{{R^2}}} - {\alpha ^2}\left( {\frac{{2{B_{11}}}}{R} - {\alpha ^2}{D_{11}}} \right),{K_{23}} = - \frac{{{k_1}A_{11}^s}}{R} - {k_1}{\alpha ^2}B_{11}^s,\\ {K_{24}} = - \frac{{{E_{11}}}}{{{R^2}}} - {\alpha ^2}\left( {\frac{{{F_{11}}}}{R} + F_{13}^s} \right) - \frac{{E_{13}^s}}{R},\\ {K_{33}} = - k_1^2\left( {D_{11}^s + {\alpha ^2}{{A'}^2}K_{55}^s} \right),{K_{34}} = - \frac{{{k_1}H_{11}^s}}{R} - {k_1}\left( {I_{13}^s + {\alpha ^2}A'K_{55}^s} \right),\\ {K_{44}} = - \frac{{{H_{11}}}}{{{R^2}}} - \frac{{2J_{13}^s}}{R} - L_{33}^s - {\alpha ^2}K_{55}^s, \end{array}$$
(23)

4 Numerical results and discussions

In this section, the static bending analysis of symmetric FG sandwich curved beams under uniform mechanical loads was investigated by using a unified kinematic model based on an efficient IHSNDT. The properties of the skins are composed of a mixture of metal (Aluminum) and ceramic (Alumina) materials with a continuous change through the thickness direction according to the power-law index/parameter, whereas the central core is made up of a homogeneous ceramic material. Since there is no available previous results based on the exact elasticity solution for the bending analysis of FG sandwich curved beams, the developed IHSNDT model is checked with several theories by addressing a problem of simply supported FG sandwich straight and curved beams. The numerical results of non-dimensional displacements, normal and shear stresses are presented in Tables 3 through 9 via several parametric studies such as power-law index, length-to-thickness ratio, skin–core-skin thickness ratio and radius of curvature then are compared with the solutions from previous studies to verify the accuracy of the proposed beam theory. The material properties used for this whole calculation are given in Table 1, whereas Table 2 shows the types of layer configurations considered for this analysis.

Table 1 Material properties of FG sandwich beams [52]
Full size table
Table 2 Types of configurations and thickness layers of FG sandwich beams
Full size table
Table 3 Comparison of non-dimensional transverse displacement of simply supported FG sandwich straight beams subjected to uniform loads
Full size table

For the simplicity, the physical quantities are presented in a non-dimensional terms as follows:

$$ \begin{aligned} \bar{u} & = 100\frac{{E_{m} h^{3} }}{{q_{0} L^{4} }}u\left( {0, - \frac{h}{2}} \right),{\text{ }}\bar{w} = 100\frac{{E_{m} h^{3} }}{{q_{0} L^{4} }}w\left( {\frac{L}{2},0} \right),{\text{ }} \hfill \\ {\text{ }}\bar{\sigma }_{x} (z) & = \frac{h}{{q_{0} L}}\sigma _{x} \left( {\frac{L}{2},\frac{h}{2}} \right),{\text{ }}\bar{\tau }_{{xz}} (z) = \frac{h}{{q_{0} L}}\tau _{{xz}} \left( {0,0} \right){\text{ }} \hfill \\ \end{aligned} $$
(24)

4.1 FG sandwich straight beams

In order to prove the validity and versatility of the present mathematical model, the first convergence study was devoted to the forecasting of the static bending phenomenon of simply supported straight FG sandwich beams with homogeneous core, by considering three types of layer configurations (2–1–2, 1–1–1, 1–2–1) and for different values of power-law index \((p = 0,{\text{ }}1,{\text{ }}2,{\text{ }}5,{\text{ }}1{\text{0}})\), as well as the length-to-thickness ratio was taken as \((L/h = 5,{\text{ }}20)\). It should be noted that the numerical results in the case of straight beams are computed by fixing the value of the radius of curvature at infinity \((R = \infty )\) in the present formulation. These results are compared with those obtained by classical beam theory (CBT) of Euler–Bernoulli, FSDT of Timoshenko, quasi-3D parabolic shear deformation theory (quasi-3D PSDT) developed by Vo et al. [52], analytical solution based on the hyperbolic shear deformation theory (HSDT) presented by Sayyad and Avhad [53], quasi-3D sinusoidal shear deformation theory (quasi-3D SSDT) used by Sayyad and Ghugal [22] and fifth-order shear and normal deformation theory (FOSNDT) recently developed by Avhad and Sayyad [29]. In particular, the FSDT results are achieved considering the shear correction factor equal to 5/6.

Examination of Tables 3, 4 and 5 reveals that the results of non-dimensional transverse displacement, axial and shear stresses obtained by using the present approach are in excellent agreement with those generated by Vo et al. [52] using quasi-3D PSDT for all types of layer configurations and all power-law indexes, except for some values of transverse shear stress, a slight difference is noted between the present model together with Vo et al. [52] compared to the analytical results of FOSNDT presented by Avhad and Sayyad [29], which is generally induced by the displacement model adopted in their study. Since the HSDT model proposed by Sayyad and Avhad [53] neglects the effects of transverse normal deformations \((\varepsilon _{z} = 0)\), the results obtained through this theory show a slight divergence with the present theory. As usual, it can always be noticed here that the classical beam theory (CBT) underestimates the results of transverse displacement as compared to the other theories due to disregard of transverse shear and normal strains. Besides, it is obvious that the measured transverse displacement values decrease as the core thickness increases with the decreasing of the power-law index, and therefore the beam structure in these conditions has become harder.

On the other hand, Table 4 shows that the increase in the thickness of the core layer has a significant effect on the reduction of the normal axial stress in the beam for both length-to-thickness ratios \((L/h = 5,{\text{ }}20)\). It is also observed from Table 5 that the non-dimensional transverse shear stress increases with respect to increase in the power-law parameter; and conversely, it can be reduced as the thickness of the middle homogeneous layer increases.

Table 4 Comparison of non-dimensional axial stress of simply supported FG sandwich straight beams subjected to uniform loads
Full size table
Table 5 Comparison of non-dimensional transverse shear stress of simply supported FG sandwich straight beams subjected to uniform loads
Full size table

4.2 FG sandwich curved beams

As the second example, let’s consider simply supported symmetric FG sandwich beams curved in elevation, which are made up of the material properties defined in Table 1 and are selected for three types of layer configurations denoted by (2–1–2, 1–1–1, 1–2–1) as shown in Table 2. The axial and transverse displacements, normal and shear stresses through the beam’s thickness defined earlier by Eq. (24) in non-dimensional form are presented in Tables 6, 7, 8, 9 and depicted in Figs. 3, 4, 5, 6 for different values of the power-law index \((p = 0,{\text{ }}1,{\text{ }}2,{\text{ }}5,{\text{ }}1{\text{0}})\) and radius of curvature \((R = 5,{\text{ }}1{\text{0}},{\text{ }}2{\text{0}})\) and for both length-to-thickness ratios \((L/h = 5,{\text{ }}20)\). For the verification of the present integral higher-order analytical model, the computed results of displacements and stresses have also been checked with the corresponding results of Sayyad and Ghugal [22] based on quasi-3D SSDT model and those achieved by Avhad and Sayyad [29] using fifth-order shear and normal deformation theory (FOSNDT).

Table 6 Comparison of non-dimensional axial displacement of simply supported FG sandwich curved beams subjected to uniform loads
Full size table
Fig. 3
figure 3

Variation of axial displacement through the thickness for three types of layer configurations FG sandwich curved beams subjected to uniform loads (L/h = 5, R/h = 5).

Full size image
Fig. 4
figure 4

Variation of transverse displacement through the thickness for three types of layer configurations FG sandwich curved beams subjected to uniform loads (L/h = 5, R/h = 5)

Full size image
Fig. 5
figure 5

Variation of axial stress through the thickness for three types of layer configurations FG sandwich curved beams subjected to uniform loads (L/h = 5, R/h = 5)

Full size image
Fig. 6
figure 6

Variation of transverse shear stress through the thickness for three types of layer configurations FG sandwich curved beams subjected to uniform loads (L/h = 5, R/h = 5).

Full size image

From the comparisons of Tables 6 and 7, one notes that the present analytical solutions of axial and transverse displacements obtained by using the present beam theory are exactly matching with those presented by Sayyad and Ghugal [22] and Avhad and Sayyad [29] for all values of power-law parameter p and radius of curvature. It can be seen again that the increment of p leads to the increase in the both displacements of simply supported FG sandwich curved beams. Furthermore, the value of the axial displacement decreases with the increase in the value of the radius of curvature for all types of layer configurations under examination, whereas the change in transverse displacement versus the change in radius of curvature is nearly negligible for the same value of p.

Table 7 Comparison of non-dimensional transverse displacement of simply supported FG sandwich curved beams subjected to uniform loads
Full size table

The non-dimensional normal and shear stresses through the beam’s thickness for simply supported boundary condition are obtained directly and reported in Tables 8 and 9 by using the constitutive relations. It is evident from the obtained results that the present computations for all types of layer configurations FG sandwich curved beams are in reasonably good agreements with those of quasi-3D SSDT solution given by Sayyad and Ghugal [22] and to those reported by Avhad and Sayyad [29] based on FOSNDT. As it is expected, increasing of the power-law parameters leads to the increases of the axial and shear stresses and this explains that the increase in this parameter causes a decrease in beam stiffness. On the other hand, for the same type of configuration and the same value of the power-law parameter, the shear stresses are identical with respect to the change in the radius of curvature.

Table 8 Comparison of non-dimensional axial stress of simply supported FG sandwich curved beams subjected to uniform loads
Full size table
Table 9 Comparison of non-dimensional shear stress of simply supported FG sandwich curved beams subjected to uniform loads
Full size table

Figures 3a–c show the variation of axial displacement through the thickness for three types of layer configurations FG sandwich curved beams subjected to uniform loads for length-to-thickness ratio L/h = 5 and radius of curvature R/h = 5, it can be seen that, the variation of axial displacement for all configurations varies linearly along the thickness of the beams, and the highest displacement values are more remarkable at the top surface of the beam \((z = - h/2)\) for different values of the power-law parameter, whereas the maximum displacement value is measured when the value of \(p\) takes 10 (i.e., a higher portion of metal phase makes the beams more flexible). It is also pointed out within the framework of the proposed beam theory that the transverse displacement observed below in Fig. 4a–c its value increases with the increase of the value of the power-law parameter and with the decrease in the thickness of the middle ceramic layer.

The variation of axial stress through the thickness of the beam computed from constitutive relations is depicted in Figs. 5a–c. For the minimum value of the power-law parameter p = 0 that corresponds to fully ceramic beams, the axial stress presents a linear variation along the thickness for all configurations of FG sandwich curved beams. However, for different values of this parameter, the linear variation is only observed in the middle homogeneous layer because of the same material properties but in nonhomogeneous skins the variation is hyperbolic for p > 0 due to the variation in the volume fraction of the constituents. Besides, the maximum axial stress is observed at the interfaces between the middle layer and the FG skins when p is greater than zero. Also, one can see the maximum axial stress for the type of configuration 1–2–1 while the minimum is observed in the type of configuration 2–1–2. Moreover, it can be seen from Figs. 6a–c that the maximum shear stress for length-to-thickness ratio L/h = 5 and radius of curvature R/h = 5 is obtained at the middle homogeneous layer of all types of FG sandwich curved beams for different values of p whereas in nonhomogeneous skins it is minimum due to gradation of material properties. From these figures, it is also underlined that the zero transverse shear stress condition at upper and lower surfaces of the beam are satisfied using the constitutive relations.

5 Conclusions

In this paper, an efficient integral higher-order shear and normal deformation theory (IHSNDT) has been developed according to the simple and unified kinematic model for static bending response of functionally graded (FG) sandwich straight and curved beams subjected to uniform mechanical loads. The novelty of this study is the use of a new kinematic, in which the axial displacement includes an undetermined integral component in order to reduce the number of unknown variables and contains a hyperbolic cosine function in terms of the thickness coordinate to describe adequately the variation of the transverse shear stress across the thickness of a beam with stretching effect. Thus, the proposed model exactly satisfies the conditions for zero shear stress on the top and bottom surface of the beam without the need for a shear correction factor. The governing differential equations and associated boundary conditions are established analytically within the framework of the principle of virtual work, and then they are solved via Navier’s technique. A variety of FG sandwich straight and curved beams with simply supported boundary conditions are studied in detail, considering the influence of different parameters such as the power-law index, length-to-thickness ratio and types of layer configurations on the static behavior of these advanced composite structures. The comparisons prove that the present numerical solutions of displacements and stresses are in excellent agreement with the analytical solutions found in the previous studies. Finally, it is possible that the proposed theory in conjunction with the new integral kinematic model can be conveniently used to analyze the bending response of FG sandwich curved beams under various loading and boundary conditions.