1 Introduction

With the current rapid development of micro- and nano-electro-mechanical systems (MEMS and NEMS), such as nanosensors, nanoactuators and nano-/microscale devices, the deformations and responses of their basic structural components become increasingly important to the optimal designs of these devices. The study of the mechanical behaviors of basic structural components, including rods, beams, plates and shells at the micro-/nanoscale, is always of scientific and technological significance and, therefore, has drawn unprecedented attention over the recent years.

Difficulties usually exist in experimental studies of nanoscopic systems because of the extreme difficulty in controlling their precision, even impossible for the nanostructures within complex environments. Atomistics (e.g., density functional theory, molecular dynamics), statistical mechanics and continuum mechanics have therefore been employed for theoretical predictions and numerical simulations [1,2,3,4]. Numerical simulations based on atomistics and statistical mechanics are, however, generally complex and time-consuming, especially for structures made of complicated composition. Continuum mechanics-based methods have hence drawn attention over the recent years. Classical mechanics of elasticity is often referred to as the “grand unified theory” of engineering technique and hence has since become the foundation of engineering science. The Cauchy’s stress principle paves the way for the rational continuum mechanics but at the same time requires a continuum assumption [5], which is, nonetheless, no longer valid as structural feature size is reduced to nanoscale in which materials have to be considered as naturally discrete nanostructures. On the other hand, these discrete points of nanostructures are interacted each other by using “long-ranged” interaction forces which have proved by various theories (such as atomistics) and experiments.

Alternatively, the nonlocal theory, as one of the well-accepted non-classical (generalized) continuum theories, is often employed to significantly reduce the complexity of atomistic simulations while retaining their most important mechanical behaviors. A scientific awareness of generalized continuum theories dates at least back to the early twentieth century. In 1909, Cosserat and Cosserat [6] proposed a micropolar continuum theory. Seminal works of the nonlocal theory of elasticity can trace to Kröner [7], Eringen [8] and several other authors [9, 10] and laid the theoretical foundational framework of nonlocality. The nonlocal theory defines a nonlocal stress concept that is completely different from that of classical mechanics (the Cauchy’s stress is the force acting on a unit area). The nonlocal stress is defined as the force crossing a plane with unit area and therefore allows for “long-ranged” forces. In the context of the nonlocal theory of elasticity [11], unlike the local theory in which stress at a “reference” point \(\mathbf{x}\) only depends on the strain at \(\mathbf{x}\), the nonlocal stress tensor \(\sigma _{ij}\) at \(\mathbf{x}\) has to be predicted based on the weighted average of the strain field at all the points \(\mathbf{x'}\) within the domain of interest. For a linear homogeneous and isotropic material, the nonlocal constitutive relation for three-dimensional (3D) structures can be expressed as

$$\begin{aligned} {\sigma _{ij}}({\mathbf{x}}) = \int _V \mathcal{K} ({\mathbf{x}},{\mathbf{x'}},\ell )\sigma _{ij}^L({\mathbf{x'}}){\mathrm{d}}V\left( {{\mathbf{x'}}} \right) , \end{aligned}$$
(1)

where \(\sigma _{ij}^L\) is the classical (local) stress tensor. According to Hooke’s law, the local constitutive law is \(\sigma _{ij}^L({\mathbf{x'}})=C_{ijkl}\varepsilon _{kl}({\mathbf{x'}})\) where \(C_{ijkl}\) is the fourth-order elasticity tensor, and \(\varepsilon _{kl}\) is the strain tensor. The kernel function \(\mathcal{K} ({\mathbf{x}},{\mathbf{x'}},\ell )\) in equation (1) is known as the nonlocal attenuation function. The intrinsic characteristic length \(\ell \) allows the nonlocal theory of elasticity to capture the size dependence of “long-ranged” forces. Often \(\ell =e_0a\) where a is a material internal characteristic length including crystal constant, and \(e_0\) is an unknown dimensionless constant to be determined from experiments or atomistic simulations.

The models in the framework of the nonlocal integral constitutive law (1) are, generally, very difficult to be analytically solved, even for a very simple structural problem, and therefore require numerical solution techniques, such as finite element methods [12,13,14,15,16], iterative methods [17]. For infinite mediums, Eringen [18] showed that the integral constitutive relation (1) can be equivalent to its differential counterpart. Compared with equation (1), the differential constitutive relation is easier to be tractable. For the differential-type problems, the nonlocal attenuation function can be treated as the Green’s function of a differential operator from the viewpoint of mathematics. That is, considering specific boundary conditions, we have [19]

$$\begin{aligned} \mathcal{D}_\mathbf{x} \mathcal{K}({\mathbf{x}},{\mathbf{x'}},\ell ) = \delta ({\mathbf{x}} - {\mathbf{x'}}), \end{aligned}$$

where \(\mathcal{D}_\mathbf{x}\) is a differential operator and \(\delta ({\mathbf{x}} - {\mathbf{x'}})\) is the Dirac delta function. The differential operator has been widely employed to simplify the integral-type constitutive models [20,21,22,23,24,25,26]. For example, this allows us to construct the differential-type constitutive law given in equation (1) as \(\mathcal{D}_\mathbf{x} {\sigma _{ij}} = C_{ijkl}\varepsilon _{kl}\) by employing specific boundary conditions. Caution must be drawn concerning the equivalent relation between differential and integral constitutive equations, which is established based on specific boundary conditions.

The classical continuum mechanics, in principle, treats beam-type structures as one-dimensional (1D) geometrical structures. Due to the simplicity of the differential constitutive relation, it has been widely and intuitively employed to study the nonlocal effect on the mechanical behaviors of finite structures without much theoretical support and physical understanding [22, 27,28,29,30,31,32,33, 33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48]. Furthermore, for the sake of simplicity in application, only the nonlocal effects in the axial direction were taken into account in the existing nonlocal beam models. Under these cases, the differential constitutive relation for nonlocal beams with \(\mathcal{D}_\mathbf{x} =\left( {1 - {{\left( {{e_0}a} \right) }^2}{\nabla ^2}} \right) \) is expressed as

$$\begin{aligned} \left( {1 - {{\left( {{e_0}a} \right) }^2}{\nabla ^2}} \right) {\sigma _{xx}} = E{\varepsilon _{xx}}, \end{aligned}$$
(2)

where the Laplacian operator is defined as \({\nabla ^2} = {\partial ^2}/\partial {x^2}\) for 1D problems. Note that the axial direction is along x, and E denotes Young’s modulus. There are a huge number of works focusing on the studies of the size-dependent effects in the framework of the differential constitutive relation in (2), the readers are encouraged to refer to the recent review papers [49, 50] and the references therein. While the integral and differential constitutive relations can be equivalent to each other in the analysis of wave propagation in infinite mediums, there exist considerable differences in finite structures due to the naturally different boundary condition implied in the integral and differential constitutive relations [51, 52]. Although there exist a lot of papers which use the differential-type constitutive laws, caution must be drawn for the boundary value problem mentioned above.

To eliminate the considerable difference, some researchers [16, 53,54,55,56,57,58,59] reconsidered the nonlocal beam problems by using the integral constitutive relation, intuitively following the one-dimensional geometrical simplification (for example, Euler–Bernoulli beam assumption). Regardless of the three-dimensional interactions between the atoms, the total stress based on the one-dimensional nonlocal beam models is expressed as

$$\begin{aligned} {\sigma _{xx}}({\mathbf{x}}) = \int _{ - L/2}^{L/2} { \mathcal{K} ({\mathbf{x}},{\mathbf{x'}},\ell )\sigma _{xx}^L({\mathbf{x'}}){\mathrm{d}}x\left( {{\mathbf{x'}}} \right) } . \end{aligned}$$
(3)

In fact, the nonlocal stress (3) in the thickness or width directions is local rather than nonlocal. This is questionable due to the fact that classical mechanics will break down firstly at the shortest dimension (beams’ width or height) when the feature size of a beam shrinks from macroscale down to the nanoscale [60]. Thus, the 1D integral constitutive relation of equation (3) may fail to capture the true nonlocal behaviors which naturally arise from the three-dimensional long-ranged forces. Furthermore, the nonlocal stress from equation (3) intuitively follows the one-dimensional geometrical simplification and as a result, lacks the necessary one-dimensional physical simplification required for nonlocal problems.

How do the nonlocal interactions in beams’ width and thickness directions affect the mechanics of beams with nanometer feature size? The objective of this work is therefore to reveal and to subsequently establish the cross-section effect on the bending behaviors of nonlocal beams. The Euler–Bernoulli beam model has the simplest formulations among many available beam models and therefore will be employed to simplify the illustration of the importance of the cross-section effect on the mechanics of beams.

The paper is outlined as follows: Preliminary concepts on the cross-section effect and a three-dimensional attenuation function will be discussed in Section 2. Then, Section 3 will reveal the cross-section effect on both the nonlocal stress and the bending moment of a three-dimensional nonlocal Euler–Bernoulli beam model. It has been found that the nonlocal physical dimension of beam-type structures is not in agreement with the 1D geometric direction of classical beam mechanics. The main contributions to size dependence should be attributed to the beam’s cross-section dimensions, rather than its widely used axial length dimension. With the proposed and developed bending moment, closed-form solutions for the deflections of both simply supported and cantilevered beams are derived. Next, Section 4 will develop a calibration method for the intrinsic characteristic length based on molecular dynamics simulations. Finally, the work will end with some concluding remarks.

2 Preliminary concepts and problem definition

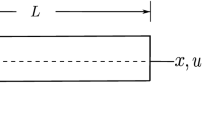
In this study, we seek to reveal the cross-section effect on the bending behaviors of nonlocal beams. The beam of interest in this study is shown in Figure 1, whose cross section is assumed to be rectangular. Let the beam’s thickness, width and length be H, W and L, respectively. For beam-type structures, these dimensions satisfy the requirements that \(H \ll L\) and \(W \ll L\).

The Cartesian coordinate system shown in Figure 1 is adopted here. Its x-axis is along the beam’s length direction through the beam’s geometric centroid. Its y-axis is along the beam’s thickness (height) direction where the beam’s deflection takes place. The y-axis is transverse to the x-axis. The x- and y-axes construct a xy-plane in the page, while the z-axis is out of the xy-plane.

Without loss of generalization, we consider the case where beam’s deflection only occurs in the y-axis direction. Under such circumstance, the deflections of beams can only be observed in their thickness directions and the displacements take only place at the xy-plane. This in turn means that the displacements in the beam’s width direction become zero.

2.1 The importance of cross-section effect

For the beam-type structures shown in Figure 1, the classical mechanics typically characterizes this structure as an one-dimensional geometrical structure (its center line) by employing, for example, Euler–Bernoulli beam hypothesis. As a very simple yet representative example, the Euler–Bernoulli hypothesis of beam bending problem states that the transverse normal line, as shown in Figure 1, remains straight and inextensible and more importantly retains normal to the geometric middle surface after bending deformation. With this hypothesis, the original 3D geometric deformation problem can be treated as a study on the transverse normal line. Therefore, beams are considered as a 1D geometric problem, just like \(H \ll L\) and \(W \ll L\). This one-dimensional geometrical simplification can significantly reduce the complexity of beam problems while retaining all the most important mechanical behaviors.

Fig. 1
figure 1

A beam with three-dimensional nonlocal elasticity

Full size image

In the current practice, by following the traditional geometrical simplification for beams, the nonlocal effect in the beams’ axial length direction is intuitively and widely considered for modeling beam-type structures in open literature. In fact, these nonlocal analyses do not take into account the main contribution of nonlocal effect due to the following reasons:

  1. (a)

    In the framework of the nonlocal theory of elasticity [11], the nonlocal stress at a “reference” point is predicted by the weighted average of the strain field at all the points in the domain of interest, as shown in equation (1). The nonlocal influence zone is a sphere illustrated in Figure 1, and therefore, nonlocality is naturally three dimensional, rather than the one-dimensional simplification currently in practice.

  2. (b)

    From the viewpoint of atomistics, the interactions between atoms take place in all the spatial directions and as a result, the long-ranged forces are expected in all the three dimensions.

  3. (c)

    When the feature size of beams is reduced to the nanoscale, classical mechanics will break down firstly at cross-section dimensions of beams due to the simple fact that beams’ cross-section dimensions are far smaller than their length dimension, as illustratively shown in Figure 1. This in turn implies that the cross-section effect is likely to play a dominant role in the contribution of size dependence.

  4. (d)

    These existing 1D nonlocal beam models, intuitively developed based on the 1D geometrical simplification of classical mechanics, suffer nonetheless from a lack of an one-dimensional physical simplification needed for nonlocal problems.

  5. (e)

    The stresses predicted by the one-dimensional nonlocal beam models in the cross-section dimensions are basically local rather than nonlocal.

All these manifest that the nonlocal problem is three dimensional in nature and should therefore be analyzed as a 3D physical problem, instead of the current 1D approach.

2.2 Three-dimensional nonlocal attenuation function

The requirements, which a nonlocal attenuation function \(\mathcal{K} ({\mathbf{x}},{\mathbf{x'}},\ell )\) in the integral constitutive relation (1) should generally fulfill, can be summarized as follows [11, 19, 61]:

  1. (a)

    The nonlocality degree should decrease as the distance of two points increases.

  2. (b)

    When \(\ell /L_{ext} \rightarrow 0\) where \(L_{ext}\) is the external characteristic length (e.g., the shortest dimension among the geometric feature lengths, the wavelength of applied loads), the nonlocal attenuation function should reduce to a Dirac delta function, that is,

    $$\begin{aligned} {\left. {\mathcal{K} ({\mathbf{x}},{\mathbf{x'}},\ell )} \right| _{\frac{\ell }{{{L_{ext}}}} \rightarrow 0}} = \delta ({\mathbf{x}} - {\mathbf{x'}}). \end{aligned}$$

    This makes sure that the nonlocal theory can be back to classical mechanics theory if the nonlocal effect is neglectable.

  3. (c)

    The maximum value of the nonlocal attenuation function must take place at the reference point, that is,

    $$\begin{aligned} \max \left\{ {\mathcal{K}({\mathbf{x}},{\mathbf{x'}},\ell )} \right\} = \mathcal{K}({\mathbf{x}},{\mathbf{x}},\ell ). \end{aligned}$$
  4. (d)

    Integrating the nonlocal attenuation function over the domain of interest should be unit. This guarantees that the integral constitutive relation (1) can be the same as the classical one when considering a constant strain.

Over the many choices of nonlocal attenuation functions, the Gaussian distribution function can satisfy the desired requirements that the nonlocal attenuation function must be positive and shall decay rapidly with the increasing distance r between the “reference” and “influence” points (\(r=\left\| {{\mathbf{x}}-{\mathbf{x'}}}\right\| \)). For the Cartesian coordinates used in Figure 1, this distance r can be written in terms of x, y and z components as

$$\begin{aligned} r = \sqrt{{{\left( {z - z'} \right) }^2} + {{\left( {x - x'} \right) }^2} + {{\left( {y - y'} \right) }^2}} . \end{aligned}$$
(4)

The Gaussian distribution function is frequently chosen due to the fact that it is not only meaningful but also relatively easy to be tractable. In the case of a three-dimensional Cartesian space, the nonlocal Gaussian attenuation function takes the form as [61]:

$$\begin{aligned} \mathcal{K}(\left\| {{\mathbf{x}} - {\mathbf{x'}}} \right\| ,\ell ) = \frac{1}{{{{\left( {\ell \sqrt{2\pi } } \right) }^{{3}}}}}\exp \left( { - \frac{{{r^2}}}{{2{\ell ^2}}}} \right) . \end{aligned}$$
(5)

Theoretically speaking, the three-dimensional Gaussian distribution function interacts between two spatial points in any distance, even for infinite domain. Owing to its rapid exponential decaying property, the three-dimensional Gaussian distribution function is often considered to work at an infinite effective zone (\(V_{\inf }\)). In the case of an isotropic and uniform medium, the nonlocal influence zone shall become a sphere, as shown in Figure 1. Further, when the small size effect is negligible, the nonlocal model is expected to be reduced to classical (local) model, and therefore, the following normalization condition is adopted:

$$\begin{aligned} \int _{{V_{\inf }}} \mathcal{K} (\left\| {{\mathbf{x}} - {\mathbf{x'}}} \right\| ,\ell ){\mathrm{d}}V\left( {{\mathbf{x'}}} \right) = 1. \end{aligned}$$
(6)

It can be checked that the local and nonlocal stresses can be the same when considering a uniform local stress field.

Remark 1

In the case of a slender beam, we assume that the beam’s thickness and width are close to its intrinsic characteristic length (\(W \sim \ell \) and \(H \sim \ell \)); however, the beam’s length is assumed to be far larger than its intrinsic characteristic length (\(L \gg \ell \)). Under such circumstances, the cross-section effect becomes the dominating contribution to the size dependence of bending behaviors, but the size-dependent effect in the length direction can be omitted.

3 Euler–Bernoulli beam theory from the viewpoint of three-dimensional nonlocality

According to the assumptions of the Euler–Bernoulli beam theory, the displacement field can be expressed as

$$\begin{aligned} {u_x}(x,y,z) = - y\frac{{\partial w(x)}}{{\partial x}}, \; {u_y}(x,y,z) = w (x), \; {u_z}(x,y,z) = 0, \end{aligned}$$

where w is only length dependent and denotes the transverse displacement of the center line (neutral axis) of the beam.

By using the strain tensor derived from the displacement, \({\varepsilon _{ij}} = 0.5({u_{i,j}} + {u_{j,i}})\), only the normal strain in the axial direction is found to be nonzero, which takes the form:

$$\begin{aligned} {\varepsilon _{xx}}(x,y) = - y\frac{{{\partial ^2}w}}{{\partial {x^2}}}. \end{aligned}$$
(7)

In this study, we only consider a constant curvature \(\kappa _0\); thus, the nonzero strain (7) can be simplified as

$$\begin{aligned} {\varepsilon _{xx}}(y) = - y\kappa _0. \end{aligned}$$
(8)

Because of the constant curvature \(\kappa _0\), the strain of interest does not vary in its axial length direction, but is only of thickness dependent.

Substituting strain (8) into the constitutive equation (1) and using the Gaussian distribution kernel function (5), the nonzero stress in the x direction for an isotropic and uniform medium can be obtained as

$$\begin{aligned} {\sigma _{xx}} = {C_{11}}\int _{ - L/2}^{L/2} {\int _{ - W/2}^{W/2} {\int _{ - H/2}^{H/2} {\frac{1}{{{{\left( {\ell \sqrt{2\pi } } \right) }^3}}}\exp \left( { - \frac{{{r^2}}}{{2{\ell ^2}}}} \right) } } } {\varepsilon '_{xx}}{\mathrm{d}}x'{\mathrm{d}}z'{\mathrm{d}}y', \end{aligned}$$
(9)

where the distance r has been defined in equation (4).

Due to the consideration of a constant curvature \(\kappa _0\), the normal stress (9) in the x-direction can be, alternatively, obtained as

$$\begin{aligned} {\sigma _{xx}} = - {\kappa _0}{C_{11}}\int _{ - L/2}^{L/2} {\int _{ - W/2}^{W/2} {\int _{ - H/2}^{H/2} {\frac{1}{{{{\left( {\ell \sqrt{2\pi } } \right) }^3}}}\exp \left( { - \frac{{{r^2}}}{{2{\ell ^2}}}} \right) } } } y'{\mathrm{d}}x'{\mathrm{d}}z'{\mathrm{d}}y'. \end{aligned}$$
(10)

3.1 Size dependence of stress

As pointed out in Remark 1, the size dependence in the axial direction can be omitted. That is,

$$\begin{aligned} \int _{ - L/2}^{L/2} {\frac{1}{{\ell \sqrt{2\pi } }}\left( { - \frac{{{{\left( {x - x'} \right) }^2}}}{{2{\ell ^2}}}} \right) } {\mathrm{d}}x' \approx \int _{ - \infty }^{ + \infty } {\frac{1}{{\ell \sqrt{2\pi } }}\left( { - \frac{{{{\left( {x - x'} \right) }^2}}}{{2{\ell ^2}}}} \right) } {\mathrm{d}}x' = 1. \end{aligned}$$
(11)

We have used the normalization condition (6) for the derivation of equation (11) and considered that \(L \gg r_{c}\) where \(r_c\) is the cutoff radius of the infinite sphere \(V_{\inf }\).

To simplify equation (10), the following mathematical property [62] will be used:

$$\begin{aligned} \frac{1}{{\sqrt{c\pi } }}\int _p^q {\exp \left( { - \frac{{{x^2}}}{c}} \right) {\mathrm{d}}x} = \frac{1}{2}\left[ {{\mathrm{erf}}\left( {\frac{q}{{\sqrt{c} }}} \right) - {\mathrm{erf}}\left( {\frac{p}{{\sqrt{c} }}} \right) } \right] , \end{aligned}$$
(12)

where \( {\mathrm{erf}}(\;) \) is the error function (or called the Gauss error function).

By using the following mathematical property (12) and equation (11), the nonlocal stress (10) can be further obtained as

$$\begin{aligned} {\sigma _{xx}} = - {c_y}{c_z}y{C_{11}}{\kappa _0} , \end{aligned}$$
(13)

where

$$\begin{aligned} {c_y} =&\frac{1}{2}\left[ {{\mathrm{erf}}\left( {\frac{{0.5H + y}}{{\sqrt{2} \ell }}} \right) + {\mathrm{erf}}\left( {\frac{{0.5H - y}}{{\sqrt{2} \ell }}} \right) } \right] \\&- \frac{\ell }{{y\sqrt{2\pi } }}\left[ {\exp \left( { - {{\left( {\frac{{0.5H - y}}{{\sqrt{2} \ell }}} \right) }^2}} \right) - \exp \left( { - {{\left( {\frac{{0.5H + y}}{{\sqrt{2} \ell }}} \right) }^2}} \right) } \right] ,\\ {c_z}&= \frac{1}{2}\left[ {{\mathrm{erf}}\left( {\frac{{0.5W + z}}{{\sqrt{2} \ell }}} \right) + {\mathrm{erf}}\left( {\frac{{0.5W - z}}{{\sqrt{2} \ell }}} \right) } \right] . \end{aligned}$$

By comparing equation (13) with its classical (local) counterpart (\( {\sigma _{xx}^L} = -y{C_{11}} {\kappa _0} \)), we note that the nonlocal stress (13) involves two new coefficients (\(c_y\) and \(c_z\)) to account for the size-dependent effects. Specifically, \({\sigma _{xx}}\left( {y = 0,z = 0} \right) = 0\), which is the same as that obtained in classical (local) stress theory.

Remark 2

It is of interest that the nonlocal stress \(\sigma _{xx}\) is dependent on both the thickness and width directions, manifesting a major difference as compared with the case of classical (local) stress theory. Due to the fact that \(c_y\) is only dependent on the location in the thickness (y) direction, coefficient \(c_y\) can be used to gauge the size-dependent effect due to the thickness. Similarly, coefficient \(c_z\) can be considered as an index for characterizing the size-dependent effect due to the width. The product of \(c_y\) and \(c_z\) close to 1 denotes no size-dependent effect, whereas its value far away from 1 shows a significant size-dependent effect. coefficients \(c_y\) and \(c_z\) are hence called stress-characteristic indices. In the case of macroscale beams where we have \(\ell \ll W\) and \(\ell \ll H\), one obtains \(c_y \rightarrow 1\) and \(c_z \rightarrow 1\), and therefore, the stress of the nonlocal theory of elasticity can be reduced to that of classical (local) theory of elasticity.

For the sake of generalization, we introduce the following dimensionless parameters:

$$\begin{aligned} \eta {\mathrm{= }}\frac{\ell }{H}, \; \gamma {\mathrm{= }}\frac{\ell }{W}, \; \bar{y} = \frac{y}{H}, \; \bar{z} = \frac{z}{W}. \end{aligned}$$
(14)

The two stress-characteristic indices (\(c_y\) and \(c_z\)) can be then given by

$$\begin{aligned} {c_y} =&\frac{1}{2}\left[ {{\mathrm{erf}}\left( {\frac{{0.5 + \bar{y}}}{{\sqrt{2} \eta }}} \right) + {\mathrm{erf}}\left( {\frac{{0.5 - \bar{y}}}{{\sqrt{2} \eta }}} \right) } \right] \nonumber \\&- \frac{\eta }{{\bar{y}\sqrt{2\pi } }}\left[ {\exp \left( { - {{\left( {\frac{{0.5 - \bar{y}}}{{\sqrt{2} \eta }}} \right) }^2}} \right) - \exp \left( { - {{\left( {\frac{{0.5 + \bar{y}}}{{\sqrt{2} \eta }}} \right) }^2}} \right) } \right] , \end{aligned}$$
(15)
$$\begin{aligned} {c_z}&= \frac{1}{2}\left[ {{\mathrm{erf}}\left( {\frac{{0.5 + \bar{z}}}{{\sqrt{2} \gamma }}} \right) + {\mathrm{erf}}\left( {\frac{{0.5 - \bar{z}}}{{\sqrt{2} \gamma }}} \right) } \right] . \end{aligned}$$
(16)

Figure 2 shows the size-dependent effect on the normal stress as two stress-characteristic indices \(c_y\) and \(c_z\) vary. Clearly, the nonlocality due to both beams’ thickness and width can be easily observed to play a vital role in the size dependence of the normal stress. When the intrinsic length parameter \(\ell \) is far smaller than the geometric characterization of the cross section of beams (\(\ell \ll W\) and \(\ell \ll H\)), one can observe that \(c_y \rightarrow 1\) and \(c_z \rightarrow 1\), leading to negligible size-dependent effect which is difficult to observe and can be therefore neglected. Under such cases, the classical local theory can be applied without much loss of accuracy. However, in the case of the intrinsic length parameter \(\ell \) close to the geometric characterization of the cross section of beams (\(\ell \sim W\) and \(\ell \sim H\)), the size-dependent effects due to beams’ both thickness and width cannot be neglected and will have to be considered. Furthermore, for both the thickness and width directions, the stresses near the free surfaces show a larger size-dependent effect than those near the neutral axis.

As shown in Figure 2, all the values of two stress-characteristic indices (\(c_y\) and \(c_z\)) are smaller than 1. This means that nonlocality has a softening effect on the stress.

What is more, the stress-characteristic index \(c_y\) takes the weighted average of linearly thickness-varying strain into consideration, while the strains in the width direction, used for obtaining the stress-characteristic index \(c_z\), are invariable. As observed from Figure 2, the value of \(c_y\) is smaller than that of \(c_z\), resulting in the size-dependent effect in the thickness direction larger than that in the width direction.

Fig. 2
figure 2

Schematic illustration of the size-dependent effects on stress: (a) the size-dependent effect in the thickness direction measured by the stress-characteristic index \(c_y\) and (b) the size-dependent effect in the width direction measured by the stress-characteristic index \(c_z\)

Full size image

Remark 3

As observed from the size dependence of the normal stress of beams, the size-dependent effect in the length direction is, as expected, the smallest in comparison with those in the other two directions due to the simple fact that the length is assumed to be the longest among all the dimensions. For the classical local theory, beams are often called a class of one-dimensional problem and therefore the geometric dimension of beams is implicitly viewed as the axial length. Currently, within the scope of the non-classical nonlocal theory, which has been investigated by many researchers [16, 27,28,29, 33, 53, 55, 56] that the geometric dimension of beams (length) is, intuitively, chosen as the nonlocal dimension, which is unusually odd given the fact that the true nonlocal effect in the physical space is three dimensional. In fact, it is shown in this study that it is the characterizing parameter of beams’ cross section (thickness and width), rather than their axial length, that is responsible for the size-dependent effect of the stress. This in turn has led to the necessary that the beam problem at nanoscale has to be viewed and treated as a “three-dimensional” geometric and physical problem due to the geometric dimension in the length direction, as well as the physical dimensions in both the thickness and width directions.

3.2 Analytical solutions of bending of nonlocal beams

Owing to its fundamental importance of the bending moment in engineering science, we will next provide a short derivation and also explore the cross-section effect on the nonlocal bending moment.

By using the expression of the normal stress (13), the bending moment M can be obtained as

$$\begin{aligned} M = \int _{ - W/2}^{W/2} {\int _{ - H/2}^{H/2} {{\sigma _{xx}}y{\mathrm{d}}y{\mathrm{d}}z} } = - {C_{11}}{\kappa _0}\int _{ - W/2}^{W/2} {{c_z}\left( {\int _{ - H/2}^{H/2} {{c_y}{y^2}{\mathrm{d}}y} } \right) {\mathrm{d}}z} . \end{aligned}$$
(17)

Upon substituting the two coefficients by equations (15) and (16) into the previous equation, we have from equation (17):

$$\begin{aligned} M = - \frac{{{H^3}W}}{{12}}{C_{11}}{\kappa _0}{\alpha _z}{\alpha _y}, \end{aligned}$$
(18)

where

$$\begin{aligned}&{\alpha _y} = {\mathrm{erf}}\left( {\frac{H}{{\sqrt{2} \ell }}} \right) + {\mathrm{3}}.{\mathrm{192}}\frac{{{\ell ^3}}}{{{H^3}}}\left[ {1 - {\mathrm{exp}}\left( { - \frac{{{H^2}}}{{2{\ell ^2}}}} \right) } \right] + 0.798\frac{\ell }{H}\left[ {{\mathrm{exp}}\left( { - \frac{{{H^2}}}{{2{\ell ^2}}}} \right) - 3} \right] , \end{aligned}$$
(19)
$$\begin{aligned}&{\alpha _z} = 0.798\frac{\ell }{W}\left[ {{\mathrm{exp}}\left( { - \frac{{{W^2}}}{{2{\ell ^2}}}} \right) - 1} \right] + {\mathrm{erf}}\left( {\frac{{0.707W}}{\ell }} \right) . \end{aligned}$$
(20)

It should be noted that in the case of macroscale (\(H/\ell \rightarrow +\infty \) and \(W/\ell \rightarrow +\infty \)), we have \(\alpha _z \rightarrow 1\) and \(\alpha _y \rightarrow 1\). Under such cases, the nonlocal effects become negligible and the classical (local) bending moment can be recovered as

$$\begin{aligned} {M^L} = - D{\kappa _0} , \end{aligned}$$
(21)

where the classical bending rigidity D can be given by

$$\begin{aligned} D=\frac{{{H^3}W}}{{12}}{C_{11}}. \end{aligned}$$
(22)

By comparing the nonlocal moment (18) with the local moment (21), the effective bending rigidity can be obtained as

$$\begin{aligned} {D_{eff}}{\mathrm{= }}\frac{{{H^3}W}}{{12}}{C_{11}}{\alpha _z}{\alpha _y}. \end{aligned}$$
(23)

With the help of equation (23), the nonlocal moment (18) can be written in a form, which is more traditional: \( {M} = - D_{eff} {\kappa _0} \).

By comparing the effective bending rigidity (23) with its classical (local) counterpart (22), two new coefficients (\(\alpha _y\) and \(\alpha _z\)) are introduced to account for the size-dependent effect of the bending rigidity. \(\alpha _y\) is responsible for the size-dependent effect in the thickness direction, while \(\alpha _z\) in the width direction. The product of \(\alpha _y\) and \(\alpha _z\) far away from 1 shows a significant size-dependent effect on moment, whereas its value close to 1 indicates no size-dependent effect. Similarly, we call \(\alpha _y\) and \(\alpha _z\) moment-characteristic indices. In the special case when \(\alpha _y=1\) and \(\alpha _z=1\), the local (classical) bending rigidity can be recovered from the effective bending rigidity. With the aid of the effective bending rigidity (23), nonlocal bending problems can be treated and analyzed in a similar way used in traditional bending analyses.

Fig. 3
figure 3

The size-dependent effect on bending moment versus the product of \( {\alpha _y} \) and \( {\alpha _z} \)

Full size image

With the aid of the first two dimensionless parameters defined in equation (14), the two indices characterizing the nonlocal effects due to beam cross section for the bending moment can be rewritten as

$$\begin{aligned}&{\alpha _y} = {\mathrm{erf}}\left( {0.707{\eta ^{ - 1}}} \right) + {\mathrm{3}}.{\mathrm{192}}{\eta ^3}\left[ {1 - {\mathrm{exp}}\left( { - 0.5{\eta ^{ - 2}}} \right) } \right] + 0.798\eta \left[ {{\mathrm{exp}}\left( { - 0.5{\eta ^{ - 2}}} \right) - 3} \right] ,\\&{\alpha _z} = 0.798\gamma \left[ {{\mathrm{exp}}\left( { - 0.5{\gamma ^{ - 2}}} \right) - 1} \right] + {\mathrm{erf}}\left( {0.707{\gamma ^{ - 1}}} \right) . \end{aligned}$$

Figure 3 illustrates the size-dependent effect on bending moment versus the product of \( {\alpha _y} \) and \({\alpha _z} \). Specifically, for the case in which the intrinsic length is far smaller than both the width and thickness of the beam, we have \(\alpha _y \rightarrow 1\) and \(\alpha _z \rightarrow 1\). Under such circumstances, the local (classical) bending moment becomes very close to the nonlocal bending moment and as a result, the nonlocal (size-dependent) effect cannot be observed. When the intrinsic length is comparable to either the width or thickness of the beam, a stiffness-softening effect can be observed.

Similarly, the linearly thickness-varying strain has a more significant contribution to the size dependent effect on the bending moment, compared with the width-invariable strain. Again, in the case of the bending moment, the nonlocal effect in the thickness direction is more sensitive than that in the width direction.

3.2.1 Simply supported beam

Here we consider a simply supported beam subjected to a constant moment \(M_b\) at its two ends, as shown in Figure 4(a).

Fig. 4
figure 4

Schematic illustrations of the considered simply supported and cantilevered beams

Full size image

The corresponding boundary conditions can be expressed as

$$\begin{aligned} w\left( { - L/2} \right) = w\left( {L/2} \right) = 0,\qquad -{D_{eff}}\frac{{{\partial ^2}w}}{{\partial {x^2}}}\left( { - L/2} \right) = -{D_{eff}}\frac{{{\partial ^2}w}}{{\partial {x^2}}}\left( { L/2} \right) = {M_b}. \end{aligned}$$
(24)

With the aid of the effective bending rigidity (23) and the assumed constant curvature \({\kappa _0} = {\partial ^2}w/\partial {x^2}\), the nonlocal bending moment (18) can be expressed as

$$\begin{aligned} M = - {D_{eff}}\frac{{{\partial ^2}w}}{{\partial {x^2}}}. \end{aligned}$$
(25)

The general solution of the deflection w can be then assumed as

$$\begin{aligned} w = - \int {\left( {\int {\frac{M}{{{D_{eff}}}}{\mathrm{d}}x} } \right) } {\mathrm{d}}x + {\beta _x}x + {\beta _0} , \end{aligned}$$
(26)

where \( {\beta _x} \) and \( {\beta _0} \) are unknown parameters which are determined by enforcing the satisfaction of boundary conditions. Using the boundary conditions (24), the deflection w in the case of simply supported beam subjected to a constant moment \(M_b\) at its ends can be solved as

$$\begin{aligned} w = - \frac{M_b}{{2{D_{eff}}}}\left( {{x^2} - \frac{{{L^2}}}{4}} \right) . \end{aligned}$$
(27)

As can be seen from (27), the maximum deflection \(w_{max}\) takes place at the middle point (\(x=0\)). Since the cross-section effect of the nonlocal beam model causes a softening behavior of the effective bending rigidity (23), the deflections from the nonlocal beam model become larger than those from classical beam model.

3.2.2 Cantilevered beam

A cantilevered beam is further considered which is subjected to a constant bending moment \(M_b\) in clockwise direction at its free end, as shown in Figure 4(b). The corresponding boundary conditions can be then expressed as

$$\begin{aligned} w\left( { - L/2} \right) = 0, \; \frac{{\partial w}}{{\partial x}}\left( { - L/2} \right) = 0, \; - {D_{eff}}\frac{{{\partial ^2}w}}{{\partial {x^2}}}\left( {L/2} \right) = {M_b}, \; \frac{{{\partial ^3}w}}{{\partial {x^3}}}\left( {L/2} \right) = 0. \end{aligned}$$
(28)

Similarly, by using the boundary conditions (28), the deflection–moment relation of the cantilevered beam can be established as

$$\begin{aligned} w = - \frac{{{M_b}}}{{2{D_{eff}}}}{\left( {x + \frac{L}{2}} \right) ^2} . \end{aligned}$$
(29)

Clearly, the maximum deflection \(w_{max}\) occurs at its free end (\(x=L/2\)). Again, the deflection from the nonlocal cantilevered beam model becomes generally larger than that from the classical cantilevered beam model.

Remark 4

It has long been recognized that if the existing 1D nonlocal differential model (3) is employed to develop nonlocal cantilevered beams, there exist some paradoxes [63,64,65]. For example, the deflection of a nonlocal cantilevered beam with a concentrated load at its free end becomes just the same as its local counterpart. Such puzzling paradoxes can now be resolved by using a three-dimensional nonlocal model developed in the present work, as shown in equation (29).

4 Calibration of the intrinsic characteristic length via molecular dynamics simulations

As observed from the two closed-form solutions established in equations (27) and (29), the effective bending rigidity \(D_{eff}\) can be determined once the deflection–moment relation is established. The intrinsic characteristic length \(\ell \) can then be calibrated if we know the variance of the effective bending rigidities corresponding to beams with different cross-section areas.

In this section, molecular dynamics (MD) simulations are utilized to establish the deflection–moment relation of beams with different cross-section areas. Here we consider silicon material, which is a diamond cubic crystal structure with its lattice constant \(a = 5.431\) Å. For the MD simulations, we consider the counterpart of the cantilevered beam discussed in subsection 3.2.2. The initial and equilibrated configurations of the MD simulations are shown in Figure 5.

Fig. 5
figure 5

The setup of molecular dynamics simulations for a cantilevered silicon beam. The left end with 2a length is clamped, and the right end with 2a length is added on a moment \(M_b\). The length–thickness ratio of simulated beams is set to be a constant, that is, \(L/H=20\)

Full size image

The well-known LAMMPS package [66] is adopted as the MD simulation tool. The Stillinger and Weber potential [67] is used to model the atom force field of silicon. To reduce the effect of thermal fluctuation, we consider a very low temperature, i.e., \( T=0.01 \) K. The moment is chosen as \(M_b=0.1\) nN\(\cdot \)Å. The length, thickness and width of the beam are along [1,0,0], [0,1,0] and [0,0,1] directions, respectively.

To obtain the elastic constant \(C_{11}\), a silicon structure in all the three directions are set to be periodic and \(C_{11}\) is predicted to be 151.42 GPa by using a small perturbation of the model in x direction. It is to be noted that the predicted \(C_{11}\) is in excellent agreement with the theoretical value 151.4 GPa for the Stillinger–Weber silicon [1]. Thus, the elastic constant \(C_{11}\) will be employed to calibrate the intrinsic characteristic length by comparing the deflection–moment relation (29) with the results of MD simulations (Figure 5).

For MD simulations, to find the maximum deflection \(w_{max}\) at the free end is relatively easy. According to the deflection–moment relation (29), the effective bending rigidity can be obtained as the following form in terms of the maximum deflection \(w_{max}\):

$$\begin{aligned} {D_{eff}}(H,W) = - \frac{{{M_b}{L^2}}}{{2{w_{\max }}}}. \end{aligned}$$
(30)

By using equation (30), we can find the effective bending rigidities as functions of the beams’ height H and width W. Finally, by comparing equations (30) with (23), we can calibrate the intrinsic characteristic length \(\ell \) by using a curve fitting data technique. As noted above, a practical numerical analysis framework based on MD simulations is proposed to calibrate the intrinsic characteristic length \(\ell \). The proposed calibration methodology developed here can also become highly beneficial to the nanomechanics of a wide variety of nanostructures, although a silicon beam is considered here for the sake of illustration.

Fig. 6
figure 6

The effective bending rigidities of beams with varying values of (a) thickness or (b) width for MD simulations, the 1D nonlocal differential model, and the 3D nonlocal integral model

Full size image

For silicon, the intrinsic characteristic length \(\ell \) is found to be 0.74253a where \(a= 5.431\) Å. With this value of the intrinsic characteristic length, the normalized bending rigidity of the silicon beams predicted by the proposed 3D nonlocal integral beam model is in reasonable agreement with that predicted by MD simulations, as shown in Figure 6. For the sake of comparison, the effective bending rigidities have been normalized by the corresponding classical bending rigidity, and the effective bending rigidities predicted by using the 1D nonlocal differential model given in equation (2), which has been widely employed to model nonlocal beams [49, 50, 68, 69] (see also the references therein), are also calculated. It is a serious unresolved paradox readily observed from Figure 6 that the 1D nonlocal differential model predicts the effective bending rigidities which are the same as those in classical mechanics. These somewhat startling results are due mainly to the fact that the cross-section effect (the nonlocal effect in both width and thickness directions) is neglected, and also the nonlocal effect predicted by the 1D nonlocal differential model cannot be observed for a concentrated moment [63, 70, 71]. The paradox can now be well resolved if the new developed 3D nonlocal integral model is employed, as shown in Figure 6.

Figure 6(a) shows the cross-section effect on the bending rigidities of beams with different thicknesses under a given constant width \(W=3a\), while Figure 6(b) plots the cross-section effect on the bending rigidities of beams with different widths under a specified constant thickness \(H=3a\). Significant size dependent influences which can be readily observed are due primarily to the fact that the dimension of one side of the beams’ cross section (the external characteristic length \(L_{ext}\)) is at least comparable to their lattice constant \(a = 5.431\) Å. Since the normalized bending rigidities are smaller than 1, MD simulations confirm that the size-dependent effect is a “rigidity-softening” effect, as observed in the nonlocal beams. Furthermore, when beams’ height or width is closer to the intrinsic characteristic length \(\ell =0.74253a\), the cross-section effect becomes more pronounced.

As mentioned previously, the 1D nonlocal integral model given in equation (3), as another widely used kind of nonlocal integral models [53, 59, 72,73,74], assumes that the nonlocal stress in the cross-section dimensions is basically local rather than nonlocal. The smallest beam considered in MD simulations has \(H=2a\), \(W=3a\) and \(L=40a\), as shown in Figure 5. In this case, corresponding ratio between the characteristic length and physical length becomes \(\ell /L = 0.01856\). Khodabakhshi and Reddy [16] employed the 1D nonlocal integral constitutive relation (3) to develop a nonlocal beam model which takes only the nonlocal effect in the length direction into consideration. Also, Khodabakhshi and Reddy [16] showed that the 1D nonlocal integral beam model produces \(\sim 108\% \) deflection of classical beam model if \(\ell /L = 0.01856\). In our new proposed 3D nonlocal integral beam model with cross-section effect being properly incorporated, the effective bending rigidity decreases to \( 27\% \) that of the classical beam model. This means that the 3D nonlocal beam model can predict as high as \(370.37\% \) deflection of classical beam model. Such increase, as discussed, is due to the dominating contributions of nonlocal behaviors from the cross-section effect, instead of the length effect whose contribution is relatively moderate. This agrees well with Remark 1.

As discussed, the 3D integral model developed in this paper bridges the gap between atomistic studies (atomistics) and the phenomenological approach (continuum mechanics) and therefore provides a new efficient and accurate tool for analyzing the mechanical behaviors of nanoscopic devices made of beam-type structures.

5 Concluding remarks

In the current practice, by intuitively following the traditional geometrical simplifications for beams, the 1D nonlocal constitutive relations are often employed to model beam-type structures, regardless of the inherent three-dimensional interactions between atoms. This work reveals for the first time how the nonlocal interactions in beams’ width and thickness directions affect the bending behaviors of nanobeams, and has established that the main nonlocal effect is due to beam cross section, rather than the length as it is commonly believed.

Based on a three-dimensional nonlocal constitutive relation, a three-dimensional nonlocal Euler–Bernoulli beam model has been developed for bending analysis of nanobeams. Closed-form solutions for the deflections of simply supported and cantilevered beams have been analytically derived. The cross-section effects on the nonlocal stress, the bending moment and the deflection have been explored and examined. Further, an effective and accurate calibration method is proposed for the determination of the intrinsic characteristic length based on molecular dynamics simulations. Some remarkable outcomes have been achieved as summarized as follows:

  1. a)

    The nonlocal physical dimension of beam-type structures has been found to be not in agreement with the 1D geometric direction of classical beam mechanics. For beam-type structures, the nonlocal physical dimensions are beams’ width and height, rather than the frequently employed beam’s length which has been somewhat blindly used in the current practices without much theoretical support and physical understanding.

  2. b)

    The beam problem at nanoscale has to be viewed and treated as a “three-dimensional” geometric and physical problem due to its geometric dimension in the length direction and its physical dimensions in both the thickness and width directions.

  3. c)

    When the intrinsic characteristic length becomes comparable to either the width or thickness of the beam, a rigidity-softening effect occurs which can be observed.

  4. d)

    The linearly thickness-varying strain has a more significant contribution to the size dependence, compared with the width-invariable strain. As a result, the nonlocal effect in the thickness direction is more sensitive than that in the width direction.

  5. e)

    The existing paradox that the deflection of a 1D nonlocal cantilevered beam with a concentrated load at its free end is the same as its local counterpart remains to be disambiguated to date. However, the proposed new three-dimensional nonlocal beam model can satisfactorily resolve such a paradox since it is largely removed.

  6. f)

    For silicon nanobeams, the all important intrinsic characteristic length \(\ell \) of the three-dimensional nonlocal beam model has been found to be 0.74253a where \(a= 5.431 \text {\AA }\) based on extensive MD simulations.