1 Introduction

Rolling element bearings as one of the most important components of rotating machines are at the core of many types of research in the literature. Nowadays, industrial companies try to increase their profits and to decrease downtime hours of machines and equipment by implementing modern maintenance methods. This important issue calls for enormous researches about rolling element bearings and their defects. Among these researches, proposing an appropriate analytical model for bearing dynamic behavior in different cases brings a correct understanding of bearing condition at real experimental tests.

One of the first comprehensive dynamic models for studying rolling element bearings was proposed by Gupta [1]. He predicted the amount of skid and resulting wear rates in an angular contact ball bearing using general partial differential equations of motions of the ball and considering the initial conditions and elastohydrodynamic traction conditions. He developed these predictions for roller bearings and other types of rolling element bearings in his later researches [2,3,4,5].

Sunnersjö [6] performed a complete analysis of vibration behavior of antifriction bearings in which the so-called varying compliance vibrations are introduced as the main causes of noise and unstable behavior of rolling element bearings even in sound cases. He was probably the first researcher that revealed the cyclic stiffness variation of rolling element bearings due to the shaft rotation.

Rolling element bearing dynamic modeling as a quasi-static analysis was presented by Hamrock and Anderson [7]. They ignored the elastohydrodynamic effect of the lubricants and implemented Coulomb friction theorem at contact surfaces between balls and inner race in addition to balls and outer race. The result was then the race control theory which is based on the pure rolling between bearing components.

The effect of geometrical defects and wear on rolling element bearing vibration was studied by Sunerjo [8]. His dynamic model focused on bearings with radial load and positive clearances. The effects of inner ring waviness and non-uniform diameters of the rolling elements were the main subjects of his researches. Spalling fatigue and abrasive wear have been studied both theoretically and experimentally.

Lim and Singh [9,10,11,12] studied vibration transmission through rolling element bearings and reported the analytical and experimental results. They showed that bearing housing is flexible and the purely in-plane-type motion cannot be a correct representation of bearing dynamic. They proposed a comprehensive bearing stiffness matrix of dimension six to couple the shaft bending motion and the flexibility of bearing housing together. The stiffness coefficients were estimated using a numerical method to solve the nonlinear algebraic equations.

Su et al. [13] considered the oil film between rolling elements and races as spring and they defined spring stiffness in different lubricating conditions according to the experimental results of previous researchers, e.g., Hamrock [7] and McFadden and Smith [14].

In 1993, Su et al. [15] proposed a mathematical model for describing frequency characteristics of rolling bearings. They observed surface imperfections induced from manufacturing errors besides lubricating film which results in waviness and geometrical irregularities. Distinguishing the real defects from error sources was one of their priorities. They found that the rolling elements at bearings induced vibration in the housing directly which is the influence of ball or roller on the outer race or vice versa and indirectly that is the influence of ball or roller on inner race or vice versa.

The induced vibrations in the inner race are primarily caused by the load changes due to inner ring rotations. Another analytical–experimental research on the dynamic behavior of rolling element bearings was conducted by Boesiger et al. [16]. They investigated the friction threshold for instability, retainer motion, and the instability frequency in precision angular contact ball bearings. Retainer-ball friction was found the most important cause of retainer instability that showed a constant characteristic frequency without any dependence on speed, external vibration, radial load, and preload.

Tandonand and Choudhury [17] predicted the vibration frequencies of rolling element bearings and the amplitudes of the main frequency of each bearing component containing the rolling element, inner ring, and outer ring due to a localized defect on the outer race in 1997. They compared the results of their analytical model with the experimental values derived from previous research which showed good agreement.

The influence of lubrication on the dynamic behavior of rolling element bearings was investigated by Wijnant et al. [18]. They studied the dynamic behavior of rolling element bearings in two conditions: at first, the bearing structure dynamic encompassing the inner and outer races in addition to the rolling element; secondly, the elastohydrodynamic lubricated (EHL) contact in the connecting surface of these elements. They employed a nonlinear spring–damper model to explain the interaction between the bearing components as structural elements. Their full EHL problem was solved using numerical methods, and they found contact angle variations as a significant cause of the shift of eigenfrequencies.

Another dynamic model for a deep groove ball bearing including localized and distributed defects was proposed by Sopanen and Mikkola [19, 20]. Their model contained the descriptions of nonlinear Hertzian contact deformation and elastohydrodynamic (EHD) fluid film for a deep groove ball bearing with six degrees of freedom. The model could explain the behavior of bearings with distributed defects, such as the waviness of the inner and outer ring and localized defects in the inner and outer races.

Damping in this model was defined in three ways: damping resulted from the oil film between bearing components, damping resulted from nonlinear Hertzian contact deformation, and damping resulted from the contact between bearing and housing which increases with increasing the clearance between these two components. The proposed model was practically appropriate for solving rotating components’ dynamic problems.

With the development of numerical methods, the study of bearing components’ dynamic employed solving nonlinear equations, whereas before this, the linear equations were solved with many simplifications and applying different assumptions.

In 2006, Harsha [21] studied the nonlinear dynamic behavior of rolling element bearings as a result of the eccentricity of the inner ring and surface waviness. The contact between different bearing components was modeled by nonlinear springs that their stiffness was calculated using the Hertzian elastic contact deformation theory. Also, the nonlinear equations of motion were derived using Lagrange’s equation. They solved the governing equations by integrating two numerical methods “Newmark-\(\beta \)” and “Newton–Raphson” simultaneously. The results of vibration response modeling presented in the form of fast Fourier transformations (FFT) and phase trajectories complied with the results of other researchers.

Some researchers introduced new simulator software for rolling element bearing defects with the extension of dynamic models. Sassi et al. [22] verified the results of modeling done with their software with the experimental method in 2007. They considered the surface localized defect of inner and outer races of the bearing in addition to the ball as a sharp-edged fault with certain dimensions. They solved the governing equations numerically regarding load distribution effect in the bearing, the elastic form of bearing structure, the existence of lubricant, transmission path effect, and assumption of the system with three degrees of freedom. They also added the noise arises from the friction between bearing components and lubricating film to the modeled signals to achieve more real signals.

Nelias et al. [23] following Gupta’s researches introduced a dynamic model for predicting the skew movement of a roller in tapered roller bearings. They defined the effect of rotating speed, inner and outer race run-out, and lubricant temperature on the skewing angle of the roller with both theoretical and experimental methods. Their researches showed that skew angle primarily depends on the angle of misalignment between the cup and the cone. Other factors that influence roller skew were the traction at the roller–flange contact, the skew angle increasing with the traction at this contact, and by the roller end geometry.

The vibration characteristics of balanced fault-free bearings with internal clearance were studied by Ghafari et al. [24]. They defined the critical clearance estimation for the equilibrium point of the bearing by employing a lumped mass–damper–spring model and using the Hertzian contact theory to calculate the stiffness of the bearing rolling elements. They found that with increasing the shaft speed depending on the bearing internal clearances, one or more chaotic attractors can appear in the vibrations of ball bearings.

Patil et al. [25] predicted the influence of dimension and location of localized defects on bearing vibration in the same year. Modeling roller elements with nonlinear spring–dampers and calculating the contact forces using Hertzian equations similar to previous researchers were performed, and different geometrical dimensions of defect at specific locations were considered to investigate and compare the results of the theoretical and experimental methods.

Tadina and Boltežar [26] proposed an improved model for vibration behavior of faulty ball bearings using the model and assumptions that Harsha had proposed before for healthy bearings. This was the first model that the defects were not considered with a sharp edge and the rolling element, i.e., the ball smoothly enters the defect location on the race or leaves it. They also considered the outer race flexible and, by adapting a FEM model, studied its behavior. They investigated the results for bearings with outer race, or inner race, or ball localized defect.

Behzad et al. [27], in the same year, developed a new model using models from other researchers, e.g., Mc. Fadden [14], and Harsha [21]. They assumed a stochastic vibration source in the bearing and the vibration source was considered metallic contact between bearing elements during rolling. With the growing defect in the bearing, the contacting surface roughness increases locally and stochastic excitation becomes stronger in the defective area. These stochastic excitations can be reliable signs of bearing fault extension.

A two-degree-of-freedom dynamic model for a cylindrical roller bearing with a localized surface defect on its race was proposed by Shao et al. [28]. The effects of defect width, depth, and types were investigated, and the load–deflection relationship between the roller and the race was considered as non-Hertzian. Moazen Ahmadi et al. [29] presented a nonlinear dynamic model of the contact forces and vibration response generated in defective rolling element bearings. They considered the finite size of the rolling elements which omitted the limitations mentioned by previous models caused by the modeling of rolling elements as point masses. They showed that a low-frequency event occurs in the measured vibration response when a rolling element enters the defect. In 2015, Kogan et al. [30] proposed a three-dimensional dynamic model for ball bearings that was based on the classic dynamic and kinematic equations. Bearing component interactions were simulated using nonlinear springs–dampers following Hertzian contact equations.

Marin et al. [31] considered the bearing faults with sharp edges and they followed the equations proposed by Harsha [21]. They also validate their theoretical results with experiments.

Harris and Kotzalas [32] introduced the array of disciplines required to evaluate and understand the performance and behavior of most types of antifriction bearings. Saruhan et al. [33] investigated the influence of defects on the vibration response of rolling element bearings. They showed that A defect at any element of the rolling element bearings transmits to all other elements such as outer/inner races, ball, and the cage of the bearing. French and Hannon [34] studied the mechanics governing spall propagation in two angular contact ball bearings experimentally. The results showed that the strain energy related to propagation reduced with thrust load, while the ball pass strain amplified.

Li et al. [35] simulated a localized defect of angular contact ball bearings with a step on the outer raceway. They showed that the size increase of localized defect leads to abrupt variations of contact angles and load distributions in the defect area. Liu and Shao [36] reported overall research about the methods for recognizing the localized and distributed faults in rolling element bearings.

Liu et al. [37] used 25 statistical features to develop an algorithm to estimate the spalling damage location and level for deep groove ball bearings. In another work, Liu et al. [39] reported a new force–deflection correlation to replace the Hertzian force–deflection relationship to define the ball–line contact between the ball and defect edge for deep groove ball bearings.

Patel et al. [38] studied the vibrations of deep groove ball bearings having single and multiple defects on surfaces of inner and outer races. Ashtekar et al. [40, 41] determined the generated force due to race defects for deep groove ball bearings. In the published researches, compared with deep groove ball bearing with race defect, there are relatively little researches on the angular contact ball bearings with the defect.

Savalia et al. [42] defined a nonlinear vibration analysis of angular contact ball bearing of a rigid rotor considering waviness of ball and races. They showed that large amplitudes of waviness enhance the vibrations. Arslan and Aktürk [43] represented a shaft–bearing model to predict the effect of the clearance defects on the vibrations of a shaft supported by angular contact ball bearings. Babu et al. [44] represented a vibration analysis of angular contact ball bearings. They simulated a waviness on surfaces of inner/outer races and ball in their model by modeling it as sinusoidal functions with waviness orders of 6, 15, and 25. Niu et al. [45] established a dynamic model to study the vibration behavior of angular contact ball bearings with ball defects. Their results proved that the frequency response of the system mainly depends on the geometry of ball defect and operating conditions.

According to the author’s literature review, there are no works about modeling of spall defect with curvature for angular contact ball bearings.

In this paper, the spall defect in the outer ring of an angular contact ball bearing is considered as an impressive circle. In this way, entering and exiting the defect location by rolling elements are very similar to that of the actual condition and more real signals can be observed. Using the equations developed by Harsha [21], the defect spalling was modeled and for validating the results, by accommodating a special test rig experimental results obtained for an angular contact ball bearing. At first, the equations are solved for a fault-free bearing. Then the fault in the outer race is considered, and with modeling and solving the nonlinear equations using 4th and 5th Rung–Kutta, the signals and fast Fourier transform (FFT) are derived.

2 Governing equations

2.1 Mathematical model and equation of motion of bearing without defect

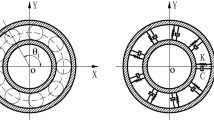
Modeling of a ball bearing is important in the vibration response simulation. In this section, according to previous researches especially models presented by Harsha [21], an angular contact ball bearing will be modeled by such spring–damper–mass system, and then, the defect on the outer race will be modeled with a new concept to predict the vibration response of the system. Figure 1 shows a multiple-degree-of-freedom model of a ball bearing. The following assumptions are considered to model the ball bearing:

  1. 1.

    The motion of the inner race, outer race, and rolling elements are in the plane of the bearing.

  2. 2.

    The outer race of the ball bearing is supported by rigid support, and also, the inner race is fixed with the shaft motion.

  3. 3.

    Elastic deformation between balls and races is simulated by nonlinear springs in compressive loading, which is obtained by the Hertzian theory.

  4. 4.

    Inertia and mass of rotating shaft are considered on the center of the inner race, and also, the elastic deformation of the rotating shaft is neglected.

  5. 5.

    The bearing cage is assumed rigid, and hence, there is no interaction between the balls with the cage and between themselves.

  6. 6.

    There is no slipping between the balls and inner and outer races.

  7. 7.

    In reality, the damping between balls and races in a ball bearing is very small. So the damping coefficient of friction and lubrication will be considered 200 N.s/m in this research as also Harsha [21] did in this way.

As the outer ring is fixed in its position, the equations of motion that describe the dynamic behavior of the complete model should be derived for the inner ring and balls. Using Lagrange’s equation for a set of independent generalized coordinates, the equation is

$$\begin{aligned} \frac{\mathrm{{d}}}{\mathrm{{d}}t}\left( \frac{\partial T}{\partial \dot{q}_{i}} \right) -\frac{\partial T}{\partial q_{i}}+\frac{\partial V}{\partial q_{i}}=Q_{i}\quad i=1,\ldots ,N_{\mathrm{{b}}} \end{aligned}$$
(1)

The total kinetic energy can be calculated with

$$\begin{aligned} T=T_{\mathrm{{b}}}+T_{\mathrm{{in}}}+T_{\mathrm{{out}}}+T_{\mathrm{{c}}} \end{aligned}$$
(2)

The potential energy due to deformations of the balls with the races follows the Hertzian contact theory of elasticity. The total potential energy of the bearing system is the sum of the balls, inner and outer races, springs, and the rotor

$$\begin{aligned} V=V_{\mathrm{{b}}}+V_{\mathrm{{in}}}+V_{\mathrm{{out}}}+V_{\mathrm{{c}}}+V_{\mathrm{{springs}}} \end{aligned}$$
(3)

where \(V_{\mathrm{{b}}}, V_{\mathrm{{in}}}, V_{\mathrm{{out}}}\), and \(V_{\mathrm{{c}}}\) are, respectively, the gravity potential energies caused by the elevation of balls, inner and outer rings, and the rotor. \(V_{\mathrm{{springs}}}\) is the potential energy produced by nonlinear spring contacts between balls and the races.

2.2 Contribution of balls

The position of ith ball is determined using the vector \(\vec {r}_{\mathrm{{out}}}+\vec {q}_{i}\), so the ball speed is described by

$$\begin{aligned} \dot{\vec {r}}_{\mathrm{{out}}} +\dot{\vec {q}}_{i} \end{aligned}$$

If the ith ball rotates with \(\dot{\vec {\alpha }}_{\text {i}}\) angular velocity, then the kinetic energy of balls is calculated with the summation of all elements’ kinetic energy

$$\begin{aligned} T_{\mathrm{{b}}}=\sum \limits _{i=1}^{N_{\mathrm{{b}}}} {T_{i}} \end{aligned}$$
(4)

Hence, the kinetic energy of the balls is written as

$$\begin{aligned} T_{i}=\frac{1}{2}m_{i}\left( \dot{\vec {r}}_{\mathrm{{out}}}+\dot{\vec {q}}_{i} \right) \left( \dot{\vec {r}}_{\mathrm{{out}}}+\dot{\vec {q}}_{i} \right) +\frac{1}{2}I_{i}\dot{\vec {\alpha }}_{i}\dot{\vec {\alpha }}_{i} \end{aligned}$$
(5)

The location of ith rolling elements is

$$\begin{aligned} \left\{ {\begin{array}{l} \vec {q}_{i}=\left( q_{i}\cos {\theta _{i} } \right) \hat{i}+(q_{i}sin\theta _{i})\hat{j} \\ \vec {r}_{\mathrm{{out}}}=\vec {x}_{\mathrm{{out}}}\hat{i}+\vec {y}_{\mathrm{{out}}}\hat{j} \\ \end{array}} \right. \end{aligned}$$
(6)

Combining the above two equations, the following is written

$$\begin{aligned}&\left( \dot{\vec {r}}_{\mathrm{{out}}}+\dot{\vec {q}}_{i} \right) \left( \dot{\vec {r}}_{\mathrm{{out}}}+\dot{\vec {q}}_{i} \right) \nonumber \\&\quad =\dot{x}_{\mathrm{{out}}}^{2}+2\dot{x}_{\mathrm{{out}}}\left( \dot{q}_{i}\cos \theta _{i}-q_{i}\theta _{i}\sin \theta _{i} \right) +\dot{y}_{\mathrm{{out}}}^{2}\nonumber \\&\qquad +\,2\dot{y}_{\mathrm{{out}}}\left( \dot{q}_{i}\cos \theta _{i}-q_{i}\theta _{i}\sin \theta _{i} \right) +\dot{q}_{i}^{2}{\sin }^{2}\theta _{i}+\dot{q}_{i}^{2}{\cos }^{2}\theta _{i}+q_{i}^{2}\dot{\theta }_{i}^{2}{\sin }^{2}\theta _{i}\nonumber \\&\qquad +\,q_{i}^{2}\dot{\theta }_{i}^{2}{\cos }^{2}\theta _{i}+2\dot{q}_{i}q_{i}\dot{\theta }_{i}\sin \theta _{i}\cos \theta _{i}-2\dot{q}_{i}q_{i}\dot{\theta }_{i}\sin \theta _{i}\cos \theta _{i} \end{aligned}$$
(7)

For the stationary outer race,

$$\begin{aligned} \dot{x}_{\mathrm{{out}}}=\dot{y}_{\mathrm{{out}}}=0 \end{aligned}$$
(8)

Therefore, the equation becomes

$$\begin{aligned}&\left( \dot{\vec {r}}_{\mathrm{{out}}}+\dot{\vec {q}}_{i} \right) \left( \dot{\vec {r}}_{\mathrm{{out}}}+\dot{\vec {q}}_{i} \right) =\dot{q}_{i}^{2}{\sin }^{2}\theta _{i}+\dot{q}_{i}^{2}{\cos }^{2}\theta _{i}+q_{i}^{2}\dot{\theta }_{i}^{2}{\sin }^{2}\theta _{i}+q_{i}^{2}\dot{\theta }_{i}^{2}{\cos }^{2}\theta _{i}\nonumber \\&\quad \left( \dot{\vec {r}}_{\mathrm{{out}}}+\dot{\vec {q}}_{i} \right) \left( \dot{\vec {r}}_{\mathrm{{out}}}+\dot{\vec {q}}_{i} \right) =\dot{q}_{i}^{2}+q_{i}^{2}\dot{\theta }_{i}^{2} \end{aligned}$$
(9)

Putting this value in Eq. (5),

$$\begin{aligned} T_{i}=\frac{1}{2}m_{i}\left( q_{i}^{2}\dot{\theta }_{i}^{2}+\dot{q}_{i}^{2} \right) +\frac{1}{2}I_{i}\dot{\vec {\alpha }}_{i}\dot{\vec {\alpha }}_{i} \end{aligned}$$
(10)

Since it is assumed to be no slip between elements of the bearing,

$$\begin{aligned} R\left( \dot{\gamma }_{\mathrm{{out}}}-\dot{\theta }_{i} \right) =-q_{\mathrm{{b}}}(\dot{\alpha }_{i}-\dot{\theta }_{i}) \end{aligned}$$
(11)

The outer race is stationary. So

$$\begin{aligned} \dot{\gamma }_{\mathrm{{out}}}=0 \end{aligned}$$
(12)

Then the angular velocity of the ith ball is

$$\begin{aligned} \dot{\alpha }_{i}=\dot{\theta }_{i}\left( 1+\frac{R}{q_{\mathrm{{b}}}} \right) \end{aligned}$$
(13)

So for the kinetic energy of balls,

$$\begin{aligned} T_{\mathrm{{b}}}=\sum \limits _{i=1}^{N_{\mathrm{{b}}}} \frac{1}{2} m_{i}\left( q_{i}^{2}\dot{\theta }_{i}^{2}+\dot{q}_{i}^{2} \right) +\frac{1}{2}I_{i}\dot{\theta }_{i}^{2}\left( 1+\frac{R}{q_{\mathrm{{b}}}} \right) ^{2} \end{aligned}$$
(14)

And for the potential energy of balls,

$$\begin{aligned} V_{\mathrm{{b}}}=\sum \limits _{i=1}^{N_{\mathrm{{b}}}} m_{i} g\left( y_{\mathrm{{out}}}+q_{i}\sin \theta _{i} \right) \end{aligned}$$
(15)

2.3 Contribution of the outer race

The kinetic energy of the outer race is zero because it is assumed to be stationary

$$\begin{aligned} \left\{ {\begin{array}{l} \dot{r}_{\mathrm{{out}}} =0 \\ \dot{\alpha }_{\mathrm{{out}}}=0 \\ \end{array}} \right. \rightarrow T_{\mathrm{{out}}}=0 \end{aligned}$$
(16)

For the potential energy of the outer race,

$$\begin{aligned} V_{\mathrm{{out}}}=m_\mathrm{{out}}\, g\, y_{\mathrm{{out}}} \end{aligned}$$
(17)

2.4 Contribution of the inner race

The kinetic energy of inner race with the effect of its mass and mass moment of inertia is

$$\begin{aligned} T_{\mathrm{{in}}}=\frac{1}{2}m_{\mathrm{{in}}}\left( \vec {\dot{r}}_{\mathrm{{in}}}.\vec {\dot{r}}_{\mathrm{{in}}} \right) +\frac{1}{2}I_{\mathrm{{in}}}\dot{\alpha }_{\mathrm{{in}}}^{2} \end{aligned}$$
(18)

where

$$\begin{aligned} \vec {r}_{\mathrm{{in}}}=\vec {x}_{\mathrm{{in}}}+ \vec {y}_{\mathrm{{in}}} \end{aligned}$$
(19)

Differentiating \(r_{\mathrm{{in}}}\) with respect to time and putting the value in Eq. (18),

$$\begin{aligned} T_{\mathrm{{in}}}=\frac{1}{2}m_{\mathrm{{in}}}\left( \vec {\dot{x}}_{\mathrm{{in}}}^{2}+\vec {\dot{y}}_{\mathrm{{in}}}^{2} \right) +\frac{1}{2}I_{\mathrm{{in}}}\dot{\alpha }_{\mathrm{{in}}}^{2} \end{aligned}$$
(20)

For the potential energy,

$$\begin{aligned} V_{\mathrm{{in}}}=m_{\mathrm{{in}}} g y_{\mathrm{{in}}} \end{aligned}$$
(21)

2.5 Contribution of cage

It is assumed that the cage’s center remains coincident with the inner race. The kinetic energy of the cage is calculated as

$$\begin{aligned} T_{\mathrm{{c}}}=\frac{1}{2}m_{\mathrm{{c}}}\left( \vec {\dot{x}}_{\mathrm{{in}}}^{2}+\vec {\dot{y}}_{\mathrm{{in}}}^{2} \right) +\frac{1}{2}I_{\mathrm{{c}}}\dot{\alpha }_{\mathrm{{c}}}^{2} \end{aligned}$$
(22)

And the potential energy is

$$\begin{aligned} V_{\mathrm{{c}}}=m_{\mathrm{{c}}}gy_{\mathrm{{in}}} \end{aligned}$$
(23)

2.6 Contribution of the elastic deformation

The contacts between races and balls are modeled by nonlinear springs. The stiffness of these springs is calculated with the Hertzian theory of elasticity. The contact deformation between balls and races

$$\begin{aligned} V_{\mathrm{{springs}}}=V_{\mathrm{{in.spring}}}+V_{\mathrm{{out.spring}}} \end{aligned}$$
(24)

is calculated as

$$\begin{aligned} V_{\mathrm{{springs}}}=\sum \limits _{i=1}^{N_{\mathrm{{b}}}} \frac{1}{2} k_{\mathrm{{in}}}\delta _{\mathrm{{in}}}^{2}+\sum \limits _{i=1}^{N_{\mathrm{{b}}}} \frac{1}{2} k_{\mathrm{{out}}}\delta _{\mathrm{{out}}}^{2} \end{aligned}$$
(25)

The contact deformation between each ball and the inner race is

$$\begin{aligned} \delta _{\mathrm{{in}}}=\left( r+q_{\mathrm{{b}}}\cos \beta \right) -X_{i} \end{aligned}$$
(26)

where r is the inner race radius and \(X_{i}\) is the nominal distance between the center of each ball from the inner race. When it becomes a positive value, it means that the elements are in pressure and contact deformation occurs; otherwise, the value is considered zero and no compression exists.

For the outer race, the deformation is calculated by

$$\begin{aligned} \delta _{\mathrm{{out}}}=R-\left( q_{i}+q_{\mathrm{{b}}} \right) \end{aligned}$$
(27)

where \(q_{i}\) is the nominal distance between the centers of balls from the outer race. If it becomes a negative value, the contact deformation happens; otherwise, the value is considered zero with no compression.

3 Equations of motion

The terms of kinetic and potential energy in Eq. (1) can be differentiated with respect to the generalized coordinates \(q_{i}\) to obtain the equations of motion of the balls as follows [21]:

$$\begin{aligned}&m_{i}\ddot{q}_{i}-\left( m_{i}q_{i}\dot{\theta }_{i}^{2} \right) +m_{i}g\sin \theta _{i}-\left[ K_{\mathrm{{in}}}\left( r+q_{\mathrm{{b}}}-X_{i} \right) +C_{\mathrm{{in}}}\dot{q}_{i} \right] _{+}+\frac{\partial X_{i}}{\partial q_{i}}\nonumber \\&\quad +\left[ K_{\mathrm{{out}}}\left( q_{\mathrm{{b}}}+q_{i}-R \right) +C_{\mathrm{{out}}}\dot{q}_{i} \right] _{+}=0 \qquad i=1, 2, \ldots , N_{\mathrm{{b}}} \end{aligned}$$
(28)
Fig. 1
figure 1

Mass–spring model of the ball bearing [21]

Full size image

Also by using Lagrange’s equation the equations of motion of inner race in the x and y directions can be derived as follows [21]:

$$\begin{aligned}&\left( m_{\mathrm{{in}}}+m_{\mathrm{{c}}}+m_{\mathrm{{r}}} \right) \ddot{x}_{\mathrm{{in}}}-\sum \limits _{i=1}^{N_{\mathrm{{b}}}} {\left[ K_{\mathrm{{in}}}\left( r+q_{\mathrm{{b}}}-X_{i} \right) +C_{\mathrm{{in}}}\dot{q}_{i} \right] _{+}+\frac{\partial X_{i}}{\partial x_{\mathrm{{in}}}}} =F_{\mathrm{{u}}}\cos {\omega t} \end{aligned}$$
(29)
$$\begin{aligned}&\left( m_{\mathrm{{in}}}+m_{\mathrm{{c}}}+m_{\mathrm{{r}}} \right) \ddot{y}_{\mathrm{{in}}}-\left( m_{\mathrm{{in}}}+m_{\mathrm{{c}}}+m_{\mathrm{{r}}} \right) g-\sum \limits _{i=1}^{N_{\mathrm{{b}}}} {\left[ K_{\mathrm{{in}}}\left( r+q_{\mathrm{{b}}}-X_{i} \right) +C_{\mathrm{{in}}}\dot{q}_{i} \right] _{+}+\frac{\partial X_{i}}{\partial y_{\mathrm{{in}}}}} =F_{\mathrm{{u}}}\sin {\omega t} \end{aligned}$$
(30)

The system represents the (\(N_{\mathrm{{b}}}+1)\) nonlinear second-order differential equations. In these equations of motion, the subscript sign “\(+\)” indicates that if the term inside the brackets had positive values, then the rolling element at angular location \(\theta _{i}\) is under compression; otherwise, the ball is not loaded, and the elastic force is considered zero. If the rotor is balanced, the unbalance force \(F_{\mathrm{{u}}}\) is considered zero.

3.1 Contact stiffness

The stress and deformation in the perfectly smooth, contacting elastic solids were practically studied by Hertz and Kotzalas [32]. The contact point between each race and ball produces an area contact which has the shape of an ellipse with semi-major axis a and semi-minor axis b.

The curvature sum and difference are needed to calculate the contact force between balls and races [32]:

$$\begin{aligned} \sum \rho= & {} \rho _{I1}+\rho _{I2}+\rho _{II1}+\rho _{II2}=\frac{1}{r_{I1}}+\frac{1}{r_{I2}}+\frac{1}{r_{II1}}+\frac{1}{r_{II2}} ;\rho =\frac{1}{r} \end{aligned}$$
(31)
$$\begin{aligned} F\left( \rho \right)= & {} \frac{\left( \rho _{I1}-\rho _{I2} \right) +\left( \rho _{II1}-\rho _{II2} \right) }{\sum \rho } \end{aligned}$$
(32)

The parameters \(r_{I1}=r_{I2}=r_{II1}=2\rho _{i}\); \(r_{II2}=R\); \(\rho _{I1}=\rho _{I2}=-\rho _{II1}=1/2\rho _{i}\); \(\rho _{II2}=-1/R\) are given dependent upon calculations referring to the outer race as shown in Fig. 2. It should be noted that \(\rho _{i}\) and R are the radius of ith rolling element and the radius of outer race, respectively.

Fig. 2
figure 2

Geometrical parameters of surfaces in contact [32]

Full size image

For the steel elements in contact, the compression value is calculated as

$$\begin{aligned} \delta =2.787\times {10}^{-8}Q^{2/3}\left( \sum \rho \right) ^{\frac{1}{3}}\delta ^{*} \end{aligned}$$
(33)

where Q is the contact force and \(\delta ^{*}\) is a function of \(F(\rho )\) obtained from Harris and Kotzalas [32].

The contact force can be written as

$$\begin{aligned} Q=\left\{ \left( 3.588\times {10}^{7} \right) ^{3/2}\left( \sum \rho \right) ^{-1/2}\left( \delta ^{*} \right) ^{-3/2} \right\} \delta ^{3/2} (\mathrm{{N}}) \end{aligned}$$
(34)

The stiffness of springs for the contact of a ball with the inner race is

$$\begin{aligned} K_{\mathrm{{in}}}=\frac{Q}{\rho _{\mathrm{{in}}}}\left\{ \left( 3.587\times {10}^{7} \right) ^{3/2}\left( \sum \rho _{i} \right) ^{-1/2}\left( \delta _{i}^{*} \right) ^{-3/2} \right\} \delta ^{1/2} (\mathrm{{N/mm}}) \end{aligned}$$
(35)

The stiffness of springs for the contact of a ball with the outer race is

$$\begin{aligned} K_{\mathrm{{out}}}=\frac{Q}{\rho _{\mathrm{{out}}}}\left\{ \left( 3.587\times {10}^{7} \right) ^{3/2}\left( \sum \rho _{\mathrm{{o}}} \right) ^{- 1/2}\left( \delta _{\mathrm{{o}}}^{*} \right) ^{-3/2} \right\} \delta ^{1/2} (\mathrm{{N/mm}}) \end{aligned}$$
(36)

In this study, the total shaft–rotor system weighs 1313.4 g (in the experimental section is described more). Due to the symmetry design of the system, 50 percent of the weight (656.7 g) is loaded on the investigated bearing. The stiffness of the spring between inner race and ball is calculated \(5.699\times 10^{\text {8}}\) N/m, and the stiffness of the spring between outer race and ball is calculated \(5.28\times 10^{\text {8}}\) N/m.

As mentioned in advance, the Hertzian theory is used for the estimation of the stiffness of springs between inner/outer races and balls [32]. The angular contact ball bearing under investigation is SKF 7202 BEP. The characteristics of the bearing in Table 1 were precisely measured using a CMM machine for geometrical parameters (± 0.001 mm). Also, all parts weighted with a very high-precision scale (± 0.001 g). For curvatures, negative values denote a concave surface.

Table 1 Characteristics of the angular contact ball bearing SKF 7202 BEP
Full size table

3.2 Mathematical model and equation of motion of bearing with a defect on the outer race

In this section, a spall defect will be modeled in the outer race of ball bearing. In some of the previous models, local defects are considered as a step with sharp corners that results in behaviors far from the real conditions. The sharp edges of the so-called defect will cause shock peaks in the simulated signals which do not exist in the experimental signals. A real spall defect in a ball bearing has a definite different pattern because of the defect expansion direction parallel to the direction of the ball’s travel. With this in mind, the balls enter the defect location and exit from it through a curved path and a circular defect is nearer to the real pattern of spall defect respect to a step with sharp corners [34]. Therefore, the defect will be considered as a circular curve on the outer race. The defect model is developed for an angular contact ball bearing which can be easily expanded to other types of ball bearings like deep groove ball bearings.

For the experimental test, an SKF angular contact ball bearing type 7202-BEP is dismantled and the spall defect is contrived using a ball end mill with 8 ± 0.01 mm diameter. The defect geometrical parameters are measured using the CMM machine and are given in Table 2.

Table 2 Characteristic defect on the outer ring of bearing
Full size table

Because of the spherical tooltip, the radius of the defect shapes in two perpendicular directions is 4.000 mm. The contrived spall defect in the outer race of bearing and the defective race is shown in Fig. 3.

Fig. 3
figure 3

Contrived spall defect in the bearing outer race

Full size image

With these values, the stiffness of the spring between the ball and outer race in the defect zone can be determined from Eq. 36. The stiffness of the outer race in the defect zone is \(4.873\times 10^{\text {8}}\) N/m. When a ball is out of the defect zone, the stiffness will have its initial value for a healthy bearing (\(5.28 \times 10^{\text {8}}\,\hbox {N/m}\)). This means that when a ball enters the defect zone, the stiffness of ball–outer race contact reduces.

The ball position is defined by the angle \(\theta \) relative to the horizontal axis or the zero angle. With the creation of the spall defect in the outer race, the diameter of the ball path curve in the outer race varies from its initial value of R. In Fig. 3, the defect generated in the bearing outer race and the important geometrical parameters are shown. When the ball enters the defect zone, it will run on a curvature different from the healthy ball bearing outer race curvature. The outer race shape curvature is also changed due to the existence of the defect. The variable radius \(R_{\mathrm{{v}}}\) is nominated for the new conditions of ball motion on the outer race. When the instantaneous contact point of the ball is outside the defect area, \(R_{\mathrm{{v}}} = R\). But if the ball is located in the defect zone, \(R_{\mathrm{{v}}}\) is to be calculated. Using trigonometry equation, the following three equations can be written:

$$\begin{aligned} c= & {} \sqrt{R_{\mathrm{{v}}}^{\text {2}}\text {+}{(R+t)}^{2}-2R_{\mathrm{{v}}}(R+t)\cos {\theta '}},\qquad c=oa \end{aligned}$$
(37)
$$\begin{aligned} c= & {} \sqrt{r_{\mathrm{{t}}}^{\text {2}}\text {+}r_{\mathrm{{t}}}^{2}-2r_{\mathrm{{t}}}^{2}\cos {\theta ^{\prime \prime }}} \end{aligned}$$
(38)
$$\begin{aligned} R_{\mathrm{{v}}}= & {} \sqrt{{(R-r_{\mathrm{{t}}}+t)}^{2}\text {+}r_{\mathrm{{t}}}^{2}-2r_{\mathrm{{t}}}(R-r_{\mathrm{{t}}}+t)\cos {\theta ^{\prime \prime }}} \end{aligned}$$
(39)
Fig. 4
figure 4

Section view of defect geometry in the outer race

Full size image

With simultaneous solving of the above three equations, the variable radius of the outer race \((R_{\mathrm{{v}}})\) at different angles shown in Fig. 4 can be calculated.

4 Experimental study

To verify the model, experimental tests have been set in different rotating speeds. The experimental test in cases of healthy bearing, and bearing with spall defect on the outer race are performed.

For this purpose, a test bench was designed with the following characteristics:

  1. 1.

    Using a small electric motor with a maximum speed of 2825 rpm and 0.37 kW

  2. 2.

    Optimized design and manufacturing of precision bearing housing

  3. 3.

    Using the angular contact ball bearings SKF 7202-BEP

Angular contact ball bearings due to their specific design should not be used alone. According to the mechanism for applying axial preload in the test bench, the bearings were installed in face to face position. For the bearing, the manufacturer company has set the maximum amount of preload applied to 80 N. In this study, as the system is not in long-term operation and the bearing temperature is controlled continuously, applying maximum preload is also available. The test bench consists of an electric motor on one side and rotating shaft including the shaft, disc, and bearings on the other side. Bearing in the electric motor side in all cases of the test is healthy, but the bearings on the other side of the test bench can be healthy or defective during research. Bearings are installed in rigid housings that have the capability of applying axial preload.

In Figs. 5 and 6, the schematic of the designed test bench, and also a section view of housing, a rotating shaft and bearings are shown.

The two ends of the shaft are threaded to fix the positions of the inner race on the shaft by nuts and also to fix the position of the outer race on the housing by tightening the socket cap screws (please see Fig. 5). The electric motor and the rotating system are connected by a flexible coupling. The type of this coupling is “curved jaw flexible coupling” which can absorb vibration, parallel, angular misalignments, and shaft end-play as shown in Fig. 6.

Fig. 5
figure 5

Section view of housing, rotating shaft, and bearings

Full size image
Fig. 6
figure 6

Schematic of designed test bench

Full size image

The special grease KluberQuiet\(\textregistered \) BQ 72-72 which produces a considerably low-level noise is used for bearing lubrication. Before data collection, the environmental conditions are controlled and the necessary equipment is provided. The test bench is leveled to avoid applying axial loads, and the bearings and electromotor’s axis are aligned with high-precision laser alignment equipment. All tests were performed at room temperature of \(25\pm 2^{\circ }\hbox { C}\) that the room temperature was controlled by air conditioning system. The test bench with the data collection equipment is shown in Fig. 7.

Acceleration of vibration on bearing No. 1 in both the vertical and horizontal directions and that of the bearing No. 2 in the vertical direction by three accelerometer sensor PCB M357B11 are measured. The sensors are shear-type accelerometers and weigh 2 grams. Their sensitivity is \(0.31\,\hbox {pC/(m/s}^{2}\)) with a measurement range of \(\pm \, 22,600\,\hbox {m/s}^{2}\hbox {pk}\) and a resonant frequency higher than 50 kHz. Accelerometers are installed on the outer surface of bearing housing with a special adhesive material.

Fig. 7
figure 7

Test bench with equipment of data collection

Full size image

Using the appropriate cables is as important as the proper installation of the sensors. The low-noise cables PCB Series 003 for data collection are used. A common approach to improve the high-impedance signal produced by a sensor is using an amplifier. For this purpose, a four-channel amplifier Nexus 2692-C was employed. Figure 8 illustrates the installation location of the three accelerometers.

Fig. 8
figure 8

Install location of the sensors on the test bench. a Bearing under investigation with spall defect on the outer race (the bearing No. 1), b healthy bearing (the bearing No. 2)

Full size image

The bearing under investigation is bearing 1, and measurement of vibration acceleration on bearing No. 2 is needed only for comparison. The electromotor speed is adjusted by changing the frequency of the electrical current in the range of rotational speed using an inverter Micromaster 420. The investigation is performed for three different rotating speeds 1500, 1800 and 2100 rpm with three repetitions. The maximum deviation of measurement results on repetitions is determined 2 percent in frequency analysis.

5 Results and discussions

Modeling for both healthy bearing and bearing with spall defect in the outer race in three different rotational speeds are done. The governing equations of motion are solved using the numerical method ODE45 with defining an objective function in MATLAB as

$$\begin{aligned} \hbox {[T,V]} = \hbox {ode}45(@ \hbox {fnc}\_{2}\_{\text {objective}}\_{\text {fcn}}, [0 \hbox {t}\_{\text {total}}],\hbox {Initial}\_{\text {value,options}}) \end{aligned}$$

Here, T represents the time and V stands for the variable under investigation. Figure 9 demonstrates the flowchart of the modeling process. The ball bearing with 10 balls and a stationary outer race set a 12-DOF system. Hence, each of these DOFs and their differentials enters the objective function. The required time for modeling is nominated as t_total.

A small damping coefficient is considered to eliminate the transient response of the system in the numerical solution. Due to the unstable behavior of the simulation in the first 0.3 s of the simulation time, the simulation is performed for 1 s at each of the three simulation cases and the responses were plotted for the 0.4–0.5 s time of the total time. For better analysis of results, FFT diagrams were derived for different cases.

Fig. 9
figure 9

Modeling code flowchart

Full size image

To obtain numerical responses, the time step for the investigation is considered \(5\times 10^{{-7}}\) s by trial-and-error approach. Due to the sensitivity of the numerical methods, increasing the time step can raise the numerical errors and thus will produce the wrong results. It is necessary to mention that the initial values are also so important for the numerical solution and convergence of results.

5.1 Results for healthy bearing

All of the rotating components of the system such as electric motor, rotating shaft, coupling, and ball bearings can create vibration. Ball bearings even if they are geometrically healthy produce vibration. The vibrations are due to the inherent properties of the bearing, and the main reason is the limited number of balls to withstand external loads. However, as mentioned before microscopic factors such as surface quality of bearing components influence vibrations. The previous studies have shown that the number of the rolling elements under load such as ball or roller or needle, and the angular position of the cage will change the dynamic behavior of the bearings. It periodically increases the total stiffness of bearing during rotation and finally produced vibration with balls rotating frequency and their harmonics. Elastic properties of the inner and outer races of the bearing are other factors to produce vibration in healthy bearings. By applying axial preload on the races, their circular form will change to almost a polygon in which the number of sides is equal to the number of rolling elements. The polygon-like inner race rotates with shaft rotation frequency and the position of balls also continuously changes, and it generates a wavy surface with the frequency of balls rotation. Vibration amplitude depends on the amount of preload. The harmonic frequencies of ball spin frequency are also produced with lower amplitudes. It can, therefore, be expected in a healthy rolling bearing; the dominant frequency is the ball spin frequency (BSF). In Table 3, the BSF and its harmonic at three rotational speeds for the bearing under study are shown. It should be noted that the value of the BSFs in Table 3 calculated and rounded according to the reference [33]. The purpose is to find these frequencies in both simulations and experimental tests.

Table 3 Ball spin frequency and its harmonic frequencies at three rotational speeds for the bearing understudy
Full size table

In the plots, hereafter the simulation results are represented by the blue color and the experimental test results are shown by the red color. For a better interpretation of the results, the vibration behavior in all cases at the time domain is demonstrated in 0.1 sec.

In Fig. 10, the time-domain signals obtained from the simulation and experimental test for the healthy bearing (bearing No. 1 in vertical direction) are shown for shaft rotating at 1500 rpm. Noise in the time signal of the experimental test causes bearing’s vibration signal to be hidden. As shown in the time-domain signal, the distance between peaks is 0.02 s, which is, in fact, the period of ball spin or the reverse of BSF. Despite the complexity of the experimental signal, it is also possible to find this period in the experimental signal.

Fig. 10
figure 10

Time-domain signal of healthy bearing at 1500 rpm

Full size image
Fig. 11
figure 11

FFT plot of healthy bearing at 1500 rpm

Full size image

The FFT diagram for the signal shown in Fig. 10 is depicted in Fig. 11. Although the rotating shaft in the experimental test is balanced, due to the residual unbalance in the system the dominant peak (25 Hz) in the frequency range is related to shaft rotation frequency. Due to the residual misalignment between the electric motor and rotating shaft, the other dominant peak with amplitude less than an unbalance peak at the frequency of twice the shaft rotation frequency (50 Hz) is observed. The frequency of ball spin, which was observed in the waveform signal, also exists in the spectrum with a small difference between simulation and experiment. The difference between the frequencies obtained by the two methods can be caused by electric motor speed oscillation. The slip between balls and races in real conditions is another cause. Also as expected, the harmonics of ball spin frequency (95 Hz) are observed in both results. Other major peaks of vibration appear in the spectrum at frequencies 100 Hz and 150 Hz which imply electrical power frequency 50 Hz of the electromotor.

For a better understanding of the results, simulation and experimental signals are also compared in the speed of 1800 rpm. The peak amplitudes with a period of ball spin (0.018 sec) in the waveform signal are again shown in Fig. 12.

Fig. 12
figure 12

Waveform signal of healthy bearing at 1800 rpm

Full size image

By increasing the rotational speed of the shaft, the vibration amplitudes are pushed to higher values. The FFT plot of the waveform signal shown in Fig. 12 is depicted in Fig. 13. Shaft rotation frequency and its harmonics, power frequency and its harmonics, and also ball spin frequency and its second harmonic are characteristics of experimental graphs. But in the graph of simulation, the frequency of ball rotation and its harmonics are observable. The proximity of ball rotation frequency and its harmonics in both results can indicate the validity of the proposed model for the healthy bearing. However, the results were evaluated for additional rotational speed. The waveform signal of bearing vibration at the speed of 2100 rpm is depicted in Fig. 14. In this case, the period of ball spin is 0.15 s, which is well matched with the frequencies listed in Table 3.

Fig. 13
figure 13

FFT plot of healthy bearing at 1800 rpm

Full size image

The third harmonic of ball spin frequency (199 Hz) is clearer at a shaft speed of 2100 rpm. The adjacent different frequencies in the FFT plot of healthy bearing add to the complexity of signal interpretation. The plots are depicted in a selected frequency domain (0–200 Hz) to investigate the exact position of each characteristic frequency (Fig. 15).

Fig. 14
figure 14

Waveform signal of healthy bearing at 2100 rpm

Full size image
Fig. 15
figure 15

FFT plot of healthy bearing at 2100 rpm

Full size image

5.2 Results for bearing with spall defect in the outer race

When a defect in the outer race exists, with the passing of each ball from the defect zone, an impact pulse appears as a dominant peak with the frequency of outer race defect in the frequency domain of bearing vibration. The calculated values of outer race defect frequency or ball pass frequency outer race (BPFO) and its harmonics for three different rotational speeds of the investigated bearing are given in Table 4. For the convenience of frequency comparison, the values are rounded.

Table 4 Outer race defect frequency and its harmonics at three rotational speeds
Full size table

It should be noted that the surface quality of the defective bearing in experimental testing decreases due to machining. The microscopic wavy surface created in the defect region will increase the amplitudes of vibration in the experimental test comparing to the simulation in which the surface quality is not degraded. But in practice, the defects in the components of a defective bearing have surface qualities much lower than even the contrived defect of our specimen. The simulation and experimental results for the speed of 1500 rpm are compared in Fig. 16.

Fig. 16
figure 16

Waveform signal of bearing with a defect in the outer race at 1500 rpm

Full size image

As shown in Fig. 16, the behavior of two signals for a bearing with spall defect in the outer race is very similar to one another in comparison with the healthy bearing condition. The distance between the impact pulses is 0.0099 s which represents the period of the outer race defect. The frequencies of dominant peaks are shown in Fig. 17. The outer race defect frequency (BPFO) and its harmonics are repeated frequently.

Defect in the outer race produces dominant peaks with a remarkable similarity to each other in both simulations and experimental tests not only in the component’s defect frequency but also in its harmonics. In the signal obtained from the experimental test, the peaks at shaft rotation frequency and its harmonics, and the peaks at power frequency are observed. There are also some peaks at frequencies of about 560 Hz and 1450 Hz that their sources are unknown. They probably occur due to resonance in the rotating parts or on the test bench. Some peaks appear where the BPFO is modulated with the shaft rotating frequency, i.e., at \(906\pm 25\,\hbox {Hz}\). These modulated peaks which are known as sidebands appear due to the unbalanced rotor. In the simulated signal, there are no sidebands because the rotor is considered completely balanced.

Fig. 17
figure 17

FFT plot of bearing with a defect in the outer race at 1500 rpm

Full size image

With increasing the shaft rotating speed to 1800 rpm, the outer race defect periodic impact reaches 0.0083 s. The vibration amplitudes also increase in both graphs (Fig. 18).

Fig. 18
figure 18

Waveform signal of bearing with a defect in the outer race at 1800 rpm

Full size image

For example, the exact value of electromotor speed in the latter is 1776 rpm. This value is read from the Tachometer which can also be obtained from the dominant frequency of the unbalanced mass force of the rotor in the FFT graph. Repeated peaks in the vicinity of 560 Hz, without moving or deleting, indicate the occurrence of resonance in the structure of the test bench (Fig. 19).

Fig. 19
figure 19

FFT plot of bearing with a defect in the outer race at 1800 rpm

Full size image

Vibration amplitudes have a greater increase at the shaft speed of 2100 rpm, and repeated impact pulses with a frequency of 0.0071 Hz occur. Figure 20 exhibits the simulated and experimental test waveform signals.

Fig. 20
figure 20

Waveform signal of bearing with a defect in the outer race at 2100 rpm

Full size image

The sidebands in the experimental test repeat. One significant point in the experimental graph is coinciding with the fourth harmonic frequency of BPFO with the resonance frequency of test bench structure which amplifies the vibration amplitude. Another result is the sidebands caused by modulating BPFO with the twice of shaft rotating frequency, i.e., at \(1409\pm 70\,\hbox {Hz}\). In this frequency region also, the harmonic BPFO\(\times \) 10 coincides with the structure resonance frequency that results in a significant amplitude peak comparing the equivalent peak in the simulated graph (Fig. 21).

Fig. 21
figure 21

FFT plot of bearing with a defect in the outer race at 2100 rpm

Full size image

6 Conclusion

In this research, a new developed dynamic model is proposed for an angular contact ball bearing with a spall defect in the outer race. The defect geometry in the model is one of the most important features. The shock peaks in the simulated signals were omitted using the presented defect shape. To validate the model, experimental tests are performed on a specially designed test bench. Comparison of the results of simulations and experimental tests shows that the proposed model can predict the dynamic behavior of the bearing in healthy and defective conditions with a substantial approximation. The results once for a healthy bearing and then for a bearing with outer race defect are obtained and compared to one another at three different rotating speeds. The frequency analysis results showed that the presented model has suitable potential for the study and prediction of vibration responses of healthy and defective angular contact ball bearings.