An enhanced scaled boundary finite element method for linear elastic fracture

Abstract

A blocked Hamiltonian Schur decomposition is herein proposed for the solution process of the scaled boundary finite element method (SBFEM), which is demonstrated to comprise a robust simulation tool for linear elastic fracture mechanics (LEFM) problems. By maintaining Hamiltonian symmetry, increased accuracy is achieved, resulting in higher rates of convergence and reduced computational toll, while the former need for adoption of a stabilizing parameter and, inevitably user supervision, is alleviated. The method is further enhanced via adoption of superconvergent patch recovery theory in the formulation of the stress intensity factors (SIFs). It is shown that in doing so, superconvergence, and in select cases ultraconvergence, is succeeded in the SIFs calculation. Based on these findings, a novel error estimator for the SIFs within the context of SBFEM is proposed. To investigate and assess the performance of SBFEM in the context of LEFM, the method is contrasted against the finite element method and the extended finite element method variants. The comparison, carried out in terms of computational toll and accuracy for a number of applications, reveals SBFEM as a highly performant method.

1 Introduction

Since its inception, the finite element method (FEM) has been advanced to handle a multitude of structural analysis problems ranging from linear to nonlinear, static to dynamic, fracture and contact problems, among others [1,2,3]. Pertaining to the field of fracture mechanics, it has been demonstrated that modeling of damage-related phenomena such as crack initiation, crack propagation and delamination can successfully be accomplished by means of the FEM [4]. Further, with the introduction of singular elements, stress singularities about crack tips may be more accurately quantified [3]. Nonetheless, various undesirable characteristics persist, which render this method computationally prohibitive for more involved analyses. Extensive mesh refinement and remeshing, as well as mesh-dependent projection errors, result in decreased accuracy and increased implementational complexity. As a result, alternative methods have been pursued such as the boundary element method (BEM) [5, 6], the discrete element method (DEM) [7], meshless methods [8], cohesive elements [9] and phase field models [10]. In general, these alternatives are not supported in commercial structural analysis software packages and are more likely to be encountered in special purpose applications.

In mitigating the aforementioned issues of the FEM, the extended finite element method (XFEM) [11] was introduced. A combination of the level set method (LSM) [12] for tracking discontinuities, combined with jump and tip enrichment for the displacement solution, is utilized to decouple both weak (material interfaces) and strong (cracks) discontinuities from the mesh. The popularity of XFEM, currently available in numerous commercial software packages, may largely be attributed to the fact that the core steps of FEM as well as its robustness are left intact, which facilitates implementation and end-user understanding alike. Although this method has aggregated significant academic interest and resolved most shortcomings of FEM-based damage simulation, a number of issues still remain. The most notable include the extension to 3D problems when using the LSM [13, 14], the larger condition number of the stiffness matrix [15, 16] and the a priori assumption for the type of tip enrichment [17]. Additionally, special integration schemes are required in order to determine the stress intensity factors (SIFs).

An alternative approach, namely the scaled boundary finite element method (SBFEM), attempts to fuse the advantageous characteristics of FEM and BEM into one method, while simultaneously introducing features that facilitate the modeling of damage-related phenomena. This method’s key feature, the introduction of a scaling center, has long been exploited for the solution of electric field problems [18]. After refinement and application to solid mechanics, it was initially termed the “Cloning Algorithm” by Dasgupta [19], where it was used to model wave propagation in unbounded soils and found applications in soil–structure interaction and earthquake engineering. Subsequent work by Wolf resulted in a similar formulation named the “infinitesimal finite element method” [20]. Wolf and Song, first coined the term SBFEM, once the derivations for various types of problems were standardized using the minimum weighted residual method [21, 22]. Deeks and Wolf [23] employed a virtual work formulation, facilitating the practical implementation of the method. Though early work on SBFEM was intended for modeling unbounded domains, it soon became apparent that it is at least equally effective for bounded domains [22].

By introducing a scaling center inside the domain, the Cartesian reference system is cast into a polar-like formulation. This can be exploited for determining an analytical solution along the radial direction, thereby only necessitating discretization along the boundary. The trade-off is the solution of a Hamiltonian eigenproblem, which essentially doubles the problem size. General purpose eigen- and Schur decompositions do not respect this special structure, and thus, numerical issues arise. The eigenproblem for generating the stiffness matrix in SBFEM may also be found in optimal control problems, as they both stem from an algebraic Riccati equation. Until recently, the solution to this Hamiltonian eigenproblem in Schur form has proven difficult to solve; developing a $O(n^3)$ backward-stable, structure-preserving algorithm, as posed in [24], came to be known as Van Loan’s curse. Chu et al. [25] proposed a new method, which seemed to resolve this issue; however, it encountered numerical difficulties when dealing with tightly packed clusters of eigenvalues, which is generally the case in SBFEM. As a response, Mehrmann et al. [26] augmented this method and subsequently proposed a “new block method for computing the Hamiltonian Schur form,” thus mitigating the aforementioned issues. Additionally, the blocked nature of the algorithm favors computational efficiency as it can better exploit cache memory. If further takes advantage of the solution symmetry, as all eigenvalues are symmetric about the real and imaginary axis. The latter results in a reduction in the computational toll as compared to a standard Schur decomposition. The main benefit to SBFEM, however, lies in its robustness, when adopted for the solution process. Previously, due to machine precision, a mesh-dependent stabilizing parameter had to be added to the input of the eigenproblem [21, 27]. Its optimal value is not known a priori. The method developed in [26], applied to SBFEM and benchmarked herein, is shown to alleviate this SBFEM-related issue, provide improved convergence rates and cut down on computational cost.

A strength of SBFEM is that damage-related phenomena can be accounted for in an elegant manner. Solution of the eigenproblem leads into straightforward identification of two singular eigenvalues and corresponding eigenmodes, which are then used to compute the stress intensity factors (SIFs). Adoption of a Schur decomposition for solution of the underlying eigenproblem ensures a better treatment of repeated eigenvalues than a standard eigendecomposition [28, 29]. Furthermore, the Schur decomposition allows to incorporate multiple types of crack tip singularities with enhanced accuracy [30], particularly for cases where the crack resides on material interfaces. This in turn allows for an improved quantification of the SIFs, which is particularly meaningful for crack propagation [31,32,33]. However, in order to quantify the quality of each step and the associated discretization level, an error estimator for the SIFs need be defined. In this paper, an efficient and elegant, a posteriori error estimator for the SIFs is presented, based on previous work by Deeks [34], where stress recovery was introduced to SBFEM utilizing superconvergent patch recovery theory (SPR) [35, 36]. Although adaptivity schemes for SBFEM have been introduced [37, 38], they focus on error estimators for the whole domain and not a single, local quantity of interest such as the SIFs. This proposed error estimator sets itself apart in that it does not require the solution of a dual problem [39, 40], which necessitates a second analysis, thus increasing its computational toll. Additionally, it is applicable to not only one [41], but all cracking modes. A further benefit of the application of SPR to the calculation of the SIFs in SBFEM is that they are shown to be superconvergent, and in select cases ultraconvergent.

To date, no comprehensive, direct comparison between SBFEM and XFEM exists, though in [33] a polygon-based SBFEM is contrasted to XFEM, while [42] compares XFEM with SBFEM tip enrichment to standard XFEM. In this paper, numerical examples are treated, which elaborate on the previous findings and fill in the remaining voids. First, the convergence behavior of SBFEM alone is treated extensively for displacements, stresses and SIFs, which in itself has not been adequately reported in the existing literature. Secondly, the convergence behavior for the SBFEM-computed SIFs is compared against those computed via XFEM in two separate numerical examples, providing novel insight into which method is better suited for linear elastic fracture mechanics (LEFM) applications.

Additional topics outside the scope of this paper also include the treatment of dynamics. Solutions based on continued fractions [43], Frobenius series expansion [44], as well as the spectral element method [45] have been proposed. Nonlinearity in SBFEM has only recently been introduced. Material nonlinearity, i.e., elastic-plastic behavior assuming associative plasticity, has been demonstrated in [46], while material and geometric nonlinearity has been incorporated in [47]. In [48], a nonlinear heat transfer problem was solved via the homotopy analysis method (HAM). Further, SBFEM has been successfully coupled with other numerical methods such as FEM [49], BEM [50] and meshless methods [51], in order to exploit SBFEM’s unique abilities to reduce the problem dimension by one. In addition, SBFEM has been used to enhance other numerical methods. This includes, but is not limited to, an XFEM variation in which SBFEM was used for crack tip enrichment [42] as well as the scaled boundary isogeometric analysis (SBIGA) [52], in which the scaled boundary concepts are fused with non-uniform rational b-splines (NURBS) from isogeometric analysis. A novel take on SBFEM, which relies on concepts from spectral element methods, results in decoupled coefficient matrices for each node [53]. The main benefit of this method is that it bypasses the need for an eigendecomposition in standard SBFEM and has thus the potential to be significantly more computationally efficient and parallelizable, especially when considering structures with more degrees of freedom (DOF) such as 3D problems.

This paper is organized as follows: Sect. 2 introduces the theoretical background of this paper. In Sect. 2.1, an abridged formulation of SBFEM theory is treated. The standard procedure for calculating SIFs is reviewed in Sect. 2.2. The novel proposed enhancements to the SIF calculation procedure, as well as the accompanying error estimator, is presented in Sect. 2.3. The newly proposed Hamiltonian Schur decomposition (HSchur), advocated for adoption in SBFEM, is treated in Sect. 2.4. Four applications are demonstrated in Sect. 3. In the first numerical example (Sect. 3.1), the issues associated with the current solution procedure in SBFEM are discussed, while demonstrating the ability of the proposed HSchur decomposition to overcome these, based on the example of an edge-cracked square plate subjected to bending. The second numerical example (Sect. 3.2) provides an exact solution for displacements, stresses and SIFs, establishing a new benchmark. The convergence behavior of SBFEM in terms of displacements, stresses and SIFs is discussed, offering a unique insight into the method. In the third numerical example (Sect. 3.3), SBFEM is contrasted to XFEM and the standard FEM, based on floating point operation counts. This type of extensive contrasting to XFEM in terms of performance and computational complexity has not so far been offered in the literature. The fourth numerical example (Sect. 3.4), a slant crack in a finite body, investigates the performance of SBFEM in the worst-case scenario and evaluates how it performs compared to XFEM and the standard FE-based approach. Section 4 summarizes the findings and provides direction for future research.

2 Theory

This paper deals with 2D elastostatics (Fig. 1), which is governed by the following strong form.

$$\begin{aligned} \text {equilibrium:}&\quad {L} {\sigma } + {b} = {0} \quad&\text {in }\quad \Omega \end{aligned}$$

(1a)

$$\begin{aligned} \text {constitutive:}&\quad {\sigma } = {D} {\varepsilon }\quad&\text {in } \quad \Omega \end{aligned}$$

(1b)

$$\begin{aligned} \text {compatibility:}&\quad {\varepsilon } = {L}^T {u} \quad&\text {in }\qquad \!\! \Omega \end{aligned}$$

(1c)

$$\begin{aligned} \text {boundary conditions:}&\quad {u} = {\hat{u}} \qquad&\text { on }\quad \varGamma _u \end{aligned}$$

(1d)

$$\begin{aligned}&\quad {\sigma } \cdot {n} = {\hat{t}} \quad&\text { on }\quad \varGamma _t \end{aligned}$$

(1e)

L is the linear differential operator, D the constitutive matrix, $\sigma$ represents stress, $\varepsilon$ strains, u displacements, and b body forces. $\hat{u}$, $\hat{t}$ are the prescribed displacements and tractions, respectively, and n is the normal vector.

Firstly, the SBFEM equations for 2D elastostatics will be derived based on a virtual work approach. Next, the solution procedure in SBFEM is described. Subsequently, the calculation of SIFs is presented, augmented by the application of SPR theory. Finally, the theory behind the new block method for computing the Hamiltonian Schur form is detailed.

2.1 Summary of SBFEM

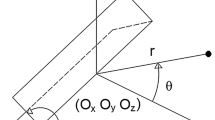
The fundamental difference between SBFEM and other numerical methods is the introduction of a scaling center O. In all but a few special cases, this scaling center must be directly visible from any point on the domain boundary. By introducing the scaling center, the Cartesian coordinate system is transformed into one similar to polar coordinates. It is in this process that a radial coordinate $\xi$ and a tangential coordinate $\eta$ are introduced (Fig. 1).

Fig. 1

Introduction of SBFEM-specific discretization of the bounded domain

Assuming that for SBFEM, an analytical solution can be found in radial direction $\xi$, which is later shown to exist (Sect. 2.1), only the tangential direction $\eta$ need be discretized in the finite element sense. Depending on the bounds for $\xi$ unbounded domains ($1 \le \xi \le \infty$), bounded domains ($0 \le \xi \le 1$) and bounded domains with similar boundaries ($\xi _{1} \le \xi \le \xi _{2}$) can be accounted for (Fig. 2).

Fig. 2

Possible domain types using SBFEM

By choosing to discretize in radial direction along the boundary, the dimension of the problem is reduced by one. Consequently, the information contained within each element on the boundary encompasses that of the triangular domain spanned by itself and the scaling center (Fig. 1).

2.1.1 Derivation based on the virtual work approach

The scaled boundary transformation of geometry, wherein Cartesian coordinates (x, y) are mapped to corresponding scaled boundary coordinates ($\xi , \eta$), is provided below. It states that any point in the domain can be equivalently expressed based on the position of the scaling center $x_0$, some scaling factor in radial direction $\xi$ and an interpolation in tangential direction $x(\eta )$.

$$\begin{aligned} x(\xi , \eta )&= x_O + \xi x(\eta ) = x_O + \xi [{N}(n)] \{{x}\} \end{aligned}$$

(2a)

$$\begin{aligned} y(\xi , \eta )&= y_O + \xi y(\eta ) = y_O + \xi [{N}(n)] \{{y}\} \end{aligned}$$

(2b)

where $[{N}(\eta )]$ corresponds to the finite element interpolation functions $[N_1(\eta ), N_2(\eta ),\ldots ,N_n(\eta )]$, $\{{x}\}$ represents the nodal coordinates $[x_1,x_2,\ldots ,x_n]^T$, and n is the number of nodes per element on the boundary. The Jacobian J, its inverse ${J}^{-1}$ and determinant |J|, which link the derivatives in Cartesian to scaled boundary coordinates on the boundary, are given as:

$$\begin{aligned}&\begin{Bmatrix} \frac{\partial }{\partial \xi } \\ \frac{\partial }{\partial \eta } \end{Bmatrix} = \begin{bmatrix} \frac{\partial x}{\partial \xi }&\frac{\partial y}{\partial \xi } \\ \frac{\partial x}{\partial \eta }&\frac{\partial y}{\partial \eta } \end{bmatrix}\quad \begin{Bmatrix} \frac{\partial }{\partial x} \\ \frac{\partial }{\partial y} \end{Bmatrix} =[{J}] \begin{Bmatrix} \frac{\partial }{\partial x} \\ \frac{\partial }{\partial y} \end{Bmatrix} \end{aligned}$$

(3a)

$$\begin{aligned}&\begin{Bmatrix} \frac{\partial }{\partial x} \\ \frac{\partial }{\partial y} \end{Bmatrix} = \frac{1}{|{J}|} \begin{bmatrix} \frac{ \partial y}{\partial \eta }&- \frac{ \partial y}{\partial \xi } \\ - \frac{ \partial x}{\partial \eta }&\frac{ \partial x}{\partial \xi } \end{bmatrix}\quad \begin{Bmatrix} \frac{\partial }{\partial \xi } \\ \frac{\partial }{\partial \eta } \end{Bmatrix} =[{J}]^{-1} \begin{Bmatrix} \frac{\partial }{\partial \xi } \\ \frac{\partial }{\partial \eta } \end{Bmatrix} \end{aligned}$$

(3b)

As a result, the differential volume unit dV is expressed as follows in scaled boundary coordinates:

$$\begin{aligned} dV = |{J}|\xi d\xi d\eta \end{aligned}$$

(4)

Subsequently, these derivatives are used to evaluate the linear differential operator L in scaled boundary coordinates. Splitting L into Cartesian components facilitates the substitution of their scaled boundary equivalents. Factoring into scaled boundary components, this results in:

$$\begin{aligned}{}[{L}]&= \begin{bmatrix} 1 \quad 0 \\ 0 \quad 0 \\ 0 \quad 1 \end{bmatrix} \frac{\partial }{\partial x} + \begin{bmatrix} 0 \quad 0 \\ 0 \quad 1 \\ 1 \quad 0 \end{bmatrix} \frac{\partial }{\partial y} = [{L^1}] \frac{\partial }{\partial x} + [{L^2}] \frac{\partial }{\partial y} \end{aligned}$$

(5a)

$$\begin{aligned}&= \frac{1}{|{J|}} \left[ [{L^1}] \left( \frac{\partial y}{\partial \eta } \frac{\partial }{\partial \xi } - \frac{\partial y}{\partial \xi } \frac{\partial }{\partial \eta }\right) + [{L^2}] \left( \frac{\partial x}{\partial \xi } \frac{\partial }{\partial \xi } - \frac{\partial x}{\partial \eta } \frac{\partial }{\partial \xi }\right) \right] \end{aligned}$$

(5b)

$$\begin{aligned}&= [{b^1}(\eta )] \frac{\partial }{\partial \xi } + \frac{1}{\xi }[{b^2}(\eta )] \frac{\partial }{\partial \eta } \end{aligned}$$

(5c)

where $[{b^1}(\eta )]$ and $[{b^2}(\eta )]$ represent:

$$\begin{aligned}{}[{b^1}(\eta )]&= \frac{1}{|{J|}} \begin{bmatrix} \frac{\partial y}{\partial \eta }&0 \\ 0&-\frac{\partial x}{\partial \eta } \\ -\frac{\partial x}{\partial \eta }&\frac{\partial y}{\partial \eta } \end{bmatrix} \end{aligned}$$

(6a)

$$\begin{aligned} {[{b^2}(\eta )]}&= \frac{1}{|{J|}} \begin{bmatrix} -\frac{\partial y}{\partial \xi }&0 \\ 0&\frac{\partial x}{\partial \xi } \\ \frac{\partial x}{\partial \xi }&-\frac{\partial y}{\partial \xi } \end{bmatrix} \end{aligned}$$

(6b)

The displacements $\{{u}(\xi , \eta )\}$ follow an isoparametric formulation. They too consist of an analytical part in radial direction $\{{u}(\xi )\}$ and an interpolatory part in tangential direction based on shape functions $[{N^u}(\eta )]$.

$$\begin{aligned} \{{u}(\xi , \eta )\} = [{N^u}(\eta )]\{{u}(\xi )\} \end{aligned}$$

(7)

where $[{N^u}(\eta )]$ represents the shape functions $[{N}(\eta )]$, which are applied to each DOF of an element separately by means of multiplication with the identity matrix [I]:

$$\begin{aligned}{}[{N^u}(\eta )] = [N^1(\eta ){I_n} , N^2(\eta ){I_n}, \ldots , N^n(\eta ){I_n}] \end{aligned}$$

(8)

As a result, an expression for the strains may be derived by substituting the formulation for the displacements into Eq. 1c.

$$\begin{aligned} \{ {{\varepsilon }} (\xi , \eta )\} = [{B^1}(\eta )]\{{u}(\xi )\}_{,\xi } + \frac{1}{\xi }[{B^2}(\eta )]\{{u}(\xi )\} \end{aligned}$$

(9)

where

$$\begin{aligned}{}[{B^1}(\eta )]= & {} [{b^1}(\eta )][{N^u}(\eta )] \end{aligned}$$

(10a)

$$\begin{aligned} {[B^2(\eta )]}= & {} [{b^2}(\eta )][{N^u}(\eta )]_{,\eta } \end{aligned}$$

(10b)

Substituting Eq. 9 into the constitutive relation 1b results in the following expression for the stress field.

$$\begin{aligned} \{ {{\sigma }} (\xi , \eta )\} = [{D}] \left( [{B^1}(\eta )]\{{u}(\xi )\}_{,\xi } + \frac{1}{\xi }[{B^2}(\eta )]\{{u}(\xi )\} \right) \end{aligned}$$

(11)

In what follows, the virtual work method is implemented. To this end, the virtual displacements $\{\delta {u}(\xi ,\eta )\}$ and strains $\{\delta {{\varepsilon }}(\xi ,\eta )\}$ are expressed as follows:

$$\begin{aligned} \{\delta {u}(\xi ,\eta )\}&= [{N(\eta )}]\{\delta {u}(\xi )\} \end{aligned}$$

(12a)

$$\begin{aligned} \{\delta {{\varepsilon }}(\xi ,\eta )\}&= [{L}] \{\delta {u}(\xi ,\eta )\} \end{aligned}$$

(12b)

Thus, by equating internal work to external work, the weak form of the scaled boundary finite element method is derived in the following form:

$$\begin{aligned} \int _V \{\delta {{\varepsilon }}(\xi ,\eta )\}^T \{{{\sigma }}(\xi ,\eta )\} dV - \int _{\partial \Omega } \{\delta {u}(\eta )\}^T \{{t}(\eta )\} = 0 \end{aligned}$$

(13)

The second term in Eq. 13 gives rise to equivalent nodal loads $\{{P}\}$, due to applied tractions ${t(\eta )}$. The corresponding displacements calculated on the boundary are termed $u_h$. Equating the internal virtual work to the external virtual work statements, we can thus formulate the complete virtual work equation:

$$\begin{aligned}&\{\delta { u}\}^T \{ [{E^0}] \{{u_h}\}_{,\xi } + [{E^1}]^T \{{u_h}\} - \{{P}\} \}\nonumber \\&\qquad - \int _{xi = 0}^{\xi = 1} \{\delta {u}(\xi )\}^T \Big \{ [{E^0}] \xi \{{u}(\xi )\}_{,\xi \xi } +\, [[{E^0}] + [{E^1}]^T - [{E^1}]] \{{u}(\xi )\}_{,\xi } - [{E^2}] \frac{1}{\xi } \{{u}(\xi )\} \Big \} d \xi = \{0\}\qquad \qquad \end{aligned}$$

(14)

A detailed derivation can be found in appendix, where the following coefficient matrices, which bare striking similarity to stiffness matrices in FEM, are introduced. The chosen approach follows [23] closely.

$$\begin{aligned}{}[E^0]= & {} \int _{\partial \Omega } [{B}^1(\eta )]^T [{D}] [{B}^1(\eta )] |{J}| d\eta \end{aligned}$$

(15a)

$$\begin{aligned} {[E^1]}= & {} \int _{\partial \Omega } [{B}^1(\eta )]^T [{D}] [{B}^2(\eta )] |{J}| d\eta \end{aligned}$$

(15b)

$$\begin{aligned} {[E^2]}= & {} \int _{\partial \Omega } [{B}^2(\eta )]^T [{D}] [{B}^2(\eta )] |{J}| d\eta \end{aligned}$$

(15c)

In order for this equation to hold for all $\xi$, which implies it should be continuously satisfied in radial direction and only compliant in the finite element sense in the tangential direction, the conditions specified by both Eq. 16 on the boundary and Eq. 17 in the domain must be satisfied:

$$\begin{aligned}&\displaystyle \{{P}\} = [{E^0}] \{{u}\}_{,\xi } + [{E^1}]^T \{{u}\} \end{aligned}$$

(16)

$$\begin{aligned}&\displaystyle [{E^0}] \xi ^2 \{{u}(\xi )\}_{,\xi \xi } + [[{E^0}] + [{E^1}]^T - [{E^1}]] \xi \{{u}(\xi )\}_{,\xi }- [{E^2}] \{{u}(\xi )\} = \{{0}\} \end{aligned}$$

(17)

The above equation is termed the scaled boundary finite element equation in displacement. Alternatively, one could also formulate the scaled boundary finite element equation in the time or frequency domain by including inertial effects into the virtual work equation. Equation 17 is equivalent to earlier work from Wolf and Song, who first used a mechanically based approach [21] and then a weighted residual method [22]. However, this derivation is more consistent with standard engineering principles and understanding. Equation 17 is characterized as a homogeneous set of Euler–Cauchy differential equations.

2.1.2 Solution procedure

The general solution to the scaled boundary finite element equation can be written in power series form as:

$$\begin{aligned} \{{u}(\xi )\}= & {} c_1\xi ^{-\lambda _1}\{{\phi }_1\} + c_2\xi ^{-\lambda _2}\{{\phi }_2\} + \cdots + c_n\xi ^{-\lambda _n}\{{\phi }_n\}\nonumber \\= & {} [{\phi }]\xi ^{\lceil {-\lambda }\rfloor }\{{c}\} \end{aligned}$$

(18)

where $\lambda _i$ and $\{{\phi _i}\}$ are the corresponding eigenvalues and vectors, respectively. The boundary conditions determine the integration constants $c_i$. As a result, the solution of SBFEM in statics strongly resembles the mode superposition method of FEM. Hence, the eigenvectors $\{{\phi _i}\}$ can be interpreted as modal displacement vectors on the boundary with a corresponding scaling factor in the radial direction $\lambda _i$ (Fig. 3).

Fig. 3

Modal interpretation of the general solution of SBFEM [54]. Dashed line original domain; solid line displacement mode

A quadratic eigenproblem results from substituting the general solution into the scaled boundary finite element equation in displacements:

$$\begin{aligned}&[ \lceil {\lambda }\rfloor ^2 [{E^0}] - \lceil {\lambda }\rfloor [ [{E^1}]^T - [{E^1}] ] - [{E^2}] ] \{{\phi } \} = \{{0}\} \end{aligned}$$

(19a)

$$\begin{aligned}&\{{q}\} = [ [{E^1}]^T - \lceil {\lambda }\rfloor [{E^0}] ] \{{\phi } \} \end{aligned}$$

(19b)

In Eq. 19b, the boundary forces are expressed in an equivalent modal formulation. Conceptually, they constitute the nodal force modes $\{{q}\}$, which balance the corresponding displacement modes on the boundary, who are directly dependent on $\{{\phi }\}$ by definition of the general solution. Linearizing the quadratic eigenproblem has been shown to be beneficial in the context of fracture mechanics [28]. Unfortunately, this means doubling the size of the eigenproblem. This is achieved by rearranging the equivalent nodal forces equation (Eq. 19b) to obtain:

$$\begin{aligned} \lceil {\lambda }\rfloor \{{\phi } \} = [{E^0}]^{-1} [ [{E^1}]^T \{{\phi } \} - \{{q}\} ] \end{aligned}$$

(20)

which is in turn substituted into the scaled boundary finite element equation (Eq. 19a):

$$\begin{aligned}&\lceil {\lambda }\rfloor [{E^0}] [{E^0}]^{-1} [ [{E^1}]^T \{{\phi } \} - \{{q}\} ] - \lceil {\lambda }\rfloor [{E^1}]^T \{{\phi } \}\nonumber \\&\qquad +\, [{E^1}] [{E^0}]^{-1} [ [{E^1}]^T \{{\phi }\} - \{{q}\} - [{E^2}] \{{\phi }\} ] = \{{0}\} \end{aligned}$$

which is equivalent to:

$$\begin{aligned} \lceil {\lambda }\rfloor \{{q}\} = [{E^1}] [{E^0}]^{-1} [ [{E^1}]^T \{{\phi }\} - \{{q}\} - [{E^2}] \{{\phi }\} ] \end{aligned}$$

(21)

The linearized, combined form of the quadratic eigenproblem can thus be expressed more compactly in matrix notation as:

$$\begin{aligned} {[Z]} \begin{Bmatrix} {\phi }\\ {q} \end{Bmatrix} = \lceil {\lambda }\rfloor \begin{Bmatrix} {\phi }\\ {q} \end{Bmatrix} \end{aligned}$$

(22)

where

$$\begin{aligned} {[Z]} = \begin{bmatrix} [{E^0}]^{-1} [{E^1}]^T&\quad - [{E^0}]^{-1} \\ [{E^1}][{E^0}]^{-1}[{E^1}]^T - [{E^2}]&\quad -[{E^1}][{E^0}]^{-1} \end{bmatrix} \end{aligned}$$

(23)

where [Z] is a Hamiltonian matrix. This special matrix form mandates symmetry about the real and the imaginary axis for all eigenvalues. As a result, the eigenvalues corresponding to rigid body translational modes can pose significant numerical issues. Machine precision can cause these eigenvalues to arbitrarily alternate in sign. Attempts by other authors to compensate for this issue resulted in:

• 1. Minimizing the condition number by

  • Preconditioning coefficient matrices [55]

  • Normalizing domain properties [21]

• 2. Addition of a mesh- and platform-dependent stabilizing parameter $\varepsilon$ to [${E^2}$]. The optimal value of this parameter is unknown a priori [21, 27]. This corresponds to physically adding small springs to the boundary.

Since eigenvalues of opposite sign contribute to the response of the system in fundamentally different ways, which will be detailed in the following paragraph, they should be sorted accordingly.

$$\begin{aligned}{}[{Z}] \begin{Bmatrix} {\phi }\\ {q} \end{Bmatrix} = \lceil {\lambda }\rfloor \begin{Bmatrix} {\phi }\\ {q} \end{Bmatrix} = \begin{bmatrix} \lceil \lambda _{\mathrm{neg}} \rfloor&\\&\lceil \lambda _{\mathrm{pos}} \rfloor \end{bmatrix} \begin{bmatrix} [\phi _1]&[\phi _2]\\ [Q_1]&[Q_2] \end{bmatrix} \end{aligned}$$

(24)

The subscripts “pos” and “neg” refer to positive and negative eigenvalues, respectively, which bear the effect of separating the bounded from the unbounded response. For negative eigenvalues, the contribution at $\xi = 0$ is bounded and at $\xi = 1$ has a finite value, which represents a solution in agreement with that of the bounded domain, whereas for positive eigenvalues, the contribution at $\xi = 1$ is finite and at $\xi = \infty$ is bounded, resembling the solution of an unbounded domain (Fig. 4).

Fig. 4

Contributions of the domain modes to the bounded and unbounded domain solutions

Having determined the eigenvalues and eigenvectors, these can be substituted into the general solution (Eq. 18) for determining the domain stiffness matrix.

$$\begin{aligned} \{{u}(\xi )\} = [{\phi _1}]\xi ^{\lceil {-\lambda _{\mathrm{neg}}}\rfloor }\{{c_1}\} + [{\phi _2}]\xi ^{\lceil {-\lambda _{\mathrm{pos}}}\rfloor }\{{c_2}\} \end{aligned}$$

(25)

Considering that only the negative eigenvalues contribute to the response of the bounded domain, the terms associated with the positive eigenvalues of Eq. 25 are discarded. Next, in order to evaluate the stiffness matrix, the displacement modes must be linked to the force modes. This is achieved by comparing the displacements on the boundary $\{{u}(\xi =1)\}$ with the acting nodal forces ${\{P\}}$. Enforcing the corresponding boundary conditions, by applying the integration constants to the force modes, results in the following formulation:

$$\begin{aligned} \{{P_{\mathrm{bounded}}}\} = {[q_1]} \{{c_1}\} \end{aligned}$$

(26)

The integration constants are obtained by evaluating Eq. 25 at $\xi = 1$.

$$\begin{aligned} \{{c_1}\} = [\varPhi _1]^{-1} \{{u}(\xi =1)\} \end{aligned}$$

(27)

In a subsequent step, the integration constants are substituted into Eq. 19b:

$$\begin{aligned} {\{P_{\mathrm{bounded}}\}} = [{q_1}][\varPhi _1]^{-1} \{{u}(\xi =1)\} \end{aligned}$$

(28)

Therefore, the stiffness matrix of a bounded domain is found to be:

$$\begin{aligned} K_{\mathrm{bounded}} = + [{q_1}][\varPhi _{1}]^{-1} \end{aligned}$$

(29)

The stiffness matrix is symmetric, though fully populated. Hence, the use of higher-order elements is not penalized by higher bandwidth as in standard FEM approaches.

Similarly, the stiffness matrix for the unbounded domain may be determined by utilizing the analogous expressions of the unbounded domain:

$$\begin{aligned} K_{\mathrm{unbounded}} = - [{q_2}][\varPhi _{2}]^{-1} \end{aligned}$$

(30)

In order to perform the back-calculation of strains and stresses, first the integration constants (Eq. 27) must be determined, next the general solution (Eq. 25) is sought, and only then are the strains (Eq. 9) and stresses (Eq. 11) derived.

Fig. 5

Flowchart of a SBFEM analysis linked to corresponding equations from Sect. 2.1

In order to better understand the steps, computational complexity and effort required for an SBFEM analysis, the flowchart in Fig. 5 is offered. Restricting discretization along the boundary when using SBFEM comes mainly at the price of the solution of an eigenproblem. Therefore, domains with minimal surface-to-volume ratio are especially suited for analysis using SBFEM.

Very similarly to standard FE-based approaches, first element-wise coefficient matrices are evaluated and assembled using a standard numerical integration procedure. However, this must be performed for three separate coefficient matrices. As opposed to XFEM though, no additional enrichment terms must be included, and thus, the need for integration of singular terms is eliminated. Since in SBFEM all elements can be treated equally, many issues pertaining to the condition number of the stiffness matrix can be avoided. Additionally, no further assumptions, for instance pertaining to what type of singularity to include in the crack tip enrichment, are put in place.

In 2D, since the domain is represented by a linked series of bar-type elements, the assembled coefficient matrices are highly sparse and their entries are clustered about the diagonals facilitating the inversion required for constructing the Hamiltonian matrix [Z]. The eigendecomposition is the central core of SBFEM analysis, as it not only is necessary for determining the stiffness matrix, but also delivers the analytical solution for the displacements in radial direction. Once the stiffness matrix is formed, the remaining steps coincide with those of the standard FEM approach. Significant differences may be identified, in the calculation of the SIFs, when compared against the XFEM approach. Not only are the SIF easily identified, efficiently extracted in post-processing, smoothed for further accuracy and used to determine an effective error estimator in SBFEM (Sect. 2.3), but they are additionally exempt from parameter-specific dependencies, such as the radius of integration and enrichment in XFEM. To see how this contributes to reducing computational complexity, approximate flop counts are listed in Table 6.

2.2 Calculation of stress intensity factors

What sets SBFEM apart from other numerical methods is how elegantly highly accurate SIFs may be obtained. The standard solution procedure by default accommodates cracks. Values for the SIFs can easily be extracted during post-processing of the stresses with only negligible additional computational effort. This is a consequence of the analytical solution in radial direction. If the scaling center is placed at the crack tip, an analytical solution for the strains and therefore additionally the stresses in radial direction may be computed. The SIFs can be determined by evaluating the limit of the stresses as $\xi \rightarrow 0$. After substituting the general solution for displacements into the definition of the stresses (Eq. 11), the stresses for any particular element can be obtained as a superposition of stress modes:

$$\begin{aligned} {\sigma }(\xi ,\eta )= \sum _{i=1}^n c_i \xi ^{-\lambda _i-1}{\varGamma _i} \end{aligned}$$

(31)

with ${\varGamma _i}$ representing the associated stress modes.

$$\begin{aligned} {\varGamma _i} = \begin{Bmatrix} \varGamma _{xx}\\ \varGamma _{yy}\\ \varGamma _{xy}\\ \end{Bmatrix}_i = {D}[-\lambda _i{B_1(\eta )} + {B_2(\eta )}] {\varPhi _i} \end{aligned}$$

(32)

The contribution of each mode to the stress response is illustrated in Fig. 7. Only the modes corresponding to eigenvalues within the range $-1< \lambda < 0$ contribute to the singular response at the crack tip ($\xi =0$). Consequently, for the purpose of determining the SIFs, all other modes can be discarded. In 2D elastostatics, only two eigenvalues and thus modes in the aforementioned range exist. As each element contains these singular modes, theoretically the SIFs could be extracted from any element in the domain. Here, the elements lying directly along the crack path extension (Fig. 6, point A) are chosen. Once the singular modes have been identified, corresponding stresses can be theoretically computed using values from anywhere within the bounded domain $0< \xi < 1$. Due to numerical concerns, the singular stresses are evaluated at the boundary ($\xi =1$) and consequently the power expression for $\xi$ in Eq. 31 is reduced to 1.

Fig. 6

Cracked SBFEM domain with crack tip location coinciding with scaling center. Additionally, the DOFs of the two elements used to compute the SIFs are identified

Fig. 7

Contribution of eigenvalues to the stress solution, reaffirming that $-1< \lambda < 0$ leads to singularities as $\xi \rightarrow 0$

Since the singular components of the stresses can be derived analytically, these can be matched directly to the definition of the SIFs. The integration constants $c_i$ correct for the boundary conditions. $L_0$ is then defined as the distance from the crack tip to the location of the evaluated stresses. Thus, the mode I and mode II SIFs assume the following form:

$$\begin{aligned} \begin{Bmatrix} K_{I}\\ K_{II}\\ \end{Bmatrix} = \sqrt{2\pi L_0} \begin{Bmatrix} \sum \nolimits _{i=I,II} c_i \varGamma _{yy}(\eta = \eta _A)_i\\ \sum \nolimits _{i=I,II} c_i \varGamma _{xy}(\eta = \eta _A)_i\\ \end{Bmatrix} \end{aligned}$$

(33)

The stress modes $\varGamma _{i}$ need only be evaluated at one specific point ($-1<\eta = \eta _A<1$) along the element. In order to accomplish this, the correct submatrix $\phi _i$ must be identified. This consists in finding the eigenvector linked to the singular eigenvalue, as well as identifying the rows representing the DOFs of the corresponding element on the boundary. Their intersection (Fig. 8) marks the relevant data for the calculation of the SIF modes. Consequently, the calculation of the SIFs requires only minimal computational effort.

Fig. 8

Singular displacement modes as columns and associated DOFs in rows of a representative element on the boundary. The dark gray intersection signifies the submatrix $\phi _i$ required in order to compute the SIFs

Fig. 9

Stress recovery based on SPR. A least square fit is constructed for the stresses in point A, based on values computed at the Gaussian integration points

2.3 Recovered stress intensity factors and error estimator

Since the SIFs are determined solely on the basis of calculated stresses, they can be easily inferred. Should the crack extension fall directly between two elements, different stresses are calculated for each element at the respective node A (Fig. 9). Trivial averaging of the stresses is an option, but not necessarily the best one. Thus, in this work, a novel application of SPR theory to SIFs is proposed, resulting in superconvergent and in select cases ultraconvergent convergence rates for the SIFs. This extends previous work by Deeks [34].

Recovered stresses are gained by least squares fit of the raw stresses sampled at the Gauss integration points over a patch of two elements. For the case of enhancing SIFs, the two elements are proposed to coincide with those in the direction of crack extension. Based on [22, 34] the fitted recovered stresses are calculated as:

$$\begin{aligned} \sigma ^{\mathrm{rec}}(\eta ) =\{P\}\{a\} \end{aligned}$$

(34)

where $-1< \eta < 3$ (Fig. 9) and for this specific application $\eta = 1$, i.e., point A. $\{P\}$ is a vector of powers of $\eta$, and $\{a\}$ is a vector of undetermined coefficients $a_i$. The vector of raw stresses computed at the Gauss integration points is denoted by $\sigma ^{\mathrm{raw}}$.

$$\begin{aligned} \{P\} = \begin{Bmatrix} \eta ^0 \\ \eta ^1 \\ \vdots \\ \eta ^i \\ \vdots \\ \eta ^n \\ \end{Bmatrix}^T,\quad \{a\} = \begin{Bmatrix} a_1 \\ a_2 \\ \vdots \\ a_i \\ \vdots \\ a_n \\ \end{Bmatrix},\quad \sigma ^{\mathrm{raw}} = \begin{Bmatrix} \sigma ^{\mathrm{raw}}_1 \\ \sigma ^{\mathrm{raw}}_2 \\ \vdots \\ \sigma ^{\mathrm{raw}}_i \\ \vdots \\ \sigma ^{\mathrm{raw}}_n\\ \end{Bmatrix} \end{aligned}$$

(35)

where n denotes the amount of Gauss integration points present in the patch. The vector of unknown coefficients $\{a\}$ can be determined by evaluating vector $\{P\}$ at each Gauss integration point, and adding its contribution to matrix $[\bar{P}]$.

$$\begin{aligned}{}[\bar{P}] = \begin{bmatrix} \eta _1^0&\eta _1^2&\ldots&\eta _1^i&\ldots&\eta _1^n\\ \\ \eta _2^0&\eta _2^2&\ldots&\eta _2^i&\ldots&\eta _2^n\\ \vdots&\vdots&\ddots&\vdots&\ddots&\vdots \\ \eta _i^0&\eta _i^2&\ldots&\eta _i^i&\ldots&\eta _i^n\\ \vdots&\vdots&\ddots&\vdots&\ddots&\vdots \\ \eta _n^0&\eta _n^2&\ldots&\eta _n^i&\ldots&\eta _n^n\\ \end{bmatrix} \end{aligned}$$

(36)

The least squares problem can then be formulated as:

$$\begin{aligned}{}[\bar{P}](\{ \sigma ^{\mathrm{raw}}\} - [\bar{P}]\{a\}) = 0 \end{aligned}$$

(37)

Subsequently, the vector of unknown coefficients is determined as:

$$\begin{aligned} \{a\} = ([\bar{P}]^T[\bar{P}])^{-1} [\bar{P}]^T \{ \sigma ^{\mathrm{raw}}\} \end{aligned}$$

(38)

Thus, recovered stresses in the direction of crack extension are determined by substituting $\eta = \eta _A$ (Fig. 9, point A) into Eq. 34. These stresses are indirectly recovered, by smoothing the stress modes $\varGamma _i$ (Eq. 32), which in turn rely on the displacement modes $[\varPhi _i]$. Since only two displacement modes contribute to the singular response, only a small subset of the eigenmodes resulting from the SBFEM solution must be smoothed. This is the first means used to reduce the computational effort for determining the SIFs. Further, since only one patch in direction of crack extension is considered, recovery over only two elements, again a small subset of the whole domain, is necessary. It is assumed that this trade-off in potential accuracy is offset by the gain in computational speed. This is later demonstrated to hold true in Sect. 3. Consequently, Eq. 31 may be rewritten as:

$$\begin{aligned} {\sigma }^{s}(\xi ,\eta )= \sum _{i=1}^2 c_i \xi ^{-\lambda _i-1} {\varGamma }^s_p \end{aligned}$$

(39)

in which superscript s denotes the singular modes and subscript p corresponds to the stress modes smoothed on the patch in direction of crack extension. Since the stresses are evaluated at the boundary, $\xi = 1$ and Eq. 39 simplifies to the extent that the SIFs can now be formulated as:

$$\begin{aligned} \begin{Bmatrix} K_{I}^{\mathrm{rec}}\\ K_{II}^{\mathrm{rec}}\\ \end{Bmatrix} = \sqrt{2\pi L_0} \begin{Bmatrix} \sum \nolimits _{i=1}^2 c_i {\varGamma }^s_{p,yy}(\eta = \eta _A)\\ \sum \nolimits _{i=1}^2 c_i {\varGamma }^s_{p,xy}(\eta = \eta _A)\\ \end{Bmatrix} \end{aligned}$$

(40)

Finally, it stands by virtue of the SPR theory that the so-recovered SIFs should be at least superconvergent.

Based on the difference in raw and recovered stresses, a novel error estimator accompanying the proposed recovery scheme for SIFs can be deduced.

$$\begin{aligned} \{e_{\sigma }^{*}(\xi ,\eta )\} = \{\sigma ^{*}(\xi ,\eta )\} - \{\sigma _{h}(\xi ,\eta )\} \end{aligned}$$

(41)

where superscript * denotes the recovered value and subscript h denotes the raw value of the stress calculated in direction of crack extension. By consequence, obtaining the error estimator is rendered computationally inexpensive.

2.4 Block Hamiltonian Schur Decomposition

The solution process in SBFEM benefits from the HSchur decomposition in multiple ways.

• It eliminates the need for an arbitrary stabilizing parameter $\varepsilon$.

• By respecting Hamiltonian symmetry of the eigenvalues, regular and steeper convergence rates can be achieved.

• The doubling of the problem size when linearizing the quadratic eigenvalue problem is reversed, and thus, computational complexity is significantly reduced.

• It still benefits from a Schur form, which allows to quantify general SIFs for bi-material interfaces.

The following is an abridged treatment of the theory first presented in [26] with emphasis placed on the parts integral to SBFEM.

A matrix $H \in \mathbb {R}^{2n \times 2n}$ is Hamiltonian iff:

$$\begin{aligned} H_{\mathrm{start}} = \begin{bmatrix} A&G\\ C&-A^T \end{bmatrix} \end{aligned}$$

(42)

Additionally, $G^T = G$ and $C^T = C$, which holds for the case of SBFEM (Eq. 23).

Matrix H is said to be in Hamiltonian real Schur form if

$$\begin{aligned} H_{\mathrm{final}} = \begin{bmatrix} T&G\\ 0&-T^T \end{bmatrix}. \end{aligned}$$

(43)

where T is quasitriangular. Any eigenvalue $+\lambda$ found in T has a corresponding eigenvalue $-\lambda$ in $-T^T$. For most applications it makes sense to group eigenvalues with same sign into T and $-T^T$, respectively.

In order to arrive at $H_{\mathrm{final}}$ from $H_{\mathrm{start}}$, a series of orthogonal symplectic similarity transformations are performed:

$$\begin{aligned} H_{i+1} \leftarrow \hat{Q}^T H_{i} \hat{Q} \end{aligned}$$

(44)

Every step is accompanied by the corresponding update, for which the starting values of $Q_0$ is chosen as $I_{2n}$:

$$\begin{aligned} Q_{i+1} \leftarrow Q_{i} \hat{Q} \end{aligned}$$

(45)

In algorithmically formulating this process of arriving at the Hamiltonian real Schur form, first a symplectic URV decomposition of H is performed. The SLICOT library [56] provides the necessary backwards stable routines:

$$\begin{aligned} H = U R_1 V^T \text { with } \,\, R_1 = \begin{bmatrix} S&\, G\\ 0&\, T^T \end{bmatrix} \end{aligned}$$

(46)

$T \in \mathbb {R}^{n \times n}$ is upper triangular, $S \in \mathbb {R}^{n \times n}$ is quasitriangular and $G \in \mathbb {R}^{n \times n}$. It is at this point that the eigenvalues of H can be determined as they are equal to the square roots of the eigenvalues of the quasitriangular matrix $-ST$.

Next, the eigenvalues of $-ST$, which correspond to the eigenvalues of $H^2$, are partitioned into blocks. Many clustering algorithms exist; however, here we choose an open ball with radius:

$$\begin{aligned} r = 10 \times \vert \vert S \vert \vert _F \vert \vert T \vert \vert _F \times \kappa \times \varepsilon \end{aligned}$$

(47)

$\vert \vert \bullet \vert \vert _F$ denotes the Frobenius norm, $\kappa$ is the condition number of the eigenvalue, $\varepsilon$ is machine precision, and the factor 10 is included to arrive at a conservative estimate as originally proposed in [26]. Eigenvalues of overlapping balls are placed in the same block. Complex conjugates are then added to the block if they exist as well. In a last operation for this step, the eigenvalues of the URV decomposition are ordered to match their blocks. The new structure of the matrix $-ST$ is given as follows:

$$\begin{aligned} -ST = B = \begin{bmatrix} B_{11}&\ldots&B_{1s}\\&\ddots&\vdots \\ 0&B_{ss} \end{bmatrix} \end{aligned}$$

(48)

The spectrum of $B_{ii}$ is given by eigenvalues $\Lambda _i$ of block $1<i<s$. At this point, the first orthogonal symplectic update is performed using the sorted output of the URV decomposition:

$$\begin{aligned} H \leftarrow U^T H U \end{aligned}$$

(49)

Henceforth, each block will be considered separately. The general procedure will be illustrated based on the first block $B_{11}$ with size k. First, a QR decomposition is performed on:

$$\begin{aligned}{}[E_{k} \,\, HE_k] = QR \end{aligned}$$

(50)

$E_k \in \mathbb {R}^{2n \times k}$ is the submatrix of $I_{2n}$ constructed from the first k columns. Next, a Schur decomposition is performed:

$$\begin{aligned} G = Q^{T} H Q \xrightarrow {Schur} \widetilde{Q} \widetilde{T} \widetilde{Q}^T \end{aligned}$$

(51)

The eigenvalues of $\widetilde{Q}$ are subsequently sorted into left- ($\widetilde{Q}_1$) and right ($\widetilde{Q}_2$) half plane, respectively:

$$\begin{aligned} \widetilde{Q} = [\widetilde{Q}_1,\widetilde{Q}_1] \end{aligned}$$

(52)

In order to construct an orthonormal basis for the invariant subspace of H, a matrix X is introduced as follows:

$$\begin{aligned} X = Q \widetilde{Q}_1 \end{aligned}$$

(53)

The main task lies in transforming X into $E_k$ and thus achieve a deflation. This is carried out by means of finding an orthogonal symplectic S such that $S^TX = E_k$, which will be subsequently used to perform an update on $H \leftarrow S^T H S$. To this end, first X is partitioned to conform to the block sizes:

$$\begin{aligned} X = \begin{bmatrix} X_{1}\\ \vdots \\ X_{s}\\ \hline X_{s+1}\\ \vdots \\ X_{2s} \end{bmatrix} \end{aligned}$$

(54)

S can be found as:

$$\begin{aligned} S = \begin{bmatrix} \hat{S}&\, 0\\ 0&\, \hat{S} \end{bmatrix} \quad \text {with} \; \hat{S} = \hbox {diag}\{\check{S},I\} \quad \text {and} \quad \check{S} = Q \widetilde{F} \end{aligned}$$

(55)

$\widetilde{F}$ is a flip vector obtained from reversing the column order of the identity matrix [I], Q results from the QR decomposition of the submatrix of X corresponding to $[X_{s+1}; X_{s+2}]$. After carrying out the updates $X \leftarrow \widetilde{S}^T X$ and $H \leftarrow \widetilde{S}^T H \widetilde{S}$, the vector X assumes the following form:

$$\begin{aligned} X = \begin{bmatrix} X_{1}\\ \vdots \\ X_{s}\\ \hline 0\\ X_{s+2}\\ \vdots \\ X_{2s} \end{bmatrix} \end{aligned}$$

(56)

Subsequent iterations on the lower blocks of X, introduce further blocks of zeros eventually resulting in:

$$\begin{aligned} X = \begin{bmatrix} X_{1}\\ \vdots \\ X_{s}\\ \hline 0\\ \vdots \\ 0\\ X_{2s} \end{bmatrix} \end{aligned}$$

(57)

For the last block, a slightly modified procedure must be applied as there is no successive block, which could be used to install a further block of zeros. For the last block, the actions are modified, by considering the submatrix $[X_{s}; X_{2s}]$. Based on the QR decomposition of the aforementioned submatrix, from which $\check{Q}$ results, the required updates $X \leftarrow \widetilde{Q}^T X$ and $H \leftarrow \widetilde{Q}^T H \widetilde{Q}$ are constructed:

$$\begin{aligned} \begin{bmatrix} X_{s}\\ X_{2s}\\ \end{bmatrix} = \begin{bmatrix} \check{Q}_1\\ \check{Q}_2\\ \end{bmatrix} R \end{aligned}$$

(58)

and

$$\begin{aligned} \widetilde{Q} = \begin{bmatrix} \widetilde{Q}_{1}&-\widetilde{Q}_{2}\\ \widetilde{Q}_{2}&\widetilde{Q}_{1} \end{bmatrix} \quad \text {and} \quad \widetilde{Q}_{1} = \hbox {diag}\{I,\check{Q}_{1}\}; \,\, \widetilde{Q}_{2} = \hbox {diag}\{I,\check{Q}_{2}\} \end{aligned}$$

(59)

This results in the entire lower portion of X running from blocks $s+1< k < 2s$ to be filled with zeros.

In a next step, an analogous procedure for the block $1< k < s$ will be applied. S can be found as:

$$\begin{aligned} S = \begin{bmatrix} \hat{S}&\, 0\\ 0&\, \hat{S} \end{bmatrix} \quad \text {with} \; \hat{S} = \hbox {diag}\{\check{S},I\} \quad \text {and} \quad \check{S} = Q \end{aligned}$$

(60)

Q results from the QR decomposition of the submatrix of X corresponding to $[X_{s-1}; X_{s}]$. Again a block of zeros is inserted into X:

$$\begin{aligned} X = \begin{bmatrix} X_{1}\\ \vdots \\ X_{s-1} 0\\ \hline 0\\ \vdots \\ 0 \end{bmatrix} \end{aligned}$$

(61)

This procedure is continued until only one block remains. After $2s-1$ updates of $X \leftarrow \widetilde{S}^T X$ and $H \leftarrow \widetilde{S}^T H \widetilde{S}$, the desired deflation is nearly achieved. At this point, the Hamiltonian matrix H is of the form:

(62)

It is now admissible to deflate the problem. Subsequent operations are performed on the following Hamiltonian submatrix:

$$\begin{aligned} H = \begin{bmatrix} A_{22}&G_{22}\\ C_{22}&-A_{22}^T \end{bmatrix} \end{aligned}$$

(63)

This deflation is repeated for each block until the real Hamiltonian Schur form is reached:

$$\begin{aligned} H = \begin{bmatrix} A&G\\ 0&-A^T \end{bmatrix} \end{aligned}$$

(64)

Q contains the orthonormal basis for the stable invariant subspace. In a last step, a sorting of the eigenvalues and vectors spanning the stable invariant subspace is performed, in order to retain only negative eigenvalues. Such routines are also available in the Slicot library [56].

It therefore becomes evident that application of the HSchur decomposition in the solution process of SBFEM as proposed will increase accuracy, while reducing complexity.

3 Numerical examples

The first numerical example illustrates the benefits to the overall robustness of the proposed SBFEM solution, incorporating the HSchur decomposition, versus the established eigen and standard Schur decomposition. This novel contribution alleviates the need for an architecture-dependent stabilizing parameter $\varepsilon$. The second numerical example demonstrates the consequently improved convergence behavior of the $L_2$ displacement and stress norms. Additionally, an efficient procedure is proposed to enhance the accuracy of the calculated SIFs. According to the latter, only local stress recovery over select few elements is performed on the boundary instead of over the whole domain, simultaneously resulting in significantly reduced computational effort. Further, it is established that the SIFs calculated by the proposed method are superconvergent for even-noded elements or even ultraconvergent for some odd-noded cases. This forms the basis for a novel error estimator for SIFs. As part of the third numerical example, the computational effort for an SBFEM solution is contrasted to that of FEM, based on a flop count, which is demonstrated for the first time herein. Additionally, the enhancement in accuracy for the proposed local recovery of the stresses compared to adoption of trivial averaging of raw stresses at nodes is demonstrated. Next, SBFEM is directly contrasted to XFEM and the FE-based commercial software Abaqus in terms of SIF reconstruction and conditioning of the stiffness matrix. To the authors knowledge, this is the first occurrence of a direct comparison between standard SBFEM and XFEM in the literature. As XFEM represents a major competing method to SBFEM within the context of LEFM, the fourth numerical example primarily considers this comparison. Furthermore, the computational time required for various parts of the SBFEM procedure are shown, illustrating the computational gains achieved by the proposed HSchur decomposition and smoothing processes.

Calculations were performed on an Intel Core i5 6600K and an Intel Xeon E3-1225 v3. SBFEM and XFEM were implemented in MATLAB 2015b. In Abaqus 6.14-1, the contour integral method was used to determine the SIFs.

3.1 Edge-cracked square plate under bending

A square, homogeneous domain with an edge crack as depicted in Fig. 10 is considered, with length $L=2$ units and crack length $a=L/2$. The domain boundary is uniformly discretized. For this special case of pure bending, an analytical solution exists for the SIFs [57]. The application of point boundary restraints in SBFEM is similarly problematic as would be in the standard FEM case, as these must be applied for eliminating rigid body motion. Since in this numerical example restraints have to be positioned along the direction of crack extension, they may induce restraining forces precisely at the position used to calculate the SIFs. This complicates the accurate determination of the SIFs, though it may be mitigated to an extent for this special test case by scaling the problem domain uniformly. This is admissible since the SIF for an edge-cracked square plate under bending only depends on the ratio of side length to crack length [57].

Fig. 10

Edge-cracked square plate subject to bending. The problem statement for the first numerical example

Numerical difficulties arise in the solution process of SBFEM due to the occurrence of rigid body modes. In 2D elastostatics, a $4 \times 4$ block of zero eigenvalues exists. Two are associated with the response of the bounded domain, whereas the other two contribute to the response of the unbounded domain (Fig. 4). Numerical issues may perturb eigenvalues, resulting in signs, which may alternate arbitrarily. A subsequent reordering of eigenvalues into left half plane and right half plane may thus result in an eigenvalue intended for the unbounded domain to falsely contribute to the bounded domain. Since the stiffness matrix is constructed from the corresponding eigenvectors, this effect leads to erroneous results. As an example, it is possible that the rigid body mode of horizontal displacement is considered twice, whereas the rigid body mode of vertical displacement is not considered at all and vice versa (Fig. 3).

Since one is not able to predict the outcome of the sorting a priori, a stabilizing parameter $\varepsilon$ is typically introduced in the existing literature [21], with the intent of shifting the eigenvalues of the rigid body modes off of the imaginary axis. This is achieved by modifying the input to the Hamiltonian matrix [Z] (Eq. 23) as follows, which physically bears the effect of introducing springs on the boundary:

$$\begin{aligned}{}[E^2] = [E^2]+\varepsilon [I] \end{aligned}$$

(65)

Table 1 summarizes the solution quality of SBFEM for various values of epsilon. According to [21], the typical values for epsilon range from $10^{-6}<\varepsilon <10^{-12}$. Below, the eigendecomposition is considered, though similar effects may also be observed for the standard Schur decomposition. It is evident that values of $\varepsilon$ exist, where incorrect solutions are obtained. Further, there exist regions for which the choice of $\varepsilon$ does not bear significant influence on the solution. Remarkable is the fact that on different CPUs, the values for epsilon, which result in solution errors due to incorrect separation of eigenvalues, differ. Consequently, the correct choice of epsilon cannot be determined prior to the analysis. In order to ensure robust results, multiple runs with different values for epsilon are necessary and usually require user intervention, which reduces the computational advantage of SBFEM. This significantly complicates modeling of crack propagation and effectively bars SBFEM from being used for problems, where successive function evaluations are required, such as optimization problems using heuristic methods.

Table 1 Correct solutions obtained as a function of the stabilizing parameter $\varepsilon$ for various CPU architectures

The main advantage of the HSchur decomposition stems from the fact that it accounts for the special structure of the Hamiltonian matrix [Z], which dictates symmetry about the real and imaginary axis for all eigenvalues. Taking advantage of symmetry by only considering the left half plane associated with the negative eigenvalues, the eigenvalues are always separated properly, and the need for a stabilizing parameter is removed. Thus, this novel approach enables a robust, parameter-independent solution process for SBFEM.

This symmetry may be observed in Fig. 11, where the eigenvalues for the square plate are plotted. The HSchur decomposition better respects symmetry in comparison with the corresponding eigen and Schur decompositions. For the Schur decomposition, the block diagonalization seems to weaken symmetry. The eigendecomposition approach does not require this step, resulting in improved symmetry. However, the issues pertaining to the sorting of the rigid body modes remains.

Fig. 11

Symmetry of eigenvalues for eigen, Schur and HSchur decomposition. Discretized with 2-noded elements and 4 elements per side

Slight variation of the stabilizing parameter induces variation in the eigenvalues, resulting in modified eigenvectors. As a result, the stiffness matrix loses its symmetry (Fig. 12), which results in solution errors.

Fig. 12

Symmetry of stiffness matrix for various choices of $\varepsilon$ compared to HSchur decomposition. Discretized with 2-noded elements and 4 elements per side

A large value for the stabilizing parameter epsilon results in loss of solution accuracy, as introducing springs on the boundary effectively results in a different structural system. On the other hand, too small values for epsilon may result in incorrect solutions due to improper separation of eigenvalues. Figure 12 visualizes that there is a region for $\varepsilon$, where the solution is better behaved. For this purpose, the values in the stiffness matrix ($K_{i,j}$) are compared to the averaged sum ($K_{\mathrm{ave}}= (1/2)*(K_{i,j}+K_{j,i})$). According to Brenner and Kressner [58], this difficulty in computing the zero and negative eigenvalues of a Hamiltonian matrix is well known for QR and Arnoldi-based decompositions, leading to loss of symmetry due to round-off errors. It is further well known that accuracy is compromised, when computing eigenvalues of a matrix whose elements differ by several orders of magnitude [59]. Since this is the case for the entries of the Hamiltonian matrix [Z], due to the contribution of the inverse of $[E^0]$, this further compounds numerical errors. Normalizing the contributions of the coefficient matrices [21] or applying a preconditioner [55] mitigates this effect partially; however, the issues discussed in [58] still remain.

Fig. 13

Evolution of the condition number for eigen and HSchur decomposition. Discretized with 2-noded elements

Further, the condition number of the stiffness matrix varies, depending on different choices of stabilizing parameter. Figure 13 depicts the evolution of the condition number for the eigendecomposition with $\varepsilon = 10^{-12.5}$ compared to the HSchur decomposition. However, since the condition number additionally varies as a function of $\varepsilon$ for the standard eigendecomposition case, box plots are further provided, indication variation for the range of $10^{-6}<\varepsilon <10^{-15}$. The observed spread in condition number may pose unpredictable, numerical challenges. This spread is not present for the proposed HSchur decomposition. The same is observed for matrix $[\varPhi ]$ (Eq. 29), whose inversion is required for the formation of the stiffness matrix and the evaluation of the vector of coefficients [c] (Eq. 27).

Fig. 14

Error in SIF $K_1$ computed by eigendecomposition as a function of $\varepsilon$, contrasted to the HSchur decomposition. Discretized with 3-noded elements and 6 elements per side

Since the HSchur decomposition results in a robust and predictable solution for SBFEM, the calculated SIFs result independently of the stabilizing parameter epsilon. Figure 14 demonstrates the fluctuation in computed SIFs by eigendecomposition, contrasted to the estimates of the HSchur decomposition. It is observed that the error in calculated SIFs via eigendecomposition with a variable $\varepsilon$ may outweigh the inherent accuracy of the method itself. Additionally, as is later demonstrated in the next numerical example, the $L_2$ displacement error for lower-order elements also fluctuates significantly with variation in $\varepsilon$ (Fig. 20). This is not the case when employing the HSchur decomposition (Fig. 21).

In [57], an exact value for $K_1$ is provided for the edge-cracked plate subjected to pure bending. In Figs. 15 and 16, respectively, the SIF $K_1$ computed using raw stress and recovered stress is depicted. Stress recovery is performed only on the two elements’ patch in the direction of crack extension (Fig. 6), and not on the entire domain. Table 2 indicates that for the proposed case of local recovery, the computational effort is drastically reduced, while achieving similar accuracy to full domain recovery. This is important, since stress recovery in SBFEM occupies a significant portion of the total execution time (Table 5). The formulation of an error estimator for SIFs based on the difference in the raw and recovered stresses, as proposed herein, may be exploited to greatly facilitate the SBFEM post-processing procedure. In Fig. 17, the computed error estimator is contrasted to the exact error for the SIF, where good agreement is noted. The proposed procedure allows for inherent checking of the accuracy of the computed SIFs, within a single analysis and with minimal computational effort.

Fig. 15

Error in SIF $K_1$ computed using raw averaged stress

Fig. 16

Error in SIF $K_1$ computed using recovered stress

3.2 Edge-cracked square plate with forced SIFs

The square, homogeneous domain with an edge crack, as depicted in Fig. 18, is considered, with length $L=2$ units and crack length $a=L/2$. The boundary is uniformly discretized. An analytical solution for displacements, stresses and SIFs is given in [60]. The expressions linking the displacements, stresses and SIFs are given in Table 3.

Table 2 Percent of total analysis time spent on calculating $K_1$ based on full or local domain stress recovery

Fig. 17

Proposed error estimator for SIFs contrasted to exact error

Fig. 18

Edge-cracked square plate problem domain subject to $K_2 = 1$ as boundary conditions. The problem statement for the second numerical example

Table 3 Analytical solution for edge-cracked plate under forced $K_2$

For this example, the mode I and mode II SIFs are chosen as $K_1= 0$ and $K_2 = 1$. The coinciding exact displacements on the boundary are then enforced as boundary conditions at each node. The improvements in convergence properties when using the novel approach based on the HSchur decomposition are investigated. To this end, first the $L_2$ error in displacements norm is considered, followed by the $L_2$ error in stresses norm. Figures 20 and 21 demonstrate the $L_2$ error in displacements norm for the eigen and HSchur decomposition, respectively. Since the boundary conditions are applied to all nodes, the error norm is calculated based on chosen displacements post-processed at 10 equally spaced points along $\xi$, as denoted by crosses in Fig. 19. The same procedure was carried out in the case of the stresses.

Fig. 19

Points at which the $L_2$ norms are calculated, denoted by crosses. The upper left quarter of the domain is depicted

Fig. 20

Convergence results of the $L_2$ displacement error based on the eigendecomposition

Fig. 21

Convergence results of the $L_2$ displacement error based on the HSchur decomposition

A significant improvement in the regularity and rate of convergence is observed between the proposed HSchur decomposition (Fig. 21) and the standard eigendecomposition (Fig. 20), as optimal convergence is almost achieved. Since the proposed HSchur decomposition is independent of a stabilizing parameter, its convergence properties do not exhibit oscillations, as is observed for the standard eigendecomposition. For the eigendecomposition, these oscillations may be amended, by appropriate variation of $\varepsilon$, a task, which, however, is not straightforward. This further implies that an increase in the employed number of DOFs does not guarantee higher accuracy in the eigendecomposition case. Furthermore, the convergence rates m of this newly proposed method, better approximate the values predicted by established FEM theory. Optimal values $m^{\mathrm{opt}}$ are equal to the order of the interpolation function. For SBFEM, this is equal to the amount of nodes present in each element.

Next, the performance of (i) the Schur decomposition as provided in MATLAB, (ii) the Hamiltonian Schur decomposition of [25], and (iii) the proposed new blocked Hamiltonian Schur decomposition, HSchur, is further investigated via the following residual metric [25]:

$$\begin{aligned} \text {Residual}_{\mathrm{Schur}} = \dfrac{||U^T H U - \hat{H} ||_2}{|| \hat{H} ||_2} \end{aligned}$$

(66)

where $\hat{H}$ represents the computed Hamiltonian Schur form and H denotes the original Hamiltonian matrix. The residual of the current MATLAB implementation of the Schur decomposition does not vary significantly with changing values of $\varepsilon$. In Table 4, the residual for all three methods is provided for different levels of discretization. The newly proposed HSchur decomposition clearly outperforms the competing methods, which results in improved convergence rates and elimination of the oscillations of the standard eigendecomposition (Fig. 20). It should be noted that the Hamiltonian Schur method (CSchur) proposed by Chu et al. [25], which is the precursor to the currently proposed method, has previously been shown to exhibit increased residuals when clusters of tightly grouped eigenvalues are present.

Table 4 Residuals for each decomposition type. Discretized with 3-noded elements

Fig. 22

Eigenvalue clustering for domains with higher levels of discretization. Discretized with 5-noded elements and 10 elements per side

Clustering of eigenvalues is generally the case for SBFEM, which is demonstrated in Fig. 11 for few DOFs and Fig. 22 for a typical amount of DOFs necessary for such an analysis. Naturally, as the amount of DOFs increases the clustering issues further propagate, and the residual of CSchur tends to accordingly increase. The block of zero eigenvalues [26] still poses a computational challenge for the proposed HSchur method. The presence of purely imaginary eigenvalues results in failure to find an invariant, isotropic subspace to working precision. By relaxing the isotropy checks, a near-real Schur form is, nonetheless, obtained, thereby forfeiting numerical accuracy. The is observed for residual values greater than machine precision $(\hbox {eps} = 2.22*10^{-16})$.

Fig. 23

Convergence results of the $L_2$ stress error based on the eigendecomposition

Fig. 24

Convergence results of the $L_2$ stress error based on the HSchur decomposition

Figures 23 and 24 plot the $L_2$ norm of the stress error vs DOFs. To this end, the stresses are first computed, and then recovered using SPR theory. The von Mises stress is adopted for this comparison. Again, the proposed HSchur decomposition outperforms the standard eigendecomposition scheme. However, certain features cannot be overcome. A change in convergence rate is observed, when few element are used to model a side of the domain. As stress recovery techniques require at least two elements to form a recovery patch, they are not applicable when one element is used to discretize a side. The lack of stress recovery options leads to a decreased rate of convergence. It is therefore proposed to discretize each side by at least two elements, in order to harness the benefits of SPR theory. Furthermore, a coarse discretization significantly limits the resolution of the mode shapes comprising part of the SBFEM solution.

Since the stress variation in the tangential direction is not smooth around corners, special consideration must be taken for these cases. In order to avoid errors, an automated procedure is proposed, based on the orientation of adjacent elements. As long as the normal vectors of two adjacent elements point along the same direction, i.e., the cosine of the angle spanned between them approaches the value of 1, then the adjacent element is added to the patch. Such a process may not be put in place for the case of corner points, an issue, which is elaborated upon in the fourth numerical example.

Figure 25 contrasts the von Mises stresses computed with only few DOF by SBFEM with the exact stresses obtained from Table 3. The largest discrepancy on the domain results around the four corners for the reason hinted at earlier. Hence, it is shown that optimal superconvergence cannot be obtained due to this limitation. Apart from this exception, the HSchur decomposition succeeds in improving the convergence behavior.

Fig. 25

Qualitative location of errors in von Mises stress, by comparing the SBFEM solution to the analytical ones provided in Table 3. Discretized with 3-noded elements and 4 elements per side

Fig. 26

Percent error in $K_2$ calculated using recovered stress

Fig. 27

Percent error in $K_2$ calculated using averaged stress

Fig. 28

Percent error in $K_2$ calculated using averaged stresses vs wall clock time. The calculations were performed on an Intel Xeon E3-1225 v3

Table 5 Percentage of computational time spent on various tasks for the solution of SBFEM. Discretized with 3-noded elements and 3 elements perside, 4-noded elements and 4 elements per side and 5-noded elements and 5 elements per side, respectively

For the current numerical example, the stresses along the boundary in the direction of crack extension are recoverable and thus the SIFs are accurately and efficiently calculated, as observed in Fig. 26. The error is determined based on the exact values for the SIFs, imposed originally through the boundary conditions. The improvement over the case with only trivial averaging of stresses at nodes (Fig. 27) is recognizable. The convergence rates m are observed as superconvergent, i.e., the stresses converge at the same rate as the displacements.

Since one of the aims is to determine the potential of SBFEM for readily determining the SIFs, the error in $K_2$ is plotted against wall clock time for each analysis (Fig. 28). It is apparent that SBFEM can compute the SIFs with subpercent accuracy in well under a second on current generation computers. Further, it seems that the odd-noded elements outperform their even-noded counterparts.

Table 5 summarizes the computational time required for completing the various tasks in SBFEM. Striking is the fact that for the current implementation of SBFEM, recovery of the stresses over the entire domain significantly extends the required computational time. In contrast, calculation of SIFs by the proposed local stress recovery scheme does not add any significant computational toll.

The associated error estimator for the SIFs is plotted in Fig. 29. Moreover, for this example, the a posteriori error estimator is highly effective and may be easily determined. In contrast to other SIF error estimators [39, 40], solving for a second right-hand side is not necessary. The absolute difference between estimated and exact error estimator is seen to decrease for all elements and is generally in the order of percent fractions (Fig. 29).

Fig. 29

Error estimator for $K_2$ based on difference between raw and recovered stress

Fig. 30

Double edge-cracked plate under tension. Problem statement for the third numerical example

3.3 Double edge-cracked plate under tension

A double edge-cracked plate under tension as depicted in Fig. 30 is considered, with length $L=1$ units and crack length $a=L/4$. The boundary is uniformly discretized. For this numerical example, SBFEM is compared to XFEM and the commercial FEM software Abaqus. Three primary metrics for a solution, i.e., accuracy of calculated SIFs, floating point operations (flops) and number of DOFs, are considered. Since the motivation for employing SBFEM to model fracture is accelerating simulations, analysis time is included as a secondary metric.

Table 6 Rough flop counts for two SBFEM variants and (X)FEM

The flops required for the solution of each method are based on simplified assumptions. Steps exist, such as the inversion of matrices and the solution of the eigenproblem, which dominate the computational toll of an analysis. For XFEM and the standard FEM, this toll is assumed to stem primarily from the inversion of the structures stiffness matrix. In SBFEM, however, multiple computationally intensive steps exist and are summarized in Table 6. The variables n and m denote the DOFs present in SBFEM and XFEM, respectively, whereas b represents the half-bandwidth of the matrix [$E^0$] (Eq. 15). The solution process in SBFEM is constrained by the computational demands of the Schur decomposition. The newly proposed HSchur decomposition reduces this burden by exploiting the symmetry conditions of the Hamiltonian matrix [Z]. Considering flops alone, the HSchur decomposition is clearly more performant. Since the method is currently implemented as proof-of-concept code written in MATLAB, execution times are similar to the generic Schur decomposition. Once this novel method is assimilated into high performance libraries, calculation times are expected to improve considerably.

In Abaqus, quadratic elements are used with the midside nodes set at the quarter points and the element sides are collapsed into a single node, in order to emulate singular elements capable of representing a square root singularity. The SIFs are calculated by a contour integral with four contours. In XFEM, linear elements are employed. The radius of enrichment is kept constant at $r_{\mathrm{e}} = 0.2$ units, while the radius of integration is fixed at $r_{\mathrm{i}} = 2.55$ times the element size. The SIFs are calculated by interaction integral. In SBFEM, the use of higher-order elements does not significantly alter the computational effort. Since the stiffness matrix is fully populated, higher-order elements do not affect the bandwidth other than in the formulation of $[E^0]^{-1}$ (Eq. 23). This operation constitutes a minor part of the overall computational complexity (Table 6). Subsequently, the worst case is assumed and the half-bandwidth is chosen to be maximal. The computational burden due to fully populated matrices is offset by symmetry and the fact that only the boundary need be discretized.

Figure 31 depicts the theoretical flop count required for analysis as a function of DOFs. A comparison focused simply on flop count favors the XFEM and FEM-based implementations. The proposed HSchur decomposition performs favorably, compared to the current standard Schur, requiring roughly an order of magnitude less flops for the same solution. However, in a direct comparison to XFEM, it still requires substantially higher computational effort at an equal level of discretization.

Fig. 31

Computational requirements for solution for (X)FEM, SBFEM using the conventional Schur decomposition and the newly proposed HSchur decomposition

In order to offer a more meaningful comparison, Fig. 32 provides the corresponding accuracy of the calculated SIFs plotted against the DOFs. To this end, a reference solution obtained from a fine mesh in Abaqus of approximately half a million DOFs is used. SBFEM evidently outperforms the competing methods, as fewer DOFs are required in order to approach the reference solution. Significantly higher rates of convergence are obtained by SBFEM by employing higher-order elements. Noteworthy are the linear, two-noded elements, which outperform XFEM and the standard FEM approach with a slope of $m=2$, calculated using recovered stresses.

Fig. 32

Accuracy of $K_1$ as a function of DOFs for SBFEM, XFEM and FEM for the double edge crack problem. For SBFEM the proposed HSchur decomposition is utilized

Figure 33 depicts the error in calculated SIF as a function of the flops required for analysis. At lower flop counts, all methods perform comparably. A slight edge goes to the FEM implementation. Since in Abaqus the integration domain is specified manually, the amount of DOFs present in the system is not uniformly distributed at coarser discretizations. Consequently, the FEM plot exhibits a plateau. Once this plateau is passed, the rate of convergence stabilizes to $m_{\mathrm{FEM}} = 0.88$. The rate of convergence for XFEM is higher at $m_{\mathrm{XFEM}} = 1.06$. At higher flop counts, SBFEM begins to separate itself from the competing methods, due to higher rates of convergence.

Fig. 33

Accuracy of $K_1$ as a function of the flops required to obtain the solution for the double edge crack problem. For SBFEM, the proposed HSchur decomposition is utilized

Fig. 34

Accuracy of $K_1$ as a function of analysis wall clock time for the double edge crack problem. For SBFEM, the proposed HSchur decomposition is utilized

Figure 34 indicates the error in computed SIFs as a function of wall clock time. For Abaqus, analysis times are extracted from the log file. For XFEM and SBFEM, the stopwatch timer in MATLAB is employed. Results for this numerical example are obtained on an Intel i5-6600K @ 3.9 GHz. As observed in Fig. 34, the current implementation of SBFEM, based on the newly adopted HSchur, outperforms XFEM by approximately an order of magnitude. This quantification must be treated with caution, since both the SBFEM and XFEM implementations have yet to undergo optimization. This discrepancy between analysis time and computation complexity (Fig. 33) is attributed to operations specific to XFEM, not incorporated in the theoretical flop count, and language-related performance limitations. Examples for the former are operations associated with the integration of the enrichment terms and the post-processing of the SIFs. Employing loops in scripting languages, such as MATLAB, is known to significantly impact run time. The number of loops performed during analysis is dependent on the amount of elements and integration points, which is significantly larger for the case of XFEM than SBFEM. These considerations are equally applicable to the fourth numerical example.

Compared to the optimized code of the commercial software Abaqus, which utilizes highly optimized numerical routines, SBFEM compares favorably. Similar accuracy in the calculated SIFs is observed at comparable analysis times. Further, for the higher noded elements, SBFEM with the adopted HSchur decomposition manages to outperform commercial software.

Figure 35 compares the accuracy of the calculated SIFs to the computational effort by proxy of flop count. The computational advantage of the HSchur decomposition over the generic Schur decomposition is demonstrated to approach an order of magnitude, with the analysis time expected to decrease with further refinement of the code.

Fig. 35

Accuracy of $K_1$ comparing the proposed HSchur and standard Schur decomposition, based solely on theoretical flop counts

A last comparison between XFEM and SBFEM considers the evolution of the condition number of the stiffness matrix for an increasing number of DOFs. Figure 36 demonstrates the numerical difficulties associated with standard XFEM. Typically, the condition number of the stiffness matrix increases rapidly, mandating preconditioning, which constitutes a computational burden. This is not the case in SBFEM since the method naturally extends to encompass fracture-related phenomena. Consequently, no terms are added, which affect the condition number adversely. However, it is evident that higher-order elements do increase the condition number steadily.

Fig. 36

Evolution of the condition number of the stiffness matrix as a function of DOFs for the double edge crack problem

3.4 Slant crack in square plate

A slant crack as depicted in Fig. 37 is considered, with length $L = 1$ unit, crack length $a=L/2$ and crack inclination angle equal to $\pi /4$. The boundary is evenly discretized. A crack inclination angle of $\pi /4$ is purposely chosen, since the largest errors in computed stresses appear at corner points (Fig. 25). The aim of this numerical example is to ascertain, how SBFEM performs in a worst-case scenario, when compared against alternatives. XFEM and the standard FE-based approach are considered in the following comparisons. For XFEM, the enrichment radius is kept constant at $r_{\mathrm{e}} = 0.2$ units, while the radius of integration is fixed at $r_{\mathrm{i}} = 2.55$ times the element size. For Abaqus, the same quadratic elements where chosen as in the previous example. Modeling the slant crack problem with SBFEM entails separating the domain into two parts. Each is inscribed its own scaling center, placed at the crack tip (Fig. 38). The results reported correspond to the SIFs calculated at the upper right sided crack tip.

Fig. 37

Slant crack in square plate under tension. The problem statement for the fourth numerical example

Fig. 38

Sample discretization scheme for modeling a slant crack with SBFEM. It can be seen that in order to accommodate different crack inclination angles, simply the scaling centers (circles) must be moved, which may be done independently of the mesh (crosses)

Figure 39 illustrates the accuracy of computed $K_2$ as a function of DOFs. To this end, a finely meshed reference solution in Abaqus was employed. The FEM-based calculation of the SIFs by Abaqus, the XFEM implementation as well as the 2-noded elements of SBFEM are observed to converge at a comparable rate, although XFEM has a slightly higher rate of convergence. Admitting higher-order elements, SBFEM outperforms the other numerical methods. The odd-noded elements outperform their even-noded counterparts. Since the computational effort per DOF for SBFEM is greater than for the two contrasted numerical methods, Fig. 40 plots the accuracy of $K_2$ as a function of flops. SBFEM compares favorably to the FE-based approach and the XFEM implementation, even in this worst-case scenario. It would seem that the calculation of SIFs at a crack inclination angle of $\pi /4$ is also a challenging task for other FE-based numerical methods.

Fig. 39

Accuracy of $K_2$ as a function of DOFs for the slant crack problem. For SBFEM, the proposed HSchur decomposition is utilized

Fig. 40

Accuracy of $K_2$ as a function of flops required for solution of the slant crack problem. For SBFEM, the proposed HSchur decomposition is utilized

Figure 41 provides the analysis times for calculating the SIFs based on all three compared methods. Calculations were performed on an Intel Xeon E3-1225 v3. Oscillatory behavior for the first few points is attributed to the method of reporting in Abaqus. Values are reported at discrete 0.1-s intervals. Since for systems with small amounts of DOFs the I/O overhead dominates the overall computational time, oscillatory values of 0.2 and 0.3 s were obtained. SBFEM is demonstrated to perform on par with current commercial software in terms of efficiently and accurately calculating the SIFs. Further, for problems with simple crack geometries, it outperforms a similarly implemented XFEM by approximately an order of magnitude at equivalent accuracy. This is attributed to the ease with which higher-order elements may be employed. However, considering only linear elements, the advantage of SBFEM over XFEM is marginal.

Figure 42 plots $K_2$ calculated based on raw stresses and the standard eigendecomposition as a function of analysis time. In particular, the lower noded elements suffer from this transition. While the XFEM implementation outperforms the 2-noded elements, the commercial software Abaqus performs similarly to the 3-noded elements. SBFEM is only observed to maintain its competitive advantage, when employing elements with four or more nodes.

Fig. 41

Accuracy of $K_2$ as a function of analysis wall clock time for the slant crack problem. For SBFEM, the proposed HSchur decomposition is utilized

Fig. 42

Accuracy of $K_2$ as a function of analysis wall clock time for the slant crack problem. For SBFEM, the eigendecomposition combined with raw stresses for the calculation of $K_2$ is utilized

In Fig. 43, the condition number of an SBFEM solution is contrasted to that of XFEM as a function of increasing DOFs. The condition numbers are not clearly separated. For finer domain discretizations, the condition number of SBFEM approaches that of XFEM. However, at that level of discretization, SBFEM is fully converged as opposed to XFEM. This escalation in condition number is dependent on the angle spanned between an element on the boundary and the scaling center. The smaller the angle, the more numerical difficulties occur. With a higher boundary discretization, these angles tend to diminish. Should severe numerical issues be encountered, a splitting of the domain perpendicular to the crack line is advised, distributing the angles spanned by the boundary elements and the scaling center more evenly.

Fig. 43

Evolution of the condition number of the stiffness matrix as a function of DOFs for the slant crack problem

One of the strengths of SBFEM is exploited to perform a study of variants. Modeling of varying crack inclination angles becomes trivial, as only the scaling centers must be repositioned. As a result, a procedure is proposed, which accommodates the application of SPR theory to the SIFs.

• 1. The direction of crack extension is determined.

• 2. The intersection point between the boundary and the crack extension line is calculated. The nearest node is calculated, and the corresponding intersection element is found.

• 3. The stresses are recovered over a patch of two elements, as described in Sect. 2.3, with the addition of a check, ensuring the chosen patch does not entail corners. This process is automated by applying the orientation checking procedure as detailed in Sect. 3.2.

• 4. The SIFs are calculated based on the locally recovered stresses, which are rotated by the crack inclination angle.

In Table 7, the SIF $K_1$ is tabulated for various discretization levels and crack inclination angles. A reference solution is obtained from a fine meshed Abaqus analysis. In order to investigate the stability of SBFEM for various crack inclination angles, the values for $K_1$ are normalized with respect to the reference solution. As observed in Table 7, $K_1$ behaves independently of the crack inclination angle. All three methods: SBFEM, XFEM and FEM, provide comparable results, with deviations lower than 1%.

Table 7 Values of computed $K_1$ as a function of the crack inclination angle ranging from 10$^{\circ }$ to 80$^{\circ }$

Table 8 summarizes the results for the case of $K_2$. It is verified that the SIFs computed by SBFEM are independent of the crack inclination angle. However, as the crack inclination angle is increased, numerical issues arise due to the introduction of small angles spanned by the elements on the boundary and the scaling center. These angles approach the values of zero as the crack inclination angle approaches 90$^{\circ }$ (Fig. 38).

Table 8 Values of computed $K_2$ as a function of the crack inclination angle ranging from 10$^{\circ }$ to 80$^{\circ }$ using the same methodology as in Table 7

4 Conclusion

In this work, the adoption of a blocked Hamiltonian Schur decomposition is proposed, which proves highly beneficial when substituted into the solution process of SBFEM. By preserving Hamiltonian symmetry, i.e., the symmetry of the eigenvalues about the real and the imaginary axis, enhanced accuracy is achieved leading to improved, near-optimal, convergence rates. Further, only half of the analysis domain need be considered, which alleviates the additional computational toll incurred in linearizing the quadratic eigenvalue problem. An additional benefit stems from the fact that the eigenvalues are automatically partitioned based on sign. Thus, errors incurred due to improper sorting, resulting in an erroneous stiffness matrix, are eliminated along with the prior need for a stabilizing parameter $\varepsilon$. By consequence, the adopted HSchur decomposition is demonstrated to significantly improve the regularity of the method.

The convergence rates of SBFEM are investigated in a benchmark example, featuring an analytical solution. The $L_2$ error in displacements, stresses as well as the error in computed stress intensity factors is recovered. Implementation of SPR theory allows for superconvergent recovery of stresses, and in select cases ultraconvergent behavior. This property is exploited to significantly improve the accuracy and convergence behavior of the calculated SIFs. It is further demonstrated that stress recovery need not be carried out for the entire domain, since similar accuracy is achieved when only considering the patch in direction of crack extension, at reduced computational cost. A local error estimator is proposed, which arises as a natural extension of the stress recovery scheme, and is highly accurate as well as computationally inexpensive.

Finally, SBFEM is explicitly contrasted against other numerical methods within the context of LEFM in terms of rough flop count, and wall clock time (albeit for unoptimized MATLAB implementations for the SBFEM and XFEM variants). It is demonstrated that for simple crack geometries, a higher-order SBFEM consistently outperforms frequently adopted alternatives.

Appendix A.1

Considering the term representing the internal virtual work first, it is rearranged after substituting Eqs. 9 and 11:

$$\begin{aligned}&\int _V \{\delta {{\varepsilon }}(\xi ,\eta )\}^T \{{{\sigma }}(\xi ,\eta )\} dV\nonumber \\&\quad =\int _V \left[ [{B^1}(\eta )]\{\delta {u}(\xi )\}_{,\xi } + \frac{1}{\xi }[{B^2}(\eta )]\{\delta {u}(\xi )\} \right] ^T\nonumber \\&\qquad \times [{D}] \left( [{B^1}(\eta )]\{{u}(\xi )\}_{,\xi } + \frac{1}{\xi }[{B^2}(\eta )]\{{u}(\xi )\} \right) dV\nonumber \\&\quad = \int _{\partial \Omega } \int _{\xi =0}^{\xi =1} \{\delta {u}(\xi )\}^T_{,\xi } [{B}^1(\eta )]^T [{D}] [{B}^1(\eta )] \xi \{{u}(\xi )\}_{,\xi } |{J}| d\xi d\eta \nonumber \\&\qquad + \int _{\partial \Omega } \int _{\xi =0}^{\xi =1} \{\delta {u}(\xi )\}^T_{,\xi } [{B}^1(\eta )]^T [{D}] [{B}^2(\eta )] \{{u}(\xi )\} |{J}| d\xi d\eta \nonumber \\&\qquad + \int _{\partial \Omega } \int _{\xi =0}^{\xi =1} \{\delta {u}(\xi )\}^T [{B}^2(\eta )]^T [{D}] [{B}^1(\eta )] \{{u}(\xi )\}_{,\xi } |{J}| d\xi d\eta \nonumber \\&\qquad + \int _{\partial \Omega } \int _{\xi =0}^{\xi =1} \{\delta {u}(\xi )\}^T [{B}^2(\eta )]^T [{D}] [{B}^2(\eta )] \frac{1}{\xi } \{{u}(\xi )\} |{J}| d\xi d\eta \end{aligned}$$

(67)

Green’s theorem leads to the following formulation:

$$\begin{aligned}&\int _V \{\delta {{\varepsilon }}(\xi ,\eta )\}^T \{{{\sigma }}(\xi ,\eta )\} dV\nonumber \\&\quad = \int _{\partial \Omega } \{\delta {u}(\xi )\}^T [{B}^1(\eta )]^T [{D}] [{B}^1(\eta )] \xi \{{u}(\xi )\}_{,\xi } |{J}| d \eta \Big |_{\xi =1}\nonumber \\&\qquad - \int _{\partial \Omega } \{\delta {u}(\xi )\}^T [{B}^1(\eta )]^T [{D}] [{B}^1(\eta )]\nonumber \\&\qquad \times \lbrace \{{u}(\xi )\}_{\xi } + \{{u}(\xi )\}_{\xi \xi } \rbrace |{J}| d\xi d\eta \nonumber \\&\qquad + \int _{\partial \Omega } \{\delta {u}(\xi )\}^T [{B}^1(\eta )]^T [{D}] [{B}^2(\eta )] \{{u}(\xi )\} |{J}| d \eta \Big |_{\xi =1}\nonumber \\&\qquad - \int _{\partial \Omega } \int _{\xi =0}^{\xi =1} \{\delta {u}(\xi )\}^T [{B}^1(\eta )]^T [{D}] [{B}^2(\eta )] \{{u}(\xi )\}_{,\xi } |{J}| d\xi d\eta \nonumber \\&\qquad + \int _{\partial \Omega } \int _{\xi =0}^{\xi =1} \{\delta {u}(\xi )\}^T [{B}^2(\eta )]^T [{D}] [{B}^1(\eta )] \{{u}(\xi )\}_{,\xi } |{J}| d\xi d\eta \nonumber \\&\qquad + \int _{\partial \Omega } \int _{\xi =0}^{\xi =1} \{\delta {u}(\xi )\}^T [{B}^2(\eta )]^T [{D}] [{B}^2(\eta )] \frac{1}{\xi } \{{u}(\xi )\} |{J}| d\xi d\eta \end{aligned}$$

(68)

In order to simplify the above equation, the following substitutions are introduced:

$$\begin{aligned}{}[E^0]= & {} \int _{\partial \Omega } [{B}^1(\eta )]^T [{D}] [{B}^1(\eta )] |{J}| d\eta \end{aligned}$$

(69a)

$$\begin{aligned} {[E^1]}= & {} \int _{\partial \Omega } [{B}^1(\eta )]^T [{D}] [{B}^2(\eta )] |{J}| d\eta \end{aligned}$$

(69b)

$$\begin{aligned} {[E^2]}= & {} \int _{\partial \Omega } [{B}^2(\eta )]^T [{D}] [{B}^2(\eta )] |{J}| d\eta \end{aligned}$$

(69c)

These simplifications are named “coefficient matrices” and resemble in structure the stiffness matrix of standard FEM schemes. They are calculated element-wise and then assembled in the standard FEM sense. Applying boundary conditions on the coefficient matrices is premature, as this will effectively delete parts of the domain corresponding to the space spanned by the DOFs on the boundary and the scaling center. Using the same notation to denote the fully assembled coefficient matrices, the previous equations are rewritten as follows using an abbreviation on the boundary $\{{u}\} \hat{=} \{{u}(\xi =1)\}$:

$$\begin{aligned}&\int _V \{\delta {{\varepsilon }}(\xi ,\eta )\}^T \{{{\sigma }}(\xi ,\eta )\} dV\nonumber \\&\quad = \{\delta { u}\}^T \{ [{E^0}] \{{u}\}_{,\xi } + [{E^1}]^T \{{u}\} \}\nonumber \\&\qquad - \int _{xi = 0}^{\xi = 1} \{\delta {u}(\xi )\}^T \Big \{ [{E^0}] \xi \{{u}(\xi )\}_{,\xi \xi }\nonumber \\&\qquad + [[{E^0}] + [{E^1}]^T - [{E^1}]] \{{u}(\xi )\}_{,\xi } - [{E^2}] \frac{1}{\xi } \{{u}(\xi )\} \Big \} d \xi \end{aligned}$$

(70)