1 Introduction

With the depletion of conventional oil and gas resources, new hydrocarbon resources are exploited gradually, such as shale gas, coal-bed gas, and the drilling engineering faces more complex formation environment. Based on the existing drilling technology, directional well, horizontal well and multilateral well are developed and applied rapidly. For example, with the increase in the target diameter of the extended reach well in the exploitation of the shale gas, the dynamic characteristics of the drill string are influenced by wellbore friction in a growing proportion, and existing research methods and conclusions cannot meet the actual needs [1,2,3]. The analysis of the wellbore friction randomness and the research of the drill string dynamics have important significances for the development of the exploitation of new hydrocarbon resources and the increase in the drilling technology of the complex well.

For the complex working conditions, the wellbore friction is influenced by many factors. On the one hand, there is loss of contact effects in the drill process, which leads that the cutting process is nonlinear [4]. The nonlinear cutting process causes the drill string vibration, including axial vibration, torsional vibration and coupled vibration, which increase the friction between the drill string and the wellbore, and then the vibration reacts on the drill string dynamics [5, 6]. On the other hand, the new conditions result new challenges for the operation safety of downhole tools [7, 8]. The importance of the issue is recognized by more scholars and research institutions. However, the accurate description method about the wellbore friction has not been given yet, and the research results are inconsistent with the actual situations [9,10,11]. In fact, if the friction randomness between the drill string and the wellbore is ignored, or the random field of the friction coefficient cannot be described correctly, the drill string dynamic characteristics cannot be reflected accurately.

On the basis of the previous researches and with the combination of the drilling field conditions, the randomness of wellbore friction and its influences on the drill string dynamics are studied. Firstly, the interaction between the wellbore and the drill string is described. Then, the dynamic model of the horizontal drill string is analyzed and constructed in the context of the exploitation of shale gas. The solutions of each force are given in the model. Considering the contact conditions of different points located in the drill pipe, the discretization method of the dynamic model is achieved. In order to verify the accuracy of the theoretical model, experimental tests and numerical examples are carried out. And the results, obtained from calculation models and experimental tests, are discussed and analyzed such as the displacement of vibration, the velocity of vibration and the related characteristics.

When facing more challenging exploitation conditions, the drill string dynamics plays the key role in drilling engineering. The results can provide a new insight into the drill string dynamics research, especially for the complex well, such as ultra-deep well, branch well or directional well, in which the wellbore friction has a significant influence on the drill string kinetic results.

2 Analysis model

2.1 Drill string dynamic model

According to the working conditions in horizontal well, the force analysis of drill string is conducted, as shown in Fig. 1, where the left boundary is the origin of coordinates of analysis segment. \(F_\mathrm{sta}\) is the equivalent force of the left boundary, \(F_\mathrm{fric}\) is the friction force, G is the gravity of drill string, m is the mass, g is the acceleration of gravity, \(F_{\mathrm{har}}\) is the force of the drilling fluid, and \(F_{\mathrm{bit}}\) is the reaction force of the rock on the drill bit, which is equal to weight on bit (WOB).

Fig. 1
figure 1

The force analysis of drill string

Full size image

Based on the force analysis, the vibration analysis model of the horizontal drill string is established to research random wellbore friction [12]. The model is expressed as

$$\begin{aligned} \left\{ {\begin{array}{l} \mathbf{M}\ddot{u}\left( {t,\xi } \right) +\mathbf{C}\dot{u}\left( {t,\xi } \right) +\mathbf{K}u\left( {t,\xi } \right) =\mathbf{F}_\mathrm{sta} +\mathbf{F}_\mathrm{har} \left( t \right) +\mathbf{F}_\mathrm{bit} \left( {\dot{u}\left( {t,\xi } \right) } \right) +\mathbf{F}_\mathrm{fric} \left( {\dot{u}\left( {t,\xi } \right) ,\xi } \right) \\ u\left( 0 \right) =u_0 \\ \dot{u}\left( 0 \right) =\dot{u}_0 \\ \end{array}} \right. \end{aligned}$$
(1)

In which, \(\mathbf{M}\), \(\mathbf{C}\) and \(\mathbf{\mathrm{K}}\) are mass matrix, damping matrix and stiffness matrix, respectively, u is the displacement function, \(\dot{u}\) is the corresponding speed, t is the time coordinate, \(\xi \) is the friction coefficient, \(\mathbf{F}_{\mathrm{sta}} \left( {x,t} \right) \), \(\mathbf{F}_{\mathrm{har}} \left( {x,t} \right) \), \(\mathbf{F}_{\mathrm{bit}} \left( {\dot{u}\left( {x,t} \right) } \right) \), \(\mathbf{F}_{\mathrm{fric}} \left( {\dot{u}\left( {x,t} \right) } \right) \), \(\mathbf{F}_{\mathrm{mass}} \left( {\ddot{u}\left( {x,t} \right) } \right) \) are the corresponding matrix of the force, respectively.

2.2 Drilling efficiency

In order to analyze drilling power consumption, the efficiency equation is defined as

$$\begin{aligned} \eta =\frac{\frac{1}{t_1 -t_0 }\int _{t_0 }^{t_1 } {f_\mathrm{sta} \dot{u}\left( {0,t} \right) +f_\mathrm{har} \dot{u}\left( {L,t} \right) {\hbox {d}}t} }{\frac{1}{t_1 -t_0 }\int _{t_0 }^{t_1 } {f_\mathrm{bit} \left( t \right) \dot{u}\left( {L,t} \right) {\hbox {d}}t} } \end{aligned}$$
(2)

With the combination of the importance and actual significance of the drilling efficiency, the mean square value analysis of the drilling efficiency is conducted to ensure the analysis result of the efficiency. And the solution method is given as

$$\begin{aligned} {\hbox {con}}\left( {n_\eta } \right) =\frac{1}{n_\eta }\sum \limits _{i=1}^{n_\eta } {\left( {\eta _i } \right) ^{2}} \end{aligned}$$
(3)

where \(n_\eta \) is different solution counts.

3 Solution of wellbore friction randomness and dynamic model

In order to solve the vibration equation, the representation of each force needs to be determined. According to the research innovation, the wellbore friction randomness is studied firstly.

3.1 The research of the wellbore friction randomness

The randomness is an important feature of the drill string friction, which is reflected in the random change of the contact position and the value of the friction coefficient. The accuracy of mathematical method has directly decisive effect on the precision of the calculation results. Considering the characteristics of the wellbore friction on drill string, the random variable \(\xi \), corresponding to the displacement u, is introduced to research the randomness of the generation location of the friction pair. For the friction coefficient, through random statistical analysis, the distribution law of the random data can be described by Gaussian distribution. The analysis method is established, and the analysis model can be defined as follows:

$$\begin{aligned} F_\mathrm{fric} \left( {\dot{u}\left( {x,t} \right) ,\xi } \right) =\rho _L g\left( {-f\left( {x,\xi } \right) } \right) \hbox {sgn}\left( {\dot{u}\left( {x,t} \right) } \right) \end{aligned}$$
(4)

where x is the coordinate value of the analysis position, \(\rho _L \) is the mass of per unit length, \(f\left( {x,\xi } \right) \) is the friction coefficient based on x and \(\xi \), and the mean value is \(\overline{f} \left( {x,\xi } \right) \), \(\hbox {sgn}\left( {\dot{u}\left( {x,t} \right) } \right) \) is the judgment function, and it can be expressed as

$$\begin{aligned} \hbox {sgn}\left( {\dot{u}\left( {x,t} \right) } \right) =\left\{ {\begin{array}{l} 1\;\;\;\;\;\;\left( {\dot{u}\left( {x,t} \right) >0} \right) \\ 0\;\;\;\;\;\;\left( {\dot{u}\left( {x,t} \right) =0} \right) \; \\ -1\;\;\;\;\left( {\dot{u}\left( {x,t} \right) <0} \right) \\ \end{array}} \right. \end{aligned}$$
(5)

The probability density of \(f\left( {x,\xi } \right) \) is calculated by

$$\begin{aligned} p\left( {f\left( {x,\xi } \right) } \right) =\frac{1}{\sqrt{2\pi }\sigma }\exp \left( {-\frac{1}{2}\left( {\frac{f\left( {x,\xi } \right) -\overline{f} \left( {x,\xi } \right) }{\sigma }} \right) ^{2}} \right) \end{aligned}$$
(6)

In which, \(\sigma \) is the standard deviation of the random variable.

In order to describe the randomness of the friction behavior, the random variable needs to be converted. Since the Gaussian distribution characteristic of the stochastic friction, Karhunen–Loève method is used to describe the random variable. According to K-L expansion, \(f\left( {x,\xi } \right) \) is expanded at the mean value \(\overline{f} \left( {x,\xi } \right) \) and the expansion can be written as

$$\begin{aligned} f\left( {x,\xi } \right) =\overline{f} \left( {x,\xi } \right) +\sum _{i=1}^\infty {\sqrt{\lambda _i }\phi _i \left( x \right) } Z_i \left( \xi \right) \end{aligned}$$
(7)

where \(\left\{ {\lambda _i } \right\} \) and \(\left\{ {\phi _i \left( x \right) } \right\} \) are eigenvalue and eigenfunction sequences, respectively, and \(Z_i \left( \xi \right) \) is uncorrelated random variable.

The expansion of Eq. (7) should be convergent in the Gaussian stationary field. Relative to other types of expansion, there is a minimum mean square error when the expansion term is same and limited. According to the downhole conditions during the drilling process, x is defined as the spatial coordinate and \(x=\left( {x_1 ,y_1 } \right) \), which can be used to research the two-dimensional random field. Similarly, based on the construction method of the two-dimensional random field, the result of one-dimensional random can be obtained.

Corresponding to the matrix form of \(Z_i \left( \xi \right) \), each row consists of an implementation of random variable vector and each line is the value of different application for the same random variable, which each line is mutually independent and satisfies the normal distribution. For Gaussian random field, the independent random variable \(Z_i \left( \xi \right) \) remains Gaussian model, and the mathematical expectation satisfies the condition, which can be expressed as

$$\begin{aligned} \left\{ {\begin{array}{l} E\left[ {Z_i \left( \xi \right) } \right] =0 \\ E\left[ {Z_i \left( \xi \right) Z_j \left( \xi \right) } \right] =\delta _{ij} \\ \end{array}} \right. \end{aligned}$$
(8)

In the two-dimensional area, the characteristic function \(\left\{ {\phi _i \left( x \right) } \right\} \) is satisfied with the following conditions.

$$\begin{aligned} \int _\Omega {\phi _i \left( {x_1 ,y_1 } \right) \phi _j \left( {x_2 ,y_2 } \right) } {\hbox {d}}\Omega =\delta _{ij} \end{aligned}$$
(9)

In which, \(\Omega \) is a two-dimensional and closed region, x and y are two-dimensional region coordinates, respectively, \(\delta _{ij} \) is K-delta function.

The analytic expression of the eigenvalue \(\left\{ {\lambda _i } \right\} \) and the eigenfunction \(\left\{ {\phi _i \left( x \right) } \right\} \) in the expansion Eq. (7) can be obtained as [13]

$$\begin{aligned} \lambda _i= & {} \frac{4\gamma _1 \gamma _2 \sigma _\phi ^2 }{\left( {\gamma _1^2 \omega _{1,m}^2 +1} \right) \left( {\gamma _2^2 \omega _{2,n}^2 +1} \right) } \end{aligned}$$
(10)
$$\begin{aligned} \phi _i^*= & {} \phi _{1,m} \left( {x_1 } \right) \phi _{2,n} \left( {x_2 } \right) \end{aligned}$$
(11)

where in \(\gamma _1 \) and \(\gamma _2 \) are correlation lengths in x and y, respectively, and when there is isotropic, for that is \(\gamma _1 =\gamma _2 \), \(\sigma _\phi ^2\) is the variance of the randomness field.

In fact, during the calculation process, the eigenvalue \(\left\{ {\lambda _i } \right\} \) and the eigenfunction \(\left\{ {\phi _i \left( x \right) } \right\} \) can be achieved by the solution of the second Fredholm equation as follows [14].

$$\begin{aligned} \int _\Omega {C\left( {x_1 ,y_1 ;x_2 ,y_2 } \right) \phi _i \left( {x_2 ,y_2 } \right) } {\hbox {d}}\Omega =\lambda _i \phi _i \left( {x_1 ,y_1 } \right) \end{aligned}$$
(12)

where \(C\left( {x_1 ,y_1 ;x_2 ,y_2 } \right) \) is the covariance function of the two-dimensional randomness field and its expression can be written as

$$\begin{aligned} C\left( {x_1 ,y_1 ;x_2 ,y_2 } \right) =\sigma ^{2}\exp \left( {-\frac{\left| {x_1 -x_2 } \right| }{\gamma _1 }-\frac{\left| {y_1 -y_2 } \right| }{\gamma _2 }} \right) \end{aligned}$$
(13)

In which, \(\left| {x_2 -x_1 } \right| \) and \(\left| {y_1 -y_2 } \right| \) are the distances of the sample points in the two-dimensional randomness field.

When Eq. (7) is work, the covariance function can be expressed as the following spectral expansion.

$$\begin{aligned} C\left( {x_1 ,y_1 ;x_2 ,y_2 } \right) =\sum _{i=0}^\infty {\lambda _i \phi _i \left( {x_1 ,y_1 } \right) } \phi _i \left( {x_2 ,y_2 } \right) \end{aligned}$$
(14)

Meanwhile, the theoretical covariance function can be represented approximately by M-order truncation analog value in the actual calculation. And the results can be obtained as follows:

$$\begin{aligned} C_M \left( {x_1 ,y_1 ;x_2 ,y_2 } \right) =\sum _{i=0}^M {\lambda _i \phi _i \left( {x_1 ,y_1 } \right) } \phi _i \left( {x_2 ,y_2 } \right) \end{aligned}$$
(15)

On the basis of the above process, the matrix relationship, corresponding to the covariance function of the multidimensional random variables, can be expressed as

$$\begin{aligned} \left[ {C\left( {x_1 ,x_2 ,\ldots x_m } \right) } \right] =\left[ {{\begin{array}{llll} {C_{1,1} }&{} {C_{1,2} }&{} \cdots &{} {C_{1,m} } \\ {C_{2,1} }&{} {C_{2,2} }&{} \cdots &{} {C_{2,m} } \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ {C_{m,1} }&{} {C_{m,2} }&{} \cdots &{} {C_{m,m} } \\ \end{array} }} \right] \end{aligned}$$
(16)

In order to conduct the error analysis, different expansion orders can be used to analyze the change trend of the eigenvalues after the solution of the above method. And the weight of orders is analyzed throughout K-L expansion. The calculation results of the covariance function can also be used to analyze the error. When Eq. (15) holds, the relationship of covariance, correlation length and expansion order can be obtained by comparing the calculation results of the M-order covariance function with the theoretical covariance function as Eq. (13).

With this, the method is achieved which is used for constructing the randomness field of the wellbore friction. The steps, using K-L expansion, are as follows that can generate the Gaussian friction randomness field between the drill string and the wellbore. The independent random variables \(f_i \left( {x,\xi } \right) \) are generated that the number is M. Then, the eigenvalue \(\left\{ {\lambda _i } \right\} \) and the eigenfunction \(\left\{ {\phi _i \left( x \right) } \right\} \) of the integral equation are solved and the results are taken into Eq. (7). Finally, the M-order truncation is taken to generate a randomness field and the P-time truncation is taken to generate P-time randomness field, and then, \(\left[ {Z_M^P \left( \xi \right) } \right] \) can be written as

$$\begin{aligned} \left[ {Z_M^P \left( \xi \right) } \right] =\left[ {{\begin{array}{llll} {Z_1^1 \left( \xi \right) }&{} {Z_2^1 \left( \xi \right) }&{} \cdots &{} {Z_M^1 \left( \xi \right) } \\ {Z_1^2 \left( \xi \right) }&{} {Z_2^2 \left( \xi \right) }&{} \cdots &{} {Z_M^2 \left( \xi \right) } \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ {Z_1^P \left( \xi \right) }&{} {Z_2^P \left( \xi \right) }&{} \cdots &{} {Z_M^P \left( \xi \right) } \\ \end{array} }} \right] \end{aligned}$$
(17)

For \(\left[ {Z_M^P \left( \xi \right) } \right] \), each row consists of an implementation of random variable vector, and each line is the value of different implementation for the same random variable, which each line is mutually independent and satisfies the normal distribution, where each element is independent Gaussian random number. Thus, M-order P-time the wellbore friction randomness field is established.

3.2 Solution method of other forces

The description and processing method of the friction force is given. The expression and the solution method of other forces are determined in this section.

$$\begin{aligned} F_\mathrm{sta} \left( {x,t} \right) =F_\mathrm{sta} \delta \left( x \right) \end{aligned}$$
(18)

where \(F_\mathrm{sta} \) is the amplitude of \(F_\mathrm{sta} \left( {x,t} \right) \), \(\delta \left( x \right) \) is the Dirac function \(\delta \) for the displacement of the analysis point.

For \(F_{\mathrm{har}} \left( {x,t} \right) \), the corresponding solution equation can be expressed as

$$\begin{aligned} F_{\mathrm{har}} \left( {x,t} \right) =F_0 \sin \left( {\omega _f t} \right) \delta \left( {x-L} \right) \end{aligned}$$
(19)

In which, \(F_0 \) is the resonant force amplitude of \(F_\mathrm{har} \left( {x,t} \right) \), \(\omega _f \) is the rotation angular velocity, \(x=L\) is the corresponding vibration equilibrium position of \(F_\mathrm{har} \left( {x,t} \right) \) and the Dirac function \(\delta \left( {x-L} \right) \) is defined based on this.

About \(F_{\mathrm{bit}} \left( {\dot{u}\left( {x,t} \right) } \right) \), the solution steps and results are more complex and the influence factors are numerous. According to the actual condition, the solution methods of the Polycrystalline Diamond Compact (PDC) drill bit and the roller cone bit are given, respectively. For the PDC drill bit, the expression is defined as [15]

$$\begin{aligned} \left\{ {\begin{array}{ll} F_\mathrm{bit} \left( {\dot{u}\left( {x,t} \right) } \right) =\left[ {C_1 \exp \left( {-C_2 \dot{u}\left( {x,t} \right) } \right) -C_1 } \right] \delta \left( {x-L} \right) &{}\quad \dot{u}\left( {L,t} \right) >0 \\ F_\mathrm{bit} \left( {\dot{u}\left( {x,t} \right) } \right) =0 &{}\quad \dot{u}\left( {L,t} \right) \le 0 \\ \end{array}} \right. \end{aligned}$$
(20)

where \(C_1\) is the coefficient which is aiming at the rate of penetration (ROP), \(C_2\) is the coefficient to describe the nonlinear characteristic between the rock and the drill bit.

For roller cone bit, according to the boundary condition, the calculation equation can be written as [16]

$$\begin{aligned} \left\{ {\begin{array}{ll} F_\mathrm{bit} \left( {\dot{u}\left( {x,t} \right) } \right) =-\sum \limits _{i=1}^I {\sum \limits _{j=1}^{J\left( i \right) } {\sum \limits _{k=1}^{K\left( {i,j} \right) } {F_{\mathrm{bit}-X} \left( {i,j,k} \right) } } } +W_0 &{}\quad \dot{u}\left( {L,t} \right) >0 \\ F_\mathrm{bit} \left( {\dot{u}\left( {x,t} \right) } \right) =0 &{}\quad \dot{u}\left( {L,t} \right) \le 0 \\ \end{array}} \right. \end{aligned}$$
(21)

where I is the number of cones, \(J\left( i \right) \) is the ring gear of the ith cone, \(K\left( {i,j} \right) \) is the teeth number of the ith cone and the jth ring gear, \(F_{\mathrm{bit}-X} \left( {i,j,k} \right) \) is the contact force between single tooth and rock, \(\sum \nolimits _{i=1}^I {\sum \nolimits _{j=1}^{J\left( i \right) } {\sum \nolimits _{k=1}^{K\left( {i,j} \right) } {F_{\mathrm{bit}-X} \left( {i,j,k} \right) } } } \) is a dynamic WOB, \(W_0\) is static WOB.

For \(F_{\mathrm{mass}} \left( {\ddot{u}\left( {x,t} \right) } \right) \), the expression is

$$\begin{aligned} F_{\mathrm{mass}} \left( {\ddot{u}\left( {x,t} \right) } \right) =-m_{\mathrm{bit}} \ddot{u}\left( {x,t} \right) \delta \left( {x-L} \right) \end{aligned}$$
(22)

where \(m_{\mathrm{bit}}\) is the mass of drill bit.

3.3 Discrete method of drill string dynamic model

Based on the completion of forces and the determination of the solution method, the dynamics vibration model of the drill string can be solved. According to Fig. 1, the discrete solution of the model is researched. With the downhole working conditions of the drill string, the discrete analysis model is established and the drill string is dispersed. The number of discrete units is n and the length of each unit is l, corresponding to \(m_1, m_2, \ldots m_{n-1}, m_n\) as shown in Fig. 2. The discrete results can be obtained, which are corresponding to the mass matrix, the damping matrix and the stiffness matrix, respectively, in Eq. (1).

Fig. 2
figure 2

The discrete method and model of dynamic solution

Full size image

The expression of unit mass matrix can be expressed as

$$\begin{aligned} \left[ M \right] ^{e}=\frac{lm^{*}}{6}\left[ {{\begin{array}{ll} 2&{} 1 \\ 1&{} 2 \\ \end{array} }} \right] \end{aligned}$$
(23)

The expression of the overall mass matrix can be written as

$$\begin{aligned} \left[ M \right] =\frac{l}{6}\left[ {{\begin{array}{l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l} {2m_n^{^{{*}}} }&{} {m_n^{^{{*}}} }&{} &{} &{} &{} &{} &{} &{} \\ {m_n^{^{{*}}} }&{} {4m_n^{^{{*}}} }&{} {m_n^{^{{*}}} }&{} &{} &{} &{} &{} &{} \\ &{} &{} &{} {m_n^{^{{*}}} }&{} {2\left( {m_n^{^{{*}}} +m_{n-1}^{^{{*}}} } \right) }&{} \cdots &{} &{} &{} \\ &{} &{} &{} &{} \cdots &{} \cdots &{} &{} &{} \\ &{} &{} &{} &{} \cdots &{} \cdots &{} &{} &{} \\ &{} &{} &{} &{} \cdots &{} {2\left( {m_2^{^{{*}}} +m_1^{^{{*}}} } \right) }&{} {m_1^{^{{*}}} }&{} &{} \\ &{} &{} &{} &{} &{} {m_1^{^{{*}}} }&{} {4m_1^{^{{*}}} }&{} {m_1^{^{{*}}} }&{} \\ &{} &{} &{} &{} &{} {m_1^{^{{*}}} }&{} {4m_1^{^{{*}}} }&{} {m_1^{^{{*}}} }&{} \\ &{} &{} &{} &{} &{} &{} &{} {m_1^{^{{*}}} }&{} {2m_1^{^{{*}}} } \\ \end{array} }} \right] \end{aligned}$$
(24)

The expression of the unit stiffness matrix is defined as follows:

$$\begin{aligned} \left[ K \right] ^{e}=\frac{EA}{l}\left[ {{\begin{array}{cc} 1&{} {-1} \\ {-1}&{} 1 \\ \end{array} }} \right] \end{aligned}$$
(25)

The expression of the overall stiffness matrix is achieved by

$$\begin{aligned} \left[ K \right] =\frac{1}{l}\left[ {{\begin{array}{llllllll} {k_{\mathrm{L}} +E_n A_n }&{} {-E_n A_n }&{} &{} &{} &{} &{} &{} \\ {-E_n A_n }&{} {2E_n A_n }&{} {-E_n A_n }&{} &{} &{} &{} &{} \\ &{} &{} &{} {-E_n A_n }&{} &{} &{} &{} \\ &{} &{} &{} \cdots &{} &{} &{} &{} \\ &{} &{} &{} &{} {\left( {E_2 A_2 +E_1 A_1 } \right) }&{} {-E_1 A_1 }&{} &{} \\ &{} &{} &{} &{} {-E_1 A_1 }&{} {2E_1 A_1 }&{} {-E_1 A_1 }&{} \\ &{} &{} &{} &{} {-E_1 A_1 }&{} {2E_1 A_1 }&{} {-E_1 A_1 }&{} \\ &{} &{} &{} &{} &{} &{} {-E_1 A_1 }&{} {2E_1 A_1 } \\ \end{array} }} \right] \end{aligned}$$
(26)

The expression of the damping matrix is obtained by [17]

$$\begin{aligned} \left[ C \right] =\alpha \left[ M \right] +\beta \left[ K \right] \end{aligned}$$
(27)

wherein \(\alpha \) and \(\beta \) are the scale coefficients, which can be determined by simulation. Different values are given to \(\alpha \) and \(\beta \). When the fluctuation of the weight on bit is within acceptable range, values of coefficients are determined.

4 Example analysis and experimental test

4.1 Basic parameters

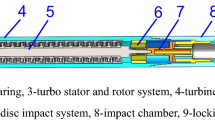
In order to verify the accuracy of the theoretical model and analyze the influence of the key parameters, the experimental test and the example analysis are carried out. Consistent with the experimental model, the relevant input parameters of example analysis are determined, and the results of the test and the theoretical calculation are compared and analyzed. The influence of key parameters on the dynamic characteristics of the drill string is also analyzed. Using the comprehensive drilling platform as shown in Fig. 3, the bench is placed at the maximum inclining position and the horizontal drilling section that is located behind the build angle section is selected to be tested. Place test point 1 at the drill bit position, and place test point 2 at the distance of 60 m away from the drill bit. The corresponding test model is shown in Fig. 4.

Fig. 3
figure 3

Experimental test of comprehensive drilling experiment platform

Full size image
Fig. 4
figure 4

The model of the correspondence to the experimental test

Full size image
Table 1 Example parameters
Full size table

With the correspondence of the experimental test, the necessary input parameters of the numerical example are determined, as shown in Table 1. And corresponding to the discrete method of the damping matrix, coefficients are defined as \(\alpha = 0.1, \beta = 0.001\) in the solution process of the vibration equation.

Fig. 5
figure 5

Simulation of the bore friction coefficient

Full size image
Fig. 6
figure 6

The vibration displacement test values of the example and experimental test. a The vibration displacement of example. b The enlarge figure of comparison result

Full size image

4.2 Analysis of calculation and experimental test results

Because of the well structure design, some parameters are not tested easily in experimental test. Therefore, referring to the above input parameters, the wellbore friction random field is analyzed according to the established theoretical model, and then, the displacement of the test point is calculated. Combined with the analysis method of the wellbore random friction forces, the friction coefficient is obtained as shown in Fig. 5. On the basis of the theoretical model, the dynamic characteristics of the drill string are solved, and the result of the vibration displacement at the test point 1 is shown in Fig. 6, in which Fig. 6a shows the vibration displacement of example and Fig. 6b obtains the enlarge figure of the results of experimental test and example calculation. Figures 5 and 6 indicate that the wellbore friction coefficient and the displacement at the test point present obvious randomness in the drilling process. Besides, the vibration displacement in numerical example model is smaller in comparison with the drilling footage.

Fig. 7
figure 7

The vibration velocity of test point 1. a The vibration velocity of random friction. b The vibration velocity of constant friction

Full size image
Fig. 8
figure 8

The vibration velocity of experimental test

Full size image

As the proportion relationship between the displacement of the test point and the footage, the comparison effect of the vibration displacement is not obvious. In order to compare the results of different methods, the vibration velocity at the test point is analyzed, including the wellbore random friction, the constant friction and the actual experimental test of the vibration velocity, as shown in Figs. 7 and 8.

Fig. 9
figure 9

Drilling efficiency

Full size image
Fig. 10
figure 10

The mean square value of drilling efficiency

Full size image
Fig. 11
figure 11

The mean square value of drilling efficiency in experimental test

Full size image

It can be obtained in the figure that the mean value of the vibration velocity is around 1.3 mm/s, but the vibration velocity, considering the friction randomness, shows the characteristic closer to the test result, which can reflect the actual motion features at the test point and verify the accuracy of the theoretical analysis. Meanwhile, it is necessary to pay more attention to the influence of the wellbore randomness on the dynamic characteristics of the drill string, especially in the horizontal drilling of deep or ultra-deep wells, or the exploitation of new oil and gas resources with larger target diameter.

The drilling efficiency is shown in Fig. 9. And the result shows that due to vibration, the corresponding forces and velocities change during the drilling process. And because of the randomness of the friction force, the drilling efficiency generates a certain random fluctuation and the average value is about 0.25.

Fig. 12
figure 12

The frequency spectrum analysis result of the vibration velocity of drill string

Full size image
Fig. 13
figure 13

The frequency spectrum analysis result of the vibration velocity in experimental test

Full size image

According to the efficiency value, different solution counts are installed to obtain the mean square value of drilling efficiency as shown in Figs. 10 and 11. With comparison to the results, although the efficiency fluctuation range is large, the average efficiency value converges to a certain value rapidly and steadily with the increase in the number of solution counts. Taking the numerical example as an example, when the number of iterations is more than 200, the mean efficiency is rapidly concentrated near 0.057.

Fig. 14
figure 14

The phase diagram of the test point 1

Full size image
Fig. 15
figure 15

The Poincare plot of the test point 1

Full size image

The accuracy and reliability of the method are verified by the comparison between the test results and the calculated results. According to the experimental test and the example calculation, the frequency spectrum of the drill string vibration velocity is obtained and the results are shown in Figs. 12 and 13. It can be seen from the figures that the frequency spectrum results show that the wellbore friction force has some influence on the frequency spectrum of the drill string vibration velocity, but in general, the dynamic input speed of the drilling platform has the greatest effect, which is at 100 rpm and its corresponding integer multiple.

Moreover, the phase diagram and the Poincare plot of the test point 1 can be obtained as shown in Figs. 14 and 15. The phase diagram shows the chaotic motion features of the system, moreover, which indicates that the attractors revolve around closed circles. Figure 14 illustrates that the system is not in a periodic or quasi-periodic vibration. Figure 15 shows the Poincare map is convergent to some irregular points, which indicates that there are some strange attractors. And the Poincare cross section is not a closed curve or fixed point but a messy assemblage, which thoroughly explains the chaotic vibration response of the system. Figures 14 and 15 show that due to the influence of the drilling parameters and the changing working conditions in downhole, the drill string produces random vibration response during the drilling process.

The key parameters, affecting the vibration characteristics of the drill string, also include the length of drill string, the radius of the wellbore friction circle, the ROP and so on. With a combination of the actual situation of oil and gas production, the above solution methods and steps can be used to get the relevant results and complete the result analysis, where the relevant parameters are transformed.

5 Conclusions

Considering the downhole condition in the drilling field, the description method of the wellbore friction randomness is presented, including the mathematic expression of the random array. Based on this, the dynamic solution models of the horizontal drill string are established. Some of the necessary input parameters are determined with experimental test, and a numerical example is carried out. The vibration displacement, the vibration velocity and the drilling efficiency are solved and analyzed, including the frequency spectrum analysis. Moreover, the phase diagram and the Poincare plot of the test point are obtained. When facing new drilling conditions including different geological parameters or wellbore structure, the experimental test is needed to accurately describe the friction randomness, which can provide the necessary inputting parameters and ensure the reliability of solution results.

According to the existing exploitation conditions of new oil and gas resources, the friction force has a more significant influence on the drill string dynamics, in particular for the complex well, such as ultra-deep well, branch well or directional well. With consideration of the friction randomness, the drill string dynamic characteristics can be evaluated accurately. The analysis models can also provide theoretical reference for the design and optimization of new downhole tools.