A feasible symmetric state of initial force design for cable-strut structures

Abstract

For a structure with given shape, to acquire feasible pre-stress states without changing its predefined shape is the main purpose of force finding as a crucial step in structural designs, since mechanical behaviors of cable-strut structures are highly sensitive to their pre-tensioning levels. One of practical ways to initial force designs is double singular value decomposition (DSVD), the essence of which is visual inspections of symmetry properties that could be arbitrary and time consuming due to its manual grouping. To reduce the iteration times of finding a proper group division, a grouping scheme was developed by utilizing the distributed static indeterminacy as a symmetry indicator that represents both geometric and stiffness symmetry. The existing DSVD method was subsequently modified using the proposed scheme that could provide an initial group classification being helpful to decrease the undesirable numbers of pre-stress states. Finally, two examples were investigated to verify the validity and accuracy of the modified method, and then it was applied in an enormous stadium with saddle-shaped roof structure showing good agreement with results obtained by a conventional approach.

1 Introduction

Possessing remarkable advantages, such as light weight, form diversity and esthetic novelty, cable-strut structures have attracted considerable attention from various fields in recent decades. They have a broad range of technological applications, including the simulations of musculoskeletal systems [1, 2], deployable aerodynamic devices [3], novel architectures [4], advanced engineering materials [5]. It is profoundly believed that as most cable-strut structures are statically and kinematically indeterminate systems whose mechanical behaviors are highly dependent on the pre-stress states, form finding analysis is naturally considered as a critical step of their design process with a view to finding the specific equilibrium configuration and its corresponding initial forces in components.

Enormous efforts were made on these form finding issues; the commonly known form finding methods contain the force density method [6,7,8], the dynamic relaxation method [4, 9, 10] and the geometrically nonlinear finite-element method [11, 12]. Furthermore, Masic et al. [13] suggested an algebraic method based on invariant tensegrity transformations. Estrada et al. [14], Zhang and Ohsaki [15], Tran and Lee [16], Lee and Lee [17] proposed numerical form finding methods for tensegrities where the force density and equilibrium matrices were iteratively decomposed by different means. Ohsaki and Zhang [18] presented a nonlinear programming approach to form finding using fictitious material properties. All these fore-mentioned approaches are useful methods for finding a new configuration with the corresponding pre-stresses; on the other hand, they are not suitable to the search of a feasible set of pre-stresses without changing the designated shapes.

Notably, seeking the initial pre-stress state for a structure with given shape is also one integral part of form finding problems. This particular issue mostly arising from preliminary design, where the geometric configuration is known and its corresponding pre-stresses are unknown, is commonly referred to as initial force design or force finding. Based on the equilibrium theory [19], the pre-stress states can be regarded as linear combinations of the independent self-stress states [20]. If the concerned structure owns more than one state, this algebraic solution can be rather difficult to exploit since each state extracted from the null-space of the equilibrium matrix normally dissatisfies the unilateral behaviors and symmetry. To find an optimal state with minimum nodal residual forces, Ströbel [21], Zhang et al. [22] and Ren et al. [23] developed numerical procedures utilizing the linear adjustment theory, which were rather useful and efficient for cable-strut systems if a reasonable pre-tension assignment could be chosen. In seeking to find compatible self-stress states, Quirant et al. [24] and Quirant [25] presented a linear program that constituted a convex polyhedral cone and its application was limited to simple cases. Sánchez et al. [26] designed strategies to identify and localize self-stress states in a modular tensegrity grid, resulting in a local state that was a less preferred option for the whole tensegrity system compared with an integral pre-stress state.

Insofar as the majority of cable-structures have inherent symmetry properties, these valuable properties have been utilized to simplify the initial force design process. Succeeding in analyzing the geometric symmetry of structures, group representation theory was adopted to find an integral pre-stress state that was extracted from the null-space of the first block matrix of the symmetry-adapted equilibrium matrix [27]. Apart from such matrix block-diagonalization, symmetry can also be used for the initial force design through element grouping that has recently been brought into strong focus of researchers [28, 29]. One recent case concerned the double singular value decomposition (DSVD) method [30] where the element grouping was adopted as the simplification and SVD as the major mathematical operation, generating feasible pre-stress states that satisfied both the unilateral behaviors and symmetry. Tran and Lee [31] carried out an exploration for proper group divisions via iterative change of group numbers, or via direct assignment of additional element forces constraints to certain groups, and then Tran and Lee [32,33,34] introduced this method to a wide variety of structural forms, including cable domes and tensegrities, with the aim of calculating their initial forces.

Despite being useful for the simplification of initial force design, these previous methods have their own limitations worth addressing. The focus of the force finding method based on group representation theory was to analyze the geometric symmetry of structures without considering the stiffness symmetry. Moreover, the essence of DSVD method was the visual inspection of symmetry properties of a structure in a way that designers manually classify different members into certain groups and impose symmetry constraints on the self-stress states. Given these, the element grouping was rather arbitrary and time consuming. Additionally, manual element grouping can be rather difficult to the point of being nearly unrealistic if the geometric configurations get far more complicated.

To this end, the distributed static indeterminacy (DSI), referred to as elastic redundancy in reference [35, 36], is used as a symmetry indicator to identify the intrinsic symmetry of cable-strut structures in terms of both geometric and stiffness geometry. The fact that the formulae provided by Ströbel [35] was only valid for kinematically determinate structures motivates this study to deduce a modified formulation of DSI that is also suitable for kinematically indeterminate systems. This symmetry indicator naturally leads to a grouping scheme that, in contrast to the visual inspection, can generate an initial group classification automatically. The DSVD method is then modified by incorporating this automatic scheme. Finally, two illustrative examples are chosen to verify the applicability and validity of this modified DSVD method; it is then applied in a colossal stadium with a saddle-like shape roof structure and compared with a conventional method.

2 Definition of distributed static indeterminacy (DSI)

To make effective use of symmetry properties in the initial force design process, the distributed static indeterminacy was introduced as a symmetry indicator that can lead to a grouping scheme to modify the existing double singular values decomposition (DSVD) method. Based on the equilibrium matrix theory, a unified formulation for DSI was derived from the relationship between the initial element elongations and the element forces in the absence of the external loads, being applicable to either kinematically determinate or indeterminate assemblies.

2.1 Formulation of DSI

For a 3-dimensional assembly with n nodes, b elements (struts and cables), and c kinematic constraints, ${\varvec{f}}_{\left( {3n-c} \right) \times 1} ,{\varvec{t}}_{b\times 1} , {\varvec{d}}_{\left( {3n-c} \right) \times 1}$ and ${\varvec{e}}_{b\times 1}$ denote a vector of its external nodal loads, element forces, nodal displacements and element elongations, respectively. Its equilibrium the compatibility and the constitutive equations are then expressed, respectively:

$$\begin{aligned} {\varvec{At}}={\varvec{f}} \end{aligned}$$

(1)

$$\begin{aligned} {\varvec{Bd}}={\varvec{e}}\end{aligned}$$

(2)

$$\begin{aligned} {\varvec{e}}={\varvec{Ft}} \end{aligned}$$

(3)

where matrix ${\varvec{A}}_{({3n-c})\times b}$ represents the equilibrium matrix, and ${\varvec{B}}_{b\times ({3n-c})} ={\varvec{A}}^{\mathrm{T}}$ the compatibility matrix; $\varvec{F}({\in \hbox {R}^{b\times b}})=\hbox {diag}({F_1 ,F_2 ,\ldots ,F_i ,\ldots ,F_b })$ is the diagonal flexibility matrix and $F_i ={l_i }/{a_i E_i }$ is the axial flexibility of the element i, (that is, the axial stiffness is $k_i =1/{F_i })$ where $a_i$ is the cross-sectional area, $l_i$ is the current element length and $E_i$ is the Young’s modulus of elasticity.

Given the effect of the initial element elongations, the expression of the element elongations e is expand to include two terms: one is caused by external nodal loads f and the other is the so-called initial elongations ${\varvec{e}}_0$, i.e.,

$$\begin{aligned} {\varvec{e}}={\varvec{e}}_0 +{\varvec{Ft}} \end{aligned}$$

(4)

Then, applying the first singular value decomposition (SVD) on the equilibrium matrix A gives a relationship between this matrix and other three relevant matrices:

$$\begin{aligned} {\varvec{A}}={\varvec{URV}}^{\mathrm{T}} \end{aligned}$$

(5)

where ${\varvec{R}}\left( {\in \hbox {R}^{\left( {3n-c} \right) \times b}} \right) =\hbox {diag}(\mu _1 ,\mu _2 ,\ldots ,\mu _{r_{\varvec{A}} } ,0,\ldots ,0)$ in which $r_{A}$ is the rank of matrix A and $\mu$ stands for its nonzero singular value; ${\varvec{U}}\left( {\in \hbox {R}^{\left( {3n-c} \right) \times \left( {3n-c} \right) }} \right) =\left[ {{\varvec{u}}_1 ,{\varvec{u}}_2 ,\ldots ,{\varvec{u}}_{3n-c} } \right]$ is the left orthogonal matrix and ${\varvec{V}}({\in \hbox {R}^{b\times b}})=\left[ {{\varvec{v}}_1 ,{\varvec{v}}_2 ,\ldots ,{\varvec{v}}_b } \right]$ is the right orthogonal matrix, both of which are implicitly normalized in this process. It is well accepted that the last $b-r_{\varvec{A}}$ columns of the matrix V can serve as the basic bases for self-stress states S:

$$\begin{aligned} {\varvec{S}}=\left[ {{\varvec{v}}_{r_{\varvec{A}} +1} ,{\varvec{v}}_{r_{\varvec{A}} +2} ,\ldots ,{\varvec{v}}_b } \right] =\left[ {{\varvec{s}}_1 ,{\varvec{s}}_2 ,\ldots ,{\varvec{s}}_s } \right] \quad {\left( {s=b-r_{\varvec{A}} } \right) } \end{aligned}$$

(6)

where s is the total degree of static indeterminacy and in most cases these states cannot be used as feasible pre-stress states directly since they normally dissatisfy with the unilateral behaviors and symmetry properties.

A general expression of the element forces t is thus obtained as:

$$\begin{aligned} {\varvec{t}}={\varvec{A}}^{+}{\varvec{f}}+{\varvec{S}}{\varvec{\alpha }} \end{aligned}$$

(7)

where ${\varvec{A}}^{+}$ stands for the generalized inverse of matrix A and $\varvec{\alpha }=\left[ {\alpha _1 ,\alpha _2 ,\ldots ,\alpha _s } \right] ^{\mathrm{T}}$ represents the coefficient vector of s independent self-stress states. Although the values of vector $\varvec{\alpha }$ are arbitrary for a statically indeterminate assembly, a specific vector $\varvec{\alpha }$ can be determined by a set of n compatibility equations. Without considering the effect of external loads f, these compatibility equations of this assembly can be obtained due to two orthogonal parts of the element elongations e including the compatible and the incompatible elongations [28]:

$$\begin{aligned} {\varvec{S}}^{\mathrm{T}}\left[ -{\varvec{e}}_0 -{\varvec{FS}}{\varvec{\alpha }} \right] ={\varvec{0}} \end{aligned}$$

(8)

therefore

$$\begin{aligned} \varvec{\alpha }=-\left( {{\varvec{S}}^{\mathrm{T}}{\varvec{FS}}} \right) ^{-1}{\varvec{S}}^{\mathrm{T}}{\varvec{e}}_0 \end{aligned}$$

(9)

Eventually, the element forces t in this case can be obtained by substituting Eq. (8) into Eq. (5):

$$\begin{aligned} t= & {} -{\varvec{S}}\left( {{\varvec{S}}^{\mathrm{T}}{\varvec{FS}}} \right) ^{-1}{\varvec{S}}^{\mathrm{T}}{\varvec{e}}_0 \nonumber \\= & {} -{\varvec{K}}\left[ {{\varvec{FS}}\left( {{\varvec{S}}^{\mathrm{T}}{\varvec{FS}}} \right) ^{-1}{\varvec{S}}^{\mathrm{T}}} \right] {\varvec{e}}_0\nonumber \\= & {} -{\varvec{K}}{\varvec{\varOmega }} {\varvec{e}}_0\end{aligned}$$

(10)

$$\begin{aligned} \varvec{\varOmega }= & {} {\varvec{FS}}\left( {{\varvec{S}}^{\mathrm{T}}{\varvec{FS}}} \right) ^{-1}{\varvec{S}}^{\mathrm{T}} \end{aligned}$$

(11)

Equation (10) is indeed a relationship between the element forces and the initial elongations; the diagonal entry of matrix $\varvec{\varOmega }$ denoted as $\gamma _i ({i=1,2,\ldots ,b})$ is then defined as the distributed static indeterminacy (DSI). Most notably, it is found that this unified formula is valid in both the kinematically determinate and the indeterminate conditions, since the matrix ${\varvec{S}}^{\mathrm{T}}{\varvec{FS}}$ is positive definite in any conditions.

2.2 Mathematical characteristic of DSI

From the viewpoint of the relationship manifested in Eq. (10), the matrix $\varvec{\varOmega }$ can be regarded as a scaling matrix reflecting the combined effect of the geometry, topology and stiffness on the structural behaviors. As it is an idempotent matrix, the summation of all the diagonal entries is equal to the total degree of static indeterminacy s; this means DSI can illustrate the contribution of each element to the total degree of static indeterminacy. It is observed from Eq. (10) that if the DSI value of one element is greater than others, its element force could be more sensitive to the change of its initial elongation, being good agreement with the Maxwell’s rule.

Furthermore, it is found that the elements holding the same symmetry properties have the same DSI values; this indicates DSI could be interpreted as a symmetric indicator representing the combined symmetry properties that in turn account for its particular mathematical characteristic. One of the combined properties is stiffness symmetry and the other is geometric symmetry.

The stiffness symmetry has a complete dependence on the stiffness assignments that sometimes are inconsistent with the geometric symmetry in order to meet the design requirements for retaining specific shapes under diverse loading conditions. In other words, the axial element stiffness values may be different at geometrically symmetric locations. This stiffness symmetry could be illustrated by the diagonal flexibility matrix F where the elements with equal stiffness values are put in the same sub-matrix:

$$\begin{aligned} {\varvec{F}}=\left[ {{\begin{array}{l} {\frac{l_1 }{a_1 E_1 }\times {\varvec{I}}_{{\bar{c}}_1 \times {\bar{c}}_1 } } \\ {{\begin{array}{l} \\ \\ {{\begin{array}{l} \\ {\varvec{0}} \\ \end{array} }} \\ \end{array} }} \\ \end{array} }{\begin{array}{l} \\ {{\begin{array}{l} \ddots \\ \\ {{\begin{array}{l} \\ \\ \end{array} }} \\ \end{array} }} \\ \end{array} }{\begin{array}{l} \\ {{\begin{array}{l} \\ {\frac{l_k }{a_k E_k }\times {\varvec{I}}_{{\bar{c}}_k \times {\bar{c}}_k } } \\ {{\begin{array}{l} \\ \\ \end{array} }} \\ \end{array} }} \\ \end{array} }{\begin{array}{l} \\ {{\begin{array}{l} \\ \\ {{\begin{array}{l} \ddots \\ \\ \end{array} }} \\ \end{array} }} \\ \end{array} }{\begin{array}{l} {\varvec{0}} \\ {{\begin{array}{l} \\ \\ {{\begin{array}{l} \\ {\frac{l_{{\bar{w}}} }{a_{{\bar{w}}} E_{{\bar{w}}} }\times {\varvec{I}}_{{\bar{c}}_{{\bar{w}}} \times {\bar{c}}_{{\bar{w}}} } } \\ \end{array} }} \\ \end{array} }} \\ \end{array} }} \right] \end{aligned}$$

(12)

in which ${\varvec{I}}_{{\bar{c}}_k \times {\bar{c}}_k }$ represents a unit matrix. As shown in Eq. (12), all the elements of this assembly can be divided into ${\bar{w}}$ groups with ${\bar{c}}_k$ elements in the kth group in terms of a specific stiffness assignment.

On the other hand, the purely geometric symmetry hidden in the self-stress matrix S can be investigated in the form of symmetric matrix ${{\varvec{SS}}}^{\mathrm{T}}$ that is essentially equivalent to matrix $\varvec{\varOmega }$ in a special case where ${\varvec{F}}={\varvec{I}}_{({b\times b})}$:

$$\begin{aligned} \varvec{\varOmega }={\varvec{S}}\left( {{\varvec{S}}^{\mathrm{T}}{\varvec{S}}} \right) ^{-1}{\varvec{S}}^{\mathrm{T}} \end{aligned}$$

(13)

where

$$\begin{aligned} {\varvec{S}}=\left[ {{\varvec{s}}_1 ,{\varvec{s}}_2 ,\ldots ,{\varvec{s}}_s } \right] =\left[ {{\begin{array}{cccc} {s_{11} }&{} {s_{21} }&{} \cdots &{} {s_{s1} } \\ {s_{12} }&{} {s_{22} }&{} \cdots &{} {s_{s2} } \\ \vdots &{} \vdots &{} \cdots &{} \vdots \\ {s_{1b} }&{} {s_{2b} }&{} \cdots &{} {s_{sb} } \\ \end{array} }} \right] =\left[ {\varvec{\tilde{s}}_1 ,\varvec{\tilde{s}}_2 ,\ldots ,\varvec{\tilde{s}}_b } \right] ^{\mathrm{T}} \end{aligned}$$

(14)

in which $\varvec{\tilde{s}}_i \left( {i=1,2,\ldots ,b} \right)$ denotes the ith row vector of the self-stress matrix S. Based on this symbolic representation, the ith diagonal element of matrix ${{\varvec{SS}}}^{\mathrm{T}}$ can be expressed as $\sum \nolimits _{\tau =1}^s {s_{i\tau }^2 }$ that is equal to the square of Euclidean norm of the ith row vector. This implies that the DSI in this special case could be rewritten as:

$$\begin{aligned} \gamma _i =\sum _{j=1}^s {\left( {s_{ji} } \right) } ^{2}=\left( {\left\| {\varvec{\tilde{s}}_{\varvec{i}} } \right\| _2 } \right) ^{2} \end{aligned}$$

(15)

where$\left\| {\varvec{\tilde{s}}_{\varvec{i}} } \right\| _2$ denotes the Euclidean norm of the ith row vector. It is in line with the previous studies [27] that $\left\| {\varvec{\tilde{s}}_{\varvec{i}} } \right\| _2$ of the ith row vector in ${\varvec{S}}$ is equal to its counterparts at symmetric locations, partially explaining the reason why symmetrically located elements always share the same DSI values. Using this DSI value calculated in Eq. (15), the entire assembly can be classified into $\tilde{w}$ groups containing $\tilde{c}_k$ elements in the kth group based on purely geometric symmetry, for the effect of stiffness symmetry in this special case is assumed to be neglected as the stiffness values of all elements are set the same.

3 Double singular value decomposition (DSVD) force finding method using DSI

Although it is considered as a conventional approach to finding initial forces, the existing DSVD method could be rather arbitrary and time consuming since its essence is the visual inspection of symmetry properties by manually classifying different members into certain groups. A feasible grouping scheme is thus on urgent demand; to this end, a grouping scheme using DSI was proposed herein under consideration of both stiffness and geometric symmetry. The DSVD method was then modified by incorporating the proposed scheme, and furthermore the calculation procedure of this modified method was outlined in this section.

3.1 A grouping scheme based on DSI

Having particular mathematical characteristic that DSI values of the elements with equal symmetry are found to be the same, DSI known as a symmetric indicator of combined symmetry properties can naturally lead to a grouping scheme. Therefore, using the formula of DSI in Eq. (11), all the elements of an assembly could be divided into w groups with $c_{k}$ elements in the kth group. This grouping scheme automatically generates an initial grouping that could be helpful to reduce the number of undesirable pre-stress states for the DSVD method.

This grouping scheme in light of DSI value is based on both stiffness and geometric symmetry, and thus various group classifications can be generated via different stiffness assignments. On the other hand, by using the DSI illustrated in Eq. (15), it can also provide an element grouping consistent with the conventional way of element grouping that depends solely on the geometric symmetry. As addressed in Sect. 2.2, the assembly could be classified into $\tilde{w}$ groups containing $\tilde{c}_k$ elements in the kth group based on purely geometric symmetry, for the effect of stiffness symmetry in this case is assumed to be ignored as all elements have the same stiffness values.

3.1.1 The modified DSVD method

The existing DSVD was modified by adding the proposed grouping scheme that made all the elements of this assembly packed into w groups. Then the elements in each group are assumed to possess the same element forces:

$$\begin{aligned} {\varvec{q}}=\left[ {{\varvec{h}}_1 ,\ldots ,{\varvec{h}}_i ,\ldots ,{\varvec{h}}_w } \right] \left[ {q_1 ,\ldots ,q_i ,\ldots ,q_w } \right] ^{\mathrm{T}} \end{aligned}$$

(16)

where ${q}_{i}$ stands for the force density of elements in the ith group; vector $[{q_1 ,\ldots ,q_i ,\ldots ,q_w }]^{\mathrm{T}}$ represents the vector of force density of all w groups; vector ${\varvec{h}}_i$ is the basis vector with a unit in the ith group and zeros in the other $w-1$ groups.

Based on the equilibrium matrix theory, a feasible pre-stress state q of this assembly can be expressed as a linear combination of the independent self-stress states, i.e.,

$$\begin{aligned} {\varvec{q}}=\alpha _1 {\varvec{s}}_1 +\alpha _2 {\varvec{s}}_2 +\cdots +\alpha _s {\varvec{s}}_s ={\varvec{S}}{\varvec{\alpha }} \end{aligned}$$

(17)

Equating Eq. (16) with Eq. (17) leads to a linear homogeneous system as follows:

$$\begin{aligned} \alpha _1 {\varvec{s}}_1 +\alpha _2 {\varvec{s}}_2 +\cdots +\alpha _s {\varvec{s}}_s -q_1 {\varvec{h}}_1 +q_2 {\varvec{h}}_2 +\cdots +q_w {\varvec{h}}_w =\underline{{\varvec{S}}}{\bar{{\varvec{\alpha }} }}={\varvec{0}} \end{aligned}$$

(18)

where

$$\begin{aligned} \varvec{{\bar{a}}}\left( {\in \hbox {R}^{\left( {s+w} \right) }} \right)= & {} \left[ {\alpha _1 ,\alpha _2 ,\ldots ,\alpha _s ,-q_1 ,-q_2 ,\ldots ,-q_w } \right] ^{\mathrm{T}}\end{aligned}$$

(19)

$$\begin{aligned} \underline{{\varvec{S}}}\left( {\in \hbox {R}^{\mathrm{s}\times \left( {s+w} \right) }} \right)= & {} \left[ {{\varvec{s}}_1 ,{\varvec{s}}_2 ,\ldots ,{\varvec{s}}_s ,{\varvec{h}}_1 ,{\varvec{h}}_2 ,\ldots ,{\varvec{h}}_w } \right] \end{aligned}$$

(20)

To solve this linear homogenous system, the SVD technique is applied on matrix $\underline{{\varvec{S}}}$ for the second time:

$$\begin{aligned} \underline{{\varvec{S}}}=\varvec{{\bar{U}}{\bar{R}}{\bar{V}}}^{\mathrm{T}} \end{aligned}$$

(21)

where the matrices ${\bar{\varvec{U}}},\bar{\varvec{R}}$ and ${\bar{\varvec{V}}}$ are similarly defined as the corresponding matrices in the first application of DSVD on the matrix A. The dimension of null-space of matrix $\underline{{\varvec{S}}}$ can be calculated by:

$$\begin{aligned} n_{\underline{{\varvec{S}}}} =\left( {s+w} \right) -r_{\underline{{\varvec{S}}}} \quad \left( ({s+w})\le b\right) \end{aligned}$$

(22)

As the sum of s and w is always less or equal to the number of elements b, the case $({s+w} )>b$ is beyond the scope of this study. If there exists the null-space of the matrix $\underline{{\varvec{S}}}$, i.e., the dimension of these space is greater than one ($n_{\underline{{\varvec{S}}}} \ge 1)$, the base of all solutions to Eq. (13) are collected in ${\bar{\varvec{v}}}_i$:

$$\begin{aligned} \underline{{\varvec{S}}}\bar{{\varvec{v}}}_i ={\varvec{0}}\quad {\left( {i=r_{\underline{{\varvec{S}}}} +1,\ldots ,s+w} \right) } \end{aligned}$$

(23)

where $r_{\underline{{\varvec{S}}}} =\textit{rank}\left( {{\varvec{{S}}}} \right)$. The $\bar{\varvec{v}}_i$ can be obtained from the last $n_{{S}}$ columns of the matrix $\varvec{{\bar{V}}}$; the first to sth components of vector $\varvec{{\bar{v}}}_i$ represent coefficients of this linear combination, and the ($s+1$)th to ($s+w)$th components denote the force densities of w groups.

Apparently, vector $\varvec{{\bar{v}}}_i$ can directly be employed as a unique pre-stress state satisfying the equilibrium, the unilateral behaviors and symmetric properties, if the dimension of null-space of matrix $\underline{{\varvec{S}}}$ is equal to one. Even if it was not found equal to one, the proposed grouping scheme could help reduce the number of undesirable self-stress states from s to $n_{\underline{{\varvec{S}}}}$, by providing an initial group classification. In the case $n_{\underline{{\varvec{S}}}} >1$, a good option for the subsequent search of initial forces is to decrease the total group numbers that is under the control of DSI values. This indicates that in this case, the elements with close DSI values can be clustered together providing a new classification with less group numbers. Its closeness threshold could be set up depending on different situations the designers are faced with and, at any rate, cables and struts could not be grouped into the same group.

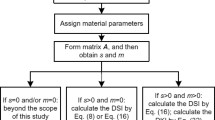
3.2 Calculation procedure of the modified DSVD method

This modified DSVD method was then coded using MATLAB 2104b, and its whole process was outlined as follows:

Step 1: Assemble the equilibrium matrix A and the diagonal flexibility matrix F.

Step 2: Apply the SVD technique on matrix A and extract the self-stress matrix S from its null-space.

Step 3: Compute the DSI values and accordingly classify the elements into different groups.

Step 4: Assemble the matrix $\underline{{\varvec{S}}}$ based on the obtained element grouping.

Step 5: Apply the SVD technique on matrix $\underline{{{\varvec{S}}}}$ does and extract the $\bar{\varvec{v}}$ from its null-space.

Step 6: If $n_{\underline{{\varvec{S}}}} =1$, then vector $\bar{\varvec{v}}$ could be chosen for the next step; if $n_{\underline{{\varvec{S}}}} >1$, go back to step 3 to decrease the total group numbers by clustering the elements with close DSI values into one groups.

Step 7: Substitute vector $\bar{\varvec{v}}$ into $\varvec{\varepsilon }={\varvec{A}}{\bar{{\varvec{v}}}}$ and then compute its Euclidean norm $\varepsilon =\left( \varvec{\varepsilon }^{\mathrm{T}}\varvec{\varepsilon } \right) ^{1/2}$.

Step 8: If $\varepsilon \le 10^{-10}$, vector $\varvec{{\bar{v}}}$ is obtained as a feasible symmetric pre-stress state satisfying the unilateral properties; if $\varepsilon >10^{-10}$, go back to step 2 to change the stiffness assignments or move backwards toward step 3 for rearrangements of element clustering.

Nevertheless, it should be emphasized that in addition to the feasible pre-stress state, another internal part of force finding is a single parameter called amplitude coefficient that represents the overall magnitude of the initial forces.

4 Examples

4.1 Example 1: A Snelson’s X beam with four modules

A Snelson’s X beam with four modules that was previously investigated in reference [31] was chosen herein as displayed in Fig. 1. It was found to be a statically and kinematically indeterminate system with four independent self-stress states and three mechanisms, for this two-dimensional free-standing assembly consisted of 10 nodes and 21 components. It was assumed that in this case each cable had the same axial stiffness and so did the struts, for example, ${ aE}_{{\text {strut}}}$ = 65940 kN and ${ aE}_{{\text {cable}}}= 3238\,{\text {kN}}$.

Fig. 1

A Snelson’s X beam with four modules: struts in thick solid lines (unit: mm)

Applying the proposed grouping scheme on this assembly, its 21 components were classified into seven groups according to the DSI values calculated by Eq. (11) as illustrated in Fig. 2. It was an element grouping depending on the combined symmetry properties. By using the DSVD method, matrix $\underline{{\varvec{S}}}$ was found to has 11 singular values and amid them there was only one value equal to zero, that is, $n_{\underline{{\varvec{{S}}}}} =1$. This means that on the grounds of this particular grouping this modified DSVD method could generate precisely one pre-stress state as shown in Fig. 3. It was apparent that this feasible state satisfied both symmetry properties and unilateral behaviors.

Fig. 2

A group classification based on DSI values

Fig. 3

A feasible symmetric pre-stress state calculated by the modified DSVD method (the greater its absolute value, the thicker its line)

Furthermore, another six typical stiffness assignments were selected for the proposed grouping scheme in such way that a comparison to the prior study [31] was easy to conduct. As listed in Table 1, $n_{\underline{{\varvec{S}}}}$ values computed under the group classifications corresponding to the stiffness changes were in general good agreement with those in the previous study, despite the case $w=9$ and $w=11$ where $n_{\underline{{\varvec{S}}}} =1$ in this method and $n_{\underline{{\varvec{S}}}} =2$ in the prior study. This slight discrepancy might be due to the occurrence of local pre-stress state in study [31]. This finding essentially confirmed that different stiffness assignments could lead to different group divisions allowing designers more freedom in the initial force design of flexible structures.

Table 1 A comparison of $n_{S}$ values computed under different group classifications

4.2 Example 2: A cable-strut tower with four modules

Similarly, a cable-strut tower with four modules in three-dimension is plotted in Fig. 4 with respect to a Cartesian coordinate system xyz. The cables parallel to plane xy were termed as horizontal cables and the others vertical cables. Being a statically and kinematically indeterminate system with 15 nodes and 39 elements, it was found to have four independent self-stress states and 10 mechanisms containing four internal mechanisms and six rigid body mechanisms. The material parameters of this assembly is set as the same with the example 1, i.e., ${ aE}_{{\text {strut}}}= 65{,}940\,\hbox {kN}$ and $aE_{{\text {cable}}}= 3238\,\hbox {kN}$.

Fig. 4

a A cable-strut tower with four modules (b) top view (c) side view of one module (unit: mm)

Based on the suggested grouping scheme, the DSI values of each element were calculated and accordingly the entire assembly was divided into five groups as demonstrated in Fig. 5. Using this obtained group classification, the dimension of matrix $\underline{{\varvec{S}}}$ was found to be equal to one meaning that this grouping was helpful to reduce the undesirable pre-stress states, in this case, from four to one; therefore, a single feasible pre-stress state was achieved as shown in Fig. 6.

Fig. 5

A group division according to DSI values

Fig. 6

A feasible symmetric pre-stress state calculated by the modified DSVD method (the greater its absolute value, the thicker its line)

Even though the obtained pre-stress state was consistent with the symmetry and the unilateral properties in light of this particular grouping, there are still other possible group divisions which can be achieved by clustering the elements with close DSI values into one groups. For example, all the vertical cables whose DSI values were rather close were put into one group to reduce the total group number from five to four, leading to $n_{\underline{{\varvec{S}}}} =1$; subsequently, all the horizontal cables were treated as one group with the total group number decreased to three, also leading to $n_{\underline{{\varvec{S}}}} =1$. Note that despite the closeness of DSI values between strut and horizontal cables in magnitude, cables and struts could not be cataloged into the one group.

4.3 Example 3: A colossal stadium with a saddle-like roof structure

A newly built stadium in Zaozhuang, China, was investigated for its initial force design using the modified DSVD method. It can be seen from Fig. 7 that there are two main characteristics distinguishing itself from other ordinary spoke structures. One is the unique shape of its inner rings closely resembling a saddle, which is fulfilled by adding extra cables as special components in a certain order, and the other is a sophisticated configuration of roof cables providing such adequate levels of stiffness that enables the design of metal shells. For simplicity, all the external ring beams were neglected in the following investigation. This assembly was constituted by 336 components and 144 nodes including 48 fully fixed boundary nodes; on this occasion, it was a statically indeterminate assembly with 48 self-stress states.

Fig. 7

a An aerial photograph of the Zaozhuang stadium during construction, taken by Pan qin b the detailed geometric relationship

There are six type of components constituting this roof structure, and their material parameters are tabulated in Table 2. It has noted that apart from the feasible pre-stress state, the amplitude coefficient as a representative of the overall magnitude of pre-tensioning also plays a significant role in the initial force design. In this situation, 35 percent of the lower ring cable’s ultimate tensile force, i.e., $2.30\times 10^{4}$ kN, was adopted to control the amplitude coefficient.

Table 2 Material parameters of different component types

The suggested grouping scheme generated the DSI values for all elements as depicted in Fig. 8, and consequently they were clustered into 86 groups. It was easy to see that the upper layer of this roof structure, including upper roof cables and upper hoop cables, has far larger DSI values compared with the rest parts. According to the context of distributed indeterminacy, this means that the element forces of these components are more sensitive to the element elongations than the rest. It was found that the dimension of matrix $\underline{{\varvec{S}}}$ was equal to one and therefore a feasible set of pre-tensions was attained as illustrated in Fig. 9.

Fig. 8

An element grouping depending on DSI values

Fig. 9

A feasible set of pre-tensions based on the result obtained from the modified DSVD method (unit: kN)

To confirm the validity of the modfied DSVD method, a numerical algorithm based on the linear adjustment theory was employed in the force finding of this example (please see reference [22] for more details). This method known as a conventional approach to force finding has been implemented in a finite-element software Easy. Since this structure is statically and kinematically indeterminate, predefined pre-tension values are needed for some particular members in the process of this numerical procedure. This manual assignment of pre-tension values that is directly related to designers’ experience can greatly affect the final result of this algorithm. In other words, the resultant pre-tensions may dissatisfy the unilateral behaviors and symmetry if this assignment is unreasonable. On this occasion, the pre-tensions of the highest and the lowest ring cables, both upper and lower, were set equal to the values as shown in Fig. 9. A optimal result of this algorithm was then obtained and illustrated in Fig. 10 as a comparison to that generated by modified DSVD method.

Fig. 10

A comparison between two pre-tension states calculated by the modified DSVD method and the numerical procedure based on linear adjustment theory

It is apparent in Fig. 10 that these two results were virtual the same apart from a fairly small difference in the upper layer, i.e., the upper roof and hoop cables. As mentioned before, possessing greater DSI values, the components of its upper layer were more sensitive to the variation of element elongations (the unstressed length minus the current length) that were generated within certain accuracy limits in the calculation process of the linear-adjustment-theory-based algorithm. This finding essentially confirms the applicability and accuracy of the modified DSVD method.

5 Conclusion

A new grouping criterion was established by using DSIs as a set of grouping indicators, since the DSI is representative of both symmetric properties; most notably, this is the first study to our knowledge to introduce the concept of DSI into a grouping criterion. The existing DSVD method was subsequently modified in the light of the new criterion that considers the combined symmetry properties.

The advantage of the proposed grouping scheme is to generate an initial grouping automatically that is helpful to reduce the iteration times of searching a proper grouping greatly deceasing the calculation time of DSVD method. On the other hand, the essence of the previous DSVD method is a manual grouping, which is arbitrary and sometimes rather time consuming. From this particular viewpoint, the modified DSVD method is much simpler and more effective. Furthermore, this modified method could allow designers more freedom to design the initial forces via the different stiffness assignments.