Torsion of a circular punch attached to an elastic half-space with a coating with periodically depth-varying elastic properties

Abstract

Torsion of a non-deformable circular punch attached to an elastic half-space with functionally graded or multilayered coating is considered. The coating is represented by a set of alternating soft and hard (in terms of shear modulus values) layers. The boundaries of the layers can be sharp (piecewise-constant variation of the shear modulus) or smooth (continuously inhomogeneous or functionally graded coatings). An approximate analytical solution of high accuracy applicable for any value of coating thickness is constructed. The influence of number of layers and type of the boundaries between them on the kernel transform of the integral equation and on the contact stresses under the punch is investigated. It is shown that for certain parameter values of the problem substantial differences between the results for the continuous and piecewise-constant variation of the shear modulus with depth are obtained.

1 Introduction

Inhomogeneous coatings of periodic structure are widely used nowadays to create optical filters as well as heat-resistant, abrasion-resistant and erosion-resistant coatings on the surface elements of gas and steam turbines and other machine parts. The number of technologies has skyrocketed in recent years that allow layered composition of alternating layers of different materials to be created, in which the thickness of the layer may be less than 100 nm but may consist of several thousand layers [1]. They include thermal spraying (in particular, vacuum-plasma spraying) and a variety of epitaxial deposition techniques (vapor deposition or deposition from the aqueous medium). Such components may be various metals, alloys and even polymeric materials (in the case of epitaxy) that can be used during the creation of such coatings.

Mechanical properties of multilayered or functionally graded coatings are being actively investigated nowadays. Dayal, Savvides and Hoffman studied [2] nanolayered aluminum/palladium thin films with smooth boundaries between the layers. Hardness and the associated microstructural deformation of such materials were investigated using transmission electron microscopy. These authors found that with just 6.5 % volume of palladium a hardness enhancement of $\sim$200 % was observed in such materials in comparison with pure aluminum films.

The influence of nitrogen partial pressure on the microstructural and morphological properties of TiN coatings has also been studied [3]. Voevodin et al. [4] developed a model to describe the resultant stress distributions in hard multilayer coatings under applied contact load, simulating coating application for wear protection, and suggested an algorithm to calculate normal and shear stress across the coating thickness for various numbers of layers and layer thicknesses. Stress analysis in specimens made of a multilayer polymer/composite used for hydrogen storage application has also been developed, and the model to predict the ultimate tensile stresses is proposed in [5].

To study the influence of material parameters and structure of such coatings on its mechanical properties, one can conduct mathematical modeling of some load (indentation, torque, heating or another) applied to a medium.

The problem of torsion of a homogeneous elastic half-space by a circular punch was first formulated and solved in a dynamic formulation by Reissner and Sagoci [6]. Using the technique of integral transforms, Sneddon [7] reduced this problem to the solution of the integral equation. Prior to this, Grilitskii [8] had constructed the solution to the problem of the isotropic two-layer medium and the orthotropic elastic layer as a power series of the ratio of first layer thickness to the radius of the punch.

There has been considerable research activity over recent years in obtaining solutions to the contact problems, related to inhomogeneous coatings. Axisymmetric and plane contact problems for a functionally graded layer on an elastic half-space and half-plane for arbitrary variation of elastic properties with depth are considered by Wang, Ke and others [9, 10]. They used piecewise linear approximation for elastic properties to reduce the problem to the solution of an integral equation, which was solved numerically.

Kulchytsky-Zhyhailo [11] considered an axially symmetric problem of the theory of elasticity for an inhomogeneous half-space loaded by Hertz’s pressure, comparing the problem for the inhomogeneous coating with the solution of the problem in which this coating is simulated by a homogenized uniform layer. But in the present paper it is shown that contact stresses under the punch significantly differ from the ones appearing on the surface of homogeneous half-space, especially for small values of coating thickness. Kulchytsky-Zhyhailo together with Matysiak and Perkowski [12] also assumes the torsion of homogeneous coating on a functionally graded substrate with power variation of the elastic properties in the substrate.

Analytical approaches are more useful for the fundamental analysis than numerical because they can mathematically show key features in the material behavior with varying geometrical and physical parameters. Also analytical solutions are more convenient for obtaining the characteristics of materials from experimental measurements [13, 14].

In this work, we present a semi-analytical solution to the axially symmetric torsion problem of a circular punch attached to an elastic half-space coated by a functionally graded (FG) layer with periodical structure (inspired by [2]). The method of analytical and numerical construction of the solutions of the problem fully explained in earlier publications [15–17]. The advantage of our approach compared with commonly used in the literature is that our method is effective in whole range of values of geometrical parameter of the problem (relative thickness of the coating). Many other methods are effective only in a specific range of layer thicknesses, and one should use different methods to analyze solution in a whole range of layer thicknesses. We also consider arbitrary variation of shear modulus in the coating while most of the results in literature were obtained only for a specific type of variation of shear modulus (exponential, linear or power variation). We have analyzed the accuracy of the solution [17] and have shown that the results provided are of high accuracy even for a coating of complicated structure, while for many other methods the precision was not discussed.

The present paper contains new results on comparison of elastic behavior for functionally graded and piecewise homogeneous layered coatings (smooth or sharp boundaries between the sublayers). It is shown that they have qualitative differences for specific values of the problem’s parameters. Novelty of the paper lies in detailed theoretical analysis of coatings of periodical structure and in comparison between the functionally graded and homogeneous “sublayers” structure. The paper provides new theoretical results on how the number of the “sublayers” in these coatings influences contact stresses for small, intermediate and large coating thicknesses. The results were also compared with the well-known results for the homogeneous half-space.

2 Statement of the problem

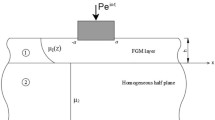
We consider a rigid punch with flat circular base attached without slipping to the boundary $\Gamma$ of elastic inhomogeneous isotropic half-space $\Omega$. The shear modulus G of the half-space varies with depth as

$$\begin{aligned} G(z)=\left\{ \begin{array}{lll} G^{c}(z)=G^{s}f(z),&{}\quad -H<z\le 0 \\ G^{s},&{}\quad -\infty \le z\le -H \\ \end{array} \right. , \quad G^{s}=\hbox {const} \end{aligned}$$

(1)

f(z) is a certain function that determines the variation of shear modulus inside the coating. Cylindrical coordinate system $r, \varphi , z$ with the origin at the center of the punch is used. The punch is subjected to a torque M. Under the action of this torque, the punch twists about the z-axis by an angle $\varepsilon$, which leads to the torsion strain in $\Omega$ (see Fig. 1). Outside of the punch, surface $\Gamma$ is traction-free:

$$\begin{aligned} z=0:\quad \quad \sigma _z =\tau _{rz} =0,\quad \left\{ \begin{array}{l} {\tau _{\varphi z} =0,\quad r>a} \\ {u_\varphi =r\varepsilon ,\quad r\le a} \\ \end{array} \right. \quad \end{aligned}$$

The stresses vanish at $r \rightarrow \infty$ and $z\rightarrow -\infty$.

Fig. 1

Statement of the problem

The coating and the substrate are assumed to be glued without sliding so the condition of continuity

$$\begin{aligned} z=-H:\quad \quad \tau _{\varphi z}^{(1)} =\tau _{\varphi z}^{(2)} ,\quad u_\varphi ^{(1)} =u_\varphi ^{(2)} \end{aligned}$$

is satisfied. Hereafter, superscripts (1) and (2) correspond to the coating and to the substrate, respectively. The quantity of primary interest is contact tangential stress under the punch

$$\begin{aligned} \tau _{\varphi z} \left| {_{z=0} } \right. =\tau _a (r),\quad r\le a \end{aligned}$$

Using Hankel integral transformation, the solution of the problem is reduced to solution of the following integral equation (assuming $G_{\varphi z} =G_{r\varphi } =G$ in [15]):

$$\begin{aligned} \mathop {\int }\limits _0^1 {\tau (\rho )\rho } \mathop {\int }\limits _0^\infty {L(u)\hbox {J}_1 (ur\lambda ^{-1})\hbox {J}_1 (u\rho \lambda ^{-1})\mathrm{d}u} \mathrm{d}\rho =\lambda G(0)r\varepsilon ,\quad r\le 1 \end{aligned}$$

(2)

where following notations are used: $r^{\prime }=r/a$, $\tau (\rho )=\tau _a (\rho a)$ (the primes were dropped), $\lambda =H/a$ is dimensionless coating thickness; $\hbox {J}_1 (x)$ is Bessel’s function of the first kind; $L(\gamma )=\gamma U_1 (\gamma ,0)\mathrm{T}^{-1}(\gamma )G(0)$ is the kernel transform of integral equation, $\gamma =u/H$; $U_1 (\gamma ,z),\mathrm{T}(\gamma )$ are the Hankel transforms of displacements $u_\varphi$ and contact stresses $\tau (r)$. Function L(u) characterizes compliance of a half-space $\Omega$ under an axially symmetric torsional loading. In case of arbitrary variation of the shear modulus in the coating, value of L(u) can be evaluated only numerically [15].

Using the bilateral asymptotic method [16], the approximate analytical solution was constructed [15]:

$$\begin{aligned} \tau (r)=\frac{4}{\pi }\varepsilon G(0)\left\{ {L_N^{-1} (0)\frac{r}{\sqrt{1-r^{2}}}+\sum _{i=1}^N {C_i } \left( {\frac{\hbox {sh}(A_i \lambda ^{-1})}{r\sqrt{1-r^{2}}}-\frac{A_i }{\lambda r}\mathop {\int }\limits _r^1 {\frac{\hbox {ch}(A_i \lambda ^{-1}t)}{\sqrt{t^{2}-r^{2}}}tdt} } \right) } \right\} \end{aligned}$$

(3)

where constants $\hbox {C}_{\mathrm{i}}$ can be obtained from the system of linear algebraic equations below

$$\begin{aligned} \sum _{i=1}^N {C_i \lambda \frac{A_i \hbox {ch}(A_i \lambda ^{-1})+B_k \hbox {sh}(A_i \lambda ^{-1})}{B_k^2 -A_i^2 }} +\frac{1+B_k \lambda ^{-1}}{L_N (0)B_k^2 \lambda ^{-2}}=0,\quad k=1, 2,\ldots ,N \end{aligned}$$

Function $L_{N}(u)$ is approximation of kernel transform of the integral equation (2) in the form:

$$\begin{aligned} L(u)\approx L_N (u)=\prod _{i=1}^N {\frac{u^{2}+A_i^2 }{u^{2}+B_i^2 }} , \end{aligned}$$

(4)

where $A_{\mathrm{i}}$, $B_{\mathrm{i}}$ are complex constants that can be calculated using an algorithm fully described in [17]. Solution (3) is asymptotically exact when $\lambda \rightarrow 0$ or $\lambda \rightarrow \infty$ [16]. The solution precision for intermediate values of coating thickness $\lambda$ depends on the error of approximation of the kernel transform L. It is shown [17] that the error of the solution is of the same order of magnitude as the error of the approximation of the kernel transform.

We consider the following types of variation of shear modulus with depth of the coating:

(1) $f_1 (z)=\frac{f_0 +1}{2}-\frac{f_0 -1}{2}\cos \left( {2\pi kz} \right)$,    (2) $f_2 (z)=\frac{f_0 +1}{2f_0 }+\frac{f_0 -1}{2f_0 }\cos \left( {2\pi kz} \right)$

(3) $f_3 (z)=\left\{ \begin{array}{lll} f_0 ,&{}\quad z\in Z_1 \\ 1,&{}\quad z\in {\left[ {-H,0} \right] }/{Z_1 } \\ \end{array} \right.$,    (4) $f_4 (z)=\left\{ \begin{array}{lll} 1/{f_0 },&{}\quad z\in Z_1 \\ 1,&{}\quad z\in {\left[ {-H,0} \right] }/{Z_1 } \\ \end{array} \right.$

$$\begin{aligned} Z_1 =\bigcup _{j=0}^{k-1} {\left[ {-\frac{4j+1}{4k}H,-\frac{4j+3}{4k}H} \right) } \end{aligned}$$

Coatings 1–4 describe periodic variation of shear modulus (Fig. 2): material A with relatively low value of G alternates material B with high G value. Shear modulus in coatings 1 and 2 varies according to the harmonic function (functionally gradient coatings (FGC) correspond to continuous variation of volume fraction of materials A and B), while coatings 3 and 4 have a distinct interface between the layers (pure deposition of each phase). Parameter k sets the number of layers. Coatings 1 and 3 have greater values of shear modulus than the substrate, while coatings 2 and 4 have lower values.

The production and deformation mechanics of such coatings and investigation using transmission electron microscopy (TEM) and nanoindentation are described in [1].

Fig. 2

Shear moduli variation in the coatings 1–4

Parameter $f_0 =\hbox {const}>1$ is the ratio of shear moduli of the materials B and A. Let us consider $f_0 =3.5$, that for example corresponds to a combination of soft (aluminum, silver, copper, lead, etc.) and hard (iron, stainless steel, palladium, molybdenum, etc.) metals.

3 Kernel transforms analysis

Integral equation (2) can be rewritten in the following form:

$$\begin{aligned} \mathop {\int }\limits _0^1 {k_s (r,\rho )\tau (\rho )\rho } \mathrm{d}\rho =\lambda G(0)r\varepsilon ,\quad r\le 1 \end{aligned}$$

where $k_s (r,\rho )=\mathop {\int }\limits _0^\infty {L(u)\hbox {J}_1 (ur\lambda ^{-1})\hbox {J}_1 (u\rho \lambda ^{-1})\mathrm{d}u}$ is the kernel of the integral equation. Properties of the kernel of integral equation largely determine the possibility of using one or another method to solve it. And, as will be shown below, the properties of the kernel transform, corresponding to a certain variation of the shear modulus in the coating, significantly affect the properties of the solution.

It was shown [18] that kernel transform of the integral equation (2) has following properties:

$$\begin{aligned} L(u)= & {} {G(0)}/{G(-H)}+Bu+Cu^{2}+\mathrm{O}(u^{3}),\quad u\rightarrow 0\\ L(u)= & {} 1+Du^{-1}+Eu^{-2}+\mathrm{O}(u^{-3}\hbox {),}\quad u\rightarrow \infty ; \end{aligned}$$

Kernel transforms for the coatings 1–4, when $k=1$, 10, 50, are illustrated in Fig. 3. Kernel transforms for functionally graded coatings 1 and 2 are illustrated by solid lines, while for the layered coatings 3 and 4, we used dashed lines. Curves corresponding to coatings made of more “hard” materials 1 and 3 are located below the line $L(u)= 1$, while curves for coatings 2 and 4 are located above the line $L(u)=1$.

Let us analyze the properties of coatings 1–4 with increasing number of layers (k).

Properties of kernel transforms common for functionally graded and multilayered coatings:

• 1. Kernel transforms have a single extremum point for all values of k (maximum—for coatings 2 and 4, minimum—for coatings 1 and 3), let’s designate it $u_{0})$.

• 2. Increasing k causes $u_{0}$ also to increase.

• 3. Value of extremum $L(u_{0})$ moves away from 1 with increasing k (value of $L(u_0)$ increases for coatings 2 and 4 and decreases for coatings 1 and 3).

• 4. Values of extremum $L(u_{0})$ for cases $k=10$ and $k=50$ are close, so we can assume that $L(u_{0})$ converges to a limit with increasing k (see Table 1).

• 5. The range of values of u for those kernel transform is significantly different from unity (expands) with increasing k.

Fig. 3

Kernel transform for coatings 1–4, cases $k=1$, 10, 50. Solid curves correspond to coatings 1 and 2, dash curves coatings 3 and 4

Table 1 Approximate values of extremum of kernel transform for coatings 1–4

Distinction between properties of kernel transform for functionally graded coatings and multilayered coatings:

• 1. Kernel transforms for functionally graded coatings (coatings 1, 2) for $u<0.5$ are almost not changed with increasing k while those with multilayered structure (coatings 3 and 4) are shifted to the right along the axis u, approaching a limit.

• 2. Extremum value of kernel transform $L(u_{0})$ for multilayered coatings is higher than those for functionally graded coatings (see Table 1).

• 3. L(u) converges to unity with $u \rightarrow \infty$ faster for multilayered coatings than for FGC.

4 Contact stresses analysis

Table 2 contains the values of the error associated with the kernel transform approximation by the expressions (4) for the coatings 1–4. The approximation error is defined by the following formula:

$$\begin{aligned} \Delta _L =\max \left| {{L_N (u)}/{L(u)}-1} \right| \cdot 100\,\% \end{aligned}$$

Table 2 Approximation errors for kernel transforms for coatings 1–4

We tried to minimize the error of approximation for kernel transforms especially for the coatings 1 and 2, $k=10$ to show the efficiency of the method even for complicated coating structures. The accuracy is as high ($\Delta _L =0.19\,\% )$ that we can expect the solution also to be of high accuracy for any value of the parameter $\lambda$ (the correlation between the error of contact stresses and approximation of kernel transform was thoroughly described in [17]).

To demonstrate the contrast of contact stresses on the surface of inhomogeneous and homogeneous half-spaces, let us introduce the function $\tau _{\mathrm{rel}} (\lambda ,r)={\tau (\lambda ,r)}/{\tau _{\mathrm{hom} } (r)}$, where $\tau (\lambda ,r)$ are the contact stresses under the punch for the coatings 1–4, and $\tau _{\mathrm{hom} } (r)$ are the contact stresses, appearing in the homogeneous half-space with the shear modulus equal to the one on the surface of coatings 1–4 (i.e., $G=G(0)$). Unlike function $\tau (\lambda ,r)$, the function $\tau _{\mathrm{rel}} (\lambda ,r)$ does not have singularity at $r = 1$.

From the physical perspective of the problem, it implies that for coatings 1–4 the condition $\tau _{\mathrm{rel}} (\lambda ,r)\rightarrow 1$ is satisfied for $\lambda \rightarrow 0$ or $\lambda \rightarrow \infty$.

Figure 4 shows the dependence of $\tau _{\mathrm{rel}} (\lambda ,r)$ with the $\lambda$ parameter for the coatings 1 and 2 for $k=1$, 2, 10 and for the coatings 3 and 4 for $k=10$ at the point $r=0.5$. Numerical experiments show that for any fixed $r\in \left[ {0...0.99} \right]$ plots do not differ qualitatively from those shown in Fig. 4.

We note the following properties of the contact stresses for coatings 1–4, arising from the results shown in Fig. 4:

• 1. Values $\tau _{\mathrm{rel}} (\lambda ,r)$ and $\tau (\lambda ,r)$ at fixed r have one extremum point at $\lambda _{0}$.

• 2. With increasing k the extremum point $\lambda _{0}$ shifts to the right along the $\lambda$ axis. This means that the maximum deviation of the contact stresses for inhomogeneous coatings 1–4 and contact stresses in a homogeneous half-space is achieved for thicker coatings as k increases.

• 3. With increasing k, the value of extremum of the function $\tau _{\mathrm{rel}} (\lambda _0 ,r)$ recedes from 1 (for coating 2—increases, for coating 1—decreases).

• 4. With increasing k the range of $\lambda$ where the value $\tau _{\mathrm{rel}} (\lambda ,r)$ significantly differs from 1 (i.e., the range of $\lambda$ values for which the distribution of contact stresses is significantly different from the case of a homogeneous medium) expands.

Fig. 4

Dependence of relative contact stresses from the parameter $\lambda$ at $r = 0.5$. Solid curves correspond to the coatings 1 and 2, dashed curves to the coatings 3 and 4

Properties 1–4 are common for layered and functionally graded coatings, and below are the main differences between them:

• 5. Extreme contact stresses in layered coatings are lower than in functionally graded coatings.

• 6. The curves of the contact stresses dependence on the parameter $\lambda$ are similar for all layered coatings and functionally graded coatings; however, the numerical values for fixed $\lambda$ may differ significantly. For example, when $k = 10$ and $\lambda = 18$ the difference in contact stresses for coatings 1 and 3 reaches 25 %.

Figure 5 shows the dependence of $\tau _{\mathrm{rel}} (\lambda ,r)$ on the coordinate r for coating 1, $k=1$ for “small” values of the parameter $\lambda$ (thin coatings), “intermediate” $\lambda$ (coating with thickness comparable to the size of a punch) and “large” $\lambda$ (thick coatings).

We analyze how the contact stresses distribution changes for “large,” “medium” and “small” values of relative layer thickness $\lambda$ on the example of the coating 1, $k=1$ below.

• 7. Contact stresses for “large” values of the parameter $\lambda$ ($\lambda > 1/2$) decreases monotonically for $r\rightarrow 1$ as compared to the case of a homogeneous half-space. For $\lambda >\lambda _{1}=8$, the difference between $\tau (\lambda ,r)$ and $\tau _{\hom } (r)$ is less than 8 % for $\lambda > \lambda _{2}=25$ is less than 1 %.

• 8. Contact stresses for “small” and “medium” values of the parameter $\lambda$ ($\lambda \le \lambda _{3}=1/2$) firstly increase and then decrease as $r\rightarrow 1$ compared with the case of a homogeneous half-space.

• 9. Figure 5 shows that with decreasing $\lambda$, regions of increasing and decreasing of the relative contact stresses by r become narrow (see property 8). Contact stresses for $\lambda < \lambda _{4}=0.01$ almost do not differ from the case of a homogeneous half-space everywhere except the neighborhood of $r=1$, where a sharp increase and then decrease in the relative values of the contact stresses can be observed.

Fig. 5

Relative contact stresses dependence on coating thickness $\lambda$ for coating 1 with $k=1$

Properties 7–9 also take place for coatings 2–4 and any value of parameter k (only values of $\lambda _{1}$, $\lambda _{2}$, $\lambda _{3}$, $\lambda _{4}$ will be different).

It should be noted that the concept of “large,” “medium” and “small” values of the parameter $\lambda$ is conventional, with change of parameter k, or when considering coatings different from 1–4, their numeric ranges may change significantly.

5 Conclusions

Contact stresses appearing on the surface of coatings on a half-space subjected to torsion were analyzed in the paper. They are of great interest for theoretical studies, because if you know these values, it becomes easy to calculate stresses, strains and displacements across the coating and within the half-space [19].

Coatings of periodical structure were considered for both functionally gradient variation of shear modulus and distinct interfaces between the layers.

Numerical results of high accuracy were obtained, illustrating the distribution of contact stresses on the surface of the coatings; detailed analysis of the properties of such coatings is provided for various ranges of parameters of the problem.

Recently, an analytical solution was obtained for the problem of torsion of a circular punch attached to a transversely isotropic elastic half-space with transversely isotropic functionally graded coating [15]. Consequentially, an extension of the same method can be used to study a periodically inhomogeneous transversely isotropic coating on a transversely isotropic half-space. Also this method can be used to study the case when the elastic modulus of the coating and the half-space differ significantly; semi-analytical solutions were obtained for indentation [20], torsion [21] and bending of a plate [22] on a half-space with a soft inhomogeneous coating (having elastic modulus smaller by 2, 5, 10, 100, 1000 times than an underlying substrate), which are proven to be correct upon comparing numerical results with results for a non-deformable substrate.