1 Introduction

The structural integrity of engineering components is always a matter of concern to the designers. The reliable prediction of the behavior of cracked structures always plays an important role being cognizant of the harmfulness of a flaw. One typical form of defect at the weld is a surface crack, which decreases the resistance of the weld to applied stresses. Lin and Smith [1] have obtained that surface cracks often grow semi-elliptically defined by geometric parameters such as an aspect ratio and relative depth. For circumferential surface cracks in pipes (Fig. 1), entirely few theoretical or experimental solutions for the SIF determination are available for both interior and exterior one, while many numerical and semi-analytical works have been carried out to determine the SIF at the deepest or at the surface point of the semi-elliptical crack. Grebner and Strathmeier [2] calculated the thermal SIFs at the deepest and surface points of circumferential surface cracks in a cylinder based on weight functions considering two different cases of thermal boundary conditions. Chen and Yu [3] derived the weight function for multiple axial cracks in hollow cylinders using FEA. Xian-Ming et al. [4] used photo-elastic experiments and caustic method to present an empirical equation for SIF for a surface crack front in a pipe under uniform tension. The results indicated that the maximum SIF occurred at the deepest point of crack. Poette and Albaladejo [5] determined the SIFs for semi-elliptic circumferential cracks in cylinders using virtual extension method. Wallbrink et al. [6] employed a semi-analytical solution to predict the SIFs for the circumferential semi-elliptical internal or external crack in a pipe involving nonlinear stress distribution reporting a highest error percentage of 15 % at the surface point of the crack. Zahoor [7] presented approximate expressions for five flaw cases. The solutions were obtained from finite element data and curve fitting. Bergman [8] employed the FEA to calculate the SIFs for a range of crack sizes and six different load cases using finite element method. Kumar et al. [9] presented elastic analysis of axial and circumferential semi-elliptical surface flaws in cylinders subjected to remote uniform tension and internal pressure using the line-spring model and a shell FEA. El Hakimi et al. [10] carried out the surface crack problem in a cylinder and a sphere using the FEA. The J-integral was employed to consider both elastic and elastic-plastic behaviors. Kamaya and Nishioka [11] used the finite element alternating method to solve an edge crack in a pipe. Alipour et al. [12] analyzed the local thermal SIFs at the whole crack front of a longitudinal semi-elliptical crack using the FEA and the weight function method. Kamaya [13] evaluated the limit load of a pipe containing two circumferential surface cracks using FEA for an elastic-perfectly plastic material.

A method for calculating the SIF is provided in Appendix C of API 579 Standard Code [14]. In this method, the stress distribution is obtained at the flaw location firstly and then fitted to a fourth-order polynomial equation. In the second step, the fitted polynomial is used with influence coefficients to calculate the SIF. Miyazaki and Mochizuki [15] calculated the SIFs of surface cracks, in plate and pipes subjected to residual stress fields by the simplified equation in API. Scarth and Xu [16] and Li et al. [17] suggested a weight function with respect to segment polynomial interpolation to calculate solutions of the SIF for applied loading. The actual stress distribution from FEA was extracted in a piecewise linear model, and the influence coefficients were applied to fit the data from API 579 [14] to derive the weight function. However, for some cases the difference between the proposed method and the others was significant. Oh et al. [18] proposed a simplified method decomposing the residual stress field by its uniform and linear components to estimate the SIFs for circumferential cracks in cylinders under both similar and dissimilar welding profiles. Katsuyama et al. [19] evaluated the effects of welding parameters on residual field by FEA. The methodology used is based on thermal-elastic-plastic analysis. The SIFs were derived by the influence function. Huh [20] proposed a three-dimensional FEA for elastic T-stress estimation of circumferential internal surface cracks in pressurized cylinders using finite element method. Kim et al. [21] and Cho et al. [22, 23] developed three-dimensional elastic-plastic finite element models to evaluate the J-integral for a circumferential surface crack in thin-walled cylinders based on a three-dimensional FEA.

Mettu and Forman [24] represented crack opening displacements to derive a WF for circumferential crack using the FEA. Varfolomeyev et al. [25] employed an approximate series, based on available numerical data, to derive crack opening displacement for determination of WF for circumferential crack in a pipe. Based on the concept of the WF, Nabavi and Ghajar [26, 27], and Nabavi and Kamyab [28] calculated thermal SIFs in circumferentially cracked pipes subjected to steady and transient thermo-mechanical loading, respectively.

As is obvious from the surveyed literature quite no closed-form expressions for the stress intensity analyses of circumferential crack subject to the residual stresses caused by welding containing wide ranges of aspect ratio and relative depth can be found. A question often posed is that for fatigue life expectancy of such circumferentially cracked pipe under welding residual stress, one needs to assess the WF formulation for SIFs as a function of residual stress field parameters and crack geometries.

Fig. 1
figure 1

Schematic view of an internal circumferential semi-elliptical crack in a pipe

Full size image
Fig. 2
figure 2

Geometrical parameters for a circumferential semi-elliptical crack

Full size image

Accordingly, as the first attempt, this paper presents a WF relation for calculation of the mode I SIF for a semi-elliptical circumferential crack depicted in Fig. 1. The crack situated at the inside of the cylinder of radii ratio \(R_\mathrm{o} /R_\mathrm{i} =1.1\) and subjected to residual stresses condition. To do so, first, based on a three-dimensional FEA a weight function is extracted for the mentioned crack to compute the SIF at the deepest point of the crack (point M in Fig. 2). Next, using the derived weight function a generalized expression for the SIF of the crack is presented as a function of arbitrary loading condition and crack geometries. Then, the computed expressions are validated in some special cases against several available solutions in the literature and the numerical results for different load cases with a good agreement. They are also extended to calculate the SIFs for complete circumferential cracks. The benefit of the obtained solution is the ability of the calculation of SIFs for a desired loading. Finally, using the proposed WF equation, the SIFs at the deepest point of semi-elliptical and fully circumferential cracks under various available welding residual stress fields are calculated and verified with the corresponding data in the literature, which provides an acceptable error percentage.

Fig. 3
figure 3

Typical finite element mesh of the cracked pipe

Full size image

2 Numerical analysis

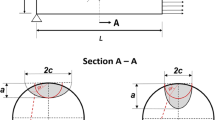
Consider an internal circumferential semi-elliptical crack with a crack depth and length of a and c, respectively, in a pipe with an outer radius-to-inner one ratio of 1.1 \((R_o /R_i =1.1)\) described by aspect ratio (a / c) and relative depth (a / t), shown in Fig. 2. Finite element program ABAQUS [29] is employed to ascertain the SIF of a surface crack located at the inner wall of a thin-walled pipe. Three-dimensional typical finite element mesh of the cracked pipe is depicted in Fig. 3; 20-node brick elements are used to model the pipe. The presence of two symmetry planes enables modeling of a quarter model. Collapsed wedge-shaped elements which midpoints are shifted to quarter points are used in the crack front area as indicated in the increased area in size of Fig. 3. The material used in the simulation assumed to be homogenous, isotopic linear elastic with Poisson’s ratio of 0.3 and module of elasticity of 200 GPa. The length of the cylinder is designated to be 15 times the thickness of the pipe [8] in order to prevent end-effects. For crack geometries, i.e., the aspect ratio (a / c) and the relative depth (a / t), the SIF may be calculated directly from the built-in J-integral solver available in the ABAQUS software established upon the domain integral technique.

Reliability of each finite element model of the cracked pipe is obtained by path independence checking of J values. Moreover, independency of the obtained SIFs to the elements number is checked doing large number of convergence tests. The axisymmetric loads were applied normal to each crack face geometry as the following form

$$\begin{aligned} \sigma _{\mathrm{ref},n} =\sigma _0 \left( \frac{r-R_i}{a}\right) ^{n} \end{aligned}$$
(1)

where n is a nonnegative integer and equal \(n=0, 1\) representing uniform and linear loading, respectively, \(\sigma _0 \) is the nominal stress and a is the crack depth. The \(r=R_i \) and \(r=R_i +a\) correspond to the internal surface of the pipe and the deepest point of the crack, respectively. Assuming the existence of plane strain condition at the deepest point of the semi-elliptical crack, the SIF formulation can be shown as

$$\begin{aligned} K_I =\sqrt{\frac{E J}{1-\nu ^{2}}} \end{aligned}$$
(2)

In Eq. (2), the mean of the values in J-integral is computed on any path surrounding the crack front at the deepest point The results of the analysis for the uniform and linear stress conditions are considered for curve fitting of reference loading to derive the WF.

3 Weight function estimation

The weight function method introduced by Bueckner [30] and Rice [31] for elastic crack analysis. The benefit of this method which is the universal features of the solution is that the weight function is independent of loading for a given cracked structure, and therefore, stresses calculated for the uncracked structure are used into an expression of Eq. (3) to obtain the SIF for the desire crack geometries and any other loads which have the same degree of symmetry

$$\begin{aligned} K=\int _{0}^{ a} {\sigma (r)} m(r,a) \mathrm{d}r \end{aligned}$$
(3)

where \(\sigma (r)\) is the normal stress field to the prospective crack face in an uncracked structure and uniform in the longitudinal direction and m(r, a) is the weight function of the crack which has been proved [31] to be only dependent on geometry and independent of loading system approximated as follows

$$\begin{aligned} m(r,a)=\frac{H}{K_\mathrm{ref}} \frac{\partial u (r,a)}{\partial r} \end{aligned}$$
(4)

where H, a and r are material constant, the crack length and the axis along the crack depth, respectively. \(K_\mathrm{ref}\) is a reference SIF obtained from a single loading case, and u(r, a) is the COD (crack opening displacement) field relevant to the reference stress field. An effective relation to approximate the reference crack opening displacement u(r, a) is hardly available especially for surface cracks in the literature, although different reference SIF solutions have been reported in the literature. Therefore, to deal with this problem, Petroski and Achenbach [32] suggested a general approximate COD, which has been shown by many authors that the accuracy of the derived weight function depends on the kind of the reference loading. In the paper by Shen and Glinka [33], a method to derive the weight function from two reference SIFs was proposed. Using the same approach, Nabavi and Azad [34] provided the form of the weight function for the deepest point of semi-elliptical cracks containing four terms as follows

$$\begin{aligned} m(r,a)=\sqrt{\frac{2}{\pi }}\sqrt{\frac{1}{R_i +a-r}}+M_1 +M_2 \sqrt{R_i +a-r}+M_3 (R_i +a-r) \end{aligned}$$
(5)

where the crack tip is at \(r=R_i +a\) and the parameters \(M_i \) rely on the geometry and crack sizes. The exactness of the three parameters \(M_i \) strongly linked the reference SIF used. The above relation includes three undefined parameters \(M_i \). One unknown in Eq. (5) can be eliminated invoking boundary conditions as the second derivative of the weight function is vanished at the crack edge. The extra condition is based on the fact that the curvature of crack contour disappears at the edge [35]. The others can be calculated from uniform \((n=0)\) and linear \((n=1)\) reference stress distributions obtained from the FEA as in Eq. (1), respectively. The SIFs for the two reference loads are predicted as

$$\begin{aligned} K_\mathrm{ref, uni}= & {} \sigma _0 Y_0 \sqrt{\pi a/Q} \end{aligned}$$
(6a)
$$\begin{aligned} K_\mathrm{ref, lin}= & {} \sigma _0 Y_1 \sqrt{\pi a/Q} \end{aligned}$$
(6b)

where \(Y_0 \) and \(Y_1 \) are geometric correction factors and Q is commonly approximated by the following empirical equation [36]

$$\begin{aligned} Q=1+1.464 ({a/c})^{1.65} \quad 0\le a/c\le 1 \end{aligned}$$
(7)
Table 1 Coefficient \(A_{kij} \) in the boundary correction factor for reference loads
Full size table

Substituting Eqs. (6) and (7) together into Eq. (3), the constants \(M_i \) in Eq. (5) can be found as

$$\begin{aligned} M_1= & {} 2\sqrt{\frac{\pi }{Q a}}\left( {Y_0 -3Y_1} \right) +\frac{24}{5}\sqrt{\frac{2}{\pi a}} \end{aligned}$$
(8a)
$$\begin{aligned} M_2= & {} 3\sqrt{\frac{2}{\pi }}\frac{1}{a} \end{aligned}$$
(8b)
$$\begin{aligned} M_3= & {} 6\sqrt{\frac{\pi }{Q a^{3}}}\left( {2Y_1 -Y_0} \right) -\frac{8}{5 a}\sqrt{\frac{2}{\pi a}} \end{aligned}$$
(8c)

The special curve fitting to suitable functions for each case of the crack geometric parameters, i.e., the aspect ratio and the relative depth, for both uniform and linear loading, is with the following closed-form expressions

$$\begin{aligned} Y_k =\sum _{i=1}^4 {\sum _{j=1}^6 {A_{kij} (a/t)^{i-1}(a/c)^{j-1}}},\qquad k=0, 1 \end{aligned}$$
(9)

where the parameters \(A_{kij} \) demonstrated in Table 1 for uniform loading \((k=0)\) and linear loading \((k=1)\), respectively. The geometric correction factors \(Y_k \) were fitted to the finite element results with average accuracy better than 1 % within the range, \(0\le a/c\le 1\) and \(0.2\le a/t\le 0.8\).

4 Determination of analytical formulation for the SIF

Substitution of Eqs. (8) and (9) into (5) gives the weight function for surface crack in a pipe with radii ratio of \(R_0/R_i =1.1\). Then, incorporating the integral of Eq. (3) together with Eq. (5) results a general form of solution for prediction of SIFs at the deepest point of a circumferential semi-elliptical crack under arbitrary loading. As a general example, consider a power-law crack face pressure with the following as in Eq. (1).

After substitution of expressions (5) and (1) together into the integral of Eq. (3), the closed-form SIF is derived as

$$\begin{aligned} K(a)= \sqrt{\frac{2 a}{\pi }} \sigma _0 \left( {B(n+1,\frac{1}{2})+\frac{1}{n+1} M_1 +\frac{\sqrt{\pi }}{2} \frac{\Gamma (n+1)}{\Gamma (n+\frac{5}{2})}M_2 +\frac{1}{n^{2}+3n+2}M_3} \right) \end{aligned}$$
(10)

where \(\Gamma \) and B are the Gamma and the Beta functions, respectively [37]. In special cases, the SIFs for uniform stress distribution on crack face (\(n=0\) in Eq. 1) are obtained as

$$\begin{aligned} K_\mathrm{uniform} (a)= \sqrt{\frac{a}{2 \pi }} \sigma _0 \left( {4+2 M_1 +\frac{4}{3}M_2 +M_3} \right) \end{aligned}$$
(11)

In addition, the SIF for linear increasing stress distribution on crack face (\(n=1\) in Eq. 1) can derive as

$$\begin{aligned} K_\mathrm{linear} (a)= \sqrt{\frac{2 a}{\pi }} \sigma _0 \left( {\frac{4}{3}+\frac{1}{2} M_1 +\frac{4}{15}M_2 +\frac{1}{6}M_3} \right) \end{aligned}$$
(12)

The SIFs for uniform and linear increasing stress field were utilized as the reference solutions. As a result, right sides of Eqs. (11) and (12) should be of the same value as correction factors \(Y_0 \) and \(Y_1 \), respectively. It should be mentioned that Eq. (10) is the only function of geometrical parameters so makes it possible to derive an expression for the SIF for any type of welding residual stress fields or thermal stresses, even though those of highly nonlinear with large number of peaks and valleys as will be discussed later. To evaluate SIFs in API 579 [14] standard code, at first, the stress over the wall thickness should be fitted by a fourth-order polynomial, and then SIFs can be calculated using the influence coefficient method. These coefficients are provided in some tables in API 579 [14]. The formulation will also allow to determine SIFs for five individual stress fields (uniform, linear, quadratic, cubic and fourth-order) normal to the crack face. However, application of this method has one problem associated with the order of fitted polynomial. It should be noted that this method will provide a conservative solution, especially for steep gradients through the wall thickness such as residual or thermal stresses. The complicated stress distributions cannot be expressed with adequate accuracy as fourth-order polynomial equations. In contrast, the unique feature of the weight function method is that once the weight function has been determined, the stress intensity factor for any loading system applied to that body can be calculated.

The limitations of this work must be noted. It has been assumed that the thermo-mechanical properties do not change during the analysis. This is an approximation, which will have to be taken account of in all cases. Because the analytical solution is generated based on the knowledge of reference load cases, only the correction factors should be redeveloped for other geometric dimension.

5 Verification and discussion

A series of computations have been carried out to recognize the precision of the derived WF expressions. At first, Eq. (10) in conjunction with Eq. (1) for a cylinder with inner radius-to-thickness ratio of \(R_i /t=10\) is used to calculate the dimensionless SIF \((K_\mathrm{N} =K_I /\sigma _0 \sqrt{\pi a/Q})\) at the deepest point of cracks with aspect ratios \(a/c=0.25, 0.5,1.0\) and relative depths of \(a/t=0.2-0.8\) subject to uniform loading \((n=0)\) perpendicular to the crack face. Both results of the closed-form expressions and a similar crack determined using appendix C of the standard API 579 [14], Bergman [8], Wallbrink [6] and Laham [38] are shown in Table 2. Moreover, another comparison has done for a same crack of aspect ratio \(a/c=0.66\) and relative depths of \(a/t=0.2-0.8\) subject to uniform loading \((n=0)\) in a similar pipe as before against experimental results [4], the line-spring model [9] and Zahoor [7], which depicted in Table 3. Both of the comparisons prove that the present results are in good accordance with those mentioned in the literature and indicate that the WF solution for the SIF (Eq. 10) approximation can predict the SIF at the deepest point of a semi-elliptical circumferential crack with maximum upper-limit difference of 2.5 % against experimental results and 4.6 and 3.5 % against standard API 579 [14] and Laham [38], respectively. Furthermore, Table 3 indicates the nearness and high accuracy of the present model in correlation with the experimental solution rather than the line-spring model and closed-form expression while implies that the present results, which supply closer SIFs to the experimental results than the line-spring model, are generally better to be used in fatigue and fracture design. For better clarification of the extracted solutions, dimensionless SIFs at the deepest point of a surface internal crack subject to linear loading \((n=1)\) of aspect ratio \(a/c=0.25, 0.5\) and 1, respectively, and various relative depths of \(a/t=0.2-0.8\) in a cylinder of inner radius-to-thickness ratio of \(R_i /t=10\) are assessed and examined to the same results by standard API 579 [14], Bergman [8], El Hakimi [10] and Laham [38] in Table 4. These comparison reveals the fact that the highest upper-limit discrepancy between the presented results and Laham’s and Bergman’s is 5.5 % for all the crack geometries under linear loading. To insist the accuracy of the presented method, the dimensionless SIFs at the deepest point of the crack of ellipticity \(a/c=0.0625\) and 1 and the relative depth varying from 0.2 to 0.8 subject to parabolic and cubic loading (\(n=2\) and \(n=3\), respectively) perpendicular to the crack face are examined against the same results presented by Laham [38], standard API 579 [14] and Bergman [8]. The SIFs for different crack geometries are shown in Table 5 and 6. In these tables, the obtained results agree well with existing solutions announcing an excellent agreement in between for both parabolic and cubic loading.

Table 2 Comparison of normalized SIF for the crack under uniform loading
Full size table
Table 3 Comparison of dimensionless SIF for the crack with aspect ratio \(a/c=0.66\) under uniform loading
Full size table
Table 4 Comparison of dimensionless SIF for the crack under linear loading
Full size table
Table 5 Comparison of dimensionless SIF for the crack under parabolic loading
Full size table
Table 6 Comparison of dimensionless SIF for the crack under cubic loading
Full size table
Table 7 Comparison of dimensionless SIF for complete circumferential crack under uniform loading
Full size table
Table 8 Comparison of dimensionless SIF for complete circumferential crack under linear, parabolic and cubic loading
Full size table

To show the universality of the model, more evidence is required to supply enough confidence in the SIF calculation procedure. Hence, for a case of complete circumferential crack prevailing at the inner wall of a pipe of inner radius-to-thickness ratio \((R_i /t=10)\) subject to four types of loading, i.e., \(n=0 ,1, 2, 3,\) respectively, normal to the crack face, the dimensionless SIF is calculated for different relative depths of \(a/t=0.2-0.8\) using Eq. (10) and compared to the similar results by API 579 [14], Nabavi and Ghajar [26], Zahoor [7] and Varfolomeyev et al. [25]. Comparisons are shown in Tables 7 and 8. It can be observed from the mentioned tables that the presented methodology and its implementation to the prediction of the SIF for a case of complete crack is acceptable and reliable with the maximum error of 0.1, 0.9 and 1.33 % for linear, parabolic and cubic loading, respectively, in comparison with the same results as in standard API 579.

6 Estimation of the influence of welding residual stresses on the SIF

Welding is one of the most extensively used methods in fabrication industry. As a useful method of joining pipes, the welding process may introduce a complex set of residual stresses in the structure which occur near the weld bead and subsequent rapid cooling results in a great deal of attention to the measurement of them in the vicinity of welded joints. Among all of factors such as residual stress, stress concentration, mechanical properties and the microstructure of the material that influence the strength of welded joints, it has been proved that residual stress has much greater effect on fatigue and stress corrosion cracking than the other factors [39, 40]. Different experimental and numerical models have been developed to investigate the residual stress distribution [41]. These residual stresses may promote brittle fractures, fatigue or stress corrosion cracking, and thus, for structural integrity assessment of such pipe, characterizing residual stresses distribution and incorporating them into fracture assessment procedure using theories of linear elastic fracture mechanics has been shown to be a priori. Additionally, when the stress distribution is highly nonlinear and has multiple peaks and valleys as in welding residual stress distribution, it is difficult to find the SIF straightforwardly. Quite no attempts have been made to find out a generalized method to estimate the SIF at the deepest point of a circumferential crack located at the inner wall of pipes under such complicated stress. Consequently, three different residual stress distributions are considered herein, and for each of them, SIFs have been derived for a cylinder cracked circumferentially using Eq. (10) proposed in previous sections. For this purpose, at first the residual stress distribution has been found using an nth-order polynomial curve fitting through the thickness to discrete data points with the profile shown in Fig. 4a which is achieved providing numerical welding residual stress analysis [18]. The fitted profile in comparison with the same results available in [18] is shown in Fig. 4a.

Fig. 4
figure 4

Normalized welding residual stress profiles for a determined from finite element analysis [18] b T-C and T-C-T [15]

Full size image
Table 9 Comparison of stress intensity factors under welding residual stress for aspect ratio \(a/c=1/3\) versus relative depth
Full size table

Furthermore, same process has incorporated for two other different residual stress distributions available in [15]. Figure 4b shows the fitted profiles to these stress distribution. The first one is tension-compression (T-C) type which is sometimes called the bending type, and the other is tension-compression-tension type (T-C-T) which is highly common in piping weld. The proposed method in this article is capable of determining the SIFs at the deepest point of both internal fully and semi-elliptical circumferential cracks under arbitrary loading situation. Thus, using fitted profiles of Fig. 4 in conjunction with Eq. (10), the SIF for different crack geometries under three mentioned welding residual stress can be estimated.

Table 9 illustrates comparison of the SIF under residual stress profile of Fig. 4a for semi-elliptical circumferential internal crack with aspect ratio of \(a/c=1/3\) and different relative depths calculated using Eq. (10), standard API 579 [14], ASME BPVC (Boiler & Pressure Vessels Code) Sec. IX. [42] and numerical results [18]. From this comparison, it follows that estimation of WF expression and finite element data and API 579 [14] are in good agreement while showing a deviation between the present result and those from the standard ASME [42] which is due to the high level of conservatism of mentioned standard.

To cover a wide range of crack geometry, Fig. 5a, b shows calculated SIFs for crack of aspect ratios \(a/c=0.1, 0.5\) and 1 in comparison with the same results of [15] for bending type stress distribution and tension-compression-tension one, respectively. These comparisons again show a reasonable accordance between the results of the proposed method and available solutions in [15]. To show the capability of the suggested method to predict the SIFs for complete circumferential cracks, another comparison is performed for a case of crack in a pipe of inner radius-to-thickness ratio of \(R_i/t=10\) under both tension-compression and tension-compression-tension residual stress fields extracted from [15]. The results of comparisons for both of mentioned stress distributions are shown in Fig 6. This figure illustrates that for both tension-compression and tension-compression-tension stress profiles, the prediction of SIF using Eq. (10) is in good correlation with the same results as in [15].

Fig. 5
figure 5

Comparison of SIFs under welding residual stress profiles determined herein and a T-C and b T-C-T [15] versus relative depth

Full size image
Fig. 6
figure 6

Comparison of SIFs under welding residual stress profiles for complete circumferential crack versus relative depth

Full size image

7 Conclusion

In the present work, a generalized theoretical solution developed for the SIFs of circumferential cracks originated from the internal surface of cylindrical vessel of inner radius-to-thickness ratio of \(R_i /t=10\) under arbitrary residual stress fields caused by welding. Three-dimensional FEA for a cracked pipe under uniform and linear increasing load has been performed employing singular elements to display the stress singularity at the crack front. Assuming the numerical results as the reference loads, a four-term weight function developed for circumferential cracks with the aspect ratio ranges between \(a/c=0\) to \(a/c=1\) and the relative depth of \(a/t=0.2-0.8\). Using the derived weight function, a closed-form relation has been proposed as a function of crack size and loading condition. The presented relation is capable of determining the SIFs at the deepest point of semi-elliptical and fully circumferential cracks under an axisymmetric stress distribution. Then, SIFs of circumferentially cracked pipes under three different residual stress distributions have obtained using the theoretical relation (Eq. 10) in conjunction with an nth-order polynomial curve fitting through the thickness to them. Comparison of the calculated SIFs from the present method and available solutions in the literature proves the high level of efficiency and precision of the derived solution.