A hybrid method for stochastic response analysis of a vibrating structure

Abstract

Response analysis of a linear structure with uncertainties in both structural parameters and external excitation is considered here. When such an analysis is carried out using the spectral stochastic finite element method (SSFEM), often the computational cost tends to be prohibitive due to the rapid growth of the number of spectral bases with the number of random variables and the order of expansion. For instance, if the excitation contains a random frequency, or if it is a general random process, then a good approximation of these excitations using polynomial chaos expansion (PCE) involves a large number of terms, which leads to very high cost. To address this issue of high computational cost, a hybrid method is proposed in this work. In this method, first the random eigenvalue problem is solved using the weak formulation of SSFEM, which involves solving a system of deterministic nonlinear algebraic equations to estimate the PCE coefficients of the random eigenvalues and eigenvectors. Then the response is estimated using a Monte Carlo (MC) simulation, where the modal bases are sampled from the PCE of the random eigenvectors estimated in the previous step, followed by a numerical time integration. It is observed through numerical studies that this proposed method successfully reduces the computational burden compared with either a pure SSFEM of a pure MC simulation and more accurate than a perturbation method. The computational gain improves as the problem size in terms of degrees of freedom grows. It also improves as the timespan of interest reduces.

1 Introduction

Consider a linearly vibrating system with $n$ degrees of freedom (DOF) with the mass, damping, and stiffness matrices denoted as $\mathbf{M}(\theta ), \mathbf{C}(\theta ), \mathbf{K}(\theta ) \in {\mathbb {R}} ^{(n\times n)}$, respectively, subjected to an external excitation ${\mathbf{f}}(t,\theta ) \in {\mathbb {R}} ^n$. Here $t$ denotes time and $\theta$ denotes an event in the probability space $(\varOmega ,{\mathcal {F}},\mu )$ used for describing the underlying uncertainty. The governing differential equation for this uncertain system subjected to stochastic loading is written as

$$\begin{aligned} \mathbf{M}(\theta )\ddot{\mathbf{u}}(t,\theta ) +\mathbf{C}(\theta )\dot{\mathbf{u}}(t,\theta )+\mathbf{K}(\theta ){\mathbf{u}}(t,\theta )={\mathbf{f}}(t, \theta ) \ a.s. \ , \end{aligned}$$

(1)

where ${\mathbf{u}}(t,\theta ) \in {\mathbb {R}}^n$ denotes the response, the dots denote derivatives with respect to time, and $a.s.$ denotes the almost sure statement. For low-frequency vibration, the modal approach is very effective in reducing the computational cost in solving this system of coupled ordinary differential equations (ODEs). Accordingly, let $k_s$ normal modes, denoted by the matrix $\varPhi (\theta ) \in {\mathbb {R}} ^{(n\times k_s)}$, be used to project the physical response as ${\mathbf{u}}(t,\theta )=\varPhi (\theta ) {\mathbf{z}}(t,\theta )$, where ${\mathbf{z}}(t,\theta ) \in {\mathbb {R}} ^{k_s}$ denotes the response in the modal coordinate. Substitution of this equation in Eq. (1) and a premultiplication by $\varPhi ^T(\theta )$ lead to

$$\begin{aligned}&\varPhi ^T(\theta )\mathbf{M}(\theta ) \varPhi (\theta ) \ddot{{\mathbf{z}}}(t,\theta ) + \varPhi ^T(\theta )\mathbf{C}(\theta ) \varPhi (\theta ) \dot{{\mathbf{z}}}(t,\theta )+ \varPhi ^T(\theta )\mathbf{K}(\theta ) \varPhi (\theta ) {\mathbf{z}}(t,\theta )\nonumber \\&\quad = \varPhi ^T(\theta ) {\mathbf{f}}(t,\theta ) \ a.s. \end{aligned}$$

(2)

Let the uncertainties in the system parameters—that is, in the coefficient matrices $\mathbf{M}(\theta ), \mathbf{C}(\theta ), \mathbf{K}(\theta )$—be modeled by a set of $q_s$ number of independent random variables $\{ \xi _i(\theta )\}_{i=1}^{i=q_s}$, and the uncertainties in the forcing function be modeled by another set of $q_f$ number of independent random variables $\{ \xi _i(\theta )\}_{i=q_s+1}^{i=q_s+q_f}$. The variables $\{ \xi _i(\theta )\}_{i=1}^{i=q_s}$ arise from (i) scalar- and vector-valued random parameters such as spring stiffness and lumped masses and (ii) Karhunen–Loève (KL) or similar discretization [1] of random field models of heterogeneous properties such as Young’s modulus, mass density. Similarly, the variables $\{ \xi _i(\theta )\}_{i=q_s+1}^{i=q_s+q_f}$ also arise from (i) scalar- or vector-valued random parameters such as frequency or phase of a harmonic loading and (ii) discretization of random process loading such as wind or earthquake loading, road unevenness, machine-induced dynamic loading. Let $\varvec{\xi }_s, \varvec{\xi }_f$ and $\varvec{\xi }$ denote the random vectors containing the elements $\{ \xi _i(\theta )\}_{i=1}^{i=q_s}, \{ \xi _i(\theta )\}_{i=q_s+1}^{i=q_s+q_f}$ and $\{ \xi _i(\theta )\}_{i=1}^{i=q_s+q_f}$, respectively. Then Eq. (2) can be written as

$$\begin{aligned}&\varPhi ^T(\varvec{\xi }_s)\mathbf{M}(\varvec{\xi }_s) \varPhi (\varvec{\xi }_s) \ddot{{\mathbf{z}}}(t,\varvec{\xi }) + \varPhi ^T(\varvec{\xi }_s)\mathbf{C}(\varvec{\xi }_s) \varPhi (\varvec{\xi }_s) \dot{{\mathbf{z}}}(t,\varvec{\xi })+ \varPhi ^T(\varvec{\xi }_s)\mathbf{K}(\varvec{\xi }_s) \varPhi (\theta ) {\mathbf{z}}(t,\varvec{\xi })\nonumber \\&\quad = \varPhi ^T(\varvec{\xi }_s) {\mathbf{f}}(t,\varvec{\xi }_f) \ a.s. \end{aligned}$$

(3)

Equation (3) can be solved using several methods such as Monte Carlo (MC) simulation [2], perturbation [3–5], polynomial approximations [6, 7], variability response functions [8, 9] and spectral stochastic finite element method (SSFEM) [10]. Generally, the MC-based methods give most accurate results, but are very expensive due to the requirement of a large number of repeated analyses. On the other hand, the perturbation methods save computational time, but are accurate only for a low level of variability, and often the expressions become very complicated. The classical random vibration methods consider deterministic systems subjected to stochastic loading [11], where a few statistical moments and the probability density function (pdf) of response are estimated by solving deterministic differential equations such as Fokker Planck equation [12]. Efficient numerical solution of this equation, especially for large systems, has received considerable attention [13–16], including parallel implementation for large-scale systems [17]. Extension of these random vibration methods to stochastic systems has received relatively limited attention [18–20] due to additional computational cost and mathematical complexity. A few other approaches are reliability methods [21, 22]—including better simulation tools such as subset simulation [23], proper generalized decomposition [24], and reduced basis [25]. A review on response analysis of stochastic structures can be found in [26] and on reliability calculations in [27]. In [10], a SSFEM-based method was developed for solving Eq. (3) where both the random eigenvalue problem to estimate $\varPhi (\varvec{\xi }_s)$ and the response analysis to estimate ${\mathbf{u}}(t,\varvec{\xi })$ were solved using a Bubnov-Galerkin projection. Accordingly, the random eigenvalues and eigenvectors were first expressed in polynomial chaos expansion (PCE), and the chaos coefficients were estimated by solving a system of deterministic nonlinear algebraic equations resulting from projecting the residual of the eigenvalue problem to the chaos bases. Then these PCE of the eigenvectors along with PCE of the response (with unknown coefficients) were substituted in Eq. (3), followed by another projection on the chaos bases. This projection led to a coupled system of ODEs, which was solved by a numerical integration to find the chaos coefficient of the response. It was successfully demonstrated for a vibrating plate example where the elastic modulus was modeled as a random field. The excitation had a deterministic component and a stochastic harmonic component with random amplitude and deterministic frequency. For this problem, the solution obtained using this method had higher accuracy than perturbation method and were comparable to estimates from MC simulation, whereas the cost of computation was considerably lower than the MC simulation. However, when the excitation has a random frequency, or for even more general random process excitations, this method suffers from very high computational cost, often prohibitive. For instance, consider the excitation is of the form

$$\begin{aligned} {\mathbf{f}}(t,{\varvec{\xi }_f})=\bar{{\mathbf{f}}}(t)+ {\mathbf{f}}_r \sin ((\bar{\omega }_{f}+\sigma _{\omega } \xi _{q_s+1}) t) \ , \end{aligned}$$

(4)

that is, the frequency is random with the mean and standard deviation be denoted by $\bar{\omega }_{f}$ and $\sigma _{\omega }, \xi _{q_s+1}$ denotes a standard normal variable, $\bar{{\mathbf{f}}}(t)$ denotes a deterministic function and ${\mathbf{f}}_r$ denotes the deterministic amplitude of the random component of the excitation. For this excitation, the accuracy of the estimate of the response was found to drop rapidly as t grows. The reason for this loss of accuracy lies in the requirement of higher-order chaos polynomial bases as time progresses. Inclusion of large number chaos bases results in significant increase in computational cost and thereby eliminates the computational advantage of the method. Similarly, when the excitation is of a more general random process of practical relevance, approximation of such excitation leads to a large dimensionality of the vector $\varvec{\xi }_f$, where $q_f$ could be in the order of tens [28, 29] or even hundred [2]. For both of these excitations, (random frequency and random process), the SSFEM suffers from the curse of dimensionality. To explain it, let q denote the number of random variables—often referred to as the basic random variables, and d denote the order of chaos expansion. Then the number of terms in PCE, denoted here as P, grows as

$$\begin{aligned} P=\frac{(q+d)!}{q!d!}, \end{aligned}$$

(5)

which is a very rapid growth. For the case of random frequency, d is high, and for general random processes, q is high.

The goal of the present paper is to propose a hybrid method to avoid this curse of dimensionality. The basic idea is as follows. Often, for a reasonable model of the uncertainties in stiffness and mass properties, the $q_s$ is low (say, about ten or less). If the random eigenvalue problem is solved using SSFEM to find the statistical nature of the natural frequencies and mode shapes, choice of $d$ as low as 2–4 yields a very good estimate, and the associated computational cost is much lower than an MC simulation [10, 30]. On the other hand, both the aforementioned excitations (random frequency and general random process) result in a large P, which is the main contributor for the prohibitive computational cost. For the random frequency loading, a large d is needed as t grows [10], whereas for the random process loading, the $q_f$ is high—can be few hundreds or even thousands, leading to the $q=q_s+q_f$ to be high. Therefore, in both the cases, Eq. (5) suggests that $P$ would be very high. However, the dimension independence property of MC can be useful in this case. Accordingly, in MC, the number of realizations for a desired level of accuracy does not depend upon the number of random variables [31]. Therefore, to take the advantage of both SSFEM and MC simulation, a hybrid method is proposed, where (i) the random eigenvalue problem is solved using SSFEM involving only $\varvec{\xi }_s$ to find the PCE of $\varPhi (\varvec{\xi }_s)$, and then (ii) the system of stochastic ODEs presented in Eq. (3) is solved using MC simulation involving the entire vector $\varvec{\xi }$.

The random eigenvalue problem has been solved using various approaches such as perturbation [4, 9, 32–34], MC simulation [35], SSFEM [30, 36–38], analytical (for very limited cases) [39], and dimensional decomposition [40]. In [30], a SSFEM characterization and solution of this problem were proposed, where the random eigenvalues and eigenvectors were expressed in PCE and the coefficients were found using a Galerkin projection. The computational speedup thus gained will be exploited here. For non-Gaussian basic random variables, a suitable basis following the Wiener–Askey scheme [41, 42] can be used. Once the PC coefficients are available for eigenpairs, for each MC simulation run, a selective number of eigenmodes can be inexpensively calculated using the PCE, which would further be used for response analysis.

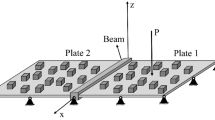
In the present paper, forced vibration of a rectangular plate is considered as a representative problem. The plate is assumed to be simply supported at four edges. In continuation to earlier investigation [10], two different load cases are considered. In the first study, an out-of-plane harmonic force with randomly varying frequency as given in Eq. (4) is applied to the central node of the plate. In the second case, a stationary Gaussian process input is considered as base excitation. Simulation of this process is performed using spectral representation of the random field [43], discussed later in detail. The model size is reduced using a simple modal truncation. The Newmark-$\beta$ time integration scheme is used for estimating response history. It is important to note that the procedure of response history analysis is not restricted to the methods used in these studies. Any suitable deterministic or stochastic scheme for size reduction and time integration [44, 45] can instead be used, if needed.

This paper is organized as follows. In the next section, the theoretical background for response prediction using the proposed hybrid method and associated issues are discussed. The difference between this method and pure SSFEM is highlighted next. Then a perturbation approach to solve the same vibration problem is discussed. A detailed numerical study is presented next. A comparison of hybrid, MC, and perturbation methods based on efficiency and other statistics extracted from the response is presented in this context. Concluding remarks and future challenges are discussed at the end.

2 Proposed hybrid method for response prediction

As mentioned in the previous section, the proposed response prediction method has two components: solving the random eigenvalue problem using SSFEM and finding the statistics of the response by sampling. These two components are described next.

2.1 The random eigenvalue problem and its solution using SSFEM

For a linear system with proportional damping and known real, symmetric, and positive definite stiffness and mass matrices $\mathbf{K}(\varvec{\xi }_s)$ and $\mathbf{M}(\varvec{\xi }_s)$, the generalized random eigenvalue problem corresponding to dynamic modes can be written as

$$\begin{aligned}&\displaystyle \mathbf{K}(\varvec{\xi }_s){\varvec{\phi }}(\varvec{\xi }_s) = {\lambda (\varvec{\xi }_s)} \mathbf{M}(\varvec{\xi }_s) {{\varvec{\phi }}(\varvec{\xi }_s)} \ a.s.;\end{aligned}$$

(6)

$$\begin{aligned}&\displaystyle \hbox {with the normalization condition} \quad {\varvec{\phi }}(\varvec{\xi }_s)^T \mathbf{M}(\varvec{\xi }_s) {\varvec{\phi }}(\varvec{\xi }_s) =1 \ a.s., \nonumber \\&\displaystyle \hbox {where} \quad \lambda (\varvec{\xi }_s)\in {\mathbb {R}}, \quad {\varvec{\phi }}(\varvec{\xi }_s)\in {{\mathbb {R}} }^n, \quad \mathbf{K}(\varvec{\xi }_s), \mathbf{M}(\varvec{\xi }_s) \in {{\mathbb {R}} }^{n\times n}. \end{aligned}$$

(7)

Here the eigenvalues $\lambda (\varvec{\xi }_s)$ and eigenvectors ${\varvec{\phi }}(\varvec{\xi }_s)$ are random in nature. In an MC simulation, these can be estimated by sampling from $\varvec{\xi }_s$, then solving a deterministic eigenvalue problem for each realization, and finally postprocessing these realizations. Here this problem is solved using SSFEM. Let ${\mathbb {E}}\{\cdot \}$ denote the mathematical expectation operator. Then the $l$-th eigenvalue and eigenvector can be represented in PCE as

$$\begin{aligned} \lambda _l(\varvec{\xi }_s) = \sum _{i=0}^{\infty } \psi _i(\varvec{\xi }_s) \lambda _l^{(i)}, \qquad {\varvec{\phi }}_l(\varvec{\xi }_s) = \sum _{i=0}^{\infty } \psi _i(\varvec{\xi }_s) {\varvec{\phi }}_l^{(i)}; \quad \lambda _l^{(i)}\in {{\mathbb {R}} }\ , \ \ {\varvec{\phi }}_l^{(i)}\in {{\mathbb {R}} }^n. \end{aligned}$$

(8)

where $\psi _{i}(\varvec{\xi }_s)$ are random polynomials of $\varvec{\xi }_s$—referred to as chaos bases or chaos polynomials—forming a set of basis in a Hilbert space, with properties

$$\begin{aligned}&\displaystyle \psi _{0}\equiv 1 , \quad {\mathbb {E}}\{\psi _{i}(\varvec{\xi }_s)\}=0 \hbox { for } i>0 ,\end{aligned}$$

(9)

$$\begin{aligned}&\displaystyle {\mathbb {E}}\{\psi _{i}(\varvec{\xi }_s)\psi _{j}(\varvec{\xi }_s)\}=\delta _{ij}{\mathbb {E}}\{\psi _{i}^2(\varvec{\xi }_s)\}. \end{aligned}$$

(10)

Square-integrability of the elements in the matrices $\mathbf{K}(\varvec{\xi }_s)$ and $\mathbf{M}(\varvec{\xi }_s)$ allows this representation [30]. When $\varvec{\xi }_s$ is a vector of standard normal variables, then the polynomials are Hermite. The series is truncated for computational purpose as

$$\begin{aligned} \hat{\lambda }_l(\varvec{\xi }_s) = \sum _{i=0}^{P-1} \psi _i(\varvec{\xi }_s) \lambda _l^{(i)}, \quad \hat{{\varvec{\phi }}}_l(\varvec{\xi }_s) = \sum _{i=0}^{P-1} \psi _i(\varvec{\xi }_s) {\varvec{\phi }}_l^{(i)};\quad \lambda _l^{(i)}\in {{\mathbb {R}} }, \quad {\varvec{\phi }}_l^{(i)}\in {{\mathbb {R}} }^n. \end{aligned}$$

(11)

The integer P can be found using Eq. (5). The deterministic chaos coefficients $\lambda _l^{(i)}$ and ${\varvec{\phi }}_l^{(i)}$ are now need to be estimated. This estimation can be done by two ways—either by a strong formulation that invokes a statistical sampling and thus expensive [36] or by a weak formulation that is computationally faster. This weak formulation, that was proposed in [30] and was used for response prediction in [10], will be used here. Accordingly, first the mass and stiffness matrices are written as

$$\begin{aligned} \mathbf{K}(\varvec{\xi }_s) = \sum _{i=0}^{L_1-1} \psi _i(\varvec{\xi }_s) \mathbf{K}^{(i)}, \quad \mathbf{M}(\varvec{\xi }_s) = \sum _{i=0}^{L_2-1} \psi _i(\varvec{\xi }_s) \mathbf{M}^{(i)}; \quad \mathbf{K}^{(i)}, \mathbf{M}^{(i)} \in {{\mathbb {R}}}^{n\times n}, \end{aligned}$$

(12)

where the deterministic coefficient matrices $\mathbf{K}^{(i)} \text {and } \mathbf{M}^{(i)}$ and the limits $L_1\text { and }L_2$ depend on the uncertainty of the system properties. Equations (11) and (12) are then substituted in the random eigenvalue problem (6) and the normalizing condition (7). Then a Bubnov–Galerkin projection of the residual of each of these two resulting equations is performed on the subspace spanned by the bases $\{\psi _m\}_{m=0}^{P-1}$. This step leads to,

$$\begin{aligned} \sum _{i=0}^{L_1-1} \sum _{j=0}^{P-1} {\mathbb {E}}\{\psi _i(\varvec{\xi }_s)\psi _j(\varvec{\xi }_s)\psi _m(\varvec{\xi }_s) \} \mathbf{K}^{(i)} {\varvec{\phi }}^{(j)}= & {} \sum _{i=0}^{P-1} \sum _{k=0}^{L_2-1} \sum _{j=0}^{P-1} {\mathbb {E}}\{\psi _i(\varvec{\xi }_s)\psi _j(\varvec{\xi }_s)\psi _k(\varvec{\xi }_s)\psi _m(\varvec{\xi }_s)\} \lambda ^{(i)} \mathbf{M}^{(k)} {\varvec{\phi }}^{(j)}, \nonumber \\&m = 0,\ldots , P-1. \end{aligned}$$

(13)

along with the constraints

$$\begin{aligned} \sum _{i=0}^{P-1} \sum _{k=0}^{L_2-1} \sum _{j=0}^{P-1} {\mathbb {E}}\{ \psi _i(\varvec{\xi }_s)\psi _j(\varvec{\xi }_s)\psi _k(\varvec{\xi }_s)\psi _m(\varvec{\xi }_s)\} {\varvec{\phi }}^{(i)T} \mathbf{M}^{(k)} {\varvec{\phi }}^{(j)} = \delta _{m0}, \quad \quad m=0,\ldots , P-1 . \end{aligned}$$

(14)

Here the subscript l is ignored for brevity. Equations (13) and (14) can be presented as a set of $(n+1)P$ number of deterministic nonlinear algebraic equations of the unknown set of coefficients $\{{\varvec{\phi }}^{(i)}\}_{i=0}^{i=P-1}$ and $\{\lambda ^{(i)}\}_{i=0}^{i=P-1}$ as

$$\begin{aligned} \mathbf{F}\left( {\varvec{\phi }}^{(0)},{\varvec{\phi }}^{(1)},\dots ,{\varvec{\phi }}^{(P-1)},\lambda ^{(0)},\lambda ^{(1)},\dots ,\lambda ^{(P-1)}\right) = \mathbf{0} \end{aligned}$$

(15)

Equation (15) can be solved using Newton–Raphson (NR) iterations, for which the implementation details can be found in [30]. However, for convenience, the expressions of the terms in the of Jacobian in Eq. (15) are given in the Appendix. Note that once the PC coefficients are known, for any realization of $\varvec{\xi }_s$, the corresponding realization of the eigenvalues and eigenvectors can be simulated with very little effort using Eq. (11).

2.2 Response prediction using sampling and modal reduction

After solving the random eigenvalue problem using SSFEM, a set of modes that primarily contribute to the response should be identified and combined. A number of schemes are available for modal truncation for deterministic harmonic excitation [46–49]. However, the combined effect of the randomness of the loading and structural parameters on the modal participation is not well understood. Some of the previous studies considered extension of the methods available for deterministic linear structures excited by deterministic harmonic loadings with some modification [50, 51]. In the present case, the structure as well as the loading is assumed to be stochastic. This makes the selection of modes even more difficult. The selection criteria used in the present implementation will be discussed in Sect. 5.2. However, this selection criteria is not a restriction on the proposed algorithm. Any other modal truncation, combination, and correction procedure can be used if required.

2.3 The proposed algorithm

The proposed hybrid method can be consolidated in an algorithmic form. First the coefficients of PCE mode shapes and frequencies are determined using SSFEM. Then within a statistical sampling loop, the mode shapes are reconstituted, and response history is obtained using a time-stepping integration scheme. Consider a $(n \times k_s)$ matrix $\varPhi _{k_s}$ whose columns are $k_s$ dominant modal vectors for the given response analysis problem. Then the hybrid method is summarized bellow in sequential steps.

• 1. Compute the KL expansion coefficients for mass, stiffness, and damping matrices.

• 2. Compute PCE coefficients by solving Eq. (15).

• 3. Generate realizations of $\varvec{\xi }$ (which includes $\varvec{\xi }_s$ and $\varvec{\xi }_f$) using a random number generator.

• 4. Statistical sampling loop: for each realizations of $\varvec{\xi }$

  • (a) Compute $\varPhi _{k_s}$ using Eqs. (11) with the help of PCE coefficients, only the value of $\varvec{\xi }_s$ is needed in this step.

  • (b) With the help of KL expansion coefficients, compute mass, stiffness and damping matrices, and their modal values for $k_s$ nodes. Once again, only the value of $\varvec{\xi }_s$ is needed in this step.

  • (c) Generate a realization of the excitation ${\mathbf{f}}(t,{\varvec{\xi }_f})$ for which only the value of $\varvec{\xi }_f$ is needed.

  • (d) For response analysis, solve the resulting deterministic system of $k_s$ ODEs by a time integrator such as Newmark-$\beta$ to obtain desired response quantities.

• 5. Find the desired statistics for postprocessing.

3 Difference with pure SSFEM-based response prediction

In the pure SSFEM, the PC expansion for the entire vector $\varvec{\xi }$ [10] is used. This means that the system properties such as mass, damping, and stiffness as well as the loading process are expanded using PCE, and then the error is projected on the PC bases. Thus, substituting Eq. (2) with Eqs. (8) and (12) and taking expectation after multiplying by $\psi _m$ as $m=1,\dots ,P-1$, the following expression emerges.

$$\begin{aligned}&\sum _{i=0}^{P-1} \sum _{j=0}^{L_2-1} \sum _{k=0}^{P-1} \sum _{l=0}^{P-1} {\mathbb {E}}\{\psi _i\psi _j\psi _k \psi _l \psi _m\} {\varPhi ^{(i)}}^T{ \mathbf M}^{(j)} \varPhi ^{(k)} \ddot{{\mathbf{z}}}^{(l)}(t)\nonumber \\&\qquad +\,\sum _{i=0}^{P-1} \sum _{j=0}^{L-1} \sum _{k=0}^{P-1} \sum _{l=0}^{P-1} {\mathbb {E}}\{\psi _i\psi _j\psi _k \psi _l \psi _m\} {\varPhi ^{(i)}}^T\mathbf{C}^{(j)} \varPhi ^{(k)}\dot{{\mathbf{z}}}^{(l)}(t) \nonumber \\&\qquad +\,\sum _{i=0}^{P-1} \sum _{j=0}^{L_1-1} \sum _{k=0}^{P-1} \sum _{l=0}^{P-1} {\mathbb {E}}\{\psi _i\psi _j\psi _k \psi _l \psi _m\} {\varPhi ^{(i)}}^T\mathbf{K}^{(j)} \varPhi ^{(k)} {\mathbf{z}}^{(l)}(t)\nonumber \\&\quad =\,\sum _{i=0}^{P-1} {\varPhi ^{(i)}}^T {\mathbb {E}}\{\psi _i\psi _m {\mathbf{f}}(t,{\varvec{\xi }})\}; \qquad m=0,1,\ldots ,P-1. \end{aligned}$$

(16)

Now the resulting system of P ODEs in Eq. (16) is solved for PCE coefficients, which can be done using a numerical integration. The statistical moments ${\mathbb {E}}\{\psi _i\psi _j\psi _k \psi _l \psi _m\}$ need to be estimated prior to this numerical integration.

While in the pure SSFEM, a system of P coupled ODE-s is solved only once, in the hybrid method, a system of $k_s$ coupled ODE-s is solved repeatedly in a statistical sampling loop. This is the major implementation difference between the two methods.

4 Response prediction using perturbation methods

In the field of structural variability, the perturbation method is a useful and well-established tool [52] and has even been used in the area of stochastic FEM [4]. In the present context, a first-order perturbation technique used for comparing the accuracy and efficiency of the hybrid method. The method can be described as follows. For any function $F({\varvec{\xi }}_s)$, the perturbation expansion about the mean of ${\varvec{\xi }}_s$ is expressed as

$$\begin{aligned} F({\varvec{\xi }}_s) = F\left( {\varvec{\xi }}_s^0\right) + \sum _{r=1}^{q_s} F^{,r}({\varvec{\xi }}_s)\varDelta \xi _r + \sum _{r=1}^{q_s}\sum _{m=1}^{q_s} F^{,mr}({\varvec{\xi }}_s)\varDelta \xi _r \varDelta \xi _m + \cdots \end{aligned}$$

(17)

Here ${\varvec{\xi }}^0_s = E\{{\varvec{\xi }}_s\}, \varDelta \xi _r = \xi _r - {\mathbb {E}}\{\xi _r\}$ and $F^{,r}({\varvec{\xi }}_s)$ is the partial derivative of $F({\varvec{\xi }}_s)$ with respect to the random variable $\xi _r$. On introducing the modal notations $\overline{\mathbf{M}}(\varvec{\xi }_s) = \varPhi ^T(\varvec{\xi }_s) \mathbf{M}(\varvec{\xi }_s) \varPhi (\varvec{\xi }_s), \overline{\mathbf{C}}(\varvec{\xi }_s) = \varPhi ^T(\varvec{\xi }_s) \mathbf{C}(\varvec{\xi }_s) \varPhi (\varvec{\xi }_s)$ and $\overline{\mathbf{K}}(\varvec{\xi }_s) = \varPhi ^T(\varvec{\xi }_s) \mathbf{K}(\varvec{\xi }_s) \varPhi (\varvec{\xi }_s)$, Eq. (3) can be rewritten as

$$\begin{aligned} \overline{\mathbf{M}}(\varvec{\xi }_s) \ddot{{\mathbf{z}}}(t,\varvec{\xi }_s,\varvec{\xi }_f) + \overline{\mathbf{C}}(\varvec{\xi }_s) \dot{{\mathbf{z}}}(t,\varvec{\xi }_s, \varvec{\xi }_f)+ \overline{\mathbf{K}}(\varvec{\xi }_s) {\mathbf{z}}(t,\varvec{\xi }_s,\varvec{\xi }_f) = \varPhi ^T(\theta ) {\mathbf{f}}(t,\varvec{\xi }_f) \ a.s.; \end{aligned}$$

(18)

Expanding $\varPhi , \overline{\mathbf{M}}(\varvec{\xi }_s), \overline{\mathbf{C}}(\varvec{\xi }_s)$ and $\overline{\mathbf{K}}(\varvec{\xi }_s)$ with respect to the mean of $\varvec{\xi }_s$ in Eq. (18), and comparing the zeroth and first-order terms in the expression, we get the following:

Zeroth-order terms: one equation

$$\begin{aligned} \overline{\mathbf{M}}\left( \varvec{\xi }^0_s\right) \ddot{{\mathbf{z}}}(t,\varvec{\xi }^0_s,\varvec{\xi }_f) + \overline{\mathbf{C}}\left( \varvec{\xi }^0_s\right) \dot{{\mathbf{z}}}(t,\varvec{\xi }^0_s, \varvec{\xi }_f) + \overline{\mathbf{K}}\left( \varvec{\xi }^0_s\right) {\mathbf{z}}(t,\varvec{\xi }^0_s,\varvec{\xi }_f) = \varPhi ^T\left( \varvec{\xi }^0_s\right) {\mathbf{f}}(t,\varvec{\xi }_f) \end{aligned}$$

(19)

First-order terms: $q_s$ number of equations

$$\begin{aligned}&\overline{\mathbf{M}}\left( \varvec{\xi }^0_s\right) \ddot{{\mathbf{z}}}^{,r}(t,\varvec{\xi }^0_s,\varvec{\xi }_f) + \overline{\mathbf{C}}\left( \varvec{\xi }^0_s\right) \dot{{\mathbf{z}}}^{,r}(t,\varvec{\xi }^0_s, \varvec{\xi }_f) + \overline{\mathbf{K}}\left( \varvec{\xi }^0_s\right) {\mathbf{z}}^{,r}(t,\varvec{\xi }^0_s,\varvec{\xi }_f) = \left( \varPhi ^{,r}\left( \varvec{\xi }^0_s\right) \right) ^T {\mathbf{f}}(t,\varvec{\xi }_f) \nonumber \\&\quad - \left[ \overline{\mathbf{M}}^{,r}\left( \varvec{\xi }^0_s\right) \ddot{{\mathbf{z}}}(t,\varvec{\xi }^0_s,\varvec{\xi }_f) + \overline{\mathbf{C}}^{,r}\left( \varvec{\xi }^0_s\right) \dot{{\mathbf{z}}}(t,\varvec{\xi }^0_s,\varvec{\xi }_f) + \overline{\mathbf{K}}^{,r}\left( \varvec{\xi }^0_s\right) {{\mathbf{z}}}(t,\varvec{\xi }^0_s,\varvec{\xi }_f) \right] \quad r=1,2,\dots ,q_s \end{aligned}$$

(20)

In Eq. (20), the first-order derivatives of the eigenvectors can be estimated using several methods [53, 54]. Here the algorithm described in [55] is used to this end. The terms $\overline{\mathbf{M}}^{,r}\left( \varvec{\xi }^0_s\right) , \overline{\mathbf{C}}^{,r}\left( \varvec{\xi }^0_s\right)$ and $\overline{\mathbf{K}}^{,r}\left( \varvec{\xi }^0_s\right)$ can be obtained from terms in KL expansion. Equations (19 and 20) have to be solved in a cascading manner. This means $\ddot{\mathbf{z}}(t,{\varvec{\xi }}_s), \dot{\mathbf{z}}(t,{\varvec{\xi }}_s)$ and ${\varvec{z}}(t,{\varvec{\xi }}_s)$ are obtained from solving Eq. (19) and used in Eq. (20). In turn we obtain $\ddot{\mathbf{z}}^{,r}(t,{\varvec{\xi }}_s), \dot{\varvec{z}}^{,r}(t,{\varvec{\xi }}_s)$ and ${\varvec{z}}^{,r}(t,{\varvec{\xi }}_s)$ by solving Eq. (20). As all the derivative terms are known at this stage, the eigenvectors and modal responses can be reconstituted for any realization of $\varvec{\xi }_s$ using Eqs. (21 and 22).

$$\begin{aligned} \varPhi (\varvec{\xi }_s)= & {} \varPhi \left( \varvec{\xi }^0_s\right) + \sum _{r=1}^{q_s} \varPhi ^{,r}(\varvec{\xi }_s)\varDelta \xi _r \end{aligned}$$

(21)

$$\begin{aligned} {\varvec{z}}(t,{\varvec{\xi }_s})= & {} {\varvec{z}}(t,{\varvec{\xi }^0_s}) + \sum _{r=1}^{q_s} {\varvec{z}}^{,r}(t,{\varvec{\xi }}_s)\varDelta \xi _r \end{aligned}$$

(22)

The response can then be obtained using mode superposition method given by ${\varvec{u}}(t,{\varvec{\xi }}_s) = \varPhi ({\varvec{\xi }}_s)\varvec{z}(t, {\varvec{\xi }}_s)$ for each realization of the force.

One notable feature is that the perturbation parameters are the variables in the random sub-vector $\varvec{\xi }_s$ and not the entire set of variables in $\varvec{\xi }$. Hence, Eqs. (19 and 20) are to be solved repeatedly inside a statistical sampling loop for each realization of ${\varvec{\xi }}_f$.

5 Numerical study

5.1 Description of the system

The proposed hybrid method is implemented on a forced vibration problem of a rectangular steel plate, simply supported at four edges, and subjected to random loading. Such vibration problems appear in a number of practical applications such as vibration of the floor panels in machine rooms, vibration of panel components of the hull of ships or aircrafts, secondary structures on satellites or printed circuit boards (PCB) in electronic packaging industry. The plate is discretized using four-noded sixteen-DOF bicubic rectangular elements [56]. The Young’s modulus of the material, $E(\varvec{x},\varvec{\xi }_s)$, is assumed to be a random Gaussian field specified by the covariance function

$$\begin{aligned} C_{EE}((x_1,y_1),(x_2,y_2)) = \sigma _E^2 \ \hbox {exp}\left[ \frac{-|x_2-x_1|}{l_x}+\frac{-|y_2-y_1|}{l_y}\right] \end{aligned}$$

(23)

where $\sigma _E$ is the standard deviation and $l_x$ and $l_y$ are the correlation lengths in two directions and for is a spatial location ${\varvec{x}}$. The rest of the material properties and parameter specifications are given in Table 1. The random field is then represented using KL expansion as

$$\begin{aligned} E({\varvec{x}},{\varvec{\xi _s}}) = E_0({\varvec{x}}) + \sum _{i=1}^{q_s} \sqrt{\eta _i} \xi _{i} \varphi _i(\varvec{x}), \quad \varvec{\xi }_s = \{ \xi _i \}_{i=1}^{q_s} \end{aligned}$$

(24)

where $\varvec{x}$ denotes a spatial location, $\eta _i$ and $\varphi _i(\varvec{x} )$ are the eigenvalues and eigenfunctions of $C_{EE}(\varvec{x})$. For simulation purpose, based on the decay of $\eta _i$—as given in Fig. 1, only first three terms are retained in the summation in Eq. (24).

Fig. 1

Decay of the eigenvalues of the covariance kernel

Table 1 Values of the parameters used in numerical study

Computation is performed for two different levels of variability in Young’s modulus, for $\sigma _E = 0.05E_0$ and $\sigma _E = 0.2E_0$. Also, two different load cases are considered, details of which are given in the following subsection. For these two load cases and two levels of variability, the response is predicted using the hybrid methods. The estimates of response and statistics derived from them are compared with perturbation method and MC method. Estimates from MC are assumed to be the benchmark for accuracy in all cases. The computational speed gain over the MC method is studied in details.

5.2 Loadings and modal truncation

The first load case considered here is a sinusoidal force with random frequency, which has the form of Eq. (4). The force is applied in the out-of-plane direction at the center of the plate. This loading is referred to as the load case I. It is assumed that $\overline{\omega }_f = 2 \pi$ rad/s and $\sigma _{\omega } = 0.05 \ \overline{\omega }_f$. The random variable $\xi _{q_s+1}$ is standard Gaussian. The pdf of different frequencies, estimated using the PCE in Eq. (11), is plotted in Fig. 2. Also, the pdf of the forcing frequency $\omega _f$ is plotted in the same figure. From this figure, it is observed that the pdfs of the first natural frequency and the forcing frequency have a significant overlap. Therefore, the contribution from the first mode is expected to be significant. From the mean of the excitation frequency, the distances of the means of first and the second natural frequencies are $1.65 \ \sigma _f$ and $21.64 \ \sigma _f$, respectively. Therefore, the participation of any other mode to the response is expected to be low, especially in the steady state. However, to be conservative, and to ensure the accuracy during the transient phase, total five modes are included in the simulation for extraction of statistical properties and efficiency estimation.

Fig. 2

Probability density function of frequencies of first five modes and the excitation frequency for load case I

The second load case a stationary Gaussian random base acceleration—referred to as load case II here. Assuming the plate to be mounted on a linear substructure, a white noise excitation on the substructure will transform into a stationary Gaussian base excitation for the plate. This random base excitation will have a power spectral density (PSD) of the form

$$\begin{aligned} S_0(\omega ) = S_i\frac{\left[ 1 + 4\lambda _g^2 \left( \frac{\omega }{\omega _g} \right) ^2 \right] }{\left[ 1 - \left( \frac{\omega }{\omega _g} \right) ^2 \right] ^2 + 4\lambda _g^2 \left( \frac{\omega }{\omega _g} \right) ^2} \end{aligned}$$

(25)

This is similar to the Kanai–Tajimi spectrum [57, 58], often used in earthquake engineering with similar mechanisms. Here $S_i = 0.0001, \zeta _g = 0.1$ and $w_g = 20$ rad/s. Thus, the inertial force generated on the plate is of the form $\varvec{F}(t,\varvec{\xi }) = -\varvec{M}(\varvec{\xi }_s) \varvec{I} f(\varvec{\xi }_f,t)$, where $\varvec{I}$ is the index of displacement degrees of freedom along the support.

For this load case, the PSD and the pdfs of first ten frequencies are plotted in Fig. 3. From the overlap between the PSD and the pdfs of frequencies, it can be observed that most of the frequency content in the force is covered by the first few natural frequencies only. In fact, from the origin to the mean of tenth mode—which has a frequency of 52.59 rad/s—99.545 % of the area under the PSD is covered. Therefore, total ten modes are included in the simulation for extraction of statistical properties and efficiency estimation.

Fig. 3

Probability density function of frequencies of first ten modes and the PSD for stationary Gaussian base excitation for load case II

5.3 Computer implementation

The computer implementation is done using Matlab [59]. The hybrid method has two major computational components : first, using SSFEM to solve the random eigenvalue problem—step 2 in Sect. 2.3, and second, using simulation for response analysis—steps 3–4 in Sect. 2.3. The first component involves solving a system of nonlinear algebraic equations. This is achieved using NR iterations for which the Jacobian is computed from available analytical expressions—given in the Appendix. The initial iterate is estimated from a short MC run of the deterministic eigensolver with a sample size of 100 and projecting the solutions on chaos bases—sometimes referred to as the nonintrusive method. This choice helped in achieving a fast convergence in NR iterations. Inside NR, the Matlab direct solver implemented using the backslash operator $(\backslash )$ is used for solving linear equations in the dense matrix format. The stopping criteria for nonlinear iterations are chosen as $\Vert \varvec{F}(\varvec{x})\Vert \,\le \,10^{-9}$.

The second component, which is the response analysis within a statistical sampling loop, is common in all the three methods: hybrid, MC, and perturbation. To accelerate the convergence in sampling, the Matlab-generated random numbers are transformed by shifting of the mean and removing the correlations. The random process loading is simulated using a spectral representation, which expresses it as a infinite sum of sinusoidal terms with random phase angles. In the truncated form, it is given by the Shinozuka’s formula

$$\begin{aligned} \bar{f}(t) = \sqrt{2}\sum _{k=1}^M A_k \hbox {cos}(\omega _kt-\phi _k) \end{aligned}$$

(26)

where $A_k = \sqrt{S_1^0(\omega _k)\varDelta \omega }, \omega _k = (k-\frac{1}{2})\varDelta \omega , \varDelta \omega =$ frequency step, $S_1^0 =$ one-sided power spectral density for the random force and $\{\phi _k\}_{k=1}^{k=M}$ are independent and uniformly distributed variables between 0 and $2\pi$. The random base acceleration is generated using Eq. (26) with maximum frequency $\omega _u = 500$ rad/s discretized in 1024 steps $(\varDelta \omega = 0.488281\,\hbox { rad/s})$. The simulated process $\bar{f}(t)$ in Eq. (26) is a superposition of harmonic terms. Hence, it is harmonic, and it can be proved that $\bar{f}(t)$ has a period $T = \frac{2\pi }{\varDelta \omega }$ sec [60]. The simulated process tends to be Gaussian for $M \rightarrow \infty$ and gives reasonably good result for $M \ge 100$ terms [60]. Nonstationary random loads can be modeled using similar formulation modified by a time-varying amplitude of the cosine terms [43]. There exists a number of different approaches to simulate stationary and nonstationary random processes developed over the years [61, 62], which can be used as deemed appropriate without any restrictions.

As discussed earlier, a Newmark-$\beta$ algorithm for time-stepping is used for all time-history analyses. For both the load cases, the out-of-plane displacement at the center of the plate is reported. In the perturbation method, the sensitivities of the eigenvectors are computed in a single-step method [55]. However, the response statistics estimation involves repeated solution of coupled ODEs stated in Eqs. (19 and 20) within a statistical simulation. Although in many applications, perturbation is a very fast method, in this case, this simulation step makes it expensive. Therefore, in this paper, the perturbation method is used to compare the accuracy only.

In the Sects. 5.4 and 5.5, the accuracy of all the three methods is compared for load cases I and II, respectively. Then in Sect. 5.6, a comparative study of the computational costs of hybrid and MC methods is presented. An analysis on the cost–benefit is also performed there.

5.4 Results for load case I: sinusoidal loading with random frequency

For extraction of the statistics of the output, the response analyses are carried out for a duration of 10 s. For the first load case, a typical realization of the response time history is plotted in Fig. 4. For 5 % standard deviation in the Young’s modulus (that is, in the system random variables $\varvec{\xi }_s$), the time history of the mean displacement is plotted in Fig. 5. Estimates using MC, hybrid, and perturbation methods are superposed in this figure. In Fig. 5a, the entire 10 s duration is plotted, whereas in Fig. 5b, a magnified view of the time histories between 7th and 8th s is plotted. From these plots, it is observed that both the hybrid and perturbation methods give accurate estimates of the mean displacement, while the estimate from the MC method serves as the benchmark for comparison. However, the magnified view in Fig. 5b reveals that the perturbation method has little error in estimate. Next, the time history of the variance of the displacement from three methods is plotted in Fig. 6. Here it is observed that for first few seconds, both hybrid and perturbation methods give a good accurate approximation. However, as the time progresses, the estimate from the perturbation method deviates from MC, while hybrid method is still very accurate.

Fig. 4

Plot of out-of-plane displacement of the central node of the plane for a typical realization of load case I for 5  % standard deviation of the system random variables

Fig. 5

Plot of the mean of out-of-plane displacement response at central node versus time for load case I a for a span of 10 s and b for a window between 7th second and 8th second for 5  % standard deviation of system random variables

Fig. 6

Plot of variance of out-of-plane displacement at central node versus time for 5  % standard deviation for load case I

The same set of experiments are repeated for 20 % standard deviation in the Young’s modulus. Estimates for the mean and variance of responses are plotted in Figs. 7 and 8, respectively. For this higher level of variability, it is observed that the hybrid method is still very accurate for the entire timespan. While the perturbation method loses accuracy in both mean and variance predictions at a very early stage, and the error grows with time. The exact match between the estimates of MC and hybrid method is attributed to the accuracy of the SSFEM in solving the random eigenvalue problem. It is worth recalling here that an attempt to use the pure SSFEM-based response prediction in [10] failed for this load case.

Fig. 7

Plot of the mean of out-of-plane displacement response at central node versus time for load case I a for a span of 10 s and b for a window between 7th second and 8th second for 20  % standard deviation of system random variables

Fig. 8

Plot of variance of out-of-plane displacement at central node versus time for 20  % standard deviation for load case I

5.5 Results for load case II: stationary Gaussian random loading

For the second load case, a typical realization of the time history of the base acceleration is presented in Fig. 9. A typical realization of the response time history is plotted in Fig. 10. For 5 % standard deviation in the Young’s modulus, the mean and variance of the response are plotted in Figs. 11 and 12, respectively. Similar to the first load case, here the estimates from the hybrid method match exactly with the MC estimates, whereas the perturbation method shows small error in predicting the mean, but accumulates large error in standard deviation prediction as time progresses. One of the widely used statistics for random vibration in structural engineering is the number of zero-crossings by the response time history within a fixed timespan. This statistic is estimated here and compared. The pdf of the zero-crossings within first 10 s is plotted in Fig. 13. It is observed from this figure that the pdf estimates from the hybrid and MC match exactly, whereas the estimate from the perturbation follows closely.

Fig. 9

Plot of random base excitation versus time for a typical realization of load case II

Fig. 10

Plot of out-of-plane displacement of the central node of the plane for a typical realization of load case II for 5  % standard deviation of the system random variables

Fig. 11

Plot of the mean of out-of-plane displacement response at central node versus time for load case II a for a span of 10 s and b for a window between seventh second and eighth second for 20  % standard deviation of system random variables

Fig. 12

Plot of variance of out-of-plane displacement at central node versus time for 5  % standard deviation for load case II

Fig. 13

Plot of probability density function (pdf) of zero-crossing statistics of displacement at central node for 5  % standard deviation for load case II

These experiments are repeated for 20 % standard deviation in the Young’s modulus. The mean, standard deviation, and the pdf of the zero-crossings are plotted in Figs. 14, 15, and 16, respectively. From these three figures, once again it is observed that the hybrid method gives very accurate result even for of the large variation, whereas the perturbation method yields large error in this region. Therefore, the hybrid method is able to predict the response due to a standard random process loading without being affected by any curse of dimensionality—generally suffered by the pure SSFEM.

Fig. 14

Plot of mean of displacement at central node versus time for a typical realization for a stationary Gaussian base excitation for a span of 10 s for 20 % variation of system parameters

Fig. 15

Plot of variance of out-of-plane displacement at central node versus time for 20  % standard deviation for load case II

Fig. 16

Plot of probability density function (pdf) of zero-crossing statistics of displacement at central node for 20  % standard deviation for load case II

5.6 Computational cost analysis

One major benefit of the proposed hybrid method is its faster computational speed compared with the MC method. A detailed study on this computational gain is carried out here. For both the load cases, the computational time taken by the hybrid and MC methods is recorded and analyzed. In this cost study, three parameters are varied : (i) the sample size in MC and the simulation step in hybrid are varied from 2000 to 10,000, (ii) the number of DOF is varied between 64 and 576, and (iii) two timespans of interest (for which the response is computed) are considered: 5 and 10 s. The gain in computational efficiency ${\mathcal {E}}$ is defined as

$$\begin{aligned} {\mathcal {E}} = \frac{\left( T_{MC} - T_{Hy} \right) }{T_{Hy}} \times 100 \ \% \end{aligned}$$

(27)

where $T_{MC}$ denotes the CPU time required to run the MC for a fixed set of aforementioned three parameters and $T_{Hy}$ denotes the CPU time to run the hybrid method for the same set of parameters. For load cases I and II, variations of the efficiency gain thus computed are plotted in Figs. 17 and 18, respectively. For ease of analysis and explanation, part of these results, along with the exact CPU timings under these two load cases, are tabulated in Tables 2 and 3, respectively. In all of these Figures and Tables, note that the gain is always positive, which means that the hybrid method is faster than MC. For studying the gain in details, first consider the load case I. In Fig. 17, it is observed that the efficiency gain ${\mathcal {E}}$ increases with both the size of the system (in terms of number of DOF) and the sample size (used in the statistical sampling loop for response analysis). This trend holds for both 5 and 10 s of response analysis. The efficiency gain is higher for 5 s of response analysis. The increase of gain against DOF can be quantitatively observed in Table 2. Here it is observed that for a fixed sample size as the number of DOF in the second column increases, the gain in efficiency in the fifth column increases. For instance, for a sample size of 2000, the efficiency gain for a 64 DOF system is 79.9 %, whereas for 576 DOF system, it is 92.8 %. Similar trend is observed for the sample size of 10000. Now for a given number of DOF, as the sample size grows, the efficiency grows. For instance, for the same 576 DOF system, the efficiency gains for 2000 and 10,000 samples are 92.8 and 143.4 %, respectively.

Fig. 17

Variation of efficiency gain with number of DOF and sample size for 5 and 10 s of response analyses under load case I

Fig. 18

Variation of efficiency gain with number of DOF and sample size for 5 and 10 s of response analyses under load case II

Table 2 Computation time (in seconds) and efficiency gain for response prediction for different numbers of elements and sample sizes under load case I

Table 3 Computation time (in seconds) and efficiency gain for response prediction for different numbers of elements and sample sizes under load case II

For load case II, the same trends are observed in Fig. 18 and Table 3. In this table, for a sample size of 2000, the efficiency gain for a 64 DOF system is 27.8 %, whereas for 576 DOF system, it is 39.1 %. Again, the same trend is observed for the sample size of 10,000. Similarly, for the same 576 DOF system, the efficiency gains for 2000 and 10,000 samples are 39.1 and 56.8 %, respectively. While comparing Tables 2 and 3, it is noted that for any mesh resolution, the efficiency gain ${\mathcal {E}}$ is lower for load case II compared with load case I. This drop in efficiency gain is attributed to the larger cost associated in generating load case II. While in load case I, only a single random variable is generated to sample from Eq. (4), generation of load case II using Eq. (26) is far more complicated and computationally expensive. This additional cost is reflected in both in $T_{MC}$ and $T_{Hy}$. Thus, for a given mesh resolution (number of DOF), the numerator $T_{MC} - T_{Hy}$ in Eq. (27) remains almost same in both the load cases as seen in Tables 2 and 3. This is true for any mesh resolution and is expected since the numerator is mainly the difference in cost of solving the random eigenvalue problem—which depends upon the mesh resolution and not on the loading. However, the denominator in Eq. (27) increases from load case I to load case II due to the additional simulation cost of the load. Therefore, the ratio ${\mathcal {E}}$ drops in load case II.

The reasons behind these trends are analyzed next. The positivity of the speed gain is due to the faster computational speed in SSFEM than MC method for solving the random eigenvalue problem [30]. As the sample size grows, this gain becomes higher since the cost in the SSFEM is independent of the sample size. Similarly, as the number of DOF grows, repeated solution of the eigenvalue problem in MC becomes more expensive compared with the SSFEM, thus leading to a relatively higher speed gain in hybrid method. In the time integration part, the cost is same for both hybrid and MC as both of them use statistical simulation. As the timespan of interest in response history increases from 5 to 10 s, cost of this time integration part increases, while the cost of the random eigenvalue solving remains unchanged. Therefore, the overall computational gain, which is achieved only through the cost saving in the random eigenvalue solving stage, is reduced.

For a detailed account on this analysis, consider the following notations. Given a fixed number of DOFs n and number of terms in PCE P, let $N_{\mathrm{run}}$ denote the sample size, $T_{\varvec{\xi }}$ denote the time needed for generating the random numbers, $T_{PC}$ denote the time needed to estimate the PC coefficients by solving Eq. (15), $T_{KL}$ denote the time needed for solving the KL eigenvalue problem, $T_{\mathrm{sys}}$ denote the time needed for computing a realization of the stiffness, mass and damping matrices, and the loading, $T_{\varPhi }$ denote the time needed for generation of realizations of eigenvectors using Eq. (11), $T_{\mathrm{res}}$ denote the time for response analysis by solving Eq. (3), and $T_{\mathrm{eig}}$ denote the time to needed for solving a deterministic eigenvalue problem—that is, solving Eq. (6) for a given realization of $\varvec{\xi }_s$. Then the time taken by the hybrid method $(T_{Hy})$ and MC methods $(T_{MC})$ is

$$\begin{aligned}&T_{MC} \approx T_{\varvec{\xi }} + T_{KL} + N_{\mathrm{run}} \times \left( T_{\mathrm{sys}} + T_{\mathrm{eig}} + T_{\mathrm{res}}\right) \end{aligned}$$

(28)

$$\begin{aligned}&T_{Hy} \approx T_{\varvec{\xi }} + T_{KL} + T_{PC} + N_{\mathrm{run}} \times \left( T_{\mathrm{sys}} + T_{\varPhi } + T_{\mathrm{res}}\right) \end{aligned}$$

(29)

These equations are valid for both the load cases. Now comparing Eqs. (28) and (29), we find that $T_{MC} > T_{Hy}$ is possible only if $N_{\mathrm{run}}T_{\mathrm{eig}} > T_{PC} + N_{\mathrm{run}}T_{\varPhi }$, which is generally the case [30] given the fact that $T_{\varPhi }$ is the cost related to only a few vector addition—which is far lower than the other costs such as solving the eigenvalue problem or the response analysis. This inequality becomes more prominent when the system size $n$ grows since the nonlinear growths of $T_{\mathrm{eig}}$ and $T_{PC}$ (with respect to n) are much faster than the linear growth of $T_{\varPhi }$; $N_{\mathrm{run}}$ usually remains in the range of a few thousands. Therefore, according to Eq. (27), the efficiency gain ${\mathcal {E}}$ is always positive and grows with n. Similarly, as $N_{\mathrm{run}}$ grows, the cost $N_{\mathrm{run}}T_{\mathrm{eig}}$ grows faster than the cost $N_{\mathrm{run}}T_{\varPhi }$, while $T_{PC}$ remains unchanged, implying that the gain increases with the sample size. Finally, as the timespan of interest increases, $T_{\mathrm{res}}$ starts growing. Then the cost $N_{\mathrm{run}}T_{\mathrm{res}}$, which is common in both the methods, becomes prominent compared with other costs, and the computational gain of $T_{PC}$ over $N_{\mathrm{run}}T_{\mathrm{eig}}$ achieved by the SSFEM starts losing its margin of advantage. Therefore, when the timespan of interest increases from 5 to 10 s, the gain ${\mathcal {E}}$ reduces. Similarly, $T_{\mathrm{res}}$ was higher in load case II compared with load case I, and thus, the gain ${\mathcal {E}}$ was lower in load case II.

6 Concluding remarks and future challenges

The proposed hybrid method succeeded in overcoming the problem of large dimensionality encountered by pure SSFEM in predicting response of linearly vibrating systems. For two loading cases—one harmonic with random frequency and another general Gaussian random process—the hybrid method accurately predicted the response where the pure SSFEM failed earlier due to prohibitive computational demand. The accuracy of the estimates is as good as MC, while the cost is much lower. Compared with the perturbation method, the relative accuracy is even better for larger variability. The cost reduction is achieved by solving the random eigenvalue problem by SSFEM, and the curse of dimensionality is avoided by using sampling in the time integration part. The efficiency gain in the hybrid method against MC method also grows with the number of DOF and the sample size.

The method is expected to work best for a range of problems in engineering where the system is linear and response of short timespan is of importance. This includes most vibration problems with damping and transient response analysis of structures. However, if the timespan of interest is very large, then the computational gain is expected to reduce.

The structure of the hybrid algorithm makes it flexible and open to improvements in its many stages. A few places for potential major improvements are finding an improved solver for the nonlinear iterations in the SSFEM stage, adopting a better sampling strategy in the response analysis. Parallelization of the method will also reduce the computational cost. To this end, parallelization of the SSFEM part will be challenging. As mentioned earlier, any other scheme for modal truncation can easily be adopted in this method.

Appendix

1.1 The Jacobian of the NR iterations

In this section, the analytical form of the Jacobian matrix is derived from Eqs. (13, 14). Note that these expressions are the modified forms of the expressions derived in [30], to include the mass matrix into consideration. For a given m between 0 and $P-1$ let $F_{m}$, denote the system of P equations in Eq. (13). Then its derivatives with respect to the components of the unknown chaos coefficients can be expressed as

$$\begin{aligned} \frac{\partial {F_{m}}}{\partial {\lambda ^{(i)}}}= & {} -\sum _{k=0}^{L_2-1}\sum _{j=0}^{P-1}{\mathbb {E}}\{\psi _i\psi _j\psi _k\psi _m\} \mathbf{M}^{(k)}{\varvec{\phi }}^{(j)} , \quad m = 0,\ldots , P-1 , \quad i = 0,\ldots , P-1, \end{aligned}$$

(30)

$$\begin{aligned} \frac{\partial {F_{m}}}{\partial {{\varvec{\phi }}^{(j)}}}= & {} \sum _{i=0}^{L_1-1}{\mathbb {E}}\{\psi _i\psi _j\psi _m\} \mathbf{K}^{(i)} - \sum _{i=0}^{P-1}\sum _{k=0}^{L_2-1}{\mathbb {E}}\{\psi _i\psi _j\psi _k\psi _m\} \lambda ^{(i)} \mathbf{M}^{(k)}, \nonumber \\ m= & {} 0,\ldots , P-1, \quad j = 0,\ldots , P-1. \end{aligned}$$

(31)

Equation (31) results in a matrix whose $(i_1,i_2)$th term is the derivative of the $i_1$-th function in $F_{m}$ with respect to the $i_2$-th element of ${\varvec{\phi }}^{(j)}$.

Similarly, from Eq. (14),

$$\begin{aligned}&\frac{\partial {f_m}}{\partial {\lambda ^{(j)}}}=0,\quad m = 0,\ldots , P-1 , j = 0,\ldots , P-1 ,\end{aligned}$$

(32)

$$\begin{aligned}&\frac{\partial {f_m}}{\partial {{\varvec{\phi }}^{(j)}}}=2\sum _{i=0}^{P-1}\sum _{k=0}^{L_2-1}\mathbf{M}^{(k)}{\varvec{\phi }}^{(i)}{\mathbb {E}}\{\psi _i\psi _j\psi _k\psi _m\},\quad m = 0,\ldots , P-1 , j = 0,\ldots , P-1 . \end{aligned}$$

(33)