Abstract
In 1454 Georg Peurbach taught astronomy at the Collegium Civium in Vienna by reading a work of his own: the Theoricae novae planetarum. In 1483 Albert of Brudzewo, teaching astronomy at Cracow University, adopted Peurbach’s text together with a commentariolum of his own. Among the numerous commentaries preserved both in manuscript and in printed form, Brudzewo’s stands out because it submits Peurbach’s work to a subtle analysis that, while recognising the merits for which it was widely accepted, also focuses on the limitations of the celestial spheres described in it. Budzewo’s commentary is of interest, in itself both for its criticism of Peurbach’s descriptions of solar, lunar and planetary theory and also for its importance to Copernicus’s own planetary theory. For Copernicus makes clear in the Commentariolus that his concern was the very same issue, violation of uniform circular motion by the rotation of spheres, that Brudzewo criticises in detail. In this way, Brudzewo’s commentary stands as the original motivation for the investigation of the motion of the planets that was eventually to lead Copernicus to a planetary theory based strictly upon uniform rotation of spheres, and through that investigation to the motion of the Earth and the heliocentric theory.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Peurbach’s Theoricae novae and their reception
Finiunt Theorice nove per magistrum Georgium de peurbach edite. anno domini 1454to Wienne in Collegio Civium penultima mensis Augusti.Footnote 1
On the penultimate day of August 1454 at the Collegium Civium in Vienna, the Magister Georg of Peurbach completed a course on the Theoricae novae which he had written himself. This course constitutes a crucial moment in the history of astronomy. The thoroughness and scientific foundation of the Theoricae novae enable them to mark a significant turning point with respect to the previous tradition. They explain, in fact, the “new” image of the celestial world, which was to persist for at least two centuries and even withstood the innovations introduced by Copernicus. From an analysis of the existing testimonies, a picture emerges of how the Theoricae, rooted in the cultural fabric of the Latin West, became the indispensable foundation for higher astronomical knowledge in the main university centres of the time, especially in contexts where it was considered imperative to renew and restore the science of the stars.Footnote 2
Although they mark an important turning point, the Theoricae novae do not actually break with the previous tradition but instead form part of it since they compose in a coherent manner the various contributions developed in the previous centuries. Peurbach gathers in a global view of the universe the most innovative results of the tradition with regard to both with the internal structure of the planetary spheres and with the superior spheres whose motions involve the overall celestial globe. His work offers a coherent and well-structured presentation of the whole universe in all its parts and according to the composition of their motions, from the sphere of the Moon up to the Prime Mover, reconciling on one side, the need of transmitting the global motions through the concentricity of the spheres, and on the other side, the need of saving the apparent irregularities through the eccentrics and the epicycles. The Theoricae novae’s universe is made of suitably structured orbs moving in an actual way and influencing one another through their movements.Footnote 3 This explains why Peurbach points out that his Theorica nova explains the real structure of the celestial spheres and their motions: “Incipit theorica nova realem sperarum habitudinem atque motum [...] declarans”.Footnote 4
Those orbs and those spheres for which Peurbach intended to be the description of the spherical reality draw their foundations from the Almagest. So, in order to place Peurbach’s contribution in perspective and understand its value, it is useful to compare the Theoricae novae with the Almagest. One can then observe the different methods characterising these astronomical texts, opposing the \(\uptau \)ò ő\(\uptau \upiota \) to the \(\updelta \upiota \)ó\(\uptau \upiota \)—or, to use the Latin expressions, the narrative exposition to the demonstrative—but it is also worth highlighting that they are closely related in terms of content.
Ptolemy’s method in the Almagest is rigorously empirical and mathematical. The descriptions of the phenomena, of the apparent motions in the heavens, are based strictly upon observations and the derivation and confirmation of the planetary systems and their parameters from those observations upon strict mathematical demonstrations. The Theoricae, written by Peurbach in 1454, are considered an isagoge to the Almagest. In contrast to Ptolemy’s highly detailed work with its extremely thorough presentation of the celestial universe, the Theoricae is very synthetic: through a sequence of statements and simply enunciated rules, it presents a comprehensive view of the celestial universe in terms both of structure of the planetary spheres and also of the composition of their motions. All of this is based on the models that Peurbach extrapolated from the Almagest. Nevertheless, a major part of the Almagest is completely absent from his text, namely the geometric demonstrations and the description of the phenomena which are both the cause and the effect of its models.
It is for this reason that once this work was adopted as the reference textbook for university teaching in the 1480s, explanatory commentaries had to be added. On the whole one can recognise that the majority of commentators, even though adopting different approachesFootnote 5 share a common purpose. These authors remain faithful to Peurbach’s text, which they examine in an uncritical way, and in its entirety, with the aim of explaining its content as thoroughly as possible, in order to prove that, even in this new structure, Peurbach’s orbs always embody the mathematical rigour and precision characterising Ptolemy’s work. By the rigour of the mathematical demonstrations, they support the consistency of the parts of the universe and the accuracy of the relations between the elements examined even when some of them remain purely geometrical abstractions interacting with the orbs of which the planetary spheres are made.
Even if one focuses solely on the printed versions—omitting the names of the numerous masters who taught Peurbach’s Theoricae novae in many universities, adding their own explanations, which have only reached us in manuscript form—the contributions of Francesco Capuano, Silvestro Mazzolini da Prierio, Oronce Finé, Peter Apian, Jacob Milich, Erasme Reinhold, E. Oswald Schreckenfuchs, Christian Wursteisen and others in centres such as Padua, Paris, Ingolstadt, Wittenberg, Freiburg and Basel...Footnote 6 increasingly strengthened and consolidated the coherence of the universe described in Peurbach’s work. This accounts for the fact that the image of the world conceived by Peurbach persisted for at least two centuries.
Nonetheless, the authority of Peurbach was by no means universally accepted. In Cracow the Theoricae novae were read in an original way according to an unusual approach by Albert of Brudzewo. It will be interesting to try to understand where the originality of the analysis developed by Brudzewo concerning the universe of the Theoricae novae does lie, and whether someone has indeed been motivated to make good use of his “unusual remarks”.
2 Aims and method
Our reading of Brudzewo’s Commentariolum reveals that his analysis of the Theoricae novae is a singular one, distinguishing him from all the other authors who examined Peurbach’s work. In this paper we will show firstly, in the section Albert of Brudzewo’s Commentariolum super Theoricas novas Georgii Purbachii, the criteria which guide Brudzewo’s lectures on the Theoricae novae and how he recognises in the Theorica Solis the embodiment of the first principle of astronomy. We will then consider the parts of the Commentariolum in which Brudzewo focuses on the weak points of Peurbach’s universe. While examining the presence of Mathematical artifices in Peurbach’s universe, we will consider his reflections on the equant circle and on the mean apogee: Peurbach derived both these elements from the Almagest but, according to Brudzewo, was unable to assimilate them to the spheres and orbs of the Theoricae.
In distinguishing Real motions and apparent motions and considering the presence of irregular motions in Peurbach’s universe, we will stress how Brudzewo demonstrates that Peurbach has built a universe that does not respect the principles of the celestial nature and in which a separation occurs between appearance and reality. In the name of the principle of the perfect circularity and uniformity of motions considered in itself and in an absolute sense “in se et absolute”, Peurbach’s statements attributing irregular motion to the celestial orbs are inadmissible. Brudzewo underlines that these equivocal, problematic statements made by Peurbach derive from the position of the observer at the centre of the world. In his analysis he perceives the Weaknesses of Peurbach’s approach: the astronomers’ point of observation. This particular point of observation represents then a serious problem for the Theoricae’s universe. Brudzewo grasps the serious weakness that could shake the very foundations of the whole structure of that universe. This gave rise to the question this paper seeks to answer: could the problems to which the Cracovian Magister drew attention, and his reflections thereon, have helped stimulate the quest for a new point of observation from which to practise astronomy?
The presence, in the same years of Brudzewo and Copernicus in Cracow, opens the possibility that Copernicus, young student at that university, knew Brudzewo’s Commentariolum. In an effort to answer this question, in the sections devoted to Copernicus’ Commentariolus: a new point of observation and to Copernicus’s De revolutionibus, we will show that without exaggerating one’s interpretation of Copernicus’s work in any way, the same objections and the same reflections as those found in Brudzewo’s work can be observed therein, although more concisely, and these were developed by the Frombork astronomer in the name of the same principles and to emphasise the same inconsistencies.
3 Albert of Brudzewo’s Commentariolum super Theoricas novas Georgii Purbachii
3.1 Brudzewo’s teaching in Cracow
In 1483 Albert of Brudzewo, an eminent figure at Cracow university, reformed the teaching of theoretical astronomy by basing his lectures on Peurbach’s new work, which he illustrated through his own commentary:
the brief commentary on the Theoricae novae of Georg Peurbach brought together by Master Albert of Brudzewo in the University of Cracow for a more appropriate introduction of younger students during a reading made of the same Theoricae novae. Footnote 7
At the end of his course he expresses his awareness of the unusual and innovative character that distinguishes his reading of the Theoricae novae and expresses an exhortation to bring further improvements:
From the unusual remarks expressed in this Commentariolum that have been set forth not according to received doctrine and science, the diligent reader should not readily rise up in indignation, but let him apply himself to bring forth anew what is more certain and profound in furtherance of this science.Footnote 8
Manuscript sources prove that from that year until at least 1495, Brudzewo’s commentary on Peurbach’s Theoricae novae became a reference work for astronomy studies at the Faculty of the Arts of that University.Footnote 9 Brudzewo was among the first Magistri to take an interest in the Theoricae novae. His Commentariolum is also the most ancient commentary on Peurbach’s work to have been printed, with two editions in 1494 and in 1495, thanks to the contribution of one of his students.Footnote 10
3.2 General approach of Brudzewo’s reading
In his commentary, Brudzewo does not adopt a uniform approach. He does not treat all the subjects of the Theoricae novae uniformly. Sometimes he refers directly to Peurbach’s words: “what the text [of Peurbach] says is proved as follows”,Footnote 11 “it is shown in the text [of Peurbach]”Footnote 12 and leaves the original text and diagrams to explain certain matters: “The Magister [Peurbach]’s text is sufficiently clear and evident looking at the diagram”;Footnote 13 in other places he merely describes the contents by means of a paraphrase, whereas the subjects in which he is particularly interested are described at length. His analysis pays particular attention to the part of the Theoricae devoted to the planets.Footnote 14 In general Brudzewo followed the same order adopted by Peurbach and examined the celestial spheres in the following order: the Sun;Footnote 15 the Moon;Footnote 16 the three superior planets, Mars, Jupiter and SaturnFootnote 17; VenusFootnote 18 and Mercury.Footnote 19 He also retained the internal division of each chapter, by devoting the first part to a description of the orbs that comprise the total spheres; the second part to the movement of each orb considered both in itself and in relation to the Sun; and the third part to the terms for using the tables.Footnote 20
Ptolemy’s astronomy is a constant presence in the whole of Brudzewo’s work, and he regularly refers to the Almagest, from which he quotes entire passages in full, or indicates the book and the chapter in which Ptolemy discusses a specific subject. In this way he establishes the foundations of the orbs of the Theoricae novae and shows how they embody the mathematical precision and rigour of the Greek work. Brudzewo starts each section of his commentary by presenting the phenomena that persuaded Ptolemy to introduce the eccentrics and the epicycles. He then shows how in the Theoricae novae the same phenomena, which, in the Almagest could be imagined as the result of the abstract combination of purely geometrical circles, can also now occur through these particular structures of “partial orbs”, that is, orbs forming the parts of an entire sphere made up of such orbs. In this sense Peurbach avoided the disadvantages that until then could only exist in the purely mathematical abstraction: he has deconstructed the motions which, in the Almagest, are carried out by a single circle, which even turned in opposite directions, preferring instead to assign each of these motions to one single orb conceived for this purpose.
3.3 The criteria which guided Brudzewo’s reading
Brudzewo makes a careful and accurate analysis of the text of the Theoricae novae. He interprets it according to his own personal beliefs. This is made possible by the way in which Peurbach explains his universe, presenting it in almost mechanical functionality, like a perfectly functioning machine, without any explicit reference to the question of the a priori principles imposed by natural philosophy. The initial lines of the Commentariolum demonstrate clearly that for Brudzewo, the “partial orbs” described by Peurbach are real:Footnote 21 “the eccentric is a real orb”Footnote 22 and the “total sphere” of each planet is made of “real partial orbs.”Footnote 23 To Brudzewo, the universe that Peurbach describes in all its constituent parts, must reflect the image of the celestial world as it is in its reality. It must then represent the part of nature that must necessarily embody the perfection in which the regular, uniform revolutions take place. These revolutions:
take place without any irregularity, since this motion is an essential attribute of the celestial bodies whose motion is different in nature to that of bodies in the sublunary world, whose motion is devoid of uniformity and order.Footnote 24
This world is governed by precise, rigorous laws, and established a priori principles to which Brudzewo constantly refers his analysis, since he considers that they are the most authentic expression of the essence of celestial nature. Thus, each celestial body must have its own unique motion which is performed in a perfectly uniform, circular manner; the same principle, in mathematical terms, requires each celestial body to move through equal angles centred on its own centre of motion, corresponding to equal arcs of the circular path through which it passes in equal intervals of time.Footnote 25 Brudzewo requires the perfect circularity and uniformity, demanded by Ptolemy for the motion of his abstract, purely mathematical circles, to be observed by the motion of the orbs conceived by Peurbach. And his assessment of the models in the Theoricae novae relies on agreement with these principles.
3.4 The Theorica Solis and astronomy’s first principle
The Sun is the first to be examined in the Theoricae and it is similarly the first to be found in Brudzewo’s Commentariolum. When describing the structure of its sphere in terms of partial orbs, Brudzewo refers to Peurbach’s text “Littera autem taliter probatur”.Footnote 26
Peurbach describes the motion of the orb carrying the Sun, saying that:
But the orb carrying the body of the Sun moves by its own motion about its centre, namely, the centre of the eccentric, uniformly in the order of the signs about 59 minutes and 8 seconds each day of the degrees of the circumference described through the centre of the body of the Sun in one complete revolution. [...] Now, since the centre of the Sun moves uniformly about the centre of the eccentric in accordance with the motion of the orb carrying it, necessarily it will move nonuniformly about any other point. Therefore, in equal times the Sun describes unequal angles about the centre of the world and unequal arcs of the circumference of the zodiac.Footnote 27
Brudzewo approves this, since the regular motion of the Sun in its eccentric constitutes the foundation of astronomy, without which any consideration of this matter becomes impossible. The validity of this principle is also confirmed by mathematical rigour:
The Sun in equal times decribes equal angles about its centre [of the eccentric] and cuts off equal arcs [of the eccentric]; therefore it moves uniformly.
Brudzewo call this the “first principle of astronomy” and defines it rigorously:
Although that the Sun moves uniformly in its eccentric is the first principle in astronomy, so that when it is denied, there is nothing more to be considered in astronomy, nevertheless, such a principle can be demonstrated by a subordinate science, namely, mathematics, in this way: The Sun in equal times decribes equal angles about its centre [of the eccentric] and cuts off equal arcs [of the eccentric]; therefore it moves uniformly.Footnote 28
In Brudzewo’s description of this sphere he explains the “quod”, that is the reasons the eccentric orb had to be included for this luminary, and also how the Theoricae’s arrangement of orbs prevents any intrusion of the vacuum and break in the celestial spheres.
Brudzewo draws attention to the optimal atmospheric conditions in the regions inhabited by the most ancient astral observers. He affirms the reliability of results achieved in a particularly limpid environment where nothing could disturb their observations.Footnote 29 On the basis of these observations, the ancient astronomers, particularly the Egyptians and the Chaldeans, “concluded that the Sun moves nonuniformly in the zodiac”.Footnote 30 Nevertheless:
Even though the Sun itself moves by an irregular motion in the zodiac, they judged, from the principles of philosophy, that it ought to move in its orb with a uniform and simple motion.Footnote 31
These ancient astronomers were then faced with two truths: one which was shown by the senses, that is the irregular motion of the Sun in the zodiac as it appeared to an observer at the centre of the world; and the other, which was based on an a priori principle, that is the circular and uniform motion of the Sun in the eccentric orb in which it had really to rotate:
And thus, pondering these two alternatives in the mind, namely, the irregular motion of the Sun in the zodiac, but the uniform and regular motion in its orb, they reasoned: If the Sun itself would have its orb concentric to the zodiac, it would in fact also move uniformly in the zodiac [...] And thus since the Sun moves irregularly in the zodiac, not finding a cause more suitable, they assigned eccentricity to the orb of the Sun, by which the eccentric is raised in one direction from the centre of the world, approaching toward the zodiac, but in the other direction it will approach towards the centre of the world, withdrawing from the zodiac. For in this way the Sun will be seen to move irregularly in the zodiac, and remain longer in one half [of the zodiac] than in the other.Footnote 32
Since the observations demonstrated that the motion of the other planets in the zodiac was also different and varied from one another, it was necessary to introduce an eccentric orb for them too. The ancient observers of the stars inquired whether all the other spheres were eccentric:
They found that the starry sphere is concentric to the world. They proved this through the Pleiades and the other stars diametrically opposed to Pleiades, namely, that when the Pleiades rise, the other stars set, and the converse. These same observers also saw that the motion of the seven planets was different and varied from one to another. Thus, if the eighth sphere is concentric and the planets among themselves move according to different motions, if their orbs were supposed to be totally eccentric, then between the eighth sphere and the sphere immediately below it, by reason of the different motion, there would occur a division of the spheres and the intrusion of a void, and the same would apply to all the inferior spheres as well, which appeared to them absurd to suppose, for otherwise the heaven would be corruptible. Therefore, they could not save entire spheres eccentric in themselves, [...] Therefore, these two contrary motives troubled them, one, on account of which they were compelled to apply the eccentric orb of the Sun to the other spheres of the planets, the other, that if entire [orbs] were totally eccentric, a division between the spheres would be permitted. Considering this from both sides, they did not find anything more suitable than that in every sphere there are at least three orbs arranged in the way the [Peurbach’s] text says.Footnote 33
Brudzewo does not name the person who conceived the solution to this problem, keeping this vague by referring to those ancient astronomers who considered that the more appropriate solution was to adopt, for each planet, a single complete sphere concentric to the eighth sphere and comprising, in the case of the Sun, three partial orbs “taliter dispositi, ut inquit littera”: arranged as described in the Theoricae novae text. Here Peurbach’s authority reappears. The sphere of the Sun has a specific internal structure made up of an eccentric orb and two surrounding orbs which are of variable thickness.
In Peurbach’s conception the surrounding (circumpositi) orbs of variable thickness prevent the generation of the division and the intrusion of a void inside the total sphere. The specific structure of these orbs surrounding the eccentric comes from the necessity of enabling the motion of the eccentric carrying the Sun or the epicycle of the other planets. Because of their shape, they are called “eccentric in a certain sense”, since they are only eccentric in one of the surfaces which contain them. In defining their movement Peurbach characterises these orbs as having propriis motibus proporcionalibus, “their motions so proportioned” that the “thinner part of the superior orb always is above the thicker part of the inferior one”.Footnote 34 Brudzewo cannot restrain expressing his personal disappointment by dwelling on this character of proportionality in their motions:
Now from this, that the principal centre of these orbs is the centre of the world, around which the motion of the eighth sphere takes place—which motion of the eighth sphere is in fact common to all the lower spheres and is passed in equal amount and in one and the same way (aequaliter et uniformiter) to them—therefore they have a motion in the amount proper to each (proportionalem) so that the thinness of one does not depart from the thickness of the other, nor the contrary. Further, the motion of any heavenly body [and then of each orb] about its centre is uniform, as was said, and the objection of some is of no effect, namely, that because these two orbs have with respect to one surface the centre of the world, but with respect to the other [surface] the centre of the eccentric, therefore if they move about the centre of the world, they will in a like way move about the centre of the eccentric. They say, therefore, it is inconceivable that the same orb move with the same motion about different centres. But in truth it is not incongruous, for on account of this, that they have different centres with respect to their different surfaces, the motions of the orbs themselves, in accordance with their different surfaces, can be assigned to different centres. Nevertheless, it would not be without incongruity that an orb, having this kind of disposition in both its surfaces, move with the same motion about different centres.Footnote 35
In the end Brudzewo’s disagreement is clearly expressed. If the eccentric orb carrying the Sun is in complete correspondence with the law of motion, the “eccentric in a certain sense” orbs, which necessarily must be in the planetary spheres, lead Brudzewo to an initial reflection which highlights how this aspect of Peurbach’s real universe holds an inconsistency between the concept of the perfection of motion, as Brudzewo conceives it with its own laws, and the motion of these orbs for which only the proporcionalibus motion is valid. Even though Brudzewo does not repeat his critique in the rest of his commentary, it applies to all the other orbs “eccentric in a certain sense”, since at least one pair of orbs of this kind is found in each planetary sphere, and Mercury even has two pair of them.
4 Mathematical artifices in Peurbach’s universe
Whenever Ptolemy’s astronomy is consistent with the Theoricae novae’s orbs, Brudzewo accepts, illustrates and comments on these passages. Unfortunately the Theoricae novae do not always represent the perfect transposition of Ptolemean geometry. When those orbs cannot explain certain celestial phenomena, Peurbach is compelled to maintain some of Ptolemy’s mathematical abstractions. Thus, in his universe there are some circles and points to which, in perfect agreement with the Almagest, he attributes a fundamental function: they become the “rule of regularity”Footnote 36 to which one can refer the irregular motions of the real orbs.
In stating the role of these artifices, Peurbach assigns them such an important function that Brudzewo cannot fail to give attention to them and their role in this universe. If Brudzewo had commented on Ptolemy’s mathematical astronomy in the Almagest, he would not have found any reason to criticise these artifices because all the discussion would have remained on a purely geometrical level. Instead, he gives Peurbach the credit for his work in inserting Ptolemy’s mathematical astronomy into a universe of orbs that really move and which have a physical effect on one another through the movement of their parts.Footnote 37 He then considers where Peurbach retained certain mathematical elements derived from Ptolemy and attributed them an active role within the physical spheres. Brudzewo cannot avoid criticising these compromises, which conflict with what he expects to find in the Theoricae. He is particularly explicit in concerning the equant, which, according to Peurbach, represents the “rule of regularity” for the motion of the eccentrics and the epicycles of the planets, and the mean apogee as the index of regularity for the motion of the celestial bodies in their epicycles.
4.1 (a) The equant
In the fifth chapter of book IX of the Almagest Ptolemy specifies that the planets’ epicycles do not physically move in the equant circle, that is in the eccentric circle in relation to whose centre, at twice the eccentricity of the eccentric, they move regularly through equal angles in equal intervals of time.Footnote 38 Instead they move in their own circle, which is different from the equant, around their own centre, which is different from the equant’s centre, and here their motion is irregular. In the Ptolemaic approach this statement cannot be criticised as it refers exclusively to purely geometric circles whose function is purely for calculation purposes. The context in which Peurbach refers to the equant is completely different. He explicitly distinguishes between orbs and the “circulus imaginatus”, called the equant eccentric:
the motion of the orb carrying the epicycle around its own centre and on its axis is nonuniform. However, this irregularity has the following rule of regularity: the centre of the epicycle moves regularly with respect to a certain point of the line of the apogee, as far from the centre of the eccentric as this centre is distant from the centre of the world. And thus this point is called the centre of the equant, and the circle imagined (circulus imaginatus) about it, in accordance with the size of the deferent and in the same plane with it, is called the equant eccentric.Footnote 39
Brudzewo remarks that, in the Theoricae, the equant always has a purely mathematical function. He states that:
insofar as it pertains to the motion of the orbs in itself, the equant is not necessary. The equant does not affect the motion of the real orb at all, since it is a circulus imaginarius. But it is useful in astronomical work or for the calculation of tables, which are calculated according to mathematical principles and conclusions that very frequently cannot be attributed or applied to the motions as they are in their nature or as they appear.Footnote 40
According to Brudzewo mathematicians must inevitably subject the motions of the celestial bodies to their art and calculations, since they cannot give a precise, regular representation of these motions in any other way.Footnote 41 Hence the equant becomes the ratio, the reason by which the apparent irregularity of the motions is reduced to regularity: by knowing how much to add or subtract to a regular motion which is calculated purely on the basis of the observations, the equant enables astronomers to locate the epicycle’s positions at any time in order to achieve the aim of astronomy:
And then, through regular motion [the astronomers] know to what extent irregular motion is greater or lesser than regular motion in terms of the size of the angles or arcs which need to be added or subtracted: this is why they assume equants.Footnote 42
Brudzewo continues his analysis:
According to the astronomers, the motion, which is in reality seen to be irregular, instead becomes regular in order to make it possible to calculate it in a more precise manner. This conviction meant that they have to put in the equants: some circuli imaginati with reference to which they make the varied, irregular motions of the orbs regular. These reduce those irregular motions to regularity in the equant circles [...]Footnote 43
In this reflection he highlights the paradoxical situation which arises in the Theoricae’s planetary spheres, where the eccentric orb carrying the epicycle actually turns, but in an irregular manner around its own centre, whereas the regularity of its motion is referred to a different point, that is the centre of this “circulus imaginatus” which is the equant: a circle, which is distinct from the orb itself and quite different in nature, since it is just a geometrical circle and does not belong to the physical reality. A single motion is thus divided with regard to its quality and its essence: the irregular motion, which belongs to the real orb; and the regular motion, which instead belongs to the purely mathematical abstraction.
This duality, in Brudzewo’s view, suggests that there is a contradiction in the Theoricae’s universe, since every part of this universe must be a physical embodiment of the perfect uniformity of all motion. But if adopting the equant satisfied Peurbach that he had found regularity of motion through a purely mathematical “rule”, Brudzewo’s criticism of the equant is not confined to rejecting it as a mathematical tool: his rejection takes on a more substantial connotation since Peurbach, by adopting the equant, has violated the very essence of celestial nature with its principle of uniformity, according to which the celestial bodies must move uniformly around the centre of their motion.
4.2 (b) The mean apogee: the Moon’s epicycle
Brudzewo’s disagreement with Peurbach for having resorted to purely mathematical abstractions also involves the mean apogee of the lunar epicycle: a geometrical point from which first Ptolemy and then Peurbach calculate the mean motion of the Moon in its sphaerula, that is in its epicycle. Peurbach defines and explains the mean apogee’s function as follows:
Nevertheless, the epicycle revolves in such a way that it moves irregularly around its own centre and axis, but this irregularity is reduced to regularity in as much as the Moon regularly moves away from the mean apogee of the epicycle, whatever this may be, by about 13 degrees and 4 minutes each natural day. The mean apogee of the epicycle is the point of the epicycle’s circumference which is located by drawing a line from the point of the small circle which is diametrically opposite the centre of the eccentric through the centre of the epicycle.Footnote 44
Brudzewo explains how the early astronomers succeeded in determining this point. He also shows how it fulfils its function. In doing this he adds further information to Peurbach’s text and shows how, here too, the Theoricae’s universe is based on the models in the Almagest. As for the equant, also for the mean apogee, he clearly draws attention to how Peurbach was unable to reconstruct the Moon’s motion, which appeared to be irregular, through actual motions of real orbs, and had to resort to mathematical artifices which, as with Ptolemy, remained pure abstractions which could not have any actual interaction with the physical reality of the Theoricae’s orbs.
Through their observations, the ancients noticed that the motion of the lunar body is irregular. So it was impossible to locate the Moon’s true position at any given time and it became necessary to find a method which allowed them to do this by finding the Moon’s regular motion in its epicycleFootnote 45 and through their observations of lunar eclipses estimating its daily mean motion.Footnote 46 They then discovered and proved that the arc of the Moon’s true motion in its epicycle compared to its mean motion is sometimes greater and sometimes smaller:
So by means of demonstrations they found out that the arc of the epicycle, included between the line of mean motion of the centre of the epicycle and the centre of the Moon, [that is, its true motion,] is sometimes greater and sometimes smaller than the arc of the Moon’s mean motion [previously calculated].Footnote 47
By the “mean motion [previously calculated]”, is meant the mean motion of the Moon already determined for the simple lunar model, derived by Ptolemy from the interval between eclipses. Thus, the mathematici had to find an effective method of transforming those irregularities into a uniform motion. In order to do this “Mathematici imaginatos fingunt circulos” the mathematicians conceived imagined circles: they considered a circulus imaginatus described by the lunar body as it traversed its epicycle. They fixed a precise point on this circle that is always invariatus, invariable or fixed, with respect to which the Moon moved regularly in its epicycle. This point is called “aux media” mean apogee or “longitudo longior aequalis” mean greatest distance, to employ Ptolemy’s expression.Footnote 48
The mean apogee of the epicycle is the point marked on the circulus imaginatus by a line drawn from the point of the “small circle” diametrically opposite the centre of the eccentric passing through the centre of the epicycle.Footnote 49 It is an index of regularity: the line marking it is directly and strictly linked to the motion of the centre of the epicycle, and indirectly linked to the motion of the centre of the eccentric. So this line causes this point of the mean apogee, to oscillate continually in longitude, and the point’s motion is one of declinatio et reflexio, here meaning a turning forward and turning back, inclining in one direction and another with reference to the true apogee. The true apogee lies on a line from the Earth passing through the centre of the epicycle extended to the far side of the epicycle:
it is evident then that, while the centre of the epicycle goes from the apogee of the eccentric to the perigee, the true apogee of the epicycle precedes the mean apogee and, while the centre of the epicycle goes from the perigee to the apogee, then the true apogee follows the mean apogee.Footnote 50

The mean apogee of the Moon. O centre of the world; D centre of the eccentric in its motion on the small circle which it describes; E point of the small circle diametrically opposite to D; C centre of the epicycle; G true apogee, determined by the line from O through C; F mean apogee, determined by the line from E through C; M body of the Moon; arc FM mean motion of the Moon on its epicycle, 13 degrees and 4 minutes per day
Brudzewo treats this subject in some detail in one of the more difficult passages of the Theoricae novae. His concern is the functioning of this purely abstract artifice, the mean apogee, depending upon the rather complex geometry of points, lines and circles in order to produce the regularity of the Moon’s motion through a motion of turning forward and turning back of the mean apogee. The aim of his commentary is to show how this component, like the equant, is not explained by Peurbach’s physical universe of spheres, even though the Viennese astronomer makes them interact with the real parts of the Theoricae’s universe.
Nevertheless, his commentary is not wholly negative and Brudzewo also proposes a possible solution to this defect in order to build as real a universe as possible. Thus for the Moon, he proposes replacing the geometry of the mean apogee and the line to the point opposite the centre of the eccentric with a solution that involves real orbs. Referring to a passage in which Ptolemy describes the appearance of lunar phases, Brudzewo states that the oscillation of the mean apogee itself is a motion of turning forward and turning back:
In these words Ptolemy appears to intimate that the turning forward and turning back arises not from computation alone, but from an apparent motion truly in the Moon. For by reason of this turning forward and turning back, the Moon follows certain appearances after its drawing away from the Sun, namely, that it appears concave or hollowed out, and this about the fifth day after conjunction. It also appears swollen, or gibbous, and this about the tenth day after conjunction.Footnote 51
Brudzewo explains that a second epicycle is imagined in order to save these specific appearances that the Moon assumes at these times in its revolution in relation to the Sun: this second epicycle would make the epicycle carrying the Moon accomplish a motion of turning forward and turning back:
Therefore, in order to save this apparent motion in the Moon, some imagine an epicycle in the Moon of such a kind that will have another [epicycle] enclosed within it, which [outer] epicycle moves the epicycle carrying the Moon in a motion of turning forward and turning back, which does not seem unsuitable.Footnote 52
The solution conceived by these astronomers, who Brudzewo does not name, could then be made of two concentric epicycles, with the outer epicycle actually oscillating with the mean apogee. In the figure that follows we show this solution by adding an outer epicycle and its motion to Ptolemy’s lunar model. To explain the lettering, O is the Earth, \(\bar{S}\) the mean Sun, M the Moon, D the centre of the eccentric with apogee A and perigee B, E the point opposite the centre of the eccentric, C the centre of the epicycle, G the true apogee lying on line OCG, F the mean apogee on line ECF. The centre of the epicycle C moves through the mean elongation \(\bar{\eta }\) from \(\bar{S}\), the centre of the eccentric D moves in the opposite direction through \(\bar{\eta }\) from \(\bar{S}\), and the Moon M moves on the epicycle through the mean anomaly \(\bar{\kappa }\) from the mean apogee F. The correction of the anomaly on the epicycle is \(c_{1}\) and the correction to the true position of the Moon seen from O is \(c_{2}\).
Our concern here is the description of the motion of F, which has a turning forward and turning back. The principle here is that an outer epicycle, within which is the epicycle carrying the Moon, has an oscillating motion, turning forward and turning back, carrying with it the inner epicycle, so that the mean apogee F lying on ECF departs from the true apogee G lying on OCG, in the motion of the centre of the epicycle C from A to B, first in the direction GF and then back to G, and in the motion of C in the other half of the eccentric, from B to A, not shown here, first in the opposite direction beyond G and then back to G. In this way, what is only geometry in Ptolemy’s model, F having an inclination towards E, lying on the line ECF, is now actually produced by a real motion of a real spherical body, an oscillating motion of the outer epicycle that is transferred, added to, the rotational motion of the inner epicycle, which thus has both the rotation through \(\bar{\kappa }\) and the oscillation through \(c_{1}\), so the motion of the Moon M with respect to the true apogee G is \(\bar{\kappa }\pm c_{1}\). What was just geometry has now become the real motions of real spherical bodies, of two concentric epicycles.Footnote 53

Note that a difficulty in interpreting this passage has been introduced by a marginal note, that interprets the second epicycle as having an entirely different purpose:
Some imagine that the Moon has two epicycles, one larger, the other smaller, in which [i.e. the smaller] its [the Moon’s] body is placed, and such that the higher [i.e. larger, outer] epicycle moves only with the motion of turning forward and turning back. And as far as concerns that spot, which is observed in the Moon, it always appears one and the same on account of this epicycle, which would not occur if there were not such an epicycle.Footnote 54
This refers to the same spot, or spots, on the Moon always facing the Earth, which is incompatible with Brudzewo’s description of the function of the outer epicycles, as its motion of turning forward and turning back cannot cause the same side of the Moon to face the Earth. It does not appear to be part of Brudzewo’s text, and its inclusion as a marginal addition, perhaps by someone who did not understand Bruzewo’s own description, is in error, or is at least extraneous, and has led to confusion in interpreting the purpose of the second epicycle, which, again, cannot cause the same side of the Moon to face the Earth.Footnote 55
4.3 (c) The mean apogee: the superior planets’ epicycle
In the analysis devoted to the three superior planets Brudzewo makes the same criticism he addressed to the mean apogee of the Moon, and in the same terms. The main difference is just the starting point of the line which marks the mean apogee of the epicycle: for the Moon it is the point of the “small circle” diametrically opposite the centre of the eccentric; but for the superior planets it is a fixed point, that is, the centre of the equant circle. His analysis of the mean apogee of the superior planets aims to show clearly how this pure geometry is not in itself sufficient to the reality of the celestial orbs. The epicycle of each planet is in fact deep in the concavity of the eccentric that contains it, and its surface touches the superior concave surface of the eccentric orb at one point. This point is called the “point of concavity” and always remains unchanged being on the line from the centre of the eccentric passing through the centre of the epicycle.Footnote 56 The line from the equant point passing through the centre of the epicycle locates a point on the epicycle called the mean apogee “from which the uniform motion of the plant in the epicycle is to be computed”. Brudzewo remarks that because of the motions in each planetary sphere, the geometrically determined point that is the mean apogee continually changes its position with respect to both the concave surface of the eccentric, the concavity at which the epicycle is located, and to the convex surface of the epicycle itself. The point of the mean apogee, however, remains “invariable” if one considers it as a mathematical point on the circumference of the circulus imaginatus produced by the motion of the planet in its epicycle:
Therefore, the planet in the epicycle will now have a regular and uniform motion about the centre of the equant, from which a line drawn through the centre of the epicycle show the point from which the uniform motion of the planet in the epicycle is to be computed, which [point] is called the mean apogee. The mean apogee is variable with respect to the concavity in which the epicycle is located, as it continually is under one and another point of that concavity. The mean apogee is also variable with respect to the actual convex surface of the epicycle itself such that it continually passes under one and another point of the surface of the real epicycle on account of the motion of the epicycle. However, the mean apogee does not vary with respect to the circumference imagined on the epicycle, in which the planet’s motion and its revolution are calculated, for it is necessary that the point of the mean apogee is always one and the same in any location for the reasons which were stated in the case of the Moon.Footnote 57
This explanation by Brudzewo aims to give a clear picture of the interaction between the mean apogee considered purely mathematically and the real structure of the celestial spheres. Adhering consistently to the criteria which guide his reading, what emerges from the analysis concerning the equant and the mean apogee is the way in which considering these physically rather than just mathematically is a serious problem for the universe as described by Peurbach.
5 Real motions and apparent motions
Peurbach brought the irregularity of the motions of his orbs back to regularity through the equant and the mean apogee of the epicycle. As we have seen, in his analysis Brudzewo does not restrict himself to the function of those mathematical artifices for astronomical calculation, but goes beyond Peurbach to show the reality of the orbs that produce those motions, to a deeper understanding of the Theoricae’s universe.Footnote 58
The same observed phenomena described in the Almagest, which determine the circles that make up each specific planetary model, are described in Brudzewo’s Commentariolum, where they now determine the partial orbs that form the models in the Theoricae novae. Indeed, Brudzewo describes the various appearances that require the eccentrics and epicycles for each planet, and also provides detailed reasons for adopting the other partial orbs. In this way, he demonstrates the reasons “quod” that determined the structure of these particular planetary spheres. In the sphere of the Moon and of the five planets, the star is fixed onto a sphaerula —the epicycle—which is carried by the eccentric. The eccentric orb, located between the two surrounding (circumpositi) orbs of variable thickness, turns around its own centre and carries the epicycle through its own complete revolution according to its own period peculiar to each planet. The zodiac is the band of the eighth sphere on which the motions of the celestial bodies are seen. The centre of the zodiac is the centre of the world, from which the centre of the eccentric is at a fixed distance, different for each planet.
In considering the movement of the celestial bodies one must therefore consider two kinds of motion:
-
the real motion, the motion the eccentric orb actually performs carrying the epicycle and the motion the epicycle performs carrying the star located within it;
-
the apparent motion, the motion of the epicycle and the motion of the star in the epicycle seen in the zodiac from the centre of the world.
Brudzewo always has in mind the distinction between the real universe, which by its nature is the realm of perfection and immutability where the motions are perfectly circular and uniform, and the phenomenal universe, as it appears on the band of the zodiac to an observer placed at the centre of the world. There is a close relationship between the real universe and the phenomena for which, according to Brudzewo, the real world must have its own identity and its own characteristics, to which the phenomenal world is subordinate, since it is the reflection of the composition of the motions of celestial reality.
6 The irregular motions in Peurbach’s universe
The text of the Theoricae novae is very concise and simply defines the quality of the motions of the orbs that carry the bodies of the planets and of the luminaries. From Peurbach we only know that:
-
(a)
The eccentric carrying the Moon’s epicycle, although it moves on its own axis and around its own poles, it does not move about them regularly: “quamvis eccentricus epicyclum deferens super axe atque polis suis moveatur, non tamen super eisdem regulariter movetur”;Footnote 59
-
(b)
The eccentric carrying the epicycle of each of the planets around its own centre and its poles is nonuniform: “Motus autem epicyclum deferentis super centro et polis suis difformis est”;Footnote 60
-
(c)
The epicycle carrying the Moon moves irregularly around its own centre and axis: “Circumvoluitur tamen epicyclus taliter ut super centro proprio atque axe irregulariter moveatur.”Footnote 61
-
(d)
The epicycle carrying each of the planets moves irregularly around its own centre: “[Huius motus] est super centro epicycli irregularis.”Footnote 62
To each of these celestial bodies Peurbach assigned an irregular motion and thus built a universe that contrasts with the true nature of the real world. On this subject, Brudzewo’s reading of the Theoricae novae proves once again to be a singular one. He stands out from the other commentators, who in their desire to confirm all Peurbach’s statements, provide demonstrations with the sole intention of supporting, in an uncritical manner, the correctness of these assumptions, even on a subject as important as this one.
Brudzewo cannot accept these assumptions since he considers that the Theoricae novae’s universe must be the description of the celestial world as it really is, and the motions that take place in that world must reflect the perfect circularity and uniformity imposed by the principles. Consequently, Peurbach’s assumptions are not true. Nevertheless, he does not deny them categorically, and his analysis becomes particularly subtle because the subject under discussion enters the most essential part of Peurbach’s universe. Orb by orb he tries to understand the logic underlying the reasoning that led the Viennese astronomer to establish an almost universal irregularity in the perfection of the celestial world. It was only once he had proved that these statements were founded on ambiguity, and thus only after he had invalidated the absoluteness of those assumptions, that Brudzewo could confirm that the motions of the celestial bodies, when considered “in se et absolute”, in themselves and in an absolute sense, are rigorously uniform. He could therefore declare that:
-
(a)
If the motion of the eccentric carrying the epicycle of the Moon is considered in an absolute sense, that is, as it is on its axis and on its poles and about its centre, without referring it to the zodiac, then its motion is regular: “si motus ecentrici Lunae absolute accipiatur (prout scilicet est in suo axe et polis et circa centrum ecentrici, non referendo ad Zodiacum), sic motus eius est regularis”;Footnote 63
-
(b)
If the motion of the eccentric carrying the epicycle of each planet is considered in itself and in an absolute sense, then de facto it is uniform: “motus deferentis epicyclum, in se et absolute consideratus, de facto uniformis est”Footnote 64;
-
(c)
If the motion of the epicycle carrying the Moon is considered simpliciter in itself and in an absolute sense, in respect only of its own centre and not in relation to any other point, then it is uniform: “epicyclus [movetur uniformiter] circa centrum suum, quod quidem verum est considerando motum epicycli simpliciter in se et absolute, sine relatione ad aliquem punctum”Footnote 65;
-
(d)
If the motion of the epicycle carrying each of the planets is considered simpliciter in itself, then it is uniform.
In the following exposition we will try to bring out the elements upon which Brudzewo’s critical analysis is based.
6.1 (a) The eccentric carrying the epicycle of the Moon
To describe the motion of the eccentric carrying the Moon’s epicycle Peurbach states that:
even if the eccentric carrying the Moon’s epicycle moves around its own axis and its own poles, it does not move about them regularly.Footnote 66
In the Theoricae novae’s universe the epicycle of the Moon, in its apparent motion, is seen to move through the zodiac uniformly while its real motion in its eccentric orb is nonuniform. To describe the motion of the eccentric carrying the epicycle of the Moon, Peurbach says:
The orb carrying the epicycle moves regularly about the centre of the world in the order of the signs, such that the centre of the epicycle moves through about 13 degrees and 11 minutes each natural day.Footnote 67
In these words Peurbach pointed out the direction and the regularity of the motion of the Moon’s eccentric in relation to the centre of the world: he has then defined the apparent motion of the Moon’s epicycle.
In the analysis of the Sun’s sphere, which Brudzewo had just completed, he noticed that the Sun, in the Theoricae’s universe, realises the essence of celestial nature and its principles: its motion is actually performed in its eccentric uniformly and the irregularity of its apparent motion is the result of its eccentricity to the centre of the universe. So it is natural for Brudzewo to state that:
the Sun moves uniformly in its eccentric is the first principle in astronomy, so that when it is denied, there is nothing more to be considered in astronomy.Footnote 68
The Sun actually represents a reference for all the celestial bodies and in particular for their motions. Brudzewo recalls Peurbach’s remark that:
Because of their motion, each of the six planets has a natural connection with the Sun: the latter’s motion is as though a kind of mirror for each of them, and a rule for measuring the motions of the planets
in order to underline how the motions of the orbs carrying the apogee and the orb carrying the Moon’s epicycle have “a natural connection with the Sun”.Footnote 69
Addressing himself directly to his students, he explained how anyone can derive the regularity of the apparent motion of the Moon’s epicycle in relation to the Sun:
you too can calculate it by proceeding in this manner: multiply the motion that the Sun performs in a day by the period of a month and add 360 degrees to the product, and there will result the degrees covered by the centre of the epicycle in a month. Divide this sum by the period of a lunation [a synodic month] and in the quotient you will find how far the centre of the epicycle, or the [orb] carrying the epicycle, moves uniformly each day in the zodiac.Footnote 70
In fact he goes on to specify that:
with the aid of mathematics, it is possible to demonstrate that the epicycle’s centre moves regularly about the centre of the world. Indeed, in relation to the line of the Sun’s mean motion the centre of the epicycle forms equal angles about the centre of the world and covers equal arcs of the zodiac in equal intervals of time. This means that it moves regularly, just as [Peurbach’s] text says, namely, 13 degrees 10 minutes, etc.Footnote 71
This regularity is referred to the elongation between the line of the Sun’s mean motion and the line of the mean motion of the epicycle of the Moon.Footnote 72 For Peurbach this regularity of motion becomes the premise from which he deduces the irregularity of the epicycle’s real motion, which he expresses in a first corollary:
From these premises it follows that, although the eccentric carrying the epicycle moves around its axis and its poles, nevertheless, it does not move around them regularly.Footnote 73
Thus, Peurbach then inserted irregular motion into the perfection of celestial reality, and this is just the first of a series of declarations of irregularity which he also extended to the eccentrics of all the planets and to the epicycles carrying both the body of the Moon and the planets.
Brudzewo could not remain impassive in the face of these declarations and refused to comment on the text of the Theoricae in an uncritical way. He tried to reconstruct the underlying logic that guided Peurbach in his deductions. Not only does Peurbach state that the real motion of the Moon’s epicycle is irregular in its eccentric and in relation to its centre, but he also shows how this can be proved geometrically:
In fact, if equal angles are marked about the centre of the world towards the apogee and the perigee [of the eccentric], the angle that is towards the apogee includes an arc of eccentric greater than [the arc included by] the other angle towards the perigee.Footnote 74

By following Peurbach’s instructions one can mark the circumference representing the zodiac centred in T as ABCD, and the circumference representing the eccentric centred in F, as GHLM, with the apsidal line AC with apogee G and perigee L. According to Peurbach, if equal angles ATB and DTC are taken at the centre of the world T, the arcs they determine on the zodiac AB and CD are equal, but the arcs they determine on the eccentric are not equal, with arc GH towards apogee greater than LM towards perigee. Hence, in equal intervals of time, measured in terms of equal angles at the centre of the world T, the centre of the epicycle covers unequal arcs on the eccentric circle: according to Peurbach, this means that the motion of the epicycle in its eccentric is irregular. But, according to Brudzewo, the regularity of the motion of the epicycle in its eccentric must be referred to the centre of the eccentric F, not to the centre of the zodiac T. Having grasped the ambiguity which had misled Peurbach, Brudzewo can affirm in his commentary that:
the first corollary has truth, namely, that the eccentric moves irregularly about its own axis and poles, and about its own centre, but—Brudzewo adds—only if its motion in the zodiac is evaluated in relation to the centre of the eccentric and not in relation to the centre of the world.Footnote 75
But in a second corollary Peurbach further specified how an irregularity such as this occurs:
Second [corollary]. The closer the Moon’s epicycle is to the deferent’s apogee, the more rapidly its centre will move, and the closer it is to the perigee of the same deferent, the more slowly [its centre will move].Footnote 76
This is shown in the figure where arc GH is greater than arc LM and both are traversed by the centre of the epicycle in the same time, a second inconsistency, which does not escape Brudzewo’s refined analysis. Peurbach has not, in fact, kept the circles and the corresponding centres about which the motions take place rigorously distinct: the zodiac, on which one observes the apparent motion of the epicycle; and the eccentric, in which the epicycles’ real motion takes place. Instead he has subordinated all the relationships between these two circles while keeping the observation point unchanged, and he has evaluated the different motions in relation to one unique point, the centre of the world T. With respect to this unique observation point, he also deduced the greatest or smallest velocity of real motion: unequal arcs on the eccentric correspond to equal angles at the centre of the universe, that is to say, that at equal intervals, evaluated about the centre of the world, the Moon’s epicycle will actually sometimes be faster and sometimes slower in its eccentric, that is in the orb where it actually moves and around the centre of its motion, because the smaller arc of the eccentric near perigee will be covered by the epicycle at a slower speed than the greater arc of the eccentric near apogee, covered in a faster speed, both arcs traversed in equal intervals of time. Thus, Peurbach had confused apparent motion with real motion or rather assimilated the two.
Having clarified the ambiguities on which Peurbach’s statements are based, Brudzewo could confirm with absolute certainty that the true nature of the eccentric orb carrying the Moon’s epicycle, as with all celestial bodies, should be expressed through perfectly circular and uniform motions around its own centre, which Peurbach has not done. In fact, “if the motion of the eccentric of the Moon is considered in an absolute sense, that is, as it is on its axis and on its poles and around the centre of the eccentric, without referring it to the zodiac, then its motion is regular”:
si motus ecentrici Lunae absolute accipiatur (prout scilicet est in suo axe et polis et circa centrum ecentrici, non referendo ad Zodiacum), sic motus eius est regularis.Footnote 77
6.2 (b) The eccentric carrying the epicycle of the planet
The superior planets—Mars, Jupiter and Saturn—are seen moving in an irregular way in the zodiac in different ways: in their latitudinal movements, their longitudinal paths, and in relation to the Sun. Brudzewo draws the description of these irregularities from the Almagest’s text, which he quotes in full to underline that the planets have an irregular motion in relation to both the zodiac and the Sun:
In these words Ptolemy explains how the five wandering stars or planets have an irregular motion in the zodiac because they sometimes move north of the ecliptic, sometimes south of it, and sometimes in the ecliptic; sometimes [they move] slowly and sometimes rapidly. Also, with respect to the Sun they have an irregular motion, for when they were seen near the Sun, their motion, especially of the three superior planets, appeared fast, when near quadrants from the Sun, they were seem not to move but to stand still, that is, their motion was so insensible that they were said more to stand still than to move, and when they were in the diameter [opposition] to the Sun they were directed opposite to the signs.Footnote 78
To describe the motion of the eccentric carrying the epicycle of the planets Peurbach states that:
The motion of the [orb] carrying the epicycle [of each planet] around its own centre and its poles is nonuniform.Footnote 79
Once again Peurbach introduced irregularity into the realm of perfection and, in no uncertain terms, Brudzewo explicitly declares the falseness “non est verum” of this:
What the Magister [Peurbach] says, that the centre of the epicycle moves irregularly around the centre of the eccentric, is not true if considered in absolute terms.Footnote 80 This would in fact be in contradiction with the principle which states that each motion of a celestial body is simple and uniform, and in contradiction with the philosophia according to which the motion of a simple body must be simple and uniform. So the motion of the orb carrying the epicycle, considered in itself and in an absolute sense, is actually uniform.Footnote 81
Once again he reveals how Peurbach’s remarks about his own universe derive from the fact that he confused apparent motion with real motion. “What the Magister [Peurbach] says” is true only in this particular, partial interpretation of these motions: that is, when the motion of the eccentric is evaluated from some point of observation inappropriate with regard to its real motion—as the centre of the world is with regard to the eccentric orb.Footnote 82 But in Peurbach’s text this distinction does not appear, and he describes the orb carrying the epicycle in itself without defining its relation to anything else:
the motion of the [orb] carrying the epicycle [of each planet] around its own centre and its poles is nonuniform.Footnote 83
In this absolute sense he attributes irregular motion to the orbs which carry the epicycles.
6.3 (c) The epicycle carrying the Moon
To describe the motion of the epicycle which carries the Moon Peurbach states that:
The epicycle turns in such a way that it moves irregularly around its own centre and axis.Footnote 84
In Peurbach’s text there is no misunderstanding, the irregularity of the motion of the epicycle occurs with respect to its own axis and to its own centre, but for Brudzewo this contradicts the principle of celestial reality. For the epicycle of the Moon, he cites Campanus of Novara:
According to Campanus, the Moon moves in its epicycle in a regular motion, and the epicycle does the same, around its own centre. And this is certainly true if one considers the motion of the epicycle simpliciter in itself and in an absolute sense, without reference to any point, for uniform motion pertains to each celestial orb because of its nature.Footnote 85
In fact, Campanus never writes in his Theorica planetarum that the motion of the Moon in its epicycle is uniform in an absolute sense, only that it is uniform with respect to the mean apogee, so it is curious that Brudzewo uses Campanus as witness to his own principle that the motion of the epicycle is uniform in an absolute sense and with respect to its centre.Footnote 86 Nevertheless, with this statement, the absolute uniformity of motion is recognised as intrinsic to the essence of celestial nature. Brudzewo makes no further reference to the principle, but appeals directly to the authority of nature: that “uniform motion is proper to each celestial orb because of its nature.”Footnote 87
But Peurbach considers the motion of the epicycle, not in an absolute sense and with respect to its centre, but with respect to another point:
what the Magister [Peurbach] says, that the epicycle turns in an irregular manner, is also true with regard to a sight (aspectum) situated at the centre of the world.Footnote 88
Peurbach ascribed irregularity to the epicycle carrying the Moon because he had evaluated its motion by reference to an improper point, a motion that by its nature is absolutely uniform becomes irregular if it is considered “with regard to a sight situated at the centre of the world”. The misunderstanding is still the same, but this time the centre of the world becomes “the sight” of the observer. Here Brudzewo offers confirmation and proof of this misunderstanding, quod sic patet, which is clear in this way:
If, in fact, the epicycle moves regularly with respect to a line to the centre of the world, then the arc of the mean motion of the epicycle would always be equal to [the arc of the same epicycle] which is situated between the centre of the Moon and the line of the mean motion of the centre of the epicycle, or, which is the same, the true apogee of the epicycle. But this does not happen. Only when the centre of the epicycle is located in the apogee or in the perigee of the eccentric are these arcs equal; while when the centre of the epicycle goes away from the apogee of the eccentric, moving towards the perigee, the arc of the Moon’s mean motion in the epicycle is always smaller than the arc in the epicycle situated between the centre of the Moon and the line of the mean motion of the centre of the epicycle, [that is, the true apogee of the epcycle]. In the other half of the eccentric, it is the opposite, [that is, the arc of the mean motion of the Moon in the epicycle is greater than the arc between the centre of the Moon and the line of the mean motion of the centre of the epicycle].Footnote 89
6.4 (d) The epicycle carrying the planet
To describe the motion of the epicycle which carries the planets, Peurbach states that:
[The motion of the epicycle carrying each of the planets] is irregular around the centre of the epicycle.Footnote 90
According to Brudzewo:
What the Magister [Peurbach] said, that the motion of the epicycle is irregular around its centre, must be understood not in an absolute sense and by considering the motion of the epicycle by itself, but with respect to the eye (oculum), which observes those motions from the centre of the sphere of the signs. For if there [in the centre of the world], the irregular motion of the epicycle [is seen to] takes place in such a way that when the centre of the epicycle is traveling from the apogee of the eccentric to the perigee, the arc of the mean motion of the planet in the epicycle is always smaller than the arc of the epicycle contained between the true apogee of the epicycle and the centre of the planet, and as much smaller as corresponds to the distance between the centre of the sphere of the signs and the centre of the equant [i.e. the equation of centre]. While in the other half [of the eccentric, the arc of the mean motion] is greater. So in this way it is irregular with respect to the centre of the world.Footnote 91
Here, the centre of the world becomes the “eye” from which motion happens, or is seen, as irregular. Brudzewo has proved successful in identifying the point of observation from which Peurbach let himself be led astray, that is, by considering the motion of the planet in the epicycle as seen from the centre of the world, from which it is irregular. Brudzewo’s conclusion is clear “sic ergo fit irregularis in ordine ad centrum mundi”: that motion becomes irregular with respect to the centre of the world or, more accurately, with respect to the eye that observes that motion from that position.
7 Weaknesses of Peurbach’s approach: the astronomers’ point of observation
In all the cases we have examined, Brudzewo highlighted the fact that Peurbach must have acknowledged that there was irregularity in the world of celestial perfection, since he shared the approach adopted by the astronomers, who relate the motions of the stars to their observation point, the Earth, which is motionless at the centre of the universe. The astronomers, in fact:
locate the positions of the stars through their visual perception, that is, as if both the eyes [of the observer] were standing at the centre of the world looking outward at the positions of the stars along lines that can be drawn from the eye to the stars: they proceed in this manner and trust to the faculty of their senses. [...] They can determine the stars’ position with reference to the centre of the world precisely because it is always motionless and immutable in relation to all the other celestial bodies.Footnote 92
This is what the astronomers do: their concern is apparent motions, and the model underlying their practice need not correspond to the real universe, but is just an instrument to assist with their calculations.
Nevertheless, Peurbach cannot permit himself the same freedom allowed to mathematical astronomers. According to Brudzewo, Peurbach, besides wishing to account for the phenomena and predict the positions of the stars, also wanted to build a universe reflecting the true essence of celestial nature with its principles of perfect uniformity and circularity of motion. The reading of the Theoricae novae by Brudzewo takes these very requirements into consideration and analyses their content in the light of these requirements. Perhaps this is the reason why, among all the commentaries on the Theoricae, Brudzewo’s Commentariolum is the only one containing an analysis which grasped the weak points and ambiguities in Peurbach’s work. Peurbach, in fact, systematically attributed the apparent motion, as seen in the zodiac from the centre of the world, directly to the eccentric orb or the epicycle, that is, to orbs, each of which actually performs its own motion in relation to its own centre, which is always different from the centre of the world. By doing this he deprived those orbs of their essential nature, to rotate uniformly in themselves and in an absolute sense. Thus, Brudzewo raised a problem that undermined the very foundations of that universe. Nevertheless, his precise, subtle analysis proved that “the irregularities in the motions of the real orbs” stated by Peurbach, if analysed in their more general context, did not possess an absolute value, but were derived from considerations of a very particular kind, related to the particular point of observation from which Peurbach derived them. As we have seen, Brudzewo does not let the apparently coherent structure of the Theoricae’s universe lead him astray. He remains consistent with his own principles and his reading never loses sight of his principal aim: to determine whether Peurbach’s orbs embody the reality of celestial nature. His analysis identified the multiple inconsistencies inherent in those planetary spheres and revealed a problem that could no longer be neglected and ignored.
8 Brudzewo and Copernicus in Cracow
Brudzewo is aware of the problems raised by his reflections and of the criticism they could attract. At the end of his course he expresses his consciousness of the unusual character and innovative scope which distinguish his reading of the Theoricae novae. He then exhorts the “diligent reader”, reflecting on the most profound and essential questions pertaining to the study of the stars, to bring forth further improvements by taking a new approach (noviter):
Here ends the Commentariolum on the Theoricae novae of Georg Peurbach brought together by Master Albert of Brudzewo for the proper introduction of students in the University of Cracow for a reading of the same [Theoricae novae]. From the unusual remarks expressed in this Commentariolum that have been set forth not according to received doctrine and science, the diligent reader should not readily rise up in indignation, but let him apply himself to bring forth anew what is more certain and profound in furtherance of this science, incited by similar effort of these kinds, if he is one who will permit [these things], and not receive those which have thus far been childishly brought forth, lest, desiring to criticize, he would openly show his own ignorance rather than more properly have remained silent.Footnote 93
The analysis we have conducted thus far of the Commentariolum allows us to grasp the meaning of this passage, with which Brudzewo ended his astronomy courses at the Faculty of the Arts at Cracow University in the academic years 1483 and 1488, that what he was doing was entirely new and his auditor or readers should not become indignant, but should also apply himself to improve this science.
In 1493 the same Commentariolum was read again in the same Faculty. This time it was Simon Sierpc who explained it to his students, and the concluding passage did not appear in the manuscripts used to teach the course.Footnote 94 That Simon Sierpc chose to adopt the work of his eminent predecessor for his lectures demonstrated that he shared the reflections made by Brudzewo which showed the inconsistencies in the traditional universe presented in Peurbach’s Theoricae novae. Further confirmation that those “unusual remarks” aroused interest and were shared by other scholars comes from the decision of one of Brudzewo’s students, Johannes Otto de Valle Uracense, to print two editions in the years 1494 and 1495.Footnote 95 Indeed, it seems likely that a common understanding arose at Cracow University in relation to this text, and a shared attitude towards the astronomy of the time. And this happened at the same period that Nicolaus Copernicus was a student at that same university.Footnote 96 Even if one excludes the possibility that Copernicus learned astronomy directly from Brudzewo’s lectures, the young student, immersed in that particularly fertile climate, could have been influenced by those reflections and particularly by Brudzewo’s singular approach to analysing the universe of the Theoricae novae. Indeed, in Copernicus’s works we can see the same objections brought forth by Brudzewo, the same inconsistencies in the name of the same principles.
9 Copernicus’ Commentariolus: a new point of observation
Copernicus opens his Commentariolus with a reflection about what astronomy had already achieved in the past. He examines both the homocentric spheres of Eudoxus and Callippus and the tradition of the eccentrics and the epicycles. Both aimed to save the apparent motions of the stars through the principle of uniformity, which was considered to be essential to the celestial spheres because of their spherical shape, saving the irregularity of apparent motions through the composition of a number of regular motions. Although he shared these a priori assumptions, none of the solutions previously proposed succeeded in reaching this objective. Copernicus, in his Commentariolus, intended to find “a more reasonable model composed of circles” which would respect those axioms in a more rigorous manner and would restore the uniformity of motions:
I understand that our predecessors assumed a large number of celestial spheres principally in order to account for the apparent motion of the planets through uniform motion, for it seemed highly unreasonable that a heavenly body should not always move uniformly in a perfectly circular figure. They have discovered that by the arrangement and combination of uniform motions in different ways it could be brought about that any body would appear to move [irregularly] to any position.
Calippus and Eudoxus, attempting to carry this out by means of concentric circles, could not by the use of these give an account of everything in the planetary motion, that is, not only those motions that appear in connection with the revolutions of the planets, but also that the planets appear to us at times to ascend and at times to descend in altitude, which concentric circles in no way permit. And for this reason a preferable theory, in which the majority of experts finally concurred, seemed to be that it is done by means of eccentrics and epicycles.
Nevertheless, the theories concerning these matters that have been put forth far and wide by Ptolemy and most others, although they correspond numerically [with the apparent motions], also seemed quite doubtful, for these theories were inadequate unless they also envisioned certain equant circles, on account of which it appeared that neither in its deferent sphere nor with respect to its proper centre does the planet always move with uniform velocity. Therefore a theory of this kind seemed neither perfect enough nor sufficiently in accordance with reason.Footnote 97
This kind of solution persuaded Copernicus to research a new order for the world:
Therefore, when I noticed these [difficulties], I often pondered whether perhaps a more reasonable model composed of circles could be found from which every apparent irregularity would follow while every [circle] in itself moved uniformly, just as the principle (ratio) of perfect motion required.Footnote 98
These words return to the criteria which guided Brudzewo’s criticism of Peurbach’s Theoricae novae: in the name of the principle of the perfect circularity and uniformity of motions considered “in se et absolute”, it is inadmissible to attribute irregular motion to the orbs which actually carry the epicycles and to the epicycles themselves, which carry the celestial bodies. But Brudzewo’s insistence throughout his Commentariolum that certain aspects are a requirement or necessity which must be respected is transformed by Copernicus into the basis on which he will found his search for an alternative solution: “a more reasonable model composed of circles [...] from which every apparent irregularity would follow.” And the focal point around which the more general structure of the new image of the world will be built is the new point of observation.
In the Theoricae novae this was fixed on the Earth, which was at the centre of the universe as required by Aristotelian and Ptolemaic tradition. But Brudzewo had demonstrated that Peurbach’s equivocal, problematic statements derived in part from the position of the observer. In his analysis he had perceived that this particular point of observation represented a serious problem for the Theoricae’s universe, for the motions of spheres that were irregular as seen from the Earth, and that this problem had led Peurbach to contradict the principles of celestial nature.
In the three first postulates of his Commentariolus, Copernicus almost seems to share Brudzewo’s reflections. He seems to be proposing the solution to the problem: he transfers the same point of observation to the fourth sphere, which becomes the sphere of the Earth, below the spheres of Saturn, Mars and Jupiter. The Earth is no longer the centre of the world, but only the centre of the Moon’s sphere; it is no longer motionless but, like the other planets, it turns around the Sun which has now become the new centre of the world.Footnote 99
First postulate: There is no one centre of all the celestial orbs or spheres.
Second postulate: The centre of the Earth is not the centre of the universe, but only the centre towards which heavy things move and the centre of the lunar sphere.
Third postulate: All spheres surround the Sun as though it were in the middle of all of them, and therefore the centre of the universe is near the Sun.Footnote 100
From this new point of observation flow four other postulates showing the consequences of this inversion of perspective. The position of the observer has changed, but so have the conditions in which he operates: he is no longer motionless, observing the celestial bodies moving in the heavens around him, but is himself in motion as he observes the celestial bodies.
The universe can assume a new physiognomy:
Fifth postulate: Whatever motion appears in the sphere of the fixed stars belongs not to it but to the Earth. Thus the entire Earth along with the nearby elements rotates with a daily motion on its fixed poles while the sphere of the fixed stars remains immovable [...]
Sixth postulate: Whatever motions appear to us to belong to the Sun are not due to [motion] of the Sun but [to the motion] of the Earth and our sphere with which we revolve around the Sun just as any other planet. And thus the Earth is carried by more than one motion.
Seventh postulate: The retrograde and direct motion that appears in the planets belongs not to them but to the [motion] of the Earth. Thus, the motion of the Earth by itself accounts for a considerable number of apparently irregular motions in the heavens.Footnote 101
These postulates, together with the a further postulate stating the immensity of the Copernican universe in comparison with the dimensions of the universe described by Aristotle and Ptolemy, will, as Copernicus himself declared, allow scholars to consider a new universe in which “the uniformity of the motions may be preserved.”Footnote 102 The requirement invoked by Brudzewo in his Commentariolum, that the real motions of the celestial bodies must be regular, was not entirely new, although it appears that he thought of it on his own; yet the image of the world that could have realised that principle was still far away.
10 Copernicus’s De revolutionibus
In books IV and V of De revolutionibus orbium coelestium, when Copernicus submits the Ancients’ theories to his critical analysis, his words echo the same objections found in Brudzewo’s writing, which Copernicus develops in the name of the same principles, showing the same inconsistencies concerning: (a) the motion of the eccentric carrying the Moon’s epicycle; (b) the motion of the epicycle which carries the lunar body; (c) the equant of the planets.
10.1 (a) The motion of the eccentric carrying the Moon’s epicycle
In the first chapter of the fourth book of De revolutionibus, Copernicus set out the model that the Ancients had conceived for the Moon and remarked that they “believe in fact that with matters so arranged, they correspond to the appearances.”Footnote 103 But in the following chapter about The faults in these assumptions he reconsidered the same concept:
Our predecessors indeed assumed such a combination of circles as though agreeing with the lunar appearances, but if we consider the reality more carefully, we shall find this hypothesis neither suitable enough nor sufficient.Footnote 104
Copernicus underlined the incoherence hidden within the hypothesis proposed by the Ancients regarding the motions of the Moon: uniform motion was attributed to appearance, while irregular motion was attributed to reality:
For when they acknowledge that the motion of the centre of the epicycle is uniform about the centre of the Earth, they must also acknowledge that in its own eccentric orb, which it describes, it is nonuniform.Footnote 105
In order to make this relationship visually clear “Quae ut oculis subiiciantur” he inserted a diagram into his text in which the circle ABCD centred in E, the centre of the Earth, represents the apparent motion of the epicycle through AB uniformly to the east with respect to E and the small circle HM represents the epicycle centred in G. The circle DG, centred in F, represents the eccentric deferent, which moves around the Earth through AD uniformly to the west so that its centre F describes a “small circle” around E.Footnote 106 The result is that the motion of the centre of the epicycle through DAB is twice its motion in the circle around the Earth, that is, DAB = 2 AB, and while the motion through DAB is uniform, the motion on the eccentric DG is nonuniform.

Copernicus, De Revolutionibus, 1543, f. 99v
By referring to the diagram, Copernicus explains the situation of the motions as conceived by the Ancients:
Since if, for example, angle AEB is assumed to be 45 degrees, that is, half a right angle, and equal to AED, so that the entire BED is a right angle, and the centre of the epicycle is taken to be in G and GF be joined, it is obvious that exterior angle GFD is greater than interior and opposite angle GEF. Therefore arcs DAB and DG, both described in the same time, are unequal, so that when DAB is a quadrant, DG, which meanwhile the centre of the epicycle describes, is greater than a quadrant of a circle. It was, however, shown that at half-Moon both DAB and DG were a semicircle, therefore the motion of the epicycle that it describes in its eccentric is nonuniform.Footnote 107
It is now that the contradiction inherent in the hypothesis of the lunar motions becomes evident. Copernicus continues his analysis:
But if this were so, what shall we reply with regard to the axiom, that the motion of the heavenly bodies is uniform and only with regard to appearance does it appear nonuniform, if the apparent uniform motion of the epicycle is in reality nonuniform, and there take place completely the opposite of the established and assumed principle?Footnote 108
But his analysis does not stop with this contradiction; he goes into the problem even more deeply, employing increasing subtlety. So he adds:
But if you were to say that the epicycle moves uniformly about the centre of the Earth, and that this is sufficient to maintain uniformity, of what sort will that uniformity be, in a foreign circle in which the motion of the epicycle does not occur, although it does occur in its eccentric?Footnote 109
Brudzewo had used the same critical terms when discussing precisely the same contradictions presented in De revolutionibus.Footnote 110
10.2 (b) The motion of the epicycle carrying the lunar body
The “defect” that Copernicus detects for the Moon in its eccentric also extends to the motion that his predecessors attributed to it in its epicycle:
Likewise, we also wonder at this, that they also intend the uniformity of the Moon in its epicycle to be understood, not in relation to the centre of the Earth through the line, namely EGM, to which with good reason the uniformity ought to be referred, in accordance with [the motion of] the centre of the epicycle, but with respect to a certain different point—and in addition that the Earth is midway between that point and the centre of the eccentric—and that the line IGH is as though the index of the uniformity [of the motion] of the Moon in the epicycle, which also sufficiently shows that this motion is in fact nonuniform.Footnote 111
The “certain different point” with the Earth halfway between it and the centre of the eccentric is the point I diametrically opposite to the centre of the eccentric F, and the line IGH is the “index of the uniformity [of the motion] of the Moon in the epicycle”, from the mean apogee H, which Brudzewo in his Commentariolum describes as having an inclinatio et reflexio, a turning forward and turning back motion. Copernicus’ criticism of the mean apogee is the same as that made by Brudzewo who, in his Commentariolum emphasised the same question: the uniformity of the motion of the Moon with reference to an abstract point.
10.3 (c) The equant of the planets
In book V of De revolutionibus, in the chapter devoted to The planets’ uniform and apparent motion, as explained by the theory of the Ancients, Copernicus analyses the incoherence of the planetary models at some length. In Copernicus’ work one find the same criticism that Brudzewo had made in the name of the uniformity of motion, regarding the equant circle, and in the same terms.Footnote 112
As we have already noticed, Brudzewo shows the paradoxical situation created in the Theoricae’s planetary spheres, where the eccentric orb carrying the epicycle actually turns around its own centre, but in an irregular way, while the regularity of its motion is referred to another point, that is, to the centre of the “circulus imaginatus” which is the equant circle. And though adopting the equant satisfied Peurbach, since he found regularity of motion in a purely mathematical “rule”, Brudzewo’s criticism of the equant goes beyond simply denouncing it as a mathematical instrument: his denunciation assumes much greater significance for him because by adopting the equant, the Viennese Magister violated the essence of celestial nature with its principle of uniformity, according to which the celestial bodies must move uniformly around the centre of their motion.Footnote 113 In his Commentariolus Copernicus had already addressed the same criticisms of the equant. In the fifth book of De revolutionibus, Copernicus explains the Ancients’ theory in order to criticise the models they had conceived for the planets:
The ancient mathematicians, who held the Earth immobile, imagined for Saturn, Jupiter, Mars, and Venus eccentrics with epicycles, and in addition, another eccentric, with respect to which the epicycle, and also the planet in the epicycle, moved uniformly.Footnote 114
Once again Copernicus uses a geometrical diagram for this analysis in order to visualise these new relationships:
For example, if there be eccentric circle AB, the centre of which is C, and the diameter ACB, in which the centre of the Earth is D, so that the apogee is in A and the perigee in B; and DC be divided into two parts at E, from which centre [E] there be described another eccentric FG equal to the previous [eccentric AB]; in which [FG], taking in any way centre H, there be drawn epicycle IK; and there be drawn through centre [H] straight line IHKC, and likewise LHME. [...] the epicycle also [moves] from west to east in consequentia in circle FHG, but [uniformly] with IHC, the line with respect to which the star also revolves uniformly in its epicycle. It is, however, certain that the uniformity [of the motion] of the epicycle ought to take place with respect to E, the centre of its deferent, and the revolution of the planet with respect to line LME. They allow, therefore, that the uniformity of this circular motion can also take place about a foreign, and not its own, centre. Likewise also in the case of Mercury this takes place even more so. But this has already been sufficiently refuted concerning the Moon.Footnote 115

Copernicus, De Revolutionibus, 1543, f. 140v
The results of this analysis, which encompassed the essential points of astronomy according to the ancient tradition, persuaded Copernicus to displace the point of observation, that is the Earth, and find a more effective solution which took into account both the uniformity of the celestial bodies’ actual motions and the irregularity of apparent motions:
These and similar questions provided the inducement for considering the mobility of the Earth and other ways by which the uniformity [of motions] and the principles of the science would be preserved and the account of the apparent nonuniformity be rendered more certain.Footnote 116
11 Concluding remarks
The need to see celestial nature realised according to authentic and rigorous principles led scholars to submit the universe to a refined analysis. Once the geometrical models of the Almagest have to be realised in the corporeal orbs of the Theoricae novae, their accuracy can no longer simply be proved purely by mathematical rigour. If those circles become physical orbs which form integral parts of the real spheres, these new models must be evaluated on the basis of how they accord with the principles of the celestial reality of which they are a part. According to this interpretation, the universe that Peurbach believed could succeed in reconciling astronomy and physics by offering the “realem sperarum habitudinem atque motum”, the real shape of the spheres and motions, can no longer be reconciled with that same celestial nature of which it forms a part, and instead becomes the object of criticism.
This was the attitude adopted by the Cracovian tradition,Footnote 117 started by Albert of Brudzewo. It analyses this universe and acknowledges the merits for which it has broadly been appreciated, but imposes the requirement that all the principles of celestial nature must to be realised in the universe, and first and foremost, the perfect circularity and uniformity of the motions. In the name of celestial perfection, Brudzewo grasped the weak elements and inconsistencies in Peurbach’s universe, focused on the limits of the astronomers, namely, to save appearances, and came to doubt the correctness of the place of the observer in the centre of the world as the location from which uniform and nonuniform motions are distinguished. For Copernicus, the perfect regularity and circularity of motions upon which Brudzewo had insisted as a necessity became the basis upon which he founded his search for an alternative solution: “to find a more reasonable model composed of circles [...] from which every apparent irregularity would follow while every [circle] in itself moved uniformly, just as the principle (ratio) of perfect motion required.” Brudzewo’s most famous “follower”, as we may now call him, thus proved that it was not just possible, but actually necessary, to formulate astronomy based upon this new principle.
We hope that this analysis has contributed a small tile to help reconstruct the great mosaic that forms the Copernican theory. The problems on which Brudzewo focused were of contemporary concern, and from Brudzewo’s Commentariolum Copernicus could find the reasons for undertaking his search for an alternative solution. How he confronted the different approaches and various theories, the way in which he dealt with the problems which emerged as the construction of his universe became more and more technical and refined, and the manner in which he always found a solution to these problems—these are all very different questions.Footnote 118
Notes
Cod. 5203, Österreichische Nationalbibliothek, Wien, f. [24r]; Codex Sancrucensis 302, Stiftbibliothek, Heiligenkreuz , f.[60v]; Cod. 5245, Österreichische Nationalbibliothek, Wien, f.[26v] (om. “Wienne in Collegio Civium penultima mensis Augusti”). For a description of these manuscripts and of the other manuscripts which transmit Peurbach’s Theoricae novae during the life of its author, see (Malpangotto 2012).
This results from the analysis of the extant manuscripts and printed editions spreading Peurbach’s Theoricae novae, alone or with commentary, from fifteenth to seventeenth century. Cf. (Malpangotto 2016 à paraître).
For a description of the way in which Peurbach, in his Theoricae novae planetarum, presents the structure of the planetary spheres, see (Malpangotto 2013b). For an analysis of what distinguishes Peurbach’s Theoricae novae from the previous tradition, see (Malpangotto 2016 à paraître). To insert Peurbach’s contribution in the previous tradition, (Duhem 1913–1915, vol. III), (Grant in Lindberg 1978), (Lerner 2008), (Barker 2011) remain the reference works and the following question in (Lerner 2008, I, 120–121) is still opened: « Faut-il voir dans cette incorporation des cercles abstraits de l’Almageste dans des orbes solides, le résultat de la diffusion progressive d’un modèle de machinerie céleste dont les origines lointaines remontent à Ptolémée lui-même? On peut le penser. En tout cas, tout se passe comme si ce processus de diffusion, qui mériterait de faire l’objet d’une étude particulière, avait trouvé chez Peurbach son aboutissement » .
Cod. 5203, Österreichische Nationalbibliothek, Wien, f. [2r]; Codex Sancrucensis 302, Stiftbibliothek, Heiligenkreuz , f.[40r]; Cod. 5245, Österreichische Nationalbibliothek, Wien, f.[1r].
Only the better known printed versions of the Theoricae novae are evoked here: (Capuano 1495), (Mazzolini de Prierio 1514), (Reinhold 1542), (Schreckenfuchs 1556), (Nunes 1566), (Wursteisen 1568). For a complete description of the spreading of Peurbach’s work and a catalogue describing both manuscripts and printed editions transmitting the Theoricae novae from 1454 to 1653, see (Malpangotto 2016 a paraître).
L, f. 69r; R, f. 79r; D, f. 149v; K, 189r. For a Latin transcription, see the “Appendix”. In 2013, in the same month of May, two studies on Brudzewo’s Commentariolum appeared: (Barker 2013) and (Malpangotto 2013a). Barker considers the vexed question of the reality of the celestial orbs to suggest that the common view of modern commentators, who usually depict Brudzewo as a fictionalist denying the physical reality of the orbs described by Peurbach in his Theoricae novae planetarum, “is an error based on selective reading and ignoring the context in which Brudzewo was writing”. (Malpangotto 2013a) presented the first French version of our analysis of Brudzewo’s text, which we here develop in more detail.
L: f. 69r; R: 79r; D: 149v; K: 189r. For a Latin transcription see the “Appendix”.
The explicit of L confirms that Brudzewo’s teaching dates back to the year 1483: “Dictum est anno domini Millesimo quadringentesimo octogesimo tertio”. The Liber diligentiarum of the Arts Faculty starts with year 1487 and does not enable to know the teachers for the previous period. According to Birkenmajer in (Brudzewo 1900: XXVII), the manuscript annotation saying “1483 Brudzew legit”, in the margin of f. sign. a3 v of the 1495 printed version Inc. 2705 of the Jagiellonian Library, confirms that in 1483 Brudzewo read his Commentariolum.
The same explicit in L also says that the text of the Commentariolum was made public to students in 1488: “Scriptum vero et in publicum editum anno domini Millesimo quadringentesimo octogesimo octavo”. This same course should be the one written in manuscripts, R, D, K (see “Appendix”).
The Liber diligentiarum of the Arts Faculty of Cracow (Wisłocki 1886: 5) reveals that Brudzewo gave a course on the Theorica planetarum in 1488. So he taught the commentary copied in these manuscripts. Manuscript C confirms that the Commentariolum is still read at Cracow University in 1493: “finitum in vigilia Circumcisionis domini a. d. 1493 Finis”. For this semester, the Liber diligentiarum says that the Theorica planetarum was taught by Simon Sierpc (Wisłocki 1886: 23).
The Commentariolum was first printed in Milan in 1494 by the printer Uldericus Scinzenzeler (M in the “Appendix”; unknown to Birkenmajer). All the extant copies of this edition M lack any f. ai and Brudzewo’s name does not appear anywhere in the volume. In 1495, the same printer published a second edition of the Commentariolum (E in the “Appendix” and in Brudzewo 1900). The titlepage on f. [ai]r does not mention Brudzewo’s name. In the dedication letter, at f. [ai]v, Johannes Otto de Valle Uracense says that this is Brudzewo’s work and states that Brudzewo was his praeceptor and the printer’s colophon at f. sign. [g viii]v explicitly attributes the work to Brudzewo.
(Brudzewo 1900: 23): “Littera autem taliter probatur”. With “littera” Brudzewo always refers to the text of Peurbach’s Theoricae novae.
(Brudzewo 1900: 47): “probatur in littera”. As usual, with “littera” Brudzewo always refers to the text of Peurbach’s Theoricae novae.
(Brudzewo 1900: 84): “Sequens etiam littera Magistri satis plana est et evidens in figura”. Usually with “Magister” Brudzewo is referring to Georg Peurbach.
Brudzewo’s Commentariolum is divided into three parts: the Tractatus primus has no title in the manuscripts, but it concerns the texts about the Sun, the Moon and the planets (Brudzewo 1900: 22–127), while the titles of Tractatus secundus: De passionibus planetarum (Brudzewo 1900: 128–145) and De motu octavae sphaerae tractatus (Brudzewo 1900: 146–151) appear in the extant manuscripts.
(Brudzewo 1900: 22–44).
(Brudzewo 1900: 44–78).
(Brudzewo 1900: 78–107).
(Brudzewo 1900: 107–110).
(Brudzewo 1900: 110–127).
At the beginning of each section of his commentary, Brudzewo presents this structure which is common to each section of Peurbach’s text. See (Brudzewo 1900: 22, 44, 78, 107, 110).
This conviction is regularly repeated and becomes particularly evident each time Brudzewo has to present the astronomical terms and the lines determining them in geometrical terms. In these passages he notices that Peurbach transforms the arrangement of the real orb carrying the celestial body into an imaginary circle represented on a plane: “In fact, the Theoristae, who know the real orbs’ arrangement, habitually subordinate to these real orbs some imaginary circles which resemble them and which are arranged in the same way that finally each one, which imitates such an arrangement, be exposed to sight in a plane, for, as Ptolemy says, sense perception frequently aids the intellect to investigate. Sensus enim saepius adiuvat intellectum ipsum speculari inquit Ptolemaeus. » (Brudzewo 1900: 34); cf. also 57, the commentary to “Vocatur autem superficies”.
(Brudzewo 1900: 57): “Iam Magister, posita declaratione ecentrici, qui est orbis realis, [...]”.
(Brudzewo 1900: 22): “In prima parte ponit Magister divisionem totius sphaerae solaris in orbes reales partiales [...]”.
(Brudzewo 1900: 79–80): “[...] in revolutionibus, quae esset absque diversitate qualibet. Talis enim motus est quasi proprietas conveniens corporibus coelestibus, alienatis a natura istorum inferiorum, quorum motus [est] absque similitudine et ordine [...]”.
Cf. (Brudzewo 1900: 23): “Omnem motum coelestis corporis simplicem et verum aequalem esse, hoc est, super aequos angulos in centro motus consistentes et in arcus cadentes aequales, aequalibus fieri temporibus”. This passage faithfully recalls the same words taken from the third book of the Abbreviatio Almagesti that Brudzewo ascribes to Albertus Magnus. Cf. manuscript Wien, Österreichische Nationalbibliothek, Cod. 5266, f. 186r.
(Brudzewo 1900: 23).
(Peurbach [1472]: ff. [1v–2r]): “Sed orbis solare corpus deferens motu proprio super suo centro scilicet eccentrici regulariter secundum successionem signorum, quotidie. lix. minutis et octo secundis fere de partibus circumferentiae per centrum corporis solaris una revolutione completa descriptae, movetur. [...] Cum autem centrum solare ad motum orbis ipsum deferentis regulariter super centro eccentrici moveatur; necesse erit ut super quocumque puncto alio irregulariter moveatur. Quare Sol super centro mundi in temporibus aequalibus inaequales angulos, et de circumferentia zodiaci inaequales arcus describit.” Here and in what follows, we have preferred to refer to Peurbach’s editio princeps and directly translate its text instead of using Aiton’s translation of the third edition of the Theoricae novae.
Cf. (Brudzewo 1900: 30–31): “Etsi Solem in suo ecentrico regulariter moveri sit primum principium in Astronomia (ideo cum negante illud, non est amplius in Astronomia disputandum), tamen tale principium potest per scientiam subalternantem, scilicet mathematice demonstrari sic. Sol in temporibus aequalibus, aequales super centrum suum describit angulos et aequales resecat arcus, ergo aequaliter movetur.”
Cf. (Brudzewo 1900: 27–28).
(Brudzewo 1900: 23): “concluserunt Solem in zodiaco inaequaliter moveri.”
(Brudzewo 1900: 23): “Et cum ipse Sol diverso motu et inaequali moveatur in zodiaco, senserunt ipsum—ex principiis philosophiae—debere moveri in suo orbe, aequali motu et simplici.”
(Brudzewo 1900: 23–24): “Haec itaque duo prae oculis pensantes, diversum scilicet motum Solis in zodiaco, uniformem vero et aequalem in suo orbe, arguebant: Si ipse Sol haberet suum orbem zodiaco concentricum, de facto etiam moveretur in zodiaco aequaliter [...] Cum itaque Sol in zodiaco moveatur irregulariter, causam non invenientes magis consonam, ecentricitatem orbis solaris assignaverunt, qui quidem ecentricus in una parte elevabitur a centro mundi ad zodiacum accedendo, in altera vero ad centrum mundi appropinquabit, removendo se a zodiaco. Hoc namque pacto Sol videbitur in zodiaco irregulariter moveri et in una medietate morari diutius quam in altera.”
Cf. (Brudzewo 1900: 25): “Amplius imaginati scrutatique sunt, an foret conveniens ipsi Soli hunc unicum habere orbem ecentricum et quaerebant, si omnes sphaerae essent ecentricae: invenerunt quidem, quod sphaera stellata est mundo concenrica. Istud enim probaverunt per Pleiades et alias stellas Pleiadibus diametraliter oppositas, videlicet, quod quando Pleiades oriebantur, illae occidebant, et e converso. Viderunt insuper motum septem planetarum, diversum et varium inter se. Si ergo octava sphaera est concentrica et planetae inter se moventur motibus diversis, positis eorum orbibus totaliter ecentricis, profecto inter sphaeram octavam et inter sibi immediate inferiorem, ratione motus diversi accideret scissio sphaerarum et commixtio vacui; et sic in aliis sphaeris inferioribus. Quod eis videbatur absurdum sentire, alias enim coelum esset corruptibile. [...] Movebant ergo eos duae causae contrariae: una propter quam coacti sunt ponere ecentricum orbem Solis cum ceteris planetarum sphaeris, altera quia si totae ecentricae fuissent, scissio sphaerarum committeretur. Hinc inde revolventes, non invenerunt aliquid magis consonum, nisi quod in unaquaque sphaera essent tres orbes ad minus taliter dispositi, ut inquit littera.”
(Peurbach [1472]: f. [1v]): “Moventur autem orbes deferentes augem Solis propriis motibus proporcionalibus ita quod semper strictior pars superioris sit supra latiore inferioris.” (Brudzewo 1900: 29) criticise the improper character of the adjective “propriis” that Peurbach attributes to the motion of these orbs.
Cf. (Brudzewo 1900: 29–30): “Ex hoc enim, quod horum orbium principale centrum sit centrum mundi [...] ideo habent motum proportionalem, sic quod moles unius crassitudinem alterius non derelinquit, nec e converso. Cuiuslibet etiam corporis coelestis circa centrum suum motus est aequalis, ut dictum est, nec procedit instantia quorumdam, videlicet quod isti duo orbes quoad unam superficiem habent centrum mundi, quoad alteram vero centrum ecentrici; ergo si movebuntur super centro mundi, simili ratione super centro ecentrici. Dicunt ergo: esse inimaginabile,eumdem orbem eodem motu super diversis centris moveri. Sed revera non est inconveniens. Ex hoc enim quod habeant diversa centra respectu diversarum suarum superficierum, motus ipsorum orbium secundum diversas eorum superficies ad diversa centra referri possunt. Orbem tamen, in utraque superficie similis dispositionis, eodem motu super diversis centris moveri, sine inconvenienti non esset.”
(Peurbach [1472]: f. [6v]): “Haec tamen difformitas hanc regularitatis habet normam [...]”.
For a description of these influences in the case of the sphere of Mercury, see (Malpangotto 2013b: 278–294).
Cf. (Brudzewo 1900: 85–86): “inquit Ptolemaeus dictione \(\hbox {IX}^{\mathrm{na}}\) capitulo \(5^{\mathrm{to}}\): Et centra orbium revolutionis neque revolvuntur super hos orbes centrorum egredientium, quorum centra per motus suos revolvuntur in revolutione aequali et perambulant in temporibus aequalibus angulos aequales. Haec ille.”
Brudzewo transcribes this passage of the Almagest which, as mentioned above, he knows from Gerard of Cremona’s Arabo-Latin version (cf. Ptolemy 1515: f. 103r). It should be noted that Brudzewo remains faithful to this Arabo-Latin version in which the circles of the Almagest are systematically called “orbs”.
(Peurbach [1472]: f. [6v]): “Motus autem epicyclum deferentis super centro et polis suis difformis est. Haec tamen difformitas hanc regularitatis habet normam ut centrum epicycli super quodam puncto in linea augis tantum a centro huius orbis quantum hoc centrum a centro mundi distat elongato: regulariter moveatur. Unde et punctus ille centrum aequantis dicitur et circulus super eo ad quantitatem deferentis secum in eadem superficie imaginatus eccentricus aequans appellatur.”
(Brudzewo 1900: 86): “Quantum est in se, ad motum orbium non est opus aequante. Nihil enim aequans facit ad motum orbis realis, cum sit circulus imaginarius, sed quantum ad opus astronomicum, seu ad calculationem Tabularum, quae calculantur iuxta principia et conclusiones mathematicas, quae quidem conclusiones, quia saepius non possunt accomodari et applicari motibus, ut sunt in sua natura, seu ut apparent.”
Cf. (Brudzewo 1900: 86): “Ideo ipsi Mathematici quandoque capiunt alio modo motus corporum coelestium, quam sunt in sua natura, vel aliter quam apparent, et considerant eos tali modo, qualiter serviunt eorum arti et operationi, cum alio modo nullatenus eos ad opus rectum et praecisum possent ponere.”
(Brudzewo 1900: 87): “Et sic per motum aequalem iterum cognoscunt, quantum motus diversus maioritate aut minoritate planorum angulorum et arcuum addat aut diminuat supra motum aequalem: propter hoc ergo ponuntur aequantes.”
(Brudzewo 1900: 86): “Imaginantur ergo aequalem esse motum, qui non aequalis videtur in se, propter opus ut rectius ponant. Et ex hoc convicti sunt et coacti ponere aequantes, circulos imaginatos, super quibus motus orbium diversos et inaequales, aequales esse considerant, reducuntque illos motus diversos primum ad aequalitatem in aequantibus, tamquam in id, ex quo iudicium diversi motus sumpturi sunt.”
(Peurbach [1472]: ff. [4r–4v]): “Circumvoluitur tamen epicyclus taliter ut super centro proprio atque axe irregulariter moveatur. Sed haec irregularitas ad uniformitatem reducitur istam ut a puncto augis epicycli mediae, quicunque sit ille, quolibet die naturali tredecim gradus et quatuor minuta fere recedendo regulariter elongetur. Aux autem media epicycli est punctus circumferentiae epicycli quem ostendit linea a puncto diametraliter opposito centro eccentrici in circulo parvo per centrum epicycli ducta.”
The “small circle” to which Peurbach refers, is determined by the motions of the secundum quid orbs and from the repositioning of their mass. Even if the sphere of the Moon has a different structure, it is the same mechanism which makes the centre of the eccentric carrying Mercury’s epicycle describe a “small circle” too. For an explanation of this, see (Malpangotto 2013b: 279–292).
Cf. (Brudzewo 1900: 62–66).
Cf. (Brudzewo 1900: 66): “Sic enim operati sunt antiqui, videlicet quod primo invenerunt revolutiones epicycli aequales et motum Lunae in epicyclo aequalem per considerationes eclipsium lunarium.” See also (Brudzewo 1900: 46–47).
(Brudzewo 1900: 66): “Tandem demonstrationibus experti sunt arcum epicycli, inter lineam medii motus centri epicycli et inter centrum Lunae interceptum, esse maiorem aut minorem arcu medii motus Lunae in epicyclo.”
See (Brudzewo 1900: 62–65).
(Peurbach [1472]: f. [4v]): “Aux autem media epicycli est punctus circumferentiae epicycli quem ostendit linea a puncto diametraliter opposito centro eccentrici in circulo parvo per centrum epicycli ducta.” For the “small circle”, see supra, n. 44.
(Brudzewo 1900: 65): “Unde est manifestum, quod—procedente centro epicycli a longitudine longiore ecentrici ad longitudinem propiorem—longitudo longior epicycli vera praecedit longitudinem longiorem aequalem, et—procedente centro epicycli a longitudine propiore ecentrici ad longitudinem longiorem— longitudo longior vera subsequitur longitudinem longiorem aequalem.”
Cf. (Brudzewo 1900: 67): “Videtur [Ptolemaeus] in istis verbis innuere, quod declinatio et reclinatio non ex sola computatione proveniat, sed ex motu realiter apparenti in Luna. Luna enim ratione istius declinationis et reflexionis consequitur quasdam figuras post elongationem eius a Sole, videlicet quod apparet concava, seu excisa, et hoc circa quintum diem fere post coniunctionem. Apparet etiam tumida vel gibbosa, et hoc circa decimum diem fere post coniunctionem.”
Cf. (Brudzewo 1900: 67–68): “Propter ergo salvare istum motum apparentem in Luna, quidam imaginantur epicyclum talem in Luna, quod habeat alium intra se inclusum, qui movet epicyclum deferentem Lunam motu declinationis et reflexionis, quod non videtur esse inconveniens.” The two figures drawn by Birkenmajer from C, L and E, although they differ in detail, show two concentric epicycles, one inside the other. There are also figures of lunar phases, including concave and gibbous.
Thanks to Noel Swerdlow we could formulate this model and give a graphical representation.
(Brudzewo 1900: 68, n.1): “Lunam quidam imaginantur habere duos epicyclos, unum maiorem, alterum minorem, in quo est eius corpus situatum, et ita epicyclus superior tantum, motu declinationis et reflexionis movetur. Et pro tanto illa macula, quae in Luna aspicitur, semper una et eadem apparet propter istum epicyclum: quod non esset, si talis epicyclus non esset.” This passage is found in the margin of f. 51r in L in the hand of the scribe and a similar annotation, literally different but on the same subject, is in the margin of f. 61v in R.
Grazyna Rosinska’s research on the astronomy teachers at Cracow University in the first half of the fifteenth century enabled her to find a double epicycle for the Moon, in Sandivogius de Czechel’s commentary on the Theorica planetarum Gerardi written in about 1430, which appears to be for this purpose. See (Rosinska 1974, 1973). The description appears to be of a second small epicycle surrounding the Moon itself that causes its body to rotate, not the two concentric epicycles described in Brudzewo’s text. Brudzewo’s text and the marginal annotation have also been considered by (Barker 2013: pp. 137–139), who reaches the same conclusion, that Brudzewo describes two concentric epicycles for the motion of the mean apogee of the epicycle and that these cannot cause the same side of the Moon to face the Earth.
(Schreckenfuchs, 1556, pp. 120–121) says this for the superior planets referring to the more explicit explanation given for the Moon at pp. 58–61.
(Brudzewo 1900: 94): “Ideo planeta in epicyclo iam habebit motum regularem et uniformem super centro aequantis, de quo linea ducta per centrum epicycli ostendit punctum, a quo computandus est aequalis motus planetae in epicyclo, qui Aux media appellatur. Quae quidem Aux media variabilis est quoad concavitatem illam, in qua situatur epicyclus, sic videlicet, quod continue sub alio et alio puncto sit concavitatis, vel etiam variabilis est in superficie convexa reali ipsius epicycli, ideo, quod continue alius et alius punctus superficiei realis epicycli succedit propter motum epicycli; non autem variabilis est quoad circumferentiam imaginatam in epicyclo, in qua motus planetae et revolutio computantur.”
See supra the analysis of Mathematical artifices in Peurbach’s universe.
(Peurbach [1472]: f. [3r]).
(Peurbach [1472]: f. [6v]).
(Peurbach [1472]: f. [4r]).
(Peurbach [1472]: f. [7r]).
(Brudzewo 1900: 55).
(Brudzewo 1900: 85).
(Brudzewo 1900: 65).
(Peurbach [1472]: f. [3r]): “quamvis eccentricus epicyclum deferens super axe atque polis suis moveatur, non tamen super eisdem regulariter movetur.”
(Peurbach [1472]: f. [2v]): “Orbis vero epicyclum deferens movetur secundum successionem signorum regulariter super centro mundi ita quod omni die naturali tali motu centrum epicycli XIII gradus et XI minuta fere perambulet.”
(Brudzewo 1900: 30): “[...] Solem in suo ecentrico regulariter moveri sit primum principium in Astronomia (ideo cum negante illud, non est amplius in Astronomia disputandum), [...]”.
Cf. (Peurbach [1472]: f. [9v]): “Ex his igitur et dictis superius manifestum est singulos sex planetas in motibus eorum aliquid cum Sole communicare: motumque illius quasi quoddam commune speculum et mensurae regulam esse motibus illorum.” Peurbach only introduces this concept in the section devoted to the sphere of Mercury, while Brudzewo brings it forward in the De Luna section. (Brudzewo 1900: 57): “Hic iam [Magister] determinat de motu eorumdem [Augem deferentium et epicyclum deferentis] per comparationem ad Solem, cum quo Luna et ceteri planetae in motibus suis naturalem habent connexionem, [...]”. He then notices that this idea had already been expressed by Haly in his commentary on the first book of Ptolemy’s Quadripartitum.
(Brudzewo 1900: 54): “[...] et tu etiam poteris reperire sic. Motum Solis, quem habet Sol in uno die per tempus unius mensis multiplica et producto 360 gradus adde: sic enim provenient gradus, quos centrum epicycli percurrit in uno mense. Hoc itaque aggregatum per tempus unius lunationis divide, et in quotiente habebis, quantum centrum epicycli, seu deferens epicyclum, movetur quolibet die naturali motu aequali in Zodiaco.”
(Brudzewo 1900: 54): “Ex his etiam, centrum epicycli moveri aequaliter super centro mundi, mathematice ostendi potest, scilicet per respectum ad lineam medii motus Solis, respectu cuius circa centrum mundi aequales constituit angulos, et aequales in temporibus aequalibus de Zodiaco resecat arcus. Ergo movetur aequaliter, sicut dicit littera, scilicet 13 gradibus 10 minutis etc.”. It is useful to note that Peurbach gives “about 13 degrees and 11 minutes.”
The line of the Sun’s mean motion is the line drawn from the centre of the world to the zodiac, parallel to the line of the Sun’s motion in its eccentric. The line of the mean motion of the Moon’s epicycle is the line passing through the centre of the epicycle, drawn from the centre of the world to the zodiac.
(Peurbach [1472]: f. [3r]): “Ex istis sequitur primo quod quamvis eccentricus epyciclum (sic) deferens super axe atque polis suis moveatur, non tamen super eisdem regulariter movetur.”
(Peurbach [1472]: f. [3r]): “Signatis enim aliquibus angulis aequalibus super centro mundi versus augem et oppositum: qui versus augem est maiorem arcum eccentrici quam alter versus oppositum complectitur.”
(Brudzewo 1900: 55): “Corellarium primum habet veritatem, scilicet quod ecentricus super axe suo et polis et circa centrum suum movetur irregulariter, motum ipsius in Zodiaco computando respectu centri ecentrici et non respectu centri mundi.”
(Peurbach [1472]: f. [3r]): “Secundo quanto epicyclus lunae augi deferentis eum vicinior fuerit tanto velocius centrum eius movetur et quanto vicinior augis eiusdem opposito tanto tardius.”
(Brudzewo 1900: 55).
(Brudzewo 1900: 79): “Et hoc patet per Ptolemaeum dictione IX capitulo \(2^{\mathrm{do}}\), ubi inquit: In inquisitione vero diversitatum ingreditur ex dubitatione non parum propterea, quod videntur cuiusque stellarum duae diversitates, quae non sunt aequales, neque in magnitudine, neque in temporibus reditionum, quarum una videtur propter Solem et altera propter partes orbis signorum. Et cum coniunxerimus eas ambas, erit semper proprietas cuiuscumque earum propter illud difficilis cognitionis. Haec ille. In istis verbis Ptolemaeus vult quomodo quinque stellae erraticae, seu planetae habent diversum motum in Zodiaco, quia moventur aliquando versus septemtrionem, aliquando versus meridiem ab ecliptica et interdum vero sub ecliptica, aliquando motu tardo, aliquando veloci. Respectu etiam Solis habent diversum motum. Cum enim videbantur prope Solem, eorum motus [...] apparebat velox, cum circa quadras a Sole non moveri quidem sed stare videbantur, [...] et cum in diametro fuerunt cum Sole, contra signa tendebant.”
(Peurbach [1472]: f. [6v]): “Motus autem epicyclum deferentis super centro et polis suis difformis est”.
(Brudzewo 1900: 85): “Quod Magister dicat: centrum epicycli super centro ecentrici irregulariter moveri, non est verum intelligendo simpliciter.” Simpliciter is used here in the same sense as absolute, taken by itself, and is translated in the same way.
(Brudzewo 1900: 85): “Hoc enim esset contra illam maximam, qua dictum est, omnem motum corporis coelestis simplicem et aequalem esse, et contra philosophiam, quae corporis simplicis et regularis motum ponit simplicem ac regularem. Et sic motus deferentis epicyclum, in se et absolute consideratus, de facto uniformis est [...]”.
Cf. (Brudzewo 1900: 85): “Et hoc quidem esse verum, videlicet quod centrum epicycli habeat diversum motum in suo ecentrico [...]”.
(Peurbach [1472]: ff. [6r-6v]): “Sed orbis epicyclum deferens super axe suo axem zodiaci secante secundum successionem signorum movetur [...] Motus autem epicyclum deferentis super centro et polis suis difformis est.”
(Peurbach [1472]: f. [4r]): “Circumvoluitur tamen epicyclus taliter ut super centro proprio atque axe irregulariter moveatur.”
(Brudzewo 1900: 65): “Secundum Campanum Luna in epicyclo movetur uniformiter et sic [movetur] et epicyclus circa centrum suum quod quidem verum est considerando motum epicycli simpliciter in se et absolute, sine relatione ad aliquem punctum. Cuilibet enim orbi coelesti motus uniformis convenit ratione suae naturae”.
The statement “without reference to any point” excludes any point other than the centre, for the epicycle must turn uniformly about its centre.
(Brudzewo 1900: 65): “Cuilibet enim orbi coelesti motus uniformis convenit ratione suae naturae”.
(Brudzewo 1900: 65): “Quod autem Magister dicit in littera, epicyclum circumvolvi irregulariter, etiam verum est in ordine ad aspectum in centro mundi constitutum.”
(Brudzewo 1900: 65): “Si enim epicyclus moveretur regulariter in ordine ad centrum mundi, extunc arcum epicycli medii motus semper staret esse tantum, quantum inter centrum Lunae et inter lineam medii motus centri epicycli, seu Augem veram epicycli (quod idem est) compraehenderetur, quod non fit. Dumtaxat, centro epicycli in Auge ecentrici vel in opposito eiusdem constituto, dicti arcus aequantur; centro autem epicycli a longitudine longiore ecentrici progrediente usque ad propiorem, semper minor est arcus medii motus Lunae in epicyclo arcu, inter centrum Lunae et lineam medii motus epicycli intercepto. In reliqua vero medietate ecentrici fit e converso [...]”.
(Peurbach [1472]: f. [7r]): “[Motus huius] est super centro epicycli irregularis
(Brudzewo 1900: 93–94): “Quod etiam Magister dicit, illum motum epicycli esse irregularem super centro suo, intelligit non simpliciter et secundum se considerando motum epicycli, sed in ordine ad oculum, qui de centro orbis signorum illum spectaret motum; si ibi (L) enim motus epicycli irregularis cadit tali modo, quod—centro epicycli discurrente ab auge ecentrici usque ad oppositum—semper minor est arcus medii motus planetae in epicyclo, quam arcus epicycli interceptus inter augem veram epicycli et inter centrum planetae, et in tantum minor, quantum correspondet distantiae inter centrum orbis signorum et inter centrum aequantis. In reliqua vero medietate iterum sit maior: sic ergo fit irregularis in ordine ad centrum mundi.” The variant “si ibi” appears only in manuscript L; all the other manuscripts and the printed editions write “sibi”.
(Brudzewo 1900: 34): “Notandum. Mathematici seu doctrinales determinant de locis astrorum modo visuali ac si uterque oculus in centro mundi esset constitutus loca astrorum prospiciens secundum lineas ab ipso per astra ducibiles; hoc faciunt iudicio sensus nostri satisfacientes. [...] Determinant etiam de locis astrorum in ordine ad centrum mundi, quoniam illud uno et eodem modo se habeat respectu omnium corporum coelestium et est immobile.”
L: f. 69r; R: 79r; D: 149v; K: 189r. For a Latin transcription see the “Appendix”.
(C: f. 154r and f. 169v). The explicit at f. 169r says that at the end of the year 1493 Michael de Ruszoczjcze copied this text which was probably adopted for a course given by one of the Faculty teachers. The student says that he finished the copy in “vigilia Circumcisionis domini”, the evening of 31 December 1493: he could have followed the course in the summer semester of 1493 (cf. “Appendix”). For this semester, the Liber diligentiarum says that the Theorica planetarum was taught by Simon Sierpc (Wisłocki 1886: 23).
In M, the editio princeps of the Commentariolum, Brudzewo’s name appears nowhere in the volume, but it is worthy to notice that all the extant copies lacks of f. ai, so it is impossible to know what appeared on the title page. The second edition (E: f. [a i]) presents a dedication letter of Johannes Otto de Valle Uracense. Here Johannes Otto says that he is a student of Brudzewo and expresses his appreciation of his master’s work: “In Theoricas planetarum Georgii Purbachii viri sane in astronomia disertissimi, interpretationem Alberti Prosevi praeceptoris mei [...] Non enim ingrato commentarium hoc iudicatum iri existimo: ubi motuum superiorum corporum diversitates reciprocationesque dispares contemplari ceperint.”
For the Cracovian milieu see (Birkenmajer 1972). More recently A. Goddu devoted an important work to the influence of the aristotelian tradition on “Copernicus’ path to heliocentrism”.
(Swerdlow 1973: 433–434). Copernicus, Commentariolus, (Prowe 1884: II, 184–202): “Multitudinem orbium caelestium maiores nostros eam maxime ob causam posuisse video, ut apparentem in sideribus motum sub regularitate salvarent. Valde enim absurdum videbatur caeleste corpus in absolutissima rotunditate non semper aeque moveri. Fieri autem posse animadverterant, ut etiam compositione atque concursu motuum regularium diversimodo ad aliquem situm moveri quippiam videretur.
Id quidem Callippus et Eudoxus per concentricos circulos deducere laborantes non potuerunt et his omnium in motu sidereo reddere rationem, non solum eorum, quae circa revolutiones siderum videntur, verum etiam, quod sidera modo scandere in sublime, modo descendere nobis videntur, quod concentricitas minime sustinet. Itaque potior sententia visa est per eccentricos et epicyclos id agi, in qua demum maxima pars sapientium convenit.
Attamen quae a Ptolemaeo et plerisque aliis passim de his prodita fuerunt, quamquam ad numerum responderent, non parvam quoque habere dubitationem. Non enim sufficiebant, nisi etiam aequantes quosdam circulos imaginarentur, quibus apparebat neque in orbe suo deferente, neque in centro proprio aequali semper velocitate sidus moveri. Quapropter non satis absoluta videbatur huiusmodi speculatio, neque rationi satis concinna.”
(Swerdlow 1973: 435). Copernicus, Commentariolus, (Prowe 1884: II, 184–202): “Igitur cum haec animadvertissem ego, saepe cogitabam, si forte rationabilior modus circulorum inveniri possit, e quibus omnis apparens diversitas dependeret, omnibus in seipsis aequaliter motis, quemadmodum ratio absoluti motus poscit.”
To be correct, one should say around the centre of the Earth’s sphere, which is “near the Sun”: cf. infra, third postulate.
(Swerdlow 1973: 436). Copernicus, Commentariolus, (Prowe 1884: II, 184–202): “Prima petitio: Omnium orbium caelestium sive sphaerarum unum centrum non esse. Secunda petitio: Centrum terrae non esse centrum mundi, sed tantum gravitatis et orbis Lunaris. Tertia petitio: Omnes orbes ambire Solem, tanquam in medio omnium existentem, ideoque circa Solem esse centrum mundi. ” To these three postulates, a fourth one is added concerning the immensity of the Copernican universe when compared to Ptolemy’s universe.
(Swerdlow 1973: 436). Copernicus, Commentariolus, (Prowe 1884: II, 184–202): “Quinta petitio: Quicquid ex motu apparet in firmamento, non esse ex parte ipsius, sed terrae. Terra igitur cum proximis elementis motu diurno tota convertitur in polis suis invariabilibus firmamento immobili permanente ac ultimo caelo. Sexta petitio: Quicquid nobis ex motibus circa Solem apparet, non esse occasione ipsius, sed telluris et nostri orbis, cum quo circa Solem volvimur ceu aliquo alio sidere, sicque terram pluribus motibus ferri. Septima petitio: Quod apparet in erraticis retrocessio ac progressus, non esse ex parte ipsarum sed telluris. huius igitur solius motus tot apparentibus in caelo diversitatibus sufficit.”
(Copernicus 1543: f. 99r): “His enim sic constitutis congruere putant apparentia.” For the purposes of our analysis, we prefer a more faithful translation of Copernicus’ text, which explicitly refers to “apparences”. In order to allow the most faithful comparison between Brudzewo’s and Copernicus’ texts, here and in what follows, we have preferred to directly refer to the Latin text of (Copernicus 1543) and directly translate its text instead of using the translation in (Rosen 1992).
(Copernicus, 1543, f. 99r): “Talem sane circulorum compositionem tanquam consencientem lunaribus apparentiis assumpserunt priores. Verum si rem ipsam diligentius expenderimus non aptam satis nec sufficientem hanc inveniemus hypothesim. Quod ratione et sensu possumus comprobare”.
(Copernicus 1543: f. 99r): “Dum enim fatentur, motum centri epicycli aequalem esse circa centrum terrae, fateri etiam oportet inaequalem esse in orbe proprio, quem describit, eccentro”.
Peurbach also refers to the path of the centre of the deferent as a “small circle”, and in his text it is the result of the movements of the two orbs eccentric in a certain sense, which shift the deferent orb, causing its centre to draw a small circle, see supra, note 44.
(Copernicus 1543: 99r-99v): “Quoniam si, verbi gratia, AEB angulus sumatur partium XLV, hoc est dimidius recti, et aequalis ipsi AED, ut totus BED rectus fiat, capiaturque centrum epicycli in G et connectatur GF, manifestum est, quod angulus GFD maior est ipsi GEF, exterior interiori et opposito. Quapropter et circumferentiae DAB, et DG dissimiles sub uno tempore ambae descriptae, ut cum DAB quadrans fuerit, DG quem interim centrum epicycli descripsit, maior sit quadrante circuli. Patuit autem in Luna dividua utramque DAB et DG semicirculum fuisse, inaequalis est ergo epicycli motus in eccentro suo quem ipse describit.”
(Copernicus, 1543, f. 99v): “Quod si sic fuerit, quid respondebimus ad axioma, Motum caelestium corporum aequalem esse, et nisi ad apparentiam inaequalem videri, si motus epicycli aequalis apparens, fuerit reipsa inaequalis? accideturque constituto principio et assumpto penitus contrarium”.
(Copernicus, 1543, f. 99v): “At si dicas aequaliter ipsum [epicyclum] moveri circa terrae centrum, atque id esse satis ad aequalitatem tuendam, qualis igitur erit illa aequalitas in circulo alieno, in quo motus eius non existit, sed in suo eccentro?”.
See supra 6—The irregular motions in Peurbach’s universe: a—The eccentric carrying the epicycle of the Moon: Brudzewo’s commentary on first corollary of Peurbach. About the same corollary Birkenmajer, in (Brudzewo 1900: 55), had already noticed that: “Correlarium hoc, nec non altera de eadem ‘maxima’ philosophica Brudzevii disceptatio [cf. p. 85], maximi sunt momenti in inquirendis exordio primoque conceptu illius admirabilis mundi systematis, quo Nicolaus Copernicus, astronomus summus, saeculo proxime posteriore inclaruit.”
(Copernicus, 1543, f. 99v): “Ita sane miramur et illud, quod ipsius Lunae quoque in epicyclo aequalitatem volunt intelligi non comparatione centri terrae per lineam, videlicet EGM, ad quam merito debebat referri aequalitas, ipso centro epicycli consentiens, sed ad punctum quoddam diversum, atque inter ipsum et eccentri centrum mediam esse terram, et lineam IGH tanquam indicem aequalitatis Lunae in epicyclo quod etiam re ipsa inaequalem satis demonstrate hunc motum.”
The commentaries on the Theoricae novae which we have already studied, in both manuscript and printed form, do not formulate any criticism of the equant similar to the one expressed by Brudzewo and Copernicus. Brudzewo and Copernicus concentrate on the fact that the epicycle moves on one circle and the uniformity of its motion is evaluated with reference to another circle. All the other authors, from Regiomontanus onward at least until Reinhold, justify this by the fact that by following a mathematical approach only one point of a circumference can move regularly in relation to a point which is not the geometrical centre of the circumference. Cf. (Regiomontanus [1475]: f. 4v) and (Reinhold 1542: ff. sign. Nv v-[Nvi] r).
About this point Birkenmajer, in (Brudzewo 1900: 85), had already noticed the relation to Copernicus: “Argumentum disceptationis proxime sequentis (“Hoc enim esset contra illam maximam”, etc.) connexionem habet intimam cum correlario pag. 55 lin. 4 seq. excuso. Utriusque loci, summam in disquisitionibus circa primitias doctrinae Copernicanae gravitatem habentis, ibidem obiter meminimus.”
(Copernicus, 1543, f. 140v): “Prisci Mathematici, qui immobilem tenebant terram, imaginati sunt in Saturno, Iove, Marte, et Venere eccentrepicyclos, et praeterea alium eccentrum ad quem epicyclus aequaliter moveretur, ac planeta in epicyclo.”
(Copernicus, 1543, f. 140v): “Quemadmodum si fuerit eccentrus AB circulus, cuius centrum sit C, dimetiens autem ACB, in quo centru terrae D, ut sit apogaeum in A, perigaeum in B, secta quoque DC bifariam in E, quo facto centro describatur alter eccentros priori aequalis FG, in quo suscepto utcunque H centro, designetur epicyclus IK, et agatur per centrum eius recta linea IHKC, similiter et LHME. [...] epicyclum quoque in consequentia in FHG circulo, sed penes IHC, lineam ad quam etiam stella revolvatur aequaliter in ipso IK epicyclo. Constat autem quod aequalitas epicycli fieri debuit ad E centrum sui differentis, et planetae revolutio ad LME lineam. Concedunt igitur et hic motus circularis aequalitatem fieri posse circa centrum alienum et non proprium. Similiter etiam in Mercurio hoc magis accidere. Sed iam circa Lunam id sufficienter refutatum est.”
(Copernicus 1543: f. 140v): “Haec et similia nobis occasionem praestiterunt de mobilitate terrae, aliisque modis cogitandi, quibus aequalitas et principia artis permanerent, et ratio inaequalitatis apparentis reddatur constantior.”
We refer to a “tradition” in the sense documented by the sources attesting that some teachers and students spread Brudzewo’s Commentariolum. See supra 8- Brudzewo and Copernicus in Cracow, and also Appendix.
For these questions one can refer to (Neugebauer and Swerdlow 1984) which remains the authoritative reference, providing the most technically founded answers that the history of science has been able to formulate until now, and to (Szczeciniarz 1998) which opens a subtle reflection involving astronomical, mathematical, philosophical and epistemological aspects intended to make the extant studies converse with a refined analysis of Copernicus’ text.
The authority of the marginal notes in this copy comes, not only from the fact that the writing is of that epoch, but especially from the fact that the person who annotated this printed copy systematically amends the variants of the printed text, integrating the manuscript version of L or of another copy transmitting the first course of Brudzewo in 1483. What is also interesting is that these same variants are common to M and E, so this person had to go back to a manuscript version.
(Brudzewo 1900): iustitiam.
References
Aiton, Eric John. 1987. Peurbach’s Theoricae Novae Planetarum: A Translation with Commentary. Osiris (2nd Series) 3: 4–43.
Barker, Peter. 2011. The Reality of Peurbach’s Orbs: Cosmological Continuity in Fifteenth and Sixteenth Century Astronomy. In Change and Continuity in Early Modern Cosmology, ed. P.J. Boner, 7–32. Dordrecht: Springer.
Barker, Peter. 2013. Albert of Brudzewo’s Little Commentary on George Peurbach’s ‘Theoricae novae planetarum’. Journal for the History of Astronomy XLIV(2): 125–148.
Birkenmajer, Alexander. 1972. Études d’histoire des sciences en Pologne (Studia Copernicana IV). Wroclaw: Polish Academy of Sciences.
Duhem, Pierre. 1913–1915. Le Système du Monde. Histoire des Doctrines cosmologiques de Platon à Copernic. Paris: Hermann.
Duhem, Pierre. 2003. Sauver les phénomènes. Essai sur la notion de théorie physique de Platon à Galilée. Paris: Vrin (1st edn. 1908, Paris: Hermann).
Goddu, André. 2010. Copernicus and the Aristotelian Tradition: Education, Reading, and Philosophy in Copernicus’ Path to Heliocentrism. Leiden: Brill.
Halma, 1813.
 Composition mathématique de Claude Ptolémée, traduite pour la première fois du grec en français ... par M. Halma et suivie des notes de M. Delambre. Paris: Henri Grand.
Composition mathématique de Claude Ptolémée, traduite pour la première fois du grec en français ... par M. Halma et suivie des notes de M. Delambre. Paris: Henri Grand.Heiberg, John Ludwig. 1898–1907. Claudii Ptolemaei opera quae exstant omnia. Leipzig: Teubner.
Jardine, Nicholas. 1984. The Birth of History and Philosophy of Science. Kepler’s A Defence of Tycho against Ursus with Essays on its Provenance and Significance. Cambridge: Cambridge University Press.
Lerner, Michel. 2008. Le monde des sphères. Paris: Les Belles Lettres (1st edn. 1996–1997).
Lindberg, David C. (ed.). 1978. Science in the Middle Ages. Chicago: The University of Chicago Press.
Malpangotto, Michela. 2012. Les premiers manuscrits des Theoricae novae planetarum de Georg Peurbach: Présentation, description, évolution d’un ouvrage. Revue d’Histoire des Sciences 65(2): 339–380.
Malpangotto, Michela. 2013a. La critique de l’univers de Peurbach développée par Albert de Brudzewo a-t-elle influencé Copernic? Un nouveau regard sur les reflexions astronomiques au \({{\rm XV}}^{\rm e}\) siècle. Almagest 4(1): 1–47.
Malpangotto, Michela. 2013. L’univers auquel s’est confronté Copernic: la sphère de Mercure dans les Theoricae novae planetarum de Georg Peurbach. Historia Mathematica 40(3): 262–308.
Malpangotto, Michela. 2016 (à paraître). Les Theoricae novae de Georg Peurbach: édition critique, traduction française et commentaire. Paris: Les Belles Lettres.
Markowski, Mieczyslaw. 1990a. Astronomica et astrologica cracoviensia ante annum 1550. Firenze: Olschki.
Neugebauer, Otto, and Noel M. Swerdlow. 1984. Mathematical Astronomy in Copernicus’s De revolutionibus. New York: Springer.
Prowe, Leopold. 1884. Nicolaus Coppernicus. Berlin: Weidmann.
Rosen, Edward. 1992. Nicholas Copernicus. Complete Works. London: The John Hopkins University Press (1st edn. 1975).
Rosinska, Grazyna. 1973. Sandivogius de Czechel et l’Ecole Astronomique de Cracovie vers 1430. Organon 9: 217–229.
Rosinska, Grazyna. 1974. Nasīr ad-Dīn al-Ṭūsī and Ibn al-Shāṭir in Cracow? Isis 65: 239–43.
Rosinska, Grazyna. 1984. Scientific Writings and Astronomical Tables in Cracow: a Census of Manuscripts Sources (14th–16th centuries) (Studia Copernicana XXII). Wroclaw: Polish Academy of Sciences.
Szczeciniarz, Jean-Jacques. 1998. Copernic et la révolution copernicienne. Paris: Flammarion.
Swerdlow, Noel M. 1973. The Derivation and the First Draft of Copernicus’s Planetary Theory: A Translation of the Commentariolus with Commentary. Proceedings of the American Philosophical Society 117(6): 423–512.
Toomer, Gerald J. 1998. Ptolemy’s Almagest. Princeton: Princeton University Press (1st edn. 1984, London, Duckworth).
Wisłocki, Wladislaus. 1886. Liber diligentiarum Facultatis artisticae Universitatis Cracoviensis, Pars I (1487–1563). Ex codice manuscripto in bibliotheca Jagellonica asservato, editionem curavit Dr. Wladislaus Wisłocki. Cracoviae, Sumptibus Academiae Litterarum. E typographia Ephemeridum “Czas” Fr. Kluczyck
Acknowledgments
I would like to warmly thank Noel Swerdlow for his advice.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by: Noel Swerdlow.
Appendices
Appendix: List of manuscripts and printed editions of Brudzewo’s Commentariolum
We present here the extant copies of Brudzewo’s Commentariolum which enrich the corpus described by Birkanmajer in (Brudzewo 1900), made up of L, C, E, of some manuscripts, we have called R, D and K, and of the editio princeps M.
The explicit of L confirms that Brudzewo’s teaching dates back to the year 1483: “Dictum est anno domini Millesimo quadringentesimo octogesimo tertio.” The Liber diligentiarum of the Arts Faculty (Wisłocki 1886) starts with year 1487, so does not contain the teachers for the previous period. According to Birkenmajer, (Brudzewo 1900: XXVII), the manuscript annotation “1483 Brudzew legit” in the margin of f. sign. a3v of the 1495 printed version, Inc. 2705 of the Jagiellonian Library, confirms that in 1483 Brudzewo read his Commentariolum.Footnote 119
The same explicit in L also says that the text of the Commentariolum was made public to students in 1488: “Scriptum vero et in publicum editum anno domini Millesimo quadringentesimo octogesimo octavo”. The Liber diligentiarum of the Arts Faculty of Cracow (Wisłocki 1886, 5) shows that Brudzewo gave a course on the Theorica planetarum in 1488. So he taught the commentary copied in manuscripts L, R, D, K.
The manuscripts, R, D, K, contain only the first part of the explicit in L, and refer solely to the 1483 course, without stating who copied the work or when. The explicit of Peurbach’s Theoricae novae in manuscript R confirms that this text was also copied in 1488. And since the Commentariolum does not present those passages of the Theoricae novae under consideration in their entirety, but only mentions the initial words of each passage, the integral copies of Peurbach’s work associated with Brudzewo’s work in these exemplars would have been read at the same time, so that the teacher’s progressive commentary would support the students’ reading of the text.
In D no other date appears, but in this manuscript (ff. 150r–150v), as in R (ff. 79 r–79 v), the Commentariolum is followed by two identical small texts that seem to be two copies of a common source. So probably both these copies, D and R, date to 1488, as stated at the end of the Theoricae novae in R.
Manuscript C confirms that the Commentariolum was still read at Cracow University in the 1490’s. The explicit at f. 169r of C says in fact that, at the end of the year 1493, Michael de Ruszoczjcze copied this text and he finished the copy in “vigilia Circumcisionis domini”, the evening of 31 December 1493; he could have followed the course in the summer semester of 1493. For this semester, the Liber diligentiarum of the Arts Faculty of Cracow (Wisłocki 1886, 23) says that the Theorica planetarum was taught by Simon Sierpc.
In all the extant copies of the editio princeps M of the Commentariolum, Brudzewo’s name appears nowhere in the volumes, but it is worthy to note that all the extant copies lack f. a i, probably the title page, so it is impossible to know what appeared on it.
The second edition E presents at f. [a i]r a dedication letter of Johannes Otto de Valle Uracense. Here Johannes Otto says that he is a student of Brudzewo and expresses his appreciation of his master’s work: “In Theoricas planetarum Georgii Purbachii viri sane in astronomia disertissimi, interpretationem Alberti Prosevi praeceptoris mei [...] Non enim ingrato commentarium hoc iudicatum iri existimo: ubi motuum superiorum corporum diversitates reciprocationesque dispares contemplari ceperint.”
1.1 Manuscripts of Brudzewo’s Commentariolum
L - Wroclaw, Ossolineum, 759/I (siglum L in Birkenmajer’s edition)
-
ff. 1r–35v, Peurbach’s Theoricae novae,
Incipit: “Sol habet tres orbes a se invicem omniquaque divisos atque sibi contiguos”
Explicit: “earum semper invariabiles Finis feliciter anno salutifere incarnacionis 1488” followed by the last diagram of the section De motu octavae sphaerae
ff. 36r–36v, blank
-
ff. 37r–41r, Brudzewo’s Prohemium to his Commentariolum
Incipit: “Astrorum observatores studiosi experti quidem sufficienter sensu ratione et instrumentis tradiderunt recte virtute primae sphaerae”
Explicit : “doctrinaliter tradiderunt se applicare poterit apte.”
-
ff. 41r–69r, Brudzewo’s Commentariolum on Peurbach’s Theoricae novae
Incipit : “Sol habet tres orbes. Theorica Solis principali divisione dividitur in tres partes. In prima parte”
Explicit: “Tantum de praedictis circa motum octavae sphaerae et per consequens circa Theoricas omnium planetarum. de quo laus et gloria in sempiternum omnipotenti deo, auctori primo coelorum et motuum eorundem, amen. Ffinit commentariolum super Theoricas novas Georgii purbachii in studio Generali Cracoviensi per Magistrum Albertum de Brudzewo pro introductione iuniorum aptiori circa lectionem earundem factam corrogatum. In quo quidem ex minus apte aut non doctrinaliter et scientifice positis, lector industrius in contumeliam facile non insurgat sed que noviter artis cerciora profundioraque in profectum edere studeat, simili provocatus labore eorum (?) si is fuerit qui neque ea que adeo pueriliter adducta sunt capiat permitat illesa ne quem reprehendere cupiens inscitiamFootnote 120 propriam quam honestius tacuisset turpiter propallaret. Dictum dictum est anno domini Millesimo quadringentesimo octogesimo tertio comutacione hiemali immediate post pestem validam que viguit Cracovie anno salutifere incarnacionis Millesimo quadringentesimo octogesimo secundo a festo Corporis Christi incipiens usque ad Michaelis. Scriptum vero et in publicum editum anno domini Millesimo quadringentesimo octogesimo octavo comutacione estivali ffinitum vero est in vigilia corporis Christi hora quasi prandii in lectorio Aristotelis Collegii urbis Cracoviensis per me Iohannem de Crobya earundem Theoricarum principaliter se applicantem auditorem. Et eciam ipso anno Illustrissimo princeps Ffredericus, serenissimi principis et domini Kazimiri dei gracia Regis Polonie filius sextogenitus more spirituali se applicans in Episcopum Cracoviensem est promotus ex convencione que tunc in Pyotrkow celebratur pro quo Deus omnipotens cuius imperium manet sit benedictus in secula seculorum amen. Telos ffinis.”
R - Rome, Biblioteca Apostolica Vaticana, Pal Lat 1385 (absent from Birkenmajer’s edition)
-
ff. 48r - 52r: Brudzewo’s Prohemium to his Commentariolum
Incipit: “Astrorum observatores studiosi experti quidem sufficienter sensu ratione et instrumentis tradiderunt recte virtute primae sphaerae”
Explicit : “doctrinaliter tradiderunt se applicare poterit apte.”
-
ff. 52r–79r, Brudzewo’s Commentariolum on Peurbach’s Theoricae novae
Incipit : “Sol habet tres orbes. Theorica Solis principali divisione dividitur in tres partes. In prima parte”
Explicit: “Tantum de praedictis circa motum octavae sphaerae et per consequens circa theoricas omnium planetarum de quo laus et gloria in sempiternum omnipotenti deo auctori primo coelorum et motuum eorundem deo gratias. \(\parallel \) Ffinit commentariolum super theoricas novas Georgii purbachii in Studio generali Cracoviensi per magistrum Albertum de Brudezuo (sic) pro introductione iuniorum apciori circa lectionem earundem factam corrogatum. In quo quidem ex minus apte autem non doctrinaliter et scientifice positis lector industrius in contumeliam facile non insurgat sed que noviter artis cerciora profundioraque in profectum edere studeat, simili provocatus labore eorum (?) si is fuerit qui neque ea que adeo pueriliter adducta sunt capiat permittatque ille ne quem reprehendere cupiens inscitiam propriam quam honestius tacuisset turpiter propallaret. Dictum est Anno domini 1483 comutacione hiemali immediate post pestem validam que viguit Cracovie anno 1482 a festo corporis Cristi incipiens usque ad Michaelis.”
-
f. 79r: List of definitions of different units
-
f. 79v: List of the distances of each planetary sphere from the Earth
-
ff. 80r–100v: Peurbach’s Theoricae novae
Incipit: “Sol habet tres orbes a se invicem omniquaque divisos atque sibi contiguos” Explicit: “semper invariabiles. Deo gratia Finis Theoricarum Anno 1488 currente per Bartholomeum Ioh. de haffurt in Cracoviensi Studio”
D - Dresden, Sächsische Landesbibliothek, N 100 (absent from Birkenmajer’s edition)
-
ff. 87r–120v, Peurbach’s Theoricae novae
Incipit: “Sol habet tres orbes a se invicem omniquaque divisos atque sibi contiguos”
Explicit: “semper invariabiles. ”
-
ff. 121r–124r, Brudzewo’s Prohemium to his Commentariolum
Incipit: “Astrorum observatores studiosi experti quidem sufficienter sensu ratione et instrumentis tradiderunt recte virtute primae sphaerae”
Explicit : “doctrinaliter tradiderunt se applicare poterit apte.”
-
ff. 124r–149v, Brudzewo’s Commentariolum on Peurbach’s Theoricae novae
Incipit: “Sol habet tres orbes. Theorica Solis principali divisione dividitur in tres partes. In prima parte”
Explicit: “Tantum de praedictis circa motum octavae sphaerae et per consequens circa theoricas omnium planetarum de quo laus et gloria in sempiternum omnipotenti deo auctori primo coelorum et motuum eorundem deo gratias. \(\parallel \) Ffinit commentariolum super theoricas novas Georgii prirbacii (sic) in Studio generali Cracoviensi per Magistrum Albertum de Brudezeuo (sic) pro introductione iuniorum aptiori circa lectionem earundem factam corrogatum. In quo quidem ex minus apte aut non doctrinaliter et scientifice positis lector industrius in contumeliam facile non insurgat sed que noviter artis cerciora profundioraque in profectum edere studeat simili provocatus labore eorum (?) si is fuerit qui neque ea que adeo pueriliter adducta sunt capiat permittatque ille ne quem reprehendere cupiens inscitiam propriam quam honestius tacuisset turpiter propallaret. Dictum est Anno domini 1483 commutacione hiemali immediate post pestem validam que viguit Cracovie anno 1482 a festo corporis Cristi incipiens usque ad Michaelis.”
According to (Rosinska 1984, 431), the annotations in the margins to the Theoricae novae in this manuscript are by Egidius de Corinthia.
-
f. 150r: List of the distances of each planetary sphere from the Earth
-
f. 150v: List of definitions of different units
K - Karlsruhe, Badische Landesbibliothek, Cod. Ratstatt 36 (absent from Birkenmajer’s edition)
-
ff. 142r–154v, Peurbach’s Theoricae novae
Only diagrams related to Peurbach’s Theoricae novae different from those of the printed tradition of Peurbach’s text.
-
ff. 155r–158r, Brudzewo’s Prohemium to his Commentariolum
Incipit: “Astrorum observatores studiosi experti quidem sufficienter sensu ratione et argumentis tradiderunt Virtute primae sphaerae”
Explicit : “doctrinaliter tradiderunt se applicare poterit apte.”
-
ff. 158r-189r, Brudzewo’s Commentariolum on Peurbach’s Theoricae novae
Incipit : “Sol habet tres orbes a se invicem. Theorica Solis principali divisione dividitur in tres partes. In prima parte”
Explicit: “Tantum de praedictis circa motum octavae sphaerae et per consequens circa theoricas omnium planetarum. de quo laus et gloria in sempiternum omnipotenti deo auctori primo coelorum et motuum eorundem \(\parallel \) Amen \(\parallel \) Ffinit Commentariolum super Theoricas novas Georgii Purbachii in studio generali Cracoviensi per Magistrum Albertum de brudezwo (sic) pro introducione maiori minori aptiorique circa lectionem earundem factam: corrogatum: In quo quidem ex minus apte aut non doctrinaliter et scientifice positis lector industrius: in contumeliam facile non insurgat. Sed qui noviter artis cerciora profundioraque in profectum edere studeat: simili provocatus labore eorum (?) si is fuerit qui neque ea que adeo pueriliter adducta sunt cupiat: permittat illesa ne quem reprehendere cupiens insciciam propriam quam honestius tacuisset turpiter propalaret. Dictum est Anno domini 1483 commutacione hiemali in mediate post pestem validam que viguit Cracovie Anno domini 1483 (sic) A festo corporis Christi incipiens usque ad festum Michaelis qui nos representat deo et sanctis in celis Amen.”
C - Krakow, Biblioteka Jagiellonska, 2703 (siglum C in Birkenmajer’s edition)
-
ff. 154r-156r, Brudzewo’s Prohemium to his Commentariolum
Incipit: “1493 Commentariolum super Theoricas Novas Georgii purbacii (sic) in Studio generali Cracoviensi per magistrum Albertum De Brudzewo diligenter corrogatum incipit. \(\mid \) Astrorum observatores studiosi experti quidem sufficienter sensu racione et instrumentis tradiderunt recte virtute primae sphaerae”
Explicit: “doctrinaliter tradiderunt se applicare poterit apte.”
-
ff. 156r-169v, Brudzewo’s Commentariolum on Peurbach’s Theoricae novae
Incipit: “Sol habet tres orbes. Theorica Solis principali divisione dividitur in tres partes. In prima parte”
Explicit: “Et his de praedictis circa motum octavae sphaerae et per consequens circa theoricas omnium planetarum Explicit Commentariolum super Theoricas novas Georgii purbacii in Studio generali Cracoviensi per magistrum Albertum De Brudzewo subtiliter corrogatum Scriptumque per me Michaelem De Ruszoczycze in bursa Ierusalem finitum in vigilia Circumcisionis domini Anno Domini 1493 Finis”
1.2 Printed editions of Brudzewo’s Commentariolum
M - Editio princeps, Milan, Uldericus Scinzenzeler, 1494 (USTC 996571, absent from Birkenmajer’s edition)
Brudzewo’s name is written nowhere in the volume.
-
f. sign. a i lacks in all the extant volumes.
-
ff. sign. a ii r–[a vi] r, Brudzewo’s Prohemium to his Commentariolum
Incipit: “Prohemium. \(\mid \) Astrorum observatores studiosi experti quidem sufficienter sensu ratione et instrumentis tradiderunt recte virtute primae sphaerae”
Explicit: “doctrinaliter tradiderunt se applicare poterit apte.”
-
ff. sign. [a vi] r–[e vi] v, Brudzewo’s Commentariolum on Peurbach’s Theoricae novae
Incipit: “Sol habet tres orbes. Theorica Solis principali divisione dividitur in tres partes. In prima parte”
Explicit: “Tantum de praedictis circa motum octave sphere et per consequens circa theoricas omnium planetarum. de quo sit laus et gloria in sempiternum omnipotenti deo auctori primo celorum et motuum eorundem Amen. \(\mid \) Impressum Mediolani per Vldericum scinzenzeler. Anno domini. MCCCCLXXXXIIII. die. viij. novembris.”
E - Second edition, Milan, Uldericus Scinzenzeler, 1495 (USTC 991670, siglum E in Birkenmajer’s edition)
-
f. [a i] recto, Frontispiece: “Commentaria utilissima in theoricis planetarum”
-
f. [a i] verso, Dedication letter: “Johannes Otto Germanus de valle vracense Magnifico Ambrosio Rosato ducali physico et Consiliario sapientissimo Rosati domino [...] Ex Papia XIIII Kalendas octobris.”
-
ff. a ij r–[a vi] r: Brudzewo’s preface to his commentary
Incipit: “Astrorum observatores studiosi experti quidem sufficienter sensu ratione et instrumentis tradiderunt recte virtute primae sphaerae”
Explicit: “doctrinaliter tradiderunt se applicare poterit apte.”
-
f. [a vi] v–[g viii] v: Brudzewo’s Commentariolum on Peurbach’s Theoricae novae
Incipit: “Sol habet tres orbes. Theorica Solis principali divisione dividitur in tres partes. In prima parte”
Explicit: “Finit Commentariolum super Theoricas novas Georgii Peurbatii in studio generali Cracoviensi per Magistrum Albertum de Brudzewo: Pro introductione Iuniorum corrogatum. Impressum arte Ulderici Scinzenzeler. Anno Christi 1495. Tertio Kalendas aprilis. Mediolani. | Ad lectorem epigramma [...]”
(Brudzewo 1900)
Albertus de Brudzewo super Theoricas novas planetarum edidit Ludovicus Antonius Birkenmajer, Cracow, Jagiellonian University, 1900.
A reference to some of these manuscripts can be found in (Brudzewo 1900, XLVI–LIII); (Rosinska 1984, 64); (Markowski 1990a, 11–13).
Sources
Copernicus, Nicolaus. 1543. De revolutionibus orbium coelestium. Nurebergae: Johannes Petreius;
-
English Translation in (Rosen, I, 1992, 3–330).
Copernicus, Nicolaus. 1884. De hypothesibus motuum caelestium a se constitutis commentariolus in (Prowe 1884, II, 184–202);
-
English translation
-
A brief description by Nicolaus Copernicus concerning the models of the motions of the heavens that he invented in (Swerdlow 1973, 433–512).
-
Peurbach, Georg. Theoricae novae planetarum
-
1454 manuscripts:
-
Cod. 5203, Österreichische Nationalbibliothek, Wien;
-
Cod. 5245, Österreichische Nationalbibliothek, Wien;
-
Codex Sancrucensis 302, Stiftbibliothek, Heiligenkreuz;
-
-
first printed editions:
-
[1472], [Nurebergae: Regiomontanus];
-
1482, Venetiis: Erhard Ratdolt;
-
1452, Venetiis: Erhard Ratdolt;
-
-
english translation of the 1485 edition in (Aiton 1987, 9–43);
-
critical edition with french translation in (Malpangotto 2016);
-
commentaries:
-
Brudzewo, Albert. 1900. Albertus de Brudzewo super Theoricas novas planetarum edidit Ludovicus Antonius Birkenmajer. Cracoviae: Typis et sumptibus Universitatis Jagellonicae.
-
Manuscripts:
-
L: 759, Zakład Narodowy im. Ossolińskich, Wrocław;
-
R: Pal. Lat. 1385, Biblioteca Apostolica Vaticana, Roma;
-
D: N 100, Sächsische Landesbibliothek, Dresde;
-
K: Cod. Ratstatt 36, Badische Landesbibliothek, Karlsruhe;
-
C: B. J. 2703, Biblioteka Jagiellonska, Cracovie;
-
Printed editions:
-
M: 1494, Mediolani: Uldericus Scinzenzeler;
-
E: 1495, Mediolani: Uldericus Scinzenzeler.
-
-
-
Capuano, Francesco. 1495. Theoricae novae Planetarum Georgii Purbachii astronomi celebratissimi ac in eas ... Domini Francisci Capuani de Manfredonia \(\ldots \) sublimis expositio et luculentissimum scriptum. Venetiis: Bevilaqua;
-
Mazzolini de Prierio, Silvestro. 1514. Clarissimi Sacre Theologie omniumque bonarum artium professoris Reverendi patris fratris Silvestri De Prierio \(\ldots \) in spheram ac Theoricas preclarissima Commentaria. Mediolani : G. de Ponte.
-
Reinhold, Erasm. 1542. Theoricae novae planetarum Georgii Purbacchii Germani ab Erasmo Reinholdo Salveldensi pluribus figuris auctae, & illustratae scholiis, quibus studiosi praeparentur, ac invitentur ad lectionem ipsius Ptolemaei. Witebergae: Lufft;
-
Schreckenfuchs, Erasm Oswald. 1556. Erasmi Osvaldi Schreckenfuchsii Commentaria in Novas theoricas planetarum Georgii Purbachii. Basileae: Henricum Petri;
-
Nunes, Pedro. 1566. In Theoricas planetarum Georgii Purbachii annotationes. Basileae: Henricpetrina; Critical edition in (Leitão 2010);
-
Wursteisen, Christian. 1568. Quaestiones novae in Theoricas novas planetarum doctissimi mathematici Georgii Purbachii Germani quae astronomiae sacris initiatis prolixi Commentarij uicem explere possint: una cum elegantibus figuris, et Isagogica Praefatione. Basileae: Henricpetrina.
Ptolemaeus, Claudius. 1515. Almagestum Claudii Ptolemei. Venetiis: Petrus Lichtenstein (First edition of the Arabo-Latin version of Gerard of Cremona);
-
critical edition of the Greek text in (Heiberg 1898–1907, I);
-
Greek text and French translation in (Halma 1813);
-
English translation in [Toomer, (1998) 1984].
Regiomontanus, Ioannes. [1475]. Dialogus inter Viennensem et Cracoviensem adversus Gerardi Cremonensis in Planetarum Theoricas deliramenta. [Nurebergae: Regiomontanus].
Rights and permissions
About this article
Cite this article
Malpangotto, M. The original motivation for Copernicus’s research: Albert of Brudzewo’s Commentariolum super Theoricas novas Georgii Purbachii . Arch. Hist. Exact Sci. 70, 361–411 (2016). https://doi.org/10.1007/s00407-015-0171-y
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00407-015-0171-y




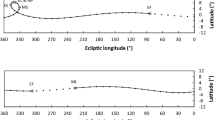
 Composition mathématique de Claude Ptolémée, traduite pour la première fois du grec en français ... par M. Halma et suivie des notes de M. Delambre. Paris: Henri Grand.
Composition mathématique de Claude Ptolémée, traduite pour la première fois du grec en français ... par M. Halma et suivie des notes de M. Delambre. Paris: Henri Grand.