Introduction

Electrorheological (ER) fluids typically consist of polarizable particles in an electrically insulating fluid (Seo and Seo 2012; Seo et al. 2012; Dong et al. 2019). When an electric field induces attractive interactions between the polarizable particles, these particles form a solid-like network of fibril shapes within a few milliseconds oriented along the direction of the electric field. Reverse transition occurs as soon as the electric field is switched off. In ER fluids, shear deformation leads to yield stress mainly because of two interactions: electrostatic interactions between the suspended ER particles and hydrodynamic interactions. At low shear rates (\( \dot{\gamma} \)), the electrostatic interactions between the suspended ER particles induced by the external electric field dominate the hydrodynamic interactions and thus lead to the formation of aggregated fibril structures (mesostructures). These fibril structures hinder the flow of the suspension, leading to yield stress before the flow starts. At high shear rates, however, the hydrodynamic interaction dominates. The fibril structures of ER fluids completely collapse, resulting in liquid-like behavior, in which the yield stress (τy) follows a power-law dependency on the electric field strength (E) such as τy∝ E1.5 ~ 2 (Seo and Seo 2012; Seo et al. 2011; Kim et al. 2016). These features lead to remarkable changes in the rheological properties of the fluid which shows wide potential applications such as dampers, brakes, shock observers, drug delivery, and robotics (Zhang et al. 2009; Yamaguchi et al. 2010).

Although many ER devices have been successfully manufactured, more effective ER fluids with higher yield stress and reduced power consumption operating at a low electric field are demanded for their further applications and commercialization. Considerable efforts have been made in recent years to improve the performance of the ER fluid, for example, by coating the suspended particles with electrically active polymers or by preparing composite particles (Armes 1996). Polypyrrole (PPy) is one of the most promising semiconducting materials because it exhibits excellent physical properties such as high electrical conductivity, polarizability, and stability. Therefore, PPy and its composite materials are frequently used in the preparation of efficient ER materials (Cheng et al. (2006a, b); Kim and Kim 2007; Sedlačík et al. 2012; Fang et al. 2013). Some years ago, Cheng et al. (2006a) reported an anhydrous ER fluid prepared by dispersing nanocomposite particles of conducting PPy and mesoporous silica (MCM-41) in the silicone oil. The PPy was synthesized in an aqueous solution of FeCl3.H2O after the pyrrole monomer was introduced into the mesoporous silica (MCM-41) channels prior to the polymerization; thus, it was confined in the silica (MCM-41) channel. Choi et al. analyzed the ER properties of mesoporous PPy/MCM-41 suspensions later (Cho et al. 2004; Liu and Choi 2009). Recently, Kim et al. 2016 also investigated the ER properties of a core-shell-structured SiO2/PPy nanoparticle suspension of which structure is opposite to Cheng et al.’s nanoparticles. Silica nanoparticles were modified by 3-(trimethoxysilyl)propyl methacrylate and a conducting PPy shell was then synthesized on the modified silica surface via oxidative polymerization with FeCl3 as the oxidant. To be used as an ER material, the SiO2/PPy particles were controlled by a dedoping process where 1 M NaOH was added to the particle suspension until the pH value reached 10 (Kim et al. (2016)). In both studies, the yield stress was dependent on the electric field, following the 1.5 power-law behavior. Thus, the ER activity mechanism was asserted to follow the conduction model as suggested by Davis and Gender (Davis and Ginder 1995). On the other hand, Goodwin et al. synthesized the PPy particles of 260 nm in diameter for the preparation of electrorheological (ER) fluids in dodecane (Goodwin et al. 1997). The particles were stabilized by a graft copolymer with poly(12-hydroxystearic acid) as the stabilizing moieties. An AC electric field at 50 Hz was applied to the fluids using field strengths up to 1 kV mm−1 and the viscometric behavior was examined. The PPy suspensions exhibited Bingham behavior and the fluid behavior could be calculated from the interparticle polarization forces. The dependence of the Bingham yield stress on the electric field strength is E2. Slightly higher values of the power-law index at lower volume fractions were possibly due to greater uncertainty in the fit of the shear stress-shear rate curves (Goodwin et al. 1997). At low volume fractions and low field strengths, the stress decreased slightly (~ 5%) at the lowest shear rates, which led to increased uncertainty in the fit. The weaker the ER effect, the more doubtful the existence of static yield stress. On the other hand, it was shown that the change in viscosity with shear rate scales with the Mason number, Mn, which expresses the ratio between polarization forces and shear forces (Parathasarathy and Klingenberg 1996). The pure PPy particle suspension shows different ER activity mechanism following the polarization model than that of two nanocomposite particle suspensions which were supposed to follow the conduction model.

In this study, we reanalyzed the experimental data of those three reports by using the Seo-Seo model (Seo and Seo 2012) to evaluate the static yield stresses (τsy) instead of the dynamic yield stresses (τdy) and to clarify the flow behavior of these ER fluids as well as the mechanism of the ER reaction. The static yield stresses were compared with the experimental data and the dynamic yield stresses (τdy) obtained with the Bingham and/or CCJ models (Cheng et al. 2006a, b; Liu and Choi 2009; Kim et al. 2016). The underlying ER mechanism was reconsidered by examining the nonlinear dependence of the static yield stress on the electric field strength (Davis and Ginder 1995; Wu and Conrad 1996).

Rheological models for the yield stress

As already mentioned, there are two yield stresses in ER fluids: the static yield stress (τsy) and the dynamic yield stress (τdy) (Fig. 1) (Seo and Seo 2012; Méheust et al. 2011). The dynamic yield stress (τdy) is obtained by extrapolating the shear stress curve versus the shear rate to the zero shear rate (Seo et al. 2018; Choi et al. 2014). The Bingham model is the simplest model to fit the yield flow behavior; the relationship between the shear stress (τ) and the shear rate (\( \dot{\gamma} \)) is as follows

$$ \uptau ={\tau}_{dy}(E)+{\eta}_{pl}\dot{\gamma},\kern0.5em \tau \ge {\tau}_0(E)\kern0.75em $$
(1)
$$ \dot{\gamma}=0,\kern0.5em \tau <{\tau}_0(E) $$
(2)

where τdy(E) is the dynamic yield stress when the electric field strength is E, and ηpl is E-dependent plastic viscosity, which approaches the suspension viscosity at a sufficiently high shear rate (Seo et al. 2018). Since the Bingham model does not adequately account for the structural change in the ER fluid during flow, Choi et al. proposed an empirical alternative model (Cho-Choi-Jhon (CCJ) model), which is a variation of the Bingham model that takes into account such structural changes (Cho et al. 2004),

$$ \tau =\frac{\tau_{dy}}{\Big(1+\left({t}_1{\dot{\gamma \Big)}}^{\alpha}\right)}+{\eta}_{\infty}\left(1+\frac{1}{\Big({t}_2{\dot{\gamma \Big)}}^{\beta }}\right)\dot{\gamma} $$
(3)

where t1 and t2 are time constants, \( \dot{\gamma} \) is the shear rate, τdy is the dynamic yield stress, and η∞ is the viscosity at high shear rates.

Fig. 1
figure 1

Schematic figure of the flow curve (broken line) for the Bingham fluid and (solid line) ER fluid. τsy is the static yield stress while τdy is the dynamic yield stress (Seo and Seo 2012)

Full size image

The yield stress of the ER fluid is the minimum stress that causes a shear flow in the undisturbed fluid state at rest (Parmar et al. 2008) The fibril-shaped structures are destroyed and the ER fluid flows when the shear stress exceeds the electric field forces that hold the fibril aggregates together. The shear stress of the flow decreases with the shear rate, but the broken structures tend to regroup to regain the aligned mesostructures because of the electrical dipoles between the particles. However, the shear stress of the fluid decreases after such reformation because the reformed structures are not as complete as those that were originally formed before the start of the shear flow process (Seo and Seo 2012; Seo et al. 2014)). The dynamic yield stress values obtained with the Bingham model are strongly influenced by the shear rate range, but are less affected when they are obtained with the CCJ model (Cho et al. 2005). When the stress value passes through a minimum during the structural change, the dynamic yield stress may or may not reach the minimum stress value depending on the depth of the minimum at which the fibril structure completely disintegrates under the continuous shearing (Seo et al. 2015).

On the other hand, the static yield stress, τsy, is the yield stress required for a static ER fluid to flow. The Seo-Seo model was used to calculate the static yield stress that met the yield criterion and to model the stress changes associated with the structural realignment (Seo and Seo 2012; McIntyre et al. 2013; Han et al. 2018).

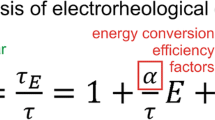
$$ \tau ={\tau}_{sy}\ \left(\ 1-\frac{\left(1-\exp \left(-a\dot{\gamma}\right)\right)}{\left(1+{\left(a\dot{\gamma}\right)}^{\alpha}\right)}\ \right)+\eta \dot{\gamma}\kern1em $$
(4)

where τsy is the static yield stress, η is the shear viscosity, a is the time constant (i.e., the reciprocal of critical shear rate for the deformation of the aligned particle structure), and α is the power-law index used to assess the degree of shear thinning (Seo and Seo 2012; Seo et al. 2014). This model has been shown to adequately account for the variation in the stress change with the shear rate described by the Papanastasiou model (Papanastasiou 1987; Seo and Seo 2012; Seo et al. 2012; McIntyre et al. 2013). Another advantage is that other models for predicting the dynamic yield stress can be included in the Seo-Seo model by varying the parameter values, for example, a Newtonian fluid (τsy = 0), the Bingham fluid (a = 0), the De Kee-Turcotte model (α = 0, a ≠ 0), and the Herschel-Bulkley model (\( a=0,\eta =\mathrm{m}{\dot{\gamma}}^{n-1} \)) (Seo and Seo 2012). The Seo-Seo model is suitable to predict the static yield stress of magnetorheological (MR) fluids as well as that of ER fluids (Seo et al. 2018).

After the yield stresses are obtained for different electric field strengths, the particle aggregation mechanism is related to the yield stress on the electric field strength. The yield stress (τy) of an ER fluid is known to exhibit a non-analytic power-law dependence on the electric field strength (E0), τy ∝ E0m (Davis 1992; Parmar et al. 2008; McIntyre et al. 2013). The τy dependence can be divided into two regions by the critical electric field strength, Ec: τy ∝ E02 for E0 < Ec because of the particle polarization and τy ∝ E03/2 for E0 > Ec due to the electrical breakdown of ER fluids under high electric field strength (Davis 1992; Davis and Ginder 1995; Wu and Conrad 1996; Choi et al. 2001). The critical electric field strength, Ec, depends on several factors such as the particle conductivity, the conduction mismatch between the particle and the medium liquid, and the particle volume fraction (Choi et al. 2001; Wu and Conrad 1996). Since a number of factors affect the value of Ec, the decision of Ec should be done before deciding the mechanism. Here, we propose a simple method to decide the Ec based on the two different fitting methods of the experimental data. Seo proposed a simple nonlinear equation that can fit the yield stress master curve after scaling of the electric field strengths,

$$ {\tau}_{sy}\left({E}_0\right)={\alpha}^{\prime }{E_0}^{3/2}\left(\ 1-\mathit{\exp}\ \left(-{m}^{\prime}\sqrt{E_0}\right)\right) $$
(5)

where m′ is a fitting parameter. This equation yields two limiting behaviors of the yield stress at low and high electric field strengths, i.e., at low electric field strengths, τsy ∝ E02 for E0 < < Ec and τsy ∝ E01.5 for E0 > > Ec (Seo 2011). Though it is an empirical equation, we have demonstrated that it fits the ER fluids yield stress behavior quite well (Seo et al. 2012, 2018). Normalizing with Ec and using τsy, 0 = α ′ Ec3/2 give the following universal fitting equation,

$$ \hat{\tau}={\hat{E}}^{3/2}\ \left(\ 1-\exp \left(-m\sqrt{\hat{E}}\right)\right) $$
(6)

where \( \hat{\tau}={\tau}_y/\alpha^{\prime }{E_c}^{3/2} \), \( \hat{E}=E/{E}_c \), and \( m=m^{\prime}\sqrt{E_c} \). After normalizing the data to produce a single curve, this simple equation was used to fit the static yield stress behavior of the three ER fluids (Figs. 3 and 4b). Excellent agreement was achieved with a single parameter, m, without requiring any arbitrary division in the range of the electric field strength (Seo et al. 2012, 2014). Since the yield stress data can be fit by the power-law model, the half region data (above or below the Ec) can be fit using a single power-law function,

$$ {\tau}_{sy}\left({E}_0\right)={m}_1{E_0}^{m_2} $$
(7)

Then, after normalization this equation is converted as

$$ \hat{\uptau}=\kern0.5em {\hat{E}}^{m_2}\kern1.25em $$
(8)

where \( \hat{\tau} \)= τ /\( {m}_1{E_c}^{m_2} \) and \( \hat{E}=E/{E}_c. \)Both the upper and lower power-law fits should meet at \( \hat{E}=1 \) and \( \hat{\tau}=1. \) The non-dimensional equation Eq. (6) should satisfy this condition, too. Then, Ec value can be approximately determined from Eqs. (6) and (8),

$$ {\alpha}^{\prime }{E_c}^{3/2}\left(\ 1-\mathit{\exp}\ \left(-{m}^{\prime}\sqrt{E_c}\right)\right)={m}_1{E_c}^{m_2}\kern0.75em $$
(9)

Modeling results and discussion

The experimental data for the PPy/ mesoporous MCM-41 particle suspensions of Cheng et al. (Cheng et al. 2006a, b; Liu and Choi 2009) were reanalyzed first by using the Bingham model, Eq. (1), and the Seo-Seo model, Eq. (4). The shear stress curves are replotted as a function of the shear rate in Fig. 2a. At a high shear rate (\( \dot{\gamma} \)), the predictions of the Bingham model are in good agreement with the experimental stress values. However, at lower shear rates, there are significant differences from the actual stress values. The flow curves display the ER fluid dynamics of the rupture and reformation of the aligned structures: the flow curve exhibits a significant stress decrease with recovery due to structural changes (Seo and Seo 2012). This demonstrates that the Bingham model is difficult to explain the ER suspension’s deformation, break-up, and realignment of fibril networks at low shear rate. On the other hand, hydrodynamic forces tend to destroy the ER structures and promote flow at high shear rates (Seo et al. 2018; Parmar et al. 2008). As the shear rate increases, the effects of the hydrodynamic forces are expected to dominate the effects of the electrostatic forces (Kim et al. 2016; Seo et al. 2015). The ER fluid is then completely broken down with no chainlike structure, and it behaves as a shear thinning fluid (Parmar et al. 2008). The results of the Seo-Seo model for PPy/MCM-41-based ER fluids show a good agreement with the experimental shear stress over the entire shear rate range (Fig. 2a).

Fig. 2
figure 2

a Flow curves of shear stress vs. shear rate for PPy /MCM-41-based ER fluids at 1 kV/mm (square), 2 kV/mm (circle), 3 kV/mm (triangle) for Seo-Seo model (solid line) and for Bingham model (3-point dot line). Data from Cheng et al. (2006a). b Flow curves of shear stress vs. shear rate for core-shell-structured SiO2/PPy nanoparticle–based ER fluid at 0.3 kV/mm (circle), 0.7 kV/mm (square), 1.0 kV/mm (diamond), 1.3 kV/mm (triangle), and 1.7 kV/mm (inverted triangle) for Seo-Seo model (solid line) and Bingham model (3-point dot line). Data from Kim et al. (2016))

Full size image

The dynamic yield stresses are strongly affected by the shear rate range used in the extrapolation and should thus be evaluated as the minimum of the shear stress if the stress value passes through a minimum during the structural change. However, this extrapolation at the minimum of the shear stress means that the breakup and realignment of the fibril network in the low and moderate shear rate region are not adequately considered (Fig. 1). For this reason, the dynamic yield stress, τdy, is not equivalent to the yield stress of an ER fluid. If the minimum-around region in the stress curve is flat, as in the case of the magnetorheological fluid, the dynamic yield stress value can be close to the static yield stress values (Seo et al. 2018; Choi et al. 2014). On the other hand, the static yield stress for an ER fluid measured under continuous shearing can be significantly different from the dynamic yield stress because ER fluids are naturally thixotropic due to the destruction of the mesostructure, which resists flow-induced particle rearrangement (Méheust et al. 2011; Seo et al. 2012). The Seo-Seo model takes into account the variation in the shear stress with the shear rate to obtain the static yield stress. The yield stress increases steadily with the electric field strengths (Table 1). In particular, the critical shear rate, which can be expressed as the inverse of the time constant a, \( {{\dot{\gamma}}_y}^{\ast }=1/a \), is the point where the ER fluids undergo a transition (McIntyre et al. 2013). It increases with the electric field strength which means that the structural change occurs at higher shear rates under the stronger electric field due to the greater cohesion between the particles. The viscosity, η, also increases with the electric field strengths because of the rapid assembly of chains. Table 1 summarizes the values of the dynamic yield stress and the static yield stress. Experimentally, the static yield stress can be measured by using the controlled shear stress (CSS) mode (Han et al. 2018). The static yield stress values predicted by the Seo-Seo model showed excellent agreement with the experimental data (Chuah et al. 2015; Choi et al. 2019).

Table 1 The optimal parameters obtained from the flow curves of PPy /MCM-41 (10 wt%) based ER fluid
Full size table

Likewise, Kim et al.’s report for the flow curves of conductive PPy-coated silica nanoparticles dispersed in silicone oil and their electrorheological (ER) characteristics under electric fields were also analyzed using the Seo-Seo model (Fig. 2b). The core-shell-structured nanoparticles have the opposite structure of the PPy/MCM41 nanocomposite particles, in which PPy is confined in the silica, in the sense that the conducting layer forms the outside. Hence, they show higher yield stress than the PPy/ mesoporous MCM-41 particle suspensions under the same electric field strength because of the stronger attraction from the higher polarization which is ascribed to the PPy coating (shell) layer (Kim et al. 2016). The Seo-Seo model that takes into account the variation in the shear stress with the shear rate demonstrates again a good agreement with the experimental data. The yield stress also increases steadily with the electric field strengths (Table 2). This suspension exhibits relatively shallow minimum region whereby a close agreement between the dynamic yield stresses from the Bingham model or CCJ model and the static yield stress from the Seo-Seo model is observed (Table 2).

Table 2 The optimal parameters obtained from the flow curves of core/shell structured SiO2/PPy nanoparticle-based ER fluid
Full size table

The particle aggregation behavior can be deduced from the dependence of the yield stress on the electric field strength. As previously stated, the τy dependence on the electric field strength is divided into two regions by the critical electric field strength, Ec: τy ∝ E02 for E0 < Ec because of the particle polarization and τy ∝ E03/2 for E0 > Ec at high electric field strengths due to the electrical breakdown of ER fluids under high electric field strength (Davis 1992; Davis and Ginder 1995; Wu and Conrad 1996; Choi et al. 2001; Wu and Conrad 1996). However, some uncertainties in the decision of the critical electric field strength Ec were not clarified yet (Espin et al. 2006; Parmar et al. 2008; Dong et al. 2019). A plot of the yield stress vs. the electric field strength after normalization is shown in Fig. 3a for the PPy/mesoporous MCM-41 nanocomposite suspensions. The static yield stress values obtained from the Seo-Seo model are close to the experimental data (Table 1).

Fig. 3
figure 3

Normalized static yield stress versus the normalized electric field strength. a ER fluid of nanocomposite of PPy confined in mesoporous silica (MCM-41). Straight line is the fit by the power-law model (∝ E1.5) and the dotted line is a nonlinear function fit (Eq. (5)). The parameter, m, value was 0.364. b ER fluids of core/shell SiO2/PPy nanocomposite particles: static yield stress (white circle) obtained from the Seo-Seo model. Experimental data (black circle), dynamic yield stress from the Bingham model (square), and dynamic yield stress (diamond) obtained from the CCJ model. Lines are the fits using the power-law dependence, Eq. (7). The power-law index is 1.5 for the Seo-Seo model data, 1.42 for the experimental data, 1.32 for the CCJ model data, and 1.31 for the Bingham mode data, respectively. In order to show the power-law dependence and the applicability of Eq. (5), the normalization was done by the lowest value of the electric field strength measured and the stress value there rather than the critical electric field strength

Full size image

More importantly, fitting the stress values with the power law is supposed to provide information about the particle aggregation mechanism (Kim et al. 2016; Kim and Kim 2007). The power-law index value, m, of the static yield stress is close to 1.5 according to the Seo-Seo model, which is possibly ascribed to the electrical breakdown of ER fluids if the electric field strength is high (Wu and Conrad 1996; Parmar et al. 2008; Kim and Kim 2007). But its true mechanism might be different from this inference. Obviously, the electric polarization mode, in which the yield stress exhibits a quadratic dependence on the electric field strength, does not appear for the PPy/MCM-41 suspensions due to the poor polarization by the surrounding non-conducting MCM-41 tube (Anderson 1994; Parathasarathy and Klingenberg 1996; Cheng et al. 2006b). The dynamic yield stress results obtained with the Bingham model or CCJ model have even lower power-law index values. Similar yield stress dependency on the electric field strengths for the Kim et al.’s suspension containing core-shell PPy/silica nanocomposite particle is also observed in Fig. 3b. Since this particle’s shell is comprised of the PPy, the polarization appears more strongly than the PPy/MCM-41 suspension which can be confirmed in Fig. 3b and Table 2. However, this suspension also shows a similar 1.5 power-law dependency, though dynamic yield stress dependency was lower than that of the static yield stress. Kim et al. presumed the ER activity mechanism to follow the conduction model (Kim et al. 2016), but it can be a hasty conclusion if we take into account of ER behavior of pure PPy particle suspensions.

The ER fluid behavior of pure PPy particle suspensions was reported by Goodwin et al. (Goodwin et al. 1997). Figure 4a shows the flow curves of the PPy ER fluid under various electric field strengths. Although these flow curves do not show the breakage and reforming of the aligned structures evidently due to the low electric field strengths (less than 1 kV/mm), thus, there is only a broad plateau in the shear stress; the static yield stress obtained after fitting the flow curves with the Seo-Seo model increases with the electric field (Fig. 4b). It shows that PPy particle suspension has an apparent quadratic dependence on the electric field strength, which may convincingly demonstrate that the 1.5 power-law dependence of the PPy/MCM-41 ER fluids may not be due to the nonlinear electrical breakdown of the ER fluids under a strong electric field but rather to the weak polarization arising from the confinement of PPy in the mesoporous silica (Goodwin et al. 1997; Choi et al. 2014). Kim et al.’s conclusion on the electrical field strength dependency of the yield stress of core/shell nanoparticle suspension might be hasty because of uncertainty in other parameters such as the conduction mismatch between the particle and the medium liquid, and the particle volume fraction (Kim et al. 2016). On the other hand, the yield stress values for PPy-coated polyethylene (PE) particle suspension were shown to be proportional to E2, which is consistent with the expected increase in electrostatic polarization with increasing particle surface conductivity (Anderson 1994; Klingenberg et al. 2007; Davis and Ginder 1995; Kim and Park 2002).

Fig. 4
figure 4

a Shear stress as a function of shear rate for PPy. Experimental points are from Goodwin et al. (1997) (200 V/mm (black circle), 300 V/mm (square), 400 V/mm (white diamond), 500 V/mm (triangle), 600 V/mm (white circle), 700 V/mm (black diamond), and 800 V/mm (inverted triangle)) and lines are calculated curves using the Seo-Seo model. b Static yield stress of PPy ER fluids versus the electric field strength. Solid line is the fit by the quadratic power-law model (∝ E2), while dotted line is a nonlinear function fit (Eq. (6)). When Eq. (5) was applied, the parameter, m, value was 0.114

Full size image

The point here is that assertion of the ER activity mechanism by the yield stress power-law index fit only can mislead the ER activity mechanism unless the basic assumption for the separation of the polarization mechanism range and the conduction mechanism range is ensured (Davis and Ginder 1995; Wu and Conrad 1996; Boissy et al. 1996). In fact, many previous studies did not check the suitability of the ER mechanism (Choi et al. 2014; Dong et al. 2019). By using the proposed method in Eq. (9), the approximate Ec values were obtained as 5.54 kV/mm for the suspension fluids containing nanocomposite particles of conducting PPy confined in a mesoporous silica (MCM-41), 4.4 kV/mm for the suspension fluids containing core/shell-structured SiO2/PPy nanoparticles, and 12.29 kV/mm for the PPy nanoparticle suspension fluids. These are much larger than the experimental electric field strengths for all three suspensions. All the electric field strengths are then below the critical electric field strength, Ec, which means the conducting model is not applicable for both nanocomposite particle suspensions. For pure PPy particle suspension fluids, polarization model is applicable and the fitting results correctly correspond to this. Since all ER fluids include many particle simultaneous cohesion, the application of the pairwise particle interaction modeling for the conduction model can be misleading, even if the basic assumption of Ec condition is satisfied (Wu and Conrad 1996). Special attentions should be paid when the yield stress dependence on the electric field strength is smaller than the quadratic dependence though the electric field strength is lower than the Ec; i.e., other factors should be checked before making an assertion on the ER fluid activity mechanism. Goodwin et al. showed that the dependence of the dynamic (Bingham) yield stress on field was E2 for pure PPy ER fluids at the higher volume fractions. The value of the power index was almost constant ~ 2 (Goodwin et al. 1997).

If the primary forces governing the behavior of ER fluids are electrostatic polarization forces induced by an applied electric field and hydrodynamic forces caused by the particle motion relative to the continuous phase, the non-dimensionalized ER fluid properties should depend only on the ratio of the electrostatic polarization force to the magnitude of the hydrodynamic force (Méheust et al. 2011; Parathasarathy and Klingenberg 1996). The dipole-dipole interactions are proportional to the square of the electric field intensity due to particle polarization, E2, whereas the shear strength acting on a particle within an ER chain is proportional to the local shear constraint, i.e., the shear rate, \( \dot{\upgamma} \). Hence, the normalized shear that allows for the comparison of the shearing process to the cohesive ER structures present in different runs is \( \dot{\upgamma} \)/E2, which is proportional to the Mason number, Mn (Mn = μ0γ/2ε0εcβ2E2, where μ0 is the medium viscosity, β is the dielectric contrast factor (= (εp−εc)/(εp + 2εc)), εp is the particle dielectric constant, εc is the dielectric constant of the liquid medium phase, and ε0 = 8.854 × 10−14 F/cm is the vacuum permittivity) (Parathasarathy and Klingenberg 1996; Méheust et al. 2011). If this reasoning works for the PPy suspensions, then the apparent viscosity η (= τ/ γ) is proportional to Mn−1, provided the volume fraction of the particle remains constant (Klingenberg et al. 2007). After the non-dimensionalization of the viscosity by dividing it with the viscosity at an electric field strength of zero (ηc) and plotting it as a function of \( \dot{\upgamma} \)/E2, the dimensionless apparent viscosities should collapse onto a single curve. All three fluid curves show that the log(viscosity) curve vs. log (\( \dot{\gamma} \)/E2) has a slope of nearly − 1 at small \( \dot{\gamma} \)/E2, whereas the curve smoothly approaches unity at large \( \dot{\gamma} \)/E2 (Fig. 5). Some scattering of the data is ascribable to the inaccuracy of the measurement due to weak ER effects as well as non-Bingham fluid behavior (Marshall et al. 1989; Klingenberg 2007).

Fig. 5
figure 5

Normalized viscosity versus the ratio of shear rate (γ)/E2 which is proportional to the modified Mason ratio. All the lines are slope of − 1. a ER fluids of nanocomposite of PPy confined in mesoporous silica (MCM-41), b ER fluids of core/shell SiO2/PPy nanocomposite particles, and c PPy nanoparticle suspension

Full size image

These results validate that the polarization mechanism works for all three particle suspensions at least within the applied electric field strengths. Also, it further elucidates that the low yield stress dependence on the electric field strengths for the nanocomposite particle suspensions is not because of the ER activity mechanism change but rather because of other reasons. Therefore, even if the yield stress plot shows 3/2 power-law dependence on the electric field strengths, we should be certain about the critical electric field strength and the applicability of conduction mechanism for general ER suspensions (Anderson 1994).

Conclusions

In this paper, the flow behavior of electrorheological fluids containing PPy nanoparticles, PPy/silica nanocomposite particles (PPy confined in a mesoporous silica), and core-shell silica-PPy nanocomposite particles was reanalyzed using the Seo-Seo model. The Seo-Seo model convincingly predicted the static yield stress data over the tested range of the electrical field strength. It describes the deformation (breakup and reformation) of aligned structures at low shear rates and the yield flow behavior at high shear rates. The static yield stress of the PPy/MCM-41 nanocomposite ER fluid was found to exhibit a 1.5 power-law dependence on the electrical field strength possibly due to the weak polarization of the nanocomposite particles that arises from the confinement of PPy in the non-conducting mesoporous silica (MCM-41). The suspension of core-shell (silica-PPy) nanoparticle also showed a similar 1.5 power-law dependence on the electrical field strength, though its structure was opposite to the PPy/MCM-41 nanocomposite particles and its polarization is much greater.

Although the 1.5 power-law dependence on the electric field strength was observed, this outcome should be distinguished from the prediction of the conduction model, which is considered to be applicable. Unless the condition that the electric field strength is higher than the critical electric field strength (Ec) which is the basic assumption for the conduction model, the 1.5 power-law dependency does not necessarily mean the ER behavior following the conduction model. In the case of the pure PPy nanocomposite particle suspension, the yield stress showed the quadratic dependence on the electric field strength, following the polarization model. We proposed a simple method to calculate the Ec that is a touchstone of differentiating the ER activity mechanisms. The nonlinear one-parameter equation proposed by Seo can be used to fit the universal plot of the static yield stress and to obtain Ec. This means if the electric field strength is lower than Ec, the polarization mechanism works for all three particle suspensions at least within the applied electric field strength range. Flow curve analysis using the Seo-Seo model in combination with dimensional analysis demonstrates to yield proper qualitative and quantitative predictions of ER fluid behaviors with relatively few experimental measurements and to elicit their working mechanism.