Introduction

Small amplitude oscillatory shear (SAOS) flow is widely used due to its simplicity and its ease of analysis. Fundamental rheological properties such as storage modulus (G’) and loss modulus (G”) are obtained through SAOS analysis, allowing the extent of elastic or viscous characteristics in various material systems to be evaluated. However, when strain amplitude (γ 0) is large, shear stress is no longer linear and has high harmonic contributions. Though it is not easy to deal with nonlinear behaviors, it is useful and informative to know the response of a material in the large amplitude oscillatory shear (LAOS) regime (Hyun et al. 2011).

To analyze nonlinear stress, several methods have been suggested by using Fourier transform (FT), characteristic functions, and Q parameter, and etc. (Wilhelm 2002; Klein et al. 2007; Hyun and Wilhelm 2009). One method to examine oscillatory shear stress is the stress decomposition method (Cho et al. 2005). It divides the total shear stress into elastic stress and viscous stress. If strain and strain rate are defined as x = γ = γ 0 sin ωt and \( \mathrm{y}=\dot{\upgamma}/\omega ={\gamma}_0\cos \upomega t \), respectively, then

$$ \sigma \left(x,y\right)=\frac{\sigma \left(x,y\right)+\sigma \left(x,-y\right)}{2}+\frac{\sigma \left(x,y\right)+\sigma \left(-x,y\right)}{2}={\sigma}_e\left(x,y\right)+{\sigma}_v\left(x,y\right) $$
(1)

where σ e indicates the elastic stress and σ v the viscous stress. This method can be expanded by using the Chebyshev polynomial (Ewoldt et al. 2008).

$$ {\sigma}_e(x)={\gamma}_0\sum \limits_{n=\mathrm{odd}}{e}_n\left(\omega, {\gamma}_0\right){T}_n(x) $$
(2)
$$ {\sigma}_v(y)={\dot{\gamma}}_0\sum \limits_{n=\mathrm{odd}}{v}_n\left(\omega, {\gamma}_0\right){T}_n(y) $$
(3)

Here, e n (ω, γ 0), v n (ω, γ 0), and T n refer elastic Chebyshev coefficients, viscous Chebyshev coefficients, and nth order Chebyshev polynomial, respectively. By analyzing elastic and viscous stress or Chebyshev coefficients, the characteristic of nonlinear stress in various systems have been investigated (Salehiyan et al. 2015; Lee et al. 2015; Park et al. 2015; Khandavalli et al. 2016; Huang et al. 2017; Goudoulas and Germann 2017). Nam et al. (2011) applied the stress decomposition method to hard sphere systems; poly(methyl methacrylate) (PMMA) particles with average diameter of 10 μm dispersed in polybutene (PB) with molecular weight 920 g/mol at volume fraction 0.514. They observed double peaks in elastic stress near the flow reversal (FR) point. However, that observation has not been reported further, and its structural origin has never been explored.

Particulate fluids are receiving wide attention due to many practical applications (Lee et al. 2017). The behaviors of hard sphere systems under oscillatory shear flow have also been studied extensively, both experimentally and via simulation (Petekidis et al. 2003; McMullan and Wagner 2009; Besseling et al. 2012; Koumakis et al. 2013; Koumakis et al. 2016). However, most studies concentrate on a system with the volume fraction near the freezing point where interesting rheological behaviors such as yielding or ordering are observed under oscillatory shear flow, and there exists only a few studies at intermediate volume fractions.

In soft particle systems, there are many reports, especially experimental studies, in which soft particle systems are analyzed by adopting a hard sphere model (Mason et al. 1997; Senff and Richtering 1999; Fuchs and Ballauff 2005; Siebenburger et al. 2009; Mohan et al. 2013; Pellet and Cloitre 2016). In simulations, soft sphere systems tends to be described by using inverse-power potential (IPP), which controls the slope of the potential (Heyes and Brańka 2005, 2008; Pieprzyk et al. 2014).

Comparisons of soft and hard sphere systems are also reported; however, they concentrate on yielding behavior at high volume fractions (Grand and Petekidis 2008; Koumakis et al. 2012; Poulos et al. 2015) or concentrate on the rheological properties under simple shear flow (Nazockdast and Morris 2012; Ding and Mittal 2015). Thus, characteristics at an intermediate volume fraction, which is lower than the freezing point, need to be investigated further under the oscillatory shear flow. Though the structure of hard sphere systems under oscillatory shear flow at an intermediate volume fraction has been described (Lin et al. 2013; Wang and Swan 2016), analyzing oscillatory shear stress through stress decomposition at intermediate volume fraction needs to be studied further.

In this paper, the stress responses of both hard and soft sphere systems at an intermediate volume fraction under oscillatory shear flow are analyzed by using the particle simulation technique. We will inceptively inspect whether double peaks, which are observed in experiments of hard sphere systems, are also created in simulation. In addition, the obtained double peaks will be quantified and their structural origin will be explored.

This paper is composed as follows. First, oscillatory shear stress for both hard and soft spheres will be analyzed by performing stress decomposition. Next, it will be shown that double peaks appear only for hard sphere systems, and they will be quantitatively analyzed. Then, the stress and structure of both hard and soft sphere systems will be compared at the same normalized volume fraction, frequency, and γ 0. Finally, the stress and structure of hard spheres at different γ 0 are compared at the same volume fraction and frequency. We draw conclusions based on the results of the comparative study.

Simulation system

There are many simulation methods for colloidal dispersions such as Brownian dynamics (BD), Stokesian dynamics (SD), multi-particle collision dynamics (MPCD), etc. (Foss and Brady 2000a, b; Gompper et al. 2009; Park et al. 2016). In this study, due to plenty of reliable references, applicability to various systems, and relatively low computational cost, a BD simulation technique is used. Hydrodynamic, potential, and Brownian forces affect the motion of the particles. The governing equation is the Langevin equation, as given in Eq. 4.

$$ m\frac{{\mathrm{dv}}_i}{\mathrm{dt}}={\mathbf{F}}_i^H+{\mathbf{F}}_i^P+{\mathbf{F}}_i^B $$
(4)

where, m, v i , \( {\boldsymbol{F}}_i^H \), \( {\boldsymbol{F}}_i^P \), and \( {\boldsymbol{F}}_i^B \) are the mass of a particle, velocity vector, hydrodynamic force, potential force, and Brownian force of the ith particle, respectively. The left-hand side term can be neglected when the time scale is sufficiently long to relax particle momentum. When the particle is a sphere, hydrodynamic force is expressed as given in Eq. 5.

$$ {\mathbf{F}}_i^H=-6\pi \eta a\left({\mathbf{v}}_i-{\mathbf{v}}_i^{\infty}\right) $$
(5)

where, η, a, and \( {\mathbf{v}}_i^{\infty } \) are the medium viscosity, radius of particle, and imposed flow velocity at ith particle, respectively. In this simulation, oscillatory shear flow \( {\mathbf{v}}_i^{\infty }={\dot{\boldsymbol{\Gamma}}}_0\bullet \mathbf{x}\ \mathrm{cos}\upomega \mathrm{t} \) is imposed, where \( {\dot{\boldsymbol{\Gamma}}}_0 \), x, and ω are the velocity gradient tensor, the position of particle and frequency, respectively.

Brownian is defined by Eqs. 6 and 7.

$$ \left\langle {\mathbf{F}}_i^B(t)\right\rangle =0 $$
(6)
$$ \left\langle {\mathbf{F}}_i^B(t){\mathbf{F}}_i^B\left({t}^{\hbox{'}}\right)\right\rangle =12{k}_B T\pi \eta a\delta \left(t-{t}^{\hbox{'}}\right)\mathbf{I} $$
(7)

where, bracket indicates an ensemble average. Here, k B , T, δ(t), and I are the Boltzmann constant, temperature, Dirac delta function and unit tensor, respectively. It can be expressed by Wiener process as in Eq. 8.

$$ {\mathbf{F}}_i^B(t)\varDelta t=\sqrt{2{k}_B T\zeta}\varDelta {\mathbf{W}}_i(t) $$
(8)

where, 〈∆ W i (t)〉 = 0 and 〈∆ W i (t)∆ W i (t ′)〉 = δ(t − t′)I∆t are satisfied.

Langevin equation can be rearranged as Eq. 9 by using previous equations, and particle position is updated by using this equation at each time step (∆t).

$$ \varDelta {\mathbf{x}}_i=\left[{\mathbf{v}}^{\infty}\left({\mathbf{x}}_i\right)+\frac{1}{6\pi \eta a}{{\mathbf{F}}_i}^p\right]\varDelta t+\sqrt{2{k}_BT/6\pi \eta a}\varDelta {\mathbf{W}}_t $$
(9)

One method used to describe hard sphere system is the potential-free (PF) method (Heyes and Melrose 1993; Foss and Brady 2000a; Wang and Swan 2016). In this method, the particles are moved by the force from the imposed flow and Brownian motion, and overlapped particles are relocated to non-overlapped states. The moving distance of the overlapped particle is determined by Eq. 10.

$$ \varDelta {x}^{\mathrm{HS}}=k\widehat{\mathbf{r}}\left(\varDelta r-2a\right)H\left(2a-\varDelta r\right) $$
(10)

where, ∆x HS, ∆r, H, and k indicate hard sphere displacement, the center-to-center distance between overlapped particles, Heaviside step function, and a constant that defines how far the overlapped particles are moved to the non-overlapped state, respectively. Moreover, \( \widehat{\mathbf{r}} \) denotes a unit vector r/r. To prevent overlap, k should be larger than 0.5. When it is 0.5, the overlapped particles are relocated to contact distance, and when k is 1, the overlapped particle are relocated to a non-overlapped state as much as their overlapped distance. In this simulation, k is set as 1 (Heyes and Melrose 1993). Interparticle force in PF is given as Eq. 11.

$$ {\mathbf{F}}_i^P=6\pi \eta a\frac{\varDelta {x}^{HS}}{\varDelta t} $$
(11)

In PF, the particle stress from the interparticle force is calculated by using the radial distribution function (RDF) at contact distance (2a) as in Eq. 12 (Foss and Brady 2000a).

$$ \left\langle {\boldsymbol{\Sigma}}_p\right\rangle =-{n}^2{k}_B Ta{\int}_{r=2a}\widehat{\mathbf{r}}\widehat{\mathbf{r}}g\left(\mathbf{r}\right) dS $$
(12)

where g(r) and n indicate RDF and the number of particles, respectively. To change particle softness, the IPP method is used, as presented in Eq. 13 (Mitchell et al. 1995).

$$ \varepsilon (r)={k}_BT{\left(\frac{2a}{r}\right)}^n $$
(13)

When the slope n is smaller than or equal to 12, it shows soft sphere characteristics. On the contrary, when n is larger than or equal to 18, it shows hard sphere characteristics (Brańka and Heyes 2006; Lange et al. 2009). When n is larger than 72, transport coefficients are hardly distinguishable at different n, and this potential describes true hard sphere systems as n goes to infinity. (Heyes and Brańka 2005). In this paper, n is 8 for soft spheres and 54 for hard spheres. Interparticle in IPP is given in Eq. 14.

$$ {\mathbf{F}}_i^P=-\sum \limits_{i\ne j}\frac{d}{d\mathbf{x}}\varepsilon \left(\left|{\mathbf{x}}_i-{\mathbf{x}}_j\right|\right) $$
(14)

Stress is obtained from the distance between two particles and the interparticle force in IPP as in eq. 15.

$$ \left\langle {\boldsymbol{\Sigma}}_p\right\rangle =-n\left\langle {\mathbf{xF}}^P\right\rangle $$
(15)

To describe hard spheres, an IPP with a slope of 54 and PF are used, whereas an IPP with a slope of 8 is used to describe soft spheres.

To revise the volume fraction of systems with different particle softness, a reduced coupling parameter (Γ/Γfreezing) is used. The effective volume fraction (Γ) is normalized by the volume fraction at the freezing point (Γfreezing) of each system. It is reported that reduced transport coefficients at equilibrium or in simple shear can be plotted on a master curve when plotting as a function of the reduced coupling parameter (Lange et al. 2009; Ding and Mittal 2015). As this value indicates how far the system is away from the freezing point, it is a useful parameter when comparing systems with different particle softness. The freezing point at specific slope n can be found in the previous paper (Agrawal and Kofke 1995). For example, the freezing point corresponds to volume fractions 0.494, 0.493, and 0.827 for the PF, IPP with n = 54, and IPP with n = 8, respectively.

Pair distribution function (g(r)) can be expressed as a series of spherical harmonic function series as in Eq. 16 (Hanley et al. 1987), and g 2, − 2(r), which is closely related with shear stress, can be calculated at each time for investigating the microstructure.

$$ g\left(\mathbf{r}\right)={g}_s(r)+{\sum}_{l=1}^{\infty }{\sum}_{m=-l}^l{g}_{lm}(r){Y}_{lm}\left(\theta, \varphi \right) $$
(16)

Moreover, to quantify the extent of particle ordering, the concept of two-body excess entropy is adopted (Truskett et al. 2000; Ding and Mittal 2015). Two-body excess entropy represents full excess entropy of the whole system (Dzugutov 1996). It can be obtained by using RDF and particle number density. This approach has advantages because the structure under oscillatory shear flow, whose structure varies as time proceeds, can be quantified as a single value at a given time as in Eq. 17.

$$ {s}_2=-\frac{\rho }{2}\int \left\{g\left(\mathbf{r}\right)\ln g\left(\mathbf{r}\right)-\left[g\left(\mathbf{r}\right)-1\right]\right\}d\mathbf{r} $$
(17)

where g(r) is RDF and ρ is number density. When -s 2 goes to infinity, it implies a highly ordered structure. When it is near zero, it implies a totally disordered structure. The extent of particle alignment during the cycle is evaluated by using this value.

In this paper, the number of particles is 253. All particles are allocated in the lattice and the initial configuration is obtained after an equilibration step. Subsequently, simulations are conducted at every γ 0 and frequency (ω) from this initial configuration. The Lees-Edwards periodic boundary condition is used when shearing (Lees and Edwards 1972). ω is normalized by multiplying it by the particle characteristic time (6πa 3 η/k B T). Normalized ω can be defined as the Deborah number.

$$ \mathrm{De}=6\pi {a}^3\omega \eta /{k}_BT $$
(18)

In this simulation, Γ/Γfreezing is fixed at 0.61 (Γ of hard sphere: 0.3, soft sphere: 0.5), and the range of De is from 20 to 100 (mostly De = 80). The stress in each oscillatory shear test is obtained by averaging the stresses during the 7 cycles after the stress is stabilized.

Stress decomposition and double peaks

Total, elastic, and viscous stresses

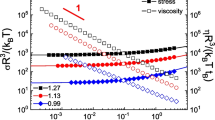
Figure 1a shows the total, elastic, and viscous stresses in a wide range of γ 0 at Γ/Γfreezing = 0.61 and De = 80 from the PF that corresponds to a hard sphere system. Figure 1b shows the elastic stresses for De from 20 to 100. Here, all stresses are normalized by their maxima.

Fig. 1
figure 1

a The total, elastic, and viscous stresses at De = 80; b elastic stresses from De = 20 to 100 for PF at Γ/Γ freezing = 0.61.

Full size image

As γ 0 increases, the total stress becomes distorted, followed by a shape change in the elastic and viscous stresses. As shown in previous studies (Koumakis et al. 2012; Koumakis et al. 2013), total stress overshoot is not observed. It is to be noted that double peaks are observed in the elastic stress near flow reversal when γ 0 is large, and this has rarely been reported. The double peaks are also observed in experimental with hard spheres (Nam et al. 2011). As seen in Fig. 1b, the double peaks appear over a wide range of De values at intermediate γ 0 in this simulation.

By increasing the slope of IPP, the particles change from soft to hard spheres. The total, elastic, and viscous stresses are shown in Fig. 2. In this simulation, the particles are soft when the slope of IPP is 8, and hard when the slope of IPP is 54. The Γ/Γfreezing is fixed to 0.61 as in the PF case. It is to be noted that the actual volume fractions are different in hard and soft sphere systems.

Fig. 2
figure 2

The total, elastic, and viscous stresses for a n = 8 (soft sphere), b n = 54 (quasi-hard sphere) for IPP method, at Γ/Γ freezing = 0.61 and De = 80

Full size image

As γ 0 increases, the shape of the total, elastic, and viscous stresses changes in both cases. At high γ 0, the shape of total stress is governed by that of viscous stress. However, in Mohan et al. (2013) and Koumakis et al. (2013), most of the stress comes from the elastic contribution. This difference can be explained by the difference in volume fraction (Poulos et al. 2015). At high volume fraction, elastic characteristic is dominant (Mohan et al. 2013), while viscous characteristic is dominant (this paper) at intermediate volume fraction. For soft spheres, double peaks are not observed in elastic stress (Fig. 2a). In contrast, in Fig. 2b, which describes a quasi-hard sphere system, double peaks are observed in elastic stress and the shape of each stress is similar to that presented in Fig. 1a which uses PF. From these results, it can be inferred that double peaks appear only in simulations that describe hard sphere system.

Peaks characteristics

To quantify the characteristics of the double peaks, both depth and width are defined as shown in Fig. 3, in which the elastic stress is plotted at Γ/Γfreezing = 0.61, De = 80, and γ 0 = 3. The horizontal axis is time, which is normalized by the duration of 1 cycle. The vertical axis is the elastic stress, which is normalized by its maximum. The depth is defined as the gap between the normalized elastic stress at peak and that at the local minimum (at normalized time of 0.25). The width is the normalized time interval between the two peaks.

Fig. 3
figure 3

The definition of depth and width when double peaks appear

Full size image

In this simulation, double peaks are observed only in the hard sphere system (i.e., PF or IPP; n = 54). The γ 0 range in which double peaks appear is wider when using PF, which better describes a hard sphere, than for the case of IPP with a slope of 54 (not shown in this paper). In Fig. 4, the open symbols connected with black solid lines represent the results from PF, while the filled symbols connected by red dashed lines represent the results from IPP.

Fig. 4
figure 4

Double peaks a depth and b width at De = 50, 80, and 100 as a function of γ 0 for PF and IPP with n = 54

Full size image

Both depth and width show maxima, and there is a range of γ 0, beyond which the peaks disappear. The depth from PF, which has better hard sphere characteristics, is larger than that obtained from IPP. The maximum locates at γ 0 = 3. For width, the variation is less pronounced, and the maximum is observed at γ 0 = 2.

Stress and structure analysis

Soft and hard spheres

The stress and structure of a hard sphere system, which shows double peaks, and a soft sphere system, which does not show double peaks, are compared when Γ/Γfreezing, De, and γ 0 are 0.61, 80, and 3, respectively. In this case, the hard sphere system is simulated using PF, and soft sphere system using IPP with n = 8. In Fig. 5a, the solid curves indicate total stress, and the dashed curves indicate elastic stress. The black curve is for the soft sphere system (IPP; n = 8) and the red one is for the hard sphere system (PF). The total and elastic stresses are normalized by the maximum value of the total stress for each system. The blue columns indicate the regime between two peaks. Point A represents the first peak before FR, and point B represents the second peak after FR. In Fig. 5b, g 2, − 2 at points A, flow reversal (FR), and B are shown. Solid line indicates hard sphere and dashed line indicates soft sphere. As the effective radius r in RDF can vary with particle softness, it is necessary to amend the radius. In this study, r is revised according to \( {\varGamma}_{\mathrm{rel}}^{1/3}={\left(\varGamma /{\varGamma}^{\mathrm{HS},\mathrm{freezing}}\right)}^{1/3} \) (Lange et al. 2009). Here, Γ HS, freezing indicates the volume fraction at the freezing point of the hard sphere system.

Fig. 5
figure 5

a The total and elastic stresses of soft sphere (S, IPP; n = 8) and hard sphere (H, PF) systems, b g 2, − 2 at points A, flow reversal (FR), and B for soft sphere and hard sphere systems when Γ/Γ freezing = 0.61, De = 80, and γ 0 = 3.

Full size image

In Fig. 5a, shape differences between the total stress of soft and hard spheres may be clearly observed in the regime where double peaks appear. The shape differences are not significant in the rest of the time domain. The differences in total stress in the blue regime also affect the elastic stress. Bases on the shape of the stress, double peaks appear when the total stress decreases rapidly before FR, which is followed by a gradual decrease after FR. In Fig. 5b, the first peak shows a negative value before flow reversal point (point A) and flow reversal point (FR), whereas it shows a positive value after flow reversal (point B). These results imply that the particle structure along the compressional axis before flow reversal is still maintained at flow reversal, whereas it is oppositely relocated along the compressional axis after flow reversal. g 2, − 2, which is closely related with the shear stress, shows a large difference between soft and hard sphere systems. For hard spheres, a sharp peak is shown near the contact point (2a, r\( {\varGamma}_{rel}^{1/3}\approx \)1.69) whereas the position of g 2, − 2 peak varies and the peak is broad for soft spheres. To obtain more information on the origin of two peaks, the structures of the hard and soft spheres at points A and B, which represent the two peak points, are compared.

Initially, the pair distribution function (PDF) needs to be inspected. The particles within a distance ±5a on the velocity-velocity gradient plane (− 5a < x, y < 5a) and ±0.05a (− 0.05a < z < 0.05a) to the vorticity direction relative to the reference particle are analyzed. Note that two systems have the same Γ/Γfreezing. Figure 6a, c, e shows the results for soft spheres, while Fig. 6b, d, f show the results for hard spheres. Figure 6a, b shows the results obtained at point A in Fig. 5, while Fig. 6e, f are the results obtained at point B. Figure 6c, d shows the results obtained at flow reversal point. In Fig. 6, the more reddish the PDF is, the more possibility that there is a particle at that point. Likewise, the more bluish the PDF is, the less possibility that there is a particle at that point. The circle at the center indicates double of the particle size. At point A in Fig. 5, the flow direction is from left to right, and at point B, the flow direction is from right to left.

Fig. 6
figure 6

PDF of a point A of soft sphere, b point A of hard sphere, c flow reversal point of soft sphere, d flow reversal point of hard sphere, e point B of soft sphere, and f point B of hard sphere

Full size image

In both cases, the particles are aligned to the compressional axis and are scarcely aligned along the extensional axis. As shown in Fig. 5b, the particle structure along the compressional axis is maintained at flow reversal point for both soft and hard sphere systems, whereas the structure along the opposite direction is observed at point B. A lot of particles are in touch for hard spheres (as evidenced by red color at contact), while particle density at contact is small (a red point is not observed at contact) and alignment to the flow direction is insignificant for soft spheres. Though not included in this paper, the difference in alignment is observed not only at points A, B, and flow reversal points but also during the whole cycle. As time proceeds from point A to point B, the particles are found less at contact distance for the hard sphere system (number of red point decreases), while for the soft sphere, the value of r of overlapped particles increases (points in inner circle area decreases), which leads the particles to locate more near the circle (contact distance). Next, the radial distribution function (RDF) at the two points is inspected. The RDF is plotted in Fig. 7. Here, only the first half cycle (0 < time/(2π / De) < 0.5) is plotted. To help comprehension, points A, B, and FR are also indicated. Legends indicate the value of g(r).

Fig. 7
figure 7

RDF of a soft sphere and b hard sphere as time proceeds. The white dashed lines represent points A and B (peaks point), and the dark gray dash-dot line represents flow reversal (FR) point. Note that the legend of soft and hard sphere systems are different

Full size image

For hard spheres, the particles do not exist in the inner area, r\( {\varGamma}_{\mathrm{rel}}^{1/3} \) is less than 1.69, which is the contact point. For soft spheres, the particles are observed in the inner area and the minimum r\( {\varGamma}_{\mathrm{rel}}^{1/3} \) of particle observation is changed with time. The maximum g(r) at each time is much higher throughout the cycle in hard sphere systems. Maximum g(r) is observed at contact point (2a, r\( {\varGamma}_{\mathrm{rel}}^{1/3}\approx \)1.69) for hard spheres, while g(r) increases with r\( {\varGamma}_{\mathrm{rel}}^{1/3} \) and maximum g(r) does not coincide with the contact distance for soft spheres. These results correspond to Fig. 5b as well as previous numerical studies, which show structures of soft and hard sphere systems in simple shear (Nazockdast and Morris 2012; Ding and Mittal 2015). In the soft sphere system, maximum g(r) throughout the cycle is observed after flow reversal. On the contrary, in the hard sphere systems, minimum g(r) at contact throughout the cycle is observed after flow reversal. As can be verified in Fig. 7, the structure formation and deformation of the particles during the whole cycle are different between two systems.

As the first peak of RDF is important for the particle system, the values of r and g(r) at the first peak during the cycle are also tracked in Fig. 8. The black symbols are for the soft sphere system, while the red symbols for the hard sphere system. The open symbols represent the results before FR, while the filled symbols are the results after FR. Only the results during a half cycle are plotted because the results after FR are the same as before FR. The solid arrows are guidelines that show the path before FR, while the dashed arrows are the guidelines that show the path after FR.

Fig. 8
figure 8

The location of the first peak in RDF during a half cycle in both soft (S, IPP; n = 8) and hard sphere (H, PF) systems

Full size image

For soft spheres, the variation of r is more pronounced than that of g(r) at the first peak. In contrast, for hard spheres, the variation of g(r) is more pronounced than that of r. When compressive force is imposed to hard spheres, most particles are located in near contact (2a, r\( {\varGamma}_{\mathrm{rel}}^{1/3}\approx \)1.69). In contrast, soft spheres can overlap, which may causes particle distribution around r\( {\varGamma}_{\mathrm{rel}}^{1/3} \). Note that the direction of force from the flow field and the interparticle force is opposite to the compressional axis. When the flow is weakened, compressed particles are pushed away as the interparticle force becomes comparatively stronger.

For soft spheres, which are indicated by the black symbols in Fig. 8, at the initial stage of the cycle where the flow is strong, the g(r) does not change much and the particles are compressed to each other. At the latter stage before FR, as the flow is weakened, the closely located particles are moved away from each other. Therefore, g(r) increases only slightly and r increases a lot. These processes are represented by arrows 1 and 2 in Fig. 8, which indicates the change of RDF before FR, which is in accordance with Fig. 7a. Shortly after FR, though flow direction is reversed, the structure formed in the previous compressional axis is maintained. As time proceeds, this maintained structure is pushed away to the extensional axis of reversed flow field (previous compressional axis), which makes both g(r) and r increase. Then the particles are spread out and no significant structure is formed. Thus, g(r) increases followed by a decrease while r increases. Long after FR, as the particles are affected continuously by the flow, the particles begin to compress again and, as a result, r continuously decreases. These processes correspond the arrows 3, 4, and 5 in the figure, which indicate the change of RDF after FR.

For a hard sphere system, which is indicated by red symbols in Fig. 8, the value of g(r) at contact is quite large at the initial stage of the cycle. As time proceeds and approaches FR, the flow velocity is reduced, which reduces compressive forces so that the particles are pushed away from each other, in a manner similar to relaxation in an equilibrium state. Therefore, r increases slightly and g(r) decreases significantly. These processes are represented by the arrows 1 and 2 in Fig. 8, which indicates the change of RDF before FR, which is in accordance with Fig. 7b. As the flow changes direction after FR, the particles, which are aligned to the compressional axis before FR, become realigned in the opposite direction for a while, and shortly after FR, the value of g(r) near the contact point decreases continuously. As the flow becomes stronger away from FR, the particles are compressed again at the contact point. Therefore, the value of r is the same as that at contact location and g(r) increases. These processes correspond the arrows 3, 4, and 5 in the figure, which indicate the change of RDF after FR.

Due to the differences in overall structural alignment of the particles as seen in PDF and the differences in structure formation and deformation mechanism during the cycle as can be seen in RDF, soft sphere systems do not show double peaks, but they appear in hard sphere system.

Hard sphere at different strain amplitudes

In this section, the stress and structure of the hard sphere system at two γ 0, one with double peaks and the other without, are compared. The simulation is performed with PF at Γ/Γfreezing = 0.61 and De = 80. In this condition, double peaks are observed in the range of γ 0 from 1 to 5. To compare cases in which double peaks appear and not, γ 0 = 0.8 and γ 0 = 1 are selected as low γ 0. Likewise, γ 0 = 5 and γ 0 = 8, are selected as high γ 0. The stresses at those four γ 0 are compared by pairing two by two. Fig. 9a shows the total and elastic stress at γ 0 = 0.8 and 1, and points C and D indicate the first and second peak, respectively, at γ 0 = 1. Fig. 9b shows the total and elastic stress at γ 0 = 5 and 8, and points E and F indicate the first and the second peak, respectively, at γ 0 = 5. The black curves indicate a condition in which double peaks do not appear, while the red curves indicate a condition in which double peaks appear. The solid lines represent total stress, and the dashed lines represent elastic stress. All stresses are normalized by the maximum of the total stress at each γ 0. Fig. 9c shows g 2, − 2 for points C and D at γ 0 = 0.8 and 1. Fig. 9d shows g 2, − 2 for points E and F at γ 0 = 5 and 8. The solid lines represent before flow reversal, and the dashed lines represent after flow reversal regime.

Fig. 9
figure 9

a Total and elastic stresses at γ 0 = 0.8 and 1, b total and elastic stresses at γ 0 = 5 and 8, c g 2, − 2 for points C and D at γ 0 = 0.8 and 1, and d g 2, − 2 for points E and F at γ 0 = 5 and 8. Double peaks are not observed at γ 0 = 0.8 and 8, but double peaks are observed at γ 0 = 1 and 5.

Full size image

The total stress shows little differences in the regimes represented by the blue columns. g 2, − 2 at two paired γ 0 are similar as total stresses is similar for the two γ 0 (especially at points C and E, which are the peak points before flow reversal). For g 2, − 2 at points D and F, which are the peak points after flow reversal, the first peak of point D is negative, whereas that of point F is positive. It means that the particle structure along the compressional axis before flow reversal is maintained at point C due to small strain rate even though the flow direction is reversed, whereas the structure is realigned to the compressional axis after flow reversal due to large strain rate at point D. The PDF obtained at peak points are illustrated in Fig. 10.

Fig. 10
figure 10

PDF for (a) γ 0 = 0.8, point C, (b) γ 0 = 1, point C, (c) γ 0 = 5, point E, (d) γ 0 = 8, point E, (e) γ 0 = 0.8, point D, (f) γ 0 = 1, point D, (g) γ 0 = 5, point F, (h) γ 0 = 8, point F

Full size image

As γ 0 increases, more particles are aligned to the compressional axis or flow direction. As confirmed in Fig. 9c and d, the structure at point D shows the same directional alignment to that of point C, whereas the structure at point F shows the opposite directional alignment to that of point E. The structures, whether double peaks appear (γ 0 = 1 or 5) or not (γ 0 = 0.8 or 8), are not much different. It is notable that the PDF at points C and D and that at points E and F are clearly different, even though the elastic stresses are the same. Though not included in the paper, the average angles at contact distance (2a) are almost same at the same time for the two γ 0 cases whether the double peaks appear or not. Moreover, the average angles at the point of same elastic stress (C and D / E and F) under the same γ 0 are different (not included in this paper). Thus, it is hard to match elastic stress and structure one-to-one at each time. So it will be necessary to adopt a different structure analysis tool to correlate elastic stress and structure.

The concept of two-body excess entropy is adopted as a new structural analysis method. This approach is useful because the structure under oscillatory shear flow, which varies with time, can be quantified as a single value at any time (Eq. 17). When the pair distribution function of every location is one, it means a totally disordered system and the excess entropy is zero. In contrast, when the excess entropy goes to minus infinity, it indicates a perfect crystal structure. Fig. 11a is the total stress and excess entropy for γ 0 = 0.8 and 1, while Fig. 11b presents those for γ 0 = 5 and 8. The solid lines represent the total stress, and the dashed lines represent the excess entropy. The red curves show the results with double peaks and the black curves show the results without double peaks. The total stress and excess entropy are normalized by their maxima.

Fig. 11
figure 11

Normalized total stress and excess entropy during half cycle at a γ 0 = 0.8 and 1 and b γ 0 = 5 and 8

Full size image

Excess entropy shows a maximum before FR and minimum after FR. The moment of minimum excess entropy is observed earlier as γ 0 increases. This indicates that the rate of realignment to the opposite direction after FR becomes large as γ 0 increases. Although the total stress or other structural analysis are not so much different between the two γ 0, the difference in excess entropy is notable in the double peaks regime. The differences between the maximum and minimum of excess entropy are larger when double peaks appear (Fig. 11, red curves) than in the absence of double peaks (Fig. 11, black curves).

At maximum excess entropy, the particles are well-packed along the compressional axis and the structure is highly ordered. In contrast, the structure is poorly ordered at minimum excess entropy. The difference between the maximum and minimum of the normalized excess entropy is plotted as a function of γ 0 in Fig. 12. When this value is large, there exists a significant structural difference between two.

Fig. 12
figure 12

The difference in the maximum and minimum of excess entropy as a function of γ 0.

Full size image

The difference between maximum and minimum excess entropy increases with the increase in γ 0, and the maximum is observed at γ 0 = 3, after which it decreases. In this simulation, double peaks are observed in the range of γ 0 from 1 to 5, as indicated in the red column of Fig. 12. When the difference between maximum and minimum exceeds a critical value (~0.4), double peaks appear. Thus, double peaks are observed only when the structural difference between the maximum-ordered state and the minimum-ordered state is large during the cycle. The subtracted excess entropy shows a similar curve with depth (Fig. 4a), which is one of the characteristic values of double peaks. Depth increases as γ 0 increases, and the maximum depth is observed at γ 0 = 3, after which it decreases. These characteristics (i.e., maxima at γ 0 = 3 and curve shape) are observed in both the depth of the elastic stress curve and in the results of quantitative structural analysis (excess entropy). And the extent of the difference between the maximum- and minimum-aligned states is related to the depth of the double peaks.

From the excess entropy results, double peaks are created when the structural difference is large during the oscillation. The variation of g(r) at contact is significant for hard sphere systems, which can lead double peaks to appear. This result also supports the observation that double peaks are observed when the structural difference during the cycle is large. Therefore, it can be concluded that double peaks appear at the systems that the difference between maximum- (before FR) and minimum-ordered states (after FR) is significant during the cycle.

Conclusions

It has been reported that double peaks are observed in elastic stress in experiments for hard sphere suspensions. However, the structural origin of those double peaks has not been reported and no quantification of the double peaks has been conducted. In this paper, to quantify the double peaks, their depth, and width are defined. The depth and widths of the double peaks were found to exhibit maxima with increased γ 0.

To investigate the structural origin of double peaks, PDF and the first peak of RDF for both soft and hard spheres were compared at the same Γ/Γfreezing, ω, and γ 0. As a result, an overall structural difference during the cycle, a difference in structural formation before FR, and a deformation mechanism after FR were observed. These differences were found to determine the appearance of double peaks.

Structures of hard sphere systems at two γ 0, one that shows double peaks and the other does not, were compared at the same Γ/Γfreezing and ω. The structures at the same time but different γ 0 are not much different, but the structures at two peaks points at the same γ 0 are clearly different. Thus, it was hard to correlate the elastic stress and structure one-to-one at each time.

To correlate elastic stress with structure and to quantify the structure during a cycle, the concept of excess entropy was applied to the hard sphere system. By applying this concept, it was concluded that double peaks are observed when the structural difference between the maximum- and minimum-ordered states is large.

By inspecting the structure of hard and soft spheres and the structure of hard sphere system at different γ 0, the conditions for the presence of double peaks are suggested. Double peaks were observed when there is a large difference between the structure before FR, in which the particles are aligned to the compressional axis, and after FR, in which particle structure on previous compressional axis is broken.