Introduction

Liquid crystal materials (LC) are classified into two main classes, namely thermotropic and lyotropic (de Gennes and Prost 1993), according to the nature of its constituent units. Classical thermotropic LC are made of elongated molecules, widely known from industrial applications like LC displays. In contrast, lyotropic LC (Figueiredo Neto and Salinas 2005; Hendrikx et al. 1983) are mixtures of amphiphilic molecules (i.e., molecules having a hydrophilic head and a hydrophobic tail) and a solvent, usually water. Surfactants can either be ionic (for instance, soap and detergents, like potassium-laurate) or nonionic (e.g., a long-chain alcohol, like 1-decanol). Generally speaking, aqueous solutions of whatever type of amphiphiles tend to form micelles at concentrations of amphiphiles higher than the critical micellar concentration. Aqueous solutions of ionic surfactants, however, are particularly interesting as in rather high concentrations they may present nematic phases. This occurs even in mixtures with only one amphiphile species (e.g., potassium-laurate/KCl/water), which form disk- or cylinder-like micelles (Figueiredo Neto and Salinas 2005). On the other hand, mixtures with more than one amphiphile (e.g., potassium-laurate/1-decanol/water or sodium decylsulfate/1-decanol/water) may display the full set of three nematic phases that are expected from symmetry considerations. Two of them are uniaxial phases: a discotic nematic phase (N D ) and a calamitic nematic phase (N C ) (Galerne and Marcerou 1983). The third one is a biaxial nematic phase (N B ), which has been found for the first time in the ternary system K-laurate/1-decanol/water (Yu and Saupe 1980), as an intermediate phase between the two uniaxial ones.

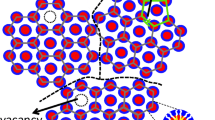
Of course, the building blocks of a biaxial nematic phase cannot be the highly symmetric micelles of either cylindrical or discotic shape as the names ‘disk-like’ or ‘cylinder-like’ referred above might suggest. Former theories tried to explain the N B phase either in terms of a mixture of oblate and prolate micelles or in terms of micelles possessing themselves biaxial symmetry. Concerning the uniaxial phases, on the other hand, this view that associates prolate and oblate micelles to the N C and the N D phases, respectively, has prevailed for a long time (Radley et al. 1976; Hendrikx et al. 1983). Later development of the structural studies, however, led to the formulation of the so called intrinsic biaxial micelle model (IBM) (Figueiredo Neto and Salinas 2005; Galerne et al. 1987). According to this model, all the three kinds of lyotropic nematic phases are just different short range orientational arrangements of micelles of essentially the same orthorhombic symmetry replicated to long range. Figure 1 shows sketches of the three different short range arrangements according to the IBM model.

Fig. 1
figure 1

Sketches of the three possible different arrangements of orthorhombic micelles according to the IBM model (Figueiredo Neto and Salinas 2005), giving rise to the uniaxial N C (a) and N D (b), and the biaxial N B (c) nematic phases of a lyotropic LC

Full size image

Viscosity measurements in lyotropic nematic LC are rather scarce in the literature (Kuzma et al. 1989; Alcantara and Vanin 1995; Sampaio et al. 2001; Kim 1999). In the present study, we report rheological characterization and shear viscosity measurements of the N C and N D phases of two kinds of lyotropic mixtures, namely a ternary and a novel quaternary ones. The later kind has been recently prepared in our laboratory (Akpinar et al. 2012a, b) and features the addition of a salt (K2SO4) on the classical ternary system potassium laurate/decanol/water mentioned above. Although marked effects of adding salt to lyotropic mixtures are known since long time ago regarding structural properties (Figueiredo Neto and Salinas 2005), much less is known about the influence of salt on the dynamic behavior of these materials.

Specifically, we carried out the rheological measurements using a cone-plate rheometer (Fig. 2) and (apparent) viscosity measurements using a rotating Couette flow viscometer (Fig. 3). The two techniques have the interesting complementary feature of allowing us to probe two different configuration in terms of order and flow coupling. Let us call n D and n C the director fields of the N D and N C phases, respectively. Assuming provisionally as true that the micelles have tendency to orient with their planes parallel to the limiting walls, we have in the Couette flow (CF) viscometer n C ∥z and n D ⊥z, where z is the rotating axis of the concentric cylinders, see Fig. 3. In contrast, in the cone-plate rheometer (CP), we have n D ∥z and n C ⊥z, where z is the rotating axis of the cone-plate system, see Fig. 2. In addition, the CF viscometer apparatus provided us with information about the density of the nematic samples. All measurements in both CP and CF techniques were taken at a fixed temperature of 20 ∘C.

Fig. 2
figure 2

a Schematic view of the meridional plane inside the gap of the cone-plate rheometer. b Sketch (half plane view) for discussing the interaction of the secondary flow velocity field profile with the micelles, assumed strongly anchored on the walls, for the case of the calamitic nematic (N C ) phase; c idem, for the case of the discotic nematic (N D ) phase

Full size image
Fig. 3
figure 3

a Schematic view of the meridional plane inside the (Couette flow type) viscometer cell. The gap containing the rotating sample is marked with an S. The dashed line is the rotation axis z either of the driven outer cylinder, C, and of the inner rotor, R. b Inside the gap, sketch (half plane view) for discussing the interaction of the secondary flow velocity field profile with the micelles, assumed strongly anchored on the walls for the case of the calamitic nematic (N C ) phase; c idem, for the case of the discotic nematic (N D ) phase

Full size image

As a summary of the results, through the rheological measurements, we verified that the ternary mixture (i.e., without salt) exhibiting the disk-like (N D ) nematic phase showed only a slight pseudo-plastic (or shear-thinning) behavior. This quasi-Newtonian behavior is drastically changed with a moderate salt addition in the quaternary sample Nd4a, which exhibits a pronounced pseudo-plastic effect. However, further addition of salt (samples Nd4b and c) makes the lyotropic system return to a relatively weak pseudo-plastic behavior.

The maximum shear rate attained (within the valid torque range) with these most salted samples was only about one third of the value reached with the N D ternary sample. In contrast, valid measurements attaining a high shear rate could be obtained with the rod-like (N C ) nematic phase mixtures, regardless they are salted or unsalted. Besides, all the N C samples showed only a weak pseudo-plastic behavior.

On the other hand, we verified that the (apparent) viscosity measured with the Couette flow viscometer is consistent with the cone-plate measurements provided the comparisons that are made in the appropriate shear rate range.

In the discussion section, we focus on two main questions. The first one is the markedly different values of the (apparent) shear viscosity measured (at comparable, moderate shear rates) in the N C and the N D phases of the ternary lyotropic LC system. We discuss this matter in terms of nematodynamic concepts which opposes tumbling and flow aligning behavior.

The second question regards the contrasting viscosity behavior between the two types of nematic phases concerning the addition of salt. While for the N D phase, η dramatically increases as the salt concentration increases, the viscosity of the N C phase is quite insensitive to the addition of salt. Again, nematodynamics are invoked to explain this difference. We show, on the other hand, that the strong effect of added salt in the N D phase can be approached in the framework of the classical theory of electrolyte solutions (Stokes and Mills 1965).

Besides these central questions, some additional discussion is done trying to made clear the connection between the rotational viscosity γ 1 (obtained mainly from light scattering data of the literature) and our measured shear viscosities for the ternary lyotropic phases. Finally, we show that the density measurements also done in this work can be comprehensively discussed by comparison with structural data from the literature. Last, but not least, this analysis brings additional evidences that favor the IBM model.

Experimental

Sample preparation

Seven lyotropic liquid crystal samples were prepared, four of them presenting the N D phase through a temperature interval of some degree Celsius around 20 ∘C, whereas three of them present the N C phase around the same temperature. For each of the two nematic phases, we have prepared one sample following the classical ternary mixture already mentioned (Yu and Saupe 1980; Figueiredo Neto et al. 1985), namely potassium laurate (KL)/1-decanol/ H2O. For example, the ternary N D sample, hereafter called Nd3, has the proportions 27.0/7.4/65.6 wt./wt.%, respectively (or 2.98/1.23/95.79 mol/mol %). This mixture exhibits a phase sequence, as a function of the temperature: N D ⇔N B ⇔N C at 22 ∘C and 27 ∘C, respectively. The N D phase was observed until (decreasing) temperatures of about 15 ∘C. The phases and phase transitions were determined by laser conoscopy (Galerne and Marcerou 1983) and optical microscopy observations. Aside the corresponding N C ternary sample, named Nc3, the remaining samples are part of a family of new quaternary mixtures (Akpinar et al. 2012b), namely KL/K2SO4/1-decanol/ H2O. Notice here two features, first the presence of salt (potassium sulfate) and second that we have kept the same cosurfactant (1-decanol) of the classical mixture in the particular quaternary system chosen. The three quaternary N D samples, hereafter called Nd4a, Nd4b, and Nd4c, have increasing salt concentrations of 1.6, 2.4, and 3.2 wt./wt.%, or equivalently, 0.25, 0.38, and 0.51 mol/mol %. The two quaternary N C samples, Nc4a and Nc4b have salt concentrations of 0.5 and 1.0 wt./wt. % (or 0.077 and 0.155 mol/mol %), respectively. The weight and molar proportions of all mixtures used in the measurements are displayed in Table 1.

Table 1 Compositionsof the lyotropic samples
Full size table

Rheometry

Rheological measurements were performed using a Brookfield cone-plate (CP) programmable rheometer model LVDV III (673 dyne cm spring torque) with CP-51 cone spindle (1.565∘ cone angle and 1.2 cm cone radius) (cf. Brookfield Manual, see website link in the References). The principle of operation of the LVDV-III rheometer is to drive a spindle (which is immersed in 0.5 ml of the test fluid) through a calibrated spring. The viscous drag of the fluid against the spindle is measured by the spring deflection. Spring deflection is measured with a rotary transducer. The full scale measuring range depends on the rotational velocity, the size and geometry of the spindle and the full scale torque of the calibrated spring.

The cleaning procedure of the cone and plate consisted of washing with soap and running water followed by several washes with distilled and deionized water. To complete the procedure, the cone and plate were washed with acetone p.a. and placed to dry with help of filtered air jet. Then, the devices were left to rest at least for 10 min before any new use. The cone and plate were then mounted on the rheometer, the LC sample was added, and the gap set.

When taking viscosity measurements with the CP/LVDV-III rheometer, there are two considerations which pertains to the low viscosity limit of effective measurement: (1) Viscosity measurements can be accepted provided the equivalent spring torque ranges from 10 to 100 %, for any combination of spindle/spinning speed. (2) Viscosity measurements should be taken under laminar flow conditions, i.e., never under turbulent flow conditions. The first consideration has to do with the precision of the instrument. The LVDV-III rheometer has a full scale range precision of ±1 % of any spindle/spinning speed. The second consideration involves the mechanics of fluid flow. In laminar flow, all particles move in layers driven by shearing forces. For rotational systems, this means that the primary fluid movement is circumferential. When the inertial forces on the fluid become too large, the fluid can break into turbulent flow wherein the movement of fluid particles becomes random. This turbulence creates a falsely high rheometer reading, with the degree of nonlinear increase in reading being directly related to the degree of turbulence in the fluid (Sherman 1970). The model LVDV-III enables speeds ranging from 0.1 to 250 rpm, in steps as small as 0.1 rpm. For the spindle CP-51, turbulent flow may appear whenever the rpm/mPa.s ratio exceeds 100 rpm/mPa.s, a situation that we have avoided in the present work. For each sample, we have also made tests that ruled out the possibility of time-dependent viscosity within the acceptable torque range described above.

Data of shear stress versus shear rate (the so-called rheograms or flow curves) were recorded at successively higher speeds until approximately 100 % of the full scale spring torque be reached, that is, the ‘up curve’. Next, the spinning speed is gradually reduced, within the appropriate waiting time, allowing the system to approach back the same rheological parameters for each speed, that is, the ‘down curve’. Here, for all rheograms, we have recorded both the ‘up curve’ and the ‘down curve’, following the usual procedure (Tanner 1970). Of course, the mentioned waiting time, that is, the time interval between data points (i.e., the amount of time for which the rheometer runs at a given step speed before taking a data point and advancing to the next program step), is an important parameter of any flow curve. For instance, for a too small time interval, the sample may not have reached the permanent flow due to the inertia of the system (Brookfield and Minard 1961).

In the present study, the maximum spinning speed of the flow curves varied from 10 rpm (shear rate; 38.4 s−1), in the samples of higher viscosity) to 80 rpm (shear rate; 307.2 s−1), in the samples of lower viscosity. All flow curves shown in this study were obtained in the absence of pre-shear, and the time interval between data points was 20 s. The temperature of the sample was maintained using a Haake DC30 K20 digital temperature control bath to within ± 0.1 ∘C. The rheometer was interfaced with a PC computer using the Brookfield Rheocalc version 1.2 operating software. Data calculation was done with the same software (cf. Brookfield Manual, see website link in the References).

Viscosity and density

As said in the Introduction, besides the rheometry, we have also employed an alternative method for measuring the shear viscosity of a similar set of lyotropic mixtures, by using a viscometer Anton Paar, model SVM 3000, which is a variation of the classic Couette flow (CF) rotational viscometer. Though being a more limited instrument (working at a fixed rpm), this viscometer has the advantage of keeping the sample within a sealed cell, so avoiding possible evaporations (as it can occurs with the cone-plate rheometer).

In addition, as pointed out in the Introduction, this CF viscometer allows probing a different configuration, in terms of order and flow coupling, when compared with the CP rheometer. Let us call n D and n C the director fields of the N D and N C phases, respectively. Assuming provisionally that the micelles have tendency to orient with their planes parallel to the limiting walls, we have in the CF viscometer n C ∥z and n D ⊥z, where z is the rotating axis of the concentric cylinders, see Fig. 3 . In contrast, in the CP rheometer, we have n D ∥z and n C ⊥z, where z is the rotating axis of the cone-plate system, see Fig. 2.

Actually, what differs the A. Paar apparatus used here from a classic Couette rotational viscometer is its specific measuring principle (Heimel et al. 1999). The sample is injected in a tube (of internal radius a) which rotates at a constant angular velocity ω o . Inside the tube, there is a hollow lightweight rotor that floats in the sample and is centered by the centrifugal forces during the measurement. The inner rotor (of external radius b) reaches a constant angular velocity ω r and contains a small magnet that produces eddy currents monitored by a Hall-effect sensor.

The sample temperature was controlled by a Peltier thermostat, with a stability of 0.005 ∘C . All the measurements were performed at 20 ∘C. A cleaning protocol was followed before each experiment. Firstly, the cylindrical sample holder was heated up to 60 ∘C. After that, the tube was filled with ethyl alcohol and the viscometer is turned on. An air pump was used to remove the alcohol from the tube. This procedure was repeated five times. After the evaporation of the alcohol, the temperature was set to 20 ∘C and, after thermal stabilization, the tube was filled with the lyotropic mixture.

The viscometer also has a density cell which uses the oscillating U-tube principle (Heimel et al. 1994). Both the density cell and the viscosity cell are filled in one single procedure and the two different measurements occur simultaneously.

Results

Starting with the cone-plate (CP) rheometer measurements, Fig. 4a, b, and c shows examples of rheograms for the discotic nematic (N D ) phase, corresponding to the ternary sample Nd3 and the quaternary samples Nd4a and Nd4c, respectively. Both ”up curve” and ”down curve” are shown. The varied range of shear rate among the different rheograms (or flow curves) is due to the need of keeping the data acquisition within the valid torque range (see “Experimental” section). All measurements were taken at 20 ∘C.

Fig. 4
figure 4

Examples of rheograms (produced via CP technique) of the N D phase, showing both ‘up curve’ and ‘down curve’ (all measurements were taken at 20 ∘C): a ternary sample Nd3; quaternary samples Nd4a (b) and Nd4c (c)

Full size image

The same remarks hold for the examples of rheograms of the calamitic nematic (N C ) phase shown in Fig. 5a, for the ternary sample Nc3, and b, for the quaternary sample Nc4a.

Fig. 5
figure 5

Idem, N C phase: a ternary sample Nc3; b quaternary sample Nc4a

Full size image

From the slopes of such rheograms one can extract the apparent viscosity for a given shear rate (which is actually done by the rheometer’s software mentioned in the “Experimental” section). Figure 6a and b show the CP viscosity data for the N D and the N C phases, respectively, for the whole set of samples.

Fig. 6
figure 6

Apparent viscosity versus shear rate extracted from the CP rheograms (only ‘up curves’ shown) for a N D samples: Nd3 (triangles), Nd4a (squares), Nd4b (diamonds), Nd4c (hexagons); b N C samples: Nc3(triangles), Nc4a(squares), Nc4b(diamonds)

Full size image

A common feature of all these data is a more or less pronounced pseudo-plastic (or shear thinning) behavior (Larson 1999). In order to give a quantitative description, it is useful at this point to introduce a parameter expressing “the degree of non-Newtonianity” of a fluid, namely

$$ d_{nN} \equiv \frac{\eta_{max}-\eta_{min}} {\dot{\gamma}_{max}-\dot{\gamma}_{min}}. $$
(1)

Along the rheological measurements, we have observed important variations of this parameter, as it can be seen on Table 2. The d n N values obtained for all samples are negative, which means pseudo-plastic behavior. Other remarkable features of the d n N values of our lyotropic mixtures are very low absolute values for the salted N C phases; the contrasting behavior of |d n N | which shows an initial increasing for the N C phase and an initial decreasing for the N D phase, as the salt concentration increases; and, finally, a strong dependence on the salt concentration for N D phase. All these features can be appreciated in Fig. 7. In this figure, we have plotted the parameter d n N versus the total molar concentration c of electrolytes, i.e., c = c(KL) + c(K2SO4), for the whole set of lyotropic mixtures. We shall come back to these features in the “Discussion” section.

Table 2 Results for viscosity obtained with CF and CP techniques and density measurements, all taken at 20 ∘C
Full size table
Fig. 7
figure 7

Proposed parameter d n N to measure the “degree of non-Newtonianity” of a fluid, see Eq. 1. Here, we have plotted d n N versus the total molar concentration c of electrolytes, i.e., c = c(K L) + c(K2SO4), for all lyotropic mixtures. Notice the negative value of d n N for all of our samples, which means pseudo-plastic behavior. Circles: N D phases; Squares: N C phases

Full size image

In Table 2, the viscosity values displayed in the column corresponding to the CP rheometric data (noted by \(\tilde {\eta }\)) have all been extracted from the high shear rate range of such measurements. These data are suitable for a proper comparison with the apparent viscosity measurements obtained with the CF viscometer (noted by η), as it can be demonstrated by the following order of magnitude calculation.

The starting point is the steady state formula for the tangential velocity in a Couette flow (Landau and Lifshitz 1988),

$$ v(r)=A/r+Br $$
(2)

where A and B are constants determined by the boundary conditions v(a)=ω r a and v(b)=ω o b, yielding,

$$ A=\frac{a^{2}b^{2}}{b^{2}-a^{2}}~ (\omega_{r} - \omega_{o})~ \text{ and }~ B=\frac{\omega_{o}~ b^{2} - \omega_{r}~ a^{2}}{b^{2}-a^{2}} . $$
(3)

Thus, it follows that the shear rate \(\dot {\gamma }= \partial v/\partial r = -A/r^{2} + B\). For a narrow gap b−a≪b, one can make the approximation r 2≈ a b, yielding

$$ \dot{\gamma}\approx \frac{2ab}{b^{2}-a^{2}} ~ (\omega_{o} - \omega_{r}) . $$
(4)

Typical numbers for the Anton Paar viscometer model SVM 3000 are b = 2.00 mm, a = 1.55 mm, with the outer cylinder spinning at 3500 rpm. For moderate viscosities, one can take about 3000 rpm for the inner rotor, yielding \(\dot {\gamma }\approx \) 200 rad/s. This is the order of magnitude of the higher shear rate range of our CP rheometric measurements. Therefore, in order to make proper comparisons with the viscosity values measured with the CF viscometer, one must be careful about choosing, whenever it is possible, the corresponding CP viscosity values at such relatively high shear rates.

Once such a care is taken, as in Table 2, the agreement between the viscosities measured by the CP and the CF techniques is quite good, within a typical deviation of 15 %, with the only exception of the lyotropic mixture Nc4a, for which \(\tilde {\eta }\) is about 30 % less than η.

Finally, Table 2 also shows the density (ρ) results, which also come from the CF apparatus. The uncertainty in the density measurements is of ± 0.0003 g cm−3 or less. We have used this precise determination of the density of the mixtures to calculate the molarities (1 M≡1 mol of solute per liter of solution) shown in the last column of Table 2, which will be useful in the forthcoming discussions.

For instance, to obtain the molar concentration of KL in the sample Nd3, we divide 27.0 g (see Table 1) by the molecular mass 238.41 g/mol, which gives 0.11325 mol. This is the amount of KL dispersed in 100 g of solution or in a volume of 0.099344 dm3, where we used the density result of 1.0066 g/cm3, yielding 1.13998 M. In the case of the quaternary samples, on the other hand, the displayed values correspond to the sum of the molarities of KL plus K 2SO4.

Discussion

Before analysing the meaning of our measurements by their own, let us make comparisons with (very few) available data in the literature. Perhaps the closest comparison we can make is between our result for the ternary sample Nc3 and a similar N C phase from Sampaio et al. (2001). Actually, their sample is slightly more concentrated in KL, and they have found, at 20 ∘C, a value for η about 20 % higher than ours. Another example contemplates measurements in a lyotropic nematic that contains salt in the composition, a mixture based on sodium decylsulfate (Alcantara and Vanin 1995). In that study, the molar fraction of salt ranges between 0.9 to 1.1 %, yielding higher viscosity values than ours. Only our most salty sample reaches the same order of magnitude.

Fluid dynamics considerations

Figure 2b and c are sketches of the flow in a meridional half-plane inside the gap between the (rotating) cone and the (stationary) plate surfaces of our CP rheometer apparatus. Specifically, parts (b) and (c) of the figure suggest a supposed preferential wall alignment effect in the N C and the N D phases, respectively. However, as a forthcoming discussion is going to show, such idealized wall effects are actually not so relevant, once they are going to be in competition with flow alignment effects.

Figure 3b and c, on the other hand, are analogous sketches for the flow inside the cylindrical sample holder of our CF viscometer apparatus. Here, the gap is limited by the outer (driven) and the inner (rotor) surfaces. The rotating sample transmits a torque across the gap to the inner rotor, which rotates at a lower speed. As the gap d = 0.45 mm, and assuming other reasonable factors in the Reynolds number expression, R e = ρ ω 0 d 2/η, one finds that R e≪1, indicating a typical creeping flow.

In spite the different geometrical configurations, the flow inside either the CF and the CP apparatus share two common features to any rotating flow. Firstly, assuming no-slip condition on all solid boundaries, it is reasonable to expect a secondary flow velocity field profile as sketched (for a discussion and computer simulations on the flow of rotating ordinary fluids, see for instance (Santos and Sørensen 1996) and references there in). Secondly, typically one expects that the primary flow (tangential velocity component) remains confined to a boundary layer region of thickness δ of the order of Landau and Lifshitz (1988), Slichting (1979), and Tritton (1987),

$$ \delta\sim\sqrt{\nu/\omega} $$
(5)

where ν is the kinematic viscosity of the fluid (i.e., the shear viscosity divided by the density) and ω is the differential angular velocity between the two (coaxial) surfaces.

Tumbling and flow aligning nematics

For a small-molecule or polymeric nematic, it is known that the behavior in a shear flow depends on the parameter λ defined in terms of either the two rotational viscosities γ 1 and γ 2 or the Leslie coeficients α 2 and α 3 by de Gennes and Prost (1993), Chan and Terentjev (2005), and Ternet et al. (1999),

$$ \lambda = -\frac{\gamma_{2}}{\gamma_{1}} = \frac{1+\alpha_{3}/\alpha_{2}}{1-\alpha_{3}/\alpha_{2}}. $$
(6)

According to the ELP continuum theory, tumbling behavior occurs when the ratio α 3/α 2<0, which implies λ < 1, while the nematic is flow-aligning if α 3/α 2 > 0, that is, λ > 1. If λ > 1, there is a certain critical angle 𝜃 between n and v, defined by de Gennes and Prost (1993) cos2𝜃 = 1/λ, for which the hydrodynamic torque vanishes. For rod-like nematics this angle is usually small, typically (Ternet et al. 1999) 𝜃 < 10∘, while for disk-like nematics (Chan and Terentjev 2005) 𝜃 ≈ 90∘. Moreover, rheological and NMR investigations either in the N C or the N D phases of a lyotropic system close to ours (Thiele et al. 2001) concluded that they belong to the flow-aligning class of nematics.

Flow aligning and apparent viscosities of the N D and the N C phases

By observing the rheological measurements of the lyotropic mixtures, a striking point to be emphasized is the pseudoplastic (or shear thinning) behavior of both the N D and the N C nematic phases. This particular rheological behavior indicates the preferred orientation of both phases when they are submitted to a steady shear. Indeed, as we have seen, both rods and disks (or rod- and disk-like arrangements of biaxial micelles, according the IBM model view) tend to align parallel to planes on which shear is taking place (Faber 1995), with consequent reduction in the apparent viscosity.

Briefly, although our experiments lack a direct observation of the flow aligning effect, indirect evidences like the above described indicate that it probably takes place. Furthermore, it has been experimentally demonstrated in the literature, for systems related to ours (Mang et al. 1994; Alcantara and Vanin 1995). Of course, it is a bulk effect, and a disordered layer near the non-treated walls of our sample holders is to be expected. However, the thickness of such a layer is quite negligible, of order of de Gennes and Prost (1993) and Larson (1999) \(\sqrt {K/\eta \dot {\gamma }}\sim 10~\mu \mathrm {m}\), where we have taken for a typical elastic constant K ∼ 2 × 10−11N (Kroin et al. 1989), η ∼ 100 mPa.s and \(\dot {\gamma }\sim 200~\mathrm {s}^{-1}\).

Interestingly enough, such alignment effects are known to occur even in the isotropic phase (Simões et al. 2001).

We now address the following question. What kind of aligning effect could potentially be produced on the lyotropic samples by the two rotating devices used in our experiments? As we have seen, whatever one considers the N D or the N C phase, the alignment effect on the micelles is similar, the difference being that the resulting direction of the director n in each case is normal to each other. Let us firstly examine closely the case of the CF viscometer geometry, see Fig. 3. If only the secondary flow was present, one would have the director confined in the meridional plane (of the figure), that is, n could point unstably either in the axial or radial directions, whatever the phase considered is the N D or the N C .

Now regarding the primary flow, one still should inquire whether or not such a tangential flow is important in the gap region Putting numbers in Eq. 5, first for pure water (w), one can take the differential angular velocity between the rotating cylinders ≈ ω o ∼ 3500 rpm ( ∼ 370 rad s−1), one has ν w = 10−3 Pa.s /103 kg m−3=10−6 m2/ s, yielding δ w ∼ 0.05 mm. Thus, one can see that, for pure water, the primary flow in our viscometer would be confined into a negligible thin boundary layer.

However, this is not true for none of our liquid crystals, as it can be seen by taking 500 rpm for the differential angular velocity and ν ∼ 50 ν w , at least, yielding δ ∼ 20, δ w , which already reaches the order of magnitude of the gap. Thus, we have to take the tangential component of the velocity field (i.e., the primary flow) into account in our discussions about order and flow coupling.

Hence, one must conclude that the primary flow is also present throughout the gap thickness (about 0.3 mm) of the CP rheometer, as the maximum spinning speed adopted in this apparatus was 80 rpm. Also, the same above conclusion about the unstable effect of the secondary flow on the alignment of either the N D or the N C phase holds for the CP rheometer.

Consequently, for now on, we can proceed with our analysis without distinction between the CP and the CF apparatus (although in a final step a distinction shall be made, see below). In the case of the N C phase, it is reasonable to assume that by effect of the primary flow a stable alignment of the director is produced normally to the meridional plane (depicted in Figs. 2 and 3), that is, n would be aligned along the tangential direction. In turn, for the N D phase, a similar alignment effect holds on the micelles, nonetheless resulting in the director confined in the meridional plane. Table 3 summarizes the expected director flow alignment effects, with the less dominant ones indicated between parentheses. Again, the same results can be inferred regardless one assumes the traditional rod/disk model (i.e., rod-like micelles for the N C phase and disk-like micelles for the N D phase) or the IBM model depicted in Fig. 1.

Table 3 Expected director flow alignment effects of the rotating N C and N D phases induced by the primary (tangential) and the secondary (predominantly axial in the CP rheometer and radial in the CF viscometer) flows
Full size table

Now, based on these predictions, it is interesting to make a connection with the so called Miesowicz viscosity coefficients η a , η b , and η c , each one associated to a particular configuration of the director n relative to a planar shear ∇v, according to the definitions appearing in de Gennes and Prost (1993), see Figs. 8:

$$\begin{array}{@{}rcl@{}} &&\eta_{a}~, \text{~for~} \mathbf{n} \perp \mathbf{v} \text{~and~} \mathbf{n} \perp \nabla \mathbf{v};\\ &&\eta_{b}~, \text{~for~} \mathbf{n} \parallel \mathbf{v} \text{~and~} \mathbf{n} \perp \nabla \mathbf{v};\\ &&\eta_{c}~, \text{~for~} \mathbf{n} \perp \mathbf{v} \text{~and~} \mathbf{n} \parallel \nabla \mathbf{v}. \end{array} $$
Fig. 8
figure 8

Density of N D and N C phases versus the molar fraction of salt

Full size image

Therefore, our predicted tangential alignment of the director of the N C phase suggests that some average of η a and η b should be associated to the measurements in this phase.

While our prediction for the director of the N D phase confined in the meridional plane suggests that the measured apparent viscosity for this case can be identified with some average of η b and η c .

Although we have arrived to these conclusions by making use of hypothetical considerations, the obtained interpretative results of Table 3 can be made consistent with the viscosity data of Table 2 (for samples with and without salt). Indeed, the observed fact that the N C phase presents viscosities much lower than the N D phase, perhaps can be explained by a simple matter of anisotropy of the viscosity coefficients.

As a matter of fact, both η a and η b are the smallest Miesowicz viscosity coefficients for a typical classical nematic (de Gennes and Prost 1993; Ternet et al. 1999), which shares with our N C phase the same symmetry properties.

For a discotic phase, on the other hand, the director is normal to the “disks”, and it is well-known (Faber 1995; Fraden and Meyer 1986) that the largest of the three Miesowicz viscosity coefficients is η b rather than η c .

The last column of Table 3 summarizes such associations, where we used the suffices ”C’ and ‘D” in order to distinguish the Miesowicz coefficients corresponding to the N C and N D phases, respectively. Here, the most intriguing case is of course the N D phase. Notice that the viscosity data suggest that \({\eta _{b}^{D}}\) should be predominant over \({\eta _{c}^{D}}\). Perhaps the only explanation to that is one that requires an additional hypothesis. That the (non-controlled) wall effect would favor the director aligned normal to the metallic surfaces both in the CF viscometer (i.e., the radial direction) and the CP rheometer (i.e., the axial direction).

The essentially two-dimensional flow problem suggested in Table 3 for the case of the N D phase can be better motivated within the framework of the nematodynamics equations. In what follows, we have adapted an approach due to Galerne (Lacerda Santos et al. 1985). Starting by writing down, the equations for the relevant viscous stress components (de Gennes and Prost 1993), \(\sigma _{xz}^{b}\) and \(\sigma _{zx}^{c}\) (z is the axial direction and x is the radial direction; notice that the director n is assumed parallel to the z-axis in both configurations, see Fig. 8),

$$ \sigma_{xz}^{b} = \alpha_{3}~N_{x} + (\alpha_{4}+\alpha_{6})\, A_{xz}, $$
(7)
$$ \sigma_{zx}^{c} = \alpha_{2}~N_{x} + (\alpha_{4}+\alpha_{5})~ A_{zx}, $$
(8)

where \(\mathbf {N}=\dot {\mathbf {n}}-{\Omega } \times \mathbf {n}\), with the vorticity \(\mathbf {\Omega } = \frac {1}{2}~\text {curl~}\mathbf {v}\), and the planar shear gradient components are given by \(A_{xz}=\frac {1}{2}~\partial v_{z}/\partial x =-{\Omega }\) and \(A_{zx}=\frac {1}{2}~\partial v_{x}/\partial z = {\Omega }\). Next, using the relationships (de Gennes and Prost 1993) \(\eta _{b}=\frac {1}{2}~(\alpha _{3}+\alpha _{4}+\alpha _{6})\) and \(\eta _{c}=\frac {1}{2}~(-\alpha _{3}+\alpha _{4}+\alpha _{5})\), we obtain,

$$ \sigma_{xz}^{b} = \alpha_{3}~\dot{n_{x}} + 2{\eta_{b}^{D}}~ A_{xz}, $$
(9)
$$ \sigma_{zx}^{c} = \alpha_{2}~\dot{n_{x}} + 2 {\eta_{c}^{D}}~ A_{zx}, $$
(10)

where now suffices D have been added to recall that we are treating specifically the case of the N D phase. Let us now assume, in a first approximation, that n is frozen in the flow. This does not mean that \(\dot {n_{x}}\) is null, but instead, that the director follows the backflow, that is, \(\dot {n_{x}}={\Omega }\) in both configurations b and c. The corresponding non-zero gradient components A x z = −A z x = −Ω can then exist without any stress applied on the fluid, i.e., σ x z = σ z x = 0.

Thus, from Eq. 9, we deduce \({\eta _{b}^{D}}= \frac {1}{2}~\alpha _{3}\), and from Eq. 10, \({\eta _{c}^{D}}= -\frac {1}{2}~\alpha _{2}\). Notice that in configuration c, the shear is parallel to the disk. Its associated viscosity \({\eta _{c}^{D}}\) is therefore of the order of the ordinary shear viscosity, say \({\eta _{c}^{D}}\approx \eta \), resulting α 2≈−2η. The relationship (de Gennes and Prost 1993) γ 1 = α 3−α 2, on the other hand, implies that \({\eta _{b}^{D}}\approx \frac {1}{2}~\gamma _{1}-\eta \).

Finally, in spite of such crude approximations, it is tempting to insert these estimates into Eq. 6 in order to obtain the tumbling parameter λ. The resulting expression, (4η/γ 1)−1, suggests indeed that a change of regime, from flow aligning (λ > 1) to tumbling (λ < 1), must occur when γ 1 grows (e.g., by influence of salt addition) beyond some threshold value. Notice, however, that the threshold of 2η predicted by these estimates is too low, as we shall see in a forthcoming section about rotational viscosity data from the literature.

Flow aligning... (specific remarks on the effect of the salt)

Moreover, the nematodynamics concepts can also help to shed some light on the effect of salt on the viscosity coefficients. Before entering into this discussion, however, let us examine briefly some considerations at the microscopic level.

Focusing firstly on the N D phase only, perhaps the simplest explanation for the increasing of the shear viscosity as the salt content increases would be assuming the micelles unchanged and to attribute all the effect to raise of the viscosity of the electrolyte solvent around them. Indeed, we shall test quantitatively such an approach in a forthcoming section.

Besides this obvious electrolyte effect, an additional, more dramatic one can be taking place if it happens that the micelles get bigger by effect of the salt. Indeed, an increase of the dimensions of the micelles and/or an augmentation of the steric micelle-to-micelle interaction due to the decrease of the Debye length and the consequent decrease of the intermicellar distance by effect of salt addition has been reported in the literature for lyotropic systems more (Saupe et al. 1991) or less (Park et al. 2008) related to ours.

In contrast, a puzzling question remains, namely why the effect of the salt on the CF data (see Table 2) of the N C phase is practically none? The explanation can come from one of the two hypotheses. In the first one, assuming that the micelles effectively get bigger by salt addition, this would not disturb their ability of getting aligned by effect of the flow in the calamitic phase. The second hypothesis, on the other hand, is that such a micellar growing caused by the salt is not favorized in the calamitic phase, as already demonstrated in lyotropic systems quite close to the ours (Saupe et al. 1991).

Now, let us turn again to the discotic phase, N D , in order to discuss a possible connection between these microscopic issues with nematodynamics concepts. Here, if one assume that the micelles get bigger by effect of the salt, then the result would be the dramatic increase observed in our viscosity measurements (for a given shear rate). Is it an effect due to reaching the tumbling regime? By the way, tumbling could also be happening in the non-salted Nc3 sample in the low shear rate range, see Fig. 6b. It is worth mentioning that a change of regime from tumbling to flow aligning as the shear rate increases has already been demonstrated by NMR measurements in a polymeric LC (Leal et al. 2004). Hopefully specially designed future experiments in low molecular weight lyotropic LC perhaps will be able to bring light on so interesting issues.

Rotational viscosities of nearby lyotropic mixtures

As a complementary topic, it is interesting to use data from the literature in order to make comparisons regarding the rotational viscosity γ 1, once such a quantity is not accessible in the present experiment. Let us first turn our attention to the ternary N D phase.

Fortunately, γ 1 of a sample of nearby composition to Nd3 can be estimated from dynamic light scattering (DLS) data (Lacerda Santos et al. 1985), namely D t w i s t = K 2/γ 1 = 1.6 × 10−12 m 2/s. Assuming the one elastic constant approximation, i.e., K 1 ∼ K 2 ∼ K 3 ∼ 2 × 10−11 N (Kroin et al. 1989), one obtains γ 1(N D ) ∼ 13 Pa.s. Thus, as we can see from Table 2, the shear viscosity η measured for the Nd3 sample is two orders of magnitude lower than γ 1. This indeed corroborates the general assumption made above that the micelles remain more or less aligned by the shear, or at least, they do not rotate along the streamlines. One could imagine that this assumption eventually breaks down in the case of quaternary samples, as the dramatic increase of η observed there might be associated to an increase of the micelle size, e.g., because of salt-mediated hydration (Figueiredo Neto and Salinas 2005; Galerne et al. 1987). However, recent DLS data (Risi et al. 2013) have shown a giant backflow effect in these salted mixtures, which implies that γ 1(N D ) ≫ η holds for such systems too.

A similar comparison can be made in the ternary N C phase, for which we can quote the DLS result (Lacerda Santos and Amato 1999) D t w i s t = 0.42 × 10−12 m2/s. By using the same K 2 value one arrives to γ 1(N c) ∼ 48 Pa.s. This perhaps surprising result of γ 1(N C ) ≫ γ 1(N D ) may seems odd in terms of an usual comparison between cylinders and disks, but it is quite acceptable in principle within the framework of the IBM model. The fact that our measurements gave η(N C ) < η(N D ), on the other hand, is a completely different matter, as we have discussed above.

Unfortunately, no DLS data is available for the quaternary N C phase, as far as we know.

Density behavior with and without salt

Now, let us comment on the meaning of the density measurements we have made using the density cell integrated into the A. Paar viscometer. Firstly, let us focus the density (ρ) of the ternary mixtures. Looking at the Table 2, one can see that ρ(N C ) is only slightly greater (0.3 %) than ρ(N D ).

An indirect comparison can be made between this result with data from the literature on structural properties. Fortunately, a very detailed study (Hendrikx et al. 1983) is available for the lyotropic system K-laurate/1-decanol/water, in which X-ray and neutron scattering data were combined in order to give both the dimensions of the oriented micelles and the distances, parallel and perpendicular to n, between them. It should be noted that the micelles in the study are assumed to be like uniaxial ellipsoids. By the way, we remark that it is indeed hard to conciliate, within such a model, the large discrepancy (in Table 2 of Hendrikx et al. (1983)) between the disk thickness and the cylinder diameter, namely 26 Å and 36 Å, respectively. On the other hand, thinking in terms of the IBM model, this large diameter could perhaps be associated to a local order involving, say, three objects, as depicted in Fig. 1a.

Now regarding the densities, the important data of Hendrikx et al. (1983) are the distances between the micelles. Using them, one can infer that the available volume per micelle is about 8 % larger in the discotic than in the calamitic phase. The study also provide data on the average aggregation number (215 for disks and 185 for cylinders), so we can infer a predicted ratio ρ(N C )/ρ(N D ) ≈ 0.93.

Taking into account the differences in composition between the samples used in the quoted study and ours, the ratio ρ(N C )/ρ(N D ) obtained from our density measurements shows a reasonable consistency with those structural data.

Next, let us consider both the ternary and the quaternary samples together. In Fig. 9, we have plotted the density data of Table 2 as a function of the molar fraction of the salt content both for the N D and the N C phases. Notice that, in case of N D phase, the range of the K2SO4 molar fraction reaches a more concentrated region, where a beginning of saturation of the density might be occurring, in the limit of the accuracy. Aside from this difference, however, a striking feature of these two curves is that the initial slope is essentially the same (about 0.05 g cm−3 per percentage point in the molar fraction of salt). This result is a strong evidence that favors the idea of common building blocks (i.e., biaxial micelles) shared by the discotic and the calamitic nematic phases, therefore also consistent with the IBM model.

Fig. 9
figure 9

Miesowicz configurations a, b, and c: sketches adapted to a discotic nematic N D

Full size image

To conclude, the analysis made here suggests that density measurements can be a useful tool to test microscopic models for the lyotropic nematic phases. For instance, computer simulations could be used to study the packing properties of the micelles either in the traditional or the IBM model, taking also into account parameters like the concentration of ions in the simulated samples, which potentially affects the density. (Recall the above mentioned decrease of the Debye length and the consequent decrease of the intermicellar distance by effect of salt addition (Saupe et al. 1991; Park et al. 2008).

The strong dependence of the N D phase shear viscosity on the added salt

As we have seen, differently than the case of the N C phase, we have observed a strong increasing of η for increasing salt concentration in the N D phase, see Fig. 10.

Fig. 10
figure 10

Plots of the apparent viscosity (measured by the CF technique) against the molar fraction of salt for N D and N C phases

Full size image

For a more quantitative discussion, let us leave for a moment the liquid crystalline aspects and turn the analysis of these viscosity data towards the electrolyte solutions viewpoint. In the following, we make a summary of the main theoretical results needed, referring to the quoted book by Stokes and Mills (1965) for further information and original references. In 1929, Jones and Dole formulated an empirical equation describing the dependence of the viscosity η of an aqueous solution on the molar concentration c of salt according to

$$ \eta/\eta_{\circ}=1+A\sqrt{c}+Bc, $$
(11)

where η ∘ is the viscosity of water (at the same temperature), A is a positive constant and B is a constant, either positive or negative. The \(\sqrt {c}\) term of Eq. 11, soon recognized to be due to long range electrostatic forces, gives significant contribution only to very dilute suspensions, up to 0.002 M. Above this concentration, a marked linear behavior of the viscosity is shown by solutions of strong electrolytes up to around 0.1 M. In this regime, the coefficient B has found to show an additive property with respect to different ionic species and is a measure of ion-solvent interactions (Lencka et al. 1998).

Notice that, regarding to lyotropic nematics, we are here still far from the concentration zone of interest, which starts around 1 M. For high concentrations, however, the rising of the viscosity caused by the presence of ions is rather due to a particle size effect, e.g., grown up by hydrated ions. The situation is similar to the one observed in suspensions of rigid particles in a continuous medium. The suspension has a viscosity higher than the medium itself, which can be explained by the interference of the particles with the streamlines of the flow (Stokes and Mills 1965). Such a hydrodynamic approach of the problem started with Einstein 1906, who dealt with the flow of a suspension of rigid spheres (Landau and Lifshitz 1988; Faber 1995). For low volume fractions ϕ of particles, he found for the viscosity η of the suspension,

$$ \eta/\eta_{\circ}=1+2.5~\phi, $$
(12)

where η ∘ is the viscosity of medium. Later treatments have elaborated this both to include departures from spherical shape, i.e., by increasing the coefficient 2.5, and to deal with higher concentrations, as the extended Vand equation (Stokes and Mills 1965; Vand 1948),

$$ \ln\frac{\eta}{\eta_{\circ}}=\frac{a~c}{1-b~c}, $$
(13)

where a is a shape coefficient, b is an interaction coefficient and the molar concentration c replaced ϕ, assuming that the volume of the attached solvent is a significant part of the whole. Whenever this is true, the following proportionality holds (Stokes and Mills 1965),

$$ \phi=c~V_{h}, $$
(14)

where V h is the molar volume of the solute including attached solvent.

Figure 11 shows a (mono-log) plot of the shear viscosity of the N D phase as a function of the total molar concentration of the electrolytes. The point at zero concentration represents pure water, where we have disregarded the 1-decanol contribution. The reasonable good fit with Eq. 13 shows that this approximation has little effect on the viscosity measurements (fit parameters a = 2.6 ± 0.3 and b = 0.29 ± 0.05). This is indeed consistent with structural studies on lyotropic materials (Figueiredo Neto and Salinas 2005) which locate the non-ionic surfactant at the micelle. Still concerning this fit, it is interesting to note that the shape coefficient a yielded 2.6. In the original context of Eq. 13, namely classical suspension of particles, a = 2.5, a > 2.5, and a < 2.5 means rigid spheres, cylinders and soft particles, respectively (Vand 1948). In our ordered fluid context, on the other hand, it would be tempting to associate the outcome a > 2.5 to a local orthorhombic ordering, somehow. However, more experimental data is necessary in order to establish such an identification.

Fig. 11
figure 11

Mono-log plot of the shear viscosity of the N D phase as a function of the total molar concentration c of the electrolytes. Point c = 0: pure water (neglecting 1-decanol contribution to η). The data were fitted with Eq. 13

Full size image

Conclusions

We presented rheological studies of micellar nematic phases of a set of potassium laurate/decanol/water mixtures with and without addition of salt (K2SO4) at a fixed temperature of 20 ∘C. With help of a cone-plate rheometer, we verified that the ternary mixture (i.e., without salt) exhibiting the discotic (N D ) nematic phase showed only a slight pseudo-plastic (or shear-thinning) behavior. This quasi-Newtonian behavior was drastically changed with a relatively small salt addition in the quaternary sample Nd4a, which exhibited a pronounced pseudo-plastic effect. However, further addition of salt (samples Nd4b and c) made the lyotropic system return to a moderate pseudo-plastic behavior.

On the other hand, all the calamitic (N C ) samples (salted or unsalted) showed only a weak pseudo-plastic behavior.

Beyond the rheological characterization, we have also done viscosity measurements using a (variation of a) rotating Couette flow viscometer, which allowed us probing a different configuration in terms of order and flow coupling. In addition, this apparatus allowed us to determine the density of the samples.

Featuring the main results, let us first point out that the markedly different shear viscosity behavior between the N C and the N D phases of either the ternary and quaternary mixtures is an intriguing puzzle founded in the present work. As a first approach, we have discussed such a behavior in terms of nematodynamic concepts. In summary, we have concluded that tumbling is likely to be occurring in some particular situations of our experiment, namely either for very salted N D samples or for the unsalted N D sample at low shear rates. Otherwise, for the majority of the investigated situations, the behavior of the discotic phase seemed to be flow aligning. Regarding the calamitic (N C ) phase, on the other hand, the observed behavior seemed to be flow aligning in all cases studied. We then attribute the mentioned high discrepancy between the behavior of the N C and the N D phases to the anisotropy of the viscosity coefficients associated to flow aligning effects in each one of these phases.

A second aspect is that our measured values for η in the N D phase dramatically increased as the salt concentration increased, while in the N C phase η was quite insensitive to the addition of salt. In order to analyse that behavior of the N D phase, we have reasonably succeeded in applying the theoretical framework of the classical theory of electrolyte solutions.

Besides these central results, we have also discussed how rotational viscosity data from light scattering literature can be related to our measured shear viscosities for the ternary lyotropic phases. In addition, in several analyses throughout the paper, we have considered the question of microscopic models for the lyotropic nematic phases, with emphasis on the so-called IBM model. Though originated from structural studies, we have considered here the possibility of finding additional evidences for it either in our viscosity or density data. Regarding viscosity, however, our conclusion is negative, that is, the analysis of such results is basically a macroscopic one, being not able to distinguish between the IBM model or some more traditional microscopic view, e.g., the one involving micelles of cylindrical and discotic shapes. In contrast, the density measurements (that, after all, were only of subsidiary importance in the present work) do have shown potential to provide additional evidences to the IBM model.