Introduction

Diffusiophoresis is the colloidal particle motion under an external concentration gradient of electrolyte and non-electrolyte [1]. Compared to the other conventional electrokinetic transport mechanisms, such as electrophoresis and dielectrophoresis, diffusiophoresis is more convenient for the manipulation of living cells. The Joule heating effect in diffusiophoresis is negligible since there is no net electric current in the medium, which makes it advantageous over other electrokinetic processes [2]. Diffusiophoresis finds vast practical applications in particle separation and characterization [1], DNA translocation and sequencing [3, 4], and flow manipulation in lab-on-a-chip devices [5], to list a few. It has excellent utilizations in controlled drug delivery governed by the concentration gradient engendered by solutes released from injured human cells [6]. Diffusiophoresis is also useful in industrial processes such as water filtration [7] and oil recovery [8].

Diffusiophoresis of a charged particle suspended in an electrolyte solution having a uniform concentration gradient is governed by two components, namely electrophoresis and chemiphoresis [9]. The uniform concentration gradient of electrolyte induces a spontaneous electric field in the bulk region when the diffusivity coefficients of the cations and anions are different. This induced electric field quickens the migration of ions with lower diffusivity and retards the motion of the ions with a higher diffusion rate to maintain electroneutrality in the bulk solution. The induced electric field exerts a force in the fluid inside the electric double layer (EDL) around the charged particle and creates a motion of the suspending particle, commonly known as electrophoresis. The electric field and, consequently, the electrophoretic motion of the colloid depend on the diffusivity difference of ions. The electrophoresis component is absent for ions with the same diffusion coefficient. The charged particle surface redistributes migrating ions within the EDL by attracting the counterions and repelling the coions. The ionic imbalance inside the EDL creates a local concentration gradient, generating a fluid flow by inducing an osmotic pressure gradient. This phenomenon is termed by researchers as chemiphoresis, which drives the particle always towards the higher concentration region. Therefore, the electrophoresis and chemiphoresis components can act in the same or opposite direction depending on the polarity of the diffusivity difference.

Prieve and co-workers [8,9,10,11] conducted a series of studies on diffusiophoresis of rigid charged particles suspending in non-electrolyte and electrolyte mediums. Based on the thin Debye layer assumption, Prieve et al. [9] analyzed the diffusiophoresis of a rigid spherical particle under an electrolyte gradient and derived a general analytical expression for the diffusiophoretic velocity. Velegol et al. [12] elaborated origins of concentration gradient causing diffusiophoresis in various physical situations. Lee and co-researchers [13,14,15,16,17,18,19,20] have theoretically studied the diffusiophoresis of rigid and non-rigid colloids in various electrokinetic circumstances. Shin and co-workers [7, 21,22,23,24,25] conducted several experimental investigations on diffusiophoresis of colloid particles of different types. Ohshima [26, 27] recently derived analytic expressions for the diffusiophoretic velocity applicable for large spherical colloidal particles bearing an arbitrary zeta potential.

Alongside rigid colloids, diffusiophoresis of non-rigid particles such as porous particles, soft particles, and liquid droplets has gained significant attention from researchers over the years. In particular, soft particles are frequently encountered in electrokinetic applications since several viruses [28], bacteria [29], humic substances [30], and core-shell nanoparticles [31, 32] used for controlled drug delivery are modeled as soft particles. These soft particles comprise a solid core covered with a fluid and ion-permeable polyelectrolyte layer (PEL) bearing functional groups which dissociate to produce volume charge density in contact with an electrolyte solution [33]. Hung and Keh [34] studied the diffusiophoresis of a charged soft particle based on a first-order perturbation from the equilibrium. Consequently, Lin and Keh [35] analyzed the diffusiophoresis in a suspension of soft particles with a similar technique. Using a pseudo-spectral method based on Chebyshev polynomials, Lee and his group [36,37,38] theoretically studied the diffusiophoresis of a highly charged soft particle. Ohshima [39] provided a general expression for the diffusiophoretic velocity of a weakly charged soft particle. Treating the particle surface planer, Ohshima [40] subsequently studied the diffusiophoresis of a soft particle, considering the particle core is much larger than the Debye layer thickness and derived general and approximate diffusiophoretic mobility expressions for simplified situations.

The consideration of equal dielectric permittivity for both the porous layer of the soft particle and the surrounding aqueous medium is justified when the soft layer density is low [41]. For soft particles with a dense polymer layer, the dielectric permittivity of the PEL, in general, is smaller than that of the adjoining electrolyte medium [42,43,44]. The distinct dielectric permittivity of the two mediums results in a difference in the Born energy of the mobile ions. This difference in Born energy between ions attenuates the penetration of mobile ions inside the PEL through the ion partitioning effect as the ions choose to stay in a medium with higher permittivity. The ion partitioning effect modifies the charge density of the soft layer and augments the electric potential within the PEL. Several studies [45,46,47,48] on electrophoresis of soft particles analyzing the impact of ion partitioning have shown that the ion partitioning effect magnifies the electric potential across the PEL, which in turn enhances the electrophoretic mobility of the particle. Majee and Bhattacharyya [49] investigated the diffusiophoresis of a pH-regulated nanogel considering the ion partitioning effect through numerical computations. They reported a growth in the effective charge of the nanogel leading to an increment in the diffusiophoretic velocity of the particle. All these studies [45,46,47,48,49] demonstrate that an enhancement in effective PEL charge due to the ion portioning effect alters the electrohydrodynamics around the charged particle. Therefore, it will be of great interest to explore how the ion partitioning effect modifies the electrophoresis and chemiphoresis components in diffusiophoresis of a soft particle.

In several practical contexts, the rigid core of a soft particle can be considered hydrophobic. For instance, synthesized composed particles used in controlled drug delivery where the drug is entrapped inside a porous layer can be modeled as a soft particle with a hydrophobic inner core [50,51,52]. The hydrophobicity of the core surface is characterized by a hydrodynamic slip length which relates the strain rate with the core surface velocity. The velocity slip at the inner core surface modifies the electrohydrodynamics of the soft particle. Several theoretical [45, 53,54,55,56] and numerical studies [57] on electrophoresis of a soft particle with a hydrophobic inner core in various electrokinetic situations have reported an enhancement in the electrophoretic mobility due to hydrophobicity of the inner core. Majhi and Bhattacharyya [58] conducted a numerical investigation on the diffusiophoresis of a hydrophobic charged colloid in a monovalent or multivalent electrolyte. They have found that the diffusiophoretic velocity augments with an enhancement of the slip length when both the chemiphoresis and electrophoresis components work jointly, and a mobility reversal occurs at a comparatively thicker Debye layer than the hydrophilic situation when these components oppose each other. In a recent study dealing with the diffusiophoresis of a hydrophobic rigid particle possessing an arbitrary \(\zeta\)-potential in a general electrolyte, Samanta et al. [59] reported that the surface hydrophobicity influences particle motion when the \(\zeta\)-potential is below a critical value. These studies suggest that surface hydrophobicity of the inner core may modify the electrokinetics and, hence, the diffusiophoretic motion of the soft particle.

For a highly charged particle surface, the mobile counterions accumulate inside the EDL from the bulk solution owing to the surface conduction effect. The accumulation of ions within the thin EDL hinders the particle motion by enhancing the shielding effect. The surface conduction effect becomes stronger for a hydrophobic surface due to a higher fluid convection. The majority of the studies on electrokinetic transport of charged colloids consider that the distribution of ions is governed by the Poisson-Boltzmann equation in which the ions are assumed as point charges. Such consideration results in an absurdly higher ionic concentration adjacent to a highly charged surface. To address this deficiency, the Poisson-Boltzmann equation is modified by considering the ions as rigid spherical particles with a finite radius [60]. The repulsions between the finite-sized ions within the Debye layer reduce the counterion accumulation leading to a finite ion concentration near the surface due to the ion steric effect. The ion steric effect diminishes the surface conduction by reducing the shielding effect and, consequently, increases the particle velocity. The main focus of the present study, however, is to develop simplified mathematical expressions for diffusiophoretic mobility of a soft particle concentrating on the impact of ion partitioning effect on the flow phenomena. The current mathematical model is based on the point-like ions assumption and therefore, it does not account the ion steric and surface conductance effects.

All the existing studies [34, 36, 38,39,40] on diffusiophoresis of charged soft particles are limited to a hydrophilic inner core, and the dielectric permittivity of the PEL is chosen to be the same as that of the surrounding electrolyte, for which the ion partitioning effect is ignored. In the present paper, we have considered the diffusiophoresis of a soft particle comprised of a rigid core covered with a charged PEL suspending in an electrolyte with a uniform concentration gradient. The surface of the rigid core is considered to exhibit surface hydrophobicity. Moreover, the ion partitioning effect is incorporated by assuming the PEL permittivity smaller than the electrolyte permittivity. The Debye layer around the particle is assumed sufficiently thinner, for which the particle surface can be treated like a flat plate. We deduced a general expression for the diffusiophoretic mobility of a soft particle with a hydrophobic core considering the ion partitioning effect, which is applicable to arbitrarily charged particles. Subsequently, we further approximated the general mobility expression under the weak PEL charge limit to provide a closed-form solution for the diffusiophoretic mobility of a weakly charged soft particle. Additionally, an approximate solution for diffusiophoretic mobility of a soft particle with a thinner PEL screening length is derived, which is appropriate for a soft particle with a hydrophilic inner core and low permeable PEL with the ion partitioning effect. The combined impacts of inner core hydrophobicity and ion partitioning on the diffusiophoresis of a soft particle are analyzed through graphical illustrations.

Mathematical model

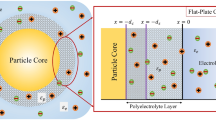
We consider the diffusiophoresis of a soft particle consisting of a hydrophobic rigid core covered with a fluid and ion permeable polyelectrolyte layer (PEL) of thickness d in an electrolyte solution with bulk ionic concentration \(n^{\infty }\). The electrolyte is considered to be binary symmetric with valence \(z_i=\pm \mathcal {Z}\). The EDL around the particle is assumed to be sufficiently thinner compared to the particle size so that the particle surface appears flat. The x-axis is taken along the surface of the PEL, and the y-axis is taken perpendicular to the surface with origin at the PEL-electrolyte interface (Fig. 1). A constant concentration gradient \(\nabla n^{\infty }\) is applied parallel to the particle surface such that the change in electrolyte concentration over the distance corresponding to the soft layer thickness is smaller, i.e., \(d|\nabla n^{\infty }|/n^{\infty }(x=0)<<1\). The PEL is assumed to possess a uniform fixed volume charge density \(\varrho _{fix}\) due to immobile ions in the PEL.

Fig. 1
figure 1

Schematics of plate like soft particle coated with a polyelectrolyte layer of thickness d

Full size image

The dielectric permittivity of the PEL \(\varepsilon _p\) is considered to be different from the electrolyte’s dielectric permittivity \(\varepsilon _e\). The difference in dielectric permittivities gives rise to a Born energy difference of ions between the two mediums. For the \(i^{th}\) ionic species, the Born energy difference is [61]

$$\begin{aligned} \Delta W_i=\frac{(z_ie)^2}{8\pi r_i}\left( \frac{1}{\varepsilon _p}-\frac{1}{\varepsilon _e}\right) , \end{aligned}$$
(1)

where \(r_i\) is the radius of the \(i^{th}\) ion with charge \(z_ie\). The Born energy difference in ions redistributes the ionic concentration within the PEL by the ion partitioning effect. The modified concentration of the \(i^{th}\) ionic species in the PEL is \(n_if_i\), where \(n_i\) is the concentration of the \(i^{th}\) ion in the electrolyte, and \(f_i\) is the ion partitioning coefficient. The ion partitioning coefficient \(f_i\) can be expressed as the Boltzmann distribution of ions as \(f_i=\exp (-\Delta W_i/k_B T)\), with \(k_B\) being the Boltzmann distribution and T being the absolute temperature. We consider the radius of ions \(r_i\) to be the same (\(r_i \approx 3.3\times 10^{-10}\)m), for which we take \(\Delta W_i=\Delta W\). With that assumption, the ion partitioning coefficient becomes \(f_{+}=f_{-}=f\).

Electrostatic potential distribution

The electrostatic potential (\(\psi\)) within and outside the PEL, taking the ion partitioning effect into account, is governed by the equations

$$\begin{aligned} -\varepsilon _p \frac{d^2\psi }{dy^2}=f\varrho _e+\varrho _{fix},\qquad \qquad (-d \le y \le 0); \end{aligned}$$
(2)
$$\begin{aligned} -\varepsilon _e \frac{d^2\psi }{dy^2}=\varrho _e,\qquad \qquad (y\ge 0); \end{aligned}$$
(3)

where \(\varrho _e=\mathcal {Z}e(n_{+}-n_{-})\) is the net charge density generated by the concentration of the mobile ions. The ions are assumed to follow the Boltzmann distribution as \(n_{\pm }=n^{\infty }\exp \left( \mp \frac{\mathcal {Z}e\psi }{k_B T}\right)\). With that, Eqs. (2) and (3) are re-written as the nonlinear Poisson-Boltzmann equation, expressed as

$$\begin{aligned} \frac{d^2 \phi }{dy^2}=\tilde{\kappa }^2 \sinh \phi -\frac{\varrho _{fix}}{\varepsilon _p \phi _0},\qquad \qquad (-d \le y \le 0); \end{aligned}$$
(4)
$$\begin{aligned} \frac{d^2 \phi }{dy^2}=\kappa ^2 \sinh \phi , \qquad \qquad (y \ge 0); \end{aligned}$$
(5)

where \(\phi =\psi /\phi _0\) is the scaled electric potential normalized by the thermal potential \(\phi _0=\mathcal {Z}e/k_BT\). Here, \(\tilde{\kappa }=\sqrt{2 \mathcal {Z}en^{\infty }(x=0)f/\varepsilon _p \phi _0}\) and \(\kappa =\sqrt{2\mathcal {Z}en^{\infty }(x=0)/\varepsilon _e \phi _0}\), respectively, are the inverse Debye lengths of the PEL and electrolyte, and they are related by the relation \(\tilde{\kappa }=\kappa \sqrt{f/\varepsilon _r}\), with \(\varepsilon _r\) ( = \(\varepsilon _p/\varepsilon _e\)) being the PEL-to-electrolyte permittivity ratio. When the PEL permittivity is the same as the electrolyte permittivity, i.e., without the ion partitioning effect, \(\tilde{\kappa }=\kappa\). The boundary conditions for the electric potential, respectively, at the inner core, particle surface, and far-field are as follows:

$$\begin{aligned} \frac{d \phi }{dy}\Bigm |_{y=-d}=0, \end{aligned}$$
(6)
$$\begin{aligned} \phi (0^{-})=\phi (0^{+}), \end{aligned}$$
(7)
$$\begin{aligned} \varepsilon _p\frac{d \phi }{dy}\Bigm |_{y=0^{-}} =\varepsilon _e\frac{d \phi }{dy}\Bigm |_{y=0^{+}}, \end{aligned}$$
(8)
$$\begin{aligned} \phi \rightarrow 0 \text { as } y \rightarrow \infty . \end{aligned}$$
(9)

In the thin Debye layer limit, the soft layer is assumed to be much thicker than the EDL thickness. The EDL potential deep inside the soft layer exhibits no variation and approaches a constant potential \(\phi _D\) known as the Donnan potential. The scaled Donnan potential \(\phi _D\) can be derived by equating the left-hand side of Eq. (4) to zero, given by

$$\begin{aligned} \phi _D=\sinh ^{-1}\Bigl (\frac{\varrho _{fix}}{\varepsilon _p\phi _0\tilde{\kappa }^2}\Bigr )=\ln \left[ \frac{\varrho _{fix}}{\varepsilon _p\phi _0\tilde{\kappa }^2}+ \sqrt{1+\Bigl (\frac{\varrho _{fix}}{\varepsilon _p\phi _0\tilde{\kappa }^2}\Bigr )^2}\right] . \end{aligned}$$
(10)

The electric potential across the PEL and in the electrolyte medium can be presented by solving Eqs.(4) and (5) with the boundary conditions (6), (7), (9) as

$$\begin{aligned} \phi (y)=\phi _D+[\phi _s-\phi _D]\text {e}^{\tilde{\kappa }_m y},~~~~~~~(-d\le y \le 0); \end{aligned}$$
(11)
$$\begin{aligned} \phi (y)=4\tanh ^{-1}\Bigl [\tanh \Bigl (\frac{\phi _s}{4}\Bigr )\text {e}^{-\kappa y}\Bigr ],~~~~~~~(y \ge 0); \end{aligned}$$
(12)

where \(\tilde{\kappa }_m=\tilde{\kappa } \sqrt{\cosh \phi _D}\) is the effective Debye length inside the soft layer, and \(\phi _s\) [ = \(\phi (y=0)\)] is the PEL-electrolyte interface potential. A relation between the scaled Donnan potential \(\phi _D\) and the surface potential \(\phi _s\) can be derived utilizing the boundary condition (8) as

$$\begin{aligned} f\varepsilon _r\Bigl [(\cosh \phi _s - \cosh \phi _D)-(\phi _s-\phi _D)\sinh \phi _D\Bigr ]=\cosh \phi _s-1, \end{aligned}$$
(13)

through which \(\phi _s\) can be obtained numerically for a prescribed \(\phi _D\). In the absence of the ion partitioning effect (i.e., \(\varepsilon _r=1\) and \(f=1\)), Eq. (13) simplifies as

$$\begin{aligned} \phi _s=\phi _D-\tanh \left( \frac{\phi _D}{2}\right) , \end{aligned}$$
(14)

which is a well known result reported by Ohshima [62, 63].

Diffusioosmotic velocity distribution

The ion flux for the \(i^{th}\) ionic species can be expressed as

$$\begin{aligned} J_{i}=-D_{i}\Bigl [ \nabla n_{i} + \frac{z_ien_{i}}{k_BT} (\nabla \psi - E_{\infty }) \Bigr ], \end{aligned}$$
(15)

where \(D_{i}\) is the diffusivity constant of the \(i^{th}\) ion. Here, \(E_{\infty }\) is the induced electric field arises spontaneously due to the imposed concentration gradient in the electrolyte. Far from the particle in the electroneutral region (\(y \rightarrow \infty\)), net current density is zero, i.e., \(J_{+}=J_{-}\), which leads to

$$\begin{aligned} E_{\infty }= \beta \biggl (\frac{k_BT}{\mathcal {Z}e}\biggr ) \frac{\nabla n^{\infty }}{n^{\infty }(0)}, \end{aligned}$$
(16)

where \(\beta =(D_{+}-D_{-})/(D_{+}+D_{-})\) is the diffusivity difference parameter.

The soft particle is considered to be translating with the diffusiophoretic velocity \(U_{DP}\) under the imposed concentration gradient \(\nabla n^{\infty }\). The flow inside the PEL and in the electrolyte is governed by the Darcy-Brinkman extended Stokes and Stokes equation, respectively. The Debye length is considered to be thinner than the particle size for which the particle surface is viewed as a flat plate and the fluid flow can be assumed to be parallel to the particle surface. The equations governing the flow field are

$$\begin{aligned} \frac{\partial p}{\partial y}+[\{H(y+d)-H(y)\}f+H(y)]\varrho _e\frac{\partial \psi }{\partial y}=0, \end{aligned}$$
(17)
$$\begin{aligned} \eta \frac{\partial ^2 u}{\partial y^2}&-\gamma u[H(y+d)-H(y)]=\frac{\partial p}{\partial x}\\&-[\{H(y+d)-H(y)\}f+H(y)]\varrho _e\Bigl (E_{\infty }-\frac{\partial \psi }{\partial x}\Bigr ), \end{aligned}$$
(18)

where u(y) is the fluid velocity parallel to the particle surface, p is the pressure, H(y) is the Heaviside function, \(\eta\) is the fluid viscosity, and \(\gamma\) is the frictional coefficient of the PEL. The pressure distributions within and outside the PEL, derived from Eq. (17), are

$$\begin{aligned} p(x)=&p^{\infty }+2n^{\infty }(x)k_BT[f\cosh \phi \\&+(1-f)\cosh \phi _s-1],\qquad(-d \le y \le 0); \end{aligned}$$
(19)
$$\begin{aligned} p(x)=p^{\infty }+2n^{\infty }(x)k_BT[\cosh \phi -1],\qquad\quad(y \ge 0); \end{aligned}$$
(20)

where \(p^{\infty }\) is the pressure at the far field \((y \rightarrow \infty )\). Incorporating Eqs. (19) and (20), Eq. (18) can be written as

$$\begin{aligned} \frac{d^2u}{dy^2}-\lambda ^2 u =&\frac{2k_B T f}{\eta }\Bigl (\frac{dn^{\infty }}{dx}\Bigr )[\cosh \phi -1]\\&+ \frac{\varepsilon _p \phi _0 E_{\infty }}{\eta } \Bigl (\frac{d^2 \phi }{dy^2}+\frac{\varrho _{fix}}{\varepsilon _p \phi _0}\Bigr ),\qquad(-d \le y \le 0); \end{aligned}$$
(21)
$$\begin{aligned} \frac{d^2u}{dy^2}=& \frac{2k_B T}{\eta }\Bigl (\frac{dn^{\infty }}{dx}\Bigr )[\cosh \phi -1]\\&+\frac{\varepsilon _e \phi _0 E_{\infty }}{\eta } \frac{d^2 \phi }{dy^2},\qquad\quad(y\ge 0); \end{aligned}$$
(22)

where \(\lambda =(\gamma /\eta )^{1/2}\) is the inverse of the Brinkman screening length, which characterizes the resistant exerted by the porous layer on the flow velocity. The boundary conditions considered for the velocity field are

$$\begin{aligned} u\Bigm |_{y=-d} =\ell _s\frac{du}{dy}\Bigm |_{y=-d}, \end{aligned}$$
(23)
$$\begin{aligned} u(0^{-}) =u(0^{+}), \end{aligned}$$
(24)
$$\begin{aligned} \frac{du}{dy}\Bigm |_{y=0^{-}} =\frac{du}{dy}\Bigm |_{y=0^{+}}, \end{aligned}$$
(25)
$$\begin{aligned} u \rightarrow -U_{DP} \text { as } y \rightarrow \infty . \end{aligned}$$
(26)

The rigid core of the soft particle is assumed to be hydrophobic in nature. The Navier slip boundary condition, which is the slip velocity at the core surface is proportional to the rate of shear strain, is imposed at \(y=-d\), as presented in Eq. (23). The proportionality constant \(\ell _s\) represents the dimensional slip length, which regulates the core hydrophobicity. For a hydrophilic core, \(\ell _s=0\). Solving Eq. (22) along with appropriate boundary conditions (23)–(25), velocity distributions within and outside the PEL can be expressed as

$$\begin{aligned} \begin{aligned} u(y)=&C_1 \cosh (\lambda y)+C_2\sinh (\lambda y) + \frac{2k_BTf}{\lambda \eta }\Bigl (\frac{dn^{\infty }}{dx}\Bigr )\\&\int _{-d}^{y}\sinh [\lambda (y-s)][\cosh \phi (s)-1]ds \\&+\frac{\varepsilon _p \phi _0 E_{\infty }}{\eta }\Bigl [\phi (y) - \phi _D\cosh \lambda (y+d) \\&+\lambda \int _{-d}^{y}\sinh [\lambda (y-s)]\phi (s)ds -\frac{\varrho _{fix}}{\lambda ^2 \varepsilon _p \phi _0} \Bigr ],~~~(-d \le y \le 0); \end{aligned} \end{aligned}$$
(27)
$$\begin{aligned} u(y)=& u(0)+\frac{\varepsilon _e \phi _0 E_{\infty }}{\eta } [\phi (y)-\phi _s]\\&+\frac{8k_BT}{\kappa ^2\eta }\ln \Bigl [\frac{\cosh (\phi (y)/4)}{\cosh (\phi _s/4)}\Bigr ]\Bigl (\frac{dn^{\infty }}{dx}\Bigr ),\qquad(y \ge 0); \end{aligned}$$
(28)

where

$$\begin{aligned} \begin{aligned} C_1=&\frac{1}{P}\biggl (\frac{\varrho _{fix} E_{\infty }}{\eta \lambda ^2} + C_2Q \biggr ), \\ C_2=&\frac{\varepsilon _p \phi _0 E_{\infty }}{\eta }\Bigl [\sinh (\lambda d)\phi _D - \lambda \int _{-d}^{0}\cosh (\lambda y)\phi (y)dy\Bigr ] \nonumber \\&-\frac{2k_BT f}{\lambda \eta }\Bigl (\frac{dn^{\infty }}{dx}\Bigr )\Bigl [ \frac{2}{\tilde{\kappa }}\Bigl (\cosh \frac{\phi _s}{2}-1\Bigr ) -\frac{\sinh (\lambda d)}{\lambda } + \int _{-d}^{0}\cosh (\lambda y)\cosh \phi (y)dy \Bigr ], \\ P=&\cosh (\lambda d)+\lambda \ell _s \sinh (\lambda d), \\ Q=&\sinh (\lambda d)+\lambda \ell _s \cosh (\lambda d). \end{aligned} \end{aligned}$$

General expressions for diffusiophoretic mobility

Imposition of the far field condition \(u(y) \rightarrow -U_{DP}\) as \(y \rightarrow \infty\) in Eq. (28) leads to

$$\begin{aligned} U_{DP}=-u(0)+\frac{\varepsilon _e \phi _0 E_{\infty }}{\eta }\phi _s+\frac{8k_BT}{\kappa ^2\eta }\ln \Bigl [\cosh \Bigl (\frac{\phi _s}{4}\Bigr )\Bigr ]\Bigl (\frac{dn^{\infty }}{dx}\Bigr ). \end{aligned}$$
(29)

We scale the diffusiophoretic velocity \(U_{DP}\) by \(\frac{\varepsilon _e\phi _0^2}{\eta d}\), and subsequently, the scaled diffusiophoretic mobility can be defined as

$$\begin{aligned} \mu _{DP}=U_{DP}/\alpha =-u^{*}(0) + \beta \phi _s+4\ln \left[ \cosh (\phi _s/4)\right] , \end{aligned}$$
(30)

where \(\alpha =\frac{d}{n^{\infty }(0)}\bigl (\frac{dn^{\infty }}{dx}\bigr )\) is the dimensionless concentration gradient parameter. The scaled surface velocity \(u^{*}(0)\) can be derived from Eq. (27) by setting \(y=0\), and the dimensionless diffusiophoretic mobility can expressed as

$$\begin{aligned} \begin{aligned} \mu _{DP}=\beta \biggl \{ \Bigl (1-\varepsilon _r\Bigr )\phi _s + \varepsilon _r\phi _D + \Bigl (1-\frac{1}{P}\Bigr )\frac{\varrho _{fix}}{\lambda ^2 \varepsilon _e \phi _0} + \frac{\varepsilon _r}{P} \frac{\phi _s-\phi _D}{1-{\tilde{\kappa }_m}^2/{\lambda }^2} \Bigl [(\cosh (\lambda d)-e^{-\tilde{\kappa }_m d})(1-\tilde{\kappa }_m \ell _s) \\ + \sinh (\lambda d)\Bigl (\lambda \ell _s-\frac{\tilde{\kappa }_m}{\lambda }\Bigr )\Bigr ] \biggr \} +4\ln \left[ \cosh (\phi _s/4)\right] - \varepsilon _r\biggl \{ \frac{2\tilde{\kappa }}{\lambda }\Bigl (\frac{Q}{P}\Bigr )(1-\cosh (\phi _s/2)) + \Bigl (1-\frac{1}{P}\Bigr )\Bigl (\frac{\tilde{\kappa }}{\lambda }\Bigr )^2 \\ - \frac{1}{P}\frac{\tilde{\kappa }^2}{\lambda }\int _{-d}^{0}[\sinh \lambda (y+d) + \lambda \ell _s \cosh \lambda (y+d)]\cosh \phi (y)dy \biggr \}. \end{aligned} \end{aligned}$$
(31)

Equation (31) represents the general diffusiophoretic mobility expression which is applicable to an arbitrarily charged soft particle with a hydrophobic inner core considering the ion partitioning effect when the Debye length is thinner than the particle size. It is worth mentioning that Eq. (31) is also valid for a large soft particle with arbitrary shape, since the particle surface can be treated as a flat plate irrespective of its form.

For a weakly charged soft particle, we can consider \(\cosh (\phi ) \approx 1+\phi ^2/2\). With that assumption, the diffusiophoretic mobility expression for a weakly charged soft particle can be derived from Eq. (31) as

$$\begin{aligned} \begin{aligned} \mu _{DP}=&\beta \biggl \{ \Bigl (1-\varepsilon _r\Bigr )\phi _s + \varepsilon _r\phi _D + \Bigl (1-\frac{1}{P}\Bigr )\frac{\varrho _{fix}}{\lambda ^2 \varepsilon _e \phi _0} \biggr \} + \Bigl [1 + \varepsilon _r\frac{2\tilde{\kappa }}{\lambda } \Bigl ( \frac{Q}{P} \Bigr ) \Bigr ]\frac{\phi _s^2}{8} + \varepsilon _r\Bigl (1-\frac{1}{P}\Bigr )\Bigl (\frac{\tilde{\kappa }}{\lambda }\Bigr )^2\frac{\phi _D^2}{2} \\&+\frac{\varepsilon _r}{P}\frac{\phi _s-\phi _D}{1-{\tilde{\kappa }_m}^2/{\lambda }^2}\Bigl [(\cosh (\lambda d)-\text {e}^{-\tilde{\kappa }_m d})(1-\tilde{\kappa }_m \ell _s) + \sinh (\lambda d)\Bigl (\lambda \ell _s-\frac{\tilde{\kappa }_m}{\lambda }\Bigr )\Bigr ] \Bigl ( \beta + \phi _D \Bigl (\frac{\tilde{\kappa }}{\lambda }\Bigr )^2 \Bigr )\\&+ \frac{\varepsilon _r}{P}\Bigl (\frac{\tilde{\kappa }}{\lambda }\Bigr )^2\frac{(\phi _s-\phi _D)^2}{2(1-{4\tilde{\kappa }_m}^2/{\lambda }^2)} \Bigl \{ (\cosh (\lambda d) -e^{-2\tilde{\kappa }_m d})(1-2\tilde{\kappa }_m \ell _s) + \sinh (\lambda d)\Bigl (\lambda \ell _s-\frac{2\tilde{\kappa }_m}{\lambda }\Bigr )\Bigr \}. \end{aligned} \end{aligned}$$
(32)

The diffusiophoretic mobility of a weakly charged soft particle without the ion partitioning effect (i.e., \(\varepsilon _r \approx 1\)) can be obtained from Eq. (32) with \(\phi _s\) being calculated explicitly from Eq. (14).

The hydrophobicity of the particle core is determined by the slip length \(\ell _s\), a proportionality constant, which associates the surface velocity with the strain rate at the core-PEL interface. For a hydrophilic surface where a no-slip velocity condition is more relevant, \(\ell _s=0\). Therefore, the diffusiophoretic mobility expression for a soft particle with a hydrophilic inner core can be obtained from Eq. (31) as

$$\begin{aligned} \begin{aligned} \mu _{DP} =&\beta \biggl \{ \Bigl (1-\varepsilon _r\Bigr )\phi _s + \varepsilon _r\phi _D + \Bigl [1-\frac{1}{\cosh (\lambda d)}\Bigr ]\frac{\varrho _{fix}}{\lambda ^2 \varepsilon _e \phi _0} +\varepsilon _r \frac{\phi _s-\phi _D}{1-\tilde{\kappa }_m^2/\lambda ^2}\Bigl [1-\frac{e^{-\tilde{\kappa }_md}}{\cosh (\lambda d)}-\frac{\tilde{\kappa }_m}{\lambda }\tanh (\lambda d)\Bigr ] \biggr \} \\&+4\ln \left[ \cosh (\phi _s/4)\right] - \varepsilon _r\biggl \{ \frac{2\tilde{\kappa }}{\lambda }(1-\cosh (\phi _s/2))\tanh (\lambda d) + \Bigl (\frac{\tilde{\kappa }}{\lambda }\Bigr )^2\Bigl [1-\frac{1}{\cosh (\lambda d)}\Bigr ] \\&-\frac{\tilde{\kappa }^2}{\lambda } \int _{-d}^{0}\frac{\sinh \lambda (y+d)}{\cosh (\lambda d)}\cosh \phi (y) dy\biggr \}. \end{aligned} \end{aligned}$$
(33)

For a low permeable soft layer, where the PEL hydrodynamic screening length is much thinner than the porous layer thickness, \(\lambda ^{-1}<<d\). Under the limit \(\lambda d>> 1\), we can consider \(\frac{1}{\cosh (\lambda d)} \approx 0\), \(\tanh (\lambda d) \approx 1\), and \(\frac{\sinh \lambda (y+d)}{\cosh (\lambda d)} \approx \text {e}^{\lambda y}\). Also, the lower limit of the integration appeared in Eq. (33) can be replaced by \(-\infty\) [40, 64]. With these approximations, Eq. (33) is reduced to

$$\begin{aligned} \begin{aligned} \mu _{DP}=&\beta \biggl \{ \Bigl ( 1-\varepsilon _r\Bigr )\phi _s + \varepsilon _r\phi _D + \frac{\varrho _{fix}}{\lambda ^2 \varepsilon _e \phi _0} +\varepsilon _r\frac{(\phi _s-\phi _D)}{1+\tilde{\kappa }_m/\lambda } \biggr \} + 4\ln [\cosh (\phi _s/4)] - \varepsilon _r\frac{2\tilde{\kappa }}{\lambda }(1-\cosh (\phi _s/2)) \\ {}&-\varepsilon _r \Bigl (\frac{\tilde{\kappa }}{\lambda } \Bigr )^2 \biggl \{1 - \sum _{n=0}^{\infty }\frac{(\phi _s-\phi _D)^{2n}(\tilde{\kappa }_m/\lambda )^{2n}}{(1+\tilde{\kappa }_m/\lambda )(1+2\tilde{\kappa }_m/\lambda )\cdots (1+2n\tilde{\kappa }_m/\lambda )}\cosh \phi _s \\ {}&+ \sum _{n=0}^{\infty }\frac{(\phi _s-\phi _D)^{2n+1}(\tilde{\kappa }_m/\lambda )^{2n+1}}{(1+\tilde{\kappa }_m/\lambda )(1+2\tilde{\kappa }_m/\lambda )\cdots (1+(2n+1)\tilde{\kappa }_m/\lambda )} \sinh \phi _s\biggr \}. \end{aligned} \end{aligned}$$
(34)

Equation (34) can be used to calculate the diffusiophoretic mobility of a soft particle with a hydrophilic core covered with a low permeable polymer layer for an arbitrary fixed charged density.

In the limit \(\lambda \rightarrow \infty\), which corresponds to a rigid colloid, Eq. (34) simplifies as

$$\begin{aligned} \mu _{DP}=\beta \phi _s+4\ln [\cosh (\phi _s/4)], \end{aligned}$$
(35)

which satisfies the diffusiophoretic mobility of a rigid particle bearing zeta potential \(\zeta =\phi _s\) [9, 65].

Results and discussion

In this section, we have graphically depicted the dependency of the diffusiophoretic mobility (\(\mu _{DP}\)) on hydrodynamic slip length (\(\ell _s\)), PEL-to-electrolyte permittivity ratio (\(\varepsilon _r\)), PEL hydrodynamic screening length (\(\lambda ^{-1}\)), PEL fixed-charged density (\(\varrho _{fix}\)), and diffusivity difference parameter (\(\beta\)) of ions in the electrolyte. For computational illustration, we have taken the thickness of the PEL, \(d=10\) nm. The hydrodynamic screening length of the PEL is selected to vary between 10 and 100 nm. The dielectric permittivity of the electrolyte \(\varepsilon _e\) is assumed to be \(78.4\varepsilon _0\), same as the dielectric permittivity of water, where \(\varepsilon _0\) is the vacuum permittivity, and the dielectric permittivity of the PEL is varied between \(0.1\varepsilon _e\) and \(\varepsilon _e\). The hydrodynamic slip length of the rigid core is considered to range from 0 to 1 \(\mu\)m. The electrolyte concentration is assumed to be sufficiently high [\(n^{\infty }(0) \sim O(10^4)\)mM] so that the Debye-Hückel parameter \(\kappa d\) (=100) is reasonably large, for which we can neglect the curvature effects of the surface and employ the flat-plate theory [48, 66,67,68] to analyze the current problem. The electrolyte solutions undertaken in the study are KCl, NaCl, and aqueous H\(_2\)CO\(_3\) solution, for which the diffusivity difference parameter \(\beta\) is \(-\)0.02,\(-\)0.2, and 0.774, respectively. All these solutions dissociate to monovalent cations and anions, e.g., KCl dissociates to K\(^{+}\) and Cl\(^{-}\) and NaCl to Na\(^{+}\) and Cl\(^{-}\) ions, while the aqueous solution of H\(_2\)CO\(_3\) produces H\(^{+}\) and HCO\(_3 ^{-}\) ions [20].

Fig. 2
figure 2

Variation of \(\mu _{DP}\) with Donnan potential \(\phi _D\) at a \(\beta =-0.02\) (KCl) and b \(\beta =-0.2\) (NaCl) for different \(\lambda ^{-1}\) ( = 0.05, 0.02, 0.1, 0.2 nm) when \(\varepsilon _p=\varepsilon _e\) and \(\ell _s=0\). Solid lines correspond to the mobility values calculated with Eq.(31); dashed lines, Eq. (32); and circular symbols, Eq. (34)

Full size image

We begin by presenting the variation of diffusiophoretic mobility of a soft particle with a hydrophilic core (\(\ell _s=0\)) with the Donnan potential (\(\phi _D\)) without considering the ion partitioning effect (\(\varepsilon _r=1\)). The Donnan potential \(\phi _D\) is directly related to the volume charge density of the PEL \(\varrho _{fix}\) through Eq. (10). Diffusiophoretic mobility obtained through Eq. (31) is presented in Fig. 2a and b for thin PEL hydrodynamic screening lengths. A numerical integration method is employed to calculate the last term of Eq. (31). Mobility values derived from Eqs. (32) and (34), respectively, correspond to the approximate expressions for weakly charged soft particles, and soft particles with a thinner Brinkman screening length are also presented. Figures 2a and b show that the weak charge solution (Eq. (32)) agrees excellently with the general mobility expression Eq. (31) when \(|\phi _D| \le 1\). For \(|\phi _D| >1\), the low potential approximation is no longer valid, and therefore, the weak charge solution, which is applicable for smaller potential, deviates from the general mobility expression. However, the solution calculated under the thinner PEL screening length assumption (Eq. (34)) satisfies Eq. (31) precisely for the entire considered range of \(\phi _D\). It may be observed from Fig. 2a that the mobility distribution is nearly symmetric around \(\phi _D=0\) when the electrolyte is KCl (\(\beta =-0.02\)), whereas for NaCl (\(\beta =-0.2\)), the diffusiophoretic mobility at a \(\phi _D\) with positive polarity is lower than that at the same \(\phi _D\) with negative polarity (Fig. 2b). For \(\beta =-0.02\), the electrophoresis component is subtle, and the diffusiophoresis is governed by the chemiphoresis component only, which always directs the particle towards the applied concentration gradient irrespective of the polarity of the particle charge. Therefore, the diffusiophoretic mobility at a certain \(\phi _D\) with same magnitude but the opposite polarity is almost the same. Nevertheless, when \(\beta =-0.2\), the electrophoresis component is prominent. For a positively charged particle (\(\phi _D>0\)), this non-negligible electrophoresis component acts against the chemiphoresis component, which in turn lowers the diffusiophoretic mobility of the particle. Whereas for a negatively charged particle (\(\phi _D<0\)), both the electrophoresis and chemiphoresis components act jointly along the direction of the concentration gradient leading to a higher diffusiophoretic mobility of the particle.

Fig. 3
figure 3

Variation of \(\mu _{DP}\) with PEL-electrolyte permittivity ratio \(\varepsilon _r\) for a \(\beta =-0.02\) (KCl), b \(\beta =-0.2\) (NaCl), and c \(\beta =0.774\) (H\(_2\)CO\(_3\)) for different \(\varrho _{fix}\) ( = [0.18, 0.9, 1.8] \(\times 10^6\) C/m\(^3\) ) when \(\ell _s=0\) and \(\lambda ^{-1}=\) 10 nm. Results are computed through Eq. (31). Inset in b represents distributions of the corresponding chemiphoresis (blue solid line) and electrophoresis components (red dashed line)

Full size image

Figures 3a–c depict the variation of diffusiophoretic mobility deduced from Eq. (31) for a soft particle with a hydrophilic rigid core as a function of PEL-electrolyte permittivity ratio \(\varepsilon _r\) for three different choices of electrolyte solutions KCl (\(\beta =-0.02\)), NaCl (\(\beta =-0.2\)), and aqueous H\(_2\)CO\(_3\) (\(\beta =0.774\)). Diffusiophoretic mobility decreases with the increase of \(\varepsilon _r\) before attaining a saturated value. The ion partitioning effect, which arises for \(\varepsilon _r<1\), restricts mobile ions from penetrating inside the PEL to enhance the effective charge of the PEL. A lower \(\varepsilon _r\) corresponds to a stronger ion partitioning effect resulting in a higher PEL effective charge and, subsequently, a higher \(\mu _{DP}\). As \(\varepsilon _r\) increases, the ion partitioning effect diminishes; hence, \(\mu _{DP}\) also reduces. It may be noted that \(\mu _{DP}\) increases with the decrease of \(\varepsilon _r\) at a faster rate for a higher \(\varrho _{fix}\), where the effective charge density of the PEL is high. Interestingly, for \(\beta =-0.2\), where the electrophoresis and chemiphoresis components oppose each other, a mobility reversal occurs when \(\varepsilon _r<1\) at a relatively higher \(\varrho _{fix}\). To explain this behavior, we have plotted the chemiphoresis and electrophoresis components separately as a function of \(\varepsilon _r\) in the inset of Fig. 3b. The chemiphoresis component (\(\mu _{CP}\)) is computed by setting \(\beta =0\) in Eq. (31), and the electrophoresis component is calculated by subtracting \(\mu _{CP}\) from \(\mu _{DP}\) (i.e., \(=\mu _{DP}-\mu _{CP}\)). It reveals that the chemiphoresis component possesses a positive value for lower \(\varepsilon _r\) (=0.1) followed by a decrement with the increase of \(\varepsilon _r\) before approaching 0 as \(\varepsilon _r\) approaches 1. On the other hand, the electrophoresis component always retains a negative value and shows no significant variation with \(\varepsilon _r\). As a result, the diffusiophoretic mobility governed by these two oppositely acting components is positive for lower values of \(\varepsilon _r\). Then, it undergoes a mobility reversal to attain negative mobility as \(\varepsilon _r\) moves towards 1. However, at \(\beta =0.774\), both the electrophoresis and chemiphoresis components act in the direction of the applied concentration gradient for a positively charged particle resulting in a positive mobility throughout the entire considered range of \(\varepsilon _r\).

Fig. 4
figure 4

Variation of \(\mu _{DP}\) with the scaled slip length \(\ell _s/d\) at a \(\beta =-0.02\) (KCl), b \(\beta =-0.2\) (NaCl), and c \(\beta =0.774\) (H\(_2\)CO\(_3\)) for different PEL-to-electrolyte permittivity ratio \(\varepsilon _r\) ( = 0.11, 0.13, 0.15, 0.2, 0.5, 1) when \(\varrho _{fix}=1.8 \times 10^6\) C/m\(^3\) and \(\lambda ^{-1}=10\) nm. Results are calculated using Eq. (31)

Full size image

Next, we have illustrated the effect of core hydrophobicity on the diffusiophoresis of a soft particle in presence of the ion partitioning effect. Variation of \(\mu _{DP}\) with the dimensionless slip length \(\ell _s/d\) scaled by the PEL thickness d for various values of \(\varepsilon _r\) is presented in Fig. 4 a–c. Results obtained through Eq. (31) are presented by choosing the background electrolyte as KCl (\(\beta =-0.02\)), NaCl (\(\beta =-0.2\)), and aqueous H\(_2\)CO\(_3\) (\(\beta =0.774\)). Figures show that \(\mu _{DP}\) enhances with the increase of \(\ell _s/d\) and attains a saturation for sufficiently larger values of the slip length. The slip length reduces the hydrodynamic drag experienced by the particle by generating a slip velocity at the inner core surface, which amplifies the diffusiophoretic mobility of the particle. For \(\varepsilon _r<1\), i.e., when the PEL dielectric permittivity is lower than the surrounding electrolyte medium, penetration of mobile ions inside the PEL gets reduced, causing a lower neutralization of the PEL charge. As a result, the effective PEL charge rises with the reduction of PEL dielectric permittivity, enhancing the diffusiophoretic mobility. At a lower \(\varepsilon _r\), where the effective charge of the PEL is high, \(\mu _{DP}\) increases at a faster rate with the increase of \(\ell _s/d\). At a large \(\ell _s/d\), neutralization of PEL charge mitigates due to a strong fluid convection, leading to a higher effective PEL charge. As a result, the influence of the ion partitioning is more profound for a larger slip length, which can be seen in Fig. 4a–c. The augmentation in diffusiophoretic mobility due to the slipping core is higher at \(\beta =0.774\), where the electrophoresis and chemiphoresis parts are cooperative, than the cases where \(\beta =-0.02\), for which the diffusiophoresis is dominated by chemiphoresis only and \(\beta =-0.2\), where the electrophoresis and chemiphoresis components compete each other.

Fig. 5
figure 5

Variation of \(\mu _{DP}\) with a \(\ell _s/d\) for different \(\lambda ^{-1}\) ( = 1, 3, 5, 7, 10 nm) at \(\varepsilon _r=0.2\) and b \(\lambda d\) for different \(\varepsilon _r\) ( = 0.11, 0.13, 0.15, 0.2, 0.5, 1) at \(\ell _s/d=0\); for different \(\beta\) ( = \(-\)0.02, \(-\)0.2, 0.774) when \(\varrho _{fix}=1.8 \times 10^6\) C/m\(^3\). Solid lines represent the results due to Eq. (31) while dashed line in b corresponds to Eq. (34) computed at \(\varepsilon _r=1\)

Full size image

Figure 5a presents the variation of \(\mu _{DP}\), given by Eq. (31), with the slip length for different choices of the PEL Brinkman screening length (\(\lambda ^{-1}\)). The PEL becomes more fluid permeable with the increase of the hydrodynamic screening length. The effect of core hydrophobicity is much sound for a higher \(\lambda ^{-1}\) due to a higher fluid convection, which can be observed from Fig. 5a. As \(\lambda ^{-1}\) increases, the neutralization of PEL charge by the mobile counterions permeated inside the PEL from the electrolyte medium attenuates due to stronger fluid convection. The effective charge of the PEL is higher for a larger \(\lambda ^{-1}\) resulting in higher diffusiophoretic mobility. On reduction of \(\lambda ^{-1}\), the effective charge of the PEL gets reduced due to a higher accumulation of counterions within the PEL, which causes lower particle mobility. It is evident from Fig. 5a that the effect of the hydrophobic core is higher for \(\beta =0.774\), where the electrophoresis and chemiphoresis components act jointly at higher \(\lambda ^{-1}\). When the dielectric permittivity of the PEL is lower than that of the surrounding electrolyte (\(\varepsilon _r<1\)), the ion partitioning effect prevents mobile counterions from entering the PEL, creating an enhancement in effective charge within the PEL. The increase of PEL effective charge due to the reduction of PEL dielectric permittivity (decreasing \(\varepsilon _r\)) augments the diffusiophoretic mobility of the particle (Fig. 5b). The impact of the ion partitioning effect is more substantial for a highly permeable PEL, as the effective PEL charge is higher for a larger screening length. Results obtained from Eq. (34) corresponding to the approximate diffusiophoretic mobility expression for a low-permeable PEL considering \(\varepsilon _r=1\) show a good agreement with the general mobility expression (31) as \(\lambda ^{-1}\) becomes smaller.

Fig. 6
figure 6

Variation of \(\mu _{DP}\) with \(\varrho _{fix}\) for different \(\varepsilon _r\) ( = 0.11, 0.13, 0.2, 0.5, 1) and different \(\beta\) (= \(-\)0.02, \(-\)0.2, 0.774) with \(\ell _s=10\) nm and \(\lambda ^{-1}=10\) nm. Solid and dotted lines correspond to Eqs. (31) and (32), respectively

Full size image

In Fig. 6, we have elucidated the influence of the ion partitioning effect on the diffusiophoretic mobility of the particle for a range of PEL volume charge density \(\varrho _{fix}\). Results based on the weak PEL charge assumption (Eq. (32)) along with the mobility values due to Eq. (31) are depicted in the figure. The impact of the ion partitioning effect is expected to grow with the increase of volume charge density as the PEL effective charge increases with it. Figure shows that our approximate mobility expression (32) derived for a weakly charged soft particle agrees with the general mobility expression (31) very well for the considered range of \(\varrho _{fix}\) at a larger value of \(\varepsilon _r\). When the dielectric permittivity is much lower than the electrolyte (lower \(\varepsilon _r\)), the weak charge solution deviates from the general mobility expression for a larger \(\varrho _{fix}\). For lower values of \(\varepsilon _r\), the effective charge of the PEL is higher, leading to a higher electric potential within the PEL, and the low potential approximation considered in Eq. (32) becomes unreasonable for a highly charged PEL. However, for a lower PEL volume charge density, the analytical solution given by Eq. (32) satisfies the general diffusiophoretic mobility expression (31) adequately.

Conclusion

A theoretical study is considered to analyze the combined impact of the ion partitioning effect and core hydrophobicity on the diffusiophoresis of a soft particle consisting of a rigid core covered with a charged porous layer. The soft particle is assumed to suspend in an electrolyte medium under an externally applied uniform concentration gradient. The electrolyte concentration is taken sufficiently high to create a thinner Debye layer around the particle compared to the particle size so that the particle surface can be treated as a flat plate and the curvature effects of the particle surface can be ignored. With these assumptions, a general expression (Eq. (31)) for diffusiophoretic mobility of a soft particle with a hydrophobic core with the ion partitioning effect is derived, which is applicable for an arbitrary PEL volume charge density. The general mobility expression is further approximated under a weak PEL charge assumption to provide a closed-form expression (Eq. (32)) for diffusiophoretic mobility for a weakly charged soft particle exhibiting core hydrophobicity with ion partitioning effect. An analytical formula (Eq. (34)) of diffusiophoretic mobility for an arbitrarily charged soft particle with a low permeable PEL and a hydrophilic core considering the ion partitioning effect is also deduced.

The ion partitioning effect, generated by the Born energy difference between the ions in the PEL and electrolyte medium having unequal dielectric permittivities, restricts counterions from accumulating inside the PEL and enhances the effective charge of the PEL. An increment in the PEL effective charge due to the ion partitioning effect increases the diffusiophoretic mobility. When the electrolyte is considered NaCl, where the chemiphoresis and electrophoresis components act against each other, a mobility reversal occurs with increased PEL permittivity. The influence of the ion partitioning effect is stronger for a large slip length and at a higher PEL volume charge density with a thicker hydrodynamic screening length where the effective charge of the PEL is high. The core hydrophobicity of the soft particle characterized by the slip length increases the particle mobility by reducing the hydrodynamic drag experienced by the particle. The effect of slipping core on diffusiophoretic mobility is substantial at a thicker PEL screening length and for a lower dielectric permittivity of the soft layer. The effect of the core hydrophobicity is higher when the electrophoresis and chemiphoresis components work collaboratively.

The present study neglects the curvature effects of the particle surface. Hence, it does not deal with the intrinsic nonlinear effects such as double layer polarization, relaxation, and counterion condensation occurring for a Debye length comparable to the particle size. Nonetheless, the analytical results presented here can be a benchmark for future studies on diffusiophoresis of soft particles with an arbitrary Debye layer thickness analyzing such nonlinear effects.