1 Introduction

Most phenomena in the atmosphere are characterized by thermodynamic irreversibility and evolve in time with increases in entropy. The circulation is maintained by the instability of the atmospheric system, and this question has been studied from a variety of different perspectives. Lorenz (1955) presented the Lorenz Energy Cycle (LEC) theory explaining the energetics of atmosphere mainly from a mechanical perspective with kinetic energy produced at the expense of available potential energy (APE), a measure of the instability of the atmosphere. A number of other groups have sought to address the question from a thermodynamic perspective focusing on the budget of atmospheric energy and entropy (e.g. Coleman and Greenberg 1967; Dutton 1973; Paltridge 1975; Livezey and Dutton 1976; Peixoto et al. 1991; Goody 2000; Paltridge 2001; Pauluis and Held 2002a, b; Ozawa et al. 2003; Romps 2008; Lucarini et al. 2011; Bannon 2005, 2012, 2013; Huang and McElroy 2014, 2015).

Lorenz (1955) defines APE as the difference in total static energy (internal plus potential) between the current state of the dry air component of the atmosphere and that of an idealized reference state, identified as the state that minimizes the static energy of the dry air component of the atmosphere after a sequence of reversible isentropic and adiabatic transformations with air parcels conserving their potential temperature, θ. The reference state is characterized by horizontal stratification with absolute stability in pressure, potential temperature and height.

For an isentropic and adiabatic adjustment of the mass field, the surface of constant θ behaves as a material surface. Thus, the average pressure over an isentropic surface, \(\tilde{p}\left( \theta \right)\), can be quantified based on the relation:

$$\tilde{p}\left( \theta \right) = \mathop {\iint }\limits_{\sigma }^{{}} p\left( {x,y,\theta } \right) \cdot dxdy / \mathop {\iint }\limits_{\sigma }^{{}} dxdy$$
(1)

where σ is the global area defined by a constant θ surface and p(x, y, θ) is the air pressure in an (x, y, θ) coordinate system. When a constant θ surface intersects the earth’s surface (θ ≤ θ surface ), p(θ) is set equal to p surface . During an isentropic and adiabatic rearrangement of mass, \(\tilde{p}\left( \theta \right)\) is conserved, representing thus the pressure of the reference state. APE is defined as

$$APE = \mathop \int \limits \left( {\varPhi + {\rm I}} \right) \cdot {\text{dm}} - \mathop \int \limits \left( {\varPhi_{r} + {\rm I}_{r} } \right) \cdot {\text{dm}}$$
(2)

where \(\varPhi\) and \(\varPhi_{\text{r}}\) represent the potential energy and the corresponding reference state of the atmosphere respectively, and I and Ir denote the internal energy for the atmosphere and for the corresponding reference state respectively (Lorenz 1967; Peixoto and Oort 1992).

Figure 1 presents a schematic illustration of APE, computed based on assimilated meteorological data from the Modern Era Retrospective-analysis for Research and Applications (MERRA). The upper panels display the zonal-average potential temperature, θ, and the zonal-average temperature, T, for year 2008. The lower panels present the zonal-average potential temperature, θ, and the zonal-average temperature, T, for the associated reference state, computed based on Eq. (1). According to the LEC theory, the maximum production of kinetic energy corresponds to the expenditure of all of the APE when the structure of θ on the upper panel collapses to the structure depicted on the lower panel. The structure of θ in the reference state (lower panels in Fig. 1) defines the condition of absolute mechanical equilibrium, since the horizontal pressure force has been eliminated and the vertical pressure force is balanced by gravity.

Fig. 1
figure 1

Schematic illustration of APE. The upper panels present zonal-average potential temperatures, θ, and zonal-average temperatures, T, for year 2008. The lower panels indicate zonal-average potential temperatures, θ, and zonal-average temperatures, T, for the associated reference state proposed by Lorenz, again for year 2008

Full size image

A number of groups have investigated the APE of the atmosphere based on the LEC theory (Oort 1964; Oort and Peixóto 1974, 1976; Li et al. 2007; Pauluis 2007; Boer and Lambert 2008; Hernández-Deckers and von Storch 2010; Marques et al. 2009; Becker 2009; Marques et al. 2010, 2011; Kim and Kim 2013). For example, using MERRA data, Kim and Kim (2013) estimated the global averaged APE as \(4.34\,{\text{MJ}}/{\text{m}}^{2}\) on an annual mean, \(4.02\,{\text{MJ}}/{\text{m}}^{2}\) for the June–August (JJA) mean and \(4.75\,{\text{MJ}}/{\text{m}}^{2}\) for the December–February (DJF) mean.

The reference state defined by Lorenz, although in mechanical equilibrium, is not in thermal equilibrium. The zonal-average temperature, T, for the associated reference state in Fig. 1 indicates the existence of a vertical temperature gradient. The reference state has the potential to produce additional kinetic energy through a thermodynamically reversible process. According to the second law of thermodynamics, motions of the atmosphere should drive the system towards thermodynamic equilibrium. A thermodynamic equilibrium state requires both mechanical and thermal equilibrium. Figure 2 presents a schematic illustration of an approach to thermodynamic equilibrium. The lower panels in Fig. 2 display the zonal-average potential temperature, θ, and zonal-average temperature, T, appropriate for a thermodynamic equilibrium state with the equilibrium temperature, T eq , set equal to 249 K. When the atmosphere reaches thermodynamic equilibrium, it is completely divested of potential to produce kinetic energy.

Fig. 2
figure 2

Schematic illustration of the approach to thermodynamic equilibrium. The upper panels display zonal-average potential temperatures, θ, and zonal-average temperatures, T, for year 2008. The lower panels indicate zonal-average potential temperatures, θ, and zonal-average temperatures, T, for the thermodynamic equilibrium state

Full size image

With respect to entropy, the atmosphere is an open system exchanging energy and matter with its surroundings. According to Prigogine (1962) and De Groot and Mazur (2013), the total variation of the entropy of the atmosphere, dS atm/dt, consists of two components: the transfer of entropy across the boundary, dS atm e /dt, and the entropy produced within the system, dS atm i /dt. The majority of the phenomena operational in the atmosphere, such as the frictional dissipation of kinetic energy, are thermodynamically irreversible. Thus dS atm i /dt is always greater than zero. dS atm/dt can be expressed as:

$$\frac{{dS^{atm} }}{dt} = \frac{{dS_{e}^{atm} }}{dt} + \frac{{dS_{i}^{atm} }}{dt}$$
(3)

Peixoto et al. (1991) provided a comprehensive analysis of the contributions to dS atm i /dt and dS atm e /dt. A relevant question is: if, since time t 0 the atmosphere had become an isolated system with zero exchange of energy and matter exchange with its environment (dS atm = dS atm i ), how much greater would be the eventual increase in entropy, \(\mathop \int \nolimits_{{t_{0} }}^{\infty } \frac{{dS^{atm} }}{dt} \cdot dt\), when the atmosphere had reached thermodynamic equilibrium. Similar to APE, \(\mathop \int \nolimits_{{t_{0} }}^{\infty } \frac{{dS^{atm} }}{dt} \cdot dt\) reflects the thermodynamic disequilibrium of the atmosphere.

The maximum entropy increase problem was studied by Coleman and Greenberg (1967) addressing a general fluid system other than specifically the atmosphere. Based on the work of Willard Gibbs (1873, 1878), they proposed a thermodynamic equilibrium state for any given fluid system together with the associated equilibrium entropy. They argued that the dynamical implication of the difference between the equilibrium state entropy and the entropy of the given system is “remarkable” because it provides a “stability criterion”. In the case of the atmosphere, this difference corresponds to \(\mathop \int \nolimits_{{t_{0} }}^{\infty } \frac{{dS^{atm} }}{dt} \cdot dt\) subject to the constraint \(\frac{{dS_{e}^{atm} }}{dt} = 0\).

Dutton (1973) extended and applied Coleman and Greenberg’s study to the atmosphere, and pointed out that every natural state of the atmosphere corresponds to a maximum entropy state, a motionless, hydrostatic state with the same mass and total energy. And this maximum entropy state is the equilibrium towards which an atmosphere in isolation will naturally tend. Bannon (2005, 2012, 2013) reexamined the question of the maximum entropy state and introduced the atmospheric available energy which is defined as a generalized Gibbs function between the atmosphere and an isothermal reference state. The reference atmosphere is in thermal and hydrostatic equilibrium and, thus, is dynamically and convectively “dead”.

Landau and Lifshitz (1980) described an approach to study the thermodynamic disequilibrium problem in an Entropy-Energy Diagram and to quantify the maximum work, W max , and maximum entropy increase, \((\Delta S)_{max}\), that a conceptual isolated system could perform or achieve. Both variables represent the level of disequilibrium for a conceptual system. Their basic idea and methodology is introduced in Sect. 3 with a simple case for demonstration. In the case of the atmosphere, the atmospheric available energy proposed by Bannon is equivalent to the maximum work concept, though without consideration of the gravitational fractionation of the dry air (Bannon 2013). In this study, we extend and apply Landau and Lifshitz’s approach to the atmosphere, investigating the level of thermodynamic disequilibrium for the atmosphere in the context of global warming using assimilated meteorological data from MERRA. The analysis provides a perspective on the relationship among temperature, energy and entropy and allows for a quantitative investigation of the deviation of the atmosphere from thermodynamic equilibrium.

2 Data

The study is based on meteorological data from the MERRA compilation covering the period January 1979 to December 2010 (Rienecker et al. 2007). Air temperatures and geopotential heights were obtained on the basis of retrospective analysis of global meteorological data using Version 5.2.0 of the GEOS-5 DAS. We use the standard 3-hourly output available for 42 pressure levels with a horizontal resolution of 1.25° latitude × 1.25° longitude. The highest pressure level at the top of the atmosphere is 0.1 hPa. The global surface temperature anomalies employed in this study are from the Goddard Institute for Space Studies (GISS) (Hansen et al. 2010).

3 Maximum work and maximum entropy increase problem

For a thermally isolated system consisting of several components out of thermal equilibrium, while equilibrium is being established, the system can perform mechanical work. The transition to equilibrium may follow a variety of possible paths. The final equilibrium states of the system represented by its energy and entropy may differ as a consequence. The total work that can be performed as well as the entropy increase that may occur from the evolution of a non-equilibrium system will depend on the manner in which equilibrium is established. Here, we explore two extreme paths to thermal equilibrium: one consistent with the performance of maximum work, W max ; the other corresponding to a maximum increase in entropy, \((\Delta S)_{max}\).

The system performs maximum work when the process of reaching thermal equilibrium is reversible. Figure 3 provides the simplest case with the thermally isolated system consisting of only two components. When the hot component at temperature T hot loses an amount of energy Q h  = −T hot δS hot , where δS h is the decrease in entropy for the hot component, the cold component at temperature T cold gains energy Q c  = T cold δS c , where δS c is the entropy increase for the cold component. If the process is reversible, then δS c  + δS h  = 0 and the work produced in the process is equal to Q h  − Q c . As the reversible process continues, T hot and T cold converge to an equilibrium temperature T S eq , with the superscript “S” denoting zero entropy change, and the thermally isolated system reaches thermal equilibrium with work output W max . In this study, the transition to thermal equilibrium with W max is identified as Evolution 1.

Fig. 3
figure 3

Illustration of W max produced from a non-equilibrium system. Initially, the thermally isolated system is out of equilibrium and can perform a maximum of mechanical work through reversible processes (\(\Delta S = 0\)). Finally, the system reaches equilibrium at T S eq in which the temperature contrast between its subcomponents has been eliminated

Full size image

The system achieves \((\Delta S)_{max}\) when the process of reaching thermal equilibrium is totally irreversible and the internal energy remains constant. Figure 4 provides the simplest case for this with energy transfer, Q, occurring directly between the components without performing any work. The process is thermally irreversible, and the entropy of the combination of the two components increases by \(Q(1/T_{cold} - 1/T_{hot} )\). As the energy transfer continues, T hot and T cold converge to another equilibrium temperature T W eq , with the superscript “W” representing the condition where no work is performed and the subscript “ eq ” defining equilibrium. T W eq is greater than T S eq , since zero work is performed on the external medium. Maximum increase in entropy, \((\Delta S)_{max}\), for the entire system occurs in the end. In this study, the transition to thermal equilibrium with \((\Delta S)_{max}\) is indicated as Evolution 2.

Fig. 4
figure 4

Illustration of \((\Delta S)_{max}\) for the entire non-equilibrium system. Initially, the thermally isolated system is energetic and out of equilibrium. There is a flux of energy Q from the high temperature component at T hot to the low temperature component at T cold . As heat transfer continues, the system reaches thermal equilibrium at T W eq in which the temperature contrast between its subcomponents has been eliminated

Full size image

The maximum work and maximum entropy increase can be depicted in an Entropy-Energy Diagram. If a system is in thermal equilibrium, its entropy, S eq , and temperature, T eq , are functions of its total energy, E eq : namely S eq  = S eq (E eq ) and T eq  = T eq (E eq ). In Fig. 5 the continuous line defines the behavior of the function S eq (E eq ) in an Entropy-Energy Diagram. For a non-equilibrium system with thermal condition \(\left( {E, S} \right)\) corresponding to point b in Fig. 5, the horizontal segment \(\Delta E\) represents the work performed as the system approaches equilibrium through Evolution 1 while the vertical segment \(\Delta S\) illustrates the increase in entropy associated with Evolution 2. Consequently T eq (E eq ) at point a corresponds to T W eq , and T eq (E eq ) at point b corresponds to T S eq . The maximum work, W max , and the maximum entropy increase, \((\Delta S)_{max}\), reflect the magnitude of the thermodynamic disequilibrium of a non-equilibrium system: if the isolated system is further removed from equilibrium, W max and \((\Delta S)_{max}\) are increased; and vice versa.

Fig. 5
figure 5

Schematic illustration of the evolution of maximum work and maximum entropy increase in an Entropy-Energy Diagram

Full size image

4 Ideal gas in a gravitational field

In a uniform gravitational field with height represented by z, the potential energy, u, of a molecule is given by u = mgz, where m is the mass of a molecule and g is the gravitational acceleration. The distribution of density for a system consisting of an ideal gas at thermodynamic equilibrium is given by the barometric formula:

$$\rho \left( {\vec{r}} \right) = \rho_{0} e^{{ - mgz/(k_{B} \cdot T_{eq} )}}$$
(4)

where ρ 0 is the mass density at level \(z = 0\), T eq is the equilibrium temperature and k B is the Boltzmann constant. The pressure in equilibrium, P eq , at height z is given by:

$$P_{eq} (z) = \mathop \int \limits_{z}^{\infty } \rho_{0} e^{{ - mgh/(k_{B} T_{eq} )}} g \cdot dh$$
(5)

or

$$P_{eq} \left( z \right) = P_{0} e^{{ - mgz/(k_{B} \cdot T_{eq} )}}$$
(6)

where P 0 is the pressure at level z = 0.

For a single mole of ideal gas, assuming temperature-independent specific heat, the associated entropy, S m , is given by:

$$S_{m} = C_{p,m} \ln T - R\ln p + S_{m0}$$
(7)

where C p,m is the molar heat capacity at constant pressure, R is the gas constant, T is the temperature of the gas, p is the pressure and S m0 is a constant of integration. Thus, the total entropy of the system is defined by:

$$S = \mathop \int \limits \left( {C_{p,m} \ln T - R\ln p + S_{m0} } \right) \cdot dn$$
(8)

and the total static energy (internal plus potential), E, is given by:

$$E = \mathop \int \limits C_{v,m} T \cdot dn + \mathop \int \limits \rho gz \cdot dv$$
(9)

where \({\text{n}}\) is the number of moles, v is volume and C v,m is the molar heat capacity at constant volume.

If the initial density distribution of a system follows Eq. (4), the system consisting of the ideal gas is in thermodynamic equilibrium at \({\text{T}}_{\text{eq}}\). For a one-dimensional equilibrium system at two temperatures T 1 eq and T 2 eq , Dutton (1973) proved that the associated equilibrium energies, E 1 eq , E 2 eq and the equilibrium entropies S 1 eq , S 2 eq are related by:

$$S_{eq}^{2} - S_{eq}^{1} = C_{p,m} \cdot \ln (E_{eq}^{2} /E_{eq}^{1} ) \cdot \mathop \int \limits dn$$
(10)

Thus:

$$S_{eq} ({\text{T}}_{\text{eq}} + \Delta {\text{T}}_{\text{eq}} ) - S_{eq} \left( {{\text{T}}_{\text{eq}} } \right) = C_{p,m} \cdot \ln (E_{eq} ({\text{T}}_{\text{eq}} + \Delta {\text{T}}_{\text{eq}} )/E_{eq} ({\text{T}}_{\text{eq}} )) \cdot \mathop \int \limits dn$$
(11)

For the case where \(\Delta {\text{T}}_{\text{eq}} \to 0\) and ln(1 + x) ~ x (x ≪ 1),

$$S_{eq}^{{}} ({\text{T}}_{\text{eq}} + \Delta {\text{T}}_{\text{eq}} ) - S_{eq}^{{}} ({\text{T}}_{\text{eq}} ) \approx C_{p,m} \cdot \frac{{E_{eq}^{{}} \left( {{\text{T}}_{\text{eq}} + \Delta {\text{T}}_{\text{eq}} } \right) - E_{eq}^{{}} ({\text{T}}_{\text{eq}} )}}{{E_{eq}^{{}} ({\text{T}}_{\text{eq}} )}} \cdot \mathop \int \limits dn$$
(12)

It follows that

$$\frac{{E_{eq}^{{}} \left( {{\text{T}}_{\text{eq}} + \Delta {\text{T}}_{\text{eq}} } \right) - E_{eq}^{{}} ({\text{T}}_{\text{eq}} )}}{{S_{eq}^{{}} ({\text{T}}_{\text{eq}} + \Delta {\text{T}}_{\text{eq}} ) - S_{eq}^{{}} ({\text{T}}_{\text{eq}} )}} \approx \frac{{E_{eq}^{{}} ({\text{T}}_{\text{eq}} )}}{{C_{p,m} \mathop \int \limits dn}}$$
(13)

Under thermodynamic equilibrium conditions, \(E_{eq}^{{}} \left( {{\text{T}}_{\text{eq}} } \right) = C_{p,m} \mathop \int \nolimits T_{eq} dn\) (Peixoto and Oort 1992). Thus:

$$\frac{{\partial E_{eq} }}{{\partial S_{eq} }} = T_{eq}$$
(14)

If the initial density distribution of a system departs from Eq. (4), the system consisting of the ideal gas will not be in equilibrium. It can approach equilibrium through a number of paths including evolution 1 depicted in Fig. 3 and evolution 2 depicted in Fig. 4 Consequently, maximum work, W max , is produced by the system if the transition to equilibrium at temperature T S eq is reversible (evolution 1 in Fig. 3), namely \(\Delta S = 0\). The maximum work, W max , is equal to \(\Delta E\), according to the first law of thermodynamics. W max may be expressed as:

$$W_{max} = \mathop \int \limits C_{v,m} \left( {T - T_{eq}^{S} } \right) \cdot dn + \mathop \int \limits \left( {\rho - \rho_{eq}^{S} } \right)gz \cdot dv$$
(15)

where \(\rho_{eq}^{S} (z) = \rho_{0}^{S} e^{{ - mgz/(k_{B} \cdot T_{eq}^{S} )}}\). Reflecting the principle of mass conservation, \(\mathop \int \nolimits \rho_{eq}^{S} \cdot dv = \mathop \int \nolimits \rho \cdot dv\), or equivalently, \(\rho_{0}^{S} = \left( {\mathop \int \nolimits \rho \cdot dv} \right)/\left( {\mathop \int \nolimits e^{{ - mgz/(k_{B} \cdot T_{eq}^{S} )}} \cdot dv} \right)\).

Similarly, the system achieves maximum entropy increase if the transition to equilibrium at temperature T W eq is thermally irreversible and produces no work (evolution 2 in Fig. 4), \(\Delta E = 0\). And the maximum entropy increase may be expressed as:

$$(\Delta S)_{max} = \mathop \int \limits \left[ {C_{p,m} \left( {\ln T_{eq}^{W} - \ln T} \right) - R\left( {\ln P_{eq}^{W} (z) - \ln p} \right)} \right] \cdot dn$$
(16)

where \(P_{eq}^{W} (z) = P_{0}^{W} e^{{ - mgz/(k_{B} \cdot T_{eq}^{W} )}}\). Because of the principle of mass conservation, \(\mathop {\iint }\nolimits_{surface}^{{}} P_{eq}^{W} (z) \cdot dxdy = \mathop {\iint }\nolimits_{surface}^{{}} P \cdot dxdy\). The equilibrium pressure P eq at level z = 0, namely P 0, can be computed as:

$$P_{0} = \mathop {\iint }\limits_{surface}^{{}} P \cdot dxdy/\mathop {\iint }\limits_{surface}^{{}} e^{{ - mgh/(k_{B} \cdot T_{eq} )}} \cdot dxdy$$
(17)

where h is the topographic height.

5 A thermodynamic perspective on the atmosphere

Oxygen (O2) occupies 20.95 % by volume of dry air in the atmosphere. Nitrogen (N2) accounts for 78.08 %. The next two most abundant gases are argon (Ar) (0.93 %) and carbon dioxide (CO2) (0.04 %). To simplify the calculation in this study we assume that O2 occupies 21 % of dry air, N2 78 % and Ar 1 % for well mixed dry air by volume and a constant gravity of \(9.8\,{\text{m}}/{\text{s}}^{2}\). The molar masses of O2, N2 and Ar equal 32, 28 and 40 g/mol respectively.

For one mole of O2, N2 and Ar, the associated entropies \(S_{m}^{{O_{2} }}\), \(S_{m}^{{N_{2} }}\) and S Ar m are given by:

$$S_{m}^{{O_{2} }} = C_{p,m}^{{O_{2} }} \ln T - R\ln P^{{O_{2} }} + S_{m0}^{{O_{2} }}$$
(18)
$$S_{m}^{{N_{2} }} = C_{p,m}^{{N_{2} }} \ln T - R\ln P^{{N_{2} }} + S_{m0}^{{N_{2} }}$$
(19)
$$S_{m}^{Ar} = C_{p,m}^{Ar} \ln T - R\ln P^{Ar} + S_{m0}^{Ar}$$
(20)

where \(C_{p,m}^{{O_{2} }}\), \(C_{p,m}^{{N_{2} }}\) and \(C_{p,m}^{Ar}\) represent the molar heat capacities at constant pressure for O2, N2 and Ar; \(P^{{O_{2} }}\), \(P^{{N_{2} }}\) and \(P^{Ar}\) denote the partial pressures for O2, N2 and Ar; and \(S_{m0}^{{O_{2} }}\), \(S_{m0}^{{N_{2} }}\) and \(S_{m0}^{Ar}\) are the related constants of integration. Since O2 and N2 are diatomic gases, \(C_{p,m}^{{O_{2} }}\) and \(C_{p,m}^{{N_{2} }}\) are set equal to \(\frac{7}{2}R\). Ar is monatomic gas, thus \(C_{p,m}^{Ar}\) is equal to \(\frac{5}{2}R\). And R is the ideal gas constant and equal to \(8.3145\,{\text{J}}/({\text{mol}}\,{\text{K}})\). Since in this study we are interested in changes in entropy, constants of integration are set to zero. The total entropy of dry air, \(S_{atm}\), in the atmosphere may be expressed then as:

$$S^{atm} = S^{{O_{2} }} + S^{{N_{2} }} + S^{Ar}$$
(21)

where \(S^{{O_{2} }} = \mathop \int \nolimits \left( {C_{p,m}^{{O_{2} }} \ln T - R\ln P^{{O_{2} }} } \right)dn_{{O_{2} }}\), \(S^{{N_{2} }} = \mathop \int \nolimits \left( {C_{p,m}^{{N_{2} }} \ln T - R\ln P^{{N_{2} }} } \right)dn_{{N_{2} }}\) and S Ar = ∫ (C Ar p,m  ln T − R ln P Ar)dn Ar respectively.

The total static energy of dry air, E atm , is given by:

$$E^{atm} = E^{{O_{2} }} + E^{{N_{2} }} + E^{Ar}$$
(22)

where \(E^{{O_{2} }} = \mathop \int \nolimits C_{v,m}^{{O_{2} }} T \cdot dn_{{O_{2} }} + \mathop \int \nolimits \rho^{{O_{2} }} gz \cdot dv\), \(E^{{N_{2} }} = \mathop \int \nolimits C_{v,m}^{{N_{2} }} T \cdot dn_{{N_{2} }} + \mathop \int \nolimits \rho^{{N_{2} }} gz \cdot dv\) and \(E^{Ar} = \mathop \int \nolimits C_{v,m}^{Ar} T \cdot dn_{Ar} + \mathop \int \nolimits \rho^{Ar} gz \cdot dv\) respectively.

For a specific equilibrium temperature, T eq , the partial pressures, \(P_{eq}^{{O_{2} }}\), \(P_{eq}^{{N_{2} }}\) and \(P_{eq}^{Ar}\), and the densities, \(\rho_{eq}^{{O_{2} }}\), \(\rho_{eq}^{{N_{2} }}\) and \(\rho_{eq}^{Ar}\), for O2, N2 and Ar in equilibrium can be quantified according to the principle of mass conservation. For example, \(\rho_{eq}^{{O_{2} }}\) can be computed based on \(\mathop \int \nolimits \rho_{eq}^{{O_{2} }} \cdot dv = \mathop \int \nolimits \rho^{{O_{2} }} \cdot dv\) and \(\rho_{eq}^{{O_{2} }} = \rho_{0}^{{O_{2} }} \cdot e^{{ - m_{{O_{2} }} gh /\left( {k_{B} \cdot T_{eq} } \right)}}\). Subsequently, the entropy, S atm eq , and the static energy, E atm eq , of the atmosphere in equilibrium at T eq can be computed based on Eqs. (15) and (16).

The highest pressure level in the dataset is 0.1 hPa. \({\text{S}}_{\text{eq}}^{\text{atm}}\) and \({\text{E}}_{\text{eq}}^{\text{atm}}\) are quantified through integrations from the ocean or land surface to the 0.1 hPa level. Figure 6 illustrates the behavior of the function S atm eq (E atm eq ) with T eq increasing from 100 to 500 K. The behavior of ∂E atm eq /∂S atm eq as a function of T eq is shown in Fig. 7. Reflecting the topographic height of the continents, ∂E atm eq /∂S atm eq is approximately equal, but not identical, to T eq . When T eq becomes warmer, the air molecules have higher kinetic energy and consequently have greater chances of moving to high altitudes and above the continents. Thus, the process of increasing T eq involves a re-distribution of air between oceanic and continental regions.

Fig. 6
figure 6

The behavior of the function \(S_{eq}^{atm} /E_{eq}^{atm}\) with T eq increasing from 100 to 500 K

Full size image
Fig. 7
figure 7

The behavior of the gradient \(\partial S_{eq}^{atm} / \partial E_{eq}^{atm}\) with T eq ranging from 100 to 500 K

Full size image

In calculating (\({\text{E}}^{\text{atm}}\), \({\text{S}}^{\text{atm}}\)) for a non-equilibrium real atmosphere, \({\text{E}}^{\text{atm}}\) and \({\text{S}}^{\text{atm}}\) are quantified through integrations from the topographic surface to 0.1 hPa level. The thermodynamic condition, (E atm, S atm), of the atmosphere on May 30, 2002 is identified by point b in the Entropy-Energy Diagram in Fig. 8, below the line of S atm eq (E atm eq ), confirming the fact that the atmosphere was out of thermodynamic equilibrium, with the associated \(W_{max} = 29.2\,{{\rm MJ/m}}^{2}\) and \((\Delta S)_{max} = 117\,{\text{kJ}}/\left( {{\text{m}}^{2} \,{\text{K}}} \right)\).

Fig. 8
figure 8

The thermodynamic condition, (\(E_{eq}^{atm} ,S_{eq}^{atm}\)), of the atmosphere on May 30, 2002 displayed in an Entropy-Energy Diagram. The \(\Delta E\) in the figure represents the maximum work, W max , that can be performed in a thermally reversible process; \(\Delta S\) represents the maximum increase in entropy, \((\Delta S)_{max},\) that can arise in a thermally irreversible process with zero work

Full size image

The seasonality of the thermodynamic condition, (E atm, \(S^{atm}\)), of the atmosphere in an Entropy-Energy Diagram is plotted in Fig. 9. The loop-shaped seasonality reflects the asymmetric distribution of land with respect to the equator in addition to the seasonally varying earth–sun distance. If the distributions of land in the Northern Hemisphere were the same as in the Southern Hemisphere and the earth–sun distance was constant, the thermodynamic condition on June 22 (summer solstice) identified in an Entropy-Energy Diagram should be the same as for December 22 (winter solstice). Similarly, the thermodynamic condition on March 21 (vernal equinox) should overlap that for September 23 (autumnal equinox) (see Fig. 10). The seasonality in Fig. 9 would have been line-shaped with the conditions of June 22 and December 22 on one end, the conditions for March 21 and September 23 on the other.

Fig. 9
figure 9

The seasonality of the thermodynamic conditions, (E atm, S atm), of the atmosphere in an Entropy-Energy Diagram

Full size image
Fig. 10
figure 10

Schematic illustration of solar radiation

Full size image

A greater content of static energy in the atmosphere does not necessarily correspond to higher thermodynamic disequilibrium and vice versa. For example, the total static energy on May 1 is close to that on October 1. Since the associated total entropy on May 1 is greater than on October 1, the atmosphere was thermodynamically more stable on May 1.

The seasonalities of W max and \((\Delta S)_{max}\) are plotted in Fig. 11. The atmosphere reaches its state of highest thermodynamic disequilibrium in late July with \(W_{max} = 31.4\,{\text{MJ}}/{\text{m}}^{2}\) and \((\Delta S)_{max} = 126\,{\text{kJ}}/\left( {{\text{m}}^{2} \,{\text{K}}} \right)\), its lowest state in mid January with \(W_{max} = 27.7\,{\text{MJ}}/{\text{m}}^{2}\) and \((\Delta S)_{max} = 112\,{\text{kJ}}/\left( {{\text{m}}^{2} \,{\text{K}}} \right)\). W max can be approximated as \(W_{max} \approx 248K \cdot (\Delta S)_{max}\). Large values of W max are associated with large values of \((\Delta S)_{max}\), corresponding to high states of thermodynamic disequilibrium. The thermodynamic condition (\(E^{atm}\), S atm) of the atmosphere is close to S atm eq (E atm eq ) as depicted by Fig. 8. Thus, \(W_{max} /(\Delta S)_{max}\) is approximately equal to \(\partial E_{eq}^{atm} /\partial S_{eq}^{atm}\), and, consequently, to T eq .

Fig. 11
figure 11

The seasonalities of W max and \((\Delta S)_{max}\) based on an average of data for the past 32 years

Full size image

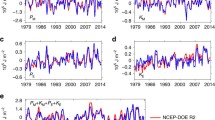
The long-term variation of W max from January 1979 to December 2010 is illustrated in Fig. 12. The conspicuous intra-seasonal fluctuation depicted by the red line reflects the strong seasonal variation of the \(W_{max}\). The blue line, computed using a 365-day running average, reflects the existence of an inter-annual variation. Linear regression of the annual mean average over this period provides a regression slope of \(2.4\,{\text{J}}/\left( {{\text{m}}^{2} \,{\text{yr}}} \right)\) with R2 = 0.004, indicating that there is no statistically significant trend in thermodynamic disequilibrium. It is not yet clear what determines the inter-annual variability of \({\text{W}}_{ \hbox{max} }\). The large scale atmosphere–ocean El Niño Southern Oscillation phenomenon could provide one possible explanation. We would note in this context that the highest peak in \({\text{W}}_{ \hbox{max} }\) is coincident with the major El Nino event of 1997–1998.

Fig. 12
figure 12

Variation of W max from January 1979 to December 2010

Full size image

The seasonalities of the equilibrium temperatures, T S eq and T W eq , are displayed in Fig. 13. T W eq is greater than T S eq , reflecting the fact that no work is performed in evolution 2. Both T S eq and T W eq reach their peak values in late July, corresponding to the highest content of static energy. The 32-year averaged values for T S eq and T W eq are \(248.9\,{\text{K}}\) and \(251.8\,{\text{K}}\) respectively. The gap between T S eq and T W eq reflects the thermodynamic disequilibrium of the atmosphere.

Fig. 13
figure 13

The seasonalities of the equilibrium temperatures, T S eq and T W eq , based on an average of data for the past 32 years

Full size image

In this study, the variation of T S eq is indicated by:

$$\Delta T_{eq}^{S} = T_{eq}^{S} - 248.5\,{\text{K}}$$
(23)

and the variation of T W eq is defined by:

$$\Delta T_{eq}^{W} = T_{eq}^{W} - 251.5\,{\text{K}}$$
(24)

The variation of \(T_{eq}^{S}\) and T W eq with the seasonal cycle removed is shown in Fig. 14. The increases of \(\Delta T_{eq}^{S}\) and \(\Delta T_{eq}^{W}\) generally follow the global surface temperature change, \(\Delta T_{surface}\), with the correlation between \(\Delta T_{eq}^{S}\) and \(\Delta T_{surface}\) equal to 0.87 and correlation between \(\Delta T_{eq}^{W}\) and \(\Delta T_{surface}\) equal to 0.91. Thus, as the global surface temperature increased from January 1979 to December 2010, the thermodynamic conditions (E atm, S atm) of the atmosphere on an Energy-Entropy Diagram moved on a trajectory parallel to the line of S atm eq (E atm eq ) in Fig. 8, resulting in increases in T S eq and T W eq , with W max and \((\Delta S)_{max}\) remaining relatively constant.

Fig. 14
figure 14

Variation of \(\Delta T_{eq}^{S}\), \(\Delta T_{eq}^{W}\) and \(\Delta T_{surface}\) from January 1979 to December 2010

Full size image

6 Discussion and summary

This study presented an approach for analysis of the interrelations of temperature, energy and entropy of the atmosphere, and proposed two variables, W max and \((\Delta S)_{max}\), as measures of the thermodynamic disequilibrium of the atmosphere. W max is approximately a linear function of \((\Delta S)_{max}\): \(W_{max} \approx 248\,{\text{K}} \cdot (\Delta S)_{max}\). The annual mean value of W max was estimated at \(29.6\,{\text{MJ}}/{\text{m}}^{2}\) with \(31.0\,{\text{MJ}}/{\text{m}}^{2}\) for JJA and \(28.0\,{\text{MJ}}/{\text{m}}^{2}\) for DJF. The conservation of mass between the atmospheric system and the isothermal reference is crucial for the quantification method developed in this study.

Based on the same assimilated meteorological dataset as used in this study, Kim and Kim (2013) estimated the global averaged APE at \(4.34\,{\text{MJ}}/{\text{m}}^{2}\) for the annual mean, \(4.02\,{\text{MJ}}/{\text{m}}^{2}\) for JJA and \(4.75\,{\text{MJ}}/{\text{m}}^{2}\) for DJF. There are considerable differences in the absolute values for APE and W max . Figure 15 provides a schematic illustration of the relationship between APE and W max with point b corresponding to the thermodynamic condition, (E atm, S atm). APE is defined as the difference in total static energy between the current state of the dry air component of the atmosphere and that of an idealized reference state corresponding to the minimum content of static energy present following a sequence of reversible isentropic transformations. When the atmosphere fully releases its APE through a isentropic and adiabatic process to perform mechanical work and reaches the associated reference state, the total value of S atm should remain constant. On the Entropy-Energy Diagram in Fig. 15, this process corresponds to a thermodynamic transition from point b to point d with entropy conserved. However, the reference state in mechanical equilibrium is not in thermal equilibrium, and the maximum work, W max , has not as yet been completely exerted. Thus, APE corresponding to the b-to-d displacement in Fig. 15 should be smaller than W max corresponding to the b-to-c displacement in Fig. 15. It follows that APE may be considered as the mechanical component of W max .

Fig. 15
figure 15

Schematic illustration of the relationship between APE and \(W_{max}\). The distance between b and d represents \(APE\), and the distance between b and c represents \(W_{max}\)

Full size image

For an isothermal well-mixed atmosphere at 250 K, W max is quantified to be 1.5 MJ/m2 using the approach described in Sect. 4. This quantity, \(1.5\,{\text{MJ}}/{\text{m}}^{2}\), represents the contribution from the gravitational separation of gases to W max for a real atmosphere. Thus the part of W max attributed to the vertical temperature contrast can be estimated as \(W_{max} - APE - 1.5\,{\text{MJ}}/{\text{m}}^{2} \approx 23.8\,{\text{MJ}}/{\text{m}}^{2}\).

Figure 16 presents a schematic illustration of the d-to-c displacement in Fig. 15. The upper panels in Fig. 16 display the zonal-average potential temperature, θ, and the zonal-average temperature, T, appropriate for the associated reference state proposed by Lorenz, with its thermodynamic condition, (E atm, S atm), corresponding to point d in Fig. 15. The lower panels display zonal-average potential temperatures, θ, and zonal-average temperatures, T, for the associated thermodynamic equilibrium state with its thermodynamic condition, (E atm, S atm), corresponding to point c in Fig. 15. When the thermally non-equilibrium reference state proposed by Lorenz approaches thermodynamic equilibrium through Evolution 1, the work performed is equal to (W max  − APE).

Fig. 16
figure 16

Schematic illustration of (W max  − APE). The upper panels display zonal-average potential temperatures, θ, and zonal-average temperatures, T, for the associated reference state proposed by Lorenz. The lower panels present zonal-average potential temperatures, θ, and zonal-average temperatures, T, for the associated thermodynamic equilibrium state

Full size image

While Lorenz’s concept of energetics is based on APE that can be extracted through a reversible adiabatic transformation of dry air, his main concern was with the rate for its generation by radiative heating and cooling, and the subsequent dissipation of this energy by mechanically irreversible processes. The fundamental question he addressed was why and how the present strength of the general circulation was determined. The main interest in this paper is to quantify the thermodynamic disequilibrium of the present climate state, although the relationship between \({\text{W}}_{ \hbox{max} }\) and APE is also investigated.

Considering the long-term variability of W max , as the global surface temperature, T surface , increased from January 1979 to December 2010, the equilibrium temperatures, \(T_{eq}^{S}\) and T W eq , increased at about the same pace as T surface . Consequently, there was no statistically significant trend in W max over this interval. It is important to understand how the atmosphere adjusted its thermodynamic structure over this period, including its vertical temperature profile in order to maintain a relatively constant \(W_{max}\). A number of studies pointed out that the lower-tropospheric temperatures have experienced slightly greater warming since 1958 than those at the surface. Lower-stratospheric temperatures have exhibited cooling since 1979 while the tropopause height has increased by 200 m between 1979 and 2001 (Randel et al. 2000; Grody et al. 2004; Santer et al. 2004; Simmons et al. 2004; Fu and Johanson 2005; Karl et al. 2006; Vinnikov et al. 2006). It is important to explore the pertinent implications for \(W_{max}\).

The global thermodynamic disequilibrium of the atmosphere was analyzed retrospectively in this study based on the MERRA data. We also estimated the thermodynamic disequilibrium corresponding to the one-dimensional international standard atmosphere (See Supplementary Material). The value of W max for the one-dimensional international standard atmosphere is estimated at \(16.8\,{\text{MJ}}/{\text{m}}^{2}\). The previous study reported a value of 12.6 MJ/m2 for a 50 km standard atmosphere (Bannon 2012). The one-dimensional international standard atmosphere doesn’t represent the thermodynamics of the time-resolved three-dimensional atmosphere. Thus, there is a difference in the values of W max between the one-dimensional model and the three dimensional atmosphere. Nevertheless, a relevant question is whether the conclusions reached here may be conditioned by the use of this specific data base. Other datasets including NCEP-1, NCEP-2, ERA-40 and JRA-25 should be employed in future work to compare with the results presented here.

This study focused on the dry air component of the atmosphere. In the real atmospheric system consisting of dry air and water, its total entropy S total and total static energy \(E^{total}\), according to thermodynamics, can be expressed as: \(S^{total} = S^{atm} + S^{{H_{2} O}}\) and \(E^{total} = E^{atm} + E^{{H_{2} O}}\), where \(S^{{H_{2} O}}\) and \(E^{{H_{2} O}}\) represent the associated entropy and static energy of the water component.

The water component plays an important role in the thermodynamics of the atmosphere, including maintenance of the general circulation (Lorenz 1978). When sunlight reaches the ocean surface, much of the energy absorbed by the ocean is used to evaporate water. Water vapor in the atmosphere acts as a reservoir for storage of heat to be released later. As the air ascends, it cools. When it becomes saturated, water vapor condenses with consequent release of latent heat. Heating is dominated in the tropical atmosphere by release of latent heat. Separate bands of relatively deep heating are observed also at mid-latitudes where active weather systems result in enhanced precipitation and release of latent heat. The condensation and evaporation of water contribute to non-uniform diabatic heating and cooling of the dry air, and, consequently, to the circulation of the atmosphere.

The water component is also an example of a thermodynamic non-equilibrium system. Under thermodynamic equilibrium conditions, liquid and solid water would be totally absent above the ground. The entire process of evaporation from the ocean, followed by condensation to form clouds and precipitation is thermodynamically irreversible. The analytical approach developed here could be used to investigate the thermodynamics of the water component by quantifying the thermodynamic condition, \((E^{{H_{2} O}} , S^{{H_{2} O}} )\) and the line of \(S_{eq}^{{H_{2} O}} \left( {E_{eq}^{{H_{2} O}} } \right)\) and by calculating W max and \((\Delta S)_{max}\) for the water component in an Entropy-Energy Diagram. The water component can further increase the thermodynamic disequilibrium of the moist atmosphere.